Hostname: page-component-7dd5485656-kp629 Total loading time: 0 Render date: 2025-10-30T13:12:54.516Z Has data issue: false hasContentIssue false
  • English
  • Français

Invariant tori and topological entropy in Tonelli Lagrangian systems on the 2-torus

Published online by Cambridge University Press:  19 March 2015

JAN PHILIPP SCHRÖDER
JAN PHILIPP SCHRÖDER*
Affiliation:
Faculty of Mathematics, Ruhr University, 44780 Bochum, Germany email jan.schroeder-a57@rub.de
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the Euler–Lagrange flow of a Tonelli Lagrangian on the 2-torus 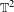$\mathbb{T}^{2}$ at a fixed energy level 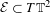${\mathcal{E}}\subset T\mathbb{T}^{2}$ strictly above Mañé’s strict critical value. We prove that, if for some rational direction 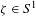${\it\zeta}\in S^{1}$ there is no invariant graph 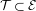${\mathcal{T}}\subset {\mathcal{E}}$ over 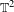$\mathbb{T}^{2}$ for the Euler–Lagrange flow with the property that all orbits on 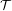${\mathcal{T}}$ have an asymptotic direction equal to 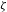${\it\zeta}$ , then there are chaotic dynamics in 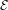${\mathcal{E}}$ . This implies that, if the topological entropy of the Euler–Lagrange flow in 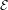${\mathcal{E}}$ vanishes, then in 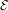${\mathcal{E}}$ there are invariant graphs for all asymptotic directions 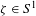${\it\zeta}\in S^{1}$ and integrable-like behavior on a large scale.

Information

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 36 , Issue 6 , September 2016 , pp. 1989 - 2014
Copyright
© Cambridge University Press, 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Angenent, S.. The topological entropy and invariant circles of an area preserving twist map. Twist Mappings and Their Applications (IMA Volumes in Mathematics and its Applications, 44) . Eds. McGehee, R. and Meyer, K. R.. Springer, New York, 1992, pp. 1–7.Google Scholar
Bosetto, E. and Serra, E.. A variational approach to chaotic dynamics in periodically forced nonlinear oscillators. Ann. Inst. H. Poincaré Non Linéaire 17(6) (2000), 673–709.Google Scholar
Contreras, G., Delgado, J. and Iturriaga, R.. Lagrangian flows: The dynamics of globally minimizing orbits II. Bol. Soc. Bras. Mat. Bul. Braz. Math. Soc. 28(2) (1997), 155–196.Google Scholar
Contreras, G. and Iturriaga, R.. Convex Hamiltonian without conjugate points. Ergod. Th. & Dynam. Sys. 19(4) (1999), 901–952.Google Scholar
Contreras, G. and Iturriaga, R.. Global minimizers of autonomous Lagrangians. 22 Coloquio Brasileiro de Matematica. IMPA, Rio de Janeiro, 1999.Google Scholar
Contreras, G., Iturriaga, R., Paternain, G. P. and Paternain, M.. Lagrangian graphs, minimizing measures and Mañé’s critical values. Geom. Funct. Anal. 8 (1998), 788–809.Google Scholar
Dubrovskiy, S.. Stokes theorem for Lipschitz forms on a smooth manifold. Preprint, 2008, arXiv:0805.4144 [math.DG].Google Scholar
Fathi, A.. Weak KAM Theorem in Lagrangian Dynamics. Cambridge University Press, to appear.Google Scholar
Glasmachers, E. and Knieper, G.. Minimal geodesic foliation on T2 in case of vanishing topological entropy. J. Topol. Anal. 3(4) (2011), 1–10.CrossRefGoogle Scholar
Glasmachers, E., Knieper, G., Ogouyandjou, C. and Schröder, J. P.. Topological entropy of minimal geodesics and volume growth on surfaces. J. Mod. Dyn. 8(1) (2014), 75–91.Google Scholar
Hedlund, G. A.. Geodesics on a two-dimensional Riemannian manifold with periodic coefficients. Ann. of Math. (2) 33(4) (1932), 719–739.Google Scholar
Katok, A.. Ergodic perturbations of degenerate integrable Hamiltonian systems. Math. USSR-Izv. 7(3) (1973), 535–571.Google Scholar
Mañé, R.. Lagrangian flows: The dynamics of globally minimizing orbits. Bol. Soc. Bras. Mat. 28(2) (1997), 141–153.Google Scholar
Mather, J. N.. Action minimizing measures for positive definite Lagrangian systems. Math. Z. 207(1) (1991), 169–207.CrossRefGoogle Scholar
Paternain, G. P.. Entropy and completely integrable Hamiltonian systems. Proc. Amer. Math. Soc. 113(3) (1991), 871–873.Google Scholar
Paternain, G. P. and Paternain, M.. Critical values of autonomous Lagrangian systems. Comment. Math. Helv. 72 (1997), 481–499.Google Scholar
Rabinowitz, P. H.. Heteroclinics for a reversible Hamiltonian system. Ergod. Th. & Dynam. Sys. 14(4) (1994), 817–829.Google Scholar
Schröder, J. P.. Tonelli Lagrangians on the 2-torus: global minimizers, invariant tori and topological entropy. PhD Thesis, Ruhr-Universität Bochum, 2013.Google Scholar
Schröder, J. P.. Global minimizers for Tonelli Lagrangians on the 2-torus. J. Topol. Anal., to appear, Preprint, 2014.Google Scholar
Schröder, J. P.. Ergodic components and topological entropy in geodesic flows of surfaces. Preprint, 2014, arXiv:1407.6259 [math.DS].Google Scholar
Sorrentino, A.. Lecture notes on Mather’s theory for Lagrangian systems. Preprint, 2010, arXiv:1011.0590 [math.DS].Google Scholar
Walters, P.. An Introduction to Ergodic Theory (Graduate Texts in Mathematics, 79) . Springer, New York, 2000.Google Scholar