Article contents
Linear rigidity of stationary stochastic processes
Published online by Cambridge University Press: 03 April 2017
Abstract
We consider stationary stochastic processes 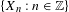 $\{X_{n}:n\in \mathbb{Z}\}$ such that
$\{X_{n}:n\in \mathbb{Z}\}$ such that 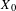 $X_{0}$ lies in the closed linear span of
$X_{0}$ lies in the closed linear span of 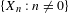 $\{X_{n}:n\neq 0\}$; following Ghosh and Peres, we call such processes linearly rigid. Using a criterion of Kolmogorov, we show that it suffices, for a stationary stochastic process to be linearly rigid, that the spectral density vanishes at zero and belongs to the Zygmund class
$\{X_{n}:n\neq 0\}$; following Ghosh and Peres, we call such processes linearly rigid. Using a criterion of Kolmogorov, we show that it suffices, for a stationary stochastic process to be linearly rigid, that the spectral density vanishes at zero and belongs to the Zygmund class 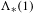 $\unicode[STIX]{x1D6EC}_{\ast }(1)$. We next give a sufficient condition for stationary determinantal point processes on
$\unicode[STIX]{x1D6EC}_{\ast }(1)$. We next give a sufficient condition for stationary determinantal point processes on  $\mathbb{Z}$ and on
$\mathbb{Z}$ and on 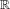 $\mathbb{R}$ to be linearly rigid. Finally, we show that the determinantal point process on
$\mathbb{R}$ to be linearly rigid. Finally, we show that the determinantal point process on 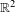 $\mathbb{R}^{2}$ induced by a tensor square of Dyson sine kernels is not linearly rigid.
$\mathbb{R}^{2}$ induced by a tensor square of Dyson sine kernels is not linearly rigid.
Information
- Type
- Original Article
- Information
- Copyright
- © Cambridge University Press, 2017
References
- 8
- Cited by

