Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
McCord, Christopher
2000.
Simplicial Models for the Global Dynamics of Attractors.
Journal of Differential Equations,
Vol. 167,
Issue. 2,
p.
316.
2002.
Vol. 2,
Issue. ,
p.
393.
Latschev, Janko
2006.
Coherent measures and the existence of smooth Lyapunov 1-forms for flows.
Topology,
Vol. 45,
Issue. 4,
p.
707.
Ban, Hyunju
and
Kalies, William D.
2006.
A Computational Approach to Conley’s Decomposition Theorem.
Journal of Computational and Nonlinear Dynamics,
Vol. 1,
Issue. 4,
p.
312.
Rot, T. O.
and
Vandervorst, R. C. A. M.
2014.
Morse–Conley–Floer homology.
Journal of Topology and Analysis,
Vol. 06,
Issue. 03,
p.
305.
D. Kalies, William
Mischaikow, Konstantin
and
C.A.M. Vandervorst, Robert
2014.
Lattice structures for attractors I.
Journal of Computational Dynamics,
Vol. 1,
Issue. 2,
p.
307.
Bartłomiejczyk, Piotr
2015.
Spectral splittings in the Conley index theory.
Journal of Fixed Point Theory and Applications,
Vol. 17,
Issue. 2,
p.
403.
Kalies, William D.
Mischaikow, Konstantin
and
Vandervorst, Robert C. A. M.
2016.
Lattice Structures for Attractors II.
Foundations of Computational Mathematics,
Vol. 16,
Issue. 5,
p.
1151.
Gukov, Sergei
2017.
RG flows and bifurcations.
Nuclear Physics B,
Vol. 919,
Issue. ,
p.
583.
Kalies, William D.
Kasti, Dinesh
and
Vandervorst, Robert
2018.
An Algorithmic Approach to Lattices and Order in Dynamics.
SIAM Journal on Applied Dynamical Systems,
Vol. 17,
Issue. 2,
p.
1617.
Harker, Shaun
Mischaikow, Konstantin
and
Spendlove, Kelly
2021.
A computational framework for connection matrix theory.
Journal of Applied and Computational Topology,
Vol. 5,
Issue. 3,
p.
459.
Kalies, W. D.
Mischaikow, K.
and
Vandervorst, R. C. A. M.
2022.
Lattice Structures for Attractors III.
Journal of Dynamics and Differential Equations,
Vol. 34,
Issue. 3,
p.
1729.
Dey, Tamal K.
Lipiński, Michał
Mrozek, Marian
and
Slechta, Ryan
2024.
Computing Connection Matrices via Persistence-Like Reductions.
SIAM Journal on Applied Dynamical Systems,
Vol. 23,
Issue. 1,
p.
81.
Mrozek, Marian
and
Wanner, Thomas
2025.
Connection Matrices in Combinatorial Topological Dynamics.
p.
119.
Spendlove, Kelly
and
Vandervorst, Robert
2025.
Graded Differential Vector Spaces, Cartan–Eilenberg Systems and Conjectures in Conley Index Theory.
Journal of Dynamics and Differential Equations,
Mrozek, Marian
and
Wanner, Thomas
2025.
Connection Matrices in Combinatorial Topological Dynamics.
p.
75.
Mrozek, Marian
and
Wanner, Thomas
2025.
Connection Matrices in Combinatorial Topological Dynamics.
p.
1.
Mrozek, Marian
and
Wanner, Thomas
2025.
Connection Matrices in Combinatorial Topological Dynamics.
p.
5.

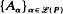 be an attractor network for a dynamical system
be an attractor network for a dynamical system 