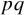1. Introduction
Cellular automata (CA) are symbolic dynamical systems that act on either
![]() $\Sigma ^{\mathbb {N}}$
(one-sided CA) or
$\Sigma ^{\mathbb {N}}$
(one-sided CA) or
![]() $\Sigma ^{\mathbb {Z}}$
(two-sided CA) for some finite symbol set
$\Sigma ^{\mathbb {Z}}$
(two-sided CA) for some finite symbol set
![]() $\Sigma $
and that are defined by using a local rule. The CA appearing in this paper are multiplication automata
$\Sigma $
and that are defined by using a local rule. The CA appearing in this paper are multiplication automata
![]() $\Pi _{\alpha ,N}$
that simulate multiplication by some
$\Pi _{\alpha ,N}$
that simulate multiplication by some
![]() $\alpha>0$
on base-N representations of numbers. These are not defined for all pairs of
$\alpha>0$
on base-N representations of numbers. These are not defined for all pairs of
![]() $\alpha $
and N. In [Reference Blanchard, Host and Maass1], possibly the first paper featuring such CA, it is shown that in the case of one-sided multiplication automata (meaning that multiplication is performed only on the fractional part of a number),
$\alpha $
and N. In [Reference Blanchard, Host and Maass1], possibly the first paper featuring such CA, it is shown that in the case of one-sided multiplication automata (meaning that multiplication is performed only on the fractional part of a number),
![]() $\Pi _{\alpha ,N}$
is defined precisely when
$\Pi _{\alpha ,N}$
is defined precisely when
![]() $\alpha $
is an integer all of whose prime factors divide N. The paper [Reference Blanchard and Maass2] shows for
$\alpha $
is an integer all of whose prime factors divide N. The paper [Reference Blanchard and Maass2] shows for
![]() $\alpha $
dividing N that
$\alpha $
dividing N that
![]() $\Pi _{\alpha ,N}$
is topologically conjugate to the left shift map on
$\Pi _{\alpha ,N}$
is topologically conjugate to the left shift map on
![]() $\Sigma _\alpha ^{\mathbb {N}}$
with
$\Sigma _\alpha ^{\mathbb {N}}$
with
![]() $\Sigma _\alpha =\{0,1,\ldots ,\alpha -1\}$
if and only if
$\Sigma _\alpha =\{0,1,\ldots ,\alpha -1\}$
if and only if
![]() $\alpha $
and N are divisible by the same prime numbers. This left shift map is in fact equal to
$\alpha $
and N are divisible by the same prime numbers. This left shift map is in fact equal to
![]() $\Pi _{\alpha ,\alpha }$
, which is the simplest way to represent the operation of multiplying by
$\Pi _{\alpha ,\alpha }$
, which is the simplest way to represent the operation of multiplying by
![]() $\alpha $
. Considering two-sided multiplication automata makes it possible to also talk about automata multiplying by proper fractions, as was done in [Reference Kari, Yen and Ibarra5] in the special case
$\alpha $
. Considering two-sided multiplication automata makes it possible to also talk about automata multiplying by proper fractions, as was done in [Reference Kari, Yen and Ibarra5] in the special case
![]() $\alpha =3/2$
,
$\alpha =3/2$
,
![]() $N=6$
. From [Reference Blanchard, Host and Maass1], one can infer that in the two-sided case,
$N=6$
. From [Reference Blanchard, Host and Maass1], one can infer that in the two-sided case,
![]() $\Pi _{\alpha ,N}$
is defined precisely when
$\Pi _{\alpha ,N}$
is defined precisely when
![]() $\alpha $
is a rational number whose numerator and denominator are products of factors of N.
$\alpha $
is a rational number whose numerator and denominator are products of factors of N.
In this paper, we consider explicitly only the case of two-sided multiplication automata and look further into topological conjugacies of multiplication automata with other multiplication automata that are not necessarily shift maps as was the case in [Reference Blanchard and Maass2]. We show in Corollary 5.10 that multiplication automata
![]() $\Pi _{\alpha ,N_1}$
and
$\Pi _{\alpha ,N_1}$
and
![]() $\Pi _{\alpha ,N_2}$
are conjugate when
$\Pi _{\alpha ,N_2}$
are conjugate when
![]() $N_1$
and
$N_1$
and
![]() $N_2$
are divisible by the same prime numbers. Even when this condition is not satisfied, we can consider topological factors. We show in Corollary 5.13 that
$N_2$
are divisible by the same prime numbers. Even when this condition is not satisfied, we can consider topological factors. We show in Corollary 5.13 that
![]() $\Pi _{\alpha ,N_1}$
has
$\Pi _{\alpha ,N_1}$
has
![]() $\Pi _{\alpha ,N_2}$
as a factor if every prime factor of
$\Pi _{\alpha ,N_2}$
as a factor if every prime factor of
![]() $N_2$
is a prime factor of
$N_2$
is a prime factor of
![]() $N_1$
. The conjugacies and factor maps we present for connecting these multiplication automata essentially transform base-
$N_1$
. The conjugacies and factor maps we present for connecting these multiplication automata essentially transform base-
![]() $N_1$
representations of any non-negative real number to base-
$N_1$
representations of any non-negative real number to base-
![]() $N_2$
representations of the same real number.
$N_2$
representations of the same real number.
To prove the results mentioned in the previous paragraph, this paper takes the approach of considering so-called multiplication tessellations formed by multiplication cubes. These turn out to be interesting mathematical objects in their own right as a family of multidimensional subshifts with good structural properties. In [Reference Rudolph11], multiplication by p and q is essentially implemented by tilings of the plane with the tiles being base-
![]() $pq$
digits and multiplication by p and q corresponding to shifting the tiling either horizontally or vertically. The tiling terminology appears explicitly in [Reference Cook, Stérin, Woods, Lakin and Sulc3] in the special case
$pq$
digits and multiplication by p and q corresponding to shifting the tiling either horizontally or vertically. The tiling terminology appears explicitly in [Reference Cook, Stérin, Woods, Lakin and Sulc3] in the special case
![]() $p=2$
,
$p=2$
,
![]() $q=3$
. Instead of restricting to two-dimensional tilings, we will introduce multiplication tessellation systems using multiplication (hyper)cubes of arbitrary dimension.
$q=3$
. Instead of restricting to two-dimensional tilings, we will introduce multiplication tessellation systems using multiplication (hyper)cubes of arbitrary dimension.
Our construction of multiplication cubes is based on mixed base representations of natural numbers, the basics of which we cover in §3. Section 4 is all about multiplication cubes, and mixed base representations of numbers are used to define multiplication cubes and their tessellations in §4.1. Briefly put, associated to any vector of positive integers
![]() $(n_1,n_2,\ldots ,n_d)$
, there will be
$(n_1,n_2,\ldots ,n_d)$
, there will be
![]() $N=n_1n_2\cdots n_d$
different d-dimensional hypercubes corresponding to the base-N digits and having various labels on their lower dimensional hyperfaces, and in valid d-dimensional tessellations, neighboring cubes have to have matching labels on adjacent
$N=n_1n_2\cdots n_d$
different d-dimensional hypercubes corresponding to the base-N digits and having various labels on their lower dimensional hyperfaces, and in valid d-dimensional tessellations, neighboring cubes have to have matching labels on adjacent
![]() $(d-1)$
-dimensional hyperfaces. The underlying idea is that then one can associate any real number
$(d-1)$
-dimensional hyperfaces. The underlying idea is that then one can associate any real number
![]() $\xi \geq 0$
with a valid tessellation containing a base-N representation of
$\xi \geq 0$
with a valid tessellation containing a base-N representation of
![]() $\xi $
along the main diagonal (Corollary 4.39), and moving along the direction of the ith coordinate axis in a tessellation corresponds to multiplication by
$\xi $
along the main diagonal (Corollary 4.39), and moving along the direction of the ith coordinate axis in a tessellation corresponds to multiplication by
![]() $n_i$
(Proposition 4.26).
$n_i$
(Proposition 4.26).
We proceed to investigate various structures appearing in multiplication tilings in later subsections of §4. In Theorem 4.6 of §4.2, it turns out that the matching condition of
![]() $(d-1)$
-dimensional hyperfaces in valid tessellations automatically implies that also the labels of lower dimensional hyperfaces in adjacent cubes match. In §4.3, we define the notion of a path integral over a path in a tessellation. This terminology is justified by Theorem 4.11, according to which the path integral over a cycle in a valid tessellation is always equal to zero. This is then used as a technical tool to define labels between directed line segments connecting any two points in a tessellation. These labels are used in §4.4, which introduces the macrotile operation. The macrotile operation groups multiplication cubes into larger cubes that can also be viewed as multiplication cubes. More generally, with some restrictions, it is possible to draw a grid of parallelepipeds within a tessellation and interpret each individual parallelelepiped as a new multiplication cube. The way this works is that the labels of the edges of the parallelepipeds in the original tessellation yield the labels of the edges of the new multiplication cubes. The grid of parallelepipeds may be of a lower dimension than the original tessellation, which in particular means that a lower dimensional cut along the
$(d-1)$
-dimensional hyperfaces in valid tessellations automatically implies that also the labels of lower dimensional hyperfaces in adjacent cubes match. In §4.3, we define the notion of a path integral over a path in a tessellation. This terminology is justified by Theorem 4.11, according to which the path integral over a cycle in a valid tessellation is always equal to zero. This is then used as a technical tool to define labels between directed line segments connecting any two points in a tessellation. These labels are used in §4.4, which introduces the macrotile operation. The macrotile operation groups multiplication cubes into larger cubes that can also be viewed as multiplication cubes. More generally, with some restrictions, it is possible to draw a grid of parallelepipeds within a tessellation and interpret each individual parallelelepiped as a new multiplication cube. The way this works is that the labels of the edges of the parallelepipeds in the original tessellation yield the labels of the edges of the new multiplication cubes. The grid of parallelepipeds may be of a lower dimension than the original tessellation, which in particular means that a lower dimensional cut along the
![]() $i_1$
th,
$i_1$
th,
![]() $i_2$
th,
$i_2$
th,
![]() $\ldots ,i_k$
th coordinate axes in a d-dimensional tessellation is a k-dimensional tessellation over the multiplication cube set associated to the vector
$\ldots ,i_k$
th coordinate axes in a d-dimensional tessellation is a k-dimensional tessellation over the multiplication cube set associated to the vector
![]() $(n_{i_1},n_{i_2},\ldots ,n_{i_k})$
. By Theorem 4.38, the macrotile operation has in some cases an inverse map, the microtile operation. Even when the macrotile operation is not invertible, by Theorem 4.40, it is always a surjection between sets of valid tessellations.
$(n_{i_1},n_{i_2},\ldots ,n_{i_k})$
. By Theorem 4.38, the macrotile operation has in some cases an inverse map, the microtile operation. Even when the macrotile operation is not invertible, by Theorem 4.40, it is always a surjection between sets of valid tessellations.
In §5, we turn to multiplication automata, which are defined in §5.1. In §5.2, multiplication automata are connected to multiplication tessellations: by Theorem 5.7, multiplication automata are topologically conjugate to shift maps on sets of valid tessellations by multiplication cubes. Due to this connection, conjugacy and factor relations between various shift dynamics on multiplication tessellations imply the conjugacy and factor relations between multiplication automata mentioned earlier in this introduction. As a minor application, we use these conjugacy and factor relations in §5.3, together with some earlier results, to completely classify multiplication automata according to their regularity status in the sense of [Reference Kůrka8].
2. Preliminaries
We denote the set of positive integers by
![]() $\mathbb {Z}_+$
and define the set of natural numbers by
$\mathbb {Z}_+$
and define the set of natural numbers by
![]() $\mathbb {N}=\mathbb {Z}_+\cup \{0\}$
. For
$\mathbb {N}=\mathbb {Z}_+\cup \{0\}$
. For
![]() $n\in \mathbb {Z}_+$
, we denote
$n\in \mathbb {Z}_+$
, we denote
![]() $\Sigma _n=\{0,1,\ldots ,n-1\}$
. Whenever A and B are sets,
$\Sigma _n=\{0,1,\ldots ,n-1\}$
. Whenever A and B are sets,
![]() $A^B$
denotes the collection of functions from B to A. We often denote the value of a function
$A^B$
denotes the collection of functions from B to A. We often denote the value of a function
![]() $f\in A^B$
at
$f\in A^B$
at
![]() $b\in B$
by
$b\in B$
by
![]() $f[b]$
instead of
$f[b]$
instead of
![]() $f(b)$
. When B is countable and A is finite, the set
$f(b)$
. When B is countable and A is finite, the set
![]() $A^B$
is a compact metrizable space with respect to the prodiscrete topology, and every closed subset of
$A^B$
is a compact metrizable space with respect to the prodiscrete topology, and every closed subset of
![]() $A^B$
is also compact and metrizable with respect to the subspace topology.
$A^B$
is also compact and metrizable with respect to the subspace topology.
We interpret the notation
![]() $A^n$
for a set A and
$A^n$
for a set A and
![]() $n\in \mathbb {N}$
as a shorthand for
$n\in \mathbb {N}$
as a shorthand for
![]() $A^{\{1,2,\ldots ,n\}}$
, the set of sequences of length n over A indexed by
$A^{\{1,2,\ldots ,n\}}$
, the set of sequences of length n over A indexed by
![]() $1,2,\ldots ,n$
. The elements of this set can be represented by
$1,2,\ldots ,n$
. The elements of this set can be represented by
![]() $(a_1,\ldots ,a_n)$
, by
$(a_1,\ldots ,a_n)$
, by
![]() $(a_i)_{i=1}^n$
, or for short, just by
$(a_i)_{i=1}^n$
, or for short, just by
![]() $(a_i)$
when the index i and the length of the sequence n are clear from the context. As in the previous paragraph, given
$(a_i)$
when the index i and the length of the sequence n are clear from the context. As in the previous paragraph, given
![]() $a=(a_1,\ldots ,a_n)\in A^n$
, we may denote
$a=(a_1,\ldots ,a_n)\in A^n$
, we may denote
![]() $a[i]=a_i$
for
$a[i]=a_i$
for
![]() $1\leq i\leq n$
. We also denote
$1\leq i\leq n$
. We also denote
![]() $a[i,j]=(a_i,a_{i+1}\ldots ,a_j)$
for
$a[i,j]=(a_i,a_{i+1}\ldots ,a_j)$
for
![]() $i,j\in \{1,2,\ldots ,n\}$
: this is the empty sequence when
$i,j\in \{1,2,\ldots ,n\}$
: this is the empty sequence when
![]() $i>j$
.
$i>j$
.
By substituting
![]() $\mathbb {R}$
for A in the previous paragraph, we get the set of n-dimensional real vectors. We define a partial order for
$\mathbb {R}$
for A in the previous paragraph, we get the set of n-dimensional real vectors. We define a partial order for
![]() $v,w\in \mathbb {R}^n$
by
$v,w\in \mathbb {R}^n$
by
![]() $v\leq w$
if
$v\leq w$
if
![]() $v[i]\leq w[i]$
for all
$v[i]\leq w[i]$
for all
![]() $1\leq i\leq n$
. A stronger inequality is
$1\leq i\leq n$
. A stronger inequality is
![]() $v\ll w$
, which means that
$v\ll w$
, which means that
![]() $v[i]<w[i]$
for all
$v[i]<w[i]$
for all
![]() $1\leq i\leq n$
. For any
$1\leq i\leq n$
. For any
![]() $x\in \mathbb {R}$
, we define the constant vector
$x\in \mathbb {R}$
, we define the constant vector
![]() ${\mathbf {x}}=(x,\ldots ,x)$
, so in particular,
${\mathbf {x}}=(x,\ldots ,x)$
, so in particular,
![]() ${\mathbf {0}}=(0,\ldots ,0)$
and
${\mathbf {0}}=(0,\ldots ,0)$
and
![]() ${\mathbf {1}}=(1,\ldots ,1)$
. The Kronecker delta is defined by
${\mathbf {1}}=(1,\ldots ,1)$
. The Kronecker delta is defined by
![]() $\delta _{ij}=0$
when
$\delta _{ij}=0$
when
![]() $i\neq j$
and
$i\neq j$
and
![]() $\delta _{ij}=1$
when
$\delta _{ij}=1$
when
![]() $i=j$
. Using this, the standard basis vectors
$i=j$
. Using this, the standard basis vectors
![]() $e_k\in \mathbb {R}^n$
for
$e_k\in \mathbb {R}^n$
for
![]() $1\leq k\leq n$
are defined by
$1\leq k\leq n$
are defined by
![]() $e_k[i]\hspace{-1pt}=\hspace{-1pt}\delta _{ki}$
for
$e_k[i]\hspace{-1pt}=\hspace{-1pt}\delta _{ki}$
for
![]() $1\hspace{-1pt}\leq\hspace{-1pt} i\hspace{-1pt}\leq\hspace{-1pt} n$
. In matrix multiplications, we interpret vectors as column vectors.
$1\hspace{-1pt}\leq\hspace{-1pt} i\hspace{-1pt}\leq\hspace{-1pt} n$
. In matrix multiplications, we interpret vectors as column vectors.
To present some of the main results of this paper, we will use the terminology of topological dynamical systems, one reference for these is [Reference Kůrka9].
Definition 2.1. If X is a compact metrizable topological space and
![]() $T:X\to X$
is a continuous map, we say that
$T:X\to X$
is a continuous map, we say that
![]() $(X,T)$
is a (topological) dynamical system.
$(X,T)$
is a (topological) dynamical system.
As a particular example, for a finite set
![]() $\Sigma $
(an alphabet),
$\Sigma $
(an alphabet),
![]() $d\in \mathbb {Z}_+$
and
$d\in \mathbb {Z}_+$
and
![]() $z\in \mathbb {Z}^d$
, we define the shift maps
$z\in \mathbb {Z}^d$
, we define the shift maps
![]() $\sigma _{z}:\Sigma ^{\mathbb {Z}^d}\to \Sigma ^{\mathbb {Z}^d}$
by
$\sigma _{z}:\Sigma ^{\mathbb {Z}^d}\to \Sigma ^{\mathbb {Z}^d}$
by
![]() $\sigma _{z}(f)[z']=f[z'+z]$
for all
$\sigma _{z}(f)[z']=f[z'+z]$
for all
![]() $f\in \Sigma ^{\mathbb {Z}^d}$
and
$f\in \Sigma ^{\mathbb {Z}^d}$
and
![]() $z'\in \mathbb {Z}^d$
. Then
$z'\in \mathbb {Z}^d$
. Then
![]() $(\Sigma ^{\mathbb {Z}^d},\sigma _z)$
is a dynamical system. Whenever
$(\Sigma ^{\mathbb {Z}^d},\sigma _z)$
is a dynamical system. Whenever
![]() $X\subseteq \Sigma ^{\mathbb {Z}^d}$
is closed and
$X\subseteq \Sigma ^{\mathbb {Z}^d}$
is closed and
![]() $\sigma _z(X)=X$
, then
$\sigma _z(X)=X$
, then
![]() $(X,\sigma _z)$
is also a dynamical system. Note that we used the same notation for both
$(X,\sigma _z)$
is also a dynamical system. Note that we used the same notation for both
![]() $\sigma _z$
and its restriction to X: in practice, this will not cause confusion. Let us also mention that if
$\sigma _z$
and its restriction to X: in practice, this will not cause confusion. Let us also mention that if
![]() $\sigma _z(X)=X$
for all
$\sigma _z(X)=X$
for all
![]() $z\in \mathbb {Z}^d$
, then X in fact becomes a system with multidimensional dynamics called a d-dimensional subshift. Throughout the text, we let
$z\in \mathbb {Z}^d$
, then X in fact becomes a system with multidimensional dynamics called a d-dimensional subshift. Throughout the text, we let
![]() $d,d',d"\in \mathbb {Z}_+$
and use
$d,d',d"\in \mathbb {Z}_+$
and use
![]() $d, d'$
, and
$d, d'$
, and
![]() $d"$
to indicate dimension. In the one-dimensional case, we define
$d"$
to indicate dimension. In the one-dimensional case, we define
![]() $\sigma :\Sigma ^{\mathbb {Z}}\to \Sigma ^{\mathbb {Z}}$
by
$\sigma :\Sigma ^{\mathbb {Z}}\to \Sigma ^{\mathbb {Z}}$
by
![]() $\sigma =\sigma _1$
and for a closed subset
$\sigma =\sigma _1$
and for a closed subset
![]() $X\subseteq \Sigma ^{\mathbb {Z}}$
satisfying
$X\subseteq \Sigma ^{\mathbb {Z}}$
satisfying
![]() $\sigma (X)=X$
, we call
$\sigma (X)=X$
, we call
![]() $(X,\sigma )$
a (one-dimensional) subshift. One can also define
$(X,\sigma )$
a (one-dimensional) subshift. One can also define
![]() $\sigma :\Sigma ^{\mathbb {N}}\to \Sigma ^{\mathbb {N}}$
by
$\sigma :\Sigma ^{\mathbb {N}}\to \Sigma ^{\mathbb {N}}$
by
![]() $\sigma (x)[i]=x[i+1]$
for
$\sigma (x)[i]=x[i+1]$
for
![]() $i\in \mathbb {N}$
, and then
$i\in \mathbb {N}$
, and then
![]() $(X,\sigma )$
for a closed
$(X,\sigma )$
for a closed
![]() $X\subseteq \Sigma ^{\mathbb {N}}$
satisfying
$X\subseteq \Sigma ^{\mathbb {N}}$
satisfying
![]() $\sigma (X)\subseteq \Sigma ^{\mathbb {N}}$
is called a one-sided subshift.
$\sigma (X)\subseteq \Sigma ^{\mathbb {N}}$
is called a one-sided subshift.
The structure preserving transformations between topological dynamical systems are known as morphisms.
Definition 2.2. We write
![]() $\psi :(X,T)\to (Y,S)$
whenever
$\psi :(X,T)\to (Y,S)$
whenever
![]() $(X,T)$
and
$(X,T)$
and
![]() $(Y,S)$
are dynamical systems and
$(Y,S)$
are dynamical systems and
![]() $\psi :X\to Y$
is a continuous map such that
$\psi :X\to Y$
is a continuous map such that
![]() $\psi \circ T=S\circ \psi $
(this equality is known as the equivariance condition). Then we say that
$\psi \circ T=S\circ \psi $
(this equality is known as the equivariance condition). Then we say that
![]() $\psi $
is a morphism. If
$\psi $
is a morphism. If
![]() $\psi $
is surjective, we say that
$\psi $
is surjective, we say that
![]() $\psi $
is a factor map and that
$\psi $
is a factor map and that
![]() $(Y,S)$
is a factor of
$(Y,S)$
is a factor of
![]() $(X,T)$
(via
$(X,T)$
(via
![]() $\psi $
). If
$\psi $
). If
![]() $\psi $
is bijective, we say that
$\psi $
is bijective, we say that
![]() $\psi $
is a conjugacy and that
$\psi $
is a conjugacy and that
![]() $(X,T)$
and
$(X,T)$
and
![]() $(Y,S)$
are conjugate (via
$(Y,S)$
are conjugate (via
![]() $\psi $
).
$\psi $
).
The particular dynamical systems under consideration in this paper will be shift maps on tilings (which are special kinds of d-dimensional subshifts) and cellular automata (which are self-maps of subshifs, particularly of
![]() $\Sigma ^{\mathbb {Z}}$
, that are continuous and satisfy the equivariance condition).
$\Sigma ^{\mathbb {Z}}$
, that are continuous and satisfy the equivariance condition).
3. Mixed base representations of numbers
A vector
![]() $m\in \mathbb {Z}_+^k$
such that
$m\in \mathbb {Z}_+^k$
such that
![]() $m[i]$
divides
$m[i]$
divides
![]() $m[i+1]$
for
$m[i+1]$
for
![]() $1\leq i<k$
is called a mixed base. Given a mixed base
$1\leq i<k$
is called a mixed base. Given a mixed base
![]() $m\in \mathbb {Z}_+^k$
, any
$m\in \mathbb {Z}_+^k$
, any
![]() $a\in \mathbb {N}$
has a base-m representation
$a\in \mathbb {N}$
has a base-m representation
![]() $a=\sum _{i=0}^k a_i m[i]$
(with the convention
$a=\sum _{i=0}^k a_i m[i]$
(with the convention
![]() $m[0]=1$
), where
$m[0]=1$
), where
![]() $a_i$
are the unique integers satisfying this equation such that
$a_i$
are the unique integers satisfying this equation such that
![]() $0\leq a_i<m[i+1]/m[i]$
for
$0\leq a_i<m[i+1]/m[i]$
for
![]() $0\leq i<k$
and
$0\leq i<k$
and
![]() $a_k\geq 0$
. For expressing such a representation, we also define the shorthand
$a_k\geq 0$
. For expressing such a representation, we also define the shorthand
![]() ${\mathrm {base}}(a,m)=(a_0,a_1,\ldots , a_k)$
, so in particular,
${\mathrm {base}}(a,m)=(a_0,a_1,\ldots , a_k)$
, so in particular,
![]() ${\mathrm {base}}(a,m)[i]=a_{i-1}$
for
${\mathrm {base}}(a,m)[i]=a_{i-1}$
for
![]() $1\leq i\leq k+1$
. For example, the base-10 representation (in the usual sense) for
$1\leq i\leq k+1$
. For example, the base-10 representation (in the usual sense) for
![]() $a\in \mathbb {N}$
arises by choosing
$a\in \mathbb {N}$
arises by choosing
![]() $m=(10,10^2,\ldots ,10^k)$
for a sufficiently large k.
$m=(10,10^2,\ldots ,10^k)$
for a sufficiently large k.
We may also use a single vector
![]() $n\in \mathbb {Z}_+^d$
as a starting point for forming many different mixed bases as various products of
$n\in \mathbb {Z}_+^d$
as a starting point for forming many different mixed bases as various products of
![]() $n[i]$
. For
$n[i]$
. For
![]() $v\in \mathbb {Z}^d$
, we let
$v\in \mathbb {Z}^d$
, we let
 $$ \begin{align*}m(n,v)=\prod_{j=1}^d n[j]^{-v[j]}\end{align*} $$
$$ \begin{align*}m(n,v)=\prod_{j=1}^d n[j]^{-v[j]}\end{align*} $$
(this is a positive integer in the special case
![]() $v\leq {\mathbf {0}}$
). For a d-directive sequence, that is, a decreasing sequence of vectors
$v\leq {\mathbf {0}}$
). For a d-directive sequence, that is, a decreasing sequence of vectors
![]() $(v_i)_{i=1}^k$
satisfying
$(v_i)_{i=1}^k$
satisfying
![]() ${\mathbf {0}}\geq v_1\geq v_2\geq \cdots \geq v_k\in \mathbb {Z}^d$
(a binary d-directive sequence in the case
${\mathbf {0}}\geq v_1\geq v_2\geq \cdots \geq v_k\in \mathbb {Z}^d$
(a binary d-directive sequence in the case
![]() $v_i\in \{-1,0\}^d$
), we define a mixed base
$v_i\in \{-1,0\}^d$
), we define a mixed base
![]() $m(n,(v_{i}))\in \mathbb {Z}_+^k$
by
$m(n,(v_{i}))\in \mathbb {Z}_+^k$
by
We also define
![]() ${\mathrm {base}}_{n}(a,(v_1,\ldots ,v_k))={\mathrm {base}}(a,m(n,(v_i)))$
for
${\mathrm {base}}_{n}(a,(v_1,\ldots ,v_k))={\mathrm {base}}(a,m(n,(v_i)))$
for
![]() $a\in \mathbb {N}$
.
$a\in \mathbb {N}$
.
Remark 3.1. Our definition of
![]() $m(n,v)$
where a negative coordinate
$m(n,v)$
where a negative coordinate
![]() $v[j]$
corresponds to raising
$v[j]$
corresponds to raising
![]() $n[j]$
to a positive power may seem strange. Throughout this paper, negative numbers will appear at points where positive numbers could be expected. Our conventions are ultimately motivated by the peculiarity that the usual method of writing down the digits of a number causes the more significant digits to appear to the left (that is, toward the negative direction of the x-axis) instead of to the right.
$n[j]$
to a positive power may seem strange. Throughout this paper, negative numbers will appear at points where positive numbers could be expected. Our conventions are ultimately motivated by the peculiarity that the usual method of writing down the digits of a number causes the more significant digits to appear to the left (that is, toward the negative direction of the x-axis) instead of to the right.
We also mention some telescoping properties for the base representations. For
![]() $x\in A^n$
and
$x\in A^n$
and
![]() $y\in A^m$
with any set A, define the insertion
$y\in A^m$
with any set A, define the insertion
![]() $x{\mathrm {\vee }}_i y\in A^{n+m}$
for
$x{\mathrm {\vee }}_i y\in A^{n+m}$
for
![]() $0\leq i\leq n$
by
$0\leq i\leq n$
by
 $$ \begin{align*} &(x{\mathrm{\vee}}_i y)[1,i]=x[1,i], \\ &(x{\mathrm{\vee}}_i y)[i+1,i+m]=y, \\ &(x{\mathrm{\vee}}_i y)[i+m+1,n+m]=x[i+1,n] \end{align*} $$
$$ \begin{align*} &(x{\mathrm{\vee}}_i y)[1,i]=x[1,i], \\ &(x{\mathrm{\vee}}_i y)[i+1,i+m]=y, \\ &(x{\mathrm{\vee}}_i y)[i+m+1,n+m]=x[i+1,n] \end{align*} $$
and the overwrite
![]() $x{\mathrm {\not \vee }}_i y\in A^{n+m-1}$
for
$x{\mathrm {\not \vee }}_i y\in A^{n+m-1}$
for
![]() $1\leq i\leq n$
by
$1\leq i\leq n$
by
 $$ \begin{align*} &(x{\mathrm{\not\vee}}_i y)[1,i-1]=x[1,i-1], \\ &(x{\mathrm{\not\vee}}_i y)[i,i+m-1]=y, \\ &(x{\mathrm{\not\vee}}_i y)[i+m,n+m-1]=x[i+1,n]. \end{align*} $$
$$ \begin{align*} &(x{\mathrm{\not\vee}}_i y)[1,i-1]=x[1,i-1], \\ &(x{\mathrm{\not\vee}}_i y)[i,i+m-1]=y, \\ &(x{\mathrm{\not\vee}}_i y)[i+m,n+m-1]=x[i+1,n]. \end{align*} $$
Lemma 3.2. Let
![]() $m\in \mathbb {Z}_+^k$
,
$m\in \mathbb {Z}_+^k$
,
![]() $m'\in \mathbb {Z}_+^{k'}$
, and
$m'\in \mathbb {Z}_+^{k'}$
, and
![]() $m{\mathrm {\vee }}_i m'\in \mathbb {Z}_+^{k+k'}$
be mixed bases with
$m{\mathrm {\vee }}_i m'\in \mathbb {Z}_+^{k+k'}$
be mixed bases with
![]() $0\leq i\leq k$
. If
$0\leq i\leq k$
. If
![]() $a\in \mathbb {N}$
and
$a\in \mathbb {N}$
and
![]() ${\mathrm {base}}(a,m)=(a_0,\ldots ,a_{k})$
, then (with the convention that
${\mathrm {base}}(a,m)=(a_0,\ldots ,a_{k})$
, then (with the convention that
![]() $m[0]=1$
)
$m[0]=1$
)
Proof. Let
![]() $(b_0,\ldots ,b_{k'})={\mathrm {base}}(a_i,m'/m[i])$
. By assumption,
$(b_0,\ldots ,b_{k'})={\mathrm {base}}(a_i,m'/m[i])$
. By assumption,
![]() $a=\sum _{j=0}^k a_j m[j]$
(
$a=\sum _{j=0}^k a_j m[j]$
(
![]() $0\leq a_j<m[j+1]/m[j]$
for
$0\leq a_j<m[j+1]/m[j]$
for
![]() $0\leq j<k$
,
$0\leq j<k$
,
![]() $a_k\geq 0$
) and
$a_k\geq 0$
) and
![]() $a_i=b_0+\sum _{j=1}^{k'} b_j(m'[j]/m[i])$
(
$a_i=b_0+\sum _{j=1}^{k'} b_j(m'[j]/m[i])$
(
![]() $0\leq b_0<m'[1]/m[i]$
,
$0\leq b_0<m'[1]/m[i]$
,
![]() $0\leq b_j<m'[j+1]/m'[j]$
for
$0\leq b_j<m'[j+1]/m'[j]$
for
![]() $1\leq j<k'$
,
$1\leq j<k'$
,
![]() $b_{k'}\geq 0$
). By substituting the base-
$b_{k'}\geq 0$
). By substituting the base-
![]() $m'$
representation of
$m'$
representation of
![]() $a_i$
into the base-m representation of a, we find that
$a_i$
into the base-m representation of a, we find that
 $$ \begin{align*}a=\sum_{j=0}^{i-1}a_j m[j]+b_0m[i]+\sum_{j=1}^{k'}b_j m'[j]+\sum_{j=i+1}^k a_j m[j].\end{align*} $$
$$ \begin{align*}a=\sum_{j=0}^{i-1}a_j m[j]+b_0m[i]+\sum_{j=1}^{k'}b_j m'[j]+\sum_{j=i+1}^k a_j m[j].\end{align*} $$
This is equivalent to the claim of the lemma,
assuming that we can verify the inequalities
 $$ \begin{align*} &0\leq a_j<m[j+1]/m[j]\quad\mbox{for }0\leq j<i\mbox{ and }i+1\leq j<k, \\ &0\leq b_0 < m'[1]/m[i], \\ &0\leq b_j<m'[j+1]/m'[j]\quad\mbox{for }1\leq j<k',\quad\mbox{and}\\ &0\leq b_{k'}<m[i+1]/m'[k'] \quad\mbox{(in the case}\ i<k\mbox{)}, \end{align*} $$
$$ \begin{align*} &0\leq a_j<m[j+1]/m[j]\quad\mbox{for }0\leq j<i\mbox{ and }i+1\leq j<k, \\ &0\leq b_0 < m'[1]/m[i], \\ &0\leq b_j<m'[j+1]/m'[j]\quad\mbox{for }1\leq j<k',\quad\mbox{and}\\ &0\leq b_{k'}<m[i+1]/m'[k'] \quad\mbox{(in the case}\ i<k\mbox{)}, \end{align*} $$
but everything except the last inequality follows directly from the definition of
![]() $a_j$
and
$a_j$
and
![]() $b_j$
. Because
$b_j$
. Because
![]() $a_i<m[i+1]/m[i]$
, it follows that
$a_i<m[i+1]/m[i]$
, it follows that
![]() $b_{k'}\leq a_i m[i]/m'[k']<m[i+1]/m'[k']$
, and we are done.
$b_{k'}\leq a_i m[i]/m'[k']<m[i+1]/m'[k']$
, and we are done.
Lemma 3.3. Let
![]() $n\in \mathbb {Z}_+^d$
, and let
$n\in \mathbb {Z}_+^d$
, and let
![]() $(v_j)_{j=1}^{k}$
,
$(v_j)_{j=1}^{k}$
,
![]() $(w_j)_{j=1}^{k'}$
and
$(w_j)_{j=1}^{k'}$
and
![]() $(v_j)_{j=1}^{k}{\mathrm {\vee }}_i (w_j)_{j=1}^{k'}$
be d-directive sequences with
$(v_j)_{j=1}^{k}{\mathrm {\vee }}_i (w_j)_{j=1}^{k'}$
be d-directive sequences with
![]() $0\leq i\leq k$
. If
$0\leq i\leq k$
. If
![]() $a\in \mathbb {N}$
and
$a\in \mathbb {N}$
and
![]() ${\mathrm {base}}_{n}(a,(v_j)_{j=1}^k)=(a_0,\ldots ,a_k)$
, then (with the convention that
${\mathrm {base}}_{n}(a,(v_j)_{j=1}^k)=(a_0,\ldots ,a_k)$
, then (with the convention that
![]() $v_0={\mathbf {0}}$
)
$v_0={\mathbf {0}}$
)
Proof. Let
![]() $M=m(n,v_i)$
. We note that for
$M=m(n,v_i)$
. We note that for
![]() $1\leq j'\leq k'$
,
$1\leq j'\leq k'$
,
 $$ \begin{align*} m(n,w_{j'}-v_i)&=\prod_{j=1}^d n[j]^{(-w_{j'}+v_i)[j]} \\ &=\prod_{j=1}^d n[j]^{-w_{j'}[j]}\prod_{j=1}^d n[j]^{v_i[j]}=m(n,w_{j'})/M. \end{align*} $$
$$ \begin{align*} m(n,w_{j'}-v_i)&=\prod_{j=1}^d n[j]^{(-w_{j'}+v_i)[j]} \\ &=\prod_{j=1}^d n[j]^{-w_{j'}[j]}\prod_{j=1}^d n[j]^{v_i[j]}=m(n,w_{j'})/M. \end{align*} $$
By assumption,
![]() ${\mathrm {base}}(a,m(n,(v_j)_{j=1}^{k}))={\mathrm {base}}_{n}(a,(v_j)_{j=1}^k)=(a_0,\ldots ,a_k)$
and
${\mathrm {base}}(a,m(n,(v_j)_{j=1}^{k}))={\mathrm {base}}_{n}(a,(v_j)_{j=1}^k)=(a_0,\ldots ,a_k)$
and
 $$ \begin{align*} &{\mathrm{base}}_{n}(a,(v_j)_{j=1}^k{\mathrm{\vee}}_i(w_j)_{j=1}^{k'})={\mathrm{base}}(a,m(n,(v_j){\mathrm{\vee}}_i(w_j))) \\ &\quad={\mathrm{base}}(a,m(n,(v_j)_{j=1}^{k}){\mathrm{\vee}}_i m(n,(w_j)_{j=1}^{k'})) \\ &\quad \overset{L.~{3.2}}{=}{\mathrm{base}}(a,m(n,(v_j)_{j=1}^{k})){\mathrm{\not\vee}}_{i+1}\ {\mathrm{base}}(a_i,m(n,(w_j)_{j=1}^{k'})/M)) \\ &\quad={\mathrm{base}}_{n}(a,(v_j)_{j=1}^k){\mathrm{\not\vee}}_{i+1}\ {\mathrm{base}}_{n}(a_i,(w_j-v_i))_{j=1}^{k'}). \end{align*} $$
$$ \begin{align*} &{\mathrm{base}}_{n}(a,(v_j)_{j=1}^k{\mathrm{\vee}}_i(w_j)_{j=1}^{k'})={\mathrm{base}}(a,m(n,(v_j){\mathrm{\vee}}_i(w_j))) \\ &\quad={\mathrm{base}}(a,m(n,(v_j)_{j=1}^{k}){\mathrm{\vee}}_i m(n,(w_j)_{j=1}^{k'})) \\ &\quad \overset{L.~{3.2}}{=}{\mathrm{base}}(a,m(n,(v_j)_{j=1}^{k})){\mathrm{\not\vee}}_{i+1}\ {\mathrm{base}}(a_i,m(n,(w_j)_{j=1}^{k'})/M)) \\ &\quad={\mathrm{base}}_{n}(a,(v_j)_{j=1}^k){\mathrm{\not\vee}}_{i+1}\ {\mathrm{base}}_{n}(a_i,(w_j-v_i))_{j=1}^{k'}). \end{align*} $$
Lemma 3.4. Let
![]() $n\in \mathbb {Z}_+^d$
, let
$n\in \mathbb {Z}_+^d$
, let
![]() $(v_j)_{j=1}^k$
and
$(v_j)_{j=1}^k$
and
![]() $(w_j)_{j=1}^{k'}$
be d-directive sequences, and let
$(w_j)_{j=1}^{k'}$
be d-directive sequences, and let
![]() $0\leq i\hspace{-1pt}<\hspace{-1pt}k$
,
$0\leq i\hspace{-1pt}<\hspace{-1pt}k$
,
![]() $0\hspace{-1pt}\leq\hspace{-1pt} i'\hspace{-1pt}<\hspace{-1pt}k'$
be such that
$0\hspace{-1pt}\leq\hspace{-1pt} i'\hspace{-1pt}<\hspace{-1pt}k'$
be such that
![]() $v_i\hspace{-1pt}=\hspace{-1pt}w_{i'}$
and
$v_i\hspace{-1pt}=\hspace{-1pt}w_{i'}$
and
![]() $v_{i+1}\hspace{-1pt}=\hspace{-1pt}w_{i'+1}$
(with the convention
$v_{i+1}\hspace{-1pt}=\hspace{-1pt}w_{i'+1}$
(with the convention
![]() $v_0\hspace{-1pt}=\hspace{-1pt}w_0\hspace{-1pt}=\hspace{-1pt}{\mathbf {0}}$
). For any
$v_0\hspace{-1pt}=\hspace{-1pt}w_0\hspace{-1pt}=\hspace{-1pt}{\mathbf {0}}$
). For any
![]() $a\in \mathbb {N}$
, it holds that
$a\in \mathbb {N}$
, it holds that
If
![]() $v_k=w_{k'}$
, then
$v_k=w_{k'}$
, then
Proof. For the first claim of the lemma concerning
![]() $0\leq i<k$
,
$0\leq i<k$
,
![]() $0\leq i'<k'$
, it suffices to show that
$0\leq i'<k'$
, it suffices to show that
![]() ${\mathrm {base}}_{n}(a,(v_i,v_{i+1}))[2]={\mathrm {base}}_{n}(a,(v_j))[i+1]$
, because from this, it follows that
${\mathrm {base}}_{n}(a,(v_i,v_{i+1}))[2]={\mathrm {base}}_{n}(a,(v_j))[i+1]$
, because from this, it follows that
 $$ \begin{align*} &{\mathrm{base}}_{n}(a,(v_j))[i+1]={\mathrm{base}}_{n}(a,(v_i,v_{i+1}))[2] \\ &\quad={\mathrm{base}}_{n}(a,(w_{i'},w_{i'+1}))[2]={\mathrm{base}}_{n}(a,(w_j))[i'+1]. \end{align*} $$
$$ \begin{align*} &{\mathrm{base}}_{n}(a,(v_j))[i+1]={\mathrm{base}}_{n}(a,(v_i,v_{i+1}))[2] \\ &\quad={\mathrm{base}}_{n}(a,(w_{i'},w_{i'+1}))[2]={\mathrm{base}}_{n}(a,(w_j))[i'+1]. \end{align*} $$
Let
![]() $(a_0,a_1,a_2)={\mathrm {base}}_{n}(a,(v_i,v_{i+1}))$
. By one application of Lemma 3.3,
$(a_0,a_1,a_2)={\mathrm {base}}_{n}(a,(v_i,v_{i+1}))$
. By one application of Lemma 3.3,
 $$ \begin{align*} &{\mathrm{base}}_{n}(a,(v_1,\ldots,v_i,v_{i+1}))={\mathrm{base}}_{n}(a,(v_i,v_{i+1}) {\mathrm{\vee}}_0(v_1,\ldots,v_{i-1})) \\ &\quad=(a_0,a_1,a_2) {\mathrm{\not\vee}}_1(b_0,\ldots,b_{i-1})=(b_0,\ldots,b_{i-1},a_1,a_2) \end{align*} $$
$$ \begin{align*} &{\mathrm{base}}_{n}(a,(v_1,\ldots,v_i,v_{i+1}))={\mathrm{base}}_{n}(a,(v_i,v_{i+1}) {\mathrm{\vee}}_0(v_1,\ldots,v_{i-1})) \\ &\quad=(a_0,a_1,a_2) {\mathrm{\not\vee}}_1(b_0,\ldots,b_{i-1})=(b_0,\ldots,b_{i-1},a_1,a_2) \end{align*} $$
for some
![]() $b_j\in \mathbb {N}$
. By another application of the same lemma,
$b_j\in \mathbb {N}$
. By another application of the same lemma,
 $$ \begin{align*} &{\mathrm{base}}_{n}(a,(v_j))={\mathrm{base}}_{n}(a,(v_1,\ldots,v_{i+1}) {\mathrm{\vee}}_{i+1}(v_{i+2},\ldots,v_k)) \\ &\quad=(b_0,\ldots,b_{i-1},a_1,a_2) {\mathrm{\not\vee}}_{i+2}(c_{i+1},\ldots,c_k)=(b_0,\ldots,b_{i-1},a_1,c_{i+1},\ldots,c_k) \end{align*} $$
$$ \begin{align*} &{\mathrm{base}}_{n}(a,(v_j))={\mathrm{base}}_{n}(a,(v_1,\ldots,v_{i+1}) {\mathrm{\vee}}_{i+1}(v_{i+2},\ldots,v_k)) \\ &\quad=(b_0,\ldots,b_{i-1},a_1,a_2) {\mathrm{\not\vee}}_{i+2}(c_{i+1},\ldots,c_k)=(b_0,\ldots,b_{i-1},a_1,c_{i+1},\ldots,c_k) \end{align*} $$
for some
![]() $c_j\in \mathbb {N}$
. Therefore,
$c_j\in \mathbb {N}$
. Therefore,
![]() ${\mathrm {base}}_{n}(a,(v_i,v_{i+1}))[2]=a_1={\mathrm {base}}_{n}(a,(v_j))[i+1]$
.
${\mathrm {base}}_{n}(a,(v_i,v_{i+1}))[2]=a_1={\mathrm {base}}_{n}(a,(v_j))[i+1]$
.
In a similar manner, for the last claim of the lemma, it suffices to show that
![]() ${\mathrm {base}}_{n}(a,(v_k))[2]={\mathrm {base}}_{n}(a,(v_j))[k+1]$
. Let
${\mathrm {base}}_{n}(a,(v_k))[2]={\mathrm {base}}_{n}(a,(v_j))[k+1]$
. Let
![]() $(a_0,a_1)={\mathrm {base}}_n(a,(v_k))$
. By Lemma 3.3,
$(a_0,a_1)={\mathrm {base}}_n(a,(v_k))$
. By Lemma 3.3,
 $$ \begin{align*} &{\mathrm{base}}_{n}(a,(v_1,\ldots,v_{k-1},v_{k}))={\mathrm{base}}_{n}(a,(v_{k}) {\mathrm{\vee}}_0(v_1,\ldots,v_{k-1})) \\ &\quad=(a_0,a_1) {\mathrm{\not\vee}}_1(b_0,\ldots,b_{k-1})=(b_0,\ldots,b_{k-1},a_1) \end{align*} $$
$$ \begin{align*} &{\mathrm{base}}_{n}(a,(v_1,\ldots,v_{k-1},v_{k}))={\mathrm{base}}_{n}(a,(v_{k}) {\mathrm{\vee}}_0(v_1,\ldots,v_{k-1})) \\ &\quad=(a_0,a_1) {\mathrm{\not\vee}}_1(b_0,\ldots,b_{k-1})=(b_0,\ldots,b_{k-1},a_1) \end{align*} $$
for some
![]() $b_j\in \mathbb {N}$
. Therefore,
$b_j\in \mathbb {N}$
. Therefore,
![]() ${\mathrm {base}}_{n}(a,(v_k))[2]=a_1={\mathrm {base}}_{n}(a,(v_j))[k+1]$
.
${\mathrm {base}}_{n}(a,(v_k))[2]=a_1={\mathrm {base}}_{n}(a,(v_j))[k+1]$
.
Lemma 3.5. Let
![]() $n\in \mathbb {Z}_+^d$
, let
$n\in \mathbb {Z}_+^d$
, let
![]() $a\in \mathbb {N}$
, and let
$a\in \mathbb {N}$
, and let
![]() $p_1,p_2,q_1,q_2\in \mathbb {Z}^d$
be such that
$p_1,p_2,q_1,q_2\in \mathbb {Z}^d$
be such that
![]() $q_1\geq q_2$
and
$q_1\geq q_2$
and
![]() $p_1\geq p_1+q_1\geq p_1+q_2\geq p_2$
are d-directive sequences. If
$p_1\geq p_1+q_1\geq p_1+q_2\geq p_2$
are d-directive sequences. If
![]() ${\mathrm {base}}_{n}(a,(p_1,p_2))=(a_0,a_1,a_2)$
, then
${\mathrm {base}}_{n}(a,(p_1,p_2))=(a_0,a_1,a_2)$
, then
Proof. By applying Lemma 3.3,
 $$ \begin{align*} &{\mathrm{base}}_{n}(a,(p_1,p_1+q_1,p_1+q_2,p_2)) \\ &\quad={\mathrm{base}}_{n}(a,(p_1,p_2)) {\mathrm{\not\vee}}_2\ {\mathrm{base}}_{n}(a_1,(q_1,q_2)), \end{align*} $$
$$ \begin{align*} &{\mathrm{base}}_{n}(a,(p_1,p_1+q_1,p_1+q_2,p_2)) \\ &\quad={\mathrm{base}}_{n}(a,(p_1,p_2)) {\mathrm{\not\vee}}_2\ {\mathrm{base}}_{n}(a_1,(q_1,q_2)), \end{align*} $$
and therefore by Lemma 3.4,
 $$ \begin{align*} &{\mathrm{base}}_{n}(a,(p_1+q_1,p_1+q_2))[2] \\ &\quad={\mathrm{base}}_{n}(a,(p_1,p_1+q_1,p_1+q_2,p_2))[3]={\mathrm{base}}_{n}(a_1,(q_1,q_2))[2]. \end{align*} $$
$$ \begin{align*} &{\mathrm{base}}_{n}(a,(p_1+q_1,p_1+q_2))[2] \\ &\quad={\mathrm{base}}_{n}(a,(p_1,p_1+q_1,p_1+q_2,p_2))[3]={\mathrm{base}}_{n}(a_1,(q_1,q_2))[2]. \end{align*} $$
For a map
![]() ${\mathrm {{\iota }}}:\{1,\ldots ,d'\}\to \{1,\ldots ,d\}$
and
${\mathrm {{\iota }}}:\{1,\ldots ,d'\}\to \{1,\ldots ,d\}$
and
![]() $p\in \mathbb {Z}^d$
, there is an affine map
$p\in \mathbb {Z}^d$
, there is an affine map
![]() ${\mathrm {I}}_{p,{\mathrm {{\iota }}}}: \mathbb {R}^{d'}\to \mathbb {R}^d$
defined by
${\mathrm {I}}_{p,{\mathrm {{\iota }}}}: \mathbb {R}^{d'}\to \mathbb {R}^d$
defined by
![]() ${\mathrm {I}}_{p,{\mathrm {{\iota }}}}({\mathbf {0}})=p$
and
${\mathrm {I}}_{p,{\mathrm {{\iota }}}}({\mathbf {0}})=p$
and
![]() ${\mathrm {I}}_{p,{\mathrm {{\iota }}}}(e_i)=p+e_{{\mathrm {{\iota }}}(i)}$
for
${\mathrm {I}}_{p,{\mathrm {{\iota }}}}(e_i)=p+e_{{\mathrm {{\iota }}}(i)}$
for
![]() $1\leq i\leq d'$
.
$1\leq i\leq d'$
.
Lemma 3.6. Let
![]() ${\mathrm {{\iota }}}:\{1,\ldots ,d'\}\to \{1,\ldots ,d\}$
be injective and let
${\mathrm {{\iota }}}:\{1,\ldots ,d'\}\to \{1,\ldots ,d\}$
be injective and let
![]() $n\in \mathbb {Z}_+^d$
,
$n\in \mathbb {Z}_+^d$
,
![]() $n'\in \mathbb {Z}_+^{d'}$
satisfy
$n'\in \mathbb {Z}_+^{d'}$
satisfy
![]() $n'[i]=n[{\mathrm {{\iota }}}(i)]$
for
$n'[i]=n[{\mathrm {{\iota }}}(i)]$
for
![]() $1\leq i\leq d'$
. For a
$1\leq i\leq d'$
. For a
![]() $d'$
-directive sequence
$d'$
-directive sequence
![]() $v_1\geq \cdots \geq v_k$
, for
$v_1\geq \cdots \geq v_k$
, for
![]() $w_i={\mathrm {I}}_{{\mathbf {0}},{\mathrm {{\iota }}}}(v_i)$
and
$w_i={\mathrm {I}}_{{\mathbf {0}},{\mathrm {{\iota }}}}(v_i)$
and
![]() $a\in \mathbb {N}$
, it holds that
$a\in \mathbb {N}$
, it holds that
![]() ${\mathrm {base}}_{n'}(a,(v_1,\ldots ,v_k))={\mathrm {base}}_{n}(a,(w_1,\ldots ,w_k))$
.
${\mathrm {base}}_{n'}(a,(v_1,\ldots ,v_k))={\mathrm {base}}_{n}(a,(w_1,\ldots ,w_k))$
.
Proof. Observe that for any
![]() $v\in \mathbb {Z}^{d'}$
,
$v\in \mathbb {Z}^{d'}$
,
![]() $1\leq j'\leq d'$
, and
$1\leq j'\leq d'$
, and
![]() $j={\mathrm {{\iota }}}(j')$
, it holds that
$j={\mathrm {{\iota }}}(j')$
, it holds that
![]() ${\mathrm {I}}_{{\mathbf {0}},{\mathrm {{\iota }}}}(v)[j]=v[j']$
. If j is not in the image of
${\mathrm {I}}_{{\mathbf {0}},{\mathrm {{\iota }}}}(v)[j]=v[j']$
. If j is not in the image of
![]() ${\mathrm {{\iota }}}$
, then
${\mathrm {{\iota }}}$
, then
![]() ${\mathrm {I}}_{{\mathbf {0}},{\mathrm {{\iota }}}}(v)[j]=0$
. Using the substitution
${\mathrm {I}}_{{\mathbf {0}},{\mathrm {{\iota }}}}(v)[j]=0$
. Using the substitution
![]() $j={\mathrm {{\iota }}}(j')$
for
$j={\mathrm {{\iota }}}(j')$
for
![]() $0\leq j'\leq d'$
below, we can compute for
$0\leq j'\leq d'$
below, we can compute for
![]() $1\leq i\leq k$
that
$1\leq i\leq k$
that
 $$ \begin{align*} m(n,w_i)&=m(n,{\mathrm{I}}_{{\mathbf{0}},{\mathrm{{\iota}}}}(v_i))=\prod_{j=1}^d n[j]^{-{\mathrm{I}}_{{\mathbf{0}},{\mathrm{{\iota}}}}(v_i))[j]} \\ &=\prod_{j'=1}^{d'}n[{\mathrm{{\iota}}}(j')]^{-{\mathrm{I}}_{{\mathbf{0}},{\mathrm{{\iota}}}}(v_i)[{\mathrm{{\iota}}}(j')]}=\prod_{j'=1}^{d'}n'[j']^{-v_i[j']}=m(n',v_i), \end{align*} $$
$$ \begin{align*} m(n,w_i)&=m(n,{\mathrm{I}}_{{\mathbf{0}},{\mathrm{{\iota}}}}(v_i))=\prod_{j=1}^d n[j]^{-{\mathrm{I}}_{{\mathbf{0}},{\mathrm{{\iota}}}}(v_i))[j]} \\ &=\prod_{j'=1}^{d'}n[{\mathrm{{\iota}}}(j')]^{-{\mathrm{I}}_{{\mathbf{0}},{\mathrm{{\iota}}}}(v_i)[{\mathrm{{\iota}}}(j')]}=\prod_{j'=1}^{d'}n'[j']^{-v_i[j']}=m(n',v_i), \end{align*} $$
and therefore
4. Multiplication cubes
4.1. Preliminaries on multiplication cubes
Our model for the d-dimensional hypercube is the set
![]() $[-1,0]^d$
. The bottom and top
$[-1,0]^d$
. The bottom and top
![]() $(d-1)$
-dimensional hyperfaces orthogonal to
$(d-1)$
-dimensional hyperfaces orthogonal to
![]() $e_i$
are
$e_i$
are
respectively.
One can take a collection of hypercubes, color their
![]() $(d-1)$
-dimensional hyperfaces
$(d-1)$
-dimensional hyperfaces
![]() ${\mathrm {\beta }}_i$
and
${\mathrm {\beta }}_i$
and
![]() ${\mathrm {\tau }}_i$
with various colors, and form tessellations of the space with these cubes in such a way that the adjacent hyperfaces of neighboring hypercubes have matching colors. An example of such a colored set of two-dimensional cubes and a part of a two-dimensional tessellation is presented in Figure 1. More precisely (and more abstractly), this is done as in the following definition.
${\mathrm {\tau }}_i$
with various colors, and form tessellations of the space with these cubes in such a way that the adjacent hyperfaces of neighboring hypercubes have matching colors. An example of such a colored set of two-dimensional cubes and a part of a two-dimensional tessellation is presented in Figure 1. More precisely (and more abstractly), this is done as in the following definition.

Figure 1 The multiplication cube set
![]() $T_{(2,5)}$
and a part of a tiling from
$T_{(2,5)}$
and a part of a tiling from
![]() $X_{(2,5)}=X_{T_{(2,5)}}$
(with the upper right corner of the cube at the origin marked by a black dot). Consecutive powers of two (starting with
$X_{(2,5)}=X_{T_{(2,5)}}$
(with the upper right corner of the cube at the origin marked by a black dot). Consecutive powers of two (starting with
![]() $4,8,16,\ldots $
) can be found in the tiling along diagonals that go from bottom left to top right: for an explanation of this, see Example 4.21 or Proposition 4.26.
$4,8,16,\ldots $
) can be found in the tiling along diagonals that go from bottom left to top right: for an explanation of this, see Example 4.21 or Proposition 4.26.
Definition 4.1. Let T and C be finite sets (the set of hypercubes and the set of colors) and for some
![]() $d\in \mathbb {Z}_+$
, let
$d\in \mathbb {Z}_+$
, let
![]() ${\mathrm {\beta }}_i:T\to C$
and
${\mathrm {\beta }}_i:T\to C$
and
![]() ${\mathrm {\tau }}_i: T\to C$
be functions for
${\mathrm {\tau }}_i: T\to C$
be functions for
![]() $1\leq i\leq d$
(the labeling functions). The set T (with associated, implicit C,
$1\leq i\leq d$
(the labeling functions). The set T (with associated, implicit C,
![]() ${\mathrm {\beta }}_i$
, and
${\mathrm {\beta }}_i$
, and
![]() ${\mathrm {\tau }}_i$
) is then called a Wang hypercube set. A valid tiling or tessellation over T is a map
${\mathrm {\tau }}_i$
) is then called a Wang hypercube set. A valid tiling or tessellation over T is a map
![]() $f:\mathbb {Z}^d\to T$
satisfying
$f:\mathbb {Z}^d\to T$
satisfying
![]() ${\mathrm {\tau }}_i(f[z])={\mathrm {\beta }}_i(f[z+e_i])$
for all
${\mathrm {\tau }}_i(f[z])={\mathrm {\beta }}_i(f[z+e_i])$
for all
![]() $z\in \mathbb {Z}^d$
and
$z\in \mathbb {Z}^d$
and
![]() $1\leq i\leq d$
. The set of all valid tilings over T is denoted by
$1\leq i\leq d$
. The set of all valid tilings over T is denoted by
![]() $X_T$
.
$X_T$
.
The pair
![]() $(X_T,\sigma _z)$
is a dynamical system for all
$(X_T,\sigma _z)$
is a dynamical system for all
![]() $z\in \mathbb {Z}^d$
, and as a d-dimensional subshift,
$z\in \mathbb {Z}^d$
, and as a d-dimensional subshift,
![]() $X_T$
is in fact an example of a so-called subshift of finite type. Wang hypercubes and their tessellations are the most commonly studied in the case
$X_T$
is in fact an example of a so-called subshift of finite type. Wang hypercubes and their tessellations are the most commonly studied in the case
![]() $d=2$
, and particularly, then the elements of T are called Wang tiles. These originate from Wang’s paper [Reference Wang13].
$d=2$
, and particularly, then the elements of T are called Wang tiles. These originate from Wang’s paper [Reference Wang13].
We will proceed to define a particular class of Wang hypercubes which could be called multiplication hypercubes, but which we will call multiplication cubes for simplicity. Two-dimensional multiplication cubes have previously appeared in [Reference Cook, Stérin, Woods, Lakin and Sulc3] as elements of the so-called Collatz tile set. Higher dimensional such cubes will in fact have labels on all of their lower-dimensional hyperfaces, not just the
![]() $(d-1)$
-dimensional ones. The set of k-dimensional hyperfaces within the d-dimensional hypercube is denoted by
$(d-1)$
-dimensional ones. The set of k-dimensional hyperfaces within the d-dimensional hypercube is denoted by
![]() $S_{d,k}$
and the set of all hyperfaces is denoted by
$S_{d,k}$
and the set of all hyperfaces is denoted by
![]() $S_d$
. Given
$S_d$
. Given
![]() $s\in S_d$
, the set of all hyperfaces that are subsets of s is denoted by
$s\in S_d$
, the set of all hyperfaces that are subsets of s is denoted by
![]() $S_d(s)$
.
$S_d(s)$
.
We develop two different sets of notation to refer to individual hyperfaces. For the first notation, whenever
![]() $p,u\in \{-1,0\}^d$
are orthogonal (in other words,
$p,u\in \{-1,0\}^d$
are orthogonal (in other words,
![]() $p[i]=u[i]=-1$
cannot happen for any
$p[i]=u[i]=-1$
cannot happen for any
![]() $1\leq i\leq d$
), we say that the hyperface at p along u is
$1\leq i\leq d$
), we say that the hyperface at p along u is
For the second notation, let
For any
![]() $(v_1,v_2)\in V_d$
, the minimal k-dimensional hyperface of
$(v_1,v_2)\in V_d$
, the minimal k-dimensional hyperface of
![]() $[-1,0]^d$
containing both
$[-1,0]^d$
containing both
![]() $v_1$
and
$v_1$
and
![]() $v_2$
is
$v_2$
is
![]() ${\mathrm {faceAt}}(v_1,v_2-v_1)$
, where k is the number of ones in
${\mathrm {faceAt}}(v_1,v_2-v_1)$
, where k is the number of ones in
![]() $v_1-v_2$
. This gives a one-to-one correspondence between
$v_1-v_2$
. This gives a one-to-one correspondence between
![]() $V_d$
and
$V_d$
and
![]() $S_d$
.
$S_d$
.
Let
![]() $n\in \mathbb {Z}_+^d$
. To any
$n\in \mathbb {Z}_+^d$
. To any
![]() $a\in \Sigma _N$
with
$a\in \Sigma _N$
with
![]() $N=\prod _{i=1}^d n[i]$
, we will associate a d-dimensional Wang hypercube, a so-called multiplication cube
$N=\prod _{i=1}^d n[i]$
, we will associate a d-dimensional Wang hypercube, a so-called multiplication cube
![]() ${\mathrm {cube}}_{n}(a)$
, whose underlying structure is that of a function:
${\mathrm {cube}}_{n}(a)$
, whose underlying structure is that of a function:
The interpretation is that
![]() ${\mathrm {cube}}_{n}(a)[v_1,v_2]$
is the label of the hyperface spanned by the vectors
${\mathrm {cube}}_{n}(a)[v_1,v_2]$
is the label of the hyperface spanned by the vectors
![]() $v_1$
and
$v_1$
and
![]() $v_2$
: this way, we get labels on all lower-dimensional hyperfaces. If
$v_2$
: this way, we get labels on all lower-dimensional hyperfaces. If
![]() $s\in S_d$
is the hyperface spanned by
$s\in S_d$
is the hyperface spanned by
![]() $v_1$
and
$v_1$
and
![]() $v_2$
, we may also define
$v_2$
, we may also define
![]() $s({\mathrm {cube}}_{n}(a))=s\ {\mathrm {cube}}_n(a)={\mathrm {cube}}_{n}(a)[v_1,v_2]$
. In particular, the labels of the bottom and top hyperfaces of
$s({\mathrm {cube}}_{n}(a))=s\ {\mathrm {cube}}_n(a)={\mathrm {cube}}_{n}(a)[v_1,v_2]$
. In particular, the labels of the bottom and top hyperfaces of
![]() ${\mathrm {cube}}_{n}(a)$
orthogonal to
${\mathrm {cube}}_{n}(a)$
orthogonal to
![]() $e_i$
are
$e_i$
are
respectively. To write this out more explicitly, let
![]() $a=a_1n[i]+a_0$
be such that
$a=a_1n[i]+a_0$
be such that
![]() ${\mathrm {base}}(a,(N,n[i]))=(0,a_1,a_0)$
and let
${\mathrm {base}}(a,(N,n[i]))=(0,a_1,a_0)$
and let
![]() $a=a_2'\prod _{j\neq i}n[j]+a_1'$
be such that
$a=a_2'\prod _{j\neq i}n[j]+a_1'$
be such that
![]() ${\mathrm {base}}(a, (\prod _{j\neq i}n[i],1))=(a_2',a_1',0)$
. Then we see that
${\mathrm {base}}(a, (\prod _{j\neq i}n[i],1))=(a_2',a_1',0)$
. Then we see that
An example of a three-dimensional multiplication cube together with (some of) the labels of faces and edges is presented in Figure 2.

Figure 2 The multiplication cube
![]() ${\mathrm {cube}}_{(2,3,5)}(10)$
with the faces
${\mathrm {cube}}_{(2,3,5)}(10)$
with the faces
![]() ${\mathrm {\tau }}_1$
(right),
${\mathrm {\tau }}_1$
(right),
![]() ${\mathrm {\beta }}_2$
(front), and
${\mathrm {\beta }}_2$
(front), and
![]() ${\mathrm {\tau }}_3$
(top) visible. One can also verify that these faces and their adjacent edges yield the lower-dimensional multiplication cubes
${\mathrm {\tau }}_3$
(top) visible. One can also verify that these faces and their adjacent edges yield the lower-dimensional multiplication cubes
![]() ${\mathrm {cube}}_{(3,5)}(10)$
,
${\mathrm {cube}}_{(3,5)}(10)$
,
![]() ${\mathrm {cube}}_{(2,5)}(3)$
, and
${\mathrm {cube}}_{(2,5)}(3)$
, and
![]() ${\mathrm {cube}}_{(2,3)}(4)$
.
${\mathrm {cube}}_{(2,3)}(4)$
.
For
![]() $n\in \mathbb {Z}_+^d$
and
$n\in \mathbb {Z}_+^d$
and
![]() $N=\prod _{i=1}^d n[i]$
, the set of base-n multiplication cubes and the valuations of cubes are defined as
$N=\prod _{i=1}^d n[i]$
, the set of base-n multiplication cubes and the valuations of cubes are defined as
In other words,
![]() ${\mathrm {val}}_{n}(t)$
is the label of the unique d-dimensional hyperface of t. More importantly, this also equals the original value that was used to form the hypercube and the maps
${\mathrm {val}}_{n}(t)$
is the label of the unique d-dimensional hyperface of t. More importantly, this also equals the original value that was used to form the hypercube and the maps
![]() ${\mathrm {val}}_{n}$
,
${\mathrm {val}}_{n}$
,
![]() ${\mathrm {cube}}_{n}$
are inverses of each other, because
${\mathrm {cube}}_{n}$
are inverses of each other, because
![]() $a=0\cdot N+a\cdot 1+0\cdot 1$
and
$a=0\cdot N+a\cdot 1+0\cdot 1$
and
![]() ${\mathrm {base}}(a,(N,1))=(0,a,0)$
for any
${\mathrm {base}}(a,(N,1))=(0,a,0)$
for any
![]() $a\in \Sigma _N$
, and therefore
$a\in \Sigma _N$
, and therefore
The set of valid tilings over
![]() $T_n$
is denoted by
$T_n$
is denoted by
![]() $X_n=X_{T_n}$
.
$X_n=X_{T_n}$
.
Later we will see that calling the elements of
![]() $T_n$
multiplication cubes is justified. If a tiling contains a base-N representation of a real number on its main diagonal, then shifting the tiling by
$T_n$
multiplication cubes is justified. If a tiling contains a base-N representation of a real number on its main diagonal, then shifting the tiling by
![]() $\sigma _{e_i}$
corresponds to multiplying this real number by
$\sigma _{e_i}$
corresponds to multiplying this real number by
![]() $n[i]$
as will be seen in Proposition 4.26. The tilings will also be connected to so-called multiplication automata in §5.2.
$n[i]$
as will be seen in Proposition 4.26. The tilings will also be connected to so-called multiplication automata in §5.2.
We observe that in the one-dimensional case
![]() $n=(N)$
, the labels of top and bottom hyperfaces satisfy
$n=(N)$
, the labels of top and bottom hyperfaces satisfy
![]() ${\mathrm {\beta }}_1({\mathrm {cube}}_{(N)}(a))={\mathrm {\tau }}_1({\mathrm {cube}}_{(N)}(a))=0$
for all
${\mathrm {\beta }}_1({\mathrm {cube}}_{(N)}(a))={\mathrm {\tau }}_1({\mathrm {cube}}_{(N)}(a))=0$
for all
![]() $a\in \Sigma _N$
and therefore
$a\in \Sigma _N$
and therefore
![]() $X_{(N)}=T_{(N)}^{\mathbb {Z}}$
. For a higher dimensional example, Figure 1 shows the tile set
$X_{(N)}=T_{(N)}^{\mathbb {Z}}$
. For a higher dimensional example, Figure 1 shows the tile set
![]() $T_{(2,5)}$
and a part of a tiling from
$T_{(2,5)}$
and a part of a tiling from
![]() $X_{(2,5)}$
. In the higher dimensional cases, it is not necessarily obvious that there exist any valid tilings except the trivial one consisting only of copies of
$X_{(2,5)}$
. In the higher dimensional cases, it is not necessarily obvious that there exist any valid tilings except the trivial one consisting only of copies of
![]() ${\mathrm {cube}}_n(0)$
, but in Corollary 4.39, we will see that any arrangement of multiplication cubes on the main diagonal of the d-dimensional space can be extended to a valid tessellation of the whole space.
${\mathrm {cube}}_n(0)$
, but in Corollary 4.39, we will see that any arrangement of multiplication cubes on the main diagonal of the d-dimensional space can be extended to a valid tessellation of the whole space.
Lemma 4.2. Let
![]() $n\in \mathbb {Z}_+^d$
. For a d-directive sequence
$n\in \mathbb {Z}_+^d$
. For a d-directive sequence
![]() $(v_j)_{j=1}^k$
and
$(v_j)_{j=1}^k$
and
![]() $a\in \mathbb {N}$
, it holds that
$a\in \mathbb {N}$
, it holds that
 $$ \begin{align*}{\mathrm{base}}_{n}(a,(v_1,v_k))[2]=\sum_{i=1}^{k-1}m(n,v_{i}-v_1)\ {\mathrm{base}}_{n}(a,(v_i,v_{i+1}))[2].\end{align*} $$
$$ \begin{align*}{\mathrm{base}}_{n}(a,(v_1,v_k))[2]=\sum_{i=1}^{k-1}m(n,v_{i}-v_1)\ {\mathrm{base}}_{n}(a,(v_i,v_{i+1}))[2].\end{align*} $$
Proof. The cases
![]() $k\leq 2$
are trivial. If
$k\leq 2$
are trivial. If
![]() $k\geq 3$
, let
$k\geq 3$
, let
![]() $(a_0',a_1',a_k')={\mathrm {base}}_{n}(a,(v_1,v_k))$
and
$(a_0',a_1',a_k')={\mathrm {base}}_{n}(a,(v_1,v_k))$
and
![]() $(a_j)_{j=0}^k={\mathrm {base}}_{n}(a,(v_j)_{j=1}^k)$
. It follows that
$(a_j)_{j=0}^k={\mathrm {base}}_{n}(a,(v_j)_{j=1}^k)$
. It follows that
 $$ \begin{align*} a_0'+a_1'm(n,v_1)+a_k'm(n,v_k)=a=\sum_{i=0}^k a_i m(n,v_i) \end{align*} $$
$$ \begin{align*} a_0'+a_1'm(n,v_1)+a_k'm(n,v_k)=a=\sum_{i=0}^k a_i m(n,v_i) \end{align*} $$
(with the convention that
![]() $v_0={\mathbf {0}}$
). From Lemma 3.4, we see that
$v_0={\mathbf {0}}$
). From Lemma 3.4, we see that
The first part of Lemma 3.4 shows that
![]() $a_0=a_0'$
and the last part of Lemma 3.4 shows that
$a_0=a_0'$
and the last part of Lemma 3.4 shows that
![]() $a_k=a_k'$
, so
$a_k=a_k'$
, so
 $$ \begin{align*} a_1'=\sum_{i=1}^{k-1}a_i m(n,v_i)/m(n,v_1)=\sum_{i=1}^{k-1}m(n,v_i-v_1)\ {\mathrm{base}}_{n}(a,(v_i,v_{i+1}))[2]. \end{align*} $$
$$ \begin{align*} a_1'=\sum_{i=1}^{k-1}a_i m(n,v_i)/m(n,v_1)=\sum_{i=1}^{k-1}m(n,v_i-v_1)\ {\mathrm{base}}_{n}(a,(v_i,v_{i+1}))[2]. \end{align*} $$
Lemma 4.3. Let
![]() $n\in \mathbb {Z}_+^d$
. For a binary d-directive sequence
$n\in \mathbb {Z}_+^d$
. For a binary d-directive sequence
![]() $(v_i)_{i=1}^k$
and
$(v_i)_{i=1}^k$
and
![]() $t\in T_{n}$
, it holds that
$t\in T_{n}$
, it holds that
 $$ \begin{align*}m(n,v_1)t[v_1,v_k]=\sum_{j=1}^{k-1}m(n,v_j)t[v_j,v_{j+1}].\end{align*} $$
$$ \begin{align*}m(n,v_1)t[v_1,v_k]=\sum_{j=1}^{k-1}m(n,v_j)t[v_j,v_{j+1}].\end{align*} $$
Proof. Let
![]() $t={\mathrm {cube}}_{n}(a)$
. We rewrite the statement of the lemma
$t={\mathrm {cube}}_{n}(a)$
. We rewrite the statement of the lemma
 $$ \begin{align*} &m(n,v_1){\mathrm{cube}}_{n}(a)[v_1,v_k]=\sum_{j=1}^{k-1}m(n,v_j)\ {\mathrm{cube}}_{n}(a)[v_j,v_{j+1}] \\ &\quad \iff m(n,v_1)\ {\mathrm{base}}_{n}(a,(v_1,v_k))[2]=\sum_{j=1}^{k-1}m(n,v_j)\ {\mathrm{base}}_{n}(a,(v_j,v_{j+1}))[2] \\ &\quad\iff {\mathrm{base}}_{n}(a,(v_1,v_k))[2]=\sum_{j=1}^{k-1}m(n,v_j-v_1)\ {\mathrm{base}}_{n}(a,(v_j,v_{j+1}))[2], \end{align*} $$
$$ \begin{align*} &m(n,v_1){\mathrm{cube}}_{n}(a)[v_1,v_k]=\sum_{j=1}^{k-1}m(n,v_j)\ {\mathrm{cube}}_{n}(a)[v_j,v_{j+1}] \\ &\quad \iff m(n,v_1)\ {\mathrm{base}}_{n}(a,(v_1,v_k))[2]=\sum_{j=1}^{k-1}m(n,v_j)\ {\mathrm{base}}_{n}(a,(v_j,v_{j+1}))[2] \\ &\quad\iff {\mathrm{base}}_{n}(a,(v_1,v_k))[2]=\sum_{j=1}^{k-1}m(n,v_j-v_1)\ {\mathrm{base}}_{n}(a,(v_j,v_{j+1}))[2], \end{align*} $$
and the last equality holds by Lemma 4.2.
4.2. Lower dimensional matchings in tilings by multiplication cubes
Throughout this subsection, let
![]() $n\in \mathbb {Z}_+^d$
. The
$n\in \mathbb {Z}_+^d$
. The
![]() $(d-1)$
-dimensional hyperfaces match in a tessellation of
$(d-1)$
-dimensional hyperfaces match in a tessellation of
![]() $X_{n}$
by definition, but there are also lower dimensional matchings as we will see in Theorem 4.6.
$X_{n}$
by definition, but there are also lower dimensional matchings as we will see in Theorem 4.6.
Recall that any
![]() $s\in S_d$
can be represented in the form
$s\in S_d$
can be represented in the form
![]() $s={\mathrm {faceAt}}(p,u)$
for some orthogonal
$s={\mathrm {faceAt}}(p,u)$
for some orthogonal
![]() $p,u\in \{-1,0\}^d$
. If u contains
$p,u\in \{-1,0\}^d$
. If u contains
![]() $d'$
non-zeroes and
$d'$
non-zeroes and
![]() ${\mathrm {{\iota }}}:\{1,\ldots ,d'\}\to \{1,\ldots ,d\}$
is an injection with the image set
${\mathrm {{\iota }}}:\{1,\ldots ,d'\}\to \{1,\ldots ,d\}$
is an injection with the image set
![]() $\{i\mid u[i]=-1\}$
, then the injective affine map
$\{i\mid u[i]=-1\}$
, then the injective affine map
![]() ${\mathrm {I}}_{p,{\mathrm {{\iota }}}}:\mathbb {R}^{d'}\to \mathbb {R}^d$
defined by
${\mathrm {I}}_{p,{\mathrm {{\iota }}}}:\mathbb {R}^{d'}\to \mathbb {R}^d$
defined by
![]() ${\mathrm {I}}_{p,{\mathrm {{\iota }}}}({\mathbf {0}})=p$
and
${\mathrm {I}}_{p,{\mathrm {{\iota }}}}({\mathbf {0}})=p$
and
![]() ${\mathrm {I}}_{p,{\mathrm {{\iota }}}}(e_i)=p+e_{{\mathrm {{\iota }}}(i)}$
for
${\mathrm {I}}_{p,{\mathrm {{\iota }}}}(e_i)=p+e_{{\mathrm {{\iota }}}(i)}$
for
![]() $1\leq i\leq d'$
satisfies
$1\leq i\leq d'$
satisfies
![]() ${\mathrm {I}}_{p,{\mathrm {{\iota }}}}([-1,0]^{d'})=s$
.
${\mathrm {I}}_{p,{\mathrm {{\iota }}}}([-1,0]^{d'})=s$
.
Lemma 4.4. Let
![]() $s={\mathrm {faceAt}}(p,u)\in S_{d,d'}$
, let
$s={\mathrm {faceAt}}(p,u)\in S_{d,d'}$
, let
![]() $s'\in S_{d'}$
, and let
$s'\in S_{d'}$
, and let
![]() $t\in T_{n}$
. Let
$t\in T_{n}$
. Let
![]() ${\mathrm {{\iota }}}:\{1,\ldots ,d'\} \to \{1,\ldots ,d\}$
be an injection with the image set
${\mathrm {{\iota }}}:\{1,\ldots ,d'\} \to \{1,\ldots ,d\}$
be an injection with the image set
![]() $D=\{i\mid u[i]=-1\}$
and let
$D=\{i\mid u[i]=-1\}$
and let
![]() $n'\in \mathbb {Z}_+^{d'}$
be defined by
$n'\in \mathbb {Z}_+^{d'}$
be defined by
![]() $n'[i]=n[{\mathrm {{\iota }}}(i)]$
for
$n'[i]=n[{\mathrm {{\iota }}}(i)]$
for
![]() $1\leq i\leq d'$
. Then
$1\leq i\leq d'$
. Then
![]() $({\mathrm {I}}_{p,{\mathrm {{\iota }}}}(s'))(t)=s'({\mathrm {cube}}_{n'}(s(t)))$
.
$({\mathrm {I}}_{p,{\mathrm {{\iota }}}}(s'))(t)=s'({\mathrm {cube}}_{n'}(s(t)))$
.
Proof. Let
![]() $p',u'\in \{-1,0\}^{d'}$
and let
$p',u'\in \{-1,0\}^{d'}$
and let
![]() $a\in \mathbb {N}$
be such that
$a\in \mathbb {N}$
be such that
![]() $s'={\mathrm {faceAt}}(p',u')$
and
$s'={\mathrm {faceAt}}(p',u')$
and
![]() $t={\mathrm {cube}}_{n}(a)$
(it follows that
$t={\mathrm {cube}}_{n}(a)$
(it follows that
![]() ${\mathrm {I}}_{p,{\mathrm {{\iota }}}}(p')\leq {\mathrm {I}}_{p,{\mathrm {{\iota }}}}({\mathbf {0}})$
and
${\mathrm {I}}_{p,{\mathrm {{\iota }}}}(p')\leq {\mathrm {I}}_{p,{\mathrm {{\iota }}}}({\mathbf {0}})$
and
![]() ${\mathrm {I}}_{p,{\mathrm {{\iota }}}}(p'+u')\geq {\mathrm {I}}_{p,{\mathrm {{\iota }}}}(-{\mathbf {1}})$
). Let
${\mathrm {I}}_{p,{\mathrm {{\iota }}}}(p'+u')\geq {\mathrm {I}}_{p,{\mathrm {{\iota }}}}(-{\mathbf {1}})$
). Let
![]() $(a_0,a_1,a_2)\hspace{-1pt}=\hspace{-1pt}{\mathrm {base}}_{n}(a,({\mathrm {I}}_{p,{\mathrm {{\iota }}}}({\mathbf {0}}),{\mathrm {I}}_{p,{\mathrm {{\iota }}}}(-{\mathbf {1}})))$
and
$(a_0,a_1,a_2)\hspace{-1pt}=\hspace{-1pt}{\mathrm {base}}_{n}(a,({\mathrm {I}}_{p,{\mathrm {{\iota }}}}({\mathbf {0}}),{\mathrm {I}}_{p,{\mathrm {{\iota }}}}(-{\mathbf {1}})))$
and
![]() $(b_0,b_1,b_2)\hspace{-1pt}=\hspace{-1pt}{\mathrm {base}}_{n}(a_1,({\mathrm {I}}_{p,{\mathrm {{\iota }}}}(p')- {\mathrm {I}}_{p,{\mathrm {{\iota }}}}({\mathbf {0}}), {\mathrm {I}}_{p,{\mathrm {{\iota }}}}(p'+u')-{\mathrm {I}}_{p,{\mathrm {{\iota }}}}({\mathbf {0}}))$
. Then by Lemma 3.3,
$(b_0,b_1,b_2)\hspace{-1pt}=\hspace{-1pt}{\mathrm {base}}_{n}(a_1,({\mathrm {I}}_{p,{\mathrm {{\iota }}}}(p')- {\mathrm {I}}_{p,{\mathrm {{\iota }}}}({\mathbf {0}}), {\mathrm {I}}_{p,{\mathrm {{\iota }}}}(p'+u')-{\mathrm {I}}_{p,{\mathrm {{\iota }}}}({\mathbf {0}}))$
. Then by Lemma 3.3,
From this, we can see that
 $$ \begin{align*} &({\mathrm{I}}_{p,{\mathrm{{\iota}}}}(s'))(t)=t[{\mathrm{I}}_{p,{\mathrm{{\iota}}}}(p'), {\mathrm{I}}_{p,{\mathrm{{\iota}}}}(p'+u')]={\mathrm{base}}_{n}(a,({\mathrm{I}}_{p,{\mathrm{{\iota}}}}(p'),{\mathrm{I}}_{p,{\mathrm{{\iota}}}}(p'+u')))[2] \\ &\quad \overset{L.~{3.4}}{=}{\mathrm{base}}_{n} (a,({\mathrm{I}}_{p,{\mathrm{{\iota}}}}({\mathbf{0}}),{\mathrm{I}}_{p,{\mathrm{{\iota}}}}(p'),{\mathrm{I}}_{p,{\mathrm{{\iota}}}}(p'+u'),{\mathrm{I}}_{p,{\mathrm{{\iota}}}}({\mathbf{-1}})))[3]=b_1. \end{align*} $$
$$ \begin{align*} &({\mathrm{I}}_{p,{\mathrm{{\iota}}}}(s'))(t)=t[{\mathrm{I}}_{p,{\mathrm{{\iota}}}}(p'), {\mathrm{I}}_{p,{\mathrm{{\iota}}}}(p'+u')]={\mathrm{base}}_{n}(a,({\mathrm{I}}_{p,{\mathrm{{\iota}}}}(p'),{\mathrm{I}}_{p,{\mathrm{{\iota}}}}(p'+u')))[2] \\ &\quad \overset{L.~{3.4}}{=}{\mathrm{base}}_{n} (a,({\mathrm{I}}_{p,{\mathrm{{\iota}}}}({\mathbf{0}}),{\mathrm{I}}_{p,{\mathrm{{\iota}}}}(p'),{\mathrm{I}}_{p,{\mathrm{{\iota}}}}(p'+u'),{\mathrm{I}}_{p,{\mathrm{{\iota}}}}({\mathbf{-1}})))[3]=b_1. \end{align*} $$
On the other hand,
and
 $$ \begin{align*} s'({\mathrm{cube}}_{n'}(s(t)))&={\mathrm{cube}}_{n'}(s(t))[p',p'+u']={\mathrm{base}}_{n'}(s(t),(p',p'+u'))[2] \\ &={\mathrm{base}}_{n'}(a_1,(p',p'+u'))[2] \\ & \overset{L.~{3.6}}{=}{\mathrm{base}}_{n} (a_1,({\mathrm{I}}_{{\mathbf{0}},{\mathrm{{\iota}}}}(p'),{\mathrm{I}}_{{\mathbf{0}},{\mathrm{{\iota}}}}(p'+u')))[2]=b_1. \end{align*} $$
$$ \begin{align*} s'({\mathrm{cube}}_{n'}(s(t)))&={\mathrm{cube}}_{n'}(s(t))[p',p'+u']={\mathrm{base}}_{n'}(s(t),(p',p'+u'))[2] \\ &={\mathrm{base}}_{n'}(a_1,(p',p'+u'))[2] \\ & \overset{L.~{3.6}}{=}{\mathrm{base}}_{n} (a_1,({\mathrm{I}}_{{\mathbf{0}},{\mathrm{{\iota}}}}(p'),{\mathrm{I}}_{{\mathbf{0}},{\mathrm{{\iota}}}}(p'+u')))[2]=b_1. \end{align*} $$
We conclude that
Lemma 4.5. Let
![]() $s_1,s_2\in S_d$
, let
$s_1,s_2\in S_d$
, let
![]() $u\in \mathbb {Z}^d$
be such that
$u\in \mathbb {Z}^d$
be such that
![]() $s_2=s_1+u$
, and let
$s_2=s_1+u$
, and let
![]() $t_1,t_2\in T_{n}$
be such that
$t_1,t_2\in T_{n}$
be such that
![]() $s_1(t_1)=s_2(t_2)$
. Then for any
$s_1(t_1)=s_2(t_2)$
. Then for any
![]() $s_1'\in S_d(s_1)$
and
$s_1'\in S_d(s_1)$
and
![]() $s_2'=s_1'+u\in S_d(s_2)$
, it holds that
$s_2'=s_1'+u\in S_d(s_2)$
, it holds that
![]() $s_1'(t_1)=s_2'(t_2)$
.
$s_1'(t_1)=s_2'(t_2)$
.
Proof. Let
![]() $p,v\in \{-1,0\}^{d}$
be such that
$p,v\in \{-1,0\}^{d}$
be such that
![]() $s_1={\mathrm {faceAt}}(p,v)$
, which means that
$s_1={\mathrm {faceAt}}(p,v)$
, which means that
![]() $s_2={\mathrm {faceAt}}(p+u,v)$
. Assume that the cardinality of
$s_2={\mathrm {faceAt}}(p+u,v)$
. Assume that the cardinality of
![]() $D=\{i\mid v[i]=-1\}$
is
$D=\{i\mid v[i]=-1\}$
is
![]() $d'$
and let
$d'$
and let
![]() $\iota :\{1,\ldots ,d'\}\to \{1,\ldots ,d\}$
be an injection with image D. Let
$\iota :\{1,\ldots ,d'\}\to \{1,\ldots ,d\}$
be an injection with image D. Let
![]() $n'\in \mathbb {Z}_+^{d'}$
be defined by
$n'\in \mathbb {Z}_+^{d'}$
be defined by
![]() $n'[i]=n[{\mathrm {{\iota }}}(i)]$
for
$n'[i]=n[{\mathrm {{\iota }}}(i)]$
for
![]() $1\leq i\leq d'$
. Let
$1\leq i\leq d'$
. Let
![]() $s'\in S_{d'}$
be such that
$s'\in S_{d'}$
be such that
![]() ${\mathrm {I}}_{p,{\mathrm {{\iota }}}}(s')=s_1'$
, which means that
${\mathrm {I}}_{p,{\mathrm {{\iota }}}}(s')=s_1'$
, which means that
![]() ${\mathrm {I}}_{p+u,{\mathrm {{\iota }}}}(s')=s_2'$
. By Lemma 4.4,
${\mathrm {I}}_{p+u,{\mathrm {{\iota }}}}(s')=s_2'$
. By Lemma 4.4,
 $$ \begin{align*} s_1'(t_1)&={\mathrm{I}}_{p,{\mathrm{{\iota}}}}(s')(t_1)=s'({\mathrm{cube}}_{n'}(s_1(t_1))) \\ &=s'({\mathrm{cube}}_{n'}(s_2(t_2)))={\mathrm{I}}_{p+u,{\mathrm{{\iota}}}}(s')(t_2)=s_2'(t_2). \end{align*} $$
$$ \begin{align*} s_1'(t_1)&={\mathrm{I}}_{p,{\mathrm{{\iota}}}}(s')(t_1)=s'({\mathrm{cube}}_{n'}(s_1(t_1))) \\ &=s'({\mathrm{cube}}_{n'}(s_2(t_2)))={\mathrm{I}}_{p+u,{\mathrm{{\iota}}}}(s')(t_2)=s_2'(t_2). \end{align*} $$
Theorem 4.6. Let
![]() $f\in X_{n}$
and let
$f\in X_{n}$
and let
![]() $s,s+v\in S_d$
for some
$s,s+v\in S_d$
for some
![]() $v\in \mathbb {Z}^d$
. For any
$v\in \mathbb {Z}^d$
. For any
![]() $z\in \mathbb {Z}^d$
, it holds that
$z\in \mathbb {Z}^d$
, it holds that
![]() $(s+v)(f[z])=s(f[z+v])$
.
$(s+v)(f[z])=s(f[z+v])$
.
Proof. Since v is a sum of vectors in the standard basis, the claim follows by induction if we show that
![]() $(s+e_i)(f[z])=s(f[z+e_i])$
for
$(s+e_i)(f[z])=s(f[z+e_i])$
for
![]() $1\leq i\leq d$
such that
$1\leq i\leq d$
such that
![]() $s,s+e_i\in S_d$
. We know that
$s,s+e_i\in S_d$
. We know that
![]() $s+e_i\in S_d({\mathrm {\tau }}_i)$
and
$s+e_i\in S_d({\mathrm {\tau }}_i)$
and
![]() $s\in S_d({\mathrm {\beta }}_i)$
. From
$s\in S_d({\mathrm {\beta }}_i)$
. From
![]() $f\in X_{n}$
, it follows that
$f\in X_{n}$
, it follows that
![]() ${\mathrm {\tau }}_i(f[z])={\mathrm {\beta }}_i(f[z+e_i])$
and Lemma 4.5 implies that
${\mathrm {\tau }}_i(f[z])={\mathrm {\beta }}_i(f[z+e_i])$
and Lemma 4.5 implies that
![]() $(s+e_i)(f[z])=s(f[z+e_i])$
.
$(s+e_i)(f[z])=s(f[z+e_i])$
.
The results of this section allow us to speak of values on edges in a tiling without referring to individual cubes. To be more precise, we imagine
![]() $\mathbb {Z}^d$
to be the vertex set of an infinite directed graph, the d-dimensional grid, having an edge
$\mathbb {Z}^d$
to be the vertex set of an infinite directed graph, the d-dimensional grid, having an edge
![]() $(z-e_i,z)$
(the edge from
$(z-e_i,z)$
(the edge from
![]() $z-e_i$
to z) for every
$z-e_i$
to z) for every
![]() $z\in \mathbb {Z}^d$
and
$z\in \mathbb {Z}^d$
and
![]() $1\leq i\leq d$
. When we consider a tiling
$1\leq i\leq d$
. When we consider a tiling
![]() $f\in X_{n}$
and say that the cube
$f\in X_{n}$
and say that the cube
![]() $f[z]$
is at position
$f[z]$
is at position
![]() $z\in \mathbb {Z}^d$
, we visualize this as the unit cube
$z\in \mathbb {Z}^d$
, we visualize this as the unit cube
![]() $[-1,0]^d$
whose ‘top-right’ corner, the point
$[-1,0]^d$
whose ‘top-right’ corner, the point
![]() ${\mathbf {0}}$
, is positioned at z. Then the edges of the cube
${\mathbf {0}}$
, is positioned at z. Then the edges of the cube
![]() $f[z]$
overlap with some of the edges of the d-dimensional grid: an edge of the form
$f[z]$
overlap with some of the edges of the d-dimensional grid: an edge of the form
![]() $s={\mathrm {faceAt}}(p,-e_i)$
overlaps the directed edge
$s={\mathrm {faceAt}}(p,-e_i)$
overlaps the directed edge
![]() ${D}_z(s)=(z+p-e_i,z+p)$
in the grid. We also define the undirected edge
${D}_z(s)=(z+p-e_i,z+p)$
in the grid. We also define the undirected edge
![]() ${E}_z(s)=\{z+p-e_i,z+p\}$
and the (undirected) label of the undirected edge
${E}_z(s)=\{z+p-e_i,z+p\}$
and the (undirected) label of the undirected edge
![]() ${E}_z(s)$
in the tessellation by
${E}_z(s)$
in the tessellation by
To see that this is well defined, let
![]() $z_1,z_2\in \mathbb {Z}^d$
and
$z_1,z_2\in \mathbb {Z}^d$
and
![]() $s_1={\mathrm {faceAt}}(p_1,-e_i)$
,
$s_1={\mathrm {faceAt}}(p_1,-e_i)$
,
![]() $s_2={\mathrm {faceAt}}(p_2,-e_i)$
be such that
$s_2={\mathrm {faceAt}}(p_2,-e_i)$
be such that
![]() ${E}_{z_1}(s_1)={E}_{z_2}(s_2)$
. Then in particular,
${E}_{z_1}(s_1)={E}_{z_2}(s_2)$
. Then in particular,
![]() $z_1+p_1=z_2+p_2$
and
$z_1+p_1=z_2+p_2$
and
![]() $s_1=s_2+(p_1-p_2)$
. Because of this,
$s_1=s_2+(p_1-p_2)$
. Because of this,
 $$ \begin{align*} &\unicode{x3bb}(f,{E}_{z_1}(s_1))=s_1 f[z_1]=(s_2+(p_1-p_2))f[z_2-(p_1-p_2)] \\ &\quad\overset{T.~{4.6}}{=}s_2 f[z_2]=\unicode{x3bb}(f,{E}_{z_2}(s_2)). \end{align*} $$
$$ \begin{align*} &\unicode{x3bb}(f,{E}_{z_1}(s_1))=s_1 f[z_1]=(s_2+(p_1-p_2))f[z_2-(p_1-p_2)] \\ &\quad\overset{T.~{4.6}}{=}s_2 f[z_2]=\unicode{x3bb}(f,{E}_{z_2}(s_2)). \end{align*} $$
We note that each edge
![]() $\{z-e_i,z\}$
has a label, because
$\{z-e_i,z\}$
has a label, because
![]() ${E}_z({\mathrm {faceAt}}({\mathbf {0}},-e_i))= \{z-e_i,z\}$
. For an example of how a tessellation yields labels on the directed edges, see the left and middle parts of Figure 3 (for the drawn part of the grid, the definition can be applied in the form
${E}_z({\mathrm {faceAt}}({\mathbf {0}},-e_i))= \{z-e_i,z\}$
. For an example of how a tessellation yields labels on the directed edges, see the left and middle parts of Figure 3 (for the drawn part of the grid, the definition can be applied in the form
![]() $\unicode{x3bb} (f,{E}_{{\mathbf {0}}}(s))=sf[{\mathbf {0}}]$
).
$\unicode{x3bb} (f,{E}_{{\mathbf {0}}}(s))=sf[{\mathbf {0}}]$
).

Figure 3 Left: A tessellation with
![]() ${\mathrm {cube}}_{(2,3,5)}(10)$
positioned at the origin in
${\mathrm {cube}}_{(2,3,5)}(10)$
positioned at the origin in
![]() $\mathbb {Z}^3$
. Middle:
$\mathbb {Z}^3$
. Middle:
![]() $\mathbb {Z}^3$
as a directed graph together with labels given by
$\mathbb {Z}^3$
as a directed graph together with labels given by
![]() ${\mathrm {cube}}_{(2,3,5)}(10)$
. Right: The weights
${\mathrm {cube}}_{(2,3,5)}(10)$
. Right: The weights
![]() ${\mathrm {wgt}}_{(2,3,5)}(v)$
of the points
${\mathrm {wgt}}_{(2,3,5)}(v)$
of the points
![]() $v\in \mathbb {Z}^3$
have been added to the grid, the point
$v\in \mathbb {Z}^3$
have been added to the grid, the point
![]() ${\mathbf {0}}$
is at the upper right with
${\mathbf {0}}$
is at the upper right with
![]() ${\mathrm {wgt}}_{(2,3,5)}({\mathbf {0}})=1$
.
${\mathrm {wgt}}_{(2,3,5)}({\mathbf {0}})=1$
.
4.3. Path integrals over tilings
Throughout this subsection, let
![]() $n\in \mathbb {Z}_+^d$
. We assign to every point
$n\in \mathbb {Z}_+^d$
. We assign to every point
![]() $v\in \mathbb {Z}^d$
a weight by
$v\in \mathbb {Z}^d$
a weight by
![]() ${\mathrm {wgt}}_{n}(v)=m(n,v)$
. A path (of length
${\mathrm {wgt}}_{n}(v)=m(n,v)$
. A path (of length
![]() $k-1$
) is a sequence
$k-1$
) is a sequence
![]() $P=(P_i)_{i=1}^k\in (\mathbb {Z}^d)^k$
, where for
$P=(P_i)_{i=1}^k\in (\mathbb {Z}^d)^k$
, where for
![]() $1\leq i< k$
, we have
$1\leq i< k$
, we have
![]() $P_{i+1}-P_i=ae_j$
for some
$P_{i+1}-P_i=ae_j$
for some
![]() $a\in \{-1,1\}$
,
$a\in \{-1,1\}$
,
![]() $1\leq j\leq d$
. For
$1\leq j\leq d$
. For
![]() $1\leq i\leq k-1$
, let
$1\leq i\leq k-1$
, let
![]() $E_P(i)=P_{i+1}-P_i$
. Given a valid tiling
$E_P(i)=P_{i+1}-P_i$
. Given a valid tiling
![]() $f\in X_{n}$
and a pair of vectors
$f\in X_{n}$
and a pair of vectors
![]() $p,p'\in \mathbb {Z}^d$
satisfying
$p,p'\in \mathbb {Z}^d$
satisfying
![]() $p'-p=ae_j$
for some
$p'-p=ae_j$
for some
![]() $a\in \{-1,1\}$
,
$a\in \{-1,1\}$
,
![]() $1\leq j\leq d$
, we denote
$1\leq j\leq d$
, we denote
![]() ${\mathrm {sign}}(p'-p)=a$
and
${\mathrm {sign}}(p'-p)=a$
and
Then the path integral of f over P is
 $$ \begin{align*}Pf=\sum_{i=1}^{k-1} (P_{i},P_{i+1})f.\end{align*} $$
$$ \begin{align*}Pf=\sum_{i=1}^{k-1} (P_{i},P_{i+1})f.\end{align*} $$
See the right part of Figure 3 containing labels given by a tessellation together with the weights of the points. Computing the path integral over a path of length
![]() $1$
consists of looking at the corresponding edge, multiplying its (undirected) label with the weight at its end point (now considered as a directed edge), and possibly multiplying the result by
$1$
consists of looking at the corresponding edge, multiplying its (undirected) label with the weight at its end point (now considered as a directed edge), and possibly multiplying the result by
![]() $-1$
in the case when the direction of the path opposes the direction of the edge.
$-1$
in the case when the direction of the path opposes the direction of the edge.
For
![]() $v\in \mathbb {Z}^d$
, we denote
$v\in \mathbb {Z}^d$
, we denote
![]() $P+v=(P_i+v)_{i=1}^k$
. We prove an equality connecting the integral of a tessellation f over a shifted path
$P+v=(P_i+v)_{i=1}^k$
. We prove an equality connecting the integral of a tessellation f over a shifted path
![]() $P+v$
to the integral of a shifted tessellation
$P+v$
to the integral of a shifted tessellation
![]() $\sigma _v(f)$
over a path P.
$\sigma _v(f)$
over a path P.
Lemma 4.7. For a path P,
![]() $f\kern1.2pt{\in}\kern1.2pt X_{n}$
, and
$f\kern1.2pt{\in}\kern1.2pt X_{n}$
, and
![]() $v\in \mathbb {Z}^d$
, it holds that
$v\in \mathbb {Z}^d$
, it holds that
![]() $(P+v)f={\mathrm {wgt}}_{n}(v)P\sigma _v(f)$
.
$(P+v)f={\mathrm {wgt}}_{n}(v)P\sigma _v(f)$
.
Proof. We denote
![]() $a_i={\mathrm {sign}}((P_{i+1}+v)-(P_i+v))={\mathrm {sign}}(P_{i+1}-P_i)$
and directly compute that
$a_i={\mathrm {sign}}((P_{i+1}+v)-(P_i+v))={\mathrm {sign}}(P_{i+1}-P_i)$
and directly compute that
 $$ \begin{align*} (P+v)f&=\sum_{i=1}^{k-1}a_i\ {\mathrm{wgt}}_{n}(\max\{P_i+v,P_{i+1}+v\})\unicode{x3bb}(f,\{P_i+v,P_{i+1}+v\})\\ &=\sum_{i=1}^{k-1}a_i\ {\mathrm{wgt}}_{n}(v)\ {\mathrm{wgt}}_{n}(\max\{P_i,P_{i+1}\})\unicode{x3bb}(\sigma_v(f),\{P_i,P_{i+1}\}) \\ &={\mathrm{wgt}}(v)P\sigma_v(f). \end{align*} $$
$$ \begin{align*} (P+v)f&=\sum_{i=1}^{k-1}a_i\ {\mathrm{wgt}}_{n}(\max\{P_i+v,P_{i+1}+v\})\unicode{x3bb}(f,\{P_i+v,P_{i+1}+v\})\\ &=\sum_{i=1}^{k-1}a_i\ {\mathrm{wgt}}_{n}(v)\ {\mathrm{wgt}}_{n}(\max\{P_i,P_{i+1}\})\unicode{x3bb}(\sigma_v(f),\{P_i,P_{i+1}\}) \\ &={\mathrm{wgt}}(v)P\sigma_v(f). \end{align*} $$
Next we note a simple cancellation property.
Lemma 4.8. Let
![]() $f\in X_{n}$
and let
$f\in X_{n}$
and let
![]() $p,p'\in \mathbb {Z}^d$
satisfy
$p,p'\in \mathbb {Z}^d$
satisfy
![]() $p'-p=ae_i$
for some
$p'-p=ae_i$
for some
![]() $a\in \{-1,1\}$
,
$a\in \{-1,1\}$
,
![]() $1\leq i\leq d$
. Then
$1\leq i\leq d$
. Then
![]() $(p,p')f+(p',p)f=0$
.
$(p,p')f+(p',p)f=0$
.
Proof. We may compute
 $$ \begin{align*} &(p,p')f+(p',p)f \\ &\quad =a\ {\mathrm{wgt}}_{n}(\max\{p,p'\})\unicode{x3bb}(f,\{p,p'\})-a\ {\mathrm{wgt}}_{n}(\max\{p',p\})\unicode{x3bb}(f,\{p',p\})=0.\qquad \end{align*} $$
$$ \begin{align*} &(p,p')f+(p',p)f \\ &\quad =a\ {\mathrm{wgt}}_{n}(\max\{p,p'\})\unicode{x3bb}(f,\{p,p'\})-a\ {\mathrm{wgt}}_{n}(\max\{p',p\})\unicode{x3bb}(f,\{p',p\})=0.\qquad \end{align*} $$
In the following lemma, we will show that the path integral over two consecutive edges around a square is equal to the path integral over the other two consecutive edges of the same square, see Figure 4. This may also be tested on the concrete examples of labels and weights in Figure 3.

Figure 4 Let P,
![]() $P'$
be the two paths between two opposite corners of a square. The path integrals of a tessellation f over P and
$P'$
be the two paths between two opposite corners of a square. The path integrals of a tessellation f over P and
![]() $P'$
are equal.
$P'$
are equal.
Lemma 4.9. Let
![]() $f\in X_{n}$
and let
$f\in X_{n}$
and let
![]() $p_0,p_1,p_2\in \mathbb {Z}^d$
satisfy
$p_0,p_1,p_2\in \mathbb {Z}^d$
satisfy
![]() $p_1-p_0=a_1e_{i_1}$
and
$p_1-p_0=a_1e_{i_1}$
and
![]() $p_2-p_1=a_2e_{i_2}$
for some
$p_2-p_1=a_2e_{i_2}$
for some
![]() $a_1,a_2\in \{-1,1\}$
and
$a_1,a_2\in \{-1,1\}$
and
![]() $1\leq i_1\neq i_2\leq d$
. If
$1\leq i_1\neq i_2\leq d$
. If
![]() $p_1'=p_0+(p_2-p_1)$
, then
$p_1'=p_0+(p_2-p_1)$
, then
![]() $(p_0,p_1')f$
and
$(p_0,p_1')f$
and
![]() $(p_1',p_2)f$
are defined, and
$(p_1',p_2)f$
are defined, and
![]() $(p_0,p_1)f+(p_1,p_2)f=(p_0,p_1')f+(p_1',p_2)f$
.
$(p_0,p_1)f+(p_1,p_2)f=(p_0,p_1')f+(p_1',p_2)f$
.
Proof. We first note that
![]() $p_1'-p_0=p_2-p_1=a_2e_{i_2}$
and
$p_1'-p_0=p_2-p_1=a_2e_{i_2}$
and
![]() $p_2-p_1'=p_1-p_0=a_1e_{i_1}$
. Therefore,
$p_2-p_1'=p_1-p_0=a_1e_{i_1}$
. Therefore,
![]() $(p_0,p_1')f$
and
$(p_0,p_1')f$
and
![]() $(p_1'+p_2)f$
are defined. To prove the lemma, it is sufficient to consider the case
$(p_1'+p_2)f$
are defined. To prove the lemma, it is sufficient to consider the case
![]() $a_1=a_2=1$
(the case in Figure 4). To see this, we show how to reduce the other cases to this one.
$a_1=a_2=1$
(the case in Figure 4). To see this, we show how to reduce the other cases to this one.
Case 1:
![]() $a_1=1, a_2=-1$
. Let
$a_1=1, a_2=-1$
. Let
![]() $q_0=p_1'$
,
$q_0=p_1'$
,
![]() $q_1=p_2$
,
$q_1=p_2$
,
![]() $q_2=p_1$
, and
$q_2=p_1$
, and
![]() $q_1'=q_0+(q_2-q_1)= p_1'+(p_1-p_2)=p_0$
. Then
$q_1'=q_0+(q_2-q_1)= p_1'+(p_1-p_2)=p_0$
. Then
![]() $q_1-q_0=p_2-p_1'=a_1e_{i_1}$
,
$q_1-q_0=p_2-p_1'=a_1e_{i_1}$
,
![]() $q_2-q_1=p_1-p_2=(-a_2)e_{i_2}$
and
$q_2-q_1=p_1-p_2=(-a_2)e_{i_2}$
and
 $$ \begin{align*} &(p_0,p_1)f+(p_1,p_2)f=(p_0,p_1')f+(p_1',p_2)f \\ &\quad \iff (q_1',q_2)f+(q_2,q_1)f=(q_1',q_0)f+(q_0,q_1)f \\ &\quad \overset{L.~{4.8}}{\iff}\hspace{-2pt} (q_0,q_1')f+(q_1',q_2)f=(q_0,q_1)f+(q_1,q_2)f. \end{align*} $$
$$ \begin{align*} &(p_0,p_1)f+(p_1,p_2)f=(p_0,p_1')f+(p_1',p_2)f \\ &\quad \iff (q_1',q_2)f+(q_2,q_1)f=(q_1',q_0)f+(q_0,q_1)f \\ &\quad \overset{L.~{4.8}}{\iff}\hspace{-2pt} (q_0,q_1')f+(q_1',q_2)f=(q_0,q_1)f+(q_1,q_2)f. \end{align*} $$
Case 2:
![]() $a_1=-1,a_2=1$
. Let
$a_1=-1,a_2=1$
. Let
![]() $q_0=p_1$
,
$q_0=p_1$
,
![]() $q_1=p_0$
,
$q_1=p_0$
,
![]() $q_2=p_1'$
, and
$q_2=p_1'$
, and
![]() $q_1'=q_0+(q_2-q_1)= p_1+(p_1'-p_0)=p_2$
. Then
$q_1'=q_0+(q_2-q_1)= p_1+(p_1'-p_0)=p_2$
. Then
![]() $q_1-q_0=p_0-p_1=(-a_1)e_{i_1}$
,
$q_1-q_0=p_0-p_1=(-a_1)e_{i_1}$
,
![]() $q_2-q_1=p_1'-p_0=a_2e_{i_2}$
and
$q_2-q_1=p_1'-p_0=a_2e_{i_2}$
and
 $$ \begin{align*} &(p_0,p_1)f+(p_1,p_2)f=(p_0,p_1')f+(p_1',p_2)f \\ &\quad \iff (q_1,q_0)f+(q_0,q_1')f=(q_1,q_2)f+(q_2,q_1')f \\ &\quad \overset{L.~{4.8}}{\iff}\hspace{-2pt} (q_0,q_1')f+(q_1',q_2)f=(q_0,q_1)f+(q_1,q_2)f. \end{align*} $$
$$ \begin{align*} &(p_0,p_1)f+(p_1,p_2)f=(p_0,p_1')f+(p_1',p_2)f \\ &\quad \iff (q_1,q_0)f+(q_0,q_1')f=(q_1,q_2)f+(q_2,q_1')f \\ &\quad \overset{L.~{4.8}}{\iff}\hspace{-2pt} (q_0,q_1')f+(q_1',q_2)f=(q_0,q_1)f+(q_1,q_2)f. \end{align*} $$
Case 3:
![]() $a_1\hspace{-1pt}=\hspace{-1pt}a_2\hspace{-1pt}=\hspace{-1pt}-1$
. Let
$a_1\hspace{-1pt}=\hspace{-1pt}a_2\hspace{-1pt}=\hspace{-1pt}-1$
. Let
![]() $q_0\hspace{-1pt}=\hspace{-1pt}p_2$
,
$q_0\hspace{-1pt}=\hspace{-1pt}p_2$
,
![]() $q_1\hspace{-1pt}=\hspace{-1pt}p_1'$
,
$q_1\hspace{-1pt}=\hspace{-1pt}p_1'$
,
![]() $q_2\hspace{-1pt}=\hspace{-1pt}p_0$
, and
$q_2\hspace{-1pt}=\hspace{-1pt}p_0$
, and
![]() $q_1'=q_0+(q_2-q_1)= p_2+ (p_0-p_1')=p_1$
. Then
$q_1'=q_0+(q_2-q_1)= p_2+ (p_0-p_1')=p_1$
. Then
![]() $q_1-q_0=p_1'-p_2=(-a_1)e_{i_1}$
,
$q_1-q_0=p_1'-p_2=(-a_1)e_{i_1}$
,
![]() $q_2-q_1=p_0-p_1'=(-a_2)e_{i_2}$
and
$q_2-q_1=p_0-p_1'=(-a_2)e_{i_2}$
and
 $$ \begin{align*} &(p_0,p_1)f+(p_1,p_2)f=(p_0,p_1')f+(p_1',p_2)f \\ &\quad\iff (q_2,q_1')f+(q_1',q_0)f=(q_2,q_1)f+(q_1,q_0)f \\ &\quad\overset{L.~{4.8}}{\iff}\hspace{-2pt} (q_0,q_1)f+(q_1,q_2)f=(q_0,q_1')f+(q_1',q_2)f. \end{align*} $$
$$ \begin{align*} &(p_0,p_1)f+(p_1,p_2)f=(p_0,p_1')f+(p_1',p_2)f \\ &\quad\iff (q_2,q_1')f+(q_1',q_0)f=(q_2,q_1)f+(q_1,q_0)f \\ &\quad\overset{L.~{4.8}}{\iff}\hspace{-2pt} (q_0,q_1)f+(q_1,q_2)f=(q_0,q_1')f+(q_1',q_2)f. \end{align*} $$
We will therefore assume that
![]() $a_1=a_2=1$
and thus
$a_1=a_2=1$
and thus
![]() $p_0<p_1<p_2$
. We will now represent all terms in the claimed equality in terms of a single cube
$p_0<p_1<p_2$
. We will now represent all terms in the claimed equality in terms of a single cube
![]() $t=f[p_2]$
in the tessellation f as follows:
$t=f[p_2]$
in the tessellation f as follows:
 $$ \begin{align*} &(p_0,p_1)f/{\mathrm{wgt}}_{n}(p_2)={\mathrm{wgt}}_{n}(p_1-p_2)\unicode{x3bb}(f,E_{p_2}({\mathrm{faceAt}}(-e_{i_2},-e_{i_1}))) \\ &\quad=n[i_2]{\mathrm{faceAt}}(-e_{i_2},-e_{i_1})t=n[i_2]t[-e_{i_2},-e_{i_2}-e_{i_1}], \\ &(p_1,p_2)f/{\mathrm{wgt}}_{n}(p_2)={\mathrm{wgt}}_{n}(p_2-p_2)\unicode{x3bb}(f,E_{p_2}({\mathrm{faceAt}}({\mathbf{0}},-e_{i_2}))) \\ &\quad={\mathrm{faceAt}}({\mathbf{0}},-e_{i_2})t=t[{\mathbf{0}},-e_{i_2}], \\&(p_0,p_1')f/{\mathrm{wgt}}_{n}(p_2)={\mathrm{wgt}}_{n}(p_1'-p_2)\unicode{x3bb}(f,E_{p_2}({\mathrm{faceAt}}(-e_{i_1},-e_{i_2})))\\ &\quad=n[i_1]{\mathrm{faceAt}}(-e_{i_1},-e_{i_2})t=n[i_1]t[-e_{i_1},-e_{i_1}-e_{i_2}]\quad\mbox{and } \\ &(p_1',p_2)f/{\mathrm{wgt}}_{n}(p_2)={\mathrm{wgt}}_{n}(p_2-p_2)\unicode{x3bb}(f,E_{p_2}({\mathrm{faceAt}}({\mathbf{0}},-e_{i_1})))\\ &\quad={\mathrm{faceAt}}(0,-e_{i_1})t=t[{\mathbf{0}},-e_1]. \end{align*} $$
$$ \begin{align*} &(p_0,p_1)f/{\mathrm{wgt}}_{n}(p_2)={\mathrm{wgt}}_{n}(p_1-p_2)\unicode{x3bb}(f,E_{p_2}({\mathrm{faceAt}}(-e_{i_2},-e_{i_1}))) \\ &\quad=n[i_2]{\mathrm{faceAt}}(-e_{i_2},-e_{i_1})t=n[i_2]t[-e_{i_2},-e_{i_2}-e_{i_1}], \\ &(p_1,p_2)f/{\mathrm{wgt}}_{n}(p_2)={\mathrm{wgt}}_{n}(p_2-p_2)\unicode{x3bb}(f,E_{p_2}({\mathrm{faceAt}}({\mathbf{0}},-e_{i_2}))) \\ &\quad={\mathrm{faceAt}}({\mathbf{0}},-e_{i_2})t=t[{\mathbf{0}},-e_{i_2}], \\&(p_0,p_1')f/{\mathrm{wgt}}_{n}(p_2)={\mathrm{wgt}}_{n}(p_1'-p_2)\unicode{x3bb}(f,E_{p_2}({\mathrm{faceAt}}(-e_{i_1},-e_{i_2})))\\ &\quad=n[i_1]{\mathrm{faceAt}}(-e_{i_1},-e_{i_2})t=n[i_1]t[-e_{i_1},-e_{i_1}-e_{i_2}]\quad\mbox{and } \\ &(p_1',p_2)f/{\mathrm{wgt}}_{n}(p_2)={\mathrm{wgt}}_{n}(p_2-p_2)\unicode{x3bb}(f,E_{p_2}({\mathrm{faceAt}}({\mathbf{0}},-e_{i_1})))\\ &\quad={\mathrm{faceAt}}(0,-e_{i_1})t=t[{\mathbf{0}},-e_1]. \end{align*} $$
From this, we see that
 $$ \begin{align*} &((p_0,p_1)f+(p_1,p_2)f)/{\mathrm{wgt}}_{n}(p_2) \\ &\quad =n[i_2]t[-e_{i_2},-e_{i_2}-e_{i_1}]+t[{\mathbf{0}},-e_{i_2}]\overset{L.~{4.3}}{=}t[{\mathbf{0}},-e_{i_1}-e_{i_2}]\quad\mbox{and}\\ &((p_0,p_1')f+(p_1',p_2)f)/{\mathrm{wgt}}_{n}(p_2) \\ &\quad =n[i_1]t[-e_{i_1},-e_{i_1}-e_{i_2}]+t[{\mathbf{0}},-e_{i_1}]\overset{L.~{4.3}}{=}t[{\mathbf{0}},-e_{i_1}-e_{i_2}]. \end{align*} $$
$$ \begin{align*} &((p_0,p_1)f+(p_1,p_2)f)/{\mathrm{wgt}}_{n}(p_2) \\ &\quad =n[i_2]t[-e_{i_2},-e_{i_2}-e_{i_1}]+t[{\mathbf{0}},-e_{i_2}]\overset{L.~{4.3}}{=}t[{\mathbf{0}},-e_{i_1}-e_{i_2}]\quad\mbox{and}\\ &((p_0,p_1')f+(p_1',p_2)f)/{\mathrm{wgt}}_{n}(p_2) \\ &\quad =n[i_1]t[-e_{i_1},-e_{i_1}-e_{i_2}]+t[{\mathbf{0}},-e_{i_1}]\overset{L.~{4.3}}{=}t[{\mathbf{0}},-e_{i_1}-e_{i_2}]. \end{align*} $$
For a path
![]() $P=(P_i)_{i=1}^k$
and for
$P=(P_i)_{i=1}^k$
and for
![]() $1\leq i<k$
, let
$1\leq i<k$
, let
![]() $a_i\in \{-1,1\}$
and let
$a_i\in \{-1,1\}$
and let
![]() $1\leq m(i)\leq d$
be such that
$1\leq m(i)\leq d$
be such that
![]() $a_i e_{m(i)}=E_P(i)$
. We say that an integer i with
$a_i e_{m(i)}=E_P(i)$
. We say that an integer i with
![]() $1\leq i<k-1$
is a return if
$1\leq i<k-1$
is a return if
![]() $m(i)=m(i+1)$
and
$m(i)=m(i+1)$
and
![]() $a_i\neq a_{i+1}$
. We say that i is an inversion if
$a_i\neq a_{i+1}$
. We say that i is an inversion if
![]() $m(i)>m(i+i)$
. The abelianization of P is the unique path
$m(i)>m(i+i)$
. The abelianization of P is the unique path
![]() ${\mathrm {Ab}}(P)=(P_i')_{i=1}^{k'}$
with
${\mathrm {Ab}}(P)=(P_i')_{i=1}^{k'}$
with
![]() $a_i' e_{m'(i)}=E_{P'}(i)$
for
$a_i' e_{m'(i)}=E_{P'}(i)$
for
![]() $1\leq i<k'$
that satisfies:
$1\leq i<k'$
that satisfies:
-
•
 $P_1'=P_1$
and
$P_1'=P_1$
and
 $P_k'=P_k$
(
$P_k'=P_k$
(
 $P'$
and P have the same start and end points);
$P'$
and P have the same start and end points); -
• if
 $1\leq i<k'-1$
, then
$1\leq i<k'-1$
, then
 $m'(i)\leq m'(i+1)$
(
$m'(i)\leq m'(i+1)$
(
 $P'$
has no inversions);
$P'$
has no inversions); -
• if
 $1\leq i<k'-1$
and
$1\leq i<k'-1$
and
 $m'(i)=m'(i+1)$
, then
$m'(i)=m'(i+1)$
, then
 $a_{i}'=a_{i+1}'$
(
$a_{i}'=a_{i+1}'$
(
 $P'$
has no returns).
$P'$
has no returns).
We will use the abelianization to show that the integral of a tiling over a path depends only on the choice of the start and end points of the path. For the proof of the following lemma, let
![]() $\ell (P)$
be the natural number whose base-d expansion is
$\ell (P)$
be the natural number whose base-d expansion is
![]() $m(1)\cdots m(k)$
.
$m(1)\cdots m(k)$
.
Lemma 4.10. For any path P and any valid tiling
![]() $f\in X_{n}$
, it holds that
$f\in X_{n}$
, it holds that
![]() $Pf={\mathrm {Ab}}(P)f$
.
$Pf={\mathrm {Ab}}(P)f$
.
Proof. We will manipulate any given path
![]() $P\neq {\mathrm {Ab}}(P)$
into another path
$P\neq {\mathrm {Ab}}(P)$
into another path
![]() $P'$
which satisfies
$P'$
which satisfies
![]() $\ell (P')<\ell (P)$
. We also make sure that
$\ell (P')<\ell (P)$
. We also make sure that
![]() $P'$
has the same start and end points as P (so
$P'$
has the same start and end points as P (so
![]() ${\mathrm {Ab}}(P')={\mathrm {Ab}}(P)$
) and that
${\mathrm {Ab}}(P')={\mathrm {Ab}}(P)$
) and that
![]() $P'f=Pf$
. Since
$P'f=Pf$
. Since
![]() $\ell (P)$
is a natural number, this argument can be repeated only finitely many times and it will eventually yield the path
$\ell (P)$
is a natural number, this argument can be repeated only finitely many times and it will eventually yield the path
![]() ${\mathrm {Ab}}(P)$
. Assume therefore that
${\mathrm {Ab}}(P)$
. Assume therefore that
![]() $P\neq {\mathrm {Ab}}(P)$
and let
$P\neq {\mathrm {Ab}}(P)$
and let
![]() $a_i e_{m(i)}=E_P(i)$
for
$a_i e_{m(i)}=E_P(i)$
for
![]() $1\leq i<k$
. There are two possibilities.
$1\leq i<k$
. There are two possibilities.
Case 1, a return:
![]() $m(i)=m(i+1)$
and
$m(i)=m(i+1)$
and
![]() $a_i\neq a_{i+1}$
for some
$a_i\neq a_{i+1}$
for some
![]() $1\leq i<k-1$
. Let
$1\leq i<k-1$
. Let
![]() ${P'=(P_1,\ldots ,P_i,P_{i+3},\ldots ,P_k)}$
. Then, using the fact that
${P'=(P_1,\ldots ,P_i,P_{i+3},\ldots ,P_k)}$
. Then, using the fact that
![]() $P_{i+2}=P_i$
, we see from Lemma 4.8 that
$P_{i+2}=P_i$
, we see from Lemma 4.8 that
![]() $(P_i,P_{i+1})f+(P_{i+1},P_{i+2})f=0$
and therefore
$(P_i,P_{i+1})f+(P_{i+1},P_{i+2})f=0$
and therefore
 $$ \begin{align*} Pf=&\sum_{j=1}^{i-1}(P_j,P_{j+1})f+(P_{i+2},P_{i+3})f+\sum_{j=i+3}^{k-1}(P_j,P_{j+1})f \\ =&\sum_{j=1}^{i-1}(P_j,P_{j+1})f+(P_i,P_{i+3})f+\sum_{j=i+3}^{k-1}(P_j,P_{j+1})=P'f. \end{align*} $$
$$ \begin{align*} Pf=&\sum_{j=1}^{i-1}(P_j,P_{j+1})f+(P_{i+2},P_{i+3})f+\sum_{j=i+3}^{k-1}(P_j,P_{j+1})f \\ =&\sum_{j=1}^{i-1}(P_j,P_{j+1})f+(P_i,P_{i+3})f+\sum_{j=i+3}^{k-1}(P_j,P_{j+1})=P'f. \end{align*} $$
The path
![]() $P'$
has the same start and end points as P, and it is shorter than P, so
$P'$
has the same start and end points as P, and it is shorter than P, so
![]() $\ell (P')<\ell (P)$
.
$\ell (P')<\ell (P)$
.
Case 2, an inversion:
![]() $m(i)>m(i+1)$
for some
$m(i)>m(i+1)$
for some
![]() $1\leq i<k-1$
. Let
$1\leq i<k-1$
. Let
![]() $P_{i+1}'=P_i +(P_{i+2} -P_{i+1})$
and let
$P_{i+1}'=P_i +(P_{i+2} -P_{i+1})$
and let
![]() $P'=(P_1,\ldots ,P_{i},P_{i+1}',P_{i+2},\ldots ,P_k)$
. It follows from Lemma 4.9 that
$P'=(P_1,\ldots ,P_{i},P_{i+1}',P_{i+2},\ldots ,P_k)$
. It follows from Lemma 4.9 that
![]() $(P_i,P_{i+1})f+(P_{i+1},P_{i+2})f=(P_i,P_{i+1}')f=(P_{i+1}',P_{i+2})f$
and therefore
$(P_i,P_{i+1})f+(P_{i+1},P_{i+2})f=(P_i,P_{i+1}')f=(P_{i+1}',P_{i+2})f$
and therefore
![]() $Pf=P'f$
. Letting
$Pf=P'f$
. Letting
![]() $b_j e_{m'(i)}=E_{P'}(j)$
for
$b_j e_{m'(i)}=E_{P'}(j)$
for
![]() $1\leq j<k$
, we check that
$1\leq j<k$
, we check that
and thus
![]() $m'(i)=m(i+1)<m(i)$
, so
$m'(i)=m(i+1)<m(i)$
, so
![]() $\ell (P')<\ell (P)$
.
$\ell (P')<\ell (P)$
.
Theorem 4.11. If two paths P,
![]() $P'$
have the same start and end points, and
$P'$
have the same start and end points, and
![]() $f\in X_{n}$
, then
$f\in X_{n}$
, then
![]() $Pf=P'f$
. In particular, if P is a cycle, then
$Pf=P'f$
. In particular, if P is a cycle, then
![]() $Pf=0$
.
$Pf=0$
.
Proof. This follows from the previous lemma, because
![]() ${\mathrm {Ab}}(P)={\mathrm {Ab}}(P')$
.
${\mathrm {Ab}}(P)={\mathrm {Ab}}(P')$
.
Remark 4.12. The inspiration for the terminology of ‘path integral’ comes from line integrals of holomorphic functions, and Theorem 4.11 is analogous to the fact that the line integral of a holomorphic function over a closed curve is equal to zero. In the case of meromorphic functions, if the line integral over a closed curve is not zero, its interior necessarily contains a non-removable singularity. Similarly, if we are given only a partial tiling of the plane and the path integral around a non-tiled part is not zero, then the interior of the path cannot be completed into a valid tiling: see Figure 5 for an example.

Figure 5 A partial valid tiling f using
![]() $T_{(2,5)}$
. There is no way to complete the tiling, because the path integral around the non-tiled part is not zero.
$T_{(2,5)}$
. There is no way to complete the tiling, because the path integral around the non-tiled part is not zero.
The situation here is reminiscent of the tiling group approach of [Reference Thurston12] for determining whether a collection of polygonal tiles can tile a finite region of the plane. In that approach, the tiles can be interpreted as describing relators in a group, and if the group element describing the boundary of the region is not the identity element, then tiling the region is not possible.
Now, given a tessellation
![]() $f\in X_{n}$
and a pair of vectors
$f\in X_{n}$
and a pair of vectors
![]() $p,p'\in \mathbb {Z}^d$
, define
$p,p'\in \mathbb {Z}^d$
, define
for any path P going from p to
![]() $p'$
: by Theorem 4.11, the choice of the path P does not matter. For the directed pair
$p'$
: by Theorem 4.11, the choice of the path P does not matter. For the directed pair
![]() $(p,p')$
, we also define the (directed) label
$(p,p')$
, we also define the (directed) label
The directed and undirected labels agree in the sense that
![]() $\unicode{x3bb} (f,(z-e_i,z))=\unicode{x3bb} (f, \{z-e_i,z\})$
for
$\unicode{x3bb} (f,(z-e_i,z))=\unicode{x3bb} (f, \{z-e_i,z\})$
for
![]() $z\in \mathbb {Z}^d$
and
$z\in \mathbb {Z}^d$
and
![]() $1\leq i\leq d$
. As one would hope, the labels do not change when the tessellation is shifted.
$1\leq i\leq d$
. As one would hope, the labels do not change when the tessellation is shifted.
Lemma 4.13. Let
![]() $f\in X_{n}$
and let
$f\in X_{n}$
and let
![]() $p,p'\in \mathbb {Z}^d$
. For any
$p,p'\in \mathbb {Z}^d$
. For any
![]() $v\in \mathbb {Z}^d$
, it holds that
$v\in \mathbb {Z}^d$
, it holds that
Proof. We have
 $$ \begin{align*} &\unicode{x3bb}(f,(p+v,p'+v))=(p+v,p'+v)f/{\mathrm{wgt}}_{n}(p'+v) \\ &\quad\overset{L.~{4.7}}{=}{\mathrm{wgt}}_{n}(v)(p,p')\sigma_v(f)/{\mathrm{wgt}}_{n}(p'+v)=(p,p')\sigma_v(f)/{\mathrm{wgt}}_{n}(p') \\ &\quad =\unicode{x3bb}(\sigma_v(f),(p,p')). \end{align*} $$
$$ \begin{align*} &\unicode{x3bb}(f,(p+v,p'+v))=(p+v,p'+v)f/{\mathrm{wgt}}_{n}(p'+v) \\ &\quad\overset{L.~{4.7}}{=}{\mathrm{wgt}}_{n}(v)(p,p')\sigma_v(f)/{\mathrm{wgt}}_{n}(p'+v)=(p,p')\sigma_v(f)/{\mathrm{wgt}}_{n}(p') \\ &\quad =\unicode{x3bb}(\sigma_v(f),(p,p')). \end{align*} $$
The labeling map inherits a summation property from the summation property of paths. The next lemma associates to any label in a tiling a mixed base representation of sorts, where the digits also come from labels in the tiling. In a special case, the base consists of powers of a single number
![]() $m(n,v)\in \mathbb {Q}$
, which is however not necessarily an integer.
$m(n,v)\in \mathbb {Q}$
, which is however not necessarily an integer.
Lemma 4.14. Let
![]() $p_0,p_1,\ldots ,p_k\in \mathbb {Z}^d$
and let
$p_0,p_1,\ldots ,p_k\in \mathbb {Z}^d$
and let
![]() $f\in X_{n}$
. Then
$f\in X_{n}$
. Then
 $$ \begin{align*}\unicode{x3bb}(f,(p_k,p_0))=\sum_{i=0}^{k-1} m(n,p_{i}-p_0)\unicode{x3bb}(f,(p_{i+1},p_{i})).\end{align*} $$
$$ \begin{align*}\unicode{x3bb}(f,(p_k,p_0))=\sum_{i=0}^{k-1} m(n,p_{i}-p_0)\unicode{x3bb}(f,(p_{i+1},p_{i})).\end{align*} $$
In particular, for
![]() $v\in \mathbb {Z}^d$
and
$v\in \mathbb {Z}^d$
and
![]() $k\in \mathbb {N}$
, it holds that
$k\in \mathbb {N}$
, it holds that
 $$ \begin{align*}\unicode{x3bb}(f,(kv+p_0,p_0))=\sum_{i=0}^{k-1} m(n,v)^i\unicode{x3bb}(f,((i+1)v+p_0,iv+p_0)).\end{align*} $$
$$ \begin{align*}\unicode{x3bb}(f,(kv+p_0,p_0))=\sum_{i=0}^{k-1} m(n,v)^i\unicode{x3bb}(f,((i+1)v+p_0,iv+p_0)).\end{align*} $$
Proof. We have
 $$ \begin{align*} &\unicode{x3bb}(f,(p_k,p_0))=(p_k,p_0)f/{\mathrm{wgt}}_{n}(p_0)=\sum_{i=0}^{k-1}(p_{i+1},p_{i})f/{\mathrm{wgt}}_{n}(p_0) \\ &\quad=\sum_{i=0}^{k-1} {\mathrm{wgt}}_{n}(p_i)\unicode{x3bb}(f,(p_{i+1},p_{i}))/{\mathrm{wgt}}_{n}(p_0)=\sum_{i=0}^{k-1} {\mathrm{wgt}}_{n}(p_i-p_0)\unicode{x3bb}(f,(p_{i+1},p_{i})). \end{align*} $$
$$ \begin{align*} &\unicode{x3bb}(f,(p_k,p_0))=(p_k,p_0)f/{\mathrm{wgt}}_{n}(p_0)=\sum_{i=0}^{k-1}(p_{i+1},p_{i})f/{\mathrm{wgt}}_{n}(p_0) \\ &\quad=\sum_{i=0}^{k-1} {\mathrm{wgt}}_{n}(p_i)\unicode{x3bb}(f,(p_{i+1},p_{i}))/{\mathrm{wgt}}_{n}(p_0)=\sum_{i=0}^{k-1} {\mathrm{wgt}}_{n}(p_i-p_0)\unicode{x3bb}(f,(p_{i+1},p_{i})). \end{align*} $$
For the latter part, choose
![]() $p_i=iv+p_0$
and note that
$p_i=iv+p_0$
and note that
 $$ \begin{align*}m(n,p_i-p_0)=m(n,iv)=\prod_{j=1}^d n[j]^{-iv[j]}=m(n,v)^i.\end{align*} $$
$$ \begin{align*}m(n,p_i-p_0)=m(n,iv)=\prod_{j=1}^d n[j]^{-iv[j]}=m(n,v)^i.\end{align*} $$
The base
![]() $m(n,v)$
of Lemma 4.14 is a natural number at least when
$m(n,v)$
of Lemma 4.14 is a natural number at least when
![]() $v\leq {\mathbf {0}}$
. In that case, the ‘digits’
$v\leq {\mathbf {0}}$
. In that case, the ‘digits’
![]() $\unicode{x3bb} (f,((i+1)v+p_0,iv+p_0))$
are actually just usual base-
$\unicode{x3bb} (f,((i+1)v+p_0,iv+p_0))$
are actually just usual base-
![]() $m(n,v)$
digits, which follows from the next lemma.
$m(n,v)$
digits, which follows from the next lemma.
Lemma 4.15. If
![]() $p\leq p'\in \mathbb {Z}^d$
and
$p\leq p'\in \mathbb {Z}^d$
and
![]() $f\in X_{n}$
, then
$f\in X_{n}$
, then
![]() $\unicode{x3bb} (f,(p,p'))\in \mathbb {N}$
and
$\unicode{x3bb} (f,(p,p'))\in \mathbb {N}$
and
![]() $0\leq \unicode{x3bb} (f,(p,p'))<m(n,p-p')$
.
$0\leq \unicode{x3bb} (f,(p,p'))<m(n,p-p')$
.
Proof. By Lemma 4.13, it is sufficient to show that if
![]() $p\leq {\mathbf {0}}$
, then
$p\leq {\mathbf {0}}$
, then
![]() $\unicode{x3bb} (f,(p,{\mathbf {0}}))\in \mathbb {N}$
and
$\unicode{x3bb} (f,(p,{\mathbf {0}}))\in \mathbb {N}$
and
![]() $\unicode{x3bb} (f,(p,{\mathbf {0}}))<m(n,p)$
. The proof is by induction on the distance of p from the origin, the base case
$\unicode{x3bb} (f,(p,{\mathbf {0}}))<m(n,p)$
. The proof is by induction on the distance of p from the origin, the base case
![]() $p={\mathbf {0}}$
is simple. Assume then that the claim holds for some
$p={\mathbf {0}}$
is simple. Assume then that the claim holds for some
![]() $p\leq {\mathbf {0}}$
and consider the vector
$p\leq {\mathbf {0}}$
and consider the vector
![]() $p-e_i$
for some
$p-e_i$
for some
![]() $1\leq i\leq d$
. Then
$1\leq i\leq d$
. Then
 $$ \begin{align*} &\unicode{x3bb}(f,(p-e_i,{\mathbf{0}}))=(p-e_i,{\mathbf{0}})f=(p-e_i,p)f+(p,{\mathbf{0}})f \\ &\quad=\underbrace{{\mathrm{wgt}}_{n}(p)}_{\in\mathbb{N}}\underbrace{\unicode{x3bb}(f,\{p-e_i,p\})}_{\in\mathbb{N}}+\underbrace{\unicode{x3bb}(f,(p,{\mathbf{0}}))}_{\in\mathbb{N}}<m(n,p)\ {\mathrm{faceAt}}({\mathbf{0}},-e_i)f[p]+m(n,p) \\ &\quad=m(n,p)({\mathrm{base}}_{n}(f[p],({\mathbf{0}},-e_i))[2]+1)\leq m(n,p) n[i]=m(n,p-e_i), \end{align*} $$
$$ \begin{align*} &\unicode{x3bb}(f,(p-e_i,{\mathbf{0}}))=(p-e_i,{\mathbf{0}})f=(p-e_i,p)f+(p,{\mathbf{0}})f \\ &\quad=\underbrace{{\mathrm{wgt}}_{n}(p)}_{\in\mathbb{N}}\underbrace{\unicode{x3bb}(f,\{p-e_i,p\})}_{\in\mathbb{N}}+\underbrace{\unicode{x3bb}(f,(p,{\mathbf{0}}))}_{\in\mathbb{N}}<m(n,p)\ {\mathrm{faceAt}}({\mathbf{0}},-e_i)f[p]+m(n,p) \\ &\quad=m(n,p)({\mathrm{base}}_{n}(f[p],({\mathbf{0}},-e_i))[2]+1)\leq m(n,p) n[i]=m(n,p-e_i), \end{align*} $$
where we use the fact that
![]() ${\mathrm {base}}_{n}(f[p],({\mathbf {0}},-e_i))[2]<m(n,-e_i)/m(n,{\mathbf {0}})=n[i]$
.
${\mathrm {base}}_{n}(f[p],({\mathbf {0}},-e_i))[2]<m(n,-e_i)/m(n,{\mathbf {0}})=n[i]$
.
Lemma 4.16. Let
![]() $p_k\leq \cdots \leq p_0$
and let
$p_k\leq \cdots \leq p_0$
and let
![]() $f\in X_{n}$
. Then for
$f\in X_{n}$
. Then for
![]() $1\leq i\leq k'\leq k$
,
$1\leq i\leq k'\leq k$
,
Proof. By Lemma 4.14,
 $$ \begin{align*} \unicode{x3bb}(f,(p_k,p_0))=\sum_{i=0}^{k-1} m(n,p_{i}-p_0)\unicode{x3bb}(f,(p_{i+1},p_{i})). \end{align*} $$
$$ \begin{align*} \unicode{x3bb}(f,(p_k,p_0))=\sum_{i=0}^{k-1} m(n,p_{i}-p_0)\unicode{x3bb}(f,(p_{i+1},p_{i})). \end{align*} $$
From this, the claim follows for
![]() $k'=k$
by the definition of a mixed base representation, because by Lemma 4.15,
$k'=k$
by the definition of a mixed base representation, because by Lemma 4.15,
![]() $0\leq \unicode{x3bb} (f,(p_{i+1},p_{i}))<m(n,p_{i+1}-p_{i})= m(n,p_{i+1}-p_0)/m(n,p_{i}-p_0)$
for
$0\leq \unicode{x3bb} (f,(p_{i+1},p_{i}))<m(n,p_{i+1}-p_{i})= m(n,p_{i+1}-p_0)/m(n,p_{i}-p_0)$
for
![]() $1\leq i\leq k$
. The claim for general
$1\leq i\leq k$
. The claim for general
![]() $k'$
follows from the case
$k'$
follows from the case
![]() $k'=k$
by Lemma 3.4.
$k'=k$
by Lemma 3.4.
Lemma 4.17. Let
![]() $f\in X_{n}$
and let
$f\in X_{n}$
and let
![]() $z\in \mathbb {Z}^d$
. Then
$z\in \mathbb {Z}^d$
. Then
![]() ${\mathrm {val}}_{n}(f[z])=\unicode{x3bb} (f,(z-{\mathbf {1}},z))$
.
${\mathrm {val}}_{n}(f[z])=\unicode{x3bb} (f,(z-{\mathbf {1}},z))$
.
Proof. Up to shifting f, we may assume that
![]() $z={\mathbf {0}}$
. Let
$z={\mathbf {0}}$
. Let
![]() $t=f[{\mathbf {0}}]$
. For
$t=f[{\mathbf {0}}]$
. For
![]() $0\leq i\leq d$
, let
$0\leq i\leq d$
, let
![]() $e_i'=\sum _{j=1}^i e_j$
. Then
$e_i'=\sum _{j=1}^i e_j$
. Then
![]() $e_i'$
form a binary d-directive sequence. Using the definition of the undirected label of a single edge, we see that
$e_i'$
form a binary d-directive sequence. Using the definition of the undirected label of a single edge, we see that
Using this, we compute that
 $$ \begin{align*} \unicode{x3bb}(f,(-{\mathbf{1}},{\mathbf{0}}))&\overset{L.~{4.14}}{=}\sum_{i=0}^{d-1}m(n,e_i')\unicode{x3bb}(f,\{e_{i+1}',e_i'\}) \\ &=\sum_{i=0}^{d-1}m(n,e_i')t[e_i',e_{i+1}']\overset{L.~{4.3}}{=}t[{\mathbf{0}},{\mathbf{1}}] ={\mathrm{val}}_{n}(t). \end{align*} $$
$$ \begin{align*} \unicode{x3bb}(f,(-{\mathbf{1}},{\mathbf{0}}))&\overset{L.~{4.14}}{=}\sum_{i=0}^{d-1}m(n,e_i')\unicode{x3bb}(f,\{e_{i+1}',e_i'\}) \\ &=\sum_{i=0}^{d-1}m(n,e_i')t[e_i',e_{i+1}']\overset{L.~{4.3}}{=}t[{\mathbf{0}},{\mathbf{1}}] ={\mathrm{val}}_{n}(t). \end{align*} $$
For a face
![]() $s={\mathrm {faceAt}}(p,v)$
and
$s={\mathrm {faceAt}}(p,v)$
and
![]() $z\in \mathbb {Z}^d$
, denote
$z\in \mathbb {Z}^d$
, denote
![]() ${D}_z(s)=(z+p+v,z+p)$
(this generalizes an earlier definition where s was an edge). We generalize the defining formula for the label of an edge in the following lemma.
${D}_z(s)=(z+p+v,z+p)$
(this generalizes an earlier definition where s was an edge). We generalize the defining formula for the label of an edge in the following lemma.
Lemma 4.18. Let
![]() $f\in X_{n}$
. For
$f\in X_{n}$
. For
![]() $s={\mathrm {faceAt}}(p,v)$
and
$s={\mathrm {faceAt}}(p,v)$
and
![]() $z\in \mathbb {Z}^d$
, it holds that
$z\in \mathbb {Z}^d$
, it holds that
Proof. Up to shifting f, we may assume that
![]() $z={\mathbf {0}}$
. Let
$z={\mathbf {0}}$
. Let
![]() $a\in \mathbb {N}$
be such that
$a\in \mathbb {N}$
be such that
![]() ${\mathrm {cube}}_{n}(a)=f[{\mathbf {0}}]$
. Then, by applying Lemma 4.16 with the choice
${\mathrm {cube}}_{n}(a)=f[{\mathbf {0}}]$
. Then, by applying Lemma 4.16 with the choice
![]() $(p_0,p_1,p_2,p_3)=({\mathbf {0}},p,p+v,{\mathbf {1}})$
,
$(p_0,p_1,p_2,p_3)=({\mathbf {0}},p,p+v,{\mathbf {1}})$
,
 $$ \begin{align*} \unicode{x3bb}(f,({D}_{{\mathbf{0}}}(s)))&=\unicode{x3bb}(f,(p+v,p))\overset{L.~{4.16}}{=}{\mathrm{base}}_{n}(\unicode{x3bb}(f,(-{\mathbf{1}},{\mathbf{0}})),(p,p+v))[2] \\ &\overset{L.~{4.17}}{=}{\mathrm{base}}_{n}(a,(p,p+v))[2]={\mathrm{cube}}_n(a)[p,p+v]=sf[{\mathbf{0}}]. \end{align*} $$
$$ \begin{align*} \unicode{x3bb}(f,({D}_{{\mathbf{0}}}(s)))&=\unicode{x3bb}(f,(p+v,p))\overset{L.~{4.16}}{=}{\mathrm{base}}_{n}(\unicode{x3bb}(f,(-{\mathbf{1}},{\mathbf{0}})),(p,p+v))[2] \\ &\overset{L.~{4.17}}{=}{\mathrm{base}}_{n}(a,(p,p+v))[2]={\mathrm{cube}}_n(a)[p,p+v]=sf[{\mathbf{0}}]. \end{align*} $$
As we shall see, by Lemma 4.17, labels along the direction of
![]() ${\mathbf {1}}$
can be found by reading the values of a sequence of cubes and interpreting this sequence of values as the representation of a number in base
${\mathbf {1}}$
can be found by reading the values of a sequence of cubes and interpreting this sequence of values as the representation of a number in base
![]() $N=\prod _{i=1}^d n[i]$
. We actually prove a more general statement by using Lemma 4.18.
$N=\prod _{i=1}^d n[i]$
. We actually prove a more general statement by using Lemma 4.18.
Lemma 4.19. Let
![]() $p_k\leq \cdots \leq p_0$
with
$p_k\leq \cdots \leq p_0$
with
![]() $p_{i+1}-p_i\geq -{\mathbf {1}}$
for
$p_{i+1}-p_i\geq -{\mathbf {1}}$
for
![]() $0\leq i<k$
and let
$0\leq i<k$
and let
![]() $f\in X_{n}$
. Then
$f\in X_{n}$
. Then
 $$ \begin{align*}\unicode{x3bb}(f,(p_k,p_0))=\sum_{i=0}^{k-1} m(n,p_{i}-p_0)\ {\mathrm{faceAt}}({\mathbf{0}},p_{i+1}-p_i)f[p_i].\end{align*} $$
$$ \begin{align*}\unicode{x3bb}(f,(p_k,p_0))=\sum_{i=0}^{k-1} m(n,p_{i}-p_0)\ {\mathrm{faceAt}}({\mathbf{0}},p_{i+1}-p_i)f[p_i].\end{align*} $$
In particular, for any
![]() $k\in \mathbb {N}$
and
$k\in \mathbb {N}$
and
![]() $v\in \mathbb {Z}^d$
,
$v\in \mathbb {Z}^d$
,
 $$ \begin{align*}\unicode{x3bb}(f,(v-{\mathbf{k}},v))=\sum_{i=0}^{k-1} N^i\ {\mathrm{val}}_n(f[v-{\mathbf{i}}]).\end{align*} $$
$$ \begin{align*}\unicode{x3bb}(f,(v-{\mathbf{k}},v))=\sum_{i=0}^{k-1} N^i\ {\mathrm{val}}_n(f[v-{\mathbf{i}}]).\end{align*} $$
Proof. The first claim follows from Lemmas 4.14 and 4.18. The second claim follows from the first with the choice
![]() $p_i=v-{\mathbf {i}}$
for
$p_i=v-{\mathbf {i}}$
for
![]() $0\leq i\leq k$
.
$0\leq i\leq k$
.
We conclude this subsection with some justification for why the elements of
![]() $T_n$
are called multiplication cubes.
$T_n$
are called multiplication cubes.
Proposition 4.20. Let
![]() $p, p'\in \mathbb {Z}^d$
,
$p, p'\in \mathbb {Z}^d$
,
![]() $v\in \mathbb {Z}^d$
, and let
$v\in \mathbb {Z}^d$
, and let
![]() $f\in X_n$
. Then
$f\in X_n$
. Then
 $$ \begin{align*} \unicode{x3bb}(f,(p+v,p'+v)) &= m(n,-v)\unicode{x3bb}(f,(p,p'))\\ &\quad + m(n,-p'-v)((p+v,p)f+(p',p'+v)f).\end{align*} $$
$$ \begin{align*} \unicode{x3bb}(f,(p+v,p'+v)) &= m(n,-v)\unicode{x3bb}(f,(p,p'))\\ &\quad + m(n,-p'-v)((p+v,p)f+(p',p'+v)f).\end{align*} $$
Proof. By Theorem 4.11,
![]() $(p+v,p'+v)f=(p+v,p)f+(p,p')f+(p',p'+v)f$
, and by replacing path integrals with labels, we find
$(p+v,p'+v)f=(p+v,p)f+(p,p')f+(p',p'+v)f$
, and by replacing path integrals with labels, we find
 $$ \begin{align*} m(n,p'+v)\ \unicode{x3bb}(f,(p+v,p'+v))&=(p+v,p)f\\ &\quad+m(n,p')\ \unicode{x3bb}(f,(p,p'))+(p',p'+v)f.\end{align*} $$
$$ \begin{align*} m(n,p'+v)\ \unicode{x3bb}(f,(p+v,p'+v))&=(p+v,p)f\\ &\quad+m(n,p')\ \unicode{x3bb}(f,(p,p'))+(p',p'+v)f.\end{align*} $$
The claim follows by dividing both sides of the equation with
![]() $m(n,p'+v)$
.
$m(n,p'+v)$
.
The message of this proposition is that moving in
![]() $\mathbb {Z}^d$
by a vector v changes the values of the labeling map by the factor of
$\mathbb {Z}^d$
by a vector v changes the values of the labeling map by the factor of
![]() $m(n,-v)$
, possibly up to an error term. In particular, moving to the direction of a basis vector
$m(n,-v)$
, possibly up to an error term. In particular, moving to the direction of a basis vector
![]() $e_i$
corresponds to multiplication by
$e_i$
corresponds to multiplication by
![]() $n[i]$
in this sense. Sometimes, the error term can be made equal to zero. We also remark that another type of tile set performing multiplication in a similar sense has appeared in [Reference Kari4].
$n[i]$
in this sense. Sometimes, the error term can be made equal to zero. We also remark that another type of tile set performing multiplication in a similar sense has appeared in [Reference Kari4].
Example 4.21. We may now explain the powers of two in Figure 1. Observe that in the figure,
![]() $(-{\mathbf {3}}+e_1,-{\mathbf {3}})f=({\mathbf {0}},e_1)f=0$
. Then by applying the previous proposition for
$(-{\mathbf {3}}+e_1,-{\mathbf {3}})f=({\mathbf {0}},e_1)f=0$
. Then by applying the previous proposition for
![]() $p=-{\mathbf {3}}$
,
$p=-{\mathbf {3}}$
,
![]() $p'={\mathbf {0}}$
, and
$p'={\mathbf {0}}$
, and
![]() $v=e_1$
, it follows that
$v=e_1$
, it follows that
Alternatively, by using the latter part of Lemma 4.19, the values
![]() $\unicode{x3bb} (f,(-{\mathbf {3}},{\mathbf {0}}))=64$
and
$\unicode{x3bb} (f,(-{\mathbf {3}},{\mathbf {0}}))=64$
and
![]() $\unicode{x3bb} (f,(-{\mathbf {3}}+e_1,e_1))=128$
can be read directly from the figure. Similar arguments connect the other powers of two appearing in the figure with each other.
$\unicode{x3bb} (f,(-{\mathbf {3}}+e_1,e_1))=128$
can be read directly from the figure. Similar arguments connect the other powers of two appearing in the figure with each other.
Next we show that Proposition 4.20 can be extended to path integrals over some infinite paths so that the error terms vanish under very natural assumptions, thus connecting multiplication operations to moving around tessellations in an even more satisfactory sense. Given vectors
![]() $p,v\in \mathbb {Z}^d$
with
$p,v\in \mathbb {Z}^d$
with
![]() $v\leq {\mathbf {0}}$
, we consider the infinite path going through p along v, and given
$v\leq {\mathbf {0}}$
, we consider the infinite path going through p along v, and given
![]() $f\in X_n$
, we denote
$f\in X_n$
, we denote
Alternatively, we can rewrite
 $$ \begin{align*} {\mathrm{frac}}_{p,v}(f)&=\sum_{i=0}^\infty(p-i v,p-(i+1)v)f \\& ={\mathrm{wgt}}_n(p)\sum_{i=0}^\infty{\mathrm{wgt}}_n(v)^{-(i+1)}\unicode{x3bb}(f,(p-i v,p-(i+1)v))\quad\mbox{and} \\{\mathrm{int}}_{p,v}(f)&=\sum_{i=0}^\infty(p+(i+1)v,p+i v)f \\&={\mathrm{wgt}}_n(p)\sum_{i=0}^\infty{\mathrm{wgt}}_n(v)^{i}\unicode{x3bb}(f,(p+(i+1)v,p+iv)), \end{align*} $$
$$ \begin{align*} {\mathrm{frac}}_{p,v}(f)&=\sum_{i=0}^\infty(p-i v,p-(i+1)v)f \\& ={\mathrm{wgt}}_n(p)\sum_{i=0}^\infty{\mathrm{wgt}}_n(v)^{-(i+1)}\unicode{x3bb}(f,(p-i v,p-(i+1)v))\quad\mbox{and} \\{\mathrm{int}}_{p,v}(f)&=\sum_{i=0}^\infty(p+(i+1)v,p+i v)f \\&={\mathrm{wgt}}_n(p)\sum_{i=0}^\infty{\mathrm{wgt}}_n(v)^{i}\unicode{x3bb}(f,(p+(i+1)v,p+iv)), \end{align*} $$
where
![]() $\unicode{x3bb} (f,(p-i v,p-(i+1)v))$
and
$\unicode{x3bb} (f,(p-i v,p-(i+1)v))$
and
![]() $\unicode{x3bb} (f,(p+(i+1)v,p+iv))$
are natural numbers less than
$\unicode{x3bb} (f,(p+(i+1)v,p+iv))$
are natural numbers less than
![]() ${\mathrm {wgt}}_n(v)$
by Lemma 4.15. The names of these quantities come from the fact that these are essentially (up to ignoring the factor
${\mathrm {wgt}}_n(v)$
by Lemma 4.15. The names of these quantities come from the fact that these are essentially (up to ignoring the factor
![]() ${\mathrm {wgt}}_n(p)$
) the fractional parts and integral parts of some quantity represented in base
${\mathrm {wgt}}_n(p)$
) the fractional parts and integral parts of some quantity represented in base
![]() ${\mathrm {wgt}}_n(v)$
:
${\mathrm {wgt}}_n(v)$
:
![]() ${\mathrm {frac}}_{p,v}(f)/{\mathrm {wgt}}_n(p)\in [0,1]$
and
${\mathrm {frac}}_{p,v}(f)/{\mathrm {wgt}}_n(p)\in [0,1]$
and
![]() ${\mathrm {int}}_{p,v}(f)/{\mathrm {wgt}}_n(p)\in \mathbb {N}$
if it is finite.
${\mathrm {int}}_{p,v}(f)/{\mathrm {wgt}}_n(p)\in \mathbb {N}$
if it is finite.
We write
 $$ \begin{align*} &{\mathrm{real}}_{p,v}(f)={\mathrm{int}}_{p,v}(f)+{\mathrm{frac}}_{p,v}(f)=\lim_{i\to\infty}(p+iv,p-iv)f \\ &\quad ={\mathrm{wgt}}_n(p)\sum_{i=-\infty}^\infty{\mathrm{wgt}}_n(v)^{i}\unicode{x3bb}(f,(p+(i+1)v,p+iv)). \end{align*} $$
$$ \begin{align*} &{\mathrm{real}}_{p,v}(f)={\mathrm{int}}_{p,v}(f)+{\mathrm{frac}}_{p,v}(f)=\lim_{i\to\infty}(p+iv,p-iv)f \\ &\quad ={\mathrm{wgt}}_n(p)\sum_{i=-\infty}^\infty{\mathrm{wgt}}_n(v)^{i}\unicode{x3bb}(f,(p+(i+1)v,p+iv)). \end{align*} $$
In the special case
![]() $p={\mathbf {0}}$
, we may omit the subscript p, and in this case, the sum above yields a base-
$p={\mathbf {0}}$
, we may omit the subscript p, and in this case, the sum above yields a base-
![]() ${\mathrm {wgt}}_n(v)$
representation for
${\mathrm {wgt}}_n(v)$
representation for
![]() ${\mathrm {real}}_v(f)$
. If additionally
${\mathrm {real}}_v(f)$
. If additionally
![]() $v=-{\mathbf {1}}$
, we may also omit the subscript v and say that the tessellation f represents the number
$v=-{\mathbf {1}}$
, we may also omit the subscript v and say that the tessellation f represents the number
![]() ${\mathrm {real}}(f)$
, but in Proposition 4.25, it will turn out that the choices of p and v do not matter much. By Lemma 4.17, the number
${\mathrm {real}}(f)$
, but in Proposition 4.25, it will turn out that the choices of p and v do not matter much. By Lemma 4.17, the number
![]() ${\mathrm {real}}(f)$
can be read directly from the cubes on the main diagonal of the tessellation f:
${\mathrm {real}}(f)$
can be read directly from the cubes on the main diagonal of the tessellation f:
 $$ \begin{align*}{\mathrm{real}}(f)=\sum_{i=-\infty}^\infty{\mathrm{wgt}}_n(-{\mathbf{1}})^{i}\ {\mathrm{val}}_n(f[-{\mathbf{i}}])=\sum_{i=-\infty}^\infty N^i\ {\mathrm{val}}_n(f[-{\mathbf{i}}]).\end{align*} $$
$$ \begin{align*}{\mathrm{real}}(f)=\sum_{i=-\infty}^\infty{\mathrm{wgt}}_n(-{\mathbf{1}})^{i}\ {\mathrm{val}}_n(f[-{\mathbf{i}}])=\sum_{i=-\infty}^\infty N^i\ {\mathrm{val}}_n(f[-{\mathbf{i}}]).\end{align*} $$
If
![]() ${\mathrm {wgt}}_n(v)>1$
, then in the sum defining
${\mathrm {wgt}}_n(v)>1$
, then in the sum defining
![]() ${\mathrm {int}}_{p,v}(f)$
, the part
${\mathrm {int}}_{p,v}(f)$
, the part
![]() ${\mathrm {wgt}}_n(v)^{i}$
tends to infinity and so the finiteness of the sum is equivalent to the equality
${\mathrm {wgt}}_n(v)^{i}$
tends to infinity and so the finiteness of the sum is equivalent to the equality
![]() $\unicode{x3bb} (f,(p+(i+1)v,p+iv))=0$
(or equivalently
$\unicode{x3bb} (f,(p+(i+1)v,p+iv))=0$
(or equivalently
![]() $(p+(i+1)v,p+i v)f=0$
) holding for all sufficiently large i. In fact, finiteness of
$(p+(i+1)v,p+i v)f=0$
) holding for all sufficiently large i. In fact, finiteness of
![]() ${\mathrm {int}}_{p,v}(f)$
also implies that many other labels are equal to zero.
${\mathrm {int}}_{p,v}(f)$
also implies that many other labels are equal to zero.
Lemma 4.22. Let
![]() $f\in X_n$
. The implications (1)
$f\in X_n$
. The implications (1)
![]() $\implies $
(2)
$\implies $
(2)
![]() $\implies $
(3) hold for the statements:
$\implies $
(3) hold for the statements:
-
(1)
 ${\mathrm {int}}_{p,v}(f)$
is finite for some
${\mathrm {int}}_{p,v}(f)$
is finite for some
 $p,v\in \mathbb {Z}^d$
with
$p,v\in \mathbb {Z}^d$
with
 $v\ll {\mathbf {0}}$
and
$v\ll {\mathbf {0}}$
and
 ${\mathrm {wgt}}_n(v)>1$
;
${\mathrm {wgt}}_n(v)>1$
; -
(2)
 $\unicode{x3bb} (f,(p_2,p_1))=(p_2,p_1)f=0$
whenever
$\unicode{x3bb} (f,(p_2,p_1))=(p_2,p_1)f=0$
whenever
 $p_2\leq p_1$
and
$p_2\leq p_1$
and
 ${\mathrm {wgt}}_n(p_1)$
is sufficiently large;
${\mathrm {wgt}}_n(p_1)$
is sufficiently large; -
(3)
 ${\mathrm {int}}_{p,v}(f)$
is finite for all
${\mathrm {int}}_{p,v}(f)$
is finite for all
 $p,v\in \mathbb {Z}^d$
with
$p,v\in \mathbb {Z}^d$
with
 $v\leq {\mathbf {0}}$
and
$v\leq {\mathbf {0}}$
and
 ${\mathrm {wgt}}_n(v)>1$
.
${\mathrm {wgt}}_n(v)>1$
.
In particular, finiteness of
![]() ${\mathrm {int}}_{p,v}(f)$
does not depend on the choice of p and v among vectors such that
${\mathrm {int}}_{p,v}(f)$
does not depend on the choice of p and v among vectors such that
![]() $v\ll {\mathbf {0}}$
and
$v\ll {\mathbf {0}}$
and
![]() ${\mathrm {wgt}}_n(v)>1$
.
${\mathrm {wgt}}_n(v)>1$
.
Proof. To show the implication (1)
![]() $\implies $
(2), assume that
$\implies $
(2), assume that
![]() ${\mathrm {int}}_{p,v}(f)$
is finite for some
${\mathrm {int}}_{p,v}(f)$
is finite for some
![]() $v\ll {\mathbf {0}}$
and
$v\ll {\mathbf {0}}$
and
![]() ${\mathrm {wgt}}_n(v)>1$
, and consider any
${\mathrm {wgt}}_n(v)>1$
, and consider any
![]() $p_2\leq p_1$
such that
$p_2\leq p_1$
such that
![]() ${\mathrm {wgt}}_n(p_1)>{\mathrm {real}}_{p,v}(f)$
. Since
${\mathrm {wgt}}_n(p_1)>{\mathrm {real}}_{p,v}(f)$
. Since
![]() ${v\ll {\mathbf {0}}}$
, we may fix some
${v\ll {\mathbf {0}}}$
, we may fix some
![]() $I\in \mathbb {N}$
such that
$I\in \mathbb {N}$
such that
![]() $p_1\leq p-I v$
and
$p_1\leq p-I v$
and
![]() $p+I v\leq p_2$
. If it were the case that
$p+I v\leq p_2$
. If it were the case that
![]() $\unicode{x3bb} (f,(p_2,p_1))>0$
, then
$\unicode{x3bb} (f,(p_2,p_1))>0$
, then
 $$ \begin{align*} &{\mathrm{real}}_{p,v}(f)\geq(p+Iv,p-I v)f=(p+Iv,p_2)f+(p_2,p_1)f+(p_1,p-Iv)f \\ &\quad \geq (p_2,p_1)f={\mathrm{wgt}}_n(p_1)\unicode{x3bb}(f,(p_2,p_1))>{\mathrm{real}}_{p,v}(f)\unicode{x3bb}(f,(p_2,p_1)) \end{align*} $$
$$ \begin{align*} &{\mathrm{real}}_{p,v}(f)\geq(p+Iv,p-I v)f=(p+Iv,p_2)f+(p_2,p_1)f+(p_1,p-Iv)f \\ &\quad \geq (p_2,p_1)f={\mathrm{wgt}}_n(p_1)\unicode{x3bb}(f,(p_2,p_1))>{\mathrm{real}}_{p,v}(f)\unicode{x3bb}(f,(p_2,p_1)) \end{align*} $$
and
![]() $\unicode{x3bb} (f,(p_2,p_1))>0$
implies that
$\unicode{x3bb} (f,(p_2,p_1))>0$
implies that
![]() ${\mathrm {real}}_{p,v}(f)>0$
, but dividing by
${\mathrm {real}}_{p,v}(f)>0$
, but dividing by
![]() ${\mathrm {real}}_{p,v}(f)$
in the inequalities yields
${\mathrm {real}}_{p,v}(f)$
in the inequalities yields
![]() $1>\unicode{x3bb} (f,(p_2,p_1))$
, which is a contradiction.
$1>\unicode{x3bb} (f,(p_2,p_1))$
, which is a contradiction.
To show the implication (2)
![]() $\implies $
(3), assume that
$\implies $
(3), assume that
![]() $\unicode{x3bb} (f,(p_2,p_1))=0$
whenever
$\unicode{x3bb} (f,(p_2,p_1))=0$
whenever
![]() $p_2\leq p_1$
and
$p_2\leq p_1$
and
![]() ${\mathrm {wgt}}_n(p_1)$
is sufficiently large. The number
${\mathrm {wgt}}_n(p_1)$
is sufficiently large. The number
![]() ${\mathrm {wgt}}_n(p+i v)$
tends to infinity as i tends to infinity, so by the assumption,
${\mathrm {wgt}}_n(p+i v)$
tends to infinity as i tends to infinity, so by the assumption,
![]() $\unicode{x3bb} (f,(p+(i+1)v,p+iv))=0$
for sufficiently large i and thus
$\unicode{x3bb} (f,(p+(i+1)v,p+iv))=0$
for sufficiently large i and thus
![]() ${\mathrm {int}}_v(f)$
is finite.
${\mathrm {int}}_v(f)$
is finite.
Lemma 4.23. For
![]() $p,q,v,w\in \mathbb {Z}^d$
satisfying
$p,q,v,w\in \mathbb {Z}^d$
satisfying
![]() $v,w\leq {\mathbf {0}}$
and
$v,w\leq {\mathbf {0}}$
and
![]() ${\mathrm {wgt}}_n(v),{\mathrm {wgt}}_n(w)>1$
, and for
${\mathrm {wgt}}_n(v),{\mathrm {wgt}}_n(w)>1$
, and for
![]() $f\in X_n$
, it holds that
$f\in X_n$
, it holds that
![]() ${\mathrm {frac}}_{p,v}(f)=(p,q)f+{\mathrm {frac}}_{q,w}(f)$
.
${\mathrm {frac}}_{p,v}(f)=(p,q)f+{\mathrm {frac}}_{q,w}(f)$
.
Proof. It suffices to prove that
![]() ${\mathrm {frac}}_{-{\mathbf {k}}}(f)=({\mathbf {0}},p)f+{\mathrm {frac}}_{p,v}(f)$
for sufficiently large
${\mathrm {frac}}_{-{\mathbf {k}}}(f)=({\mathbf {0}},p)f+{\mathrm {frac}}_{p,v}(f)$
for sufficiently large
![]() $k\in \mathbb {N}$
, because then,
$k\in \mathbb {N}$
, because then,
Let therefore
![]() $k\in \mathbb {N}$
be so large that
$k\in \mathbb {N}$
be so large that
![]() $-{\mathbf {k}}=v+v'$
for some
$-{\mathbf {k}}=v+v'$
for some
![]() $v'\ll {\mathbf {0}}$
. For sufficiently large
$v'\ll {\mathbf {0}}$
. For sufficiently large
![]() ${i\in \mathbb {N}}$
, it holds that
${i\in \mathbb {N}}$
, it holds that
![]() $p-iv\leq -iv-iv'$
, and so an application of Lemma 4.15 at the position indicated below shows that the following expression is non-negative and simultaneously bounds it from above:
$p-iv\leq -iv-iv'$
, and so an application of Lemma 4.15 at the position indicated below shows that the following expression is non-negative and simultaneously bounds it from above:
 $$ \begin{align*} &{\mathrm{frac}}_{-{\mathbf{k}}}(f)-{\mathrm{frac}}_{p,v}(f)-({\mathbf{0}},p)f=\lim_{i\to\infty}({\mathbf{0}},i{\mathbf{k}})f-(p,p-iv)f-({\mathbf{0}},p)f \\ &\quad =\lim_{i\to\infty}({\mathbf{0}},i{\mathbf{k}})f-({\mathbf{0}},p-iv) f=\lim_{i\to\infty}(p-iv,i{\mathbf{k}})f \\ &\quad =\lim_{i\to\infty}(p-iv,-iv-iv')f=\lim_{i\to\infty}\unicode{x3bb}(f,(p-iv,-iv-iv'))\ {\mathrm{wgt}}_n(v+v')^{-i} \\ &\quad \overset{L.~{4.15}}{\leq}\lim_{i\to\infty}{\mathrm{wgt}}_n(p+iv'){\mathrm{wgt}}_n(v+v')^{-i}=\lim_{i\to\infty}{\mathrm{wgt}}_n(p)\ {\mathrm{wgt}}_n(v)^{-i}=0. \end{align*} $$
$$ \begin{align*} &{\mathrm{frac}}_{-{\mathbf{k}}}(f)-{\mathrm{frac}}_{p,v}(f)-({\mathbf{0}},p)f=\lim_{i\to\infty}({\mathbf{0}},i{\mathbf{k}})f-(p,p-iv)f-({\mathbf{0}},p)f \\ &\quad =\lim_{i\to\infty}({\mathbf{0}},i{\mathbf{k}})f-({\mathbf{0}},p-iv) f=\lim_{i\to\infty}(p-iv,i{\mathbf{k}})f \\ &\quad =\lim_{i\to\infty}(p-iv,-iv-iv')f=\lim_{i\to\infty}\unicode{x3bb}(f,(p-iv,-iv-iv'))\ {\mathrm{wgt}}_n(v+v')^{-i} \\ &\quad \overset{L.~{4.15}}{\leq}\lim_{i\to\infty}{\mathrm{wgt}}_n(p+iv'){\mathrm{wgt}}_n(v+v')^{-i}=\lim_{i\to\infty}{\mathrm{wgt}}_n(p)\ {\mathrm{wgt}}_n(v)^{-i}=0. \end{align*} $$
Lemma 4.24. Let
![]() $p,q,v,w\in \mathbb {Z}^d$
satisfy
$p,q,v,w\in \mathbb {Z}^d$
satisfy
![]() $v\ll {\mathbf {0}}$
,
$v\ll {\mathbf {0}}$
,
![]() $w\leq {\mathbf {0}}$
and
$w\leq {\mathbf {0}}$
and
![]() ${\mathrm {wgt}}_n(v),{\mathrm {wgt}}_n(w)>1$
, and let
${\mathrm {wgt}}_n(v),{\mathrm {wgt}}_n(w)>1$
, and let
![]() $f\in X_n$
. If
$f\in X_n$
. If
![]() ${\mathrm {int}}_{p,v}(f)$
is finite, it holds that
${\mathrm {int}}_{p,v}(f)$
is finite, it holds that
![]() ${\mathrm {int}}_{p,v}(f)+(p,q)f={\mathrm {int}}_{q,w}(f)$
.
${\mathrm {int}}_{p,v}(f)+(p,q)f={\mathrm {int}}_{q,w}(f)$
.
Proof. From Lemma 4.22, it follows that
![]() ${\mathrm {int}}_{q,w}(f)$
is also finite. By using Lemma 4.22, choose a sufficiently large
${\mathrm {int}}_{q,w}(f)$
is also finite. By using Lemma 4.22, choose a sufficiently large
![]() $I\in \mathbb {N}$
so that
$I\in \mathbb {N}$
so that
![]() $(p',p+Iv)f=0$
and
$(p',p+Iv)f=0$
and
![]() $(q',q+Iw)f=0$
whenever
$(q',q+Iw)f=0$
whenever
![]() $p'\leq p+Iv$
and
$p'\leq p+Iv$
and
![]() $q'\leq q+Iw$
. In particular,
$q'\leq q+Iw$
. In particular,
![]() ${\mathrm {int}}_{p,v}(f)=(p+Iv,p)f$
and
${\mathrm {int}}_{p,v}(f)=(p+Iv,p)f$
and
![]() ${\mathrm {int}}_{q,w}(f)= (q+Iw,q)f$
. Fix some
${\mathrm {int}}_{q,w}(f)= (q+Iw,q)f$
. Fix some
![]() $r\in \mathbb {Z}^d$
such that
$r\in \mathbb {Z}^d$
such that
![]() $r\leq p+Iv$
and
$r\leq p+Iv$
and
![]() $r\leq p+Iw$
. Then
$r\leq p+Iw$
. Then
 $$ \begin{align*} &{\mathrm{int}}_{p,v}(f)+(p,q)f=(r,p+Iv)f+(p+Iv,p)f+(p,q)f=(r,q)f \\ &\quad =(r,q+Iw)f+(q+Iw,q)f={\mathrm{int}}_{q,w}(f). \end{align*} $$
$$ \begin{align*} &{\mathrm{int}}_{p,v}(f)+(p,q)f=(r,p+Iv)f+(p+Iv,p)f+(p,q)f=(r,q)f \\ &\quad =(r,q+Iw)f+(q+Iw,q)f={\mathrm{int}}_{q,w}(f). \end{align*} $$
Proposition 4.25. Let
![]() $p,q,v,w\in \mathbb {Z}^d$
be such that
$p,q,v,w\in \mathbb {Z}^d$
be such that
![]() $v\ll {\mathbf {0}}$
,
$v\ll {\mathbf {0}}$
,
![]() $w\leq {\mathbf {0}}$
, and
$w\leq {\mathbf {0}}$
, and
![]() ${\mathrm {wgt}}_n(v),{\mathrm {wgt}}_n (w)>1$
, and let
${\mathrm {wgt}}_n(v),{\mathrm {wgt}}_n (w)>1$
, and let
![]() $f\in X_n$
. If
$f\in X_n$
. If
![]() ${\mathrm {real}}_{p,v}(f)$
is finite, it holds that
${\mathrm {real}}_{p,v}(f)$
is finite, it holds that
![]() ${\mathrm {real}}_{p,v}(f)={\mathrm {real}}_{q,w}(f)$
.
${\mathrm {real}}_{p,v}(f)={\mathrm {real}}_{q,w}(f)$
.
Proof. Combine the two previous lemmas to see that
and subtract
![]() $(p,q)f$
from both sides of the equality.
$(p,q)f$
from both sides of the equality.
We are now ready to present the analogue of Proposition 4.20 for infinite paths. The following proposition shows that shifting a tessellation by
![]() $\sigma _v$
multiplies the real number it represents by
$\sigma _v$
multiplies the real number it represents by
![]() ${\mathrm {wgt}}_n(-v)$
without additional error terms.
${\mathrm {wgt}}_n(-v)$
without additional error terms.
Proposition 4.26. For
![]() $f\in X_n$
such that
$f\in X_n$
such that
![]() ${\mathrm {real}}(f)$
is finite and
${\mathrm {real}}(f)$
is finite and
![]() $v\in \mathbb {Z}^d$
, it holds that
$v\in \mathbb {Z}^d$
, it holds that
![]() ${\mathrm {real}}(\sigma _v(f))={\mathrm {wgt}}_n(-v){\mathrm {real}}(f)$
.
${\mathrm {real}}(\sigma _v(f))={\mathrm {wgt}}_n(-v){\mathrm {real}}(f)$
.
Proof. We compute
 $$ \begin{align*} &{\mathrm{real}}(\sigma_v(f))\overset{P.~{4.25}}{=}{\mathrm{real}}_{-v,-{\mathbf{1}}}(\sigma_v(f))=\lim_{i\to\infty}(-v-{\mathbf{i}},-v+{\mathbf{i}})\sigma_v(f)\\ &\quad \overset{L.~{4.7}}{=}{\mathrm{wgt}}_n(-v)\lim_{i\to\infty}(-{\mathbf{i}},{\mathbf{i}})f={\mathrm{wgt}}_n(-v)\ {\mathrm{real}}(f). \end{align*} $$
$$ \begin{align*} &{\mathrm{real}}(\sigma_v(f))\overset{P.~{4.25}}{=}{\mathrm{real}}_{-v,-{\mathbf{1}}}(\sigma_v(f))=\lim_{i\to\infty}(-v-{\mathbf{i}},-v+{\mathbf{i}})\sigma_v(f)\\ &\quad \overset{L.~{4.7}}{=}{\mathrm{wgt}}_n(-v)\lim_{i\to\infty}(-{\mathbf{i}},{\mathbf{i}})f={\mathrm{wgt}}_n(-v)\ {\mathrm{real}}(f). \end{align*} $$
4.4. Macrotiles and microtiles
In Figure 6, tiles of
![]() $T_{(2,5)}$
(left) are grouped into
$T_{(2,5)}$
(left) are grouped into
![]() $2\times 2$
squares (middle), values in the centers of the new squares are given by computing the labels from the bottom left to the top right in the original
$2\times 2$
squares (middle), values in the centers of the new squares are given by computing the labels from the bottom left to the top right in the original
![]() $2\times 2$
squares, and labels for the edges of the new squares are given by computing the labels of the boundaries of the original
$2\times 2$
squares, and labels for the edges of the new squares are given by computing the labels of the boundaries of the original
![]() $2\times 2$
squares. For example, assuming that the top right corner of the top right square is at the origin of a tiling f, the value in the center of the new top right square comes from computing
$2\times 2$
squares. For example, assuming that the top right corner of the top right square is at the origin of a tiling f, the value in the center of the new top right square comes from computing
 $$ \begin{align*}\unicode{x3bb}(f,(-{\mathbf{2}},{\mathbf{0}}))\overset{L.~{4.19}}{=}\sum_{i=0}^{1} (2\cdot 5)^i\ {\mathrm{val}}_n(f[-{\mathbf{i}}]) = 8 + 10\cdot 3 = 38\end{align*} $$
$$ \begin{align*}\unicode{x3bb}(f,(-{\mathbf{2}},{\mathbf{0}}))\overset{L.~{4.19}}{=}\sum_{i=0}^{1} (2\cdot 5)^i\ {\mathrm{val}}_n(f[-{\mathbf{i}}]) = 8 + 10\cdot 3 = 38\end{align*} $$
and the label for the right edge of the new top right square comes from computing (with the choices
![]() $p_0={\mathbf {0}}$
,
$p_0={\mathbf {0}}$
,
![]() $p_1=-e_2$
, and
$p_1=-e_2$
, and
![]() $p_2=-2e_2$
in Lemma 4.19)
$p_2=-2e_2$
in Lemma 4.19)
 $$ \begin{align*} &\unicode{x3bb}(f,(-2e_2,{\mathbf{0}}))\overset{L.~{4.19}}{=}\sum_{i=0}^{1} m((2,5),p_{i}-p_0)\ {\mathrm{faceAt}}({\mathbf{0}},p_{i+1}-p_i)f[p_i]\\ &\quad ={\mathrm{faceAt}}({\mathbf{0}},-e_2)f[{\mathbf{0}}] + 5\cdot {\mathrm{faceAt}}({\mathbf{0}},-e_2)f[-e_2] = 3 + 5\cdot 2 = 13. \end{align*} $$
$$ \begin{align*} &\unicode{x3bb}(f,(-2e_2,{\mathbf{0}}))\overset{L.~{4.19}}{=}\sum_{i=0}^{1} m((2,5),p_{i}-p_0)\ {\mathrm{faceAt}}({\mathbf{0}},p_{i+1}-p_i)f[p_i]\\ &\quad ={\mathrm{faceAt}}({\mathbf{0}},-e_2)f[{\mathbf{0}}] + 5\cdot {\mathrm{faceAt}}({\mathbf{0}},-e_2)f[-e_2] = 3 + 5\cdot 2 = 13. \end{align*} $$
It turns out that the resulting squares are tiles of
![]() $T_{(4,25)}$
. Grouping these new tiles again into
$T_{(4,25)}$
. Grouping these new tiles again into
![]() $2\times 2$
squares yields tiles of
$2\times 2$
squares yields tiles of
![]() $T_{(16,625)}$
. In this subsection, we show how partitioning a valid tessellation into larger squares, and even into more general (multidimensional) parallelepipeds, yields new multiplication cubes.
$T_{(16,625)}$
. In this subsection, we show how partitioning a valid tessellation into larger squares, and even into more general (multidimensional) parallelepipeds, yields new multiplication cubes.

Figure 6 Tiles from
![]() $T_{(2,5)}$
(left) grouped into larger macrotiles of
$T_{(2,5)}$
(left) grouped into larger macrotiles of
![]() $T_{(4,25)}$
(middle) and
$T_{(4,25)}$
(middle) and
![]() $T_{(16,625)}$
(right).
$T_{(16,625)}$
(right).
Throughout this subsection, let
![]() $n\in \mathbb {Z}_+^d$
and let A be a
$n\in \mathbb {Z}_+^d$
and let A be a
![]() $d\times d'$
natural number matrix. We interpret the columns
$d\times d'$
natural number matrix. We interpret the columns
![]() $Ae_i$
of A as the generating vectors of the parallelepiped which will yield the new multiplication cubes, e.g., in the case of Figure 6, we would choose
$Ae_i$
of A as the generating vectors of the parallelepiped which will yield the new multiplication cubes, e.g., in the case of Figure 6, we would choose
![]() $A={\mathrm {diag}}(2,2)$
. We denote
$A={\mathrm {diag}}(2,2)$
. We denote
![]() $n^A=m(n,(-Ae_i)_{i=1}^{d'})$
, in particular,
$n^A=m(n,(-Ae_i)_{i=1}^{d'})$
, in particular,
![]() $n^I=n$
for the identity matrix I. We define the A-macrotile map
$n^I=n$
for the identity matrix I. We define the A-macrotile map
![]() ${\mathrm {M}}_{A,n}:X_{n}\to X_{n^{A}}$
(usually written just as
${\mathrm {M}}_{A,n}:X_{n}\to X_{n^{A}}$
(usually written just as
![]() ${\mathrm {M}}_A$
) by
${\mathrm {M}}_A$
) by
for
![]() $f\in X_{n}$
,
$f\in X_{n}$
,
![]() $v\in \mathbb {Z}^{d'}$
. One needs to check that
$v\in \mathbb {Z}^{d'}$
. One needs to check that
![]() ${\mathrm {M}}_A(f)$
really belongs to
${\mathrm {M}}_A(f)$
really belongs to
![]() $X_{n^A}$
. It is simple to verify that
$X_{n^A}$
. It is simple to verify that
![]() $\unicode{x3bb} (f,(A(v-{\mathbf {1}}),Av))\in \Sigma _{N'}$
with
$\unicode{x3bb} (f,(A(v-{\mathbf {1}}),Av))\in \Sigma _{N'}$
with
 $$ \begin{align*}N'=\prod_{i=1}^{d'} n^A[i]=\prod_{i=1}^{d'} m(n,-Ae_i)=m(n,-A{\mathbf{1}}),\end{align*} $$
$$ \begin{align*}N'=\prod_{i=1}^{d'} n^A[i]=\prod_{i=1}^{d'} m(n,-Ae_i)=m(n,-A{\mathbf{1}}),\end{align*} $$
because
![]() $\unicode{x3bb} (f,(A(v-{\mathbf {1}}),Av))<m(n,-A{\mathbf {1}})=N'$
by Lemma 4.15.
$\unicode{x3bb} (f,(A(v-{\mathbf {1}}),Av))<m(n,-A{\mathbf {1}})=N'$
by Lemma 4.15.
In Theorem 4.27, it will turn out that labels in the original tiling correspond to the labels of faces in the macrotiling. From this, it follows that the hyperfaces of neighboring cubes match in
![]() ${\mathrm {M}}_A(f)$
and that
${\mathrm {M}}_A(f)$
and that
![]() ${\mathrm {M}}_A(f)\in X_{n^A}$
.
${\mathrm {M}}_A(f)\in X_{n^A}$
.
Let us observe that
 $$ \begin{align*}m(n^A,v_i)=\prod_{j=1}^{d'}m(n,-Ae_j)^{-v_i[j]}=\prod_{j=1}^{d'}m(n,A(v_i[j]e_j))=m(n,Av_i)\end{align*} $$
$$ \begin{align*}m(n^A,v_i)=\prod_{j=1}^{d'}m(n,-Ae_j)^{-v_i[j]}=\prod_{j=1}^{d'}m(n,A(v_i[j]e_j))=m(n,Av_i)\end{align*} $$
and
Theorem 4.27. Let
![]() $f\in X_{n}$
, let
$f\in X_{n}$
, let
![]() $z\in \mathbb {Z}^{d'}$
, and let
$z\in \mathbb {Z}^{d'}$
, and let
![]() $t={\mathrm {M}}_A(f)[z]$
. For
$t={\mathrm {M}}_A(f)[z]$
. For
![]() $s={\mathrm {faceAt}}(p,u)$
with
$s={\mathrm {faceAt}}(p,u)$
with
![]() $p,u\in \mathbb {Z}^{d'}$
, it holds that
$p,u\in \mathbb {Z}^{d'}$
, it holds that
![]() $st=\unicode{x3bb} (f,(A(z+p+u),A(z+p)))$
. In particular,
$st=\unicode{x3bb} (f,(A(z+p+u),A(z+p)))$
. In particular,
![]() ${\mathrm {\tau }}_i({\mathrm {M}}_A(f)[z])={\mathrm {\beta }}_i({\mathrm {M}}_A(f)[z+e_i])$
for any
${\mathrm {\tau }}_i({\mathrm {M}}_A(f)[z])={\mathrm {\beta }}_i({\mathrm {M}}_A(f)[z+e_i])$
for any
![]() $1\leq i\leq d'$
.
$1\leq i\leq d'$
.
Proof. By applying Lemma 4.16 with the choice
we have
 $$ \begin{align*} st&=s\ {\mathrm{cube}}_{n^A}(\unicode{x3bb}(f,(A(z-{\mathbf{1}}),Az))) \\ &={\mathrm{base}}_{n^A}(\unicode{x3bb}(f,(A(z-{\mathbf{1}}),Az),(p,p+u))[2] \\ &={\mathrm{base}}_{n}(\unicode{x3bb}(f,(A(z-{\mathbf{1}}),Az)),(Ap,A(p+u)))[2] \\ &\overset{L.~{4.16}}{=}\unicode{x3bb}(f,(A(z+p+u),A(z+p))), \end{align*} $$
$$ \begin{align*} st&=s\ {\mathrm{cube}}_{n^A}(\unicode{x3bb}(f,(A(z-{\mathbf{1}}),Az))) \\ &={\mathrm{base}}_{n^A}(\unicode{x3bb}(f,(A(z-{\mathbf{1}}),Az),(p,p+u))[2] \\ &={\mathrm{base}}_{n}(\unicode{x3bb}(f,(A(z-{\mathbf{1}}),Az)),(Ap,A(p+u)))[2] \\ &\overset{L.~{4.16}}{=}\unicode{x3bb}(f,(A(z+p+u),A(z+p))), \end{align*} $$
which proves the first claim. To prove the second claim, we apply the first claim twice:
 $$ \begin{align*} &{\mathrm{\tau}}_i({\mathrm{M}}_A(f)[z])={\mathrm{faceAt}}({\mathbf{0}},-{\mathbf{1}}+e_i)\ {\mathrm{M}}_A(f)[z]=\unicode{x3bb}(f,(A(z-{\mathbf{1}}+e_i),Az)) \\ &\quad ={\mathrm{faceAt}}(-e_i,-{\mathbf{1}}+e_i)\ {\mathrm{M}}_k(f)[z+e_i]={\mathrm{\beta}}_i({\mathrm{M}}_A(f)[z+e_i]). \end{align*} $$
$$ \begin{align*} &{\mathrm{\tau}}_i({\mathrm{M}}_A(f)[z])={\mathrm{faceAt}}({\mathbf{0}},-{\mathbf{1}}+e_i)\ {\mathrm{M}}_A(f)[z]=\unicode{x3bb}(f,(A(z-{\mathbf{1}}+e_i),Az)) \\ &\quad ={\mathrm{faceAt}}(-e_i,-{\mathbf{1}}+e_i)\ {\mathrm{M}}_k(f)[z+e_i]={\mathrm{\beta}}_i({\mathrm{M}}_A(f)[z+e_i]). \end{align*} $$
Remark 4.28. Consider the special case where the columns of A are the first
![]() $d'$
elementary basis vectors of
$d'$
elementary basis vectors of
![]() $\mathbb {Z}^d$
. Then for every
$\mathbb {Z}^d$
. Then for every
![]() $z'\in \mathbb {Z}^{d'}$
, we have
$z'\in \mathbb {Z}^{d'}$
, we have
![]() $Az'=z'{\mathrm {\vee }}_{d'}{\mathbf {0}}$
, where
$Az'=z'{\mathrm {\vee }}_{d'}{\mathbf {0}}$
, where
![]() ${\mathbf {0}}\in \mathbb {Z}^{d-d'}$
. Fix
${\mathbf {0}}\in \mathbb {Z}^{d-d'}$
. Fix
![]() $z'\in \mathbb {Z}^{d'}$
and let
$z'\in \mathbb {Z}^{d'}$
and let
![]() $z=Az'$
. Let
$z=Az'$
. Let
![]() $s'={\mathrm {faceAt}}(p',u')$
for
$s'={\mathrm {faceAt}}(p',u')$
for
![]() $p',u'\in \mathbb {Z}^{d'}$
and let
$p',u'\in \mathbb {Z}^{d'}$
and let
![]() $p=Ap'$
,
$p=Ap'$
,
![]() $u=Au'$
. Then
$u=Au'$
. Then
![]() $p,u\in \{-1,0\}^d$
are orthogonal, so we may define
$p,u\in \{-1,0\}^d$
are orthogonal, so we may define
![]() $s={\mathrm {faceAt}}(p,u)$
and it follows that
$s={\mathrm {faceAt}}(p,u)$
and it follows that
 $$ \begin{align*} s'({\mathrm{M}}_A(f)[z'])&\overset{T.~{4.27}}{=}\unicode{x3bb}(f,(A(z'+p'+u'),A(z'+p'))) \\ &=\unicode{x3bb}(f,{D}_z(s))\overset{L.~{4.18}}{=}sf[z]. \end{align*} $$
$$ \begin{align*} s'({\mathrm{M}}_A(f)[z'])&\overset{T.~{4.27}}{=}\unicode{x3bb}(f,(A(z'+p'+u'),A(z'+p'))) \\ &=\unicode{x3bb}(f,{D}_z(s))\overset{L.~{4.18}}{=}sf[z]. \end{align*} $$
The meaning of this equality is that the tessellation
![]() ${\mathrm {M}}_A(f)$
is formed by looking at a cut of the tessellation f along the first
${\mathrm {M}}_A(f)$
is formed by looking at a cut of the tessellation f along the first
![]() $d'$
coordinate axes.
$d'$
coordinate axes.
As a more concrete example, consider
![]() $f\in X_{(2,3,5)}$
, and let the columns of A be the basis vectors
$f\in X_{(2,3,5)}$
, and let the columns of A be the basis vectors
![]() $e_1=(1,0,0)$
and
$e_1=(1,0,0)$
and
![]() $e_2=(0,1,0)$
. For any
$e_2=(0,1,0)$
. For any
![]() $z'=(z_1,z_2)\in \mathbb {Z}^2$
and any face of the two-dimensional cube
$z'=(z_1,z_2)\in \mathbb {Z}^2$
and any face of the two-dimensional cube
![]() $s={\mathrm {faceAt}}((p_1,p_2),(u_1,u_2))$
, one finds that
$s={\mathrm {faceAt}}((p_1,p_2),(u_1,u_2))$
, one finds that
 $$ \begin{align*} &{\mathrm{faceAt}}((p_1,p_2),(u_1,u_2))\ {\mathrm{M}}_A(f)[(z_1,z_2)] \\ &\quad ={\mathrm{faceAt}}((p_1,p_2,0),(u_1,u_2,0))f[(z_1,z_2,0)]. \end{align*} $$
$$ \begin{align*} &{\mathrm{faceAt}}((p_1,p_2),(u_1,u_2))\ {\mathrm{M}}_A(f)[(z_1,z_2)] \\ &\quad ={\mathrm{faceAt}}((p_1,p_2,0),(u_1,u_2,0))f[(z_1,z_2,0)]. \end{align*} $$
Assuming that the cube in Figure 2 is equal to
![]() $f[(z_1,z_2,0)]$
, then the values of all the hyperfaces of
$f[(z_1,z_2,0)]$
, then the values of all the hyperfaces of
![]() ${\mathrm {M}}_A(f)[(z_1,z_2)]$
are equal to the values on the corresponding hyperfaces of
${\mathrm {M}}_A(f)[(z_1,z_2)]$
are equal to the values on the corresponding hyperfaces of
![]() $f[(z_1,z_2,0)]$
on the plane
$f[(z_1,z_2,0)]$
on the plane
![]() $z=0$
. This explains why the top face and its adjacent edges in Figure 2 yield a multiplication cube from
$z=0$
. This explains why the top face and its adjacent edges in Figure 2 yield a multiplication cube from
![]() $T_{(2,3)}$
.
$T_{(2,3)}$
.
Lemma 4.29. Let
![]() $f\in X_{n}$
and let
$f\in X_{n}$
and let
![]() $p,p'\in \mathbb {Z}^{d'}$
. Then
$p,p'\in \mathbb {Z}^{d'}$
. Then
Proof. The two equalities are equivalent, so it suffices to prove the first one. We first show for
![]() $z,v\in \mathbb {Z}^d$
,
$z,v\in \mathbb {Z}^d$
,
![]() $v\geq {\mathbf {0}}$
, that
$v\geq {\mathbf {0}}$
, that
In the special case
![]() $v=e_i$
for some
$v=e_i$
for some
![]() $1\leq i\leq d'$
, let
$1\leq i\leq d'$
, let
![]() $t={\mathrm {M}}_A(f)[z]$
and
$t={\mathrm {M}}_A(f)[z]$
and
![]() $s={\mathrm {faceAt}}({\mathbf {0}},-e_i)$
. Then by Theorem 4.27,
$s={\mathrm {faceAt}}({\mathbf {0}},-e_i)$
. Then by Theorem 4.27,
In general,
![]() $v=\sum _{k=1}^m e_{i_k}$
for some
$v=\sum _{k=1}^m e_{i_k}$
for some
![]() $m\in \mathbb {N}$
. Denote
$m\in \mathbb {N}$
. Denote
![]() $v_j=\sum _{k=1}^j e_{i_k}$
for
$v_j=\sum _{k=1}^j e_{i_k}$
for
![]() $0\leq j\leq m$
. Then
$0\leq j\leq m$
. Then
 $$ \begin{align*} \unicode{x3bb}({\mathrm{M}}_A(f),(z-v,z))&\overset{L.~{4.14}}{=}\sum_{i=0}^{m-1}m(n^A,-v_i)\ \unicode{x3bb}({\mathrm{M}}_A(f),(z-v_{i}-e_{i+1},z-v_i)) \\ &=\sum_{i=0}^{m-1}m(n,-Av_i)\ \unicode{x3bb}(f,(A(z-v_{i}-e_{i+1}),A(z-v_i))) \\ &\overset{L.~{4.14}}{=}\unicode{x3bb}(f,(A(z-v),Az). \end{align*} $$
$$ \begin{align*} \unicode{x3bb}({\mathrm{M}}_A(f),(z-v,z))&\overset{L.~{4.14}}{=}\sum_{i=0}^{m-1}m(n^A,-v_i)\ \unicode{x3bb}({\mathrm{M}}_A(f),(z-v_{i}-e_{i+1},z-v_i)) \\ &=\sum_{i=0}^{m-1}m(n,-Av_i)\ \unicode{x3bb}(f,(A(z-v_{i}-e_{i+1}),A(z-v_i))) \\ &\overset{L.~{4.14}}{=}\unicode{x3bb}(f,(A(z-v),Az). \end{align*} $$
To prove the statement of the lemma, let
![]() $p"\in \mathbb {Z}^d$
such that
$p"\in \mathbb {Z}^d$
such that
![]() $p"\geq p$
and
$p"\geq p$
and
![]() $p"\geq p'$
. The previous part is applied in the following with the choices
$p"\geq p'$
. The previous part is applied in the following with the choices
![]() $z=p"$
and
$z=p"$
and
![]() $v=p"-p$
or
$v=p"-p$
or
![]() $v=p"-p'$
, thus yielding
$v=p"-p'$
, thus yielding
 $$ \begin{align*} &\unicode{x3bb}({\mathrm{M}}_A(f),(p,p')) \\ &\quad \overset{L.~{4.14}}{=}m(n^A,p"-p')\unicode{x3bb}({\mathrm{M}}_A(f),(p,p"))+\unicode{x3bb}({\mathrm{M}}_A(f),(p",p')) \\ &\quad =m(n,A(p"-p'))\unicode{x3bb}(f,(Ap,Ap"))+\unicode{x3bb}(f,(Ap",Ap'))\\ &\quad\overset{L.~{4.14}}{=}\unicode{x3bb}(f,(Ap,Ap')).\end{align*} $$
$$ \begin{align*} &\unicode{x3bb}({\mathrm{M}}_A(f),(p,p')) \\ &\quad \overset{L.~{4.14}}{=}m(n^A,p"-p')\unicode{x3bb}({\mathrm{M}}_A(f),(p,p"))+\unicode{x3bb}({\mathrm{M}}_A(f),(p",p')) \\ &\quad =m(n,A(p"-p'))\unicode{x3bb}(f,(Ap,Ap"))+\unicode{x3bb}(f,(Ap",Ap'))\\ &\quad\overset{L.~{4.14}}{=}\unicode{x3bb}(f,(Ap,Ap')).\end{align*} $$
Now we can show that the real number represented by a tessellation is preserved by the macrotile map
![]() ${\mathrm {M}}_A$
.
${\mathrm {M}}_A$
.
Proposition 4.30. Let A be a
![]() $d\times d'$
natural number matrix such that
$d\times d'$
natural number matrix such that
![]() $N'={\mathrm {wgt}}_n(-A{\mathbf {1}})>1$
. For any
$N'={\mathrm {wgt}}_n(-A{\mathbf {1}})>1$
. For any
![]() $f\in X_n$
such that
$f\in X_n$
such that
![]() ${\mathrm {real}}(f)$
is finite, it holds that
${\mathrm {real}}(f)$
is finite, it holds that
![]() ${\mathrm {real}}({\mathrm {M}}_A(f))={\mathrm {real}}(f)$
.
${\mathrm {real}}({\mathrm {M}}_A(f))={\mathrm {real}}(f)$
.
Proof. Finiteness of
![]() ${\mathrm {real}}(f)$
will be required for applying Lemma 4.25. We compute
${\mathrm {real}}(f)$
will be required for applying Lemma 4.25. We compute
 $$ \begin{align*} {\mathrm{real}}({\mathrm{M}}_A(f))&=\lim_{i\to\infty}(-{\mathbf{i}},{\mathbf{i}})\ {\mathrm{M}}_A(f) \\ &\overset{L.~{4.29}}{=}\lim_{i\to\infty}(-iA{\mathbf{1}},iA{\mathbf{1}})f={\mathrm{real}}_{-A{\mathbf{1}}}(f)\overset{P.~{4.25}}{=}{\mathrm{real}}(f). \end{align*} $$
$$ \begin{align*} {\mathrm{real}}({\mathrm{M}}_A(f))&=\lim_{i\to\infty}(-{\mathbf{i}},{\mathbf{i}})\ {\mathrm{M}}_A(f) \\ &\overset{L.~{4.29}}{=}\lim_{i\to\infty}(-iA{\mathbf{1}},iA{\mathbf{1}})f={\mathrm{real}}_{-A{\mathbf{1}}}(f)\overset{P.~{4.25}}{=}{\mathrm{real}}(f). \end{align*} $$
In the following lemmas, we show that the composition of macrotile maps corresponds to matrix multiplication.
Lemma 4.31. Let A be a
![]() $d\times d'$
and let B be a
$d\times d'$
and let B be a
![]() $d'\times d"$
natural number matrix. Then
$d'\times d"$
natural number matrix. Then
![]() $(n^A)^B=n^{AB}$
.
$(n^A)^B=n^{AB}$
.
Proof.
Lemma 4.32. Let A be a
![]() $d\times d'$
and let B be a
$d\times d'$
and let B be a
![]() $d'\times d"$
natural number matrix. Then
$d'\times d"$
natural number matrix. Then
![]() ${\mathrm {M}}_{B,n^A}\circ {\mathrm {M}}_{A,n}={\mathrm {M}}_{AB,n}$
.
${\mathrm {M}}_{B,n^A}\circ {\mathrm {M}}_{A,n}={\mathrm {M}}_{AB,n}$
.
Proof. For
![]() $f\in X_{n}$
and
$f\in X_{n}$
and
![]() $v\in \mathbb {Z}^{d"}$
, we compute
$v\in \mathbb {Z}^{d"}$
, we compute
 $$ \begin{align*} {\mathrm{M}}_{B,n^A}({\mathrm{M}}_{A,n}(f))[v]&\overset{L.~{4.31}}{=} {\mathrm{cube}}_{n^{AB}}(\unicode{x3bb}({\mathrm{M}}_{A,n}(f),(B(v-{\mathbf{1}}),Bv))) \\ &\overset{L.~{4.29}}{=}{\mathrm{cube}}_{n^{AB}} (\unicode{x3bb}(f,(AB(v-{\mathbf{1}}),ABv)))={\mathrm{M}}_{AB,n}(f)[v].\quad \end{align*} $$
$$ \begin{align*} {\mathrm{M}}_{B,n^A}({\mathrm{M}}_{A,n}(f))[v]&\overset{L.~{4.31}}{=} {\mathrm{cube}}_{n^{AB}}(\unicode{x3bb}({\mathrm{M}}_{A,n}(f),(B(v-{\mathbf{1}}),Bv))) \\ &\overset{L.~{4.29}}{=}{\mathrm{cube}}_{n^{AB}} (\unicode{x3bb}(f,(AB(v-{\mathbf{1}}),ABv)))={\mathrm{M}}_{AB,n}(f)[v].\quad \end{align*} $$
Now let A be a
![]() $d\times d'$
natural number matrix all of whose rows contain a positive integer. Then the A-macrotile map is going to have an inverse, the A-microtile map
$d\times d'$
natural number matrix all of whose rows contain a positive integer. Then the A-macrotile map is going to have an inverse, the A-microtile map
![]() ${{\mathrm {\mu }}_{A,n}:X_{n^{A}}\to X_{n}}$
. By the assumption on A for every element
${{\mathrm {\mu }}_{A,n}:X_{n^{A}}\to X_{n}}$
. By the assumption on A for every element
![]() $x\in \mathbb {Z}^d$
, there is a
$x\in \mathbb {Z}^d$
, there is a
![]() $z_1\in \mathbb {Z}^{d'}$
such that
$z_1\in \mathbb {Z}^{d'}$
such that
![]() $Az_1\geq x$
and thus x can be written in the form
$Az_1\geq x$
and thus x can be written in the form
![]() $x=Az_1-v$
with
$x=Az_1-v$
with
![]() $v\in \mathbb {Z}^d$
,
$v\in \mathbb {Z}^d$
,
![]() $v\geq {\mathbf {0}}$
. Let
$v\geq {\mathbf {0}}$
. Let
![]() $z_2\in \mathbb {Z}^{d'}$
satisfy
$z_2\in \mathbb {Z}^{d'}$
satisfy
![]() $z_1\geq z_2$
,
$z_1\geq z_2$
,
![]() $x-{\mathbf {1}}\geq Az_2$
, let
$x-{\mathbf {1}}\geq Az_2$
, let
![]() $a=\unicode{x3bb} (f,(z_2,z_1))$
for
$a=\unicode{x3bb} (f,(z_2,z_1))$
for
![]() $f\in X_{n^A}$
and define the map
$f\in X_{n^A}$
and define the map
![]() ${\mathrm {\mu }}_{A,n}$
(usually written just as
${\mathrm {\mu }}_{A,n}$
(usually written just as
![]() ${\mathrm {\mu }}_A$
) by
${\mathrm {\mu }}_A$
) by
We need to verify that
![]() ${\mathrm {\mu }}_A(f)[x]$
is well defined (which we will do in Lemma 4.33) and that
${\mathrm {\mu }}_A(f)[x]$
is well defined (which we will do in Lemma 4.33) and that
![]() ${\mathrm {\mu }}_A(f)$
is indeed in
${\mathrm {\mu }}_A(f)$
is indeed in
![]() $X_{n}$
(which we will do in Theorem 4.35). It is simple that
$X_{n}$
(which we will do in Theorem 4.35). It is simple that
![]() ${\mathrm {base}}_{n}(a,(-v,-v-{\mathbf {1}}))[2])\in \Sigma _N$
with
${\mathrm {base}}_{n}(a,(-v,-v-{\mathbf {1}}))[2])\in \Sigma _N$
with
![]() $N=\prod _{i=1}^d n[i]$
, since
$N=\prod _{i=1}^d n[i]$
, since
The assumption that all the rows of A contain a positive integer will hold until Theorem 4.40. Frequent appearances of the map
![]() $\mu _A$
(which is not defined for other kinds of matrices) are also reminders of this.
$\mu _A$
(which is not defined for other kinds of matrices) are also reminders of this.
Lemma 4.33. Let
![]() $f\in X_{n^A}$
and let
$f\in X_{n^A}$
and let
![]() $x\in \mathbb {Z}^d$
. Let
$x\in \mathbb {Z}^d$
. Let
![]() $z_1,z_1'\in \mathbb {Z}^d$
,
$z_1,z_1'\in \mathbb {Z}^d$
,
![]() $v,v'\in \mathbb {Z}^{d}$
,
$v,v'\in \mathbb {Z}^{d}$
,
![]() $v,v'\geq {\mathbf {0}}$
be such that
$v,v'\geq {\mathbf {0}}$
be such that
![]() $x=Az_1-v=Az_1'-v'$
. Let
$x=Az_1-v=Az_1'-v'$
. Let
![]() $z_2,z_2'\in \mathbb {Z}^{d'}$
satisfy
$z_2,z_2'\in \mathbb {Z}^{d'}$
satisfy
![]() $z_1\geq z_2$
,
$z_1\geq z_2$
,
![]() $z_1'\geq z_2'$
,
$z_1'\geq z_2'$
,
![]() $x-{\mathbf {1}}\geq Az_2, Az_2'$
. Denote
$x-{\mathbf {1}}\geq Az_2, Az_2'$
. Denote
![]() $a=\unicode{x3bb} (f,(z_2,z_1))$
and
$a=\unicode{x3bb} (f,(z_2,z_1))$
and
![]() $a'=\unicode{x3bb} (f,(z_2',z_1'))$
. Then
$a'=\unicode{x3bb} (f,(z_2',z_1'))$
. Then
Proof. It is possible to choose
![]() $z_1",z_2"\in \mathbb {Z}^{d'}$
and
$z_1",z_2"\in \mathbb {Z}^{d'}$
and
![]() $v"\in \mathbb {Z}^d$
,
$v"\in \mathbb {Z}^d$
,
![]() $v"\geq {\mathbf {0}}$
so that
$v"\geq {\mathbf {0}}$
so that
![]() $x=Az_1"-v"$
,
$x=Az_1"-v"$
,
![]() $z_1"\geq z_2"$
,
$z_1"\geq z_2"$
,
![]() $x-{\mathbf {1}}\geq Az_2"$
, and furthermore,
$x-{\mathbf {1}}\geq Az_2"$
, and furthermore,
![]() $z_1"\geq z_1,z_1'$
and
$z_1"\geq z_1,z_1'$
and
![]() $z_2"\leq z_2,z_2'$
, that is,
$z_2"\leq z_2,z_2'$
, that is,
![]() $z_1"$
and
$z_1"$
and
![]() $z_2"$
are common upper and lower bounds for
$z_2"$
are common upper and lower bounds for
![]() $z_1,z_1'$
and
$z_1,z_1'$
and
![]() $z_2,z_2'$
. Therefore, to prove the lemma, it is sufficient to consider the case of
$z_2,z_2'$
. Therefore, to prove the lemma, it is sufficient to consider the case of
![]() $z_1'\geq z_1$
and
$z_1'\geq z_1$
and
![]() $z_2'\leq z_2$
.
$z_2'\leq z_2$
.
Observe that
 $$ \begin{align*} \unicode{x3bb}(f,(z_2',z_1'))&\overset{L.~{4.14}}{=}m(n^A,z_2-z_1')\unicode{x3bb}(f,(z_2',z_2)) \\ &\quad +m(n^A,z_1-z_1')\unicode{x3bb}(f,(z_2,z_1))+\unicode{x3bb}(f,(z_1,z_1')) \\ &=m(n,A(z_2-z_1'))\underbrace{\unicode{x3bb}(f,(z_2',z_2))}_{a_2} \\ &\quad +m(n,A(z_1-z_1'))\underbrace{\unicode{x3bb}(f,(z_2,z_1))}_{a_1}+\underbrace{\unicode{x3bb}(f,(z_1,z_1'))}_{a_0}. \end{align*} $$
$$ \begin{align*} \unicode{x3bb}(f,(z_2',z_1'))&\overset{L.~{4.14}}{=}m(n^A,z_2-z_1')\unicode{x3bb}(f,(z_2',z_2)) \\ &\quad +m(n^A,z_1-z_1')\unicode{x3bb}(f,(z_2,z_1))+\unicode{x3bb}(f,(z_1,z_1')) \\ &=m(n,A(z_2-z_1'))\underbrace{\unicode{x3bb}(f,(z_2',z_2))}_{a_2} \\ &\quad +m(n,A(z_1-z_1'))\underbrace{\unicode{x3bb}(f,(z_2,z_1))}_{a_1}+\underbrace{\unicode{x3bb}(f,(z_1,z_1'))}_{a_0}. \end{align*} $$
By Lemma 4.15,
 $$ \begin{align*} a_0&<m(n^A,z_1-z_1')=m(n,A(z_1-z_1')), \\ a_1&<m(n^A,z_2-z_1')/m(n^A,z_1-z_1')=m(n,A(z_2-z_1'))/m(n,A(z_1-z_1')), \end{align*} $$
$$ \begin{align*} a_0&<m(n^A,z_1-z_1')=m(n,A(z_1-z_1')), \\ a_1&<m(n^A,z_2-z_1')/m(n^A,z_1-z_1')=m(n,A(z_2-z_1'))/m(n,A(z_1-z_1')), \end{align*} $$
and therefore,
Let
 $$ \begin{align*} (b_0,b_1,b_2)&={\mathrm{base}}_{n}(\unicode{x3bb}(f,(z_2,z_1))),(-v,-v-{\mathbf{1}})) \\ &={\mathrm{base}}_{n}(a_1,(-v'-A(z_1-z_1'),-v'-A(z_1-z_1')-{\mathbf{1}})). \end{align*} $$
$$ \begin{align*} (b_0,b_1,b_2)&={\mathrm{base}}_{n}(\unicode{x3bb}(f,(z_2,z_1))),(-v,-v-{\mathbf{1}})) \\ &={\mathrm{base}}_{n}(a_1,(-v'-A(z_1-z_1'),-v'-A(z_1-z_1')-{\mathbf{1}})). \end{align*} $$
To see that the mixed base expression after this paragraph contains a valid d-directive sequence, we need to check that
![]() $A(z_1-z_1')\geq -v'$
and
$A(z_1-z_1')\geq -v'$
and
![]() $-v'-{\mathbf {1}}\geq A(z_2-z_1')$
. By definition,
$-v'-{\mathbf {1}}\geq A(z_2-z_1')$
. By definition,
![]() $Az_1-v=Az_1'-v'$
and thus
$Az_1-v=Az_1'-v'$
and thus
![]() $-v'=A(z_1-z_1')-v\leq A(z_1-z_1')$
. The other inequality is shown by
$-v'=A(z_1-z_1')-v\leq A(z_1-z_1')$
. The other inequality is shown by
By Lemma 3.3,
We conclude by computing
 $$ \begin{align*} &{\mathrm{base}}_{n}(a,(-v,-v-{\mathbf{1}}))[2]={\mathrm{base}}_{n}(\unicode{x3bb}(f,(z_1,z_2))),(-v,-v-{\mathbf{1}}))[2]=b_1 \\ &\quad ={\mathrm{base}}_{n}(\unicode{x3bb}(f,(z_2',z_1')),(A(z_1-z_1'),-v',-v'-{\mathbf{1}},A(z_2-z_1')))[3] \\ &\quad\overset{L.~{3.4}}{=}{\mathrm{base}}_{n}(\unicode{x3bb}(f,(z_2',z_1')),(-v',-v'-{\mathbf{1}}))[2]={\mathrm{base}}_{n}(a',(-v',-v'-{\mathbf{1}}))[2].\qquad \end{align*} $$
$$ \begin{align*} &{\mathrm{base}}_{n}(a,(-v,-v-{\mathbf{1}}))[2]={\mathrm{base}}_{n}(\unicode{x3bb}(f,(z_1,z_2))),(-v,-v-{\mathbf{1}}))[2]=b_1 \\ &\quad ={\mathrm{base}}_{n}(\unicode{x3bb}(f,(z_2',z_1')),(A(z_1-z_1'),-v',-v'-{\mathbf{1}},A(z_2-z_1')))[3] \\ &\quad\overset{L.~{3.4}}{=}{\mathrm{base}}_{n}(\unicode{x3bb}(f,(z_2',z_1')),(-v',-v'-{\mathbf{1}}))[2]={\mathrm{base}}_{n}(a',(-v',-v'-{\mathbf{1}}))[2].\qquad \end{align*} $$
Lemma 4.34. Let
![]() $f\in X_{n^A}$
and let
$f\in X_{n^A}$
and let
![]() $x\in \mathbb {Z}^d$
. Let
$x\in \mathbb {Z}^d$
. Let
![]() $z_1\in \mathbb {Z}^{d'}$
,
$z_1\in \mathbb {Z}^{d'}$
,
![]() $v\in \mathbb {Z}^{d}$
,
$v\in \mathbb {Z}^{d}$
,
![]() $v\geq {\mathbf {0}}$
be such that
$v\geq {\mathbf {0}}$
be such that
![]() $x=Az_1-v$
. Let
$x=Az_1-v$
. Let
![]() $z_2\in \mathbb {Z}^{d'}$
satisfy
$z_2\in \mathbb {Z}^{d'}$
satisfy
![]() $z_1\geq z_2$
and
$z_1\geq z_2$
and
![]() $x-{\mathbf {1}}\geq Az_2$
. Denote
$x-{\mathbf {1}}\geq Az_2$
. Denote
![]() $a=\unicode{x3bb} (f,(z_2,z_1))$
. For any face
$a=\unicode{x3bb} (f,(z_2,z_1))$
. For any face
![]() $s={\mathrm {faceAt}}(p,u)$
, it holds that
$s={\mathrm {faceAt}}(p,u)$
, it holds that
Proof. Let
![]() $(a_0,a_1,a_2)={\mathrm {base}}_{n}(a,(-v,-v-{\mathbf {1}}))$
. By Lemma 3.5,
$(a_0,a_1,a_2)={\mathrm {base}}_{n}(a,(-v,-v-{\mathbf {1}}))$
. By Lemma 3.5,
so we can compute
 $$ \begin{align*} &{\mathrm{faceAt}}(p,u)({\mathrm{\mu}}_A(f)[Az_1-v])={\mathrm{base}}_{n}({\mathrm{base}}_{n}(a,(-v,-v-{\mathbf{1}}))[2],(p,p+u))[2] \\ &\quad ={\mathrm{base}}_{n}(a_1,(p,p+u))[2]={\mathrm{base}}_{n}(a,(-v+p,-v+p+u))[2]. \end{align*} $$
$$ \begin{align*} &{\mathrm{faceAt}}(p,u)({\mathrm{\mu}}_A(f)[Az_1-v])={\mathrm{base}}_{n}({\mathrm{base}}_{n}(a,(-v,-v-{\mathbf{1}}))[2],(p,p+u))[2] \\ &\quad ={\mathrm{base}}_{n}(a_1,(p,p+u))[2]={\mathrm{base}}_{n}(a,(-v+p,-v+p+u))[2]. \end{align*} $$
Theorem 4.35. Let
![]() $f\in X_{n^A}$
. Then
$f\in X_{n^A}$
. Then
![]() ${\mathrm {\mu }}_A(f)\in X_{n}$
.
${\mathrm {\mu }}_A(f)\in X_{n}$
.
Proof. We need to show that
![]() ${\mathrm {\tau }}_i({\mathrm {\mu }}_A(f)[w])={\mathrm {\beta }}_i({\mathrm {\mu }}_A(f)[w+e_i])$
for any
${\mathrm {\tau }}_i({\mathrm {\mu }}_A(f)[w])={\mathrm {\beta }}_i({\mathrm {\mu }}_A(f)[w+e_i])$
for any
![]() $w\in \mathbb {Z}^d$
and
$w\in \mathbb {Z}^d$
and
![]() $1\leq i\leq d$
. Let
$1\leq i\leq d$
. Let
![]() $z_1,z_2\in \mathbb {Z}^{d'}$
be such that Lemma 4.34 can be applied at coordinates w and
$z_1,z_2\in \mathbb {Z}^{d'}$
be such that Lemma 4.34 can be applied at coordinates w and
![]() $w+e_i$
. Let
$w+e_i$
. Let
![]() $w=Az_1-v$
and
$w=Az_1-v$
and
![]() $w+e_i=Az_1-u$
, from which it follows that
$w+e_i=Az_1-u$
, from which it follows that
![]() ${-v+e_i=-u}$
. Denote
${-v+e_i=-u}$
. Denote
![]() $a=\unicode{x3bb} (f,(z_2,z_1))$
. By applying Lemma 4.34 two times, we see that
$a=\unicode{x3bb} (f,(z_2,z_1))$
. By applying Lemma 4.34 two times, we see that
 $$ \begin{align*} {\mathrm{\tau}}_i({\mathrm{\mu}}_A(f)[w])&={\mathrm{base}}_{n}(a,(-v,-v-{\mathbf{1}}+e_i))[2] \\ &={\mathrm{base}}_{n}(a,((-v+e_i)-e_i,(-v+e_i)-e_i+(-{\mathbf{1}}+e_i)))[2] \\ &={\mathrm{base}}_{n}(a,(-u-e_i,-u-e_i+(-{\mathbf{1}}+e_i)))[2] \\ &={\mathrm{\beta}}_i({\mathrm{\mu}}_A(f)[w+e_i]). \end{align*} $$
$$ \begin{align*} {\mathrm{\tau}}_i({\mathrm{\mu}}_A(f)[w])&={\mathrm{base}}_{n}(a,(-v,-v-{\mathbf{1}}+e_i))[2] \\ &={\mathrm{base}}_{n}(a,((-v+e_i)-e_i,(-v+e_i)-e_i+(-{\mathbf{1}}+e_i)))[2] \\ &={\mathrm{base}}_{n}(a,(-u-e_i,-u-e_i+(-{\mathbf{1}}+e_i)))[2] \\ &={\mathrm{\beta}}_i({\mathrm{\mu}}_A(f)[w+e_i]). \end{align*} $$
Lemma 4.36. Let
![]() $f\in X_{n^A}$
and let
$f\in X_{n^A}$
and let
![]() $p,p'\in \mathbb {Z}^{d'}$
. Then
$p,p'\in \mathbb {Z}^{d'}$
. Then
Proof. The two equalities are equivalent, so it suffices to prove the first one. We first show for
![]() $z_1\in \mathbb {Z}^{d'},v\in \mathbb {Z}^d$
,
$z_1\in \mathbb {Z}^{d'},v\in \mathbb {Z}^d$
,
![]() $v\geq {\mathbf {0}}$
that
$v\geq {\mathbf {0}}$
that
We can represent
![]() $Av=\sum _{k=1}^m e_{i_k}$
for some
$Av=\sum _{k=1}^m e_{i_k}$
for some
![]() $m\in \mathbb {N}$
. Denote
$m\in \mathbb {N}$
. Denote
![]() $v^{\prime }_j=\sum _{k=1}^j e_{i_k}$
for
$v^{\prime }_j=\sum _{k=1}^j e_{i_k}$
for
![]() $0\leq j\leq m$
, so in particular,
$0\leq j\leq m$
, so in particular,
![]() $Av=v^{\prime }_m$
. Denote
$Av=v^{\prime }_m$
. Denote
![]() $s_i={\mathrm {faceAt}}({\mathbf {0}},-e_i)$
for any
$s_i={\mathrm {faceAt}}({\mathbf {0}},-e_i)$
for any
![]() $1\leq i\leq m$
. Choose
$1\leq i\leq m$
. Choose
![]() ${z_2\in \mathbb {Z}^{d'}}$
so that Lemma 4.34 can be applied to faces
${z_2\in \mathbb {Z}^{d'}}$
so that Lemma 4.34 can be applied to faces
![]() $s_{i_{j+1}}$
of the microtiles at coordinates of the form
$s_{i_{j+1}}$
of the microtiles at coordinates of the form
![]() $Az_1-v^{\prime }_j$
. Let
$Az_1-v^{\prime }_j$
. Let
![]() $a=\unicode{x3bb} (f,(z_2,z_1))$
. Then
$a=\unicode{x3bb} (f,(z_2,z_1))$
. Then
 $$ \begin{align*} \unicode{x3bb}({\mathrm{\mu}}_A(f),(A(z-v),Az))&=\unicode{x3bb}({\mathrm{\mu}}_A(f),(Az-v^{\prime}_m,Az-v^{\prime}_0)) \\ &\overset{L.~{4.14}}{=}\sum_{j=0}^{m-1}m(n,-v^{\prime}_j)\ \unicode{x3bb}({\mathrm{\mu}}_A(f),(Az-v^{\prime}_{j+1},Az-v^{\prime}_j)) \\ &=\sum_{j=0}^{m-1}m(n,-v^{\prime}_j)\ s_{i_{j+1}}({\mathrm{\mu}}_A(f)[Az-v^{\prime}_j]) \\ &\overset{L.~{4.34}}{=}\sum_{j=0}^{m-1}m(n,-v^{\prime}_j)\ {\mathrm{base}}_{n}(a,(-v^{\prime}_j,\underbrace{-v^{\prime}_j-e_{i_{j+1}}}_{-v^{\prime}_{j+1}}))[2] \\ &\overset{L.~{4.2}}{=}{\mathrm{base}}_{n}(a,(-v^{\prime}_0,-v^{\prime}_m))[2]={\mathrm{base}}_{n}(a,({\mathbf{0}},-Av))[2] \\ &={\mathrm{base}}_{n^A}(\unicode{x3bb}(f,(z_2,z_1)),({\mathbf{0}},-v))[2]\overset{L.~{4.16}}{=}\unicode{x3bb}(f,(z_1-v,z_1)). \end{align*} $$
$$ \begin{align*} \unicode{x3bb}({\mathrm{\mu}}_A(f),(A(z-v),Az))&=\unicode{x3bb}({\mathrm{\mu}}_A(f),(Az-v^{\prime}_m,Az-v^{\prime}_0)) \\ &\overset{L.~{4.14}}{=}\sum_{j=0}^{m-1}m(n,-v^{\prime}_j)\ \unicode{x3bb}({\mathrm{\mu}}_A(f),(Az-v^{\prime}_{j+1},Az-v^{\prime}_j)) \\ &=\sum_{j=0}^{m-1}m(n,-v^{\prime}_j)\ s_{i_{j+1}}({\mathrm{\mu}}_A(f)[Az-v^{\prime}_j]) \\ &\overset{L.~{4.34}}{=}\sum_{j=0}^{m-1}m(n,-v^{\prime}_j)\ {\mathrm{base}}_{n}(a,(-v^{\prime}_j,\underbrace{-v^{\prime}_j-e_{i_{j+1}}}_{-v^{\prime}_{j+1}}))[2] \\ &\overset{L.~{4.2}}{=}{\mathrm{base}}_{n}(a,(-v^{\prime}_0,-v^{\prime}_m))[2]={\mathrm{base}}_{n}(a,({\mathbf{0}},-Av))[2] \\ &={\mathrm{base}}_{n^A}(\unicode{x3bb}(f,(z_2,z_1)),({\mathbf{0}},-v))[2]\overset{L.~{4.16}}{=}\unicode{x3bb}(f,(z_1-v,z_1)). \end{align*} $$
On the last line, we need that
![]() $(z_1,z_1-v,z_2)$
is a
$(z_1,z_1-v,z_2)$
is a
![]() $d'$
-directive sequence, but this can be achieved by choosing
$d'$
-directive sequence, but this can be achieved by choosing
![]() $z_2$
suitably.
$z_2$
suitably.
For the general case, let
![]() $p"\in \mathbb {Z}^d$
such that
$p"\in \mathbb {Z}^d$
such that
![]() $p"\geq p$
and
$p"\geq p$
and
![]() $p"\geq p'$
. The previous part is applied in the following with the choices
$p"\geq p'$
. The previous part is applied in the following with the choices
![]() $z=p"$
and
$z=p"$
and
![]() $v=p"-p$
or
$v=p"-p$
or
![]() $v=p"-p'$
, thus yielding
$v=p"-p'$
, thus yielding
 $$ \begin{align*} \unicode{x3bb}({\mathrm{\mu}}_A(f),(Ap,Ap')) &\overset{L.~{4.14}}{=}m(n,A(p"-p'))\unicode{x3bb}({\mathrm{\mu}}_A(f),(Ap,Ap"))+\unicode{x3bb}({\mathrm{\mu}}_A(f),(Ap",Ap')) \\ &=m(n^A,p"-p')\unicode{x3bb}(f,(p,p"))+\unicode{x3bb}(f,(p",p'))\overset{L.~{4.14}}{=}\unicode{x3bb}(f,(p,p')). \end{align*} $$
$$ \begin{align*} \unicode{x3bb}({\mathrm{\mu}}_A(f),(Ap,Ap')) &\overset{L.~{4.14}}{=}m(n,A(p"-p'))\unicode{x3bb}({\mathrm{\mu}}_A(f),(Ap,Ap"))+\unicode{x3bb}({\mathrm{\mu}}_A(f),(Ap",Ap')) \\ &=m(n^A,p"-p')\unicode{x3bb}(f,(p,p"))+\unicode{x3bb}(f,(p",p'))\overset{L.~{4.14}}{=}\unicode{x3bb}(f,(p,p')). \end{align*} $$
Now we can show that the real number represented by a tessellation is preserved also by the microtile map
![]() ${\mathrm {\mu }}_A$
.
${\mathrm {\mu }}_A$
.
Proposition 4.37. Let A be a
![]() $d\times d'$
natural number matrix all of whose rows contain a positive integer. For any
$d\times d'$
natural number matrix all of whose rows contain a positive integer. For any
![]() $f\in X_{n^A}$
, it holds that
$f\in X_{n^A}$
, it holds that
![]() ${\mathrm {real}}({\mathrm {\mu }}_A(f))={\mathrm {real}}(f)$
.
${\mathrm {real}}({\mathrm {\mu }}_A(f))={\mathrm {real}}(f)$
.
Proof. We observe that
![]() ${\mathrm {wgt}}_n(-{\mathbf {1}})>1$
if and only if
${\mathrm {wgt}}_n(-{\mathbf {1}})>1$
if and only if
![]() ${\mathrm {wgt}}_n(-A{\mathbf {1}})>1$
. The case
${\mathrm {wgt}}_n(-A{\mathbf {1}})>1$
. The case
![]() ${\mathrm {wgt}}_n(-{\mathbf {1}})={\mathrm {wgt}}_n(-A{\mathbf {1}})=1$
is simple because then
${\mathrm {wgt}}_n(-{\mathbf {1}})={\mathrm {wgt}}_n(-A{\mathbf {1}})=1$
is simple because then
![]() ${\mathrm {real}}({\mathrm {\mu }}_A(f))={\mathrm {real}}(f)=0$
.
${\mathrm {real}}({\mathrm {\mu }}_A(f))={\mathrm {real}}(f)=0$
.
Assume then that
![]() ${\mathrm {wgt}}_n(-{\mathbf {1}})>1$
and
${\mathrm {wgt}}_n(-{\mathbf {1}})>1$
and
![]() ${\mathrm {wgt}}_n(-A{\mathbf {1}})>1$
. Because
${\mathrm {wgt}}_n(-A{\mathbf {1}})>1$
. Because
![]() $-{\mathbf {1}}\ll {\mathbf {0}}$
and
$-{\mathbf {1}}\ll {\mathbf {0}}$
and
![]() $-A{\mathbf {1}}\ll {\mathbf {0}}$
, it follows from Proposition 4.25 that the equality
$-A{\mathbf {1}}\ll {\mathbf {0}}$
, it follows from Proposition 4.25 that the equality
![]() ${\mathrm {real}}({\mathrm {\mu }}_A(f))={\mathrm {real}}_{-A{\mathbf {1}}}({\mathrm {\mu }}_A(f))$
holds if one these quantities is finite (and it trivially holds if both of them are infinite). Therefore,
${\mathrm {real}}({\mathrm {\mu }}_A(f))={\mathrm {real}}_{-A{\mathbf {1}}}({\mathrm {\mu }}_A(f))$
holds if one these quantities is finite (and it trivially holds if both of them are infinite). Therefore,
 $$ \begin{align*} {\mathrm{real}}({\mathrm{\mu}}_A(f))&={\mathrm{real}}_{-A{\mathbf{1}}}({\mathrm{\mu}}_A(f))=\lim_{i\to\infty}(-iA{\mathbf{1}},iA{\mathbf{1}}) {\mathrm{\mu}}_A(f) \\ &\overset{L.~{4.36}}{=}\lim_{i\to\infty}(-{\mathbf{i}},{\mathbf{i}})f={\mathrm{real}}(f). \end{align*} $$
$$ \begin{align*} {\mathrm{real}}({\mathrm{\mu}}_A(f))&={\mathrm{real}}_{-A{\mathbf{1}}}({\mathrm{\mu}}_A(f))=\lim_{i\to\infty}(-iA{\mathbf{1}},iA{\mathbf{1}}) {\mathrm{\mu}}_A(f) \\ &\overset{L.~{4.36}}{=}\lim_{i\to\infty}(-{\mathbf{i}},{\mathbf{i}})f={\mathrm{real}}(f). \end{align*} $$
Theorem 4.38. Let A be a natural number matrix all of whose rows contain a positive integer. Then
![]() ${\mathrm {M}}_{A,n}$
and
${\mathrm {M}}_{A,n}$
and
![]() ${\mathrm {\mu }}_{A,n}$
are inverse maps of each other.
${\mathrm {\mu }}_{A,n}$
are inverse maps of each other.
Proof. Let
![]() $f\in X_{n}$
and consider
$f\in X_{n}$
and consider
![]() $x=Az_1-v$
with
$x=Az_1-v$
with
![]() $z_1\in \mathbb {Z}^{d'}$
,
$z_1\in \mathbb {Z}^{d'}$
,
![]() $v\in \mathbb {Z}^{d}$
,
$v\in \mathbb {Z}^{d}$
,
![]() $v\geq {\mathbf {0}}$
. Let
$v\geq {\mathbf {0}}$
. Let
![]() $z_2\in \mathbb {Z}^{d'}$
satisfy
$z_2\in \mathbb {Z}^{d'}$
satisfy
![]() $z_1\geq z_2$
and
$z_1\geq z_2$
and
![]() $x-{\mathbf {1}}\geq Az_2$
. Then
$x-{\mathbf {1}}\geq Az_2$
. Then
 $$ \begin{align*} {\mathrm{\mu}}_A({\mathrm{M}}_A(f))[Az_1-v]&={\mathrm{cube}}_{n}({\mathrm{base}}_{n}(\unicode{x3bb}({\mathrm{M}}_A(f),(z_2,z_1)),(-v,-v-{\mathbf{1}}))[2]) \\ &\overset{L.~{4.29}}{=}{\mathrm{cube}}_{n}({\mathrm{base}}_{n}(\unicode{x3bb}(f,(Az_2,Az_1)),(-v,-v-{\mathbf{1}}))[2]) \\ &\overset{L.~{4.16}}{=}{\mathrm{cube}}_{n}(\unicode{x3bb}(f,(Az_1-v-{\mathbf{1}},Az_1-v))) \\ &\overset{L.~{4.17}}{=}{\mathrm{cube}}_{n}({\mathrm{val}}_{n}(f[Az_1-v]))=f[Az_1-v]. \end{align*} $$
$$ \begin{align*} {\mathrm{\mu}}_A({\mathrm{M}}_A(f))[Az_1-v]&={\mathrm{cube}}_{n}({\mathrm{base}}_{n}(\unicode{x3bb}({\mathrm{M}}_A(f),(z_2,z_1)),(-v,-v-{\mathbf{1}}))[2]) \\ &\overset{L.~{4.29}}{=}{\mathrm{cube}}_{n}({\mathrm{base}}_{n}(\unicode{x3bb}(f,(Az_2,Az_1)),(-v,-v-{\mathbf{1}}))[2]) \\ &\overset{L.~{4.16}}{=}{\mathrm{cube}}_{n}(\unicode{x3bb}(f,(Az_1-v-{\mathbf{1}},Az_1-v))) \\ &\overset{L.~{4.17}}{=}{\mathrm{cube}}_{n}({\mathrm{val}}_{n}(f[Az_1-v]))=f[Az_1-v]. \end{align*} $$
For the other direction, let
![]() $f\in X_{n^A}$
and
$f\in X_{n^A}$
and
![]() $z\in \mathbb {Z}^{d'}$
. Then
$z\in \mathbb {Z}^{d'}$
. Then
 $$ \begin{align*} {\mathrm{M}}_A({\mathrm{\mu}}_A(f))[z]&={\mathrm{cube}}_{n^A}(\unicode{x3bb}({\mathrm{\mu}}_A(f),(A(z-{\mathbf{1}}),Az))) \\ &\overset{L.~{4.36}}{=}{\mathrm{cube}}_{n^A}(\unicode{x3bb}(f,(z-{\mathbf{1}},z)))\overset{L.~{4.17}}{=}{\mathrm{cube}}_{n^A}({\mathrm{val}}_{n^A}(f[z]))=f[z].\qquad \end{align*} $$
$$ \begin{align*} {\mathrm{M}}_A({\mathrm{\mu}}_A(f))[z]&={\mathrm{cube}}_{n^A}(\unicode{x3bb}({\mathrm{\mu}}_A(f),(A(z-{\mathbf{1}}),Az))) \\ &\overset{L.~{4.36}}{=}{\mathrm{cube}}_{n^A}(\unicode{x3bb}(f,(z-{\mathbf{1}},z)))\overset{L.~{4.17}}{=}{\mathrm{cube}}_{n^A}({\mathrm{val}}_{n^A}(f[z]))=f[z].\qquad \end{align*} $$
As a corollary, we can show that any bi-infinite sequence of cubes occurs on the main diagonal of precisely one valid tessellation.
Corollary 4.39. For every
![]() $x\in \Sigma _N^{\mathbb {Z}}$
with
$x\in \Sigma _N^{\mathbb {Z}}$
with
![]() $N={\mathrm {wgt}}_n(-{\mathbf {1}})$
, there is a unique
$N={\mathrm {wgt}}_n(-{\mathbf {1}})$
, there is a unique
![]() $f\in X_n$
such that
$f\in X_n$
such that
![]() ${\mathrm {val}}_n(f[{\mathbf {i}}])=x[i]$
for all
${\mathrm {val}}_n(f[{\mathbf {i}}])=x[i]$
for all
![]() $i\in \mathbb {Z}$
.
$i\in \mathbb {Z}$
.
Proof. Let A be the
![]() $d\times 1$
matrix with all entries equal to
$d\times 1$
matrix with all entries equal to
![]() $1$
, so
$1$
, so
![]() $n^A=(N)$
and there is a
$n^A=(N)$
and there is a
![]() $g\in X_{n^A}=X_{(N)}=T_{(N)}^{\mathbb {Z}}$
such that
$g\in X_{n^A}=X_{(N)}=T_{(N)}^{\mathbb {Z}}$
such that
![]() ${\mathrm {val}}_{(N)}(g[i])=x[i]$
for all
${\mathrm {val}}_{(N)}(g[i])=x[i]$
for all
![]() $i\in \mathbb {Z}$
. For
$i\in \mathbb {Z}$
. For
![]() $f\in X_n$
, the equality
$f\in X_n$
, the equality
![]() ${\mathrm {M}}_A(f)=g$
holds if and only if
${\mathrm {M}}_A(f)=g$
holds if and only if
 $$ \begin{align*} {\mathrm{val}}_n(f)[{\mathbf{i}}]&=\unicode{x3bb}(f,({\mathbf{i-1}},{\mathbf{i}}))=\unicode{x3bb}(f,(A(i-1),Ai))\overset{L.~{4.29}}{=}\unicode{x3bb}({\mathrm{M}}_A(f),(i-1,i)) \\ &={\mathrm{val}}_{(N)}({\mathrm{M}}_A(f)[i])={\mathrm{val}}_{(N)}(g[i])=x[i]\quad\mbox{for all }i\in\mathbb{Z}, \end{align*} $$
$$ \begin{align*} {\mathrm{val}}_n(f)[{\mathbf{i}}]&=\unicode{x3bb}(f,({\mathbf{i-1}},{\mathbf{i}}))=\unicode{x3bb}(f,(A(i-1),Ai))\overset{L.~{4.29}}{=}\unicode{x3bb}({\mathrm{M}}_A(f),(i-1,i)) \\ &={\mathrm{val}}_{(N)}({\mathrm{M}}_A(f)[i])={\mathrm{val}}_{(N)}(g[i])=x[i]\quad\mbox{for all }i\in\mathbb{Z}, \end{align*} $$
so we need to show that there is a unique
![]() $f\in X_n$
such that
$f\in X_n$
such that
![]() ${\mathrm {M}}_A(f)=g$
. This follows because by Theorem 4.38, the map
${\mathrm {M}}_A(f)=g$
. This follows because by Theorem 4.38, the map
![]() ${\mathrm {M}}_A$
is bijective.
${\mathrm {M}}_A$
is bijective.
We will show that
![]() ${\mathrm {M}}_A$
is surjective for a
${\mathrm {M}}_A$
is surjective for a
![]() $d\times d'$
natural number matrix A even without the assumption that all its rows contain a positive integer.
$d\times d'$
natural number matrix A even without the assumption that all its rows contain a positive integer.
Theorem 4.40. Let A be a
![]() $d\times d'$
natural number matrix. Then
$d\times d'$
natural number matrix. Then
![]() ${\mathrm {M}}_A$
is surjective.
${\mathrm {M}}_A$
is surjective.
Proof. We have
![]() ${\mathrm {M}}_A={\mathrm {M}}_{A,n}$
with
${\mathrm {M}}_A={\mathrm {M}}_{A,n}$
with
![]() $n\in \mathbb {Z}_+^d$
. Let B be a
$n\in \mathbb {Z}_+^d$
. Let B be a
![]() $d'\times 1$
matrix with all entries equal to
$d'\times 1$
matrix with all entries equal to
![]() $1$
. By Theorem 4.38, the map
$1$
. By Theorem 4.38, the map
![]() ${\mathrm {M}}_{B,n^A}$
is bijective, so
${\mathrm {M}}_{B,n^A}$
is bijective, so
![]() ${\mathrm {M}}_{A,n}$
is surjective if and only if
${\mathrm {M}}_{A,n}$
is surjective if and only if
![]() ${\mathrm {M}}_{AB,n}={\mathrm {M}}_{B,n^A}\circ {\mathrm {M}}_{A,n}$
is surjective. Since
${\mathrm {M}}_{AB,n}={\mathrm {M}}_{B,n^A}\circ {\mathrm {M}}_{A,n}$
is surjective. Since
![]() $AB$
is a
$AB$
is a
![]() $d\times 1$
matrix, by rewriting
$d\times 1$
matrix, by rewriting
![]() $AB$
as A, we may assume without loss of generality that A is a
$AB$
as A, we may assume without loss of generality that A is a
![]() $d\times 1$
matrix. Then
$d\times 1$
matrix. Then
![]() $n^A=(N')$
for some
$n^A=(N')$
for some
![]() $N'\in \mathbb {Z}_+$
and
$N'\in \mathbb {Z}_+$
and
![]() $X_{n^A}=T_{(N')}^{\mathbb {Z}}$
.
$X_{n^A}=T_{(N')}^{\mathbb {Z}}$
.
The case
![]() $N'=1$
is simple because then
$N'=1$
is simple because then
![]() $X_{n^A}$
contains only one point, so we may assume that
$X_{n^A}$
contains only one point, so we may assume that
![]() $N'>1$
. By continuity of
$N'>1$
. By continuity of
![]() ${\mathrm {M}}_A$
, it is sufficient to show that the image of
${\mathrm {M}}_A$
, it is sufficient to show that the image of
![]() ${\mathrm {M}}_A$
contains a dense subset of
${\mathrm {M}}_A$
contains a dense subset of
![]() $X_{n^A}$
. One dense subset is given by
$X_{n^A}$
. One dense subset is given by
![]() $g\in X_{n^A}$
such that
$g\in X_{n^A}$
such that
![]() ${\mathrm {real}}(g)=\xi $
for some
${\mathrm {real}}(g)=\xi $
for some
![]() $\xi \in \mathbb {R}\setminus \mathbb {Q}$
, and for any other
$\xi \in \mathbb {R}\setminus \mathbb {Q}$
, and for any other
![]() $g'\in X_{n^A}$
with
$g'\in X_{n^A}$
with
![]() ${\mathrm {real}}(g')=\xi $
, it follows that
${\mathrm {real}}(g')=\xi $
, it follows that
![]() $g'=g$
, because irrational numbers have a unique representation in any integer base. Thus, for any fixed
$g'=g$
, because irrational numbers have a unique representation in any integer base. Thus, for any fixed
![]() $\xi \in \mathbb {R}\setminus \mathbb {Q}$
and
$\xi \in \mathbb {R}\setminus \mathbb {Q}$
and
![]() $g\in X_{n^A}$
with
$g\in X_{n^A}$
with
![]() ${\mathrm {real}}(g)=\xi $
, we will present an
${\mathrm {real}}(g)=\xi $
, we will present an
![]() $f\in X_n$
such that
$f\in X_n$
such that
![]() ${{\mathrm {M}}_{A}(f)=g}$
. We choose
${{\mathrm {M}}_{A}(f)=g}$
. We choose
![]() $f\in X_n$
with the property that
$f\in X_n$
with the property that
![]() ${\mathrm {real}}(f)={\mathrm {real}}(g)$
. This is possible, because
${\mathrm {real}}(f)={\mathrm {real}}(g)$
. This is possible, because
![]() ${\mathrm {real}}(f)$
depends only on the choice of cubes on the main diagonal of f, and these can be chosen freely by Corollary 4.39. By Proposition 4.30, we have
${\mathrm {real}}(f)$
depends only on the choice of cubes on the main diagonal of f, and these can be chosen freely by Corollary 4.39. By Proposition 4.30, we have
![]() ${\mathrm {real}}({\mathrm {M}}_{A}(f))={\mathrm {real}}(f)={\mathrm {real}}(g)=\xi $
. But because for any
${\mathrm {real}}({\mathrm {M}}_{A}(f))={\mathrm {real}}(f)={\mathrm {real}}(g)=\xi $
. But because for any
![]() $g'\in X_{n^A}$
the equality
$g'\in X_{n^A}$
the equality
![]() ${\mathrm {real}}(g')=\xi $
implies
${\mathrm {real}}(g')=\xi $
implies
![]() $g'=g$
, it follows that
$g'=g$
, it follows that
![]() ${\mathrm {M}}_A(f)=g$
.
${\mathrm {M}}_A(f)=g$
.
Corollary 4.41. Let A be a
![]() $d\times d'$
natural number matrix. Then
$d\times d'$
natural number matrix. Then
![]() $(X_n,\sigma _{Az})$
has
$(X_n,\sigma _{Az})$
has
![]() $(X_{n^A},\sigma _z)$
as a factor for every
$(X_{n^A},\sigma _z)$
as a factor for every
![]() $z\in \mathbb {Z}^{d'}$
via
$z\in \mathbb {Z}^{d'}$
via
![]() ${\mathrm {M}}_A$
. If every row of A contains a positive number, the map
${\mathrm {M}}_A$
. If every row of A contains a positive number, the map
![]() ${\mathrm {M}}_A$
is a conjugacy.
${\mathrm {M}}_A$
is a conjugacy.
Proof. By Theorem 4.40, the map
![]() ${\mathrm {M}}_A$
is surjective, so it remains to show that
${\mathrm {M}}_A$
is surjective, so it remains to show that
![]() $\sigma _z\circ {\mathrm {M}}_A={\mathrm {M}}_A \circ \sigma _{Az}$
. Let
$\sigma _z\circ {\mathrm {M}}_A={\mathrm {M}}_A \circ \sigma _{Az}$
. Let
![]() $f\in X_{n}$
and
$f\in X_{n}$
and
![]() $v\in \mathbb {Z}^{d'}$
be arbitrary. Then
$v\in \mathbb {Z}^{d'}$
be arbitrary. Then
 $$ \begin{align*} \sigma_z({\mathrm{M}}_A(f))[v]&={\mathrm{M}}_A(f)[z+v]={\mathrm{cube}}_{n^A}(\unicode{x3bb}(f,(A(z+v-{\mathbf{1}}),A(z+v)))) \\ &\overset{L.~{4.13}}{=}{\mathrm{cube}}_{n^A} (\unicode{x3bb}(\sigma_{Az}(f),(A(v-{\mathbf{1}}),Av)))={\mathrm{M}}_A(\sigma_{Az}(f))[v]. \end{align*} $$
$$ \begin{align*} \sigma_z({\mathrm{M}}_A(f))[v]&={\mathrm{M}}_A(f)[z+v]={\mathrm{cube}}_{n^A}(\unicode{x3bb}(f,(A(z+v-{\mathbf{1}}),A(z+v)))) \\ &\overset{L.~{4.13}}{=}{\mathrm{cube}}_{n^A} (\unicode{x3bb}(\sigma_{Az}(f),(A(v-{\mathbf{1}}),Av)))={\mathrm{M}}_A(\sigma_{Az}(f))[v]. \end{align*} $$
In the case when every row of A contains a positive number, the map
![]() ${\mathrm {M}}_A$
is bijective by Theorem 4.38.
${\mathrm {M}}_A$
is bijective by Theorem 4.38.
5. Multiplication automata
5.1. Preliminaries on multiplication automata
Let
![]() $\Sigma $
be an alphabet. Concatenations of symbols from
$\Sigma $
be an alphabet. Concatenations of symbols from
![]() $\Sigma $
are called words, and for
$\Sigma $
are called words, and for
![]() $k\in \mathbb {Z}_+$
, the set of words of length k is denoted by
$k\in \mathbb {Z}_+$
, the set of words of length k is denoted by
![]() $\Sigma ^k$
. Elements of the one-dimensional subshift
$\Sigma ^k$
. Elements of the one-dimensional subshift
![]() $\Sigma ^{\mathbb {Z}}$
are bi-infinite sequences that are called configurations. As previously in this paper, the value of
$\Sigma ^{\mathbb {Z}}$
are bi-infinite sequences that are called configurations. As previously in this paper, the value of
![]() $x\in \Sigma ^{\mathbb {Z}}$
at a coordinate
$x\in \Sigma ^{\mathbb {Z}}$
at a coordinate
![]() $i\in \mathbb {Z}$
is denoted by
$i\in \mathbb {Z}$
is denoted by
![]() $x[i]$
. More generally, given an interval
$x[i]$
. More generally, given an interval
![]() $I=[i,j]$
with
$I=[i,j]$
with
![]() $i\leq j\in \mathbb {Z}$
, x has a finite subword denoted by
$i\leq j\in \mathbb {Z}$
, x has a finite subword denoted by
![]() $x[I]=x[i,j]=x[i]x[i+1]\cdots x[j]\in \Sigma ^{j-i+1}$
.
$x[I]=x[i,j]=x[i]x[i+1]\cdots x[j]\in \Sigma ^{j-i+1}$
.
Definition 5.1. Let
![]() $\Sigma $
be an alphabet. We say that a map
$\Sigma $
be an alphabet. We say that a map
![]() $F:\Sigma ^{\mathbb {Z}}\to \Sigma ^{\mathbb {Z}}$
is a cellular automaton if for some
$F:\Sigma ^{\mathbb {Z}}\to \Sigma ^{\mathbb {Z}}$
is a cellular automaton if for some
![]() $m\leq n\in \mathbb {N}$
, there exists a map
$m\leq n\in \mathbb {N}$
, there exists a map
![]() $f:\Sigma ^{m-n+1}\to \Sigma $
(a so-called
$f:\Sigma ^{m-n+1}\to \Sigma $
(a so-called
![]() $(m,n)$
local rule for F) such that
$(m,n)$
local rule for F) such that
![]() $F(x)[i]=f(x[i+m,i+n])$
for
$F(x)[i]=f(x[i+m,i+n])$
for
![]() $i\in \mathbb {Z}$
.
$i\in \mathbb {Z}$
.
If
![]() $F:\Sigma ^{\mathbb {Z}}\to \Sigma ^{\mathbb {Z}}$
is a cellular automaton, then
$F:\Sigma ^{\mathbb {Z}}\to \Sigma ^{\mathbb {Z}}$
is a cellular automaton, then
![]() $(\Sigma ^{\mathbb {Z}},F)$
is a dynamical system. Bijective cellular automata are often called reversible, because their inverse maps are also cellular automata (see e.g., [Reference Kari6, Theorem 2]).
$(\Sigma ^{\mathbb {Z}},F)$
is a dynamical system. Bijective cellular automata are often called reversible, because their inverse maps are also cellular automata (see e.g., [Reference Kari6, Theorem 2]).
For a CA
![]() $F:\Sigma ^{\mathbb {Z}}\to \Sigma ^{\mathbb {Z}}$
, a configuration
$F:\Sigma ^{\mathbb {Z}}\to \Sigma ^{\mathbb {Z}}$
, a configuration
![]() $x\in X$
, and an interval
$x\in X$
, and an interval
![]() $I=[i,j]$
with
$I=[i,j]$
with
![]() ${i\leq j\in \mathbb {Z}}$
, the I-trace of x (with respect to F) is the sequence
${i\leq j\in \mathbb {Z}}$
, the I-trace of x (with respect to F) is the sequence
![]() ${\mathrm {Tr}}_{F,I}(x)$
over the alphabet
${\mathrm {Tr}}_{F,I}(x)$
over the alphabet
![]() $\Sigma ^{j-i+1}$
(that is, the symbols of the alphabet are words over
$\Sigma ^{j-i+1}$
(that is, the symbols of the alphabet are words over
![]() $\Sigma $
) defined by
$\Sigma $
) defined by
![]() ${\mathrm {Tr}}_{F,I}(x)[t]=F^t(x)[I]$
for
${\mathrm {Tr}}_{F,I}(x)[t]=F^t(x)[I]$
for
![]() $t\in \mathbb {N}$
. If
$t\in \mathbb {N}$
. If
![]() $I=\{i\}$
is the degenerate interval, we may write
$I=\{i\}$
is the degenerate interval, we may write
![]() ${\mathrm {Tr}}_{F,i}(x)$
and if
${\mathrm {Tr}}_{F,i}(x)$
and if
![]() $i=0$
, we may write
$i=0$
, we may write
![]() ${\mathrm {Tr}}_F(x)$
. If the CA F is clear from the context, we may write
${\mathrm {Tr}}_F(x)$
. If the CA F is clear from the context, we may write
![]() ${\mathrm {Tr}}_I(x)$
. The I-trace subshift of F is
${\mathrm {Tr}}_I(x)$
. The I-trace subshift of F is
![]() $(\Xi _I(F),\sigma )$
, where
$(\Xi _I(F),\sigma )$
, where
It is easy to see that
![]() $\Xi _{[i,j]}(F)=\Xi _{[i-j,0]}(F)$
and, therefore, the set of all trace subshifts satisfies
$\Xi _{[i,j]}(F)=\Xi _{[i-j,0]}(F)$
and, therefore, the set of all trace subshifts satisfies
We call
![]() $(\Xi _{[-(k-1),0]},\sigma )$
the width k trace subshift of F.
$(\Xi _{[-(k-1),0]},\sigma )$
the width k trace subshift of F.
For examining multiplication CA, it is convenient to define
 $$ \begin{align*} {\mathcal{N}(\Sigma_N)}&=\{x\in\Sigma_N^{\mathbb{Z}}\mid \text{there exists } j\in\mathbb{Z}: x[i]=0\mbox{ for }i<j\}\quad\mbox{and} \\ {\mathcal{F}(\Sigma_N)}&=\{x\in\Sigma_N^{\mathbb{Z}}\mid x[i]\neq 0\mbox{ for finitely many }i\in\mathbb{Z}\}\subseteq {\mathcal{N}(\Sigma_N)}. \end{align*} $$
$$ \begin{align*} {\mathcal{N}(\Sigma_N)}&=\{x\in\Sigma_N^{\mathbb{Z}}\mid \text{there exists } j\in\mathbb{Z}: x[i]=0\mbox{ for }i<j\}\quad\mbox{and} \\ {\mathcal{F}(\Sigma_N)}&=\{x\in\Sigma_N^{\mathbb{Z}}\mid x[i]\neq 0\mbox{ for finitely many }i\in\mathbb{Z}\}\subseteq {\mathcal{N}(\Sigma_N)}. \end{align*} $$
The elements of
![]() ${\mathcal {N}(\Sigma _N)}$
are analogous to the usual base-N representations of positive numbers, where there may be infinitely many digits to the right of the decimal point but always a finite number of digits to the left of the decimal point (and then the representation can be extended to a bi-infinite sequence by adding an infinite sequence of zeroes to the left end). The elements of
${\mathcal {N}(\Sigma _N)}$
are analogous to the usual base-N representations of positive numbers, where there may be infinitely many digits to the right of the decimal point but always a finite number of digits to the left of the decimal point (and then the representation can be extended to a bi-infinite sequence by adding an infinite sequence of zeroes to the left end). The elements of
![]() ${\mathcal {F}(\Sigma _N)}$
correspond to numbers whose representations are finite to both directions.
${\mathcal {F}(\Sigma _N)}$
correspond to numbers whose representations are finite to both directions.
Definition 5.2. Let
![]() $N>1$
be an integer. If
$N>1$
be an integer. If
![]() $\xi \geq 0$
is a real number and
$\xi \geq 0$
is a real number and
![]() $\xi =\sum _{i=-\infty }^{\infty }{\xi _i N^{i}}$
is the unique base-N expansion of
$\xi =\sum _{i=-\infty }^{\infty }{\xi _i N^{i}}$
is the unique base-N expansion of
![]() $\xi $
such that
$\xi $
such that
![]() $\xi _i\neq N-1$
for infinitely many
$\xi _i\neq N-1$
for infinitely many
![]() $i<0$
, we define
$i<0$
, we define
![]() ${\mathrm {config}}_N(\xi )\in {\mathcal {N}(\Sigma _N)}$
by
${\mathrm {config}}_N(\xi )\in {\mathcal {N}(\Sigma _N)}$
by
for all
![]() $i\in \mathbb {Z}$
. In reverse, for
$i\in \mathbb {Z}$
. In reverse, for
![]() $x\in \Sigma _N^{\mathbb {Z}}$
, we define
$x\in \Sigma _N^{\mathbb {Z}}$
, we define
 $$ \begin{align*}{\mathrm{real}}_N(x)=\sum_{i=-\infty}^{\infty}{x[-i] N^{i}}.\end{align*} $$
$$ \begin{align*}{\mathrm{real}}_N(x)=\sum_{i=-\infty}^{\infty}{x[-i] N^{i}}.\end{align*} $$
Clearly,
![]() ${\mathrm {real}}_N({\mathrm {config}}_N(\xi ))=\xi $
and
${\mathrm {real}}_N({\mathrm {config}}_N(\xi ))=\xi $
and
![]() ${\mathrm {config}}_N({\mathrm {real}}_N(x))=x$
for every
${\mathrm {config}}_N({\mathrm {real}}_N(x))=x$
for every
![]() $\xi \geq 0$
and every
$\xi \geq 0$
and every
![]() ${x\in {\mathcal {N}(\Sigma _N)}}$
such that
${x\in {\mathcal {N}(\Sigma _N)}}$
such that
![]() $x[i]\neq N-1$
for infinitely many
$x[i]\neq N-1$
for infinitely many
![]() $i>0$
.
$i>0$
.
Additionally, in the special case
![]() $N=1$
, we define
$N=1$
, we define
![]() ${\mathrm {config}}_1:\{0\}\to \Sigma _1^{\mathbb {Z}}$
and
${\mathrm {config}}_1:\{0\}\to \Sigma _1^{\mathbb {Z}}$
and
![]() ${\mathrm {real}}_1:\Sigma _1^{\mathbb {Z}}\to \{0\}$
in the only possible way.
${\mathrm {real}}_1:\Sigma _1^{\mathbb {Z}}\to \{0\}$
in the only possible way.
Definition 5.3. (Multiplication CA)
Let
![]() $N\in \mathbb {Z}_+$
. For
$N\in \mathbb {Z}_+$
. For
![]() $p\in \mathbb {Z}_+$
dividing N, we define a
$p\in \mathbb {Z}_+$
dividing N, we define a
![]() $(0,1)$
local rule
$(0,1)$
local rule
![]() $g_{p,N}:\Sigma _{N}\times \Sigma _{N}\to \Sigma _{N}$
for a CA
$g_{p,N}:\Sigma _{N}\times \Sigma _{N}\to \Sigma _{N}$
for a CA
![]() $\Pi _{p,N}$
as follows. Let
$\Pi _{p,N}$
as follows. Let
![]() $q\in \mathbb {Z}_+$
be such that
$q\in \mathbb {Z}_+$
be such that
![]() $N=pq$
. The numbers
$N=pq$
. The numbers
![]() $a,b\in \Sigma _{N}$
are represented as
$a,b\in \Sigma _{N}$
are represented as
![]() $a=a_1q+a_0$
and
$a=a_1q+a_0$
and
![]() $b=b_1q+b_0$
, where
$b=b_1q+b_0$
, where
![]() $a_0,b_0\in \Sigma _q$
and
$a_0,b_0\in \Sigma _q$
and
![]() $a_1,b_1\in \Sigma _p$
: such representations always exist and they are unique. Then
$a_1,b_1\in \Sigma _p$
: such representations always exist and they are unique. Then
It can be shown that the map
![]() $g_{p,N}$
performs multiplication by p in base N in the sense that
$g_{p,N}$
performs multiplication by p in base N in the sense that
![]() $\Pi _{p,n}({\mathcal {F}(\Sigma _N)})\subseteq {\mathcal {F}(\Sigma _N)}$
,
$\Pi _{p,n}({\mathcal {F}(\Sigma _N)})\subseteq {\mathcal {F}(\Sigma _N)}$
,
![]() $\Pi _{p,N}({\mathcal {N}(\Sigma _N)})\subseteq {\mathcal {N}(\Sigma _N)}$
, and
$\Pi _{p,N}({\mathcal {N}(\Sigma _N)})\subseteq {\mathcal {N}(\Sigma _N)}$
, and
![]() ${\mathrm {real}}_N(\Pi _{p,N}(x))=p{\mathrm {real}}_N(x)$
for
${\mathrm {real}}_N(\Pi _{p,N}(x))=p{\mathrm {real}}_N(x)$
for
![]() $x\in {\mathcal {N}(\Sigma _N)}$
. To put it shortly, this is because
$x\in {\mathcal {N}(\Sigma _N)}$
. To put it shortly, this is because
![]() $g_{p,N}$
encodes the usual algorithm for long multiplication by p in base N (for more details, see e.g., [Reference Kari, Yen and Ibarra5, Reference Kopra7]). All these maps commute because
$g_{p,N}$
encodes the usual algorithm for long multiplication by p in base N (for more details, see e.g., [Reference Kari, Yen and Ibarra5, Reference Kopra7]). All these maps commute because
for
![]() $p_1,p_2$
dividing N and for x in the dense set
$p_1,p_2$
dividing N and for x in the dense set
![]() ${\mathcal {F}(\Sigma _N)}$
. They are reversible, because for
${\mathcal {F}(\Sigma _N)}$
. They are reversible, because for
![]() $pq=N$
,
$pq=N$
,
for x in the dense set
![]() ${\mathcal {F}(\Sigma _N)}$
and
${\mathcal {F}(\Sigma _N)}$
and
![]() $\sigma $
is reversible. Whenever
$\sigma $
is reversible. Whenever
![]() $\alpha =p/q$
, where p and q are products of factors
$\alpha =p/q$
, where p and q are products of factors
![]() $p_i$
and
$p_i$
and
![]() $q_i$
of N, we may define
$q_i$
of N, we may define
![]() $\Pi _{\alpha ,N}$
as the composition of corresponding
$\Pi _{\alpha ,N}$
as the composition of corresponding
![]() $\Pi _{p_i,N}$
and
$\Pi _{p_i,N}$
and
![]() $\Pi _{q_i,N}^{-1}$
. The map
$\Pi _{q_i,N}^{-1}$
. The map
![]() $\Pi _{\alpha ,N}$
does not depend on the choice of the composition into
$\Pi _{\alpha ,N}$
does not depend on the choice of the composition into
![]() $p_i$
and
$p_i$
and
![]() $q_i$
by arguments similar to those above.
$q_i$
by arguments similar to those above.
5.2. The connection between multiplication cube tessellations and multiplication automata
Throughout this subsection, let
![]() $n\in \mathbb {Z}_+^d$
and let
$n\in \mathbb {Z}_+^d$
and let
![]() $N=\prod _{i=1}^d n[i]$
. From any configuration
$N=\prod _{i=1}^d n[i]$
. From any configuration
![]() $x\in \Sigma _N^{\mathbb {Z}}$
, one can form a tessellation
$x\in \Sigma _N^{\mathbb {Z}}$
, one can form a tessellation
![]() ${\mathrm {tess}}_{n}(x)\in X_{n}$
as follows: for any
${\mathrm {tess}}_{n}(x)\in X_{n}$
as follows: for any
![]() $z\in \mathbb {Z}^d$
, we define
$z\in \mathbb {Z}^d$
, we define
![]() $\alpha (z,n)=\prod _{i=1}^d n[i]^{z[i]}$
and define
$\alpha (z,n)=\prod _{i=1}^d n[i]^{z[i]}$
and define
(one still has to verify that this is indeed a valid tiling, which we will do in Lemma 5.4). On the other hand, from any tessellation
![]() $f\in X_{n}$
, one can extract a configuration
$f\in X_{n}$
, one can extract a configuration
![]() ${{\mathrm {diag}}_{n}(f)\in \Sigma _N^{\mathbb {Z}}}$
by looking at the tiles on the main diagonal: let
${{\mathrm {diag}}_{n}(f)\in \Sigma _N^{\mathbb {Z}}}$
by looking at the tiles on the main diagonal: let
Lemma 5.4. For every
![]() $x\in \Sigma _N^{\mathbb {Z}}$
, it holds that
$x\in \Sigma _N^{\mathbb {Z}}$
, it holds that
![]() ${\mathrm {tess}}_{n}(x)\in X_{n}$
.
${\mathrm {tess}}_{n}(x)\in X_{n}$
.
Proof. Let
![]() $z\in \mathbb {Z}^d$
and
$z\in \mathbb {Z}^d$
and
![]() $1\leq i\leq d$
be arbitrary. We need to show that
$1\leq i\leq d$
be arbitrary. We need to show that
![]() ${\mathrm {\tau }}_i({\mathrm {tess}}_{n}(x)[z])={\mathrm {\beta }}_i({\mathrm {tess}}_{n}(x)[z+e_i])$
. Let
${\mathrm {\tau }}_i({\mathrm {tess}}_{n}(x)[z])={\mathrm {\beta }}_i({\mathrm {tess}}_{n}(x)[z+e_i])$
. Let
![]() $y=\Pi _{\alpha (z,n),N}(x)$
. By writing
$y=\Pi _{\alpha (z,n),N}(x)$
. By writing
![]() $y[0]=a_1\prod _{j\neq i}n[j]+a_0$
for
$y[0]=a_1\prod _{j\neq i}n[j]+a_0$
for
![]() ${0\leq a_0<\prod _{j\neq i}n[i]}$
and
${0\leq a_0<\prod _{j\neq i}n[i]}$
and
![]() $0\leq a_1<n[i]$
, we see that
$0\leq a_1<n[i]$
, we see that
![]() $\Pi _{n[i],N}(y)[0]=a_0n[i]+a_1'$
for some
$\Pi _{n[i],N}(y)[0]=a_0n[i]+a_1'$
for some
![]() $0\leq a_1'<n[i]$
. Then
$0\leq a_1'<n[i]$
. Then
 $$ \begin{align*} &{\mathrm{\tau}}_i({\mathrm{tess}}_{n}(x)[z])={\mathrm{\tau}}_i({\mathrm{cube}}_{n}(\Pi_{\alpha(z,n),N}(x)[0])) \\ &\quad ={\mathrm{\tau}}_i({\mathrm{cube}}_{n}(y[0]))={\mathrm{\tau}}_i({\mathrm{cube}}_{n}(a_1\prod_{j\neq i}n[j]+a_0))=a_0\quad\mbox{and} \\ &{\mathrm{\beta}}_i({\mathrm{tess}}_{n}(x)[z+e_i])={\mathrm{\beta}}_i({\mathrm{cube}}_{n}(\Pi_{\alpha(z+e_i,n),N}(x)[0])) \\ &\quad ={\mathrm{\beta}}_i({\mathrm{cube}}_{n}(\Pi_{n[i],N}(y)[0]))={\mathrm{\beta}}_i({\mathrm{cube}}_{n}(a_0n[i]+a_1'))=a_0. \end{align*} $$
$$ \begin{align*} &{\mathrm{\tau}}_i({\mathrm{tess}}_{n}(x)[z])={\mathrm{\tau}}_i({\mathrm{cube}}_{n}(\Pi_{\alpha(z,n),N}(x)[0])) \\ &\quad ={\mathrm{\tau}}_i({\mathrm{cube}}_{n}(y[0]))={\mathrm{\tau}}_i({\mathrm{cube}}_{n}(a_1\prod_{j\neq i}n[j]+a_0))=a_0\quad\mbox{and} \\ &{\mathrm{\beta}}_i({\mathrm{tess}}_{n}(x)[z+e_i])={\mathrm{\beta}}_i({\mathrm{cube}}_{n}(\Pi_{\alpha(z+e_i,n),N}(x)[0])) \\ &\quad ={\mathrm{\beta}}_i({\mathrm{cube}}_{n}(\Pi_{n[i],N}(y)[0]))={\mathrm{\beta}}_i({\mathrm{cube}}_{n}(a_0n[i]+a_1'))=a_0. \end{align*} $$
Theorem 5.5. For any
![]() $z\in \mathbb {Z}^d$
, it holds that
$z\in \mathbb {Z}^d$
, it holds that
![]() $\sigma _z{\circ }\ {\mathrm {tess}}_{n}={\mathrm {tess}}_{n}\; {\circ }\;\Pi _{\alpha (z,n),N}$
.
$\sigma _z{\circ }\ {\mathrm {tess}}_{n}={\mathrm {tess}}_{n}\; {\circ }\;\Pi _{\alpha (z,n),N}$
.
Proof. Let
![]() $x\in \Sigma _N^{\mathbb {Z}}$
and
$x\in \Sigma _N^{\mathbb {Z}}$
and
![]() $z'\in \mathbb {Z}^d$
be arbitrary. Then
$z'\in \mathbb {Z}^d$
be arbitrary. Then
 $$ \begin{align*} &\sigma_z({\mathrm{tess}}_{n}(x))[z']={\mathrm{tess}}_{n}(x)[z'+z]={\mathrm{cube}}_{n}(\Pi_{\alpha(z'+z,n),N}(x)[0]) \\ &\quad ={\mathrm{cube}}_{n}(\Pi_{\alpha(z',n),N}(\Pi_{\alpha(z,n),N}(x))[0])={\mathrm{tess}}_{n}(\Pi_{\alpha(z,n),N}(x))[z']. \end{align*} $$
$$ \begin{align*} &\sigma_z({\mathrm{tess}}_{n}(x))[z']={\mathrm{tess}}_{n}(x)[z'+z]={\mathrm{cube}}_{n}(\Pi_{\alpha(z'+z,n),N}(x)[0]) \\ &\quad ={\mathrm{cube}}_{n}(\Pi_{\alpha(z',n),N}(\Pi_{\alpha(z,n),N}(x))[0])={\mathrm{tess}}_{n}(\Pi_{\alpha(z,n),N}(x))[z']. \end{align*} $$
We define ‘partial’ shifts on macrotilings by conjugating to a microtiling. For the rest of this subsection (unless specified otherwise), let A be a
![]() $d\times d'$
natural number matrix and let
$d\times d'$
natural number matrix and let
![]() $N'=\prod _{i=1}^{d'} n^A[i]$
. If additionally all the rows of A contain a positive integer, we define
$N'=\prod _{i=1}^{d'} n^A[i]$
. If additionally all the rows of A contain a positive integer, we define
![]() $\sigma _{A,z}:X_{n^A}\to X_{n^A}$
by
$\sigma _{A,z}:X_{n^A}\to X_{n^A}$
by
![]() $\sigma _{A,z}={\mathrm {M}}_A\circ \;\sigma _z\circ {\mathrm {\mu }}_A$
for any
$\sigma _{A,z}={\mathrm {M}}_A\circ \;\sigma _z\circ {\mathrm {\mu }}_A$
for any
![]() $z\in \mathbb {Z}^d$
. The assumption that all the rows of A contain a positive integer will hold until Theorem 5.12. Appearances of the maps
$z\in \mathbb {Z}^d$
. The assumption that all the rows of A contain a positive integer will hold until Theorem 5.12. Appearances of the maps
![]() $\sigma _{A,z}$
and
$\sigma _{A,z}$
and
![]() $\mu _A$
(which are not defined for other kinds of matrices) are also reminders of this.
$\mu _A$
(which are not defined for other kinds of matrices) are also reminders of this.
Lemma 5.6. For any
![]() $z\in \mathbb {Z}^d$
, it holds that
$z\in \mathbb {Z}^d$
, it holds that
![]() $\Pi _{\alpha (z,n),N'}{\circ }{\mathrm {diag}}_{n^A}={\mathrm {diag}}_{n^A}\;{\circ }\;\sigma _{A,z}$
. In the special case
$\Pi _{\alpha (z,n),N'}{\circ }{\mathrm {diag}}_{n^A}={\mathrm {diag}}_{n^A}\;{\circ }\;\sigma _{A,z}$
. In the special case
![]() $A=I$
, it holds that
$A=I$
, it holds that
![]() $\Pi _{\alpha (z,n),N}{\circ }{\mathrm {diag}}_{n}={\mathrm {diag}}_{n}\;{\circ }\;\sigma _z$
.
$\Pi _{\alpha (z,n),N}{\circ }{\mathrm {diag}}_{n}={\mathrm {diag}}_{n}\;{\circ }\;\sigma _z$
.
Proof. First observe that
![]() $\Pi _{\alpha (z,n),N'}$
always exists, because every factor of N is a factor of
$\Pi _{\alpha (z,n),N'}$
always exists, because every factor of N is a factor of
![]() $N'$
. It is sufficient to show for any
$N'$
. It is sufficient to show for any
![]() $1\leq k\leq d$
that
$1\leq k\leq d$
that
![]() $\Pi _{n[k],N'}\circ {\mathrm {diag}}_{n^A}={\mathrm {diag}}_{n^A}\circ \;\sigma _{A,e_k}$
. After composing by
$\Pi _{n[k],N'}\circ {\mathrm {diag}}_{n^A}={\mathrm {diag}}_{n^A}\circ \;\sigma _{A,e_k}$
. After composing by
![]() ${\mathrm {M}}_A$
on the right, we need to show for all
${\mathrm {M}}_A$
on the right, we need to show for all
![]() $f\in X_{n}$
and
$f\in X_{n}$
and
![]() $i\in \mathbb {Z}$
that
$i\in \mathbb {Z}$
that
![]() $\Pi _{n[k],N'}({\mathrm {diag}}_{n^A}({\mathrm {M}}_A(f)))[i]={\mathrm {diag}}_{n^A}({\mathrm {M}}_A(\sigma _{e_k}(f)))[i]$
. We compute
$\Pi _{n[k],N'}({\mathrm {diag}}_{n^A}({\mathrm {M}}_A(f)))[i]={\mathrm {diag}}_{n^A}({\mathrm {M}}_A(\sigma _{e_k}(f)))[i]$
. We compute
 $$ \begin{align*} &\Pi_{n[k],N'}({\mathrm{diag}}_{n^A}({\mathrm{M}}_A(f)))[i]=g_{n[k],N'}({\mathrm{diag}}_{n^A}({\mathrm{M}}_A(f))[i],\ {\mathrm{diag}}_{n^A}({\mathrm{M}}_A(f))[i+1]) \\ &\quad =g_{n[k],N'}(\underbrace{\unicode{x3bb}(f,(A({\mathbf{i-1}}),A{\mathbf{i}}))}_{a},\underbrace{\unicode{x3bb}(f,(A{\mathbf{i}},A({\mathbf{i+1}})))}_{b}) \end{align*} $$
$$ \begin{align*} &\Pi_{n[k],N'}({\mathrm{diag}}_{n^A}({\mathrm{M}}_A(f)))[i]=g_{n[k],N'}({\mathrm{diag}}_{n^A}({\mathrm{M}}_A(f))[i],\ {\mathrm{diag}}_{n^A}({\mathrm{M}}_A(f))[i+1]) \\ &\quad =g_{n[k],N'}(\underbrace{\unicode{x3bb}(f,(A({\mathbf{i-1}}),A{\mathbf{i}}))}_{a},\underbrace{\unicode{x3bb}(f,(A{\mathbf{i}},A({\mathbf{i+1}})))}_{b}) \end{align*} $$
and
 $$ \begin{align*} &{\mathrm{diag}}_{n^A}({\mathrm{M}}_A(\sigma_{e_k}(f)))[i]={\mathrm{val}}_{n^A}({\mathrm{M}}_A(\sigma_{e_k}(f)))[{\mathbf{i}}] \\ &\quad =\unicode{x3bb}(\sigma_{e_i}(f),(A({\mathbf{i-1}}),A{\mathbf{i}}))=\underbrace{\unicode{x3bb}(f,(A({\mathbf{i-1}})+e_i,A{\mathbf{i}}+e_i))}_{c}, \end{align*} $$
$$ \begin{align*} &{\mathrm{diag}}_{n^A}({\mathrm{M}}_A(\sigma_{e_k}(f)))[i]={\mathrm{val}}_{n^A}({\mathrm{M}}_A(\sigma_{e_k}(f)))[{\mathbf{i}}] \\ &\quad =\unicode{x3bb}(\sigma_{e_i}(f),(A({\mathbf{i-1}}),A{\mathbf{i}}))=\underbrace{\unicode{x3bb}(f,(A({\mathbf{i-1}})+e_i,A{\mathbf{i}}+e_i))}_{c}, \end{align*} $$
where
![]() $a,b,c<N'=m(n,-A{\mathbf {1}})$
. We need to show that
$a,b,c<N'=m(n,-A{\mathbf {1}})$
. We need to show that
![]() $g_{n[k],N'}(a,b)=c$
. After defining
$g_{n[k],N'}(a,b)=c$
. After defining
![]() $a_0,a_1,b_0,b_1$
by
$a_0,a_1,b_0,b_1$
by
 $$ \begin{align*} (a_0,a_1)&={\mathrm{base}}(a,(N'/n[k]))={\mathrm{base}}_{n}(a,(-A{\mathbf{1}}+e_k,-A{\mathbf{1}}))[0,1] \\ &={\mathrm{base}}_{n}(a,((A({\mathbf{i-1}})+e_k)-A{\mathbf{i}},A({\mathbf{i-1}})-A{\mathbf{i}}))[0,1]\quad\mbox{and} \\ (b_0,b_1)&={\mathrm{base}}(b,(N'/n[k]))={\mathrm{base}}_{n}(b,(-A{\mathbf{1}}+e_k,-A{\mathbf{1}}))[0,1] \\ &={\mathrm{base}}_{n}(b,((A{\mathbf{i}}+e_k)-A({\mathbf{i+1}}),A{\mathbf{i}}-A({\mathbf{i+1}})))[0,1], \end{align*} $$
$$ \begin{align*} (a_0,a_1)&={\mathrm{base}}(a,(N'/n[k]))={\mathrm{base}}_{n}(a,(-A{\mathbf{1}}+e_k,-A{\mathbf{1}}))[0,1] \\ &={\mathrm{base}}_{n}(a,((A({\mathbf{i-1}})+e_k)-A{\mathbf{i}},A({\mathbf{i-1}})-A{\mathbf{i}}))[0,1]\quad\mbox{and} \\ (b_0,b_1)&={\mathrm{base}}(b,(N'/n[k]))={\mathrm{base}}_{n}(b,(-A{\mathbf{1}}+e_k,-A{\mathbf{1}}))[0,1] \\ &={\mathrm{base}}_{n}(b,((A{\mathbf{i}}+e_k)-A({\mathbf{i+1}}),A{\mathbf{i}}-A({\mathbf{i+1}})))[0,1], \end{align*} $$
it amounts to showing that
![]() $c=a_0n[k]+b_1$
. By Lemma 4.16, we see that
$c=a_0n[k]+b_1$
. By Lemma 4.16, we see that
By Lemma 4.14, we see that
 $$ \begin{align*} &a_1N'+c \\ &\quad =\unicode{x3bb}(f,(A({\mathbf{i-1}}),A({\mathbf{i-1}})+e_i))m(n,-A{\mathbf{1}})+\unicode{x3bb}(f,(A({\mathbf{i-1}})+e_i,A{\mathbf{i}}+e_i)) \\ &\quad =\unicode{x3bb}(f,(A({\mathbf{i-1}}),A{\mathbf{i}}+e_i)) \\ &\quad =\unicode{x3bb}(f,(A({\mathbf{i-1}}),A{\mathbf{i}}))m(n,-e_k)+\unicode{x3bb}(f,(A{\mathbf{i}},A{\mathbf{i}}+e_i))=an[k]+b_1. \end{align*} $$
$$ \begin{align*} &a_1N'+c \\ &\quad =\unicode{x3bb}(f,(A({\mathbf{i-1}}),A({\mathbf{i-1}})+e_i))m(n,-A{\mathbf{1}})+\unicode{x3bb}(f,(A({\mathbf{i-1}})+e_i,A{\mathbf{i}}+e_i)) \\ &\quad =\unicode{x3bb}(f,(A({\mathbf{i-1}}),A{\mathbf{i}}+e_i)) \\ &\quad =\unicode{x3bb}(f,(A({\mathbf{i-1}}),A{\mathbf{i}}))m(n,-e_k)+\unicode{x3bb}(f,(A{\mathbf{i}},A{\mathbf{i}}+e_i))=an[k]+b_1. \end{align*} $$
From this, one can solve
![]() $c=(a-a_1N'/n[k])n[k]+b_1=a_0n[k]+b_1$
, and we are done.
$c=(a-a_1N'/n[k])n[k]+b_1=a_0n[k]+b_1$
, and we are done.
Theorem 5.7. The maps
![]() ${\mathrm {tess}}_{n}$
and
${\mathrm {tess}}_{n}$
and
![]() ${\mathrm {diag}}_{n}$
are inverse maps of each other. For any
${\mathrm {diag}}_{n}$
are inverse maps of each other. For any
![]() $z\in \mathbb {Z}^d$
, the system
$z\in \mathbb {Z}^d$
, the system
![]() $(\Sigma _{N'}^{\mathbb {Z}},\Pi _{\alpha (z,n),N'})$
is conjugate to
$(\Sigma _{N'}^{\mathbb {Z}},\Pi _{\alpha (z,n),N'})$
is conjugate to
![]() $(X_{n^A},\sigma _{A,z})$
via
$(X_{n^A},\sigma _{A,z})$
via
![]() ${\mathrm {tess}}_{n^A}$
and
${\mathrm {tess}}_{n^A}$
and
![]() $(\Sigma _N^{\mathbb {Z}},\Pi _{\alpha (z,n),N})$
is conjugate to
$(\Sigma _N^{\mathbb {Z}},\Pi _{\alpha (z,n),N})$
is conjugate to
![]() $(X_n,\sigma _{z})$
via
$(X_n,\sigma _{z})$
via
![]() ${\mathrm {tess}}_{n}$
.
${\mathrm {tess}}_{n}$
.
Proof. First, let
![]() $x\in \Sigma _N^{\mathbb {Z}}$
and
$x\in \Sigma _N^{\mathbb {Z}}$
and
![]() $i\in \mathbb {Z}$
be arbitrary. It holds that
$i\in \mathbb {Z}$
be arbitrary. It holds that
and therefore
![]() ${\mathrm {diag}}_{n}({\mathrm {tess}}_{n}(x))[i]={\mathrm {val}}_{n}({\mathrm {cube}}_{n}(x[i]))=x[i]$
.
${\mathrm {diag}}_{n}({\mathrm {tess}}_{n}(x))[i]={\mathrm {val}}_{n}({\mathrm {cube}}_{n}(x[i]))=x[i]$
.
Next let
![]() $f\in X_{n}$
and
$f\in X_{n}$
and
![]() $z\in \mathbb {Z}^d$
be arbitrary, and denote
$z\in \mathbb {Z}^d$
be arbitrary, and denote
![]() $f'=\sigma _z(f)$
. It holds that
$f'=\sigma _z(f)$
. It holds that
 $$ \begin{align*} {\mathrm{tess}}_{n}({\mathrm{diag}}_{n}(f))[z]&=\sigma_z({\mathrm{tess}}_{n}({\mathrm{diag}}_{n}(f)))[{\mathbf{0}}] \\ &\overset{T. {5.5}}{=}{\mathrm{tess}}_{n}(\Pi_{\alpha(z,n),N}({\mathrm{diag}}_{n}(f)))[{\mathbf{0}}] \overset{L. {5.6}}{=}{\mathrm{tess}}_{n}({\mathrm{diag}}_{n}(f'))[{\mathbf{0}}] \\ &={\mathrm{cube}}_{n}({\mathrm{diag}}_{n}(f')[0])={\mathrm{cube}}_{n}({\mathrm{val}}_{n}(f'[{\mathbf{0}}]))=f'[{\mathbf{0}}]=f[z]. \end{align*} $$
$$ \begin{align*} {\mathrm{tess}}_{n}({\mathrm{diag}}_{n}(f))[z]&=\sigma_z({\mathrm{tess}}_{n}({\mathrm{diag}}_{n}(f)))[{\mathbf{0}}] \\ &\overset{T. {5.5}}{=}{\mathrm{tess}}_{n}(\Pi_{\alpha(z,n),N}({\mathrm{diag}}_{n}(f)))[{\mathbf{0}}] \overset{L. {5.6}}{=}{\mathrm{tess}}_{n}({\mathrm{diag}}_{n}(f'))[{\mathbf{0}}] \\ &={\mathrm{cube}}_{n}({\mathrm{diag}}_{n}(f')[0])={\mathrm{cube}}_{n}({\mathrm{val}}_{n}(f'[{\mathbf{0}}]))=f'[{\mathbf{0}}]=f[z]. \end{align*} $$
Since
![]() ${\mathrm {tess}}_{n}$
is the inverse of
${\mathrm {tess}}_{n}$
is the inverse of
![]() ${\mathrm {diag}}_n$
, the last claim follows from Lemma 5.6.
${\mathrm {diag}}_n$
, the last claim follows from Lemma 5.6.
It is a simple observation that the maps we have defined for mapping between tessellations and configurations are such that the represented real numbers are preserved.
Proposition 5.8. It holds that
![]() ${\mathrm {real}}_N\circ {\mathrm {diag}}_n={\mathrm {real}}_{{\mathbf {0}},-{\mathbf {1}}}$
and
${\mathrm {real}}_N\circ {\mathrm {diag}}_n={\mathrm {real}}_{{\mathbf {0}},-{\mathbf {1}}}$
and
![]() ${\mathrm {real}}_{{\mathbf {0}},-{\mathbf {1}}}\circ {\mathrm {tess}}_n={\mathrm {real}}_N$
.
${\mathrm {real}}_{{\mathbf {0}},-{\mathbf {1}}}\circ {\mathrm {tess}}_n={\mathrm {real}}_N$
.
Proof. The first equality follows directly from definitions. The second equality follows from the first one because
![]() ${\mathrm {tess}}_{n}$
is the inverse of
${\mathrm {tess}}_{n}$
is the inverse of
![]() ${\mathrm {diag}}_{n}$
by Theorem 5.7.
${\mathrm {diag}}_{n}$
by Theorem 5.7.
Theorem 5.9. The system
![]() $(\Sigma _{N'}^{\mathbb {Z}},\Pi _{\alpha (z,n),N'})$
is conjugate to
$(\Sigma _{N'}^{\mathbb {Z}},\Pi _{\alpha (z,n),N'})$
is conjugate to
![]() $(\Sigma _N^{\mathbb {Z}},\Pi _{\alpha (z,n),N})$
via
$(\Sigma _N^{\mathbb {Z}},\Pi _{\alpha (z,n),N})$
via
![]() $\phi ={\mathrm {diag}}_{n}\circ {\mathrm {\mu }}_{A,n}\circ {\mathrm {tess}}_{n^A}$
. Additionally,
$\phi ={\mathrm {diag}}_{n}\circ {\mathrm {\mu }}_{A,n}\circ {\mathrm {tess}}_{n^A}$
. Additionally,
![]() ${\mathrm {real}}_{N}\circ \;\phi ={\mathrm {real}}_{N'}$
.
${\mathrm {real}}_{N}\circ \;\phi ={\mathrm {real}}_{N'}$
.
Proof. The system
![]() $(\Sigma _{N'}^{\mathbb {Z}},\Pi _{\alpha (z,n),N'})$
is conjugate to
$(\Sigma _{N'}^{\mathbb {Z}},\Pi _{\alpha (z,n),N'})$
is conjugate to
![]() $(X_{n^A},\sigma _{A,z})$
via
$(X_{n^A},\sigma _{A,z})$
via
![]() ${\mathrm {tess}}_{n^A}$
by Theorem 5.7. The system
${\mathrm {tess}}_{n^A}$
by Theorem 5.7. The system
![]() $(X_{n^A},\sigma _{A,z})$
is conjugate to
$(X_{n^A},\sigma _{A,z})$
is conjugate to
![]() $(X_n,\sigma _z)$
via
$(X_n,\sigma _z)$
via
![]() ${\mathrm {\mu }}_A$
by definition. The system
${\mathrm {\mu }}_A$
by definition. The system
![]() $(X_n,\sigma _z)$
is conjugate to
$(X_n,\sigma _z)$
is conjugate to
![]() $(\Sigma _N^{\mathbb {Z}},\Pi _{\alpha (z,n),N})$
via
$(\Sigma _N^{\mathbb {Z}},\Pi _{\alpha (z,n),N})$
via
![]() ${\mathrm {diag}}_{n}$
by Theorem 5.7. The last claim follows by Propositions 4.37 and 5.8.
${\mathrm {diag}}_{n}$
by Theorem 5.7. The last claim follows by Propositions 4.37 and 5.8.
Let us specify one particular type of conjugacy. For any
![]() $N>1$
, let
$N>1$
, let
![]() $N=\prod _{i=1}^d p_i^{k_i}$
be its prime decomposition (with
$N=\prod _{i=1}^d p_i^{k_i}$
be its prime decomposition (with
![]() $k_i\in \mathbb {Z}_+$
and with the
$k_i\in \mathbb {Z}_+$
and with the
![]() $p_i$
in rising order) and let
$p_i$
in rising order) and let
![]() ${n=(p_1^{k_i},\ldots ,p_d^{k_d})}$
. Then, let
${n=(p_1^{k_i},\ldots ,p_d^{k_d})}$
. Then, let
![]() $m=(p_1,\ldots ,p_d)$
and
$m=(p_1,\ldots ,p_d)$
and
![]() $M=\prod _{i=1}^d p_i$
. If
$M=\prod _{i=1}^d p_i$
. If
![]() $A_{N}$
is the diagonal matrix
$A_{N}$
is the diagonal matrix
![]() ${\mathrm {diag}}(k_1,\ldots ,k_d)$
, it is easy to see that
${\mathrm {diag}}(k_1,\ldots ,k_d)$
, it is easy to see that
![]() $n=m^{A_N}$
. Then we define
$n=m^{A_N}$
. Then we define
![]() ${\mathrm {Conj}}_{N,M}={\mathrm {diag}}_{m}\circ {\mathrm {\mu }}_{A_{N},m}\circ {\mathrm {tess}}_{n}$
.
${\mathrm {Conj}}_{N,M}={\mathrm {diag}}_{m}\circ {\mathrm {\mu }}_{A_{N},m}\circ {\mathrm {tess}}_{n}$
.
If
![]() $N'>1$
is divisible by the same prime numbers as N, we extend the definition to
$N'>1$
is divisible by the same prime numbers as N, we extend the definition to
![]() ${\mathrm {Conj}}_{N,N'}={\mathrm {Conj}}_{N',M}^{-1}\circ {\mathrm {Conj}}_{N,M}$
. This agrees with the previous definition in the case
${\mathrm {Conj}}_{N,N'}={\mathrm {Conj}}_{N',M}^{-1}\circ {\mathrm {Conj}}_{N,M}$
. This agrees with the previous definition in the case
![]() $N'=M$
, because
$N'=M$
, because
![]() ${\mathrm {Conj}}_{M,M}$
is the identity map.
${\mathrm {Conj}}_{M,M}$
is the identity map.
Corollary 5.10. Assume that
![]() $N_1,N_2>1$
are divisible by the same prime numbers. Then
$N_1,N_2>1$
are divisible by the same prime numbers. Then
![]() $(\Sigma _{N_1}^{\mathbb {Z}},\Pi _{\alpha ,N_1})$
is conjugate to
$(\Sigma _{N_1}^{\mathbb {Z}},\Pi _{\alpha ,N_1})$
is conjugate to
![]() $(\Sigma _{N_2}^{\mathbb {Z}},\Pi _{\alpha ,N_2})$
via
$(\Sigma _{N_2}^{\mathbb {Z}},\Pi _{\alpha ,N_2})$
via
![]() ${\mathrm {Conj}}_{N_1,N_2}$
for any
${\mathrm {Conj}}_{N_1,N_2}$
for any
![]() $\alpha>0$
such that these maps are defined. Additionally,
$\alpha>0$
such that these maps are defined. Additionally,
![]() ${\mathrm {real}}_{N_2}\circ {\mathrm {Conj}}_{N_1,N_2}={\mathrm {real}}_{N_1}$
.
${\mathrm {real}}_{N_2}\circ {\mathrm {Conj}}_{N_1,N_2}={\mathrm {real}}_{N_1}$
.
Proof. Let
![]() $N=\prod _{i=1}^d p_i$
, where
$N=\prod _{i=1}^d p_i$
, where
![]() $p_i$
is the rising sequence of prime numbers that divide
$p_i$
is the rising sequence of prime numbers that divide
![]() $N_1$
and
$N_1$
and
![]() $N_2$
. Then also
$N_2$
. Then also
![]() $\Pi _{\alpha ,N}$
is defined. By the previous theorem,
$\Pi _{\alpha ,N}$
is defined. By the previous theorem,
![]() $(\Sigma _{N_1}^{\mathbb {Z}},\Pi _{\alpha ,N_1})$
is conjugate to
$(\Sigma _{N_1}^{\mathbb {Z}},\Pi _{\alpha ,N_1})$
is conjugate to
![]() $(\Sigma _N^{\mathbb {Z}},\Pi _{\alpha ,N})$
via
$(\Sigma _N^{\mathbb {Z}},\Pi _{\alpha ,N})$
via
![]() ${\mathrm {Conj}}_{N_1,N}$
and
${\mathrm {Conj}}_{N_1,N}$
and
![]() $(\Sigma _N^{\mathbb {Z}},\Pi _{\alpha ,N})$
is conjugate to
$(\Sigma _N^{\mathbb {Z}},\Pi _{\alpha ,N})$
is conjugate to
![]() $(\Sigma _{N_2}^{\mathbb {Z}},\Pi _{\alpha ,N_2})$
via
$(\Sigma _{N_2}^{\mathbb {Z}},\Pi _{\alpha ,N_2})$
via
![]() $({\mathrm {Conj}}_{N_2,N})^{-1}$
, so
$({\mathrm {Conj}}_{N_2,N})^{-1}$
, so
![]() $\Pi _{\alpha ,N_1}$
is conjugate to
$\Pi _{\alpha ,N_1}$
is conjugate to
![]() $\Pi _{\alpha ,N_2}$
via
$\Pi _{\alpha ,N_2}$
via
![]() ${\mathrm {Conj}}_{N_1,N_2}$
. The last claim also follows from the previous theorem.
${\mathrm {Conj}}_{N_1,N_2}$
. The last claim also follows from the previous theorem.
We highlight that, as it turns out, the conjugacy of the particular form
![]() ${\mathrm {Conj}}_{N,N^k}$
works in a very transparent way: cells in a configuration
${\mathrm {Conj}}_{N,N^k}$
works in a very transparent way: cells in a configuration
![]() $x\in \Sigma _N^{\mathbb {Z}}$
are grouped into blocks of k cells, and the k symbols of
$x\in \Sigma _N^{\mathbb {Z}}$
are grouped into blocks of k cells, and the k symbols of
![]() $\Sigma _N$
in each block are interpreted as a base-N representation of a number in
$\Sigma _N$
in each block are interpreted as a base-N representation of a number in
![]() $\Sigma _{N^k}$
. We define the block map
$\Sigma _{N^k}$
. We define the block map
![]() ${\mathrm {B}}_{N,k}:\Sigma _N^k\to \Sigma _{N^k}$
by
${\mathrm {B}}_{N,k}:\Sigma _N^k\to \Sigma _{N^k}$
by
![]() ${\mathrm {B}}_{N,k}(a_{k-1}\cdots a_1a_0)=\sum _{i=0}^{k-1}a_i N^i$
for
${\mathrm {B}}_{N,k}(a_{k-1}\cdots a_1a_0)=\sum _{i=0}^{k-1}a_i N^i$
for
![]() $N>1$
,
$N>1$
,
![]() $k\geq 1$
, and
$k\geq 1$
, and
![]() $a_i\in \Sigma _N$
.
$a_i\in \Sigma _N$
.
Theorem 5.11. Let
![]() $N>1$
, let
$N>1$
, let
![]() $k\geq 1$
, let
$k\geq 1$
, let
![]() $x\in \Sigma _N^{\mathbb {Z}}$
, and let
$x\in \Sigma _N^{\mathbb {Z}}$
, and let
![]() $i\in \mathbb {Z}$
. Then
$i\in \mathbb {Z}$
. Then
![]() ${\mathrm {Conj}}_{N,N^k}(x)[i]={\mathrm {B}}_{N,k}(x[ik-(k-1),ik])$
.
${\mathrm {Conj}}_{N,N^k}(x)[i]={\mathrm {B}}_{N,k}(x[ik-(k-1),ik])$
.
Proof. As in the definition of
![]() ${\mathrm {Conj}}_{N,M}$
, let
${\mathrm {Conj}}_{N,M}$
, let
![]() $N=\prod _{i=1}^d p_i^{k_i}$
be the prime decomposition of N, and thus
$N=\prod _{i=1}^d p_i^{k_i}$
be the prime decomposition of N, and thus
![]() $N^k=\prod _{i=1}^d p_i^{kk_i}$
. Define vectors
$N^k=\prod _{i=1}^d p_i^{kk_i}$
. Define vectors
![]() $n=(p_1^{k_1},\ldots ,p_d^{k_d})$
,
$n=(p_1^{k_1},\ldots ,p_d^{k_d})$
,
![]() $n'=(p^{kk_1},\ldots ,p^{kk_d})$
, and
$n'=(p^{kk_1},\ldots ,p^{kk_d})$
, and
![]() $m=(p_1,\ldots ,p_d)$
. Define the diagonal matrix
$m=(p_1,\ldots ,p_d)$
. Define the diagonal matrix
![]() $K={\mathrm {diag}}(k,\ldots ,k)$
. We note that
$K={\mathrm {diag}}(k,\ldots ,k)$
. We note that
![]() $A_{N^k}=A_N K$
, so by Lemma 4.32,
$A_{N^k}=A_N K$
, so by Lemma 4.32,
![]() ${\mathrm {M}}_{A_{N^k},m}={\mathrm {M}}_{K,n}\circ {\mathrm {M}}_{A_{N},m}$
. We simplify the defining formula of
${\mathrm {M}}_{A_{N^k},m}={\mathrm {M}}_{K,n}\circ {\mathrm {M}}_{A_{N},m}$
. We simplify the defining formula of
![]() ${\mathrm {Conj}}_{N,N^k}$
as follows:
${\mathrm {Conj}}_{N,N^k}$
as follows:
 $$ \begin{align*} {\mathrm{Conj}}_{N,N^k}&={\mathrm{Conj}}_{N^k,M}^{-1}\circ{\mathrm{Conj}}_{N,M} \\ &=({\mathrm{diag}}_{n'}\circ{\mathrm{M}}_{A_{N^k},m}\circ{\mathrm{tess}}_{m})\circ({\mathrm{diag}}_{m}\circ {\mathrm{\mu}}_{A_{N},m}\circ {\mathrm{tess}}_{n}) \\ &={\mathrm{diag}}_{n^K}\circ{\mathrm{M}}_{A_{N^k},m}\circ {\mathrm{\mu}}_{A_{N},m}\circ {\mathrm{tess}}_{n}={\mathrm{diag}}_{n^K}\circ{\mathrm{M}}_{K,n}\circ {\mathrm{tess}}_{n}.\end{align*} $$
$$ \begin{align*} {\mathrm{Conj}}_{N,N^k}&={\mathrm{Conj}}_{N^k,M}^{-1}\circ{\mathrm{Conj}}_{N,M} \\ &=({\mathrm{diag}}_{n'}\circ{\mathrm{M}}_{A_{N^k},m}\circ{\mathrm{tess}}_{m})\circ({\mathrm{diag}}_{m}\circ {\mathrm{\mu}}_{A_{N},m}\circ {\mathrm{tess}}_{n}) \\ &={\mathrm{diag}}_{n^K}\circ{\mathrm{M}}_{A_{N^k},m}\circ {\mathrm{\mu}}_{A_{N},m}\circ {\mathrm{tess}}_{n}={\mathrm{diag}}_{n^K}\circ{\mathrm{M}}_{K,n}\circ {\mathrm{tess}}_{n}.\end{align*} $$
We apply this to compute
 $$ \begin{align*} {\mathrm{Conj}}_{N,N^k}(x)[i]&={\mathrm{diag}}_{n^K}({\mathrm{M}}_{K}({\mathrm{tess}}_{n}(x)))[i]={\mathrm{val}}_{n^K}({\mathrm{M}}_K({\mathrm{tess}}_{n}(x))[{\mathbf{i}}]) \\ &=\unicode{x3bb}({\mathrm{tess}}_{n}(x),(K({\mathbf{i-1}}),K{\mathbf{i}}))=\unicode{x3bb}({\mathrm{tess}}_{n}(x),(k({\mathbf{i-1}}),k{\mathbf{i}})) \\ &\overset{L.~{4.14}}{=}\sum_{j=0}^{k-1}N^j \unicode{x3bb}({\mathrm{tess}}_{n}(x),(k{\mathbf{i}}-{\mathbf{j}}-{\mathbf{1}}),k{\mathbf{i}}-{\mathbf{j}})) \\ &=\sum_{j=0}^{k-1}N^j{\mathrm{val}}_n({\mathrm{tess}}_n(x)[k{\mathbf{i}}-{\mathbf{j}}])\\ &=\sum_{j=0}^{k-1}N^j x[ik-j]={\mathrm{B}}_{N,k}(x[ik-(k-1),ik]). \end{align*} $$
$$ \begin{align*} {\mathrm{Conj}}_{N,N^k}(x)[i]&={\mathrm{diag}}_{n^K}({\mathrm{M}}_{K}({\mathrm{tess}}_{n}(x)))[i]={\mathrm{val}}_{n^K}({\mathrm{M}}_K({\mathrm{tess}}_{n}(x))[{\mathbf{i}}]) \\ &=\unicode{x3bb}({\mathrm{tess}}_{n}(x),(K({\mathbf{i-1}}),K{\mathbf{i}}))=\unicode{x3bb}({\mathrm{tess}}_{n}(x),(k({\mathbf{i-1}}),k{\mathbf{i}})) \\ &\overset{L.~{4.14}}{=}\sum_{j=0}^{k-1}N^j \unicode{x3bb}({\mathrm{tess}}_{n}(x),(k{\mathbf{i}}-{\mathbf{j}}-{\mathbf{1}}),k{\mathbf{i}}-{\mathbf{j}})) \\ &=\sum_{j=0}^{k-1}N^j{\mathrm{val}}_n({\mathrm{tess}}_n(x)[k{\mathbf{i}}-{\mathbf{j}}])\\ &=\sum_{j=0}^{k-1}N^j x[ik-j]={\mathrm{B}}_{N,k}(x[ik-(k-1),ik]). \end{align*} $$
We conclude by presenting some factor maps between multiplication automata. Now A may be a general
![]() $d\times d'$
natural number matrix.
$d\times d'$
natural number matrix.
Theorem 5.12. The system
![]() $(\Sigma _N^{\mathbb {Z}},\Pi _{\alpha (z,n^A),N})$
has
$(\Sigma _N^{\mathbb {Z}},\Pi _{\alpha (z,n^A),N})$
has
![]() $(\Sigma _{N'}^{\mathbb {Z}},\Pi _{\alpha (z,n^A),N'})$
as a factor via
$(\Sigma _{N'}^{\mathbb {Z}},\Pi _{\alpha (z,n^A),N'})$
as a factor via
![]() $\phi ={\mathrm {diag}}_{n^A}\circ {\mathrm {M}}_{A,n}\circ {\mathrm {tess}}_{n}$
. Additionally, if
$\phi ={\mathrm {diag}}_{n^A}\circ {\mathrm {M}}_{A,n}\circ {\mathrm {tess}}_{n}$
. Additionally, if
![]() $N'>1$
and
$N'>1$
and
![]() $x\in \Sigma _N^{\mathbb {Z}}$
is such that
$x\in \Sigma _N^{\mathbb {Z}}$
is such that
![]() ${\mathrm {real}}_N(x)$
is finite, then
${\mathrm {real}}_N(x)$
is finite, then
![]() ${\mathrm {real}}_{N'}(\phi (x))={\mathrm {real}}_N(x)$
.
${\mathrm {real}}_{N'}(\phi (x))={\mathrm {real}}_N(x)$
.
Proof. We note that
so
![]() $\Pi _{\alpha (z,n^A),N}=\Pi _{\alpha (Az,n),N}$
and it is defined.
$\Pi _{\alpha (z,n^A),N}=\Pi _{\alpha (Az,n),N}$
and it is defined.
The system
![]() $(\Sigma _N^{\mathbb {Z}},\Pi _{\alpha (Az,n),N})$
has
$(\Sigma _N^{\mathbb {Z}},\Pi _{\alpha (Az,n),N})$
has
![]() $(X_n,\sigma _{Az})$
as a factor via
$(X_n,\sigma _{Az})$
as a factor via
![]() ${\mathrm {tess}}_{n}$
by Theorem 5.7. The system
${\mathrm {tess}}_{n}$
by Theorem 5.7. The system
![]() $(X_n,\sigma _{Az})$
has
$(X_n,\sigma _{Az})$
has
![]() $(X_{n^A},\sigma _{z})$
as a factor via
$(X_{n^A},\sigma _{z})$
as a factor via
![]() ${\mathrm {M}}_A$
by Corollary 4.41. The system
${\mathrm {M}}_A$
by Corollary 4.41. The system
![]() $(X_{n^A},\sigma _{z})$
has
$(X_{n^A},\sigma _{z})$
has
![]() $(\Sigma _{N'}^{\mathbb {Z}},\Pi _{\alpha (z,n^A),N'})$
as a factor via
$(\Sigma _{N'}^{\mathbb {Z}},\Pi _{\alpha (z,n^A),N'})$
as a factor via
![]() ${\mathrm {diag}}_{n^A}$
by Theorem 5.7. The last claim follows from Propositions 4.30 and 5.8.
${\mathrm {diag}}_{n^A}$
by Theorem 5.7. The last claim follows from Propositions 4.30 and 5.8.
Let us specify one particular type of factor map. Consider any
![]() $M>1$
with a prime decomposition of the form
$M>1$
with a prime decomposition of the form
![]() $M=\prod _{i=1}^d p_i$
(with the
$M=\prod _{i=1}^d p_i$
(with the
![]() $p_i$
distinct and in rising order) and let
$p_i$
distinct and in rising order) and let
![]() $m=(p_1,\ldots ,p_d)$
. If
$m=(p_1,\ldots ,p_d)$
. If
![]() $M'$
divides M, there is a subsequence
$M'$
divides M, there is a subsequence
![]() $(k_i)_{i=1}^{d'}$
of
$(k_i)_{i=1}^{d'}$
of
![]() $(1,2,\ldots ,d)$
such that
$(1,2,\ldots ,d)$
such that
![]() $M=\prod _{i=1}^{d'} p_{k_i}$
. Let
$M=\prod _{i=1}^{d'} p_{k_i}$
. Let
![]() $m'=(p_{k_1},\ldots ,p_{k_{d'}})$
. If
$m'=(p_{k_1},\ldots ,p_{k_{d'}})$
. If
![]() $A_{M,M'}$
is the
$A_{M,M'}$
is the
![]() $d\times d'$
matrix having
$d\times d'$
matrix having
![]() $e_{k_i}\in \mathbb {Z}^d$
as the ith column for
$e_{k_i}\in \mathbb {Z}^d$
as the ith column for
![]() $1\leq i\leq d'$
, it is easy to see that
$1\leq i\leq d'$
, it is easy to see that
![]() $m'=m^{A_{M,M'}}$
. Then we define
$m'=m^{A_{M,M'}}$
. Then we define
![]() ${\mathrm {Fact}}_{M,M'}={\mathrm {diag}}_{m'}\circ {\mathrm {M}}_{A_{M,M'},m}\circ {\mathrm {tess}}_{m}$
.
${\mathrm {Fact}}_{M,M'}={\mathrm {diag}}_{m'}\circ {\mathrm {M}}_{A_{M,M'},m}\circ {\mathrm {tess}}_{m}$
.
If
![]() $N,N'>1$
are divisible by the same prime numbers as
$N,N'>1$
are divisible by the same prime numbers as
![]() $M,M'$
, respectively, we extend the definition to
$M,M'$
, respectively, we extend the definition to
![]() ${\mathrm {Fact}}_{N,N'}={\mathrm {Conj}}_{M',N'}\circ {\mathrm {Fact}}_{M,M'}\circ {\mathrm {Conj}}_{N,M}$
. This agrees with the previous definition in the case when
${\mathrm {Fact}}_{N,N'}={\mathrm {Conj}}_{M',N'}\circ {\mathrm {Fact}}_{M,M'}\circ {\mathrm {Conj}}_{N,M}$
. This agrees with the previous definition in the case when
![]() $N=M$
and
$N=M$
and
![]() $N'=M'$
, because
$N'=M'$
, because
![]() ${\mathrm {Conj}}_{M,M}$
and
${\mathrm {Conj}}_{M,M}$
and
![]() ${\mathrm {Conj}}_{M',M'}$
are identity maps.
${\mathrm {Conj}}_{M',M'}$
are identity maps.
Corollary 5.13. Let
![]() $N_1,N_2>1$
be such that every prime factor of
$N_1,N_2>1$
be such that every prime factor of
![]() $N_2$
is a prime factor of
$N_2$
is a prime factor of
![]() $N_1$
. Then
$N_1$
. Then
![]() $(\Sigma _{N_1}^{\mathbb {Z}},\Pi _{\alpha ,N_1})$
has
$(\Sigma _{N_1}^{\mathbb {Z}},\Pi _{\alpha ,N_1})$
has
![]() $(\Sigma _{N_2}^{\mathbb {Z}},\Pi _{\alpha ,N_2})$
as a factor via
$(\Sigma _{N_2}^{\mathbb {Z}},\Pi _{\alpha ,N_2})$
as a factor via
![]() ${\mathrm {Fact}}_{N_1,N_2}$
for any
${\mathrm {Fact}}_{N_1,N_2}$
for any
![]() $\alpha>0$
such that these maps are defined. Additionally, if
$\alpha>0$
such that these maps are defined. Additionally, if
![]() $x\in \Sigma _{N_1}^{\mathbb {Z}}$
is such that
$x\in \Sigma _{N_1}^{\mathbb {Z}}$
is such that
![]() ${\mathrm {real}}_{N_1}(x)$
is finite, then
${\mathrm {real}}_{N_1}(x)$
is finite, then
![]() ${\mathrm {real}}_{N_2}({\mathrm {Fact}}_{N_1,N_2}(x))={\mathrm {real}}_{N_1}(x)$
.
${\mathrm {real}}_{N_2}({\mathrm {Fact}}_{N_1,N_2}(x))={\mathrm {real}}_{N_1}(x)$
.
Proof. Let
![]() $M_1=\prod _{i=1}^{d} p_i$
where
$M_1=\prod _{i=1}^{d} p_i$
where
![]() $p_i$
are the prime numbers that divide
$p_i$
are the prime numbers that divide
![]() $N_1$
(in rising order), and let
$N_1$
(in rising order), and let
![]() $M_2=\prod _{i=1}^{d} q_i$
where
$M_2=\prod _{i=1}^{d} q_i$
where
![]() $q_i$
are the prime numbers that divide
$q_i$
are the prime numbers that divide
![]() $N_2$
. Then
$N_2$
. Then
![]() $M_2$
divides
$M_2$
divides
![]() $M_1$
.
$M_1$
.
The system
![]() $(\Sigma _{N_1}^{\mathbb {Z}},\Pi _{\alpha ,N_1})$
has
$(\Sigma _{N_1}^{\mathbb {Z}},\Pi _{\alpha ,N_1})$
has
![]() $(\Sigma _{M_1}^{\mathbb {Z}},\Pi _{\alpha ,M_1})$
as a factor via
$(\Sigma _{M_1}^{\mathbb {Z}},\Pi _{\alpha ,M_1})$
as a factor via
![]() ${\mathrm {Conj}}_{N_1,M_1}$
by Corollary 5.10. The system
${\mathrm {Conj}}_{N_1,M_1}$
by Corollary 5.10. The system
![]() $(\Sigma _{M_1}^{\mathbb {Z}},\Pi _{\alpha ,M_1})$
has
$(\Sigma _{M_1}^{\mathbb {Z}},\Pi _{\alpha ,M_1})$
has
![]() $(\Sigma _{M_2}^{\mathbb {Z}},\Pi _{\alpha ,M_2})$
as a factor via
$(\Sigma _{M_2}^{\mathbb {Z}},\Pi _{\alpha ,M_2})$
as a factor via
![]() ${\mathrm {Fact}}_{M_1,M_2}$
by the previous theorem. The system
${\mathrm {Fact}}_{M_1,M_2}$
by the previous theorem. The system
![]() $(\Sigma _{M_2}^{\mathbb {Z}},\Pi _{\alpha ,M_2})$
has
$(\Sigma _{M_2}^{\mathbb {Z}},\Pi _{\alpha ,M_2})$
has
![]() $(\Sigma _{N_2}^{\mathbb {Z}},\Pi _{\alpha ,N_2})$
as a factor via
$(\Sigma _{N_2}^{\mathbb {Z}},\Pi _{\alpha ,N_2})$
as a factor via
![]() ${\mathrm {Conj}}_{M_2,N_2}$
. Therefore,
${\mathrm {Conj}}_{M_2,N_2}$
. Therefore,
![]() $(\Sigma _{N_1}^{\mathbb {Z}},\Pi _{\alpha ,N_1})$
has
$(\Sigma _{N_1}^{\mathbb {Z}},\Pi _{\alpha ,N_1})$
has
![]() $(\Sigma _{N_2},\Pi _{\alpha ,N_2})$
as a factor via
$(\Sigma _{N_2},\Pi _{\alpha ,N_2})$
as a factor via
![]() ${\mathrm {Fact}}_{N_1,N_2}$
. The last claim follows from Corollary 5.10 and Theorem 5.12.
${\mathrm {Fact}}_{N_1,N_2}$
. The last claim follows from Corollary 5.10 and Theorem 5.12.
We conclude this subsection by highlighting an alternative characterization for the maps
![]() ${\mathrm {Conj}}_{N_1,N_2}$
and
${\mathrm {Conj}}_{N_1,N_2}$
and
![]() ${\mathrm {Fact}}_{N_1,N_2}$
which may be used to ignore the details of their construction: they are fully determined by the requirement of continuity and the fact that they change representations of real numbers in base
${\mathrm {Fact}}_{N_1,N_2}$
which may be used to ignore the details of their construction: they are fully determined by the requirement of continuity and the fact that they change representations of real numbers in base
![]() $N_1$
to representations of the same real numbers in base
$N_1$
to representations of the same real numbers in base
![]() $N_2$
.
$N_2$
.
Theorem 5.14. Let
![]() $N_1,N_2>1$
be such that every prime factor of
$N_1,N_2>1$
be such that every prime factor of
![]() $N_2$
is a prime factor of
$N_2$
is a prime factor of
![]() $N_1$
. If
$N_1$
. If
![]() $\phi :\Sigma _{N_1}^{\mathbb {Z}}\to \Sigma _{N_2}^{\mathbb {Z}}$
is a continuous map and for any
$\phi :\Sigma _{N_1}^{\mathbb {Z}}\to \Sigma _{N_2}^{\mathbb {Z}}$
is a continuous map and for any
![]() $x\in \Sigma _{N_1}^{\mathbb {Z}}$
such that
$x\in \Sigma _{N_1}^{\mathbb {Z}}$
such that
![]() ${\mathrm {real}}_{N_1}(x)$
is finite, it holds that
${\mathrm {real}}_{N_1}(x)$
is finite, it holds that
![]() ${\mathrm {real}}_{N_2}(\phi (x))={\mathrm {real}}_{N_1}(x)$
, then
${\mathrm {real}}_{N_2}(\phi (x))={\mathrm {real}}_{N_1}(x)$
, then
![]() $\phi ={\mathrm {Fact}}_{N_1,N_2}$
. Additionally, if
$\phi ={\mathrm {Fact}}_{N_1,N_2}$
. Additionally, if
![]() $N_1$
and
$N_1$
and
![]() $N_2$
have the same prime factors, then
$N_2$
have the same prime factors, then
![]() $\phi ={\mathrm {Conj}}_{N_1,N_2}$
, and
$\phi ={\mathrm {Conj}}_{N_1,N_2}$
, and
![]() $\phi $
is injective only in this case. If on the other hand
$\phi $
is injective only in this case. If on the other hand
![]() $N_2$
has a prime factor that does not divide
$N_2$
has a prime factor that does not divide
![]() $N_1$
, then a map
$N_1$
, then a map
![]() $\phi $
satisfying the conditions does not exist.
$\phi $
satisfying the conditions does not exist.
Proof. The claims that
![]() $\phi ={\mathrm {Fact}}_{N_1,N_2}$
or
$\phi ={\mathrm {Fact}}_{N_1,N_2}$
or
![]() $\phi ={\mathrm {Conj}}_{N_1,N_2}$
follow from Corollaries 5.10 and 5.13 if we show that the map
$\phi ={\mathrm {Conj}}_{N_1,N_2}$
follow from Corollaries 5.10 and 5.13 if we show that the map
![]() $\phi $
satisfying the conditions in the statement of the theorem is unique, that is, if
$\phi $
satisfying the conditions in the statement of the theorem is unique, that is, if
![]() $\phi '$
is another such map then
$\phi '$
is another such map then
![]() $\phi =\phi '$
. Since
$\phi =\phi '$
. Since
![]() $\phi $
and
$\phi $
and
![]() $\phi '$
are continuous, it is sufficient to show that
$\phi '$
are continuous, it is sufficient to show that
![]() $\phi (x)=\phi '(x)$
in a dense subset of
$\phi (x)=\phi '(x)$
in a dense subset of
![]() $\Sigma _{N_1}^{\mathbb {Z}}$
, so let
$\Sigma _{N_1}^{\mathbb {Z}}$
, so let
![]() $x\in \Sigma _{N_1}^{\mathbb {Z}}$
be such that
$x\in \Sigma _{N_1}^{\mathbb {Z}}$
be such that
![]() ${\mathrm {real}}_{N_1}(x)\in \mathbb {R}\setminus \mathbb {Q}$
. Then
${\mathrm {real}}_{N_1}(x)\in \mathbb {R}\setminus \mathbb {Q}$
. Then
 $$ \begin{align*} \phi(x)&={\mathrm{config}}_{N_2}({\mathrm{real}}_{N_2}(\phi(x)))={\mathrm{config}}_{N_2}({\mathrm{real}}_{N_1}(x)) \\ &={\mathrm{config}}_{N_2}({\mathrm{real}}_{N_2}(\phi'(x)))=\phi'(x). \end{align*} $$
$$ \begin{align*} \phi(x)&={\mathrm{config}}_{N_2}({\mathrm{real}}_{N_2}(\phi(x)))={\mathrm{config}}_{N_2}({\mathrm{real}}_{N_1}(x)) \\ &={\mathrm{config}}_{N_2}({\mathrm{real}}_{N_2}(\phi'(x)))=\phi'(x). \end{align*} $$
Next we show that if
![]() $N_1$
has some prime factor p not dividing
$N_1$
has some prime factor p not dividing
![]() $N_2$
, then
$N_2$
, then
![]() $\phi $
is not injective. The number
$\phi $
is not injective. The number
![]() $p^{-1}$
has a finite base-
$p^{-1}$
has a finite base-
![]() $N_1$
representation
$N_1$
representation
![]() $0.(N_1/p)$
, so
$0.(N_1/p)$
, so
![]() $p^{-1}$
has two different representations in base
$p^{-1}$
has two different representations in base
![]() $N_1$
. On the other hand,
$N_1$
. On the other hand,
![]() $p^{-1}$
does not have a finite base-
$p^{-1}$
does not have a finite base-
![]() $N_2$
representation, because otherwise,
$N_2$
representation, because otherwise,
![]() $N_2^ip^{-1}$
would be an integer for a sufficiently large
$N_2^ip^{-1}$
would be an integer for a sufficiently large
![]() $i\in \mathbb {N}$
even though p does not divide
$i\in \mathbb {N}$
even though p does not divide
![]() $N_2$
. Therefore,
$N_2$
. Therefore,
![]() $p^{-1}$
has only one representation in base
$p^{-1}$
has only one representation in base
![]() $N_2$
. Let
$N_2$
. Let
![]() $x,y\in \Sigma _{N_1}^{\mathbb {Z}}$
be distinct configurations such that
$x,y\in \Sigma _{N_1}^{\mathbb {Z}}$
be distinct configurations such that
![]() ${\mathrm {real}}_{N_1}(x)={\mathrm {real}}_{N_1}(y)=p^{-1}$
. Then it also holds that
${\mathrm {real}}_{N_1}(x)={\mathrm {real}}_{N_1}(y)=p^{-1}$
. Then it also holds that
![]() ${\mathrm {real}}_{N_2}(\phi (x))={\mathrm {real}}_{N_2}(\phi (y))=p^{-1}$
. Because
${\mathrm {real}}_{N_2}(\phi (x))={\mathrm {real}}_{N_2}(\phi (y))=p^{-1}$
. Because
![]() $p^{-1}$
has only one representation in base
$p^{-1}$
has only one representation in base
![]() $N_2$
, from this, it follows that
$N_2$
, from this, it follows that
![]() $\phi (x)=\phi (y)$
and
$\phi (x)=\phi (y)$
and
![]() $\phi $
is not injective.
$\phi $
is not injective.
To show the last claim, assume to the contrary that
![]() $N_2$
has a prime factor not dividing
$N_2$
has a prime factor not dividing
![]() $N_1$
and that a map
$N_1$
and that a map
![]() $\phi $
satisfying the conditions exists. For
$\phi $
satisfying the conditions exists. For
![]() $i\in \mathbb {N}$
, let
$i\in \mathbb {N}$
, let
![]() $x_i={\mathrm {config}}_{N_1}(N_1^i)$
, meaning that
$x_i={\mathrm {config}}_{N_1}(N_1^i)$
, meaning that
![]() $\lim _{i\to \infty }x_i=0^{\mathbb {Z}}$
. For all
$\lim _{i\to \infty }x_i=0^{\mathbb {Z}}$
. For all
![]() $i\in \mathbb {N}$
, it holds that
$i\in \mathbb {N}$
, it holds that
and therefore
![]() $\phi (x_i)[0]\neq 0$
or
$\phi (x_i)[0]\neq 0$
or
![]() $\phi (x_i)[1]\neq 0$
. But then it follows that
$\phi (x_i)[1]\neq 0$
. But then it follows that
which contradicts the assumption of continuity of
![]() $\phi $
.
$\phi $
.
5.3. The regularity status of multiplication automata
In this subsection, we consider the question of which multiplication automata are regular. Regularity is presented in [Reference Kůrka8] as one way to classify dynamical systems according to the complexity of their time evolution: non-regular systems are in some sense more complex than regular systems. We will use the notions of sofic subshifts and subshifts of finite type (SFT) (for definitions, see e.g., [Reference Lind and Marcus10]), but for our purposes, it is for the most part sufficient to know that sofic subshifts are precisely the subshift factors of SFTs. From this, it also follows that all subshift factors of sofic subshifts are sofic. The following definition was given in [Reference Kůrka8].
Definition 5.15. A dynamical system
![]() $(X,T)$
with X a zero-dimensional compact metrizable space is called regular if all its one-sided subshift factors are sofic shifts.
$(X,T)$
with X a zero-dimensional compact metrizable space is called regular if all its one-sided subshift factors are sofic shifts.
In [Reference Kůrka8, §3], it is also observed that to check the regularity of
![]() $(X,F)$
for a CA F, it is sufficient to check whether all of its trace subshifts are sofic shifts, that is, whether the trace subshifts of all widths are sofic. Lower width trace subshifts are factors of higher width trace subshifts, so it is sufficient to check whether trace subshifts of arbitrarily large width are sofic.
$(X,F)$
for a CA F, it is sufficient to check whether all of its trace subshifts are sofic shifts, that is, whether the trace subshifts of all widths are sofic. Lower width trace subshifts are factors of higher width trace subshifts, so it is sufficient to check whether trace subshifts of arbitrarily large width are sofic.
We will give in Theorems 5.17 and 5.19 a complete characterization of regular multiplication automata based on earlier results [Reference Blanchard and Maass2, Reference Kopra7].
Theorem 5.16. [Reference Kopra7, Corollary 4.19]
The system
![]() $(\Sigma _{pq}^{\mathbb {Z}},\Pi _{p/q,pq})$
is not regular for coprime
$(\Sigma _{pq}^{\mathbb {Z}},\Pi _{p/q,pq})$
is not regular for coprime
![]() $p,q>2$
.
$p,q>2$
.
Theorem 5.17. The system
![]() $(\Sigma _N^{\mathbb {Z}},\Pi _{p/q,N})$
is not regular for any coprime
$(\Sigma _N^{\mathbb {Z}},\Pi _{p/q,N})$
is not regular for any coprime
![]() $p,q>2$
such that this map is defined.
$p,q>2$
such that this map is defined.
Proof. Since
![]() $\Pi _{p/q,N}$
is defined, all the prime factors of p and q divide N, so by Corollary 5.13, the system
$\Pi _{p/q,N}$
is defined, all the prime factors of p and q divide N, so by Corollary 5.13, the system
![]() $(\Sigma _N^{\mathbb {Z}},\Pi _{p/q,N})$
has
$(\Sigma _N^{\mathbb {Z}},\Pi _{p/q,N})$
has
![]() $(\Sigma _{pq}^{\mathbb {Z}},\Pi _{p/q,pq})$
as a factor. By the previous theorem,
$(\Sigma _{pq}^{\mathbb {Z}},\Pi _{p/q,pq})$
as a factor. By the previous theorem,
![]() $(\Sigma _{pq}^{\mathbb {Z}},\Pi _{p/q,pq})$
has a non-sofic subshift
$(\Sigma _{pq}^{\mathbb {Z}},\Pi _{p/q,pq})$
has a non-sofic subshift
![]() $(X,\sigma )$
as a factor. Therefore,
$(X,\sigma )$
as a factor. Therefore,
![]() $(\Sigma _N^{\mathbb {Z}},\Pi _{p/q,N})$
has the non-sofic subshift
$(\Sigma _N^{\mathbb {Z}},\Pi _{p/q,N})$
has the non-sofic subshift
![]() $(X,\sigma )$
as a factor and
$(X,\sigma )$
as a factor and
![]() $(\Sigma _N^{\mathbb {Z}},\Pi _{p/q,N})$
is not regular.
$(\Sigma _N^{\mathbb {Z}},\Pi _{p/q,N})$
is not regular.
Theorem 5.18. [Reference Blanchard and Maass2, §4]
The width
![]() $1$
trace subshift of the CA
$1$
trace subshift of the CA
![]() $\Pi _{p,pq}$
for
$\Pi _{p,pq}$
for
![]() $p,q\geq 1$
is an SFT.
$p,q\geq 1$
is an SFT.
Theorem 5.19. The systems
![]() $(\Sigma _N^{\mathbb {Z}},\Pi _{p,N})$
and
$(\Sigma _N^{\mathbb {Z}},\Pi _{p,N})$
and
![]() $(\Sigma _N^{\mathbb {Z}},\Pi _{1/p,N})$
are regular for any
$(\Sigma _N^{\mathbb {Z}},\Pi _{1/p,N})$
are regular for any
![]() ${p,N\in \mathbb {Z}_+}$
such that these maps are defined.
${p,N\in \mathbb {Z}_+}$
such that these maps are defined.
Proof. The maps
![]() $\Pi _{p,N}$
and
$\Pi _{p,N}$
and
![]() $\Pi _{1/p,N}$
are inverses of each other, so it is sufficient to show that
$\Pi _{1/p,N}$
are inverses of each other, so it is sufficient to show that
![]() $(\Sigma _N^{\mathbb {Z}},\Pi _{p,N})$
is regular. For
$(\Sigma _N^{\mathbb {Z}},\Pi _{p,N})$
is regular. For
![]() $N=1$
, the CA
$N=1$
, the CA
![]() $\Pi _{p,N}$
is the identity map on the set with a single point, so we may assume that
$\Pi _{p,N}$
is the identity map on the set with a single point, so we may assume that
![]() $N>1$
. Regularity is equivalent to showing that for some
$N>1$
. Regularity is equivalent to showing that for some
![]() $M\geq 1$
, the trace subshift of arbitrary width
$M\geq 1$
, the trace subshift of arbitrary width
![]() $k\geq M$
is sofic. Let M be such that p divides
$k\geq M$
is sofic. Let M be such that p divides
![]() $N^M$
and fix any
$N^M$
and fix any
![]() $k\geq M$
. Let
$k\geq M$
. Let
![]() $I=[-(k-1),0]$
. We need to show that
$I=[-(k-1),0]$
. We need to show that
![]() $(X,\sigma )$
with
$(X,\sigma )$
with
![]() $X=\Xi _I(F)$
is sofic. Let
$X=\Xi _I(F)$
is sofic. Let
![]() ${\mathrm {B}}_{N,k}$
be the map defined before Theorem 5.11 and for
${\mathrm {B}}_{N,k}$
be the map defined before Theorem 5.11 and for
![]() $z\in ((\Sigma _N)^k)^{\mathbb {N}}$
, denote by
$z\in ((\Sigma _N)^k)^{\mathbb {N}}$
, denote by
![]() ${\mathrm {B}}_{N,k}(z)$
the coordinatewise application of
${\mathrm {B}}_{N,k}(z)$
the coordinatewise application of
![]() ${\mathrm {B}}_{N,k}$
to the symbols of z. We need to show that the subshift
${\mathrm {B}}_{N,k}$
to the symbols of z. We need to show that the subshift
![]() $({\mathrm {B}}_{N,k}(X),\sigma )$
conjugate to
$({\mathrm {B}}_{N,k}(X),\sigma )$
conjugate to
![]() $(X,\sigma )$
is sofic. Its configurations
$(X,\sigma )$
is sofic. Its configurations
![]() ${\mathrm {B}}_{N,k}({\mathrm {Tr}}_{\Pi _{p,N},I}(x))$
for
${\mathrm {B}}_{N,k}({\mathrm {Tr}}_{\Pi _{p,N},I}(x))$
for
![]() $x\in \Sigma _N^{\mathbb {Z}}$
are precisely of the form
$x\in \Sigma _N^{\mathbb {Z}}$
are precisely of the form
 $$ \begin{align*} {\mathrm{B}}_{N,k}({\mathrm{Tr}}_{\Pi_{p,N},I}(x))[i]&={\mathrm{B}}_{N,k}(\Pi_{p,N}^i(x)[-(k-1),0]) \\ &\overset{T.~{5.11}}{=}{\mathrm{Conj}}_{N,N^k}(\Pi_{p,N}^i(x))[0]\overset{C.~{5.10}}{=}\Pi_{p,N^k}^i({\mathrm{Conj}}_{N,N^k}(x))[0] \\ &=\Pi_{p,N^k}^i(x')[0]={\mathrm{Tr}}_{\Pi_{p,N^k}}(x')[i]\mbox{ for }i\in\mathbb{N}, \end{align*} $$
$$ \begin{align*} {\mathrm{B}}_{N,k}({\mathrm{Tr}}_{\Pi_{p,N},I}(x))[i]&={\mathrm{B}}_{N,k}(\Pi_{p,N}^i(x)[-(k-1),0]) \\ &\overset{T.~{5.11}}{=}{\mathrm{Conj}}_{N,N^k}(\Pi_{p,N}^i(x))[0]\overset{C.~{5.10}}{=}\Pi_{p,N^k}^i({\mathrm{Conj}}_{N,N^k}(x))[0] \\ &=\Pi_{p,N^k}^i(x')[0]={\mathrm{Tr}}_{\Pi_{p,N^k}}(x')[i]\mbox{ for }i\in\mathbb{N}, \end{align*} $$
where
![]() $x'={\mathrm {Conj}}_{N,N^k}(x)\in (\Sigma _{N^k})^{\mathbb {Z}}$
, so
$x'={\mathrm {Conj}}_{N,N^k}(x)\in (\Sigma _{N^k})^{\mathbb {Z}}$
, so
![]() ${\mathrm {B}}_{N,k}({\mathrm {Tr}}_{\Pi _{p,N},I}(x))\in \Xi _{[0,0]}(\Pi _{p,N^k})$
. Since
${\mathrm {B}}_{N,k}({\mathrm {Tr}}_{\Pi _{p,N},I}(x))\in \Xi _{[0,0]}(\Pi _{p,N^k})$
. Since
![]() ${\mathrm {Conj}}_{N,N^k}$
is a bijection, in fact,
${\mathrm {Conj}}_{N,N^k}$
is a bijection, in fact,
![]() ${\mathrm {B}}_{N,k}(X)=\Xi _{[0,0]}(\Pi _{p,N^k})$
. Therefore,
${\mathrm {B}}_{N,k}(X)=\Xi _{[0,0]}(\Pi _{p,N^k})$
. Therefore,
![]() $({\mathrm {B}}_{N,k}(X),\sigma )$
is the trace subshift of width
$({\mathrm {B}}_{N,k}(X),\sigma )$
is the trace subshift of width
![]() $1$
of the CA
$1$
of the CA
![]() $\Pi _{p,N^k}$
, and it is sofic by the previous theorem.
$\Pi _{p,N^k}$
, and it is sofic by the previous theorem.
Acknowledgements
I thank Tristan Stérin for helpful discussions on representing multiplication by Wang tiles. The work was supported by the Finnish Cultural Foundation (grant number 00220510).