Hostname: page-component-76fb5796d-vfjqv Total loading time: 0 Render date: 2024-04-29T23:32:49.110Z Has data issue: false hasContentIssue false
  • English
  • Français

Natural boundary for the susceptibility function of generic piecewise expanding unimodal maps

Published online by Cambridge University Press:  25 January 2013

V. BALADI ,
S. MARMI  and
D. SAUZIN
V. BALADI
Affiliation:
D.M.A., UMR 8553, École Normale Supérieure, 75005 Paris, France (email: baladi@math.ku.dk)
S. MARMI
Affiliation:
Scuola Normale Superiore, CNRS–UMI 3483 Fibonacci, 56126 Pisa, Italy (email: s.marmi@sns.it)
D. SAUZIN
Affiliation:
Scuola Normale Superiore, CNRS–UMI 3483 Fibonacci, 56126 Pisa, Italy (email: david.sauzin@sns.it)
Get access Rights & Permissions [Opens in a new window]

Abstract

For a piecewise expanding unimodal interval map 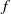$f$ with unique absolutely continuous invariant probability measure 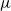$\mu $, a perturbation 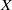$X$, and an observable 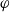$\varphi $, the susceptibility function is 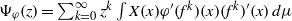$\Psi _\varphi (z)= \sum _{k=0}^\infty z^k \int X(x) \varphi '( f^k)(x) (f^k)'(x) \, d\mu $. Combining previous results [V. Baladi, On the susceptibility function of piecewise expanding interval maps. Comm. Math. Phys.275 (2007), 839–859; V. Baladi and D. Smania, Linear response for piecewise expanding unimodal maps. Nonlinearity21 (2008), 677–711] (deduced from spectral properties of Ruelle transfer operators) with recent work of Breuer–Simon [Natural boundaries and spectral theory. Adv. Math.226 (2011), 4902–4920] (based on techniques from the spectral theory of Jacobi matrices and a classical paper of Agmon [Sur les séries de Dirichlet. Ann. Sci. Éc. Norm. Supér. (3) 66 (1949), 263–310]), we show that density of the postcritical orbit (a generic condition) implies that 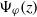$\Psi _\varphi (z)$ has a strong natural boundary on the unit circle. The Breuer–Simon method provides uncountably many candidates for the outer functions of 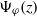$\Psi _\varphi (z)$, associated with precritical orbits. If the perturbation 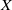$X$ is horizontal, a generic condition (Birkhoff typicality of the postcritical orbit) implies that the non-tangential limit of 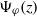$\Psi _\varphi (z)$ as 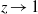$z\to 1$ exists and coincides with the derivative of the absolutely continuous invariant probability measure with respect to the map (‘linear response formula’). Applying the Wiener–Wintner theorem, we study the singularity type of non-tangential limits of 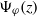$\Psi _\varphi (z)$ as 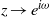$z\to e^{i\omega }$ for real 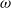$\omega $. An additional ‘law of the iterated logarithm’ typicality assumption on the postcritical orbit gives stronger results.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 34 , Issue 3 , June 2014 , pp. 777 - 800
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Agmon, S.. Sur les séries de Dirichlet. Ann. Sci. Éc. Norm. Supér. (3) 66 (1949), 263–310.CrossRefGoogle Scholar
[2]Assani, I.. Wiener–Wintner Ergodic Theorems. World Scientific, Singapore, 2003.CrossRefGoogle Scholar
[3]Assani, I.. Private communication, 2012.Google Scholar
[4]Baladi, V.. Positive Transfer Operators and Decay of Correlations (Advanced Series in Nonlinear Dynamics, 16). World Scientific, Singapore, 2000.Google Scholar
[5]Baladi, V.. On the susceptibility function of piecewise expanding interval maps. Comm. Math. Phys. 275 (2007), 839–859.Google Scholar
[6]Baladi, V. and Smania, D.. Linear response for piecewise expanding unimodal maps. Nonlinearity 21 (2008), 677–711. Corrigendum Nonlinearity 25 (2012), 2203–2205.Google Scholar
[7]Baladi, V. and Smania, D.. Linear response for smooth deformations of generic non-uniformly hyperbolic unimodal maps. Preprint. 2010. Ann. Sci. Éc. Norm. Supér. 45 (2012).Google Scholar
[8]Baladi, V.. Linear response despite critical points. Nonlinearity 21 (2008), T81–T90.CrossRefGoogle Scholar
[9]Baladi, V., Benedicks, M. and Schnellmann, D.. Whitney Hölder continuity of the SRB measure for transversal families of smooth unimodal maps. In preparation, 2012.Google Scholar
[10]Benedicks, M.. Private communication, 2011.Google Scholar
[11]Block, L. S. and Coppel, W. A.. Dynamics in One Dimension (Lecture Notes in Mathematics, 1513). Springer, New York, 1992.Google Scholar
[12]Borel, E.. Leçons sur les fonctions monogènes uniformes d’une variable complexe. Gauthier-Villars, Paris, 1917.Google Scholar
[13]Breuer, J. and Simon, B.. Natural boundaries and spectral theory. Adv. Math. 226 (2011), 4902–4920.Google Scholar
[14]Broise, A.. Transformations dilatantes de l’intervalle et théorèmes limites. Etudes spectrales d’opérateurs de transfert et applications. Astérisque 238 (1996), 1–109.Google Scholar
[15]Bruin, H.. Private communication, 2012.Google Scholar
[16]Buzzi, J.. Specification on the interval. Trans. Amer. Math. Soc. 349 (1997), 2737–2754.Google Scholar
[17]Cohen, G. and Conze, J.-P.. The CLT for rotated ergodic sums and related processes. Preprint, 2012.Google Scholar
[18]Field, M., Melbourne, I. and Török, A.. Decay of correlations, central limit theorems and approximation by Brownian motion for compact Lie group extensions. Ergod. Th. & Dynam. Sys. 23 (2003), 87–110.Google Scholar
[19]Gouëzel, S.. Almost sure invariance principle for dynamical systems by spectral methods. Ann. Probab. 38 (2010), 1639–1671.Google Scholar
[20]Hofbauer, F. and Keller, G.. Ergodic properties of invariant measures for piecewise monotonic transformations. Math. Z. 180 (1982), 119–140.Google Scholar
[21]Keller, G.. Piecewise monotonic transformations and exactness. Collection: Seminar on Probability, University of Rennes, Rennes, 1978, Exp. 6.Google Scholar
[22]Kowalski, Z. S.. Invariant measure for piecewise monotonic transformations has a lower bound on its support. Bull. Pol. Acad. Sci. Math. 27 (1979), 53–57.Google Scholar
[23]Kuipers, L. and Niederreiter, H.. Uniform Distribution of Sequences. Wiley, New York, 1974.Google Scholar
[24]Liverani, C.. Decay of correlations in piecewise expanding maps. J. Stat. Phys. 78 (1995), 1111–1129.CrossRefGoogle Scholar
[25]Marmi, S. and Sauzin, D.. Quasianalytic monogenic solutions of a cohomological equation. Mem. Amer. Math. Soc. 164 (2003), 780.Google Scholar
[26]Marmi, S. and Sauzin, D.. A quasianalyticity property for monogenic solutions of small divisor problems. Bull. Braz. Math. Soc. (N.S.) 42 (2011), 45–74.Google Scholar
[27]Marmi, S., Sauzin, D. and Tiozzo, G.. Generalised continuation by means of right limits, in preparation.Google Scholar
[28]Melbourne, I. and Nicol, M.. Statistical properties of endomorphisms and compact group extensions. J. Lond. Math. Soc. 70 (2004), 427–446.Google Scholar
[29]Melbourne, I. and Nicol, M.. Statistical limit laws for equivariant observations. Stoch. Dyn. 4 (2004), 1–13.Google Scholar
[30]Nicol, M., Melbourne, I. and Ashwin, P.. Euclidean extensions of dynamical systems. Nonlinearity 14 (2001), 275–300.Google Scholar
[31]Ross, W. T. and Shapiro, H. S.. Generalised Analytic Continuation (University Lecture Series, 25). American Mathematical Society, Providence, RI, 2002.Google Scholar
[32]Rohlin, V. A.. Exact endomorphisms of a Lebesgue space. Izv. Akad. Nauk SSSR Ser. Mat. 25 (1961), 499–530 (in Russian).Google Scholar
[33]Ruelle, D.. Application of hyperbolic dynamics to physics: some problems and conjectures. Bull. Amer. Math. Soc. 41 (2004), 275–278.Google Scholar
[34]Ruelle, D.. Differentiating the A.C.I.M. of an interval map with respect to $f$. Comm. Math. Phys. 258 (2005), 445–453.Google Scholar
[35]Ruelle, D.. Structure and f-dependence of the A.C.I.M. for a unimodal map f is Misiurewicz type. Comm. Math. Phys. 287 (2009), 1039–1070.Google Scholar
[36]Schnellmann, D.. Typical points for one-parameter families of piecewise expanding maps of the interval. Discrete Contin. Dyn. Syst. 31 (2011), 877–911.CrossRefGoogle Scholar
[37]Shen, W.. Private communication, 2011.Google Scholar
[38]Van Den Bedem, H. and Chernov, N.. Expanding maps of an interval with holes. Ergod. Th. & Dynam. Sys. 22 (2002), 637–654.Google Scholar
[39]Wittmann, R.. A general law of iterated logarithm. Z. Wahrsch. Verw. Gebiete 68 (1985), 521–543.Google Scholar