Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Mukherjee, Sabyasachi
2015.
Orbit portraits of unicritical antiholomorphic polynomials.
Conformal Geometry and Dynamics of the American Mathematical Society,
Vol. 19,
Issue. 3,
p.
35.
Bergweiler, Walter
and
Eremenko, Alexandre
2016.
Green’s function and anti-holomorphic dynamics on a torus.
Proceedings of the American Mathematical Society,
Vol. 144,
Issue. 7,
p.
2911.
Mukherjee, Sabyasachi
2017.
Parabolic arcs of the multicorns: Real-analyticity of Hausdorff dimension, and singularities of $\mathrm{Per}_n(1)$ curves.
Discrete & Continuous Dynamical Systems - A,
Vol. 37,
Issue. 5,
p.
2565.
Bogdanov, Konstantin
Mamayusupov, Khudoyor
Mukherjee, Sabyasachi
and
Schleicher, Dierk
2017.
Antiholomorphic perturbations of Weierstrass Zeta functions and Green’s function on tori.
Nonlinearity,
Vol. 30,
Issue. 8,
p.
3241.
Zhang, Xiuming
2019.
Cross-sections of the multicorns.
Proceedings - Mathematical Sciences,
Vol. 129,
Issue. 2,
Inou, Hiroyuki
2019.
Self-Similarity for the Tricorn.
Experimental Mathematics,
Vol. 28,
Issue. 4,
p.
440.
Inou, Hiroyuki
and
Mukherjee, Sabyasachi
2020.
On the support of the bifurcation measure of cubic polynomials.
Mathematische Annalen,
Vol. 378,
Issue. 1-2,
p.
1.
Sète, Olivier
and
Zur, Jan
2020.
A Newton method for harmonic mappings in the plane.
IMA Journal of Numerical Analysis,
Vol. 40,
Issue. 4,
p.
2777.
Chávez, C. Abraham T.
and
Curilef, Sergio
2020.
Tricorn-like structures in an optically injected semiconductor laser.
Chaos: An Interdisciplinary Journal of Nonlinear Science,
Vol. 30,
Issue. 2,
Wang, Wei
Hu, Xiaohui
Shahid, Abdul Aziz
and
Wang, Mingye
2020.
Generation of Antifractals via Hybrid Picard-Mann Iteration.
IEEE Access,
Vol. 8,
Issue. ,
p.
83974.
Kawahira, Tomoki
2020.
Zalcman functions and similarity between the Mandelbrot set, Julia sets, and the tricorn.
Analysis and Mathematical Physics,
Vol. 10,
Issue. 2,
Inou, Hiroyuki
and
Mukherjee, Sabyasachi
2021.
Discontinuity of Straightening in Anti-holomorphic Dynamics: I.
Transactions of the American Mathematical Society,
Vol. 374,
Issue. 9,
p.
6445.
Lee, Seung-Yeop
Lyubich, Mikhail
Makarov, Nikolai G.
and
Mukherjee, Sabyasachi
2021.
Schwarz reflections and anti-holomorphic correspondences.
Advances in Mathematics,
Vol. 385,
Issue. ,
p.
107766.
Lundberg, Erik
and
Ramachandran, Koushik
2021.
A note on the critical points of the localization landscape.
Complex Analysis and its Synergies,
Vol. 7,
Issue. 2,
Mj, Mahan
and
Mukherjee, Sabyasachi
2022.
In the Tradition of Thurston II.
p.
331.
Inou, Hiroyuki
and
Mukherjee, Sabyasachi
2022.
Discontinuity of Straightening in Anti-Holomorphic Dynamics: II.
International Mathematics Research Notices,
Vol. 2022,
Issue. 9,
p.
6948.
Lodge, Russell
Luo, Yusheng
and
Mukherjee, Sabyasachi
2022.
On deformation space analogies between Kleinian reflection groups and antiholomorphic rational maps.
Geometric and Functional Analysis,
Vol. 32,
Issue. 6,
p.
1428.
GODIN, JONATHAN
and
ROUSSEAU, CHRISTIANE
2022.
Analytic classification of germs of parabolic antiholomorphic diffeomorphisms of codimension k.
Ergodic Theory and Dynamical Systems,
Vol. 42,
Issue. 12,
p.
3619.
Lee, Seung-Yeop
Lyubich, Mikhail
Makarov, Nikolai G.
and
Mukherjee, Sabyasachi
2025.
Schwarz reflections and the Tricorn.
Annales de l'Institut Fourier,
Vol. 75,
Issue. 5,
p.
1987.
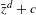 $\bar{z}^{d}+c$ . We investigate the structure of boundaries of hyperbolic components: we prove that the structure of bifurcations from hyperbolic components of even period is as one would expect for maps that depend holomorphically on a complex parameter (for instance, as for the Mandelbrot set; in this setting, this is a non-obvious fact), while the bifurcation structure at hyperbolic components of odd period is very different. In particular, the boundaries of odd period hyperbolic components consist only of parabolic parameters, and there are bifurcations between hyperbolic components along entire arcs, but only of bifurcation ratio 2. We also count the number of hyperbolic components of any period of the multicorns. Since antiholomorphic polynomials depend only real-analytically on the parameters, most of the techniques used in this paper are quite different from the ones used to prove the corresponding results in a holomorphic setting.
$\bar{z}^{d}+c$ . We investigate the structure of boundaries of hyperbolic components: we prove that the structure of bifurcations from hyperbolic components of even period is as one would expect for maps that depend holomorphically on a complex parameter (for instance, as for the Mandelbrot set; in this setting, this is a non-obvious fact), while the bifurcation structure at hyperbolic components of odd period is very different. In particular, the boundaries of odd period hyperbolic components consist only of parabolic parameters, and there are bifurcations between hyperbolic components along entire arcs, but only of bifurcation ratio 2. We also count the number of hyperbolic components of any period of the multicorns. Since antiholomorphic polynomials depend only real-analytically on the parameters, most of the techniques used in this paper are quite different from the ones used to prove the corresponding results in a holomorphic setting.
