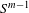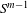Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Mukhamedov, Farrukh
and
Ganikhodjaev, Nasir
2015.
Quantum Quadratic Operators and Processes.
Vol. 2133,
Issue. ,
p.
7.
Badocha, Michał
and
Bartoszek, Wojciech
2018.
Quadratic stochastic operators on Banach lattices.
Positivity,
Vol. 22,
Issue. 2,
p.
477.
Abdulghafor, Rawad
Abdullah, Shahrum Shah
Turaev, Sherzod
and
Hassan, Raini
2019.
The nonlinear limit control of EDSQOs on finite dimensional simplex.
Automatika,
Vol. 60,
Issue. 4,
p.
404.
Homburg, A J
Jamilov, U U
and
Scheutzow, M
2019.
Asymptotics for a class of iterated random cubic operators.
Nonlinearity,
Vol. 32,
Issue. 10,
p.
3646.
Saburov, Mansoor
2020.
Ergodicity of non-homogeneous $$\mathbf {p}$$-majorizing quadratic stochastic operators.
Positivity,
Vol. 24,
Issue. 5,
p.
1191.
Jamilov, Uygun
and
Ladra, Manuel
2020.
The dynamics of (π, α)-cubic stochastic operators.
Journal of Difference Equations and Applications,
Vol. 26,
Issue. 11-12,
p.
1514.
Jamilov, Uygun
and
Ladra, Manuel
2020.
On a Family of Non-Volterra Quadratic Operators Acting on a Simplex.
Qualitative Theory of Dynamical Systems,
Vol. 19,
Issue. 3,
Jamilov, U. U.
Khudoyberdiev, Kh. O.
and
Ladra, M.
2020.
Quadratic operators corresponding to permutations.
Stochastic Analysis and Applications,
Vol. 38,
Issue. 5,
p.
929.
Kurganov, K. A.
Jamilov, U. U.
and
Okhunova, M. O.
2021.
On a Family of Volterra Cubic Stochastic Operators.
Lobachevskii Journal of Mathematics,
Vol. 42,
Issue. 12,
p.
2867.
Jamilov, U. U.
2021.
Certain Polynomial Stochastic Operators.
Mathematical Notes,
Vol. 109,
Issue. 5-6,
p.
828.
Jamilov, Uygun
and
Ladra, Manuel
2022.
Evolution algebras and dynamical systems of a worm propagation model.
Linear and Multilinear Algebra,
Vol. 70,
Issue. 19,
p.
4097.
Khudoyberdiev, Khayotjon O.
2022.
Infinite Dimensional Analysis, Quantum Probability and Applications.
Vol. 390,
Issue. ,
p.
369.
Jamilov, Uygun U.
and
Ziyodullaev, Elbek Kh.
2022.
Infinite Dimensional Analysis, Quantum Probability and Applications.
Vol. 390,
Issue. ,
p.
341.
Jamilov, Uygun
and
Mukhamedov, Farrukh
2022.
A Class of Lotka-Volterra Operators with Historical Behavior.
Results in Mathematics,
Vol. 77,
Issue. 4,
Aralova, K. A.
and
Jamilov, U. U.
2022.
The dynamics of superposition of non-Volterra quadratic stochastic operators.
Journal of Difference Equations and Applications,
Vol. 28,
Issue. 9,
p.
1178.
Jamilov, U. U.
and
Mamurov, B. J.
2022.
Asymptotical Behavior of Trajectories of Non-Volterra Quadratic Stochastic Operators.
Lobachevskii Journal of Mathematics,
Vol. 43,
Issue. 11,
p.
3174.
Jamilov, Uygun
and
Aralova, Kamola
2022.
Infinite Dimensional Analysis, Quantum Probability and Applications.
Vol. 390,
Issue. ,
p.
357.
Khamrayev, A. Yu.
2023.
Periodic and Regular Trajectories of Non-Volterra Quadratic Stochastic Operators.
Lobachevskii Journal of Mathematics,
Vol. 44,
Issue. 10,
p.
4321.
Jamilov, Uygun
Mukhamedov, Farrukh
and
Mukhamedova, Farzona
2023.
Discrete time model of sexual systems.
Heliyon,
Vol. 9,
Issue. 7,
p.
e17913.
Embong, Ahmad Fadillah
and
Mukhamedov, Farrukh
2023.
Lyapunov functions and dynamics of infinite dimensional Volterra operators.
Chaos, Solitons & Fractals,
Vol. 173,
Issue. ,
p.
113625.