Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Veerman, Peter
1987.
Symbolic dynamics of order-preserving orbits.
Physica D: Nonlinear Phenomena,
Vol. 29,
Issue. 1-2,
p.
191.
Casdagli, Martin
1988.
Rotational chaos in dissipative systems.
Physica D: Nonlinear Phenomena,
Vol. 29,
Issue. 3,
p.
365.
Sotomayor, J.
1989.
Stability and regularity in bifurcations of planar vector fields.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 113,
Issue. 3-4,
p.
243.
Veerman, J J P
1989.
Irrational rotation numbers.
Nonlinearity,
Vol. 2,
Issue. 3,
p.
419.
MacKay, R. S.
1991.
Chaos, Order, and Patterns.
Vol. 280,
Issue. ,
p.
35.
Baesens, C.
Guckenheimer, J.
Kim, S.
and
MacKay, R.S.
1991.
Three coupled oscillators: mode-locking, global bifurcations and toroidal chaos.
Physica D: Nonlinear Phenomena,
Vol. 49,
Issue. 3,
p.
387.
Siegel, Ralph M.
Tresser, Charles
and
Zettler, George
1992.
A decoding problem in dynamics and in number theory.
Chaos: An Interdisciplinary Journal of Nonlinear Science,
Vol. 2,
Issue. 4,
p.
473.
Uherka, David J.
Tresser, Charles
Galeeva, Roza
and
Campbell, David K.
1992.
Solvable models for the quasi-periodic transition to chaos.
Physics Letters A,
Vol. 170,
Issue. 3,
p.
189.
Zaks, Mikhail A.
1993.
Scaling properties and renormalization invariants for the “homoclinic quasiperiodicity”.
Physica D: Nonlinear Phenomena,
Vol. 62,
Issue. 1-4,
p.
300.
Ashwin, P
and
Swift, J W
1994.
Measuring rotation sets of coupled oscillators.
Nonlinearity,
Vol. 7,
Issue. 3,
p.
925.
Graczyk, J.
Jonker, L. B.
Świątek, G.
Tangerman, F. M.
and
Veerman, J. J. P.
1995.
Differentiable circle maps with a flat interval.
Communications in Mathematical Physics,
Vol. 173,
Issue. 3,
p.
599.
Campbell, David K.
Galeeva, Roza
Tresser, Charles
and
Uherka, David J.
1996.
Piecewise linear models for the quasiperiodic transition to chaos.
Chaos: An Interdisciplinary Journal of Nonlinear Science,
Vol. 6,
Issue. 2,
p.
121.
Aranson, S.
and
Zhuzhoma, E.
1998.
Qualitative theory of flows on surfaces (A review).
Journal of Mathematical Sciences,
Vol. 90,
Issue. 3,
p.
2051.
Zaks, Michael A.
2001.
Fractal Fourier spectra of Cherry flows.
Physica D: Nonlinear Phenomena,
Vol. 149,
Issue. 4,
p.
237.
Maistrenko, Yu.
Popovych, O.
Burylko, O.
and
Tass, P. A.
2004.
Mechanism of Desynchronization in the Finite-Dimensional Kuramoto Model.
Physical Review Letters,
Vol. 93,
Issue. 8,
Maistrenko, Y.L.
Popovych, O.V.
and
Tass, P.A.
2005.
Dynamics of Coupled Map Lattices and of Related Spatially Extended Systems.
Vol. 671,
Issue. ,
p.
285.
MAISTRENKO, YURI L.
POPOVYCH, OLEKSANDR V.
and
TASS, PETER A.
2005.
CHAOTIC ATTRACTOR IN THE KURAMOTO MODEL.
International Journal of Bifurcation and Chaos,
Vol. 15,
Issue. 11,
p.
3457.
Morales, C.A.
2008.
A singular-hyperbolic closing lemma.
Michigan Mathematical Journal,
Vol. 56,
Issue. 1,
Anagnostopoulou, V
Díaz-Ordaz, K
Jenkinson, O
and
Richard, C
2010.
Entrance time functions for flat spot maps.
Nonlinearity,
Vol. 23,
Issue. 6,
p.
1477.
Anagnostopoulou, V.
Díaz-Ordaz, K.
Jenkinson, O.
and
Richard, C.
2012.
The flat spot standard family: variation of the entrance time median.
Dynamical Systems,
Vol. 27,
Issue. 1,
p.
29.

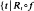 has irrational rotation number}, where ƒ is a certain map of the circle and
has irrational rotation number}, where ƒ is a certain map of the circle and 