Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Przytycki, Feliks
1998.
Iterations of holomorphic Collet-Eckmann maps: conformal and invariant measures. Appendix: On non-renormalizable quadratic polynomials.
Transactions of the American Mathematical Society,
Vol. 350,
Issue. 2,
p.
717.
Haydn, Nicolai
1999.
The Distribution of the First Return Time for Rational Maps.
Journal of Statistical Physics,
Vol. 94,
Issue. 5-6,
p.
1027.
2002.
Vol. 1,
Issue. ,
p.
599.
Urbański, Mariusz
2003.
Measures and dimensions in conformal dynamics.
Bulletin of the American Mathematical Society,
Vol. 40,
Issue. 3,
p.
281.
Yuri, Michiko
2003.
Thermodynamic formalism for countable to one Markov systems.
Transactions of the American Mathematical Society,
Vol. 355,
Issue. 7,
p.
2949.
Dinh, Tien-Cuong
and
Sibony, Nessim
2005.
Equidistribution for meromorphic transforms and the ddc-method.
Science in China Series A: Mathematics,
Vol. 48,
Issue. S1,
p.
180.
Dinh, Tien‐Cuong
and
Sibony, Nessim
2006.
Decay of correlations and the central limit theorem for meromorphic maps.
Communications on Pure and Applied Mathematics,
Vol. 59,
Issue. 5,
p.
754.
Pollicott, Mark
and
Sridharan, Shrihari
2007.
Large Deviation Results for Periodic Points of a Rational Map.
Journal of Dynamical Systems and Geometric Theories,
Vol. 5,
Issue. 1,
p.
69.
Dutkay, Dorin Ervin
and
Røysland, Kjetil
2007.
The algebra of harmonic functions for a matrix-valued transfer operator.
Journal of Functional Analysis,
Vol. 252,
Issue. 2,
p.
734.
Denker, Manfred
Duan, Jinqiao
and
McCourt, Michael
2009.
Pseudorandom numbers for conformal measures.
Dynamical Systems,
Vol. 24,
Issue. 4,
p.
439.
Dinh, Tien-Cuong
and
Sibony, Nessim
2010.
Equidistribution speed for endomorphisms of projective spaces.
Mathematische Annalen,
Vol. 347,
Issue. 3,
p.
613.
Varandas, Paulo
and
Viana, Marcelo
2010.
Existence, uniqueness and stability of equilibrium states for non-uniformly expanding maps.
Annales de l'Institut Henri Poincaré C, Analyse non linéaire,
Vol. 27,
Issue. 2,
p.
555.
Gelfert, Katrin
Przytycki, Feliks
and
Rams, Michał
2010.
On the Lyapunov spectrum for rational maps.
Mathematische Annalen,
Vol. 348,
Issue. 4,
p.
965.
Dupont, Christophe
2010.
Bernoulli coding map and almost sure invariance principle for endomorphisms of $${\mathbb P^k}$$
.
Probability Theory and Related Fields,
Vol. 146,
Issue. 3-4,
p.
337.
COMMAN, HENRI
and
RIVERA-LETELIER, JUAN
2011.
Large deviation principles for non-uniformly hyperbolic rational maps.
Ergodic Theory and Dynamical Systems,
Vol. 31,
Issue. 2,
p.
321.
Pinheiro, Vilton
2011.
Expanding measures.
Annales de l'Institut Henri Poincaré C, Analyse non linéaire,
Vol. 28,
Issue. 6,
p.
889.
Denker, Manfred
and
Stratmann, Bernd O.
2012.
Contributions in Analytic and Algebraic Number Theory.
Vol. 9,
Issue. ,
p.
171.
Castro, A.
and
Varandas, P.
2013.
Equilibrium states for non-uniformly expanding maps: Decay of correlations and strong stability.
Annales de l'Institut Henri Poincaré C, Analyse non linéaire,
Vol. 30,
Issue. 2,
p.
225.
Li, Huaibin
and
Rivera-Letelier, Juan
2014.
Equilibrium States of Weakly Hyperbolic One-Dimensional Maps for Hölder Potentials.
Communications in Mathematical Physics,
Vol. 328,
Issue. 1,
p.
397.
Sridharan, Shrihari
2014.
Spectral Triple and Sinai–Ruelle–Bowen Measures.
Complex Analysis and Operator Theory,
Vol. 8,
Issue. 7,
p.
1513.
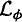 the transfer operator of a Hölder-continuous function φ on J satisfying P(T,φ) > supz∈Jφ(z). We study the behavior of {
the transfer operator of a Hölder-continuous function φ on J satisfying P(T,φ) > supz∈Jφ(z). We study the behavior of {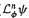 : n ≥ 1} for Hölder-continuous functions ψ and show that the sequence is (uniformly) normbounded in the space of Hölder-continuous functions for sufficiently small exponent. As a consequence we obtain that the density of the equilibrium measure μ for φ with respect to the
: n ≥ 1} for Hölder-continuous functions ψ and show that the sequence is (uniformly) normbounded in the space of Hölder-continuous functions for sufficiently small exponent. As a consequence we obtain that the density of the equilibrium measure μ for φ with respect to the 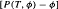 -conformal measure is Höolder-continuous. We also prove that the rate of convergence of {
-conformal measure is Höolder-continuous. We also prove that the rate of convergence of {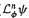 ψ to this density in sup-norm is
ψ to this density in sup-norm is 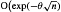 . From this we deduce the corresponding decay of the correlation integral and the central limit theorem for ψ.
. From this we deduce the corresponding decay of the correlation integral and the central limit theorem for ψ.
