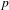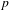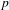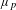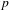Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ueki, Jun
2021.
Profinite rigidity for twisted Alexander polynomials.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2021,
Issue. 771,
p.
171.
Tange, Ryoto
and
Ueki, Jun
2024.
Twisted Iwasawa invariants of knots.
Mathematische Nachrichten,
Vol. 297,
Issue. 4,
p.
1519.
Morishita, Masanori
2024.
Knots and Primes.
p.
171.
UEKI, JUN
and
YOSHIZAKI, HYUGA
2025.
The p-adic limits of class numbers in
${\mathbb{Z}}_p$
-towers.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 179,
Issue. 2,
p.
299.
PENGO, RICCARDO
and
VALLIÈRES, DANIEL
2025.
SPANNING TREES IN
$\mathbb {Z}$
-COVERS OF A FINITE GRAPH AND MAHLER MEASURES.
Journal of the Australian Mathematical Society,
Vol. 118,
Issue. 1,
p.
108.