Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Zhang, Fang
and
Zhou, Yunhua
2017.
On the limit quasi-shadowing property.
Discrete & Continuous Dynamical Systems - A,
Vol. 37,
Issue. 5,
p.
2861.
Bonatti, Christian
and
Zhang, Jinhua
2020.
Transitive partially hyperbolic diffeomorphisms with one-dimensional neutral center.
Science China Mathematics,
Vol. 63,
Issue. 9,
p.
1647.
DE MARTINO, VERÓNICA
and
MARTINCHICH, SANTIAGO
2020.
Codimension one compact center foliations are uniformly compact.
Ergodic Theory and Dynamical Systems,
Vol. 40,
Issue. 9,
p.
2349.
Li, Zhiping
and
Zhou, Yunhua
2020.
Quasi-shadowing and limit quasi-shadowing for quasi-partially hyperbolic strings of flows.
Journal of Differential Equations,
Vol. 269,
Issue. 12,
p.
11062.
Backes, Lucas
and
Dragičević, Davor
2020.
Quasi-shadowing for partially hyperbolic dynamics on Banach spaces.
Journal of Mathematical Analysis and Applications,
Vol. 492,
Issue. 1,
p.
124445.
Castro, A.
Rodrigues, F.
and
Varandas, P.
2020.
Leafwise shadowing property for partially hyperbolic diffeomorphisms.
Dynamical Systems,
Vol. 35,
Issue. 2,
p.
306.
Pan, Juan
Zhang, Wenda
and
Zhou, Yunhua
2021.
Shadowing properties for weakly hyperbolic Zd-actions.
Journal of Mathematical Analysis and Applications,
Vol. 496,
Issue. 2,
p.
124814.
Lee, Manseob
and
Ahn, Jiweon
2022.
Partial hyperbolicity and pseudo orbit tracing properties.
Topology and its Applications,
Vol. 314,
Issue. ,
p.
108095.
Guelman, Nancy
and
Martinchich, Santiago
2022.
Uniqueness of minimal unstable lamination for discretized Anosov flows.
Mathematische Zeitschrift,
Vol. 300,
Issue. 2,
p.
1401.
Lin, Wang
Xinsheng, Wang
and
Yujun, Zhu
2022.
Subsystems with the shadowing 性质 for bm$\mathbb{Z}^{k}$-actions.
SCIENTIA SINICA Mathematica,
Vol. 52,
Issue. 10,
p.
1145.
Wang, Lin
Wang, Xinsheng
and
Wang, Lei
2023.
Measurable Versions of Some Topological Properties for Diffeomorphisms with Continuous Foliations.
Mathematical Problems in Engineering,
Vol. 2023,
Issue. 1,
Martinchich, Santiago
2023.
Global stability of discretized Anosov flows.
Journal of Modern Dynamics,
Vol. 19,
Issue. 0,
p.
561.
Pan, Juan
Ren, Xian Kun
and
Zhou, Yun Hua
2024.
Quasi-shadowing for ℤd-actions.
Acta Mathematica Sinica, English Series,
Vol. 40,
Issue. 6,
p.
1563.
Piñeyrúa, Luis Pedro
and
Sambarino, Martín
2024.
Dynamical coherence in isotopy classes of fibered lifted partially hyperbolic diffeomorphisms.
Mathematische Zeitschrift,
Vol. 307,
Issue. 3,
DOUCETTE, MEG
2024.
Smooth models for certain fibered partially hyperbolic systems.
Ergodic Theory and Dynamical Systems,
Vol. 44,
Issue. 8,
p.
2173.
Damjanović, Danijela
Wilkinson, Amie
and
Xu, Disheng
2024.
Transitive Centralizer and Fibered Partially Hyperbolic Systems.
International Mathematics Research Notices,
Vol. 2024,
Issue. 12,
p.
9686.
Chen, Lin
and
Zhou, Yunhua
2025.
Bi-quasi-shadowing for semi-partially hyperbolic families.
Journal of Mathematical Analysis and Applications,
Vol. 549,
Issue. 2,
p.
129550.
Espitia, Marcielis
Martinchich, Santiago
and
Potrie, Rafael
2025.
Quasi-isometric center action in dimension 3.
Proceedings of the American Mathematical Society,
Wang, Lin
and
Wang, Xinsheng
2026.
A characterization of <i>ω</i>-leaf-limit sets for systems with foliations.
Discrete and Continuous Dynamical Systems,
Vol. 47,
Issue. 0,
p.
576.
 $C^{1}$-diffeomorphism
$C^{1}$-diffeomorphism 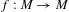 $f:M\rightarrow M$ with a uniformly compact
$f:M\rightarrow M$ with a uniformly compact 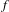 $f$-invariant center foliation
$f$-invariant center foliation 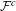 ${\mathcal{F}}^{c}$ is dynamically coherent. Further, the induced homeomorphism
${\mathcal{F}}^{c}$ is dynamically coherent. Further, the induced homeomorphism 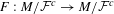 $F:M/{\mathcal{F}}^{c}\rightarrow M/{\mathcal{F}}^{c}$ on the quotient space of the center foliation has the shadowing property, i.e. for every
$F:M/{\mathcal{F}}^{c}\rightarrow M/{\mathcal{F}}^{c}$ on the quotient space of the center foliation has the shadowing property, i.e. for every 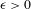 ${\it\epsilon}>0$ there exists
${\it\epsilon}>0$ there exists 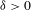 ${\it\delta}>0$ such that every
${\it\delta}>0$ such that every 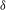 ${\it\delta}$-pseudo-orbit of center leaves is
${\it\delta}$-pseudo-orbit of center leaves is  ${\it\epsilon}$-shadowed by an orbit of center leaves. Although the shadowing orbit is not necessarily unique, we prove the density of periodic center leaves inside the chain recurrent set of the quotient dynamics. Other interesting properties of the quotient dynamics are also discussed.
${\it\epsilon}$-shadowed by an orbit of center leaves. Although the shadowing orbit is not necessarily unique, we prove the density of periodic center leaves inside the chain recurrent set of the quotient dynamics. Other interesting properties of the quotient dynamics are also discussed.
