Article contents
Periodic domains of quasiregular maps
Published online by Cambridge University Press: 14 March 2017
Abstract
We consider the iteration of quasiregular maps of transcendental type from 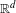 $\mathbb{R}^{d}$ to
$\mathbb{R}^{d}$ to 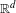 $\mathbb{R}^{d}$. We give a bound on the rate at which the iterates of such a map can escape to infinity in a periodic component of the quasi-Fatou set. We give examples which show that this result is the best possible. Under an additional hypothesis, which is satisfied by all uniformly quasiregular maps, this bound can be improved to be the same as those in a Baker domain of a transcendental entire function. We construct a quasiregular map of transcendental type from
$\mathbb{R}^{d}$. We give a bound on the rate at which the iterates of such a map can escape to infinity in a periodic component of the quasi-Fatou set. We give examples which show that this result is the best possible. Under an additional hypothesis, which is satisfied by all uniformly quasiregular maps, this bound can be improved to be the same as those in a Baker domain of a transcendental entire function. We construct a quasiregular map of transcendental type from 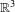 $\mathbb{R}^{3}$ to
$\mathbb{R}^{3}$ to 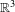 $\mathbb{R}^{3}$ with a periodic domain in which all iterates tend locally uniformly to infinity. This is the first example of such behaviour in a dimension greater than two. Our construction uses a general result regarding the extension of bi-Lipschitz maps. In addition, we show that there is a quasiregular map of transcendental type from
$\mathbb{R}^{3}$ with a periodic domain in which all iterates tend locally uniformly to infinity. This is the first example of such behaviour in a dimension greater than two. Our construction uses a general result regarding the extension of bi-Lipschitz maps. In addition, we show that there is a quasiregular map of transcendental type from 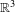 $\mathbb{R}^{3}$ to
$\mathbb{R}^{3}$ to 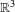 $\mathbb{R}^{3}$ which is equal to the identity map in a half-space.
$\mathbb{R}^{3}$ which is equal to the identity map in a half-space.
Information
- Type
- Original Article
- Information
- Copyright
- © Cambridge University Press, 2017
References
- 6
- Cited by

