Hostname: page-component-848d4c4894-75dct Total loading time: 0 Render date: 2024-05-06T12:43:45.795Z Has data issue: false hasContentIssue false
  • English
  • Français

Pointwise characteristic factors for Wiener–Wintner double recurrence theorem

Published online by Cambridge University Press:  11 February 2015

IDRIS ASSANI ,
DAVID DUNCAN  and
RYO MOORE
IDRIS ASSANI
Affiliation:
Department of Mathematics, The University of North Carolina at Chapel Hill, Chapel Hill, NC 27599, USA email assani@math.unc.edu, ryom@live.unc.edu
DAVID DUNCAN
Affiliation:
Department of Mathematics & Statistics, Coastal Carolina University, Conway, SC 29528, USA email dduncan@coastal.edu
RYO MOORE
Affiliation:
Department of Mathematics, The University of North Carolina at Chapel Hill, Chapel Hill, NC 27599, USA email assani@math.unc.edu, ryom@live.unc.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we extend Bourgain’s double recurrence result to the Wiener–Wintner averages. Let 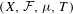$(X,{\mathcal{F}},{\it\mu},T)$ be a standard ergodic system. We will show that for any 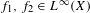$f_{1},f_{2}\in L^{\infty }(X)$, the double recurrence Wiener–Wintner average

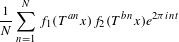$$\begin{eqnarray}\frac{1}{N}\mathop{\sum }_{n=1}^{N}f_{1}(T^{an}x)f_{2}(T^{bn}x)e^{2{\it\pi}int}\end{eqnarray}$$
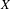converges off a single null set of $X$ independent of $t$ as 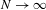$N\rightarrow \infty$. Furthermore, we will show a uniform Wiener–Wintner double recurrence result: if either 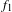$f_{1}$ or 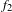$f_{2}$ belongs to the orthogonal complement of the Conze–Lesigne factor, then there exists a set of full measure such that the supremum on $t$ of the absolute value of the averages above converges to $0$.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 36 , Issue 4 , June 2016 , pp. 1037 - 1066
Copyright
© Cambridge University Press, 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Assani, I.. Characteristic factors for some nonconventional ergodic averages. Preprint, 2003.Google Scholar
Assani, I.. Wiener Wintner Ergodic Theorems. World Scientific, River Edge, NJ, 2003.Google Scholar
Assani, I.. Pointwise convergence of ergodic averages along cubes. J. Anal. Math. 110 (2010), 241–269.CrossRefGoogle Scholar
Assani, I. and Moore, R.. New universal weight for the pointwise ergodic theorem, in preparation.Google Scholar
Assani, I. and Moore, R.. Extension of double recurrence Wiener–Wintner theorem to polynomials. Preliminary Version, 2014, arXiv:1408.3064.Google Scholar
Assani, I. and Moore, R.. Extension of double recurrence Wiener–Wintner theorem to polynomials II. Preprint, 2014, arXiv:1409.0463.Google Scholar
Assani, I. and Presser, K.. Pointwise charateristic factors for multiple term return times theorem. Preprint, 2003.Google Scholar
Assani, I. and Presser, K.. Pointwise characteristic factors for the multiterm return times theorem. Ergod. Th. & Dynam. Sys. 32 (2012), 341–360.Google Scholar
Bourgain, J.. Double recurrence and almost sure convergence. J. Reine Angew. Math. 404 (1990), 140–161.Google Scholar
Conze, J.-P. and Lesigne, E.. Théorèmes ergodiques pour des mesures diagonales. Bull. Soc. Math. France 112 (1984), 143–175.Google Scholar
Conze, J.-P. and Lesigne, E.. Sur un théorème ergodique pour des mesures diagonaless. Publ. Inst. Rech. Math. Rennes Probab. 1987‐1 (1988), 1–31.Google Scholar
Duncan, D.. A Wiener–Wintner double recurrence theorem. PhD Thesis, The University of North Carolina at Chapel Hill, 2001, Advisor: I. Assani.Google Scholar
Furstenberg, H.. Ergodic behavior of diagonal measures and a theorem of Szemerédi on arithmetic progressions. J. Anal. Math. 31 (1977), 204–256.Google Scholar
Furstenberg, H. and Weiss, B.. A mean ergodic theorem for (1/N)∑n=1Nf (T nx)g (T n 2x). Convergence in Ergodic Theory and Probability. Ohio State University Mathematical Research Institute Publications, De Gruyter, Berlin, 1996.Google Scholar
Gowers, W. T.. A new proof of Szemerédi’s theorem. Geom. Funct. Anal. 11 (2001), 465–588.CrossRefGoogle Scholar
Host, B. and Kra, B.. Average along cubes. Modern Dynamical Systems and Applications. Cambridge University Press, Cambridge, 2004, pp. 369–432.Google Scholar
Host, B. and Kra, B.. Nonconventional ergodic averages and nilmanifolds. Ann. of Math. (2) 161 (2005), 387–488.Google Scholar
Kuipers, L. and Niederreiter, H.. Uniform Distribution of Sequences. John Wiley & Sons, New York, 1974.Google Scholar
Leibman, A.. Pointwise convergence of ergodic averages for polynomial sequence of translations on a nilmanifold. Ergod. Th. & Dynam. Sys. 25 (2005), 201–213.Google Scholar
Queffélec, M.. Substitution Dynamical Systems—Spectral Analysis, 2nd edn. Springer, Berlin, 2010.Google Scholar
Rudolph, D.. Eigenfunctions of T × S and the Conze–Lesigne algebra. Ergodic Theory and Harmonic Analysis. Cambridge University Press, Cambridge, 1993.Google Scholar
Ziegler, T.. Universal characteristic factors and Furstenberg averages. J. Amer. Math. Soc. 20(1) (2006), 53–97.Google Scholar