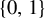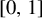Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kanigowski, Adam
Lemańczyk, Mariusz
Richter, Florian K
and
Teräväinen, Joni
2024.
On the Local Fourier Uniformity Problem for Small Sets.
International Mathematics Research Notices,
Vol. 2024,
Issue. 15,
p.
11488.
Eisner, Tanja
and
Farkas, Bálint
2025.
A Journey Through Ergodic Theorems.
p.
483.