No CrossRef data available.
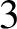 $3$-colorings of
$3$-colorings of 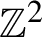 $\mathbb {Z}^{2}$ are Bernoulli
$\mathbb {Z}^{2}$ are BernoulliPublished online by Cambridge University Press: 27 April 2022
We consider the unique measure of maximal entropy for proper 3-colorings of
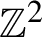 $\mathbb {Z}^{2}$
, or equivalently, the so-called zero-slope Gibbs measure. Our main result is that this measure is Bernoulli, or equivalently, that it can be expressed as the image of a translation-equivariant function of independent and identically distributed random variables placed on
$\mathbb {Z}^{2}$
, or equivalently, the so-called zero-slope Gibbs measure. Our main result is that this measure is Bernoulli, or equivalently, that it can be expressed as the image of a translation-equivariant function of independent and identically distributed random variables placed on
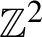 $\mathbb {Z}^{2}$
. Along the way, we obtain various estimates on the mixing properties of this measure.
$\mathbb {Z}^{2}$
. Along the way, we obtain various estimates on the mixing properties of this measure.