Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Ferenczi, Sébastien
1997.
Measure-theoretic complexity of ergodic systems.
Israel Journal of Mathematics,
Vol. 100,
Issue. 1,
p.
189.
Béal, M.-P
Mignosi, F
Restivo, A
and
Sciortino, M
2000.
Forbidden Words in Symbolic Dynamics.
Advances in Applied Mathematics,
Vol. 25,
Issue. 2,
p.
163.
Damanik, David
2001.
Schrödinger operators with low-complexity potentials.
Ferroelectrics,
Vol. 250,
Issue. 1,
p.
143.
Ferenczi, Sébastien
Holton, Charles
and
Zamboni, Luca Q.
2001.
Automata, Languages and Programming.
Vol. 2076,
Issue. ,
p.
567.
Ferenczi, Sébastien
Holton, Charles
and
Zamboni, Luca Q.
2003.
Structure of three-interval exchange transformations II: a combinatorial description of the tranjectories.
Journal d'Analyse Mathématique,
Vol. 89,
Issue. 1,
p.
239.
Bruin, H.
2003.
Minimal Cantor Systems and Unimodal Maps.
Journal of Difference Equations and Applications,
Vol. 9,
Issue. 3-4,
p.
305.
Arnoux, Pierre
Berthé, Valérie
and
Siegel, Anne
2004.
Two-dimensional iterated morphisms and discrete planes.
Theoretical Computer Science,
Vol. 319,
Issue. 1-3,
p.
145.
Balogh, József
and
Bollobás, Béla
2005.
Hereditary properties of words.
RAIRO - Theoretical Informatics and Applications,
Vol. 39,
Issue. 1,
p.
49.
Fernique, Thomas
2005.
Developments in Language Theory.
Vol. 3572,
Issue. ,
p.
236.
Bruin, H.
and
Volkova, O.
2005.
The complexity of Fibonacci-like kneading sequences.
Theoretical Computer Science,
Vol. 337,
Issue. 1-3,
p.
379.
THOMAS, FERNIQUE
2006.
MULTIDIMENSIONAL STURMIAN SEQUENCES AND GENERALIZED SUBSTITUTIONS.
International Journal of Foundations of Computer Science,
Vol. 17,
Issue. 03,
p.
575.
Ferenczi, Sébastien
and
Zamboni, Luca Q.
2010.
Structure of K-interval exchange transformations: Induction, trajectories, and distance theorems.
Journal d'Analyse Mathématique,
Vol. 112,
Issue. 1,
p.
289.
Leroy, Julien
2012.
Some improvements of the S-adic conjecture.
Advances in Applied Mathematics,
Vol. 48,
Issue. 1,
p.
79.
Durand, Fabien
and
Leroy, Julien
2012.
S-adic conjecture and Bratteli diagrams.
Comptes Rendus. Mathématique,
Vol. 350,
Issue. 21-22,
p.
979.
CHAIKA, JON
2012.
There exists a topologically mixing interval exchange transformation.
Ergodic Theory and Dynamical Systems,
Vol. 32,
Issue. 3,
p.
869.
Gähler, Franz
and
Maloney, Gregory R.
2013.
Cohomology of one-dimensional mixed substitution tiling spaces.
Topology and its Applications,
Vol. 160,
Issue. 5,
p.
703.
Pacheco, Rui
and
Vilarinho, Helder
2013.
Statistical stability for multi-substitution tiling spaces.
Discrete & Continuous Dynamical Systems - A,
Vol. 33,
Issue. 10,
p.
4579.
Bourgain, J.
Sarnak, P.
and
Ziegler, T.
2013.
From Fourier Analysis and Number Theory to Radon Transforms and Geometry.
Vol. 28,
Issue. ,
p.
67.
2014.
Formal Languages, Automata and Numeration Systems 2.
p.
193.
Matte Bon, Nicolás
2014.
Subshifts with slow complexity and simple groups with the Liouville property.
Geometric and Functional Analysis,
Vol. 24,
Issue. 5,
p.
1637.
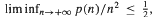 , but give examples with lim
, but give examples with lim  for any prescribed function G with G (n) = 0(an) for every a > 1. We give exact computations for examples of the ‘staircase’ type, which are strongly mixing systems with quadratic complexity. Conversely, for minimal sequences, if p(n) < an + b for some a ≥ 1, the rank is at most 2[a], with bounded strings of spacers, and the system is generated by a finite number of substitutions.
for any prescribed function G with G (n) = 0(an) for every a > 1. We give exact computations for examples of the ‘staircase’ type, which are strongly mixing systems with quadratic complexity. Conversely, for minimal sequences, if p(n) < an + b for some a ≥ 1, the rank is at most 2[a], with bounded strings of spacers, and the system is generated by a finite number of substitutions.
