Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ratner, Marina
1987.
Rigid reparametrizations and cohomology for horocycle flows.
Inventiones Mathematicae,
Vol. 88,
Issue. 2,
p.
341.
de la Llave, R.
and
Moriyón, R.
1988.
Invariants for smooth conjugacy of hyperbolic dynamical systems. IV.
Communications in Mathematical Physics,
Vol. 116,
Issue. 2,
p.
185.
Witte, Dave
1989.
Rigidity of horospherical foliations.
Ergodic Theory and Dynamical Systems,
Vol. 9,
Issue. 1,
p.
191.
Croke, Christopher B.
1990.
Rigidity for surfaces of non-positive curvature.
Commentarii Mathematici Helvetici,
Vol. 65,
Issue. 1,
p.
150.
Pollicott, Mark
1990.
C k-rigidity for hyperbolic flows II.
Israel Journal of Mathematics,
Vol. 69,
Issue. 3,
p.
351.
Flaminio, L.
and
Spatzier, R. J.
1990.
Geometrically finite groups, Patterson-Sullivan measures and Ratner's ridigity theorem.
Inventiones Mathematicae,
Vol. 99,
Issue. 1,
p.
601.
Troubetzkoy, Serge E.
1991.
Extreme instability of the horocycle flow.
Journal d’Analyse Mathématique,
Vol. 57,
Issue. 1,
p.
37.
Ornstein, D. S.
and
Weiss, B.
1991.
Statistical properties of chaotic systems.
Bulletin of the American Mathematical Society,
Vol. 24,
Issue. 1,
p.
11.
de la Llave, R.
1992.
Mathematical Physics X.
p.
3.
Croke, C.
Fathi, A.
and
Feldman, J.
1992.
The marked length-spectrum of a surface of nonpositive curvature.
Topology,
Vol. 31,
Issue. 4,
p.
847.
de la Llave, R.
1992.
Smooth conjugacy and S-R-B measures for uniformly and non-uniformly hyperbolic systems.
Communications in Mathematical Physics,
Vol. 150,
Issue. 2,
p.
289.
Green, Leon W.
1992.
When is an Anosov flow geodesic?.
Ergodic Theory and Dynamical Systems,
Vol. 12,
Issue. 2,
p.
227.
Hamenstädt, Ursula
1993.
Regularity of time-preserving conjugacies for contact Anosov flows withC1-Anosov splitting.
Ergodic Theory and Dynamical Systems,
Vol. 13,
Issue. 1,
p.
65.
Hamenstädt, Ursula
1994.
Regularity at infinity of compact negatively curved manifolds.
Ergodic Theory and Dynamical Systems,
Vol. 14,
Issue. 3,
p.
493.
Besson, G�rard
Courtois, Gilles
and
Gallot, Sylvestre
1994.
Les vari�t�s hyperboliques sont des minima locaux de l'entropie topologique.
Inventiones Mathematicae,
Vol. 117,
Issue. 1,
p.
403.
Ratner, Marina
1995.
Proceedings of the International Congress of Mathematicians.
p.
157.
Safonov, A. V.
Starkov, A. N.
and
Stepin, A. M.
1995.
Dynamical Systems IX.
Vol. 66,
Issue. ,
p.
177.
Cao, Jianguo
1995.
Rigidity for non-compact surfaces of finite area and certain Kähler manifolds.
Ergodic Theory and Dynamical Systems,
Vol. 15,
Issue. 3,
p.
475.
Старков, Александр Николаевич
and
Starkov, Aleksandr Nikolaevich
1997.
Новый прогресс в теории однородных потоков.
Успехи математических наук,
Vol. 52,
Issue. 4,
p.
87.
Pollicott, Mark
and
Sharp, Richard
2001.
Asymptotic Expansions for Closed Orbits in Homology Classes.
Geometriae Dedicata,
Vol. 87,
Issue. 1-3,
p.
123.

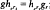 such a flow exists, leaves μ invariant, and is unique up to constant scaling of the parameter (Margulis). We show that any measure-theoretic conjugacy: (
such a flow exists, leaves μ invariant, and is unique up to constant scaling of the parameter (Margulis). We show that any measure-theoretic conjugacy: (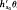 θ, where θ is a homeomorphic conjugacy:
θ, where θ is a homeomorphic conjugacy: 