[AM10]
Austin, T. and Moore, C. C.. Continuity properties of measurable group cohomology. Math. Ann.
356 (2013), 885–937.
[AO74]
Akemann, C. A. and Ostrand, P. A.. On a tensor product C∗ -algebra associated with the free group on two generators. J. Math. Soc. Japan
27 (1975), 589–599.
[BHR12]
Boutonnet, R., Houdayer, C. and Raum, S.. Amalgamated free product type III factors with at most one Cartan subalgebra. Compos. Math.
150 (2014), 143–174.
[BISG15]
Boutonnet, R., Ioana, A. and Salehi Golsefidy, A.. Local spectral gap in simple Lie groups and applications. Invent. Math.
208 (2017), 715–802.
[BO08]
Brown, N. P. and Ozawa, N.. C∗ -Algebras and Finite-Dimensional Approximations
(Graduate Studies in Mathematics, 88)
. American Mathematical Society, Providence, RI, 2008.
[CFW81]
Connes, A., Feldman, J. and Weiss, B.. An amenable equivalence relation is generated by a single transformation. Ergod. Th. & Dynam. Sys.
1 (1981), 431–450.
[CJ81]
Connes, A. and Jones, V. F. R.. A II1 factor with two non-conjugate Cartan subalgebras. Bull. Amer. Math. Soc. (N.S.)
6 (1982), 211–212.
[Co72]
Connes, A.. Une classification des facteurs de type III. Ann. Sci. Éc. Norm. Supér. (4)
6 (1973), 133–252.
[Co74]
Connes, A.. Almost periodic states and factors of type III1
. J. Funct. Anal.
16 (1974), 415–445.
[Co75a]
Connes, A.. Outer conjugacy classes of automorphisms of factors. Ann. Sci. Éc. Norm. Supér. (4)
8 (1975), 383–419.
[Co75b]
Connes, A.. Classification of injective factors. Cases II1 , II
∞
, III𝜆 , 𝜆≠1. Ann. of Math. (2)
74 (1976), 73–115.
[FM75]
Feldman, J. and Moore, C. C.. Ergodic equivalence relations, cohomology, and von Neumann algebras. I, II. Trans. Amer. Math. Soc.
234 (1977), 289–324; 325–359.
[Ha85]
Haagerup, U.. Connes’ bicentralizer problem and uniqueness of the injective factor of type III1
. Acta Math.
69 (1986), 95–148.
[HI15]
Houdayer, C. and Isono, Y.. Bi-exact groups, strongly ergodic actions and group measure space type III factors with no central sequence. Comm. Math. Phys.
348 (2016), 991–1015.
[HMV16]
Houdayer, C., Marrakchi, A. and Verraedt, P.. Fullness and Connes’
$\unicode[STIX]{x1D70F}$
invariant of type
$\text{III}$
tensor product factors. Preprint, 2016, arXiv:1611.07914.
[Jo81]
Jones, V. F. R.. Central sequences in crossed products of full factors. Duke Math. J.
49 (1982), 29–33.
[Kr67]
Krieger, W.. On non-singular transformations of a measure space. I, II. Z. Wahrscheinlichkeitstheorie und Verw. Gebiete
11 (1969), 83–97; 98–119.
[Kr75]
Krieger, W.. On ergodic flows and the isomorphism of factors. Math. Ann.
223 (1976), 19–70.
[KT06]
Kechris, A. S. and Tsankov, T.. Amenable actions and almost invariant sets. Proc. Amer. Math. Soc.
136 (2008), 687–697.
[Ma16]
Marrakchi, A.. Spectral gap characterization of full type III factors. J. Reine Angew. Math. to appear. Published online 12 January 2017, doi:10.1515/crelle-2016-0071.
[Mo75]
Moore, C. C.. Group extensions and cohomology for locally compact groups. III. Trans. Amer. Math. Soc.
221 (1976), 1–33.
[Oz03]
Ozawa, N.. Solid von Neumann algebras. Acta Math.
192 (2004), 111–117.
[Oz04]
Ozawa, N.. A Kurosh type theorem for type II1 factors. Int. Math. Res. Not. IMRN (2006), Art. ID 97560.
[Oz08]
Ozawa, N.. An example of a solid von Neumann algebra. Hokkaido Math. J.
38 (2009), 557–561.
[Oz16]
Ozawa, N.. A remark on fullness of some group measure space von Neumann algebras. Compos. Math.
152 (2016), 2493–2502.
[Po04]
Popa, S.. Some computations of 1-cohomology groups and construction of non orbit equivalent actions. J. Inst. Math. Jussieu
5 (2006), 309–332.
[Sc79]
Schmidt, K.. Asymptotically invariant sequences and an action of SL(2, ℤ) on the 2-sphere. Israel J. Math.
37 (1980), 193–208.
[Sc80]
Schmidt, K.. Amenability, Kazhdan’s property T, strong ergodicity and invariant means for ergodic group-actions. Ergod. Th. & Dynam. Sys.
1 (1981), 223–236.
[Sk88]
Skandalis, G.. Une notion de nucléarité en K-théorie (d’après J. Cuntz). J. K-Theory
1 (1988), 549–573.
[Ta03a]
Takesaki, M.. Theory of operator algebras. II. Encyclopaedia of Mathematical Sciences. Vol. 125
(Operator Algebras and Non-commutative Geometry, 6)
. Springer, Berlin, 2003.
[Ta03b]
Takesaki, M.. Theory of operator algebras. III. Encyclopaedia of Mathematical Sciences. Vol. 127
(Operator Algebras and Non-commutative Geometry, 8)
. Springer, Berlin, 2003.
[VV14]
Vaes, S. and Verraedt, P.. Classification of type III Bernoulli crossed products. Adv. Math.
281 (2015), 296–332.
[VW17]
Vaes, S. and Wahl, J.. Bernoulli actions of type
$\text{III}_{1}$
and
$\text{L}^{2}$
-cohomology. Preprint, 2017, arXiv:1705.00439.
[Zi76]
Zimmer, R.. Extensions of ergodic group actions. Illinois J. Math.
20 (1976), 373–409.
[Zi84]
Zimmer, R.. Ergodic theory and semisimple groups. Monographs in Mathematics. Vol. 81. Birkhäuser, Basel, 1984.
$1$
-cocycles with values in locally compact abelian groups are strongly ergodic. By analogy with the work of Connes on full factors, we introduce the Sd and
$\unicode[STIX]{x1D70F}$
invariants for type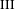
$\text{III}$
strongly ergodic equivalence relations. As a corollary to our main results, we show that for any type
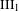$\text{III}_{1}$
ergodic equivalence relation
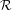${\mathcal{R}}$
, the Maharam extension
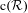$\text{c}({\mathcal{R}})$
is strongly ergodic if and only if
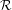${\mathcal{R}}$
is strongly ergodic and the invariant
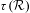$\unicode[STIX]{x1D70F}({\mathcal{R}})$
is the usual topology on
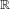$\mathbb{R}$
. We also obtain a structure theorem for almost periodic strongly ergodic equivalence relations analogous to Connes’ structure theorem for almost periodic full factors. Finally, we prove that for arbitrary strongly ergodic free actions of bi-exact groups (e.g. hyperbolic groups), the Sd and
$\unicode[STIX]{x1D70F}$
invariants of the orbit equivalence relation and of the associated group measure space von Neumann factor coincide.