No CrossRef data available.
Article contents
Subshifts and colorings on ascending HNN-extensions of finitely generated abelian groups
Part of:
Hamiltonian and Lagrangian mechanics
Finite-dimensional Hamiltonian, Lagrangian, contact, and nonholonomic systems
Published online by Cambridge University Press: 08 September 2021
Abstract
For an ascending HNN-extension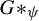 
$G*_{\psi }$
of a finitely generated abelian group G, we study how a synchronization between the geometry of the group and weak periodicity of a configuration in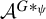 
$\mathcal {A}^{G*_{\psi }}$
forces global constraints on it, as well as in subshifts containing it. A particular case are Baumslag–Solitar groups 
$\mathrm {BS}(1,N)$
, 
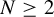$N\ge 2$
, for which our results imply that a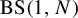 
$\mathrm {BS}(1,N)$
-subshift of finite type which contains a configuration with period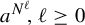 
$a^{N^\ell }\!, \ell \ge 0$
, must contain a strongly periodic configuration with monochromatic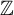 
$\mathbb {Z}$
-sections. Then we study proper n-colorings,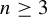 
$n\ge 3$
, of the (right) Cayley graph of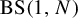 
$\mathrm {BS}(1,N)$
, estimating the entropy of the associated subshift together with its mixing properties. We prove that 
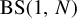$\mathrm {BS}(1,N)$
admits a frozen n-coloring if and only if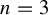 
$n=3$
. We finally suggest generalizations of the latter results to n-colorings of ascending HNN-extensions of finitely generated abelian groups.
MSC classification
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
Alon, N., Briceño, R., Chandgotia, N., Magazinov, A. and Spinka, Y.. Mixing properties of colourings of the
${\mathbb{Z}}^d$
lattice. Combin. Probab. Comput. 30(3) (2020), 1–14.Google Scholar
${\mathbb{Z}}^d$
lattice. Combin. Probab. Comput. 30(3) (2020), 1–14.Google ScholarAubrun, N. and Kari, J.. Tiling problems on Baumslag–Solitar groups. Electron. Proc. Theor. Comput. Sci. (EPTCS) 128 (2013), 35–46.CrossRefGoogle Scholar
Baumslag, G. and Solitar, D.. Some two-generator one-relator non-Hopfian groups. Bull. Amer. Math. Soc. 68(3) (1962), 199–202.CrossRefGoogle Scholar
Ceccherini-Silberstein, T. and Coornaert, M.. Cellular Automata and Groups (Springer Monographs in Mathematics, 44). Springer, Berlin, 2010.CrossRefGoogle Scholar
Cyr, V., Franks, J., Kra, B. and Petite, S.. Distortion and the automorphism group of a shift. J. Mod. Dyn. 13(1) (2018), 147–161.CrossRefGoogle Scholar
de La Harpe, P.. Topics in Geometric Group Theory. University of Chicago Press, Chicago, IL, 2003.Google Scholar
Esnay, J. and Moutot, E.. Weakly and strongly aperiodic subshifts of finite type on Baumslag–Solitar groups. Preprint, 2021, arXiv:2004.02534.CrossRefGoogle Scholar
Higman, G., Neumann, B. H. and Neuman, H.. Embedding theorems for groups. J. Lond. Math. Soc. s1–24(4) (1949), 247–254.CrossRefGoogle Scholar
Kerr, D. and Li, H.. Ergodic Theory (Springer Monographs in Mathematics). Springer International Publishing, Cham, 2016.CrossRefGoogle Scholar
Löh, C.. Geometric Group Theory: An Introduction (Universitext). Springer, Cham, 2017.CrossRefGoogle Scholar
Lyndon, R. C. and Schupp, P. E.. Combinatorial Group Theory. Springer-Verlag, Berlin, 1977.Google Scholar
Meskin, S.. Nonresidually finite one-relator groups. Trans. Amer. Math. Soc. 164 (1972), 105–114.CrossRefGoogle Scholar
Peled, R. and Spinka, Y.. Rigidity of proper colorings of
${\mathbb{Z}}^d$
. Preprint, 2020, arXiv:1808.03597.Google Scholar
${\mathbb{Z}}^d$
. Preprint, 2020, arXiv:1808.03597.Google ScholarRay, G. and Spinka, Y.. Proper 3-colorings of
${\mathbb{Z}}^2$
are Bernoulli. Preprint, 2020, arXiv:2004.00028.Google Scholar
${\mathbb{Z}}^2$
are Bernoulli. Preprint, 2020, arXiv:2004.00028.Google Scholar