In this paper, we address the problem of computing the topological entropy of a map 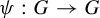$\psi : G \to G$, where G is a Lie group, given by some power 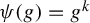$\psi (g) = g^k$, with k a positive integer. When G is abelian, 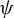$\psi $ is an endomorphism and its topological entropy is given by 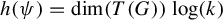$h(\psi ) = \dim (T(G)) \log (k)$, where 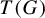$T(G)$ is the maximal torus of G, as shown by Patrão [The topological entropy of endomorphisms of Lie groups. Israel J. Math. 234 (2019), 55–80]. However, when G is not abelian, 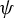$\psi $ is no longer an endomorphism and these previous results cannot be used. Still, 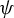$\psi $ has some interesting symmetries, for example, it commutes with the conjugations of G. In this paper, the structure theory of Lie groups is used to show that 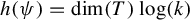$h(\psi ) = \dim (T)\log (k)$, where T is a maximal torus of G, generalizing the formula in the abelian case. In particular, the topological entropy of powers on compact Lie groups with discrete center is always positive, in contrast to what happens to endomorphisms of such groups, which always have null entropy.