Article contents
Topological structure and entropy of mixing graph maps
Published online by Cambridge University Press: 30 April 2013
Abstract
Let 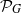 ${ \mathcal{P} }_{G} $ be the family of all topologically mixing, but not exact self-maps of a topological graph
${ \mathcal{P} }_{G} $ be the family of all topologically mixing, but not exact self-maps of a topological graph 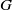 $G$. It is proved that the infimum of topological entropies of maps from
$G$. It is proved that the infimum of topological entropies of maps from 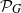 ${ \mathcal{P} }_{G} $ is bounded from below by
${ \mathcal{P} }_{G} $ is bounded from below by 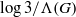 $\log 3/ \Lambda (G)$, where
$\log 3/ \Lambda (G)$, where 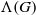 $\Lambda (G)$ is a constant depending on the combinatorial structure of
$\Lambda (G)$ is a constant depending on the combinatorial structure of 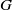 $G$. The exact value of the infimum on
$G$. The exact value of the infimum on 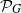 ${ \mathcal{P} }_{G} $ is calculated for some families of graphs. The main tool is a refined version of the structure theorem for mixing graph maps. It also yields new proofs of some known results, including Blokh’s theorem (topological mixing implies the specification property for maps on graphs).
${ \mathcal{P} }_{G} $ is calculated for some families of graphs. The main tool is a refined version of the structure theorem for mixing graph maps. It also yields new proofs of some known results, including Blokh’s theorem (topological mixing implies the specification property for maps on graphs).
Information
- Type
- Research Article
- Information
- Copyright
- Copyright ©2013 Cambridge University Press
References
- 9
- Cited by

