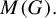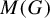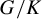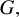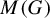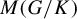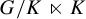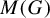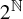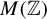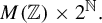1 Introduction
The structure theory of minimal flows dates back to the origins of topological dynamics. Among the most notable achievements is the structure theorem on minimal metrizable distal flows of countable discrete groups by Furstenberg [Reference FurstenbergF]. Furstenberg’s result was extended to non-metrizable minimal distal flows by Ellis in [Reference EllisE2] and to locally compact groups by Zimmer in [Reference ZimmerZ, Reference ZimmerZ2]. However, little is known about the structure of general minimal flows. A well-known theorem by Ellis states that, up to isomorphism, every topological group G admits a unique universal minimal flow
![]() $M(G)$
(mapping onto every minimal flow preserving the respective actions). For discrete groups, it is know that the universal minimal flow is zero-dimensional [Reference EllisE] and extremally disconnected (attributed independently to Ellis and Balcar, first in print by van Douwen in [Reference van DouwenvDo]). Using methods from the theory of Boolean algebras, Balcar and Błaszczyk showed in [Reference Balcar and BłaszczykBB] that the underlying space (phase space) of
$M(G)$
(mapping onto every minimal flow preserving the respective actions). For discrete groups, it is know that the universal minimal flow is zero-dimensional [Reference EllisE] and extremally disconnected (attributed independently to Ellis and Balcar, first in print by van Douwen in [Reference van DouwenvDo]). Using methods from the theory of Boolean algebras, Balcar and Błaszczyk showed in [Reference Balcar and BłaszczykBB] that the underlying space (phase space) of
![]() $M(G)$
of any countably infinite discrete group G is homeomorphic to the Gleason cover
$M(G)$
of any countably infinite discrete group G is homeomorphic to the Gleason cover
![]() $G(2^{\kappa })$
of the Cantor cube
$G(2^{\kappa })$
of the Cantor cube
![]() $2^{\kappa }$
for some uncountable cardinal
$2^{\kappa }$
for some uncountable cardinal
![]() $\kappa \leq 2^{\aleph _0}$
. This is the unique compact extremely disconnected space that has an irreducible map onto
$\kappa \leq 2^{\aleph _0}$
. This is the unique compact extremely disconnected space that has an irreducible map onto
![]() $2^{\kappa }$
, that is,
$2^{\kappa }$
, that is,
![]() $2^{\kappa }$
is not the image of any proper closed and open (clopen) subset of
$2^{\kappa }$
is not the image of any proper closed and open (clopen) subset of
![]() $G(2^{\kappa })$
. In other words, the algebra of clopen subsets of
$G(2^{\kappa })$
. In other words, the algebra of clopen subsets of
![]() $G(2^{\kappa })$
is the completion of the free Boolean algebra on
$G(2^{\kappa })$
is the completion of the free Boolean algebra on
![]() $\kappa $
generators. It was proved that
$\kappa $
generators. It was proved that
![]() $\kappa =2^{\aleph _0}$
for
$\kappa =2^{\aleph _0}$
for
![]() $\mathbb {Z}$
in [Reference Balcar and BłaszczykBB], for Abelian groups by Turek in [Reference TurekT], and in general by a recent paper of Glasner et al. [Reference Glasner, Tsankov, Weiss and ZuckerGTWZ].
$\mathbb {Z}$
in [Reference Balcar and BłaszczykBB], for Abelian groups by Turek in [Reference TurekT], and in general by a recent paper of Glasner et al. [Reference Glasner, Tsankov, Weiss and ZuckerGTWZ].
Theorem 1.1. (Balcar and Błaszczyk [Reference Balcar and BłaszczykBB], Turek [Reference TurekT], Glasner et al. [Reference Glasner, Tsankov, Weiss and ZuckerGTWZ])
Let G be a discrete countably infinite group. Then the phase space of
![]() $M(G)$
is homeomorphic to the Gleason cover of the Cantor cube
$M(G)$
is homeomorphic to the Gleason cover of the Cantor cube
![]() $2^{2^{\aleph _0}}.$
$2^{2^{\aleph _0}}.$
To date, we lack a concrete description of the universal minimal action even in the case of the discrete group of integers
![]() $\mathbb {Z}$
.
$\mathbb {Z}$
.
On the other hand, there are topological groups for which the universal minimal flow (and therefore any minimal flow) is metrizable (e.g., the group of permutations of a countable set
![]() $S_{\infty }$
[Reference Glasner and WeissGW], the group of homeomorphisms of the Lelek fan [Reference Bartošová and KwiatkowskaBK]), or even trivializes (e.g., the group of automorphisms of the rational linear order [Reference PestovP], group of unitaries of the separable Hilbert space [Reference Gromov and MilmanGM]). These results are obtained via structural Ramsey theory [Reference Glasner and WeissGW, Reference Kechris, Pestov and TodorcevicKPT, Reference PestovP] or concentration of measure phenomena [Reference Gromov and MilmanGM, Reference PestovP2], and provide a concrete description. If the group G can be represented as a group of automorphisms of a countable first-order structure, then the phase space of
$S_{\infty }$
[Reference Glasner and WeissGW], the group of homeomorphisms of the Lelek fan [Reference Bartošová and KwiatkowskaBK]), or even trivializes (e.g., the group of automorphisms of the rational linear order [Reference PestovP], group of unitaries of the separable Hilbert space [Reference Gromov and MilmanGM]). These results are obtained via structural Ramsey theory [Reference Glasner and WeissGW, Reference Kechris, Pestov and TodorcevicKPT, Reference PestovP] or concentration of measure phenomena [Reference Gromov and MilmanGM, Reference PestovP2], and provide a concrete description. If the group G can be represented as a group of automorphisms of a countable first-order structure, then the phase space of
![]() $M(G)$
is either finite or homeomorphic to the Cantor set
$M(G)$
is either finite or homeomorphic to the Cantor set
![]() $2^{\mathbb {N}}.$
However, we lack a group topological characterization of such groups.
$2^{\mathbb {N}}.$
However, we lack a group topological characterization of such groups.
Generalizing Theorem 1.1, Bandlow showed in [Reference BandlowBa] that if an
![]() $\omega $
-bounded group G (every maximal system of pairwise disjoint translates of a neighbourhood in G is countable) has an infinite minimal flow, then the phase space of
$\omega $
-bounded group G (every maximal system of pairwise disjoint translates of a neighbourhood in G is countable) has an infinite minimal flow, then the phase space of
![]() $M(G)$
has the same Gleason cover as
$M(G)$
has the same Gleason cover as
![]() $2^{\kappa }$
for some infinite cardinal
$2^{\kappa }$
for some infinite cardinal
![]() $\kappa $
(for a simplified proof, see [Reference TurekT2]). Błaszczyk, Kucharski, and Turek demonstrated in [Reference Błaszczyk, Kucharski and TurekBKT] that every infinite minimal flow of such a group maps irreducibly onto
$\kappa $
(for a simplified proof, see [Reference TurekT2]). Błaszczyk, Kucharski, and Turek demonstrated in [Reference Błaszczyk, Kucharski and TurekBKT] that every infinite minimal flow of such a group maps irreducibly onto
![]() $2^{\kappa }$
for some infinite
$2^{\kappa }$
for some infinite
![]() $\kappa $
.
$\kappa $
.
Our original motivation was to prove an analogue of Theorem 1.1 for Polish (separable and completely metrizable) locally compact groups with a basis at the neutral element of open subgroups. They are a natural direction from discrete groups since their topology is determined by cosets of basic open (compact) subgroups and their universal minimal flow can be viewed from the Boolean algebraic perspective. This class of groups coincides with the class of locally compact groups of automorphisms of countable first-order structures, which in turn by van Dantzig’s theorem [Reference van DantzigvDa] coincides with the class of Polish totally disconnected locally compact (t.d.l.c.) groups. We succeed in the case where G possesses a compact open normal subgroup.
Theorem 1.2. Let G be a Polish t.d.l.c. group with a compact normal open subgroup
![]() $K.$
Then
$K.$
Then
![]() $M(G)$
is homeomorphic to a finite set,
$M(G)$
is homeomorphic to a finite set,
![]() $M(\mathbb {Z}), 2^{\mathbb {N}},$
or
$M(\mathbb {Z}), 2^{\mathbb {N}},$
or
![]() $M(\mathbb {Z})\times 2^{\mathbb {N}}$
.
$M(\mathbb {Z})\times 2^{\mathbb {N}}$
.
If G admits a basis of compact open normal subgroups then we also recover the action. Among Polish groups, these are the t.d.l.c. groups admitting a two-sided invariant metric, in particular, Abelian groups. These are consequences of the main results of the present paper, which can be summarized as follows.
Theorem 1.3. Let G be a topological group with a compact normal subgroup K such that K acts freely on
![]() $M(G)$
and the quotient mapping
$M(G)$
and the quotient mapping
![]() $G\to G/K$
admits a uniformly continuous cross-section. Then the phase space of
$G\to G/K$
admits a uniformly continuous cross-section. Then the phase space of
![]() $M(G)$
is homeomorphic to the product of the phase space of
$M(G)$
is homeomorphic to the product of the phase space of
![]() $M(G/K)$
and
$M(G/K)$
and
![]() $K.$
If the left and right uniformities on G coincide or the cross-section is a group homomorphism, then the homeomorphism is an isomorphism of flows.
$K.$
If the left and right uniformities on G coincide or the cross-section is a group homomorphism, then the homeomorphism is an isomorphism of flows.
As a corollary, we obtain a result by Kechris and Sokić.
Corollary 1.4. [Reference Kechris and SokićKS]
Let G be a Polish group with a metrizable
![]() $M(G)$
and let K be a compact metrizable group. Suppose that G acts continuously on K by automorphisms. Then
$M(G)$
and let K be a compact metrizable group. Suppose that G acts continuously on K by automorphisms. Then
![]() $M(G\ltimes K)$
is isomorphic to
$M(G\ltimes K)$
is isomorphic to
![]() $M(G)\times K.$
$M(G)\times K.$
In §4 we verify that an analogue of Theorem 1.3 holds when K is closed (not necessarily compact), but
![]() $G/K$
is compact, extending another result of Kechris and Sokić from [Reference Kechris and SokićKS].
$G/K$
is compact, extending another result of Kechris and Sokić from [Reference Kechris and SokićKS].
The strategy is to prove statements in Theorem 1.3 for the greatest ambit of G that contains
![]() $M(G)$
as its minimal subflow.
$M(G)$
as its minimal subflow.
Let us remark that recently Basso and Zucker isolated in [Reference Basso and ZuckerBZ] a class of topological groups, the CAP groups, for which
![]() $M(G\times H)\cong M(G)\times M(H).$
It includes, for instance, groups with metrizable universal minimal flows. In contrast, for any two infinite discrete groups
$M(G\times H)\cong M(G)\times M(H).$
It includes, for instance, groups with metrizable universal minimal flows. In contrast, for any two infinite discrete groups
![]() $G,H$
,
$G,H$
,
![]() $M(G\times H)\not \cong M(G)\times M(H).$
In fact, the phase spaces are not even homeomorphic, since
$M(G\times H)\not \cong M(G)\times M(H).$
In fact, the phase spaces are not even homeomorphic, since
![]() $M(G\times H)$
is extremally disconnected, but a product of two infinite compact spaces is never extremally disconnected (see [Reference Koppelberg and Donald MonkK, Proposition 11.9]).
$M(G\times H)$
is extremally disconnected, but a product of two infinite compact spaces is never extremally disconnected (see [Reference Koppelberg and Donald MonkK, Proposition 11.9]).
2 Background
Let G be a topological group with neutral element e. The topology on G is fully determined by a basis at e of open neighbourhoods, which will be denoted by
![]() ${\mathcal {N}}_e(G).$
Without loss of generality, we can assume that
${\mathcal {N}}_e(G).$
Without loss of generality, we can assume that
![]() $V=V^{-1}$
for every
$V=V^{-1}$
for every
![]() $V\in {\mathcal {N}}_e(G).$
$V\in {\mathcal {N}}_e(G).$
A G-flow is a continuous left action
![]() $\alpha :G\times X\to X$
of G on a compact Hausdorff space X, which we refer to as the phase space of
$\alpha :G\times X\to X$
of G on a compact Hausdorff space X, which we refer to as the phase space of
![]() $\alpha $
. We typically write
$\alpha $
. We typically write
![]() $gx$
in place of
$gx$
in place of
![]() $\alpha (g,x).$
The action is free if G acts without fixed points on X, that is, for every
$\alpha (g,x).$
The action is free if G acts without fixed points on X, that is, for every
![]() $g\neq e$
and
$g\neq e$
and
![]() $x\in X, gx\neq x.$
A homomorphism between two G-flows
$x\in X, gx\neq x.$
A homomorphism between two G-flows
![]() $G\times X\to X$
and
$G\times X\to X$
and
![]() $G\times Y\to Y$
is a continuous map
$G\times Y\to Y$
is a continuous map
![]() $\phi :X\to Y$
such that
$\phi :X\to Y$
such that
![]() $\phi (gx)=g\phi (x).$
An isomorphism is a bijective homomorphism (recall that a bijective continuous map between compact spaces is a homeomorphism). We will use
$\phi (gx)=g\phi (x).$
An isomorphism is a bijective homomorphism (recall that a bijective continuous map between compact spaces is a homeomorphism). We will use
![]() $\cong $
for the isomorphism relation on flows. An ambit is a G-flow X with a base point
$\cong $
for the isomorphism relation on flows. An ambit is a G-flow X with a base point
![]() $x_0\in X$
that has a dense orbit, that is,
$x_0\in X$
that has a dense orbit, that is,
![]() $Gx_0=\{gx_0:g\in G\}$
is dense in X. An ambit homomorphism is a homomorphism between ambits
$Gx_0=\{gx_0:g\in G\}$
is dense in X. An ambit homomorphism is a homomorphism between ambits
![]() $(X,x_0)$
and
$(X,x_0)$
and
![]() $(Y,y_0)$
sending
$(Y,y_0)$
sending
![]() $x_0$
to
$x_0$
to
![]() $y_0.$
There is, up to isomorphism, a unique ambit
$y_0.$
There is, up to isomorphism, a unique ambit
![]() $(S(G),e)$
that homomorphically maps onto every ambit, the greatest ambit. Topologically,
$(S(G),e)$
that homomorphically maps onto every ambit, the greatest ambit. Topologically,
![]() $S(G)$
is the Samuel compactification of G with respect to the right uniformity on G generated by open covers
$S(G)$
is the Samuel compactification of G with respect to the right uniformity on G generated by open covers
A compact space X admits a unique compatible uniformity (generated by finite open covers). We will say that a map
![]() $G\to X$
is right uniformly continuous if it is uniformly continuous with respect to the right uniformity on G and the unique compatible uniformity on
$G\to X$
is right uniformly continuous if it is uniformly continuous with respect to the right uniformity on G and the unique compatible uniformity on
![]() $X.$
Similarly, we define left uniformity, right action, and the greatest ambit with respect to the right action. In what follows, ‘uniformly continuous’ will mean right uniformly continuous, unless otherwise stated.
$X.$
Similarly, we define left uniformity, right action, and the greatest ambit with respect to the right action. In what follows, ‘uniformly continuous’ will mean right uniformly continuous, unless otherwise stated.
We call a topological group SIN (an abbreviation for small invariant neighbourhoods) if the left and right uniformities coincide. It is easy to see that a group G is SIN if and only if it admits a basis of e consisting of conjugation invariant neighbourhoods, that is, V such that
![]() $gVg^{-1}=V$
for every
$gVg^{-1}=V$
for every
![]() $g\in G.$
Multiplication and inversion in SIN groups are (right, left) uniformly continuous.
$g\in G.$
Multiplication and inversion in SIN groups are (right, left) uniformly continuous.
The Samuel compactification is the smallest compactification of G (that is, there is an embedding of G into
![]() $S(G)$
with dense image) such that every right uniformly continuous function from G to a compact space (uniquely) extends to
$S(G)$
with dense image) such that every right uniformly continuous function from G to a compact space (uniquely) extends to
![]() $S(G).$
We will describe Samuel’s original construction (see [Reference SamuelS]) of
$S(G).$
We will describe Samuel’s original construction (see [Reference SamuelS]) of
![]() $S(G)$
. For a discrete group
$S(G)$
. For a discrete group
![]() $H,$
the Samuel compactification coincides with the Čech–Stone compactification
$H,$
the Samuel compactification coincides with the Čech–Stone compactification
![]() $\beta H \cdot \beta H$
consists of ultrafilters on H with a basis for topology of clopen sets
$\beta H \cdot \beta H$
consists of ultrafilters on H with a basis for topology of clopen sets
![]() $\hat {A}=\{u\in \beta (H), A\in u\}$
for
$\hat {A}=\{u\in \beta (H), A\in u\}$
for
![]() $A\subset H$
. We can identify H with a dense subset of
$A\subset H$
. We can identify H with a dense subset of
![]() $\beta H$
via principal ultrafilters. The action
$\beta H$
via principal ultrafilters. The action
![]() $H\times \beta H\to \beta H$
given by
$H\times \beta H\to \beta H$
given by
![]() $hu=\{hA:A\in u\}$
is the greatest ambit
$hu=\{hA:A\in u\}$
is the greatest ambit
![]() $(\beta H,e).$
Given a topological group G, we denote by
$(\beta H,e).$
Given a topological group G, we denote by
![]() $G_d$
the same algebraic group with the discrete topology. Then the greatest ambit action of G remains an ambit action
$G_d$
the same algebraic group with the discrete topology. Then the greatest ambit action of G remains an ambit action
![]() $G_d\times (S(G),e)\to (S(G),e).$
Since
$G_d\times (S(G),e)\to (S(G),e).$
Since
![]() $\beta G_d$
is the greatest ambit for
$\beta G_d$
is the greatest ambit for
![]() $G_d,$
there is an ambit homomorphism
$G_d,$
there is an ambit homomorphism
![]() $\pi :\beta G_d\to S(G).$
For an ultrafilter u in
$\pi :\beta G_d\to S(G).$
For an ultrafilter u in
![]() $\beta G_d,$
we let the envelope of u be its subfilter
$\beta G_d,$
we let the envelope of u be its subfilter
generated by
![]() $\{VA:V\in {\mathcal {N}}_e(G),A\in u\}.$
Given
$\{VA:V\in {\mathcal {N}}_e(G),A\in u\}.$
Given
![]() $u,v\in \beta G_d,$
we set
$u,v\in \beta G_d,$
we set
![]() $u\sim v$
if and only if
$u\sim v$
if and only if
![]() $u^*=v^*$
. Then
$u^*=v^*$
. Then
![]() $\sim $
is an equivalence relation whose equivalence classes are exactly preimages of
$\sim $
is an equivalence relation whose equivalence classes are exactly preimages of
![]() $\pi .$
The collection of
$\pi .$
The collection of
for
![]() $A\subset G$
forms a basis for closed sets in
$A\subset G$
forms a basis for closed sets in
![]() $S(G).$
$S(G).$
A G-flow on X is minimal if X contains no closed proper non-empty invariant subset, that is, no proper subflow. Equivalently, for every
![]() $x\in X,$
the orbit
$x\in X,$
the orbit
![]() $Gx$
is dense in X. Up to isomorphism, there is a unique minimal flow that admits a homomorphism onto every minimal flow, called the universal minimal flow of G and denoted by
$Gx$
is dense in X. Up to isomorphism, there is a unique minimal flow that admits a homomorphism onto every minimal flow, called the universal minimal flow of G and denoted by
![]() $M(G)$
. The universal minimal flow is isomorphic to any minimal subflow of
$M(G)$
. The universal minimal flow is isomorphic to any minimal subflow of
![]() $S(G)$
. If G is compact, then
$S(G)$
. If G is compact, then
![]() $M(G)\cong G$
with the left translation action; if G is locally compact, then G acts freely on
$M(G)\cong G$
with the left translation action; if G is locally compact, then G acts freely on
![]() $M(G)$
, by a theorem of Veech [Reference VeechV], and if G is locally compact, non-compact, then M(G) is non-metrizable [Reference Kechris, Pestov and TodorcevicKPT].
$M(G)$
, by a theorem of Veech [Reference VeechV], and if G is locally compact, non-compact, then M(G) is non-metrizable [Reference Kechris, Pestov and TodorcevicKPT].
3 Extensions of compact groups
Given topological groups
![]() $G,K,H,$
we say that G is an extension of K by H if there is a short exact sequence
$G,K,H,$
we say that G is an extension of K by H if there is a short exact sequence
where each arrow is a continuous group homomorphism onto its image (which, moreover, implies that
![]() $\pi $
is open). We focus on the case where K is compact. Identifying K with the image of
$\pi $
is open). We focus on the case where K is compact. Identifying K with the image of
![]() $\iota $
, we can assume that K is a compact normal subgroup of G and H is isomorphic to
$\iota $
, we can assume that K is a compact normal subgroup of G and H is isomorphic to
![]() $G/K.$
For the rest of this section, we fix a topological group G together with a compact normal subgroup
$G/K.$
For the rest of this section, we fix a topological group G together with a compact normal subgroup
![]() $K.$
We investigate the relationship between
$K.$
We investigate the relationship between
![]() $S(G)$
and
$S(G)$
and
![]() $S(G/K)\times K,$
respectively,
$S(G/K)\times K,$
respectively,
![]() $M(G)$
and
$M(G)$
and
![]() $M(G/K)\times K.$
$M(G/K)\times K.$
Let
![]() $S(G)/K$
denote the orbit space
$S(G)/K$
denote the orbit space
![]() $\{Kx:x\in S(G)\}$
of the restricted action
$\{Kx:x\in S(G)\}$
of the restricted action
![]() $K\times S(G)\to S(G)$
. Since K is compact, K-orbits are equivalence classes of a closed equivalence relation on
$K\times S(G)\to S(G)$
. Since K is compact, K-orbits are equivalence classes of a closed equivalence relation on
![]() $S(G),$
and therefore
$S(G),$
and therefore
![]() $S(G)/K$
(with the quotient topology) is a compact Hausdorff space. We have that
$S(G)/K$
(with the quotient topology) is a compact Hausdorff space. We have that
![]() $G/K\times S(G)/K\to S(G)/K$
, defined by
$G/K\times S(G)/K\to S(G)/K$
, defined by
![]() $(Kg)Kx=Kgx$
, is a continuous ambit action with the base point
$(Kg)Kx=Kgx$
, is a continuous ambit action with the base point
![]() $K.$
$K.$
Lemma 3.1.
![]() $S(G/K)\cong S(G)/K.$
$S(G/K)\cong S(G)/K.$
Proof. We can define an ambit action
![]() $G\times S(G/K)\to S(G/K)$
by
$G\times S(G/K)\to S(G/K)$
by
![]() $gx=Kgx$
. Since
$gx=Kgx$
. Since
![]() $S(G)$
is the greatest G-ambit, there is an ambit homomorphism
$S(G)$
is the greatest G-ambit, there is an ambit homomorphism
![]() $\phi :S(G)\to S(G/K)$
. Clearly,
$\phi :S(G)\to S(G/K)$
. Clearly,
![]() $\phi $
is constant on every K-orbit, so
$\phi $
is constant on every K-orbit, so
![]() $\phi $
factors through
$\phi $
factors through
![]() $\psi :S(G)\to S(G)/K$
and
$\psi :S(G)\to S(G)/K$
and
![]() $\xi :S(G)/K\to S(G/K).$
Since
$\xi :S(G)/K\to S(G/K).$
Since
![]() $\xi $
maps
$\xi $
maps
![]() $Ke\in S(G)/K$
to
$Ke\in S(G)/K$
to
![]() $K\in G/K\subset S(G/K)$
, it is a
$K\in G/K\subset S(G/K)$
, it is a
![]() $G/K$
-ambit homomorphism. But
$G/K$
-ambit homomorphism. But
![]() $S(G/K)$
is the greatest
$S(G/K)$
is the greatest
![]() $G/K$
-ambit, therefore
$G/K$
-ambit, therefore
![]() $\xi $
must be an ambit isomorphism.
$\xi $
must be an ambit isomorphism.
Remark 3.2. By Lemma 3.1 and (Δ), we have that, for any
![]() $u\in \beta G_d,$
the K-orbit
$u\in \beta G_d,$
the K-orbit
![]() $Ku^*=\{ku^*:k\in K\}$
is a closed subset of
$Ku^*=\{ku^*:k\in K\}$
is a closed subset of
![]() $S(G)$
corresponding to the filter
$S(G)$
corresponding to the filter
That is, elements of
![]() $Ku^*$
are exactly those
$Ku^*$
are exactly those
![]() $v^*$
that extend this filter.
$v^*$
that extend this filter.
Lemma 3.3.
![]() $M(G/K)\cong M(G)/K.$
$M(G/K)\cong M(G)/K.$
Proof. Since
![]() $M(G)$
is isomorphic to a minimal G-subflow of
$M(G)$
is isomorphic to a minimal G-subflow of
![]() $S(G), M(G)/K$
is isomorphic to a minimal
$S(G), M(G)/K$
is isomorphic to a minimal
![]() $G/K$
-subflow of
$G/K$
-subflow of
![]() $S(G)/K.$
By Lemma 3.1,
$S(G)/K.$
By Lemma 3.1,
![]() $S(G)/K$
is isomorphic to the greatest ambit
$S(G)/K$
is isomorphic to the greatest ambit
![]() $S(G/K)$
and therefore its minimal subflows are isomorphic to
$S(G/K)$
and therefore its minimal subflows are isomorphic to
![]() $M(G/K).$
$M(G/K).$
Let us remark that we can prove this fact directly as in the proof of Lemma 3.1 from universality and uniqueness of
![]() $M(G).$
$M(G).$
Definition 3.1. Let X be a topological space and let
![]() $\pi :X\to X/E$
be a quotient map. A cross-section is a map
$\pi :X\to X/E$
be a quotient map. A cross-section is a map
![]() $\phi :X/E \to X$
such that
$\phi :X/E \to X$
such that
![]() $\pi \circ \phi =\text {id}_{X/E}.$
$\pi \circ \phi =\text {id}_{X/E}.$
Theorem 3.4. Suppose that there exists a uniformly continuous cross-section
![]() $s:G/K\to ~G.$
Then there is a continuous cross-section
$s:G/K\to ~G.$
Then there is a continuous cross-section
![]() $s':S(G)/K\to S(G)$
.
$s':S(G)/K\to S(G)$
.
Proof. Let
![]() $\pi :S(G)\to S(G/K)$
be the natural G-ambit homomorphism as in Lemma 3.1. Let
$\pi :S(G)\to S(G/K)$
be the natural G-ambit homomorphism as in Lemma 3.1. Let
![]() $s:G/K\to G$
be a uniformly continuous cross-section. Since uniformly continuous maps from
$s:G/K\to G$
be a uniformly continuous cross-section. Since uniformly continuous maps from
![]() $G/K$
to compact spaces uniquely extend to
$G/K$
to compact spaces uniquely extend to
![]() $S(G/K),$
there is a continuous map
$S(G/K),$
there is a continuous map
![]() $\bar {s}:S(G/K)\to S(G)$
extending s. Concretely (see [Reference BartošováB]), denoting by S the image of
$\bar {s}:S(G/K)\to S(G)$
extending s. Concretely (see [Reference BartošováB]), denoting by S the image of
![]() $s,$
for any
$s,$
for any
![]() $u\in \beta G_d,$
$u\in \beta G_d,$
Since S intersects every coset of K and
![]() $\{KA:A\in u\}$
is an ultrafilter in
$\{KA:A\in u\}$
is an ultrafilter in
![]() $\beta (G/K)_d,$
we get that
$\beta (G/K)_d,$
we get that
![]() $v=\langle \{KA:A\in u\}\cup \{S\}\rangle $
is an ultrafilter in
$v=\langle \{KA:A\in u\}\cup \{S\}\rangle $
is an ultrafilter in
![]() $\beta G_d$
such that
$\beta G_d$
such that
![]() $\{KA:A\in u\}=\{KB:B\in v\}.$
By Remark 3.2, it follows that
$\{KA:A\in u\}=\{KB:B\in v\}.$
By Remark 3.2, it follows that
![]() $\bar {s}\pi (u^*)$
lies in the orbit
$\bar {s}\pi (u^*)$
lies in the orbit
![]() $Ku^*$
. Precomposing with
$Ku^*$
. Precomposing with
![]() $\xi $
from Lemma 3.1, we obtain a continuous cross-section
$\xi $
from Lemma 3.1, we obtain a continuous cross-section
![]() $s':S(G)/K\to S(G).$
$s':S(G)/K\to S(G).$
Remark 3.5. Continuity of
![]() $s'$
means that for every open
$s'$
means that for every open
![]() $U\subset S(G)$
there is an open
$U\subset S(G)$
there is an open
![]() $V\subset S(G)$
such that
$V\subset S(G)$
such that
![]() $s'(KV)\subset U$
from the definition of the quotient topology on
$s'(KV)\subset U$
from the definition of the quotient topology on
![]() $S(G)/K.$
$S(G)/K.$
Corollary 3.6. Suppose that K acts freely on
![]() $S(G).$
If there exists a uniformly continuous cross-section
$S(G).$
If there exists a uniformly continuous cross-section
![]() $s:G/K\to G,$
then the phase space of
$s:G/K\to G,$
then the phase space of
![]() $S(G)$
is homeomorphic to
$S(G)$
is homeomorphic to
![]() $S(G/K)\times K.$
$S(G/K)\times K.$
Proof. Denote by
![]() $s':S(G)/K\to S(G)$
the continuous cross-section as in Theorem 3.4. Define a map
$s':S(G)/K\to S(G)$
the continuous cross-section as in Theorem 3.4. Define a map
![]() $\phi :S(G)/K\times K\to S(G)$
by
$\phi :S(G)/K\times K\to S(G)$
by
![]() $\phi (Ku,k)=ks'(Ku).$
As K acts freely,
$\phi (Ku,k)=ks'(Ku).$
As K acts freely,
![]() $\phi $
is a bijection. Since
$\phi $
is a bijection. Since
![]() $\phi $
is multiplication of two continuous maps, it is continuous, hence a homeomorphism. The statement follows by Lemma 3.1.
$\phi $
is multiplication of two continuous maps, it is continuous, hence a homeomorphism. The statement follows by Lemma 3.1.
Corollary 3.7. If there exists a uniformly continuous cross-section
![]() $s:G/K\to G,$
then the phase space of
$s:G/K\to G,$
then the phase space of
![]() $M(G)$
is homeomorphic to
$M(G)$
is homeomorphic to
![]() $M(G/K)\times K.$
$M(G/K)\times K.$
If G is SIN, we can fully describe the greatest ambit and the universal minimal actions.
Theorem 3.8. Let G be SIN. Suppose that K acts freely on
![]() $S(G)$
and that there is a uniformly continuous cross-section
$S(G)$
and that there is a uniformly continuous cross-section
![]() $s:G/K\to G.$
Then we can explicitly describe an action of G on
$s:G/K\to G.$
Then we can explicitly describe an action of G on
![]() $S(G/K)\times K$
such that
$S(G/K)\times K$
such that
![]() $S(G)\cong S(G/K)\times K$
as ambits.
$S(G)\cong S(G/K)\times K$
as ambits.
Proof. Let
![]() $S_L(G)$
(respectively,
$S_L(G)$
(respectively,
![]() $S_R(G)$
) denote the greatest ambit of G with respect to the right (respectively, left) actions of G. The anti-isomorphism
$S_R(G)$
) denote the greatest ambit of G with respect to the right (respectively, left) actions of G. The anti-isomorphism
![]() $G\to G, g\mapsto g^{-1}$
induces a homeomorphism
$G\to G, g\mapsto g^{-1}$
induces a homeomorphism
![]() $S_L(G)\to S_R(G)$
by
$S_L(G)\to S_R(G)$
by
![]() $u^*\mapsto (u^{-1})^*$
, where
$u^*\mapsto (u^{-1})^*$
, where
![]() $u^{-1}$
denotes
$u^{-1}$
denotes
![]() $\{A^{-1}=\{a^{-1}:a\in A\}: A\in u\}$
and
$\{A^{-1}=\{a^{-1}:a\in A\}: A\in u\}$
and
![]() $u^*$
is the Samuel envelope of
$u^*$
is the Samuel envelope of
![]() $u\in \beta (G_d)$
. This witnesses a correspondence between the left action of G on
$u\in \beta (G_d)$
. This witnesses a correspondence between the left action of G on
![]() $S_L(G)$
and the right action of G on
$S_L(G)$
and the right action of G on
![]() $S_R(G)$
.
$S_R(G)$
.
Since G is SIN, we can choose
![]() ${\mathcal {N}}_e(G)$
to be a neighbourhood basis of G at e consisting of V such that
${\mathcal {N}}_e(G)$
to be a neighbourhood basis of G at e consisting of V such that
![]() $gVg^{-1}=V$
for every
$gVg^{-1}=V$
for every
![]() $g\in G.$
Then for every
$g\in G.$
Then for every
![]() $A\subset G, VA=AV,$
therefore the construction by Samuel of the (left, right) greatest ambit via envelopes shows that
$A\subset G, VA=AV,$
therefore the construction by Samuel of the (left, right) greatest ambit via envelopes shows that
![]() $S_L(G)$
and
$S_L(G)$
and
![]() $S_R(G)$
coincide, and will further be denoted by
$S_R(G)$
coincide, and will further be denoted by
![]() $S(G)$
. As K acts freely on the left on
$S(G)$
. As K acts freely on the left on
![]() $S(G),$
by the first paragraph K also acts freely on the right on
$S(G),$
by the first paragraph K also acts freely on the right on
![]() $S(G).$
Since K is normal in
$S(G).$
Since K is normal in
![]() $G, VKA=AKV,$
and we have that the quotient maps
$G, VKA=AKV,$
and we have that the quotient maps
![]() $S(G)\to S(G/K)$
and
$S(G)\to S(G/K)$
and
![]() $S(G)\to S(K\backslash G)$
define the same equivalence relation on
$S(G)\to S(K\backslash G)$
define the same equivalence relation on
![]() $S(G).$
By Lemma 3.1, the orbit spaces
$S(G).$
By Lemma 3.1, the orbit spaces
![]() $S(G)/K=\{Ku:u\in S(G)\}$
and
$S(G)/K=\{Ku:u\in S(G)\}$
and
![]() $K\backslash S(G)=\{uK:u\in S(G)\}$
are the same. It means that for every
$K\backslash S(G)=\{uK:u\in S(G)\}$
are the same. It means that for every
![]() $k\in K, u\in S(G)$
there is
$k\in K, u\in S(G)$
there is
![]() $k'\in K$
such that
$k'\in K$
such that
![]() $ku=uk'.$
$ku=uk'.$
Suppose that there is a uniformly continuous cross-section
![]() $s:G/K\to G;$
by shifting we can assume that
$s:G/K\to G;$
by shifting we can assume that
![]() $s(K)=e.$
By Theorem 3.4, s uniquely extends to a cross-section
$s(K)=e.$
By Theorem 3.4, s uniquely extends to a cross-section
![]() $s':S(G)/K\to S(G)$
.
$s':S(G)/K\to S(G)$
.
We define a cocycle
![]() $\rho : G\times S(G)/K\to K$
to ‘correct’ that s may not be a group homomorphism by the rule
$\rho : G\times S(G)/K\to K$
to ‘correct’ that s may not be a group homomorphism by the rule
Since left and right K-orbits in
![]() $S(G)$
coincide and K acts freely on
$S(G)$
coincide and K acts freely on
![]() $S(G)$
on the right,
$S(G)$
on the right,
![]() $\rho $
is well defined.
$\rho $
is well defined.
We will prove that
![]() $\rho $
is continuous. Fix
$\rho $
is continuous. Fix
![]() $g\in G$
and
$g\in G$
and
![]() $Ku\in S(G)/K$
, and denote
$Ku\in S(G)/K$
, and denote
![]() ${k=\rho (g, Ku).}$
Let
${k=\rho (g, Ku).}$
Let
![]() $k\in O$
be a basic open neighbourhood of k in K. By Corollary 3.6 for right actions, we have that
$k\in O$
be a basic open neighbourhood of k in K. By Corollary 3.6 for right actions, we have that
![]() $ S(G)/K\times K\to S(G)$
defined by
$ S(G)/K\times K\to S(G)$
defined by
![]() $(Ku,l)\mapsto s'(Ku)l$
is a homeomorphism. Consequently,
$(Ku,l)\mapsto s'(Ku)l$
is a homeomorphism. Consequently,
![]() $s'(S(G)/K)\times O$
is an open neighbourhood of
$s'(S(G)/K)\times O$
is an open neighbourhood of
![]() $gs'(Ku)$
in
$gs'(Ku)$
in
![]() $S(G).$
Since the action of G on
$S(G).$
Since the action of G on
![]() $S(G)$
is continuous, there are open neighbourhoods
$S(G)$
is continuous, there are open neighbourhoods
![]() $V\in \mathcal {N}_e(G)$
and U of
$V\in \mathcal {N}_e(G)$
and U of
![]() $s'(u)$
such that
$s'(u)$
such that
![]() $VgU\subset s'(S(G)/K)\times O.$
Since
$VgU\subset s'(S(G)/K)\times O.$
Since
![]() $s'$
is continuous, there is an open neighbourhood
$s'$
is continuous, there is an open neighbourhood
![]() $U'$
of u such that
$U'$
of u such that
![]() $s'(KU')\subset U.$
Since
$s'(KU')\subset U.$
Since
![]() $U'$
is open in
$U'$
is open in
![]() $S(G)$
and G acts by homeomorphisms,
$S(G)$
and G acts by homeomorphisms,
![]() $VgU'=\bigcup _{h\in Vg}hU',$
is open in
$VgU'=\bigcup _{h\in Vg}hU',$
is open in
![]() $S(G).$
Therefore,
$S(G).$
Therefore,
![]() $VgU'k^{-1}$
is an open neighbourhood of
$VgU'k^{-1}$
is an open neighbourhood of
![]() $s'(gKu).$
By continuity of
$s'(gKu).$
By continuity of
![]() $s'$
and of the action of G on
$s'$
and of the action of G on
![]() $G/K$
, there are neighbourhoods
$G/K$
, there are neighbourhoods
![]() $V'\in \mathcal {N}_e(G)$
and
$V'\in \mathcal {N}_e(G)$
and
![]() $U"$
of u in
$U"$
of u in
![]() $S(G)$
such that
$S(G)$
such that
![]() $s'(V'gKU")\subset VgU'k^{-1}.$
Finally, we get that
$s'(V'gKU")\subset VgU'k^{-1}.$
Finally, we get that
![]() $s'((V\cap V')gK(U'\cap U"))\times O\supset (V\cap V')gs'(K(U'\cap U")),$
so
$s'((V\cap V')gK(U'\cap U"))\times O\supset (V\cap V')gs'(K(U'\cap U")),$
so
![]() $\rho ((V\cap V')g,K(U\cap U"))\subset O.$
$\rho ((V\cap V')g,K(U\cap U"))\subset O.$
The function
![]() $\rho $
is a cocycle in the sense that for every
$\rho $
is a cocycle in the sense that for every
![]() $g,h\in G$
we have
$g,h\in G$
we have
 $$ \begin{align*} s'(Kghu)\rho(gh, Ku)&=ghs'(Ku),\\ s'(Kghu)\rho(g,Khu)&=gs'(Khu),\\ s'(Khu)\rho(h,Ku)&=hs'(Ku),\\ s'(Kghu)\rho(gh, Ku)&=gs'(Khu)\rho(h,Ku)=s'(Kghu)\rho(g,Khu)\rho(h,Ku), \end{align*} $$
$$ \begin{align*} s'(Kghu)\rho(gh, Ku)&=ghs'(Ku),\\ s'(Kghu)\rho(g,Khu)&=gs'(Khu),\\ s'(Khu)\rho(h,Ku)&=hs'(Ku),\\ s'(Kghu)\rho(gh, Ku)&=gs'(Khu)\rho(h,Ku)=s'(Kghu)\rho(g,Khu)\rho(h,Ku), \end{align*} $$
and (*) follows from freeness of the action by
![]() $K.$
$K.$
We define an action
![]() $\alpha :G\times (S(G/K)\times K)\to S(G/K)\times K$
by
$\alpha :G\times (S(G/K)\times K)\to S(G/K)\times K$
by
By (*),
![]() $\alpha $
is an action and it is obviously continuous.
$\alpha $
is an action and it is obviously continuous.
We define
Then
![]() $\phi $
is an ambit homomorphism:
$\phi $
is an ambit homomorphism:
-
(1)
 $\phi $
is continuous as it is a composition of multiplication with continuous functions;
$\phi $
is continuous as it is a composition of multiplication with continuous functions; -
(2)
 $\phi (K,e)=s'(K)e=ee=e$
;
$\phi (K,e)=s'(K)e=ee=e$
; -
(3)
 $\phi (g(Ku,k))=\phi ((Kgu,\rho (g,Ku)k))=s'(Kgu)\rho (g,Ku)k=gs'(Ku)k= g(\phi (Ku, k))$
, where the penultimate equality holds by the definition of
$\phi (g(Ku,k))=\phi ((Kgu,\rho (g,Ku)k))=s'(Kgu)\rho (g,Ku)k=gs'(Ku)k= g(\phi (Ku, k))$
, where the penultimate equality holds by the definition of
 $\rho .$
$\rho .$
By universality of
![]() $S(G),$
we can conclude that
$S(G),$
we can conclude that
![]() $\phi $
is an isomorphism.
$\phi $
is an isomorphism.
Corollary 3.9. Let G be SIN. Then we can explicitly describe an action of G on
![]() $M(G/K)\times K$
such that
$M(G/K)\times K$
such that
![]() $M(G)\cong M(G/K)\times K$
as G-flows.
$M(G)\cong M(G/K)\times K$
as G-flows.
4 Extensions by compact groups
In this section we will consider short exact sequences
where K is compact. We verify that a result of Kechris and Sokić for Polish G in [Reference Kechris and SokićKS] generalizes to arbitrary topological groups and works for the greatest ambit as well as the universal minimal flow. Our proof is slightly shorter, but the idea is the same.
Theorem 4.1. Let G be a topological group with a closed normal subgroup N such that
![]() $G/N$
is compact. Suppose that there is a continuous cross-section
$G/N$
is compact. Suppose that there is a continuous cross-section
![]() $s:G/N\to G$
(which is automatically uniformly continuous by compactness of
$s:G/N\to G$
(which is automatically uniformly continuous by compactness of
![]() $G/N$
). Then
$G/N$
). Then
![]() $S(G)\cong S(N)\times G/N$
.
$S(G)\cong S(N)\times G/N$
.
Proof. By shifting, we can assume that
![]() $s(N)=e.$
$s(N)=e.$
We again define a cocycle
![]() $\rho : G\times G/N\to N$
by
$\rho : G\times G/N\to N$
by
We have that
![]() $\rho (g, Nh)=s(Ngh)^{-1}gs(Nh),$
so
$\rho (g, Nh)=s(Ngh)^{-1}gs(Nh),$
so
![]() $\rho $
is continuous. By (*) in the proof of Theorem 3.8,
$\rho $
is continuous. By (*) in the proof of Theorem 3.8,
![]() $\rho (gg', Nh)=\rho (g, Ng'h)\rho (g',Nh).$
Therefore, the map
$\rho (gg', Nh)=\rho (g, Ng'h)\rho (g',Nh).$
Therefore, the map
![]() $G\times (S(N)\times G/N)\to S(N)\times G/N$
defined by
$G\times (S(N)\times G/N)\to S(N)\times G/N$
defined by
is an ambit action.
Viewing
![]() $S(G)$
as an N-flow, there is an N-ambit homomorphism
$S(G)$
as an N-flow, there is an N-ambit homomorphism
![]() $\mu :(S(N),e)\to (S(G),e)$
. We define
$\mu :(S(N),e)\to (S(G),e)$
. We define
![]() $\phi :S(N)\times G/N \to S(G)$
by
$\phi :S(N)\times G/N \to S(G)$
by
![]() $(u, Nh)\mapsto s(Nh)\mu (u).$
Then
$(u, Nh)\mapsto s(Nh)\mu (u).$
Then
![]() $\phi $
is a G-ambit homomorphism.
$\phi $
is a G-ambit homomorphism.
-
(1)
 $\phi $
is continuous since,
$\phi $
is continuous since,
 $s, \mu ,$
and the action of G on
$s, \mu ,$
and the action of G on
 $S(G)$
are.
$S(G)$
are. -
(2)
 $\phi (e,N)=s(N)\mu (e)=ee=e.$
$\phi (e,N)=s(N)\mu (e)=ee=e.$
-
(3) Since
 $\mu $
is a homomorphism of N-flows, we have
$\mu $
is a homomorphism of N-flows, we have
 $\mu (\rho (g,Nh)u)=\rho (g,Nh)\mu (u)$
:
$\mu (\rho (g,Nh)u)=\rho (g,Nh)\mu (u)$
:  $$ \begin{align*} \phi(g(u,Nh))&=\phi(\rho(g,Nh)u, Ngh)=s(Ngh)\mu(\rho(g,Nh)u) \\ &= s(Ngh)\rho(g,Nh)\mu(u) \quad(\mu \textrm{ homomorphism})\\ &=gs(Nh)\mu(u)= g\phi(u,Nh) \quad(\rho \textrm{ cocycle}). \end{align*} $$
$$ \begin{align*} \phi(g(u,Nh))&=\phi(\rho(g,Nh)u, Ngh)=s(Ngh)\mu(\rho(g,Nh)u) \\ &= s(Ngh)\rho(g,Nh)\mu(u) \quad(\mu \textrm{ homomorphism})\\ &=gs(Nh)\mu(u)= g\phi(u,Nh) \quad(\rho \textrm{ cocycle}). \end{align*} $$
Since
![]() $S(G)$
is the greatest ambit,
$S(G)$
is the greatest ambit,
![]() $\phi $
is an isomorphism.
$\phi $
is an isomorphism.
Corollary 4.2. Let G be a topological group with a closed normal subgroup N such that
![]() $G/N$
is compact. Suppose that there is a continuous cross-section
$G/N$
is compact. Suppose that there is a continuous cross-section
![]() $s:G/N\to G.$
Then
$s:G/N\to G.$
Then
![]() $M(G)\cong M(N)\times G/N$
.
$M(G)\cong M(N)\times G/N$
.
Proof. For every
![]() $Nh\in G/N,$
the evaluation map
$Nh\in G/N,$
the evaluation map
![]() $G\to N, g\mapsto \rho (g, Nh) $
given by the cocycle
$G\to N, g\mapsto \rho (g, Nh) $
given by the cocycle
![]() $\rho $
defined in the proof of Theorem 4.1 is onto. Viewing
$\rho $
defined in the proof of Theorem 4.1 is onto. Viewing
![]() $M(N)$
as a subflow of
$M(N)$
as a subflow of
![]() $S(N)$
, for any
$S(N)$
, for any
![]() $m\in M(N)$
,
$m\in M(N)$
,
![]() $\{\rho (g,Nh)m:g\in G\}=Nm$
, so
$\{\rho (g,Nh)m:g\in G\}=Nm$
, so
![]() $M(N)\times G/N$
is a minimal subflow of
$M(N)\times G/N$
is a minimal subflow of
![]() $S(N)\times G/N.$
$S(N)\times G/N.$
5 Applications
5.1 Totally disconnected locally compact groups
Totally disconnected locally compact groups coincide with locally compact groups of automorphisms of first-order structures. T.d.l.c. groups admit a local basis at the neutral element e consisting of open compact subgroups. Systematic study of Polish t.d.l.c. groups was started by the book by Wesolek [Reference WesolekW]. By van Dantzig’s theorem, the underlying topological space of a Polish t.d.l.c. group is homeomorphic to either a countable set, the Cantor space
![]() $2^{\mathbb {N}}$
, or
$2^{\mathbb {N}}$
, or
![]() $\mathbb {N}\times 2^{\mathbb {N}}$
. By Veech’s theorem [Reference VeechV], every locally compact group acts freely on its greatest ambit, and consequently on its universal minimal flow. If K is a compact open normal subgroup of
$\mathbb {N}\times 2^{\mathbb {N}}$
. By Veech’s theorem [Reference VeechV], every locally compact group acts freely on its greatest ambit, and consequently on its universal minimal flow. If K is a compact open normal subgroup of
![]() $G,$
then
$G,$
then
![]() $G/K$
is a discrete group. Therefore, any cross-section
$G/K$
is a discrete group. Therefore, any cross-section
![]() $G/K\to G$
is uniformly continuous and we can apply Corollary 3.7 to derive the following theorem.
$G/K\to G$
is uniformly continuous and we can apply Corollary 3.7 to derive the following theorem.
Theorem 5.1. Let G be a t.d.l.c. group with a normal compact open subgroup
![]() $K.$
Then the phase space of
$K.$
Then the phase space of
![]() $M(G)$
is homeomorphic to
$M(G)$
is homeomorphic to
![]() $M(G/K)\times K.$
$M(G/K)\times K.$
In the case of Polish t.d.l.c. groups we get a complete characterization of phase spaces of universal minimal flows.
Corollary 5.2. If G is a Polish t.d.l.c. group with a normal compact open subgroup
![]() $K,$
then
$K,$
then
![]() $M(G)$
is homeomorphic to a finite set,
$M(G)$
is homeomorphic to a finite set,
![]() $M(\mathbb {Z}), 2^{\mathbb {N}}$
, or
$M(\mathbb {Z}), 2^{\mathbb {N}}$
, or
![]() $M(\mathbb {Z})\times 2^{\mathbb {N}}.$
$M(\mathbb {Z})\times 2^{\mathbb {N}}.$
Moreover, if G in Theorem 5.1 is SIN, we can also define the action as in Corollary 3.9.
Theorem 5.3. If G is a SIN t.d.l.c. group and K any normal compact open subgroup, then
![]() $M(G)$
is isomorphic to
$M(G)$
is isomorphic to
![]() $M(G/K)\times K.$
$M(G/K)\times K.$
Polish SIN t.d.l.c. groups are exactly locally compact groups of automorphisms of countable first-order structures admitting a two-sided invariant metric, or equivalently, Polish groups admitting a countable basis at the neutral element consisting of compact open normal subgroups.
5.2 Semi-direct products
In [Reference Kechris and SokićKS], Kechris and Sokić studied universal minimal flows of semidirect products of Polish groups with one of the factors compact. Their proof can be modified to apply to groups that are not Polish as well. We include the results for completeness and extend them to the greatest ambit.
In Theorem 3.8 we required G to be SIN, and in Theorem 4.1 we proved that
![]() $S(G/N)=G/N,$
which allowed us to define the cocycle
$S(G/N)=G/N,$
which allowed us to define the cocycle
![]() $\rho $
to compensate for s not being necessarily a group homomorphism. If s is a group homomorphism, that is, the respective short exact sequence splits, then G is a semidirect product, and we do not need
$\rho $
to compensate for s not being necessarily a group homomorphism. If s is a group homomorphism, that is, the respective short exact sequence splits, then G is a semidirect product, and we do not need
![]() $\rho $
.
$\rho $
.
Theorem 5.4. Let
![]() $G\cong H\ltimes K,$
where K is compact. Then
$G\cong H\ltimes K,$
where K is compact. Then
![]() $S(G)\cong S(H)\times K$
and
$S(G)\cong S(H)\times K$
and
![]() $M(G)\cong M(H)\times K.$
$M(G)\cong M(H)\times K.$
Proof. Let
![]() $s:H\to G$
be a cross-section that is a continuous homomorphism and let
$s:H\to G$
be a cross-section that is a continuous homomorphism and let
![]() $\pi :G\to H$
be the natural projection. Define
$\pi :G\to H$
be the natural projection. Define
![]() $\alpha : G\times (S(H)\times K)\to (S(H)\times K)$
by
$\alpha : G\times (S(H)\times K)\to (S(H)\times K)$
by
![]() $g(u,k)=(\pi (g)u,gks(\pi (g))^{-1}).$
Since
$g(u,k)=(\pi (g)u,gks(\pi (g))^{-1}).$
Since
![]() $\pi $
and s are continuous group homomorphisms,
$\pi $
and s are continuous group homomorphisms,
![]() $\alpha $
is a continuous action. Also,
$\alpha $
is a continuous action. Also,
![]() $G(e,e)=(He, K)$
is dense in
$G(e,e)=(He, K)$
is dense in
![]() $S(H)\times K,$
so
$S(H)\times K,$
so
![]() $\alpha $
is an ambit action. Since s is a continuous homomorphism, we can define a continuous ambit action
$\alpha $
is an ambit action. Since s is a continuous homomorphism, we can define a continuous ambit action
![]() $H\times S(G)\to S(G)$
by
$H\times S(G)\to S(G)$
by
![]() $(h,u)\mapsto s(h)u.$
Therefore, there is an H-ambit homomorphism
$(h,u)\mapsto s(h)u.$
Therefore, there is an H-ambit homomorphism
![]() $s':S(H)\to S(G)$
extending s. Define
$s':S(H)\to S(G)$
extending s. Define
![]() $\phi :S(H)\times K\to S(G)$
by
$\phi :S(H)\times K\to S(G)$
by
![]() $(u,k)\mapsto ks'(u)$
. Then
$(u,k)\mapsto ks'(u)$
. Then
![]() $\phi $
is a G-ambit homomorphism:
$\phi $
is a G-ambit homomorphism:
 $$ \begin{align} \phi(g(u,k))&=\phi((\pi(g)u, gk(s(\pi(g)))^{-1}))=gk(s(\pi(g)))^{-1}s'(\pi(g)u)\nonumber\\ &= gk(s(\pi(g)))^{-1}s(\pi(g))s'(u)=gks'(u)=g\phi(u,k). \end{align} $$
$$ \begin{align} \phi(g(u,k))&=\phi((\pi(g)u, gk(s(\pi(g)))^{-1}))=gk(s(\pi(g)))^{-1}s'(\pi(g)u)\nonumber\\ &= gk(s(\pi(g)))^{-1}s(\pi(g))s'(u)=gks'(u)=g\phi(u,k). \end{align} $$
As
![]() $S(G)$
is the greatest G-ambit, we can conclude that
$S(G)$
is the greatest G-ambit, we can conclude that
![]() $\phi $
is an isomorphism.
$\phi $
is an isomorphism.
Because
![]() $M(H)$
is a minimal subflow of
$M(H)$
is a minimal subflow of
![]() $S(H),$
we have that
$S(H),$
we have that
![]() $M(H)\times K$
is a minimal subflow of
$M(H)\times K$
is a minimal subflow of
![]() $S(H)\times K$
, and therefore isomorphic to
$S(H)\times K$
, and therefore isomorphic to
![]() $M(G).$
$M(G).$
The following result is an immediate application of Theorem 4.1.
Theorem 5.5. Let
![]() $G\cong K\ltimes H,$
where K is compact. Then
$G\cong K\ltimes H,$
where K is compact. Then
![]() $S(G)\cong S(H)\times K$
and
$S(G)\cong S(H)\times K$
and
![]() $M(G)\cong M(H)\times K.$
$M(G)\cong M(H)\times K.$
6 Concluding remarks and questions
A natural question is whether we can prove a version of Theorem 3.8 with relaxed requirements.
If K is not normal, we can still prove that the Samuel compactification
![]() $S(G/K)$
of the quotient space
$S(G/K)$
of the quotient space
![]() $G/K$
is homeomorphic to the orbit space
$G/K$
is homeomorphic to the orbit space
![]() $S(G)/K$
, and if there is a uniformly continuous cross-section
$S(G)/K$
, and if there is a uniformly continuous cross-section
![]() $s:G/K\to G$
, then
$s:G/K\to G$
, then
![]() $S(G)$
is homeomorphic to
$S(G)$
is homeomorphic to
![]() $S(G/K)\times ~K.$
However,
$S(G/K)\times ~K.$
However,
![]() $G/K$
is not a group, so there is no notion of a
$G/K$
is not a group, so there is no notion of a
![]() $G/K$
-flow on
$G/K$
-flow on
![]() $S(G/K)$
. A natural test problem is whether Corollary 5.1 holds for all Polish t.d.l.c. groups. Among the easiest examples of Polish t.d.l.c. groups that are not SIN are groups of automorphisms of graphs of finite degree. Answering the following concrete question will likely shed light on this problem.
$S(G/K)$
. A natural test problem is whether Corollary 5.1 holds for all Polish t.d.l.c. groups. Among the easiest examples of Polish t.d.l.c. groups that are not SIN are groups of automorphisms of graphs of finite degree. Answering the following concrete question will likely shed light on this problem.
Question 6.1. What is the universal minimal flow of the group of automorphisms of a countable regular n-branching tree for
![]() $n\geq 3$
?
$n\geq 3$
?
Grosser and Moskowitz showed in [Reference Grosser and MoskowitzGrM] that a locally compact SIN group G contains a compact normal subgroup K such that
![]() $G/K$
is a Lie SIN group. To reduce computation of
$G/K$
is a Lie SIN group. To reduce computation of
![]() $M(G)$
to computation of
$M(G)$
to computation of
![]() $M(G/K)$
using methods in this paper, we would need to have a uniformly continuous cross-section
$M(G/K)$
using methods in this paper, we would need to have a uniformly continuous cross-section
![]() $G/K\to G.$
However, continuous cross-sections may not exist, even in compact groups. Using this decomposition, they showed that connected locally compact SIN groups are extensions of compact groups by vector groups
$G/K\to G.$
However, continuous cross-sections may not exist, even in compact groups. Using this decomposition, they showed that connected locally compact SIN groups are extensions of compact groups by vector groups
![]() $\mathbb {R}^n$
. More generally, they proved that every locally compact SIN group G is an extension of
$\mathbb {R}^n$
. More generally, they proved that every locally compact SIN group G is an extension of
![]() $\mathbb {R}^n\times K$
with K compact by a discrete group. It is natural to ask whether it is the case that
$\mathbb {R}^n\times K$
with K compact by a discrete group. It is natural to ask whether it is the case that
![]() $M(G)$
can be computed from
$M(G)$
can be computed from
![]() $M(H),$
where H is an extension of
$M(H),$
where H is an extension of
![]() $\mathbb {R}^n$
by a discrete group. Let us remark that
$\mathbb {R}^n$
by a discrete group. Let us remark that
![]() $M(\mathbb {R})$
was computed by Turek in [Reference TurekT3] as a quotient of
$M(\mathbb {R})$
was computed by Turek in [Reference TurekT3] as a quotient of
![]() $M(\mathbb {Z})\times [0,1],$
and his method has recently been generalized to
$M(\mathbb {Z})\times [0,1],$
and his method has recently been generalized to
![]() $M(\mathbb {R}^n)$
by Vishnubhotla (see [Reference VishnubhotlaVi]).
$M(\mathbb {R}^n)$
by Vishnubhotla (see [Reference VishnubhotlaVi]).
Acknowledgements
This research was partially supported by National Science Foundation grant no. DMS-1953955.