Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Band, Ram
and
Lévy, Guillaume
2017.
Quantum Graphs which Optimize the Spectral Gap.
Annales Henri Poincaré,
Vol. 18,
Issue. 10,
p.
3269.
Li, Yuhua
Li, Fuyi
and
Shi, Junping
2018.
Ground states of nonlinear Schrödinger equation on star metric graphs.
Journal of Mathematical Analysis and Applications,
Vol. 459,
Issue. 2,
p.
661.
Berkolaiko, Gregory
Latushkin, Yuri
and
Sukhtaiev, Selim
2019.
Limits of quantum graph operators with shrinking edges.
Advances in Mathematics,
Vol. 352,
Issue. ,
p.
632.
Leugering, Günter
2020.
Mathematical Modelling, Optimization, Analytic and Numerical Solutions.
p.
77.

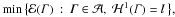 min{ℰ(
min{ℰ( 𝒟 = {
𝒟 = { 