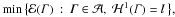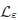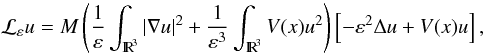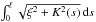Refine listing
Actions for selected content:
Contents
Research Article
A deterministic affine-quadratic optimal control problem∗
-
- Published online by Cambridge University Press:
- 21 May 2014, pp. 633-661
-
- Article
- Export citation
Shape optimization problems for metric graphs
-
- Published online by Cambridge University Press:
- 29 August 2013, pp. 1-22
-
- Article
- Export citation
On torsional rigidity and principal frequencies: an invitationto the Kohler−Jobin rearrangement technique
-
- Published online by Cambridge University Press:
- 06 February 2014, pp. 315-338
-
- Article
- Export citation
On asymptotic exit-time control problems lacking coercivity∗
-
- Published online by Cambridge University Press:
- 05 August 2014, pp. 957-982
-
- Article
- Export citation
Exact boundary synchronization for a coupled system of 1-D waveequations
-
- Published online by Cambridge University Press:
- 06 February 2014, pp. 339-361
-
- Article
- Export citation
Control of underwater vehicles in inviscidfluids: I. Irrotational flows
-
- Published online by Cambridge University Press:
- 27 May 2014, pp. 662-703
-
- Article
- Export citation
Controllability of Schrödinger equation with a nonlocalterm
-
- Published online by Cambridge University Press:
- 29 August 2013, pp. 23-41
-
- Article
- Export citation
Quasi-static rate-independent evolutions: characterization, existence, approximation and application to fracture mechanics∗
-
- Published online by Cambridge University Press:
- 04 August 2014, pp. 983-1008
-
- Article
- Export citation
Second-order sufficient conditions for strong solutions to optimal control problems∗
-
- Published online by Cambridge University Press:
- 14 March 2014, pp. 704-724
-
- Article
- Export citation
𝒞1,β regularity for Dirichlet problems associated to fully nonlineardegenerate elliptic equations
-
- Published online by Cambridge University Press:
- 13 August 2014, pp. 1009-1024
-
- Article
- Export citation
Global minimizer of the ground state for two phase conductorsin low contrast regime∗∗∗
-
- Published online by Cambridge University Press:
- 03 March 2014, pp. 362-388
-
- Article
- Export citation
Dimension reduction for −Δ1
-
- Published online by Cambridge University Press:
- 03 September 2013, pp. 42-77
-
- Article
- Export citation
Multiplicity and concentration behavior of positive solutionsfor a Schrödinger–Kirchhoff type problem via penalization method∗∗∗
-
- Published online by Cambridge University Press:
- 03 March 2014, pp. 389-415
-
- Article
- Export citation
Differential games of partial information forward-backward doubly SDE and applications∗
-
- Published online by Cambridge University Press:
- 10 October 2013, pp. 78-94
-
- Article
- Export citation
Linearized plastic plate models as Γ-limits of 3D finiteelastoplasticity
-
- Published online by Cambridge University Press:
- 27 May 2014, pp. 725-747
-
- Article
- Export citation
Relating phase field and sharp interface approaches tostructural topology optimization
-
- Published online by Cambridge University Press:
- 05 August 2014, pp. 1025-1058
-
- Article
- Export citation
Approximation of the pareto optimal set for multiobjective optimal control problems using viability kernels
-
- Published online by Cambridge University Press:
- 10 October 2013, pp. 95-115
-
- Article
- Export citation
Ground states of singularly perturbed convection-diffusionequation with oscillating coefficients
-
- Published online by Cambridge University Press:
- 04 August 2014, pp. 1059-1077
-
- Article
- Export citation
A certified reduced basis method for parametrized ellipticoptimal control problems∗
-
- Published online by Cambridge University Press:
- 07 March 2014, pp. 416-441
-
- Article
- Export citation
Curve cuspless reconstruction via sub-Riemannian geometry∗∗∗
-
- Published online by Cambridge University Press:
- 27 May 2014, pp. 748-770
-
- Article
- Export citation