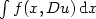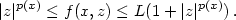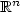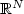Refine listing
Actions for selected content:
Contents
Research Article
Integral representation and Γ-convergence of variational integrals with p(x)-growth
-
- Published online by Cambridge University Press:
- 15 September 2002, pp. 495-519
-
- Article
- Export citation
A stability result in the localization of cavities in a thermic conducting medium
-
- Published online by Cambridge University Press:
- 15 September 2002, pp. 521-565
-
- Article
- Export citation
Stabilisation d'une poutre. Étude du taux optimalde décroissance de l'énergie élastique
-
- Published online by Cambridge University Press:
- 15 September 2002, pp. 567-595
-
- Article
- Export citation
A positive solution for an asymptotically linear elliptic problem on $\mathbb{R}^N$
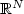 autonomous at infinity
autonomous at infinity
-
- Published online by Cambridge University Press:
- 15 September 2002, pp. 597-614
-
- Article
- Export citation