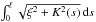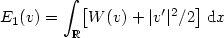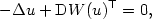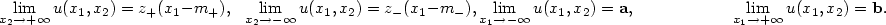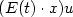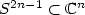Refine listing
Actions for selected content:
Most cited
This page lists all time most cited articles for this title. Please use the publication date filters on the left if you would like to restrict this list to recently published content, for example to articles published in the last three years. The number of times each article was cited is displayed to the right of its title and can be clicked to access a list of all titles this article has been cited by.
Contents
- Cited by 23
Nonlinear feedback stabilizationof a two-dimensional Burgers equation
-
- Published online by Cambridge University Press:
- 31 July 2009, pp. 929-955
-
- Article
- Export citation
- Cited by 23
Vector variational problems and applications to optimal design
-
- Published online by Cambridge University Press:
- 15 July 2005, pp. 357-381
-
- Article
- Export citation
- Cited by 23
Boundary feedback stabilization of a three-layer sandwichbeam: Riesz basis approach
-
- Published online by Cambridge University Press:
- 15 December 2005, pp. 12-34
-
- Article
- Export citation
- Cited by 23
Curve cuspless reconstruction via sub-Riemannian geometry∗∗∗
-
- Published online by Cambridge University Press:
- 27 May 2014, pp. 748-770
-
- Article
- Export citation
- Cited by 23
Adaptive finite element method for shape optimization∗
-
- Published online by Cambridge University Press:
- 16 January 2012, pp. 1122-1149
-
- Article
- Export citation
- Cited by 23
Input-to-state stability with respect to measurement disturbances for one-dimensional systems
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 99-121
-
- Article
- Export citation
- Cited by 22
Global non-negative controllability of the semilinear parabolic equation governed by bilinear control
-
- Published online by Cambridge University Press:
- 15 September 2002, pp. 269-283
-
- Article
- Export citation
- Cited by 22
Turnpike theorems by a value function approach
-
- Published online by Cambridge University Press:
- 15 February 2004, pp. 123-141
-
- Article
- Export citation
- Cited by 22
Dynamic stabilization of systems via decoupling techniques
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 577-593
-
- Article
- Export citation
- Cited by 22
Optimal control for distributed systems subjectto null-controllability. Application to discriminating sentinels
-
- Published online by Cambridge University Press:
- 05 September 2007, pp. 623-638
-
- Article
- Export citation
- Cited by 22
Asymmetric heteroclinicdouble layers
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 965-1005
-
- Article
- Export citation
- Cited by 22
The formation of a tree leaf
-
- Published online by Cambridge University Press:
- 12 May 2007, pp. 359-377
-
- Article
- Export citation
- Cited by 22
Limitations on the control of Schrödinger equations
-
- Published online by Cambridge University Press:
- 11 October 2006, pp. 615-635
-
- Article
- Export citation
- Cited by 22
Geometrical aspects of exact boundary controllability for the wave equation - anumerical study
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 163-212
-
- Article
- Export citation
- Cited by 22
Stabilization of walls for nano-wires of finite length
-
- Published online by Cambridge University Press:
- 02 December 2010, pp. 1-21
-
- Article
- Export citation
- Cited by 22
Quasistatic crack evolution for a cohesive zone modelwith different response to loading and unloading:a Young measures approach
-
- Published online by Cambridge University Press:
- 09 October 2009, pp. 1-27
-
- Article
- Export citation
- Cited by 22
Relaxation of singular functionals definedon Sobolev spaces
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 71-85
-
- Article
- Export citation
- Cited by 21
Analysis of M-stationary points to an EPEC modelingoligopolistic competition in an electricity spot market∗
-
- Published online by Cambridge University Press:
- 19 January 2011, pp. 295-317
-
- Article
- Export citation
- Cited by 21
An estimation of the controllability time forsingle-input systems on compact Lie Groups
-
- Published online by Cambridge University Press:
- 20 June 2006, pp. 409-441
-
- Article
- Export citation
- Cited by 21
Resonance of minimizers for n-level quantum systemswith an arbitrary cost
-
- Published online by Cambridge University Press:
- 15 October 2004, pp. 593-614
-
- Article
- Export citation