Article contents
Cops-on-the-dots: The linear stability of crime hotspots for a 1-D reaction-diffusion model of urban crime
Published online by Cambridge University Press: 11 November 2019
Abstract
In a singularly perturbed limit, we analyse the existence and linear stability of steady-state hotspot solutions for an extension of the 1-D three-component reaction-diffusion (RD) system formulated and studied numerically in Jones et. al. [Math. Models. Meth. Appl. Sci., 20, Suppl., (2010)], which models urban crime with police intervention. In our extended RD model, the field variables are the attractiveness field for burglary, the criminal population density and the police population density. Our model includes a scalar parameter that determines the strength of the police drift towards maxima of the attractiveness field. For a special choice of this parameter, we recover the ‘cops-on-the-dots’ policing strategy of Jones et. al., where the police mimic the drift of the criminals towards maxima of the attractiveness field. For our extended model, the method of matched asymptotic expansions is used to construct 1-D steady-state hotspot patterns as well as to derive nonlocal eigenvalue problems (NLEPs) that characterise the linear stability of these hotspot steady states to 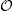 ${\cal O}$(1) timescale instabilities. For a cops-on-the-dots policing strategy, we prove that a multi-hotspot steady state is linearly stable to synchronous perturbations of the hotspot amplitudes. Alternatively, for asynchronous perturbations of the hotspot amplitudes, a hybrid analytical–numerical method is used to construct linear stability phase diagrams in the police vs. criminal diffusivity parameter space. In one particular region of these phase diagrams, the hotspot steady states are shown to be unstable to asynchronous oscillatory instabilities in the hotspot amplitudes that arise from a Hopf bifurcation. Within the context of our model, this provides a parameter range where the effect of a cops-on-the-dots policing strategy is to only displace crime temporally between neighbouring spatial regions. Our hybrid approach to study the NLEPs combines rigorous spectral results with a numerical parameterisation of any Hopf bifurcation threshold. For the cops-on-the-dots policing strategy, our linear stability predictions for steady-state hotspot patterns are confirmed from full numerical PDE simulations of the three-component RD system.
${\cal O}$(1) timescale instabilities. For a cops-on-the-dots policing strategy, we prove that a multi-hotspot steady state is linearly stable to synchronous perturbations of the hotspot amplitudes. Alternatively, for asynchronous perturbations of the hotspot amplitudes, a hybrid analytical–numerical method is used to construct linear stability phase diagrams in the police vs. criminal diffusivity parameter space. In one particular region of these phase diagrams, the hotspot steady states are shown to be unstable to asynchronous oscillatory instabilities in the hotspot amplitudes that arise from a Hopf bifurcation. Within the context of our model, this provides a parameter range where the effect of a cops-on-the-dots policing strategy is to only displace crime temporally between neighbouring spatial regions. Our hybrid approach to study the NLEPs combines rigorous spectral results with a numerical parameterisation of any Hopf bifurcation threshold. For the cops-on-the-dots policing strategy, our linear stability predictions for steady-state hotspot patterns are confirmed from full numerical PDE simulations of the three-component RD system.
Keywords
MSC classification
Information
- Type
- Papers
- Information
- Copyright
- © Cambridge University Press 2019
References
- 12
- Cited by


