Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Silberstein, Natalia
Etzion, Tuvi
and
Schwartz, Moshe
2017.
Locality and availability of array codes constructed from subspaces.
p.
829.
Braun, Michael
Kiermaier, Michael
Kohnert, Axel
and
Laue, Reinhard
2017.
Large sets of subspace designs.
Journal of Combinatorial Theory, Series A,
Vol. 147,
Issue. ,
p.
155.
Heinlein, Daniel
and
Kurz, Sascha
2017.
Coding Theory and Applications.
Vol. 10495,
Issue. ,
p.
163.
Arias, Francisco
de la Cruz, Javier
Rosenthal, Joachim
and
Willems, Wolfgang
2018.
On q-Steiner systems from rank metric codes.
Discrete Mathematics,
Vol. 341,
Issue. 10,
p.
2729.
Kiermaier, Michael
Kurz, Sascha
and
Wassermann, Alfred
2018.
The order of the automorphism group of a binary
$${\varvec{q}}$$
q
-analog of the Fano plane is at most two.
Designs, Codes and Cryptography,
Vol. 86,
Issue. 2,
p.
239.
Braun, Michael
and
Wassermann, Alfred
2018.
Disjoint q -Steiner systems in dimension 13.
Electronic Notes in Discrete Mathematics,
Vol. 65,
Issue. ,
p.
23.
Gnilke, Oliver Wilhelm
Greferath, Marcus
and
Pavčević, Mario Osvin
2018.
Mosaics of combinatorial designs.
Designs, Codes and Cryptography,
Vol. 86,
Issue. 1,
p.
85.
Otal, Kamil
and
Özbudak, Ferruh
2018.
Network Coding and Subspace Designs.
p.
43.
Xu, Liqing
and
Chen, Hao
2018.
New Constant-Dimension Subspace Codes from Maximum Rank Distance Codes.
IEEE Transactions on Information Theory,
Vol. 64,
Issue. 9,
p.
6315.
Braun, Michael
Kiermaier, Michael
and
Wassermann, Alfred
2018.
Network Coding and Subspace Designs.
p.
171.
Heinlein, Daniel
Honold, Thomas
Kiermaier, Michael
Kurz, Sascha
and
Wassermann, Alfred
2019.
Classifying optimal binary subspace codes of length 8, constant dimension 4 and minimum distance 6.
Designs, Codes and Cryptography,
Vol. 87,
Issue. 2-3,
p.
375.
Silberstein, Natalia
Etzion, Tuvi
and
Schwartz, Moshe
2019.
Locality and Availability of Array Codes Constructed From Subspaces.
IEEE Transactions on Information Theory,
Vol. 65,
Issue. 5,
p.
2648.
Buratti, Marco
and
Nakić, Anamari
2019.
Designs over finite fields by difference methods.
Finite Fields and Their Applications,
Vol. 57,
Issue. ,
p.
128.
Byrne, Eimear
and
Ravagnani, Alberto
2019.
An Assmus--Mattson Theorem for Rank Metric Codes.
SIAM Journal on Discrete Mathematics,
Vol. 33,
Issue. 3,
p.
1242.
Buratti, Marco
and
Merola, Francesca
2019.
Fano Kaleidoscopes and their generalizations.
Designs, Codes and Cryptography,
Vol. 87,
Issue. 4,
p.
769.
Etzion, Tuvi
and
Zhang, Hui
2019.
Grassmannian Codes With New Distance Measures for Network Coding.
IEEE Transactions on Information Theory,
Vol. 65,
Issue. 7,
p.
4131.
Etzion, Tuvi
Kurz, Sascha
Otal, Kamil
and
Özbudak, Ferruh
2020.
Subspace packings: constructions and bounds.
Designs, Codes and Cryptography,
Vol. 88,
Issue. 9,
p.
1781.
Chen, Hao
He, Xianmang
Weng, Jian
and
Xu, Liqing
2020.
New Constructions of Subspace Codes Using Subsets of MRD Codes in Several Blocks.
IEEE Transactions on Information Theory,
Vol. 66,
Issue. 9,
p.
5317.
Wang, Gang
Niu, Min-Yao
and
Fu, Fang-Wei
2020.
Deterministic construction of compressed sensing matrices from constant dimension codes.
Discrete Applied Mathematics,
Vol. 285,
Issue. ,
p.
9.
Potapov, V. N.
and
Avgustinovich, S. V.
2020.
Combinatorial Designs, Difference Sets, and Bent Functions as Perfect Colorings of Graphs and Multigraphs.
Siberian Mathematical Journal,
Vol. 61,
Issue. 5,
p.
867.
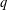 $q$-ANALOGS OF STEINER SYSTEMS
$q$-ANALOGS OF STEINER SYSTEMS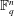 $\mathbb{F}_{q}^{n}$ be a vector space of dimension
$\mathbb{F}_{q}^{n}$ be a vector space of dimension  $n$ over the finite field
$n$ over the finite field 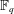 $\mathbb{F}_{q}$. A
$\mathbb{F}_{q}$. A 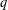 $q$-analog of a Steiner system (also known as a
$q$-analog of a Steiner system (also known as a 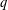 $q$-Steiner system), denoted
$q$-Steiner system), denoted 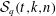 ${\mathcal{S}}_{q}(t,\!k,\!n)$, is a set
${\mathcal{S}}_{q}(t,\!k,\!n)$, is a set 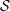 ${\mathcal{S}}$ of
${\mathcal{S}}$ of 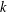 $k$-dimensional subspaces of
$k$-dimensional subspaces of 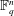 $\mathbb{F}_{q}^{n}$ such that each
$\mathbb{F}_{q}^{n}$ such that each  $t$-dimensional subspace of
$t$-dimensional subspace of 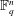 $\mathbb{F}_{q}^{n}$ is contained in exactly one element of
$\mathbb{F}_{q}^{n}$ is contained in exactly one element of 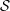 ${\mathcal{S}}$. Presently,
${\mathcal{S}}$. Presently, 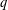 $q$-Steiner systems are known only for
$q$-Steiner systems are known only for 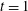 $t\,=\,1\!$, and in the trivial cases
$t\,=\,1\!$, and in the trivial cases 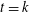 $t\,=\,k$ and
$t\,=\,k$ and 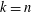 $k\,=\,n$. In this paper, the first nontrivial
$k\,=\,n$. In this paper, the first nontrivial 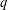 $q$-Steiner systems with
$q$-Steiner systems with 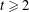 $t\,\geqslant \,2$ are constructed. Specifically, several nonisomorphic
$t\,\geqslant \,2$ are constructed. Specifically, several nonisomorphic 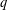 $q$-Steiner systems
$q$-Steiner systems 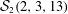 ${\mathcal{S}}_{2}(2,3,13)$ are found by requiring that their automorphism groups contain the normalizer of a Singer subgroup of
${\mathcal{S}}_{2}(2,3,13)$ are found by requiring that their automorphism groups contain the normalizer of a Singer subgroup of 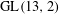 $\text{GL}(13,2)$. This approach leads to an instance of the exact cover problem, which turns out to have many solutions.
$\text{GL}(13,2)$. This approach leads to an instance of the exact cover problem, which turns out to have many solutions.