Hostname: page-component-5db58dd55d-jnbmb Total loading time: 0 Render date: 2026-06-10T07:04:00.507Z Has data issue: false hasContentIssue false
  • English
  • Français

SIMPLE GROUPS STABILIZING POLYNOMIALS

Part of: Basic linear algebra Linear algebraic groups and related topics

Published online by Cambridge University Press:  15 June 2015

SKIP GARIBALDI  and
ROBERT M. GURALNICK
SKIP GARIBALDI
Affiliation:
Institute for Pure and Applied Mathematics, UCLA, 460 Portola Plaza, Box 957121, Los Angeles, CA 90095-7121, USA; skip@member.ams.org
ROBERT M. GURALNICK
Affiliation:
Department of Mathematics, University of Southern California, Los Angeles, CA 90089-2532, USA; guralnic@usc.edu

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the 'Save PDF' action button.

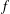We study the problem of determining, for a polynomial function $f$ on a vector space 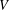$V$, the linear transformations 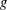$g$ of 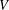$V$ such that 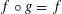$f\circ g=f$. When 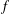$f$ is invariant under a simple algebraic group 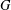$G$ acting irreducibly on 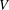$V$, we note that the subgroup of 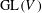$\text{GL}(V)$ stabilizing 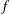$f$ often has identity component 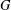$G$, and we give applications realizing various groups, including the largest exceptional group 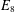$E_{8}$, as automorphism groups of polynomials and algebras. We show that, starting with a simple group 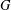$G$ and an irreducible representation 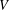$V$, one can almost always find an 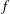$f$ whose stabilizer has identity component 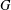$G$, and that no such 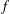$f$ exists in the short list of excluded cases. This relies on our core technical result, the enumeration of inclusions $G<H\leqslant \text{SL}(V)$ such that 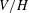$V/H$ has the same dimension as 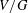$V/G$. The main results of this paper are new even in the special case where 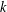$k$ is the complex numbers.

MSC classification

Primary: 20G15: Linear algebraic groups over arbitrary fields
Secondary: 15A72: Vector and tensor algebra, theory of invariants 20G41: Exceptional groups

Information

Type
Research Article
Information
Forum of Mathematics, Pi , Volume 3 , 2015 , e3
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/3.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2015

References

Andreev, E. M., Vinberg, E. B. and Elashvili, A. G., ‘Orbits of greatest dimension in semi-simple linear Lie groups’, Funct. Anal. Appl. 1 (1968), 257–261.CrossRefGoogle Scholar
Azad, H., Barry, M. and Seitz, G., ‘On the structure of parabolic subgroups’, Comm. Algebra 18(2) (1990), 551–562.Google Scholar
Bate, M., Martin, B. and Röhrle, G., ‘A geometric approach to complete reducibility’, Invent. Math. 161(1) (2005), 177–218.Google Scholar
Bermudez, H., Garibaldi, S. and Larsen, V., ‘Linear preservers and representations with a 1-dimensional ring of invariants’, Trans. Amer. Math. Soc. 366 (2014), 4755–4780. doi:10.1090/S0002-9947-2014-06081-9.Google Scholar
Bermudez, H. and Ruozzi, A., ‘Classifying simple groups via their invariant polynomials’, J. Algebra 424 (2015), 448–463. doi:10.1016/j.jalgebra.2014.08.057.Google Scholar
Block, R. E. and Zassenhaus, H., ‘The Lie algebras with a nondegenerate trace form’, Illinois J. Math. 8 (1964), 543–549.CrossRefGoogle Scholar
Borel, A. and Tits, J., ‘Groupes réductifs’, Publ. Math. Inst. Hautes Études Sci. 27 (1965), 55–150.CrossRefGoogle Scholar
Borel, A. and Tits, J., ‘Compléments à l’article: Groupes réductifs’, Publ. Math. Inst. Hautes Études Sci. 41 (1972), 253–276.Google Scholar
Borel, A. and Tits, J., ‘Homomorphismes “abstraits” de groupes algébriques simples’, Ann. of Math. (2) 97 (1973), 499–571.CrossRefGoogle Scholar
Borthwick, D. and Garibaldi, S., ‘Did a 1-dimensional magnet detect a 248-dimensional algebra?’, Notices Amer. Math. Soc. 58(8) (2011), 1055–1066.Google Scholar
Bourbaki, N., Lie Groups and Lie Algebras (Springer, Berlin, 2005).Google Scholar
Cartan, E., ‘Sur la structure des groupes de transformations finis et continus’, Thesis, Paris (1894); 2nd edn, Vuibert, 1933 ($=$ Oe, part 1, vol 1 (1952), 137–287).Google Scholar
Cartan, E., ‘Les groupes réels simples et continus’, Ann. É. Norm. Supér. 31 (1914), 263–355.CrossRefGoogle Scholar
Cederwall, M. and Palmkvist, J., ‘The octic E 8 invariant’, J. Math. Phys. (2007), 073505.CrossRefGoogle Scholar
Chen, Z. J., ‘A new prehomogeneous vector space of characteristic p’, Chin. Ann. Math. Ser. B 8(1) (1987), 22–35.Google Scholar
Chevalley, C. and Schafer, R. D., ‘The exceptional simple Lie algebras F 4 and E 6’, Proc. Natl Acad. Sci. USA 36 (1950), 137–141.CrossRefGoogle ScholarPubMed
Cohen, A. M. and Wales, D. B., ‘GL (4)-orbits in a 16-dimensional module for characteristic 3’, J. Algebra 185 (1996), 85–107.CrossRefGoogle Scholar
Coldea, R., Tennant, D. A., Wheeler, E. M., Wawrzynska, E., Prabhakaran, D., Telling, M., Habicht, K., Smibidl, P. and Kiefer, K., ‘Quantum criticality in an Ising chain: experimental evidence for emergent E 8 symmetry’, Science 327 (2010), 177–180.Google Scholar
Conrad, B., Gabber, O. and Prasad, G., Pseudo-Reductive Groups (Cambridge University Press, Cambridge, 2010).CrossRefGoogle Scholar
Demazure, M., ‘Invariants symétriques entiers des groupes de Weyl et torsion’, Invent. Math. 21 (1973), 287–301.CrossRefGoogle Scholar
Demazure, M., ‘Automorphismes et déformations des variétés de Borel’, Invent. Math. 39(2) (1977), 179–186.CrossRefGoogle Scholar
Demazure, M. and Grothendieck, A., Schémas en groupes, (Société Mathématique de France, 2011), re-edition edited by P. Gille and P. Polo.Google Scholar
Dieudonné, J. A., ‘Sur une généralisation du groupe orthogonal à quatre variables’, Arch. Math. 1 (1949), 282–287.Google Scholar
Dixmier, J., ‘Champs de vecteurs adjoints sur les groupes et algèbres de Lie semisimples’, J. reine angew. Math. 309 (1979), 183–190.Google Scholar
Grothendieck, A., ‘Éléments de géométrie algébrique IV. Etude locale des schémas et des morphismes de schémas, Troisième partie’, Publ. Math. Inst. Hautes Études Sci. 28 (1966), 5–255.Google Scholar
Engel, F., ‘Ein neues, dem linearen Komplexe analoges Gebilde’, Berichte über die Verhandlungen der Königlich Sächsischen Gesellschaft der Wissenschaften zu Leipzig. Math.-Phys. Kl. 52 (1900), 63–76. 220–239.Google Scholar
Freudenthal, H., ‘Sur le groupe exceptionnel E 7’, Nederl. Akad. Wetensch. Proc. Ser. A 56 = Indagationes Math. 15 (1953), 81–89.CrossRefGoogle Scholar
Frobenius, G., ‘Über die Darstellung der endlichen Gruppen durch lineare Substitutionen’, Sitzungsberichte Deutsch. Akad. Wiss. Berlin (1897), 994–1015.Google Scholar
Garibaldi, S. and Saltman, D. J., ‘Quaternion algebras with the same subfields’, inQuadratic Forms, Linear Algebraic Groups, and Cohomology, Developments in Mathematics, 18 (Springer, New York, 2010), 225–238.CrossRefGoogle Scholar
Goldstein, D. and Guralnick, R., ‘Alternating forms and self-adjoint operators’, J. Algebra 308(1) (2007), 330–349.Google Scholar
Gordeev, N. L. and Popov, V. L., ‘Automorphism groups of finite dimensional simple algebras’, Ann. of Math. (2) 158(3) (2003), 1041–1065.CrossRefGoogle Scholar
Guralnick, R. M., Liebeck, M. W., Macpherson, D. and Seitz, G. M., ‘Modules for algebraic groups with finitely many orbits on subspaces’, J. Algebra 196 (1997), 211–250.Google Scholar
Helenius, F., ‘Freudenthal triple systems by root system methods’, J. Algebra 357 (2012), 116–137.Google Scholar
Hiss, G., ‘Die adjungierten Darstellungen der Chevalley–Gruppen’, Arch. Math. (Basel) 42 (1984), 408–416.Google Scholar
Hoffmann, D. W., ‘On Elman and Lam’s filtration of the u-invariant’, J. reine angew. Math. 495 (1998), 175–186.Google Scholar
Hoffmann, D. W., ‘Pythagoras numbers of fields’, J. Amer. Math. Soc. 12(3) (1999), 839–848.Google Scholar
Hoffmann, D. W., ‘Isotropy of quadratic forms and field invariants’, inQuadratic Forms and their Applications (Dublin, 1999), Contemporary Mathematics, 272 (American Mathematical Society, Providence, RI, 2000), 73–102.CrossRefGoogle Scholar
Hogeweij, G. M. D., ‘Almost-classical Lie algebras. I, II’, Nederl. Akad. Wetensch. Indag. Math. 44(4) (1982), 441–460.CrossRefGoogle Scholar
Igusa, J.-I., ‘A classification of spinors up to dimension twelve’, Amer. J. Math. 92 (1970), 997–1028.Google Scholar
Izhboldin, O. T., ‘Fields of u-invariant 9’, Ann. of Math. (2) 154(3) (2001), 529–587.Google Scholar
Jacobson, N., ‘Some groups of transformations defined by Jordan algebras I’, J. reine angew. Math. 201 (1959), 178–195. ($=$ Coll. Math. Papers 63).Google Scholar
Kac, V. G., ‘Some remarks on nilpotent orbits’, J. Algebra 64 (1980), 190–213.Google Scholar
Kac, V. G., Popov, V. L. and Vinberg, E. B., ‘Sur les groupes linéaires algébriques dont l’algèbre des invariants est libre’, C. R. Acad. Sci. Paris A–B 283(12) (1976), A875–A878.Google Scholar
Kac, V. and Weisfeiler, B., ‘Coadjoint action of a semi-simple algebraic group and the center of the enveloping algebra in characteristic p’, Nederl. Akad. Wetensch. Proc. Ser. A 79 = Indag. Math. 38(2) (1976), 136–151.Google Scholar
Kemper, G. and Malle, G., ‘The finite irreducible linear groups with polynomial ring of invariants’, Transform. Groups 2(1) (1997), 57–89.Google Scholar
Kenneally, D. J., ‘On eigenvectors for semisimple elements in actions of algebraic groups’, PhD Thesis, University of Cambridge, 2010.Google Scholar
Killing, W., ‘Die Zusammensetzung der stetigen endlichen Transformationsgruppen. Zweiter Theil’, Math. Ann. 33 (1889), 1–48.CrossRefGoogle Scholar
Knus, M.-A., Merkurjev, A. S., Rost, M. and Tignol, J.-P., The Book of Involutions, Colloquium Publications, 44 (American Mathematical Society, Providence, RI, 1998).Google Scholar
Lemire, N., ‘Essential dimension of algebraic groups and integral representations of Weyl groups’, Transform. Groups 9(4) (2004), 337–379.CrossRefGoogle Scholar
Levy, P., ‘Vinberg’s 𝜃-groups in positive characteristic and Kostant–Weierstrass slices’, Transform. Groups 14(2) (2009), 417–461.Google Scholar
Liebeck, M. W., ‘The affine permutation groups of rank three’, Proc. Lond. Math. Soc. (3) 54(3) (1987), 477–516.Google Scholar
Liebeck, M. W. and Seitz, G. M., ‘The maximal subgroups of positive dimension in exceptional algebraic groups’, Mem. Amer. Math. Soc. 169(802) (2004), vi+227.Google Scholar
Lübeck, F., ‘Small degree representations of finite Chevalley groups in defining characteristic’, LMS J. Comput. Math. 4 (2001), 135–169.Google Scholar
Lurie, J., ‘On simply laced Lie algebras and their minuscule representations’, Comment. Math. Helv. 76 (2001), 515–575.Google Scholar
Luzgarev, A. Yu., ‘Fourth-degree invariants for G (E 7, R) not depending on the characteristic’, Vestnik St. Petersburg Univ. Math. 46(1) (2013), 29–34.Google Scholar
Martin, B., ‘Reductive subgroups of reductive groups in nonzero characteristic’, J. Algebra 262(2) (2003), 265–286.Google Scholar
Martin, B., ‘Conjugacy classes of maximal subgroups of a reductive algebraic group’, Preprint, 2013.Google Scholar
Matzri, E. and Vishne, U., ‘Composition algebras and cyclic p-algebras in characteristic 3’, Manuscripta Math. 143 (2014), 1–18.Google Scholar
Mehta, M. L., ‘Basic sets of invariant polynomials for finite reflection groups’, Comm. Algebra 16(5) (1988), 1083–1098.Google Scholar
Merkurjev, A., ‘Simple algebras and quadratic forms’, Math. USSR Izv. 38(1) (1992), 215–221.Google Scholar
Meyer, J. S., ‘A division algebra with infinite genus’, Bull. Lond. Math. Soc. 46(3) (2014), 463–468. doi:10.1112/blms/bdt104.CrossRefGoogle Scholar
Mulmuley, K. D. and Sohoni, M., ‘Geometric complexity theory I: an approach to the P vs. NP and related problems’, SIAM J. Comput. 31 (2001), 496–526.CrossRefGoogle Scholar
Nakajima, H., ‘Invariants of finite groups generated by pseudoreflections in positive characteristic’, Tsukuba J. Math. 3(1) (1979), 109–122.Google Scholar
Popov, V. L., ‘Classification of spinors of dimension 14’, Trans. Moscow Math. Soc. (1) (1980), 181–232.Google Scholar
Popov, V. L., Groups, Generators, Syzygies, and Orbits in Invariant Theory, Translations of Mathematical Monographs, 100 (American Mathematical Society, Providence, RI, 1992).Google Scholar
Popov, V. L. and Vinberg, E. B., Invariant Theory, Encyclopedia of Mathematical Sciences, 55 (Springer, 1994), 123–284.Google Scholar
Premet, A. A., ‘Inner ideals in modular Lie algebras’, Vestsi Akad. Navuk BSSR Ser. Fiz.-Mat. Navuk (5) (1986), 11–15. 123.Google Scholar
Premet, A. A., ‘Lie algebras without strong degeneration’, Math. USSR Sb. 57(1) (1987), 151–164.Google Scholar
Reichstein, Z., ‘Essential dimension’, inProceedings of the International Congress of Mathematicians, Vol. II (Hindustan Book Agency, New Delhi, 2010), 162–188.Google Scholar
Reichstein, Z., ‘What is …essential dimension?’, Not. AMS 59(10) (2012), 1432–1434.Google Scholar
Richardson, R. W., ‘Affine coset spaces of reductive algebraic groups’, Bull. Lond. Math. Soc. 9(1) (1977), 38–41.Google Scholar
Richardson, R. W., ‘Conjugacy classes of n-tuples in Lie algebras and algebraic groups’, Duke Math. J. 57 (1988), 1–35.Google Scholar
Rosenlicht, M., ‘Some basic theorems on algebraic groups’, Amer. J. Math. 78 (1956), 401–443.Google Scholar
Rubenthaler, H., ‘Non-parabolic prehomogeneous vector spaces and exceptional Lie algebras’, J. Algebra 281(1) (2004), 366–394.Google Scholar
Rudakov, A. N., ‘Deformations of simple Lie algebras’, Math. USSR Izv. 5(5) (1971), 1120–1126.CrossRefGoogle Scholar
Saito, K., ‘On a linear structure of the quotient variety by a finite reflexion group’, Publ. RIMS 29 (1993), 535–579. text written in 1979.CrossRefGoogle Scholar
Saito, K., Yano, T. and Sekiguchi, J., ‘On a certain generator system of the ring of invariants of a finite reflection group’, Comm. Algebra 8(4) (1980), 373–408.CrossRefGoogle Scholar
Sato, M. and Kimura, T., ‘A classification of irreducible prehomogeneous vector spaces and their relative invariants’, Nagoya Math. J. 65 (1977), 1–155.CrossRefGoogle Scholar
Schwarz, G. W., ‘Representations of simple Lie groups with regular rings of invariants’, Invent. Math. 49(2) (1978), 167–191.CrossRefGoogle Scholar
Schwarz, G. W., ‘Linear maps preserving invariants’, Proc. Amer. Math. Soc. 136(12) (2008), 4197–4200.CrossRefGoogle Scholar
Seitz, G. M., ‘The maximal subgroups of classical algebraic groups’, Mem. Amer. Math. Soc. 67(365) (1987), iv+286.Google Scholar
Seshadri, C. S., ‘Geometric reductivity over arbitrary base’, Adv. Math. 26 (1977), 225–274.CrossRefGoogle Scholar
Skryabin, S., ‘Invariants of finite group schemes’, J. Lond. Math. Soc. (2) 65(2) (2002), 339–360.CrossRefGoogle Scholar
Solomon, S., ‘Irreducible linear group-subgroup pairs with the same invariants’, J. Lie Theory 15 (2005), 105–123.Google Scholar
Springer, T. A., Linear Algebraic Groups, second edn, (Birkhäuser, Boston, MA, 1998).CrossRefGoogle Scholar
Springer, T. A. and Steinberg, R., ‘Conjugacy classes’, inSeminar on Algebraic Groups and Related Finite Groups (The Institute for Advanced Study, Princeton, NJ, 1968/69), Lecture Notes in Mathematics, 131 (Springer, Berlin, 1970), 167–266.CrossRefGoogle Scholar
Steinberg, R., ‘Automorphisms of classical Lie algebras’, Pacific J. Math. 11 (1961), 1119–1129. ($=$ Collected Papers, pp. 101–111).CrossRefGoogle Scholar
Steinberg, R., ‘Representations of algebraic groups’, Nagoya Math. J. 22 (1963), 33–56. ($=$ Collected Papers, pp. 149–172).Google Scholar
Talamini, V., ‘Flat bases of invariant polynomials and P̂-matrices of E 7 and E 8’, J. Math. Phys. 51 (2010), 023520.Google Scholar
Tits, J., ‘Représentations linéaires irréductibles d’un groupe réductif sur un corps quelconque’, J. reine angew. Math. 247 (1971), 196–220.Google Scholar
Tits, J., Buildings of Spherical Type and Finite BN-Pairs, Lecture Notes in Mathematics, 386 (Springer, New York, 1974).Google Scholar
Vinberg, E. B., ‘The Weyl group of a graded Lie algebra’, Math. USSR Izv. 10 (1976), 463–495.CrossRefGoogle Scholar