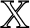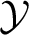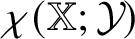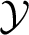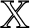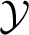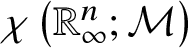1 Introduction
Ramsey theory is a central part of modern combinatorics with many connections to other areas, such as logic, number theory and computer science. Its topic is to find homogeneous substructures in sufficiently large or dense structures. The early examples include Schur's lemma, van der Waerden's theorem and Ramsey's theorem. We refer the reader to the classical book [Reference Graham, Rothschild and Spencer12] for a survey of early developments of Ramsey theory.
Most early results were concerned with finding homogeneous substructures in combinatorial structures (such as monochromatic complete subgraphs in any two-colouring of edges of a large complete graph). The problems we are interested in in this article are of geometric nature.
In 1950, Nelson posed the following question: What is the minimal number of colours needed to colour all points of the Euclidean plane ![]() $\mathbb {R}^2$ such that no two points at unit distance apart receive the same colour? This quantity is called the chromatic number of the plane and is denoted by
$\mathbb {R}^2$ such that no two points at unit distance apart receive the same colour? This quantity is called the chromatic number of the plane and is denoted by ![]() $\chi ( \mathbb {R}^2) $. This problem received great interest from the mathematics community, and even the origins of the questions spurred heated debates, partly because Nelson asked his question in private communication. We refer to the book of Soifer [Reference Soifer33] and surveys of Raigorodskii [Reference Raigorodskii26, Reference Raigorodskii28] for a comprehensive account of the problem.
$\chi ( \mathbb {R}^2) $. This problem received great interest from the mathematics community, and even the origins of the questions spurred heated debates, partly because Nelson asked his question in private communication. We refer to the book of Soifer [Reference Soifer33] and surveys of Raigorodskii [Reference Raigorodskii26, Reference Raigorodskii28] for a comprehensive account of the problem.
For almost 70 years, the problem resisted attacks from numerous researchers, and the state of the art was at the easy-to-get lower and upper bounds ![]() $4\leq \chi ({{\mathbb R}}^2)\leq 7$ due to Nelson and Isbell, respectively (or due to Mosers [Reference Moser and Moser20] and Hadwiger [Reference Hadwiger13]; see the Soifer’s historical research [Reference Soifer33]). Recently, the combinatorics community was shaken when an amateur mathematician, de Grey [Reference de Grey4], improved the lower bound to
$4\leq \chi ({{\mathbb R}}^2)\leq 7$ due to Nelson and Isbell, respectively (or due to Mosers [Reference Moser and Moser20] and Hadwiger [Reference Hadwiger13]; see the Soifer’s historical research [Reference Soifer33]). Recently, the combinatorics community was shaken when an amateur mathematician, de Grey [Reference de Grey4], improved the lower bound to ![]() $\chi ({{\mathbb R}}^2)\geq 5$. A few weeks later, Exoo and Ismailescu [Reference Exoo and Ismailescu9] gave another proof of this bound. Since then, the initial de Grey’s construction has been simplified several times within the framework of the Polymath16 Project (the current record is due to Parts [Reference Parts22]).
$\chi ({{\mathbb R}}^2)\geq 5$. A few weeks later, Exoo and Ismailescu [Reference Exoo and Ismailescu9] gave another proof of this bound. Since then, the initial de Grey’s construction has been simplified several times within the framework of the Polymath16 Project (the current record is due to Parts [Reference Parts22]).
One natural generalisation of Nelson’s problem concerns chromatic numbers of Euclidean spaces of other dimensions. One can find the current best lower and upper bounds on ![]() $\chi (\mathbb {R}^n)$ for several small values of n in [Reference Bogoliubsky and Raigorodskii1, Reference Cherkashin, Kulikov and Raigorodskii3]. As for n large, Frankl and Wilson [Reference Frankl and Wilson11] showed that the function
$\chi (\mathbb {R}^n)$ for several small values of n in [Reference Bogoliubsky and Raigorodskii1, Reference Cherkashin, Kulikov and Raigorodskii3]. As for n large, Frankl and Wilson [Reference Frankl and Wilson11] showed that the function ![]() $\chi ( \mathbb {R}^n) $ grows exponentially with n. The best known asymptotic lower and upper bounds are
$\chi ( \mathbb {R}^n) $ grows exponentially with n. The best known asymptotic lower and upper bounds are ![]() $\left (1.239...+o(1)\right )^n \leq \chi (\mathbb {R}^n) \leq \left (3+o(1)\right )^n$ as
$\left (1.239...+o(1)\right )^n \leq \chi (\mathbb {R}^n) \leq \left (3+o(1)\right )^n$ as ![]() $n \rightarrow \infty $ (see Larman and Rogers [Reference Larman and Rogers17] or Prosanov [Reference Prosanov23] for the upper bound and Raigorodskii [Reference Raigorodskii25] for the lower bound).
$n \rightarrow \infty $ (see Larman and Rogers [Reference Larman and Rogers17] or Prosanov [Reference Prosanov23] for the upper bound and Raigorodskii [Reference Raigorodskii25] for the lower bound).
A systematic study of such questions on the interface of geometry and Ramsey theory, named Euclidean Ramsey theory, began with three papers [Reference Erdős, Graham, Montgomery, Rothschild, Spencer and Straus5, Reference Erdős, Graham, Montgomery, Rothschild, Spencer and Straus6, Reference Erdős, Graham, Montgomery, Rothschild, Spencer and Straus7] of Erdős, Graham, Montgomery, Rothschild, Spencer and Straus. Given a subset ![]() $S \subset \mathbb {R}^d$ (with induced metric), the value
$S \subset \mathbb {R}^d$ (with induced metric), the value ![]() $\chi ( \mathbb {R}^n; S)$ is defined to be the minimum number of colours needed to colour all points of Euclidean space
$\chi ( \mathbb {R}^n; S)$ is defined to be the minimum number of colours needed to colour all points of Euclidean space ![]() $\mathbb {R}^n$ with no monochromatic isometric copy
$\mathbb {R}^n$ with no monochromatic isometric copy ![]() $S' \subset \mathbb {R}^n$ of S. Note this this definition only makes sense if
$S' \subset \mathbb {R}^n$ of S. Note this this definition only makes sense if ![]() $|S|\ge 2$. In this case, the value
$|S|\ge 2$. In this case, the value ![]() $\chi ( \mathbb {R}^n; S)$ is well defined; that is, the corresponding minimum always exists, because we trivially have
$\chi ( \mathbb {R}^n; S)$ is well defined; that is, the corresponding minimum always exists, because we trivially have ![]() $\chi ( \mathbb {R}^n; S) \le \chi (\mathbb {R}^n)$.
$\chi ( \mathbb {R}^n; S) \le \chi (\mathbb {R}^n)$.
A set ![]() $S \subset \mathbb {R}^d$ is called
$S \subset \mathbb {R}^d$ is called ![]() $\ell _2-$Ramsey if
$\ell _2-$Ramsey if ![]() $\chi ( \mathbb {R}^n; S) $ tends to infinity as
$\chi ( \mathbb {R}^n; S) $ tends to infinity as ![]() $n \rightarrow \infty $. Similarly, a set S is called exponentially
$n \rightarrow \infty $. Similarly, a set S is called exponentially ![]() $\ell _2-$Ramsey if there is a constant
$\ell _2-$Ramsey if there is a constant ![]() $\chi _S> 1$ such that
$\chi _S> 1$ such that ![]() $\chi ( \mathbb {R}^n; S)> \left ( \chi _S+o(1)\right )^n$ as
$\chi ( \mathbb {R}^n; S)> \left ( \chi _S+o(1)\right )^n$ as ![]() $n \rightarrow \infty $. Relatively few sets are known to be exponentially
$n \rightarrow \infty $. Relatively few sets are known to be exponentially ![]() $\ell _2-$Ramsey. Frankl and Rödl [Reference Frankl and Rödl10] proved that the vertex sets of simplices and bricks (or hyperrectangles) are exponentially
$\ell _2-$Ramsey. Frankl and Rödl [Reference Frankl and Rödl10] proved that the vertex sets of simplices and bricks (or hyperrectangles) are exponentially ![]() $\ell _2-$Ramsey. One can find several explicit exponential lower and upper bounds for these sets in [Reference Naslund21, Reference Prosanov24, Reference Sagdeev29, Reference Sagdeev30, Reference Sagdeev and Raigorodskii31]. More sets are known to have a weaker property of being
$\ell _2-$Ramsey. One can find several explicit exponential lower and upper bounds for these sets in [Reference Naslund21, Reference Prosanov24, Reference Sagdeev29, Reference Sagdeev30, Reference Sagdeev and Raigorodskii31]. More sets are known to have a weaker property of being ![]() $\ell _2-$Ramsey. Kříž [Reference Kříž14] proved that each ‘fairly symmetric’ set is
$\ell _2-$Ramsey. Kříž [Reference Kříž14] proved that each ‘fairly symmetric’ set is ![]() $\ell _2-$Ramsey. Later, this was used by him [Reference Kříž15] and Cantwell [Reference Cantwell2] to show that the set of vertices of each regular polytope is
$\ell _2-$Ramsey. Later, this was used by him [Reference Kříž15] and Cantwell [Reference Cantwell2] to show that the set of vertices of each regular polytope is ![]() $\ell _2-$Ramsey. Note that it is unknown whether there is an
$\ell _2-$Ramsey. Note that it is unknown whether there is an ![]() $\ell _2-$Ramsey set that is not exponentially
$\ell _2-$Ramsey set that is not exponentially ![]() $\ell _2-$Ramsey.
$\ell _2-$Ramsey.
At the same time, we know a strong necessary condition for a set to be ![]() $\ell _2-$Ramsey. Erdős et al. showed that each
$\ell _2-$Ramsey. Erdős et al. showed that each ![]() $\ell _2-$Ramsey set must be finite [Reference Erdős, Graham, Montgomery, Rothschild, Spencer and Straus6] and spherical [Reference Erdős, Graham, Montgomery, Rothschild, Spencer and Straus5]; that is, be isometric to a subset of a sphere of some dimension. There is a popular conjecture stating that this is also sufficient. There is also a ‘rival’ conjecture proposed in [Reference Leader, Russell and Walters18] that states that only so-called subtransitive sets are
$\ell _2-$Ramsey set must be finite [Reference Erdős, Graham, Montgomery, Rothschild, Spencer and Straus6] and spherical [Reference Erdős, Graham, Montgomery, Rothschild, Spencer and Straus5]; that is, be isometric to a subset of a sphere of some dimension. There is a popular conjecture stating that this is also sufficient. There is also a ‘rival’ conjecture proposed in [Reference Leader, Russell and Walters18] that states that only so-called subtransitive sets are ![]() $\ell _2-$Ramsey.
$\ell _2-$Ramsey.
Another direction for generalisations that was explored is to work with other metrics than the Euclidean one. The natural candidates are the ![]() $\ell _p-$metrics, defined for
$\ell _p-$metrics, defined for ![]() $\mathbf {x}, \mathbf {y} \in \mathbb {R}^n$ by
$\mathbf {x}, \mathbf {y} \in \mathbb {R}^n$ by  $\|\mathbf {x}-\mathbf {y}\|_{p} = (\left |x_1-y_1\right |^p+\dots +\left |x_n-y_n\right |^p)^{1/p}$, or the Chebyshev metric (also known as the maximum metric)
$\|\mathbf {x}-\mathbf {y}\|_{p} = (\left |x_1-y_1\right |^p+\dots +\left |x_n-y_n\right |^p)^{1/p}$, or the Chebyshev metric (also known as the maximum metric) ![]() $\ell _\infty $ defined by
$\ell _\infty $ defined by ![]() $\|\mathbf {x}-\mathbf {y}\|_{\infty } = \max _{1 \leq i \leq n} \left \{ \left |x_i-y_i\right |\right \}.$ We denote the corresponding spaces by
$\|\mathbf {x}-\mathbf {y}\|_{\infty } = \max _{1 \leq i \leq n} \left \{ \left |x_i-y_i\right |\right \}.$ We denote the corresponding spaces by ![]() ${{\mathbb R}}^n_{p}$ and the corresponding chromatic numbers by
${{\mathbb R}}^n_{p}$ and the corresponding chromatic numbers by ![]() $\chi (\mathbb {R}^n_p)$. For all
$\chi (\mathbb {R}^n_p)$. For all ![]() $1<p<\infty $,
$1<p<\infty $, ![]() $p \neq 2$, the best known lower bound due to Frankl and Wilson [Reference Frankl and Wilson11] is
$p \neq 2$, the best known lower bound due to Frankl and Wilson [Reference Frankl and Wilson11] is ![]() $ \chi (\mathbb {R}^n_p) \ge (1.207...+o(1))^n$ as
$ \chi (\mathbb {R}^n_p) \ge (1.207...+o(1))^n$ as ![]() $n \rightarrow \infty $, whereas in case
$n \rightarrow \infty $, whereas in case ![]() $p=1$ – that is, in case of the taxicab or Manhattan metric – Raigorodskii [Reference Raigorodskii27] proved a better lower bound
$p=1$ – that is, in case of the taxicab or Manhattan metric – Raigorodskii [Reference Raigorodskii27] proved a better lower bound ![]() $\chi (\mathbb {R}^n_1) \ge (1.366...+o(1))^n$. As for the upper bound, the best result for all real
$\chi (\mathbb {R}^n_1) \ge (1.366...+o(1))^n$. As for the upper bound, the best result for all real ![]() $p \neq 2$ due to the first author [Reference Kupavskiy16] is
$p \neq 2$ due to the first author [Reference Kupavskiy16] is ![]() $\chi (\mathbb {R}^n_p) \le (4+o(1))^n$ as
$\chi (\mathbb {R}^n_p) \le (4+o(1))^n$ as ![]() $n \rightarrow \infty $ (also valid for any norm). The case
$n \rightarrow \infty $ (also valid for any norm). The case ![]() $p = \infty $ stands out here because of the folklore equality
$p = \infty $ stands out here because of the folklore equality ![]() $\chi ( \mathbb {R}^n_\infty ) = 2^n,$ valid for each
$\chi ( \mathbb {R}^n_\infty ) = 2^n,$ valid for each ![]() $n \in \mathbb {N}$. For completeness, we will give its simple proof in the next section.
$n \in \mathbb {N}$. For completeness, we will give its simple proof in the next section.
The questions mentioned above can be described using the following general setup. Let ![]() ${{\mathbb X}} = \left ( X, \rho _X\right ), {{\mathcal{Y}}} = ( Y, \rho _Y)$ be two metric spaces. A subset
${{\mathbb X}} = \left ( X, \rho _X\right ), {{\mathcal{Y}}} = ( Y, \rho _Y)$ be two metric spaces. A subset ![]() $Y' \subset X$ is called a copy of
$Y' \subset X$ is called a copy of ![]() ${{\mathcal{Y}}}$ if there is an isometry
${{\mathcal{Y}}}$ if there is an isometry ![]() $f: Y \rightarrow Y'$; that is, a bijection such that
$f: Y \rightarrow Y'$; that is, a bijection such that ![]() $\rho _Y(y_1,y_2) = \rho _X\big (f(y_1), f(y_2)\big )$ for all
$\rho _Y(y_1,y_2) = \rho _X\big (f(y_1), f(y_2)\big )$ for all ![]() $y_1, y_2 \in Y$. The chromatic number
$y_1, y_2 \in Y$. The chromatic number ![]() $\chi ({{\mathbb X}};{{\mathcal{Y}}})$ of the space
$\chi ({{\mathbb X}};{{\mathcal{Y}}})$ of the space ![]() ${{\mathbb X}}$ with a forbidden subspace
${{\mathbb X}}$ with a forbidden subspace ![]() $\mathcal {Y}$ is the minimal k such that there is a colouring of elements of X with k colours and no monochromatic copy of
$\mathcal {Y}$ is the minimal k such that there is a colouring of elements of X with k colours and no monochromatic copy of ![]() ${{\mathcal{Y}}}$.
${{\mathcal{Y}}}$.
In this article, we focus on the case of ![]() ${{\mathbb X}} = \mathbb {R}^n_\infty $. Recall that for each finite metric space
${{\mathbb X}} = \mathbb {R}^n_\infty $. Recall that for each finite metric space ![]() $\mathcal {M}$ of size at least
$\mathcal {M}$ of size at least ![]() $2$ we trivially have
$2$ we trivially have ![]() $\chi (\mathbb {R}^n_\infty; \mathcal {M}) \le \chi (\mathbb {R}^n_\infty ) = 2^n$ for all
$\chi (\mathbb {R}^n_\infty; \mathcal {M}) \le \chi (\mathbb {R}^n_\infty ) = 2^n$ for all ![]() $n \in \mathbb {N}$. As for the lower bound, observe that it is not even obvious that
$n \in \mathbb {N}$. As for the lower bound, observe that it is not even obvious that ![]() $\chi (\mathbb {R}^n_\infty; \mathcal {M})> 1$ for some n. This inequality follows from a result due to Fréchet (see, e.g., [Reference Matoušek19]) that states that every finite metric space can be embedded into
$\chi (\mathbb {R}^n_\infty; \mathcal {M})> 1$ for some n. This inequality follows from a result due to Fréchet (see, e.g., [Reference Matoušek19]) that states that every finite metric space can be embedded into ![]() $\mathbb {R}^n_\infty $ for some
$\mathbb {R}^n_\infty $ for some ![]() $n \in \mathbb {N}$. We give the precise statement along with the short proof in Section 3 for completeness (see Lemma 2). The following theorem, which is the main result of our article, gives a much stronger lower bound.
$n \in \mathbb {N}$. We give the precise statement along with the short proof in Section 3 for completeness (see Lemma 2). The following theorem, which is the main result of our article, gives a much stronger lower bound.
Theorem 1. Any finite metric space ![]() $\mathcal {M}$ that contains at least two points is exponentially
$\mathcal {M}$ that contains at least two points is exponentially ![]() $\ell _\infty -$Ramsey; that is, there is a constant
$\ell _\infty -$Ramsey; that is, there is a constant ![]() $\chi _{\mathcal {M}}> 1$ such that
$\chi _{\mathcal {M}}> 1$ such that ![]() $\chi (\mathbb {R}^n_\infty; \mathcal {M})> \left ( \chi _{\mathcal {M}}+o(1)\right )^n$ as
$\chi (\mathbb {R}^n_\infty; \mathcal {M})> \left ( \chi _{\mathcal {M}}+o(1)\right )^n$ as ![]() $n \rightarrow \infty $.
$n \rightarrow \infty $.
The rest of the article is organised as follows. We start Section 2 by reciting the proof of ![]() $\chi ( \mathbb {R}^n_\infty )=2^n$ and then prove Theorem 1 for ‘
$\chi ( \mathbb {R}^n_\infty )=2^n$ and then prove Theorem 1 for ‘![]() $1-$dimensional’ metric spaces, called batons. This step is crucial in the proof of Theorem 1, and the results in that section are also of independent interest. In Section 3 we deduce Theorem 1 from the results of Section 2. In Section 4 we provide upper bounds on the values
$1-$dimensional’ metric spaces, called batons. This step is crucial in the proof of Theorem 1, and the results in that section are also of independent interest. In Section 3 we deduce Theorem 1 from the results of Section 2. In Section 4 we provide upper bounds on the values ![]() $\chi (\mathbb {R}^n_\infty; \mathcal {M})$. Finally, Section 5 contains a discussion of the results and some open problems.
$\chi (\mathbb {R}^n_\infty; \mathcal {M})$. Finally, Section 5 contains a discussion of the results and some open problems.
In what follows, whenever not specified, the distances are taken in the Chebyshev metric. We also slightly abuse notation and identify each set ![]() $S \subset {{\mathbb R}}^d$ with the corresponding metric space
$S \subset {{\mathbb R}}^d$ with the corresponding metric space ![]() $\left (S, \ell _\infty \right )$, which is a subspace of
$\left (S, \ell _\infty \right )$, which is a subspace of ![]() ${{\mathbb R}}^d_\infty $.
${{\mathbb R}}^d_\infty $.
2 Batons
For a ![]() $k \in \mathbb {N}$, denote
$k \in \mathbb {N}$, denote ![]() $\left [k\right ]_0 = \left \{0,1, 2,\, \dots \,,k\right \}$ (note that this is a slightly nonstandard notation). Given a sequence of positive real numbers
$\left [k\right ]_0 = \left \{0,1, 2,\, \dots \,,k\right \}$ (note that this is a slightly nonstandard notation). Given a sequence of positive real numbers ![]() $\alpha _1,\, \dots \, , \alpha _k$, a baton
$\alpha _1,\, \dots \, , \alpha _k$, a baton ![]() $\mathcal {B}(\alpha _1,\, \dots \, , \alpha _k)$ is a metric space isometric to a set of points
$\mathcal {B}(\alpha _1,\, \dots \, , \alpha _k)$ is a metric space isometric to a set of points  $\left \{0, \alpha _1, \alpha _1+\alpha _2,\, \dots \,,\sum _{i=1}^{k}\alpha _i \right \} \subset \mathbb {R}$ with the metric induced from
$\left \{0, \alpha _1, \alpha _1+\alpha _2,\, \dots \,,\sum _{i=1}^{k}\alpha _i \right \} \subset \mathbb {R}$ with the metric induced from ![]() $\mathbb {R}$. If
$\mathbb {R}$. If ![]() $\alpha _1=\dots =\alpha _k=1$ then we denote this space
$\alpha _1=\dots =\alpha _k=1$ then we denote this space ![]() $\mathcal {B}_k$ for shorthand.
$\mathcal {B}_k$ for shorthand.
2.1  $\chi ( \mathbb {R}^n_\infty )=2^n$
$\chi ( \mathbb {R}^n_\infty )=2^n$
We start the proofs with the simple but instructive case of ![]() $\chi ( \mathbb {R}^n_\infty ) = \chi ( \mathbb {R}^n_\infty ,\mathcal B_1)$. As we have already mentioned, the equality
$\chi ( \mathbb {R}^n_\infty ) = \chi ( \mathbb {R}^n_\infty ,\mathcal B_1)$. As we have already mentioned, the equality ![]() $\chi ( \mathbb {R}^n_\infty )=2^n$ is folklore, and we give its proof for completeness.
$\chi ( \mathbb {R}^n_\infty )=2^n$ is folklore, and we give its proof for completeness.
Given ![]() $n \in \mathbb {N}$, let us denote
$n \in \mathbb {N}$, let us denote ![]() $m=2^n$ for convenience. Let
$m=2^n$ for convenience. Let ![]() $\mathbf {v}_1, \,\dots \, , \mathbf {v}_m$ be a set of vertices of a standard (discrete) unit cube
$\mathbf {v}_1, \,\dots \, , \mathbf {v}_m$ be a set of vertices of a standard (discrete) unit cube ![]() $\{0,1\}^n$. Note that
$\{0,1\}^n$. Note that ![]() $\|\mathbf {v}_i-\mathbf {v}_j\|_\infty = 1$ for all
$\|\mathbf {v}_i-\mathbf {v}_j\|_\infty = 1$ for all ![]() $i\neq j$, and thus
$i\neq j$, and thus ![]() $\chi ( \mathbb {R}^n_\infty ) \geq 2^n$ because we need to use a distinct colour for each
$\chi ( \mathbb {R}^n_\infty ) \geq 2^n$ because we need to use a distinct colour for each ![]() $\mathbf v_i$.
$\mathbf v_i$.
To prove the matching upper bound, we explicitly describe the colouring. Let
 $$ \begin{align*}\mathcal{C} = \bigsqcup_{\mathbf{w}\in {{\mathbb Z}}^n} \big( \left[0;1\right)^n+2\mathbf{w} \big)\end{align*} $$
$$ \begin{align*}\mathcal{C} = \bigsqcup_{\mathbf{w}\in {{\mathbb Z}}^n} \big( \left[0;1\right)^n+2\mathbf{w} \big)\end{align*} $$be a disjoint union of unit cubes. It is clear that for each ![]() $\mathbf {x},\mathbf {y} \in \mathcal {C}$ we have
$\mathbf {x},\mathbf {y} \in \mathcal {C}$ we have ![]() $\|\mathbf {x}-\mathbf {y}\|_\infty \neq 1$. Indeed, one has
$\|\mathbf {x}-\mathbf {y}\|_\infty \neq 1$. Indeed, one has ![]() $\|\mathbf {x}-\mathbf {y}\|_\infty < 1$ whenever
$\|\mathbf {x}-\mathbf {y}\|_\infty < 1$ whenever ![]() $\mathbf {x}$ and
$\mathbf {x}$ and ![]() $\mathbf {y}$ come from the same unit cube, and
$\mathbf {y}$ come from the same unit cube, and ![]() $\|\mathbf {x}-\mathbf {y}\|_\infty> 1$ whenever they are from different cubes. Given
$\|\mathbf {x}-\mathbf {y}\|_\infty> 1$ whenever they are from different cubes. Given ![]() $i \leq m$, let us denote
$i \leq m$, let us denote ![]() $\mathcal {C}_i = \mathcal {C} + \mathbf {v}_i$ (where
$\mathcal {C}_i = \mathcal {C} + \mathbf {v}_i$ (where ![]() $\mathbf {v}_i$ were defined in the previous paragraph). Colour each point of
$\mathbf {v}_i$ were defined in the previous paragraph). Colour each point of ![]() $\mathcal {C}_i$ with the ith colour. We have
$\mathcal {C}_i$ with the ith colour. We have ![]() $\bigsqcup _{i=1}^m \mathcal {C}_i = {{\mathbb R}}^n$, and thus it is a well-defined proper colouring of
$\bigsqcup _{i=1}^m \mathcal {C}_i = {{\mathbb R}}^n$, and thus it is a well-defined proper colouring of ![]() ${{\mathbb R}}^n$. This shows that
${{\mathbb R}}^n$. This shows that ![]() $\chi ( \mathbb {R}^n_\infty ) \leq 2^n$.
$\chi ( \mathbb {R}^n_\infty ) \leq 2^n$.
2.2  $\mathcal B_k$ is exponentially
$\mathcal B_k$ is exponentially  $\ell _\infty -$Ramsey
$\ell _\infty -$Ramsey
Theorem 2. Let ![]() $k, n$ be positive integers. Then each subset
$k, n$ be positive integers. Then each subset ![]() $X \subset \left [k\right ]_0^n \subset \mathbb {R}^n_\infty $ of cardinality
$X \subset \left [k\right ]_0^n \subset \mathbb {R}^n_\infty $ of cardinality ![]() $\left |X\right |>k^n$ contains a copy of
$\left |X\right |>k^n$ contains a copy of ![]() $\mathcal {B}_k$.
$\mathcal {B}_k$.
Proof . The proof is by induction on n. For ![]() $n=1$, there is nothing to prove. Indeed, if
$n=1$, there is nothing to prove. Indeed, if ![]() $X \subset \left [k\right ]_0$ and
$X \subset \left [k\right ]_0$ and ![]() $\left |X\right |> k$, then
$\left |X\right |> k$, then ![]() $X = \left [k\right ]_0$ is the required copy of
$X = \left [k\right ]_0$ is the required copy of ![]() $\mathcal {B}_k.$
$\mathcal {B}_k.$
Next, assume that ![]() $n>1$. We employ a certain shifting-type argument. For a vector
$n>1$. We employ a certain shifting-type argument. For a vector ![]() $\mathbf {x}=\left (x_1,\, \dots \,, x_n\right )\in \left [k\right ]_0^n$ define its head
$\mathbf {x}=\left (x_1,\, \dots \,, x_n\right )\in \left [k\right ]_0^n$ define its head ![]() $h\left ( \mathbf {x} \right )=x_n$ and tail
$h\left ( \mathbf {x} \right )=x_n$ and tail ![]() $t(\mathbf {x})=\left (x_1,\, \dots \,, x_{n-1}\right )$. Given
$t(\mathbf {x})=\left (x_1,\, \dots \,, x_{n-1}\right )$. Given  $\mathbf {y} \in \left [k\right ]_0^{n-1}$, let
$\mathbf {y} \in \left [k\right ]_0^{n-1}$, let ![]() $H(\mathbf {y}) = \left \{i \in [k]_0: \left (\mathbf {y}, i\right ) \in X\right \}$. It should be clear that if
$H(\mathbf {y}) = \left \{i \in [k]_0: \left (\mathbf {y}, i\right ) \in X\right \}$. It should be clear that if ![]() $H(\mathbf {y}) = \left [k\right ]_0$ for some
$H(\mathbf {y}) = \left [k\right ]_0$ for some  $\mathbf y\in [k]_0^{n-1}$, then a subset
$\mathbf y\in [k]_0^{n-1}$, then a subset ![]() $\left \{ \left (\mathbf {y},0\right ), \left (\mathbf {y}, 1\right ),\,\dots \,,\left (\mathbf {y},k\right )\right \} \subset X$ is the required copy of
$\left \{ \left (\mathbf {y},0\right ), \left (\mathbf {y}, 1\right ),\,\dots \,,\left (\mathbf {y},k\right )\right \} \subset X$ is the required copy of ![]() $\mathcal {B}_k.$ In what follows, we assume that
$\mathcal {B}_k.$ In what follows, we assume that ![]() $H(\mathbf {y}) \neq \left [k\right ]_0$ for all
$H(\mathbf {y}) \neq \left [k\right ]_0$ for all  $\mathbf {y} \in \left [k\right ]_0^{n-1}$.
$\mathbf {y} \in \left [k\right ]_0^{n-1}$.
Let us define a function ![]() $f:X\rightarrow \left [k\right ]_0^n$ that increases the last coordinate of a vector by
$f:X\rightarrow \left [k\right ]_0^n$ that increases the last coordinate of a vector by ![]() $1$ ‘whenever possible’ as follows. For a vector
$1$ ‘whenever possible’ as follows. For a vector ![]() $\mathbf x\in X$,
$\mathbf x\in X$,
 $$ \begin{align*} f\left(\mathbf{x}\right) = \begin{cases} \left(t(\mathbf{x}),h(\mathbf x)+1\right) & \mbox{if } \exists\, j \in \left[k\right]_0\setminus H\left(t(\mathbf{x})\right) \mbox{ such that } j> h(\mathbf{x});\\ \mathbf{x} & \mbox{otherwise.} \end{cases} \end{align*} $$
$$ \begin{align*} f\left(\mathbf{x}\right) = \begin{cases} \left(t(\mathbf{x}),h(\mathbf x)+1\right) & \mbox{if } \exists\, j \in \left[k\right]_0\setminus H\left(t(\mathbf{x})\right) \mbox{ such that } j> h(\mathbf{x});\\ \mathbf{x} & \mbox{otherwise.} \end{cases} \end{align*} $$We show that ![]() $f(\cdot )$ is an injection. Indeed, it is clear that
$f(\cdot )$ is an injection. Indeed, it is clear that ![]() $f(\mathbf {x}^1)\neq f(\mathbf {x}^2)$ for all
$f(\mathbf {x}^1)\neq f(\mathbf {x}^2)$ for all ![]() $\mathbf {x}^1, \mathbf {x}^2$ such that
$\mathbf {x}^1, \mathbf {x}^2$ such that ![]() $t(\mathbf {x}^1) \neq t(\mathbf {x}^2)$ or
$t(\mathbf {x}^1) \neq t(\mathbf {x}^2)$ or ![]() $|h(\mathbf {x}^1)-h(\mathbf {x}^2)| \ge 2$. Thus, let us consider
$|h(\mathbf {x}^1)-h(\mathbf {x}^2)| \ge 2$. Thus, let us consider  $\mathbf {y} \in [k]_0^{n-1}$,
$\mathbf {y} \in [k]_0^{n-1}$, ![]() $0 \le i < k$, such that both
$0 \le i < k$, such that both ![]() $(\mathbf {y},i)$ and
$(\mathbf {y},i)$ and ![]() $(\mathbf {y},i+1)$ belong to X. It is not hard to see that either
$(\mathbf {y},i+1)$ belong to X. It is not hard to see that either ![]() $f((\mathbf {y},i)) = (\mathbf {y},i+1), f((\mathbf {y},i+1)) = (\mathbf {y},i+2)$ or
$f((\mathbf {y},i)) = (\mathbf {y},i+1), f((\mathbf {y},i+1)) = (\mathbf {y},i+2)$ or ![]() $f((\mathbf {y},i)) = (\mathbf {y},i), f((\mathbf {y},i+1)) = (\mathbf {y},i+1)$. In both cases we have
$f((\mathbf {y},i)) = (\mathbf {y},i), f((\mathbf {y},i+1)) = (\mathbf {y},i+1)$. In both cases we have ![]() $f((\mathbf {y},i))\neq f((\mathbf {y},i+1))$. Thus,
$f((\mathbf {y},i))\neq f((\mathbf {y},i+1))$. Thus, ![]() $f(\cdot )$ is really an injection. Let
$f(\cdot )$ is really an injection. Let ![]() $f\left (X\right )$ be the image of X under
$f\left (X\right )$ be the image of X under ![]() $f(\cdot )$. Hence,
$f(\cdot )$. Hence,
Partition ![]() $f\left (X\right )=X_0\,\sqcup \dots \,\sqcup X_{k}$ based on the last coordinate:
$f\left (X\right )=X_0\,\sqcup \dots \,\sqcup X_{k}$ based on the last coordinate:
Because ![]() $H(\mathbf y)\ne [k]_0$ for all
$H(\mathbf y)\ne [k]_0$ for all  $\mathbf y\in [k]_0^{n-1}$, it is easy to see that
$\mathbf y\in [k]_0^{n-1}$, it is easy to see that ![]() $X_0$ is empty. We conclude that
$X_0$ is empty. We conclude that
It easily follows from comparing (1) and (2) that there is an ![]() $i \in \left \{1, \, \dots \,, k\right \}$ such that
$i \in \left \{1, \, \dots \,, k\right \}$ such that ![]() $\left |X_i\right |> k^{n-1}.$ Because distinct elements of
$\left |X_i\right |> k^{n-1}.$ Because distinct elements of ![]() $X_i$ have distinct tails, by the induction hypothesis one can find a set
$X_i$ have distinct tails, by the induction hypothesis one can find a set ![]() $\{\mathbf {y}^0,\,\dots \,,\mathbf {y}^k\}\subset \{t(\mathbf x): \mathbf x\in X_i\}$ that forms a copy of
$\{\mathbf {y}^0,\,\dots \,,\mathbf {y}^k\}\subset \{t(\mathbf x): \mathbf x\in X_i\}$ that forms a copy of ![]() $\mathcal {B}_k$. For each
$\mathcal {B}_k$. For each ![]() $j \in [k]_0$, let
$j \in [k]_0$, let ![]() $\mathbf {x}^j = f^{-1}(\mathbf {y}^j, i)\in X$ be the preimage of
$\mathbf {x}^j = f^{-1}(\mathbf {y}^j, i)\in X$ be the preimage of ![]() $(\mathbf {y}^j, i) \in X_i$. Note that we have
$(\mathbf {y}^j, i) \in X_i$. Note that we have ![]() $h(\mathbf {x}^j)\in \{i-1,i\}$ for each j, and thus
$h(\mathbf {x}^j)\in \{i-1,i\}$ for each j, and thus ![]() $|h(\mathbf {x}^j ) - h(\mathbf {x}^{j'} )|\in \{0,1\}$ for all
$|h(\mathbf {x}^j ) - h(\mathbf {x}^{j'} )|\in \{0,1\}$ for all ![]() $j,j' \in [k]_0$. This immediately implies that
$j,j' \in [k]_0$. This immediately implies that ![]() $\|\mathbf {x}^j-\mathbf {x}^{j'}\|_\infty = \|\mathbf {y}^j- \mathbf {y}^{j'}\|_\infty $ for all
$\|\mathbf {x}^j-\mathbf {x}^{j'}\|_\infty = \|\mathbf {y}^j- \mathbf {y}^{j'}\|_\infty $ for all ![]() $j,j' \in [k]_0$. Hence, the subset
$j,j' \in [k]_0$. Hence, the subset ![]() $\{ \mathbf {x}^0,\,\dots \,, \mathbf {x}^k\} \subset X$ is isometric to
$\{ \mathbf {x}^0,\,\dots \,, \mathbf {x}^k\} \subset X$ is isometric to ![]() $\mathcal {B}_k$.
$\mathcal {B}_k$.
Theorem 2 implies that if the colouring of ![]() ${{\mathbb R}}^n_\infty $ contains no monochromatic copy of
${{\mathbb R}}^n_\infty $ contains no monochromatic copy of ![]() $\mathcal {B}_k$, then each of its colours can intersect
$\mathcal {B}_k$, then each of its colours can intersect ![]() $[k]_0^n$ in at most
$[k]_0^n$ in at most ![]() $k^n$ points. Using the pigeonhole principle, we get the following corollary.
$k^n$ points. Using the pigeonhole principle, we get the following corollary.
Corollary 1. For each positive integer ![]() $k,n$ one has
$k,n$ one has  $\chi (\mathbb {R}^n_\infty; \mathcal {B}_k) \geq \left (\frac {k+1}{k}\right )^n$.
$\chi (\mathbb {R}^n_\infty; \mathcal {B}_k) \geq \left (\frac {k+1}{k}\right )^n$.
2.3  $\mathcal {B}\left ( 1,\ {\alpha} \right )$ is exponentially
$\mathcal {B}\left ( 1,\ {\alpha} \right )$ is exponentially  $\ell _\infty -$Ramsey
$\ell _\infty -$Ramsey
In this and the following two subsections we generalise Theorem 2 and Corollary 1 to the case of arbitrary batons. However, the proof in the general case is nontrivial, and we wanted to illustrate some of its ideas on a much simpler case of ![]() $\mathcal {B}\left ( 1,\alpha \right )$, which is a set
$\mathcal {B}\left ( 1,\alpha \right )$, which is a set ![]() $\{0,1,1+\alpha \}$ with the natural metric.
$\{0,1,1+\alpha \}$ with the natural metric.
Theorem 3. Let ![]() $\alpha>1$ be a real number. Then there is a subset
$\alpha>1$ be a real number. Then there is a subset ![]() $A\subset \mathbb {R}$ of cardinality
$A\subset \mathbb {R}$ of cardinality ![]() $\left \lceil \alpha \right \rceil +2$ such that the following holds. Given a positive integer n, each subset
$\left \lceil \alpha \right \rceil +2$ such that the following holds. Given a positive integer n, each subset ![]() $B \subset A^n \subset \mathbb {R}^n_{\infty }$ of cardinality
$B \subset A^n \subset \mathbb {R}^n_{\infty }$ of cardinality ![]() $\left |B\right |>\left (\left \lceil \alpha \right \rceil +1\right )^n$ contains a copy of
$\left |B\right |>\left (\left \lceil \alpha \right \rceil +1\right )^n$ contains a copy of ![]() $\mathcal {B}\left (1,\alpha \right )$.
$\mathcal {B}\left (1,\alpha \right )$.
Proof . Denote ![]() $m=\left \lceil \alpha \right \rceil $. Consider
$m=\left \lceil \alpha \right \rceil $. Consider ![]() $A = \left \{a_0,\,\dots \,, a_{m+1}\right \} \subset \mathbb {R},$ where
$A = \left \{a_0,\,\dots \,, a_{m+1}\right \} \subset \mathbb {R},$ where ![]() $a_l$ are defined as follows:
$a_l$ are defined as follows:
 $$ \begin{align*} a_0 = 0, \ \ a_l = 1+\frac{l-1}{m-1}\left(\alpha-1\right) \mbox{ for } 1 \leq l \leq m, \ \ a_{m+1} = \alpha+1. \end{align*} $$
$$ \begin{align*} a_0 = 0, \ \ a_l = 1+\frac{l-1}{m-1}\left(\alpha-1\right) \mbox{ for } 1 \leq l \leq m, \ \ a_{m+1} = \alpha+1. \end{align*} $$In particular, ![]() $a_1 = 1, a_{m} = \alpha $. Define a bijection
$a_1 = 1, a_{m} = \alpha $. Define a bijection ![]() $f: [m+1]_0^n\to A^n$ by
$f: [m+1]_0^n\to A^n$ by ![]() $f((x_1, \,\ldots \,,x_n)) = (a_{x_1}, \,\dots \,, a_{x_n})$.
$f((x_1, \,\ldots \,,x_n)) = (a_{x_1}, \,\dots \,, a_{x_n})$.
Let ![]() $B\subset A^n$ be an arbitrary subset of cardinality
$B\subset A^n$ be an arbitrary subset of cardinality ![]() $\left |B\right |>\left (m+1\right )^n$. From Theorem 2 it follows that there is a subset
$\left |B\right |>\left (m+1\right )^n$. From Theorem 2 it follows that there is a subset  $\left \{\mathbf {x}^0,\,\dots \,,\mathbf {x}^{m+1}\right \} \subset f^{-1}(B) \subset \left [m+1\right ]_0^n$ that is a copy of
$\left \{\mathbf {x}^0,\,\dots \,,\mathbf {x}^{m+1}\right \} \subset f^{-1}(B) \subset \left [m+1\right ]_0^n$ that is a copy of ![]() $\mathcal {B}_{m+1}$. Without loss of generality, we can assume that
$\mathcal {B}_{m+1}$. Without loss of generality, we can assume that ![]() $\|\mathbf {x}^s- \mathbf {x}^t\|_\infty = \left |s-t\right |$ for all
$\|\mathbf {x}^s- \mathbf {x}^t\|_\infty = \left |s-t\right |$ for all ![]() $s,t \in \left [m+1\right ]_0.$ In particular, it is easy to see that
$s,t \in \left [m+1\right ]_0.$ In particular, it is easy to see that  $\left \{\mathbf {x}^0, \mathbf {x}^1, \mathbf {x}^{m+1}\right \}$ is a copy of
$\left \{\mathbf {x}^0, \mathbf {x}^1, \mathbf {x}^{m+1}\right \}$ is a copy of ![]() $\mathcal {B}\left (1,m\right )$. For convenience, let us denote
$\mathcal {B}\left (1,m\right )$. For convenience, let us denote ![]() $\mathbf {x}^0, \mathbf {x}^1$ and
$\mathbf {x}^0, \mathbf {x}^1$ and ![]() $\mathbf {x}^{m+1}$ by
$\mathbf {x}^{m+1}$ by ![]() $\mathbf {x}, \mathbf {y}$ and
$\mathbf {x}, \mathbf {y}$ and ![]() $\mathbf {z},$ respectively. Then the following two statements hold:
$\mathbf {z},$ respectively. Then the following two statements hold:
 $$ \begin{align} \mbox{for all } i \in \{1,\,\dots\,,n\} \mbox{ one has } \begin{cases} \left|x_i-y_i\right| \leq 1, \\ \left|y_i-z_i\right| \leq m; \end{cases} \end{align} $$
$$ \begin{align} \mbox{for all } i \in \{1,\,\dots\,,n\} \mbox{ one has } \begin{cases} \left|x_i-y_i\right| \leq 1, \\ \left|y_i-z_i\right| \leq m; \end{cases} \end{align} $$ $$ \begin{align} \mbox{there is } j \in \{1,\,\dots\,,n\} \mbox{ such that either } \begin{cases} x_j=0,\\ y_j=1,\\ z_j=m\!+\!1, \end{cases} \mbox{ or } \begin{cases} x_j=m\!+\!1,\\ y_j=m,\\ z_j=0. \end{cases} \end{align} $$
$$ \begin{align} \mbox{there is } j \in \{1,\,\dots\,,n\} \mbox{ such that either } \begin{cases} x_j=0,\\ y_j=1,\\ z_j=m\!+\!1, \end{cases} \mbox{ or } \begin{cases} x_j=m\!+\!1,\\ y_j=m,\\ z_j=0. \end{cases} \end{align} $$The first statement is straightforward from the definition of ![]() $\mathcal B(1,m)$. As for the second, the equality
$\mathcal B(1,m)$. As for the second, the equality ![]() $\|\mathbf {x}- \mathbf {z}\|_\infty = m+1$ implies that there is
$\|\mathbf {x}- \mathbf {z}\|_\infty = m+1$ implies that there is ![]() $j \in \{1,\,\dots \,,n\}$ such that
$j \in \{1,\,\dots \,,n\}$ such that  $\left |x_j-z_j\right | = m+1$, and thus either
$\left |x_j-z_j\right | = m+1$, and thus either ![]() $x_j=0$ and
$x_j=0$ and ![]() $z_j=m+1$ or
$z_j=m+1$ or ![]() $x_j=m+1$ and
$x_j=m+1$ and ![]() $z_j=0$. Then it follows from (3) that
$z_j=0$. Then it follows from (3) that ![]() $y_j = 1$ in the former case and
$y_j = 1$ in the former case and ![]() $y_j=m$ in the latter.
$y_j=m$ in the latter.
We claim that ![]() $\{f(\mathbf {x}), f(\mathbf {y}), f(\mathbf {z})\} \subset B$ is a copy of
$\{f(\mathbf {x}), f(\mathbf {y}), f(\mathbf {z})\} \subset B$ is a copy of ![]() $\mathcal {B}\left (1,\alpha \right )$. To check that, we need to verify that the distances between
$\mathcal {B}\left (1,\alpha \right )$. To check that, we need to verify that the distances between ![]() $f(\mathbf x), f(\mathbf y), f(\mathbf z)$ are the same as the distances between points in
$f(\mathbf x), f(\mathbf y), f(\mathbf z)$ are the same as the distances between points in ![]() $\mathcal B(1,\alpha )$.
$\mathcal B(1,\alpha )$.
Clearly, ![]() $\|\mathbf a^1-\mathbf a^2\|_\infty \leq \alpha +1$ for all
$\|\mathbf a^1-\mathbf a^2\|_\infty \leq \alpha +1$ for all ![]() $\mathbf a^1,\mathbf a^2\in A^n$. At the same time, it follows from (4) that
$\mathbf a^1,\mathbf a^2\in A^n$. At the same time, it follows from (4) that ![]() $|f(\mathbf x)_j-f(\mathbf z)_j|= |a_{x_j}-a_{z_j}| = \alpha +1,$ and thus
$|f(\mathbf x)_j-f(\mathbf z)_j|= |a_{x_j}-a_{z_j}| = \alpha +1,$ and thus ![]() $\|f(\mathbf x)-f(\mathbf z)\|_\infty =\alpha +1.$
$\|f(\mathbf x)-f(\mathbf z)\|_\infty =\alpha +1.$
Similarly, ![]() $|f(\mathbf x)_j-f(\mathbf y)_j| = 1$ and
$|f(\mathbf x)_j-f(\mathbf y)_j| = 1$ and ![]() $|f(\mathbf y)_j-f(\mathbf z)_j| = \alpha ,$ implying
$|f(\mathbf y)_j-f(\mathbf z)_j| = \alpha ,$ implying ![]() $\|f(\mathbf x)-f(\mathbf y)\|_\infty \geq 1$ and
$\|f(\mathbf x)-f(\mathbf y)\|_\infty \geq 1$ and ![]() $\|f(\mathbf y)-f(\mathbf z)\|_\infty \geq \alpha .$ We actually have equality in both of these inequalities. Let us show it for the former, and the latter is analogous. Indeed, if
$\|f(\mathbf y)-f(\mathbf z)\|_\infty \geq \alpha .$ We actually have equality in both of these inequalities. Let us show it for the former, and the latter is analogous. Indeed, if ![]() $\|f(\mathbf x)-f(\mathbf y)\|_\infty> 1$, then there is
$\|f(\mathbf x)-f(\mathbf y)\|_\infty> 1$, then there is ![]() $j' \in \{1,\,\dots \,,n\}$ such that
$j' \in \{1,\,\dots \,,n\}$ such that ![]() $|f(\mathbf x)_{j'}-f(\mathbf y)_{j'}|> 1$. It follows from the definition of
$|f(\mathbf x)_{j'}-f(\mathbf y)_{j'}|> 1$. It follows from the definition of ![]() $a_l$ that if
$a_l$ that if ![]() $|a_l-a_r|> 1$, then
$|a_l-a_r|> 1$, then ![]() $|l-r|\geq 2$. Hence,
$|l-r|\geq 2$. Hence, ![]() $|x_{j'}-y_{j'}|\geq 2$, which contradicts (3).
$|x_{j'}-y_{j'}|\geq 2$, which contradicts (3).
Observe that now one can easily deduce from Theorem 3 that for all ![]() $\alpha>1$ and
$\alpha>1$ and ![]() $n \in \mathbb {N}$, we have
$n \in \mathbb {N}$, we have  $\chi ({{\mathbb R}}_\infty ^n; \mathcal {B}(1,\alpha )) \ge \left (\frac {\lceil \alpha \rceil +2}{ \lceil \alpha \rceil +1}\right )^n$. In particular, this implies that the metric space
$\chi ({{\mathbb R}}_\infty ^n; \mathcal {B}(1,\alpha )) \ge \left (\frac {\lceil \alpha \rceil +2}{ \lceil \alpha \rceil +1}\right )^n$. In particular, this implies that the metric space ![]() $\mathcal {B}(1,\alpha )$ is exponentially
$\mathcal {B}(1,\alpha )$ is exponentially ![]() $\ell _\infty -$Ramsey.
$\ell _\infty -$Ramsey.
2.4  $\mathcal {B}\left (\alpha _1,\, \dots \, , \alpha _k\right )$ is exponentially
$\mathcal {B}\left (\alpha _1,\, \dots \, , \alpha _k\right )$ is exponentially  $\ell _\infty -$Ramsey
$\ell _\infty -$Ramsey
In this subsection we deal with the general case of ![]() $\mathcal {B}\left ( \alpha _1,\, \dots \, , \alpha _k\right )$. We use the same idea of reduction to the integer case and applying the pigeonhole principle. In the notation of the previous subsection, the main difficulty here is to find an appropriate A and bijection f.
$\mathcal {B}\left ( \alpha _1,\, \dots \, , \alpha _k\right )$. We use the same idea of reduction to the integer case and applying the pigeonhole principle. In the notation of the previous subsection, the main difficulty here is to find an appropriate A and bijection f.
Theorem 4. Let k be a positive integer and ![]() $\alpha _1,\, \dots \, , \alpha _k$ be positive real numbers. Then there is an integer m and a subset
$\alpha _1,\, \dots \, , \alpha _k$ be positive real numbers. Then there is an integer m and a subset ![]() $A\subset \mathbb {R}$ of cardinality
$A\subset \mathbb {R}$ of cardinality ![]() $m+1$ such that the following holds. Given a positive integer n, each subset
$m+1$ such that the following holds. Given a positive integer n, each subset ![]() $B \subset A^n \subset \mathbb {R}^n_\infty $ of cardinality
$B \subset A^n \subset \mathbb {R}^n_\infty $ of cardinality ![]() $\left |B\right |>m^n$ contains a copy of
$\left |B\right |>m^n$ contains a copy of ![]() $\mathcal {B}\left ( \alpha _1,\, \dots \, , \alpha _k\right )$.
$\mathcal {B}\left ( \alpha _1,\, \dots \, , \alpha _k\right )$.
First, we suppose that there exists an ‘appropriate’ finite subset ![]() $A =\{a_0, \, \ldots \, ,a_m\} \subset \mathbb {R}$ that satisfies several conditions and deduce Theorem 4 using it. Then we prove the existence of this ‘appropriate’ A.
$A =\{a_0, \, \ldots \, ,a_m\} \subset \mathbb {R}$ that satisfies several conditions and deduce Theorem 4 using it. Then we prove the existence of this ‘appropriate’ A.
Lemma 1. Let k be a positive integer and ![]() $\alpha _1,\, \dots \, , \alpha _k$ be positive real numbers. Set
$\alpha _1,\, \dots \, , \alpha _k$ be positive real numbers. Set
 $$ \begin{align*} \Gamma = \big\{\gamma : \gamma &\leq \alpha_1+\dots+ \alpha_k \mbox{ and } \\ \gamma &= d_1\alpha_1+\dots+ d_k\alpha_k \mbox{ for some } d_1,\,\dots\,, d_k \in \mathbb{N}\cup\{0\} \big\}. \end{align*} $$
$$ \begin{align*} \Gamma = \big\{\gamma : \gamma &\leq \alpha_1+\dots+ \alpha_k \mbox{ and } \\ \gamma &= d_1\alpha_1+\dots+ d_k\alpha_k \mbox{ for some } d_1,\,\dots\,, d_k \in \mathbb{N}\cup\{0\} \big\}. \end{align*} $$Then there are positive integers ![]() $p_1,\, \dots \, , p_k$ and a sequence of real numbers
$p_1,\, \dots \, , p_k$ and a sequence of real numbers ![]() $a_0 < \dots < a_m$, where
$a_0 < \dots < a_m$, where ![]() $m=p_1+\dots +p_k$, such that the following two statements hold. First, for all positive integers l and r such that
$m=p_1+\dots +p_k$, such that the following two statements hold. First, for all positive integers l and r such that ![]() $l+r \leq m$, one has
$l+r \leq m$, one has
Second, for each ![]() $\gamma = d_1\alpha _1+\dots + d_k\alpha _k \in \Gamma $, one has
$\gamma = d_1\alpha _1+\dots + d_k\alpha _k \in \Gamma $, one has ![]() $d_1p_1+\dots + d_kp_k \leq m$ and
$d_1p_1+\dots + d_kp_k \leq m$ and
Proof of Theorem 4. This proof essentially repeats the argument from the previous subsection. Take ![]() $p_1, \,\ldots \, , p_k, m,$ and
$p_1, \,\ldots \, , p_k, m,$ and ![]() $a_0<\ldots <a_m$ as in Lemma 1. Set
$a_0<\ldots <a_m$ as in Lemma 1. Set ![]() $A = \{a_0, \,\ldots \,, a_m\}$. Define a bijection
$A = \{a_0, \,\ldots \,, a_m\}$. Define a bijection ![]() $a: [m]_0 \to A$ by
$a: [m]_0 \to A$ by ![]() $a(l) = a_l$ for all
$a(l) = a_l$ for all ![]() $l \in [m]_0$. This function is strictly increasing by construction. Given
$l \in [m]_0$. This function is strictly increasing by construction. Given ![]() $n \geq 1$, let
$n \geq 1$, let ![]() $f: [m]_0^n\to A^n$ be a bijection defined by
$f: [m]_0^n\to A^n$ be a bijection defined by ![]() $f((x_1,\,\ldots \,,x_n)) = (a_{x_1}, \,\dots \,, a_{x_n})$. Note that we have
$f((x_1,\,\ldots \,,x_n)) = (a_{x_1}, \,\dots \,, a_{x_n})$. Note that we have ![]() $f(\mathbf {x})_i = a(x_i) = a_{x_i}$ for all
$f(\mathbf {x})_i = a(x_i) = a_{x_i}$ for all ![]() $\mathbf {x} = (x_1,\,\ldots \,,x_n) \in [m]_0^n, 1 \leq i \leq n$.
$\mathbf {x} = (x_1,\,\ldots \,,x_n) \in [m]_0^n, 1 \leq i \leq n$.
Let ![]() $B \subset A^n$ be an arbitrary subset of cardinality
$B \subset A^n$ be an arbitrary subset of cardinality ![]() $\left |B\right |>m^n$. From Theorem 2 it follows that there is a subset
$\left |B\right |>m^n$. From Theorem 2 it follows that there is a subset ![]() $\{\mathbf {x}^0,\,\dots \,,\mathbf {x}^{m}\} \subset f^{-1}(B) \subset \left [m\right ]_0^n$ that is a copy of
$\{\mathbf {x}^0,\,\dots \,,\mathbf {x}^{m}\} \subset f^{-1}(B) \subset \left [m\right ]_0^n$ that is a copy of ![]() $\mathcal {B}_{m}$. Without loss of generality, we can assume that
$\mathcal {B}_{m}$. Without loss of generality, we can assume that ![]() $\|\mathbf {x}^s- \mathbf {x}^t\|_\infty = \left |s-t\right |$ for all
$\|\mathbf {x}^s- \mathbf {x}^t\|_\infty = \left |s-t\right |$ for all ![]() $s,t \in \left [m\right ]_0.$ In particular, it is easy to see that
$s,t \in \left [m\right ]_0.$ In particular, it is easy to see that ![]() $\{\mathbf {x}^0, \mathbf {x}^{p_1}, \mathbf {x}^{p_1+p_2},\, \dots \,, \mathbf {x}^{ p_1+p_2+\dots +p_k}\}$ is a copy of
$\{\mathbf {x}^0, \mathbf {x}^{p_1}, \mathbf {x}^{p_1+p_2},\, \dots \,, \mathbf {x}^{ p_1+p_2+\dots +p_k}\}$ is a copy of ![]() $\mathcal {B}\left ( p_1,\, \dots \, , p_k\right )$. For convenience, let us denote
$\mathcal {B}\left ( p_1,\, \dots \, , p_k\right )$. For convenience, let us denote ![]() $\mathbf {x}^0, \mathbf {x}^{p_1}, \mathbf {x}^{p_1+p_2},\, \dots \,, \mathbf {x}^{ p_1+p_2+\dots +p_k}$ by
$\mathbf {x}^0, \mathbf {x}^{p_1}, \mathbf {x}^{p_1+p_2},\, \dots \,, \mathbf {x}^{ p_1+p_2+\dots +p_k}$ by ![]() $\mathbf {y}^0, \mathbf {y}^{1}, \, \dots \,, \mathbf {y}^{k}$, respectively. They satisfy the following two properties:
$\mathbf {y}^0, \mathbf {y}^{1}, \, \dots \,, \mathbf {y}^{k}$, respectively. They satisfy the following two properties:
 $$ \begin{align} \mbox{for all } 0 \leq s<t\leq k &\mbox{ and for all } i \in \{1,\,\dots\,,n\}, \mbox{ one has } \nonumber \\ &\left|y_{i}^s-y_{i}^t\right| \leq p_{s+1}+\dots+p_{t}, \end{align} $$
$$ \begin{align} \mbox{for all } 0 \leq s<t\leq k &\mbox{ and for all } i \in \{1,\,\dots\,,n\}, \mbox{ one has } \nonumber \\ &\left|y_{i}^s-y_{i}^t\right| \leq p_{s+1}+\dots+p_{t}, \end{align} $$ $$ \begin{align} &\mbox{there is } j \in \{1,\,\dots\,,n\} \mbox{ such that } \nonumber \\ &\mbox{either } \begin{cases} y_{j}^0=0,\\ y_{j}^1=p_1,\\ \dots\\ y_{j}^k=p_1+\dots+p_k, \end{cases} \mbox{ or } \begin{cases} y_{j}^0=p_1+\dots+p_k,\\ y_{j}^1=p_1+\dots+p_{k-1},\\ \dots\\ y_{j}^k=0. \end{cases} \end{align} $$
$$ \begin{align} &\mbox{there is } j \in \{1,\,\dots\,,n\} \mbox{ such that } \nonumber \\ &\mbox{either } \begin{cases} y_{j}^0=0,\\ y_{j}^1=p_1,\\ \dots\\ y_{j}^k=p_1+\dots+p_k, \end{cases} \mbox{ or } \begin{cases} y_{j}^0=p_1+\dots+p_k,\\ y_{j}^1=p_1+\dots+p_{k-1},\\ \dots\\ y_{j}^k=0. \end{cases} \end{align} $$The first property immediately follows from ![]() $\|\mathbf y^s-\mathbf y^t\|_{\infty } = p_{s+1}+\dots +p_{t}$. As for the second, given that
$\|\mathbf y^s-\mathbf y^t\|_{\infty } = p_{s+1}+\dots +p_{t}$. As for the second, given that ![]() $\|\mathbf y^0-\mathbf y^k\|_{\infty } = m$ and
$\|\mathbf y^0-\mathbf y^k\|_{\infty } = m$ and  $\mathbf y^0, \mathbf y^k \in [m]_0^n,$ we must have a j such that either
$\mathbf y^0, \mathbf y^k \in [m]_0^n,$ we must have a j such that either  $y^0_j=0$ and
$y^0_j=0$ and  $y^k_j=m$ or
$y^k_j=m$ or  $y^0_j=m$ and
$y^0_j=m$ and  $y^k_j=0.$ In the rest of this subsection we assume that the former holds (the other case is symmetric). Then for each
$y^k_j=0.$ In the rest of this subsection we assume that the former holds (the other case is symmetric). Then for each ![]() $1\leq s\leq k-1,$ given the distances
$1\leq s\leq k-1,$ given the distances ![]() $\|\mathbf y^0-\mathbf y^s\|_{\infty } = p_1+\ldots +p_s, \|\mathbf y^s-\mathbf y^k\|_{\infty } = p_{s+1}+\ldots +p_k = m-\|\mathbf y^0-\mathbf y^s\|_{\infty },$ we clearly must have
$\|\mathbf y^0-\mathbf y^s\|_{\infty } = p_1+\ldots +p_s, \|\mathbf y^s-\mathbf y^k\|_{\infty } = p_{s+1}+\ldots +p_k = m-\|\mathbf y^0-\mathbf y^s\|_{\infty },$ we clearly must have  $y^s_j = p_1+\ldots +p_s.$
$y^s_j = p_1+\ldots +p_s.$
Using these two properties, we conclude the proof of Theorem 4 by showing that the set ![]() $\{f(\mathbf {y}^0), f(\mathbf {y}^{1}), \, \dots \,, f(\mathbf {y}^{k})\} \subset B$ is a copy of
$\{f(\mathbf {y}^0), f(\mathbf {y}^{1}), \, \dots \,, f(\mathbf {y}^{k})\} \subset B$ is a copy of ![]() $\mathcal {B}\left ( \alpha _1,\, \dots \, , \alpha _k\right )$.
$\mathcal {B}\left ( \alpha _1,\, \dots \, , \alpha _k\right )$.
On the one hand, given ![]() $0 \leq s<t\leq k$, we use (6) and (8) to get that
$0 \leq s<t\leq k$, we use (6) and (8) to get that ![]() $f(\mathbf {y}^s)_j = \alpha _1+\ldots +\alpha _s$ and
$f(\mathbf {y}^s)_j = \alpha _1+\ldots +\alpha _s$ and ![]() $f(\mathbf {y}^t)_j = \alpha _{1}+\ldots +\alpha _t$. This implies that
$f(\mathbf {y}^t)_j = \alpha _{1}+\ldots +\alpha _t$. This implies that
On the other hand, fix any ![]() $j'\in \{1, \,\dots \,, n\}$ and without loss of generality, assume that
$j'\in \{1, \,\dots \,, n\}$ and without loss of generality, assume that  $y^s_{j'}\geq y^t_{j'}.$ Using the monotonicity of
$y^s_{j'}\geq y^t_{j'}.$ Using the monotonicity of ![]() $a(\cdot )$ and (5), we get that
$a(\cdot )$ and (5), we get that
 $$ \begin{align} 0 \leq f(\mathbf{y}^s)_{j'} - f(\mathbf{y}^t)_{j'} = a(y^s_{j'}) - a(y^t_{j'}) = a(y^s_{j'}- y^t_{j'} +y^t_{j'}) - a(y^t_{j'}) \leq a(y^s_{j'}-y^t_{j'}). \end{align} $$
$$ \begin{align} 0 \leq f(\mathbf{y}^s)_{j'} - f(\mathbf{y}^t)_{j'} = a(y^s_{j'}) - a(y^t_{j'}) = a(y^s_{j'}- y^t_{j'} +y^t_{j'}) - a(y^t_{j'}) \leq a(y^s_{j'}-y^t_{j'}). \end{align} $$It follows from (7) that  $y^s_{j'}- y^t_{j'} \leq p_{s+1}+\dots +p_{t}$. Using the monotonicity of
$y^s_{j'}- y^t_{j'} \leq p_{s+1}+\dots +p_{t}$. Using the monotonicity of ![]() $a(\cdot )$ and (6), we get that
$a(\cdot )$ and (6), we get that
 $$ \begin{align} a(y^s_{j'}-y^t_{j'}) \leq a(p_{s+1}+\dots+p_{t}) = \alpha_{s+1}+\dots+\alpha_t. \end{align} $$
$$ \begin{align} a(y^s_{j'}-y^t_{j'}) \leq a(p_{s+1}+\dots+p_{t}) = \alpha_{s+1}+\dots+\alpha_t. \end{align} $$We substitute (11) in (10) and get that ![]() $|f(\mathbf {y}^s)_{j'} - f(\mathbf {y}^t)_{j'}| \leq \alpha _{s+1}+\dots +\alpha _t$. Together with (9) this gives
$|f(\mathbf {y}^s)_{j'} - f(\mathbf {y}^t)_{j'}| \leq \alpha _{s+1}+\dots +\alpha _t$. Together with (9) this gives ![]() $\|f(\mathbf {y}^s)-f(\mathbf {y}^t)\|_{\infty } = \alpha _{s+1}+\ldots +\alpha _t$ for all
$\|f(\mathbf {y}^s)-f(\mathbf {y}^t)\|_{\infty } = \alpha _{s+1}+\ldots +\alpha _t$ for all ![]() $0 \leq s<t\leq k$. This implies that
$0 \leq s<t\leq k$. This implies that ![]() $\{f(\mathbf {y}^0), f(\mathbf {y}^{1}), \, \dots \,, f(\mathbf {y}^{k})\} \subset B$ is indeed a copy of
$\{f(\mathbf {y}^0), f(\mathbf {y}^{1}), \, \dots \,, f(\mathbf {y}^{k})\} \subset B$ is indeed a copy of ![]() $\mathcal {B}\left ( \alpha _1,\, \dots \, , \alpha _k\right )$.
$\mathcal {B}\left ( \alpha _1,\, \dots \, , \alpha _k\right )$.
It only remains to prove Lemma 1 in order to finish the proof of Theorem 4.
2.5 The proof of Lemma 1
Suppose that ![]() $\Gamma = \{\gamma _0, \,\ldots \,, \gamma _t\}$, where
$\Gamma = \{\gamma _0, \,\ldots \,, \gamma _t\}$, where ![]() $\gamma _0 < \dots < \gamma _t$. In particular,
$\gamma _0 < \dots < \gamma _t$. In particular, ![]() $\gamma _0 = 0, \gamma _1 = \min _{1\leq i \leq k} \{\alpha _i\}$ and
$\gamma _0 = 0, \gamma _1 = \min _{1\leq i \leq k} \{\alpha _i\}$ and ![]() $\gamma _t = \alpha _1+\dots +\alpha _k$. Let
$\gamma _t = \alpha _1+\dots +\alpha _k$. Let ![]() $\gamma _{t+1}$ be the smallest linear combination of
$\gamma _{t+1}$ be the smallest linear combination of ![]() $\alpha _1,\, \dots \, , \alpha _k$ with nonnegative integer coefficients that is greater than
$\alpha _1,\, \dots \, , \alpha _k$ with nonnegative integer coefficients that is greater than ![]() $\gamma _t$; that is,
$\gamma _t$; that is,
 $$ \begin{align*} \gamma_{t+1} = \min\big\{\gamma: \gamma> \gamma_t \mbox{ and } \gamma = d_1\alpha_1+\dots+d_k\alpha_k \mbox{ for some } d_1, \,\ldots\, , d_k \in \mathbb{N}\cup\{0\}\big\}. \end{align*} $$
$$ \begin{align*} \gamma_{t+1} = \min\big\{\gamma: \gamma> \gamma_t \mbox{ and } \gamma = d_1\alpha_1+\dots+d_k\alpha_k \mbox{ for some } d_1, \,\ldots\, , d_k \in \mathbb{N}\cup\{0\}\big\}. \end{align*} $$ Put ![]() $\delta = \min _{1\leq i \leq t+1}\{\gamma _{i}-\gamma _{i-1}\}$ and
$\delta = \min _{1\leq i \leq t+1}\{\gamma _{i}-\gamma _{i-1}\}$ and ![]() $\theta = \gamma _{t}/\gamma _1$. Let
$\theta = \gamma _{t}/\gamma _1$. Let ![]() $q_0$ be a large enough integer such that
$q_0$ be a large enough integer such that
 $$ \begin{align*} \frac{1}{q_0} < \delta \ \ \text{and} \ \ \frac{\theta}{q_0^{1+1/k}} < \frac{1}{2q_0}. \end{align*} $$
$$ \begin{align*} \frac{1}{q_0} < \delta \ \ \text{and} \ \ \frac{\theta}{q_0^{1+1/k}} < \frac{1}{2q_0}. \end{align*} $$We will apply the following result of Dirichlet on Diophantine approximations (see, e.g., [Reference Schmidt32], Section 2, Theorem 1A).
Theorem 5. Given ![]() $\alpha _1',\, \dots \, , \alpha _k'\in \mathbb R$ and
$\alpha _1',\, \dots \, , \alpha _k'\in \mathbb R$ and ![]() $q_0'\in \mathbb N$, there is an integer
$q_0'\in \mathbb N$, there is an integer ![]() $q> q_0'$ such that the following holds. There are
$q> q_0'$ such that the following holds. There are ![]() $p_1,\, \dots \, , p_k \in \mathbb {Z}$ such that for each
$p_1,\, \dots \, , p_k \in \mathbb {Z}$ such that for each ![]() $1 \leq i \leq k$, one has
$1 \leq i \leq k$, one has
 $$ \begin{align*} \left|\alpha_i'-\frac{p_i}{q}\right| < \frac{1}{q^{1+1/k}}. \end{align*} $$
$$ \begin{align*} \left|\alpha_i'-\frac{p_i}{q}\right| < \frac{1}{q^{1+1/k}}. \end{align*} $$ Apply this theorem with ![]() $\alpha _i$ playing the role of
$\alpha _i$ playing the role of ![]() $\alpha ^{\prime }_i$ and
$\alpha ^{\prime }_i$ and ![]() $q_0$ playing the role of
$q_0$ playing the role of ![]() $q_0'$. Let
$q_0'$. Let ![]() $q, p_1, \,\dots \,, p_k$ be as in the conclusion of this theorem. Given
$q, p_1, \,\dots \,, p_k$ be as in the conclusion of this theorem. Given ![]() $\gamma \in {{\mathbb R}}$, denote by
$\gamma \in {{\mathbb R}}$, denote by ![]() $c(\gamma ) = \left \lfloor q\gamma \right \rceil $ the numerator of the best rational approximation of
$c(\gamma ) = \left \lfloor q\gamma \right \rceil $ the numerator of the best rational approximation of ![]() $\gamma $ with denominator equal to q. Note that
$\gamma $ with denominator equal to q. Note that  $ |\gamma - \frac {c(\gamma )}{q}| \leq \frac {1}{2q}$ for all
$ |\gamma - \frac {c(\gamma )}{q}| \leq \frac {1}{2q}$ for all ![]() $\gamma $. Moreover, if
$\gamma $. Moreover, if  $|\gamma - \frac {c}{q}| < \frac {1}{2q}$ for some
$|\gamma - \frac {c}{q}| < \frac {1}{2q}$ for some ![]() $\gamma \in {{\mathbb R}}, c \in \mathbb {N}$, then
$\gamma \in {{\mathbb R}}, c \in \mathbb {N}$, then ![]() $c = c(\gamma )$. The following two propositions show that the function
$c = c(\gamma )$. The following two propositions show that the function ![]() $c(\cdot )$ is strictly increasing and ‘linear’ on
$c(\cdot )$ is strictly increasing and ‘linear’ on ![]() $\Gamma $.
$\Gamma $.
Proposition 1. One has ![]() $c(\gamma _{i})> c(\gamma _{i-1})$ for all
$c(\gamma _{i})> c(\gamma _{i-1})$ for all ![]() $1 \leq i \leq t$.
$1 \leq i \leq t$.
Proof . Given ![]() $1 \leq i \leq t$, it is clear that
$1 \leq i \leq t$, it is clear that ![]() $c(\gamma _{i}) \geq c(\gamma _{i-1})$. Assume that
$c(\gamma _{i}) \geq c(\gamma _{i-1})$. Assume that ![]() $c(\gamma _{i}) = c(\gamma _{i-1})$. Now it follows by the triangle inequality that
$c(\gamma _{i}) = c(\gamma _{i-1})$. Now it follows by the triangle inequality that
 $$ \begin{align*} \delta \leq \left|\gamma_{i}-\gamma_{i-1}\right| \leq \left|\gamma_{i}-\frac{c(\gamma_{i})}{q}\right| + \left|\gamma_{i-1}- \frac{c(\gamma_{i-1})}{q}\right| \leq \frac{1}{2q} + \frac{1}{2q} = \frac{1}{q} < \frac{1}{q_0}, \end{align*} $$
$$ \begin{align*} \delta \leq \left|\gamma_{i}-\gamma_{i-1}\right| \leq \left|\gamma_{i}-\frac{c(\gamma_{i})}{q}\right| + \left|\gamma_{i-1}- \frac{c(\gamma_{i-1})}{q}\right| \leq \frac{1}{2q} + \frac{1}{2q} = \frac{1}{q} < \frac{1}{q_0}, \end{align*} $$which contradicts the definition of ![]() $q_0$.
$q_0$.
Proposition 2. Let ![]() $\gamma = d_1\alpha _1+\dots + d_k\alpha _k \in \Gamma $. Then
$\gamma = d_1\alpha _1+\dots + d_k\alpha _k \in \Gamma $. Then ![]() $c(\gamma ) = d_1p_1+\dots + d_kp_k$. In particular, for all
$c(\gamma ) = d_1p_1+\dots + d_kp_k$. In particular, for all ![]() $\gamma _{i}, \gamma _{i'} \in \Gamma $ such that
$\gamma _{i}, \gamma _{i'} \in \Gamma $ such that ![]() $\gamma _{i}+\gamma _{i'} \in \Gamma $, one has
$\gamma _{i}+\gamma _{i'} \in \Gamma $, one has ![]() $c(\gamma _{i}+\gamma _{i'}) = c(\gamma _{i})+c(\gamma _{i'})$.
$c(\gamma _{i}+\gamma _{i'}) = c(\gamma _{i})+c(\gamma _{i'})$.
Proof . Set  $ \varepsilon _i = \left |\alpha _i- \frac {p_i}{q}\right |$ and recall that
$ \varepsilon _i = \left |\alpha _i- \frac {p_i}{q}\right |$ and recall that ![]() $\varepsilon _i\leq q^{-(1+1/k)}$. Recall that
$\varepsilon _i\leq q^{-(1+1/k)}$. Recall that
 $$ \begin{align*} \theta= \frac{\gamma_t}{\gamma_1} = \frac{\alpha_1+ \dots+\alpha_k}{\min_{1\leq i \leq k} \left\{\alpha_i\right\}}. \end{align*} $$
$$ \begin{align*} \theta= \frac{\gamma_t}{\gamma_1} = \frac{\alpha_1+ \dots+\alpha_k}{\min_{1\leq i \leq k} \left\{\alpha_i\right\}}. \end{align*} $$Because ![]() $\gamma \leq \alpha _1+\dots +\alpha _k$, it is easy to see that
$\gamma \leq \alpha _1+\dots +\alpha _k$, it is easy to see that ![]() $d_1+\dots + d_k \leq \theta $. Now it is clear that
$d_1+\dots + d_k \leq \theta $. Now it is clear that
 $$ \begin{align*} \left|\gamma - \frac{d_1p_1+\dots+ d_kp_k}{q}\right| \leq d_1\varepsilon_1+\dots+ d_k\varepsilon_k \leq \frac{d_1+\dots+ d_k}{q^{1+1/k}} \leq \frac{\theta}{q^{1+1/k}} < \frac{1}{2q}, \end{align*} $$
$$ \begin{align*} \left|\gamma - \frac{d_1p_1+\dots+ d_kp_k}{q}\right| \leq d_1\varepsilon_1+\dots+ d_k\varepsilon_k \leq \frac{d_1+\dots+ d_k}{q^{1+1/k}} \leq \frac{\theta}{q^{1+1/k}} < \frac{1}{2q}, \end{align*} $$because ![]() $q> q_0$. This implies that
$q> q_0$. This implies that ![]() $c(\gamma ) = d_1p_1+\ldots +d_kp_k.$ The second part of the proposition is immediate from the first part by the ‘linearity’ of
$c(\gamma ) = d_1p_1+\ldots +d_kp_k.$ The second part of the proposition is immediate from the first part by the ‘linearity’ of ![]() $c(\gamma )$ on
$c(\gamma )$ on ![]() $\gamma \in \Gamma $.
$\gamma \in \Gamma $.
Proposition 2 implies that ![]() $c(\gamma _0) = 0$ and
$c(\gamma _0) = 0$ and ![]() $c(\gamma _{t}) = p_1+\dots +p_k=m$. We define the desired sequence
$c(\gamma _{t}) = p_1+\dots +p_k=m$. We define the desired sequence ![]() $a_0, \,\dots \,, a_m$ as follows. Set
$a_0, \,\dots \,, a_m$ as follows. Set ![]() $a_0 = 0$. Given
$a_0 = 0$. Given ![]() $0 < l \leq m$, it follows from Proposition 1 that there is a unique
$0 < l \leq m$, it follows from Proposition 1 that there is a unique ![]() $1\leq i \leq t$ such that
$1\leq i \leq t$ such that ![]() $ c(\gamma _{i-1}) < l \leq c(\gamma _{i})$. We set
$ c(\gamma _{i-1}) < l \leq c(\gamma _{i})$. We set
 $$ \begin{align*} a_l = \gamma_{i} - \frac{c(\gamma_{i})-l}{2m}\delta. \end{align*} $$
$$ \begin{align*} a_l = \gamma_{i} - \frac{c(\gamma_{i})-l}{2m}\delta. \end{align*} $$To finish the proof of Lemma 1 we need to verify that this sequence is strictly increasing and satisfies (5) and (6).
First, we show that ![]() $a_{l}> a_{l-1}$ for all
$a_{l}> a_{l-1}$ for all ![]() $1 \leq l \leq m$. If there is
$1 \leq l \leq m$. If there is ![]() $1 \leq i \leq t$ such that
$1 \leq i \leq t$ such that ![]() $c(\gamma _{i-1})< l-1 < l \leq c(\gamma _{i})$, then
$c(\gamma _{i-1})< l-1 < l \leq c(\gamma _{i})$, then  $a_{l} - a_{l-1} = \frac {1}{2m}\delta> 0$. Moreover, for all
$a_{l} - a_{l-1} = \frac {1}{2m}\delta> 0$. Moreover, for all ![]() $1 \leq i \leq t$, one has
$1 \leq i \leq t$, one has
 $$ \begin{align*} a_{c(\gamma_{i-1})+1}-a_{c(\gamma_{i-1})} = \left( \gamma_{i}- \frac{c(\gamma_{i}) -c(\gamma_{i-1})-1}{2m}\delta\right)-\gamma_{i-1}> (\gamma_{i} - \gamma_{i-1}) - \frac{\delta}{2} \geq \frac{\delta}{2} > 0. \end{align*} $$
$$ \begin{align*} a_{c(\gamma_{i-1})+1}-a_{c(\gamma_{i-1})} = \left( \gamma_{i}- \frac{c(\gamma_{i}) -c(\gamma_{i-1})-1}{2m}\delta\right)-\gamma_{i-1}> (\gamma_{i} - \gamma_{i-1}) - \frac{\delta}{2} \geq \frac{\delta}{2} > 0. \end{align*} $$ Second, for all ![]() $0 \leq i \leq t$ we have
$0 \leq i \leq t$ we have ![]() $a_{c(\gamma _{i})} = \gamma _{i}$ by construction. Therefore, Proposition 2 implies that the sequence
$a_{c(\gamma _{i})} = \gamma _{i}$ by construction. Therefore, Proposition 2 implies that the sequence ![]() $a_0, \,\dots \,, a_m$ satisfies (6).
$a_0, \,\dots \,, a_m$ satisfies (6).
Finally, given ![]() $0 \leq l,r \leq m$ such that
$0 \leq l,r \leq m$ such that ![]() $l+r \leq m$, we need to check that
$l+r \leq m$, we need to check that ![]() $a_{l+r} \leq a_l + a_r$. Observe that there is nothing to check if either
$a_{l+r} \leq a_l + a_r$. Observe that there is nothing to check if either ![]() $l=0$ or
$l=0$ or ![]() $r=0$. Thus, without loss of generality, we assume that both l and r are greater than
$r=0$. Thus, without loss of generality, we assume that both l and r are greater than ![]() $0$. Under this assumption there are unique
$0$. Under this assumption there are unique ![]() $1 \leq i, i',j \leq t$ such that
$1 \leq i, i',j \leq t$ such that ![]() $c(\gamma _{i-1}) < l \leq c(\gamma _{i})$,
$c(\gamma _{i-1}) < l \leq c(\gamma _{i})$, ![]() $c(\gamma _{i'-1}) < r \leq c(\gamma _{i'})$ and
$c(\gamma _{i'-1}) < r \leq c(\gamma _{i'})$ and ![]() $c(\gamma _{j-1}) < l+r \leq c(\gamma _{j})$. Set
$c(\gamma _{j-1}) < l+r \leq c(\gamma _{j})$. Set ![]() $\gamma = \gamma _{i}+\gamma _{i'}$.
$\gamma = \gamma _{i}+\gamma _{i'}$.
Assume that ![]() $\gamma < \gamma _{j}$. Then
$\gamma < \gamma _{j}$. Then ![]() $\gamma \in \Gamma $ and we can apply Proposition 2 to get that
$\gamma \in \Gamma $ and we can apply Proposition 2 to get that ![]() $c(\gamma _{j-1}) <l+r \leq c(\gamma _{i})+c(\gamma _{i'}) = c(\gamma )$. Thus, by Proposition 1 we get that
$c(\gamma _{j-1}) <l+r \leq c(\gamma _{i})+c(\gamma _{i'}) = c(\gamma )$. Thus, by Proposition 1 we get that ![]() $\gamma> \gamma _{j-1}$ and so
$\gamma> \gamma _{j-1}$ and so ![]() $\gamma \geq \gamma _j$, a contradiction. Thus,
$\gamma \geq \gamma _j$, a contradiction. Thus, ![]() $\gamma \geq \gamma _{j}$.
$\gamma \geq \gamma _{j}$.
Suppose that ![]() $\gamma = \gamma _{j}$. Then Proposition 2 implies that
$\gamma = \gamma _{j}$. Then Proposition 2 implies that ![]() $c(\gamma ) = c(\gamma _{i})+ c(\gamma _{i'})$, and we have
$c(\gamma ) = c(\gamma _{i})+ c(\gamma _{i'})$, and we have
 $$ \begin{align*} a_l+a_r-a_{l+r} =& \left( \gamma_{i} - \frac{c(\gamma_{i})-l}{2m}\delta \right) + \left( \gamma_{i'} - \frac{c(\gamma_{i'})-r}{2m}\delta \right) - \left( \gamma_{j} - \frac{c(\gamma_{j})-l-r}{2m}\delta \right) \\ =& (\gamma_{i}+\gamma_{i'}-\gamma)+\frac{c(\gamma)-c(\gamma_{i})- c(\gamma_{i'})}{2m}\delta = 0. \end{align*} $$
$$ \begin{align*} a_l+a_r-a_{l+r} =& \left( \gamma_{i} - \frac{c(\gamma_{i})-l}{2m}\delta \right) + \left( \gamma_{i'} - \frac{c(\gamma_{i'})-r}{2m}\delta \right) - \left( \gamma_{j} - \frac{c(\gamma_{j})-l-r}{2m}\delta \right) \\ =& (\gamma_{i}+\gamma_{i'}-\gamma)+\frac{c(\gamma)-c(\gamma_{i})- c(\gamma_{i'})}{2m}\delta = 0. \end{align*} $$ Suppose that ![]() $\gamma> \gamma _{j}$ and, consequently,
$\gamma> \gamma _{j}$ and, consequently, ![]() $\gamma \geq \gamma _{j+1}$. The sequence of
$\gamma \geq \gamma _{j+1}$. The sequence of ![]() $a_i$s is increasing, and so
$a_i$s is increasing, and so ![]() $a_{l+r} \leq a_{c(\gamma _{j})} = \gamma _{j}$. We conclude that
$a_{l+r} \leq a_{c(\gamma _{j})} = \gamma _{j}$. We conclude that
 $$ \begin{align*} a_l+a_r-a_{l+r} \geq& \left( \gamma_{i} - \frac{c(\gamma_{i})-l}{2m}\delta \right) + \left( \gamma_{i'} - \frac{c(\gamma_{i'})-r}{2m}\delta \right) - \gamma_{j} \\>& (\gamma_{i}+\gamma_{i'}-\gamma_{j}) -\frac{\delta}{2} -\frac{\delta}{2} \geq (\gamma_{j+1}-\gamma_{j}) -\delta \geq 0. \end{align*} $$
$$ \begin{align*} a_l+a_r-a_{l+r} \geq& \left( \gamma_{i} - \frac{c(\gamma_{i})-l}{2m}\delta \right) + \left( \gamma_{i'} - \frac{c(\gamma_{i'})-r}{2m}\delta \right) - \gamma_{j} \\>& (\gamma_{i}+\gamma_{i'}-\gamma_{j}) -\frac{\delta}{2} -\frac{\delta}{2} \geq (\gamma_{j+1}-\gamma_{j}) -\delta \geq 0. \end{align*} $$This concludes the proof of Lemma 1.
3 The proof of Theorem 1
We begin with some notation that was introduced (in a slightly different form) by Frankl and Rödl [Reference Frankl and Rödl10]. Given a real ![]() $p \ge 1$ or
$p \ge 1$ or ![]() $p=\infty $, a metric space
$p=\infty $, a metric space ![]() $\mathcal {M}$ is called
$\mathcal {M}$ is called ![]() $\ell _p-$super-Ramsey (with parameters
$\ell _p-$super-Ramsey (with parameters ![]() $F_{\mathcal {M}}$ and
$F_{\mathcal {M}}$ and ![]() $\chi _{\mathcal {M}}$) if there exist constants
$\chi _{\mathcal {M}}$) if there exist constants ![]() $F_{\mathcal {M}} \geq \chi _{\mathcal {M}}> 1$ and a sequence of sets
$F_{\mathcal {M}} \geq \chi _{\mathcal {M}}> 1$ and a sequence of sets ![]() $V_{\mathcal {M}}(n) \subset \mathbb {R}^n_p$ such that
$V_{\mathcal {M}}(n) \subset \mathbb {R}^n_p$ such that ![]() $\left | V_{\mathcal {M}}(n)\right | \leq \left ( F_{\mathcal {M}}+o(1) \right )^n$ and each subset of
$\left | V_{\mathcal {M}}(n)\right | \leq \left ( F_{\mathcal {M}}+o(1) \right )^n$ and each subset of ![]() $V_{\mathcal M}(n)$ of size greater than
$V_{\mathcal M}(n)$ of size greater than ![]() $\left |V_{\mathcal M} (n)\right | \left ( \chi _{\mathcal {M}}+o(1) \right )^{-n}$,
$\left |V_{\mathcal M} (n)\right | \left ( \chi _{\mathcal {M}}+o(1) \right )^{-n}$, ![]() $n \rightarrow \infty $, contains a copy of
$n \rightarrow \infty $, contains a copy of ![]() $\mathcal M$. An easy application of the pigeonhole principle as in Corollary 1 shows that for each
$\mathcal M$. An easy application of the pigeonhole principle as in Corollary 1 shows that for each ![]() $\ell _p-$super-Ramsey metric space
$\ell _p-$super-Ramsey metric space ![]() $\mathcal {M}$ with parameters
$\mathcal {M}$ with parameters ![]() $F_{\mathcal {M}}$ and
$F_{\mathcal {M}}$ and ![]() $\chi _{\mathcal {M}}$ that contains at least two points, one has
$\chi _{\mathcal {M}}$ that contains at least two points, one has ![]() $\chi (\mathbb {R}^n_p; \mathcal {M}) \geq \left ( \chi _{\mathcal {M}}+o(1) \right )^n$ as
$\chi (\mathbb {R}^n_p; \mathcal {M}) \geq \left ( \chi _{\mathcal {M}}+o(1) \right )^n$ as ![]() $n \rightarrow \infty $. So, the
$n \rightarrow \infty $. So, the ![]() $\ell _p-$super-Ramsey property implies the exponentially
$\ell _p-$super-Ramsey property implies the exponentially ![]() $\ell _p-$Ramsey one. Therefore, in order to prove Theorem 1 it is sufficient to prove the following statement.
$\ell _p-$Ramsey one. Therefore, in order to prove Theorem 1 it is sufficient to prove the following statement.
Theorem 6. Any finite metric space is ![]() $\ell _\infty -$super-Ramsey.
$\ell _\infty -$super-Ramsey.
Given a real ![]() $p\ge 1$ and given two metric spaces
$p\ge 1$ and given two metric spaces ![]() $\mathcal {X} = \left ( X, \rho _X\right )$ and
$\mathcal {X} = \left ( X, \rho _X\right )$ and ![]() $\mathcal {Y} = \left ( Y, \rho _Y\right )$, their Cartesian product
$\mathcal {Y} = \left ( Y, \rho _Y\right )$, their Cartesian product ![]() $\mathcal {X} \times \mathcal {Y}$ is the metric space
$\mathcal {X} \times \mathcal {Y}$ is the metric space ![]() $\left ( X\times Y, \rho \right )$, where
$\left ( X\times Y, \rho \right )$, where
for all ![]() $x_1,x_2 \in X$ and
$x_1,x_2 \in X$ and ![]() $y_1,y_2 \in Y$. In a special case
$y_1,y_2 \in Y$. In a special case ![]() $p=\infty $, to which we devote the present article, we set
$p=\infty $, to which we devote the present article, we set
Frankl and Rödl [Reference Frankl and Rödl10] showed that a Cartesian product of any two ![]() $\ell _2-$super-Ramsey finite metric spaces is also
$\ell _2-$super-Ramsey finite metric spaces is also ![]() $\ell _2-$super-Ramsey. Their proof actually works for the
$\ell _2-$super-Ramsey. Their proof actually works for the ![]() $\ell _p$ metric for all p. In case
$\ell _p$ metric for all p. In case ![]() $p=\infty $, the proof is spelled out in a paper by the second author [Reference Sagdeev29], where he also gives an explicit dependence of the parameters.
$p=\infty $, the proof is spelled out in a paper by the second author [Reference Sagdeev29], where he also gives an explicit dependence of the parameters.
Theorem 7 [Reference Frankl and Rödl10], Theorem 2.2; [Reference Sagdeev29], Proposition 1.
Let ![]() $\mathcal {X}$ and
$\mathcal {X}$ and ![]() $\mathcal {Y}$ be
$\mathcal {Y}$ be ![]() $\ell _\infty -$super-Ramsey finite metric spaces. Then
$\ell _\infty -$super-Ramsey finite metric spaces. Then ![]() $\mathcal {X} \times \mathcal {Y}$ is also
$\mathcal {X} \times \mathcal {Y}$ is also ![]() $\ell _\infty -$super-Ramsey.
$\ell _\infty -$super-Ramsey.
Note that Theorem 4 implies that each baton ![]() $\mathcal {B}$ is
$\mathcal {B}$ is ![]() $\ell _\infty -$super-Ramsey (with the parameters
$\ell _\infty -$super-Ramsey (with the parameters ![]() $F_{\mathcal {B}} = m+1$ and
$F_{\mathcal {B}} = m+1$ and  $\chi _{\mathcal {B}} = \frac {m+1}{m}$, where m is from Theorem 4). Thus, by Theorem 7, we conclude that for all
$\chi _{\mathcal {B}} = \frac {m+1}{m}$, where m is from Theorem 4). Thus, by Theorem 7, we conclude that for all ![]() $d \in \mathbb {N}$, each
$d \in \mathbb {N}$, each ![]() $d-$dimensional grid – that is, a Cartesian product of d batons – is also
$d-$dimensional grid – that is, a Cartesian product of d batons – is also ![]() $\ell _\infty -$super-Ramsey. It should be clear that the property of being
$\ell _\infty -$super-Ramsey. It should be clear that the property of being ![]() $\ell _\infty -$super-Ramsey (with parameters F and
$\ell _\infty -$super-Ramsey (with parameters F and ![]() $\chi $) is hereditary with respect to taking subsets. Because each finite subset
$\chi $) is hereditary with respect to taking subsets. Because each finite subset ![]() $\{\mathbf x^0, \,\ldots \, ,\mathbf x^k\}\subset {{\mathbb R}}^d$ is a subset of the
$\{\mathbf x^0, \,\ldots \, ,\mathbf x^k\}\subset {{\mathbb R}}^d$ is a subset of the ![]() $d-$dimensional grid
$d-$dimensional grid  $\prod _{i=1}^d\{x^0_i, \,\ldots \, , x^k_i\}$, we get the following corollary.
$\prod _{i=1}^d\{x^0_i, \,\ldots \, , x^k_i\}$, we get the following corollary.
Corollary 2. Given ![]() $d \in \mathbb {N}$, any finite
$d \in \mathbb {N}$, any finite ![]() $S\subset {{\mathbb R}}^d_\infty $ is
$S\subset {{\mathbb R}}^d_\infty $ is ![]() $\ell _\infty -$super-Ramsey.
$\ell _\infty -$super-Ramsey.
The following simple proposition due to Fréchet (see [Reference Matoušek19]) concludes the proof of Theorem 6.
Lemma 2. Any metric space ![]() $\mathcal M = (M,\rho )$ with
$\mathcal M = (M,\rho )$ with ![]() $|M| = d$ is isometric to a subset
$|M| = d$ is isometric to a subset ![]() $S\subset {{\mathbb R}}^d_{\infty }$.
$S\subset {{\mathbb R}}^d_{\infty }$.
Proof . Let ![]() $M = \{u_1,\ldots , u_d\}$. The desired set S is given by the rows of the distance matrix
$M = \{u_1,\ldots , u_d\}$. The desired set S is given by the rows of the distance matrix  $D= \big (\rho (u_i,u_j)\big )_{i,j=1}^d$.
$D= \big (\rho (u_i,u_j)\big )_{i,j=1}^d$.
4 Upper bounds
Let ![]() $\mathcal {M} = \left (M, \rho _M\right )$ be a finite metric space that contains at least two points. Theorem 1 guarantees the existence of an exponential lower bound on
$\mathcal {M} = \left (M, \rho _M\right )$ be a finite metric space that contains at least two points. Theorem 1 guarantees the existence of an exponential lower bound on ![]() $\chi (\mathbb {R}^n_\infty; \mathcal {M})$. Recall that we also have
$\chi (\mathbb {R}^n_\infty; \mathcal {M})$. Recall that we also have ![]() $\chi ({{\mathbb R}}^n_\infty ;\mathcal M)\leq \chi ({{\mathbb R}}^n_{\infty })=2^n$. In this section we give a better upper bound. Essentially the same proof appeared in [Reference Prosanov24], [Reference Prosanov23].
$\chi ({{\mathbb R}}^n_\infty ;\mathcal M)\leq \chi ({{\mathbb R}}^n_{\infty })=2^n$. In this section we give a better upper bound. Essentially the same proof appeared in [Reference Prosanov24], [Reference Prosanov23].
For a metric space ![]() $\mathcal M$, let
$\mathcal M$, let ![]() $d( \mathcal {M})$ be the diameter of
$d( \mathcal {M})$ be the diameter of ![]() $\mathcal {M}$; that is, the maximum over distances between pair of points of
$\mathcal {M}$; that is, the maximum over distances between pair of points of ![]() $\mathcal M$. Let
$\mathcal M$. Let ![]() $l( \mathcal {M})> 0$ be the smallest number such that for each two points
$l( \mathcal {M})> 0$ be the smallest number such that for each two points ![]() $x,y \in M$ there are
$x,y \in M$ there are ![]() $z_0, z_1, \,\dots \,, z_t \in M$ such that
$z_0, z_1, \,\dots \,, z_t \in M$ such that ![]() $z_0=x, z_t = y$, and
$z_0=x, z_t = y$, and ![]() $\rho _M(z_i,z_{i+1}) \leq l$ for all
$\rho _M(z_i,z_{i+1}) \leq l$ for all ![]() $0 \le i \le t-1$.
$0 \le i \le t-1$.
In what follows, we denote the natural logarithm by ![]() $\log (\cdot )$.
$\log (\cdot )$.
Theorem 8. For each finite metric space ![]() $\mathcal {M}$ that contains at least two points, one has
$\mathcal {M}$ that contains at least two points, one has
 $$ \begin{align*}\chi(\mathbb{R}^n_\infty; \mathcal{M}) < (1+o(1))n\log n\left( 1+\frac{l(\mathcal M)}{d(\mathcal M)}\right)^n\end{align*} $$
$$ \begin{align*}\chi(\mathbb{R}^n_\infty; \mathcal{M}) < (1+o(1))n\log n\left( 1+\frac{l(\mathcal M)}{d(\mathcal M)}\right)^n\end{align*} $$as ![]() $n \rightarrow \infty $.
$n \rightarrow \infty $.
Proof . Fix arbitrary positive ![]() $d' < d(\mathcal M)$ and
$d' < d(\mathcal M)$ and ![]() $l'>l(\mathcal M)$. Let
$l'>l(\mathcal M)$. Let ![]() $C = \left [0;d'\right ]^n$ be an
$C = \left [0;d'\right ]^n$ be an ![]() $n-$dimensional cube and put
$n-$dimensional cube and put ![]() $\mathcal {C}=\bigsqcup _{\mathbf {v} \in \mathbb {Z}^n}\left ( C+\left ( d'+l'\right )\mathbf {v} \right ) \subset {{\mathbb R}}^n$.
$\mathcal {C}=\bigsqcup _{\mathbf {v} \in \mathbb {Z}^n}\left ( C+\left ( d'+l'\right )\mathbf {v} \right ) \subset {{\mathbb R}}^n$.
Assume that there is a subset ![]() $M' \subset \mathcal {C}$ that is a copy of
$M' \subset \mathcal {C}$ that is a copy of ![]() $\mathcal M$ and consider any
$\mathcal M$ and consider any ![]() $ \mathbf {x}, \mathbf {y} \in M'$. Let
$ \mathbf {x}, \mathbf {y} \in M'$. Let ![]() $\mathbf {z}_0, \mathbf {z}_1, \,\dots \,, \mathbf {z}_t \in M'$ be a sequence of points of
$\mathbf {z}_0, \mathbf {z}_1, \,\dots \,, \mathbf {z}_t \in M'$ be a sequence of points of ![]() $M'$ such that
$M'$ such that ![]() $\mathbf {z}_0=\mathbf {x}, \mathbf {z}_t = \mathbf {y}$ and
$\mathbf {z}_0=\mathbf {x}, \mathbf {z}_t = \mathbf {y}$ and ![]() $\|\mathbf {z}_i-\mathbf {z}_{i+1}\|_\infty \leq l(M)$ for all
$\|\mathbf {z}_i-\mathbf {z}_{i+1}\|_\infty \leq l(M)$ for all ![]() $0 \le i \le t-1$. Because the distance between any two different translates of C in
$0 \le i \le t-1$. Because the distance between any two different translates of C in ![]() $\mathcal {C}$ is at least
$\mathcal {C}$ is at least ![]() $l'> l(\mathcal {M})$, we conclude that
$l'> l(\mathcal {M})$, we conclude that ![]() $\mathbf {z}_i$ and
$\mathbf {z}_i$ and ![]() $\mathbf {z}_{i+1}$ belong to the same translate of C for all
$\mathbf {z}_{i+1}$ belong to the same translate of C for all ![]() $0 \le i \le t-1$. Hence,
$0 \le i \le t-1$. Hence, ![]() $\mathbf {x}$ and
$\mathbf {x}$ and ![]() $\mathbf {y}$ belong to the same translate of C, and thus
$\mathbf {y}$ belong to the same translate of C, and thus ![]() $M'$ lies entirely within the same translate of C. However, this is impossible, because the diameter of C is equal to
$M'$ lies entirely within the same translate of C. However, this is impossible, because the diameter of C is equal to ![]() $d' < d(\mathcal {M})$. Thus,
$d' < d(\mathcal {M})$. Thus, ![]() $\mathcal C$ does not contain a copy of
$\mathcal C$ does not contain a copy of ![]() $\mathcal M$.
$\mathcal M$.
To conclude the proof, we use the classical Erdős–Rogers result [Reference Erdős and Rogers8], which states that  $(1+o(1))n\log n\left (1+\frac {l'}{d'}\right )^n $ translates of
$(1+o(1))n\log n\left (1+\frac {l'}{d'}\right )^n $ translates of ![]() $\mathcal C$ are sufficient to cover
$\mathcal C$ are sufficient to cover ![]() ${{\mathbb R}}^n$. Colour all points of the ith translate of
${{\mathbb R}}^n$. Colour all points of the ith translate of ![]() $\mathcal C$ from the covering in one colour. This is clearly a valid colouring. We also remark that
$\mathcal C$ from the covering in one colour. This is clearly a valid colouring. We also remark that ![]() $o(1)$ in the last formula does not depend on
$o(1)$ in the last formula does not depend on ![]() $d'$ and
$d'$ and ![]() $l'$. Hence, letting
$l'$. Hence, letting ![]() $d' \rightarrow d$ and
$d' \rightarrow d$ and ![]() $l' \rightarrow l$, we obtain the claimed upper bound.
$l' \rightarrow l$, we obtain the claimed upper bound.
It is straightforward from the definition that ![]() $l(\mathcal {M}) \leq d(\mathcal {M})$ for all metric spaces
$l(\mathcal {M}) \leq d(\mathcal {M})$ for all metric spaces ![]() $\mathcal {M}$. Note that the upper bound from Theorem 8 is slightly worse than the trivial bound
$\mathcal {M}$. Note that the upper bound from Theorem 8 is slightly worse than the trivial bound ![]() $\chi (\mathbb {R}^n_\infty; \mathcal {M}) \leq 2^n$ if
$\chi (\mathbb {R}^n_\infty; \mathcal {M}) \leq 2^n$ if ![]() $l(\mathcal {M}) = d(\mathcal {M})$ but is asymptotically better if
$l(\mathcal {M}) = d(\mathcal {M})$ but is asymptotically better if ![]() $l(\mathcal {M}) < d(\mathcal {M})$.
$l(\mathcal {M}) < d(\mathcal {M})$.
Let ![]() $\mathcal {M}$ be a metric space such that
$\mathcal {M}$ be a metric space such that ![]() $l(\mathcal {M}) < d(\mathcal {M})$ and
$l(\mathcal {M}) < d(\mathcal {M})$ and  $\frac {l(\mathcal {M})}{d(\mathcal {M})} \in \mathbb {Q}$. Applying a proper homothety, one can assume without loss of generality that
$\frac {l(\mathcal {M})}{d(\mathcal {M})} \in \mathbb {Q}$. Applying a proper homothety, one can assume without loss of generality that ![]() $l(\mathcal {M}), d(\mathcal {M}) \in \mathbb {N}$. We can slightly improve the result of Theorem 8 for such metric spaces using a simpler probabilistic argument.
$l(\mathcal {M}), d(\mathcal {M}) \in \mathbb {N}$. We can slightly improve the result of Theorem 8 for such metric spaces using a simpler probabilistic argument.
Theorem 9. Let ![]() $\mathcal {M}= (M,\rho _M)$ be a finite metric space such that
$\mathcal {M}= (M,\rho _M)$ be a finite metric space such that ![]() $|M| \ge 2$,
$|M| \ge 2$, ![]() $l(\mathcal {M})$ and
$l(\mathcal {M})$ and ![]() $d(\mathcal {M})$ are integers satisfying
$d(\mathcal {M})$ are integers satisfying ![]() $l(\mathcal {M}) < d(\mathcal {M})$. Then, we have
$l(\mathcal {M}) < d(\mathcal {M})$. Then, we have
 $$ \begin{align*}\chi(\mathbb{R}^n_\infty; \mathcal{M}) < (1+o(1))n\log d(\mathcal{M})\left( 1+\frac{l(\mathcal M)}{d(\mathcal M)}\right)^n\end{align*} $$
$$ \begin{align*}\chi(\mathbb{R}^n_\infty; \mathcal{M}) < (1+o(1))n\log d(\mathcal{M})\left( 1+\frac{l(\mathcal M)}{d(\mathcal M)}\right)^n\end{align*} $$as ![]() $n \rightarrow \infty $.
$n \rightarrow \infty $.
Proof . For shorthand, denote ![]() $l = l(\mathcal {M}), d = d(\mathcal {M})$ and
$l = l(\mathcal {M}), d = d(\mathcal {M})$ and ![]() $m=d+l \in \mathbb {N}$. Let
$m=d+l \in \mathbb {N}$. Let ![]() $C = [0;d)^n$ and
$C = [0;d)^n$ and ![]() $\mathcal {C}=\bigsqcup _{\mathbf {v} \in \mathbb {Z}^n}\left ( C+m\mathbf {v} \right ) \subset {{\mathbb R}}^n$. As in the proof of Theorem 8, one can see that
$\mathcal {C}=\bigsqcup _{\mathbf {v} \in \mathbb {Z}^n}\left ( C+m\mathbf {v} \right ) \subset {{\mathbb R}}^n$. As in the proof of Theorem 8, one can see that ![]() $\mathcal C$ does not contain a copy of
$\mathcal C$ does not contain a copy of ![]() $\mathcal M$, and we can use the same colour for all of its points. It only remains to cover
$\mathcal M$, and we can use the same colour for all of its points. It only remains to cover ![]() ${{\mathbb R}}^n$ using as few translates of
${{\mathbb R}}^n$ using as few translates of ![]() $\mathcal {C}$ as possible.
$\mathcal {C}$ as possible.
Set  $s = \lfloor n\log d \left ( \frac {m}{d}\right )^n \rfloor $ and let
$s = \lfloor n\log d \left ( \frac {m}{d}\right )^n \rfloor $ and let ![]() $\mathbf {v}_1, \,\dots \, ,\mathbf {v}_s$ be the elements of
$\mathbf {v}_1, \,\dots \, ,\mathbf {v}_s$ be the elements of ![]() $[m-1]_0^n$ chosen uniformly and independently at random. Let
$[m-1]_0^n$ chosen uniformly and independently at random. Let ![]() $X \subset [m-1]_0^n$ be the subset consisting of all points
$X \subset [m-1]_0^n$ be the subset consisting of all points ![]() $\mathbf {x} \in [m-1]_0^n$ that do not belong to any
$\mathbf {x} \in [m-1]_0^n$ that do not belong to any ![]() $\mathcal C + \mathbf {v}_i$, where
$\mathcal C + \mathbf {v}_i$, where ![]() $1 \leq i \leq s$.
$1 \leq i \leq s$.
It is easy to see that for ![]() $\mathbf {x} \in [m-1]_0^n$ and
$\mathbf {x} \in [m-1]_0^n$ and ![]() $1 \leq i \leq s$, we have
$1 \leq i \leq s$, we have  $\Pr [\mathbf {x} \in \mathcal C + \mathbf {v}_i] = \left ( \frac {d}{m} \right )^n$. Hence, from the mutual independence of the choice of
$\Pr [\mathbf {x} \in \mathcal C + \mathbf {v}_i] = \left ( \frac {d}{m} \right )^n$. Hence, from the mutual independence of the choice of ![]() $\mathbf v_i$s it follows that
$\mathbf v_i$s it follows that
 $$ \begin{align*} \Pr [\mathbf{x} \in X] = \left( 1-\Big( \frac{d}{m} \Big)^n\right)^s. \end{align*} $$
$$ \begin{align*} \Pr [\mathbf{x} \in X] = \left( 1-\Big( \frac{d}{m} \Big)^n\right)^s. \end{align*} $$The linearity of the expectation gives
 $$ \begin{align*} \mathrm{E}[|X|] = \left( 1-\Big( \frac{d}{m} \Big)^n\right)^s m^n < \left( 1-\Big( \frac{d}{m} \Big)^n\right)^{n\log d \left( \frac{m}{d}\right)^n} m^n < e^{-n\log d} m^n = \left( \frac{m}{d} \right)^n. \end{align*} $$
$$ \begin{align*} \mathrm{E}[|X|] = \left( 1-\Big( \frac{d}{m} \Big)^n\right)^s m^n < \left( 1-\Big( \frac{d}{m} \Big)^n\right)^{n\log d \left( \frac{m}{d}\right)^n} m^n < e^{-n\log d} m^n = \left( \frac{m}{d} \right)^n. \end{align*} $$ Thus, there is a way to fix the choice of ![]() $\mathbf {v}_1, \,\dots \, ,\mathbf {v}_s \in [m-1]_0^n$ such that
$\mathbf {v}_1, \,\dots \, ,\mathbf {v}_s \in [m-1]_0^n$ such that  $|X| \leq \left ( \frac {m}{d} \right )^n$. Consider the translates
$|X| \leq \left ( \frac {m}{d} \right )^n$. Consider the translates ![]() $\{\mathcal {C}+\mathbf {v}_i: 1 \leq i \leq s\} \cup \{\mathcal {C}+\mathbf {x}: \mathbf {x} \in X\}.$ Together, they cover all points of
$\{\mathcal {C}+\mathbf {v}_i: 1 \leq i \leq s\} \cup \{\mathcal {C}+\mathbf {x}: \mathbf {x} \in X\}.$ Together, they cover all points of ![]() $[m-1]_0^n$ by construction. Moreover, they cover all points of
$[m-1]_0^n$ by construction. Moreover, they cover all points of ![]() ${{\mathbb R}}^n$ by periodicity. Finally, the number of translates we used is equal to
${{\mathbb R}}^n$ by periodicity. Finally, the number of translates we used is equal to  $s+|X| = (1+o(1))n\log d\left ( \frac {m}{d}\right )^n$ as required.
$s+|X| = (1+o(1))n\log d\left ( \frac {m}{d}\right )^n$ as required.
5 Concluding remarks and open problems
One of the key objects in this article are the batons ![]() $\mathcal {B}_k$. It follows from Corollary 1 and Theorem 9 that
$\mathcal {B}_k$. It follows from Corollary 1 and Theorem 9 that  $\chi (\mathbb {R}^n_\infty; \mathcal {B}_k) = \left (\frac {k+1}{k} + o(1) \right )^n$ as
$\chi (\mathbb {R}^n_\infty; \mathcal {B}_k) = \left (\frac {k+1}{k} + o(1) \right )^n$ as ![]() $n \rightarrow \infty $. However, by calculating the exact values of
$n \rightarrow \infty $. However, by calculating the exact values of ![]() $\chi (\mathbb {R}^n_\infty; \mathcal {B}_k)$ for some pairs of fixed small n and k, we found that both the lower and upper bounds are not tight.
$\chi (\mathbb {R}^n_\infty; \mathcal {B}_k)$ for some pairs of fixed small n and k, we found that both the lower and upper bounds are not tight.
For other batons the situation is much worse. For instance, given ![]() $\alpha> 1$, it follows from Theorems 3 and 8 that
$\alpha> 1$, it follows from Theorems 3 and 8 that  $ \big ( \frac { \left \lceil \alpha \right \rceil +2 } {\left \lceil \alpha \right \rceil +1} \big )^n \leq \chi \left ( \mathbb {R}^n_\infty; \mathcal B(1,\alpha ) \right ) \leq \big ( 1+\frac {\alpha }{1+\alpha } +o(1) \big )^n$. Neither of these two bounds appears to be tight in general, and it is an interesting problem to determine the correct base of the exponent for this function.
$ \big ( \frac { \left \lceil \alpha \right \rceil +2 } {\left \lceil \alpha \right \rceil +1} \big )^n \leq \chi \left ( \mathbb {R}^n_\infty; \mathcal B(1,\alpha ) \right ) \leq \big ( 1+\frac {\alpha }{1+\alpha } +o(1) \big )^n$. Neither of these two bounds appears to be tight in general, and it is an interesting problem to determine the correct base of the exponent for this function.
For metric spaces other than batons, Theorem 1 does not immediately give an explicit exponential lower bound. One may, of course, directly follow its proof to extract the lower bound on ![]() $\chi _{\mathcal {M}}> 1$ for each specific
$\chi _{\mathcal {M}}> 1$ for each specific ![]() $\mathcal {M}$. The resulting bound would strongly depend on the dimension of the grid in which we embed
$\mathcal {M}$. The resulting bound would strongly depend on the dimension of the grid in which we embed ![]() $\mathcal {M}$, because each application of Theorem 7 weakens the lower bound significantly. For example, a lower bound for
$\mathcal {M}$, because each application of Theorem 7 weakens the lower bound significantly. For example, a lower bound for ![]() $2-$dimensional grid
$2-$dimensional grid  $\mathcal {B}_2^2 = \mathcal {B}_2 \times \mathcal {B}_2$ one can extract from our proof is only
$\mathcal {B}_2^2 = \mathcal {B}_2 \times \mathcal {B}_2$ one can extract from our proof is only  $\chi \left ( \mathbb {R}^n_\infty; \mathcal {B}_2^2\right ) \geq \left ( 1.0667... +o(1)\right )^n$. We managed to generalise the argument from Section 2 to make it applicable not only for batons but also for different multidimensional grids. One of the results that we are able to obtain is that for each fixed k and m, one has
$\chi \left ( \mathbb {R}^n_\infty; \mathcal {B}_2^2\right ) \geq \left ( 1.0667... +o(1)\right )^n$. We managed to generalise the argument from Section 2 to make it applicable not only for batons but also for different multidimensional grids. One of the results that we are able to obtain is that for each fixed k and m, one has  $\chi (\mathbb {R}^n_\infty; \mathcal {B}_k^m) = \left (\frac {k+1}{k} + o(1) \right )^n$ as
$\chi (\mathbb {R}^n_\infty; \mathcal {B}_k^m) = \left (\frac {k+1}{k} + o(1) \right )^n$ as ![]() $n \rightarrow \infty $; that is, the base of the exponent does not depend on m. This result will be one of the subjects of a separate paper that is currently in preparation.
$n \rightarrow \infty $; that is, the base of the exponent does not depend on m. This result will be one of the subjects of a separate paper that is currently in preparation.
Finally, let us explicitly state a question that arises in connection with the covering technique from Section 4.
Problem 1. What is the smallest number ![]() $c(n)$ of translates of cubes
$c(n)$ of translates of cubes ![]() $\{0,1\}^n$ that is needed to cover the torus
$\{0,1\}^n$ that is needed to cover the torus ![]() ${{\mathbb Z}}_3^n$?
${{\mathbb Z}}_3^n$?
The best upper and lower bounds that we know of are ![]() $C_1 (3/2)^n\le c(n)\le C_2 n (3/2)^n$ for some constants
$C_1 (3/2)^n\le c(n)\le C_2 n (3/2)^n$ for some constants ![]() $C_1,C_2$. Although the problem might appear simple, it seems to contain the difficulties that one is typically faced with when working with coverings as in Section 4.
$C_1,C_2$. Although the problem might appear simple, it seems to contain the difficulties that one is typically faced with when working with coverings as in Section 4.
Acknowledgments
We thank A.M. Raigorodskii for his helpful suggestions and active interest in our work during the preparation of this article. We also thank the referee for their helpful comments.
Conflict of Interest
None.
Financial Support
The authors acknowledge the financial support from the Ministry of Education and Science of the Russian Federation in the framework of MegaGrant No. 075-15-2019-1926, the Russian Foundation for Basic Research Grant No. 20-31-70039 and No. 20-31-90009 and the Council for the Support of Leading Scientific Schools of the President of the Russian Federation (Grant No. N.Sh.-2540.2020.1). The research of the second author was supported in part by the Simons Foundation and by the Moebius Contest Foundation for Young Scientists. The second author is a Young Russian Mathematics award winner and would like to thank its sponsors and jury.