Hostname: page-component-76c49bb84f-65mhm Total loading time: 0 Render date: 2025-07-12T02:28:16.815Z Has data issue: false hasContentIssue false
  • English
  • Français

THE AUTOMORPHISM GROUP OF A SHIFT OF LINEAR GROWTH: BEYOND TRANSITIVITY

Part of: Discrete mathematics in relation to computer science Topological dynamics

Published online by Cambridge University Press:  02 March 2015

VAN CYR  and
BRYNA KRA
VAN CYR
Affiliation:
Bucknell University, Lewisburg, PA 17837, USA; van.cyr@bucknell.edu
BRYNA KRA
Affiliation:
Northwestern University, Evanston, IL 60208, USA; kra@math.northwestern.edu

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

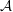For a finite alphabet ${\mathcal{A}}$ and shift 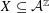$X\subseteq {\mathcal{A}}^{\mathbb{Z}}$ whose factor complexity function grows at most linearly, we study the algebraic properties of the automorphism group 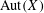$\text{Aut}(X)$. For such systems, we show that every finitely generated subgroup of 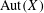$\text{Aut}(X)$ is virtually 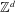$\mathbb{Z}^{d}$, in contrast to the behavior when the complexity function grows more quickly. With additional dynamical assumptions we show more: if 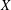$X$ is transitive, then 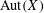$\text{Aut}(X)$ is virtually 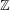$\mathbb{Z}$; if 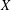$X$ has dense aperiodic points, then 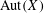$\text{Aut}(X)$ is virtually 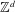$\mathbb{Z}^{d}$. We also classify all finite groups that arise as the automorphism group of a shift.

MSC classification

Primary: 37B50: Multi-dimensional shifts of finite type, tiling dynamics
Secondary: 68R15: Combinatorics on words 37B10: Symbolic dynamics

Information

Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 3 , 2015 , e5
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/3.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2015

References

Boshernitzan, M., ‘A unique ergodicity of minimal symbolic flows with linear block growth’, J. Anal. Math. 44(1) (1984), 77–96.CrossRefGoogle Scholar
Boyle, M. and Krieger, W., ‘Periodic points and automorphisms of the shift’, Trans. Amer. Math. Soc. 302 (1987), 125–149.Google Scholar
Boyle, M., Lind, D. and Rudolph, D., ‘The automorphism group of a shift of finite type’, Trans. Amer. Math. Soc. 306(1) (1988), 71–114.CrossRefGoogle Scholar
Cassaigne, J., ‘Special factors of sequences with linear subword complexity’, inDevelopments in Language Theorem, II (Magdeburg, 1995) (World Science Publications, River Edge, NJ, 1996), 25–34.Google Scholar
Cyr, V. and Kra, B., ‘The automorphism group of s shift of subquadratic growth’, Proc. Amer. Math. Soc. (to appear), Preprint, arXiv:1403.0238.Google Scholar
Donoso, S., Durand, F., Maass, A. and Petite, S., ‘On automorphism groups of low complexity minimal subshifts’, Preprint, arXiv:1501.00510.Google Scholar
Fiebig, D. and Fiebig, U., ‘The automorphism group of a coded system’, Trans. Amer. Math. Soc. 348(8) (1996), 3173–3191.Google Scholar
Hedlund, G. A., ‘Endomorphisms and automorphisms of the shift dynamical system’, Math. Systems Theory 3 (1969), 320–375.Google Scholar
Hochman, M., ‘On the automorphism groups of multidimensional shifts of finite type’, Ergodic Theory Dynam. Systems 30(3) (2010), 809–840.CrossRefGoogle Scholar
Kim, K. H., Roush, F. W. and Wagoner, J. B., ‘Automorphisms of the dimension group and gyration numbers’, J. Amer. Math. Soc. 5 (1993), 191–212.CrossRefGoogle Scholar
Morse, M. and Hedlund, G. A., ‘Symbolic dynamics II. Sturmian trajectories’, Amer. J. Math. 62 (1940), 1–42.Google Scholar
Olli, J., ‘Endomorphisms of Sturmian systems and the discrete chair substitution tiling system’, Discrete Contin. Dyn. Syst. 33(9) (2013), 4173–4186.CrossRefGoogle Scholar
Osima, M., ‘Some remarks on the characters of the symmetric group II’, Canad. J. Math. 6 (1954), 511–521.Google Scholar
Salo, V. and Törmä, I., ‘Block maps between primitive uniform and Pisot substitutions’, Ergodic Theory Dynam. Systems (to appear), Preprint, arXiv:1306.3777.Google Scholar
Scott, P. and Wall, T., ‘Topological methods in group theory’, inHomological Group Theory (Proc. Sympos., Durham, 1977), London Mathematical Society Lecture Note Series, 36 (Cambridge University Press, Cambridge–New York, 1979), 137–203.Google Scholar
Ward, T., ‘Automorphisms of Z d -subshifts of finite type’, Indag. Math. (N.S.) 5(4) (1994), 495–504.CrossRefGoogle Scholar