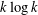Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Aramayona, Javier
Patel, Priyam
and
Vlamis, Nicholas G
2020.
The First Integral Cohomology of Pure Mapping Class Groups.
International Mathematics Research Notices,
Gaster, Jonah
Lopez, Miguel
Rexer, Emily
Riell, Zoë
and
Xiao, Yang
2020.
Combinatorics of $k$-Farey graphs.
Rocky Mountain Journal of Mathematics,
Vol. 50,
Issue. 1,