Hostname: page-component-cb9f654ff-lqqdg Total loading time: 0 Render date: 2025-08-24T21:24:58.125Z Has data issue: false hasContentIssue false
  • English
  • Français

Dynamics of plane partitions: Proof of the Cameron–Fon-Der-Flaass conjecture

Part of: Algebraic combinatorics Combinatorics

Published online by Cambridge University Press:  07 December 2020

Rebecca Patrias  and
Oliver Pechenik Open the ORCID record for Oliver Pechenik [Opens in a new window]
Rebecca Patrias
Affiliation:
Department of Mathematics, University of St. Thomas, St. Paul, MN 55105, USA; E-mail: patr0028@stthomas.edu
Oliver Pechenik
Affiliation:
Department of Combinatorics & Optimization, University of Waterloo, Waterloo, ON N2L 3G1, Canada; E-mail: oliver.pechenik@uwaterloo.ca

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

One of the oldest outstanding problems in dynamical algebraic combinatorics is the following conjecture of P. Cameron and D. Fon-Der-Flaass (1995): consider a plane partition P in an 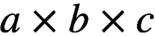$a \times b \times c$ box 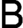${\sf B}$. Let 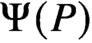$\Psi (P)$ denote the smallest plane partition containing the minimal elements of 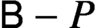${\sf B} - P$. Then if 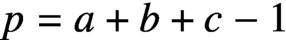$p= a+b+c-1$ is prime, Cameron and Fon-Der-Flaass conjectured that the cardinality of the 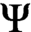$\Psi $-orbit of P is always a multiple of p.

This conjecture was established for 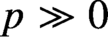$p \gg 0$ by Cameron and Fon-Der-Flaass (1995) and for slightly smaller values of p in work of K. Dilks, J. Striker and the second author (2017). Our main theorem specializes to prove this conjecture in full generality.

MSC classification

Primary: 05E18: Group actions on combinatorial structures
Secondary: 05A17: Partitions of integers

Information

Type
Discrete Mathematics
Information
Forum of Mathematics, Sigma , Volume 8 , 2020 , 62
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s), 2020. Published by Cambridge University Press

References

Armstrong, D., Stump, C. and Thomas, H., ‘A uniform bijection between nonnesting and noncrossing partitions’, Trans. Amer. Math. Soc. 365(8) (2013), 4121–4151.CrossRefGoogle Scholar
Buch, A. S. and Samuel, M. J., ‘ $K$ -theory of minuscule varieties’, J. Reine Angew. Math. 719 (2016), 133–171.Google Scholar
Brouwer, A. E. and Schrijver, A., On the Period of an Operator, Defined on Antichains, Mathematisch Centrum Afdeling Zuivere Wiskunde ZW, 24/74 (Mathematisch Centrum, Amsterdam, 1974).Google Scholar
Cameron, P. J. and Fon-Der-Flaass, D. G., ‘Orbits of antichains revisited’, European J. Combin. 16(6) (1995), 545–554.CrossRefGoogle Scholar
Dilks, K., Pechenik, O. and Striker, J., ‘Resonance in orbits of plane partitions and increasing tableaux’, J. Combin. Theory Ser. A 148 (2017), 244–274.CrossRefGoogle Scholar
Duchet, P., ‘Sur les hypergraphes invariantes’, Discrete Math. 8 (1974), 269–280.CrossRefGoogle Scholar
Mandel, H. and Pechenik, O., ‘Orbits of plane partitions of exceptional Lie type’, European J. Combin. 74 (2018), 90–109.CrossRefGoogle Scholar
Panyushev, D. I., ‘On orbits of antichains of positive roots’, European J. Combin. 30(2) (2009), 586–594.CrossRefGoogle Scholar
Pechenik, O., ‘Cyclic sieving of increasing tableaux and small Schröder paths’, J. Combin. Theory Ser. A 125 (2014), 357–378.CrossRefGoogle Scholar
Pechenik, O., ‘Promotion of increasing tableaux: Frames and homomesies’, Electron. J. Combin. 24(3) (2017), 3.50.CrossRefGoogle Scholar
Propp, J. and Roby, T., ‘Homomesy in products of two chains’, Electron. J. Combin. 22(3) (2015), 3.4.CrossRefGoogle Scholar
Rush, D. B. and Shi, X., ‘On orbits of order ideals of minuscule posets’, J. Algebraic Combin. 37(3) (2013), 545–569.CrossRefGoogle Scholar
Reiner, V., Stanton, D. and White, D., ‘The cyclic sieving phenomenon’, J. Combin. Theory Ser. A 108(1) (2004), 17–50.CrossRefGoogle Scholar
Schützenberger, M. P., ‘Promotion des morphismes d’ensembles ordonnés’, Discrete Math. 2 (1972), 73–94.CrossRefGoogle Scholar
Striker, J., ‘Dynamical algebraic combinatorics: Promotion, rowmotion, and resonance’, Notices Amer. Math. Soc. 64(6) (2017), 543–549.CrossRefGoogle Scholar
Striker, J. and Williams, N., ‘Promotion and rowmotion’, European J. Combin. 33(8) (2012), 1919–1942.CrossRefGoogle Scholar
Thomas, H. and Yong, A., ‘A jeu de taquin theory for increasing tableaux, with applications to $K$ -theoretic Schubert calculus’, Algebra Number Theory 3(2) (2009), 121–148.CrossRefGoogle Scholar
Thomas, H. and Yong, A., ‘Longest increasing subsequences, Plancherel-type measure and the Hecke insertion algorithm’, Adv. in Appl. Math. 46(1-4) (2011), 610–642.CrossRefGoogle Scholar
Vorland, C., ‘Homomesy in products of three chains and multidimensional recombination’, Electron. J. Combin. 26(4) (2019), 4.30.CrossRefGoogle Scholar