Hostname: page-component-5d84bcc8dc-xsbxj Total loading time: 0 Render date: 2026-09-15T11:19:51.993Z Has data issue: false hasContentIssue false
  • English
  • Français

EXPONENTIAL IMPROVEMENT IN PRECISION FOR SIMULATING SPARSE HAMILTONIANS

Part of: Theory of computing

Published online by Cambridge University Press:  02 March 2017

DOMINIC W. BERRY ,
ANDREW M. CHILDS ,
RICHARD CLEVE ,
ROBIN KOTHARI  and
ROLANDO D. SOMMA
DOMINIC W. BERRY
Affiliation:
Department of Physics and Astronomy, Macquarie University, Sydney, NSW 2109, Australia; dominic.berry@mq.edu.au
ANDREW M. CHILDS
Affiliation:
Department of Combinatorics & Optimization and Institute for Quantum Computing, University of Waterloo, Waterloo, ON N2L 3G1, Canada Department of Computer Science, Institute for Advanced Computer Studies, and Joint Center for Quantum Information and Computer Science, University of Maryland, College Park, MD 20742, USA; amchilds@umd.edu
RICHARD CLEVE
Affiliation:
David R. Cheriton School of Computer Science and Institute for Quantum Computing, University of Waterloo, Waterloo, ON N2L 3G1, Canada; cleve@uwaterloo.ca Canadian Institute for Advanced Research, Toronto, ON M5G 1Z8, Canada
ROBIN KOTHARI
Affiliation:
David R. Cheriton School of Computer Science and Institute for Quantum Computing, University of Waterloo, Waterloo, ON N2L 3G1, Canada; cleve@uwaterloo.ca Center for Theoretical Physics, Massachusetts Institute of Technology, Cambridge, MA 02139, USA; rkothari@mit.edu
ROLANDO D. SOMMA
Affiliation:
Theoretical Division, Los Alamos National Laboratory, Los Alamos, NM 87545, USA; somma@lanl.gov

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the 'Save PDF' action button.

We provide a quantum algorithm for simulating the dynamics of sparse Hamiltonians with complexity sublogarithmic in the inverse error, an exponential improvement over previous methods. Specifically, we show that a 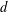$d$ -sparse Hamiltonian 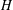$H$ acting on $n$ qubits can be simulated for time $t$ with precision $\unicode[STIX]{x1D716}$ using 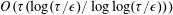$O(\unicode[STIX]{x1D70F}(\log (\unicode[STIX]{x1D70F}/\unicode[STIX]{x1D716})/\log \log (\unicode[STIX]{x1D70F}/\unicode[STIX]{x1D716})))$ queries and 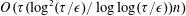$O(\unicode[STIX]{x1D70F}(\log ^{2}(\unicode[STIX]{x1D70F}/\unicode[STIX]{x1D716})/\log \log (\unicode[STIX]{x1D70F}/\unicode[STIX]{x1D716}))n)$ additional 2-qubit gates, where 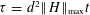$\unicode[STIX]{x1D70F}=d^{2}\Vert H\Vert _{\max }t$ . Unlike previous approaches based on product formulas, the query complexity is independent of the number of qubits acted on, and for time-varying Hamiltonians, the gate complexity is logarithmic in the norm of the derivative of the Hamiltonian. Our algorithm is based on a significantly improved simulation of the continuous- and fractional-query models using discrete quantum queries, showing that the former models are not much more powerful than the discrete model even for very small error. We also simplify the analysis of this conversion, avoiding the need for a complex fault-correction procedure. Our simplification relies on a new form of ‘oblivious amplitude amplification’ that can be applied even though the reflection about the input state is unavailable. Finally, we prove new lower bounds showing that our algorithms are optimal as a function of the error.

MSC classification

Primary: 68Q12: Quantum algorithms and complexity
Secondary: 81P68: Quantum computation

Information

Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 5 , 2017 , e8
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2017

References

Aharonov, D. and Ta-Shma, A., ‘Adiabatic quantum state generation and statistical zero knowledge’, inProceedings of the 35th ACM Symposium on Theory of Computing (ACM, New York, 2003), 20–29.Google Scholar
Ambainis, A., Childs, A. M., Reichardt, B. W., Špalek, R. and Zhang, S., ‘Any AND-OR formula of size N can be evaluated in time N 1/2+o (1) on a quantum computer’, SIAM J. Comput. 39(6) (2010), 2513–2530.CrossRefGoogle Scholar
Ambainis, A., Magnin, L., Roetteler, M. and Roland, J., ‘Symmetry-assisted adversaries for quantum state generation’, inProceedings of the 26th IEEE Conference on Computational Complexity (IEEE, Piscataway, NJ, 2011), 167–177.Google Scholar
Babbush, R., Berry, D. W., Kivlichan, I. D., Wei, A. Y., Love, P. J. and Aspuru-Guzik, A., ‘Exponentially more precise quantum simulation of fermions II: Quantum chemistry in the CI matrix representation’, Preprint, 2015, arXiv:1506.01029.CrossRefGoogle Scholar
Babbush, R., Berry, D. W., Kivlichan, I. D., Wei, A. Y., Love, P. J. and Aspuru-Guzik, A., ‘Exponentially more precise quantum simulation of fermions in second quantization’, New J. Phys. 18 (2016), 033032.CrossRefGoogle Scholar
Beals, R., Buhrman, H., Cleve, R., Mosca, M. and de Wolf, R., ‘Quantum lower bounds by polynomials’, J. ACM 48(4) (2001), 778–797.CrossRefGoogle Scholar
Belovs, A., ‘Variations on quantum adversary’, Preprint, 2015, arXiv:1504.06943.Google Scholar
Berry, D. W., Ahokas, G., Cleve, R. and Sanders, B. C., ‘Efficient quantum algorithms for simulating sparse Hamiltonians’, Commun. Math. Phys. 270(2) (2007), 359–371.CrossRefGoogle Scholar
Berry, D. W. and Childs, A. M., ‘Black-box Hamiltonian simulation and unitary implementation’, Quantum Inf. Comput. 12(1–2) (2012), 29–62.Google Scholar
Berry, D. W., Childs, A. M., Cleve, R., Kothari, R. and Somma, R. D., ‘Exponential improvement in precision for simulating sparse Hamiltonians’, inProceedings of the 46th ACM Symposium on Theory of Computing (ACM, New York, 2014), 283–292.Google Scholar
Berry, D. W., Childs, A. M., Cleve, R., Kothari, R. and Somma, R. D., ‘Simulating Hamiltonian dynamics with a truncated Taylor series’, Phys. Rev. Lett. 114(9) (2015), 090502.CrossRefGoogle ScholarPubMed
Berry, D. W., Childs, A. M. and Kothari, R., ‘Hamiltonian simulation with nearly optimal dependence on all parameters’, inProceedings of the 56th IEEE Symposium on Foundations of Computer Science (IEEE, Piscataway, NJ, 2015), 792–809.Google Scholar
Berry, D. W., Cleve, R. and Gharibian, S., ‘Gate-efficient discrete simulations of continuous-time quantum query algorithms’, Quantum Inf. Comput. 14(1–2) (2014), 1–30.Google Scholar
Childs, A. M., ‘Quantum information processing in continuous time’, PhD Thesis, Massachusetts Institute of Technology, 2004.Google Scholar
Childs, A. M., ‘On the relationship between continuous- and discrete-time quantum walk’, Comm. Math. Phys. 294(2) (2010), 581–603.CrossRefGoogle Scholar
Childs, A. M., Cleve, R., Deotto, E., Farhi, E., Gutmann, S. and Spielman, D. A., ‘Exponential algorithmic speedup by quantum walk’, inProceedings of the 35th ACM Symposium on Theory of Computing (ACM, New York, 2003), 59–68.Google Scholar
Childs, A. M., Cleve, R., Jordan, S. P. and Yonge-Mallo, D., ‘Discrete-query quantum algorithm for NAND trees’, Theory Comput. 5(5) (2009), 119–123.CrossRefGoogle Scholar
Childs, A. M., Gosset, D. and Webb, Z., ‘Universal computation by multi-particle quantum walk’, Science 339(6121) (2013), 791–794.CrossRefGoogle Scholar
Childs, A. M. and Kothari, R., ‘Simulating sparse Hamiltonians with star decompositions’, inTheory of Quantum Computation, Communication, and Cryptography (TQC 2010), Lecture Notes in Computer Science, 6519 (Springer, Berlin, Heidelberg, 2011), 94–103.CrossRefGoogle Scholar
Childs, A. M. and Wiebe, N., ‘Hamiltonian simulation using linear combinations of unitary operations’, Quantum Inf. Comput. 12(11–12) (2012), 901–924.Google Scholar
Christandl, M., Datta, N., Ekert, A. and Landahl, A. J., ‘Perfect state transfer in quantum spin networks’, Phys. Rev. Lett. 92(18) (2004), 187902.CrossRefGoogle ScholarPubMed
Clader, B. D., Jacobs, B. C. and Sprouse, C. R., ‘Preconditioned quantum linear system algorithm’, Phys. Rev. Lett. 110(25) (2013), 250504.CrossRefGoogle ScholarPubMed
Cleve, R., Gottesman, D., Mosca, M., Somma, R. D. and Yonge-Mallo, D., ‘Efficient discrete-time simulations of continuous-time quantum query algorithms’, inProceedings of the 41st ACM Symposium on Theory of Computing (ACM, New York, 2009), 409–416.Google Scholar
Farhi, E., Goldstone, J. and Gutmann, S., ‘A quantum algorithm for the Hamiltonian NAND tree’, Theory Comput. 4(8) (2008), 169–190.CrossRefGoogle Scholar
Farhi, E., Goldstone, J., Gutmann, S. and Sipser, M., ‘Limit on the speed of quantum computation in determining parity’, Phys. Rev. Lett. 81(24) (1998), 5442–5444.CrossRefGoogle Scholar
Farhi, E. and Gutmann, S., ‘Analog analogue of a digital quantum computation’, Phys. Rev. A 57(4) (1998), 2403–2406.CrossRefGoogle Scholar
Feynman, R. P., ‘Simulating physics with computers’, Int. J. Theor. Phys. 21(6) (1982), 467–488.CrossRefGoogle Scholar
Harrow, A. W., Hassidim, A. and Lloyd, S., ‘Quantum algorithm for linear systems of equations’, Phys. Rev. Lett. 103(15) (2009), 150502.CrossRefGoogle ScholarPubMed
Huyghebaert, J. and Raedt, H. D., ‘Product formula methods for time-dependent Schrödinger problems’, J. Phys. A 23(24) (1990), 5777.CrossRefGoogle Scholar
Jordan, C., ‘Essai sur la géométrie à n dimensions’, Bull. Soc. Math. France 3 (1875), 103–174.CrossRefGoogle Scholar
Lee, T., Mittal, R., Reichardt, B. W., Špalek, R. and Szegedy, M., ‘Quantum query complexity of state conversion’, inProceedings of the 52nd IEEE Symposium on Foundations of Computer Science (IEEE, Piscataway, NJ, 2011), 344–353.Google Scholar
Lloyd, S., ‘Universal quantum simulators’, Science 273(5278) (1996), 1073–1078.CrossRefGoogle ScholarPubMed
Marriott, C. and Watrous, J., ‘Quantum Arthur–Merlin games’, Comput. Complexity 14(2) (2005), 122–152.CrossRefGoogle Scholar
Mochon, C., ‘Hamiltonian oracles’, Phys. Rev. A 75(4) (2007), 042313.CrossRefGoogle Scholar
Motwani, R. and Raghavan, P., Randomized Algorithms (Cambridge University Press, 1995).CrossRefGoogle Scholar
Nagaj, D., Wocjan, P. and Zhang, Y., ‘Fast amplification of QMA’, Quantum Inf. Comput. 9(11–12) (2009), 1053–1068.Google Scholar
Paetznick, A. and Svore, K. M., ‘Repeat-until-success: Non-deterministic decomposition of single-qubit unitaries’, Quantum Inf. Comput. 14(15–16) (2014), 1277–1301.Google Scholar
Poulin, D., Qarry, A., Somma, R. D. and Verstraete, F., ‘Quantum simulation of time-dependent Hamiltonians and the convenient illusion of Hilbert space’, Phys. Rev. Lett. 106(17) (2011), 170501.CrossRefGoogle ScholarPubMed
Scherer, A., Valiron, B., Mau, S.-C., Alexander, S., van den Berg, E. and Chapuran, T. E., ‘Concrete resource analysis of the quantum linear system algorithm used to compute the electromagnetic scattering cross section of a 2D target’, Quantum Inf. Process. 16(3) (2017), 60.CrossRefGoogle Scholar
Suzuki, M., ‘General theory of fractal path integrals with applications to many-body theories and statistical physics’, J. Math. Phys. 32(2) (1991), 400–407.CrossRefGoogle Scholar
Watrous, J., ‘Zero-knowledge against quantum attacks’, SIAM J. Comput. 39(1) (2009), 25–38.CrossRefGoogle Scholar
Watson, G. N., A Treatise on the Theory of Bessel Functions (Cambridge University Press, Cambridge, UK, 1922).Google Scholar
Wiebe, N., Berry, D. W., Høyer, P. and Sanders, B. C., ‘Simulating quantum dynamics on a quantum computer’, J. Phys. A 44(44) (2011), 445308.CrossRefGoogle Scholar
Wiebe, N. and Roetteler, M., ‘Quantum arithmetic and numerical analysis using Repeat-Until-Success circuits’, Quantum Inf. Comput. 16(1–2) (2016), 134–178.Google Scholar