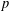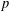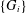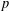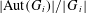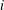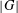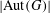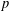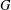Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Abdollahi, Alireza
Ahmadi, Marzieh
and
Ghoraishi, S. Mohsen
2017.
Finite p-groups with the least number of outer p-automorphisms.
Journal of Algebra and Its Applications,
Vol. 16,
Issue. 06,
p.
1750111.
Sambale, Benjamin
2020.
On a Theorem of Ledermann and Neumann.
The American Mathematical Monthly,
Vol. 127,
Issue. 9,
p.
827.
Goyal, Ashish
Kalra, Hemant
and
Gumber, Deepak
2020.
On the probability that an automorphism of a group fixes an element of the group.
Journal of Algebra and Its Applications,
Vol. 19,
Issue. 10,
p.
2050198.
Zhang, Qinhai
2022.
Some unsolvable conjectures in finite p-groups.
Frontiers of Mathematics in China,
Vol. 17,
Issue. 1,
p.
1.
Kalra, Hemant
and
Gumber, Deepak
2025.
Automorphisms of finite p-groups.
Archiv der Mathematik,
Vol. 124,
Issue. 4,
p.
357.