1 Introduction
Recently, we witnessed huge progress on K-stability of Fano varieties [Reference Abban and Zhuang1, Reference Fujita15, Reference Li18, Reference Xu22], which resulted in an immense breakthrough in the solution of the following problem:
Problem. Find all K-polystable smooth Fano threefolds.
Let us describe what is done in this direction. To do this, fix a smooth Fano threefold X. Then X belongs to one of the
![]() $105$
deformation families found by Iskovskikh, Mori, Mukai. These families are often labeled as
$105$
deformation families found by Iskovskikh, Mori, Mukai. These families are often labeled as ![]() , where the first digit stands for the rank of the Picard group of the threefolds in the family. For the detailed descriptions of the
, where the first digit stands for the rank of the Picard group of the threefolds in the family. For the detailed descriptions of the
![]() $105$
families, we refer the reader to [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3].
$105$
families, we refer the reader to [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3].
The valuative criterion for K-stability [Reference Fujita15, Reference Li18] allows us to explain when X is K-stable in relatively simple terms. To do this, let us remind what are
![]() $\beta $
-invariant and
$\beta $
-invariant and
![]() $\delta $
-invariant. Recall that E is a prime divisor over X if there is a birational morphism
$\delta $
-invariant. Recall that E is a prime divisor over X if there is a birational morphism
![]() $f\colon \widetilde {X}\to X$
with normal
$f\colon \widetilde {X}\to X$
with normal
![]() $\widetilde {X}$
and a prime divisor
$\widetilde {X}$
and a prime divisor
![]() $E\subset \widetilde {X}$
. We set
$E\subset \widetilde {X}$
. We set
![]() $\beta (E)=A_X(E)-S_X(E)$
, where
$\beta (E)=A_X(E)-S_X(E)$
, where
and
![]() $A_X(E)$
is the log discrepancy of the divisor E. Then, for every point
$A_X(E)$
is the log discrepancy of the divisor E. Then, for every point
![]() $P\in X$
, we let
$P\in X$
, we let
 $$ \begin{align*}\delta_P(X)=\inf_{\substack{F/X\\ P\in C_X(F)}}\frac{A_{X}(F)}{S_X(F)}, \end{align*} $$
$$ \begin{align*}\delta_P(X)=\inf_{\substack{F/X\\ P\in C_X(F)}}\frac{A_{X}(F)}{S_X(F)}, \end{align*} $$
where the infimum is taken over all prime divisors over X whose centers on X contain P. Finally, we set
The valuative criterion says that X is K-stable (respectively, K-semistable) if
![]() $\beta (F)>0$
(respectively,
$\beta (F)>0$
(respectively,
![]() $\beta (F)\geqslant 0$
) for any prime divisor F over X. Hence, X is K-stable if
$\beta (F)\geqslant 0$
) for any prime divisor F over X. Hence, X is K-stable if
![]() $\delta (X)>1$
. We say that X is K-unstable if it is not K-semistable.
$\delta (X)>1$
. We say that X is K-unstable if it is not K-semistable.
The simplest way to apply the valuative criterion is to check whether
![]() $\beta (S)<0$
or not for some irreducible surface S in the threefold X. This has been done in [Reference Fujita15]. As a result, we know that X is K-unstable if it belongs to any of the following
$\beta (S)<0$
or not for some irreducible surface S in the threefold X. This has been done in [Reference Fujita15]. As a result, we know that X is K-unstable if it belongs to any of the following
![]() $26$
families:
$26$
families:

To be precise, if X is contained in one of these
![]() $26$
families, then it contains an irreducible surface S such that
$26$
families, then it contains an irreducible surface S such that
![]() $\beta (S)<0$
, so that X is K-unstable, which implies that X does not admit a Kähler–Einstein metric. Almost in every case, such surface S is not hard to find. For instance, if X is the unique smooth Fano threefold in the deformation family
$\beta (S)<0$
, so that X is K-unstable, which implies that X does not admit a Kähler–Einstein metric. Almost in every case, such surface S is not hard to find. For instance, if X is the unique smooth Fano threefold in the deformation family ![]() , then X is a blow up of
, then X is a blow up of
![]() $\mathbb {P}^3$
at a point, and S is the exceptional surface of the blow up.
$\mathbb {P}^3$
at a point, and S is the exceptional surface of the blow up.
We listed
![]() $26$
families of smooth Fano threefolds that contain no K-semistable members. There is another family that does not contain K-polystable members – the family
$26$
families of smooth Fano threefolds that contain no K-semistable members. There is another family that does not contain K-polystable members – the family ![]() . This family is quite special; see [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, § 5.10] for its detailed description, and it contains exactly two smooth Fano threefolds. One of them is K-semistable and not K-polystable, while another one is K-unstable. Moreover, it follows from [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Main Theorem] that general members of the remaining
. This family is quite special; see [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, § 5.10] for its detailed description, and it contains exactly two smooth Fano threefolds. One of them is K-semistable and not K-polystable, while another one is K-unstable. Moreover, it follows from [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Main Theorem] that general members of the remaining
![]() $78$
families of smooth Fano threefolds are K-polystable.
$78$
families of smooth Fano threefolds are K-polystable.
Further, all K-polystable smooth Fano threefolds in
![]() $53$
families among these
$53$
families among these
![]() $78$
families are described in [Reference Abban and Zhuang2, Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Reference Belousov and Loginov4, Reference Cheltsov and Park9, Reference Denisova13, Reference Giovenzana, Guerreiro and Viswanathan17, Reference Liu19, Reference Malbon20, Reference Xu and Liu23, Reference Cheltsov, Fujita, Kishimoto and Okada7, Reference Cheltsov, Fujita, Kishimoto and Park8]. The remaining
$78$
families are described in [Reference Abban and Zhuang2, Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Reference Belousov and Loginov4, Reference Cheltsov and Park9, Reference Denisova13, Reference Giovenzana, Guerreiro and Viswanathan17, Reference Liu19, Reference Malbon20, Reference Xu and Liu23, Reference Cheltsov, Fujita, Kishimoto and Okada7, Reference Cheltsov, Fujita, Kishimoto and Park8]. The remaining
![]() $25$
families are:
$25$
families are:
The deformation families ![]() contain non-K-polystable members, and [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, § 7] provides conjectures that describe K-polystable smooth Fano threefolds in these four families. On the other hand, all smooth Fano threefolds in the
contain non-K-polystable members, and [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, § 7] provides conjectures that describe K-polystable smooth Fano threefolds in these four families. On the other hand, all smooth Fano threefolds in the
![]() $21$
families
$21$
families

are conjectured to be K-stable [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3]. The goal of this paper is to prove this for six families:
Main Theorem. Let X be a smooth Fano threefold contained in one of the following deformation families: ![]() . Then X is K-stable.
. Then X is K-stable.
Therefore, to solve the problem posed above, it remains to find all K-polystable smooth Fano threefolds in the following
![]() $19$
families:
$19$
families:
We hope that this will be done in a nearest future.
To prove Main Theorem, we use Abban–Zhuang theory [Reference Abban and Zhuang1] and its applications [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Reference Fujita16]. A similar approach also works for almost all smooth Fano threefolds in the family ![]() . Namely, if X is a smooth Fano threefold in the family
. Namely, if X is a smooth Fano threefold in the family ![]() , we show that
, we show that
![]() $\delta _P(X)>1$
for every point
$\delta _P(X)>1$
for every point
![]() $P\in X$
that satisfy certain geometric conditions. As a result, we obtained
$P\in X$
that satisfy certain geometric conditions. As a result, we obtained
Auxiliary Theorem. Let X be a smooth Fano threefold in the deformation family ![]() . Recall that there exists the following Sarkisov link:
. Recall that there exists the following Sarkisov link:

where V is a smooth cubic threefold in
![]() $\mathbb {P}^4$
, the morphism
$\mathbb {P}^4$
, the morphism
![]() $\pi $
is a blow up of a smooth plane cubic curve, and
$\pi $
is a blow up of a smooth plane cubic curve, and
![]() $\phi $
is a morphism whose fibers are normal cubic surfaces. Suppose that
$\phi $
is a morphism whose fibers are normal cubic surfaces. Suppose that
Then X is K-stable.
Let us describe the structure of this paper. In Section 2, we prove auxiliary theorem, and we prove that all smooth Fano threefolds in the families ![]() and
and ![]() are K-stable. In Sections 3, 4, 5, 6, we prove that all smooth Fano threefolds in the families
are K-stable. In Sections 3, 4, 5, 6, we prove that all smooth Fano threefolds in the families ![]() are K-stable, respectively. Note that Section 6 is very technical and long.
are K-stable, respectively. Note that Section 6 is very technical and long.
As we already mentioned, we use applications of Abban–Zhuang theory [Reference Abban and Zhuang1] which have been discovered in [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Reference Fujita16]. For the background material, we refer the reader to [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Reference Fujita16, Reference Xu22].
2 Families 
Fix
![]() $d\in \{1,2,3\}$
. Let V be one of the following smooth Fano threefolds:
$d\in \{1,2,3\}$
. Let V be one of the following smooth Fano threefolds:
-
 $\boxed{d=1}$
a smooth sextic hypersurface in
$\boxed{d=1}$
a smooth sextic hypersurface in
 $\mathbb {P}(1,1,1,2,3)$
;
$\mathbb {P}(1,1,1,2,3)$
; -
 $\boxed{d=2}$
a smooth quartic hypersurface in
$\boxed{d=2}$
a smooth quartic hypersurface in
 $\mathbb {P}(1,1,1,1,2)$
;
$\mathbb {P}(1,1,1,1,2)$
; -
 $\boxed{d=3}$
a smooth cubic threefold in
$\boxed{d=3}$
a smooth cubic threefold in
 $\mathbb {P}^4$
.
$\mathbb {P}^4$
.
Then
![]() $-K_{V}\sim 2H$
for an ample divisor
$-K_{V}\sim 2H$
for an ample divisor
![]() $H\in \mathrm {Pic}(V)$
such that
$H\in \mathrm {Pic}(V)$
such that
![]() $H^3=d$
and
$H^3=d$
and
![]() $\mathrm {Pic}(V)=\mathbb {Z}[H]$
. Let
$\mathrm {Pic}(V)=\mathbb {Z}[H]$
. Let
![]() $S_1$
and
$S_1$
and
![]() $S_2$
be two distinct surfaces in the linear system
$S_2$
be two distinct surfaces in the linear system
![]() $|H|$
, and let
$|H|$
, and let
![]() $\mathcal {C}=S_1\cap S_2$
. Suppose that the curve
$\mathcal {C}=S_1\cap S_2$
. Suppose that the curve
![]() $\mathcal {C}$
is smooth. Then
$\mathcal {C}$
is smooth. Then
![]() $\mathcal {C}$
is an elliptic curve by the adjunction formula. Let
$\mathcal {C}$
is an elliptic curve by the adjunction formula. Let
![]() $\pi \colon X\to V$
be the blow up of the curve
$\pi \colon X\to V$
be the blow up of the curve
![]() $\mathcal {C}$
, and let E be the
$\mathcal {C}$
, and let E be the
![]() $\pi $
-exceptional surface.
$\pi $
-exceptional surface.
-
• If
 $d=1$
, then X is a smooth Fano threefold in the deformation family
$d=1$
, then X is a smooth Fano threefold in the deformation family  .
. -
• If
 $d=2$
, then X is a smooth Fano threefold in the deformation family
$d=2$
, then X is a smooth Fano threefold in the deformation family  .
. -
• If
 $d=3$
, then X is a smooth Fano threefold in the deformation family
$d=3$
, then X is a smooth Fano threefold in the deformation family  .
.
Moreover, all smooth Fano threefolds in these families can be obtained in this way.
Note that
![]() $(-K_X)^3=4d$
. Moreover, we have the following commutative diagram:
$(-K_X)^3=4d$
. Moreover, we have the following commutative diagram:

where ![]() is the rational map given by the pencil that is generated by
is the rational map given by the pencil that is generated by
![]() $S_1$
and
$S_1$
and
![]() $S_2$
, and
$S_2$
, and
![]() $\phi $
is a morphism whose general fiber is a smooth del Pezzo surface of degree d.
$\phi $
is a morphism whose general fiber is a smooth del Pezzo surface of degree d.
The goal of this section is to show that X is K-stable in the case when
![]() $d=1$
or
$d=1$
or
![]() $d=2$
, and to show that X is K-stable in the case when
$d=2$
, and to show that X is K-stable in the case when
![]() $d=3$
and X satisfies the condition (★). To show that X is K-stable, it is enough to show that
$d=3$
and X satisfies the condition (★). To show that X is K-stable, it is enough to show that
![]() $\delta _O(X)>1$
for every point
$\delta _O(X)>1$
for every point
![]() $O\in X$
. This follows from the valuative criterion for K-stability [Reference Fujita15, Reference Li18].
$O\in X$
. This follows from the valuative criterion for K-stability [Reference Fujita15, Reference Li18].
Lemma 2.1. Let O be a point in X; let A be the fiber of the morphism
![]() $\phi $
such that
$\phi $
such that
![]() $O\in A$
. Suppose that A has at most Du Val singularities at the point O. Then
$O\in A$
. Suppose that A has at most Du Val singularities at the point O. Then
 $$ \begin{align*}\delta_O(X)\geqslant\left\{\begin{aligned} &\mathrm{min}\Big\{\frac{16}{11},\frac{16}{15}\delta_O(A)\Big\}\ \text{if }O\not\in E, \\ &\mathrm{min}\Big\{\frac{16}{11},\frac{16\delta_{O}(A)}{\delta_{O}(A)+15}\Big\}\ \text{if }O\in E. \end{aligned} \right. \end{align*} $$
$$ \begin{align*}\delta_O(X)\geqslant\left\{\begin{aligned} &\mathrm{min}\Big\{\frac{16}{11},\frac{16}{15}\delta_O(A)\Big\}\ \text{if }O\not\in E, \\ &\mathrm{min}\Big\{\frac{16}{11},\frac{16\delta_{O}(A)}{\delta_{O}(A)+15}\Big\}\ \text{if }O\in E. \end{aligned} \right. \end{align*} $$
Proof. Let u be a nonnegative real number. Then
![]() $-K_X-uA\sim _{\mathbb {R}} (2-u)A+E$
, which implies that divisor
$-K_X-uA\sim _{\mathbb {R}} (2-u)A+E$
, which implies that divisor
![]() $-K_X-uA$
is pseudoeffective if and only if
$-K_X-uA$
is pseudoeffective if and only if
![]() $u\leqslant 2$
. For every
$u\leqslant 2$
. For every
![]() $u\in [0,2]$
, let us denote by
$u\in [0,2]$
, let us denote by
![]() $P(u)$
the positive part of Zariski decomposition of the divisor
$P(u)$
the positive part of Zariski decomposition of the divisor
![]() $-K_X-uA$
, and let us denote by
$-K_X-uA$
, and let us denote by
![]() $N(u)$
its negative part. Then
$N(u)$
its negative part. Then
 $$ \begin{align*}P(u)=\left\{\begin{aligned} &(2-u)A+E\ \text{if }0\leqslant u\leqslant 1, \\ &(2-u)H\ \text{if }1\leqslant u\leqslant 2, \end{aligned} \right. \end{align*} $$
$$ \begin{align*}P(u)=\left\{\begin{aligned} &(2-u)A+E\ \text{if }0\leqslant u\leqslant 1, \\ &(2-u)H\ \text{if }1\leqslant u\leqslant 2, \end{aligned} \right. \end{align*} $$
and
 $$ \begin{align*}N(u)=\left\{\begin{aligned} &0\ \text{if }0\leqslant u\leqslant 1, \\ &(u-1)E\ \text{if }1\leqslant u\leqslant 2. \end{aligned} \right. \end{align*} $$
$$ \begin{align*}N(u)=\left\{\begin{aligned} &0\ \text{if }0\leqslant u\leqslant 1, \\ &(u-1)E\ \text{if }1\leqslant u\leqslant 2. \end{aligned} \right. \end{align*} $$
Integrating, we get
![]() $S_X(A)=\frac {11}{16}$
. Using [Reference Abban and Zhuang1, Theorem 3.3] and [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Corollary 1.102], we get
$S_X(A)=\frac {11}{16}$
. Using [Reference Abban and Zhuang1, Theorem 3.3] and [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Corollary 1.102], we get
 $$ \begin{align} \delta_O(X)\geqslant \min\left\{\frac{1}{S_X(A)},\inf_{\substack{F/A\\ O\in C_A(F)}}\frac{A_A(F)}{S(W_{\bullet,\bullet}^A;F)}\right\}=\min\left\{\frac{16}{11},\inf_{\substack{F/A\\ O\in C_A(F)}}\frac{A_A(F)}{S(W_{\bullet,\bullet}^A;F)}\right\}, \end{align} $$
$$ \begin{align} \delta_O(X)\geqslant \min\left\{\frac{1}{S_X(A)},\inf_{\substack{F/A\\ O\in C_A(F)}}\frac{A_A(F)}{S(W_{\bullet,\bullet}^A;F)}\right\}=\min\left\{\frac{16}{11},\inf_{\substack{F/A\\ O\in C_A(F)}}\frac{A_A(F)}{S(W_{\bullet,\bullet}^A;F)}\right\}, \end{align} $$
where the infimum is taken by all prime divisors F over the surface A with
![]() $O\in C_A(F)$
. The value
$O\in C_A(F)$
. The value
![]() $S(W_{\bullet ,\bullet }^A;F)$
can be computed using [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Corollary 1.108] as follows:
$S(W_{\bullet ,\bullet }^A;F)$
can be computed using [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Corollary 1.108] as follows:
 $$ \begin{align*}S\big(W_{\bullet,\bullet}^A; F\big)= \frac{3}{4d}\int_1^{2}\big(P(u)\big\vert_{A}\big)^2(u-1)\mathrm{ord}_{F}\big(E\big\vert_{A}\big)du+ \frac{3}{4d}\int_{0}^{2}\int_0^\infty \mathrm{vol}\big(P(u)\big\vert_{A}-vF\big)dvdu. \end{align*} $$
$$ \begin{align*}S\big(W_{\bullet,\bullet}^A; F\big)= \frac{3}{4d}\int_1^{2}\big(P(u)\big\vert_{A}\big)^2(u-1)\mathrm{ord}_{F}\big(E\big\vert_{A}\big)du+ \frac{3}{4d}\int_{0}^{2}\int_0^\infty \mathrm{vol}\big(P(u)\big\vert_{A}-vF\big)dvdu. \end{align*} $$
Now, let F be any prime divisor over the surface A such that
![]() $O\in C_A(F)$
. Since
$O\in C_A(F)$
. Since
 $$ \begin{align*}P(u)\big\vert_{A}=\left\{\begin{aligned} &-K_A\ \text{if }0\leqslant u\leqslant 1, \\ &(2-u)(-K_A)\ \text{if }1\leqslant u\leqslant 2, \end{aligned} \right. \end{align*} $$
$$ \begin{align*}P(u)\big\vert_{A}=\left\{\begin{aligned} &-K_A\ \text{if }0\leqslant u\leqslant 1, \\ &(2-u)(-K_A)\ \text{if }1\leqslant u\leqslant 2, \end{aligned} \right. \end{align*} $$
we have
 $$ \begin{align*} S\big(W_{\bullet,\bullet}^A; F\big)&= \frac{3}{4d}\int_1^{2}d(2-u)^2(u-1)\mathrm{ord}_{F}\big(E\big\vert_{A}\big)du+\\ &\quad+\frac{3}{4d}\int_{0}^{1} \int_{0}^{\infty}\mathrm{vol}\big(-K_A-vF\big)dvdu+\frac{3}{4d}\int_{1}^{2}\int_{0}^{\infty}\mathrm{vol}\big((2-u)(-K_A)-vF\big)dvdu=\\ &=\frac{\mathrm{ord}_{F}\big(E\big\vert_{A}\big)}{16}+\frac{3}{4d}\int_{0}^{\infty}\mathrm{vol}\big(-K_A-vF\big)dv+\frac{3}{4d}\int_{1}^{2}(2-u)^3\int_{0}^{\infty}\mathrm{vol}\big(-K_A-vF\big)dvdu=\\ &=\frac{\mathrm{ord}_{F}\big(E\big\vert_{A}\big)}{16}+\frac{3}{4d}\int_{0}^{\infty}\mathrm{vol}\big(-K_A-vF\big)dv+\frac{3}{16d}\int_{0}^{\infty}\mathrm{vol}\big(-K_A-vF\big)dv=\\ &=\frac{\mathrm{ord}_{F}\big(E\big\vert_{A}\big)}{16}+\frac{15}{16d}\int_{0}^{\infty}\mathrm{vol}\big(-K_A-vF\big)dv=\\ &=\frac{\mathrm{ord}_{F}\big(E\big\vert_{A}\big)}{16}+\frac{15}{16}S_A(F)\leqslant\frac{\mathrm{ord}_{F}\big(E\big\vert_{A}\big)}{16}+\frac{15A_{A}(F)}{16\delta_{O}(A)}.\end{align*} $$
$$ \begin{align*} S\big(W_{\bullet,\bullet}^A; F\big)&= \frac{3}{4d}\int_1^{2}d(2-u)^2(u-1)\mathrm{ord}_{F}\big(E\big\vert_{A}\big)du+\\ &\quad+\frac{3}{4d}\int_{0}^{1} \int_{0}^{\infty}\mathrm{vol}\big(-K_A-vF\big)dvdu+\frac{3}{4d}\int_{1}^{2}\int_{0}^{\infty}\mathrm{vol}\big((2-u)(-K_A)-vF\big)dvdu=\\ &=\frac{\mathrm{ord}_{F}\big(E\big\vert_{A}\big)}{16}+\frac{3}{4d}\int_{0}^{\infty}\mathrm{vol}\big(-K_A-vF\big)dv+\frac{3}{4d}\int_{1}^{2}(2-u)^3\int_{0}^{\infty}\mathrm{vol}\big(-K_A-vF\big)dvdu=\\ &=\frac{\mathrm{ord}_{F}\big(E\big\vert_{A}\big)}{16}+\frac{3}{4d}\int_{0}^{\infty}\mathrm{vol}\big(-K_A-vF\big)dv+\frac{3}{16d}\int_{0}^{\infty}\mathrm{vol}\big(-K_A-vF\big)dv=\\ &=\frac{\mathrm{ord}_{F}\big(E\big\vert_{A}\big)}{16}+\frac{15}{16d}\int_{0}^{\infty}\mathrm{vol}\big(-K_A-vF\big)dv=\\ &=\frac{\mathrm{ord}_{F}\big(E\big\vert_{A}\big)}{16}+\frac{15}{16}S_A(F)\leqslant\frac{\mathrm{ord}_{F}\big(E\big\vert_{A}\big)}{16}+\frac{15A_{A}(F)}{16\delta_{O}(A)}.\end{align*} $$
Therefore, if
![]() $O\not \in E$
, then
$O\not \in E$
, then
![]() $\mathrm {ord}_{F}(E\vert _{A})=0$
, which implies that
$\mathrm {ord}_{F}(E\vert _{A})=0$
, which implies that
Similarly, if
![]() $O\in E$
, then
$O\in E$
, then
![]() $\mathrm {ord}_{F}(E\vert _{A})\leqslant A_A(F)$
because
$\mathrm {ord}_{F}(E\vert _{A})\leqslant A_A(F)$
because
![]() $(A,E\vert _A)$
is log canonical, so that
$(A,E\vert _A)$
is log canonical, so that
 $$ \begin{align*}S\big(W_{\bullet,\bullet}^A; F\big)=\frac{\mathrm{ord}_{F}\big(E\big\vert_{A}\big)}{16}+\frac{15}{16}S_A(F)\leqslant\frac{A_A(F)}{16}+\frac{15A_{A}(F)}{16\delta_{O}(A)}=\frac{\delta_{O}(A)+15}{16\delta_{O}(A)}A_{A}(F). \end{align*} $$
$$ \begin{align*}S\big(W_{\bullet,\bullet}^A; F\big)=\frac{\mathrm{ord}_{F}\big(E\big\vert_{A}\big)}{16}+\frac{15}{16}S_A(F)\leqslant\frac{A_A(F)}{16}+\frac{15A_{A}(F)}{16\delta_{O}(A)}=\frac{\delta_{O}(A)+15}{16\delta_{O}(A)}A_{A}(F). \end{align*} $$
Now, using Equation (2.1), we obtain the required inequality.
Suppose X is not K-stable. Let us seek for a contradiction. Using the valuative criterion for K-stability [Reference Fujita15, Reference Li18], we see that there exists a prime divisor
![]() $\mathbf {F}$
over X such that
$\mathbf {F}$
over X such that
where
![]() $A_X(\mathbf {F})$
is a log discrepancy of the divisor
$A_X(\mathbf {F})$
is a log discrepancy of the divisor
![]() $\mathbf {F}$
, and
$\mathbf {F}$
, and
![]() $S_X(\mathbf {F})$
is defined in [Reference Fujita15] or [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, § 1.2]. Let Z be the center of the divisor
$S_X(\mathbf {F})$
is defined in [Reference Fujita15] or [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, § 1.2]. Let Z be the center of the divisor
![]() $\mathbf {F}$
on X. Then Z is not a surface [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Theorem 3.17]. We see that Z is an irreducible curve or a point. Let P be a point in Z. Then
$\mathbf {F}$
on X. Then Z is not a surface [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Theorem 3.17]. We see that Z is an irreducible curve or a point. Let P be a point in Z. Then
![]() $\delta _P(X)\leqslant 1$
.
$\delta _P(X)\leqslant 1$
.
Lemma 2.2. One has
![]() $P\not \in E$
.
$P\not \in E$
.
Proof. Let us compute
![]() $S_X(E)$
. Note that
$S_X(E)$
. Note that
![]() $S_X(E)<1$
by [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Theorem 3.17]. Fix
$S_X(E)<1$
by [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Theorem 3.17]. Fix
![]() $u\in \mathbb {R}_{\geqslant 0}$
. Then
$u\in \mathbb {R}_{\geqslant 0}$
. Then
![]() $-K_X-uE$
is pseudoeffective
$-K_X-uE$
is pseudoeffective
![]() $\iff -K_X-uE$
is nef
$\iff -K_X-uE$
is nef
![]() $\iff u\leqslant 1$
. Thus, we have
$\iff u\leqslant 1$
. Thus, we have
 $$ \begin{align*}S_X(E)=\frac{1}{4d}\int_{0}^{1}\big(-K_X-uE\big)^3du=\frac{1}{4d}\int_{0}^{1}d(2u^3-6u+4)du=\frac{3}{8}. \end{align*} $$
$$ \begin{align*}S_X(E)=\frac{1}{4d}\int_{0}^{1}\big(-K_X-uE\big)^3du=\frac{1}{4d}\int_{0}^{1}d(2u^3-6u+4)du=\frac{3}{8}. \end{align*} $$
Suppose that
![]() $P\in E$
. Let us seek for a contradiction.
$P\in E$
. Let us seek for a contradiction.
Note that
![]() $E\cong \mathcal {C}\times \mathbb {P}^1$
. Let
$E\cong \mathcal {C}\times \mathbb {P}^1$
. Let
![]() $\mathbf {s}$
be a fiber of the projection
$\mathbf {s}$
be a fiber of the projection
![]() $\phi \vert _{E}\colon E\to \mathbb {P}^1$
that contains P, and let
$\phi \vert _{E}\colon E\to \mathbb {P}^1$
that contains P, and let
![]() $\mathbf {f}$
be a fiber of the projection
$\mathbf {f}$
be a fiber of the projection
![]() $\pi \vert _{E}\colon E\to \mathcal {C}$
. Fix
$\pi \vert _{E}\colon E\to \mathcal {C}$
. Fix
![]() $u\in [0,1]$
, and take
$u\in [0,1]$
, and take
![]() $v\in \mathbb {R}_{\geqslant 0}$
. Then
$v\in \mathbb {R}_{\geqslant 0}$
. Then
This implies that
Therefore, using [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Corollary 1.109], we get
 $$ \begin{align*}S\left(W_{\bullet,\bullet}^{E};\mathbf{s}\right)=\frac{3}{4d} \int_{0}^{1} \int_{0}^{1+u} 2d(1-u)(1+u-v)dvdu=\frac{11}{16}. \end{align*} $$
$$ \begin{align*}S\left(W_{\bullet,\bullet}^{E};\mathbf{s}\right)=\frac{3}{4d} \int_{0}^{1} \int_{0}^{1+u} 2d(1-u)(1+u-v)dvdu=\frac{11}{16}. \end{align*} $$
Similarly, using [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Theorem 1.112], we get
 $$ \begin{align*}S\left(W_{\bullet,\bullet, \bullet}^{E,\mathbf{s}};P\right)=\frac{3}{4d}\int_{0}^{1} \int_{0}^{1+u}\big(d(1-u)\big)^{2}dvdu=\frac{5d}{16}. \end{align*} $$
$$ \begin{align*}S\left(W_{\bullet,\bullet, \bullet}^{E,\mathbf{s}};P\right)=\frac{3}{4d}\int_{0}^{1} \int_{0}^{1+u}\big(d(1-u)\big)^{2}dvdu=\frac{5d}{16}. \end{align*} $$
Therefore, it follows from [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Theorem 1.112] that
 $$ \begin{align*}1\geqslant\frac{A_X(\mathbf{F})}{S_X(\mathbf{F})}\geqslant \min\left\{\frac{1}{S_{X}(E)}, \frac{1}{S\left(W_{\bullet,\bullet}^E,\mathbf{s}\right)}, \frac{1}{S\left(W_{\bullet,\bullet,\bullet}^{E,\mathbf{s}};P\right)}\right\}=\min \left\{\frac{8}{3}, \frac{16}{11}, \frac{16}{5d}\right\}\geqslant\frac{16}{15}>1, \end{align*} $$
$$ \begin{align*}1\geqslant\frac{A_X(\mathbf{F})}{S_X(\mathbf{F})}\geqslant \min\left\{\frac{1}{S_{X}(E)}, \frac{1}{S\left(W_{\bullet,\bullet}^E,\mathbf{s}\right)}, \frac{1}{S\left(W_{\bullet,\bullet,\bullet}^{E,\mathbf{s}};P\right)}\right\}=\min \left\{\frac{8}{3}, \frac{16}{11}, \frac{16}{5d}\right\}\geqslant\frac{16}{15}>1, \end{align*} $$
which is a contradiction.
Let A be the fiber of the del Pezzo fibration
![]() $\phi $
such that A passes through the point P. Then A is a del Pezzo surface of degree
$\phi $
such that A passes through the point P. Then A is a del Pezzo surface of degree
![]() $d\in \{1,2,3\}$
that has at most isolated singularities. In particular, we see that A is normal. Applying Lemmas 2.1 and 2.2, we obtain
$d\in \{1,2,3\}$
that has at most isolated singularities. In particular, we see that A is normal. Applying Lemmas 2.1 and 2.2, we obtain
Corollary 2.3. One has
![]() $\delta _P(A)\leqslant \frac {15}{16}$
.
$\delta _P(A)\leqslant \frac {15}{16}$
.
Proof. Since
![]() $1\geqslant \frac {A_X(\mathbf {F})}{S_X(\mathbf {F})}\geqslant \delta _P(X)$
, we get
$1\geqslant \frac {A_X(\mathbf {F})}{S_X(\mathbf {F})}\geqslant \delta _P(X)$
, we get
![]() $\delta _P(A)\leqslant \frac {15}{16}$
by Lemmas 2.1 and 2.2.
$\delta _P(A)\leqslant \frac {15}{16}$
by Lemmas 2.1 and 2.2.
Corollary 2.4. The surface A is singular.
Proof. If A is smooth, then
![]() $\delta _P(A)\geqslant \delta (A)\geqslant \frac {3}{2}$
[Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, § 2], which contradicts Corollary 2.3.
$\delta _P(A)\geqslant \delta (A)\geqslant \frac {3}{2}$
[Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, § 2], which contradicts Corollary 2.3.
Let
![]() $\overline {S}$
be a general surface in
$\overline {S}$
be a general surface in
![]() $|H|$
that passes through
$|H|$
that passes through
![]() $\pi (P)$
, and let S be the proper transform on X of the surface
$\pi (P)$
, and let S be the proper transform on X of the surface
![]() $\overline {S}$
. Then
$\overline {S}$
. Then
-
• the surface
 $\overline {S}$
is a smooth del Pezzo surface of degree d,
$\overline {S}$
is a smooth del Pezzo surface of degree d, -
• the surface
 $\overline {S}$
intersects the curve
$\overline {S}$
intersects the curve
 $\mathcal {C}$
transversally at d points,
$\mathcal {C}$
transversally at d points, -
• the induced morphism
 $\pi \vert _{S}\colon S\to \overline {S}$
is a blow up of the points
$\pi \vert _{S}\colon S\to \overline {S}$
is a blow up of the points
 $\overline {S}\cap \mathcal {C}$
.
$\overline {S}\cap \mathcal {C}$
.
Observe that
![]() $\phi \vert _S\colon S\to \mathbb {P}^1$
is an elliptic fibration given by the pencil
$\phi \vert _S\colon S\to \mathbb {P}^1$
is an elliptic fibration given by the pencil
![]() $|-K_S|$
. Set
$|-K_S|$
. Set
![]() $C=A\big \vert _{S}$
. Then C is a reduced curve of arithmetic genus
$C=A\big \vert _{S}$
. Then C is a reduced curve of arithmetic genus
![]() $1$
in
$1$
in
![]() $|-K_S|$
that has at most d components. In particular, if
$|-K_S|$
that has at most d components. In particular, if
![]() $d=1$
, then C is irreducible. Therefore, the following cases may happen:
$d=1$
, then C is irreducible. Therefore, the following cases may happen:
-
(1) the curve C is irreducible, and C is smooth at P,
-
(2) the curve C is irreducible, and C has an ordinary node at P,
-
(3) the curve C is irreducible, and C has an ordinary cusp at P,
-
(4) the curve C is reducible.
Fix
![]() $u\in \mathbb {R}_{\geqslant 0}$
. Then
$u\in \mathbb {R}_{\geqslant 0}$
. Then
![]() $-K_X-uS$
is nef
$-K_X-uS$
is nef
![]() $\iff u\leqslant 1 \iff -K_X-uS$
is pseudoeffective. Using this, we see that
$\iff u\leqslant 1 \iff -K_X-uS$
is pseudoeffective. Using this, we see that
 $$ \begin{align*}S_X(S)=\frac{1}{4d}\int_{0}^{1}(-K_X-uS)^3du=\frac{1}{4d}\int_{0}^{1}d(4-u)(1-u)^2du=\frac{5}{16}<1, \end{align*} $$
$$ \begin{align*}S_X(S)=\frac{1}{4d}\int_{0}^{1}(-K_X-uS)^3du=\frac{1}{4d}\int_{0}^{1}d(4-u)(1-u)^2du=\frac{5}{16}<1, \end{align*} $$
which also follows from [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Theorem 3.17]. Moreover, if
![]() $u\in [0,1]$
, then
$u\in [0,1]$
, then
 $$ \begin{align*}(-K_X-uS)|_S\sim_{\mathbb{R}}(1-u)(\pi\vert_{S})^*(-K_{\overline{S}})-K_S\sim_{\mathbb{R}}(1-u)\sum_{i=1}^{d}\mathbf{e}_i+(2-u)(-K_S), \end{align*} $$
$$ \begin{align*}(-K_X-uS)|_S\sim_{\mathbb{R}}(1-u)(\pi\vert_{S})^*(-K_{\overline{S}})-K_S\sim_{\mathbb{R}}(1-u)\sum_{i=1}^{d}\mathbf{e}_i+(2-u)(-K_S), \end{align*} $$
where
![]() $\mathbf {e}_1,\ldots ,\mathbf {e}_d$
are exceptional curves of the blow up
$\mathbf {e}_1,\ldots ,\mathbf {e}_d$
are exceptional curves of the blow up
![]() $\pi \vert _{S}\colon S\to \overline {S}$
.
$\pi \vert _{S}\colon S\to \overline {S}$
.
Lemma 2.5. Suppose that C is irreducible. Then C is singular at the point P.
Proof. As in the proof of Lemma 2.2, it follows from [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Theorem 1.112] that
 $$ \begin{align*}1\geqslant \frac{A_X(\mathbf{F})}{S_X(\mathbf{F})}\geqslant \min\left\{\frac{1}{S_X(S)},\frac{1}{S(W_{\bullet,\bullet}^S;C)}, \frac{1}{S(W_{\bullet, \bullet,\bullet}^{S,C};P)}\right\}, \end{align*} $$
$$ \begin{align*}1\geqslant \frac{A_X(\mathbf{F})}{S_X(\mathbf{F})}\geqslant \min\left\{\frac{1}{S_X(S)},\frac{1}{S(W_{\bullet,\bullet}^S;C)}, \frac{1}{S(W_{\bullet, \bullet,\bullet}^{S,C};P)}\right\}, \end{align*} $$
where
![]() $S(W_{\bullet ,\bullet }^S;C)$
and
$S(W_{\bullet ,\bullet }^S;C)$
and
![]() $S(W_{\bullet , \bullet ,\bullet }^{S,C};P)$
are defined in [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, § 1.7]. Since we know that
$S(W_{\bullet , \bullet ,\bullet }^{S,C};P)$
are defined in [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, § 1.7]. Since we know that
![]() $S_X(S)<1$
, we see that
$S_X(S)<1$
, we see that
![]() $S(W_{\bullet ,\bullet }^S;C)\geqslant 1$
or
$S(W_{\bullet ,\bullet }^S;C)\geqslant 1$
or
![]() $S(W_{\bullet , \bullet ,\bullet }^{S,C};P)\geqslant 1$
. Let us compute these numbers.
$S(W_{\bullet , \bullet ,\bullet }^{S,C};P)\geqslant 1$
. Let us compute these numbers.
Let
![]() $P(u,v)$
be the positive part of the Zariski decomposition of
$P(u,v)$
be the positive part of the Zariski decomposition of
![]() $(-K_X-uS)\vert _{S}-vC$
, and let
$(-K_X-uS)\vert _{S}-vC$
, and let
![]() $N(u,v)$
be its negative part, where
$N(u,v)$
be its negative part, where
![]() $u\in [0,1]$
and
$u\in [0,1]$
and
![]() $v\in \mathbb {R}_{\geqslant 0}$
. Since
$v\in \mathbb {R}_{\geqslant 0}$
. Since
 $$ \begin{align*}(-K_X-uS)\vert_{S}-vC\sim_{\mathbb{R}}(1-u)\sum_{i=1}^{d}\mathbf{e}_i+(2-u-v)C, \end{align*} $$
$$ \begin{align*}(-K_X-uS)\vert_{S}-vC\sim_{\mathbb{R}}(1-u)\sum_{i=1}^{d}\mathbf{e}_i+(2-u-v)C, \end{align*} $$
we see that
![]() $(-K_X-uS)\vert _{S}-vC$
is pseudoeffective
$(-K_X-uS)\vert _{S}-vC$
is pseudoeffective
![]() $\iff v\leqslant 2-u$
. Moreover, we have
$\iff v\leqslant 2-u$
. Moreover, we have
 $$ \begin{align*}P(u,v)=\left\{\begin{aligned} &(1-u)\sum_{i=1}^{d}\mathbf{e}_i+(2-u-v)C\ \text{if }0\leqslant v\leqslant 1, \\ &(2-u-v)\Big(C+\sum_{i=1}^{d}\mathbf{e}_i\Big)\ \text{if }1\leqslant v\leqslant 2-u, \\ \end{aligned} \right. \end{align*} $$
$$ \begin{align*}P(u,v)=\left\{\begin{aligned} &(1-u)\sum_{i=1}^{d}\mathbf{e}_i+(2-u-v)C\ \text{if }0\leqslant v\leqslant 1, \\ &(2-u-v)\Big(C+\sum_{i=1}^{d}\mathbf{e}_i\Big)\ \text{if }1\leqslant v\leqslant 2-u, \\ \end{aligned} \right. \end{align*} $$
and
 $$ \begin{align*}N(u,v)=\left\{\begin{aligned} &0\ \text{if }0\leqslant v\leqslant 1, \\ &(v-1)\sum_{i=1}^{d}\mathbf{e}_i\ \text{if }1\leqslant v\leqslant 2-u. \\ \end{aligned} \right. \end{align*} $$
$$ \begin{align*}N(u,v)=\left\{\begin{aligned} &0\ \text{if }0\leqslant v\leqslant 1, \\ &(v-1)\sum_{i=1}^{d}\mathbf{e}_i\ \text{if }1\leqslant v\leqslant 2-u. \\ \end{aligned} \right. \end{align*} $$
Thus, it follows from [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Corollary 1.109] that
 $$ \begin{align*} S\big(W^S_{\bullet,\bullet};C\big)& =\frac{3}{4d}\int_0^1\int_0^{2-u}P(u,v)^2dvdu=\\ &=\frac{3}{4d}\int_0^1\int_0^1d(1-u)(3-u-2v)dvdu+\frac{3}{4d}\int_0^1\int_1^{2-u}d(2-u-v)^2dvdu=\frac{11}{16}<1. \end{align*} $$
$$ \begin{align*} S\big(W^S_{\bullet,\bullet};C\big)& =\frac{3}{4d}\int_0^1\int_0^{2-u}P(u,v)^2dvdu=\\ &=\frac{3}{4d}\int_0^1\int_0^1d(1-u)(3-u-2v)dvdu+\frac{3}{4d}\int_0^1\int_1^{2-u}d(2-u-v)^2dvdu=\frac{11}{16}<1. \end{align*} $$
Thus, we conclude that
![]() $S(W_{\bullet , \bullet ,\bullet }^{S,C};P)\geqslant 1$
.
$S(W_{\bullet , \bullet ,\bullet }^{S,C};P)\geqslant 1$
.
Since
![]() $P\not \in \mathbf {e}_1\cup \cdots \cup \mathbf {e}_d$
by Lemma 2.2, it follows from [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Theorem 1.112] that
$P\not \in \mathbf {e}_1\cup \cdots \cup \mathbf {e}_d$
by Lemma 2.2, it follows from [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Theorem 1.112] that
 $$ \begin{align*} S\big(W_{\bullet, \bullet,\bullet}^{S,C};P\big)&=\frac{3}{4d}\int_0^1\int_0^{2-u}\big(P(u,v)\cdot C\big)^2dvdu=\\ &=\frac{3}{4d}\int_0^1\int_0^1d^2(u-1)^2dvdu+\frac{3}{4d}\int_0^1\int_1^{2-u}d^2(2-u-v)^2dvdu=\frac{5d}{16}<1, \end{align*} $$
$$ \begin{align*} S\big(W_{\bullet, \bullet,\bullet}^{S,C};P\big)&=\frac{3}{4d}\int_0^1\int_0^{2-u}\big(P(u,v)\cdot C\big)^2dvdu=\\ &=\frac{3}{4d}\int_0^1\int_0^1d^2(u-1)^2dvdu+\frac{3}{4d}\int_0^1\int_1^{2-u}d^2(2-u-v)^2dvdu=\frac{5d}{16}<1, \end{align*} $$
which is a contradiction.
Now, let us show that C is reducible for
![]() $d\in \{1,2\}$
.
$d\in \{1,2\}$
.
Lemma 2.6. Suppose that C is irreducible. Then
![]() $d=3$
and C has a cusp at P.
$d=3$
and C has a cusp at P.
Proof. By Lemma 2.5, the curve C is singular at the point P.
Now, let
![]() $\sigma \colon \widetilde {S}\to S$
be the blow up of the point P; let
$\sigma \colon \widetilde {S}\to S$
be the blow up of the point P; let
![]() $\mathbf {f}$
be the
$\mathbf {f}$
be the
![]() $\sigma $
-exceptional curve, and let
$\sigma $
-exceptional curve, and let
![]() $\widetilde {\mathbf {e}}_1,\ldots ,\widetilde {\mathbf {e}}_d,\widetilde {C}$
be the proper transforms on
$\widetilde {\mathbf {e}}_1,\ldots ,\widetilde {\mathbf {e}}_d,\widetilde {C}$
be the proper transforms on
![]() $\widetilde {S}$
of the curves
$\widetilde {S}$
of the curves
![]() $\mathbf {e}_1,\ldots ,\mathbf {e}_d,C$
, respectively. Then the curve
$\mathbf {e}_1,\ldots ,\mathbf {e}_d,C$
, respectively. Then the curve
![]() $\widetilde {C}$
is smooth, and it follows from [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Remark 1.113] that
$\widetilde {C}$
is smooth, and it follows from [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Remark 1.113] that
 $$ \begin{align*}1\geqslant \frac{A_X(\mathbf{F})}{S_X(\mathbf{F})}\geqslant\min\left\{\inf_{O\in\mathbf{f}}\frac{1}{S(W_{\bullet,\bullet,\bullet}^{\widetilde{S},\mathbf{f}};O)}, \frac{2}{S(V_{\bullet,\bullet}^{S};\mathbf{f})},\frac{1}{S_X(S)}\right\}, \end{align*} $$
$$ \begin{align*}1\geqslant \frac{A_X(\mathbf{F})}{S_X(\mathbf{F})}\geqslant\min\left\{\inf_{O\in\mathbf{f}}\frac{1}{S(W_{\bullet,\bullet,\bullet}^{\widetilde{S},\mathbf{f}};O)}, \frac{2}{S(V_{\bullet,\bullet}^{S};\mathbf{f})},\frac{1}{S_X(S)}\right\}, \end{align*} $$
where
![]() $S(W_{\bullet , \bullet ,\bullet }^{\widetilde {S},\mathbf {f}};O)$
and
$S(W_{\bullet , \bullet ,\bullet }^{\widetilde {S},\mathbf {f}};O)$
and
![]() $S(V_{\bullet ,\bullet }^{S};\mathbf {f})$
are defined in [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, § 1.7]. Since we know that
$S(V_{\bullet ,\bullet }^{S};\mathbf {f})$
are defined in [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, § 1.7]. Since we know that
![]() $S_X(S)<1$
, we see that
$S_X(S)<1$
, we see that
![]() $S(V_{\bullet ,\bullet }^{S};\mathbf {f})\geqslant 2$
or there exists a point
$S(V_{\bullet ,\bullet }^{S};\mathbf {f})\geqslant 2$
or there exists a point
![]() $O\in \mathbf {f}$
such that
$O\in \mathbf {f}$
such that
![]() $S(W_{\bullet ,\bullet ,\bullet }^{\widetilde {S},\mathbf {f}};O)\geqslant 1$
.
$S(W_{\bullet ,\bullet ,\bullet }^{\widetilde {S},\mathbf {f}};O)\geqslant 1$
.
Let us compute
![]() $S(V_{\bullet ,\bullet }^{S};\mathbf {f})$
. Fix
$S(V_{\bullet ,\bullet }^{S};\mathbf {f})$
. Fix
![]() $u\in [0,1]$
and
$u\in [0,1]$
and
![]() $v\in \mathbb {R}_{\geqslant 0}$
. Since
$v\in \mathbb {R}_{\geqslant 0}$
. Since
![]() $\sigma ^*(C)\sim \widetilde {C}+2\mathbf {f}$
, we get
$\sigma ^*(C)\sim \widetilde {C}+2\mathbf {f}$
, we get
 $$ \begin{align*}\sigma^*\big((-K_X-uS)\vert_{S}\big)-v\mathbf{f}\sim_{\mathbb{R}}(2-u)\widetilde{C}+(4-2u-v)\mathbf{f}+(1-u)\sum_{i=1}^{d}\widetilde{\mathbf{e}}_i. \end{align*} $$
$$ \begin{align*}\sigma^*\big((-K_X-uS)\vert_{S}\big)-v\mathbf{f}\sim_{\mathbb{R}}(2-u)\widetilde{C}+(4-2u-v)\mathbf{f}+(1-u)\sum_{i=1}^{d}\widetilde{\mathbf{e}}_i. \end{align*} $$
Then the divisor
![]() $\sigma ^*((-K_X-uS)\vert _{S})-v\mathbf {f}$
is pseudoeffective
$\sigma ^*((-K_X-uS)\vert _{S})-v\mathbf {f}$
is pseudoeffective
![]() $\iff v\leqslant 4-2u$
.
$\iff v\leqslant 4-2u$
.
Let
![]() $P(u,v)$
be the positive part of the Zariski decomposition of
$P(u,v)$
be the positive part of the Zariski decomposition of
![]() $\sigma ^*((-K_X-uS)\vert _{S})-v\mathbf {f}$
, and let
$\sigma ^*((-K_X-uS)\vert _{S})-v\mathbf {f}$
, and let
![]() $N(u,v)$
be its negative part. Then
$N(u,v)$
be its negative part. Then
 $$ \begin{align*}P(u,v)=\left\{\begin{aligned} &(2-u)\widetilde{C}+(4-2u-v)\mathbf{f}+(1-u)\sum_{i=1}^{d}\widetilde{\mathbf{e}}_i\ \text{if }0\leqslant v\leqslant \frac{d-du}{2}, \\ &\frac{8+d-4u-du-2v}{4}\widetilde{C}+(4-2u-v)\mathbf{f}+(1-u)\sum_{i=1}^{d}\widetilde{\mathbf{e}}_i\ \text{if }\frac{d-du}{2}\leqslant v\leqslant \frac{4+d-du}{2}, \\ &\frac{4-2u-v}{4-d}\Big(2\widetilde{C}+(4-d)\mathbf{f}+2\sum_{i=1}^{d}\widetilde{\mathbf{e}}_i\Big)\ \text{if }\frac{4+d-du}{2}\leqslant v\leqslant 4-2u, \end{aligned} \right. \end{align*} $$
$$ \begin{align*}P(u,v)=\left\{\begin{aligned} &(2-u)\widetilde{C}+(4-2u-v)\mathbf{f}+(1-u)\sum_{i=1}^{d}\widetilde{\mathbf{e}}_i\ \text{if }0\leqslant v\leqslant \frac{d-du}{2}, \\ &\frac{8+d-4u-du-2v}{4}\widetilde{C}+(4-2u-v)\mathbf{f}+(1-u)\sum_{i=1}^{d}\widetilde{\mathbf{e}}_i\ \text{if }\frac{d-du}{2}\leqslant v\leqslant \frac{4+d-du}{2}, \\ &\frac{4-2u-v}{4-d}\Big(2\widetilde{C}+(4-d)\mathbf{f}+2\sum_{i=1}^{d}\widetilde{\mathbf{e}}_i\Big)\ \text{if }\frac{4+d-du}{2}\leqslant v\leqslant 4-2u, \end{aligned} \right. \end{align*} $$
and
 $$ \begin{align*}N(u,v)=\left\{\begin{aligned} &0\ \text{if }0\leqslant v\leqslant \frac{d-du}{2}, \\ &\frac{2v+du-d}{4}\widetilde{C}\ \text{if }\frac{d-du}{2}\leqslant v\leqslant \frac{4+d-du}{2}, \\ &\frac{2v+du-2d}{4-d}\widetilde{C}+\frac{2v+du-4-d}{4-d}\sum_{i=1}^{d}\widetilde{\mathbf{e}}_i\ \text{if }\frac{4+d-du}{2}\leqslant v\leqslant 4-2u. \end{aligned} \right. \end{align*} $$
$$ \begin{align*}N(u,v)=\left\{\begin{aligned} &0\ \text{if }0\leqslant v\leqslant \frac{d-du}{2}, \\ &\frac{2v+du-d}{4}\widetilde{C}\ \text{if }\frac{d-du}{2}\leqslant v\leqslant \frac{4+d-du}{2}, \\ &\frac{2v+du-2d}{4-d}\widetilde{C}+\frac{2v+du-4-d}{4-d}\sum_{i=1}^{d}\widetilde{\mathbf{e}}_i\ \text{if }\frac{4+d-du}{2}\leqslant v\leqslant 4-2u. \end{aligned} \right. \end{align*} $$
Thus, using [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Corollary 1.109], we get
 $$ \begin{align*} S\big(W_{\bullet,\bullet}^S;\mathbf{f}\big)&=\frac{3}{4d}\int_0^1\int_0^{\frac{d-du}{2}}\big(du^2-4du-v^2+3d\big)dvdu+\\ &\quad+\frac{3}{4d}\int_0^1\int_{\frac{d-du}{2}}^{\frac{4+d-du}{2}}\frac{d(1-u)(12-du+d-4u-4v)}{4}dvdu+\\ &\quad+\frac{3}{4d}\int_0^1\int_{\frac{4+d-du}{2}}^{4-2u}\frac{d(4-2u-v)^2}{4-d}dvdu=\frac{44+5d}{32}<2. \end{align*} $$
$$ \begin{align*} S\big(W_{\bullet,\bullet}^S;\mathbf{f}\big)&=\frac{3}{4d}\int_0^1\int_0^{\frac{d-du}{2}}\big(du^2-4du-v^2+3d\big)dvdu+\\ &\quad+\frac{3}{4d}\int_0^1\int_{\frac{d-du}{2}}^{\frac{4+d-du}{2}}\frac{d(1-u)(12-du+d-4u-4v)}{4}dvdu+\\ &\quad+\frac{3}{4d}\int_0^1\int_{\frac{4+d-du}{2}}^{4-2u}\frac{d(4-2u-v)^2}{4-d}dvdu=\frac{44+5d}{32}<2. \end{align*} $$
Therefore, there exists a point
![]() $O\in \mathbf {f}$
such that
$O\in \mathbf {f}$
such that
![]() $S(W_{\bullet ,\bullet ,\bullet }^{\widetilde {S},\mathbf {f}};O)\geqslant 1$
.
$S(W_{\bullet ,\bullet ,\bullet }^{\widetilde {S},\mathbf {f}};O)\geqslant 1$
.
Let us compute
![]() $S(W_{\bullet ,\bullet ,\bullet }^{\widetilde {S},\mathbf {f}};O)$
. Observe that
$S(W_{\bullet ,\bullet ,\bullet }^{\widetilde {S},\mathbf {f}};O)$
. Observe that
 $$ \begin{align*}P(u,v)\cdot\mathbf{f}=\left\{\begin{aligned} &v\ \text{if }0\leqslant v\leqslant \frac{d-du}{2}, \\ &\frac{d-du}{2}\ \text{if }\frac{d-du}{2}\leqslant v\leqslant \frac{4+d-du}{2}, \\ &\frac{d(4-2u-v)}{4-d}\ \text{if }\frac{4+d-du}{2}\leqslant v\leqslant 4-2u. \end{aligned} \right. \end{align*} $$
$$ \begin{align*}P(u,v)\cdot\mathbf{f}=\left\{\begin{aligned} &v\ \text{if }0\leqslant v\leqslant \frac{d-du}{2}, \\ &\frac{d-du}{2}\ \text{if }\frac{d-du}{2}\leqslant v\leqslant \frac{4+d-du}{2}, \\ &\frac{d(4-2u-v)}{4-d}\ \text{if }\frac{4+d-du}{2}\leqslant v\leqslant 4-2u. \end{aligned} \right. \end{align*} $$
Hence, it follows from [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Remark 1.113] that
 $$ \begin{align*} S(W_{\bullet,\bullet,\bullet}^{\widetilde{S},\mathbf{f}};O)&=\frac{3}{4d}\int_0^1\int_0^{4-2u}\Big(\big(P(u,v)\cdot\mathbf{f}\big)\Big)^2dvdu+\\ &\quad+\frac{6}{4d}\int_0^1\int_0^{4-2u}\big(P(u,v)\cdot\mathbf{f}\big)\mathrm{ord}_O\big(N(u,v)\big|_{\mathbf{f}}\big)dvdu=\\ &=\frac{3}{4d}\int_0^1\int_0^{\frac{d-du}{2}}v^2dvdu+\\ &\quad+\frac{3}{4d}\int_{\frac{d-du}{2}}^{\frac{4+d-du}{2}}\Big(\frac{d-du}{2}\Big)^2dvdu+ \frac{3}{4d}\int_0^1\int_{\frac{4+d-du}{2}}^{4-2u}\Big(\frac{d(4-2u-v)}{4-d}\Big)^2dvdu+\\ &\quad+\frac{6}{4d}\int_0^1\int_0^{4-2u}\big(P(u,v)\cdot\mathbf{f}\big)\mathrm{ord}_O\big(N(u,v)\big|_{\mathbf{f}}\big)dvdu=\\ &=\frac{5d}{32}+\frac{3}{2}\int_0^1\int_0^{4-2u}\big(P(u,v)\cdot\mathbf{f}\big)\mathrm{ord}_O\big(N(u,v)\big|_{\mathbf{f}}\big)dvdu. \end{align*} $$
$$ \begin{align*} S(W_{\bullet,\bullet,\bullet}^{\widetilde{S},\mathbf{f}};O)&=\frac{3}{4d}\int_0^1\int_0^{4-2u}\Big(\big(P(u,v)\cdot\mathbf{f}\big)\Big)^2dvdu+\\ &\quad+\frac{6}{4d}\int_0^1\int_0^{4-2u}\big(P(u,v)\cdot\mathbf{f}\big)\mathrm{ord}_O\big(N(u,v)\big|_{\mathbf{f}}\big)dvdu=\\ &=\frac{3}{4d}\int_0^1\int_0^{\frac{d-du}{2}}v^2dvdu+\\ &\quad+\frac{3}{4d}\int_{\frac{d-du}{2}}^{\frac{4+d-du}{2}}\Big(\frac{d-du}{2}\Big)^2dvdu+ \frac{3}{4d}\int_0^1\int_{\frac{4+d-du}{2}}^{4-2u}\Big(\frac{d(4-2u-v)}{4-d}\Big)^2dvdu+\\ &\quad+\frac{6}{4d}\int_0^1\int_0^{4-2u}\big(P(u,v)\cdot\mathbf{f}\big)\mathrm{ord}_O\big(N(u,v)\big|_{\mathbf{f}}\big)dvdu=\\ &=\frac{5d}{32}+\frac{3}{2}\int_0^1\int_0^{4-2u}\big(P(u,v)\cdot\mathbf{f}\big)\mathrm{ord}_O\big(N(u,v)\big|_{\mathbf{f}}\big)dvdu. \end{align*} $$
Therefore, if
![]() $O\not \in \widetilde {C}$
, we obtain
$O\not \in \widetilde {C}$
, we obtain
![]() $S(W_{\bullet ,\bullet ,\bullet }^{\widetilde {S},\mathbf {f}};O)=\frac {5d}{32}$
, which contradicts to
$S(W_{\bullet ,\bullet ,\bullet }^{\widetilde {S},\mathbf {f}};O)=\frac {5d}{32}$
, which contradicts to
![]() $S(W_{\bullet ,\bullet ,\bullet }^{\widetilde {S},\mathbf {f}};O)\geqslant 1$
. Similarly, if
$S(W_{\bullet ,\bullet ,\bullet }^{\widetilde {S},\mathbf {f}};O)\geqslant 1$
. Similarly, if
![]() $O\in \widetilde {C}$
and
$O\in \widetilde {C}$
and
![]() $\widetilde {C}$
intersects the curve
$\widetilde {C}$
intersects the curve
![]() $\mathbf {f}$
transversally at the point O, then
$\mathbf {f}$
transversally at the point O, then
 $$ \begin{align*}S(W_{\bullet,\bullet,\bullet}^{\widetilde{S},\mathbf{f}};O)=\frac{5d}{32}+\frac{6}{4d}\int_0^1\int_0^{4-2u}\big(P(u,v)\cdot\mathbf{f}\big)\mathrm{ord}_O\big(N(u,v)\big|_{\mathbf{f}}\big)dvdu=\frac{44+5d}{64}<1, \end{align*} $$
$$ \begin{align*}S(W_{\bullet,\bullet,\bullet}^{\widetilde{S},\mathbf{f}};O)=\frac{5d}{32}+\frac{6}{4d}\int_0^1\int_0^{4-2u}\big(P(u,v)\cdot\mathbf{f}\big)\mathrm{ord}_O\big(N(u,v)\big|_{\mathbf{f}}\big)dvdu=\frac{44+5d}{64}<1, \end{align*} $$
which again contradicts
![]() $S(W_{\bullet ,\bullet ,\bullet }^{\widetilde {S},\mathbf {f}};O)\geqslant 1$
. Therefore, the curves
$S(W_{\bullet ,\bullet ,\bullet }^{\widetilde {S},\mathbf {f}};O)\geqslant 1$
. Therefore, the curves
![]() $\widetilde {C}$
and
$\widetilde {C}$
and
![]() $\mathbf {f}$
are tangent at O, which implies that C has a cusp at the point P.
$\mathbf {f}$
are tangent at O, which implies that C has a cusp at the point P.
Thus, to proceed, we may assume that
![]() $d=1$
or
$d=1$
or
![]() $d=2$
.
$d=2$
.
Now, let us consider the following commutative diagram:

where
-
•
 $\rho $
is the blow up of the point
$\rho $
is the blow up of the point
 $\widetilde {C}\cap \mathbf {f}$
,
$\widetilde {C}\cap \mathbf {f}$
, -
•
 $\eta $
is the blow up of the intersection point of the
$\eta $
is the blow up of the intersection point of the
 $\rho $
-exceptional curve and the proper transform of the curve
$\rho $
-exceptional curve and the proper transform of the curve
 $\widetilde {C}$
,
$\widetilde {C}$
, -
•
 $\psi $
is the contraction of the proper transforms of both
$\psi $
is the contraction of the proper transforms of both
 $(\sigma \circ \rho )$
-exceptional curves,
$(\sigma \circ \rho )$
-exceptional curves, -
•
 $\upsilon $
is the birational contraction of the proper transform of the
$\upsilon $
is the birational contraction of the proper transform of the
 $\eta $
-exceptional curve.
$\eta $
-exceptional curve.
Let
![]() $\mathscr {F}$
be the
$\mathscr {F}$
be the
![]() $\upsilon $
-exceptional curve; let
$\upsilon $
-exceptional curve; let
![]() $\mathscr {C}$
be the proper transform on
$\mathscr {C}$
be the proper transform on
![]() $\mathscr {S}$
of the curve C. Then
$\mathscr {S}$
of the curve C. Then
![]() $\mathscr {F}$
and
$\mathscr {F}$
and
![]() $\mathscr {C}$
are smooth,
$\mathscr {C}$
are smooth,
![]() $\mathscr {C}^2=-6$
,
$\mathscr {C}^2=-6$
,
![]() $\mathscr {F}^{2}=-\frac {1}{6}$
,
$\mathscr {F}^{2}=-\frac {1}{6}$
,
![]() $\mathscr {C}\cdot \mathscr {F}=1$
, and
$\mathscr {C}\cdot \mathscr {F}=1$
, and
![]() $\upsilon ^*(C)=\mathscr {C}+6\mathscr {F}$
.
$\upsilon ^*(C)=\mathscr {C}+6\mathscr {F}$
.
Observe that
![]() $\mathscr {F}$
contains two singular points of the surfaces
$\mathscr {F}$
contains two singular points of the surfaces
![]() $\mathscr {S}$
, which are quotient singular points of type
$\mathscr {S}$
, which are quotient singular points of type
![]() $\frac {1}{2}(1,1)$
and
$\frac {1}{2}(1,1)$
and
![]() $\frac {1}{3}(1,1)$
. Denote these points by
$\frac {1}{3}(1,1)$
. Denote these points by
![]() $Q_2$
and
$Q_2$
and
![]() $Q_3$
, respectively. Note that
$Q_3$
, respectively. Note that
![]() $\mathscr {C}$
does not contain
$\mathscr {C}$
does not contain
![]() $Q_2$
and
$Q_2$
and
![]() $Q_3$
. Write
$Q_3$
. Write
![]() $\Delta _{\mathscr {F}}=\frac {1}{2}Q_2+\frac {2}{3}Q_3$
. Then, since
$\Delta _{\mathscr {F}}=\frac {1}{2}Q_2+\frac {2}{3}Q_3$
. Then, since
![]() $A_S(\mathscr {F})=5$
, it follows from [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Remark 1.113] that
$A_S(\mathscr {F})=5$
, it follows from [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Remark 1.113] that
 $$ \begin{align*}1\geqslant \frac{A_X(\mathbf{F})}{S_X(\mathbf{F})}\geqslant\min\left\{\inf_{Q\in\mathscr{F}}\frac{1-\mathrm{ord}_{Q}(\Delta_{\mathscr{F}})}{S(W_{\bullet,\bullet,\bullet}^{\mathscr{S},\mathscr{F}};Q)}, \frac{5}{S(V_{\bullet,\bullet}^{S};\mathscr{F})},\frac{1}{S_X(S)}\right\}. \end{align*} $$
$$ \begin{align*}1\geqslant \frac{A_X(\mathbf{F})}{S_X(\mathbf{F})}\geqslant\min\left\{\inf_{Q\in\mathscr{F}}\frac{1-\mathrm{ord}_{Q}(\Delta_{\mathscr{F}})}{S(W_{\bullet,\bullet,\bullet}^{\mathscr{S},\mathscr{F}};Q)}, \frac{5}{S(V_{\bullet,\bullet}^{S};\mathscr{F})},\frac{1}{S_X(S)}\right\}. \end{align*} $$
But we already proved that
![]() $S_X(S)<1$
. Hence, we conclude that
$S_X(S)<1$
. Hence, we conclude that
![]() $S(V_{\bullet ,\bullet }^{S};\mathscr {F})\geqslant 5$
or there exists a point
$S(V_{\bullet ,\bullet }^{S};\mathscr {F})\geqslant 5$
or there exists a point
![]() $Q\in \mathscr {F}$
such that
$Q\in \mathscr {F}$
such that
![]() $S(W_{\bullet ,\bullet ,\bullet }^{\mathscr {S},\mathscr {F}};Q)\geqslant 1-\mathrm {ord}_{Q}(\Delta _{\mathscr {F}})$
.
$S(W_{\bullet ,\bullet ,\bullet }^{\mathscr {S},\mathscr {F}};Q)\geqslant 1-\mathrm {ord}_{Q}(\Delta _{\mathscr {F}})$
.
Let us compute
![]() $S(V_{\bullet ,\bullet }^{S};\mathscr {F})$
. Take
$S(V_{\bullet ,\bullet }^{S};\mathscr {F})$
. Take
![]() $v\in \mathbb {R}_{\geqslant 0}$
. Set
$v\in \mathbb {R}_{\geqslant 0}$
. Set
![]() $P(u)=-K_X-u S$
. Then
$P(u)=-K_X-u S$
. Then
 $$ \begin{align*}\upsilon^*\big(P(u)|_S\big)-v\mathscr{F}\sim_{\mathbb{R}}(2-u)\mathscr{C}+(1-u)\sum_{i=1}^{d}\mathscr{E}_i+(12-6u-v)\mathscr{F}, \end{align*} $$
$$ \begin{align*}\upsilon^*\big(P(u)|_S\big)-v\mathscr{F}\sim_{\mathbb{R}}(2-u)\mathscr{C}+(1-u)\sum_{i=1}^{d}\mathscr{E}_i+(12-6u-v)\mathscr{F}, \end{align*} $$
where
![]() $\mathscr {E}_i$
is the proper transform on
$\mathscr {E}_i$
is the proper transform on
![]() $\mathscr {S}$
of the
$\mathscr {S}$
of the
![]() $(-1)$
-curve
$(-1)$
-curve
![]() $\mathbf {e}_i$
. Using this, we conclude that the divisor
$\mathbf {e}_i$
. Using this, we conclude that the divisor
![]() $\upsilon ^*(P(u)|_S)-v\mathscr {F}$
is pseudoeffective
$\upsilon ^*(P(u)|_S)-v\mathscr {F}$
is pseudoeffective
![]() $\iff v\leqslant 12-6u$
.
$\iff v\leqslant 12-6u$
.
Let
![]() $\mathscr {P}(u,v)$
be the positive part of the Zariski decomposition of
$\mathscr {P}(u,v)$
be the positive part of the Zariski decomposition of
![]() $\upsilon ^*(P(u)|_S)-v\mathscr {F}$
, and let
$\upsilon ^*(P(u)|_S)-v\mathscr {F}$
, and let
![]() $\mathscr {N}(u,v)$
be its negative part. Then
$\mathscr {N}(u,v)$
be its negative part. Then
 $$ \begin{align*}\mathscr{P}(u,v)=\left\{\begin{aligned} &(2-u)\mathscr{C}+(1-u)\sum_{i=1}^{d}\mathscr{E}_i+(12-6u-v)\mathscr{F}\ \text{if }0\leqslant v\leqslant d(1-u), \\ &\frac{12+d-(6+d)u-v}{6}\mathscr{C}+(1-u)\sum_{i=1}^{d}\mathscr{E}_i+(12-6u-v)\mathscr{F}\ \text{if }d(1-u)\leqslant v\leqslant 6+d-du, \\ &\frac{12-6u-v}{6-d}\Big(\mathscr{C}+\sum_{i=1}^{d}\mathscr{E}_i+(6-d)\mathscr{F}\Big)\ \text{if }6+d-du\leqslant v\leqslant 12-6u, \end{aligned} \right. \end{align*} $$
$$ \begin{align*}\mathscr{P}(u,v)=\left\{\begin{aligned} &(2-u)\mathscr{C}+(1-u)\sum_{i=1}^{d}\mathscr{E}_i+(12-6u-v)\mathscr{F}\ \text{if }0\leqslant v\leqslant d(1-u), \\ &\frac{12+d-(6+d)u-v}{6}\mathscr{C}+(1-u)\sum_{i=1}^{d}\mathscr{E}_i+(12-6u-v)\mathscr{F}\ \text{if }d(1-u)\leqslant v\leqslant 6+d-du, \\ &\frac{12-6u-v}{6-d}\Big(\mathscr{C}+\sum_{i=1}^{d}\mathscr{E}_i+(6-d)\mathscr{F}\Big)\ \text{if }6+d-du\leqslant v\leqslant 12-6u, \end{aligned} \right. \end{align*} $$
and
 $$ \begin{align*}\mathscr{N}(u,v)=\left\{\begin{aligned} &0\ \text{if }0\leqslant v\leqslant d(1-u), \\ &\frac{v+d(u-1)}{6}\mathscr{C}\ \text{if }d(1-u)\leqslant v\leqslant 6+d-du, \\ &\frac{v+du-2d}{6-d}\mathscr{C}+\frac{v+du-6-d}{6-d}\sum_{i=1}^{d}\mathscr{E}_i\ \text{if }6+d-du\leqslant v\leqslant 12-6u. \end{aligned} \right. \end{align*} $$
$$ \begin{align*}\mathscr{N}(u,v)=\left\{\begin{aligned} &0\ \text{if }0\leqslant v\leqslant d(1-u), \\ &\frac{v+d(u-1)}{6}\mathscr{C}\ \text{if }d(1-u)\leqslant v\leqslant 6+d-du, \\ &\frac{v+du-2d}{6-d}\mathscr{C}+\frac{v+du-6-d}{6-d}\sum_{i=1}^{d}\mathscr{E}_i\ \text{if }6+d-du\leqslant v\leqslant 12-6u. \end{aligned} \right. \end{align*} $$
This gives
 $$ \begin{align*}\mathscr{P}(u,v)^2=\left\{\begin{aligned} &\frac{6du^2-24du-v^2+18d}{6}\ \text{if }0\leqslant v\leqslant d(1-u), \\ &\frac{d(1-u)(18-(d+6)u+d-2v)}{6}\ \text{if }d(1-u)\leqslant v\leqslant 6+d-du, \\ &\frac{d(12-6u-v)^2}{6(6-d)}\ \text{if }6+d-du\leqslant v\leqslant 12-6u. \end{aligned} \right. \end{align*} $$
$$ \begin{align*}\mathscr{P}(u,v)^2=\left\{\begin{aligned} &\frac{6du^2-24du-v^2+18d}{6}\ \text{if }0\leqslant v\leqslant d(1-u), \\ &\frac{d(1-u)(18-(d+6)u+d-2v)}{6}\ \text{if }d(1-u)\leqslant v\leqslant 6+d-du, \\ &\frac{d(12-6u-v)^2}{6(6-d)}\ \text{if }6+d-du\leqslant v\leqslant 12-6u. \end{aligned} \right. \end{align*} $$
Thus, using [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Corollary 1.109] and integrating, we get
 $$ \begin{align*}S(W_{\bullet,\bullet}^{\mathscr{S}};\mathscr{F})=\frac{3}{4d}\int_0^1\int_0^{12-6u}\mathscr{P}(u,v)^2dvdu=\frac{66+5d}{16}\leqslant\frac{19}{4}<5=A_S(\mathscr{F}) \end{align*} $$
$$ \begin{align*}S(W_{\bullet,\bullet}^{\mathscr{S}};\mathscr{F})=\frac{3}{4d}\int_0^1\int_0^{12-6u}\mathscr{P}(u,v)^2dvdu=\frac{66+5d}{16}\leqslant\frac{19}{4}<5=A_S(\mathscr{F}) \end{align*} $$
since
![]() $d=1$
or
$d=1$
or
![]() $d=2$
. Thus, there is a point
$d=2$
. Thus, there is a point
![]() $Q\in \mathscr {F}$
such that
$Q\in \mathscr {F}$
such that
![]() $S(W_{\bullet ,\bullet ,\bullet }^{\mathscr {S},\mathscr {F}};Q)\geqslant 1-\mathrm {ord}_{Q}(\Delta _{\mathscr {F}})$
.
$S(W_{\bullet ,\bullet ,\bullet }^{\mathscr {S},\mathscr {F}};Q)\geqslant 1-\mathrm {ord}_{Q}(\Delta _{\mathscr {F}})$
.
Now, using [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Remark 1.103] again, we see that
 $$ \begin{align*}S\big(W_{\bullet,\bullet,\bullet}^{\mathscr{S},\mathscr{F}};Q\big)&=\frac{3}{4d}\int_0^1\int_0^{12-6u}\Big(\big(\mathscr{P}(u,v)\cdot\mathscr{F}\big)\Big)^2dvdu+\\&\quad +\frac{6}{4d}\int_0^1\int_0^{12-6u}\big(P(u,v)\cdot\mathscr{F}\big)\mathrm{ord}_Q\big(\mathscr{N}(u,v)\big|_{\mathscr{F}}\big)dvdu.\end{align*} $$
$$ \begin{align*}S\big(W_{\bullet,\bullet,\bullet}^{\mathscr{S},\mathscr{F}};Q\big)&=\frac{3}{4d}\int_0^1\int_0^{12-6u}\Big(\big(\mathscr{P}(u,v)\cdot\mathscr{F}\big)\Big)^2dvdu+\\&\quad +\frac{6}{4d}\int_0^1\int_0^{12-6u}\big(P(u,v)\cdot\mathscr{F}\big)\mathrm{ord}_Q\big(\mathscr{N}(u,v)\big|_{\mathscr{F}}\big)dvdu.\end{align*} $$
On the other hand, we have
 $$ \begin{align*}\mathscr{P}(u,v)\cdot\mathscr{F}=\left\{\begin{aligned} &\frac{v}{6}\ \text{if }0\leqslant v\leqslant d(1-u), \\ &\frac{d(1-u)}{6}\ \text{if }d(1-u)\leqslant v\leqslant 6+d-du, \\ &\frac{d(12-6u-v)}{6(6-d)}\ \text{if }6+d-du\leqslant v\leqslant 12-6u, \end{aligned} \right. \end{align*} $$
$$ \begin{align*}\mathscr{P}(u,v)\cdot\mathscr{F}=\left\{\begin{aligned} &\frac{v}{6}\ \text{if }0\leqslant v\leqslant d(1-u), \\ &\frac{d(1-u)}{6}\ \text{if }d(1-u)\leqslant v\leqslant 6+d-du, \\ &\frac{d(12-6u-v)}{6(6-d)}\ \text{if }6+d-du\leqslant v\leqslant 12-6u, \end{aligned} \right. \end{align*} $$
and
 $$ \begin{align*}\mathscr{N}(u,v)\cdot\mathscr{F}=\left\{\begin{aligned} &0\ \text{if }0\leqslant v\leqslant d(1-u), \\ &\frac{v-d(1-u)}{6}\ \text{if }d(1-u)\leqslant v\leqslant 6+d-du, \\ &\frac{v+du-2d}{6-d}\ \text{if }6+d-du\leqslant v\leqslant 12-6u. \end{aligned} \right. \end{align*} $$
$$ \begin{align*}\mathscr{N}(u,v)\cdot\mathscr{F}=\left\{\begin{aligned} &0\ \text{if }0\leqslant v\leqslant d(1-u), \\ &\frac{v-d(1-u)}{6}\ \text{if }d(1-u)\leqslant v\leqslant 6+d-du, \\ &\frac{v+du-2d}{6-d}\ \text{if }6+d-du\leqslant v\leqslant 12-6u. \end{aligned} \right. \end{align*} $$
In particular, we have
 $$ \begin{align*}S(W_{\bullet,\bullet,\bullet}^{\mathscr{S},\mathscr{F}};Q)=\frac{5d}{96}+\frac{6}{4d}\int_0^1\int_0^{12-6u}\big(P(u,v)\cdot\mathscr{F}\big)\mathrm{ord}_Q\big(\mathscr{N}(u,v)\big|_{\mathscr{F}}\big)dvdu. \end{align*} $$
$$ \begin{align*}S(W_{\bullet,\bullet,\bullet}^{\mathscr{S},\mathscr{F}};Q)=\frac{5d}{96}+\frac{6}{4d}\int_0^1\int_0^{12-6u}\big(P(u,v)\cdot\mathscr{F}\big)\mathrm{ord}_Q\big(\mathscr{N}(u,v)\big|_{\mathscr{F}}\big)dvdu. \end{align*} $$
Hence, if
![]() $Q\not \in \mathscr {C}$
, then
$Q\not \in \mathscr {C}$
, then
![]() $\frac {1}{3}\leqslant 1-\mathrm {ord}_{Q}(\Delta _{\mathscr {F}})\leqslant S(W_{\bullet ,\bullet ,\bullet }^{\mathscr {S},\mathscr {F}};Q)=\frac {5d}{96}<\frac {1}{3}$
, which is absurd. Thus, we conclude that
$\frac {1}{3}\leqslant 1-\mathrm {ord}_{Q}(\Delta _{\mathscr {F}})\leqslant S(W_{\bullet ,\bullet ,\bullet }^{\mathscr {S},\mathscr {F}};Q)=\frac {5d}{96}<\frac {1}{3}$
, which is absurd. Thus, we conclude that
![]() $Q=\mathscr {C}\cap \mathscr {F}$
. Then
$Q=\mathscr {C}\cap \mathscr {F}$
. Then
 $$ \begin{align*} S(W_{\bullet,\bullet,\bullet}^{\mathscr{S},\mathscr{F}};Q)&=\frac{5d}{96}+\frac{6}{4d}\int_0^1\int_0^{12-6u}\big(P(u,v)\cdot\mathscr{F}\big)\mathrm{ord}_Q\big(\mathscr{N}(u,v)\big|_{\mathscr{F}}\big)dvdu\leqslant\\ &\quad\leqslant\frac{5d}{96}+\frac{6}{4d}\int_0^1\int_0^{12-6u}\big(P(u,v)\cdot\mathscr{F}\big)\big(\mathscr{N}(u,v)\cdot\mathscr{F}\big)dvdu=\frac{11}{16}<1, \end{align*} $$
$$ \begin{align*} S(W_{\bullet,\bullet,\bullet}^{\mathscr{S},\mathscr{F}};Q)&=\frac{5d}{96}+\frac{6}{4d}\int_0^1\int_0^{12-6u}\big(P(u,v)\cdot\mathscr{F}\big)\mathrm{ord}_Q\big(\mathscr{N}(u,v)\big|_{\mathscr{F}}\big)dvdu\leqslant\\ &\quad\leqslant\frac{5d}{96}+\frac{6}{4d}\int_0^1\int_0^{12-6u}\big(P(u,v)\cdot\mathscr{F}\big)\big(\mathscr{N}(u,v)\cdot\mathscr{F}\big)dvdu=\frac{11}{16}<1, \end{align*} $$
which is a contradiction, since
![]() $S(W_{\bullet ,\bullet ,\bullet }^{\mathscr {S},\mathscr {F}};Q)\geqslant 1-\mathrm {ord}_{Q}(\Delta _{\mathscr {F}})=1$
.
$S(W_{\bullet ,\bullet ,\bullet }^{\mathscr {S},\mathscr {F}};Q)\geqslant 1-\mathrm {ord}_{Q}(\Delta _{\mathscr {F}})=1$
.
In particular, we conclude that either
![]() $d=2$
or
$d=2$
or
![]() $d=3$
.
$d=3$
.
Corollary 2.7. All smooth Fano threefolds in the family ![]() are K-stable.
are K-stable.
Recall that A is the fiber of the del Pezzo fibration
![]() $\phi \colon X\to \mathbb {P}^1$
that passes through P. Note also that we have the following possibilities:
$\phi \colon X\to \mathbb {P}^1$
that passes through P. Note also that we have the following possibilities:
-
•
 $d=2$
, and A is a double cover of
$d=2$
, and A is a double cover of
 $\mathbb {P}^2$
branched over a reduced quartic curve;
$\mathbb {P}^2$
branched over a reduced quartic curve; -
•
 $d=3$
, and A is a normal cubic surface in
$d=3$
, and A is a normal cubic surface in
 $\mathbb {P}^3$
.
$\mathbb {P}^3$
.
Observe that
![]() $C=S\cap A$
, where S is a general surface in
$C=S\cap A$
, where S is a general surface in
![]() $|\pi ^*(H)|$
that contains the point P. Since C is singular at P, the surface A must be singular at P, which confirms Corollary 2.4. Now, using classifications of reduced singular plane quartic curves and singular normal cubic surfaces [Reference Bruce and Wall6], we see that
$|\pi ^*(H)|$
that contains the point P. Since C is singular at P, the surface A must be singular at P, which confirms Corollary 2.4. Now, using classifications of reduced singular plane quartic curves and singular normal cubic surfaces [Reference Bruce and Wall6], we see that
![]() $P=\mathrm {Sing}(A)$
, and one of the following three cases holds:
$P=\mathrm {Sing}(A)$
, and one of the following three cases holds:
-
•
 $d=2$
, and A is a double cover of
$d=2$
, and A is a double cover of
 $\mathbb {P}^2$
branched over four lines intersecting in a point;
$\mathbb {P}^2$
branched over four lines intersecting in a point; -
•
 $d=3$
, and A is a cone in
$d=3$
, and A is a cone in
 $\mathbb {P}^3$
over a smooth plane cubic curve;
$\mathbb {P}^3$
over a smooth plane cubic curve; -
•
 $d=3$
, and A has Du Val singular point of type
$d=3$
, and A has Du Val singular point of type
 $\mathbb {D}_4$
,
$\mathbb {D}_4$
,
 $\mathbb {D}_5$
, or
$\mathbb {D}_5$
, or
 $\mathbb {E}_6$
.
$\mathbb {E}_6$
.
Let us show that the first case is impossible.
Lemma 2.8. One has
![]() $d=3$
.
$d=3$
.
Proof. Suppose that
![]() $d=2$
. Then
$d=2$
. Then
![]() $P=\mathrm {Sing}(A)$
, and A is a double cover of
$P=\mathrm {Sing}(A)$
, and A is a double cover of
![]() $\mathbb {P}^2$
branched over a reduced reducible plane quartic curve that is a union of four distinct lines passing through one point. Let us seek for a contradiction.
$\mathbb {P}^2$
branched over a reduced reducible plane quartic curve that is a union of four distinct lines passing through one point. Let us seek for a contradiction.
Let
![]() $\alpha \colon \widetilde {X}\to X$
be the blow up of the point P, let
$\alpha \colon \widetilde {X}\to X$
be the blow up of the point P, let
![]() $E_P$
be the
$E_P$
be the
![]() $\alpha $
-exceptional divisor and let
$\alpha $
-exceptional divisor and let
![]() $\widetilde {A}$
be the proper transform on
$\widetilde {A}$
be the proper transform on
![]() $\widetilde {X}$
of the surface A. Then
$\widetilde {X}$
of the surface A. Then
![]() $\widetilde {A}\cap E_P$
is a line
$\widetilde {A}\cap E_P$
is a line
![]() $L\subset E_P\cong \mathbb {P}^2$
, and the surface
$L\subset E_P\cong \mathbb {P}^2$
, and the surface
![]() $\widetilde {A}$
is singular along this line. Let
$\widetilde {A}$
is singular along this line. Let
![]() $\beta \colon \overline {X}\to \widetilde {X}$
be the blow up of the line L, let
$\beta \colon \overline {X}\to \widetilde {X}$
be the blow up of the line L, let
![]() $E_L$
be the
$E_L$
be the
![]() $\beta $
-exceptional divisor, let
$\beta $
-exceptional divisor, let
![]() $\overline {A}$
be the proper transform on
$\overline {A}$
be the proper transform on
![]() $\overline {X}$
of the surface
$\overline {X}$
of the surface
![]() $\widetilde {A}$
and let
$\widetilde {A}$
and let
![]() $\overline {E}_P$
be the proper transforms on
$\overline {E}_P$
be the proper transforms on
![]() $\overline {X}$
of the surface
$\overline {X}$
of the surface
![]() $E_P$
. Then
$E_P$
. Then
-
•
 $E_L\cong \mathbb {F}_2$
,
$E_L\cong \mathbb {F}_2$
, -
• the intersection
 $\overline {E}_P\cap E_L$
is the
$\overline {E}_P\cap E_L$
is the
 $(-2)$
-curve in
$(-2)$
-curve in
 $E_L$
,
$E_L$
, -
• the surface
 $\overline {A}$
is smooth, and there exists a
$\overline {A}$
is smooth, and there exists a
 $\mathbb {P}^1$
-bundle
$\mathbb {P}^1$
-bundle
 $\overline {A}\to \mathcal {C}$
,
$\overline {A}\to \mathcal {C}$
, -
•
 $\overline {A}\cap E_L$
is a smooth elliptic curve that is a section of the
$\overline {A}\cap E_L$
is a smooth elliptic curve that is a section of the
 $\mathbb {P}^1$
-bundle
$\mathbb {P}^1$
-bundle
 $\overline {A}\to \mathcal {C}$
,
$\overline {A}\to \mathcal {C}$
, -
• the surfaces
 $\overline {A}$
and
$\overline {A}$
and
 $\overline {E}_P$
are disjoint,
$\overline {E}_P$
are disjoint, -
•
 $\overline {E}_P\cong \mathbb {P}^2$
and
$\overline {E}_P\cong \mathbb {P}^2$
and
 $\overline {E}_P\vert _{\overline {E}_P}\cong \mathcal {O}_{\mathbb {P}^2}(-2)$
.
$\overline {E}_P\vert _{\overline {E}_P}\cong \mathcal {O}_{\mathbb {P}^2}(-2)$
.
There is a birational contraction
![]() $\gamma \colon \overline {X}\to \widehat {X}$
of the surface
$\gamma \colon \overline {X}\to \widehat {X}$
of the surface
![]() $\overline {E}_P$
such that
$\overline {E}_P$
such that
![]() $\widehat {X}$
is a projective threefold that has one singular point
$\widehat {X}$
is a projective threefold that has one singular point
![]() $O=\gamma (\overline {E}_P)$
, which is a terminal cyclic quotient singularities of type
$O=\gamma (\overline {E}_P)$
, which is a terminal cyclic quotient singularities of type
![]() $\frac {1}{2}(1,1,1)$
. Thus, there exists the following commutative diagram
$\frac {1}{2}(1,1,1)$
. Thus, there exists the following commutative diagram

where
![]() $\sigma $
is a birational morphism that contracts the surface
$\sigma $
is a birational morphism that contracts the surface
![]() $\gamma (E_L)$
to the point P.
$\gamma (E_L)$
to the point P.
Let
![]() $G=\gamma (E_L)$
, let
$G=\gamma (E_L)$
, let
![]() $\widehat {A}=\gamma (\overline {A})$
and let
$\widehat {A}=\gamma (\overline {A})$
and let
![]() $\widehat {E}$
be the proper transform on
$\widehat {E}$
be the proper transform on
![]() $\widehat {X}$
of the surface E. Then
$\widehat {X}$
of the surface E. Then
![]() $A_{X}(G)=4$
. Moreover, we have
$A_{X}(G)=4$
. Moreover, we have
 $$ \begin{align*} \sigma^{*}(-K_X)&\sim 2\widehat{A}+\widehat{E}+8G, \\ \sigma^{*}(A)&\sim\widehat{A}+4G. \end{align*} $$
$$ \begin{align*} \sigma^{*}(-K_X)&\sim 2\widehat{A}+\widehat{E}+8G, \\ \sigma^{*}(A)&\sim\widehat{A}+4G. \end{align*} $$
Note that
![]() $\widehat {A}\cong \overline {A}$
and
$\widehat {A}\cong \overline {A}$
and
![]() $G\cong \mathbb {P}(1,1,2)$
, so we can identify G with a quadric cone in
$G\cong \mathbb {P}(1,1,2)$
, so we can identify G with a quadric cone in
![]() $\mathbb {P}^3$
. Note also that O is the vertex of the cone G. Moreover, by construction, we have
$\mathbb {P}^3$
. Note also that O is the vertex of the cone G. Moreover, by construction, we have
![]() $O\not \in \widehat {A}$
. Furthermore, the exists a
$O\not \in \widehat {A}$
. Furthermore, the exists a
![]() $\mathbb {P}^1$
-bundle
$\mathbb {P}^1$
-bundle
![]() $\widehat {A}\to \mathcal {C}$
such that
$\widehat {A}\to \mathcal {C}$
such that
![]() $G\vert _{\widehat {A}}$
is its section.
$G\vert _{\widehat {A}}$
is its section.
Let
![]() $\mathbf {g}$
be a ruling of the quadric cone G, let
$\mathbf {g}$
be a ruling of the quadric cone G, let
![]() $\mathbf {l}$
be a fiber of the
$\mathbf {l}$
be a fiber of the
![]() $\mathbb {P}^1$
-bundle
$\mathbb {P}^1$
-bundle
![]() $\widehat {A}\to \mathcal {C}$
and let
$\widehat {A}\to \mathcal {C}$
and let
![]() $\mathbf {f}$
be a fiber of the
$\mathbf {f}$
be a fiber of the
![]() $\mathbb {P}^1$
-bundle
$\mathbb {P}^1$
-bundle
![]() $\pi \circ \sigma \vert _{\widehat {E}}\colon \widehat {E}\to \mathcal {C}$
. Then
$\pi \circ \sigma \vert _{\widehat {E}}\colon \widehat {E}\to \mathcal {C}$
. Then
![]() $G\vert _{G}\sim _{\mathbb {Q}}-\mathbf {g}$
and
$G\vert _{G}\sim _{\mathbb {Q}}-\mathbf {g}$
and
![]() $\widehat {A}\vert _{G}\sim _{\mathbb {Q}}4\mathbf {g}$
. Moreover, the intersections of the surfaces G,
$\widehat {A}\vert _{G}\sim _{\mathbb {Q}}4\mathbf {g}$
. Moreover, the intersections of the surfaces G,
![]() $\widehat {A}$
,
$\widehat {A}$
,
![]() $\widehat {E}$
with the curves
$\widehat {E}$
with the curves
![]() $\mathbf {g}$
,
$\mathbf {g}$
,
![]() $\mathbf {l}$
,
$\mathbf {l}$
,
![]() $\mathbf {f}$
are given here:
$\mathbf {f}$
are given here:

Fix a nonnegative real number u. We have
![]() $\sigma ^{*}(-K_X)-uG\sim _{\mathbb {R}} 2\widehat {A}+\widehat {E}+(8-u)G$
, which implies that
$\sigma ^{*}(-K_X)-uG\sim _{\mathbb {R}} 2\widehat {A}+\widehat {E}+(8-u)G$
, which implies that
![]() $\sigma ^{*}(-K_X)-uG$
is pseudoeffective
$\sigma ^{*}(-K_X)-uG$
is pseudoeffective
![]() $\iff u\in [0,8]$
. Furthermore, if
$\iff u\in [0,8]$
. Furthermore, if
![]() $u\in [0,8]$
, then the Zariski decomposition of the divisor
$u\in [0,8]$
, then the Zariski decomposition of the divisor
![]() $\sigma ^{*}(-K_X)-uG$
can be described as follows:
$\sigma ^{*}(-K_X)-uG$
can be described as follows:
 $$ \begin{align*}P(u)=\left\{\begin{aligned} &2\widehat{A}+\widehat{E}+(8-u)G\ \text{if }0\leqslant u\leqslant 1, \\ &\frac{9-u}{4}\widehat{A}+\widehat{E}+(8-u)G \ \text{if }1\leqslant u\leqslant 5, \\ &\frac{8-u}{3}\big(\widehat{A}+\widehat{E}+3G\big)\ \text{if }5\leqslant u\leqslant 8, \\ \end{aligned} \right. \end{align*} $$
$$ \begin{align*}P(u)=\left\{\begin{aligned} &2\widehat{A}+\widehat{E}+(8-u)G\ \text{if }0\leqslant u\leqslant 1, \\ &\frac{9-u}{4}\widehat{A}+\widehat{E}+(8-u)G \ \text{if }1\leqslant u\leqslant 5, \\ &\frac{8-u}{3}\big(\widehat{A}+\widehat{E}+3G\big)\ \text{if }5\leqslant u\leqslant 8, \\ \end{aligned} \right. \end{align*} $$
and
 $$ \begin{align*}N(u)=\left\{\begin{aligned} &0\ \text{if }0\leqslant u\leqslant 1, \\ &\frac{u-1}{4}\widehat{A}\ \text{if }1\leqslant u\leqslant 5, \\ &\frac{u-2}{3}\widehat{A}+\frac{u-5}{3}\widehat{E}\ \text{if }5\leqslant u\leqslant 8, \\ \end{aligned} \right. \end{align*} $$
$$ \begin{align*}N(u)=\left\{\begin{aligned} &0\ \text{if }0\leqslant u\leqslant 1, \\ &\frac{u-1}{4}\widehat{A}\ \text{if }1\leqslant u\leqslant 5, \\ &\frac{u-2}{3}\widehat{A}+\frac{u-5}{3}\widehat{E}\ \text{if }5\leqslant u\leqslant 8, \\ \end{aligned} \right. \end{align*} $$
where
![]() $P(u)$
and
$P(u)$
and
![]() $N(u)$
are the positive and the negative parts of the decomposition. Then
$N(u)$
are the positive and the negative parts of the decomposition. Then
 $$ \begin{align*}\mathrm{vol}\big(\sigma^{*}(-K_X)-uG\big)=P(u)^3=\left\{\begin{aligned} &8-\frac{u^3}{8}\ \text{if }0\leqslant u\leqslant 1, \\ &\frac{18-3u}{2}\ \text{if }1\leqslant u\leqslant 5, \\ &\frac{(8-u)^{3}}{18}\ \text{if }5\leqslant u\leqslant 8. \\ \end{aligned} \right. \end{align*} $$
$$ \begin{align*}\mathrm{vol}\big(\sigma^{*}(-K_X)-uG\big)=P(u)^3=\left\{\begin{aligned} &8-\frac{u^3}{8}\ \text{if }0\leqslant u\leqslant 1, \\ &\frac{18-3u}{2}\ \text{if }1\leqslant u\leqslant 5, \\ &\frac{(8-u)^{3}}{18}\ \text{if }5\leqslant u\leqslant 8. \\ \end{aligned} \right. \end{align*} $$
Integrating, we get
![]() $S_{X}(G)=\frac {27}{8}<4=A_{X}(G)$
. But [Reference Fujita16, Corollary 4.18] gives
$S_{X}(G)=\frac {27}{8}<4=A_{X}(G)$
. But [Reference Fujita16, Corollary 4.18] gives
 $$ \begin{align*}1\geqslant \frac{A_X(\mathbf{F})}{S_X(\mathbf{F})}\geqslant\min\left\{\frac{A_{X}(G)}{S_{X}(G)}, \inf_{Q\in G}\delta_{Q}\big(G,V^G_{\bullet,\bullet}\big)\right\}=\min\left\{\frac{32}{27},\inf_{Q\in G}\delta_{Q}\big(G,V^G_{\bullet,\bullet}\big)\right\}, \end{align*} $$
$$ \begin{align*}1\geqslant \frac{A_X(\mathbf{F})}{S_X(\mathbf{F})}\geqslant\min\left\{\frac{A_{X}(G)}{S_{X}(G)}, \inf_{Q\in G}\delta_{Q}\big(G,V^G_{\bullet,\bullet}\big)\right\}=\min\left\{\frac{32}{27},\inf_{Q\in G}\delta_{Q}\big(G,V^G_{\bullet,\bullet}\big)\right\}, \end{align*} $$
where
![]() $\delta _{Q}(G,V^G_{\bullet ,\bullet })$
is defined in [Reference Fujita16]. Moreover, if Q is a point in G and Z is a smooth curve in G that passes through Q, then it follows from [Reference Fujita16, Corollary 4.18] that
$\delta _{Q}(G,V^G_{\bullet ,\bullet })$
is defined in [Reference Fujita16]. Moreover, if Q is a point in G and Z is a smooth curve in G that passes through Q, then it follows from [Reference Fujita16, Corollary 4.18] that
 $$ \begin{align*}\delta_{Q}\big(G,V^G_{\bullet,\bullet}\big) \geqslant\min\left\{\frac{1}{S\big(V^G_{\bullet,\bullet};Z\big)},\frac{1-\mathrm{ord}_Q(\Delta_Z)}{S\big(W^{G,Z}_{\bullet,\bullet,\bullet};Q\big)}\right\}, \end{align*} $$
$$ \begin{align*}\delta_{Q}\big(G,V^G_{\bullet,\bullet}\big) \geqslant\min\left\{\frac{1}{S\big(V^G_{\bullet,\bullet};Z\big)},\frac{1-\mathrm{ord}_Q(\Delta_Z)}{S\big(W^{G,Z}_{\bullet,\bullet,\bullet};Q\big)}\right\}, \end{align*} $$
where
![]() $S(V^G_{\bullet ,\bullet };Z)$
and
$S(V^G_{\bullet ,\bullet };Z)$
and
![]() $S(W^{G,Z}_{\bullet ,\bullet ,\bullet };Q)$
are defined in [Reference Fujita16], and
$S(W^{G,Z}_{\bullet ,\bullet ,\bullet };Q)$
are defined in [Reference Fujita16], and
 $$ \begin{align*}\Delta_Z=\left\{\begin{aligned} &0\ \text{if }O\not\in Z, \\ &\frac{1}{2}O\ \text{if }O\in Z. \end{aligned} \right. \end{align*} $$
$$ \begin{align*}\Delta_Z=\left\{\begin{aligned} &0\ \text{if }O\not\in Z, \\ &\frac{1}{2}O\ \text{if }O\in Z. \end{aligned} \right. \end{align*} $$
Let us show that
![]() $\delta _{Q}\big (G,V^G_{\bullet ,\bullet }\big )>1$
for every
$\delta _{Q}\big (G,V^G_{\bullet ,\bullet }\big )>1$
for every
![]() $Q\in G$
, which would imply a contradiction.
$Q\in G$
, which would imply a contradiction.
Let
![]() $\mathscr {C}=\widehat {A}\vert _{G}$
, and let
$\mathscr {C}=\widehat {A}\vert _{G}$
, and let
![]() $\ell $
be the curve in
$\ell $
be the curve in
![]() $|\mathbf {f}|$
that contains Q. Then
$|\mathbf {f}|$
that contains Q. Then
![]() $O\not \in \mathscr {C}$
and
$O\not \in \mathscr {C}$
and
![]() $O\in \ell $
so that
$O\in \ell $
so that
![]() $\Delta _{\mathscr {C}}=0$
and
$\Delta _{\mathscr {C}}=0$
and
![]() $\Delta _{\ell }=\frac {1}{2}O$
. Take
$\Delta _{\ell }=\frac {1}{2}O$
. Take
![]() $v\in \mathbb {R}_{\geqslant 0}$
. Then
$v\in \mathbb {R}_{\geqslant 0}$
. Then
 $$ \begin{align*}P(u)\big\vert_{G}-v\ell\sim_{\mathbb{R}}\left\{\begin{aligned} &(u-v)\mathbf{g}\ \text{if }0\leqslant u\leqslant 1, \\ &(1-v)\mathbf{g}\ \text{if }1\leqslant u\leqslant 5, \\ &\frac{8-u-3v}{3}\mathbf{g}\ \text{if }5\leqslant u\leqslant 8.\\ \end{aligned} \right. \end{align*} $$
$$ \begin{align*}P(u)\big\vert_{G}-v\ell\sim_{\mathbb{R}}\left\{\begin{aligned} &(u-v)\mathbf{g}\ \text{if }0\leqslant u\leqslant 1, \\ &(1-v)\mathbf{g}\ \text{if }1\leqslant u\leqslant 5, \\ &\frac{8-u-3v}{3}\mathbf{g}\ \text{if }5\leqslant u\leqslant 8.\\ \end{aligned} \right. \end{align*} $$
Now, using [Reference Fujita16, Theorem 4.8], we get
 $$ \begin{align*} S\big(W^{G}_{\bullet,\bullet};\ell\big)&= \frac{3}{8}\int_0^8\int_0^\infty \mathrm{vol}\big(P(u)\big\vert_{G}-v\ell\big)dvdu=\frac{3}{8}\int_{0}^{1}\int_{0}^{u}\frac{(u-v)^{2}}{2}dvdu+\\ &\quad+\frac{3}{12}\int_{1}^{5}\int_{0}^{1}\frac{(1-v)^{2}}{4}dvdu+\frac{3}{12}\int_{5}^{8}\int_{0}^{\frac{8-u}{3}}\frac{(8-u-3v)^2}{18}dvdu=\frac{5}{16}. \end{align*} $$
$$ \begin{align*} S\big(W^{G}_{\bullet,\bullet};\ell\big)&= \frac{3}{8}\int_0^8\int_0^\infty \mathrm{vol}\big(P(u)\big\vert_{G}-v\ell\big)dvdu=\frac{3}{8}\int_{0}^{1}\int_{0}^{u}\frac{(u-v)^{2}}{2}dvdu+\\ &\quad+\frac{3}{12}\int_{1}^{5}\int_{0}^{1}\frac{(1-v)^{2}}{4}dvdu+\frac{3}{12}\int_{5}^{8}\int_{0}^{\frac{8-u}{3}}\frac{(8-u-3v)^2}{18}dvdu=\frac{5}{16}. \end{align*} $$
Similarly, if
![]() $Q\not \in \mathscr {C}$
, then it follows from [Reference Fujita16, Theorem 4.17] that
$Q\not \in \mathscr {C}$
, then it follows from [Reference Fujita16, Theorem 4.17] that
 $$ \begin{align*} S\big(W_{\bullet,\bullet,\bullet}^{G,\ell};Q\big)&= \frac{3}{8}\int_{0}^{1}\int_{0}^{u}\Big(\big(P(u)\big\vert_{G}-v\ell\big)\cdot\ell\Big)^2dvdu+ \frac{3}{8}\int_{1}^{5}\int_{0}^{1}\Big(\big(P(u)\big\vert_{G}-v\ell\big)\cdot\ell\Big)^2dvdu+\\ &\quad+\frac{3}{8}\int_{5}^{8}\int_{0}^{\frac{8-u}{3}}\Big(\big(P(u)\big\vert_{G}-v\ell\big)\cdot\ell\Big)^2dvdu+F_Q= \frac{3}{8}\int_{0}^{1}\int_{0}^{u}\frac{(u-v)^{2}}{4}dvdu+\\ &\quad+\frac{3}{8}\int_{1}^{5}\int_{0}^{1}\frac{(1-v)^{2}}{4}dvdu+ \frac{3}{8}\int_{5}^{8}\int_{0}^{\frac{8-u}{3}}\frac{(8-u-3v)^2}{36}dvdu=\frac{5}{32} \end{align*} $$
$$ \begin{align*} S\big(W_{\bullet,\bullet,\bullet}^{G,\ell};Q\big)&= \frac{3}{8}\int_{0}^{1}\int_{0}^{u}\Big(\big(P(u)\big\vert_{G}-v\ell\big)\cdot\ell\Big)^2dvdu+ \frac{3}{8}\int_{1}^{5}\int_{0}^{1}\Big(\big(P(u)\big\vert_{G}-v\ell\big)\cdot\ell\Big)^2dvdu+\\ &\quad+\frac{3}{8}\int_{5}^{8}\int_{0}^{\frac{8-u}{3}}\Big(\big(P(u)\big\vert_{G}-v\ell\big)\cdot\ell\Big)^2dvdu+F_Q= \frac{3}{8}\int_{0}^{1}\int_{0}^{u}\frac{(u-v)^{2}}{4}dvdu+\\ &\quad+\frac{3}{8}\int_{1}^{5}\int_{0}^{1}\frac{(1-v)^{2}}{4}dvdu+ \frac{3}{8}\int_{5}^{8}\int_{0}^{\frac{8-u}{3}}\frac{(8-u-3v)^2}{36}dvdu=\frac{5}{32} \end{align*} $$
so that
![]() $S(W_{\bullet ,\bullet ,\bullet }^{G,\ell };Q)=\frac {5}{32}$
, which implies that
$S(W_{\bullet ,\bullet ,\bullet }^{G,\ell };Q)=\frac {5}{32}$
, which implies that
![]() $\delta _{Q}(G,V^G_{\bullet ,\bullet })\geqslant \frac {16}{5}$
. Likewise, if
$\delta _{Q}(G,V^G_{\bullet ,\bullet })\geqslant \frac {16}{5}$
. Likewise, if
![]() $Q\in \mathscr {C}$
, then
$Q\in \mathscr {C}$
, then
 $$ \begin{align*} S\big(W^{G}_{\bullet,\bullet};\mathscr{C}\big)&= \frac{3}{8}\int_{0}^{8}\big(P(u)^{2}\cdot G\big)\cdot\mathrm{ord}_{\mathscr{C}}\Big(N(u)\big\vert_{G}\Big)du+ \frac{3}{8}\int_0^8\int_0^\infty \mathrm{vol}\big(P(u)\big\vert_{G}-v\mathscr{C}\big)dvdu=\\ &=\frac{3}{8}\int_{1}^{5}\frac{u-1}{8}du+\frac{3}{8}\int_{5}^{8}\frac{(u-2)(8-u)^{2}}{54}du+\frac{3}{8}\int_0^1\int_{0}^{\frac{u}{4}}\frac{(u-4v)^{2}}{2}dvdu+\\ &\quad+\frac{3}{8}\int_{1}^{5}\int_{0}^{\frac{1}{4}} \frac{(1-4v)^{2}}{2}dvdu+\frac{3}{8}\int_{5}^{8}\int_{0}^{\frac{8-u}{12}}\frac{(8-u-12v)^{2}}{18}dvdu=\frac{11}{16} \end{align*} $$
$$ \begin{align*} S\big(W^{G}_{\bullet,\bullet};\mathscr{C}\big)&= \frac{3}{8}\int_{0}^{8}\big(P(u)^{2}\cdot G\big)\cdot\mathrm{ord}_{\mathscr{C}}\Big(N(u)\big\vert_{G}\Big)du+ \frac{3}{8}\int_0^8\int_0^\infty \mathrm{vol}\big(P(u)\big\vert_{G}-v\mathscr{C}\big)dvdu=\\ &=\frac{3}{8}\int_{1}^{5}\frac{u-1}{8}du+\frac{3}{8}\int_{5}^{8}\frac{(u-2)(8-u)^{2}}{54}du+\frac{3}{8}\int_0^1\int_{0}^{\frac{u}{4}}\frac{(u-4v)^{2}}{2}dvdu+\\ &\quad+\frac{3}{8}\int_{1}^{5}\int_{0}^{\frac{1}{4}} \frac{(1-4v)^{2}}{2}dvdu+\frac{3}{8}\int_{5}^{8}\int_{0}^{\frac{8-u}{12}}\frac{(8-u-12v)^{2}}{18}dvdu=\frac{11}{16} \end{align*} $$
and
 $$ \begin{align*} S\big(W_{\bullet,\bullet,\bullet}^{G,\mathscr{C}};Q\big)&= \frac{3}{8}\int_{0}^{1}\int_{0}^{\frac{u}{4}}\Big(\big(P(u)\big\vert_{G}-v\mathscr{C}\big)\cdot\mathscr{C}\Big)^2dvdu+\\ &\quad+\frac{3}{8}\int_{1}^{5}\int_{0}^{\frac{1}{4}}\Big(\big(P(u)\big\vert_{G}-v\mathscr{C}\big)\cdot\mathscr{C}\Big)^2dvdu+\frac{3}{8}\int_{5}^{8}\int_{0}^{\frac{8-u}{12}}\Big(\big(P(u)\big\vert_{G}-v\mathscr{C}\big)\cdot\mathscr{C}\Big)^2dvdu=\\ &=\frac{3}{8}\int_{0}^{1} \int_{0}^{\frac{u}{4}}(2u-8v)^{2}dvdu+\frac{3}{8}\int_{1}^{5} \int_{0}^{\frac{1}{4}}(2-8v)^{2}dvdu+\\ &\quad+\frac{3}{8}\int_{5}^{8}\int_{0}^{\frac{8-u}{12}}(\frac{(16-2u-24v)^2}{9}dvdu=\frac{5}{8}. \end{align*} $$
$$ \begin{align*} S\big(W_{\bullet,\bullet,\bullet}^{G,\mathscr{C}};Q\big)&= \frac{3}{8}\int_{0}^{1}\int_{0}^{\frac{u}{4}}\Big(\big(P(u)\big\vert_{G}-v\mathscr{C}\big)\cdot\mathscr{C}\Big)^2dvdu+\\ &\quad+\frac{3}{8}\int_{1}^{5}\int_{0}^{\frac{1}{4}}\Big(\big(P(u)\big\vert_{G}-v\mathscr{C}\big)\cdot\mathscr{C}\Big)^2dvdu+\frac{3}{8}\int_{5}^{8}\int_{0}^{\frac{8-u}{12}}\Big(\big(P(u)\big\vert_{G}-v\mathscr{C}\big)\cdot\mathscr{C}\Big)^2dvdu=\\ &=\frac{3}{8}\int_{0}^{1} \int_{0}^{\frac{u}{4}}(2u-8v)^{2}dvdu+\frac{3}{8}\int_{1}^{5} \int_{0}^{\frac{1}{4}}(2-8v)^{2}dvdu+\\ &\quad+\frac{3}{8}\int_{5}^{8}\int_{0}^{\frac{8-u}{12}}(\frac{(16-2u-24v)^2}{9}dvdu=\frac{5}{8}. \end{align*} $$
This implies that
![]() $\delta _{Q}(G,V^G_{\bullet ,\bullet })\geqslant \min \left \{\frac {16}{11},\frac {8}{5}\right \}=\frac {16}{11}$
, which is a contradiction.
$\delta _{Q}(G,V^G_{\bullet ,\bullet })\geqslant \min \left \{\frac {16}{11},\frac {8}{5}\right \}=\frac {16}{11}$
, which is a contradiction.
Corollary 2.9. All smooth Fano threefolds in the family ![]() are K-stable.
are K-stable.
We see that
![]() $d=3$
so that A is a singular cubic surface in
$d=3$
so that A is a singular cubic surface in
![]() $\mathbb {P}^3$
such that
$\mathbb {P}^3$
such that
![]() $P=\mathrm {Sing}(A)$
. Let
$P=\mathrm {Sing}(A)$
. Let
![]() $\sigma \colon \widehat {X}\to X$
be the blow up of the point P, and let G be the
$\sigma \colon \widehat {X}\to X$
be the blow up of the point P, and let G be the
![]() $\sigma $
-exceptional surface. Denote by
$\sigma $
-exceptional surface. Denote by
![]() $\widehat {A}$
and
$\widehat {A}$
and
![]() $\widehat {E}$
the proper transforms on
$\widehat {E}$
the proper transforms on
![]() $\widehat {X}$
of the surfaces A and E, respectively.
$\widehat {X}$
of the surfaces A and E, respectively.
Lemma 2.10. The surface A has Du Val singularities.
Proof. Suppose that A is a cone in
![]() $\mathbb {P}^3$
with vertex P. Take
$\mathbb {P}^3$
with vertex P. Take
![]() $u\in \mathbb {R}_{\geqslant 0}$
. Then
$u\in \mathbb {R}_{\geqslant 0}$
. Then
Thus, the divisor
![]() $\sigma ^*(-K_X)-vG$
is pseudoeffective
$\sigma ^*(-K_X)-vG$
is pseudoeffective
![]() $\iff u\in [0,6]$
. Moreover, if
$\iff u\in [0,6]$
. Moreover, if
![]() $u\in [0,6]$
, then the Zariski decomposition of the divisor
$u\in [0,6]$
, then the Zariski decomposition of the divisor
![]() $\sigma ^*(-K_X)-vG$
can be described as follows:
$\sigma ^*(-K_X)-vG$
can be described as follows:
 $$ \begin{align*}P(u)=\left\{\begin{aligned} &2\widehat{A}+E+(6-u)G\ \text{if }0\leqslant u\leqslant 1, \\ &\frac{7-u}{3}\widehat{A}+\widehat{E}+(6-u)G\ \text{if }1\leqslant u\leqslant 4, \\ &\frac{6-u}{2}(\widehat{A}+\widehat{E}+2G)\ \text{if }4\leqslant u\leqslant 6, \\ \end{aligned} \right. \end{align*} $$
$$ \begin{align*}P(u)=\left\{\begin{aligned} &2\widehat{A}+E+(6-u)G\ \text{if }0\leqslant u\leqslant 1, \\ &\frac{7-u}{3}\widehat{A}+\widehat{E}+(6-u)G\ \text{if }1\leqslant u\leqslant 4, \\ &\frac{6-u}{2}(\widehat{A}+\widehat{E}+2G)\ \text{if }4\leqslant u\leqslant 6, \\ \end{aligned} \right. \end{align*} $$
and
 $$ \begin{align*}N(u)=\left\{\begin{aligned} &0\ \text{if }0\leqslant u\leqslant 1, \\ &\frac{u-1}{3}\widehat{A}\ \text{if }1\leqslant u\leqslant 4, \\ &\frac{u-2}{2}\widehat{A}+\frac{u-4}{2}\widehat{E}\ \text{if }4\leqslant u\leqslant 6, \\ \end{aligned} \right. \end{align*} $$
$$ \begin{align*}N(u)=\left\{\begin{aligned} &0\ \text{if }0\leqslant u\leqslant 1, \\ &\frac{u-1}{3}\widehat{A}\ \text{if }1\leqslant u\leqslant 4, \\ &\frac{u-2}{2}\widehat{A}+\frac{u-4}{2}\widehat{E}\ \text{if }4\leqslant u\leqslant 6, \\ \end{aligned} \right. \end{align*} $$
where
![]() $P(u)$
and
$P(u)$
and
![]() $N(u)$
are the positive and the negative parts of the Zariski decomposition, respectively. Using this, we compute
$N(u)$
are the positive and the negative parts of the Zariski decomposition, respectively. Using this, we compute
 $$ \begin{align*}S_{X}(G)=\frac{3}{12}\int_{0}^{1}u^{3}du+\frac{3}{12}\int_{1}^{4}udu+\frac{3}{12}\int_{4}^{6}\frac{u(6-u)^{2}}{4}du=\frac{43}{16}<3=A_X(G). \end{align*} $$
$$ \begin{align*}S_{X}(G)=\frac{3}{12}\int_{0}^{1}u^{3}du+\frac{3}{12}\int_{1}^{4}udu+\frac{3}{12}\int_{4}^{6}\frac{u(6-u)^{2}}{4}du=\frac{43}{16}<3=A_X(G). \end{align*} $$
Let us apply [Reference Fujita16, Theorem 4.8], [Reference Fujita16, Corollary 4.17], [Reference Fujita16, Corollary 4.18] using notations introduced in [Reference Fujita16, § 4]. To start with, we apply [Reference Fujita16, Corollary 4.18] to get
 $$ \begin{align} 1\geqslant \frac{A_X(\mathbf{F})}{S_X(\mathbf{F})}\geqslant\min\left\{\frac{A_{X}(G)}{S_{X}(G)}, \inf_{Q\in G}\delta_{Q}\big(G,V^G_{\bullet,\bullet}\big)\right\}=\min\left\{\frac{48}{43},\inf_{Q\in G}\delta_{Q}\big(G,V^G_{\bullet,\bullet}\big)\right\}, \end{align} $$
$$ \begin{align} 1\geqslant \frac{A_X(\mathbf{F})}{S_X(\mathbf{F})}\geqslant\min\left\{\frac{A_{X}(G)}{S_{X}(G)}, \inf_{Q\in G}\delta_{Q}\big(G,V^G_{\bullet,\bullet}\big)\right\}=\min\left\{\frac{48}{43},\inf_{Q\in G}\delta_{Q}\big(G,V^G_{\bullet,\bullet}\big)\right\}, \end{align} $$
where
![]() $\delta _{Q}(G,V^G_{\bullet ,\bullet })$
is defined in [Reference Fujita16, § 4]. Let Q be an arbitrary point in the surface G, and let
$\delta _{Q}(G,V^G_{\bullet ,\bullet })$
is defined in [Reference Fujita16, § 4]. Let Q be an arbitrary point in the surface G, and let
![]() $\ell $
is a general line in
$\ell $
is a general line in
![]() $G\cong \mathbb {P}^2$
that contains Q. Then [Reference Fujita16, Corollary 4.18] gives
$G\cong \mathbb {P}^2$
that contains Q. Then [Reference Fujita16, Corollary 4.18] gives
 $$ \begin{align*}\delta_{Q}\big(G,V^G_{\bullet,\bullet}\big) \geqslant\min\left\{\frac{1}{S\big(V^G_{\bullet,\bullet};\ell\big)},\frac{1}{S\big(W^{G,\ell}_{\bullet,\bullet,\bullet};Q\big)}\right\}, \end{align*} $$
$$ \begin{align*}\delta_{Q}\big(G,V^G_{\bullet,\bullet}\big) \geqslant\min\left\{\frac{1}{S\big(V^G_{\bullet,\bullet};\ell\big)},\frac{1}{S\big(W^{G,\ell}_{\bullet,\bullet,\bullet};Q\big)}\right\}, \end{align*} $$
where
![]() $S(V^F_{\bullet ,\bullet };\ell )$
and
$S(V^F_{\bullet ,\bullet };\ell )$
and
![]() $S(W^{G,\ell }_{\bullet ,\bullet ,\bullet };Q)$
are defined in [Reference Fujita16, § 4]. Take
$S(W^{G,\ell }_{\bullet ,\bullet ,\bullet };Q)$
are defined in [Reference Fujita16, § 4]. Take
![]() $v\in \mathbb {R}_{\geqslant 0}$
. Then
$v\in \mathbb {R}_{\geqslant 0}$
. Then
 $$ \begin{align*}P(u)\big\vert_{G}-v\ell\sim_{\mathbb{R}}\left\{\begin{aligned} &(u-v)\ell\ \text{if }0\leqslant u\leqslant 1, \\ &(1-v)\ell\ \text{if }1\leqslant u\leqslant 4, \\ &\frac{6-u-2v}{2}\ell\ \text{if }4\leqslant u\leqslant 6.\\ \end{aligned} \right. \end{align*} $$
$$ \begin{align*}P(u)\big\vert_{G}-v\ell\sim_{\mathbb{R}}\left\{\begin{aligned} &(u-v)\ell\ \text{if }0\leqslant u\leqslant 1, \\ &(1-v)\ell\ \text{if }1\leqslant u\leqslant 4, \\ &\frac{6-u-2v}{2}\ell\ \text{if }4\leqslant u\leqslant 6.\\ \end{aligned} \right. \end{align*} $$
Let
![]() $\mathscr {C}=\widehat {A}\vert _{G}$
. Then
$\mathscr {C}=\widehat {A}\vert _{G}$
. Then
![]() $\mathscr {C}$
is a smooth cubic curve in
$\mathscr {C}$
is a smooth cubic curve in
![]() $G\cong \mathbb {P}^2$
. Let
$G\cong \mathbb {P}^2$
. Let
 $$ \begin{align*}N^\prime(u)=N(u)\big\vert_{G}=\left\{\begin{aligned} &0\ \text{if }0\leqslant u\leqslant 1, \\ &\frac{u-1}{3}\mathscr{C}\ \text{if }1\leqslant u\leqslant 4, \\ &\frac{u-2}{2}\mathscr{C}\ \text{if }4\leqslant u\leqslant 6. \end{aligned} \right. \end{align*} $$
$$ \begin{align*}N^\prime(u)=N(u)\big\vert_{G}=\left\{\begin{aligned} &0\ \text{if }0\leqslant u\leqslant 1, \\ &\frac{u-1}{3}\mathscr{C}\ \text{if }1\leqslant u\leqslant 4, \\ &\frac{u-2}{2}\mathscr{C}\ \text{if }4\leqslant u\leqslant 6. \end{aligned} \right. \end{align*} $$
Now, using [Reference Fujita16, Theorem 4.8], we get
 $$ \begin{align*} S\big(W^{G}_{\bullet,\bullet};\ell\big)&=\frac{3}{12}\int_0^6\int_0^\infty \mathrm{vol}\big(P(u)\big\vert_{G}-v\ell\big)dvdu=\frac{3}{12}\int_{0}^{1}\int_{0}^{u}(u-v)^{2}dvdu+\\ &\quad+\frac{3}{12}\int_{1}^{4}\int_{0}^{1}(1-v)^{2}dvdu+\frac{3}{12}\int_{4}^{6}\int_{0}^{\frac{6-u}{2}}\left(\frac{6-u-2v}{2}\right)^{2}dvdu=\frac{5}{16}. \end{align*} $$
$$ \begin{align*} S\big(W^{G}_{\bullet,\bullet};\ell\big)&=\frac{3}{12}\int_0^6\int_0^\infty \mathrm{vol}\big(P(u)\big\vert_{G}-v\ell\big)dvdu=\frac{3}{12}\int_{0}^{1}\int_{0}^{u}(u-v)^{2}dvdu+\\ &\quad+\frac{3}{12}\int_{1}^{4}\int_{0}^{1}(1-v)^{2}dvdu+\frac{3}{12}\int_{4}^{6}\int_{0}^{\frac{6-u}{2}}\left(\frac{6-u-2v}{2}\right)^{2}dvdu=\frac{5}{16}. \end{align*} $$
Similarly, it follows from [Reference Fujita16, Theorem 4.17] that
 $$ \begin{align*} S\big(W_{\bullet,\bullet,\bullet}^{G,\ell};Q\big)&= \frac{3}{12}\int_{0}^{1}\int_{0}^{u}\Big(\big(P(u)\big\vert_{G}-v\ell\big)\cdot\ell\Big)^2dvdu+ \frac{3}{12}\int_{1}^{4}\int_{0}^{1}\Big(\big(P(u)\big\vert_{G}-v\ell\big)\cdot\ell\Big)^2dvdu+\\ &\quad+\frac{3}{12}\int_{4}^{6}\int_{0}^{\frac{6-u}{2}}\Big(\big(P(u)\big\vert_{G}-v\ell\big)\cdot\ell\Big)^2dvdu+F_Q=\frac{3}{12}\int_{0}^{1}\int_{0}^{u}(u-v)^{2}dvdu+\\ &\quad+\frac{3}{12}\int_{1}^{4}\int_{0}^{1}(1-v)^{2}dvdu+\frac{3}{12}\int_{4}^{6}\int_{0}^{\frac{6-u}{2}}\left(\frac{6-u-2v}{2}\right)^{2}dvdu+F_Q=\frac{5}{16}+F_Q, \end{align*} $$
$$ \begin{align*} S\big(W_{\bullet,\bullet,\bullet}^{G,\ell};Q\big)&= \frac{3}{12}\int_{0}^{1}\int_{0}^{u}\Big(\big(P(u)\big\vert_{G}-v\ell\big)\cdot\ell\Big)^2dvdu+ \frac{3}{12}\int_{1}^{4}\int_{0}^{1}\Big(\big(P(u)\big\vert_{G}-v\ell\big)\cdot\ell\Big)^2dvdu+\\ &\quad+\frac{3}{12}\int_{4}^{6}\int_{0}^{\frac{6-u}{2}}\Big(\big(P(u)\big\vert_{G}-v\ell\big)\cdot\ell\Big)^2dvdu+F_Q=\frac{3}{12}\int_{0}^{1}\int_{0}^{u}(u-v)^{2}dvdu+\\ &\quad+\frac{3}{12}\int_{1}^{4}\int_{0}^{1}(1-v)^{2}dvdu+\frac{3}{12}\int_{4}^{6}\int_{0}^{\frac{6-u}{2}}\left(\frac{6-u-2v}{2}\right)^{2}dvdu+F_Q=\frac{5}{16}+F_Q, \end{align*} $$
where
 $$ \begin{align*} F_Q&=\frac{6}{12}\int_{1}^{4}\int_{0}^{1}\Big(\big(P(u)\big\vert_{G}-v\ell\big)\cdot\ell\Big)\mathrm{ord}_Q\big(N^\prime(u)\big|_\ell\big)dvdu+\\ &\quad+\frac{6}{12}\int_{4}^{6} \int_{0}^{\frac{6-u}{2}}\Big(\big(P(u)\big\vert_{G}-v\ell\big)\cdot\ell\Big)\mathrm{ord}_Q\big(N^\prime(u)\big|_\ell\big)dvdu\leqslant\\ &\quad\leqslant\frac{6}{12}\int_{1}^{4} \int_{0}^{1}\frac{(1-v)(u-1)}{3}dvdu+ \frac{6}{12}\int_{4}^{6} \int_{0}^{\frac{6-u}{2}}\frac{(6-u-2v)(u-2)}{4}dvdu=\frac{7}{12}. \end{align*} $$
$$ \begin{align*} F_Q&=\frac{6}{12}\int_{1}^{4}\int_{0}^{1}\Big(\big(P(u)\big\vert_{G}-v\ell\big)\cdot\ell\Big)\mathrm{ord}_Q\big(N^\prime(u)\big|_\ell\big)dvdu+\\ &\quad+\frac{6}{12}\int_{4}^{6} \int_{0}^{\frac{6-u}{2}}\Big(\big(P(u)\big\vert_{G}-v\ell\big)\cdot\ell\Big)\mathrm{ord}_Q\big(N^\prime(u)\big|_\ell\big)dvdu\leqslant\\ &\quad\leqslant\frac{6}{12}\int_{1}^{4} \int_{0}^{1}\frac{(1-v)(u-1)}{3}dvdu+ \frac{6}{12}\int_{4}^{6} \int_{0}^{\frac{6-u}{2}}\frac{(6-u-2v)(u-2)}{4}dvdu=\frac{7}{12}. \end{align*} $$
So, we have
![]() $S(W_{\bullet ,\bullet ,\bullet }^{G,\ell };Q)\leqslant \frac {43}{48}$
. Then
$S(W_{\bullet ,\bullet ,\bullet }^{G,\ell };Q)\leqslant \frac {43}{48}$
. Then
![]() $\delta _{Q}(G,V^G_{\bullet ,\bullet })>1$
, which contradicts Equation (2.2).
$\delta _{Q}(G,V^G_{\bullet ,\bullet })>1$
, which contradicts Equation (2.2).
Thus, we see that P is a Du Val singular point of the surface A of type
![]() $\mathbb {D}_4$
,
$\mathbb {D}_4$
,
![]() $\mathbb {D}_5$
,
$\mathbb {D}_5$
,
![]() $\mathbb {E}_6$
. Now, arguing as in the proof of [Reference Xu22, Lemma 9.11], we see that
$\mathbb {E}_6$
. Now, arguing as in the proof of [Reference Xu22, Lemma 9.11], we see that
![]() $\beta (\mathbf {F})>0$
if
$\beta (\mathbf {F})>0$
if
-
(1) the inequality
 $\beta (G)>0$
holds,
$\beta (G)>0$
holds, -
(2) and for every prime divisor
 $\mathbf {E}$
over X such that
$\mathbf {E}$
over X such that
 $C_X(\mathbf {E})$
is a curve containing P, the following inequality holds:
$C_X(\mathbf {E})$
is a curve containing P, the following inequality holds:  $$ \begin{align*}\frac{A_X(\mathbf{E})}{S_X(\mathbf{E})}\geqslant\frac{4}{3}. \end{align*} $$
$$ \begin{align*}\frac{A_X(\mathbf{E})}{S_X(\mathbf{E})}\geqslant\frac{4}{3}. \end{align*} $$
Since
![]() $\beta (\mathbf {F})\leqslant 0$
by our assumption, we see that at least one of these conditions must fail.
$\beta (\mathbf {F})\leqslant 0$
by our assumption, we see that at least one of these conditions must fail.
Lemma 2.11. One has
![]() $\beta (G)\geqslant \frac {465}{2048}$
.
$\beta (G)\geqslant \frac {465}{2048}$
.
Proof. Let
![]() $\widehat {A}$
and
$\widehat {A}$
and
![]() $\widehat {E}$
be the proper transforms on
$\widehat {E}$
be the proper transforms on
![]() $\widehat {X}$
of the surfaces A and E, respectively. Take
$\widehat {X}$
of the surfaces A and E, respectively. Take
![]() $u\in \mathbb {R}_{\geqslant 0}$
. Then
$u\in \mathbb {R}_{\geqslant 0}$
. Then
which easily implies that the divisor
![]() $-K_{\widehat {X}}-G$
is pseudoeffective
$-K_{\widehat {X}}-G$
is pseudoeffective
![]() $\iff u\leqslant 4$
because we can contract the surfaces
$\iff u\leqslant 4$
because we can contract the surfaces
![]() $\widehat {A}$
and
$\widehat {A}$
and
![]() $\widehat {E}$
simultaneously after flops. Then
$\widehat {E}$
simultaneously after flops. Then
 $$ \begin{align*}\beta(G)=A_X(G)-S_X(G)=3-\frac{1}{12}\int_0^4\mathrm{vol}\big(\sigma^*(-K_{X})-uG\big)du. \end{align*} $$
$$ \begin{align*}\beta(G)=A_X(G)-S_X(G)=3-\frac{1}{12}\int_0^4\mathrm{vol}\big(\sigma^*(-K_{X})-uG\big)du. \end{align*} $$
Note that
![]() $\sigma ^*(-K_{X})-uG$
is nef for
$\sigma ^*(-K_{X})-uG$
is nef for
![]() $u\in [0,1]$
because the divisor
$u\in [0,1]$
because the divisor
![]() $-K_X$
is very ample. Thus, if
$-K_X$
is very ample. Thus, if
![]() $u\in [0,1]$
, then
$u\in [0,1]$
, then
Similarly, if
![]() $1\leqslant u\leqslant \frac {3}{2}$
, then
$1\leqslant u\leqslant \frac {3}{2}$
, then
Finally, let us estimate
![]() $\mathrm {vol}(\sigma ^*(-K_{X})-uG)$
in the case when
$\mathrm {vol}(\sigma ^*(-K_{X})-uG)$
in the case when
![]() $4\geqslant u>\frac {3}{2}$
.
$4\geqslant u>\frac {3}{2}$
.
Let Z be a general hyperplane section of the cubic surface A that passes through P, and let
![]() $\widehat {Z}$
be its proper transform on the threefold
$\widehat {Z}$
be its proper transform on the threefold
![]() $\widehat {X}$
. Then Z is an irreducible cuspidal cubic curve, and
$\widehat {X}$
. Then Z is an irreducible cuspidal cubic curve, and
![]() $\widehat {Z}\subset \widehat {A}$
. Observe that
$\widehat {Z}\subset \widehat {A}$
. Observe that
![]() $(\sigma ^*(-K_{X})-uG)\cdot \widehat {Z}=3-2u$
and
$(\sigma ^*(-K_{X})-uG)\cdot \widehat {Z}=3-2u$
and
![]() $\widehat {A}\cdot \widehat {Z}=-4$
, so
$\widehat {A}\cdot \widehat {Z}=-4$
, so
![]() $\widehat {A}$
is contained in the asymptotic base locus of the divisor
$\widehat {A}$
is contained in the asymptotic base locus of the divisor
![]() $\sigma ^*(-K_{X})-uG$
for
$\sigma ^*(-K_{X})-uG$
for
![]() $u>\frac {3}{2}$
. Moreover, if
$u>\frac {3}{2}$
. Moreover, if
![]() $\sigma ^*(-K_{X})-uG\sim _{\mathbb {R}}\widehat {D}+\lambda \widehat {A}$
for
$\sigma ^*(-K_{X})-uG\sim _{\mathbb {R}}\widehat {D}+\lambda \widehat {A}$
for
![]() $\lambda \in \mathbb {R}_{\geqslant 0}$
and an effective
$\lambda \in \mathbb {R}_{\geqslant 0}$
and an effective
![]() $\mathbb {R}$
-divisor
$\mathbb {R}$
-divisor
![]() $\widehat {D}$
whose support does not contain
$\widehat {D}$
whose support does not contain
![]() $\widehat {A}$
, then
$\widehat {A}$
, then
![]() $\widehat {Z}\not \subset \widehat {D}$
, which implies that
$\widehat {Z}\not \subset \widehat {D}$
, which implies that
so that
![]() $\lambda \geqslant \frac {3-2u}{4}$
. Thus, if
$\lambda \geqslant \frac {3-2u}{4}$
. Thus, if
![]() $4\geqslant u>\frac {3}{2}$
, then
$4\geqslant u>\frac {3}{2}$
, then
Moreover, if
![]() $4\geqslant u>\frac {3}{2}$
, then
$4\geqslant u>\frac {3}{2}$
, then
Therefore, if
![]() $4\geqslant u>\frac {3}{2}$
, then
$4\geqslant u>\frac {3}{2}$
, then
Furthermore, if
![]() $\frac {7}{2}\geqslant u>\frac {3}{2}$
, then
$\frac {7}{2}\geqslant u>\frac {3}{2}$
, then
![]() $\frac {11-2u}{4}H-\frac {7-2u}{2}E$
is nef so that
$\frac {11-2u}{4}H-\frac {7-2u}{2}E$
is nef so that
Similarly, if
![]() $4\geqslant u>\frac {7}{2}$
, then
$4\geqslant u>\frac {7}{2}$
, then
Now, we can estimate
![]() $\beta (G)$
as follows
$\beta (G)$
as follows
 $$ \begin{align*} \beta(G)&=3-\frac{1}{12}\int_0^4\mathrm{vol}\big(\sigma^*(-K_{X})-uG\big)du\geqslant 3-\frac{1}{12}\int_0^{1}(12-u^3)du-\frac{1}{12}\int_1^{\frac{3}{2}}11du-\\&\quad-\frac{1}{12}\int_{\frac{3}{2}}^{\frac{7}{2}}\frac{25-6u}{16}du-\frac{1}{12}\int_{\frac{7}{2}}^4\frac{(11-2u)^3}{256}du=3-\frac{5679}{2048}=\frac{465}{2048} \end{align*} $$
$$ \begin{align*} \beta(G)&=3-\frac{1}{12}\int_0^4\mathrm{vol}\big(\sigma^*(-K_{X})-uG\big)du\geqslant 3-\frac{1}{12}\int_0^{1}(12-u^3)du-\frac{1}{12}\int_1^{\frac{3}{2}}11du-\\&\quad-\frac{1}{12}\int_{\frac{3}{2}}^{\frac{7}{2}}\frac{25-6u}{16}du-\frac{1}{12}\int_{\frac{7}{2}}^4\frac{(11-2u)^3}{256}du=3-\frac{5679}{2048}=\frac{465}{2048} \end{align*} $$
as claimed.
Therefore, there exists a prime divisor
![]() $\mathbf {E}$
over X such that
$\mathbf {E}$
over X such that
![]() $C_X(\mathbf {E})$
is a curve,
$C_X(\mathbf {E})$
is a curve,
![]() $P\in C_X(\mathbf {E})$
, and
$P\in C_X(\mathbf {E})$
, and
![]() $A_X(\mathbf {E})<\frac {4}{3}S_X(\mathbf {E})$
. Set
$A_X(\mathbf {E})<\frac {4}{3}S_X(\mathbf {E})$
. Set
![]() $Z=C_X(\mathbf {E})$
. Then
$Z=C_X(\mathbf {E})$
. Then
![]() $\delta _O(X)<\frac {4}{3}$
for every point
$\delta _O(X)<\frac {4}{3}$
for every point
![]() $O\in Z$
.
$O\in Z$
.
Lemma 2.12. One has
![]() $Z\subset A$
, and Z is a line in the cubic surface A.
$Z\subset A$
, and Z is a line in the cubic surface A.
Proof. Let O be a general point in Z, and let
![]() $A_O$
be the fiber of
$A_O$
be the fiber of
![]() $\phi $
that passes through O. If
$\phi $
that passes through O. If
![]() $Z\not \subset A$
, then
$Z\not \subset A$
, then
![]() $A_O$
is smooth, so that
$A_O$
is smooth, so that
![]() $\delta _O(A_O)\geqslant \frac {3}{2}$
by [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Lemma 2.13], which gives
$\delta _O(A_O)\geqslant \frac {3}{2}$
by [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Lemma 2.13], which gives
 $$ \begin{align*}\frac{4}{3}>\frac{A_X(\mathbf{E})}{S_X(\mathbf{E})}\geqslant\delta_O(X)\geqslant\mathrm{min}\Bigg\{\frac{16}{11},\frac{16\delta_O(A_O)}{\delta_O(A_O)+15}\Bigg\}\geqslant\mathrm{min}\Bigg\{\frac{16}{11},\frac{16\times\frac{3}{2}}{\frac{3}{2}+15}\Bigg\}=\frac{16}{11}>\frac{4}{3} \end{align*} $$
$$ \begin{align*}\frac{4}{3}>\frac{A_X(\mathbf{E})}{S_X(\mathbf{E})}\geqslant\delta_O(X)\geqslant\mathrm{min}\Bigg\{\frac{16}{11},\frac{16\delta_O(A_O)}{\delta_O(A_O)+15}\Bigg\}\geqslant\mathrm{min}\Bigg\{\frac{16}{11},\frac{16\times\frac{3}{2}}{\frac{3}{2}+15}\Bigg\}=\frac{16}{11}>\frac{4}{3} \end{align*} $$
by Lemma 2.1. This shows that
![]() $Z\subset A$
and
$Z\subset A$
and
![]() $A_O=A$
.
$A_O=A$
.
To complete the proof of the lemma, we have to show that Z is a line in the surface A. Suppose that Z is not a line. Then the point O is not contained in a line in the surface A because A contains finitely many lines [Reference Bruce and Wall6]. Now, arguing as in the proof of [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Lemma 2.13], we get
![]() $\delta _O(A)\geqslant \frac {3}{2}$
. So, applying Lemma 2.1 again, we get a contradiction as above.
$\delta _O(A)\geqslant \frac {3}{2}$
. So, applying Lemma 2.1 again, we get a contradiction as above.
Now, our auxiliary theorem follows from the following lemma:
Lemma 2.13. The surface A does not have a singular point of type
![]() $\mathbb {D}_4$
.
$\mathbb {D}_4$
.
Proof. Suppose A has singularity of type
![]() $\mathbb {D}_4$
. Then it follows from [Reference Bruce and Wall6] that, for a suitable choice of coordinates x, y, z, t on the projective space
$\mathbb {D}_4$
. Then it follows from [Reference Bruce and Wall6] that, for a suitable choice of coordinates x, y, z, t on the projective space
![]() $\mathbb {P}^3$
, one of the following cases hold:
$\mathbb {P}^3$
, one of the following cases hold:
-
(A)
 $A=\{tx^2=y^3-z^3\}\subset \mathbb {P}^3$
,
$A=\{tx^2=y^3-z^3\}\subset \mathbb {P}^3$
, -
(B)
 $A=\{tx^2=y^3-z^3+xyz\}\subset \mathbb {P}^3$
.
$A=\{tx^2=y^3-z^3+xyz\}\subset \mathbb {P}^3$
.
Note that
![]() $P=[0:0:0:1]$
, and A contains six lines [Reference Bruce and Wall6]. In case (A), these lines are
$P=[0:0:0:1]$
, and A contains six lines [Reference Bruce and Wall6]. In case (A), these lines are
 $$ \begin{align*} L_1&=\{x=y-z=0\},\\[3pt] L_2&=\{x=y-\omega_3z=0\},\\[3pt] L_3&=\{x=y+\omega_3^2z=0\},\\[3pt]L_4&=\{t=y-z=0\},\\[3pt] L_5&=\{t=y+\omega_3z=0\},\\[3pt] L_6&=\{t=y+\omega_3^2z=0\}, \end{align*} $$
$$ \begin{align*} L_1&=\{x=y-z=0\},\\[3pt] L_2&=\{x=y-\omega_3z=0\},\\[3pt] L_3&=\{x=y+\omega_3^2z=0\},\\[3pt]L_4&=\{t=y-z=0\},\\[3pt] L_5&=\{t=y+\omega_3z=0\},\\[3pt] L_6&=\{t=y+\omega_3^2z=0\}, \end{align*} $$
where
![]() $\omega _3$
is a primitive cube root of unity. In case (B), these lines are
$\omega _3$
is a primitive cube root of unity. In case (B), these lines are
 $$ \begin{align*} L_1&=\{x=y-z=0\},\\ L_2&=\{x=y-\omega_3z=0\},\\ L_3&=\{x=y-\omega_3^2z=0\},\\ L_4&=\{x+3(y-z)=y-z-9t=0\},\\ L_5&=\{x+3\omega_3(y-\omega_3z)=\omega_3y-\omega_3^2z-9t=0\},\\ L_6&=\{x+3\omega_3^2(y-\omega_3^2z)=\omega_3^2y-\omega_3z-9t=0\}. \end{align*} $$
$$ \begin{align*} L_1&=\{x=y-z=0\},\\ L_2&=\{x=y-\omega_3z=0\},\\ L_3&=\{x=y-\omega_3^2z=0\},\\ L_4&=\{x+3(y-z)=y-z-9t=0\},\\ L_5&=\{x+3\omega_3(y-\omega_3z)=\omega_3y-\omega_3^2z-9t=0\},\\ L_6&=\{x+3\omega_3^2(y-\omega_3^2z)=\omega_3^2y-\omega_3z-9t=0\}. \end{align*} $$
Note that
![]() $P=L_1\cap L_3\cap L_3$
,
$P=L_1\cap L_3\cap L_3$
,
![]() $P\not \in L_4\cup L_5\cup L_6$
and
$P\not \in L_4\cup L_5\cup L_6$
and
![]() $-K_A\sim 2L_1+L_4\sim 2L_2+L_5\sim 2L_3+L_6$
.
$-K_A\sim 2L_1+L_4\sim 2L_2+L_5\sim 2L_3+L_6$
.
By Lemma 2.12, we may assume that
![]() $Z=L_1$
.
$Z=L_1$
.
Recall that
![]() $S_X(A)=\frac {11}{16}$
; see the proof of Lemma 2.1. Using [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Theorem 1.112], we get
$S_X(A)=\frac {11}{16}$
; see the proof of Lemma 2.1. Using [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Theorem 1.112], we get
 $$ \begin{align*}\frac{4}{3}>\frac{A_X(\mathbf{E})}{S_X(\mathbf{E})}\geqslant \min\left\{\frac{1}{S_X(A)},\frac{1}{S(W_{\bullet,\bullet}^A;L_1)}\right\}=\min\left\{\frac{16}{11},\frac{1}{S(W_{\bullet,\bullet}^A;L_1)}\right\}, \end{align*} $$
$$ \begin{align*}\frac{4}{3}>\frac{A_X(\mathbf{E})}{S_X(\mathbf{E})}\geqslant \min\left\{\frac{1}{S_X(A)},\frac{1}{S(W_{\bullet,\bullet}^A;L_1)}\right\}=\min\left\{\frac{16}{11},\frac{1}{S(W_{\bullet,\bullet}^A;L_1)}\right\}, \end{align*} $$
where
![]() $S(W_{\bullet ,\bullet }^A;L_1)$
is defined in [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, § 1.7]. Therefore, we conclude that
$S(W_{\bullet ,\bullet }^A;L_1)$
is defined in [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, § 1.7]. Therefore, we conclude that
![]() $S(W_{\bullet ,\bullet }^A;L_1)<\frac {4}{3}$
. Let us compute
$S(W_{\bullet ,\bullet }^A;L_1)<\frac {4}{3}$
. Let us compute
![]() $S(W_{\bullet ,\bullet }^A;L_1)$
using [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Corollary 1.109].
$S(W_{\bullet ,\bullet }^A;L_1)$
using [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Corollary 1.109].
To do this, we use notations introduced in the proof of Lemma 2.1 applied to
![]() $O=P$
. Then using [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Corollary 1.109] and computations from the proof of Lemma 2.1, we get
$O=P$
. Then using [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Corollary 1.109] and computations from the proof of Lemma 2.1, we get
 $$ \begin{align*}S\big(W_{\bullet,\bullet}^A; L_1\big)=\frac{1}{4}\int_{0}^{1}\int_0^\infty \mathrm{vol}\big(-K_A-vL_1\big)dvdu+\frac{1}{4}\int_{1}^{2}\int_0^\infty \mathrm{vol}\big((2-u)(-K_A)-vL_1\big)dvdu \end{align*} $$
$$ \begin{align*}S\big(W_{\bullet,\bullet}^A; L_1\big)=\frac{1}{4}\int_{0}^{1}\int_0^\infty \mathrm{vol}\big(-K_A-vL_1\big)dvdu+\frac{1}{4}\int_{1}^{2}\int_0^\infty \mathrm{vol}\big((2-u)(-K_A)-vL_1\big)dvdu \end{align*} $$
since
![]() $L_1\not \subset \mathrm {Supp}(N(u))$
since
$L_1\not \subset \mathrm {Supp}(N(u))$
since
![]() $L_1\not \subset E$
. Let us compute
$L_1\not \subset E$
. Let us compute
![]() $S(W_{\bullet ,\bullet }^A; L_1)$
. Take
$S(W_{\bullet ,\bullet }^A; L_1)$
. Take
![]() $v\in \mathbb {R}_{\geqslant 0}$
. Then
$v\in \mathbb {R}_{\geqslant 0}$
. Then
Thus, the divisor
![]() $-K_A-vL_1$
is pseudoeffective
$-K_A-vL_1$
is pseudoeffective
![]() $\iff v\leqslant 2$
since
$\iff v\leqslant 2$
since
![]() $L_4^2=-1$
. Fix
$L_4^2=-1$
. Fix
![]() $v\in [0,2]$
. Let
$v\in [0,2]$
. Let
![]() $P(u,v)$
be the positive part of the Zariski decomposition of the divisor
$P(u,v)$
be the positive part of the Zariski decomposition of the divisor
![]() $-K_A-vL_1$
, and let
$-K_A-vL_1$
, and let
![]() $N(u,v)$
be its negative part. Then
$N(u,v)$
be its negative part. Then
 $$ \begin{align*}P(u,v)=\left\{\begin{aligned} &(2-v)L_1+L_4\ \text{if }0\leqslant v\leqslant 1, \\ &(2-v)(L_1+L_4)\ \text{if }1\leqslant v\leqslant 2, \\ \end{aligned} \right. \end{align*} $$
$$ \begin{align*}P(u,v)=\left\{\begin{aligned} &(2-v)L_1+L_4\ \text{if }0\leqslant v\leqslant 1, \\ &(2-v)(L_1+L_4)\ \text{if }1\leqslant v\leqslant 2, \\ \end{aligned} \right. \end{align*} $$
and
 $$ \begin{align*}N(u,v)=\left\{\begin{aligned} &0\ \text{if }0\leqslant v\leqslant 1, \\ &(v-1)L_4\ \text{if }1\leqslant v\leqslant 2. \end{aligned} \right. \end{align*} $$
$$ \begin{align*}N(u,v)=\left\{\begin{aligned} &0\ \text{if }0\leqslant v\leqslant 1, \\ &(v-1)L_4\ \text{if }1\leqslant v\leqslant 2. \end{aligned} \right. \end{align*} $$
Thus, if
![]() $0\leqslant v\leqslant 1$
, then
$0\leqslant v\leqslant 1$
, then
![]() $\mathrm {vol}(-K_A-vL_1)=3-2v$
because
$\mathrm {vol}(-K_A-vL_1)=3-2v$
because
![]() $L_1^2=0$
and
$L_1^2=0$
and
![]() $L_1\cdot L_4=0$
. Similarly, if
$L_1\cdot L_4=0$
. Similarly, if
![]() $1\leqslant v\leqslant 2$
, then
$1\leqslant v\leqslant 2$
, then
![]() $\mathrm {vol}(-K_A-vL_1)=(v-2)^2$
. This gives
$\mathrm {vol}(-K_A-vL_1)=(v-2)^2$
. This gives
 $$ \begin{align*}\frac{1}{4}\int_{0}^{1}\int_0^\infty \mathrm{vol}\big(-K_A-vL_1\big)dvdu= \frac{1}{4}\int_{0}^{1}\int_0^1(3-2v)dvdu+\frac{1}{4}\int_{0}^{1}\int_1^2(v-2)^2dvdu=\frac{7}{12} \end{align*} $$
$$ \begin{align*}\frac{1}{4}\int_{0}^{1}\int_0^\infty \mathrm{vol}\big(-K_A-vL_1\big)dvdu= \frac{1}{4}\int_{0}^{1}\int_0^1(3-2v)dvdu+\frac{1}{4}\int_{0}^{1}\int_1^2(v-2)^2dvdu=\frac{7}{12} \end{align*} $$
and
 $$ \begin{align*} &\frac{1}{4}\int_{1}^{2}\int_0^\infty \mathrm{vol}\big((2-u)(-K_A)-vL_1\big)dvdu= \frac{1}{4}\int_{1}^{2}\int_0^\infty(2-u)^3\mathrm{vol}\big((-K_A)-vL_1\big)dvdu=\\ &\quad=\frac{1}{4}\int_{1}^{2}\int_0^1(2-u)^3(3-2v)dvdu+\frac{1}{4}\int_{1}^{2}\int_1^2(2-u)^3(v-2)^2dvdu=\frac{7}{48}. \end{align*} $$
$$ \begin{align*} &\frac{1}{4}\int_{1}^{2}\int_0^\infty \mathrm{vol}\big((2-u)(-K_A)-vL_1\big)dvdu= \frac{1}{4}\int_{1}^{2}\int_0^\infty(2-u)^3\mathrm{vol}\big((-K_A)-vL_1\big)dvdu=\\ &\quad=\frac{1}{4}\int_{1}^{2}\int_0^1(2-u)^3(3-2v)dvdu+\frac{1}{4}\int_{1}^{2}\int_1^2(2-u)^3(v-2)^2dvdu=\frac{7}{48}. \end{align*} $$
Combining, we get
![]() $S(W_{\bullet ,\bullet }^A;L_1)=\frac {35}{48}<\frac {3}{4}$
. This is a contradiction.
$S(W_{\bullet ,\bullet }^A;L_1)=\frac {35}{48}<\frac {3}{4}$
. This is a contradiction.
3 Family  .
.
Let R be a smooth surface of degree
![]() $(2,4)$
in
$(2,4)$
in
![]() $\mathbb {P}^1\times \mathbb {P}^2$
; let
$\mathbb {P}^1\times \mathbb {P}^2$
; let
![]() $\pi \colon X\to \mathbb {P}^1\times \mathbb {P}^2$
be a double cover ramified over the surface R. Then X is a smooth Fano threefold in the family
$\pi \colon X\to \mathbb {P}^1\times \mathbb {P}^2$
be a double cover ramified over the surface R. Then X is a smooth Fano threefold in the family ![]() . Moreover, all smooth Fano threefolds in this family can be obtained this way.
. Moreover, all smooth Fano threefolds in this family can be obtained this way.
Let
![]() $\mathrm {pr}_1\colon \mathbb {P}^1\times \mathbb {P}^2\to \mathbb {P}^1$
and
$\mathrm {pr}_1\colon \mathbb {P}^1\times \mathbb {P}^2\to \mathbb {P}^1$
and
![]() $\mathrm {pr}_2\colon \mathbb {P}^1\times \mathbb {P}^2\to \mathbb {P}^2$
be the projections to the first and the second factors, respectively. Set
$\mathrm {pr}_2\colon \mathbb {P}^1\times \mathbb {P}^2\to \mathbb {P}^2$
be the projections to the first and the second factors, respectively. Set
![]() $p_1=\mathrm {pr}_1\circ \pi $
and
$p_1=\mathrm {pr}_1\circ \pi $
and
![]() $p_2=\mathrm {pr}_2\circ \pi $
. We have the following commutative diagram:
$p_2=\mathrm {pr}_2\circ \pi $
. We have the following commutative diagram:

where
![]() $p_1$
is a fibration into del Pezzo surfaces of degree
$p_1$
is a fibration into del Pezzo surfaces of degree
![]() $2$
, and
$2$
, and
![]() $p_2$
is a conic bundle.
$p_2$
is a conic bundle.
Lemma 3.1. Let S be a fiber of the morphism
![]() $p_1$
. Then S is irreducible and normal.
$p_1$
. Then S is irreducible and normal.
Proof. Since
![]() $p_1\colon X\to \mathbb {P}^1$
is a Mori fiber space, any fiber of
$p_1\colon X\to \mathbb {P}^1$
is a Mori fiber space, any fiber of
![]() $p_1$
is irreducible and reduced. Moreover, any fiber of
$p_1$
is irreducible and reduced. Moreover, any fiber of
![]() $\mathrm {pr}_1|_R$
is reduced by local computations. Thus, the assertion follows.
$\mathrm {pr}_1|_R$
is reduced by local computations. Thus, the assertion follows.
Lemma 3.2. Let S be a fiber of the morphism
![]() $p_1$
, let C be a fiber of the morphism
$p_1$
, let C be a fiber of the morphism
![]() $p_2$
and let P be a point in
$p_2$
and let P be a point in
![]() $S\cap C$
. Then S or C is smooth at P.
$S\cap C$
. Then S or C is smooth at P.
Proof. Local computations.
Now, we are ready to prove that X is K-stable. Recall from [Reference Cheltsov, Przyjalkowski and Shramov10] that
![]() $\mathrm {Aut}(X)$
is finite. Thus, the threefold X is K-stable if and only if it is K-polystable [Reference Xu22].
$\mathrm {Aut}(X)$
is finite. Thus, the threefold X is K-stable if and only if it is K-polystable [Reference Xu22].
Let
![]() $\tau $
be the Galois involution of the double cover
$\tau $
be the Galois involution of the double cover
![]() $\pi \colon X\to \mathbb {P}^1\times \mathbb {P}^2$
, and let
$\pi \colon X\to \mathbb {P}^1\times \mathbb {P}^2$
, and let
![]() $G=\langle \tau \rangle $
. Suppose that X is not K-polystable. Then it follows from [Reference Zhuang24, Corollary 4.14] that there exists a G-invariant prime divisor
$G=\langle \tau \rangle $
. Suppose that X is not K-polystable. Then it follows from [Reference Zhuang24, Corollary 4.14] that there exists a G-invariant prime divisor
![]() $\mathbf {F}$
over X such that
$\mathbf {F}$
over X such that
Let Z be the center of this divisor on X. Then Z is not a surface by [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Theorem 3.17]. Hence, we see that either Z is a G-invariant irreducible curve, or Z is a G-fixed point. Let us seek for a contradiction.
Let P be a general point in Z, and let S be the fiber of
![]() $p_1$
that passes through P.
$p_1$
that passes through P.
Lemma 3.3. The surface S is singular at P.
Proof. Suppose that S is smooth at P. Let B be a general curve in
![]() $|-K_S|$
that contains P. Then B is a smooth curve in S. Applying [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Theorem 1.112], we get
$|-K_S|$
that contains P. Then B is a smooth curve in S. Applying [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Theorem 1.112], we get
 $$ \begin{align*}1\geqslant \frac{A_X(\mathbf{F})}{S_X(\mathbf{F})}\geqslant \min\left\{\frac{1}{S_X(S)},\frac{1}{S(W_{\bullet,\bullet}^S;B)},\frac{1}{S(W_{\bullet, \bullet,\bullet}^{S,B};P)}\right\}. \end{align*} $$
$$ \begin{align*}1\geqslant \frac{A_X(\mathbf{F})}{S_X(\mathbf{F})}\geqslant \min\left\{\frac{1}{S_X(S)},\frac{1}{S(W_{\bullet,\bullet}^S;B)},\frac{1}{S(W_{\bullet, \bullet,\bullet}^{S,B};P)}\right\}. \end{align*} $$
Since
![]() $S_X(S)<1$
by [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Theorem 3.17], we see that
$S_X(S)<1$
by [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Theorem 3.17], we see that
![]() $S(W_{\bullet ,\bullet }^S;B)\geqslant 1$
or
$S(W_{\bullet ,\bullet }^S;B)\geqslant 1$
or
![]() $S(W_{\bullet , \bullet ,\bullet }^{S,B};P)\geqslant 1$
. We refer the reader to [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, § 1.7] for definitions of
$S(W_{\bullet , \bullet ,\bullet }^{S,B};P)\geqslant 1$
. We refer the reader to [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, § 1.7] for definitions of
![]() $S_X(S)$
,
$S_X(S)$
,
![]() $S(W_{\bullet ,\bullet }^S;B)$
,
$S(W_{\bullet ,\bullet }^S;B)$
,
![]() $S(W_{\bullet , \bullet ,\bullet }^{S,B};P)$
.
$S(W_{\bullet , \bullet ,\bullet }^{S,B};P)$
.
Note that [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Theorem 1.112] requires S to have Du Val singularities, but S may have non-Du Val singularities. Nevertheless, we still can apply [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Theorem 1.112] here since the proof of [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Theorem 1.112] remains valid in our case because S is smooth along B.
Let us compute
![]() $S(W_{\bullet ,\bullet }^S;B)$
and
$S(W_{\bullet ,\bullet }^S;B)$
and
![]() $S(W_{\bullet , \bullet ,\bullet }^{S,B};P)$
. Take
$S(W_{\bullet , \bullet ,\bullet }^{S,B};P)$
. Take
![]() $u\in \mathbb {R}_{\geqslant 0}$
and
$u\in \mathbb {R}_{\geqslant 0}$
and
![]() $v\in \mathbb {R}_{\geqslant 0}$
. Then
$v\in \mathbb {R}_{\geqslant 0}$
. Then
Similarly, if
![]() $u\in [0,1]$
, then
$u\in [0,1]$
, then
![]() $(-K_X-uS)\vert _{S}-vB\sim _{\mathbb {R}}(1-v)(-K_S)$
, so
$(-K_X-uS)\vert _{S}-vB\sim _{\mathbb {R}}(1-v)(-K_S)$
, so
Now, applying [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Corollary 1.109], we get
 $$ \begin{align*}S(W_{\bullet,\bullet}^S;B)=\frac{3}{6}\int_0^1\int_0^1\big((1-v)(-K_S)\big)^2dvdu=\frac{1}{2}\int_0^1\int_0^12(1-v)^2dv=\frac{1}{3}<1. \end{align*} $$
$$ \begin{align*}S(W_{\bullet,\bullet}^S;B)=\frac{3}{6}\int_0^1\int_0^1\big((1-v)(-K_S)\big)^2dvdu=\frac{1}{2}\int_0^1\int_0^12(1-v)^2dv=\frac{1}{3}<1. \end{align*} $$
Similarly, using [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Theorem 1.112], we get
 $$ \begin{align*}S(W_{\bullet,\bullet,\bullet}^{S,B},P)=\frac{3}{6}\int_0^1\int_0^1\big((1-v)(-K_S)\cdot B\big)^2dvdu=\frac{2}{3}<1. \end{align*} $$
$$ \begin{align*}S(W_{\bullet,\bullet,\bullet}^{S,B},P)=\frac{3}{6}\int_0^1\int_0^1\big((1-v)(-K_S)\cdot B\big)^2dvdu=\frac{2}{3}<1. \end{align*} $$
But we already know that
![]() $S(W_{\bullet ,\bullet }^S;B)\geqslant 1$
or
$S(W_{\bullet ,\bullet }^S;B)\geqslant 1$
or
![]() $S(W_{\bullet , \bullet ,\bullet }^{S,B};P)\geqslant 1$
. This is a contradiction.
$S(W_{\bullet , \bullet ,\bullet }^{S,B};P)\geqslant 1$
. This is a contradiction.
If Z is a curve, then S is smooth at P by Lemma 3.1 because P is a general point in Z. Hence, we conclude that
![]() $Z=P$
because S is singular at the point P by Lemma 3.3. Recall that Z is G-invariant. This implies that
$Z=P$
because S is singular at the point P by Lemma 3.3. Recall that Z is G-invariant. This implies that
![]() $\tau (P)\in R$
.
$\tau (P)\in R$
.
Let C be the fiber of
![]() $p_2$
that passes through P. Then C is smooth at P by Lemma 3.2 because S is singular at P. Since
$p_2$
that passes through P. Then C is smooth at P by Lemma 3.2 because S is singular at P. Since
![]() $\tau (P)\in R$
, we see that C is irreducible and smooth.
$\tau (P)\in R$
, we see that C is irreducible and smooth.
Let T be a sufficiently general surface in linear system
![]() $|p_2^*(\mathcal {O}_{\mathbb {P}^2}(1))|$
that contains C. Since C is smooth, it follows from Bertini’s theorem that the surface T is smooth.
$|p_2^*(\mathcal {O}_{\mathbb {P}^2}(1))|$
that contains C. Since C is smooth, it follows from Bertini’s theorem that the surface T is smooth.
As in the proof of Lemma 3.3, it follows from [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Theorem 1.112] that
 $$ \begin{align*}1\geqslant \frac{A_X(\mathbf{F})}{S_X(\mathbf{F})}\geqslant\min\left\{\frac{1}{S_X(T)},\frac{1}{S(W_{\bullet,\bullet}^T;C)},\frac{1}{S(W_{\bullet, \bullet,\bullet}^{T,C};P)}\right\}. \end{align*} $$
$$ \begin{align*}1\geqslant \frac{A_X(\mathbf{F})}{S_X(\mathbf{F})}\geqslant\min\left\{\frac{1}{S_X(T)},\frac{1}{S(W_{\bullet,\bullet}^T;C)},\frac{1}{S(W_{\bullet, \bullet,\bullet}^{T,C};P)}\right\}. \end{align*} $$
Moreover, it follows from [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Theorem 3.17] that
![]() $S_X(T)<1$
. Thus, we conclude that
$S_X(T)<1$
. Thus, we conclude that
In fact, since P is the center of the divisor
![]() $\mathbf {F}$
on X, [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Theorem 3.17] gives
$\mathbf {F}$
on X, [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Theorem 3.17] gives
Now, let us compute
![]() $S(W_{\bullet ,\bullet }^T;C)$
and
$S(W_{\bullet ,\bullet }^T;C)$
and
![]() $S(W_{\bullet , \bullet ,\bullet }^{T,C};P)$
using the results obtained in [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, § 1.7].
$S(W_{\bullet , \bullet ,\bullet }^{T,C};P)$
using the results obtained in [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, § 1.7].
Take
![]() $u\in \mathbb {R}_{\geqslant 0}$
and
$u\in \mathbb {R}_{\geqslant 0}$
and
![]() $v\in \mathbb {R}_{\geqslant 0}$
. Then
$v\in \mathbb {R}_{\geqslant 0}$
. Then
Similarly, if
![]() $u\in [0,1]$
, then
$u\in [0,1]$
, then
because
![]() $(-K_X-uT)\vert _{T}-vC\sim _{\mathbb {R}}S|_T+(1-u-v)C$
. So, using [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Corollary 1.109], we get
$(-K_X-uT)\vert _{T}-vC\sim _{\mathbb {R}}S|_T+(1-u-v)C$
. So, using [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Corollary 1.109], we get
 $$ \begin{align*}S(W_{\bullet,\bullet}^T;C)=\frac{3}{6}\int_0^1\int_0^{1-u}\big(S|_T+(1-u-v)C\big)^2dvdu=\frac{1}{2}\int_0^1\int_0^{1-u}4(1-u-v)dvdu=\frac{1}{3}<1. \end{align*} $$
$$ \begin{align*}S(W_{\bullet,\bullet}^T;C)=\frac{3}{6}\int_0^1\int_0^{1-u}\big(S|_T+(1-u-v)C\big)^2dvdu=\frac{1}{2}\int_0^1\int_0^{1-u}4(1-u-v)dvdu=\frac{1}{3}<1. \end{align*} $$
Hence, it follows from Equation (3.1) that
![]() $S(W_{\bullet ,\bullet ,\bullet }^{T,C},P)>1$
. Now, using [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Theorem 1.112], we get
$S(W_{\bullet ,\bullet ,\bullet }^{T,C},P)>1$
. Now, using [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Theorem 1.112], we get
 $$ \begin{align*}S(W_{\bullet,\bullet,\bullet}^{T,C},P)=\frac{3}{6}\int_0^1\int_0^{1-u}\Big(\big(S|_T+(1-u-v)C\big)\cdot C\Big)^2dvdu=\frac{3}{6}\int_0^1\int_0^{1-u}4\,dvdu=1, \end{align*} $$
$$ \begin{align*}S(W_{\bullet,\bullet,\bullet}^{T,C},P)=\frac{3}{6}\int_0^1\int_0^{1-u}\Big(\big(S|_T+(1-u-v)C\big)\cdot C\Big)^2dvdu=\frac{3}{6}\int_0^1\int_0^{1-u}4\,dvdu=1, \end{align*} $$
which is a contradiction. This shows that X is K-stable.
Corollary 3.4. All smooth Fano threefolds in the family ![]() are K-stable.
are K-stable.
4 Family  .
.
Let
![]() $\mathscr {S}$
and
$\mathscr {S}$
and
![]() $\mathscr {S}^\prime $
be smooth cubic surfaces in
$\mathscr {S}^\prime $
be smooth cubic surfaces in
![]() $\mathbb {P}^3$
such that their intersection is a smooth curve of genus
$\mathbb {P}^3$
such that their intersection is a smooth curve of genus
![]() $10$
. Set
$10$
. Set
![]() $\mathscr {C}=\mathscr {S}\cap \mathscr {S}^\prime $
, and let
$\mathscr {C}=\mathscr {S}\cap \mathscr {S}^\prime $
, and let
![]() $\pi \colon X\to \mathbb {P}^3$
be the blow up of the curve
$\pi \colon X\to \mathbb {P}^3$
be the blow up of the curve
![]() $\mathscr {C}$
. Then X is a smooth Fano threefold in the family
$\mathscr {C}$
. Then X is a smooth Fano threefold in the family ![]() , and every smooth Fano threefold in this family can be obtained in this way. Moreover, there exists a commutative diagram
, and every smooth Fano threefold in this family can be obtained in this way. Moreover, there exists a commutative diagram

where ![]() is a map that is given by the pencil generated by the surfaces
is a map that is given by the pencil generated by the surfaces
![]() $\mathscr {S}$
and
$\mathscr {S}$
and
![]() $\mathscr {S}^\prime $
, and
$\mathscr {S}^\prime $
, and
![]() $\phi $
is a fibration into cubic surfaces. Note that
$\phi $
is a fibration into cubic surfaces. Note that
![]() $-K_X^3=10$
and
$-K_X^3=10$
and
![]() $\mathrm {Aut}(X)$
is finite [Reference Cheltsov, Przyjalkowski and Shramov10].
$\mathrm {Aut}(X)$
is finite [Reference Cheltsov, Przyjalkowski and Shramov10].
Let
![]() $H=\pi ^*(\mathcal {O}_{\mathbb {P}^3}(1))$
, and let E be the
$H=\pi ^*(\mathcal {O}_{\mathbb {P}^3}(1))$
, and let E be the
![]() $\pi $
-exceptional surface. Then
$\pi $
-exceptional surface. Then
![]() $-K_X\sim 4H-E$
, the morphism
$-K_X\sim 4H-E$
, the morphism
![]() $\phi $
is given by the linear system
$\phi $
is given by the linear system
![]() $|3H-E|$
, and
$|3H-E|$
, and
![]() $E\cong \mathscr {S}\times \mathbb {P}^1$
.
$E\cong \mathscr {S}\times \mathbb {P}^1$
.
The goal of this section is to prove that X is K-stable. Suppose that X is not K-stable. Let us seek for a contradiction. First, using the valuative criterion for K-stability [Reference Fujita15, Reference Li18], we see that there exists a prime divisor
![]() $\mathbf {F}$
over X such that
$\mathbf {F}$
over X such that
Let Z be the center of the divisor
![]() $\mathbf {F}$
on X. Then Z is not a surface by [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Theorem 3.17]. Therefore, either Z is an irreducible curve or Z is a point. Fix a point
$\mathbf {F}$
on X. Then Z is not a surface by [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Theorem 3.17]. Therefore, either Z is an irreducible curve or Z is a point. Fix a point
![]() $P\in Z$
.
$P\in Z$
.
Let A be the surface in
![]() $|3H-E|$
that contains P. Fix
$|3H-E|$
that contains P. Fix
![]() $u\in \mathbb {R}_{\geqslant 0}$
. Let
$u\in \mathbb {R}_{\geqslant 0}$
. Let
![]() $\mathscr {P}(u)$
be the positive part of the Zariski decomposition of
$\mathscr {P}(u)$
be the positive part of the Zariski decomposition of
![]() $-K_X-uA$
, and let
$-K_X-uA$
, and let
![]() $\mathscr {N}(u)$
be its negative part. Then
$\mathscr {N}(u)$
be its negative part. Then
This implies that
![]() $-K_X-uA$
is pseudoeffective
$-K_X-uA$
is pseudoeffective
![]() $\iff u\leqslant \frac {4}{3}$
. Moreover, we have
$\iff u\leqslant \frac {4}{3}$
. Moreover, we have
 $$ \begin{align*}\mathscr{P}(u)=\left\{\begin{aligned} &(4-3u)H-(1-u)E\ \text{if }0\leqslant u\leqslant 1, \\ &(4-3u)H\ \text{if }1\leqslant v\leqslant \frac{4}{3}, \\ \end{aligned} \right. \end{align*} $$
$$ \begin{align*}\mathscr{P}(u)=\left\{\begin{aligned} &(4-3u)H-(1-u)E\ \text{if }0\leqslant u\leqslant 1, \\ &(4-3u)H\ \text{if }1\leqslant v\leqslant \frac{4}{3}, \\ \end{aligned} \right. \end{align*} $$
and
 $$ \begin{align*}\mathscr{N}(u)=\left\{\begin{aligned} &0\ \text{if }0\leqslant u\leqslant 1, \\ &(u-1)E\ \text{if }1\leqslant u\leqslant \frac{4}{3}. \\ \end{aligned} \right. \end{align*} $$
$$ \begin{align*}\mathscr{N}(u)=\left\{\begin{aligned} &0\ \text{if }0\leqslant u\leqslant 1, \\ &(u-1)E\ \text{if }1\leqslant u\leqslant \frac{4}{3}. \\ \end{aligned} \right. \end{align*} $$
Integrating, we obtain
![]() $S_X(A)=\frac {67}{120}<1$
, which also follows from [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Theorem 3.17].
$S_X(A)=\frac {67}{120}<1$
, which also follows from [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Theorem 3.17].
Note that
![]() $\pi (A)$
is a normal cubic surface in
$\pi (A)$
is a normal cubic surface in
![]() $\mathbb {P}^3$
, and
$\mathbb {P}^3$
, and
![]() $\pi (A)$
is smooth along the curve
$\pi (A)$
is smooth along the curve
![]() $\mathscr {C}$
. In particular, we see that
$\mathscr {C}$
. In particular, we see that
![]() $A\cong \pi (A)$
, and A is smooth along the intersection
$A\cong \pi (A)$
, and A is smooth along the intersection
![]() $E\cap A$
.
$E\cap A$
.
Lemma 4.1. The surface A is singular at the point P.
Proof. Suppose that A is smooth at P. Let C be a general curve in
![]() $|-K_A|$
that passes through the point P. Then C is a smooth irreducible elliptic curve. Take
$|-K_A|$
that passes through the point P. Then C is a smooth irreducible elliptic curve. Take
![]() $v\in \mathbb {R}_{\geqslant 0}$
. Then
$v\in \mathbb {R}_{\geqslant 0}$
. Then
 $$ \begin{align*}\mathscr{P}(u)\vert_{S}-vC\sim_{\mathbb{R}}\left\{\begin{aligned} &(1-v)C\ \text{if }0\leqslant u\leqslant 1, \\ &(4-3u-v)C\ \text{if }1\leqslant u\leqslant \frac{4}{3}. \end{aligned} \right. \end{align*} $$
$$ \begin{align*}\mathscr{P}(u)\vert_{S}-vC\sim_{\mathbb{R}}\left\{\begin{aligned} &(1-v)C\ \text{if }0\leqslant u\leqslant 1, \\ &(4-3u-v)C\ \text{if }1\leqslant u\leqslant \frac{4}{3}. \end{aligned} \right. \end{align*} $$
Therefore, using [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Corollary 1.109], we obtain
 $$ \begin{align*}S\big(W_{\bullet,\bullet}^A;C\big)=\frac{3}{10}\int_0^1\int_0^13(1-v)^2dvdu+\frac{3}{10}\int_1^{\frac{4}{3}}\int_0^{4-3u}3(4-3u-v)^2dvdu=\frac{13}{40}. \end{align*} $$
$$ \begin{align*}S\big(W_{\bullet,\bullet}^A;C\big)=\frac{3}{10}\int_0^1\int_0^13(1-v)^2dvdu+\frac{3}{10}\int_1^{\frac{4}{3}}\int_0^{4-3u}3(4-3u-v)^2dvdu=\frac{13}{40}. \end{align*} $$
Similarly, using [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Theorem 1.112], we obtain
 $$ \begin{align*} S\big(W_{\bullet,\bullet,\bullet}^{A,C};P\big)\leqslant \frac{3}{10}\int_0^1\int_0^1\big(3(1-v)\big)^2dvdu+\frac{3}{10}\int_1^{\frac{4}{3}}\int_0^{4-3u}\big(3(4-3u-v)\big)^2dvdu+\\ +\underbrace{\frac{6}{10}\int_1^{\frac{4}{3}}\int_0^{4-3u}3(4-3u-v)(u-1)dvdu}_{\text{if } P\in E}=\frac{39}{40}+\frac{1}{120}=\frac{59}{60}. \end{align*} $$
$$ \begin{align*} S\big(W_{\bullet,\bullet,\bullet}^{A,C};P\big)\leqslant \frac{3}{10}\int_0^1\int_0^1\big(3(1-v)\big)^2dvdu+\frac{3}{10}\int_1^{\frac{4}{3}}\int_0^{4-3u}\big(3(4-3u-v)\big)^2dvdu+\\ +\underbrace{\frac{6}{10}\int_1^{\frac{4}{3}}\int_0^{4-3u}3(4-3u-v)(u-1)dvdu}_{\text{if } P\in E}=\frac{39}{40}+\frac{1}{120}=\frac{59}{60}. \end{align*} $$
Therefore, it follows from [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Theorem 1.112] that
 $$ \begin{align*}1\geqslant \frac{A_X(\mathbf{F})}{S_X(\mathbf{F})}\geqslant\min\left\{\frac{1}{S_X(A)},\frac{1}{S(W_{\bullet,\bullet}^A;C)},\frac{1}{S(W_{\bullet, \bullet,\bullet}^{A,C};P)}\right\} \geqslant\min\left\{\frac{120}{67},\frac{40}{13},\frac{60}{59}\right\}>1, \end{align*} $$
$$ \begin{align*}1\geqslant \frac{A_X(\mathbf{F})}{S_X(\mathbf{F})}\geqslant\min\left\{\frac{1}{S_X(A)},\frac{1}{S(W_{\bullet,\bullet}^A;C)},\frac{1}{S(W_{\bullet, \bullet,\bullet}^{A,C};P)}\right\} \geqslant\min\left\{\frac{120}{67},\frac{40}{13},\frac{60}{59}\right\}>1, \end{align*} $$
which is absurd.
Corollary 4.2. The point P is not contained in the surface E.
Since
![]() $A\cong \pi (A)$
, we may consider A as a cubic surface in
$A\cong \pi (A)$
, we may consider A as a cubic surface in
![]() $\mathbb {P}^3$
. Then
$\mathbb {P}^3$
. Then
-
• either
 $\mathrm {mult}_P(A)=2$
and A has Du Val singularities.
$\mathrm {mult}_P(A)=2$
and A has Du Val singularities. -
• or
 $\mathrm {mult}_P(A)=3$
and A is a cone over a plane smooth cubic curve with vertex P.
$\mathrm {mult}_P(A)=3$
and A is a cone over a plane smooth cubic curve with vertex P.
Lemma 4.3. One has
![]() $\mathrm {mult}_P(A)\ne 3$
.
$\mathrm {mult}_P(A)\ne 3$
.
Proof. Let
![]() $\sigma \colon \widehat {X}\to X$
be a blow up of the point P, and let G be the
$\sigma \colon \widehat {X}\to X$
be a blow up of the point P, and let G be the
![]() $\sigma $
-exceptional surface. Denote by
$\sigma $
-exceptional surface. Denote by
![]() $\widehat {A}$
and
$\widehat {A}$
and
![]() $\widehat {E}$
the proper transforms on
$\widehat {E}$
the proper transforms on
![]() $\widehat {X}$
of the surfaces A and E, respectively. Suppose that
$\widehat {X}$
of the surfaces A and E, respectively. Suppose that
![]() $\mathrm {mult}_P(A)=3$
. Take
$\mathrm {mult}_P(A)=3$
. Take
![]() $u\in \mathbb {R}_{\geqslant 0}$
. Then
$u\in \mathbb {R}_{\geqslant 0}$
. Then
Thus, the divisor
![]() $\sigma ^*(-K_X)-vG$
is pseudoeffective
$\sigma ^*(-K_X)-vG$
is pseudoeffective
![]() $\iff u\in [0,4]$
. Moreover, if
$\iff u\in [0,4]$
. Moreover, if
![]() $u\in [0,4]$
, then the Zariski decomposition of the divisor
$u\in [0,4]$
, then the Zariski decomposition of the divisor
![]() $\sigma ^*(-K_X)-vG$
can be described as follows:
$\sigma ^*(-K_X)-vG$
can be described as follows:
 $$ \begin{align*}P(u)=\left\{\begin{aligned} &\frac{1}{3}\widehat{E}+\frac{4}{3}\widehat{A}+(4-u)G\ \text{if }0\leqslant u\leqslant 1, \\ &\frac{1}{3}\widehat{E}+\frac{5-u}{3}\widehat{A}+(4-u)G\ \text{if }1\leqslant u\leqslant 4, \\ \end{aligned} \right. \end{align*} $$
$$ \begin{align*}P(u)=\left\{\begin{aligned} &\frac{1}{3}\widehat{E}+\frac{4}{3}\widehat{A}+(4-u)G\ \text{if }0\leqslant u\leqslant 1, \\ &\frac{1}{3}\widehat{E}+\frac{5-u}{3}\widehat{A}+(4-u)G\ \text{if }1\leqslant u\leqslant 4, \\ \end{aligned} \right. \end{align*} $$
and
 $$ \begin{align*}N(u)=\left\{\begin{aligned} &0\ \text{if }0\leqslant u\leqslant 1, \\ &\frac{u-1}{3}\widehat{A}\ \text{if }1\leqslant u\leqslant 4, \\ \end{aligned} \right. \end{align*} $$
$$ \begin{align*}N(u)=\left\{\begin{aligned} &0\ \text{if }0\leqslant u\leqslant 1, \\ &\frac{u-1}{3}\widehat{A}\ \text{if }1\leqslant u\leqslant 4, \\ \end{aligned} \right. \end{align*} $$
where
![]() $P(u)$
and
$P(u)$
and
![]() $N(u)$
are the positive and the negative parts of the Zariski decomposition, respectively. Using this, we compute
$N(u)$
are the positive and the negative parts of the Zariski decomposition, respectively. Using this, we compute
 $$ \begin{align*}S_{X}(G)=\frac{3}{10}\int_{0}^{1}u^{3},du+\frac{3}{10}\int_{1}^{4}udu=\frac{93}{40}<3=A_{X}(G). \end{align*} $$
$$ \begin{align*}S_{X}(G)=\frac{3}{10}\int_{0}^{1}u^{3},du+\frac{3}{10}\int_{1}^{4}udu=\frac{93}{40}<3=A_{X}(G). \end{align*} $$
As in the proof of Lemma 2.10, let us use results from [Reference Fujita16, § 4] to get a contradiction. Namely, applying [Reference Fujita16, Corollary 4.18], we get
 $$ \begin{align*}1\geqslant \frac{A_X(\mathbf{F})}{S_X(\mathbf{F})}\geqslant\min\left\{\frac{A_{X}(G)}{S_{X}(G)}, \inf_{Q\in G}\delta_{Q}\big(G,V^G_{\bullet,\bullet}\big)\right\}= \min\left\{\frac{40}{31},\inf_{Q\in G}\delta_{Q}\big(G,V^G_{\bullet,\bullet}\big)\right\}, \end{align*} $$
$$ \begin{align*}1\geqslant \frac{A_X(\mathbf{F})}{S_X(\mathbf{F})}\geqslant\min\left\{\frac{A_{X}(G)}{S_{X}(G)}, \inf_{Q\in G}\delta_{Q}\big(G,V^G_{\bullet,\bullet}\big)\right\}= \min\left\{\frac{40}{31},\inf_{Q\in G}\delta_{Q}\big(G,V^G_{\bullet,\bullet}\big)\right\}, \end{align*} $$
where
![]() $\delta _{Q}(G,V^G_{\bullet ,\bullet })$
is defined in [Reference Fujita16, § 4]. So, there is
$\delta _{Q}(G,V^G_{\bullet ,\bullet })$
is defined in [Reference Fujita16, § 4]. So, there is
![]() $Q\in G$
such that
$Q\in G$
such that
![]() $\delta _{Q}(G,V^G_{\bullet ,\bullet })<\frac {40}{31}$
.
$\delta _{Q}(G,V^G_{\bullet ,\bullet })<\frac {40}{31}$
.
Let
![]() $\ell $
is a general line in
$\ell $
is a general line in
![]() $G\cong \mathbb {P}^2$
that contains Q. Then [Reference Fujita16, Corollary 4.18] gives
$G\cong \mathbb {P}^2$
that contains Q. Then [Reference Fujita16, Corollary 4.18] gives
 $$ \begin{align*}\delta_{Q}\big(G,V^G_{\bullet,\bullet}\big) \geqslant\min\left\{\frac{1}{S\big(V^F_{\bullet,\bullet};\ell\big)},\frac{1}{S\big(W^{G,\ell}_{\bullet,\bullet,\bullet};Q\big)}\right\}. \end{align*} $$
$$ \begin{align*}\delta_{Q}\big(G,V^G_{\bullet,\bullet}\big) \geqslant\min\left\{\frac{1}{S\big(V^F_{\bullet,\bullet};\ell\big)},\frac{1}{S\big(W^{G,\ell}_{\bullet,\bullet,\bullet};Q\big)}\right\}. \end{align*} $$
Let us compute
![]() $S(V^G_{\bullet ,\bullet };\ell )$
and
$S(V^G_{\bullet ,\bullet };\ell )$
and
![]() $S(W^{G,\ell }_{\bullet ,\bullet ,\bullet };Q)$
. Take
$S(W^{G,\ell }_{\bullet ,\bullet ,\bullet };Q)$
. Take
![]() $v\in \mathbb {R}_{\geqslant 0}$
. Then
$v\in \mathbb {R}_{\geqslant 0}$
. Then
 $$ \begin{align*}P(u)\big\vert_{G}-v\ell\sim_{\mathbb{R}}\left\{\begin{aligned} &(u-v)\ell\ \text{if }0\leqslant u\leqslant 1, \\ &(1-v)\ell\ \text{if }1\leqslant u\leqslant 4. \end{aligned} \right. \end{align*} $$
$$ \begin{align*}P(u)\big\vert_{G}-v\ell\sim_{\mathbb{R}}\left\{\begin{aligned} &(u-v)\ell\ \text{if }0\leqslant u\leqslant 1, \\ &(1-v)\ell\ \text{if }1\leqslant u\leqslant 4. \end{aligned} \right. \end{align*} $$
Let
![]() $\widehat {\mathscr {C}}=\widehat {A}\vert _{G}$
. Then
$\widehat {\mathscr {C}}=\widehat {A}\vert _{G}$
. Then
![]() $\widehat {\mathscr {C}}$
is a smooth cubic curve in
$\widehat {\mathscr {C}}$
is a smooth cubic curve in
![]() $G\cong \mathbb {P}^2$
. Let
$G\cong \mathbb {P}^2$
. Let
 $$ \begin{align*}N^\prime(u)=N(u)\big\vert_{G}=\left\{\begin{aligned} &0\ \text{if }0\leqslant u\leqslant 1, \\ &\frac{u-1}{3}\widehat{\mathscr{C}}\ \text{if }1\leqslant u\leqslant 4. \end{aligned} \right. \end{align*} $$
$$ \begin{align*}N^\prime(u)=N(u)\big\vert_{G}=\left\{\begin{aligned} &0\ \text{if }0\leqslant u\leqslant 1, \\ &\frac{u-1}{3}\widehat{\mathscr{C}}\ \text{if }1\leqslant u\leqslant 4. \end{aligned} \right. \end{align*} $$
Now, using [Reference Fujita16, Theorem 4.8], we get
 $$ \begin{align*} S\big(W^{G}_{\bullet,\bullet};\ell\big)&=\frac{3}{10}\int_0^4\int_0^\infty \mathrm{vol}\big(P(u)\big\vert_{G}-v\ell\big)dvdu=\\ &=\frac{3}{10}\int_{0}^{1}\int_{0}^{u}(u-v)^{2}dvdu+\frac{3}{10}\int_{1}^{4}\int_{0}^{1}(1-v)^{2}dvdu=\frac{13}{40}. \end{align*} $$
$$ \begin{align*} S\big(W^{G}_{\bullet,\bullet};\ell\big)&=\frac{3}{10}\int_0^4\int_0^\infty \mathrm{vol}\big(P(u)\big\vert_{G}-v\ell\big)dvdu=\\ &=\frac{3}{10}\int_{0}^{1}\int_{0}^{u}(u-v)^{2}dvdu+\frac{3}{10}\int_{1}^{4}\int_{0}^{1}(1-v)^{2}dvdu=\frac{13}{40}. \end{align*} $$
Similarly, it follows from [Reference Fujita16, Theorem 4.17] that
![]() $S(W_{\bullet ,\bullet ,\bullet }^{G,\ell };Q)$
can be computes as follows:
$S(W_{\bullet ,\bullet ,\bullet }^{G,\ell };Q)$
can be computes as follows:
 $$ \begin{align*} &\frac{3}{10}\int_{0}^{1}\int_{0}^{u}\Big(\big(P(u)\big\vert_{G}-v\ell\big)\cdot\ell\Big)^2dvdu+\frac{3}{10}\int_{1}^{4}\int_{0}^{1}\Big(\big(P(u)\big\vert_{G}-v\ell\big)\cdot\ell\Big)^2dvdu+F_Q=\\ &\quad=\frac{3}{12}\int_{0}^{1}\int_{0}^{u}(u-v)^{2}dvdu+\frac{3}{10}\int_{1}^{4}\int_{0}^{1}(1-v)^{2}dvdu+F_Q=\frac{13}{40}+F_Q, \end{align*} $$
$$ \begin{align*} &\frac{3}{10}\int_{0}^{1}\int_{0}^{u}\Big(\big(P(u)\big\vert_{G}-v\ell\big)\cdot\ell\Big)^2dvdu+\frac{3}{10}\int_{1}^{4}\int_{0}^{1}\Big(\big(P(u)\big\vert_{G}-v\ell\big)\cdot\ell\Big)^2dvdu+F_Q=\\ &\quad=\frac{3}{12}\int_{0}^{1}\int_{0}^{u}(u-v)^{2}dvdu+\frac{3}{10}\int_{1}^{4}\int_{0}^{1}(1-v)^{2}dvdu+F_Q=\frac{13}{40}+F_Q, \end{align*} $$
where
![]() $F_Q=0$
if
$F_Q=0$
if
![]() $Q\not \in \widehat {A}\vert _{G}$
, and
$Q\not \in \widehat {A}\vert _{G}$
, and
 $$ \begin{align*}F_Q=\frac{6}{10} \int_{1}^{4} \int_{0}^{1}\frac{(1-v)(u-1)}{3}dvdu=\frac{9}{20} \end{align*} $$
$$ \begin{align*}F_Q=\frac{6}{10} \int_{1}^{4} \int_{0}^{1}\frac{(1-v)(u-1)}{3}dvdu=\frac{9}{20} \end{align*} $$
otherwise. This gives
![]() $S(W_{\bullet ,\bullet ,\bullet }^{G,\ell };Q)\leqslant \frac {31}{40}$
. Combining the estimates, we get
$S(W_{\bullet ,\bullet ,\bullet }^{G,\ell };Q)\leqslant \frac {31}{40}$
. Combining the estimates, we get
![]() $\delta _{Q}(G,V^G_{\bullet ,\bullet })\geqslant \frac {40}{31}$
, which is a contradiction. This completes the proof of the lemma.
$\delta _{Q}(G,V^G_{\bullet ,\bullet })\geqslant \frac {40}{31}$
, which is a contradiction. This completes the proof of the lemma.
Hence, we see that the surface A has Du Val singularities. Let S be a general surface in the linear system
![]() $|H|$
that contains P. Then S is smooth, and
$|H|$
that contains P. Then S is smooth, and
![]() $-K_X-uS\sim _{\mathbb {R}} (4-u)H-E$
. Hence, the divisor
$-K_X-uS\sim _{\mathbb {R}} (4-u)H-E$
. Hence, the divisor
![]() $-K_X-uS$
is pseudoeffective
$-K_X-uS$
is pseudoeffective
![]() $\iff $
it is nef
$\iff $
it is nef
![]() $\iff u\leqslant 1$
. Then
$\iff u\leqslant 1$
. Then
 $$ \begin{align*}S_X(S)=\frac{3}{10}\int_{0}^{1}(-K_X-uS)^3du=\frac{3}{10}\int_{0}^{1}u(1-u)(7-u)du=\frac{13}{40}<1. \end{align*} $$
$$ \begin{align*}S_X(S)=\frac{3}{10}\int_{0}^{1}(-K_X-uS)^3du=\frac{3}{10}\int_{0}^{1}u(1-u)(7-u)du=\frac{13}{40}<1. \end{align*} $$
Let
![]() $C=A\vert _{S}$
. Then C is a reduced curve in
$C=A\vert _{S}$
. Then C is a reduced curve in
![]() $|-K_S|$
that is singular at P, and
$|-K_S|$
that is singular at P, and
![]() $C\cong \pi (C)$
. Moreover, the curve
$C\cong \pi (C)$
. Moreover, the curve
![]() $\pi (C)$
is a general hyperplane section of the cubic surface
$\pi (C)$
is a general hyperplane section of the cubic surface
![]() $\pi (A)\subset \mathbb {P}^3$
that passes through the point
$\pi (A)\subset \mathbb {P}^3$
that passes through the point
![]() $\pi (P)$
. Therefore, since
$\pi (P)$
. Therefore, since
![]() $\pi (A)$
is not a cone by Lemma 4.3, we conclude that the curve C is irreducible. Hence, one of the following two cases holds:
$\pi (A)$
is not a cone by Lemma 4.3, we conclude that the curve C is irreducible. Hence, one of the following two cases holds:
-
(1) the curve C has an ordinary node at P,
-
(2) the curve C has an ordinary cusp at P.
Let
![]() $\Pi =\pi (S)$
. Then
$\Pi =\pi (S)$
. Then
![]() $\Pi $
is a plane in
$\Pi $
is a plane in
![]() $\mathbb {P}^3$
such that
$\mathbb {P}^3$
such that
![]() $\pi (P)\in \Pi $
and
$\pi (P)\in \Pi $
and
![]() $\Pi \cap \pi (A)=\pi (C)$
, and the morphism
$\Pi \cap \pi (A)=\pi (C)$
, and the morphism
![]() $\pi \vert _{S}\colon S\to \Pi $
is a composition of blow ups of
$\pi \vert _{S}\colon S\to \Pi $
is a composition of blow ups of
![]() $9$
intersection points
$9$
intersection points
![]() $\Pi \cap \mathscr {C}$
, which we denote by
$\Pi \cap \mathscr {C}$
, which we denote by
![]() $O_1,\ldots ,O_9$
. Note that
$O_1,\ldots ,O_9$
. Note that
![]() $\pi (C)$
is a reduced plane cubic curve that passes through these nine points, and
$\pi (C)$
is a reduced plane cubic curve that passes through these nine points, and
![]() $\pi (C)$
is smooth away from
$\pi (C)$
is smooth away from
![]() $\pi (P)$
.
$\pi (P)$
.
Lemma 4.4. The curve C cannot have an ordinary double point at the point P.
Proof. For each
![]() $i\in \{1,\ldots ,9\}$
, let
$i\in \{1,\ldots ,9\}$
, let
![]() $L_i$
be the proper transform on S of the line in
$L_i$
be the proper transform on S of the line in
![]() $\Pi $
that passes through P and
$\Pi $
that passes through P and
![]() $O_i$
. Then
$O_i$
. Then
![]() $L_i\ne L_j$
for
$L_i\ne L_j$
for
![]() $i\ne j$
since
$i\ne j$
since
![]() $\pi (C)$
is irreducible. We have
$\pi (C)$
is irreducible. We have
 $$ \begin{align*}(-K_X-uS)\big\vert_{S}\sim_{\mathbb{R}}\frac{1-u}{6}\sum_{i=1}^9L_i. \end{align*} $$
$$ \begin{align*}(-K_X-uS)\big\vert_{S}\sim_{\mathbb{R}}\frac{1-u}{6}\sum_{i=1}^9L_i. \end{align*} $$
Let
![]() $\sigma \colon \widehat {S}\to S$
be the blow up of S at the point P, let
$\sigma \colon \widehat {S}\to S$
be the blow up of S at the point P, let
![]() $\mathbf {f}$
be the
$\mathbf {f}$
be the
![]() $\sigma $
-exceptional curve and let
$\sigma $
-exceptional curve and let
![]() $\widehat {C},\widehat {L}_1,\ldots ,\widehat {L}_{9}$
be the proper transforms on
$\widehat {C},\widehat {L}_1,\ldots ,\widehat {L}_{9}$
be the proper transforms on
![]() $\widehat {S}$
of the curves
$\widehat {S}$
of the curves
![]() $C,L_1,\ldots ,L_9$
, respectively. Then
$C,L_1,\ldots ,L_9$
, respectively. Then
![]() $\widehat {L}_1,\ldots ,\widehat {L}_{9}$
are disjoint. On the surface
$\widehat {L}_1,\ldots ,\widehat {L}_{9}$
are disjoint. On the surface
![]() $\widehat {S}$
, we have
$\widehat {S}$
, we have
and
![]() $\widehat {C}\cdot \widehat {L}_1=\cdots =\widehat {C}\cdot \widehat {L}_9=0$
.
$\widehat {C}\cdot \widehat {L}_1=\cdots =\widehat {C}\cdot \widehat {L}_9=0$
.
Fix
![]() $u\in [0,1]$
. Let v be a nonnegative real number. Then
$u\in [0,1]$
. Let v be a nonnegative real number. Then
 $$ \begin{align} \sigma^*\big((-K_X-uS)\big\vert_S\big)-v\mathbf{f}\sim_{\mathbb{R}}\frac{5+u}{6}\widehat{C}+\frac{1-u}{6}\sum_i^9\widehat{L}_i+\frac{19-7u-6v}{6}\mathbf{f}. \end{align} $$
$$ \begin{align} \sigma^*\big((-K_X-uS)\big\vert_S\big)-v\mathbf{f}\sim_{\mathbb{R}}\frac{5+u}{6}\widehat{C}+\frac{1-u}{6}\sum_i^9\widehat{L}_i+\frac{19-7u-6v}{6}\mathbf{f}. \end{align} $$
So, the divisor
![]() $\sigma ^*((-K_X-uS)|_S)-v\mathbf {f}$
is pseudoeffective
$\sigma ^*((-K_X-uS)|_S)-v\mathbf {f}$
is pseudoeffective
![]() $\iff $
it is nef
$\iff $
it is nef
![]() $\iff v\leqslant \frac {19-7u}{6}$
. Let
$\iff v\leqslant \frac {19-7u}{6}$
. Let
![]() $P(u,v)$
and
$P(u,v)$
and
![]() $N(u,v)$
be the positive and the negative parts of its Zariski decomposition. Then, using Equation (4.1), we compute
$N(u,v)$
be the positive and the negative parts of its Zariski decomposition. Then, using Equation (4.1), we compute
 $$ \begin{align*}P(u,v)=\left\{\begin{aligned} &\frac{5+u}{6}\widehat{C}+\frac{1-u}{6}\sum_i^9\widehat{L}_i+\frac{19-7u-6v}{6}\mathbf{f}\ \text{if }0\leqslant v\leqslant \frac{3-3u}{2}, \\ &\frac{19-7u-6v}{12}\widehat{C}+\frac{1-u}{6}\sum_i^9\widehat{L}_i+\frac{19-7u-6v}{6}\mathbf{f}\ \text{if }\frac{3-3u}{2}\leqslant v\leqslant 3-u, \\ &\frac{19-7u-6v}{12}\big(\widehat{C}+2\sum_i^9\widehat{L}_i+2\mathbf{f}\big)\ \text{if }3-u\leqslant v\leqslant \frac{19-7u}{6}, \end{aligned} \right. \end{align*} $$
$$ \begin{align*}P(u,v)=\left\{\begin{aligned} &\frac{5+u}{6}\widehat{C}+\frac{1-u}{6}\sum_i^9\widehat{L}_i+\frac{19-7u-6v}{6}\mathbf{f}\ \text{if }0\leqslant v\leqslant \frac{3-3u}{2}, \\ &\frac{19-7u-6v}{12}\widehat{C}+\frac{1-u}{6}\sum_i^9\widehat{L}_i+\frac{19-7u-6v}{6}\mathbf{f}\ \text{if }\frac{3-3u}{2}\leqslant v\leqslant 3-u, \\ &\frac{19-7u-6v}{12}\big(\widehat{C}+2\sum_i^9\widehat{L}_i+2\mathbf{f}\big)\ \text{if }3-u\leqslant v\leqslant \frac{19-7u}{6}, \end{aligned} \right. \end{align*} $$
 $$ \begin{align*}N(u,v)=\left\{\begin{aligned} &0\ \text{if }0\leqslant v\leqslant \frac{3-3u}{2}, \\ &\frac{-3+3u+2v}{4}\widehat{C}\ \text{if }\frac{3-3u}{2}\leqslant v\leqslant 3-u, \\ &\frac{2v+3u-3}{4}\widehat{C}+(v+u-3)\sum_i^9\widehat{L}_i\ \text{if }3-u\leqslant v\leqslant \frac{19-7u}{6}, \end{aligned} \right. \end{align*} $$
$$ \begin{align*}N(u,v)=\left\{\begin{aligned} &0\ \text{if }0\leqslant v\leqslant \frac{3-3u}{2}, \\ &\frac{-3+3u+2v}{4}\widehat{C}\ \text{if }\frac{3-3u}{2}\leqslant v\leqslant 3-u, \\ &\frac{2v+3u-3}{4}\widehat{C}+(v+u-3)\sum_i^9\widehat{L}_i\ \text{if }3-u\leqslant v\leqslant \frac{19-7u}{6}, \end{aligned} \right. \end{align*} $$
 $$ \begin{align*}\mathrm{vol}\Big(\sigma^*\big((-K_X-uS)\big|_S\big)-v\mathbf{f}\Big)=\left\{\begin{aligned} &(1-u)(7-u)-v^2\ \text{if }0\leqslant v\leqslant \frac{3-3u}{2}, \\ &\frac{(1-u)(37-13u-12v)}{4}\ \text{if }\frac{3-3u}{2}\leqslant v\leqslant 3-u, \\ &\frac{(19-7u-6v)^2}{4}\ \text{if }3-u\leqslant v\leqslant \frac{19-7u}{6}, \end{aligned} \right. \end{align*} $$
$$ \begin{align*}\mathrm{vol}\Big(\sigma^*\big((-K_X-uS)\big|_S\big)-v\mathbf{f}\Big)=\left\{\begin{aligned} &(1-u)(7-u)-v^2\ \text{if }0\leqslant v\leqslant \frac{3-3u}{2}, \\ &\frac{(1-u)(37-13u-12v)}{4}\ \text{if }\frac{3-3u}{2}\leqslant v\leqslant 3-u, \\ &\frac{(19-7u-6v)^2}{4}\ \text{if }3-u\leqslant v\leqslant \frac{19-7u}{6}, \end{aligned} \right. \end{align*} $$
 $$ \begin{align*}P(u,v)\cdot\mathbf{f}=\left\{\begin{aligned} &v \ \text{if }0\leqslant v\leqslant \frac{3-3u}{2}, \\ &\frac{3(1-u)}{2} \ \text{if }\frac{3-3u}{2}\leqslant v\leqslant 3-u, \\ &\frac{3(19-7u-6v)}{2}\ \text{if }3-u\leqslant v\leqslant \frac{19-7u}{6}. \end{aligned} \right. \end{align*} $$
$$ \begin{align*}P(u,v)\cdot\mathbf{f}=\left\{\begin{aligned} &v \ \text{if }0\leqslant v\leqslant \frac{3-3u}{2}, \\ &\frac{3(1-u)}{2} \ \text{if }\frac{3-3u}{2}\leqslant v\leqslant 3-u, \\ &\frac{3(19-7u-6v)}{2}\ \text{if }3-u\leqslant v\leqslant \frac{19-7u}{6}. \end{aligned} \right. \end{align*} $$
Indeed, the divisor
![]() $P(u,v)$
above is effective, and it has a nonnegative intersection with every irreducible component of
$P(u,v)$
above is effective, and it has a nonnegative intersection with every irreducible component of
![]() $\operatorname {Supp}\left (P(u,v)\right )$
, which implies that it is nef in every case. Now, using [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Corollary 1.109], we get
$\operatorname {Supp}\left (P(u,v)\right )$
, which implies that it is nef in every case. Now, using [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Corollary 1.109], we get
 $$ \begin{align*} S\big(W_{\bullet,\bullet}^{\widehat{S}};\mathbf{f}\big)&= \frac{3}{10}\int_0^1\int_{0}^{\frac{19-7u}{6}}\mathrm{vol}\Big(\sigma^*\big((-K_X-uS)\big|_S\big)-v\mathbf{f}\Big)dudv=\\ &=\frac{3}{10}\int_0^1\int_0^{\frac{3-3u}{2}}\big((1-u)(7-u)-v^2\big)dv+\frac{3}{10}\int_0^1\int_{\frac{3-3u}{2}}^{3-u}\frac{(1-u)(37-13u-12v)}{4}dv+\\ &\quad+\frac{3}{10}\int_0^1\int_{3-u}^{\frac{19-7u}{6}}\frac{(19-7u-6v)^2}{4}dvdu=\frac{767}{480}<2=A_S(\mathbf{f}). \end{align*} $$
$$ \begin{align*} S\big(W_{\bullet,\bullet}^{\widehat{S}};\mathbf{f}\big)&= \frac{3}{10}\int_0^1\int_{0}^{\frac{19-7u}{6}}\mathrm{vol}\Big(\sigma^*\big((-K_X-uS)\big|_S\big)-v\mathbf{f}\Big)dudv=\\ &=\frac{3}{10}\int_0^1\int_0^{\frac{3-3u}{2}}\big((1-u)(7-u)-v^2\big)dv+\frac{3}{10}\int_0^1\int_{\frac{3-3u}{2}}^{3-u}\frac{(1-u)(37-13u-12v)}{4}dv+\\ &\quad+\frac{3}{10}\int_0^1\int_{3-u}^{\frac{19-7u}{6}}\frac{(19-7u-6v)^2}{4}dvdu=\frac{767}{480}<2=A_S(\mathbf{f}). \end{align*} $$
Moreover, if Q is a point in
![]() $\mathbf {f}$
, then [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Remark 1.113] gives
$\mathbf {f}$
, then [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Remark 1.113] gives
 $$ \begin{align*} &S\big(W_{\bullet,\bullet,\bullet}^{\widehat{S},\mathbf{f}};Q\big)= F_{Q}+\frac{3}{10}\int_{0}^{1}\int_{0}^{\frac{19-7u}{6}}\big(P(u,v)\cdot\mathbf{f}\big)^2dvdu=F_Q+\frac{3}{10}\int_0^1\int_0^{\frac{3-3u}{2}}v^2dv+\\ &\quad+\frac{3}{10}\int_0^1\int_{\frac{3-3u}{2}}^{3-u}\Bigg(\frac{3(1-u)}{2}\Bigg)^2dv+\frac{3}{10}\int_0^1\int_{3-u}^{\frac{19-7u}{6}}\Bigg(\frac{3(19-7u-6v)}{2}\Bigg)^2dvdu=F_Q+\frac{147}{320}, \end{align*} $$
$$ \begin{align*} &S\big(W_{\bullet,\bullet,\bullet}^{\widehat{S},\mathbf{f}};Q\big)= F_{Q}+\frac{3}{10}\int_{0}^{1}\int_{0}^{\frac{19-7u}{6}}\big(P(u,v)\cdot\mathbf{f}\big)^2dvdu=F_Q+\frac{3}{10}\int_0^1\int_0^{\frac{3-3u}{2}}v^2dv+\\ &\quad+\frac{3}{10}\int_0^1\int_{\frac{3-3u}{2}}^{3-u}\Bigg(\frac{3(1-u)}{2}\Bigg)^2dv+\frac{3}{10}\int_0^1\int_{3-u}^{\frac{19-7u}{6}}\Bigg(\frac{3(19-7u-6v)}{2}\Bigg)^2dvdu=F_Q+\frac{147}{320}, \end{align*} $$
where
 $$ \begin{align*}F_Q=\frac{6}{10}\int_{0}^{1}\int_{0}^{\frac{19-7u}{6}}\big(P(u,v)\cdot\mathbf{f}\big)\mathrm{ord}_Q\Big(N(u,v)\big\vert_{\mathbf{f}}\Big)dvdu, \end{align*} $$
$$ \begin{align*}F_Q=\frac{6}{10}\int_{0}^{1}\int_{0}^{\frac{19-7u}{6}}\big(P(u,v)\cdot\mathbf{f}\big)\mathrm{ord}_Q\Big(N(u,v)\big\vert_{\mathbf{f}}\Big)dvdu, \end{align*} $$
which implies the following assertions:
-
• if
 $Q\not \in \widehat {C}\cup \widehat {L}_1\cup \cdots \cup \widehat {L}_{9}$
, then
$Q\not \in \widehat {C}\cup \widehat {L}_1\cup \cdots \cup \widehat {L}_{9}$
, then
 $F_Q=0$
;
$F_Q=0$
; -
• if
 $Q\in \widehat {L}_1\cup \cdots \cup \widehat {L}_{9}$
, then
$Q\in \widehat {L}_1\cup \cdots \cup \widehat {L}_{9}$
, then  $$ \begin{align*}F_Q=\frac{6}{10}\int_0^1\int_{3-u}^{\frac{19-7u}{6}}\frac{3(19-7u-6v)(v+u-3)}{2}dvdu=\frac{1}{960}; \end{align*} $$
$$ \begin{align*}F_Q=\frac{6}{10}\int_0^1\int_{3-u}^{\frac{19-7u}{6}}\frac{3(19-7u-6v)(v+u-3)}{2}dvdu=\frac{1}{960}; \end{align*} $$
-
• if
 $Q\in \widehat {C}$
and
$Q\in \widehat {C}$
and
 $\widehat {C}$
intersects
$\widehat {C}$
intersects
 $\mathbf {f}$
transversally at P, then
$\mathbf {f}$
transversally at P, then  $$ \begin{align*} F_Q=&\frac{6}{10}\int_0^1\int_{\frac{3-3u}{2}}^{3-u}\frac{3(1-u)(2v+3u-3)}{8}dvdu+\\ &\frac{6}{10}\int_0^1\int_{3-u}^{\frac{19-7u}{6}}\frac{3(19-7u-6v)(2v+3u-3)}{8}dvdu=\frac{643}{1920};\quad \quad \quad \quad \quad \end{align*} $$
$$ \begin{align*} F_Q=&\frac{6}{10}\int_0^1\int_{\frac{3-3u}{2}}^{3-u}\frac{3(1-u)(2v+3u-3)}{8}dvdu+\\ &\frac{6}{10}\int_0^1\int_{3-u}^{\frac{19-7u}{6}}\frac{3(19-7u-6v)(2v+3u-3)}{8}dvdu=\frac{643}{1920};\quad \quad \quad \quad \quad \end{align*} $$
-
• if
 $Q\in \widehat {C}$
and
$Q\in \widehat {C}$
and
 $\widehat {C}$
is tangent to
$\widehat {C}$
is tangent to
 $\mathbf {f}$
at the point P, then
$\mathbf {f}$
at the point P, then
 $F_Q=\frac {643}{960}$
.
$F_Q=\frac {643}{960}$
.
Thus, if C has a node at P, then
![]() $S(W_{\bullet ,\bullet ,\bullet }^{\widehat {S},\mathbf {f}};Q)\leqslant \frac {305}{384}$
, so [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Remark 1.113] gives
$S(W_{\bullet ,\bullet ,\bullet }^{\widehat {S},\mathbf {f}};Q)\leqslant \frac {305}{384}$
, so [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Remark 1.113] gives
 $$ \begin{align*}1\geqslant \frac{A_X(\mathbf{F})}{S_X(\mathbf{F})}\geqslant\min\left\{\inf_{Q\in\mathbf{f}}\frac{1}{S(W_{\bullet,\bullet,\bullet}^{\widehat{S},\mathbf{f}};Q)}, \frac{2}{S(V_{\bullet,\bullet}^{S};\mathbf{f})},\frac{1}{S_X(S)}\right\} \geqslant\min\left\{\frac{384}{305},\frac{960}{767},\frac{40}{13}\right\}=\frac{960}{767}>1, \end{align*} $$
$$ \begin{align*}1\geqslant \frac{A_X(\mathbf{F})}{S_X(\mathbf{F})}\geqslant\min\left\{\inf_{Q\in\mathbf{f}}\frac{1}{S(W_{\bullet,\bullet,\bullet}^{\widehat{S},\mathbf{f}};Q)}, \frac{2}{S(V_{\bullet,\bullet}^{S};\mathbf{f})},\frac{1}{S_X(S)}\right\} \geqslant\min\left\{\frac{384}{305},\frac{960}{767},\frac{40}{13}\right\}=\frac{960}{767}>1, \end{align*} $$
which is a contradiction.
Lemma 4.5. The curve C cannot have an ordinary cusp at the point P.
Proof. Suppose C has a cusp. Let L be an irreducible curve in S such that
![]() $\pi (L)$
is a line and
$\pi (L)$
is a line and
![]() $\pi (L)\cap \pi (C)=\pi (P)$
. Then
$\pi (L)\cap \pi (C)=\pi (P)$
. Then
![]() $(-K_X-uS)\vert _{S}\sim _{\mathbb {R}}(1-u)L+C$
.
$(-K_X-uS)\vert _{S}\sim _{\mathbb {R}}(1-u)L+C$
.
Now, we consider the following commutative diagram:

where
![]() $\sigma _1$
is the blow up of P,
$\sigma _1$
is the blow up of P,
![]() $\sigma _2$
is the blow up of the point in the
$\sigma _2$
is the blow up of the point in the
![]() $\sigma _1$
-exceptional curve contained in the proper transform of C,
$\sigma _1$
-exceptional curve contained in the proper transform of C,
![]() $\sigma _3$
is the blow up of the point in the
$\sigma _3$
is the blow up of the point in the
![]() $\sigma _2$
-exceptional curve contained in the proper transform of C,
$\sigma _2$
-exceptional curve contained in the proper transform of C,
![]() $\upsilon $
is the birational contraction of the proper transforms of
$\upsilon $
is the birational contraction of the proper transforms of
![]() $\sigma _1\circ \sigma _2$
-exceptional curves and
$\sigma _1\circ \sigma _2$
-exceptional curves and
![]() $\sigma $
is the birational contraction of the proper transform of the
$\sigma $
is the birational contraction of the proper transform of the
![]() $\sigma _3$
-exceptional curve. Then
$\sigma _3$
-exceptional curve. Then
![]() $\widehat {S}$
has two singular points:
$\widehat {S}$
has two singular points:
-
(1) a cyclic quotient singularity of type
 $\frac {1}{2}(1,1)$
, which we denote by
$\frac {1}{2}(1,1)$
, which we denote by
 $Q_2$
;
$Q_2$
; -
(2) a cyclic quotient singularity of type
 $\frac {1}{3}(1,1)$
, which we denote by
$\frac {1}{3}(1,1)$
, which we denote by
 $Q_3$
.
$Q_3$
.
Let
![]() $\mathbf {f}$
be the
$\mathbf {f}$
be the
![]() $\sigma $
-exceptional curve, let
$\sigma $
-exceptional curve, let
![]() $\widehat {C}$
be the proper transform on
$\widehat {C}$
be the proper transform on
![]() $\widehat {S}$
of the curve C and let
$\widehat {S}$
of the curve C and let
![]() $\widehat {L}$
be the proper transform of the curve L. Then the curves
$\widehat {L}$
be the proper transform of the curve L. Then the curves
![]() $\mathbf {f}$
,
$\mathbf {f}$
,
![]() $\widehat {C}$
,
$\widehat {C}$
,
![]() $\widehat {L}$
are smooth. Moreover, it is not very difficult to check that
$\widehat {L}$
are smooth. Moreover, it is not very difficult to check that
![]() $Q_2\in \mathbf {f}\ni Q_3$
,
$Q_2\in \mathbf {f}\ni Q_3$
,
![]() $Q_2\not \in \widehat {C}\not \ni Q_3$
,
$Q_2\not \in \widehat {C}\not \ni Q_3$
,
![]() $Q_2\in \widehat {L}\not \ni Q_3$
. Further, we have
$Q_2\in \widehat {L}\not \ni Q_3$
. Further, we have
![]() $A_S(\mathbf {f})=5$
,
$A_S(\mathbf {f})=5$
,
![]() $\sigma ^*(C)\sim \widehat {C}+6\mathbf {f}$
,
$\sigma ^*(C)\sim \widehat {C}+6\mathbf {f}$
,
![]() $\sigma ^*(L)\sim \widehat {L}+3\mathbf {f}$
. On the surface
$\sigma ^*(L)\sim \widehat {L}+3\mathbf {f}$
. On the surface
![]() $\widehat {S}$
, we have
$\widehat {S}$
, we have
Note that
![]() $Q_2=\mathbf {f}\cap \widehat {L}$
, and
$Q_2=\mathbf {f}\cap \widehat {L}$
, and
![]() $\widehat {C}$
intersects
$\widehat {C}$
intersects
![]() $\mathbf {f}$
transversally by one point.
$\mathbf {f}$
transversally by one point.
Fix
![]() $u\in [0,1]$
. Let v be a nonnegative real number. Then
$u\in [0,1]$
. Let v be a nonnegative real number. Then
Thus, the divisor
![]() $\sigma ^*((-K_X-uS)|_S)-v\mathbf {f}$
is pseudoeffective
$\sigma ^*((-K_X-uS)|_S)-v\mathbf {f}$
is pseudoeffective
![]() $\iff $
it is nef
$\iff $
it is nef
![]() $\iff v\leqslant 9-3u$
. Let
$\iff v\leqslant 9-3u$
. Let
![]() $P(u,v)$
be the positive part of the Zariski decomposition of
$P(u,v)$
be the positive part of the Zariski decomposition of
![]() $\sigma ^*((-K_X-uS)|_S)-v\mathbf {f}$
, and let
$\sigma ^*((-K_X-uS)|_S)-v\mathbf {f}$
, and let
![]() $N(u,v)$
be the negative part. Then, using Equation (4.2), we compute
$N(u,v)$
be the negative part. Then, using Equation (4.2), we compute
 $$ \begin{align*}P(u,v)=\left\{\begin{aligned} &(1-u)\widehat{L}+\widehat{C}+(9-3u-v)\mathbf{f}\ \text{if }0\leqslant v\leqslant 3-3u, \\ &(1-u)\widehat{L}+\frac{9-3u-v}{6}\widehat{C}+(9-3u-v)\mathbf{f}\ \text{if }3-3u\leqslant v\leqslant 8-2u, \\ &\frac{9-3u-v}{6}\big(6\widehat{L}+\widehat{C}+6\mathbf{f}\big)\ \text{if }8-2u\leqslant v\leqslant 9-3u, \end{aligned} \right. \end{align*} $$
$$ \begin{align*}P(u,v)=\left\{\begin{aligned} &(1-u)\widehat{L}+\widehat{C}+(9-3u-v)\mathbf{f}\ \text{if }0\leqslant v\leqslant 3-3u, \\ &(1-u)\widehat{L}+\frac{9-3u-v}{6}\widehat{C}+(9-3u-v)\mathbf{f}\ \text{if }3-3u\leqslant v\leqslant 8-2u, \\ &\frac{9-3u-v}{6}\big(6\widehat{L}+\widehat{C}+6\mathbf{f}\big)\ \text{if }8-2u\leqslant v\leqslant 9-3u, \end{aligned} \right. \end{align*} $$
and
 $$ \begin{align*}N(u,v)=\left\{\begin{aligned} &0\ \text{if }0\leqslant v\leqslant 3-3u, \\ &\frac{v+3u-3}{6}\widehat{C}\ \text{if }3-3u\leqslant v\leqslant 8-2u, \\ &\frac{v+3u-3}{6}\widehat{C}+(v+2u-8)\widehat{L}\ \text{if }8-2u\leqslant v\leqslant 9-3u. \end{aligned} \right. \end{align*} $$
$$ \begin{align*}N(u,v)=\left\{\begin{aligned} &0\ \text{if }0\leqslant v\leqslant 3-3u, \\ &\frac{v+3u-3}{6}\widehat{C}\ \text{if }3-3u\leqslant v\leqslant 8-2u, \\ &\frac{v+3u-3}{6}\widehat{C}+(v+2u-8)\widehat{L}\ \text{if }8-2u\leqslant v\leqslant 9-3u. \end{aligned} \right. \end{align*} $$
This gives
 $$ \begin{align*}\mathrm{vol}\Big(\sigma^*\big((-K_X-uS)\big|_S\big)-v\mathbf{f}\Big)=\left\{\begin{aligned} &(1-u)(7-u)-\frac{v^2}{6}\ \text{if }0\leqslant v\leqslant 3-3u, \\ &\frac{(1-u)(17-5u-2v)}{2}\ \text{if }3-3u\leqslant v\leqslant 8-2u, \\ &\frac{(9-3u-v)^2}{2}\ \text{if }8-2u\leqslant v\leqslant 9-3u, \end{aligned} \right. \end{align*} $$
$$ \begin{align*}\mathrm{vol}\Big(\sigma^*\big((-K_X-uS)\big|_S\big)-v\mathbf{f}\Big)=\left\{\begin{aligned} &(1-u)(7-u)-\frac{v^2}{6}\ \text{if }0\leqslant v\leqslant 3-3u, \\ &\frac{(1-u)(17-5u-2v)}{2}\ \text{if }3-3u\leqslant v\leqslant 8-2u, \\ &\frac{(9-3u-v)^2}{2}\ \text{if }8-2u\leqslant v\leqslant 9-3u, \end{aligned} \right. \end{align*} $$
and
 $$ \begin{align*}P(u,v)\cdot\mathbf{f}=\left\{\begin{aligned} &\frac{v}{6}\ \text{if }0\leqslant v\leqslant 3-3u, \\ &\frac{1-u}{2}\ \text{if }3-3u\leqslant v\leqslant 8-2u, \\ &\frac{9-3u-v}{2}\ \text{if }8-2u\leqslant v\leqslant 9-3u. \end{aligned} \right. \end{align*} $$
$$ \begin{align*}P(u,v)\cdot\mathbf{f}=\left\{\begin{aligned} &\frac{v}{6}\ \text{if }0\leqslant v\leqslant 3-3u, \\ &\frac{1-u}{2}\ \text{if }3-3u\leqslant v\leqslant 8-2u, \\ &\frac{9-3u-v}{2}\ \text{if }8-2u\leqslant v\leqslant 9-3u. \end{aligned} \right. \end{align*} $$
Now, we use [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Corollary 1.109] to get
 $$ \begin{align*} S\big(W_{\bullet,\bullet}^{\widehat{S}};\mathbf{f}\big)&=\frac{3}{10}\int_0^1\int_0^{3-3u}\Big((1-u)(7-u)-\frac{v^2}{6}\Big)dv+\\ &\quad+\frac{3}{10}\int_0^1\int_{3-3u}^{8-2u}\frac{(1-u)(17-5u-2v)}{2}dv+\frac{3}{10}\int_0^1\int_{8-2u}^{9-3u}\frac{(9-3u-v)^2}{2}dvdu=\frac{173}{40}. \end{align*} $$
$$ \begin{align*} S\big(W_{\bullet,\bullet}^{\widehat{S}};\mathbf{f}\big)&=\frac{3}{10}\int_0^1\int_0^{3-3u}\Big((1-u)(7-u)-\frac{v^2}{6}\Big)dv+\\ &\quad+\frac{3}{10}\int_0^1\int_{3-3u}^{8-2u}\frac{(1-u)(17-5u-2v)}{2}dv+\frac{3}{10}\int_0^1\int_{8-2u}^{9-3u}\frac{(9-3u-v)^2}{2}dvdu=\frac{173}{40}. \end{align*} $$
Similarly, if Q is a point in
![]() $\mathbf {f}$
, then [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Remark 1.113] gives
$\mathbf {f}$
, then [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Remark 1.113] gives
 $$ \begin{align*} S\big(W_{\bullet,\bullet,\bullet}^{\widehat{S},\mathbf{f}};Q\big)&=F_{Q}+\frac{3}{10}\int_{0}^{1}\int_{0}^{9-3u}\big(P(u,v)\cdot\mathbf{f}\big)^2dvdu=\\ &=F_Q+\frac{3}{10}\int_0^1\int_0^{3-3u}\Big(\frac{v}{6}\Big)^2dvdu+\frac{3}{10}\int_0^1\int_{3-3u}^{8-2u}\Big(\frac{1-u}{2}\Big)^2dvdu+\\ &\quad+\frac{3}{10}\int_0^1\int_{8-2u}^{9-3u}\Big(\frac{9-3u-v}{2}\Big)^2dvdu=F_Q+\frac{5}{32}, \end{align*} $$
$$ \begin{align*} S\big(W_{\bullet,\bullet,\bullet}^{\widehat{S},\mathbf{f}};Q\big)&=F_{Q}+\frac{3}{10}\int_{0}^{1}\int_{0}^{9-3u}\big(P(u,v)\cdot\mathbf{f}\big)^2dvdu=\\ &=F_Q+\frac{3}{10}\int_0^1\int_0^{3-3u}\Big(\frac{v}{6}\Big)^2dvdu+\frac{3}{10}\int_0^1\int_{3-3u}^{8-2u}\Big(\frac{1-u}{2}\Big)^2dvdu+\\ &\quad+\frac{3}{10}\int_0^1\int_{8-2u}^{9-3u}\Big(\frac{9-3u-v}{2}\Big)^2dvdu=F_Q+\frac{5}{32}, \end{align*} $$
where
![]() $F_Q$
can be computes as follows:
$F_Q$
can be computes as follows:
-
• if
 $Q\ne \widehat {C}\cap \mathbf {f}$
and
$Q\ne \widehat {C}\cap \mathbf {f}$
and
 $Q\ne \widehat {L}\cap \mathbf {f}$
, then
$Q\ne \widehat {L}\cap \mathbf {f}$
, then
 $F_Q=0$
;
$F_Q=0$
; -
• if
 $Q=\widehat {L}\cap \mathbf {f}$
, then
$Q=\widehat {L}\cap \mathbf {f}$
, then  $$ \begin{align*}F_Q=\frac{6}{10}\int_0^1\int_{8-2u}^{9-3u}\frac{(9-3u-v)(v+2u-8)}{2}dvdu=\frac{1}{80}; \end{align*} $$
$$ \begin{align*}F_Q=\frac{6}{10}\int_0^1\int_{8-2u}^{9-3u}\frac{(9-3u-v)(v+2u-8)}{2}dvdu=\frac{1}{80}; \end{align*} $$
-
• if
 $Q=\widehat {C}\cap \mathbf {f}$
, then
$Q=\widehat {C}\cap \mathbf {f}$
, then  $$ \begin{align*} F_Q=&\frac{6}{10}\int_0^1\int_{3-3u}^{8-2u}\frac{(1-u)(v+3u-3)}{12}dv+\\ &+\frac{6}{10}\int_0^1\int_{8-2u}^{9-3u}\frac{(9-3u-v)(v+3u-3)}{12}dudv=\frac{193}{480}. \end{align*} $$
$$ \begin{align*} F_Q=&\frac{6}{10}\int_0^1\int_{3-3u}^{8-2u}\frac{(1-u)(v+3u-3)}{12}dv+\\ &+\frac{6}{10}\int_0^1\int_{8-2u}^{9-3u}\frac{(9-3u-v)(v+3u-3)}{12}dudv=\frac{193}{480}. \end{align*} $$
Therefore, we conclude that
 $$ \begin{align*}S\big(W_{\bullet,\bullet,\bullet}^{\widehat{S},\mathbf{f}};Q\big)= \left\{\begin{aligned} &\frac{5}{32}\ \text{if }Q\not\in\widehat{C}\cup\widehat{L}, \\[5pt] &\frac{27}{80} \ \text{if }Q=\widehat{L}\cap\mathbf{f}, \\[5pt] &\frac{67}{120}\ \text{if }Q=\widehat{C}\cap\mathbf{f}. \end{aligned} \right. \end{align*} $$
$$ \begin{align*}S\big(W_{\bullet,\bullet,\bullet}^{\widehat{S},\mathbf{f}};Q\big)= \left\{\begin{aligned} &\frac{5}{32}\ \text{if }Q\not\in\widehat{C}\cup\widehat{L}, \\[5pt] &\frac{27}{80} \ \text{if }Q=\widehat{L}\cap\mathbf{f}, \\[5pt] &\frac{67}{120}\ \text{if }Q=\widehat{C}\cap\mathbf{f}. \end{aligned} \right. \end{align*} $$
Let
![]() $\Delta _{\mathbf {f}}=\frac {1}{2}Q_2+\frac {2}{3}Q_3$
. Then, using [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Remark 1.113] and our computations, we get
$\Delta _{\mathbf {f}}=\frac {1}{2}Q_2+\frac {2}{3}Q_3$
. Then, using [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Remark 1.113] and our computations, we get
 $$ \begin{align*}1\geqslant \frac{A_X(\mathbf{F})}{S_X(\mathbf{F})}\geqslant\min\left\{\inf_{Q\in\mathbf{f}}\frac{1-\mathrm{ord}_Q\big(\Delta_{\mathbf{f}}\big)}{S(W_{\bullet,\bullet,\bullet}^{\widehat{S},\mathbf{f}};Q)}, \frac{5}{S(V_{\bullet,\bullet}^{S};\mathbf{f})},\frac{1}{S_X(S)}\right\} \geqslant \min \left\{\frac{40}{13}, \frac{200}{173}, \frac{120}{67}\right\}=\frac{200}{173}>1, \end{align*} $$
$$ \begin{align*}1\geqslant \frac{A_X(\mathbf{F})}{S_X(\mathbf{F})}\geqslant\min\left\{\inf_{Q\in\mathbf{f}}\frac{1-\mathrm{ord}_Q\big(\Delta_{\mathbf{f}}\big)}{S(W_{\bullet,\bullet,\bullet}^{\widehat{S},\mathbf{f}};Q)}, \frac{5}{S(V_{\bullet,\bullet}^{S};\mathbf{f})},\frac{1}{S_X(S)}\right\} \geqslant \min \left\{\frac{40}{13}, \frac{200}{173}, \frac{120}{67}\right\}=\frac{200}{173}>1, \end{align*} $$
which is a contradiction.
Combining Lemmas 4.4 and 4.5, we obtain a contradiction.
Corollary 4.6. All smooth Fano threefolds in the family ![]() are K-stable.
are K-stable.
5 Family  (Verra threefolds)
(Verra threefolds)
Smooth Fano threefolds in the family ![]() can be described as follows:
can be described as follows:
-
(a) smooth divisors of degree
 $(2,2)$
in
$(2,2)$
in
 $\mathbb {P}^2\times \mathbb {P}^2$
, which are known as Verra threefolds,
$\mathbb {P}^2\times \mathbb {P}^2$
, which are known as Verra threefolds, -
(b) double covers of the (unique) smooth divisor in
 $\mathbb {P}^2\times \mathbb {P}^2$
of degree
$\mathbb {P}^2\times \mathbb {P}^2$
of degree
 $(1,1)$
branched over smooth anticanonical K3 surfaces.
$(1,1)$
branched over smooth anticanonical K3 surfaces.
Note that every double cover of a smooth divisor in
![]() $\mathbb {P}^2\times \mathbb {P}^2$
of degree
$\mathbb {P}^2\times \mathbb {P}^2$
of degree
![]() $(1,1)$
branched over a smooth anticanonical surface is K-stable [Reference Dervan14, Example 4.4]. In fact, this also implies that general Verra threefold is K-stable [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Example 3.14].
$(1,1)$
branched over a smooth anticanonical surface is K-stable [Reference Dervan14, Example 4.4]. In fact, this also implies that general Verra threefold is K-stable [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Example 3.14].
The goal of this section is to prove that all smooth Verra threefolds are K-stable.
Let X be a smooth divisor of degree
![]() $(2,2)$
in
$(2,2)$
in
![]() $\mathbb {P}^2\times \mathbb {P}^2$
, let
$\mathbb {P}^2\times \mathbb {P}^2$
, let
![]() $\pi _1\colon X\to \mathbb {P}^2$
be the projection to the first factor of
$\pi _1\colon X\to \mathbb {P}^2$
be the projection to the first factor of
![]() $\mathbb {P}^2\times \mathbb {P}^2$
, and let
$\mathbb {P}^2\times \mathbb {P}^2$
, and let
![]() $\pi _2\colon X\to \mathbb {P}^2$
be the projection to the second factor. Then
$\pi _2\colon X\to \mathbb {P}^2$
be the projection to the second factor. Then
![]() $\pi _1$
and
$\pi _1$
and
![]() $\pi _2$
are conic bundles [Reference Prokhorov21]. Set
$\pi _2$
are conic bundles [Reference Prokhorov21]. Set
![]() $H_1=\pi _1^*(\mathcal {O}_{\mathbb {P}^2}(1))$
and
$H_1=\pi _1^*(\mathcal {O}_{\mathbb {P}^2}(1))$
and
![]() $H_2=\pi _2^*(\mathcal {O}_{\mathbb {P}^2}(1))$
. Then
$H_2=\pi _2^*(\mathcal {O}_{\mathbb {P}^2}(1))$
. Then
and the group
![]() $\mathrm {Pic}(X)$
is generated by
$\mathrm {Pic}(X)$
is generated by
![]() $H_1$
and
$H_1$
and
![]() $H_2$
. Note that
$H_2$
. Note that
![]() $\mathrm {Aut}(X)$
is finite [Reference Cheltsov, Przyjalkowski and Shramov10]. Thus, the threefold X is K-stable
$\mathrm {Aut}(X)$
is finite [Reference Cheltsov, Przyjalkowski and Shramov10]. Thus, the threefold X is K-stable
![]() $\iff $
it is K-polystable. See [Reference Xu22] for details.
$\iff $
it is K-polystable. See [Reference Xu22] for details.
Lemma 5.1. Fix a point
![]() $P\in X$
. Let
$P\in X$
. Let
![]() $C_1$
be the fiber of the conic bundle
$C_1$
be the fiber of the conic bundle
![]() $\pi _1$
that contains P, and let
$\pi _1$
that contains P, and let
![]() $C_2$
be the fiber of
$C_2$
be the fiber of
![]() $\pi _2$
that contains P. Then
$\pi _2$
that contains P. Then
![]() $C_1$
or
$C_1$
or
![]() $C_2$
is smooth at P.
$C_2$
is smooth at P.
Proof. Local computations.
Let
![]() $\Delta _1$
and
$\Delta _1$
and
![]() $\Delta _2$
be the discriminant curves of the conic bundles
$\Delta _2$
be the discriminant curves of the conic bundles
![]() $\pi _1$
and
$\pi _1$
and
![]() $\pi _2$
, respectively. Then
$\pi _2$
, respectively. Then
![]() $\Delta _1$
and
$\Delta _1$
and
![]() $\Delta _2$
are reduced curves of degree
$\Delta _2$
are reduced curves of degree
![]() $6$
that have at most ordinary double points as singularities. For basic properties of the discriminant curves
$6$
that have at most ordinary double points as singularities. For basic properties of the discriminant curves
![]() $\Delta _1$
and
$\Delta _1$
and
![]() $\Delta _2$
, see [Reference Prokhorov21, § 3.8]. In particular, we know that no line in
$\Delta _2$
, see [Reference Prokhorov21, § 3.8]. In particular, we know that no line in
![]() $\mathbb {P}^2$
can be an irreducible component of these curves.
$\mathbb {P}^2$
can be an irreducible component of these curves.
Lemma 5.2. Fix a point
![]() $P\in X$
. Let
$P\in X$
. Let
![]() $C_2$
be the fiber of the conic bundle
$C_2$
be the fiber of the conic bundle
![]() $\pi _2$
that contains P, let S be a general surface in
$\pi _2$
that contains P, let S be a general surface in
![]() $|H_2|$
that contains
$|H_2|$
that contains
![]() $C_2$
. Then one of the following cases holds:
$C_2$
. Then one of the following cases holds:
-
(1)
 $C_2$
is smooth, S is smooth, the divisor
$C_2$
is smooth, S is smooth, the divisor
 $-K_S$
is ample;
$-K_S$
is ample; -
(2)
 $C_2$
is smooth, S is smooth, the divisor
$C_2$
is smooth, S is smooth, the divisor
 $-K_S$
is nef, the surface S has exactly four irreducible curves that have trivial intersection with the divisor
$-K_S$
is nef, the surface S has exactly four irreducible curves that have trivial intersection with the divisor
 $-K_S$
, these curves are disjoint and none of them passes through P, and
$-K_S$
, these curves are disjoint and none of them passes through P, and
 $C_2\subset \mathrm {Sing}(\pi _1^{-1}(\Delta _1))$
;
$C_2\subset \mathrm {Sing}(\pi _1^{-1}(\Delta _1))$
; -
(3)
 $C_2$
is singular and reduced, S is smooth, the divisor
$C_2$
is singular and reduced, S is smooth, the divisor
 $-K_S$
is ample;
$-K_S$
is ample; -
(4)
 $C_2$
is not reduced,
$C_2$
is not reduced,
 $P\not \in \mathrm {Sing}(S)\subset \mathrm {Supp}(C_2)$
, and
$P\not \in \mathrm {Sing}(S)\subset \mathrm {Supp}(C_2)$
, and
 $\mathrm {Sing}(S)$
consists of two points, which are ordinary double points of the surface S, and
$\mathrm {Sing}(S)$
consists of two points, which are ordinary double points of the surface S, and
 $-K_S$
is ample.
$-K_S$
is ample.
Proof. The assertion about the singularities of the surface S are local and well known.
We have
![]() $-K_S\sim H_1\vert _S$
and
$-K_S\sim H_1\vert _S$
and
![]() $K_S^2=2$
, so S is a weak del Pezzo surface of degree
$K_S^2=2$
, so S is a weak del Pezzo surface of degree
![]() $2$
, and the restriction
$2$
, and the restriction
![]() $\pi _1\vert _{S}\colon S\to \mathbb {P}^2$
is the anticanonical morphism. Let
$\pi _1\vert _{S}\colon S\to \mathbb {P}^2$
is the anticanonical morphism. Let
![]() $\ell $
be an irreducible curve in the surface S such that
$\ell $
be an irreducible curve in the surface S such that
Then
![]() $\ell $
is an irreducible component of the fiber
$\ell $
is an irreducible component of the fiber
![]() $\pi _1^{-1}(\pi _1(\ell ))$
. But
$\pi _1^{-1}(\pi _1(\ell ))$
. But
![]() $\pi _2(\ell )$
is the line
$\pi _2(\ell )$
is the line
![]() $\pi _2(S)$
, which implies that the scheme fiber
$\pi _2(S)$
, which implies that the scheme fiber
![]() $\pi _1^{-1}(\pi _1(\ell ))$
is singular, which implies that
$\pi _1^{-1}(\pi _1(\ell ))$
is singular, which implies that
![]() $\pi _1(\ell )\in \Delta _1$
. Since
$\pi _1(\ell )\in \Delta _1$
. Since
![]() $\ell \cap C_2\ne \varnothing $
and
$\ell \cap C_2\ne \varnothing $
and
![]() $\pi _2(S)$
is a general line in
$\pi _2(S)$
is a general line in
![]() $\mathbb {P}^2$
that passes through the point
$\mathbb {P}^2$
that passes through the point
![]() $\pi _2(P)$
, we see that
$\pi _2(P)$
, we see that
![]() $\pi _1(C_2)\subset \Delta _1$
. This implies that
$\pi _1(C_2)\subset \Delta _1$
. This implies that
![]() $C_2$
is irreducible and reduced.
$C_2$
is irreducible and reduced.
Let
![]() $R=\pi _1^{-1}(\pi _1(C_2))$
. Then the surface R is singular along a curve that is isomorphic to the conic
$R=\pi _1^{-1}(\pi _1(C_2))$
. Then the surface R is singular along a curve that is isomorphic to the conic
![]() $\pi _1(C_2)\cong C_2$
. Let
$\pi _1(C_2)\cong C_2$
. Let
![]() $f\colon \widetilde {R}\to R$
be the blow up of this curve. Then
$f\colon \widetilde {R}\to R$
be the blow up of this curve. Then
![]() $\widetilde {R}$
is smooth, and the composition morphism
$\widetilde {R}$
is smooth, and the composition morphism
![]() $\pi _1\circ f$
induces a
$\pi _1\circ f$
induces a
![]() $\mathbb {P}^1$
-bundle
$\mathbb {P}^1$
-bundle
![]() $\widetilde {R}\to \widetilde {C}_2$
, where
$\widetilde {R}\to \widetilde {C}_2$
, where
![]() $\widetilde {C}_2$
is double cover of the conic
$\widetilde {C}_2$
is double cover of the conic
![]() $\pi _1(C_2)$
that is branched over the eight points
$\pi _1(C_2)$
that is branched over the eight points
![]() $\pi _1(C_2)\cap (\Delta _1-\pi _1(C_2))$
. In particular, we see that
$\pi _1(C_2)\cap (\Delta _1-\pi _1(C_2))$
. In particular, we see that
![]() $\widetilde {C}_2$
is an irrational curve, which implies that
$\widetilde {C}_2$
is an irrational curve, which implies that
![]() $C_2=\mathrm {Sing}(R)$
.
$C_2=\mathrm {Sing}(R)$
.
Vice versa, if the fiber
![]() $C_2$
is a smooth conic, and the conic
$C_2$
is a smooth conic, and the conic
![]() $\pi _1(C_2)$
is an irreducible component of the discriminant curve
$\pi _1(C_2)$
is an irreducible component of the discriminant curve
![]() $\Delta _1$
, then it follows from the Bertini theorem that
$\Delta _1$
, then it follows from the Bertini theorem that
where
![]() $\ell _1,\ell _2,\ldots ,\ell _k$
are k distinct irreducible reduced curves in X that are irreducible components of the fibers of the natural projection
$\ell _1,\ell _2,\ldots ,\ell _k$
are k distinct irreducible reduced curves in X that are irreducible components of the fibers of the natural projection
![]() $\pi _1^{-1}(\pi _1(C_2))\to \pi _1(C_2)$
. Since
$\pi _1^{-1}(\pi _1(C_2))\to \pi _1(C_2)$
. Since
 $$ \begin{align*}4=2H_2^2\cdot H_1=H_2\cdot S\cdot\pi_1^{-1}(\pi_1(C_2))=H_2\cdot\Big(2C_2+\sum_{i=1}^k\ell_i\Big)=k, \end{align*} $$
$$ \begin{align*}4=2H_2^2\cdot H_1=H_2\cdot S\cdot\pi_1^{-1}(\pi_1(C_2))=H_2\cdot\Big(2C_2+\sum_{i=1}^k\ell_i\Big)=k, \end{align*} $$
we see that S contains exactly
![]() $4$
irreducible curves that intersects trivially with
$4$
irreducible curves that intersects trivially with
![]() $-K_S$
. Now, the generality in the choice of S implies that none of these curves contains P.
$-K_S$
. Now, the generality in the choice of S implies that none of these curves contains P.
Example 5.3. Actually, the case (2) in Lemma 5.2 can happen. Indeed, in the assumption and notations of Lemma 5.2, let
![]() $P=([0:0:1],[0:0:1])$
, and suppose that X is given by
$P=([0:0:1],[0:0:1])$
, and suppose that X is given by
where
![]() $([u:v:w],[x:y:z])$
are coordinates on
$([u:v:w],[x:y:z])$
are coordinates on
![]() $\mathbb {P}^2\times \mathbb {P}^2$
. Then the threefold X is smooth. For instance, this can be checked using the following Magma script:
$\mathbb {P}^2\times \mathbb {P}^2$
. Then the threefold X is smooth. For instance, this can be checked using the following Magma script:

Observe that the fiber
![]() $C_1$
is a singular reduced curve given by
$C_1$
is a singular reduced curve given by
![]() $u=v=2x^2-xy+y^2=0$
, the fiber
$u=v=2x^2-xy+y^2=0$
, the fiber
![]() $C_2$
is a smooth curve that is given by
$C_2$
is a smooth curve that is given by
![]() $x=y=uw+v^2=0$
, and the discriminant curve
$x=y=uw+v^2=0$
, and the discriminant curve
![]() $\Delta _1$
is a union of the conic
$\Delta _1$
is a union of the conic
![]() $\pi _1(C_2)$
and the irreducible quartic plane curve given by
$\pi _1(C_2)$
and the irreducible quartic plane curve given by
 $$ \begin{align*} 8u^3v-4u^3w-11u^2v^2+16u^2vw-12u^2w^2+8uv^3-\\ -28uv^2w+14uvw^2-16uw^3-12v^4-28v^2w^2-7w^4=0. \end{align*} $$
$$ \begin{align*} 8u^3v-4u^3w-11u^2v^2+16u^2vw-12u^2w^2+8uv^3-\\ -28uv^2w+14uvw^2-16uw^3-12v^4-28v^2w^2-7w^4=0. \end{align*} $$
As in case (2) in Lemma 5.2, we have
![]() $C_2=\mathrm {Sing}(\pi _1^{-1}(\pi _1(C_2)))$
.
$C_2=\mathrm {Sing}(\pi _1^{-1}(\pi _1(C_2)))$
.
Let us prove that X is K-stable. Suppose it is not. Using the valuative criterion [Reference Fujita15, Reference Li18], we see that there exists a prime divisor
![]() $\mathbf {F}$
over X such that
$\mathbf {F}$
over X such that
Let Z be the center of the divisor
![]() $\mathbf {F}$
on X. Then Z is not a surface by [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Theorem 3.17].
$\mathbf {F}$
on X. Then Z is not a surface by [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Theorem 3.17].
Let P be any point in Z, let
![]() $C_1$
be the fiber of the conic bundle
$C_1$
be the fiber of the conic bundle
![]() $\pi _1$
that contains P and let
$\pi _1$
that contains P and let
![]() $C_2$
be the fiber of the conic bundle
$C_2$
be the fiber of the conic bundle
![]() $\pi _2$
that contains P. By Lemma 5.1, at least one curve among
$\pi _2$
that contains P. By Lemma 5.1, at least one curve among
![]() $C_1$
or
$C_1$
or
![]() $C_2$
is smooth at P. We may assume that
$C_2$
is smooth at P. We may assume that
![]() $C_2$
is smooth at P.
$C_2$
is smooth at P.
Let S be a general surface in
![]() $|H_2|$
that contains
$|H_2|$
that contains
![]() $C_2$
. Then S is smooth by Lemma 5.2. Moreover, one of the following three cases holds:
$C_2$
. Then S is smooth by Lemma 5.2. Moreover, one of the following three cases holds:
-
(1)
 $C_2$
is smooth, the divisor
$C_2$
is smooth, the divisor
 $-K_S$
is ample;
$-K_S$
is ample; -
(2)
 $C_2$
is smooth,
$C_2$
is smooth,
 $\pi _1(C_2)\subset \Delta _1$
, the divisor
$\pi _1(C_2)\subset \Delta _1$
, the divisor
 $-K_S$
is nef, the surface S has exactly four irreducible curves that have trivial intersection with the divisor
$-K_S$
is nef, the surface S has exactly four irreducible curves that have trivial intersection with the divisor
 $-K_S$
, these curves are disjoint and none of them passes through P;
$-K_S$
, these curves are disjoint and none of them passes through P; -
(3)
 $C_2$
is singular and reduced, the divisor
$C_2$
is singular and reduced, the divisor
 $-K_S$
is ample.
$-K_S$
is ample.
Let C be the curve in X that is defined as follows:
-
• if
 $C_2$
is smooth and irreducible, we let
$C_2$
is smooth and irreducible, we let
 $C=C_2$
.
$C=C_2$
. -
• if
 $C_2$
is reducible, we let C be its irreducible component that contains P.
$C_2$
is reducible, we let C be its irreducible component that contains P.
Note that
![]() $-K_S\sim H_1\vert _{S}$
and
$-K_S\sim H_1\vert _{S}$
and
![]() $K_S^2=2$
. Let
$K_S^2=2$
. Let
![]() $\eta \colon S\to \mathbb {P}^2$
be the restriction morphism
$\eta \colon S\to \mathbb {P}^2$
be the restriction morphism
![]() $\pi _1\vert _{S}$
. Then
$\pi _1\vert _{S}$
. Then
![]() $\eta $
is an anticanonical morphism of the surface S, which is generically two-to-one. Hence, the morphism
$\eta $
is an anticanonical morphism of the surface S, which is generically two-to-one. Hence, the morphism
![]() $\eta $
induces an involution
$\eta $
induces an involution
![]() $\tau \in \mathrm {Aut}(S)$
. We let
$\tau \in \mathrm {Aut}(S)$
. We let
![]() $C^\prime =\tau (C)$
.
$C^\prime =\tau (C)$
.
Now, let u be a nonnegative real number. Then we have
![]() $-K_X-uS\sim _{\mathbb {R}} H_1+(1-u)H_2$
, so
$-K_X-uS\sim _{\mathbb {R}} H_1+(1-u)H_2$
, so
![]() $-K_X-uS$
is nef
$-K_X-uS$
is nef
![]() $\iff -K_X-uS$
is pseudoeffective
$\iff -K_X-uS$
is pseudoeffective
![]() $\iff u\leqslant 1$
. Then
$\iff u\leqslant 1$
. Then
![]() $S_X(S)=\frac {5}{12}$
. Now, let us use notations introduced in [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, § 1.7]. Using [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Theorem 1.112], we get
$S_X(S)=\frac {5}{12}$
. Now, let us use notations introduced in [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, § 1.7]. Using [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Theorem 1.112], we get
 $$ \begin{align*}1\geqslant \frac{A_X(\mathbf{F})}{S_X(\mathbf{F})}\geqslant \min\left\{\frac{1}{S_X(S)},\frac{1}{S(W_{\bullet,\bullet}^S;C)},\frac{1}{S(W_{\bullet, \bullet,\bullet}^{S,C};P)}\right\}, \end{align*} $$
$$ \begin{align*}1\geqslant \frac{A_X(\mathbf{F})}{S_X(\mathbf{F})}\geqslant \min\left\{\frac{1}{S_X(S)},\frac{1}{S(W_{\bullet,\bullet}^S;C)},\frac{1}{S(W_{\bullet, \bullet,\bullet}^{S,C};P)}\right\}, \end{align*} $$
where
![]() $S(W_{\bullet ,\bullet }^S;C)$
and
$S(W_{\bullet ,\bullet }^S;C)$
and
![]() $S(W_{\bullet , \bullet ,\bullet }^{S,C};P)$
are defined in [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, § 1.7]. Hence, since
$S(W_{\bullet , \bullet ,\bullet }^{S,C};P)$
are defined in [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, § 1.7]. Hence, since
![]() $S_X(S)<1$
, we get
$S_X(S)<1$
, we get
Moreover, if
![]() $Z=P$
, then it also follows from [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Theorem 1.112] that
$Z=P$
, then it also follows from [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Theorem 1.112] that
Let us estimate
![]() $S(W_{\bullet ,\bullet }^S;C)$
and
$S(W_{\bullet ,\bullet }^S;C)$
and
![]() $S(W_{\bullet , \bullet ,\bullet }^{S,C};P)$
using results obtained in [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, § 1.7].
$S(W_{\bullet , \bullet ,\bullet }^{S,C};P)$
using results obtained in [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, § 1.7].
Let
![]() $P(u)=-K_X-uS$
. Then [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Corollary 1.109] gives
$P(u)=-K_X-uS$
. Then [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Corollary 1.109] gives
 $$ \begin{align*}S\big(W^S_{\bullet,\bullet};C\big)=\frac{1}{4}\int_0^1\int_0^\infty \mathrm{vol}\big(P(u)\big\vert_{S}-vC\big)dvdu. \end{align*} $$
$$ \begin{align*}S\big(W^S_{\bullet,\bullet};C\big)=\frac{1}{4}\int_0^1\int_0^\infty \mathrm{vol}\big(P(u)\big\vert_{S}-vC\big)dvdu. \end{align*} $$
Let
![]() $P(u,v)$
be the positive part of the Zariski decomposition of the divisor
$P(u,v)$
be the positive part of the Zariski decomposition of the divisor
![]() $P(u)\vert _{S}-vC$
, and let
$P(u)\vert _{S}-vC$
, and let
![]() $N(u,v)$
be its negative part, where
$N(u,v)$
be its negative part, where
![]() $u\in [0,1]$
and
$u\in [0,1]$
and
![]() $v\in \mathbb {R}_{\geqslant 0}$
. Then
$v\in \mathbb {R}_{\geqslant 0}$
. Then
 $$ \begin{align*}S\big(W_{\bullet,\bullet,\bullet}^{S,C};P\big)=F_{P}+\frac{1}{4}\int_{0}^{1}\int_{0}^{\infty}\big(P(u,v)\cdot C\big)^2dvdu \end{align*} $$
$$ \begin{align*}S\big(W_{\bullet,\bullet,\bullet}^{S,C};P\big)=F_{P}+\frac{1}{4}\int_{0}^{1}\int_{0}^{\infty}\big(P(u,v)\cdot C\big)^2dvdu \end{align*} $$
by [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Theorem 1.112], where
 $$ \begin{align*}F_P=\frac{1}{2}\int_{0}^{1}\int_{0}^{\infty}\big(P(u,v)\cdot C\big)\mathrm{ord}_P\Big(N(u,v)\big\vert_{C}\Big)dvdu. \end{align*} $$
$$ \begin{align*}F_P=\frac{1}{2}\int_{0}^{1}\int_{0}^{\infty}\big(P(u,v)\cdot C\big)\mathrm{ord}_P\Big(N(u,v)\big\vert_{C}\Big)dvdu. \end{align*} $$
Lemma 5.4. Suppose that
![]() $C_2$
is smooth, and
$C_2$
is smooth, and
![]() $-K_S$
is ample. Then
$-K_S$
is ample. Then
 $$ \begin{align*} S(W_{\bullet,\bullet}^S;C)&=\frac{13}{24},\\ S(W_{\bullet, \bullet,\bullet}^{S,C};P)&=1. \end{align*} $$
$$ \begin{align*} S(W_{\bullet,\bullet}^S;C)&=\frac{13}{24},\\ S(W_{\bullet, \bullet,\bullet}^{S,C};P)&=1. \end{align*} $$
Proof. We have
![]() $C\cdot C^\prime =4$
and
$C\cdot C^\prime =4$
and
![]() $(C^\prime )^2=C^2=0$
. Fix
$(C^\prime )^2=C^2=0$
. Fix
![]() $u\in [0,1]$
and
$u\in [0,1]$
and
![]() $v\in \mathbb {R}_{\geqslant 0}$
. Then
$v\in \mathbb {R}_{\geqslant 0}$
. Then
which implies that
![]() $P(u)\vert _{S}-vC$
is pseudoeffective
$P(u)\vert _{S}-vC$
is pseudoeffective
![]() $\iff P(u)\vert _{S}-vC$
is nef
$\iff P(u)\vert _{S}-vC$
is nef
![]() $\iff v\leqslant \frac {3}{2}-u$
. If
$\iff v\leqslant \frac {3}{2}-u$
. If
![]() $0\leqslant u\leqslant 1$
and
$0\leqslant u\leqslant 1$
and
![]() $0\leqslant v\leqslant \frac {3}{2}-u$
, then
$0\leqslant v\leqslant \frac {3}{2}-u$
, then
![]() $P(u,v)=(\frac {3}{2}-u-v)C+\frac {1}{2}C^\prime $
and
$P(u,v)=(\frac {3}{2}-u-v)C+\frac {1}{2}C^\prime $
and
![]() $N(u,v)=0$
, so
$N(u,v)=0$
, so
 $$ \begin{align*}S\big(W^S_{\bullet,\bullet};C\big)=\frac{1}{4}\int_0^1\int_0^{\frac{3}{2}-u}\Bigg(\Big(\frac{3}{2}-u-v)C+\frac{1}{2}C^\prime\Bigg)^2dvdu= \frac{1}{4}\int_0^1\int_0^{\frac{3}{2}-u}6-4u-4v\,dvdu=\frac{13}{24}. \end{align*} $$
$$ \begin{align*}S\big(W^S_{\bullet,\bullet};C\big)=\frac{1}{4}\int_0^1\int_0^{\frac{3}{2}-u}\Bigg(\Big(\frac{3}{2}-u-v)C+\frac{1}{2}C^\prime\Bigg)^2dvdu= \frac{1}{4}\int_0^1\int_0^{\frac{3}{2}-u}6-4u-4v\,dvdu=\frac{13}{24}. \end{align*} $$
Similarly, we see that
![]() $F_P=0$
and
$F_P=0$
and
![]() $P(u,v)\cdot C=2$
, which gives
$P(u,v)\cdot C=2$
, which gives
![]() $S(W_{\bullet ,\bullet ,\bullet }^{S,C};P)=1$
.
$S(W_{\bullet ,\bullet ,\bullet }^{S,C};P)=1$
.
Lemma 5.5. Suppose that
![]() $C_2$
is smooth,
$C_2$
is smooth,
![]() $-K_S$
is not ample. Then
$-K_S$
is not ample. Then
 $$ \begin{align*} S(W_{\bullet,\bullet}^S;C)&=\frac{7}{12},\\ S(W_{\bullet, \bullet,\bullet}^{S,C};P)&=\frac{5}{6}. \end{align*} $$
$$ \begin{align*} S(W_{\bullet,\bullet}^S;C)&=\frac{7}{12},\\ S(W_{\bullet, \bullet,\bullet}^{S,C};P)&=\frac{5}{6}. \end{align*} $$
Proof. In this case, we have the following commutative diagram:

where
![]() $\phi $
is a birational map that contracts four disjoint
$\phi $
is a birational map that contracts four disjoint
![]() $(-2)$
-curves, and
$(-2)$
-curves, and
![]() $\overline {S}$
is a del Pezzo surface of degree
$\overline {S}$
is a del Pezzo surface of degree
![]() $2$
that has
$2$
that has
![]() $4$
isolated ordinary double points, and
$4$
isolated ordinary double points, and
![]() $\pi $
is a double cover that is ramified in a reducible quartic curve that is a union of two irreducible conics such that
$\pi $
is a double cover that is ramified in a reducible quartic curve that is a union of two irreducible conics such that
![]() $\eta (C)$
is one of these two conics. In particular, we have
$\eta (C)$
is one of these two conics. In particular, we have
![]() $C=\tau (C)$
.
$C=\tau (C)$
.
Let
![]() $E_1$
,
$E_1$
,
![]() $E_2$
,
$E_2$
,
![]() $E_3$
,
$E_3$
,
![]() $E_4$
be the
$E_4$
be the
![]() $\phi $
-exceptional curves. Fix
$\phi $
-exceptional curves. Fix
![]() $u\in [0,1]$
and
$u\in [0,1]$
and
![]() $v\in \mathbb {R}_{\geqslant 0}$
. Then
$v\in \mathbb {R}_{\geqslant 0}$
. Then
so the divisor
![]() $P(u)\vert _{S}-vC$
is pseudoeffective
$P(u)\vert _{S}-vC$
is pseudoeffective
![]() $\iff v\leqslant 2-u$
. Moreover, we have
$\iff v\leqslant 2-u$
. Moreover, we have
 $$ \begin{align*}P(u,v)=\left\{\begin{aligned} &(2-u-v)C+\frac{1}{2}(E_1+E_2+E_3+E_4)\ \text{if }0\leqslant v\leqslant 1-u, \\ &(2-u-v)\Big(C+\frac{1}{2}(E_1+E_2+E_3+E_4)\Big)\ \text{if }1-u\leqslant v\leqslant 2-u, \\ \end{aligned} \right. \end{align*} $$
$$ \begin{align*}P(u,v)=\left\{\begin{aligned} &(2-u-v)C+\frac{1}{2}(E_1+E_2+E_3+E_4)\ \text{if }0\leqslant v\leqslant 1-u, \\ &(2-u-v)\Big(C+\frac{1}{2}(E_1+E_2+E_3+E_4)\Big)\ \text{if }1-u\leqslant v\leqslant 2-u, \\ \end{aligned} \right. \end{align*} $$
 $$ \begin{align*}N(u,v)=\left\{\begin{aligned} &0\ \text{if }0\leqslant v\leqslant 1-u, \\ &\frac{u+v-1}{2}(E_1+E_2+E_3+E_4)\ \text{if }1-u\leqslant v\leqslant 2-u, \\ \end{aligned} \right. \end{align*} $$
$$ \begin{align*}N(u,v)=\left\{\begin{aligned} &0\ \text{if }0\leqslant v\leqslant 1-u, \\ &\frac{u+v-1}{2}(E_1+E_2+E_3+E_4)\ \text{if }1-u\leqslant v\leqslant 2-u, \\ \end{aligned} \right. \end{align*} $$
 $$ \begin{align*}\mathrm{vol}\big(P(u)\vert_{S}-vC\big)= \left\{\begin{aligned} &(6-4u)-4\ \text{if }0\leqslant v\leqslant 1-u, \\ &2(2-u-v)^2\ \text{if }1-u\leqslant v\leqslant 2-u. \\ \end{aligned} \right. \end{align*} $$
$$ \begin{align*}\mathrm{vol}\big(P(u)\vert_{S}-vC\big)= \left\{\begin{aligned} &(6-4u)-4\ \text{if }0\leqslant v\leqslant 1-u, \\ &2(2-u-v)^2\ \text{if }1-u\leqslant v\leqslant 2-u. \\ \end{aligned} \right. \end{align*} $$
Now, integrating
![]() $\mathrm {vol}(P(u)\vert _{S}-vC)$
, we obtain
$\mathrm {vol}(P(u)\vert _{S}-vC)$
, we obtain
![]() $S(W_{\bullet ,\bullet }^S;C)=\frac {7}{12}$
.
$S(W_{\bullet ,\bullet }^S;C)=\frac {7}{12}$
.
To compute
![]() $S(W_{\bullet ,\bullet ,\bullet }^{S,C};P)$
, we first observe that
$S(W_{\bullet ,\bullet ,\bullet }^{S,C};P)$
, we first observe that
![]() $F_{P}=0$
because
$F_{P}=0$
because
![]() $P\not \in E_1\cup E_2\cup E_3\cup E_4$
since S is a general surface in
$P\not \in E_1\cup E_2\cup E_3\cup E_4$
since S is a general surface in
![]() $|H_2|$
that contains
$|H_2|$
that contains
![]() $C_2$
. On the other hand, we have
$C_2$
. On the other hand, we have
 $$ \begin{align*}P(u,v)\cdot C=\left\{\begin{aligned} &2\ \text{if }0\leqslant v\leqslant 1-u, \\ &4-2u-2v\ \text{if }1-u\leqslant v\leqslant 2-u. \\ \end{aligned} \right. \end{align*} $$
$$ \begin{align*}P(u,v)\cdot C=\left\{\begin{aligned} &2\ \text{if }0\leqslant v\leqslant 1-u, \\ &4-2u-2v\ \text{if }1-u\leqslant v\leqslant 2-u. \\ \end{aligned} \right. \end{align*} $$
Hence, integrating
![]() $(P(u,v)\cdot C)^2$
, we get
$(P(u,v)\cdot C)^2$
, we get
![]() $S(W_{\bullet ,\bullet ,\bullet }^{S,C};P)=\frac {5}{6}$
as required.
$S(W_{\bullet ,\bullet ,\bullet }^{S,C};P)=\frac {5}{6}$
as required.
Lemma 5.6. Suppose that
![]() $C_2$
is singular. Then
$C_2$
is singular. Then
 $$ \begin{align*} S(W_{\bullet,\bullet}^S;C)&=\frac{3}{4},\\ S(W_{\bullet, \bullet,\bullet}^{S,C};P)&\leqslant \frac{11}{12}. \end{align*} $$
$$ \begin{align*} S(W_{\bullet,\bullet}^S;C)&=\frac{3}{4},\\ S(W_{\bullet, \bullet,\bullet}^{S,C};P)&\leqslant \frac{11}{12}. \end{align*} $$
Proof. The curve
![]() $C_2$
consists of two irreducible components: the curve C and another curve, which we denote by L. The curves C and L are smooth and intersects transversally at one point. Note that
$C_2$
consists of two irreducible components: the curve C and another curve, which we denote by L. The curves C and L are smooth and intersects transversally at one point. Note that
![]() $P\ne C\cap L$
since
$P\ne C\cap L$
since
![]() $C_2$
is smooth at the point P by assumption.
$C_2$
is smooth at the point P by assumption.
The intersections of the curves C, L and
![]() $C^\prime =\tau (C)$
on S are given in the table below.
$C^\prime =\tau (C)$
on S are given in the table below.

Fix
![]() $u\in [0,1]$
and
$u\in [0,1]$
and
![]() $v\in \mathbb {R}_{\geqslant 0}$
. Since
$v\in \mathbb {R}_{\geqslant 0}$
. Since
![]() $C+C^\prime \sim -K_S$
, we have
$C+C^\prime \sim -K_S$
, we have
so
![]() $P(u)\vert _{S}-vC$
is pseudoeffective
$P(u)\vert _{S}-vC$
is pseudoeffective
![]() $\iff v\leqslant 2-u$
. Moreover, if
$\iff v\leqslant 2-u$
. Moreover, if
![]() $0\leqslant u\leqslant \frac {1}{2}$
, then
$0\leqslant u\leqslant \frac {1}{2}$
, then
 $$ \begin{align*}P(u,v)=\left\{\begin{aligned} &(2-u-v)C+(1-u)L+C^\prime\ \text{if }0\leqslant v\leqslant 1, \\ &(2-u-v)(C+L)+C^\prime\ \text{if }1\leqslant v\leqslant \frac{3}{2}-u, \\ &(2-u-v)(C+L+C^\prime)\ \text{if }\frac{3}{2}-u\leqslant v\leqslant 2-u, \end{aligned} \right. \end{align*} $$
$$ \begin{align*}P(u,v)=\left\{\begin{aligned} &(2-u-v)C+(1-u)L+C^\prime\ \text{if }0\leqslant v\leqslant 1, \\ &(2-u-v)(C+L)+C^\prime\ \text{if }1\leqslant v\leqslant \frac{3}{2}-u, \\ &(2-u-v)(C+L+C^\prime)\ \text{if }\frac{3}{2}-u\leqslant v\leqslant 2-u, \end{aligned} \right. \end{align*} $$
 $$ \begin{align*}N(u,v)=\left\{\begin{aligned} &0\ \text{if }0\leqslant v\leqslant 1, \\ &(v-1)L\ \text{if }1\leqslant v\leqslant \frac{3}{2}-u, \\ &(v-1)L+(2v+2u-3)C^\prime\ \text{if }\frac{3}{2}-u\leqslant v\leqslant 2-u, \end{aligned} \right. \end{align*} $$
$$ \begin{align*}N(u,v)=\left\{\begin{aligned} &0\ \text{if }0\leqslant v\leqslant 1, \\ &(v-1)L\ \text{if }1\leqslant v\leqslant \frac{3}{2}-u, \\ &(v-1)L+(2v+2u-3)C^\prime\ \text{if }\frac{3}{2}-u\leqslant v\leqslant 2-u, \end{aligned} \right. \end{align*} $$
 $$ \begin{align*}\mathrm{vol}\big(P(u)\vert_{S}-vC\big)= \left\{\begin{aligned} &6-v^2-4u-2v\ \text{if }0\leqslant v\leqslant 1, \\ &7-4u-4v \ \text{if }1\leqslant v\leqslant \frac{3}{2}-u, \\ &4(u+v-2)^2\ \text{if }\frac{3}{2}-u\leqslant v\leqslant 2-u. \end{aligned} \right. \end{align*} $$
$$ \begin{align*}\mathrm{vol}\big(P(u)\vert_{S}-vC\big)= \left\{\begin{aligned} &6-v^2-4u-2v\ \text{if }0\leqslant v\leqslant 1, \\ &7-4u-4v \ \text{if }1\leqslant v\leqslant \frac{3}{2}-u, \\ &4(u+v-2)^2\ \text{if }\frac{3}{2}-u\leqslant v\leqslant 2-u. \end{aligned} \right. \end{align*} $$
Similarly, if
![]() $\frac {1}{2}\leqslant u\leqslant 1$
, then
$\frac {1}{2}\leqslant u\leqslant 1$
, then
 $$ \begin{align*}P(u,v)=\left\{\begin{aligned} &(2-u-v)C+(1-u)L+C^\prime\ \text{if }0\leqslant v\leqslant \frac{3}{2}-u, \\ &(2-u-v)(C+2C^\prime)+(1-u)L\ \text{if }\frac{3}{2}-u\leqslant v\leqslant 1, \\ &(2-u-v)(C+L+C^\prime)\ \text{if }1\leqslant v\leqslant 2-u, \end{aligned} \right. \end{align*} $$
$$ \begin{align*}P(u,v)=\left\{\begin{aligned} &(2-u-v)C+(1-u)L+C^\prime\ \text{if }0\leqslant v\leqslant \frac{3}{2}-u, \\ &(2-u-v)(C+2C^\prime)+(1-u)L\ \text{if }\frac{3}{2}-u\leqslant v\leqslant 1, \\ &(2-u-v)(C+L+C^\prime)\ \text{if }1\leqslant v\leqslant 2-u, \end{aligned} \right. \end{align*} $$
 $$ \begin{align*}N(u,v)=\left\{\begin{aligned} &0\ \text{if }0\leqslant v\leqslant \frac{3}{2}-u, \\ &(2v+2u-3)C^\prime\ \text{if }\frac{3}{2}-u\leqslant v\leqslant 1, \\ &(v-1)L+(2v+2u-3)C^\prime\ \text{if }1\leqslant v\leqslant 2-u, \end{aligned} \right. \end{align*} $$
$$ \begin{align*}N(u,v)=\left\{\begin{aligned} &0\ \text{if }0\leqslant v\leqslant \frac{3}{2}-u, \\ &(2v+2u-3)C^\prime\ \text{if }\frac{3}{2}-u\leqslant v\leqslant 1, \\ &(v-1)L+(2v+2u-3)C^\prime\ \text{if }1\leqslant v\leqslant 2-u, \end{aligned} \right. \end{align*} $$
 $$ \begin{align*}\mathrm{vol}\big(P(u)\vert_{S}-vC\big)= \left\{\begin{aligned} &6-v^2-4u-2v\ \text{if }0\leqslant v\leqslant \frac{3}{2}-u, \\ &(5-2u-3v)(3-2u-v)\ \text{if }\frac{3}{2}-u\leqslant v\leqslant 1, \\ &4(u+v-2)^2\ \text{if }1\leqslant v\leqslant 2-u. \end{aligned} \right. \end{align*} $$
$$ \begin{align*}\mathrm{vol}\big(P(u)\vert_{S}-vC\big)= \left\{\begin{aligned} &6-v^2-4u-2v\ \text{if }0\leqslant v\leqslant \frac{3}{2}-u, \\ &(5-2u-3v)(3-2u-v)\ \text{if }\frac{3}{2}-u\leqslant v\leqslant 1, \\ &4(u+v-2)^2\ \text{if }1\leqslant v\leqslant 2-u. \end{aligned} \right. \end{align*} $$
Hence, integrating
![]() $\mathrm {vol}(P(u)\vert _{S}-vC)$
, we get
$\mathrm {vol}(P(u)\vert _{S}-vC)$
, we get
![]() $S(W_{\bullet ,\bullet }^S;C)=\frac {3}{4}$
.
$S(W_{\bullet ,\bullet }^S;C)=\frac {3}{4}$
.
Now, let us compute
![]() $S(W_{\bullet , \bullet ,\bullet }^{S,C};P)$
. If
$S(W_{\bullet , \bullet ,\bullet }^{S,C};P)$
. If
![]() $0\leqslant u\leqslant \frac {1}{2}$
, then
$0\leqslant u\leqslant \frac {1}{2}$
, then
 $$ \begin{align*}P(u,v)\cdot C=\left\{\begin{aligned} &1+v\ \text{if }0\leqslant v\leqslant 1, \\ &2\ \text{if }1\leqslant v\leqslant \frac{3}{2}-u, \\ &8-4u-4v\ \text{if }\frac{3}{2}-u\leqslant v\leqslant 2-u. \end{aligned} \right. \end{align*} $$
$$ \begin{align*}P(u,v)\cdot C=\left\{\begin{aligned} &1+v\ \text{if }0\leqslant v\leqslant 1, \\ &2\ \text{if }1\leqslant v\leqslant \frac{3}{2}-u, \\ &8-4u-4v\ \text{if }\frac{3}{2}-u\leqslant v\leqslant 2-u. \end{aligned} \right. \end{align*} $$
Similarly, if
![]() $\frac {1}{2}\leqslant u\leqslant 1$
, then
$\frac {1}{2}\leqslant u\leqslant 1$
, then
 $$ \begin{align*}P(u,v)\cdot C=\left\{\begin{aligned} &1+v\ \text{if }0\leqslant v\leqslant \frac{3}{2}-u, \\ &7-4u-3v\ \text{if }\frac{3}{2}-u\leqslant v\leqslant 1, \\ &8-4u-4v\ \text{if }1\leqslant v\leqslant 2-u. \end{aligned} \right. \end{align*} $$
$$ \begin{align*}P(u,v)\cdot C=\left\{\begin{aligned} &1+v\ \text{if }0\leqslant v\leqslant \frac{3}{2}-u, \\ &7-4u-3v\ \text{if }\frac{3}{2}-u\leqslant v\leqslant 1, \\ &8-4u-4v\ \text{if }1\leqslant v\leqslant 2-u. \end{aligned} \right. \end{align*} $$
Then integrating, we get
![]() $S(W_{\bullet ,\bullet ,\bullet }^{S,C};P)=\frac {145}{192}+F_{P}$
. To compute
$S(W_{\bullet ,\bullet ,\bullet }^{S,C};P)=\frac {145}{192}+F_{P}$
. To compute
![]() $F_{P}$
, let us recall that
$F_{P}$
, let us recall that
![]() $P\not \in L$
. Hence, if
$P\not \in L$
. Hence, if
![]() $P\not \in C^\prime $
, then
$P\not \in C^\prime $
, then
![]() $F_{P}=0$
, which implies that
$F_{P}=0$
, which implies that
![]() $S(W_{\bullet ,\bullet ,\bullet }^{S,C};P)=\frac {145}{192}<\frac {11}{12}$
as required.
$S(W_{\bullet ,\bullet ,\bullet }^{S,C};P)=\frac {145}{192}<\frac {11}{12}$
as required.
We may assume that
![]() $P\in C\cap C^\prime $
. If
$P\in C\cap C^\prime $
. If
![]() $C^\prime $
intersects C transversally at P, then
$C^\prime $
intersects C transversally at P, then
 $$ \begin{align*}\mathrm{ord}_P\Big(N(u,v)\big\vert_{C}\Big)=\left\{\begin{aligned} &0\ \text{if }0\leqslant v\leqslant\frac{3}{2}-u, \\ &2u+2v-3\ \text{if }\frac{3}{2}-u\leqslant v\leqslant 2-u, \end{aligned} \right. \end{align*} $$
$$ \begin{align*}\mathrm{ord}_P\Big(N(u,v)\big\vert_{C}\Big)=\left\{\begin{aligned} &0\ \text{if }0\leqslant v\leqslant\frac{3}{2}-u, \\ &2u+2v-3\ \text{if }\frac{3}{2}-u\leqslant v\leqslant 2-u, \end{aligned} \right. \end{align*} $$
which gives
 $$ \begin{align*} F_P&=\frac{1}{2}\int_{0}^{\frac{1}{2}}\int_{\frac{3}{2}-u}^{2-u}(8-4u-4v)(2u+2v-3)dvdu+\\ &\quad+\frac{1}{2}\int_{\frac{1}{2}}^{1}\int_{1}^{\frac{3}{2}-u}(7-4u-3v)(2u+2v-3)dvdu\\&\quad+\frac{1}{2}\int_{\frac{1}{2}}^{1}\int_{\frac{3}{2}-u}^{2-u}(8-4u-4v)(2u+2v-3)dvdu=\frac{31}{384}, \end{align*} $$
$$ \begin{align*} F_P&=\frac{1}{2}\int_{0}^{\frac{1}{2}}\int_{\frac{3}{2}-u}^{2-u}(8-4u-4v)(2u+2v-3)dvdu+\\ &\quad+\frac{1}{2}\int_{\frac{1}{2}}^{1}\int_{1}^{\frac{3}{2}-u}(7-4u-3v)(2u+2v-3)dvdu\\&\quad+\frac{1}{2}\int_{\frac{1}{2}}^{1}\int_{\frac{3}{2}-u}^{2-u}(8-4u-4v)(2u+2v-3)dvdu=\frac{31}{384}, \end{align*} $$
so
![]() $S(W_{\bullet ,\bullet ,\bullet }^{S,C};P)=\frac {145}{192}+\frac {31}{384}=\frac {107}{128}<\frac {11}{12}$
. If
$S(W_{\bullet ,\bullet ,\bullet }^{S,C};P)=\frac {145}{192}+\frac {31}{384}=\frac {107}{128}<\frac {11}{12}$
. If
![]() $C^\prime $
is tangent to C at the point P, then
$C^\prime $
is tangent to C at the point P, then
 $$ \begin{align*}\mathrm{ord}_P\Big(N(u,v)\big\vert_{C}\Big)=\left\{\begin{aligned} &0\ \text{if }0\leqslant v\leqslant\frac{3}{2}-u, \\ &2(2u+2v-3)\ \text{if }\frac{3}{2}-u\leqslant v\leqslant 2-u,\\ \end{aligned} \right. \end{align*} $$
$$ \begin{align*}\mathrm{ord}_P\Big(N(u,v)\big\vert_{C}\Big)=\left\{\begin{aligned} &0\ \text{if }0\leqslant v\leqslant\frac{3}{2}-u, \\ &2(2u+2v-3)\ \text{if }\frac{3}{2}-u\leqslant v\leqslant 2-u,\\ \end{aligned} \right. \end{align*} $$
which gives
![]() $F_P=\frac {31}{192}$
, so
$F_P=\frac {31}{192}$
, so
![]() $S(W_{\bullet ,\bullet }^{S,C};P)=\frac {145}{192}+\frac {31}{192}=\frac {11}{12}$
.
$S(W_{\bullet ,\bullet }^{S,C};P)=\frac {145}{192}+\frac {31}{192}=\frac {11}{12}$
.
Now, using Equation (5.2) and Lemmas 5.4, 5.5, 5.6, we see that Z is a curve.
Lemma 5.7. One has
![]() $H_1\cdot Z\geqslant 1$
and
$H_1\cdot Z\geqslant 1$
and
![]() $H_2\cdot Z\geqslant 1$
.
$H_2\cdot Z\geqslant 1$
.
Proof. If
![]() $H_2\cdot Z=0$
, then
$H_2\cdot Z=0$
, then
![]() $Z=C$
, which is impossible by Equation (5.1) and Lemmas 5.4, 5.5, 5.6. Hence, we see that
$Z=C$
, which is impossible by Equation (5.1) and Lemmas 5.4, 5.5, 5.6. Hence, we see that
![]() $H_2\cdot Z\geqslant 1$
and
$H_2\cdot Z\geqslant 1$
and
![]() $\pi _2(Z)$
is a curve. Let us show that
$\pi _2(Z)$
is a curve. Let us show that
![]() $H_1\cdot Z\geqslant 1$
.
$H_1\cdot Z\geqslant 1$
.
Suppose that
![]() $H_1\cdot Z=0$
. Then Z must be an irreducible component of the curve
$H_1\cdot Z=0$
. Then Z must be an irreducible component of the curve
![]() $C_1$
. If
$C_1$
. If
![]() $C_1$
is reduced, then arguing exactly as in the proofs of Lemmas 5.4, 5.5, 5.6, we obtain a contradiction with [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Corollary 1.109]. Thus, we see that
$C_1$
is reduced, then arguing exactly as in the proofs of Lemmas 5.4, 5.5, 5.6, we obtain a contradiction with [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Corollary 1.109]. Thus, we see that
![]() $C_1$
is not reduced.
$C_1$
is not reduced.
So far, the point P was a point in Z. Let us choose
![]() $P\in Z$
such that
$P\in Z$
such that
![]() $\pi _2(P)\in \pi _2(Z)\cap \Delta _2$
. Then
$\pi _2(P)\in \pi _2(Z)\cap \Delta _2$
. Then
![]() $C_2$
is singular. But it is smooth at P by Lemma 5.1, which fits our assumption above. Then
$C_2$
is singular. But it is smooth at P by Lemma 5.1, which fits our assumption above. Then
![]() $S(W_{\bullet ,\bullet }^S;C)=\frac {3}{4}$
and
$S(W_{\bullet ,\bullet }^S;C)=\frac {3}{4}$
and
![]() $S(W_{\bullet , \bullet ,\bullet }^{S,C};P)\leqslant \frac {11}{12}$
by Lemma 5.6, which contradicts Equation (5.1).
$S(W_{\bullet , \bullet ,\bullet }^{S,C};P)\leqslant \frac {11}{12}$
by Lemma 5.6, which contradicts Equation (5.1).
Both
![]() $\pi _1(Z)$
and
$\pi _1(Z)$
and
![]() $\pi _2(Z)$
are curves. Similar to what we did in the proof of Lemma 5.7, let us choose the point
$\pi _2(Z)$
are curves. Similar to what we did in the proof of Lemma 5.7, let us choose the point
![]() $P\in Z$
such that
$P\in Z$
such that
![]() $\pi _1(P)\in \Delta _1$
. Then
$\pi _1(P)\in \Delta _1$
. Then
![]() $C_1$
is singular at P, which implies that
$C_1$
is singular at P, which implies that
![]() $C_2$
is smooth at P by Lemma 5.1. Now, using Equation (5.1) and Lemmas 5.5 and 5.6, we see that
$C_2$
is smooth at P by Lemma 5.1. Now, using Equation (5.1) and Lemmas 5.5 and 5.6, we see that
![]() $C=C_2$
, the curve
$C=C_2$
, the curve
![]() $C_2$
is smooth, the divisor
$C_2$
is smooth, the divisor
![]() $-K_S$
is ample.
$-K_S$
is ample.
We see that S is a del Pezzo surface, and
![]() $\eta \colon S\to \mathbb {P}^2$
is a double cover ramified in a smooth quartic curve, so we are almost in the same position as in the proof of Lemma 5.4. But now, we have one small advantage: the point
$\eta \colon S\to \mathbb {P}^2$
is a double cover ramified in a smooth quartic curve, so we are almost in the same position as in the proof of Lemma 5.4. But now, we have one small advantage: the point
![]() $\eta (P)$
is contained in the ramification divisor of the double cover
$\eta (P)$
is contained in the ramification divisor of the double cover
![]() $\eta $
because
$\eta $
because
![]() $C_1$
is singular at P. Then
$C_1$
is singular at P. Then
![]() $|-K_S|$
contains a unique curve that is singular at P. Denote this curve by R. We have the following possibilities:
$|-K_S|$
contains a unique curve that is singular at P. Denote this curve by R. We have the following possibilities:
-
(a) R is an irreducible curve that has a nodal singularity at P;
-
(b) R is an irreducible curve that has a cuspidal singularity at P;
-
(c)
 $R=R_1+R_2$
for two
$R=R_1+R_2$
for two
 $(-1)$
-curves in S that intersect transversally at P;
$(-1)$
-curves in S that intersect transversally at P; -
(d)
 $R=R_1+R_2$
for two
$R=R_1+R_2$
for two
 $(-1)$
-curves in S that are tangent at P.
$(-1)$
-curves in S that are tangent at P.
Let
![]() $f\colon \widetilde {S}\to S$
be the blow up of the point P. Denote by
$f\colon \widetilde {S}\to S$
be the blow up of the point P. Denote by
![]() $\widetilde {R}$
and
$\widetilde {R}$
and
![]() $\widetilde {C}$
the proper transforms on the surface
$\widetilde {C}$
the proper transforms on the surface
![]() $\widetilde {S}$
of the curves R and C, respectively. Fix
$\widetilde {S}$
of the curves R and C, respectively. Fix
![]() $u\in [0,1]$
and
$u\in [0,1]$
and
![]() $v\in \mathbb {R}_{\geqslant 0}$
. Then
$v\in \mathbb {R}_{\geqslant 0}$
. Then
Let
![]() $\widetilde {P}(u,v)$
be the positive part of the Zariski decomposition of
$\widetilde {P}(u,v)$
be the positive part of the Zariski decomposition of
![]() $\widetilde {R}+(1-u)\widetilde {C}+(3-u-v)E$
, and let
$\widetilde {R}+(1-u)\widetilde {C}+(3-u-v)E$
, and let
![]() $\widetilde {N}(u,v)$
its negative part. Then it follows from [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Remark 1.113] that
$\widetilde {N}(u,v)$
its negative part. Then it follows from [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Remark 1.113] that
 $$ \begin{align} 1\geqslant \frac{A_X(\mathbf{F})}{S_X(\mathbf{F})}\geqslant\min\left\{\frac{1}{S_X(S)}, \frac{2}{S(W_{\bullet,\bullet}^{\widetilde{S}};E)},\inf_{O\in E}\frac{1}{S(W_{\bullet, \bullet,\bullet}^{\widetilde{S},E};O)}\right\}, \end{align} $$
$$ \begin{align} 1\geqslant \frac{A_X(\mathbf{F})}{S_X(\mathbf{F})}\geqslant\min\left\{\frac{1}{S_X(S)}, \frac{2}{S(W_{\bullet,\bullet}^{\widetilde{S}};E)},\inf_{O\in E}\frac{1}{S(W_{\bullet, \bullet,\bullet}^{\widetilde{S},E};O)}\right\}, \end{align} $$
where
![]() $S(W_{\bullet ,\bullet }^{\widetilde {S}};E)$
and
$S(W_{\bullet ,\bullet }^{\widetilde {S}};E)$
and
![]() $S(W_{\bullet , \bullet ,\bullet }^{\widetilde {S},E};O)$
are defined in [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3] similar to
$S(W_{\bullet , \bullet ,\bullet }^{\widetilde {S},E};O)$
are defined in [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3] similar to
![]() $S(W_{\bullet ,\bullet }^S;C)$
and
$S(W_{\bullet ,\bullet }^S;C)$
and
![]() $S(W_{\bullet , \bullet ,\bullet }^{S,C};P)$
. These two numbers can be computed using [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Remark 1.113]. Namely, we have
$S(W_{\bullet , \bullet ,\bullet }^{S,C};P)$
. These two numbers can be computed using [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Remark 1.113]. Namely, we have
 $$ \begin{align*}S\big(W_{\bullet,\bullet}^{\widetilde{S}};E\big)=\frac{1}{4}\int_0^1\int_0^{\infty}\big(\widetilde{P}(u,v)\big)^2dvdu \end{align*} $$
$$ \begin{align*}S\big(W_{\bullet,\bullet}^{\widetilde{S}};E\big)=\frac{1}{4}\int_0^1\int_0^{\infty}\big(\widetilde{P}(u,v)\big)^2dvdu \end{align*} $$
and
 $$ \begin{align*}S\big(W_{\bullet, \bullet,\bullet}^{\widetilde{S},E};O\big)=\frac{1}{4}\int_0^1\int_0^{\infty}\Big(\big(\widetilde{P}(u,v)\cdot E\big)\Big)^2dvdu+ F_O, \end{align*} $$
$$ \begin{align*}S\big(W_{\bullet, \bullet,\bullet}^{\widetilde{S},E};O\big)=\frac{1}{4}\int_0^1\int_0^{\infty}\Big(\big(\widetilde{P}(u,v)\cdot E\big)\Big)^2dvdu+ F_O, \end{align*} $$
where O is a point in E and
 $$ \begin{align*}F_O=\frac{1}{2}\int_0^1\int_0^{\infty}\big(\widetilde{P}(u,v)\cdot E\big)\mathrm{ord}_O\Big(\widetilde{N}(u,v)\big|_{E}\Big)dvdu. \end{align*} $$
$$ \begin{align*}F_O=\frac{1}{2}\int_0^1\int_0^{\infty}\big(\widetilde{P}(u,v)\cdot E\big)\mathrm{ord}_O\Big(\widetilde{N}(u,v)\big|_{E}\Big)dvdu. \end{align*} $$
Let us use these formulas to estimate
![]() $S(W_{\bullet ,\bullet }^{\widetilde {S}};E)$
and
$S(W_{\bullet ,\bullet }^{\widetilde {S}};E)$
and
![]() $S(W_{\bullet , \bullet ,\bullet }^{\widetilde {S},E};O)$
.
$S(W_{\bullet , \bullet ,\bullet }^{\widetilde {S},E};O)$
.
If the curve R is irreducible, the intersections of the curves
![]() $\widetilde {C}$
,
$\widetilde {C}$
,
![]() $\widetilde {R}$
, E can be computed as follows:
$\widetilde {R}$
, E can be computed as follows:
![]() $\widetilde {C}^2=-1$
,
$\widetilde {C}^2=-1$
,
![]() $\widetilde {C}\cdot \widetilde {R}=0$
,
$\widetilde {C}\cdot \widetilde {R}=0$
,
![]() $\widetilde {C}\cdot E=1$
,
$\widetilde {C}\cdot E=1$
,
![]() $\widetilde {R}^2=-2$
,
$\widetilde {R}^2=-2$
,
![]() $\widetilde {R}\cdot E=2$
,
$\widetilde {R}\cdot E=2$
,
![]() $E^2=-1$
. If R is reducible, then
$E^2=-1$
. If R is reducible, then
![]() $\widetilde {R}=\widetilde {R}_1+\widetilde {R}_2$
for two smooth irreducible curves
$\widetilde {R}=\widetilde {R}_1+\widetilde {R}_2$
for two smooth irreducible curves
![]() $\widetilde {R}_1+\widetilde {R}_2$
such that the intersection form of the curves
$\widetilde {R}_1+\widetilde {R}_2$
such that the intersection form of the curves
![]() $\widetilde {C}$
,
$\widetilde {C}$
,
![]() $\widetilde {R}_1$
,
$\widetilde {R}_1$
,
![]() $\widetilde {R}_1$
and E is given in the following table:
$\widetilde {R}_1$
and E is given in the following table:

Then
![]() $\widetilde {R}+(1-u)\widetilde {C}+(3-u-v)E$
is pseudoeffective
$\widetilde {R}+(1-u)\widetilde {C}+(3-u-v)E$
is pseudoeffective
![]() $\iff v\leqslant 3-u$
. Moreover, we have
$\iff v\leqslant 3-u$
. Moreover, we have
 $$ \begin{align*}\widetilde{P}(u,v)=\left\{\begin{aligned} &\widetilde{R}+(1-u)\widetilde{C}+(3-u-v)E\ \text{if }0\leqslant v\leqslant 2-u, \\ &(1-u)\widetilde{C}+(3-u-v)(E+\widetilde{R})\ \text{if }2-u\leqslant v\leqslant 2, \\ &(3-u-v)(E+\widetilde{R}+\widetilde{C})\ \text{if }2\leqslant v\leqslant 3-u, \\ \end{aligned} \right. \end{align*} $$
$$ \begin{align*}\widetilde{P}(u,v)=\left\{\begin{aligned} &\widetilde{R}+(1-u)\widetilde{C}+(3-u-v)E\ \text{if }0\leqslant v\leqslant 2-u, \\ &(1-u)\widetilde{C}+(3-u-v)(E+\widetilde{R})\ \text{if }2-u\leqslant v\leqslant 2, \\ &(3-u-v)(E+\widetilde{R}+\widetilde{C})\ \text{if }2\leqslant v\leqslant 3-u, \\ \end{aligned} \right. \end{align*} $$
 $$ \begin{align*}\widetilde{N}(u,v)=\left\{\begin{aligned} &0\ \text{if }0\leqslant v\leqslant 2-u, \\ &(v+u-2)\widetilde{R}\ \text{if }2-u\leqslant v\leqslant 2, \\ &(v+u-2)\widetilde{R}+(v-2)\widetilde{C}\ \text{if }2\leqslant v\leqslant 3-u,\\ \end{aligned} \right. \end{align*} $$
$$ \begin{align*}\widetilde{N}(u,v)=\left\{\begin{aligned} &0\ \text{if }0\leqslant v\leqslant 2-u, \\ &(v+u-2)\widetilde{R}\ \text{if }2-u\leqslant v\leqslant 2, \\ &(v+u-2)\widetilde{R}+(v-2)\widetilde{C}\ \text{if }2\leqslant v\leqslant 3-u,\\ \end{aligned} \right. \end{align*} $$
 $$ \begin{align*}\big(\widetilde{P}(u,v)\big)^2= \left\{\begin{aligned} &6-v^2-4u\ \text{if }0\leqslant v\leqslant 2-u, \\ &14+2u^2+4uv+v^2-12u-8v\ \text{if }2-u\leqslant v\leqslant 2, \\ &2(3-u-v)^2\ \text{if }2\leqslant v\leqslant 3-u, \\ \end{aligned} \right. \end{align*} $$
$$ \begin{align*}\big(\widetilde{P}(u,v)\big)^2= \left\{\begin{aligned} &6-v^2-4u\ \text{if }0\leqslant v\leqslant 2-u, \\ &14+2u^2+4uv+v^2-12u-8v\ \text{if }2-u\leqslant v\leqslant 2, \\ &2(3-u-v)^2\ \text{if }2\leqslant v\leqslant 3-u, \\ \end{aligned} \right. \end{align*} $$
Now, integrating, we obtain
![]() $S(W_{\bullet ,\bullet }^{\widetilde {S}};E)=\frac {17}{12}$
.
$S(W_{\bullet ,\bullet }^{\widetilde {S}};E)=\frac {17}{12}$
.
Fix a point
![]() $O\in E$
. To estimate
$O\in E$
. To estimate
![]() $S(W_{\bullet , \bullet ,\bullet }^{\widetilde {S},E};O)$
, first we observe that
$S(W_{\bullet , \bullet ,\bullet }^{\widetilde {S},E};O)$
, first we observe that
 $$ \begin{align*}\widetilde{P}(u,v)\cdot E= \left\{\begin{aligned} &v\ \text{if }0\leqslant v\leqslant 2-u, \\ &4-2u-v\ \text{if }2-u\leqslant v\leqslant 2, \\ &6-2u-2v\ \text{if }2\leqslant v\leqslant 3-u.\\ \end{aligned} \right. \end{align*} $$
$$ \begin{align*}\widetilde{P}(u,v)\cdot E= \left\{\begin{aligned} &v\ \text{if }0\leqslant v\leqslant 2-u, \\ &4-2u-v\ \text{if }2-u\leqslant v\leqslant 2, \\ &6-2u-2v\ \text{if }2\leqslant v\leqslant 3-u.\\ \end{aligned} \right. \end{align*} $$
Therefore, integrating
![]() $(\widetilde {P}(u,v)\cdot E)^2$
, we obtain
$(\widetilde {P}(u,v)\cdot E)^2$
, we obtain
![]() $S(W_{\bullet , \bullet ,\bullet }^{Y,\widetilde {S}};O)=\frac {13}{24}+F_O$
.
$S(W_{\bullet , \bullet ,\bullet }^{Y,\widetilde {S}};O)=\frac {13}{24}+F_O$
.
If
![]() $O\not \in \widetilde {C}\cup \widetilde {R}$
, then
$O\not \in \widetilde {C}\cup \widetilde {R}$
, then
![]() $F_O=0$
. Similarly, if
$F_O=0$
. Similarly, if
![]() $O\in \widetilde {C}$
, then
$O\in \widetilde {C}$
, then
![]() $O\not \in \widetilde {R}$
, which gives
$O\not \in \widetilde {R}$
, which gives
 $$ \begin{align*}F_O=\frac{1}{2}\int_0^1\int_2^{3-u}(6-2u-2v)(v-2)dvdu=\frac{1}{24}. \end{align*} $$
$$ \begin{align*}F_O=\frac{1}{2}\int_0^1\int_2^{3-u}(6-2u-2v)(v-2)dvdu=\frac{1}{24}. \end{align*} $$
Finally, if
![]() $O\in \widetilde {R}$
, then
$O\in \widetilde {R}$
, then
![]() $O\not \in \widetilde {C}$
, which gives
$O\not \in \widetilde {C}$
, which gives
 $$ \begin{align*}F_O\leqslant\frac{1}{2}\int_0^1\int_{2-u}^{2}2(4-2u-v)(v+u-2)dvdu+\frac{1}{2}\int_0^1\int_{2}^{3-u}2(6-2u-2v)(v+u-2)dvdu=\frac{7}{24}. \end{align*} $$
$$ \begin{align*}F_O\leqslant\frac{1}{2}\int_0^1\int_{2-u}^{2}2(4-2u-v)(v+u-2)dvdu+\frac{1}{2}\int_0^1\int_{2}^{3-u}2(6-2u-2v)(v+u-2)dvdu=\frac{7}{24}. \end{align*} $$
Summarizing, we get
![]() $S(W_{\bullet , \bullet ,\bullet }^{\widetilde {S},E};O)\leqslant \frac {5}{6}$
for every point
$S(W_{\bullet , \bullet ,\bullet }^{\widetilde {S},E};O)\leqslant \frac {5}{6}$
for every point
![]() $O\in E$
, which contradicts Equation (5.3) because
$O\in E$
, which contradicts Equation (5.3) because
![]() $S_X(S)=\frac {5}{12}$
and
$S_X(S)=\frac {5}{12}$
and
![]() $S(W_{\bullet ,\bullet }^{\widetilde {S}};E)=\frac {17}{12}<2$
. This shows that X is K-stable.
$S(W_{\bullet ,\bullet }^{\widetilde {S}};E)=\frac {17}{12}<2$
. This shows that X is K-stable.
Corollary 5.8. All smooth Fano threefolds in the family ![]() are K-stable.
are K-stable.
6 Family 
Now, let us fix three smooth quadric hypersurfaces
![]() $\mathscr {Q}$
,
$\mathscr {Q}$
,
![]() $\mathscr {Q}^\prime $
and
$\mathscr {Q}^\prime $
and
![]() $\mathscr {Q}^{\prime \prime }$
in
$\mathscr {Q}^{\prime \prime }$
in
![]() $\mathbb {P}^4$
such that their intersection is a smooth curve of degree
$\mathbb {P}^4$
such that their intersection is a smooth curve of degree
![]() $8$
and genus
$8$
and genus
![]() $5$
. We set
$5$
. We set
![]() $\mathscr {C}=\mathscr {Q}\cap \mathscr {Q}^\prime \cap \mathscr {Q}^{\prime \prime }$
. Let
$\mathscr {C}=\mathscr {Q}\cap \mathscr {Q}^\prime \cap \mathscr {Q}^{\prime \prime }$
. Let
![]() $\pi \colon X\to \mathscr {Q}$
be the blow up of the smooth curve
$\pi \colon X\to \mathscr {Q}$
be the blow up of the smooth curve
![]() $\mathscr {C}$
. Then X is a smooth Fano threefold, which is contained in the family
$\mathscr {C}$
. Then X is a smooth Fano threefold, which is contained in the family ![]() . Moreover, all smooth Fano threefolds in this family can be obtained in this way. Note that
. Moreover, all smooth Fano threefolds in this family can be obtained in this way. Note that
![]() $-K_X^3=14$
and
$-K_X^3=14$
and
![]() $\mathrm {Aut}(X)$
is finite [Reference Cheltsov, Przyjalkowski and Shramov10].
$\mathrm {Aut}(X)$
is finite [Reference Cheltsov, Przyjalkowski and Shramov10].
The pencil generated by the surfaces
![]() $\mathscr {Q}^\prime \vert _{\mathscr {Q}}$
and
$\mathscr {Q}^\prime \vert _{\mathscr {Q}}$
and
![]() $\mathscr {Q}^{\prime \prime }\vert _{\mathscr {Q}}$
gives a rational map
$\mathscr {Q}^{\prime \prime }\vert _{\mathscr {Q}}$
gives a rational map ![]() , which fits the following commutative diagram:
, which fits the following commutative diagram:

where
![]() $\phi $
is a fibration into quartic del Pezzo surfaces. Let E be the
$\phi $
is a fibration into quartic del Pezzo surfaces. Let E be the
![]() $\pi $
-exceptional surface, and let
$\pi $
-exceptional surface, and let
![]() $H=\pi ^*(\mathcal {O}_{\mathbb {P}^4}(1)\vert _{\mathscr {Q}})$
. Then
$H=\pi ^*(\mathcal {O}_{\mathbb {P}^4}(1)\vert _{\mathscr {Q}})$
. Then
![]() $-K_X\sim 3H-E$
, the morphism
$-K_X\sim 3H-E$
, the morphism
![]() $\phi $
is given by the linear system
$\phi $
is given by the linear system
![]() $|2H-E|$
, and
$|2H-E|$
, and
![]() $E\cong \mathscr {C}\times \mathbb {P}^1$
.
$E\cong \mathscr {C}\times \mathbb {P}^1$
.
Lemma 6.1. Let S be a fiber of the morphism
![]() $\phi $
. Then S has at most Du Val singularities.
$\phi $
. Then S has at most Du Val singularities.
Proof. Since
![]() $E\vert _{S}$
is a smooth curve, the surface S is smooth along
$E\vert _{S}$
is a smooth curve, the surface S is smooth along
![]() $E\vert _{S}$
, which implies that it has at most isolated singularities. Hence, we conclude that S is normal and irreducible.
$E\vert _{S}$
, which implies that it has at most isolated singularities. Hence, we conclude that S is normal and irreducible.
Note that
![]() $S\cong \pi (S)$
. Suppose that the singularities of the surface
$S\cong \pi (S)$
. Suppose that the singularities of the surface
![]() $\pi (S)$
are not Du Val. Then it follows from [Reference Brenton5, Theorem 1] that
$\pi (S)$
are not Du Val. Then it follows from [Reference Brenton5, Theorem 1] that
![]() $\pi (S)$
is a cone in
$\pi (S)$
is a cone in
![]() $\mathbb {P}^4$
over a quartic elliptic curve. Let P be the vertex of the cone
$\mathbb {P}^4$
over a quartic elliptic curve. Let P be the vertex of the cone
![]() $\pi (S)$
, and let
$\pi (S)$
, and let
![]() $T_P$
be the hyperplane section of the quadric hypersurface
$T_P$
be the hyperplane section of the quadric hypersurface
![]() $\mathscr {Q}$
that is singular at P. Then
$\mathscr {Q}$
that is singular at P. Then
![]() $T_P$
contains all lines in
$T_P$
contains all lines in
![]() $\mathscr {Q}$
that pass through P, which implies that
$\mathscr {Q}$
that pass through P, which implies that
![]() $T_P$
contains
$T_P$
contains
![]() $\pi (S)$
. This is impossible since
$\pi (S)$
. This is impossible since
![]() $T_P$
is a quadric cone.
$T_P$
is a quadric cone.
The goal of this section is to prove that X is K-stable. To do this, we fix a point
![]() $P\in X$
. By [Reference Fujita15, Reference Li18], to prove that X is K-stable, it is enough to show that
$P\in X$
. By [Reference Fujita15, Reference Li18], to prove that X is K-stable, it is enough to show that
![]() $\delta _P(X)>1$
.
$\delta _P(X)>1$
.
Let S be the fiber of the morphism
![]() $\phi $
containing P. Then S is a quartic del Pezzo surface, and S has at most Du Val singularity at P by Lemma 6.1. Moreover, if S is singular at P, then P is a singular point of the surface S of type
$\phi $
containing P. Then S is a quartic del Pezzo surface, and S has at most Du Val singularity at P by Lemma 6.1. Moreover, if S is singular at P, then P is a singular point of the surface S of type
![]() $\mathbb {A}_1$
,
$\mathbb {A}_1$
,
![]() $\mathbb {A}_2$
,
$\mathbb {A}_2$
,
![]() $\mathbb {A}_3$
,
$\mathbb {A}_3$
,
![]() $\mathbb {A}_4$
,
$\mathbb {A}_4$
,
![]() $\mathbb {D}_4$
or
$\mathbb {D}_4$
or
![]() $\mathbb {D}_5$
, see [Reference Coray and Tsfasman12].
$\mathbb {D}_5$
, see [Reference Coray and Tsfasman12].
Lemma 6.2. If
![]() $\delta _P(S)>\frac {54}{55}$
or
$\delta _P(S)>\frac {54}{55}$
or
![]() $P\in \mathrm {Sing}(S)$
and
$P\in \mathrm {Sing}(S)$
and
![]() $\delta _P(S)>\frac {27}{28}$
, then
$\delta _P(S)>\frac {27}{28}$
, then
![]() $\delta _P(X)>1$
.
$\delta _P(X)>1$
.
Proof. Take
![]() $u\in \mathbb {R}_{\geqslant 0}$
. Since
$u\in \mathbb {R}_{\geqslant 0}$
. Since
![]() $S\sim 2H-E$
, we have
$S\sim 2H-E$
, we have
Using this, we conclude that the divisor
![]() $-K_X-uS$
is pseudoeffective if and only if
$-K_X-uS$
is pseudoeffective if and only if
![]() $u\leqslant \frac {3}{2}$
. For
$u\leqslant \frac {3}{2}$
. For
![]() $u\leqslant \frac {3}{2}$
, let
$u\leqslant \frac {3}{2}$
, let
![]() $P(u)$
be the positive part of Zariski decomposition of the divisor
$P(u)$
be the positive part of Zariski decomposition of the divisor
![]() $-K_X-uS$
, and let
$-K_X-uS$
, and let
![]() $N(u)$
be the negative part of Zariski decomposition of the divisor
$N(u)$
be the negative part of Zariski decomposition of the divisor
![]() $-K_X-uS$
. Then
$-K_X-uS$
. Then
 $$ \begin{align*}P(u)=\left\{\begin{aligned} &-K_X-uS\ \text{if }0\leqslant u\leqslant 1, \\ &(3-2u)H\ \text{if }1\leqslant u\leqslant \frac{3}{2}, \end{aligned} \right. \end{align*} $$
$$ \begin{align*}P(u)=\left\{\begin{aligned} &-K_X-uS\ \text{if }0\leqslant u\leqslant 1, \\ &(3-2u)H\ \text{if }1\leqslant u\leqslant \frac{3}{2}, \end{aligned} \right. \end{align*} $$
and
 $$ \begin{align*}N(u)=\left\{\begin{aligned} &0\ \text{if }0\leqslant u\leqslant 1, \\ &(u-1)E\ \text{if }1\leqslant u\leqslant \frac{3}{2}. \end{aligned} \right. \end{align*} $$
$$ \begin{align*}N(u)=\left\{\begin{aligned} &0\ \text{if }0\leqslant u\leqslant 1, \\ &(u-1)E\ \text{if }1\leqslant u\leqslant \frac{3}{2}. \end{aligned} \right. \end{align*} $$
This gives
 $$ \begin{align*}S_{X}(S)=\frac{1}{14}\int_{0}^{\frac{3}{2}}\big(P(u)\big)^3du=\frac{1}{14}\int_{0}^{1}(14-12u)du+\frac{1}{14}\int_{1}^{\frac{3}{2}} 2(3-2u)^{3}du=\frac{33}{56}<1. \end{align*} $$
$$ \begin{align*}S_{X}(S)=\frac{1}{14}\int_{0}^{\frac{3}{2}}\big(P(u)\big)^3du=\frac{1}{14}\int_{0}^{1}(14-12u)du+\frac{1}{14}\int_{1}^{\frac{3}{2}} 2(3-2u)^{3}du=\frac{33}{56}<1. \end{align*} $$
Now, using [Reference Abban and Zhuang1, Theorem 3.3] and [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Corollary 1.102], we get
 $$ \begin{align} \delta_P(X)\geqslant \min\left\{\frac{1}{S_X(S)},\inf_{\substack{F/S\\ P\in C_S(F)}}\frac{A_S(F)}{S(W_{\bullet,\bullet}^S;F)}\right\}, \end{align} $$
$$ \begin{align} \delta_P(X)\geqslant \min\left\{\frac{1}{S_X(S)},\inf_{\substack{F/S\\ P\in C_S(F)}}\frac{A_S(F)}{S(W_{\bullet,\bullet}^S;F)}\right\}, \end{align} $$
where the infimum is taken by all prime divisors F over the surface S such that
![]() $P\in C_S(F)$
, and
$P\in C_S(F)$
, and
![]() $S(W_{\bullet ,\bullet }^S;F)$
can be computed using [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Corollary 1.108] as follows:
$S(W_{\bullet ,\bullet }^S;F)$
can be computed using [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Corollary 1.108] as follows:
 $$ \begin{align*}S\big(W_{\bullet,\bullet}^S; F\big)=\frac{3}{14}\int_0^{\frac{3}{2}}\big(P(u)\big\vert_{S}\big)^2\mathrm{ord}_{F}\big(N(u)\big\vert_{S}\big)du+\frac{3}{14}\int_{0}^{\frac{3}{2}}\int_0^\infty \mathrm{vol}\big(P(u)\big\vert_{S}-vF\big)dvdu. \end{align*} $$
$$ \begin{align*}S\big(W_{\bullet,\bullet}^S; F\big)=\frac{3}{14}\int_0^{\frac{3}{2}}\big(P(u)\big\vert_{S}\big)^2\mathrm{ord}_{F}\big(N(u)\big\vert_{S}\big)du+\frac{3}{14}\int_{0}^{\frac{3}{2}}\int_0^\infty \mathrm{vol}\big(P(u)\big\vert_{S}-vF\big)dvdu. \end{align*} $$
Let
![]() $E_S=E|_S$
. Then
$E_S=E|_S$
. Then
![]() $E_S\in |-2K_S|$
and
$E_S\in |-2K_S|$
and
![]() $E_S\cong \mathscr {C}$
. Moreover, the surface S is smooth in a neighborhood of the curve
$E_S\cong \mathscr {C}$
. Moreover, the surface S is smooth in a neighborhood of the curve
![]() $E_S$
. Furthermore, we have
$E_S$
. Furthermore, we have
 $$ \begin{align*}P(u)\big\vert_{S}=\left\{\begin{aligned} &-K_S\ \text{if }0\leqslant u\leqslant 1, \\ &(3-2u)(-K_S)\ \text{if }1\leqslant u\leqslant \frac{3}{2}, \end{aligned} \right. \end{align*} $$
$$ \begin{align*}P(u)\big\vert_{S}=\left\{\begin{aligned} &-K_S\ \text{if }0\leqslant u\leqslant 1, \\ &(3-2u)(-K_S)\ \text{if }1\leqslant u\leqslant \frac{3}{2}, \end{aligned} \right. \end{align*} $$
and
 $$ \begin{align*}N(u)\big\vert_{S}=\left\{\begin{aligned} &0\ \text{if }0\leqslant u\leqslant 1, \\ &(u-1)E_S\ \text{if }1\leqslant u\leqslant \frac{3}{2}. \end{aligned} \right. \end{align*} $$
$$ \begin{align*}N(u)\big\vert_{S}=\left\{\begin{aligned} &0\ \text{if }0\leqslant u\leqslant 1, \\ &(u-1)E_S\ \text{if }1\leqslant u\leqslant \frac{3}{2}. \end{aligned} \right. \end{align*} $$
Let F be any prime divisor over S such that
![]() $P\in C_S(F)$
. Then
$P\in C_S(F)$
. Then
 $$ \begin{align*} S\big(W_{\bullet,\bullet}^S; F\big)&=\frac{3}{14}\int_{1}^{\frac{3}{2}}4(u-1)(3-2u)^{2}\mathrm{ord}_{F}\big(E_{S}\big)du+\\ &\quad+\frac{3}{14}\int_{0}^{1} \int_{0}^{\infty}\mathrm{vol}\big(-K_S-vF\big)dvdu+\\ &\quad+\frac{3}{14}\int_{1}^{\frac{3}{2}}\int_{0}^{\infty}\mathrm{vol}\big((3-2u)(-K_S)-vF\big)dvdu=\\ &=\frac{\mathrm{ord}_{F}\big(E_{S}\big)}{56}+\frac{3}{14}\int_{0}^{\infty}\!\mathrm{vol}\big(-K_S-vF\big)dv+\frac{3}{14}\int_{1}^{\frac{3}{2}}\!(3-2u)^3\int_{0}^{\infty}\!\mathrm{vol}\big(-K_S-vF\big)dvdu=\\ &=\frac{\mathrm{ord}_{F}\big(E_{S}\big)}{56}+\frac{3}{14}\int_{0}^{\infty}\mathrm{vol}\big(-K_S-vF\big)dv+\frac{3}{112}\int_{0}^{\infty}\mathrm{vol}\big(-K_S-vF\big)dv=\\ &=\frac{\mathrm{ord}_{F}\big(E_{S}\big)}{56}+\frac{27}{112}\kern-1pt\int_{0}^{\infty}\!\kern-1pt\mathrm{vol}\big(-K_S-vF\big)dv=\frac{\mathrm{ord}_{F}\big(E_{S}\big)}{56}+\frac{27}{28}S_S(F)\kern1.3pt{\leqslant}\kern1.3pt\frac{A_{S}(F)}{56}+\frac{27A_{S}(F)}{28\delta_{P}(S)} \end{align*} $$
$$ \begin{align*} S\big(W_{\bullet,\bullet}^S; F\big)&=\frac{3}{14}\int_{1}^{\frac{3}{2}}4(u-1)(3-2u)^{2}\mathrm{ord}_{F}\big(E_{S}\big)du+\\ &\quad+\frac{3}{14}\int_{0}^{1} \int_{0}^{\infty}\mathrm{vol}\big(-K_S-vF\big)dvdu+\\ &\quad+\frac{3}{14}\int_{1}^{\frac{3}{2}}\int_{0}^{\infty}\mathrm{vol}\big((3-2u)(-K_S)-vF\big)dvdu=\\ &=\frac{\mathrm{ord}_{F}\big(E_{S}\big)}{56}+\frac{3}{14}\int_{0}^{\infty}\!\mathrm{vol}\big(-K_S-vF\big)dv+\frac{3}{14}\int_{1}^{\frac{3}{2}}\!(3-2u)^3\int_{0}^{\infty}\!\mathrm{vol}\big(-K_S-vF\big)dvdu=\\ &=\frac{\mathrm{ord}_{F}\big(E_{S}\big)}{56}+\frac{3}{14}\int_{0}^{\infty}\mathrm{vol}\big(-K_S-vF\big)dv+\frac{3}{112}\int_{0}^{\infty}\mathrm{vol}\big(-K_S-vF\big)dv=\\ &=\frac{\mathrm{ord}_{F}\big(E_{S}\big)}{56}+\frac{27}{112}\kern-1pt\int_{0}^{\infty}\!\kern-1pt\mathrm{vol}\big(-K_S-vF\big)dv=\frac{\mathrm{ord}_{F}\big(E_{S}\big)}{56}+\frac{27}{28}S_S(F)\kern1.3pt{\leqslant}\kern1.3pt\frac{A_{S}(F)}{56}+\frac{27A_{S}(F)}{28\delta_{P}(S)} \end{align*} $$
because log pair
![]() $(S,E_S)$
is log canonical. Therefore, if
$(S,E_S)$
is log canonical. Therefore, if
![]() $\delta _P(S)>\frac {54}{55}$
, Equation (6.1) gives
$\delta _P(S)>\frac {54}{55}$
, Equation (6.1) gives
![]() $\delta _P(X)>1$
. Similarly, if
$\delta _P(X)>1$
. Similarly, if
![]() $P\in \mathrm {Sing}(S)$
,
$P\in \mathrm {Sing}(S)$
,
![]() $P\not \in E_S$
, so
$P\not \in E_S$
, so
![]() $\mathrm {ord}_{F}(E_{S})=0$
, which implies that
$\mathrm {ord}_{F}(E_{S})=0$
, which implies that
Hence, in this case, it follows from Equation (6.1) that
![]() $\delta _P(X)>1$
provided that
$\delta _P(X)>1$
provided that
![]() $\delta _P(S)>\frac {27}{28}$
.
$\delta _P(S)>\frac {27}{28}$
.
Corollary 6.3. If S is smooth, then
![]() $\delta _P(X)>1$
.
$\delta _P(X)>1$
.
Proof. If S is smooth, then
![]() $\delta (S)=\frac {4}{3}$
by [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Lemma 2.12]. Now, apply Lemma 6.2.
$\delta (S)=\frac {4}{3}$
by [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Lemma 2.12]. Now, apply Lemma 6.2.
Corollary 6.4. If P is not contained in a line in S, then
![]() $\delta _P(X)>1$
.
$\delta _P(X)>1$
.
Proof. If P is not contained in a line in S, then P is a smooth point of the surface S, and the blow up of the surface S at this point is a (possibly singular) cubic surface in
![]() $\mathbb {P}^3$
. Thus, arguing exactly as in the end of the proof of [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Lemma 2.12], we obtain
$\mathbb {P}^3$
. Thus, arguing exactly as in the end of the proof of [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Lemma 2.12], we obtain
![]() $\delta _P(S)\geqslant \frac {3}{2}$
, which implies that
$\delta _P(S)\geqslant \frac {3}{2}$
, which implies that
![]() $\delta _P(X)>1$
by Lemma 6.2.
$\delta _P(X)>1$
by Lemma 6.2.
Now, let T be a surface in the linear system
![]() $|H|$
such that
$|H|$
such that
![]() $P\in T$
, and let
$P\in T$
, and let
![]() $\mathcal {Q}=\pi (T)$
. Then
$\mathcal {Q}=\pi (T)$
. Then
![]() $\mathcal {Q}$
is a hyperplane section of the hypersurface
$\mathcal {Q}$
is a hyperplane section of the hypersurface
![]() $\mathscr {Q}$
, so both
$\mathscr {Q}$
, so both
![]() $\mathcal {Q}$
and T are irreducible. In the following, we will choose T such that the surface
$\mathcal {Q}$
and T are irreducible. In the following, we will choose T such that the surface
![]() $\mathcal {Q}$
is smooth so that
$\mathcal {Q}$
is smooth so that
![]() $\mathcal {Q}\cong \mathbb {P}^1\times \mathbb {P}^1$
.
$\mathcal {Q}\cong \mathbb {P}^1\times \mathbb {P}^1$
.
Lemma 6.5. Suppose that T is a general surface in the linear system
![]() $|H|$
such that
$|H|$
such that
![]() $P\in T$
. Then the (scheme) intersection
$P\in T$
. Then the (scheme) intersection
![]() $S\cap T$
is an irreducible reduced curve.
$S\cap T$
is an irreducible reduced curve.
Proof. Let
![]() $\rho \colon \widetilde {S}\to S$
be a blow up of the quartic del Pezzo surface S at the point P, and let Z be the proper transform of the curve
$\rho \colon \widetilde {S}\to S$
be a blow up of the quartic del Pezzo surface S at the point P, and let Z be the proper transform of the curve
![]() $T\vert _{S}$
on the surface
$T\vert _{S}$
on the surface
![]() $\widetilde {S}$
. Then
$\widetilde {S}$
. Then
![]() $|Z|$
has no base points and gives the morphism
$|Z|$
has no base points and gives the morphism
![]() $\eta \colon \widetilde {S}\to \mathbb {P}^3$
that fits the following commutative diagram:
$\eta \colon \widetilde {S}\to \mathbb {P}^3$
that fits the following commutative diagram:

where ![]() is a projection from P. Moreover, if P is a smooth point of the surface S, then
is a projection from P. Moreover, if P is a smooth point of the surface S, then
![]() $Z^2=3$
, and the image of the morphism
$Z^2=3$
, and the image of the morphism
![]() $\eta $
is an irreducible cubic surface in
$\eta $
is an irreducible cubic surface in
![]() $\mathbb {P}^3$
. Similarly, if P is a singular point of the surface S, then we have
$\mathbb {P}^3$
. Similarly, if P is a singular point of the surface S, then we have
![]() $Z^2=4-\mathrm {mult}_P(S)=2$
, and the image of the morphism
$Z^2=4-\mathrm {mult}_P(S)=2$
, and the image of the morphism
![]() $\eta $
is an irreducible quadric surface. Therefore, we conclude that the curve Z must be irreducible and reduced (by Bertini theorem), which implies that the intersection
$\eta $
is an irreducible quadric surface. Therefore, we conclude that the curve Z must be irreducible and reduced (by Bertini theorem), which implies that the intersection
![]() $S\cap T$
is also irreducible and reduced.
$S\cap T$
is also irreducible and reduced.
Remark 6.6. Suppose that S is singular at P, and T is a general surface in
![]() $|H|$
that passes through the point P. Then, choosing appropriate coordinates
$|H|$
that passes through the point P. Then, choosing appropriate coordinates
![]() $[x:y:z:t:w]$
on
$[x:y:z:t:w]$
on
![]() $\mathbb {P}^4$
, we may assume that
$\mathbb {P}^4$
, we may assume that
![]() $\pi (P)=[0:0:0:0:1]$
, and the surface
$\pi (P)=[0:0:0:0:1]$
, and the surface
![]() $\pi (S)$
is given in
$\pi (S)$
is given in
![]() $\mathbb {P}^4$
by
$\mathbb {P}^4$
by
 $$ \begin{align*}\left\{\begin{aligned} &at^2+btx+f_2(x,y,z)=0, \\ &wt=g_2(x,y,z), \\ \end{aligned} \right. \end{align*} $$
$$ \begin{align*}\left\{\begin{aligned} &at^2+btx+f_2(x,y,z)=0, \\ &wt=g_2(x,y,z), \\ \end{aligned} \right. \end{align*} $$
where a and b are complex numbers,
![]() $f_2(x,y,z)$
and
$f_2(x,y,z)$
and
![]() $g_2(x,y,z)$
are nonzero quadratic homogeneous polynomials. In the chart
$g_2(x,y,z)$
are nonzero quadratic homogeneous polynomials. In the chart
![]() $w\ne 0$
, the surface
$w\ne 0$
, the surface
![]() $\pi (S)$
is given by
$\pi (S)$
is given by
 $$ \begin{align*}\left\{\begin{aligned} &at^2+btx+f_2(x,y,z)=0, \\ &t=g_2(x,y,z), \\ \end{aligned} \right. \end{align*} $$
$$ \begin{align*}\left\{\begin{aligned} &at^2+btx+f_2(x,y,z)=0, \\ &t=g_2(x,y,z), \\ \end{aligned} \right. \end{align*} $$
where now we consider x, y, z, t as affine coordinates on
![]() $\mathbb {C}^4$
. Then
$\mathbb {C}^4$
. Then
![]() $\pi (S)\cap \mathcal {Q}$
is cut out on the surface
$\pi (S)\cap \mathcal {Q}$
is cut out on the surface
![]() $\pi (S)$
by
$\pi (S)$
by
![]() $c_1x+c_2y+c_3z+c_4t=0$
, where
$c_1x+c_2y+c_3z+c_4t=0$
, where
![]() $c_1$
,
$c_1$
,
![]() $c_2$
,
$c_2$
,
![]() $c_3$
,
$c_3$
,
![]() $c_4$
are general numbers. The affine part of the surface
$c_4$
are general numbers. The affine part of the surface
![]() $\pi (S)$
is isomorphic to the hypersurface in
$\pi (S)$
is isomorphic to the hypersurface in
![]() $\mathbb {C}^3$
given by
$\mathbb {C}^3$
given by
and the affine part of the curve
![]() $\pi (S)\cap \mathcal {Q}$
is cut out by
$\pi (S)\cap \mathcal {Q}$
is cut out by
![]() $c_1x+c_2y+c_3z+c_4g_2(x,y,z)=0$
. If P is a singular point of the surface S of type
$c_1x+c_2y+c_3z+c_4g_2(x,y,z)=0$
. If P is a singular point of the surface S of type
![]() $\mathbb {D}_4$
or
$\mathbb {D}_4$
or
![]() $\mathbb {D}_5$
, then
$\mathbb {D}_5$
, then
![]() $S\cap T$
has an ordinary cusp at the point P, which easily implies that the intersection
$S\cap T$
has an ordinary cusp at the point P, which easily implies that the intersection
![]() $S\cap T$
is reduced and irreducible. Similarly, if P is a Du Val singular point of the surface S of type
$S\cap T$
is reduced and irreducible. Similarly, if P is a Du Val singular point of the surface S of type
![]() $\mathbb {A}_1$
,
$\mathbb {A}_1$
,
![]() $\mathbb {A}_2$
,
$\mathbb {A}_2$
,
![]() $\mathbb {A}_3$
or
$\mathbb {A}_3$
or
![]() $\mathbb {A}_4$
, then the intersection
$\mathbb {A}_4$
, then the intersection
![]() $S\cap T$
has an isolated ordinary double singularity at P.
$S\cap T$
has an isolated ordinary double singularity at P.
Observe that the morphism
![]() $\pi \colon X\to \mathscr {Q}$
induces a birational morphism
$\pi \colon X\to \mathscr {Q}$
induces a birational morphism
![]() $\varpi \colon T\to \mathcal {Q}$
, and the morphism
$\varpi \colon T\to \mathcal {Q}$
, and the morphism
![]() $\phi \colon X\to \mathbb {P}^1$
induces a fibration
$\phi \colon X\to \mathbb {P}^1$
induces a fibration
![]() $\varphi \colon T\to \mathbb {P}^1$
that both fit the following commutative diagram:
$\varphi \colon T\to \mathbb {P}^1$
that both fit the following commutative diagram:

where ![]() is a map given by the pencil generated by the curves
is a map given by the pencil generated by the curves
![]() $\mathscr {Q}^\prime \vert _{\mathcal {Q}}$
and
$\mathscr {Q}^\prime \vert _{\mathcal {Q}}$
and
![]() $\mathscr {Q}^{\prime \prime }\vert _{\mathcal {Q}}$
. In the following, we will always choose
$\mathscr {Q}^{\prime \prime }\vert _{\mathcal {Q}}$
. In the following, we will always choose
![]() $T\in |H|$
such that the quadric surface
$T\in |H|$
such that the quadric surface
![]() $\mathcal {Q}$
is smooth, and T is either smooth or has one isolated ordinary singularity, which would imply that a general fiber of the induced fibration
$\mathcal {Q}$
is smooth, and T is either smooth or has one isolated ordinary singularity, which would imply that a general fiber of the induced fibration
![]() $\varphi \colon T\to \mathbb {P}^1$
is a smooth elliptic curve. Let
$\varphi \colon T\to \mathbb {P}^1$
is a smooth elliptic curve. Let
![]() $\mathcal {C}=S\vert _{T}$
. Then
$\mathcal {C}=S\vert _{T}$
. Then
![]() $\mathcal {C}$
is the fiber of the (elliptic) fibration
$\mathcal {C}$
is the fiber of the (elliptic) fibration
![]() $\varphi $
that contains the point P.
$\varphi $
that contains the point P.
Let u be a nonnegative real number. Then
![]() $-K_X-uT\sim _{\mathbb {R}}(3-u)H-E\sim _{\mathbb {R}}(1-u)H+S$
, which implies that
$-K_X-uT\sim _{\mathbb {R}}(3-u)H-E\sim _{\mathbb {R}}(1-u)H+S$
, which implies that
![]() $-K_X-uT$
is nef
$-K_X-uT$
is nef
![]() $\iff -K_X-uT$
is pseudoeffective
$\iff -K_X-uT$
is pseudoeffective
![]() $\iff u\in [0,1]$
. Integrating, we get
$\iff u\in [0,1]$
. Integrating, we get
![]() $S_{X}(T)=\frac {9}{28}<1$
. For simplicity, we let
$S_{X}(T)=\frac {9}{28}<1$
. For simplicity, we let
![]() $P(u)=-K_X-uT$
.
$P(u)=-K_X-uT$
.
Lemma 6.7. Suppose that S is singular at P. Then
![]() $\delta _P(X)>1$
.
$\delta _P(X)>1$
.
Proof. Now, let us choose
![]() $T\in |H|$
such that T is a general surface in
$T\in |H|$
such that T is a general surface in
![]() $|H|$
that contains P. Then T and
$|H|$
that contains P. Then T and
![]() $\mathcal {Q}$
are smooth, and
$\mathcal {Q}$
are smooth, and
![]() $\varpi $
is a blow up of the eight intersection points
$\varpi $
is a blow up of the eight intersection points
![]() $\mathscr {C}\cap \mathcal {Q}$
. Moreover, by Lemma 6.5, the curve
$\mathscr {C}\cap \mathcal {Q}$
. Moreover, by Lemma 6.5, the curve
![]() $\mathcal {C}$
is an irreducible singular curve of arithmetic genus
$\mathcal {C}$
is an irreducible singular curve of arithmetic genus
![]() $1$
. Thus, we have
$1$
. Thus, we have
![]() $P=\mathrm {Sing}(\mathcal {C})$
. Furthermore, using Remark 6.6, we see that
$P=\mathrm {Sing}(\mathcal {C})$
. Furthermore, using Remark 6.6, we see that
-
• either
 $\mathcal {C}$
has an isolated ordinary double singularity at P,
$\mathcal {C}$
has an isolated ordinary double singularity at P, -
• or the curve
 $\mathcal {C}$
has an ordinary cusp at the point P.
$\mathcal {C}$
has an ordinary cusp at the point P.
Recall that
![]() $\mathcal {Q}$
is a smooth quadric surface, so that it contains exactly two lines that pass though
$\mathcal {Q}$
is a smooth quadric surface, so that it contains exactly two lines that pass though
![]() $\pi (P)$
. Since T is chosen to be general, these lines are disjoint from
$\pi (P)$
. Since T is chosen to be general, these lines are disjoint from
![]() $\mathscr {C}\cap \mathcal {Q}$
. Denote by
$\mathscr {C}\cap \mathcal {Q}$
. Denote by
![]() $L_1$
and
$L_1$
and
![]() $L_2$
the proper transforms of these lines on T. Then
$L_2$
the proper transforms of these lines on T. Then
Now, we let
![]() $\sigma \colon \widetilde {T}\to T$
be the blow up of the point P, we let
$\sigma \colon \widetilde {T}\to T$
be the blow up of the point P, we let
![]() $\mathbf {e}$
be the
$\mathbf {e}$
be the
![]() $\sigma $
-exceptional curve, and we denote by
$\sigma $
-exceptional curve, and we denote by
![]() $\widetilde {\mathcal {C}}$
,
$\widetilde {\mathcal {C}}$
,
![]() $\widetilde {L}_1$
,
$\widetilde {L}_1$
,
![]() $\widetilde {L}_2$
the proper transforms on
$\widetilde {L}_2$
the proper transforms on
![]() $\widetilde {T}$
of the curves
$\widetilde {T}$
of the curves
![]() $\mathcal {C}$
,
$\mathcal {C}$
,
![]() $L_1$
,
$L_1$
,
![]() $L_2$
, respectively. Take a nonnegative real number v. Then
$L_2$
, respectively. Take a nonnegative real number v. Then
Note that the curves
![]() $\widetilde {\mathcal {C}}$
,
$\widetilde {\mathcal {C}}$
,
![]() $\widetilde {L}_1$
,
$\widetilde {L}_1$
,
![]() $\widetilde {L}_2$
are disjoint. Moreover, we have
$\widetilde {L}_2$
are disjoint. Moreover, we have
![]() $\widetilde {L}_{1}^2=\widetilde {L}_{2}^2=-1$
and
$\widetilde {L}_{1}^2=\widetilde {L}_{2}^2=-1$
and
![]() $\widetilde {\mathcal {C}}^2=-4$
. Thus, using Equation (6.2), we see that
$\widetilde {\mathcal {C}}^2=-4$
. Thus, using Equation (6.2), we see that
![]() $\sigma ^*(P(u)\vert _{T})-v\mathbf {e}$
is pseudoeffective
$\sigma ^*(P(u)\vert _{T})-v\mathbf {e}$
is pseudoeffective
![]() $\iff v\leqslant 4-2u$
.
$\iff v\leqslant 4-2u$
.
Let
![]() $\widetilde {P}(u,v)$
be the positive part of Zariski decomposition of the divisor
$\widetilde {P}(u,v)$
be the positive part of Zariski decomposition of the divisor
![]() $\sigma ^*(P(u)\vert _{T})-v\mathbf {e}$
, and let
$\sigma ^*(P(u)\vert _{T})-v\mathbf {e}$
, and let
![]() $\widetilde {N}(u,v)$
be its negative part. Then it follows from [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Remark 1.113] that
$\widetilde {N}(u,v)$
be its negative part. Then it follows from [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Remark 1.113] that
 $$ \begin{align} \delta_P(X)\geqslant\min\left\{\frac{1}{S_X(T)}, \frac{2}{S(W_{\bullet,\bullet}^{\widetilde{T}};\mathbf{e})},\inf_{O\in \mathbf{e}}\frac{1}{S(W_{\bullet, \bullet,\bullet}^{\widetilde{T},\mathbf{e}};O)}\right\}, \end{align} $$
$$ \begin{align} \delta_P(X)\geqslant\min\left\{\frac{1}{S_X(T)}, \frac{2}{S(W_{\bullet,\bullet}^{\widetilde{T}};\mathbf{e})},\inf_{O\in \mathbf{e}}\frac{1}{S(W_{\bullet, \bullet,\bullet}^{\widetilde{T},\mathbf{e}};O)}\right\}, \end{align} $$
where
![]() $S(W_{\bullet ,\bullet }^{\widetilde {T}};\mathbf {e})$
and
$S(W_{\bullet ,\bullet }^{\widetilde {T}};\mathbf {e})$
and
![]() $S(W_{\bullet , \bullet ,\bullet }^{\widetilde {T},\mathbf {e}};O)$
are defined in [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, § 1.7], and these two numbers can be computed using formulas described in [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Remark 1.113]. Namely, we have
$S(W_{\bullet , \bullet ,\bullet }^{\widetilde {T},\mathbf {e}};O)$
are defined in [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, § 1.7], and these two numbers can be computed using formulas described in [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Remark 1.113]. Namely, we have
 $$ \begin{align*}S\big(W_{\bullet,\bullet}^{\widetilde{T}};\mathbf{e}\big)=\frac{3}{14}\int_0^1\int_0^{4-2u}\big(\widetilde{P}(u,v)\big)^2dvdu \end{align*} $$
$$ \begin{align*}S\big(W_{\bullet,\bullet}^{\widetilde{T}};\mathbf{e}\big)=\frac{3}{14}\int_0^1\int_0^{4-2u}\big(\widetilde{P}(u,v)\big)^2dvdu \end{align*} $$
and
 $$ \begin{align*}S\big(W_{\bullet, \bullet,\bullet}^{\widetilde{T},\mathbf{e}};O\big)=\frac{3}{14}\int_0^1\!\int_0^{4-2u}\Big(\big(\widetilde{P}(u,v)\cdot\mathbf{e}\big)\Big)^2dvdu+\frac{3}{7}\int_0^1\!\int_0^{4-2u}\kern-1.5pt\big(\widetilde{P}(u,v)\cdot\mathbf{e}\big)\mathrm{ord}_O\Big(\widetilde{N}(u,v)\big|_{\mathbf{e}}\Big)dvdu, \end{align*} $$
$$ \begin{align*}S\big(W_{\bullet, \bullet,\bullet}^{\widetilde{T},\mathbf{e}};O\big)=\frac{3}{14}\int_0^1\!\int_0^{4-2u}\Big(\big(\widetilde{P}(u,v)\cdot\mathbf{e}\big)\Big)^2dvdu+\frac{3}{7}\int_0^1\!\int_0^{4-2u}\kern-1.5pt\big(\widetilde{P}(u,v)\cdot\mathbf{e}\big)\mathrm{ord}_O\Big(\widetilde{N}(u,v)\big|_{\mathbf{e}}\Big)dvdu, \end{align*} $$
where O is a point in
![]() $\mathbf {e}$
. Moreover, using Equation (6.2), we compute
$\mathbf {e}$
. Moreover, using Equation (6.2), we compute
![]() $\widetilde {P}(u,v)$
and
$\widetilde {P}(u,v)$
and
![]() $\widetilde {N}(u,v)$
as follows:
$\widetilde {N}(u,v)$
as follows:
 $$ \begin{align*}\widetilde{P}(u,v)=\left\{\begin{aligned} &\widetilde{\mathcal{C}}+(1-u)(\widetilde{L}_{1}+\widetilde{L}_{2})+(4-2u-v)\mathbf{e}\ \text{if }0\leqslant v\leqslant 2-2u, \\ &\frac{4-2u-v}{2}\widetilde{\mathcal{C}}+(1-u)(\widetilde{L}_{1}+\widetilde{L}_{2})+(4-2u-v)\mathbf{e}\ \text{if }2-2u\leqslant v\leqslant 3-u, \\ &\frac{4-2u-v}{2}\big(\widetilde{\mathcal{C}}+2(\widetilde{L}_{1}+\widetilde{L}_{2})+2\mathbf{e}\big)\ \text{if }3-u\leqslant v\leqslant 4-2u, \\ \end{aligned} \right. \end{align*} $$
$$ \begin{align*}\widetilde{P}(u,v)=\left\{\begin{aligned} &\widetilde{\mathcal{C}}+(1-u)(\widetilde{L}_{1}+\widetilde{L}_{2})+(4-2u-v)\mathbf{e}\ \text{if }0\leqslant v\leqslant 2-2u, \\ &\frac{4-2u-v}{2}\widetilde{\mathcal{C}}+(1-u)(\widetilde{L}_{1}+\widetilde{L}_{2})+(4-2u-v)\mathbf{e}\ \text{if }2-2u\leqslant v\leqslant 3-u, \\ &\frac{4-2u-v}{2}\big(\widetilde{\mathcal{C}}+2(\widetilde{L}_{1}+\widetilde{L}_{2})+2\mathbf{e}\big)\ \text{if }3-u\leqslant v\leqslant 4-2u, \\ \end{aligned} \right. \end{align*} $$
and
 $$ \begin{align*}\widetilde{N}(u,v)=\left\{\begin{aligned} &0\ \text{if }0\leqslant v\leqslant 2-2u, \\ &\frac{v-2+2u}{2}\widetilde{\mathcal{C}}\ \text{if }2-2u\leqslant v\leqslant 3-u, \\ &\frac{v-2+2u}{2}\widetilde{\mathcal{C}}+(v-3+u)(\widetilde{L}_{1}+\widetilde{L}_{2}) \ \text{if }3-u\leqslant v\leqslant 4-2u.\\ \end{aligned} \right. \end{align*} $$
$$ \begin{align*}\widetilde{N}(u,v)=\left\{\begin{aligned} &0\ \text{if }0\leqslant v\leqslant 2-2u, \\ &\frac{v-2+2u}{2}\widetilde{\mathcal{C}}\ \text{if }2-2u\leqslant v\leqslant 3-u, \\ &\frac{v-2+2u}{2}\widetilde{\mathcal{C}}+(v-3+u)(\widetilde{L}_{1}+\widetilde{L}_{2}) \ \text{if }3-u\leqslant v\leqslant 4-2u.\\ \end{aligned} \right. \end{align*} $$
Thus, we have
 $$ \begin{align*}\big(\widetilde{P}(u,v)\big)^2=\left\{\begin{aligned} &2(1-u)(5-u)-v^{2}\ \text{if }0\leqslant v\leqslant 2-2u, \\ &2(1-u)(7-3u-2v)\ \text{if }2-2u\leqslant v\leqslant 3-u, \\ &2(4-2 u-v)^{2}\ \text{if }3-u\leqslant v\leqslant 4-2u, \\ \end{aligned} \right. \end{align*} $$
$$ \begin{align*}\big(\widetilde{P}(u,v)\big)^2=\left\{\begin{aligned} &2(1-u)(5-u)-v^{2}\ \text{if }0\leqslant v\leqslant 2-2u, \\ &2(1-u)(7-3u-2v)\ \text{if }2-2u\leqslant v\leqslant 3-u, \\ &2(4-2 u-v)^{2}\ \text{if }3-u\leqslant v\leqslant 4-2u, \\ \end{aligned} \right. \end{align*} $$
and
 $$ \begin{align*}\widetilde{P}(u,v)\cdot\mathbf{e}=\left\{\begin{aligned} &v\ \text{if }0\leqslant v\leqslant 2-2u, \\ &2(1-u)\ \text{if }2-2u\leqslant v\leqslant 3-u, \\ &2(4-2u-v)\ \text{if }3-u\leqslant v\leqslant 4-2u. \\ \end{aligned} \right. \end{align*} $$
$$ \begin{align*}\widetilde{P}(u,v)\cdot\mathbf{e}=\left\{\begin{aligned} &v\ \text{if }0\leqslant v\leqslant 2-2u, \\ &2(1-u)\ \text{if }2-2u\leqslant v\leqslant 3-u, \\ &2(4-2u-v)\ \text{if }3-u\leqslant v\leqslant 4-2u. \\ \end{aligned} \right. \end{align*} $$
Now, integrating, we get
![]() $S(W_{\bullet ,\bullet }^{\widetilde {T}};\mathbf {e})=\frac {51}{28}<2$
.
$S(W_{\bullet ,\bullet }^{\widetilde {T}};\mathbf {e})=\frac {51}{28}<2$
.
Let O be an arbitrary point in
![]() $\mathbf {e}$
. If
$\mathbf {e}$
. If
![]() $O\not \in \widetilde {L}_1\cup \widetilde {L}_2\cup \widetilde {\mathcal {C}}$
, then we compute
$O\not \in \widetilde {L}_1\cup \widetilde {L}_2\cup \widetilde {\mathcal {C}}$
, then we compute
![]() $S(W_{\bullet , \bullet ,\bullet }^{\widetilde {T},\mathbf {e}};O)=\frac {4}{7}$
. Similarly, if
$S(W_{\bullet , \bullet ,\bullet }^{\widetilde {T},\mathbf {e}};O)=\frac {4}{7}$
. Similarly, if
![]() $O\in \widetilde {L}_1\cup \widetilde {L}_2$
, then
$O\in \widetilde {L}_1\cup \widetilde {L}_2$
, then
![]() $S(W_{\bullet , \bullet ,\bullet }^{\widetilde {T},\mathbf {e}};O)=\frac {17}{28}$
. Finally, if
$S(W_{\bullet , \bullet ,\bullet }^{\widetilde {T},\mathbf {e}};O)=\frac {17}{28}$
. Finally, if
![]() $O\in \widetilde {\mathcal {C}}$
, then
$O\in \widetilde {\mathcal {C}}$
, then
 $$ \begin{align*} S\big(W_{\bullet, \bullet,\bullet}^{\widetilde{T},\mathbf{e}};O\big)&=\frac{4}{7}+\frac{3}{7}\int_{0}^{1}\int_{2-2u}^{3-u} 2(1-u)\frac{v-2+2 u}{2}\mathrm{ord}_O\big(\widetilde{\mathcal{C}}\big\vert_{\mathbf{e}}\big)dvdu+\\ &\quad+\frac{3}{7}\int_{0}^{1}\int_{3-u}^{4-2u} 2(4-2u-v)\frac{v-2+2 u}{2}\mathrm{ord}_O\big(\widetilde{\mathcal{C}}\big\vert_{\mathbf{e}}\big)dvdu=\frac{4}{7}+\frac{17}{56}\mathrm{ord}_O\big(\widetilde{\mathcal{C}}\big\vert_{\mathbf{e}}\big). \end{align*} $$
$$ \begin{align*} S\big(W_{\bullet, \bullet,\bullet}^{\widetilde{T},\mathbf{e}};O\big)&=\frac{4}{7}+\frac{3}{7}\int_{0}^{1}\int_{2-2u}^{3-u} 2(1-u)\frac{v-2+2 u}{2}\mathrm{ord}_O\big(\widetilde{\mathcal{C}}\big\vert_{\mathbf{e}}\big)dvdu+\\ &\quad+\frac{3}{7}\int_{0}^{1}\int_{3-u}^{4-2u} 2(4-2u-v)\frac{v-2+2 u}{2}\mathrm{ord}_O\big(\widetilde{\mathcal{C}}\big\vert_{\mathbf{e}}\big)dvdu=\frac{4}{7}+\frac{17}{56}\mathrm{ord}_O\big(\widetilde{\mathcal{C}}\big\vert_{\mathbf{e}}\big). \end{align*} $$
Hence, if
![]() $\widetilde {\mathcal {C}}$
intersects
$\widetilde {\mathcal {C}}$
intersects
![]() $\mathbf {e}$
transversally, then
$\mathbf {e}$
transversally, then
![]() $S(W_{\bullet , \bullet ,\bullet }^{\widetilde {T},\mathbf {e}};O)<1$
so that
$S(W_{\bullet , \bullet ,\bullet }^{\widetilde {T},\mathbf {e}};O)<1$
so that
![]() $\delta _P(X)>1$
by Equation (6.3).
$\delta _P(X)>1$
by Equation (6.3).
Therefore, to complete the proof of the lemma, we may assume that
![]() $\widetilde {\mathcal {C}}$
is tangent to
$\widetilde {\mathcal {C}}$
is tangent to
![]() $\mathbf {e}$
. This means that
$\mathbf {e}$
. This means that
![]() $\mathcal {C}$
has a cusp at P, and the intersection
$\mathcal {C}$
has a cusp at P, and the intersection
![]() $\widetilde {\mathcal {C}}\cap \mathbf {e}$
consists of a single point.
$\widetilde {\mathcal {C}}\cap \mathbf {e}$
consists of a single point.
Now, as in the proof of Lemma 4.5, we consider the following commutative diagram:

where
![]() $\gamma $
is a composition of the blow up of the point
$\gamma $
is a composition of the blow up of the point
![]() $\widetilde {\mathcal {C}}\cap \mathbf {e}$
with the blow up of the unique intersection point of the proper transforms of the curves
$\widetilde {\mathcal {C}}\cap \mathbf {e}$
with the blow up of the unique intersection point of the proper transforms of the curves
![]() $\widetilde {\mathcal {C}}$
and
$\widetilde {\mathcal {C}}$
and
![]() $\mathbf {e}$
,
$\mathbf {e}$
,
![]() $\upsilon $
is the birational contraction of all
$\upsilon $
is the birational contraction of all
![]() $(\sigma \circ \gamma )$
-exceptional curves that are not
$(\sigma \circ \gamma )$
-exceptional curves that are not
![]() $(-1)$
-curve, and
$(-1)$
-curve, and
![]() $\varsigma $
is the birational contraction of the proper transform of the unique
$\varsigma $
is the birational contraction of the proper transform of the unique
![]() $\gamma $
-exceptional curve that is
$\gamma $
-exceptional curve that is
![]() $(-1)$
-curve. Then
$(-1)$
-curve. Then
![]() $\widehat {T}$
has two singular points:
$\widehat {T}$
has two singular points:
-
(1) a cyclic quotient singularity of type
 $\frac {1}{2}(1,1)$
, which we denote by
$\frac {1}{2}(1,1)$
, which we denote by
 $O_2$
;
$O_2$
; -
(2) a cyclic quotient singularity of type
 $\frac {1}{3}(1,1)$
, which we denote by
$\frac {1}{3}(1,1)$
, which we denote by
 $O_3$
.
$O_3$
.
Let
![]() $\mathbf {f}$
be the
$\mathbf {f}$
be the
![]() $\varsigma $
-exceptional curve, let
$\varsigma $
-exceptional curve, let
![]() $\widehat {\mathcal {C}}$
be the proper transform on
$\widehat {\mathcal {C}}$
be the proper transform on
![]() $\widehat {T}$
of the curve
$\widehat {T}$
of the curve
![]() $\mathcal {C}$
and let
$\mathcal {C}$
and let
![]() $\widehat {L}_1$
and
$\widehat {L}_1$
and
![]() $\widehat {L}_2$
be the proper transforms on
$\widehat {L}_2$
be the proper transforms on
![]() $\widehat {T}$
of the curves
$\widehat {T}$
of the curves
![]() $L_1$
and
$L_1$
and
![]() $L_2$
, respectively. Then the curves
$L_2$
, respectively. Then the curves
![]() $\mathbf {f}$
,
$\mathbf {f}$
,
![]() $\widehat {\mathcal {C}}$
,
$\widehat {\mathcal {C}}$
,
![]() $\widehat {L}_1$
,
$\widehat {L}_1$
,
![]() $\widehat {L}_2$
are smooth, and the curve
$\widehat {L}_2$
are smooth, and the curve
![]() $\mathbf {f}$
contains both points
$\mathbf {f}$
contains both points
![]() $O_2$
and
$O_2$
and
![]() $O_3$
, which are not contained in
$O_3$
, which are not contained in
![]() $\widehat {\mathcal {C}}$
. Moreover, we have
$\widehat {\mathcal {C}}$
. Moreover, we have
Furthermore, we have
![]() $A_T(\mathbf {f})=5$
,
$A_T(\mathbf {f})=5$
,
![]() $\varsigma ^*(\mathcal {C})\sim \widehat {\mathcal {C}}+6\mathbf {f}$
,
$\varsigma ^*(\mathcal {C})\sim \widehat {\mathcal {C}}+6\mathbf {f}$
,
![]() $\varsigma ^*(L_1)\sim \widehat {L}_1+2\mathbf {f}$
,
$\varsigma ^*(L_1)\sim \widehat {L}_1+2\mathbf {f}$
,
![]() $\varsigma ^*(L_2)\sim \widehat {L}_2+2\mathbf {f}$
, and the intersection form of the curves
$\varsigma ^*(L_2)\sim \widehat {L}_2+2\mathbf {f}$
, and the intersection form of the curves
![]() $\mathbf {f}$
,
$\mathbf {f}$
,
![]() $\widehat {\mathcal {C}}$
,
$\widehat {\mathcal {C}}$
,
![]() $\widehat {L}_1$
and
$\widehat {L}_1$
and
![]() $\widehat {L}_2$
is given in the following table:
$\widehat {L}_2$
is given in the following table:

For a nonnegative real number v, we have
which implies that the divisor
![]() $\varsigma ^*(P(u)\vert _{T})-v\mathbf {f}$
is pseudoeffective if and only if
$\varsigma ^*(P(u)\vert _{T})-v\mathbf {f}$
is pseudoeffective if and only if
![]() $v\leqslant 10-4u$
because the intersection form of the curves
$v\leqslant 10-4u$
because the intersection form of the curves
![]() $\widehat {\mathcal {C}}$
,
$\widehat {\mathcal {C}}$
,
![]() $\widehat {L}_1$
,
$\widehat {L}_1$
,
![]() $\widehat {L}_2$
is negative definite.
$\widehat {L}_2$
is negative definite.
Let
![]() $\widehat {P}(u,v)$
be the positive part of Zariski decomposition of the divisor
$\widehat {P}(u,v)$
be the positive part of Zariski decomposition of the divisor
![]() $\varsigma ^*(P(u)\vert _{T})-v\mathbf {f}$
, and let
$\varsigma ^*(P(u)\vert _{T})-v\mathbf {f}$
, and let
![]() $\widehat {N}(u,v)$
be its negative part. Set
$\widehat {N}(u,v)$
be its negative part. Set
![]() $\Delta _{\mathbf {f}}=\frac {1}{2}O_2+\frac {2}{3}O_3$
. By [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Remark 1.113], we get
$\Delta _{\mathbf {f}}=\frac {1}{2}O_2+\frac {2}{3}O_3$
. By [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Remark 1.113], we get
 $$ \begin{align} \delta_P(X)\geqslant\min\left\{\frac{1}{S_X(T)}, \frac{5}{S(W_{\bullet,\bullet}^{\widehat{T}};\mathbf{f})},\inf_{O\in \mathbf{f}}\frac{1-\mathrm{ord}_O\big(\Delta_{\mathbf{f}}\big)}{S(W_{\bullet, \bullet,\bullet}^{\widehat{T},\mathbf{f}};O)}\right\}, \end{align} $$
$$ \begin{align} \delta_P(X)\geqslant\min\left\{\frac{1}{S_X(T)}, \frac{5}{S(W_{\bullet,\bullet}^{\widehat{T}};\mathbf{f})},\inf_{O\in \mathbf{f}}\frac{1-\mathrm{ord}_O\big(\Delta_{\mathbf{f}}\big)}{S(W_{\bullet, \bullet,\bullet}^{\widehat{T},\mathbf{f}};O)}\right\}, \end{align} $$
where
![]() $S(W_{\bullet ,\bullet }^{\widehat {T}};\mathbf {f})$
and
$S(W_{\bullet ,\bullet }^{\widehat {T}};\mathbf {f})$
and
![]() $S(W_{\bullet , \bullet ,\bullet }^{\widehat {T},\mathbf {f}};O)$
are defined as
$S(W_{\bullet , \bullet ,\bullet }^{\widehat {T},\mathbf {f}};O)$
are defined as
![]() $S(W_{\bullet ,\bullet }^{\widetilde {T}};\mathbf {e})$
and
$S(W_{\bullet ,\bullet }^{\widetilde {T}};\mathbf {e})$
and
![]() $S(W_{\bullet , \bullet ,\bullet }^{\widetilde {T},\mathbf {e}};O)$
used earlier. Moreover, it follows from [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Remark 1.113] that
$S(W_{\bullet , \bullet ,\bullet }^{\widetilde {T},\mathbf {e}};O)$
used earlier. Moreover, it follows from [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Remark 1.113] that
 $$ \begin{align*}S\big(W_{\bullet,\bullet}^{\widehat{T}};\mathbf{f}\big)=\frac{3}{14}\int_0^1\int_0^{10-4u}\big(\widehat{P}(u,v)\big)^2dvdu \end{align*} $$
$$ \begin{align*}S\big(W_{\bullet,\bullet}^{\widehat{T}};\mathbf{f}\big)=\frac{3}{14}\int_0^1\int_0^{10-4u}\big(\widehat{P}(u,v)\big)^2dvdu \end{align*} $$
and
 $$ \begin{align*}S\big(W_{\bullet, \bullet,\bullet}^{\widehat{T},\mathbf{f}};O\big)=\frac{3}{14}\int_0^1\!\kern-1pt\int_0^{10-4u}\!\Big(\big(\widehat{P}(u,v)\cdot\mathbf{f}\big)\Big)^2dvdu+\frac{3}{7}\int_0^1\!\kern-1pt\int_0^{10-4u}\!\big(\widehat{P}(u,v)\cdot\mathbf{f}\big)\mathrm{ord}_O\Big(\widehat{N}(u,v)\big|_{\mathbf{f}}\Big)dvdu. \end{align*} $$
$$ \begin{align*}S\big(W_{\bullet, \bullet,\bullet}^{\widehat{T},\mathbf{f}};O\big)=\frac{3}{14}\int_0^1\!\kern-1pt\int_0^{10-4u}\!\Big(\big(\widehat{P}(u,v)\cdot\mathbf{f}\big)\Big)^2dvdu+\frac{3}{7}\int_0^1\!\kern-1pt\int_0^{10-4u}\!\big(\widehat{P}(u,v)\cdot\mathbf{f}\big)\mathrm{ord}_O\Big(\widehat{N}(u,v)\big|_{\mathbf{f}}\Big)dvdu. \end{align*} $$
Moreover, we compute
![]() $\widehat {P}(u,v)$
and
$\widehat {P}(u,v)$
and
![]() $\widehat {N}(u,v)$
as follows:
$\widehat {N}(u,v)$
as follows:
 $$ \begin{align*}\widehat{P}(u,v)=\left\{\begin{aligned} &\widetilde{\mathcal{C}}+(1-u)(\widetilde{L}_{1}+\widetilde{L}_{2})+(10-4u-v)\mathbf{f}\ \text{if }0\leqslant v\leqslant 4-4u, \\ &\frac{10-4u-v}{6}\widetilde{\mathcal{C}}+(1-u)(\widetilde{L}_{1}+\widetilde{L}_{2})+(10-4u-v)\mathbf{f}\ \text{if }4-4u\leqslant v\leqslant 9-3u, \\ &\frac{10-4u-v}{6}\big(\widehat{\mathcal{C}}+6(\widehat{L}_{1}+\widehat{L}_{2})+6\mathbf{f}\big)\ \text{if }9-3u\leqslant v\leqslant 10-4u, \\ \end{aligned} \right. \end{align*} $$
$$ \begin{align*}\widehat{P}(u,v)=\left\{\begin{aligned} &\widetilde{\mathcal{C}}+(1-u)(\widetilde{L}_{1}+\widetilde{L}_{2})+(10-4u-v)\mathbf{f}\ \text{if }0\leqslant v\leqslant 4-4u, \\ &\frac{10-4u-v}{6}\widetilde{\mathcal{C}}+(1-u)(\widetilde{L}_{1}+\widetilde{L}_{2})+(10-4u-v)\mathbf{f}\ \text{if }4-4u\leqslant v\leqslant 9-3u, \\ &\frac{10-4u-v}{6}\big(\widehat{\mathcal{C}}+6(\widehat{L}_{1}+\widehat{L}_{2})+6\mathbf{f}\big)\ \text{if }9-3u\leqslant v\leqslant 10-4u, \\ \end{aligned} \right. \end{align*} $$
and
 $$ \begin{align*}\widehat{N}(u,v)=\left\{\begin{aligned} &0\ \text{if }0\leqslant v\leqslant 4-4u, \\ &\frac{v-4+4u}{6}\widehat{\mathcal{C}}\ \text{if }4-4u\leqslant v\leqslant 9-3u, \\ &\frac{v-4+4u}{6}\widehat{\mathcal{C}}+(v-9+3u)(\widetilde{L}_{1}+\widetilde{L}_{2})\ \text{if }9-3u\leqslant v\leqslant 10-4u. \\ \end{aligned} \right. \end{align*} $$
$$ \begin{align*}\widehat{N}(u,v)=\left\{\begin{aligned} &0\ \text{if }0\leqslant v\leqslant 4-4u, \\ &\frac{v-4+4u}{6}\widehat{\mathcal{C}}\ \text{if }4-4u\leqslant v\leqslant 9-3u, \\ &\frac{v-4+4u}{6}\widehat{\mathcal{C}}+(v-9+3u)(\widetilde{L}_{1}+\widetilde{L}_{2})\ \text{if }9-3u\leqslant v\leqslant 10-4u. \\ \end{aligned} \right. \end{align*} $$
This gives
 $$ \begin{align*}\big(\widehat{P}(u,v)\big)^2=\left\{\begin{aligned} &2(1-u)(5-u)-\frac{v^{2}}{6}\ \text{if }0\leqslant v\leqslant 4-4u, \\ &\frac{2(1-u)(19-7u-2v)}{3}\ \text{if }4-4u\leqslant v\leqslant 9-3u, \\ &\frac{2(10-4u-v)^{2}}{3}\ \text{if }9-3u\leqslant v\leqslant 10-4u, \\ \end{aligned} \right. \end{align*} $$
$$ \begin{align*}\big(\widehat{P}(u,v)\big)^2=\left\{\begin{aligned} &2(1-u)(5-u)-\frac{v^{2}}{6}\ \text{if }0\leqslant v\leqslant 4-4u, \\ &\frac{2(1-u)(19-7u-2v)}{3}\ \text{if }4-4u\leqslant v\leqslant 9-3u, \\ &\frac{2(10-4u-v)^{2}}{3}\ \text{if }9-3u\leqslant v\leqslant 10-4u, \\ \end{aligned} \right. \end{align*} $$
and
 $$ \begin{align*}\widehat{P}(u,v)\cdot\mathbf{f}=\left\{\begin{aligned} &\frac{v}{6}\ \text{if }0\leqslant v\leqslant 4-4u, \\ &\frac{2(1-u)}{3}\ \text{if }4-4u\leqslant v\leqslant 9-3u, \\ &\frac{2(10-4 u-v)}{3}\ \text{if }9-3u\leqslant v\leqslant 10-4u. \\ \end{aligned} \right. \end{align*} $$
$$ \begin{align*}\widehat{P}(u,v)\cdot\mathbf{f}=\left\{\begin{aligned} &\frac{v}{6}\ \text{if }0\leqslant v\leqslant 4-4u, \\ &\frac{2(1-u)}{3}\ \text{if }4-4u\leqslant v\leqslant 9-3u, \\ &\frac{2(10-4 u-v)}{3}\ \text{if }9-3u\leqslant v\leqslant 10-4u. \\ \end{aligned} \right. \end{align*} $$
Now, integrating, we get
![]() $S(W_{\bullet ,\bullet }^{\widehat {T}};\mathbf {f})=\frac {135}{28}<A_{T}(\mathbf {f})=5$
.
$S(W_{\bullet ,\bullet }^{\widehat {T}};\mathbf {f})=\frac {135}{28}<A_{T}(\mathbf {f})=5$
.
Let O be a point in
![]() $\mathbf {f}$
. If
$\mathbf {f}$
. If
![]() $O\not \in \widehat {L}_1\cup \widehat {L}_2\cup \widehat {\mathcal {C}}$
, then
$O\not \in \widehat {L}_1\cup \widehat {L}_2\cup \widehat {\mathcal {C}}$
, then
 $$ \begin{align*} S\big(W_{\bullet, \bullet,\bullet}^{\widehat{T},\mathbf{f}};O\big)&=\frac{3}{14}\int_{0}^{1}\int_{0}^{4-4u}\left(\frac{v}{6}\right)^{2}dvdu+\frac{3}{14}\int_{0}^{1}\int_{4-4u}^{9-3u}\left(\frac{2(1-u)}{3}\right)^{2}dvdu+\\ &\quad+\frac{3}{14}\int_{0}^{1}\int_{9-3u}^{10-4 u}\left(\frac{2(10-4 u-v)}{3}\right)^{2}dvdu=\frac{13}{63}.\quad\quad\quad \end{align*} $$
$$ \begin{align*} S\big(W_{\bullet, \bullet,\bullet}^{\widehat{T},\mathbf{f}};O\big)&=\frac{3}{14}\int_{0}^{1}\int_{0}^{4-4u}\left(\frac{v}{6}\right)^{2}dvdu+\frac{3}{14}\int_{0}^{1}\int_{4-4u}^{9-3u}\left(\frac{2(1-u)}{3}\right)^{2}dvdu+\\ &\quad+\frac{3}{14}\int_{0}^{1}\int_{9-3u}^{10-4 u}\left(\frac{2(10-4 u-v)}{3}\right)^{2}dvdu=\frac{13}{63}.\quad\quad\quad \end{align*} $$
Similarly, if
![]() $O=\mathbf {f}\cap \widetilde {\mathcal {C}}$
, then
$O=\mathbf {f}\cap \widetilde {\mathcal {C}}$
, then
 $$ \begin{align*} S\big(W_{\bullet, \bullet,\bullet}^{\widehat{T},\mathbf{f}};O\big)&=\frac{13}{63}+ \frac{3}{7}\int_{0}^{1}\int_{4-4u}^{9-3u}\frac{2(1-u)}{3}\times\frac{v-4+4 u}{6}dvdu+\\[5pt] &\quad+\frac{3}{7}\int_{0}^{1}\int_{9-3u}^{10-4u}\frac{2(10-4 u-v)}{3}\times\frac{v-4+4u}{6}dvdu=\frac{13}{63}+\frac{193}{504}=\frac{33}{56}. \end{align*} $$
$$ \begin{align*} S\big(W_{\bullet, \bullet,\bullet}^{\widehat{T},\mathbf{f}};O\big)&=\frac{13}{63}+ \frac{3}{7}\int_{0}^{1}\int_{4-4u}^{9-3u}\frac{2(1-u)}{3}\times\frac{v-4+4 u}{6}dvdu+\\[5pt] &\quad+\frac{3}{7}\int_{0}^{1}\int_{9-3u}^{10-4u}\frac{2(10-4 u-v)}{3}\times\frac{v-4+4u}{6}dvdu=\frac{13}{63}+\frac{193}{504}=\frac{33}{56}. \end{align*} $$
Likewise, if
![]() $O=O_3$
, we compute
$O=O_3$
, we compute
![]() $S(W_{\bullet , \bullet ,\bullet }^{\widehat {T},\mathbf {f}};O)=\frac {3}{14}$
. So, using Equation (6.4), we get
$S(W_{\bullet , \bullet ,\bullet }^{\widehat {T},\mathbf {f}};O)=\frac {3}{14}$
. So, using Equation (6.4), we get
![]() $\delta _P(X)>1$
.
$\delta _P(X)>1$
.
Thus, to prove that
![]() $\delta _P(X)>1$
, we may assume that S is singular, but
$\delta _P(X)>1$
, we may assume that S is singular, but
![]() $P\not \in \mathrm {Sing}(S)$
.
$P\not \in \mathrm {Sing}(S)$
.
Lemma 6.8. Suppose that
![]() $P\not \in E$
. Then
$P\not \in E$
. Then
![]() $\delta _P(X)>1$
.
$\delta _P(X)>1$
.
Proof. Recall that E is the
![]() $\pi $
-exceptional surface. Using Corollary 6.4, we may assume that S contains a line L that passes through P. Then
$\pi $
-exceptional surface. Using Corollary 6.4, we may assume that S contains a line L that passes through P. Then
![]() $\pi (L)$
is a line in
$\pi (L)$
is a line in
![]() $\mathscr {Q}$
,
$\mathscr {Q}$
,
![]() $\pi (L)\cap \mathscr {C}\ne \varnothing $
, and one of the following cases holds:
$\pi (L)\cap \mathscr {C}\ne \varnothing $
, and one of the following cases holds:
-
Case 1: the line
 $\pi (L)$
intersects the curve
$\pi (L)$
intersects the curve
 $\mathscr {C}$
transversally at two points,
$\mathscr {C}$
transversally at two points, -
Case 2: the line
 $\pi (L)$
is tangent to the curve
$\pi (L)$
is tangent to the curve
 $\mathscr {C}$
at their single intersection point.
$\mathscr {C}$
at their single intersection point.
Now, let us choose T to be a sufficiently general surface in
![]() $|H|$
that passes through L. If the intersection
$|H|$
that passes through L. If the intersection
![]() $\pi (L)\cap \mathscr {C}$
consists of two points, then
$\pi (L)\cap \mathscr {C}$
consists of two points, then
![]() $\varpi \colon T\to \mathcal {Q}$
is a blow up of eight distinct points of the transversal intersection
$\varpi \colon T\to \mathcal {Q}$
is a blow up of eight distinct points of the transversal intersection
![]() $\mathcal {Q}\cap \mathscr {C}$
, which implies that T is smooth. On the other hand, if
$\mathcal {Q}\cap \mathscr {C}$
, which implies that T is smooth. On the other hand, if
![]() $L\cap \mathscr {C}$
consists of one point, then T has one ordinary double point, which is not contained in the curve L. We have
$L\cap \mathscr {C}$
consists of one point, then T has one ordinary double point, which is not contained in the curve L. We have
![]() $\mathcal {C}=S\vert _{T}=L+Z$
, where Z is a smooth rational irreducible curve such that
$\mathcal {C}=S\vert _{T}=L+Z$
, where Z is a smooth rational irreducible curve such that
![]() $\pi (Z)$
is a smooth twisted cubic in
$\pi (Z)$
is a smooth twisted cubic in
![]() $\mathscr {Q}$
. The twisted cubic curve
$\mathscr {Q}$
. The twisted cubic curve
![]() $\pi (Z)$
in
$\pi (Z)$
in
![]() $\mathscr {Q}$
intersects the curve
$\mathscr {Q}$
intersects the curve
![]() $\mathscr {C}$
transversally by six distinct points, which we denote by
$\mathscr {C}$
transversally by six distinct points, which we denote by
![]() $Q_3,Q_4,Q_5,Q_6,Q_7,Q_8$
. Moreover, if
$Q_3,Q_4,Q_5,Q_6,Q_7,Q_8$
. Moreover, if
![]() $\pi (L)\cap \mathscr {C}$
consists of two distinct points, we denote these points by
$\pi (L)\cap \mathscr {C}$
consists of two distinct points, we denote these points by
![]() $Q_1$
and
$Q_1$
and
![]() $Q_2$
. Likewise, if
$Q_2$
. Likewise, if
![]() $\pi (L)\cap \mathscr {C}$
consists of one point, we let
$\pi (L)\cap \mathscr {C}$
consists of one point, we let
![]() $Q_1=Q_2=\pi (Z)\cap \mathscr {C}$
. Then
$Q_1=Q_2=\pi (Z)\cap \mathscr {C}$
. Then
-
Case 1: the morphism
 $\varpi \colon T\to \mathcal {Q}$
is the blow up of the points
$\varpi \colon T\to \mathcal {Q}$
is the blow up of the points
 $Q_1,Q_2,\ldots ,Q_8$
,
$Q_1,Q_2,\ldots ,Q_8$
, -
Case 2: the morphism
 $\varpi \colon T\to \mathcal {Q}$
is a composition of the blow up of the points
$\varpi \colon T\to \mathcal {Q}$
is a composition of the blow up of the points
 $Q_3,\ldots ,Q_8$
with a weighted blow up with weights
$Q_3,\ldots ,Q_8$
with a weighted blow up with weights
 $(1,2)$
of the point
$(1,2)$
of the point
 $Q_1=Q_2$
.
$Q_1=Q_2$
.
Since T is a general surface in
![]() $|H|$
that contains the line L, we may assume that
$|H|$
that contains the line L, we may assume that
![]() $P\not \in Z$
. Likewise, we may assume further that Z is contained in the smooth locus of the surface T. Moreover, we may also assume that the quadric surface
$P\not \in Z$
. Likewise, we may assume further that Z is contained in the smooth locus of the surface T. Moreover, we may also assume that the quadric surface
![]() $\mathcal {Q}$
does not contain lines that pass through one point in the set
$\mathcal {Q}$
does not contain lines that pass through one point in the set
![]() $\{Q_1,Q_2,\pi (P)\}$
and one point in
$\{Q_1,Q_2,\pi (P)\}$
and one point in
![]() $\{Q_3,Q_4,Q_5,Q_6,Q_7,Q_8\}$
. Indeed, let
$\{Q_3,Q_4,Q_5,Q_6,Q_7,Q_8\}$
. Indeed, let
![]() $\mathcal {Q}^\prime $
,
$\mathcal {Q}^\prime $
,
![]() $\mathcal {Q}^{\prime \prime }$
,
$\mathcal {Q}^{\prime \prime }$
,
![]() $\mathcal {Q}^{\prime \prime \prime }$
be the hyperplane sections of the quadric
$\mathcal {Q}^{\prime \prime \prime }$
be the hyperplane sections of the quadric
![]() $\mathscr {Q}$
that are singular at the points
$\mathscr {Q}$
that are singular at the points
![]() $Q_1$
,
$Q_1$
,
![]() $Q_2$
,
$Q_2$
,
![]() $\pi (P)$
, respectively. Then
$\pi (P)$
, respectively. Then
![]() $\mathcal {Q}^\prime $
,
$\mathcal {Q}^\prime $
,
![]() $\mathcal {Q}^{\prime \prime }$
,
$\mathcal {Q}^{\prime \prime }$
,
![]() $\mathcal {Q}^{\prime \prime \prime }$
are cones,
$\mathcal {Q}^{\prime \prime \prime }$
are cones,
![]() $\pi (L)\subset \mathcal {Q}^\prime \cap \mathcal {Q}^{\prime \prime }\cap \mathcal {Q}^{\prime \prime \prime }$
, and every line in
$\pi (L)\subset \mathcal {Q}^\prime \cap \mathcal {Q}^{\prime \prime }\cap \mathcal {Q}^{\prime \prime \prime }$
, and every line in
![]() $\mathscr {Q}$
containing a point in
$\mathscr {Q}$
containing a point in
![]() $\{Q_1,Q_2,\pi (P)\}$
is a ruling of one of these cones. On the other hand, we have
$\{Q_1,Q_2,\pi (P)\}$
is a ruling of one of these cones. On the other hand, we have
![]() $\mathscr {C}\not \subset \mathcal {Q}^\prime \cup \mathcal {Q}^{\prime \prime }\cup \mathcal {Q}^{\prime \prime \prime }$
because
$\mathscr {C}\not \subset \mathcal {Q}^\prime \cup \mathcal {Q}^{\prime \prime }\cup \mathcal {Q}^{\prime \prime \prime }$
because
![]() $\mathscr {C}$
is not contained in a hyperplane. This implies that the quadric threefold
$\mathscr {C}$
is not contained in a hyperplane. This implies that the quadric threefold
![]() $\mathscr {Q}$
contains at most finitely many lines that pass through a point in
$\mathscr {Q}$
contains at most finitely many lines that pass through a point in
![]() $\{Q_1,Q_2,\pi (P)\}$
and a point in
$\{Q_1,Q_2,\pi (P)\}$
and a point in
![]() $\mathscr {C}\setminus \{Q_1,Q_2\}$
. Therefore, we can choose the surface
$\mathscr {C}\setminus \{Q_1,Q_2\}$
. Therefore, we can choose the surface
![]() $T\in |H|$
such that
$T\in |H|$
such that
![]() $L\subset T$
, but
$L\subset T$
, but
![]() $\mathcal {Q}=\pi (T)$
does not contain any of these lines.
$\mathcal {Q}=\pi (T)$
does not contain any of these lines.
Let us identify
![]() $\mathcal {Q}=\mathbb {P}^1\times \mathbb {P}^1$
such that the line
$\mathcal {Q}=\mathbb {P}^1\times \mathbb {P}^1$
such that the line
![]() $\pi (L)$
is a curve in
$\pi (L)$
is a curve in
![]() $\mathcal {Q}$
of degree
$\mathcal {Q}$
of degree
![]() $(0,1)$
. Denote by
$(0,1)$
. Denote by
![]() $\mathbf {e}_1,\ldots ,\mathbf {e}_8$
the
$\mathbf {e}_1,\ldots ,\mathbf {e}_8$
the
![]() $\varpi $
-exceptional curves such that
$\varpi $
-exceptional curves such that
![]() $\varpi (\mathbf {e}_1)=Q_1,\ldots ,\varpi (\mathbf {e}_8)=Q_8$
. Let
$\varpi (\mathbf {e}_1)=Q_1,\ldots ,\varpi (\mathbf {e}_8)=Q_8$
. Let
![]() $\mathbf {g}_3,\ldots ,\mathbf {g}_8$
be the strict transforms on T of the curves in
$\mathbf {g}_3,\ldots ,\mathbf {g}_8$
be the strict transforms on T of the curves in
![]() $\mathcal {Q}$
of degree
$\mathcal {Q}$
of degree
![]() $(1,0)$
that pass through the points
$(1,0)$
that pass through the points
![]() $Q_3,\ldots ,Q_8$
, respectively. Then
$Q_3,\ldots ,Q_8$
, respectively. Then
![]() $L,Z,\mathbf {e}_1,\ldots ,\mathbf {e}_8,\mathbf {g}_3,\ldots ,\mathbf {g}_8$
are smooth irreducible rational curves. In Case 1, their intersections are given in the following table:
$L,Z,\mathbf {e}_1,\ldots ,\mathbf {e}_8,\mathbf {g}_3,\ldots ,\mathbf {g}_8$
are smooth irreducible rational curves. In Case 1, their intersections are given in the following table:

In Case 2, we have
![]() $\mathbf {e}_1=\mathbf {e}_2$
, and
$\mathbf {e}_1=\mathbf {e}_2$
, and
![]() $\mathbf {e}_1$
contains the singular point of T so that
$\mathbf {e}_1$
contains the singular point of T so that
![]() $\mathbf {e}_1^2=-\frac {1}{2}$
. The remaining intersection numbers are exactly the same as in Case 1.
$\mathbf {e}_1^2=-\frac {1}{2}$
. The remaining intersection numbers are exactly the same as in Case 1.
Observe that
![]() $P\not \in Z\cup \mathbf {g}_3\cup \mathbf {g}_4\cup \mathbf {g}_5\cup \mathbf {g}_6\cup \mathbf {g}_7\cup \mathbf {g}_8\cup \mathbf {e}_1\cup \mathbf {e}_2$
since
$P\not \in Z\cup \mathbf {g}_3\cup \mathbf {g}_4\cup \mathbf {g}_5\cup \mathbf {g}_6\cup \mathbf {g}_7\cup \mathbf {g}_8\cup \mathbf {e}_1\cup \mathbf {e}_2$
since
![]() $P\not \in E$
by assumption.
$P\not \in E$
by assumption.
Recall that
![]() $P(u)=-K_X-uT$
is nef
$P(u)=-K_X-uT$
is nef
![]() $\iff P(u)$
is pseudoeffective
$\iff P(u)$
is pseudoeffective
![]() $\iff u\in [0,1]$
. Let v be a nonnegative real number. Then, in both Cases 1 and 2, we have
$\iff u\in [0,1]$
. Let v be a nonnegative real number. Then, in both Cases 1 and 2, we have
 $$ \begin{align} P(u)\big\vert_{T}-vL\sim_{\mathbb{R}}\frac{9-5u-4v}{4}L+\frac{3+u}{4}Z+\frac{5-5u}{4}\big(\mathbf{e}_1+\mathbf{e}_2\big)+\frac{1-u}{4}\sum_{i=3}^8\mathbf{g}_i, \end{align} $$
$$ \begin{align} P(u)\big\vert_{T}-vL\sim_{\mathbb{R}}\frac{9-5u-4v}{4}L+\frac{3+u}{4}Z+\frac{5-5u}{4}\big(\mathbf{e}_1+\mathbf{e}_2\big)+\frac{1-u}{4}\sum_{i=3}^8\mathbf{g}_i, \end{align} $$
which implies that the divisor
![]() $P(u)\vert _{T}-vL$
is pseudoeffective
$P(u)\vert _{T}-vL$
is pseudoeffective
![]() $\iff v\leqslant \frac {9-5u}{4}$
.
$\iff v\leqslant \frac {9-5u}{4}$
.
Let
![]() $P(u,v)$
be the positive part of Zariski decomposition of the divisor
$P(u,v)$
be the positive part of Zariski decomposition of the divisor
![]() $P(u)\vert _{T}-vL$
, and let
$P(u)\vert _{T}-vL$
, and let
![]() $N(u,v)$
be its negative part. Then it follows from [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Theorem 1.112] that
$N(u,v)$
be its negative part. Then it follows from [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Theorem 1.112] that
 $$ \begin{align} \delta_P(X)\geqslant\min\left\{\frac{1}{S_X(T)},\frac{1}{S(W_{\bullet,\bullet}^{T};L)},\frac{1}{S(W_{\bullet, \bullet,\bullet}^{T,L};P)}\right\}, \end{align} $$
$$ \begin{align} \delta_P(X)\geqslant\min\left\{\frac{1}{S_X(T)},\frac{1}{S(W_{\bullet,\bullet}^{T};L)},\frac{1}{S(W_{\bullet, \bullet,\bullet}^{T,L};P)}\right\}, \end{align} $$
where
 $$ \begin{align*}S\big(W_{\bullet,\bullet}^{T};L\big)=\frac{3}{14}\int_0^1\int_0^{\frac{9-5u}{4}}\big(P(u,v)\big)^2dvdu \end{align*} $$
$$ \begin{align*}S\big(W_{\bullet,\bullet}^{T};L\big)=\frac{3}{14}\int_0^1\int_0^{\frac{9-5u}{4}}\big(P(u,v)\big)^2dvdu \end{align*} $$
and
 $$ \begin{align*}S\big(W_{\bullet, \bullet,\bullet}^{T,L};P\big)=\frac{3}{14}\int_0^1\!\int_0^{\frac{9-5u}{4}}\Big(\big(P(u,v)\cdot L\big)\Big)^2dvdu+\frac{3}{7}\int_0^1\!\int_0^{\frac{9-5u}{4}}\big(P(u,v)\cdot L\big)\mathrm{ord}_P\Big(N(u,v)\big|_{L}\Big)dvdu. \end{align*} $$
$$ \begin{align*}S\big(W_{\bullet, \bullet,\bullet}^{T,L};P\big)=\frac{3}{14}\int_0^1\!\int_0^{\frac{9-5u}{4}}\Big(\big(P(u,v)\cdot L\big)\Big)^2dvdu+\frac{3}{7}\int_0^1\!\int_0^{\frac{9-5u}{4}}\big(P(u,v)\cdot L\big)\mathrm{ord}_P\Big(N(u,v)\big|_{L}\Big)dvdu. \end{align*} $$
Let us compute
![]() $S(W_{\bullet ,\bullet }^{T};L)$
and
$S(W_{\bullet ,\bullet }^{T};L)$
and
![]() $S(W_{\bullet , \bullet ,\bullet }^{T,L};P)$
. If
$S(W_{\bullet , \bullet ,\bullet }^{T,L};P)$
. If
![]() $0\leqslant u\leqslant \frac {1}{3}$
, then, using Equation (6.5), we get
$0\leqslant u\leqslant \frac {1}{3}$
, then, using Equation (6.5), we get
 $$ \begin{align*}P(u,v)=\left\{\begin{aligned} &\frac{9-5u-4v}{4}L+\frac{3+u}{4}Z+\frac{5-5u}{4}\big(\mathbf{e}_1+\mathbf{e}_2\big)+\frac{1-u}{4}\sum_{i=3}^8\mathbf{g}_i\ \text{if }0\leqslant v\leqslant 1, \\[-1pt] &\frac{9-5u-4v}{4}\big(L+\mathbf{e}_1+\mathbf{e}_2\big)+\frac{3+u}{4}Z+\frac{1-u}{4}\sum_{i=3}^8\mathbf{g}_i\ \text{if }1\leqslant v\leqslant \frac{3-3u}{2}, \\[-1pt] &\frac{9-5u-4v}{4}\big(L+Z+\mathbf{e}_1+\mathbf{e}_2\big)+\frac{1-u}{4}\sum_{i=3}^8\mathbf{g}_i\ \text{if }\frac{3-3u}{2}\leqslant v\leqslant 2-u, \\[-1pt] &\frac{9-5 u-4 v}{4}\Big(L+Z+\mathbf{e}_1+\mathbf{e}_2+\sum_{i=3}^8\mathbf{g}_i\Big)\ \text{if }2-u\leqslant v\leqslant \frac{9-5u}{4}, \\ \end{aligned} \right. \end{align*} $$
$$ \begin{align*}P(u,v)=\left\{\begin{aligned} &\frac{9-5u-4v}{4}L+\frac{3+u}{4}Z+\frac{5-5u}{4}\big(\mathbf{e}_1+\mathbf{e}_2\big)+\frac{1-u}{4}\sum_{i=3}^8\mathbf{g}_i\ \text{if }0\leqslant v\leqslant 1, \\[-1pt] &\frac{9-5u-4v}{4}\big(L+\mathbf{e}_1+\mathbf{e}_2\big)+\frac{3+u}{4}Z+\frac{1-u}{4}\sum_{i=3}^8\mathbf{g}_i\ \text{if }1\leqslant v\leqslant \frac{3-3u}{2}, \\[-1pt] &\frac{9-5u-4v}{4}\big(L+Z+\mathbf{e}_1+\mathbf{e}_2\big)+\frac{1-u}{4}\sum_{i=3}^8\mathbf{g}_i\ \text{if }\frac{3-3u}{2}\leqslant v\leqslant 2-u, \\[-1pt] &\frac{9-5 u-4 v}{4}\Big(L+Z+\mathbf{e}_1+\mathbf{e}_2+\sum_{i=3}^8\mathbf{g}_i\Big)\ \text{if }2-u\leqslant v\leqslant \frac{9-5u}{4}, \\ \end{aligned} \right. \end{align*} $$
 $$ \begin{align*}N(u,v)=\left\{\begin{aligned} &0\ \text{if }0\leqslant v\leqslant 1, \\[-1pt] &(v-1)\big(\mathbf{e}_1+\mathbf{e}_2\big) \ \text{if }1\leqslant v\leqslant \frac{3-3u}{2}, \\[-1pt] &(v-1)\big(\mathbf{e}_1+\mathbf{e}_2\big)+\frac{2v+3u-3}{2}Z\ \text{if }\frac{3-3u}{2}\leqslant v\leqslant 2-u, \\[-1pt] &(v-1)\big(\mathbf{e}_1+\mathbf{e}_2\big)+\frac{2v+3u-3}{2}Z+(v-2+u)\sum_{i=3}^{8}\mathbf{g}_{i}\ \text{if }2-u\leqslant v\leqslant \frac{9-5u}{4}, \\ \end{aligned} \right. \end{align*} $$
$$ \begin{align*}N(u,v)=\left\{\begin{aligned} &0\ \text{if }0\leqslant v\leqslant 1, \\[-1pt] &(v-1)\big(\mathbf{e}_1+\mathbf{e}_2\big) \ \text{if }1\leqslant v\leqslant \frac{3-3u}{2}, \\[-1pt] &(v-1)\big(\mathbf{e}_1+\mathbf{e}_2\big)+\frac{2v+3u-3}{2}Z\ \text{if }\frac{3-3u}{2}\leqslant v\leqslant 2-u, \\[-1pt] &(v-1)\big(\mathbf{e}_1+\mathbf{e}_2\big)+\frac{2v+3u-3}{2}Z+(v-2+u)\sum_{i=3}^{8}\mathbf{g}_{i}\ \text{if }2-u\leqslant v\leqslant \frac{9-5u}{4}, \\ \end{aligned} \right. \end{align*} $$
 $$ \begin{align*}\big(P(u,v)\big)^2=\left\{\begin{aligned} &2u^2+(2v-12)u-2v^2-2v+10 \ \text{if }0\leqslant v\leqslant 1, \\[-1pt] &2u^2+(2v-12)u-6v+12\ \text{if }1\leqslant v\leqslant \frac{3-3u}{2}, \\[-1pt] &\frac{13u^2+16uv+4v^2-42u-24v+33}{2}\ \text{if }\frac{3-3u}{2}\leqslant v\leqslant 2-u, \\[-1pt] &\frac{(9-5u-4v)^{2}}{2}\ \text{if }2-u\leqslant v\leqslant \frac{9-5u}{4}, \\ \end{aligned} \right. \end{align*} $$
$$ \begin{align*}\big(P(u,v)\big)^2=\left\{\begin{aligned} &2u^2+(2v-12)u-2v^2-2v+10 \ \text{if }0\leqslant v\leqslant 1, \\[-1pt] &2u^2+(2v-12)u-6v+12\ \text{if }1\leqslant v\leqslant \frac{3-3u}{2}, \\[-1pt] &\frac{13u^2+16uv+4v^2-42u-24v+33}{2}\ \text{if }\frac{3-3u}{2}\leqslant v\leqslant 2-u, \\[-1pt] &\frac{(9-5u-4v)^{2}}{2}\ \text{if }2-u\leqslant v\leqslant \frac{9-5u}{4}, \\ \end{aligned} \right. \end{align*} $$
and
 $$ \begin{align*}P(u,v)\cdot L=\left\{\begin{aligned} &1-u+2v\ \text{if }0\leqslant v\leqslant 1, \\[-1pt] &3-u\ \text{if }1\leqslant v\leqslant \frac{3-3u}{2}, \\[-1pt] &6-4u-2v\ \text{if }\frac{3-3u}{2}\leqslant v\leqslant 2-u, \\[-1pt] &2(9-5u-4v)\ \text{if }2-u\leqslant v\leqslant \frac{9-5u}{4}. \\ \end{aligned} \right. \end{align*} $$
$$ \begin{align*}P(u,v)\cdot L=\left\{\begin{aligned} &1-u+2v\ \text{if }0\leqslant v\leqslant 1, \\[-1pt] &3-u\ \text{if }1\leqslant v\leqslant \frac{3-3u}{2}, \\[-1pt] &6-4u-2v\ \text{if }\frac{3-3u}{2}\leqslant v\leqslant 2-u, \\[-1pt] &2(9-5u-4v)\ \text{if }2-u\leqslant v\leqslant \frac{9-5u}{4}. \\ \end{aligned} \right. \end{align*} $$
Similarly, if
![]() $\frac {1}{3}\leqslant u\leqslant 1$
, then, using Equation (6.5), we get
$\frac {1}{3}\leqslant u\leqslant 1$
, then, using Equation (6.5), we get
 $$ \begin{align*}P(u,v)=\left\{\begin{aligned} &\frac{9-5u-4v}{4}L+\frac{3+u}{4}Z+\frac{5-5u}{4}\big(\mathbf{e}_1+\mathbf{e}_2\big)+\frac{1-u}{4}\sum_{i=3}^8\mathbf{g}_i\ \text{if }0\leqslant v\leqslant \frac{3-3u}{2}, \\[-1pt] &\frac{9-5u-4v}{4}(L+Z)+\frac{5-5u}{4}\big(\mathbf{e}_1+\mathbf{e}_2\big)+\frac{1-u}{4}\sum_{i=3}^8\mathbf{g}_i\ \text{if }\frac{3-3u}{2}\leqslant v\leqslant 1, \\[-1pt] &\frac{9-5u-4v}{4}\big(L+Z+\mathbf{e}_1+\mathbf{e}_2\big)+\frac{1-u}{4}\sum_{i=3}^8\mathbf{g}_i\ \text{if }1\leqslant v\leqslant 2-u, \\[-1pt] &\frac{9-5 u-4 v}{4}\Big(L+Z+\mathbf{e}_1+\mathbf{e}_2+\sum_{i=3}^8\mathbf{g}_i\Big)\ \text{if }2-u\leqslant v\leqslant \frac{9-5u}{4}, \\ \end{aligned} \right. \end{align*} $$
$$ \begin{align*}P(u,v)=\left\{\begin{aligned} &\frac{9-5u-4v}{4}L+\frac{3+u}{4}Z+\frac{5-5u}{4}\big(\mathbf{e}_1+\mathbf{e}_2\big)+\frac{1-u}{4}\sum_{i=3}^8\mathbf{g}_i\ \text{if }0\leqslant v\leqslant \frac{3-3u}{2}, \\[-1pt] &\frac{9-5u-4v}{4}(L+Z)+\frac{5-5u}{4}\big(\mathbf{e}_1+\mathbf{e}_2\big)+\frac{1-u}{4}\sum_{i=3}^8\mathbf{g}_i\ \text{if }\frac{3-3u}{2}\leqslant v\leqslant 1, \\[-1pt] &\frac{9-5u-4v}{4}\big(L+Z+\mathbf{e}_1+\mathbf{e}_2\big)+\frac{1-u}{4}\sum_{i=3}^8\mathbf{g}_i\ \text{if }1\leqslant v\leqslant 2-u, \\[-1pt] &\frac{9-5 u-4 v}{4}\Big(L+Z+\mathbf{e}_1+\mathbf{e}_2+\sum_{i=3}^8\mathbf{g}_i\Big)\ \text{if }2-u\leqslant v\leqslant \frac{9-5u}{4}, \\ \end{aligned} \right. \end{align*} $$
 $$ \begin{align*}N(u,v)=\left\{\begin{aligned} &0\ \text{if }0\leqslant v\leqslant \frac{3-3u}{2}, \\ &\frac{2v+3u-3}{2}Z\ \text{if }\frac{3-3u}{2}\leqslant v\leqslant 1, \\ &(v-1)\big(\mathbf{e}_1+\mathbf{e}_2\big)+\frac{2v+3u-3}{2}Z\ \text{if }1\leqslant v\leqslant 2-u, \\ &(v-1)\big(\mathbf{e}_1+\mathbf{e}_2\big)+\frac{2v+3u-3}{2}Z+(v-2+u)\sum_{i=3}^{8}\mathbf{g}_{i}\ \text{if }2-u\leqslant v\leqslant \frac{9-5u}{4}, \\ \end{aligned} \right. \end{align*} $$
$$ \begin{align*}N(u,v)=\left\{\begin{aligned} &0\ \text{if }0\leqslant v\leqslant \frac{3-3u}{2}, \\ &\frac{2v+3u-3}{2}Z\ \text{if }\frac{3-3u}{2}\leqslant v\leqslant 1, \\ &(v-1)\big(\mathbf{e}_1+\mathbf{e}_2\big)+\frac{2v+3u-3}{2}Z\ \text{if }1\leqslant v\leqslant 2-u, \\ &(v-1)\big(\mathbf{e}_1+\mathbf{e}_2\big)+\frac{2v+3u-3}{2}Z+(v-2+u)\sum_{i=3}^{8}\mathbf{g}_{i}\ \text{if }2-u\leqslant v\leqslant \frac{9-5u}{4}, \\ \end{aligned} \right. \end{align*} $$
 $$ \begin{align*}\big(P(u,v)\big)^2=\left\{\begin{aligned} &2u^2+(2v-12)u-2v^2-2v+10\ \text{if }0\leqslant v\leqslant \frac{3-3u}{2}, \\ &\frac{(1-u)(29-13u-16v)}{2}\ \text{if }\frac{3-3u}{2}\leqslant v\leqslant 1, \\ &\frac{13u^2+16uv+4v^2-42u-24v+33}{2}\ \text{if }1\leqslant v\leqslant 2-u, \\ &\frac{(9-5u-4v)^{2}}{2}\ \text{if }2-u\leqslant v\leqslant \frac{9-5u}{4}, \\ \end{aligned} \right. \end{align*} $$
$$ \begin{align*}\big(P(u,v)\big)^2=\left\{\begin{aligned} &2u^2+(2v-12)u-2v^2-2v+10\ \text{if }0\leqslant v\leqslant \frac{3-3u}{2}, \\ &\frac{(1-u)(29-13u-16v)}{2}\ \text{if }\frac{3-3u}{2}\leqslant v\leqslant 1, \\ &\frac{13u^2+16uv+4v^2-42u-24v+33}{2}\ \text{if }1\leqslant v\leqslant 2-u, \\ &\frac{(9-5u-4v)^{2}}{2}\ \text{if }2-u\leqslant v\leqslant \frac{9-5u}{4}, \\ \end{aligned} \right. \end{align*} $$
and
 $$ \begin{align*}P(u,v)\cdot L=\left\{\begin{aligned} &1-u+2v\ \text{if }0\leqslant v\leqslant \frac{3-3u}{2}, \\ &4-4u\ \text{if }\frac{3-3u}{2}\leqslant v\leqslant 1, \\ &6-4u-2v\ \text{if }1\leqslant v\leqslant 2-u, \\ &2(9-5u-4v)\ \text{if }2-u\leqslant v\leqslant \frac{9-5u}{4}. \\ \end{aligned} \right. \end{align*} $$
$$ \begin{align*}P(u,v)\cdot L=\left\{\begin{aligned} &1-u+2v\ \text{if }0\leqslant v\leqslant \frac{3-3u}{2}, \\ &4-4u\ \text{if }\frac{3-3u}{2}\leqslant v\leqslant 1, \\ &6-4u-2v\ \text{if }1\leqslant v\leqslant 2-u, \\ &2(9-5u-4v)\ \text{if }2-u\leqslant v\leqslant \frac{9-5u}{4}. \\ \end{aligned} \right. \end{align*} $$
Therefore, we have
![]() $P\not \in \mathrm {Supp}(N(u,v))$
because
$P\not \in \mathrm {Supp}(N(u,v))$
because
![]() $P\not \in Z\cup \mathbf {g}_3\cup \mathbf {g}_4\cup \mathbf {g}_5\cup \mathbf {g}_6\cup \mathbf {g}_7\cup \mathbf {g}_8\cup \mathbf {e}_1\cup \mathbf {e}_2$
. So, integrating
$P\not \in Z\cup \mathbf {g}_3\cup \mathbf {g}_4\cup \mathbf {g}_5\cup \mathbf {g}_6\cup \mathbf {g}_7\cup \mathbf {g}_8\cup \mathbf {e}_1\cup \mathbf {e}_2$
. So, integrating
![]() $(P(u,v))^2$
and
$(P(u,v))^2$
and
![]() $(P(u,v)\cdot L)^2$
, we get
$(P(u,v)\cdot L)^2$
, we get
![]() $S(W_{\bullet ,\bullet }^{T};L)=\frac {423}{448}$
and
$S(W_{\bullet ,\bullet }^{T};L)=\frac {423}{448}$
and
![]() $S(W_{\bullet , \bullet ,\bullet }^{T,L};P)=\frac {79}{84}$
, which implies that
$S(W_{\bullet , \bullet ,\bullet }^{T,L};P)=\frac {79}{84}$
, which implies that
![]() $\delta _P(X)>1$
by Equation (6.6).
$\delta _P(X)>1$
by Equation (6.6).
By Lemma 6.8, to show that
![]() $\delta _P(X)>1$
, we may assume that
$\delta _P(X)>1$
, we may assume that
![]() $P\in E$
. Then
$P\in E$
. Then
![]() $\pi (P)\in \mathscr {C}$
. Now, let us choose T to be a sufficiently general surface in
$\pi (P)\in \mathscr {C}$
. Now, let us choose T to be a sufficiently general surface in
![]() $|H|$
that contains the point P so that
$|H|$
that contains the point P so that
![]() $\mathcal {Q}$
is a sufficiently general hyperplane section of the quadric
$\mathcal {Q}$
is a sufficiently general hyperplane section of the quadric
![]() $\mathscr {Q}$
that contains
$\mathscr {Q}$
that contains
![]() $\pi (P)$
. Then T is smooth, and
$\pi (P)$
. Then T is smooth, and
![]() $\varpi \colon T\to \mathcal {Q}$
is a blow up of eight points of the intersection
$\varpi \colon T\to \mathcal {Q}$
is a blow up of eight points of the intersection
![]() $\mathcal {Q}\cap \mathscr {C}$
.
$\mathcal {Q}\cap \mathscr {C}$
.
Let
![]() $Q_1=\pi (P)$
, let
$Q_1=\pi (P)$
, let
![]() $Q_2,\ldots ,Q_8$
be the remaining seven points of the intersection
$Q_2,\ldots ,Q_8$
be the remaining seven points of the intersection
![]() $\mathcal {Q}\cap \mathscr {C}$
and let
$\mathcal {Q}\cap \mathscr {C}$
and let
![]() $\mathbf {e}_1,\ldots ,\mathbf {e}_8$
be the
$\mathbf {e}_1,\ldots ,\mathbf {e}_8$
be the
![]() $\varpi $
-exceptional curves such that
$\varpi $
-exceptional curves such that
![]() $\varpi (\mathbf {e}_1)=Q_1,\ldots ,\varpi (\mathbf {e}_8)=Q_8$
. For every
$\varpi (\mathbf {e}_1)=Q_1,\ldots ,\varpi (\mathbf {e}_8)=Q_8$
. For every
![]() $u\in [0,1]$
, set
$u\in [0,1]$
, set
and fix a real number
![]() $v\in [0, t(u)]$
. Let
$v\in [0, t(u)]$
. Let
![]() $P(u,v)$
and
$P(u,v)$
and
![]() $N(u,v)$
be the positive and the negative parts of the Zariski decomposition of the
$N(u,v)$
be the positive and the negative parts of the Zariski decomposition of the
![]() $\mathbb {R}$
-divisor
$\mathbb {R}$
-divisor
![]() $P(u)|_T-v\mathbf {e}_1$
, respectively. Then
$P(u)|_T-v\mathbf {e}_1$
, respectively. Then
 $$ \begin{align} \delta_P(X)\geqslant\min\left\{\frac{1}{S_X(T)},\frac{1}{S(W_{\bullet,\bullet}^{T};\mathbf{e}_1)},\frac{1}{S(W_{\bullet, \bullet,\bullet}^{T,\mathbf{e}_1};P)}\right\} \end{align} $$
$$ \begin{align} \delta_P(X)\geqslant\min\left\{\frac{1}{S_X(T)},\frac{1}{S(W_{\bullet,\bullet}^{T};\mathbf{e}_1)},\frac{1}{S(W_{\bullet, \bullet,\bullet}^{T,\mathbf{e}_1};P)}\right\} \end{align} $$
by [Reference Araujo, Castravet, Cheltsov, Fujita, Kaloghiros, Martinez-Garcia, Shramov, Süß and Viswanathan3, Theorem 1.112], where
 $$ \begin{align*}S\big(W_{\bullet,\bullet}^{T};\mathbf{e}_1\big)=\frac{3}{14}\int_0^1\int_0^{t(u)}\big(P(u,v)\big)^2dvdu \end{align*} $$
$$ \begin{align*}S\big(W_{\bullet,\bullet}^{T};\mathbf{e}_1\big)=\frac{3}{14}\int_0^1\int_0^{t(u)}\big(P(u,v)\big)^2dvdu \end{align*} $$
and
 $$ \begin{align*} S\big(W_{\bullet, \bullet,\bullet}^{T,\mathbf{e}_1};P\big)&=\frac{3}{14}\int_0^1\int_0^{t(u)}\Big(\big(P(u,v)\cdot\mathbf{e}_1\big)\Big)^2dvdu+\\[5pt] &\quad+\frac{3}{7}\int_0^1\int_0^{t(u)}\big(P(u,v)\cdot \mathbf{e}_1\big)\mathrm{ord}_P\Big(N(u,v)\big|_{\mathbf{e}_1}\Big)dvdu. \end{align*} $$
$$ \begin{align*} S\big(W_{\bullet, \bullet,\bullet}^{T,\mathbf{e}_1};P\big)&=\frac{3}{14}\int_0^1\int_0^{t(u)}\Big(\big(P(u,v)\cdot\mathbf{e}_1\big)\Big)^2dvdu+\\[5pt] &\quad+\frac{3}{7}\int_0^1\int_0^{t(u)}\big(P(u,v)\cdot \mathbf{e}_1\big)\mathrm{ord}_P\Big(N(u,v)\big|_{\mathbf{e}_1}\Big)dvdu. \end{align*} $$
Let us compute
![]() $S(W_{\bullet ,\bullet }^{T};\mathbf {e}_1)$
and
$S(W_{\bullet ,\bullet }^{T};\mathbf {e}_1)$
and
![]() $S(W_{\bullet , \bullet ,\bullet }^{T,\mathbf {e}_1};P)$
.
$S(W_{\bullet , \bullet ,\bullet }^{T,\mathbf {e}_1};P)$
.
Recall that
![]() $\varphi \colon T\to \mathbb {P}^1$
is an elliptic fibration, which is given by the linear system
$\varphi \colon T\to \mathbb {P}^1$
is an elliptic fibration, which is given by the linear system
![]() $|-K_T|$
. As in the proof of Lemma 6.8, let us identify
$|-K_T|$
. As in the proof of Lemma 6.8, let us identify
![]() $\mathcal {Q}=\mathbb {P}^1\times \mathbb {P}^1$
.
$\mathcal {Q}=\mathbb {P}^1\times \mathbb {P}^1$
.
Lemma 6.9. Let F be a curve in
![]() $|-K_T|$
. Then F is irreducible and reduced.
$|-K_T|$
. Then F is irreducible and reduced.
Proof. Suppose that F is reducible or nonreduced. Then the curve
![]() $\pi (F)$
is also reducible or nonreduced, and every irreducible component of the curve F is a smooth
$\pi (F)$
is also reducible or nonreduced, and every irreducible component of the curve F is a smooth
![]() $(-2)$
-curve. But
$(-2)$
-curve. But
![]() $\pi (F)$
is a curve in
$\pi (F)$
is a curve in
![]() $\mathcal {Q}$
of degree
$\mathcal {Q}$
of degree
![]() $(2,2)$
that passes through the points
$(2,2)$
that passes through the points
![]() $Q_1,Q_2,\ldots ,Q_8$
. Therefore, we have one of the following possibilities:
$Q_1,Q_2,\ldots ,Q_8$
. Therefore, we have one of the following possibilities:
-
(1)
 $\mathcal {Q}$
contains a line that passes through
$\mathcal {Q}$
contains a line that passes through
 $Q_1$
and one point among
$Q_1$
and one point among
 $Q_2,\ldots ,Q_8$
,
$Q_2,\ldots ,Q_8$
, -
(2)
 $\mathcal {Q}$
contains a line that passes through two points among
$\mathcal {Q}$
contains a line that passes through two points among
 $Q_2,\ldots ,Q_8$
,
$Q_2,\ldots ,Q_8$
, -
(3)
 $\mathcal {Q}$
contains a conic that passes through
$\mathcal {Q}$
contains a conic that passes through
 $Q_1$
and three points among
$Q_1$
and three points among
 $Q_2,\ldots ,Q_8$
.
$Q_2,\ldots ,Q_8$
.
Recall that
![]() $\mathcal {Q}$
is a general hyperplane section of the quadric
$\mathcal {Q}$
is a general hyperplane section of the quadric
![]() $\mathscr {Q}$
that contains
$\mathscr {Q}$
that contains
![]() $Q_1=\pi (P)$
. As we already mentioned in the proof of Lemma 6.8, the quadric
$Q_1=\pi (P)$
. As we already mentioned in the proof of Lemma 6.8, the quadric
![]() $\mathscr {Q}$
contains finitely many lines that pass through
$\mathscr {Q}$
contains finitely many lines that pass through
![]() $Q_1$
and a point in
$Q_1$
and a point in
![]() $\mathscr {C}\setminus Q_1$
. Thus, since
$\mathscr {C}\setminus Q_1$
. Thus, since
![]() $\mathcal {Q}$
is assumed to be general, the quadric
$\mathcal {Q}$
is assumed to be general, the quadric
![]() $\mathcal {Q}$
does not contain any of these lines so that
$\mathcal {Q}$
does not contain any of these lines so that
![]() $\mathcal {Q}$
does not contain a line that passes through
$\mathcal {Q}$
does not contain a line that passes through
![]() $Q_1$
and a point among
$Q_1$
and a point among
![]() $Q_2,\ldots ,Q_8$
.
$Q_2,\ldots ,Q_8$
.
Similarly, a parameter count implies that
![]() $\mathcal {Q}$
does not contain secant lines of the curve
$\mathcal {Q}$
does not contain secant lines of the curve
![]() $\mathscr {C}$
so that
$\mathscr {C}$
so that
![]() $\mathcal {Q}$
does not contain a line that passes through two points among
$\mathcal {Q}$
does not contain a line that passes through two points among
![]() $Q_2,\ldots ,Q_8$
,
$Q_2,\ldots ,Q_8$
,
Finally, we suppose that
![]() $\mathcal {Q}$
contains an irreducible conic C that passes through
$\mathcal {Q}$
contains an irreducible conic C that passes through
![]() $Q_1$
and three points among
$Q_1$
and three points among
![]() $Q_2,\ldots ,Q_8$
. Let
$Q_2,\ldots ,Q_8$
. Let ![]() be a linear projection from the point
be a linear projection from the point
![]() $Q_1$
. Then
$Q_1$
. Then
![]() $\rho (\mathscr {C})$
is a curve of degree
$\rho (\mathscr {C})$
is a curve of degree
![]() $7$
, and the induced map
$7$
, and the induced map ![]() is an isomorphism because
is an isomorphism because
![]() $\mathscr {C}$
is an intersection of quadrics. Similarly, all points
$\mathscr {C}$
is an intersection of quadrics. Similarly, all points
![]() $\rho (Q_2),\ldots ,\rho (Q_8)$
are distinct. Then
$\rho (Q_2),\ldots ,\rho (Q_8)$
are distinct. Then
![]() $\rho (C)$
is a three-secant line of the curve
$\rho (C)$
is a three-secant line of the curve
![]() $\rho (\mathscr {C})$
. Note that
$\rho (\mathscr {C})$
. Note that
![]() $\rho (\mathscr {C})$
contains one-parameter family of three-secants [Reference Cheltsov and Shramov11, Appendix A]. But
$\rho (\mathscr {C})$
contains one-parameter family of three-secants [Reference Cheltsov and Shramov11, Appendix A]. But
![]() $\rho (\mathcal {Q})$
is a general plane in
$\rho (\mathcal {Q})$
is a general plane in
![]() $\mathbb {P}^3$
, which implies that
$\mathbb {P}^3$
, which implies that
![]() $\rho (\mathcal {Q})$
does not contain three-secant lines of the curve
$\rho (\mathcal {Q})$
does not contain three-secant lines of the curve
![]() $\rho (\mathscr {C})$
– a contradiction.
$\rho (\mathscr {C})$
– a contradiction.
Corollary 6.10. Let
![]() $\gamma $
be a class in the group
$\gamma $
be a class in the group
![]() $\mathrm {Pic}(T)$
such that
$\mathrm {Pic}(T)$
such that
![]() $-K_T\cdot \gamma =1$
and
$-K_T\cdot \gamma =1$
and
![]() $\gamma ^2=-1$
. Then the linear system
$\gamma ^2=-1$
. Then the linear system
![]() $|\gamma |$
consists of a unique
$|\gamma |$
consists of a unique
![]() $(-1)$
-curve.
$(-1)$
-curve.
Proof. Apply the Riemann–Roch theorem, Serre duality and Lemma 6.9.
Let us use Corollary 6.10 to describe infinitely many
![]() $(-1)$
-curves in the surface T. Namely, let
$(-1)$
-curves in the surface T. Namely, let
![]() $\ell _1$
and
$\ell _1$
and
![]() $\ell _2$
be any curves in
$\ell _2$
be any curves in
![]() $\mathcal {Q}=\mathbb {P}^1\times \mathbb {P}^1$
of degrees
$\mathcal {Q}=\mathbb {P}^1\times \mathbb {P}^1$
of degrees
![]() $(1,0)$
and
$(1,0)$
and
![]() $(0,1)$
, respectively. For
$(0,1)$
, respectively. For
![]() $n\in \mathbb {Z}_{\geqslant 0}$
and
$n\in \mathbb {Z}_{\geqslant 0}$
and
![]() $i\in \{2,3,4,5,6,7,8\}$
, let
$i\in \{2,3,4,5,6,7,8\}$
, let
![]() $B_{n,1,1}$
,
$B_{n,1,1}$
,
![]() $B_{n,1,2}$
,
$B_{n,1,2}$
,
![]() $B_{n,2,i}$
,
$B_{n,2,i}$
,
![]() $B_{n,3}$
,
$B_{n,3}$
,
![]() $B_{n,4,i}$
be the classes
$B_{n,4,i}$
be the classes
 $$ \begin{align*}\varpi^*\big(a_1\ell_1+a_2\ell_2\big)-\sum_{i=1}^8b_i\mathbf{e}_i\in\mathrm{Pic}(T), \end{align*} $$
$$ \begin{align*}\varpi^*\big(a_1\ell_1+a_2\ell_2\big)-\sum_{i=1}^8b_i\mathbf{e}_i\in\mathrm{Pic}(T), \end{align*} $$
where
![]() $a_1,a_2,b_1,\ldots ,b_8$
are nonnegative integers given in the following table:
$a_1,a_2,b_1,\ldots ,b_8$
are nonnegative integers given in the following table:

By Corollary 6.10, each linear system
![]() $|B_{n,1,1}|$
,
$|B_{n,1,1}|$
,
![]() $|B_{n,1,2}|$
,
$|B_{n,1,2}|$
,
![]() $|B_{n,2,i}|$
,
$|B_{n,2,i}|$
,
![]() $|B_{n,3}|$
,
$|B_{n,3}|$
,
![]() $|B_{n,4,i}|$
contains a unique
$|B_{n,4,i}|$
contains a unique
![]() $(-1)$
-curve. Hence, we can identify the classes
$(-1)$
-curve. Hence, we can identify the classes
![]() $B_{n,1,1}$
,
$B_{n,1,1}$
,
![]() $B_{n,1,2}$
,
$B_{n,1,2}$
,
![]() $B_{n,2,i}$
,
$B_{n,2,i}$
,
![]() $B_{n,3}$
,
$B_{n,3}$
,
![]() $B_{n,4,i}$
with
$B_{n,4,i}$
with
![]() $(-1)$
-curves in
$(-1)$
-curves in
![]() $|B_{n,1,1}|$
,
$|B_{n,1,1}|$
,
![]() $|B_{n,1,2}|$
,
$|B_{n,1,2}|$
,
![]() $|B_{n,2,i}|$
,
$|B_{n,2,i}|$
,
![]() $|B_{n,3}|$
,
$|B_{n,3}|$
,
![]() $|B_{n,4,i}|$
, respectively. Set
$|B_{n,4,i}|$
, respectively. Set
 $$ \begin{align*} B_{n, 1}&=B_{n, 1, 1}+B_{n, 1, 2},\\ B_{n, 2}&=B_{n,2,2}+B_{n,2,3}+B_{n,2,4}+B_{n,2,5}+B_{n,2,6}+B_{n,2,7}+B_{n,2,8},\\ B_{n, 4}&=B_{n,4,2}+B_{n,4,3}+B_{n,4,4}+B_{n,4,5}+B_{n,4,6}+B_{n,4,7}+B_{n,4,8}. \end{align*} $$
$$ \begin{align*} B_{n, 1}&=B_{n, 1, 1}+B_{n, 1, 2},\\ B_{n, 2}&=B_{n,2,2}+B_{n,2,3}+B_{n,2,4}+B_{n,2,5}+B_{n,2,6}+B_{n,2,7}+B_{n,2,8},\\ B_{n, 4}&=B_{n,4,2}+B_{n,4,3}+B_{n,4,4}+B_{n,4,5}+B_{n,4,6}+B_{n,4,7}+B_{n,4,8}. \end{align*} $$
Note that irreducible components of each curve
![]() $B_{n,1}$
,
$B_{n,1}$
,
![]() $B_{n,2}$
,
$B_{n,2}$
,
![]() $B_{n,4}$
are disjoint
$B_{n,4}$
are disjoint
![]() $(-1)$
-curves, and
$(-1)$
-curves, and
![]() $B_{n,1}\cap B_{n,2}=\varnothing $
,
$B_{n,1}\cap B_{n,2}=\varnothing $
,
![]() $B_{n,2}\cap B_{n,3}=\varnothing $
,
$B_{n,2}\cap B_{n,3}=\varnothing $
,
![]() $B_{n,3}\cap B_{n,4}=\varnothing $
,
$B_{n,3}\cap B_{n,4}=\varnothing $
,
![]() $B_{n,4} \cap B_{n+1,1}=\varnothing $
for each
$B_{n,4} \cap B_{n+1,1}=\varnothing $
for each
![]() $n\geqslant 0$
.
$n\geqslant 0$
.
Now, we let
![]() $I^\prime _{0,1}=[0,\frac {1}{3}]$
and
$I^\prime _{0,1}=[0,\frac {1}{3}]$
and
![]() $I^{\prime \prime }_{0,1}=[\frac {1}{3},\frac {3}{8}]$
. For every
$I^{\prime \prime }_{0,1}=[\frac {1}{3},\frac {3}{8}]$
. For every
![]() $n\in \mathbb {Z}_{> 0}$
, we also let
$n\in \mathbb {Z}_{> 0}$
, we also let
 $$ \begin{align*} I_{n, 1}^{\prime}&=\left[\frac{-1+4 n+14 n^{2}}{6 n+14 n^{2}}, \frac{1+13 n+21 n^{2}}{3+16 n+21 n^{2}}\right],\\ I_{n, 1}^{\prime \prime}&=\left[\frac{1+13n+21n^{2}}{3+16n+21n^{2}}, \frac{3+35n+49 n^{2}}{8+42 n+49 n^{2}}\right]. \end{align*} $$
$$ \begin{align*} I_{n, 1}^{\prime}&=\left[\frac{-1+4 n+14 n^{2}}{6 n+14 n^{2}}, \frac{1+13 n+21 n^{2}}{3+16 n+21 n^{2}}\right],\\ I_{n, 1}^{\prime \prime}&=\left[\frac{1+13n+21n^{2}}{3+16n+21n^{2}}, \frac{3+35n+49 n^{2}}{8+42 n+49 n^{2}}\right]. \end{align*} $$
For every
![]() $n\in \mathbb {Z}_{\geqslant 0}$
, we let
$n\in \mathbb {Z}_{\geqslant 0}$
, we let
 $$ \begin{align*} I_{n,2}^{\prime}&=\left[\frac{3+35 n+49n^{2}}{8+42 n+49 n^{2}}, \frac{3+22 n+28 n^{2}}{6+26 n+28 n^{2}}\right],\\ I_{n,2}^{\prime\prime}&=\left[\frac{3+22n+28 n^{2}}{6+26 n+28 n^{2}}, \frac{2+7 n}{3+7 n}\right],\\ I_{n,3}^{\prime}&=\left[\frac{2+7 n}{3+7 n}, \frac{21+50 n+28 n^{2}}{26+54 n+28 n^{2}}\right],\\ I_{n, 3}^{\prime\prime}&=\left[\frac{21+50 n+28 n^{2}}{26+54 n+28 n^{2}}, \frac{39+91 n+49 n^{2}}{48+98 n+49 n^{2}}\right],\\ I_{n,4}^{\prime}&=\left[\frac{39+91 n+49 n^{2}}{48+98 n+49 n^{2}}, \frac{19+41 n+21 n^{2}}{23+44 n+21 n^{2}}\right],\\ I_{n,4}^{\prime\prime}&=\left[\frac{19+41 n+21 n^{2}}{23+44 n+21 n^{2}}, \frac{17+32 n+14 n^{2}}{20+34 n+14 n^{2}}\right]. \end{align*} $$
$$ \begin{align*} I_{n,2}^{\prime}&=\left[\frac{3+35 n+49n^{2}}{8+42 n+49 n^{2}}, \frac{3+22 n+28 n^{2}}{6+26 n+28 n^{2}}\right],\\ I_{n,2}^{\prime\prime}&=\left[\frac{3+22n+28 n^{2}}{6+26 n+28 n^{2}}, \frac{2+7 n}{3+7 n}\right],\\ I_{n,3}^{\prime}&=\left[\frac{2+7 n}{3+7 n}, \frac{21+50 n+28 n^{2}}{26+54 n+28 n^{2}}\right],\\ I_{n, 3}^{\prime\prime}&=\left[\frac{21+50 n+28 n^{2}}{26+54 n+28 n^{2}}, \frac{39+91 n+49 n^{2}}{48+98 n+49 n^{2}}\right],\\ I_{n,4}^{\prime}&=\left[\frac{39+91 n+49 n^{2}}{48+98 n+49 n^{2}}, \frac{19+41 n+21 n^{2}}{23+44 n+21 n^{2}}\right],\\ I_{n,4}^{\prime\prime}&=\left[\frac{19+41 n+21 n^{2}}{23+44 n+21 n^{2}}, \frac{17+32 n+14 n^{2}}{20+34 n+14 n^{2}}\right]. \end{align*} $$
Set
![]() $I_{n,1}=I_{n,1}^\prime \cup I_{n,1}^{\prime \prime }$
,
$I_{n,1}=I_{n,1}^\prime \cup I_{n,1}^{\prime \prime }$
,
![]() $I_{n,2}=I_{n,2}^\prime \cup I_{n,2}^{\prime \prime }$
,
$I_{n,2}=I_{n,2}^\prime \cup I_{n,2}^{\prime \prime }$
,
![]() $I_{n,3}=I_{n,3}^\prime \cup I_{n,3}^{\prime \prime }$
,
$I_{n,3}=I_{n,3}^\prime \cup I_{n,3}^{\prime \prime }$
,
![]() $I_{n,4}=I_{n,4}^\prime \cup I_{n,4}^{\prime \prime }$
. Then
$I_{n,4}=I_{n,4}^\prime \cup I_{n,4}^{\prime \prime }$
. Then
 $$ \begin{align*}[0,1)=\bigcup_{n \in \mathbb{Z}_{\geqslant 0}} \Big(I_{n, 1} \cup I_{n, 2} \cup I_{n, 3} \cup I_{n, 4}\Big), \end{align*} $$
$$ \begin{align*}[0,1)=\bigcup_{n \in \mathbb{Z}_{\geqslant 0}} \Big(I_{n, 1} \cup I_{n, 2} \cup I_{n, 3} \cup I_{n, 4}\Big), \end{align*} $$
the intervals
![]() $I_{n,1}$
,
$I_{n,1}$
,
![]() $I_{n,2}$
,
$I_{n,2}$
,
![]() $I_{n,3}$
,
$I_{n,3}$
,
![]() $I_{n,4}$
have positive volumes, and all their interiors are disjoint. Let us analyze
$I_{n,4}$
have positive volumes, and all their interiors are disjoint. Let us analyze
![]() $P(u,v)$
and
$P(u,v)$
and
![]() $N(u,v)$
when u is contained in one of these intervals.
$N(u,v)$
when u is contained in one of these intervals.
First, we deal with
![]() $u\in I_{n,1}$
. If
$u\in I_{n,1}$
. If
![]() $u\in I_{n,1}^{\prime }$
and
$u\in I_{n,1}^{\prime }$
and
![]() $v\in \left [0,\frac {2+14 n+28 n^{2}-u(1+14 n+28 n^{2})}{1+7 n+7 n^{2}}\right ]$
, then
$v\in \left [0,\frac {2+14 n+28 n^{2}-u(1+14 n+28 n^{2})}{1+7 n+7 n^{2}}\right ]$
, then
 $$ \begin{align*} P(u, v)&=\frac{19+70 n+84 n^{2}-u\left(16+70 n+84 n^{2}\right)-v\left(8+28 n+21 n^{2}\right)}{8+28 n+21 n^{2}}\mathbf{e}_{1}+\\ &\quad+\frac{3+35n+49 n^{2}-u\left(8+42 n+49 n^{2}\right)}{8+28 n+21 n^{2}}B_{n, 1}+ \frac{1-4n-14n^{2}+u\left(6 n+14 n^{2}\right)}{8+28 n+21 n^{2}}B_{n, 2} \end{align*} $$
$$ \begin{align*} P(u, v)&=\frac{19+70 n+84 n^{2}-u\left(16+70 n+84 n^{2}\right)-v\left(8+28 n+21 n^{2}\right)}{8+28 n+21 n^{2}}\mathbf{e}_{1}+\\ &\quad+\frac{3+35n+49 n^{2}-u\left(8+42 n+49 n^{2}\right)}{8+28 n+21 n^{2}}B_{n, 1}+ \frac{1-4n-14n^{2}+u\left(6 n+14 n^{2}\right)}{8+28 n+21 n^{2}}B_{n, 2} \end{align*} $$
and
![]() $N(u,v)=0$
. The same holds if
$N(u,v)=0$
. The same holds if
![]() $u\in I_{n,1}^{\prime \prime }$
and
$u\in I_{n,1}^{\prime \prime }$
and
![]() $v\in \left [0,\frac {7+26 n+28n^{2}-u(6+26 n+28 n^{2})}{3+10 n+7 n^{2}}\right ]$
. Then
$v\in \left [0,\frac {7+26 n+28n^{2}-u(6+26 n+28 n^{2})}{3+10 n+7 n^{2}}\right ]$
. Then
 $$ \begin{align*} \big(P(u,v)\big)^{2}&=10-12u+2u^{2}-2v-v^{2},\\ P(u,v)\cdot\mathbf{e}_1&=1+v. \end{align*} $$
$$ \begin{align*} \big(P(u,v)\big)^{2}&=10-12u+2u^{2}-2v-v^{2},\\ P(u,v)\cdot\mathbf{e}_1&=1+v. \end{align*} $$
Similarly, if
![]() $u\in I_{n,1}^\prime $
and
$u\in I_{n,1}^\prime $
and
![]() $v\in \left [\frac {2+14 n+28 n^{2}-u\left (1+14 n+28 n^{2}\right )}{1+7 n+7 n^{2}}, \frac {7+26 n+28 n^{2}-u\left (6+26 n+28 n^{2}\right )}{3+10 n+7 n^{2}}\right ]$
, then
$v\in \left [\frac {2+14 n+28 n^{2}-u\left (1+14 n+28 n^{2}\right )}{1+7 n+7 n^{2}}, \frac {7+26 n+28 n^{2}-u\left (6+26 n+28 n^{2}\right )}{3+10 n+7 n^{2}}\right ]$
, then
 $$ \begin{align*} P(u, v)&=\frac{19+70n+84n^{2}-u(16+70 n+84 n^{2})-v(8+28 n+21 n^{2})}{8+28 n+21 n^{2}}\mathbf{e}_{1}+\\ &\quad+\frac{\big(19+70n+84n^{2}-u(16+70 n+84 n^{2})-v(8+28 n+21 n^{2})\big)(1+7n+7n^{2})}{8+28n+21n^{2}}B_{n,1}+\\ &\quad+\frac{1-4n-14n^{2}+u(6 n+14 n^{2})}{8+28 n+21 n^{2}}B_{n,2} \end{align*} $$
$$ \begin{align*} P(u, v)&=\frac{19+70n+84n^{2}-u(16+70 n+84 n^{2})-v(8+28 n+21 n^{2})}{8+28 n+21 n^{2}}\mathbf{e}_{1}+\\ &\quad+\frac{\big(19+70n+84n^{2}-u(16+70 n+84 n^{2})-v(8+28 n+21 n^{2})\big)(1+7n+7n^{2})}{8+28n+21n^{2}}B_{n,1}+\\ &\quad+\frac{1-4n-14n^{2}+u(6 n+14 n^{2})}{8+28 n+21 n^{2}}B_{n,2} \end{align*} $$
and
Then
 $$ \begin{align*} \big(P(u,v)\big)^{2}&=10-12 u+2 u^{2}-2 v-v^{2}+\\ &\quad+2\left(u\left(1+14 n+28 n^{2}\right)+v\left(1+7 n+7 n^{2}\right)-2-14n-28n^{2}\right)^{2}\quad\quad\quad\quad \end{align*} $$
$$ \begin{align*} \big(P(u,v)\big)^{2}&=10-12 u+2 u^{2}-2 v-v^{2}+\\ &\quad+2\left(u\left(1+14 n+28 n^{2}\right)+v\left(1+7 n+7 n^{2}\right)-2-14n-28n^{2}\right)^{2}\quad\quad\quad\quad \end{align*} $$
and
 $$ \begin{align*} P(u,v)\cdot\mathbf{e}_1&=5+56n+280n^2+588n^3+392n^4-\\ &\quad-2u(1+7n+7n^2)(1+14n+28n^2)-v(1+28n+126n^2+196n^3+98n^4). \end{align*} $$
$$ \begin{align*} P(u,v)\cdot\mathbf{e}_1&=5+56n+280n^2+588n^3+392n^4-\\ &\quad-2u(1+7n+7n^2)(1+14n+28n^2)-v(1+28n+126n^2+196n^3+98n^4). \end{align*} $$
Likewise, if
![]() $u\in I_{n,1}^{\prime \prime }$
and
$u\in I_{n,1}^{\prime \prime }$
and
![]() $v \in \left [\frac {7+26 n+28 n^{2}-u\left (6+26 n+28 n^{2}\right )}{3+10 n+7 n^{2}}, \frac {2+14 n+28 n^{2}-u\left (1+14 n+28 n^{2}\right )}{1+7 n+7 n^{2}}\right ]$
, then
$v \in \left [\frac {7+26 n+28 n^{2}-u\left (6+26 n+28 n^{2}\right )}{3+10 n+7 n^{2}}, \frac {2+14 n+28 n^{2}-u\left (1+14 n+28 n^{2}\right )}{1+7 n+7 n^{2}}\right ]$
, then
 $$ \begin{align*} P(u, v)&=\frac{(19+70 n+84 n^{2}-u(16+70 n+84 n^{2})-v(8+28 n+21 n^{2})}{8+28 n+21 n^{2}}\mathbf{e}_{1}+\\ &\quad+\frac{\big(19+70 n+84 n^{2}-u(16+70 n+84 n^{2})-v(8+28 n+21 n^{2})\big)(1+n)(3+7n)}{8+28 n+21 n^{2}}B_{n,2}+\\ &\quad+\frac{3+35 n+49 n^{2}-u\left(8+42 n+49 n^{2}\right)}{8+28 n+21 n^{2}}B_{n,1} \end{align*} $$
$$ \begin{align*} P(u, v)&=\frac{(19+70 n+84 n^{2}-u(16+70 n+84 n^{2})-v(8+28 n+21 n^{2})}{8+28 n+21 n^{2}}\mathbf{e}_{1}+\\ &\quad+\frac{\big(19+70 n+84 n^{2}-u(16+70 n+84 n^{2})-v(8+28 n+21 n^{2})\big)(1+n)(3+7n)}{8+28 n+21 n^{2}}B_{n,2}+\\ &\quad+\frac{3+35 n+49 n^{2}-u\left(8+42 n+49 n^{2}\right)}{8+28 n+21 n^{2}}B_{n,1} \end{align*} $$
and
Then
 $$ \begin{align*} &\big(P(u,v)\big)^{2}=10-12 u+2 u^{2}-2 v-v^{2}+\\ &\quad+7\left(u\left(6+26 n+28 n^{2}\right)+v\left(3+10 n+7 n^{2}\right)-7-26n-28n^{2}\right)^{2}\end{align*} $$
$$ \begin{align*} &\big(P(u,v)\big)^{2}=10-12 u+2 u^{2}-2 v-v^{2}+\\ &\quad+7\left(u\left(6+26 n+28 n^{2}\right)+v\left(3+10 n+7 n^{2}\right)-7-26n-28n^{2}\right)^{2}\end{align*} $$
and
 $$ \begin{align*} P(u,v)\cdot\mathbf{e}_1&=148+1036 n+2751 n^{2}+3234 n^{3}+1372 n^{4}-\\ &\quad-14u(1+n)(1+2 n)(3+7 n)^{2}-v\left(62+420 n+994 n^{2}+980 n^{3}+343 n^{4}\right). \end{align*} $$
$$ \begin{align*} P(u,v)\cdot\mathbf{e}_1&=148+1036 n+2751 n^{2}+3234 n^{3}+1372 n^{4}-\\ &\quad-14u(1+n)(1+2 n)(3+7 n)^{2}-v\left(62+420 n+994 n^{2}+980 n^{3}+343 n^{4}\right). \end{align*} $$
If
![]() $u \in I_{n, 1}^{\prime }$
and
$u \in I_{n, 1}^{\prime }$
and
![]() $v\in \left [\frac {7+26 n+28 n^{2}-u\left (6+26 n+28 n^{2}\right )}{3+10 n+7 n^{2}}, \frac {19+70 n+84 n^{2}-u\left (16+70 n+84 n^{2}\right )}{8+28 n+21 n^{2}}\right ]$
, then
$v\in \left [\frac {7+26 n+28 n^{2}-u\left (6+26 n+28 n^{2}\right )}{3+10 n+7 n^{2}}, \frac {19+70 n+84 n^{2}-u\left (16+70 n+84 n^{2}\right )}{8+28 n+21 n^{2}}\right ]$
, then
 $$ \begin{align*} P(u,v)&=\frac{19+70 n+84 n^{2}-u\left(16+70 n+84 n^{2}\right)-v\left(8+28 n+21 n^{2}\right)}{8+28 n+21 n^{2}}\mathbf{e}_1+\\ &\quad+\frac{\big(19+70 n+84 n^{2}-u\left(16+70 n+84 n^{2}\right)-v\left(8+28 n+21 n^{2}\right)\big)\left(1+7n+7 n^{2}\right)}{8+28 n+21 n^{2}}B_{n,1}+\\ &\quad+\frac{\big(19+70 n+84 n^{2}-u\left(16+70 n+84 n^{2}\right)-v\left(8+28 n+21 n^{2}\right)\big)(1+n)(3+7n)}{8+28 n+21 n^{2}}B_{n,2} \end{align*} $$
$$ \begin{align*} P(u,v)&=\frac{19+70 n+84 n^{2}-u\left(16+70 n+84 n^{2}\right)-v\left(8+28 n+21 n^{2}\right)}{8+28 n+21 n^{2}}\mathbf{e}_1+\\ &\quad+\frac{\big(19+70 n+84 n^{2}-u\left(16+70 n+84 n^{2}\right)-v\left(8+28 n+21 n^{2}\right)\big)\left(1+7n+7 n^{2}\right)}{8+28 n+21 n^{2}}B_{n,1}+\\ &\quad+\frac{\big(19+70 n+84 n^{2}-u\left(16+70 n+84 n^{2}\right)-v\left(8+28 n+21 n^{2}\right)\big)(1+n)(3+7n)}{8+28 n+21 n^{2}}B_{n,2} \end{align*} $$
and
 $$ \begin{align*} N(u,v)&=\left(u\left(1+14 n+28 n^{2}\right)+v\left(1+7 n+7 n^{2}\right)-2-14n-28n^{2}\right)B_{n,1}+ \\ &\quad+\left(u\left(6+26 n+28 n^{2}\right)+v\left(3+10 n+7 n^{2}\right)-7-26n-28n^{2}\right)B_{n,2}. \end{align*} $$
$$ \begin{align*} N(u,v)&=\left(u\left(1+14 n+28 n^{2}\right)+v\left(1+7 n+7 n^{2}\right)-2-14n-28n^{2}\right)B_{n,1}+ \\ &\quad+\left(u\left(6+26 n+28 n^{2}\right)+v\left(3+10 n+7 n^{2}\right)-7-26n-28n^{2}\right)B_{n,2}. \end{align*} $$
The same holds if
![]() $u\in I_{n,1}^{\prime \prime }$
and
$u\in I_{n,1}^{\prime \prime }$
and
![]() $v\in \left [\frac {2+14 n+28 n^{2}-u\left (1+14 n+28 n^{2}\right )}{1+7 n+7 n^{2}}, \frac {19+70 n+84 n^{2}-u\left (16+70 n+84 n^{2}\right )}{8+28 n+21 n^{2}}\right ]$
. In both cases, we have
$v\in \left [\frac {2+14 n+28 n^{2}-u\left (1+14 n+28 n^{2}\right )}{1+7 n+7 n^{2}}, \frac {19+70 n+84 n^{2}-u\left (16+70 n+84 n^{2}\right )}{8+28 n+21 n^{2}}\right ]$
. In both cases, we have
 $$ \begin{align*} \big(P(u,v)\big)^{2}&=\left(19+70 n+84 n^{2}-u\left(16+70 n+84 n^{2}\right)-v\left(8+28 n+21 n^{2}\right)\right)^{2},\\ P(u,v)\cdot\mathbf{e}_1&=\left(8+28 n+21 n^{2}\right)\left(19+70 n+84 n^{2}-u\left(16+70 n+84 n^{2}\right)-v\left(8+28 n+21 n^{2}\right)\right). \end{align*} $$
$$ \begin{align*} \big(P(u,v)\big)^{2}&=\left(19+70 n+84 n^{2}-u\left(16+70 n+84 n^{2}\right)-v\left(8+28 n+21 n^{2}\right)\right)^{2},\\ P(u,v)\cdot\mathbf{e}_1&=\left(8+28 n+21 n^{2}\right)\left(19+70 n+84 n^{2}-u\left(16+70 n+84 n^{2}\right)-v\left(8+28 n+21 n^{2}\right)\right). \end{align*} $$
Hence, if
![]() $u\in I_{n,1}$
, then
$u\in I_{n,1}$
, then
 $$ \begin{align*}t(u)=\frac{19+70 n+84 n^{2}-u\left(16+70 n+84 n^{2}\right)}{8+28 n+21 n^{2}}. \end{align*} $$
$$ \begin{align*}t(u)=\frac{19+70 n+84 n^{2}-u\left(16+70 n+84 n^{2}\right)}{8+28 n+21 n^{2}}. \end{align*} $$
Now, we deal with
![]() $u\in I_{n,2}$
. If
$u\in I_{n,2}$
. If
![]() $u\in I_{n,2}^{\prime }$
and
$u\in I_{n,2}^{\prime }$
and
![]() $v\in \left [0,\frac {7+26 n+28 n^{2}-u\left (6+26 n+28 n^{2}\right )}{3+10 n+7 n^{2}}\right ]$
, then
$v\in \left [0,\frac {7+26 n+28 n^{2}-u\left (6+26 n+28 n^{2}\right )}{3+10 n+7 n^{2}}\right ]$
, then
 $$ \begin{align*} P(u,v)&=\frac{17+56 n+56 n^{2}-u\left(15+56 n+56 n^{2}\right)-7v(1+n)(1+2 n)}{7(1+n)(1+2n)}\mathbf{e}_{1}+ \\ &\quad+\frac{(1+n)(2+7 n)-u(1+n)(3+7n)}{7(1+n)(1+2n)} B_{n, 2}+\frac{u\left(8+42 n+49 n^{2}\right)-3-35n-49n^{2}}{7(1+n)(1+2n)}B_{n, 3} \end{align*} $$
$$ \begin{align*} P(u,v)&=\frac{17+56 n+56 n^{2}-u\left(15+56 n+56 n^{2}\right)-7v(1+n)(1+2 n)}{7(1+n)(1+2n)}\mathbf{e}_{1}+ \\ &\quad+\frac{(1+n)(2+7 n)-u(1+n)(3+7n)}{7(1+n)(1+2n)} B_{n, 2}+\frac{u\left(8+42 n+49 n^{2}\right)-3-35n-49n^{2}}{7(1+n)(1+2n)}B_{n, 3} \end{align*} $$
and
![]() $N(u,v)=0$
. The same holds if
$N(u,v)=0$
. The same holds if
![]() $u\in I_{n,2}^{\prime \prime }$
and
$u\in I_{n,2}^{\prime \prime }$
and
![]() $v\in \left [0,\frac {15+42n+28n^{2}-u\left (14+42 n+28 n^{2}\right )}{6+14 n+7 n^{2}}\right ]$
. Then
$v\in \left [0,\frac {15+42n+28n^{2}-u\left (14+42 n+28 n^{2}\right )}{6+14 n+7 n^{2}}\right ]$
. Then
 $$ \begin{align*} \big(P(u,v)\big)^{2}&=10-12u+2u^{2}-2v-v^{2},\\ P(u,v)\cdot\mathbf{e}_1&=v+1. \end{align*} $$
$$ \begin{align*} \big(P(u,v)\big)^{2}&=10-12u+2u^{2}-2v-v^{2},\\ P(u,v)\cdot\mathbf{e}_1&=v+1. \end{align*} $$
If
![]() $u\in I_{n,2}^\prime $
and
$u\in I_{n,2}^\prime $
and
![]() $v \in \left [\frac {7+26 n+28 n^{2}-u\left (6+26 n+28 n^{2}\right )}{3+10 n+7 n^{2}}, \frac {15+42 n+28 n^{2}-u\left (14+42 n+28 n^{2}\right )}{6+14 n+7 n^{2}}\right ]$
, then
$v \in \left [\frac {7+26 n+28 n^{2}-u\left (6+26 n+28 n^{2}\right )}{3+10 n+7 n^{2}}, \frac {15+42 n+28 n^{2}-u\left (14+42 n+28 n^{2}\right )}{6+14 n+7 n^{2}}\right ]$
, then
 $$ \begin{align*} P(u,v)&=\frac{17+56n+56 n^{2}-u(15+56 n+56 n^{2})-7v(1+n)(1+2n)}{7(1+n)(1+2n)}\mathbf{e}_{1}+\\&\quad +\frac{(1+n)(3+7n)\big(17+56n+56 n^{2}-u(15+56 n+56 n^{2})-7v(1+n)(1+2n)\big)}{7(1+n)(1+2n)}B_{n, 2}+\\ &\quad+\frac{u\left(8+42 n+49 n^{2}\right)-3-35n-49n^{2}}{7(1+n)(1+2 n)}B_{n,3}, \end{align*} $$
$$ \begin{align*} P(u,v)&=\frac{17+56n+56 n^{2}-u(15+56 n+56 n^{2})-7v(1+n)(1+2n)}{7(1+n)(1+2n)}\mathbf{e}_{1}+\\&\quad +\frac{(1+n)(3+7n)\big(17+56n+56 n^{2}-u(15+56 n+56 n^{2})-7v(1+n)(1+2n)\big)}{7(1+n)(1+2n)}B_{n, 2}+\\ &\quad+\frac{u\left(8+42 n+49 n^{2}\right)-3-35n-49n^{2}}{7(1+n)(1+2 n)}B_{n,3}, \end{align*} $$
 $$ \begin{align*} \big(P(u,v)\big)^{2}&=10-12 u+2 u^{2}-2 v-v^{2}+\\ &\quad+7\left(u\left(6+26 n+28 n^{2}\right)+v\left(3+10 n+7 n^{2}\right)-7-26n-28n^{2}\right)^{2}, \end{align*} $$
$$ \begin{align*} \big(P(u,v)\big)^{2}&=10-12 u+2 u^{2}-2 v-v^{2}+\\ &\quad+7\left(u\left(6+26 n+28 n^{2}\right)+v\left(3+10 n+7 n^{2}\right)-7-26n-28n^{2}\right)^{2}, \end{align*} $$
 $$ \begin{align*} P(u,v)\cdot\mathbf{e}_1&=148+1036 n+2751 n^{2}+3234 n^{3}+1372 n^{4}-\\ &\quad-14u(1+n)(1+2 n)(3+7 n)^{2}-\\ &\quad-v\left(62+420 n+994 n^{2}+980 n^{3}+343 n^{4}\right). \end{align*} $$
$$ \begin{align*} P(u,v)\cdot\mathbf{e}_1&=148+1036 n+2751 n^{2}+3234 n^{3}+1372 n^{4}-\\ &\quad-14u(1+n)(1+2 n)(3+7 n)^{2}-\\ &\quad-v\left(62+420 n+994 n^{2}+980 n^{3}+343 n^{4}\right). \end{align*} $$
Similarly, if
![]() $u\in I_{n,2}^{\prime \prime }$
and
$u\in I_{n,2}^{\prime \prime }$
and
![]() $v\in \left [\frac {15+42 n+28 n^{2}-u\left (14+42 n+28 n^{2}\right )}{6+14 n+7 n^{2}}, \frac {7+26 n+28 n^{3}-u\left (6+26 n+28 n^{2}\right )}{3+10 n+7 n^{2}}\right ]$
, then
$v\in \left [\frac {15+42 n+28 n^{2}-u\left (14+42 n+28 n^{2}\right )}{6+14 n+7 n^{2}}, \frac {7+26 n+28 n^{3}-u\left (6+26 n+28 n^{2}\right )}{3+10 n+7 n^{2}}\right ]$
, then
 $$ \begin{align*} P(u,v)&=\frac{17+56+56 n^{2}-u\left(15+56 n+56 n^{2}\right)-7v(1+n)(1+2 n)}{7(1+n)(1+2n)}\mathbf{e}_{1}+\\ &\quad+\frac{(6+14 n+7 n^{2})\big(17+56+56 n^{2}-u\left(15+56 n+56 n^{2}\right)-7v(1+n)(1+2 n)\big)}{7(1+n)(1+2 n)}B_{n, 3}+\\ &\quad+\frac{(1+n)(2+7n)-u(1+n)(3+7n)}{7(1+n)(1+2n)}B_{n,2}, \end{align*} $$
$$ \begin{align*} P(u,v)&=\frac{17+56+56 n^{2}-u\left(15+56 n+56 n^{2}\right)-7v(1+n)(1+2 n)}{7(1+n)(1+2n)}\mathbf{e}_{1}+\\ &\quad+\frac{(6+14 n+7 n^{2})\big(17+56+56 n^{2}-u\left(15+56 n+56 n^{2}\right)-7v(1+n)(1+2 n)\big)}{7(1+n)(1+2 n)}B_{n, 3}+\\ &\quad+\frac{(1+n)(2+7n)-u(1+n)(3+7n)}{7(1+n)(1+2n)}B_{n,2}, \end{align*} $$
 $$ \begin{align*} \big(P(u, v)\big)^{2}=10-12 u+2 u^{2}-2 v-v^{2}+\\ +\left(u\left(14+42 n+28 n^{2}\right)+v\left(6+14 n+7 n^{2}\right)-15-42n-28n^{2}\right)^{2}, \end{align*} $$
$$ \begin{align*} \big(P(u, v)\big)^{2}=10-12 u+2 u^{2}-2 v-v^{2}+\\ +\left(u\left(14+42 n+28 n^{2}\right)+v\left(6+14 n+7 n^{2}\right)-15-42n-28n^{2}\right)^{2}, \end{align*} $$
 $$ \begin{align*} P(u,v)\cdot\mathbf{e}_1&=7(1+n)(13+53 n+70n^{2}+28 n^{3})-\\&\quad -14u(1+n)(1+2n)\left(6+14 n+7 n^{2}\right)-7v(1+n)^2\left(5+14 n+7 n^{2}\right). \end{align*} $$
$$ \begin{align*} P(u,v)\cdot\mathbf{e}_1&=7(1+n)(13+53 n+70n^{2}+28 n^{3})-\\&\quad -14u(1+n)(1+2n)\left(6+14 n+7 n^{2}\right)-7v(1+n)^2\left(5+14 n+7 n^{2}\right). \end{align*} $$
Likewise, if
![]() $u\in I_{n,2}^{\prime }$
and
$u\in I_{n,2}^{\prime }$
and
![]() $v\in \left [\frac {15+42 n+28 n^{2}-u\left (14+42 n+28 n^{2}\right )}{6+14 n+7 n^{2}}, \frac {17+56 n+56 n^{2}-u\left (15+56 n+56 n^{2}\right )}{7(1+n)(1+2 n)}\right ]$
, then
$v\in \left [\frac {15+42 n+28 n^{2}-u\left (14+42 n+28 n^{2}\right )}{6+14 n+7 n^{2}}, \frac {17+56 n+56 n^{2}-u\left (15+56 n+56 n^{2}\right )}{7(1+n)(1+2 n)}\right ]$
, then
 $$ \begin{align*} P(u,v)&=\frac{17+56n+56 n^{2}-u\left(15+56 n+56 n^{2}\right)-v(7(1+n)(1+2 n))}{7(1+n)(1+2n)}\mathbf{e}_{1}+\\ &\quad+\frac{(1+n)(3+7n)\big(17+56n+56 n^{2}-u\left(15+56 n+56 n^{2}\right)-7v(1+n)(1+2 n)\big)}{7(1+n)(1+2n)}B_{n, 2}+\\ &\quad+\frac{\left(6+14 n+7 n^{2}\right)\big(17+56n+56 n^{2}-u\left(15+56 n+56 n^{2}\right)-7v(1+n)(1+2n)\big)}{7(1+n)(1+2n)}B_{n,3} \end{align*} $$
$$ \begin{align*} P(u,v)&=\frac{17+56n+56 n^{2}-u\left(15+56 n+56 n^{2}\right)-v(7(1+n)(1+2 n))}{7(1+n)(1+2n)}\mathbf{e}_{1}+\\ &\quad+\frac{(1+n)(3+7n)\big(17+56n+56 n^{2}-u\left(15+56 n+56 n^{2}\right)-7v(1+n)(1+2 n)\big)}{7(1+n)(1+2n)}B_{n, 2}+\\ &\quad+\frac{\left(6+14 n+7 n^{2}\right)\big(17+56n+56 n^{2}-u\left(15+56 n+56 n^{2}\right)-7v(1+n)(1+2n)\big)}{7(1+n)(1+2n)}B_{n,3} \end{align*} $$
and
 $$ \begin{align*} N(u,v)&=\big(u(6+26 n+28 n^{2})+v(3+10 n+7 n^{2})-7-26n-28n^{2}\big) B_{n, 2}+\\ &\quad+\big(u\left(14+42 n+28 n^{2}\right)+v\left(6+14 n+7 n^{2}\right)-15-42n-28 n^{2}\big)B_{n,3}. \end{align*} $$
$$ \begin{align*} N(u,v)&=\big(u(6+26 n+28 n^{2})+v(3+10 n+7 n^{2})-7-26n-28n^{2}\big) B_{n, 2}+\\ &\quad+\big(u\left(14+42 n+28 n^{2}\right)+v\left(6+14 n+7 n^{2}\right)-15-42n-28 n^{2}\big)B_{n,3}. \end{align*} $$
The same holds if
![]() $u\in I_{n,2}^{\prime \prime }$
and
$u\in I_{n,2}^{\prime \prime }$
and
![]() $v\in \left [\frac {7+26 n+28 n^{2}-u\left (6+26 n+28 n^{2}\right )}{3+10 n+7 n^{2}}, \frac {17+56 n+56 n^{2}-u\left (15+56 n+56 n^{2}\right )}{7(1+n)(1+2 n)}\right ]$
. Moreover, in both cases, we have
$v\in \left [\frac {7+26 n+28 n^{2}-u\left (6+26 n+28 n^{2}\right )}{3+10 n+7 n^{2}}, \frac {17+56 n+56 n^{2}-u\left (15+56 n+56 n^{2}\right )}{7(1+n)(1+2 n)}\right ]$
. Moreover, in both cases, we have
and
Thus, if
![]() $u\in I_{n,2}$
, then
$u\in I_{n,2}$
, then
 $$ \begin{align*}t(u)=\frac{17+56n+56n^{2}-u\left(15+56n+56n^{2}\right)}{7(1+n)(1+2n)}. \end{align*} $$
$$ \begin{align*}t(u)=\frac{17+56n+56n^{2}-u\left(15+56n+56n^{2}\right)}{7(1+n)(1+2n)}. \end{align*} $$
Now, we deal with
![]() $u\in I_{n,3}$
. If
$u\in I_{n,3}$
. If
![]() $u\in I_{n,3}^{\prime }$
and
$u\in I_{n,3}^{\prime }$
and
![]() $v\in \left [0,\frac {15+42 n+28 n^{2}-u\left (14+42 n+28 n^{2}\right )}{6+14 n+7 n^{2}}\right ]$
, then
$v\in \left [0,\frac {15+42 n+28 n^{2}-u\left (14+42 n+28 n^{2}\right )}{6+14 n+7 n^{2}}\right ]$
, then
 $$ \begin{align*} P(u,v)&=\frac{59+112 n+56 n^{2}-u\left(57+112 n+56n^{2}\right)-7v(1+n)(3+2n)}{7(1+n)(3+2n)}\mathbf{e}_{1}+ \\ &\quad+\frac{39+91 n+49 n^{2}-u\left(48+98 n+49 n^{2}\right)}{7(1+n)(3+2n)}B_{n, 3}+\frac{u(1+n)(3+7n)-(1+n)(2+7n)}{7(1+n)(3+2n)}B_{n,4} \end{align*} $$
$$ \begin{align*} P(u,v)&=\frac{59+112 n+56 n^{2}-u\left(57+112 n+56n^{2}\right)-7v(1+n)(3+2n)}{7(1+n)(3+2n)}\mathbf{e}_{1}+ \\ &\quad+\frac{39+91 n+49 n^{2}-u\left(48+98 n+49 n^{2}\right)}{7(1+n)(3+2n)}B_{n, 3}+\frac{u(1+n)(3+7n)-(1+n)(2+7n)}{7(1+n)(3+2n)}B_{n,4} \end{align*} $$
and
![]() $N(u,v)=0$
. The same holds if
$N(u,v)=0$
. The same holds if
![]() $u\in I_{n,3}^{\prime \prime }$
and
$u\in I_{n,3}^{\prime \prime }$
and
![]() $v\in \left [0,\frac {31+58 n+28 n^{2}-u\left (30+58 n+28 n^{2}\right )}{11+18 n+7 n^{2}}\right ]$
. Then
$v\in \left [0,\frac {31+58 n+28 n^{2}-u\left (30+58 n+28 n^{2}\right )}{11+18 n+7 n^{2}}\right ]$
. Then
 $$ \begin{align*} \big(P(u,v)\big)^{2}&=10-12u+2u^{2}-2v-v^{2},\\ P(u,v)\cdot\mathbf{e}_1&=1+v. \end{align*} $$
$$ \begin{align*} \big(P(u,v)\big)^{2}&=10-12u+2u^{2}-2v-v^{2},\\ P(u,v)\cdot\mathbf{e}_1&=1+v. \end{align*} $$
If
![]() $u\in I_{n,3}^\prime $
and
$u\in I_{n,3}^\prime $
and
![]() $v \in \left [\frac {15+42 n+28 n^{2}-u\left (14+42 n+28 n^{2}\right )}{6+14 n+7 n^{2}}, \frac {31+58 n+28 n^{2}-u\left (30+58 n+28 n^{2}\right )}{11+18 n+7 n^{2}}\right ]$
, then
$v \in \left [\frac {15+42 n+28 n^{2}-u\left (14+42 n+28 n^{2}\right )}{6+14 n+7 n^{2}}, \frac {31+58 n+28 n^{2}-u\left (30+58 n+28 n^{2}\right )}{11+18 n+7 n^{2}}\right ]$
, then
 $$ \begin{align*} P(u,v)&=\frac{59+112n+56 n^{2}-u\left(57+112 n+56 n^{2}\right)-7v(1+n)(3+2n)}{7(1+n)(3+2n)}\mathbf{e}_{1}+\\ &\quad+\frac{\left(6+14n+7 n^{2}\right)\big(59+112n+56 n^{2}-u\left(57+112 n+56 n^{2}\right)-7v(1+n)(3+2n)\big)}{7(1+n)(3+2n)}B_{n, 3}+\\&\quad +\frac{u(1+n)(3+7n)-(1+n)(2+7n)}{7(1+n)(3+2n)}B_{n,4} \end{align*} $$
$$ \begin{align*} P(u,v)&=\frac{59+112n+56 n^{2}-u\left(57+112 n+56 n^{2}\right)-7v(1+n)(3+2n)}{7(1+n)(3+2n)}\mathbf{e}_{1}+\\ &\quad+\frac{\left(6+14n+7 n^{2}\right)\big(59+112n+56 n^{2}-u\left(57+112 n+56 n^{2}\right)-7v(1+n)(3+2n)\big)}{7(1+n)(3+2n)}B_{n, 3}+\\&\quad +\frac{u(1+n)(3+7n)-(1+n)(2+7n)}{7(1+n)(3+2n)}B_{n,4} \end{align*} $$
 $$ \begin{align*} \big(P(u, v)\big)^{2}&=10-12 u+2 u^{2}-2 v-v^{2}+\\ &\quad+\left(u\left(14+42 n+28 n^{2}\right)+v\left(6+14 n+7 n^{2}\right)-15-42n-28 n^{2}\right)^{2}, \end{align*} $$
$$ \begin{align*} \big(P(u, v)\big)^{2}&=10-12 u+2 u^{2}-2 v-v^{2}+\\ &\quad+\left(u\left(14+42 n+28 n^{2}\right)+v\left(6+14 n+7 n^{2}\right)-15-42n-28 n^{2}\right)^{2}, \end{align*} $$
 $$ \begin{align*} P(u,v)\cdot\mathbf{e}_1&=7(1+n)\big(13+53 n+70 n^{2}+28 n^{3}\big)-\\&\quad -14u(1+n)(1+2n)\left(6+14 n+7 n^{2}\right)-7v(1+n)^2\left(5+14n+7n^{2}\right). \end{align*} $$
$$ \begin{align*} P(u,v)\cdot\mathbf{e}_1&=7(1+n)\big(13+53 n+70 n^{2}+28 n^{3}\big)-\\&\quad -14u(1+n)(1+2n)\left(6+14 n+7 n^{2}\right)-7v(1+n)^2\left(5+14n+7n^{2}\right). \end{align*} $$
Similarly, if
![]() $u\in I_{n,3}^{\prime \prime }$
and
$u\in I_{n,3}^{\prime \prime }$
and
![]() $v \in \left [\frac {31+58 n+28 n^{2}-u\left (30+58 n+28 n^{2}\right )}{11+18 n+7 n^{2}}, \frac {15+42 n+28 n^{2}-u\left (14+42 n+28 n^{2}\right )}{6+14 n+7 n^{2}}\right ]$
, then
$v \in \left [\frac {31+58 n+28 n^{2}-u\left (30+58 n+28 n^{2}\right )}{11+18 n+7 n^{2}}, \frac {15+42 n+28 n^{2}-u\left (14+42 n+28 n^{2}\right )}{6+14 n+7 n^{2}}\right ]$
, then
 $$ \begin{align*} P(u,v)&=\frac{59+112n+56n^{2}-u(57+112n+56n^{2})-7v(1+n)(3+2n)}{7(1+n)(3+2n)}\mathbf{e}_{1}+\\ &\quad+\frac{(1+n)(11+7n)\big(59+112n+56n^{2}-u(57+112n+56n^{2})-7v(1+n)(3+2n)\big)}{7(1+n)(3+2n)}B_{n,4}+\\ &\quad+\frac{39+91n+49n^{2}-u\left(48+98n+49n^{2}\right)}{7(1+n)(3+2n)}B_{n,3},\end{align*} $$
$$ \begin{align*} P(u,v)&=\frac{59+112n+56n^{2}-u(57+112n+56n^{2})-7v(1+n)(3+2n)}{7(1+n)(3+2n)}\mathbf{e}_{1}+\\ &\quad+\frac{(1+n)(11+7n)\big(59+112n+56n^{2}-u(57+112n+56n^{2})-7v(1+n)(3+2n)\big)}{7(1+n)(3+2n)}B_{n,4}+\\ &\quad+\frac{39+91n+49n^{2}-u\left(48+98n+49n^{2}\right)}{7(1+n)(3+2n)}B_{n,3},\end{align*} $$
 $$ \begin{align*} \big(P(u, v)\big)^{2}&=10-12 u+2 u^{2}-2v-v^{2}+\\ &\quad+7\left(u\left(30+58n+28n^{2}\right)+v\left(11+18n+7n^{2}\right)-31-58n-28n^{2}\right)^{2}, \end{align*} $$
$$ \begin{align*} \big(P(u, v)\big)^{2}&=10-12 u+2 u^{2}-2v-v^{2}+\\ &\quad+7\left(u\left(30+58n+28n^{2}\right)+v\left(11+18n+7n^{2}\right)-31-58n-28n^{2}\right)^{2}, \end{align*} $$
 $$ \begin{align*} P(u,v)\cdot\mathbf{e}_1&=2388+8372 n+10983 n^{2}+6370 n^{3}+1372 n^{4}-\\ &\quad-14u(1+n)^{2}(11+7n)(15+14n)-v\left(846+2772 n+3346 n^{2}+1764 n^{3}+343 n^{4}\right). \end{align*} $$
$$ \begin{align*} P(u,v)\cdot\mathbf{e}_1&=2388+8372 n+10983 n^{2}+6370 n^{3}+1372 n^{4}-\\ &\quad-14u(1+n)^{2}(11+7n)(15+14n)-v\left(846+2772 n+3346 n^{2}+1764 n^{3}+343 n^{4}\right). \end{align*} $$
If
![]() $u\in I_{n,3}^{\prime }$
and
$u\in I_{n,3}^{\prime }$
and
![]() $v\in \left [\frac {31+58 n+28 n^{2}-u\left (30+58 n+28 n^{2}\right )}{11+18 n+7 n^{2}}, \frac {59+112 n+56 n^{2}-u\left (57+112 n+56 n^{2}\right )}{7(1+n)(3+2 n)}\right ]$
, then
$v\in \left [\frac {31+58 n+28 n^{2}-u\left (30+58 n+28 n^{2}\right )}{11+18 n+7 n^{2}}, \frac {59+112 n+56 n^{2}-u\left (57+112 n+56 n^{2}\right )}{7(1+n)(3+2 n)}\right ]$
, then
 $$ \begin{align*} P(u, v)&=\frac{59+112 n+56 n^{2}-u\left(57+112 n+56 n^{2}\right)-7v(1+n)(3+2n)}{7(1+n)(3+2n)}\mathbf{e}_1+\\&\quad +\frac{\left(6+14 n+7 n^{2}\right)\big(59+112 n+56 n^{2}-u\left(57+112 n+56 n^{2}\right)-7v(1+n)(3+2n)\big)}{7(1+n)(3+2n)}B_{n,3 }+\\ &\quad+\frac{(1+n)\left(11+7n\right)\big(59+112 n+56 n^{2}-u\left(57+112 n+56 n^{2}\right)-7v(1+n)(3+2n)\big)}{7(1+n)(3+2n)}B_{n, 4} \end{align*} $$
$$ \begin{align*} P(u, v)&=\frac{59+112 n+56 n^{2}-u\left(57+112 n+56 n^{2}\right)-7v(1+n)(3+2n)}{7(1+n)(3+2n)}\mathbf{e}_1+\\&\quad +\frac{\left(6+14 n+7 n^{2}\right)\big(59+112 n+56 n^{2}-u\left(57+112 n+56 n^{2}\right)-7v(1+n)(3+2n)\big)}{7(1+n)(3+2n)}B_{n,3 }+\\ &\quad+\frac{(1+n)\left(11+7n\right)\big(59+112 n+56 n^{2}-u\left(57+112 n+56 n^{2}\right)-7v(1+n)(3+2n)\big)}{7(1+n)(3+2n)}B_{n, 4} \end{align*} $$
and
 $$ \begin{align*} N(u,v)&=\left(u\left(14+42 n+28 n^{2}\right)+v\left(6+14 n+7 n^{2}\right)-15-42n-28n^{2}\right)B_{n,3}+\\ &\quad+\left(u\left(30+58n+28n^{2}\right)+v\left(11+18n+7n^{2}\right)-31-58n-28n^{2}\right)B_{n, 4}. \end{align*} $$
$$ \begin{align*} N(u,v)&=\left(u\left(14+42 n+28 n^{2}\right)+v\left(6+14 n+7 n^{2}\right)-15-42n-28n^{2}\right)B_{n,3}+\\ &\quad+\left(u\left(30+58n+28n^{2}\right)+v\left(11+18n+7n^{2}\right)-31-58n-28n^{2}\right)B_{n, 4}. \end{align*} $$
The same holds if
![]() $u\in I_{u,3}^{\prime \prime }$
and
$u\in I_{u,3}^{\prime \prime }$
and
![]() $v\in \left [\frac {15+42 n+28 n^{2}-u\left (14+42 n+28 n^{2}\right )}{6+14 n+7 n^{2}}, \frac {59+112 n+56 n^{2}-u\left (57+112 n+56 n^{2}\right )}{7(1+n)(3+2n)}\right ]$
. In both cases, we have
$v\in \left [\frac {15+42 n+28 n^{2}-u\left (14+42 n+28 n^{2}\right )}{6+14 n+7 n^{2}}, \frac {59+112 n+56 n^{2}-u\left (57+112 n+56 n^{2}\right )}{7(1+n)(3+2n)}\right ]$
. In both cases, we have
and
Therefore, if
![]() $u\in I_{n,3}$
, then
$u\in I_{n,3}$
, then
 $$ \begin{align*}t(u)=\frac{59+112n+56n^{2}-u\left(57+112n+56n^{2}\right)}{7(1+n)(3+2n)}. \end{align*} $$
$$ \begin{align*}t(u)=\frac{59+112n+56n^{2}-u\left(57+112n+56n^{2}\right)}{7(1+n)(3+2n)}. \end{align*} $$
Finally, we deal with
![]() $u\in I_{n,4}$
. If
$u\in I_{n,4}$
. If
![]() $u\in I_{n,4}^{\prime }$
and
$u\in I_{n,4}^{\prime }$
and
![]() $v\in \left [0,\frac {31+58n+28n^{2}-u\left (30+58n+28n^{2}\right )}{11+18n+7n^{2}}\right ]$
, then
$v\in \left [0,\frac {31+58n+28n^{2}-u\left (30+58n+28n^{2}\right )}{11+18n+7n^{2}}\right ]$
, then
 $$ \begin{align*} P(u, v)&=\frac{103+182 n+84 n^{2}-u\left(100+182 n+84 n^{2}\right)-v\left(36+56 n+21 n^{2}\right)}{36+56n+21 n^{2}}\mathbf{e}_{1}+\\ &\quad+\frac{17+32 n+14 n^{2}-u\left(20+34 n+14 n^{2}\right)}{36+56n+21n^{2}}B_{n,4}+\frac{u\left(48+98 n+49 n^{2}\right)-39-91n-49n^{2}}{36+56n+21 n^{2}}B_{n+1,1} \end{align*} $$
$$ \begin{align*} P(u, v)&=\frac{103+182 n+84 n^{2}-u\left(100+182 n+84 n^{2}\right)-v\left(36+56 n+21 n^{2}\right)}{36+56n+21 n^{2}}\mathbf{e}_{1}+\\ &\quad+\frac{17+32 n+14 n^{2}-u\left(20+34 n+14 n^{2}\right)}{36+56n+21n^{2}}B_{n,4}+\frac{u\left(48+98 n+49 n^{2}\right)-39-91n-49n^{2}}{36+56n+21 n^{2}}B_{n+1,1} \end{align*} $$
and
![]() $N(u,v)=0$
. The same holds when
$N(u,v)=0$
. The same holds when
![]() $u\in I_{n,4}^{\prime \prime }$
and
$u\in I_{n,4}^{\prime \prime }$
and
![]() $v\in \left [0,\frac {44+70 n+28 n^{2}-u\left (43+70 n+28 n^{2}\right )}{15+21 n+7 n^{2}}\right ]$
. In both cases, we compute
$v\in \left [0,\frac {44+70 n+28 n^{2}-u\left (43+70 n+28 n^{2}\right )}{15+21 n+7 n^{2}}\right ]$
. In both cases, we compute
 $$ \begin{align*} \big(P(u,v)\big)^{2}&=10-12u+2u^{2}-2 v-v^{2},\\ P(u,v)\cdot\mathbf{e}_1&=1+v. \end{align*} $$
$$ \begin{align*} \big(P(u,v)\big)^{2}&=10-12u+2u^{2}-2 v-v^{2},\\ P(u,v)\cdot\mathbf{e}_1&=1+v. \end{align*} $$
If
![]() $u\in I_{n,4}^\prime $
and
$u\in I_{n,4}^\prime $
and
![]() $v \in \left [\frac {31+58 n+28 n^{2}-u\left (30+58 n+28 n^{2}\right )}{11+18 n+7 n^{2}}, \frac {44+70 n+28 n^{2}-u\left (43+70 n+28 n^{2}\right )}{15+21 n+7 n^{2}}\right ]$
, then
$v \in \left [\frac {31+58 n+28 n^{2}-u\left (30+58 n+28 n^{2}\right )}{11+18 n+7 n^{2}}, \frac {44+70 n+28 n^{2}-u\left (43+70 n+28 n^{2}\right )}{15+21 n+7 n^{2}}\right ]$
, then
 $$ \begin{align*} P(u, v)&=\frac{103+182n+84n^{2}-u(100+182n+84n^{2})-v(36+56n+21n^{2})}{36+56n+21n^{2}}\mathbf{e}_{1}+\\ &\quad+\frac{(1+n)(11+7n)\big(103+182n+84n^{2}-u(100+182n+84n^{2})-v(36+56n+21n^{2})\big)}{36+56n+21n^{2}}B_{n,4}+\\ &\quad+\frac{u(48+98n+49n^{2})-39-91n-49n^{2}}{36+56n+21n^{2}}B_{n+1,1}, \end{align*} $$
$$ \begin{align*} P(u, v)&=\frac{103+182n+84n^{2}-u(100+182n+84n^{2})-v(36+56n+21n^{2})}{36+56n+21n^{2}}\mathbf{e}_{1}+\\ &\quad+\frac{(1+n)(11+7n)\big(103+182n+84n^{2}-u(100+182n+84n^{2})-v(36+56n+21n^{2})\big)}{36+56n+21n^{2}}B_{n,4}+\\ &\quad+\frac{u(48+98n+49n^{2})-39-91n-49n^{2}}{36+56n+21n^{2}}B_{n+1,1}, \end{align*} $$
 $$ \begin{align*} \big(P(u,v)\big)^{2}&=10-12 u+2 u^{2}-2 v-v^{2}+\\ &\quad+7\left(u\left(30+58 n+28 n^{2}\right)+v\left(11+18 n+7 n^{2}\right)-31-58n-28n^{2}\right)^{2}, \end{align*} $$
$$ \begin{align*} \big(P(u,v)\big)^{2}&=10-12 u+2 u^{2}-2 v-v^{2}+\\ &\quad+7\left(u\left(30+58 n+28 n^{2}\right)+v\left(11+18 n+7 n^{2}\right)-31-58n-28n^{2}\right)^{2}, \end{align*} $$
 $$ \begin{align*} P(u,v)\cdot\mathbf{e}_1&=2388+8372 n+10983 n^{2}+6370 n^{2}+1372 n^{4}-\\ &\quad-14u(1+n)^{2}(11+7n)(15+14 n)-\\ &\quad-v\left(846+2772 n+3346 n^{2}+1764 n^{3}+343 n^{4}\right). \end{align*} $$
$$ \begin{align*} P(u,v)\cdot\mathbf{e}_1&=2388+8372 n+10983 n^{2}+6370 n^{2}+1372 n^{4}-\\ &\quad-14u(1+n)^{2}(11+7n)(15+14 n)-\\ &\quad-v\left(846+2772 n+3346 n^{2}+1764 n^{3}+343 n^{4}\right). \end{align*} $$
If
![]() $u\in I_{n,4}^{\prime \prime }$
and
$u\in I_{n,4}^{\prime \prime }$
and
![]() $v \in \left [\frac {44+70 n+28 n^{2}-u\left (43+70 n+28 n^{2}\right )}{15+21 n+7 n^{2}}, \frac {31+58 n+28 n^{2}-u\left (30+58 n+28 n^{2}\right )}{11+18 n+7 n^{2}}\right ]$
, then
$v \in \left [\frac {44+70 n+28 n^{2}-u\left (43+70 n+28 n^{2}\right )}{15+21 n+7 n^{2}}, \frac {31+58 n+28 n^{2}-u\left (30+58 n+28 n^{2}\right )}{11+18 n+7 n^{2}}\right ]$
, then
 $$ \begin{align*} P(u,v)&=\frac{103+182n+84n^{2}-u(100+182n+84n^{2})-v(36+56n+21n^{2})}{36+56 n+21n^{2}}\mathbf{e}_{1}+\\ &\quad+\frac{(15+21n+7n^{2})\big(103+182n+84n^{2}-u(100+182n+84n^{2})-v(36+56n+21n^{2})\big)}{36+56 n+21n^{2}}B_{n+1,1}+\\ &\quad+\frac{17+32n+14n^{2}-u\left(20+34n+14n^{2}\right)}{36+56 n+21n^{2}}B_{n,4} \end{align*} $$
$$ \begin{align*} P(u,v)&=\frac{103+182n+84n^{2}-u(100+182n+84n^{2})-v(36+56n+21n^{2})}{36+56 n+21n^{2}}\mathbf{e}_{1}+\\ &\quad+\frac{(15+21n+7n^{2})\big(103+182n+84n^{2}-u(100+182n+84n^{2})-v(36+56n+21n^{2})\big)}{36+56 n+21n^{2}}B_{n+1,1}+\\ &\quad+\frac{17+32n+14n^{2}-u\left(20+34n+14n^{2}\right)}{36+56 n+21n^{2}}B_{n,4} \end{align*} $$
and
Moreover, in this case, we have
 $$ \begin{align*} \big(P(u,v)\big)^{2}&=10-12 u+2 u^{2}-2 v-v^{2}+\\ &\quad+2\left(u\left(43+70 n+28 n^{2}\right)+v\left(15+21 n+7 n^{2}\right)-44-70n-28n^{2}\right)^{2}\end{align*} $$
$$ \begin{align*} \big(P(u,v)\big)^{2}&=10-12 u+2 u^{2}-2 v-v^{2}+\\ &\quad+2\left(u\left(43+70 n+28 n^{2}\right)+v\left(15+21 n+7 n^{2}\right)-44-70n-28n^{2}\right)^{2}\end{align*} $$
and
 $$ \begin{align*} P(u,v)\cdot\mathbf{e}_1&=1321+3948 n+4396 n^{2}+2156 n^{3}+392 n^{4}-\\ &\quad-2u\left(15+21 n+7 n^{2}\right)\left(43+70 n+28 n^{2}\right)-\\&\quad -v\left(449+1260 n+1302 n^{2}+588 n^{3}+98 n^{4}\right). \end{align*} $$
$$ \begin{align*} P(u,v)\cdot\mathbf{e}_1&=1321+3948 n+4396 n^{2}+2156 n^{3}+392 n^{4}-\\ &\quad-2u\left(15+21 n+7 n^{2}\right)\left(43+70 n+28 n^{2}\right)-\\&\quad -v\left(449+1260 n+1302 n^{2}+588 n^{3}+98 n^{4}\right). \end{align*} $$
If
![]() $u\in I_{n,4}^{\prime }$
and
$u\in I_{n,4}^{\prime }$
and
![]() $v\in \left [\frac {44+70 n+28 n^{2}-u\left (43+70 n+28 n^{2}\right )}{15+21 n+7 n^{2}},\frac {103+182 n+84 n^{2}-u\left (100+182 n+84 n^{2}\right )}{36+56 n+21 n^{2}}\right ]$
, then
$v\in \left [\frac {44+70 n+28 n^{2}-u\left (43+70 n+28 n^{2}\right )}{15+21 n+7 n^{2}},\frac {103+182 n+84 n^{2}-u\left (100+182 n+84 n^{2}\right )}{36+56 n+21 n^{2}}\right ]$
, then
 $$ \begin{align*} P(u,v)&=\frac{103+182n+84n^{2}-u(100+182n+84n^{2})-v(36+56n+21n^{2})}{36+56n+21n^{2}}\mathbf{e}_1+\\ &\quad+\frac{(1+n)(11+7n)\big(103+182n+84n^{2}-u(100+182n+84n^{2})-v(36+56n+21n^{2})\big)}{36+56n+21n^{2}}B_{n,4}+\\ &\quad+\frac{(15+21 n+7n^{2})\big(103+182n+84n^{2}-u(100+182n+84n^{2})-v(36+56n+21n^{2})\big)}{36+56n+21n^{2}}B_{n+1,1} \end{align*} $$
$$ \begin{align*} P(u,v)&=\frac{103+182n+84n^{2}-u(100+182n+84n^{2})-v(36+56n+21n^{2})}{36+56n+21n^{2}}\mathbf{e}_1+\\ &\quad+\frac{(1+n)(11+7n)\big(103+182n+84n^{2}-u(100+182n+84n^{2})-v(36+56n+21n^{2})\big)}{36+56n+21n^{2}}B_{n,4}+\\ &\quad+\frac{(15+21 n+7n^{2})\big(103+182n+84n^{2}-u(100+182n+84n^{2})-v(36+56n+21n^{2})\big)}{36+56n+21n^{2}}B_{n+1,1} \end{align*} $$
and
 $$ \begin{align*} N(u,v) &=\big(u(30+58 n+28 n^{2})+v(11+18 n+7 n^{2})-31-58n-28n^{2}\big)B_{n,4} +\\&\quad +\big(u(43+70 n+28 n^{2})+v(15+21 n+7 n^{2})-44-70n-28n^{2}\big)B_{n+1,1}. \end{align*} $$
$$ \begin{align*} N(u,v) &=\big(u(30+58 n+28 n^{2})+v(11+18 n+7 n^{2})-31-58n-28n^{2}\big)B_{n,4} +\\&\quad +\big(u(43+70 n+28 n^{2})+v(15+21 n+7 n^{2})-44-70n-28n^{2}\big)B_{n+1,1}. \end{align*} $$
The same holds when
![]() $u\in I_{n,4}^{\prime \prime }$
and
$u\in I_{n,4}^{\prime \prime }$
and
![]() $v \in \left [\frac {31+58n+28 n^{2}-u\left (30+58n+28 n^{2}\right )}{11+18n+7 n^{2}},\frac {103+182n+84n^{2}-u\left (100+182 n+84n^{2}\right )}{36+56n+21n^{2}}\right ]$
. Moreover, in both cases, we have
$v \in \left [\frac {31+58n+28 n^{2}-u\left (30+58n+28 n^{2}\right )}{11+18n+7 n^{2}},\frac {103+182n+84n^{2}-u\left (100+182 n+84n^{2}\right )}{36+56n+21n^{2}}\right ]$
. Moreover, in both cases, we have
and
Thus, if
![]() $u\in I_{n,4}$
, then
$u\in I_{n,4}$
, then
 $$ \begin{align*}t(u)=\frac{103+182n+84n^{2}-u\left(100+182n+84n^{2}\right)}{36+56n+21n^{2}}. \end{align*} $$
$$ \begin{align*}t(u)=\frac{103+182n+84n^{2}-u\left(100+182n+84n^{2}\right)}{36+56n+21n^{2}}. \end{align*} $$
Now, we are ready to compute
![]() $S(W_{\bullet ,\bullet }^{T};\mathbf {e}_1)$
. Namely, for every
$S(W_{\bullet ,\bullet }^{T};\mathbf {e}_1)$
. Namely, for every
![]() $i\in \{1,2,3,4\}$
, we set
$i\in \{1,2,3,4\}$
, we set
 $$ \begin{align*}S_{n,i}=\frac{3}{14}\int_{I_{n,i}}\int_0^{t(u)}\big(P(u,v)\big)^2dvdu. \end{align*} $$
$$ \begin{align*}S_{n,i}=\frac{3}{14}\int_{I_{n,i}}\int_0^{t(u)}\big(P(u,v)\big)^2dvdu. \end{align*} $$
Then
 $$ \begin{align*}S\big(W_{\bullet,\bullet}^{T};\mathbf{e}_1\big)=\sum_{n=0}^{\infty}\Big(S_{n,1}+S_{n,2}+S_{n,3}+S_{n,4}\Big). \end{align*} $$
$$ \begin{align*}S\big(W_{\bullet,\bullet}^{T};\mathbf{e}_1\big)=\sum_{n=0}^{\infty}\Big(S_{n,1}+S_{n,2}+S_{n,3}+S_{n,4}\Big). \end{align*} $$
On the other hand, integrating, we get
 $$ \begin{align*}S_{n,1}= \left\{\begin{aligned} &\frac{84365}{114688}\ \text{if }n=0, \\ &\frac{(8+28n+21n^{2})A_{n,1}}{448 n^{4}(1+n)(2+7n)^{4}(3+7n)^{4}(4+7n)^{4} (1+7n+7n^{2})}\ \text{if }n\geqslant 1, \\ \end{aligned} \right. \end{align*} $$
$$ \begin{align*}S_{n,1}= \left\{\begin{aligned} &\frac{84365}{114688}\ \text{if }n=0, \\ &\frac{(8+28n+21n^{2})A_{n,1}}{448 n^{4}(1+n)(2+7n)^{4}(3+7n)^{4}(4+7n)^{4} (1+7n+7n^{2})}\ \text{if }n\geqslant 1, \\ \end{aligned} \right. \end{align*} $$
where
 $$ \begin{align*} A_{n,1}&=1536+109312 n+2935552 n^{2}+42681728 n^{3}+386407488 n^{4}+2335296292 n^{5}+\\ &\quad+9789648099 n^{6}+29038364761 n^{7}+61312905318 n^{8}+91454579804 n^{9}+\\ &\quad+94035837280 n^{10}+63317750608 n^{11}+25088413952 n^{12}+4427367168 n^{13}.\quad\quad \end{align*} $$
$$ \begin{align*} A_{n,1}&=1536+109312 n+2935552 n^{2}+42681728 n^{3}+386407488 n^{4}+2335296292 n^{5}+\\ &\quad+9789648099 n^{6}+29038364761 n^{7}+61312905318 n^{8}+91454579804 n^{9}+\\ &\quad+94035837280 n^{10}+63317750608 n^{11}+25088413952 n^{12}+4427367168 n^{13}.\quad\quad \end{align*} $$
Similarly, we get
where
 $$ \begin{align*} A_{n,2}&=1618654+31459234 n+271069253 n^{2}+1362423916 n^{3}+4419070194 n^{4}+9654348284n^{5}+\\ &\quad+14368501182 n^{6}+14362052096 n^{7}+9209328422 n^{8}+3412762192n^9+553420896n^{10}. \end{align*} $$
$$ \begin{align*} A_{n,2}&=1618654+31459234 n+271069253 n^{2}+1362423916 n^{3}+4419070194 n^{4}+9654348284n^{5}+\\ &\quad+14368501182 n^{6}+14362052096 n^{7}+9209328422 n^{8}+3412762192n^9+553420896n^{10}. \end{align*} $$
Likewise, we get
where
 $$ \begin{align*} A_{n,3}&=1167997914+15454923336 n+91492878645 n^{2}+319934133575 n^{3}+\\ &\quad+734395997090 n^{4}+1162203105378 n^{5}+1294197714054 n^{6}+1014406754242 n^{7}+\\ &\quad+548632346402 n^{8}+195059453722 n^{9}+41045383120 n^{10}+3873946272n^{11}. \end{align*} $$
$$ \begin{align*} A_{n,3}&=1167997914+15454923336 n+91492878645 n^{2}+319934133575 n^{3}+\\ &\quad+734395997090 n^{4}+1162203105378 n^{5}+1294197714054 n^{6}+1014406754242 n^{7}+\\ &\quad+548632346402 n^{8}+195059453722 n^{9}+41045383120 n^{10}+3873946272n^{11}. \end{align*} $$
Finally, we get
 $$ \begin{align*}S_{n,4}=\frac{(36+56 n+21 n^{2})A_{n,4}}{448(1+n)^{4}(6+7n)^{4}(8+7n)^{4}(10+7n)^{4}(11+7n)(15+21n+7 n^{2})}, \end{align*} $$
$$ \begin{align*}S_{n,4}=\frac{(36+56 n+21 n^{2})A_{n,4}}{448(1+n)^{4}(6+7n)^{4}(8+7n)^{4}(10+7n)^{4}(11+7n)(15+21n+7 n^{2})}, \end{align*} $$
where
 $$ \begin{align*} A_{n,4}&=365613573312+4021500121920 n+20341847967024 n^{2}+\\ &\quad+62650071283024 n^{3}+131072047236004 n^{4}+196698030664492 n^{5}+217823761840153 n^{6}+\\ &\quad+180219167765455 n^{7}+111395400841326 n^{8}+50802960251820 n^{9}+16615457209344 n^{10}+\\ &\quad+3690223711216 n^{11}+498816700928 n^{12}+30991570176 n^{13}. \end{align*} $$
$$ \begin{align*} A_{n,4}&=365613573312+4021500121920 n+20341847967024 n^{2}+\\ &\quad+62650071283024 n^{3}+131072047236004 n^{4}+196698030664492 n^{5}+217823761840153 n^{6}+\\ &\quad+180219167765455 n^{7}+111395400841326 n^{8}+50802960251820 n^{9}+16615457209344 n^{10}+\\ &\quad+3690223711216 n^{11}+498816700928 n^{12}+30991570176 n^{13}. \end{align*} $$
Then, adding, we get
 $$ \begin{align*}S\big(W_{\bullet,\bullet}^{T};\mathbf{e}_1\big)=\sum_{n=0}^{\infty}\Big(S_{n,1}+S_{n,2}+S_{n,3}+S_{n,4}\Big)\approx 0.976712233\ldots<1. \end{align*} $$
$$ \begin{align*}S\big(W_{\bullet,\bullet}^{T};\mathbf{e}_1\big)=\sum_{n=0}^{\infty}\Big(S_{n,1}+S_{n,2}+S_{n,3}+S_{n,4}\Big)\approx 0.976712233\ldots<1. \end{align*} $$
Finally, let us compute
![]() $S(W_{\bullet , \bullet ,\bullet }^{T,\mathbf {e}_1};P)$
. For every
$S(W_{\bullet , \bullet ,\bullet }^{T,\mathbf {e}_1};P)$
. For every
![]() $i\in \{1,2,3,4\}$
, we set
$i\in \{1,2,3,4\}$
, we set
 $$ \begin{align*} M_{n,i}^\prime&=\frac{3}{14}\int_{I_{n,i}^\prime}\int_0^{t(u)}\Big(\big(P(u,v)\cdot\mathbf{e}_1\big)\Big)^2dvdu,\\ M_{n,i}^{\prime\prime}&=\frac{3}{14}\int_{I_{n,i}^{\prime\prime}}\int_0^{t(u)}\Big(\big(P(u,v)\cdot\mathbf{e}_1\big)\Big)^2dvdu.\quad\quad\quad\quad\quad\quad\quad \end{align*} $$
$$ \begin{align*} M_{n,i}^\prime&=\frac{3}{14}\int_{I_{n,i}^\prime}\int_0^{t(u)}\Big(\big(P(u,v)\cdot\mathbf{e}_1\big)\Big)^2dvdu,\\ M_{n,i}^{\prime\prime}&=\frac{3}{14}\int_{I_{n,i}^{\prime\prime}}\int_0^{t(u)}\Big(\big(P(u,v)\cdot\mathbf{e}_1\big)\Big)^2dvdu.\quad\quad\quad\quad\quad\quad\quad \end{align*} $$
Then
 $$ \begin{align*}S\big(W_{\bullet, \bullet,\bullet}^{T,\mathbf{e}_1};P\big)= \sum_{n=0}^{\infty}\sum_{i=1}^{4}\Big(M_{n,i}^\prime+M_{n,i}^{\prime\prime}\Big)+\frac{3}{7}\int_{0}^1\int_0^{t(u)}\big(P(u,v)\cdot \mathbf{e}_1\big)\mathrm{ord}_P\Big(N(u,v)\big|_{\mathbf{e}_1}\Big)dvdu. \end{align*} $$
$$ \begin{align*}S\big(W_{\bullet, \bullet,\bullet}^{T,\mathbf{e}_1};P\big)= \sum_{n=0}^{\infty}\sum_{i=1}^{4}\Big(M_{n,i}^\prime+M_{n,i}^{\prime\prime}\Big)+\frac{3}{7}\int_{0}^1\int_0^{t(u)}\big(P(u,v)\cdot \mathbf{e}_1\big)\mathrm{ord}_P\Big(N(u,v)\big|_{\mathbf{e}_1}\Big)dvdu. \end{align*} $$
On the other hand, integrating, we get
 $$ \begin{align*}M_{n,1}^\prime= \left\{\begin{aligned} &\frac{1403}{22268}\ \text{if }n=0, \\ &\frac{(1+n)A_{n,1}^\prime}{448n^{4}(1+3n)^{4}(3+7n)^{4}(1+7n+7 n^{2})}\ \text{if }n\geqslant 1, \\ \end{aligned} \right. \end{align*} $$
$$ \begin{align*}M_{n,1}^\prime= \left\{\begin{aligned} &\frac{1403}{22268}\ \text{if }n=0, \\ &\frac{(1+n)A_{n,1}^\prime}{448n^{4}(1+3n)^{4}(3+7n)^{4}(1+7n+7 n^{2})}\ \text{if }n\geqslant 1, \\ \end{aligned} \right. \end{align*} $$
where
 $$ \begin{align*} A_{n,1}^\prime&=1+81 n+2535 n^{2}+37209 n^{3}+301046 n^{4}+1459736 n^{5}+\\ &\quad+4420190 n^{6}+8425410 n^{7}+9821448 n^{8}+6392736 n^{9}+1778112 n^{10}. \end{align*} $$
$$ \begin{align*} A_{n,1}^\prime&=1+81 n+2535 n^{2}+37209 n^{3}+301046 n^{4}+1459736 n^{5}+\\ &\quad+4420190 n^{6}+8425410 n^{7}+9821448 n^{8}+6392736 n^{9}+1778112 n^{10}. \end{align*} $$
Similarly, we get
 $$ \begin{align*}M_{n, 1}^{\prime\prime}=\frac{(1+7 n+7 n^{2})A_{n,1}^{\prime\prime}}{28(1+n)(1+3 n)^{4}(2+7 n)^{4}(3+7 n)^{4}(4+7 n)^{4}}, \end{align*} $$
$$ \begin{align*}M_{n, 1}^{\prime\prime}=\frac{(1+7 n+7 n^{2})A_{n,1}^{\prime\prime}}{28(1+n)(1+3 n)^{4}(2+7 n)^{4}(3+7 n)^{4}(4+7 n)^{4}}, \end{align*} $$
where
 $$ \begin{align*} A_{n,1}^{\prime\prime}&=480574+12906866 n+157271760 n^{2}+1149521334 n^{3}+5612285145 n^{4}+\\&\quad +19278934535 n^{5}+47770884833 n^{6}+86016481159 n^{7} +111679016743 n^{8}+\\ &\quad+101939513907 n^{9}+62077730148 n^{10}+22635902898 n^{11}+3735591048 n^{12}. \end{align*} $$
$$ \begin{align*} A_{n,1}^{\prime\prime}&=480574+12906866 n+157271760 n^{2}+1149521334 n^{3}+5612285145 n^{4}+\\&\quad +19278934535 n^{5}+47770884833 n^{6}+86016481159 n^{7} +111679016743 n^{8}+\\ &\quad+101939513907 n^{9}+62077730148 n^{10}+22635902898 n^{11}+3735591048 n^{12}. \end{align*} $$
Likewise, we have
 $$ \begin{align*}M_{n,2}^{\prime}=\frac{(6+14n+7n^{2})A_{n,2}^{\prime}}{224(1+n)(1+2 n)^{3}(2+7 n)^{4}(3+7 n)^{4}(4+7 n)^{4}}, \end{align*} $$
$$ \begin{align*}M_{n,2}^{\prime}=\frac{(6+14n+7n^{2})A_{n,2}^{\prime}}{224(1+n)(1+2 n)^{3}(2+7 n)^{4}(3+7 n)^{4}(4+7 n)^{4}}, \end{align*} $$
and
 $$ \begin{align*}M_{n,2}^{\prime\prime}=\frac{11780+111142 n+430951 n^{2}+875637 n^{3}+978656 n^{4}+566832 n^{5}+131712 n^{6}}{224(1+2 n)^{3}(3+7 n)^{4}( 6+14 n+7 n^{2})}, \end{align*} $$
$$ \begin{align*}M_{n,2}^{\prime\prime}=\frac{11780+111142 n+430951 n^{2}+875637 n^{3}+978656 n^{4}+566832 n^{5}+131712 n^{6}}{224(1+2 n)^{3}(3+7 n)^{4}( 6+14 n+7 n^{2})}, \end{align*} $$
where
 $$ \begin{align*} A_{n,2}^{\prime}&=1561176+35176776 n+356105548 n^{2}+2137950448 n^{3}+\\ &\quad+8458603286 n^{4}+23158717414 n^{5}+44778314889 n^{6}+61151030584 n^{7}+\\ &\quad+57807289939 n^{8}+36026947376 n^{9}+13321631568 n^{10}+2213683584 n^{11}. \end{align*} $$
$$ \begin{align*} A_{n,2}^{\prime}&=1561176+35176776 n+356105548 n^{2}+2137950448 n^{3}+\\ &\quad+8458603286 n^{4}+23158717414 n^{5}+44778314889 n^{6}+61151030584 n^{7}+\\ &\quad+57807289939 n^{8}+36026947376 n^{9}+13321631568 n^{10}+2213683584 n^{11}. \end{align*} $$
Similarly, we have
 $$ \begin{align*}M_{n,3}^{\prime}=\frac{(11+7n)A_{n,3}^{\prime}}{224(1+n)^{3}(3+7 n)^{4}(13+14 n)^{4} (6+14 n+7 n^{2})}, \end{align*} $$
$$ \begin{align*}M_{n,3}^{\prime}=\frac{(11+7n)A_{n,3}^{\prime}}{224(1+n)^{3}(3+7 n)^{4}(13+14 n)^{4} (6+14 n+7 n^{2})}, \end{align*} $$
where
 $$ \begin{align*} A_{n,3}^{\prime}&=13726028+164541190 n+859036123 n^{2}+2564002455 n^{3}+4823323519 n^{4}+\\&\quad +5933644367 n^{5}+4776917782 n^{6}+2428774768 n^{7}+708314208 n^{8}+90354432 n^{9}. \end{align*} $$
$$ \begin{align*} A_{n,3}^{\prime}&=13726028+164541190 n+859036123 n^{2}+2564002455 n^{3}+4823323519 n^{4}+\\&\quad +5933644367 n^{5}+4776917782 n^{6}+2428774768 n^{7}+708314208 n^{8}+90354432 n^{9}. \end{align*} $$
Likewise, we have
![]() $M_{n,3}^{\prime \prime }=\frac {(6+14 n+7 n^{2})A_{n,3}^{\prime \prime }}{224(1+n)^{3}(6+7 n)^{4}(8+7 n)^{4}(11+7 n)(13+14n)^{4}}$
, where
$M_{n,3}^{\prime \prime }=\frac {(6+14 n+7 n^{2})A_{n,3}^{\prime \prime }}{224(1+n)^{3}(6+7 n)^{4}(8+7 n)^{4}(11+7 n)(13+14n)^{4}}$
, where
 $$ \begin{align*} A_{n,3}^{\prime\prime}&=67760261208+703706084640 n+3313300067388 n^{2}+9335574166156 n^{3}+\\ &\quad+17489294547578 n^{4}+22873117200584 n^{5}+21308562209725 n^{6}+14139587568253 n^{7}+\\ &\quad+6548997703738 n^{8}+2016283621072 n^{9}+371345421216 n^{10}+30991570176 n^{11}. \end{align*} $$
$$ \begin{align*} A_{n,3}^{\prime\prime}&=67760261208+703706084640 n+3313300067388 n^{2}+9335574166156 n^{3}+\\ &\quad+17489294547578 n^{4}+22873117200584 n^{5}+21308562209725 n^{6}+14139587568253 n^{7}+\\ &\quad+6548997703738 n^{8}+2016283621072 n^{9}+371345421216 n^{10}+30991570176 n^{11}. \end{align*} $$
Similarly, we see that
 $$ \begin{align*}M_{n,4}^{\prime}=\frac{(15+21n+7n^{2})A_{n,4}^{\prime}}{28(1+n)^{4}(6+7 n)^{4}(8+7 n)^{4}(11+7 n)(23+21 n)^{4}}, \end{align*} $$
$$ \begin{align*}M_{n,4}^{\prime}=\frac{(15+21n+7n^{2})A_{n,4}^{\prime}}{28(1+n)^{4}(6+7 n)^{4}(8+7 n)^{4}(11+7 n)(23+21 n)^{4}}, \end{align*} $$
where
 $$ \begin{align*} A_{n,4}^{\prime}&=88135013250+967134809574 n+4853884596732 n^{2}+\\ &\quad+14732868828434 n^{3}+30120687035243 n^{4}+43697011451345 n^{5}+46124583653603 n^{6}+\\ &\quad+35692827118809 n^{7}+20096052100397 n^{8}+8028312817917 n^{9}+\\ &\quad+2160120347280 n^{10}+351456857766 n^{11}+26149137336 n^{12}. \end{align*} $$
$$ \begin{align*} A_{n,4}^{\prime}&=88135013250+967134809574 n+4853884596732 n^{2}+\\ &\quad+14732868828434 n^{3}+30120687035243 n^{4}+43697011451345 n^{5}+46124583653603 n^{6}+\\ &\quad+35692827118809 n^{7}+20096052100397 n^{8}+8028312817917 n^{9}+\\ &\quad+2160120347280 n^{10}+351456857766 n^{11}+26149137336 n^{12}. \end{align*} $$
Finally, we have
 $$ \begin{align*}M_{n,4}^{\prime\prime}=\frac{(11+7n)A_{n,4}^{\prime\prime}}{448(1+n)^{4}(10+7 n)^{4}(23+21 n)^{4} (15+21 n+7 n^{2})}, \end{align*} $$
$$ \begin{align*}M_{n,4}^{\prime\prime}=\frac{(11+7n)A_{n,4}^{\prime\prime}}{448(1+n)^{4}(10+7 n)^{4}(23+21 n)^{4} (15+21 n+7 n^{2})}, \end{align*} $$
where
 $$ \begin{align*} A_{n,4}^{\prime\prime}&=7582266167+59702225967 n+210973884925 n^{2}+440580768679 n^{3}+\\ &\quad+602090743422 n^{4}+562572998512 n^{5}+363945674554 n^{6}+160955181870 n^{7}+\\ &\quad+46566357768 n^{8}+7957643904 n^{9}+609892416 n^{10}. \end{align*} $$
$$ \begin{align*} A_{n,4}^{\prime\prime}&=7582266167+59702225967 n+210973884925 n^{2}+440580768679 n^{3}+\\ &\quad+602090743422 n^{4}+562572998512 n^{5}+363945674554 n^{6}+160955181870 n^{7}+\\ &\quad+46566357768 n^{8}+7957643904 n^{9}+609892416 n^{10}. \end{align*} $$
Now, adding terms together, we see that
 $$ \begin{align} S\big(W_{\bullet, \bullet,\bullet}^{T,\mathbf{e}_1};P\big)\leqslant 0.974+\frac{3}{7}\int_{0}^1\int_0^{t(u)}\big(P(u,v)\cdot \mathbf{e}_1\big)\mathrm{ord}_P\Big(N(u,v)\big|_{\mathbf{e}_1}\Big)dvdu. \end{align} $$
$$ \begin{align} S\big(W_{\bullet, \bullet,\bullet}^{T,\mathbf{e}_1};P\big)\leqslant 0.974+\frac{3}{7}\int_{0}^1\int_0^{t(u)}\big(P(u,v)\cdot \mathbf{e}_1\big)\mathrm{ord}_P\Big(N(u,v)\big|_{\mathbf{e}_1}\Big)dvdu. \end{align} $$
Now, for every
![]() $i\in \{1,2,3,4\}$
and any irreducible component
$i\in \{1,2,3,4\}$
and any irreducible component
![]() $\ell $
of the curve
$\ell $
of the curve
![]() $B_{n,i}$
, we let
$B_{n,i}$
, we let
 $$ \begin{align*} F_{n,i}&=\frac{3}{7}\int_{0}^1\int_0^{t(u)}\big(P(u,v)\cdot \mathbf{e}_1\big)\mathrm{ord}_\ell\big(N(u,v)\big)\big(\ell\cdot\mathbf{e}_1\big)dvdu=\\ &=\frac{3}{7}\int_{I_{n,i-1}}\int_0^{t(u)}\big(P(u,v)\cdot \mathbf{e}_1\big)\mathrm{ord}_\ell\big(N(u,v)\big)\big(\ell\cdot\mathbf{e}_1\big)dvdu+\\ &\quad+\frac{3}{7}\int_{I_{n,i}}\int_0^{t(u)}\big(P(u,v)\cdot \mathbf{e}_1\big)\mathrm{ord}_\ell\big(N(u,v)\big)\big(\ell\cdot\mathbf{e}_1\big)dvdu+\\ &\quad+\frac{3}{7}\int_{I_{n,i+1}}\int_0^{t(u)}\big(P(u,v)\cdot \mathbf{e}_1\big)\mathrm{ord}_\ell\big(N(u,v)\big)\big(\ell\cdot\mathbf{e}_1\big)dvdu, \end{align*} $$
$$ \begin{align*} F_{n,i}&=\frac{3}{7}\int_{0}^1\int_0^{t(u)}\big(P(u,v)\cdot \mathbf{e}_1\big)\mathrm{ord}_\ell\big(N(u,v)\big)\big(\ell\cdot\mathbf{e}_1\big)dvdu=\\ &=\frac{3}{7}\int_{I_{n,i-1}}\int_0^{t(u)}\big(P(u,v)\cdot \mathbf{e}_1\big)\mathrm{ord}_\ell\big(N(u,v)\big)\big(\ell\cdot\mathbf{e}_1\big)dvdu+\\ &\quad+\frac{3}{7}\int_{I_{n,i}}\int_0^{t(u)}\big(P(u,v)\cdot \mathbf{e}_1\big)\mathrm{ord}_\ell\big(N(u,v)\big)\big(\ell\cdot\mathbf{e}_1\big)dvdu+\\ &\quad+\frac{3}{7}\int_{I_{n,i+1}}\int_0^{t(u)}\big(P(u,v)\cdot \mathbf{e}_1\big)\mathrm{ord}_\ell\big(N(u,v)\big)\big(\ell\cdot\mathbf{e}_1\big)dvdu, \end{align*} $$
where we set
![]() $I_{0,0}=\varnothing $
,
$I_{0,0}=\varnothing $
,
![]() $I_{n,5}=I_{n+1,1}$
for
$I_{n,5}=I_{n+1,1}$
for
![]() $n\geqslant 0$
and
$n\geqslant 0$
and
![]() $I_{n,0}=I_{n-1,4}$
for
$I_{n,0}=I_{n-1,4}$
for
![]() $n\geqslant 1$
. Since irreducible components of the curve
$n\geqslant 1$
. Since irreducible components of the curve
![]() $B_{n,i}$
are disjoint, we get
$B_{n,i}$
are disjoint, we get
 $$ \begin{align*}\frac{3}{7}\int_{0}^1\int_0^{t(u)}\big(P(u,v)\cdot \mathbf{e}_1\big)\mathrm{ord}_P\Big(N(u,v)\big|_{\mathbf{e}_1}\Big)dvdu\leqslant \sum_{n=0}^{\infty}\sum_{i=1}^{4}F_{n,i}. \end{align*} $$
$$ \begin{align*}\frac{3}{7}\int_{0}^1\int_0^{t(u)}\big(P(u,v)\cdot \mathbf{e}_1\big)\mathrm{ord}_P\Big(N(u,v)\big|_{\mathbf{e}_1}\Big)dvdu\leqslant \sum_{n=0}^{\infty}\sum_{i=1}^{4}F_{n,i}. \end{align*} $$
On the other hand, each
![]() $F_{n,i}$
is not difficult to compute. For instance, we have
$F_{n,i}$
is not difficult to compute. For instance, we have
 $$ \begin{align*} F_{0,1}&=\frac{3}{7}\int_{0}^{\frac{1}{3}}\int_{2-u}^{\frac{7-6u}{3}}(v+u-2)(5-2u-v)dvdu+\\ &\quad+\frac{3}{7}\int_{0}^{\frac{1}{3}}\int_{\frac{7-6 u}{3}}^{\frac{19-16u}{8}}8(u+v-2)(19-16u-8v)dvdu+\\ &\quad+\frac{3}{7}\int_{\frac{1}{3}}^{\frac{3}{8}}\int_{2-u}^{\frac{19-16 u}{8}}8(u+v-2)(19-16u-8v)dvdu=\frac{281}{32256}. \end{align*} $$
$$ \begin{align*} F_{0,1}&=\frac{3}{7}\int_{0}^{\frac{1}{3}}\int_{2-u}^{\frac{7-6u}{3}}(v+u-2)(5-2u-v)dvdu+\\ &\quad+\frac{3}{7}\int_{0}^{\frac{1}{3}}\int_{\frac{7-6 u}{3}}^{\frac{19-16u}{8}}8(u+v-2)(19-16u-8v)dvdu+\\ &\quad+\frac{3}{7}\int_{\frac{1}{3}}^{\frac{3}{8}}\int_{2-u}^{\frac{19-16 u}{8}}8(u+v-2)(19-16u-8v)dvdu=\frac{281}{32256}. \end{align*} $$
Similarly, we see that
 $$ \begin{align*}F_{n,1}=\frac{3(1+7 n+7 n^{2} )^{2}}{2 n^{2}(1+3 n)(-1+7 n)(1+7 n)(2+7 n)(3+7 n)^{2}(4+7 n)(2+21 n)} \end{align*} $$
$$ \begin{align*}F_{n,1}=\frac{3(1+7 n+7 n^{2} )^{2}}{2 n^{2}(1+3 n)(-1+7 n)(1+7 n)(2+7 n)(3+7 n)^{2}(4+7 n)(2+21 n)} \end{align*} $$
for
![]() $n\geqslant 1$
. Likewise, we get
$n\geqslant 1$
. Likewise, we get
 $$ \begin{align*}F_{n,2}= \left\{\begin{aligned} &\frac{5}{3584}\ \text{if }n=0, \\ &\frac{1+n}{112 n(1+2 n)(1+3 n)(2+7 n)(3+7 n)^{2}(4+7 n)}\ \text{if }n\geqslant 1. \\ \end{aligned} \right. \end{align*} $$
$$ \begin{align*}F_{n,2}= \left\{\begin{aligned} &\frac{5}{3584}\ \text{if }n=0, \\ &\frac{1+n}{112 n(1+2 n)(1+3 n)(2+7 n)(3+7 n)^{2}(4+7 n)}\ \text{if }n\geqslant 1. \\ \end{aligned} \right. \end{align*} $$
Likewise, for every
![]() $n\geqslant 0$
, we have
$n\geqslant 0$
, we have
 $$ \begin{align*}F_{n,3}=\frac{15 (6+14n+7n^{2})^{2}}{4(1+n)^{2}(1+2 n)(2+7 n)(3+7 n)^{2}(4+7 n)(6+7 n)(8+7 n)(13+14 n)} \end{align*} $$
$$ \begin{align*}F_{n,3}=\frac{15 (6+14n+7n^{2})^{2}}{4(1+n)^{2}(1+2 n)(2+7 n)(3+7 n)^{2}(4+7 n)(6+7 n)(8+7 n)(13+14 n)} \end{align*} $$
and
 $$ \begin{align*}F_{n,4}=\frac{(11+7 n)^{2}}{112(1+n)^{2}(3+7 n)(6+7 n)(8+7 n)(10+7 n)(13+14 n)(23+21 n)}. \end{align*} $$
$$ \begin{align*}F_{n,4}=\frac{(11+7 n)^{2}}{112(1+n)^{2}(3+7 n)(6+7 n)(8+7 n)(10+7 n)(13+14 n)(23+21 n)}. \end{align*} $$
Now, one can easily check that the total sum of all
![]() $F_{n,1}$
,
$F_{n,1}$
,
![]() $F_{n,2}$
,
$F_{n,2}$
,
![]() $F_{n,3}$
,
$F_{n,3}$
,
![]() $F_{n,4}$
is at most
$F_{n,4}$
is at most
![]() $0.014$
. This and Equation (6.8) give
$0.014$
. This and Equation (6.8) give
![]() $S(W_{\bullet , \bullet ,\bullet }^{T,\mathbf {e}_1};P)\leqslant 0.974+0.014=0.988$
. Using Equation (6.7), we get
$S(W_{\bullet , \bullet ,\bullet }^{T,\mathbf {e}_1};P)\leqslant 0.974+0.014=0.988$
. Using Equation (6.7), we get
![]() $\delta _P(X)>1$
.
$\delta _P(X)>1$
.
Corollary 6.11. All smooth Fano threefolds in the family ![]() are K-stable.
are K-stable.
Competing interests
The authors have no competing interest to declare.
Financial support
Cheltsov has been supported by EPSRC grant ![]() . Fujita has been supported by JSPS KAKENHI Grant
. Fujita has been supported by JSPS KAKENHI Grant ![]() .
.
This paper has been written during Cheltsov’s stay at IHES (Bures-sur-Yvette, France). He thanks the institute for the hospitality and excellent working conditions.

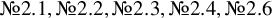 and
and 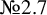 are K-stable, and we also prove that smooth Fano threefolds in the family
are K-stable, and we also prove that smooth Fano threefolds in the family 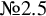 that satisfy one very explicit generality condition are K-stable.
that satisfy one very explicit generality condition are K-stable.





