Published online by Cambridge University Press: 30 October 2015
We investigate the interplay between the local and asymptotic geometry of a set 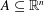 $A\subseteq \mathbb{R}^{n}$ and the geometry of model sets
$A\subseteq \mathbb{R}^{n}$ and the geometry of model sets 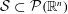 ${\mathcal{S}}\subset {\mathcal{P}}(\mathbb{R}^{n})$, which approximate
${\mathcal{S}}\subset {\mathcal{P}}(\mathbb{R}^{n})$, which approximate 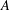 $A$ locally uniformly on small scales. The framework for local set approximation developed in this paper unifies and extends ideas of Jones, Mattila and Vuorinen, Reifenberg, and Preiss. We indicate several applications of this framework to variational problems that arise in geometric measure theory and partial differential equations. For instance, we show that the singular part of the support of an
$A$ locally uniformly on small scales. The framework for local set approximation developed in this paper unifies and extends ideas of Jones, Mattila and Vuorinen, Reifenberg, and Preiss. We indicate several applications of this framework to variational problems that arise in geometric measure theory and partial differential equations. For instance, we show that the singular part of the support of an 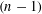 $(n-1)$-dimensional asymptotically optimally doubling measure in
$(n-1)$-dimensional asymptotically optimally doubling measure in 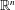 $\mathbb{R}^{n}$ (
$\mathbb{R}^{n}$ (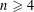 $n\geqslant 4$) has upper Minkowski dimension at most
$n\geqslant 4$) has upper Minkowski dimension at most 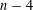 $n-4$.
$n-4$.