Article contents
LOCALLY NORMAL SUBGROUPS OF TOTALLY DISCONNECTED GROUPS. PART II: COMPACTLY GENERATED SIMPLE GROUPS
Published online by Cambridge University Press: 22 May 2017
Abstract
We use the structure lattice, introduced in Part I, to undertake a systematic study of the class 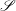 $\mathscr{S}$ consisting of compactly generated, topologically simple, totally disconnected locally compact groups that are nondiscrete. Given
$\mathscr{S}$ consisting of compactly generated, topologically simple, totally disconnected locally compact groups that are nondiscrete. Given 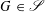 $G\in \mathscr{S}$ , we show that compact open subgroups of
$G\in \mathscr{S}$ , we show that compact open subgroups of 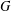 $G$ involve finitely many isomorphism types of composition factors, and do not have any soluble normal subgroup other than the trivial one. By results of Part I, this implies that the centralizer lattice and local decomposition lattice of
$G$ involve finitely many isomorphism types of composition factors, and do not have any soluble normal subgroup other than the trivial one. By results of Part I, this implies that the centralizer lattice and local decomposition lattice of 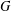 $G$ are Boolean algebras. We show that the
$G$ are Boolean algebras. We show that the 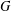 $G$ -action on the Stone space of those Boolean algebras is minimal, strongly proximal, and microsupported. Building upon those results, we obtain partial answers to the following key problems: Are all groups in
$G$ -action on the Stone space of those Boolean algebras is minimal, strongly proximal, and microsupported. Building upon those results, we obtain partial answers to the following key problems: Are all groups in  $\mathscr{S}$ abstractly simple? Can a group in
$\mathscr{S}$ abstractly simple? Can a group in 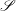 $\mathscr{S}$ be amenable? Can a group in
$\mathscr{S}$ be amenable? Can a group in 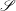 $\mathscr{S}$ be such that the contraction groups of all of its elements are trivial?
$\mathscr{S}$ be such that the contraction groups of all of its elements are trivial?
MSC classification
Information
- Type
- Research Article
- Information
- Creative Commons
- This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
- Copyright
- © The Author(s) 2017
References
- 13
- Cited by


