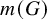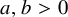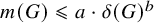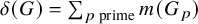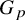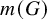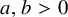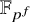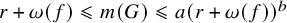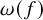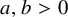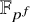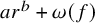1 Introduction
Since a generating set for a group remains a generating set if additional elements are added, it is natural to focus on generating sets for which no proper subset is a generating set; we call these minimal generating sets (they are also known as independent generating sets). A minimal generating set need not have minimum possible size. For instance, if
![]() $n \geqslant 4$
, then
$n \geqslant 4$
, then
![]() $\{ (1 \ 2), (2 \ 3), \dots , (n-1 \ n) \}$
is a minimal generating set for
$\{ (1 \ 2), (2 \ 3), \dots , (n-1 \ n) \}$
is a minimal generating set for
![]() $S_n$
, but it has size
$S_n$
, but it has size
![]() $n-1$
, which exceeds the minimum size possible size of
$n-1$
, which exceeds the minimum size possible size of
![]() $2$
. How large can a minimal generating set be?
$2$
. How large can a minimal generating set be?
Let G be a finite group. We begin by comparing what is known about the minimum size
![]() $d(G)$
and maximum size
$d(G)$
and maximum size
![]() $m(G)$
of a minimal generating set for G. If G is a p-group, then
$m(G)$
of a minimal generating set for G. If G is a p-group, then
![]() $d(G) = m(G)$
(this follows from Burnside’s basis theorem), so if G is nilpotent, then
$d(G) = m(G)$
(this follows from Burnside’s basis theorem), so if G is nilpotent, then
![]() $d(G) = \max _{p \text { prime}} d(G_p)$
and
$d(G) = \max _{p \text { prime}} d(G_p)$
and
![]() $m(G) = \sum _{p \text { prime}} d(G_p)$
, where
$m(G) = \sum _{p \text { prime}} d(G_p)$
, where
![]() $G_p$
is a Sylow p-subgroup of G. In 1989, Guralnick [Reference Guralnick14] and Lucchini [Reference Lucchini23] independently proved that all finite groups G satisfy
$G_p$
is a Sylow p-subgroup of G. In 1989, Guralnick [Reference Guralnick14] and Lucchini [Reference Lucchini23] independently proved that all finite groups G satisfy
![]() $d(G) \leqslant \max _{p \text { prime}} d(G_p) + 1$
. Do all finite groups satisfy
$d(G) \leqslant \max _{p \text { prime}} d(G_p) + 1$
. Do all finite groups satisfy
![]() $m(G) \leqslant \sum _{p \text { prime}} d(G_p)+ 1$
? Writing
$m(G) \leqslant \sum _{p \text { prime}} d(G_p)+ 1$
? Writing
![]() $\delta (G) = \sum _{p \text { prime}} d(G_p)$
, Lucchini, Moscatiello and Spiga [Reference Lucchini, Moscatiello and Spiga24] showed that
$\delta (G) = \sum _{p \text { prime}} d(G_p)$
, Lucchini, Moscatiello and Spiga [Reference Lucchini, Moscatiello and Spiga24] showed that
![]() $m(G) \leqslant \delta (G)+1$
is false in general, but they conjectured that there exist
$m(G) \leqslant \delta (G)+1$
is false in general, but they conjectured that there exist
![]() $a,b> 0$
such that every finite group G satisfies
$a,b> 0$
such that every finite group G satisfies
![]() $m(G) \leqslant a \cdot \delta (G)^b$
. Our first theorem confirms this local-to-global conjecture.
$m(G) \leqslant a \cdot \delta (G)^b$
. Our first theorem confirms this local-to-global conjecture.
Theorem 1. There exist
![]() $a,b> 0$
such that if G is any finite group, then
$a,b> 0$
such that if G is any finite group, then
![]() $m(G) \leqslant a \cdot \delta (G)^b$
. Moreover, this is true for
$m(G) \leqslant a \cdot \delta (G)^b$
. Moreover, this is true for
![]() $a = 10^{10}$
and
$a = 10^{10}$
and
![]() $b=10$
.
$b=10$
.
In [Reference Lucchini, Moscatiello and Spiga24], Theorem 1 is reduced to a statement about almost simple groups. (A group G is almost simple if
![]() $G_0 \leqslant G \leqslant \mathrm {Aut}(G_0)$
for a nonabelian simple group
$G_0 \leqslant G \leqslant \mathrm {Aut}(G_0)$
for a nonabelian simple group
![]() $G_0$
.) Even for finite simple groups G, while it has long been known that
$G_0$
.) Even for finite simple groups G, while it has long been known that
![]() $d(G) \leqslant 2$
(see [Reference Aschbacher and Guralnick2]), little is known about
$d(G) \leqslant 2$
(see [Reference Aschbacher and Guralnick2]), little is known about
![]() $m(G)$
. In 2000, Whiston [Reference Whiston29] (using the Classification of Finite Simple Groups) proved
$m(G)$
. In 2000, Whiston [Reference Whiston29] (using the Classification of Finite Simple Groups) proved
![]() $m(A_n) = n-2$
. Later, in 2002, Whiston and Saxl [Reference Whiston and Saxl30] proved that
$m(A_n) = n-2$
. Later, in 2002, Whiston and Saxl [Reference Whiston and Saxl30] proved that
![]() $m(\mathrm {PSL}_2(p^f)) \leqslant \max \{ 6, \omega (f) + 2 \}$
with equality if
$m(\mathrm {PSL}_2(p^f)) \leqslant \max \{ 6, \omega (f) + 2 \}$
with equality if
![]() $\omega (f) \geqslant 4$
, and the exact value of
$\omega (f) \geqslant 4$
, and the exact value of
![]() $m(\mathrm {PSL}_2(p))$
is given in [Reference Jambor16]. (Throughout,
$m(\mathrm {PSL}_2(p))$
is given in [Reference Jambor16]. (Throughout,
![]() $\omega (n)$
is the number of distinct prime divisors of n, and
$\omega (n)$
is the number of distinct prime divisors of n, and
![]() $\Omega (n)$
is the number of prime divisors of n counted with multiplicity.) Except for the three-dimensional classical groups studied in [Reference Keen17], no nontrivial bounds exist for any other finite simple group. This motivates our second theorem, which we will use to prove Theorem 1.
$\Omega (n)$
is the number of prime divisors of n counted with multiplicity.) Except for the three-dimensional classical groups studied in [Reference Keen17], no nontrivial bounds exist for any other finite simple group. This motivates our second theorem, which we will use to prove Theorem 1.
Theorem 2. There exist
![]() $\alpha ,\beta> 0$
such that if G is an almost simple group of Lie type of rank r over
$\alpha ,\beta> 0$
such that if G is an almost simple group of Lie type of rank r over
![]() $\mathbb {F}_{p^f}$
(where p is prime), then
$\mathbb {F}_{p^f}$
(where p is prime), then
![]() $m(G) \leqslant \alpha (r+\omega (f))^\beta $
. Moreover, this is true for
$m(G) \leqslant \alpha (r+\omega (f))^\beta $
. Moreover, this is true for
![]() $\alpha =10^5$
and
$\alpha =10^5$
and
![]() $\beta =10$
.
$\beta =10$
.
Up to improving the values of
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
, Theorem 2 is best possible since if G is a finite simple group of Lie type of rank r over
$\beta $
, Theorem 2 is best possible since if G is a finite simple group of Lie type of rank r over
![]() $\mathbb {F}_{p^f}$
, then
$\mathbb {F}_{p^f}$
, then
![]() $m(G) \geqslant r+\omega (f)$
(see Proposition 3.2).
$m(G) \geqslant r+\omega (f)$
(see Proposition 3.2).
The invariant
![]() $m(G)$
also plays a role in the product replacement algorithm for producing random elements of G (see [Reference Celler, Leedham-Green, Murray, Niemeyer and O’Brien7]). This algorithm involves a random walk on the product replacement graph
$m(G)$
also plays a role in the product replacement algorithm for producing random elements of G (see [Reference Celler, Leedham-Green, Murray, Niemeyer and O’Brien7]). This algorithm involves a random walk on the product replacement graph
![]() $\Gamma _n(G)$
, and Diaconis and Saloff-Coste [Reference Diaconis and Saloff-Coste8] proved that for large enough n this random walk reaches the uniform distribution in time
$\Gamma _n(G)$
, and Diaconis and Saloff-Coste [Reference Diaconis and Saloff-Coste8] proved that for large enough n this random walk reaches the uniform distribution in time
![]() $|G|^{O(m(G))}n^2\log {n}$
.
$|G|^{O(m(G))}n^2\log {n}$
.
To prove Theorem 2, we relate
![]() $m(G)$
to some well-studied invariants in permutation group theory. Let G be a finite group acting faithfully on a set X. A sequence
$m(G)$
to some well-studied invariants in permutation group theory. Let G be a finite group acting faithfully on a set X. A sequence
![]() $(x_1,\dots ,x_k)$
of points in X is a base if the pointwise stabiliser
$(x_1,\dots ,x_k)$
of points in X is a base if the pointwise stabiliser
![]() $G_{(x_1, \dots , x_k)}$
is trivial. This subject has a long history, with many connections to abstract group theory, computational group theory and graph theory; see the survey [Reference Bailey and Cameron3]. A base
$G_{(x_1, \dots , x_k)}$
is trivial. This subject has a long history, with many connections to abstract group theory, computational group theory and graph theory; see the survey [Reference Bailey and Cameron3]. A base
![]() $(x_1, \dots , x_k)$
is irredundant if we have a proper subgroup chain
$(x_1, \dots , x_k)$
is irredundant if we have a proper subgroup chain
![]() $G> G_{(x_1)} > G_{(x_1,x_2)} > \cdots > G_{(x_1,x_2,\dots ,x_k)} = 1$
, and it is minimal if no proper subsequence of
$G> G_{(x_1)} > G_{(x_1,x_2)} > \cdots > G_{(x_1,x_2,\dots ,x_k)} = 1$
, and it is minimal if no proper subsequence of
![]() $(x_1, \dots , x_k)$
is a base. A minimal base is irredundant, but the converse need not hold. Let
$(x_1, \dots , x_k)$
is a base. A minimal base is irredundant, but the converse need not hold. Let
![]() $I(G,X)$
and
$I(G,X)$
and
![]() $B(G,X)$
be the maximum size of an irredundant and minimal base, respectively.
$B(G,X)$
be the maximum size of an irredundant and minimal base, respectively.
Much is known about the minimum size of a base, for instance the resolutions of Pyber’s conjecture [Reference Duyan, Halasi and Maróti9] and Cameron’s conjecture [Reference Burness, Liebeck and Shalev5], but less is known about
![]() $I(G,X)$
and
$I(G,X)$
and
![]() $B(G,X)$
. However, Gill and Liebeck [Reference Gill and Liebeck10] recently proved that any almost simple group of Lie type of rank r over
$B(G,X)$
. However, Gill and Liebeck [Reference Gill and Liebeck10] recently proved that any almost simple group of Lie type of rank r over
![]() $\mathbb {F}_{p^f}$
(where p is prime) acting faithfully and primitively on X satisfies the bound
$\mathbb {F}_{p^f}$
(where p is prime) acting faithfully and primitively on X satisfies the bound
![]() $B(G,X) \leqslant I(G,X) \leqslant 177r^8 + \Omega (f)$
. As explained in [Reference Gill and Liebeck10, Example 5.1],
$B(G,X) \leqslant I(G,X) \leqslant 177r^8 + \Omega (f)$
. As explained in [Reference Gill and Liebeck10, Example 5.1],
![]() $I(G,X)$
must depend on
$I(G,X)$
must depend on
![]() $\Omega (f)$
, but Gill and Liebeck conjecture that
$\Omega (f)$
, but Gill and Liebeck conjecture that
![]() $B(G,X)$
should only depend on
$B(G,X)$
should only depend on
![]() $\omega (f)$
(see [Reference Gill and Liebeck10, Conjecture 5.2] for a precise statement). Our final theorem proves this conjecture.
$\omega (f)$
(see [Reference Gill and Liebeck10, Conjecture 5.2] for a precise statement). Our final theorem proves this conjecture.
We actually prove a stronger result (also conjectured in [Reference Gill and Liebeck10]) that is more convenient for proving Theorem 2. For a finite group G acting on X, a sequence S in X is independent if
![]() $G_{(S')}> G_{(S)}$
for proper all subsequences
$G_{(S')}> G_{(S)}$
for proper all subsequences
![]() $S'$
of S, and the height, denoted
$S'$
of S, and the height, denoted
![]() $H(G,X)$
, is the maximum size of an independent sequence. Note that
$H(G,X)$
, is the maximum size of an independent sequence. Note that
![]() $B(G,X) \leqslant H(G,X) \leqslant I(G,X)$
.
$B(G,X) \leqslant H(G,X) \leqslant I(G,X)$
.
Theorem 3. There exist
![]() $A,B> 0$
such that if G is an almost simple group of Lie type of rank r over
$A,B> 0$
such that if G is an almost simple group of Lie type of rank r over
![]() $\mathbb {F}_{p^f}$
(where p is prime) acting faithfully and primitively on a set X, then
$\mathbb {F}_{p^f}$
(where p is prime) acting faithfully and primitively on a set X, then
![]() $H(G,X) \leqslant Ar^B+\omega (f)$
. Moreover, this is true for
$H(G,X) \leqslant Ar^B+\omega (f)$
. Moreover, this is true for
![]() $A = 177$
and
$A = 177$
and
![]() $B=8$
.
$B=8$
.
For a finite group G acting on X, the height
![]() $H(G,X)$
is related to the relational complexity
$H(G,X)$
is related to the relational complexity
![]() $RC(G,X)$
via the inequality
$RC(G,X)$
via the inequality
![]() $RC(G,X) \leqslant H(G,X)+1$
. Relational complexity arose in model theory, and it has been the subject recent work, including Gill, Liebeck and Spiga’s recent proof [Reference Gill, Liebeck and Spiga11] of Cherlin’s conjecture that classifies the primitive actions satisfying
$RC(G,X) \leqslant H(G,X)+1$
. Relational complexity arose in model theory, and it has been the subject recent work, including Gill, Liebeck and Spiga’s recent proof [Reference Gill, Liebeck and Spiga11] of Cherlin’s conjecture that classifies the primitive actions satisfying
![]() $RC(G,X)=2$
.
$RC(G,X)=2$
.
Corollary 4. If G is an almost simple group of Lie type of rank r over
![]() $\mathbb {F}_{p^f}$
(where p is prime) acting faithfully and primitively on a set X, then the following hold:
$\mathbb {F}_{p^f}$
(where p is prime) acting faithfully and primitively on a set X, then the following hold:
-
(i)
 $B(G,X) \leqslant 177r^8 + \omega (f)$
$B(G,X) \leqslant 177r^8 + \omega (f)$
-
(ii)
 $RC(G,X) \leqslant 177r^8 + \omega (f) + 1$
.
$RC(G,X) \leqslant 177r^8 + \omega (f) + 1$
.
2 Preliminaries
2.1 Maximal subgroups of almost simple groups
The maximal subgroups of almost simple groups of Lie type are described by Theorem 2.1, which combines two theorems of Liebeck and Seitz [Reference Liebeck and Seitz19, Theorem 2] and [Reference Liebeck and Seitz20, Theorem 2].
Let p be prime, and let X be a linear algebraic group over
![]() $\overline {\mathbb {F}}_p$
, which from now on we call an algebraic group. For a Steinberg endomorphism
$\overline {\mathbb {F}}_p$
, which from now on we call an algebraic group. For a Steinberg endomorphism
![]() $\sigma $
of X, write
$\sigma $
of X, write
![]() $X_\sigma = \{ x \in X \mid x^\sigma = x \}$
. A finite group
$X_\sigma = \{ x \in X \mid x^\sigma = x \}$
. A finite group
![]() $O^{p'}(X_\sigma )$
for a simple algebraic group X of adjoint type and a Steinberg endomorphism
$O^{p'}(X_\sigma )$
for a simple algebraic group X of adjoint type and a Steinberg endomorphism
![]() $\sigma $
is usually simple, and in this case we call it a finite simple group of Lie type. (Here,
$\sigma $
is usually simple, and in this case we call it a finite simple group of Lie type. (Here,
![]() $O^{p'}(G)$
is the subgroup generated by the p-elements of G.) In particular, for us, the Tits group
$O^{p'}(G)$
is the subgroup generated by the p-elements of G.) In particular, for us, the Tits group
![]() ${}^2F_4(2)'$
is not a finite simple group of Lie type. Throughout, by rank we mean untwisted rank.
${}^2F_4(2)'$
is not a finite simple group of Lie type. Throughout, by rank we mean untwisted rank.
Theorem 2.1. Let G be an almost simple group of Lie type. Write
![]() $\mathrm {soc}(G) = O^{p'}(X_\sigma )$
for a simple algebraic group X of adjoint type and a Steinberg endomorphism
$\mathrm {soc}(G) = O^{p'}(X_\sigma )$
for a simple algebraic group X of adjoint type and a Steinberg endomorphism
![]() $\sigma $
of X. Let M be a maximal subgroup of G not containing
$\sigma $
of X. Let M be a maximal subgroup of G not containing
![]() $\mathrm {soc}(G)$
. Then M is one of the following:
$\mathrm {soc}(G)$
. Then M is one of the following:
-
(I)
 $N_G(Y_\sigma \cap \mathrm {soc}(G))$
for a maximal closed
$N_G(Y_\sigma \cap \mathrm {soc}(G))$
for a maximal closed
 $\sigma $
-stable positive-dimensional subgroup Y of X
$\sigma $
-stable positive-dimensional subgroup Y of X -
(II)
 $N_G(X_\alpha \cap \mathrm {soc}(G))$
for a Steinberg endomorphism
$N_G(X_\alpha \cap \mathrm {soc}(G))$
for a Steinberg endomorphism
 $\alpha $
of X such that
$\alpha $
of X such that
 $\alpha ^k=\sigma $
for a prime k
$\alpha ^k=\sigma $
for a prime k -
(III) a local subgroup not in (I)
-
(IV) an almost simple group not in (I) or (II)
-
(V) the Borovik subgroup:
 $M \cap \mathrm {soc}(G) = (A_5 \times A_6).2^2$
with
$M \cap \mathrm {soc}(G) = (A_5 \times A_6).2^2$
with
 $\mathrm {soc}(G) = E_8(q)$
and
$\mathrm {soc}(G) = E_8(q)$
and
 $p \geqslant 7$
.
$p \geqslant 7$
.
We say that a core-free maximal subgroup of an almost simple group of Lie type has type (I), (II), (III), (IV) or (V) if it arises in case (I), (II), (III), (IV) or (V) of Theorem 2.1, respectively.
In the remainder of this section, we collect together information about the subgroups appearing in cases (I)–(V) that we will use in the proof of Theorem 2.
2.2 Aschbacher’s theorem and type (I*) subgroups
One usually categorises the maximal subgroups of an almost simple classical group G via Aschbacher’s subgroup structure theorem [Reference Aschbacher1]. Following the notation of Kleidman and Liebeck in [Reference Kleidman and Liebeck18], one can define a geometric class of subgroups
![]() $\mathcal {C} = \mathcal {C}_1 \cup \dots \cup \mathcal {C}_8$
(see [Reference Kleidman and Liebeck18, Chapter 3]) and a class
$\mathcal {C} = \mathcal {C}_1 \cup \dots \cup \mathcal {C}_8$
(see [Reference Kleidman and Liebeck18, Chapter 3]) and a class
![]() $\mathcal {S}$
of almost simple groups (see [Reference Kleidman and Liebeck18, Section 1.2]) such that for every subgroup H of G not containing
$\mathcal {S}$
of almost simple groups (see [Reference Kleidman and Liebeck18, Section 1.2]) such that for every subgroup H of G not containing
![]() $\mathrm {soc}(G)$
either
$\mathrm {soc}(G)$
either
![]() $H \leqslant M$
for a maximal subgroup
$H \leqslant M$
for a maximal subgroup
![]() $M \in \mathcal {C}$
or else
$M \in \mathcal {C}$
or else
![]() $H \in \mathcal {S}$
. The subgroups in
$H \in \mathcal {S}$
. The subgroups in
![]() $\mathcal {C}$
are all of type (I), (II) or (III) (with (II) and (III) broadly overlapping with
$\mathcal {C}$
are all of type (I), (II) or (III) (with (II) and (III) broadly overlapping with
![]() $\mathcal {C}_5$
and
$\mathcal {C}_5$
and
![]() $\mathcal {C}_6$
subgroups, respectively). However, Case (I) also includes almost simple groups in
$\mathcal {C}_6$
subgroups, respectively). However, Case (I) also includes almost simple groups in
![]() $\mathcal {S}$
whose socle is a group of Lie type in defining characteristic. Therefore, it is convenient to make the following definitions.
$\mathcal {S}$
whose socle is a group of Lie type in defining characteristic. Therefore, it is convenient to make the following definitions.
Let G be an almost simple group of Lie type. If G is classical, then let (I*) be the set of all maximal subgroups M of G that are in (I) and are in the geometric class
![]() $\mathcal {C}$
or are twisted tensor product subgroups (see [Reference Schaffer27]), and define (IV*) as (IV) without the groups of Lie type in defining characteristic. (It is natural to include the twisted tensor product subgroups in (I*) as they arise as geometric subgroups of the ambient algebraic group, see [Reference Liebeck and Seitz20, Theorem 2] and the remark that follows it.) If G is exceptional, then let (I*) be (I) and (IV*) be (IV).
$\mathcal {C}$
or are twisted tensor product subgroups (see [Reference Schaffer27]), and define (IV*) as (IV) without the groups of Lie type in defining characteristic. (It is natural to include the twisted tensor product subgroups in (I*) as they arise as geometric subgroups of the ambient algebraic group, see [Reference Liebeck and Seitz20, Theorem 2] and the remark that follows it.) If G is exceptional, then let (I*) be (I) and (IV*) be (IV).
Proposition 2.2. Let G be an almost simple classical group defined over
![]() $\mathbb {F}_q$
, and let
$\mathbb {F}_q$
, and let
![]() $H \leqslant G$
not contain
$H \leqslant G$
not contain
![]() $\mathrm {soc}(G)$
. Then either
$\mathrm {soc}(G)$
. Then either
![]() $H \leqslant M$
for a maximal subgroup M of G of type (I*), (II), (III) or (IV*), or H is an almost simple group of Lie type defined over a subfield of
$H \leqslant M$
for a maximal subgroup M of G of type (I*), (II), (III) or (IV*), or H is an almost simple group of Lie type defined over a subfield of
![]() $\mathbb {F}_q$
satisfying
$\mathbb {F}_q$
satisfying
![]() $\mathrm {rank}(H) < \mathrm {rank}(G)$
.
$\mathrm {rank}(H) < \mathrm {rank}(G)$
.
Proof. Assume that H does not lie in a maximal subgroup of type (I*), (II), (III) or (IV*). Let
![]() $q=p^f$
, where p is prime, and let
$q=p^f$
, where p is prime, and let
![]() $\mathbb {F}_q^n$
be the natural module for G. Since (I*), (II) and (III) cover the entire geometric class
$\mathbb {F}_q^n$
be the natural module for G. Since (I*), (II) and (III) cover the entire geometric class
![]() $\mathcal {C}$
of maximal subgroups of G, we know that H is not a subgroup of any maximal subgroup M contained in the geometric class
$\mathcal {C}$
of maximal subgroups of G, we know that H is not a subgroup of any maximal subgroup M contained in the geometric class
![]() $\mathcal {C}$
. Therefore, by the main theorem of [Reference Aschbacher1], we deduce that H is contained in
$\mathcal {C}$
. Therefore, by the main theorem of [Reference Aschbacher1], we deduce that H is contained in
![]() $\mathcal {S}$
. Since H is not in (IV*), H must be a group of Lie type defined over
$\mathcal {S}$
. Since H is not in (IV*), H must be a group of Lie type defined over
![]() $\mathbb {F}_{p^e}$
for some e. By [Reference Kleidman and Liebeck18, Proposition 5.4.6] (which is an application of Steinberg’s twisted tensor product theorem), f divides
$\mathbb {F}_{p^e}$
for some e. By [Reference Kleidman and Liebeck18, Proposition 5.4.6] (which is an application of Steinberg’s twisted tensor product theorem), f divides
![]() $de$
, for some
$de$
, for some
![]() $d \in \{1,2,3\}$
, and the embedding of H in G affords an irreducible
$d \in \{1,2,3\}$
, and the embedding of H in G affords an irreducible
![]() $\mathbb {F}_{p^e}H$
-module V of dimension
$\mathbb {F}_{p^e}H$
-module V of dimension
![]() $n^{f/de}$
. Since H is not contained in any maximal twisted tensor product subgroup, by [Reference Seitz28, Corollary 6], we must have
$n^{f/de}$
. Since H is not contained in any maximal twisted tensor product subgroup, by [Reference Seitz28, Corollary 6], we must have
![]() $f=de$
, so H is defined over
$f=de$
, so H is defined over
![]() $\mathbb {F}_{p^{f/d}}$
and
$\mathbb {F}_{p^{f/d}}$
and
![]() $\dim {V} = n$
.
$\dim {V} = n$
.
It remains to prove that
![]() $\mathrm {rank}(H) < \mathrm {rank}(G)$
. Referring to the bounds on the dimension of the minimal module in [Reference Kleidman and Liebeck18, Proposition 5.4.13], since H has an irreducible module of dimension n either
$\mathrm {rank}(H) < \mathrm {rank}(G)$
. Referring to the bounds on the dimension of the minimal module in [Reference Kleidman and Liebeck18, Proposition 5.4.13], since H has an irreducible module of dimension n either
![]() $\mathrm {rank}(H) < \mathrm {rank}(G)$
or
$\mathrm {rank}(H) < \mathrm {rank}(G)$
or
![]() $(H,V)$
is one of a small number of possibilities all of which arise in the geometric class
$(H,V)$
is one of a small number of possibilities all of which arise in the geometric class
![]() $\mathcal {C}$
or case (II). For instance, if
$\mathcal {C}$
or case (II). For instance, if
![]() $G = \mathrm {PSp}_n(q)$
with
$G = \mathrm {PSp}_n(q)$
with
![]() $n> 8$
, then n is strictly smaller than the dimension of the minimal module of any finite simple group of Lie type of
$n> 8$
, then n is strictly smaller than the dimension of the minimal module of any finite simple group of Lie type of
![]() $\mathrm {rank}(G) = n/2$
except
$\mathrm {rank}(G) = n/2$
except
![]() $\mathrm {PSL}^\pm _{n/2+1}(q)$
or
$\mathrm {PSL}^\pm _{n/2+1}(q)$
or
![]() $\mathrm {P}\Omega ^\pm _n(q)$
, and, by [Reference Kleidman and Liebeck18, Proposition 5.4.11], the former groups have no irreducible modules of dimension n and latter groups embed in G as
$\mathrm {P}\Omega ^\pm _n(q)$
, and, by [Reference Kleidman and Liebeck18, Proposition 5.4.11], the former groups have no irreducible modules of dimension n and latter groups embed in G as
![]() $\mathcal {C}_8$
subgroups if at all. However, H is not in
$\mathcal {C}_8$
subgroups if at all. However, H is not in
![]() $\mathcal {C}$
or (II), so
$\mathcal {C}$
or (II), so
![]() $\mathrm {rank}(H) < \mathrm {rank}(G)$
.
$\mathrm {rank}(H) < \mathrm {rank}(G)$
.
2.3 Length and type (IV*) subgroups
Let us introduce an invariant that we use throughout the paper. Let G be a finite group. A subgroup chain of G of length k is a sequence
![]() $G = G_0> G_1 > \dots > G_k = 1$
, and the length of G, written
$G = G_0> G_1 > \dots > G_k = 1$
, and the length of G, written
![]() $\ell (G)$
, is the maximal length of a subgroup chain of G. To see the significance for this paper, note that if
$\ell (G)$
, is the maximal length of a subgroup chain of G. To see the significance for this paper, note that if
![]() $X = \{ x_1, \dots , x_k \}$
is a minimal generating set for G, then
$X = \{ x_1, \dots , x_k \}$
is a minimal generating set for G, then
is a subgroup chain, so
![]() $m(G) \leqslant \ell (G)$
. There are many results on length, and we highlight one result that we will use later. Cameron, Solomon and Turull proved in [Reference Cameron, Solomon and Turull6, Theorem 1] that
$m(G) \leqslant \ell (G)$
. There are many results on length, and we highlight one result that we will use later. Cameron, Solomon and Turull proved in [Reference Cameron, Solomon and Turull6, Theorem 1] that
where
![]() $b_n$
is the number of ones in the base
$b_n$
is the number of ones in the base
![]() $2$
expansion of n.
$2$
expansion of n.
Proposition 2.3. There exists
![]() $C> 0$
such that if G is an almost simple group of Lie type of rank r and M is a type (IV*) maximal subgroup of G, then
$C> 0$
such that if G is an almost simple group of Lie type of rank r and M is a type (IV*) maximal subgroup of G, then
![]() $\ell (M) \leqslant C r$
. Moreover, this is true with
$\ell (M) \leqslant C r$
. Moreover, this is true with
![]() $C = 192$
.
$C = 192$
.
Proof. First, assume that
![]() $\mathrm {soc}(M)$
is sporadic. Then
$\mathrm {soc}(M)$
is sporadic. Then
![]() $\ell (\mathrm {soc}(M))$
is given in [Reference Cameron, Solomon and Turull6, Tables III & IV] (the ‘probable values’ have since been verified), whence we deduce that
$\ell (\mathrm {soc}(M))$
is given in [Reference Cameron, Solomon and Turull6, Tables III & IV] (the ‘probable values’ have since been verified), whence we deduce that
![]() $\ell (M) \leqslant 52$
.
$\ell (M) \leqslant 52$
.
Next, assume that
![]() $\mathrm {soc}(M) = A_d$
for some
$\mathrm {soc}(M) = A_d$
for some
![]() $d \geqslant 5$
. If G is exceptional, then
$d \geqslant 5$
. If G is exceptional, then
![]() $d \leqslant 18$
by [Reference Liebeck and Seitz22, Theorem 8], so
$d \leqslant 18$
by [Reference Liebeck and Seitz22, Theorem 8], so
![]() $\ell (M) \leqslant \ell (S_d) + 1 \leqslant 28$
by equation (2.1), and if G is classical in dimension n, then [Reference Kleidman and Liebeck18, Proposition 5.3.7] implies that
$\ell (M) \leqslant \ell (S_d) + 1 \leqslant 28$
by equation (2.1), and if G is classical in dimension n, then [Reference Kleidman and Liebeck18, Proposition 5.3.7] implies that
![]() $d \leqslant 2n-1$
, so
$d \leqslant 2n-1$
, so
![]() $\ell (M) \leqslant 3n-1 \leqslant 6r+2$
, again by equation (2.1).
$\ell (M) \leqslant 3n-1 \leqslant 6r+2$
, again by equation (2.1).
Finally, assume that
![]() $\mathrm {soc}(M)$
is a group of Lie type of rank
$\mathrm {soc}(M)$
is a group of Lie type of rank
![]() $r_0$
over
$r_0$
over
![]() $\mathbb {F}_{q_0}$
, where
$\mathbb {F}_{q_0}$
, where
![]() $q_0$
is a power of a prime
$q_0$
is a power of a prime
![]() $p_0$
. If G is classical in dimension n, then
$p_0$
. If G is classical in dimension n, then
![]() $p_0 \neq p$
and [Reference Kleidman and Liebeck18, Theorem 5.3.9] implies that
$p_0 \neq p$
and [Reference Kleidman and Liebeck18, Theorem 5.3.9] implies that
![]() $q_0^{r_0} \leqslant n^2$
, so using the facts that
$q_0^{r_0} \leqslant n^2$
, so using the facts that
![]() $|M| \leqslant q_0^{12r_0^2}$
and
$|M| \leqslant q_0^{12r_0^2}$
and
![]() $n \leqslant 4r$
, we have
$n \leqslant 4r$
, we have
If G is exceptional, then there are only finitely many possibilities for M. Consulting [Reference Liebeck and Seitz21, Tables 10.3 and 10.4] for the case
![]() $p_0 \neq p$
and [Reference Liebeck and Seitz22, Theorem 8] for the case
$p_0 \neq p$
and [Reference Liebeck and Seitz22, Theorem 8] for the case
![]() $p_0 = p$
, we see that in all cases
$p_0 = p$
, we see that in all cases
![]() $|M| < 2^{200}$
, so
$|M| < 2^{200}$
, so
![]() $\ell (M) \leqslant 200 \leqslant 100r$
.
$\ell (M) \leqslant 200 \leqslant 100r$
.
2.4 Enumerating maximal subgroups
In this section, we prove the following result, which gives a bound on the number of maximal subgroups of various types in almost simple groups of Lie type.
Proposition 2.4. Let G be an almost simple group of Lie type of rank r over
![]() $\mathbb {F}_{p^f}$
. Then there are
$\mathbb {F}_{p^f}$
. Then there are
-
(i) at most
 $2r+\omega (f)+10$
maximal subgroups of G that contain
$2r+\omega (f)+10$
maximal subgroups of G that contain
 $\mathrm {soc}(G)$
$\mathrm {soc}(G)$
-
(ii) at most
 $100r$
conjugacy classes of maximal subgroups of G that have type (I*), (III) or (V)
$100r$
conjugacy classes of maximal subgroups of G that have type (I*), (III) or (V) -
(iii) at most
 $(r+1)(\omega (f)+2)$
conjugacy classes of maximal subgroups of G that have type (II).
$(r+1)(\omega (f)+2)$
conjugacy classes of maximal subgroups of G that have type (II).
We establish some lemmas before proving Proposition 2.4.
Lemma 2.5. Let H be a subgroup of
![]() $S_4$
, and let n be a positive integer. Then
$S_4$
, and let n be a positive integer. Then
![]() $G = H \times C_n$
has at most
$G = H \times C_n$
has at most
![]() $9+\omega (n)$
maximal subgroups.
$9+\omega (n)$
maximal subgroups.
Proof. Write
![]() $\mathcal {M}(X)$
for the set of maximal subgroups of X and
$\mathcal {M}(X)$
for the set of maximal subgroups of X and
![]() $\mathrm {Hom}(X,Y)$
for the set of homomorphisms from X to Y. Goursat’s lemma (see [Reference Scott31, (4.3.1)], for example) implies that
$\mathrm {Hom}(X,Y)$
for the set of homomorphisms from X to Y. Goursat’s lemma (see [Reference Scott31, (4.3.1)], for example) implies that
 $$ \begin{align} |\mathcal{M}(G)| = |\mathcal{M}(H)|+|\mathcal{M}(C_n)|+\sum_{\text{prime } p \mid n}(|\mathrm{Hom}(H,C_p)|-1). \end{align} $$
$$ \begin{align} |\mathcal{M}(G)| = |\mathcal{M}(H)|+|\mathcal{M}(C_n)|+\sum_{\text{prime } p \mid n}(|\mathrm{Hom}(H,C_p)|-1). \end{align} $$
Note that
![]() $|\mathcal {M}(C_n)| = \omega (n)$
and
$|\mathcal {M}(C_n)| = \omega (n)$
and
![]() $|\mathrm {Hom}(H,C_p)|=1$
unless
$|\mathrm {Hom}(H,C_p)|=1$
unless
![]() $p \in \{2,3\}$
. It remains to check that
$p \in \{2,3\}$
. It remains to check that
![]() $|\mathcal {M}(H)|+|\mathrm {Hom}(H,C_2)|+|\mathrm {Hom}(H,C_3)| \leqslant 11$
, which is easy to do for each
$|\mathcal {M}(H)|+|\mathrm {Hom}(H,C_2)|+|\mathrm {Hom}(H,C_3)| \leqslant 11$
, which is easy to do for each
![]() $H \leqslant S_4$
.
$H \leqslant S_4$
.
Lemma 2.6. Let m and n be positive integers. Then
-
(i) any semidirect product
 $C_m{:}C_n$
has at most
$C_m{:}C_n$
has at most
 $m+\omega (n)$
maximal subgroups
$m+\omega (n)$
maximal subgroups -
(ii) any semidirect product
 $C_m{:}(C_n \times C_2)$
, where the generator of the
$C_m{:}(C_n \times C_2)$
, where the generator of the
 $C_2$
subgroup inverts every element of the
$C_2$
subgroup inverts every element of the
 $C_m$
subgroup, has at most
$C_m$
subgroup, has at most
 $2m+\omega (n)+2$
maximal subgroups.
$2m+\omega (n)+2$
maximal subgroups.
Proof. For part (i), write
![]() $G = \langle a, b \mid a^m, b^n, a^ba^{-k} \rangle $
and
$G = \langle a, b \mid a^m, b^n, a^ba^{-k} \rangle $
and
![]() $H = \langle b\rangle \cong C_n$
, and for part (ii) write
$H = \langle b\rangle \cong C_n$
, and for part (ii) write
![]() $G = \langle a, b,c \mid a^m, b^n, c^2, a^ba^{-k}, a^ca, [b,c] \rangle $
and
$G = \langle a, b,c \mid a^m, b^n, c^2, a^ba^{-k}, a^ca, [b,c] \rangle $
and
![]() $H = \langle b, c\rangle \cong C_n \times C_2$
(in both cases, we assume that
$H = \langle b, c\rangle \cong C_n \times C_2$
(in both cases, we assume that
![]() $\mathrm {gcd}(k,m)=1$
and
$\mathrm {gcd}(k,m)=1$
and
![]() $m \mid (k^n-1)$
).
$m \mid (k^n-1)$
).
Let M be a maximal subgroup of G, and write
![]() $A = M \cap \langle a\rangle $
. The possibilities for M correspond to the maximal subgroups of
$A = M \cap \langle a\rangle $
. The possibilities for M correspond to the maximal subgroups of
![]() $G/A$
. If
$G/A$
. If
![]() $A = \langle a\rangle $
, then
$A = \langle a\rangle $
, then
![]() $G/A = H$
, so applying equation (2.2) as in the proof of Lemma 2.5, we see that the number of possibilities for M is at
$G/A = H$
, so applying equation (2.2) as in the proof of Lemma 2.5, we see that the number of possibilities for M is at
![]() $\omega (n)$
and
$\omega (n)$
and
![]() $\omega (n)+2$
in cases (i) and (ii), respectively. Now, assume that
$\omega (n)+2$
in cases (i) and (ii), respectively. Now, assume that
![]() $A < \langle a\rangle $
. First, note that M projects into H, for otherwise
$A < \langle a\rangle $
. First, note that M projects into H, for otherwise
![]() $M < \langle a, M_0\rangle $
for a maximal subgroup
$M < \langle a, M_0\rangle $
for a maximal subgroup
![]() $M_0$
of H, contradicting the maximality of M. We next claim that
$M_0$
of H, contradicting the maximality of M. We next claim that
![]() $|\langle a\rangle :A|$
is prime. For a contradiction, suppose otherwise. Then
$|\langle a\rangle :A|$
is prime. For a contradiction, suppose otherwise. Then
![]() $A < \langle a^p\rangle $
for some prime divisor p of m. Now,
$A < \langle a^p\rangle $
for some prime divisor p of m. Now,
![]() $M < \langle M, a^p \rangle $
. If
$M < \langle M, a^p \rangle $
. If
![]() $\langle M, a^p \rangle = G$
, then
$\langle M, a^p \rangle = G$
, then
![]() $a \in \langle M, a^p\rangle = \langle a^p\rangle M$
which is impossible since
$a \in \langle M, a^p\rangle = \langle a^p\rangle M$
which is impossible since
![]() $M \cap \langle a \rangle = A \leqslant \langle a^p\rangle $
, so
$M \cap \langle a \rangle = A \leqslant \langle a^p\rangle $
, so
![]() $M < \langle M, a^p \rangle < G$
, which contradicts the maximality of M. Therefore,
$M < \langle M, a^p \rangle < G$
, which contradicts the maximality of M. Therefore,
![]() $|\langle a\rangle :A|$
is a prime divisor of m. To finish, we divide into the cases (i) and (ii).
$|\langle a\rangle :A|$
is a prime divisor of m. To finish, we divide into the cases (i) and (ii).
For (i), if
![]() $|\langle a\rangle :A| = p$
, then
$|\langle a\rangle :A| = p$
, then
![]() $M = \langle A, a^ib\rangle $
, where
$M = \langle A, a^ib\rangle $
, where
![]() $0 \leqslant i < p$
, so there are at most p possibilities for M. This means that if
$0 \leqslant i < p$
, so there are at most p possibilities for M. This means that if
![]() $m = p_1^{e_1} \dots p_k^{e_k}$
, where
$m = p_1^{e_1} \dots p_k^{e_k}$
, where
![]() $p_1, \dots , p_k$
are the distinct prime divisors of m, there are at most
$p_1, \dots , p_k$
are the distinct prime divisors of m, there are at most
![]() $p_1+\dots +p_k+\omega (n) \leqslant m+\omega (n)$
maximal subgroups of G.
$p_1+\dots +p_k+\omega (n) \leqslant m+\omega (n)$
maximal subgroups of G.
For (ii), if
![]() $|\langle a\rangle :A| = p$
, then
$|\langle a\rangle :A| = p$
, then
![]() $M = \langle A, a^ib, a^jc\rangle $
, where
$M = \langle A, a^ib, a^jc\rangle $
, where
![]() $0 \leqslant i,j < p$
. Now,
$0 \leqslant i,j < p$
. Now,
![]() $[a^ib,a^jc] \in \langle a\rangle \cap M = A$
, but
$[a^ib,a^jc] \in \langle a\rangle \cap M = A$
, but
![]() $[a^ib,a^jc] = a^{(1-k)j-2ik}$
, so
$[a^ib,a^jc] = a^{(1-k)j-2ik}$
, so
![]() $Aa^{2ik} = Aa^{(1-k)j}$
, and thus there are at most two choices for i for each choice of j. Since there are at most p choices for j, there are at most
$Aa^{2ik} = Aa^{(1-k)j}$
, and thus there are at most two choices for i for each choice of j. Since there are at most p choices for j, there are at most
![]() $2p$
choices for M. As in the previous case, if
$2p$
choices for M. As in the previous case, if
![]() $m = p_1^{e_1} \dots p_k^{e_k}$
, then there are at most
$m = p_1^{e_1} \dots p_k^{e_k}$
, then there are at most
![]() $2p_1+\dots +2p_k+\omega (n)+2 \leqslant 2m+\omega (n)+2$
maximal subgroups of G.
$2p_1+\dots +2p_k+\omega (n)+2 \leqslant 2m+\omega (n)+2$
maximal subgroups of G.
Lemma 2.7. Let G be an almost simple group with socle
![]() $\mathrm {PSL}^\varepsilon _n(q)$
. Then G has at most n conjugacy classes of maximal
$\mathrm {PSL}^\varepsilon _n(q)$
. Then G has at most n conjugacy classes of maximal
![]() $\mathcal {C}_7$
subgroups.
$\mathcal {C}_7$
subgroups.
Proof. Let t be the largest integer such that
![]() $n=s^t$
for some integer s. Then every maximal
$n=s^t$
for some integer s. Then every maximal
![]() $\mathcal {C}_7$
subgroup of G has type
$\mathcal {C}_7$
subgroup of G has type
![]() $\mathrm {GL}^\varepsilon _m(q) \wr S_k$
, where k divides t and
$\mathrm {GL}^\varepsilon _m(q) \wr S_k$
, where k divides t and
![]() $n=m^k$
and by [Reference Kleidman and Liebeck18, Tables 3.5.A and 3.5.B], there are at most
$n=m^k$
and by [Reference Kleidman and Liebeck18, Tables 3.5.A and 3.5.B], there are at most
![]() $n/m \ G$
-classes of subgroups of a given type. Therefore, the number of G-classes of
$n/m \ G$
-classes of subgroups of a given type. Therefore, the number of G-classes of
![]() $\mathcal {C}_7$
subgroups is at most
$\mathcal {C}_7$
subgroups is at most
![]() $\sum _{k \mid t} s^{t-t/k} \leqslant \sum _{i=0}^{t-1} s^i = (s^t-1)/(s-1) < s^t = n$
.
$\sum _{k \mid t} s^{t-t/k} \leqslant \sum _{i=0}^{t-1} s^i = (s^t-1)/(s-1) < s^t = n$
.
Proof of Proposition 2.4.
First, consider part (i). For now, assume that
![]() $\mathrm {soc}(G) \neq \mathrm {PSL}^\pm _n(q)$
. Then
$\mathrm {soc}(G) \neq \mathrm {PSL}^\pm _n(q)$
. Then
![]() $\mathrm {Out}(\mathrm {soc}(G)) = H \times C_{df}$
, where
$\mathrm {Out}(\mathrm {soc}(G)) = H \times C_{df}$
, where
![]() $H \leqslant S_4$
and
$H \leqslant S_4$
and
![]() $d \leqslant 3$
; see [Reference Burness, Guralnick and Harper4, Table 2] for exceptional groups and [Reference Harper15, Section 5.2] for classical groups. Therefore, Lemma 2.5 implies that
$d \leqslant 3$
; see [Reference Burness, Guralnick and Harper4, Table 2] for exceptional groups and [Reference Harper15, Section 5.2] for classical groups. Therefore, Lemma 2.5 implies that
![]() $\mathrm {Out}(\mathrm {soc}(G))$
has at most
$\mathrm {Out}(\mathrm {soc}(G))$
has at most
![]() $\omega (f)+10$
maximal subgroups. It remains to assume that
$\omega (f)+10$
maximal subgroups. It remains to assume that
![]() $\mathrm {soc}(G) = \mathrm {PSL}^\pm _n(q)$
. In this case, Lemma 2.6 implies that
$\mathrm {soc}(G) = \mathrm {PSL}^\pm _n(q)$
. In this case, Lemma 2.6 implies that
![]() $\mathrm {Out}(\mathrm {PSL}_n(q)) = C_{\mathrm {gcd}(q-1,n)}{:}(C_2 \times C_f)$
has at most
$\mathrm {Out}(\mathrm {PSL}_n(q)) = C_{\mathrm {gcd}(q-1,n)}{:}(C_2 \times C_f)$
has at most
![]() $2n+\omega (f)+2 = 2r+\omega (f)+4$
maximal subgroups and
$2n+\omega (f)+2 = 2r+\omega (f)+4$
maximal subgroups and
![]() $\mathrm {Out}(\mathrm {PSU}_n(q)) = C_{\mathrm {gcd}(q+1,n)}{:}C_{2f}$
has at most
$\mathrm {Out}(\mathrm {PSU}_n(q)) = C_{\mathrm {gcd}(q+1,n)}{:}C_{2f}$
has at most
![]() $n+\omega (2f) \leqslant r+\omega (f)+2$
maximal subgroups. This proves part (i).
$n+\omega (2f) \leqslant r+\omega (f)+2$
maximal subgroups. This proves part (i).
For parts (ii) and (iii), an
![]() $\mathrm {Inndiag}(\mathrm {soc}(G))$
-class yields at most
$\mathrm {Inndiag}(\mathrm {soc}(G))$
-class yields at most
![]() $|\mathrm {Inndiag}(\mathrm {soc}(G)):\mathrm {soc}(G)|$
classes in G, and
$|\mathrm {Inndiag}(\mathrm {soc}(G)):\mathrm {soc}(G)|$
classes in G, and
![]() $|\mathrm {Inndiag}(\mathrm {soc}(G)):\mathrm {soc}(G)| \leqslant 4$
unless
$|\mathrm {Inndiag}(\mathrm {soc}(G)):\mathrm {soc}(G)| \leqslant 4$
unless
![]() $\mathrm {soc}(G) = \mathrm {PSL}^\pm _n(q)$
, in which case we have
$\mathrm {soc}(G) = \mathrm {PSL}^\pm _n(q)$
, in which case we have
![]() $|\mathrm {Inndiag}(\mathrm {soc}(G)):\mathrm {soc}(G)| \leqslant n = r+1$
. Part (iii) now follows by the observation that there are at most
$|\mathrm {Inndiag}(\mathrm {soc}(G)):\mathrm {soc}(G)| \leqslant n = r+1$
. Part (iii) now follows by the observation that there are at most
![]() $\omega (f)+2$
classes in
$\omega (f)+2$
classes in
![]() $\mathrm {Inndiag}(\mathrm {soc}(G))$
. Part (ii) is easily verified by consulting [Reference Liebeck and Seitz19, Theorem 2] for exceptional groups and [Reference Kleidman and Liebeck18, Chapter 3] and [Reference Schaffer27] for classical groups (we use Lemma 2.7 in the one slightly more difficult case).
$\mathrm {Inndiag}(\mathrm {soc}(G))$
. Part (ii) is easily verified by consulting [Reference Liebeck and Seitz19, Theorem 2] for exceptional groups and [Reference Kleidman and Liebeck18, Chapter 3] and [Reference Schaffer27] for classical groups (we use Lemma 2.7 in the one slightly more difficult case).
3 Proofs of the main theorems
3.1 Independent sets for primitive actions of almost simple groups
This section is devoted to proving Theorem 3. In the introduction, we defined height in terms of sequences of points, but clearly the ordering is irrelevant, so from now on we focus on sets of points. That is, for a group G acting on a set
![]() $\Omega $
, a subset
$\Omega $
, a subset
![]() $S \subseteq \Omega $
is independent if
$S \subseteq \Omega $
is independent if
![]() $G_{(S')}> G_{(S)}$
for all proper subsets
$G_{(S')}> G_{(S)}$
for all proper subsets
![]() $S'$
of S, and the height, denoted
$S'$
of S, and the height, denoted
![]() $H(G,\Omega )$
, is the maximum size of an independent subset of G on
$H(G,\Omega )$
, is the maximum size of an independent subset of G on
![]() $\Omega $
.
$\Omega $
.
Lemma 3.1. Let G be a finite group acting on a set
![]() $\Omega $
. Let N be a normal subgroup of G such that
$\Omega $
. Let N be a normal subgroup of G such that
![]() $G/N$
is cyclic. Then
$G/N$
is cyclic. Then
![]() $H(G,\Omega ) \leqslant H(N,\Omega ) + \omega (|G/N|)$
.
$H(G,\Omega ) \leqslant H(N,\Omega ) + \omega (|G/N|)$
.
Proof. Let
![]() $\Gamma \subseteq \Omega $
be an independent set for G of size
$\Gamma \subseteq \Omega $
be an independent set for G of size
![]() $H(G,\Omega )$
. Fix
$H(G,\Omega )$
. Fix
![]() $\Delta \subseteq \Gamma $
such that
$\Delta \subseteq \Gamma $
such that
![]() $\Delta $
is independent for N and
$\Delta $
is independent for N and
![]() $N_{(\Delta )} = N_{(\Gamma )}$
, so, in particular,
$N_{(\Delta )} = N_{(\Gamma )}$
, so, in particular,
![]() $|\Delta | \leqslant H(N,\Omega )$
. This is always possible by [Reference Gill, Lodá and Spiga12, Lemma 2.4], but the argument is short so we give it: If
$|\Delta | \leqslant H(N,\Omega )$
. This is always possible by [Reference Gill, Lodá and Spiga12, Lemma 2.4], but the argument is short so we give it: If
![]() $\Gamma $
is independent for N, then let
$\Gamma $
is independent for N, then let
![]() $\Delta = \Gamma $
; otherwise, there exists a proper subset
$\Delta = \Gamma $
; otherwise, there exists a proper subset
![]() $\Gamma ' \subseteq \Gamma $
such that
$\Gamma ' \subseteq \Gamma $
such that
![]() $N_{(\Gamma ')} = N_{(\Gamma )}$
, and we repeat the argument replacing
$N_{(\Gamma ')} = N_{(\Gamma )}$
, and we repeat the argument replacing
![]() $\Gamma $
with
$\Gamma $
with
![]() $\Gamma '$
.
$\Gamma '$
.
Let
![]() $\varphi \colon G \to G/N$
be the quotient map, and let
$\varphi \colon G \to G/N$
be the quotient map, and let
![]() $p_1 < \dots < p_k$
be the prime divisors of
$p_1 < \dots < p_k$
be the prime divisors of
![]() $|G/N|$
, so, in particular,
$|G/N|$
, so, in particular,
![]() $k = \omega (|G/N|)$
. Write
$k = \omega (|G/N|)$
. Write
![]() $|\varphi (G_{(\Gamma )})| = p_1^{e_1} \cdots p_k^{e_k}$
. Fix
$|\varphi (G_{(\Gamma )})| = p_1^{e_1} \cdots p_k^{e_k}$
. Fix
![]() $1 \leqslant i \leqslant k$
. Suppose that for all
$1 \leqslant i \leqslant k$
. Suppose that for all
![]() $\alpha \in \Gamma \setminus \Delta $
, the
$\alpha \in \Gamma \setminus \Delta $
, the
![]() $p_i$
-part of
$p_i$
-part of
![]() $|\varphi (G_{(\Delta \cup \{\alpha \})})|$
strictly exceeds
$|\varphi (G_{(\Delta \cup \{\alpha \})})|$
strictly exceeds
![]() $p_i^{e_i}$
. Then since
$p_i^{e_i}$
. Then since
![]() $G_{(\Gamma )} = \bigcap _{\alpha \in \Gamma \setminus \Delta } G_{(\Delta \cup \{\alpha \})}$
and
$G_{(\Gamma )} = \bigcap _{\alpha \in \Gamma \setminus \Delta } G_{(\Delta \cup \{\alpha \})}$
and
![]() $\varphi (G)$
is cyclic, the
$\varphi (G)$
is cyclic, the
![]() $p_i$
-part of
$p_i$
-part of
![]() $|\varphi (G_{(\Gamma )})|$
strictly exceeds
$|\varphi (G_{(\Gamma )})|$
strictly exceeds
![]() $p_i^{e_i}$
, which is a contradiction. Therefore, there exists
$p_i^{e_i}$
, which is a contradiction. Therefore, there exists
![]() $\alpha _i \in \Gamma \setminus \Delta $
such that the
$\alpha _i \in \Gamma \setminus \Delta $
such that the
![]() $p_i$
-part of
$p_i$
-part of
![]() $|\varphi (G_{(\Delta \cup \{\alpha _i\})})|$
is
$|\varphi (G_{(\Delta \cup \{\alpha _i\})})|$
is
![]() $p_i^{e_i}$
. Thus,
$p_i^{e_i}$
. Thus,
![]() $|\varphi (G_{(\Delta \cup \{\alpha _1, \dots , \alpha _k\})})| = p_1^{e_1} \cdots p_k^{e_k} = |\varphi (G_{(\Gamma )})|$
. However,
$|\varphi (G_{(\Delta \cup \{\alpha _1, \dots , \alpha _k\})})| = p_1^{e_1} \cdots p_k^{e_k} = |\varphi (G_{(\Gamma )})|$
. However,
![]() $N_{(\Delta \cup \{\alpha _1, \dots , \alpha _k\})} = N_{(\Gamma )}$
, so we have
$N_{(\Delta \cup \{\alpha _1, \dots , \alpha _k\})} = N_{(\Gamma )}$
, so we have
![]() $G_{(\Delta \cup \{\alpha _1, \dots , \alpha _k\})} = G_{(\Gamma )}$
. Since
$G_{(\Delta \cup \{\alpha _1, \dots , \alpha _k\})} = G_{(\Gamma )}$
. Since
![]() $\Gamma $
is independent for G, we deduce that
$\Gamma $
is independent for G, we deduce that
![]() $\Gamma = \Delta \cup \{\alpha _1, \dots , \alpha _k\}$
, which implies that
$\Gamma = \Delta \cup \{\alpha _1, \dots , \alpha _k\}$
, which implies that
![]() $H(G,\Omega ) = |\Gamma | \leqslant |\Delta | + k \leqslant H(N,\Omega ) + \omega (f)$
, as sought.
$H(G,\Omega ) = |\Gamma | \leqslant |\Delta | + k \leqslant H(N,\Omega ) + \omega (f)$
, as sought.
Proof of Theorem 3.
Let G be an almost simple group of Lie type of rank r over
![]() $\mathbb {F}_{p^f}$
, where p is prime, acting primitively on
$\mathbb {F}_{p^f}$
, where p is prime, acting primitively on
![]() $\Omega $
. Let
$\Omega $
. Let
![]() $G_0 = \mathrm {soc}(G)$
, so
$G_0 = \mathrm {soc}(G)$
, so
![]() $G_0 \leqslant G \leqslant \mathrm {Aut}(G_0)$
. Now, [Reference Gorenstein, Lyons and Solomon13, Theorem 2.5.12] implies that
$G_0 \leqslant G \leqslant \mathrm {Aut}(G_0)$
. Now, [Reference Gorenstein, Lyons and Solomon13, Theorem 2.5.12] implies that
![]() $\mathrm {Aut}(G_0)$
has a normal subgroup N such that
$\mathrm {Aut}(G_0)$
has a normal subgroup N such that
![]() $\mathrm {Aut}(G_0)/N = C_f$
and
$\mathrm {Aut}(G_0)/N = C_f$
and
![]() $|N/G_0| \leqslant 6r$
. Since
$|N/G_0| \leqslant 6r$
. Since
![]() $G/(G \cap N) \cong GN/N$
, by Lemma 3.1,
$G/(G \cap N) \cong GN/N$
, by Lemma 3.1,
and, by [Reference Gill, Lodá and Spiga12, Lemma 2.8],
Now,
![]() $\ell (N/G_0) \leqslant \log _2{|N/G_0|} \leqslant \log _2(6r) \leqslant 3r^3$
, so
$\ell (N/G_0) \leqslant \log _2{|N/G_0|} \leqslant \log _2(6r) \leqslant 3r^3$
, so
![]() $H(G,\Omega ) \leqslant H(G_0,\Omega ) + 3r^3 + \omega (f)$
. While the action of
$H(G,\Omega ) \leqslant H(G_0,\Omega ) + 3r^3 + \omega (f)$
. While the action of
![]() $G_0$
on
$G_0$
on
![]() $\Omega $
need not be primitive, as explained in the final paragraph of the proof of [Reference Gill and Liebeck10, Corollary 3], we still have
$\Omega $
need not be primitive, as explained in the final paragraph of the proof of [Reference Gill and Liebeck10, Corollary 3], we still have
![]() $H(G_0,\Omega ) \leqslant 174r^8$
, so
$H(G_0,\Omega ) \leqslant 174r^8$
, so
![]() $H(G_0,\Omega ) \leqslant 177r^8 + \omega (f)$
.
$H(G_0,\Omega ) \leqslant 177r^8 + \omega (f)$
.
3.2 Minimal generating sets for almost simple groups of Lie type
We are now in a position to prove Theorem 2.
Proof of Theorem 2.
By Theorem 3 and Proposition 2.3, there exist constants
![]() $A,B,C> 0$
such that for all almost simple groups of Lie type G of rank r over
$A,B,C> 0$
such that for all almost simple groups of Lie type G of rank r over
![]() $\mathbb {F}_{p^f}$
, where p is prime, the following both hold
$\mathbb {F}_{p^f}$
, where p is prime, the following both hold
-
(i) if G acts faithfully and primitively on a set
 $\Omega $
, then
$\Omega $
, then
 $H(G,\Omega ) \leqslant Ar^B+\omega (f)$
$H(G,\Omega ) \leqslant Ar^B+\omega (f)$
-
(ii) if M is a maximal subgroup of G of type (IV*), then
 $\ell (M) \leqslant C r$
.
$\ell (M) \leqslant C r$
.
Define
![]() $\alpha = \max \{ 100A, C \}$
and
$\alpha = \max \{ 100A, C \}$
and
![]() $\beta =B+2$
(note that
$\beta =B+2$
(note that
![]() $(\alpha ,\beta ) = (17700,10)$
is a valid choice here since
$(\alpha ,\beta ) = (17700,10)$
is a valid choice here since
![]() $(A,B) = (177,8)$
and
$(A,B) = (177,8)$
and
![]() $C=192$
are valid for Theorem 3 and Proposition 2.3).
$C=192$
are valid for Theorem 3 and Proposition 2.3).
Let G be an almost simple group of Lie type of rank r over
![]() $\mathbb {F}_{p^f}$
where p is prime. Then we claim that
$\mathbb {F}_{p^f}$
where p is prime. Then we claim that
Let X be a minimal generating set for G. For each
![]() $x \in X$
, write
$x \in X$
, write
![]() $H_x = \langle X \setminus \{x\} \rangle $
and let
$H_x = \langle X \setminus \{x\} \rangle $
and let
![]() $M_x$
be a maximal subgroup of G such that
$M_x$
be a maximal subgroup of G such that
![]() $H_x \leqslant M_x$
. For distinct
$H_x \leqslant M_x$
. For distinct
![]() $x,y \in X$
note that
$x,y \in X$
note that
![]() $M_x \neq M_y$
, for otherwise
$M_x \neq M_y$
, for otherwise
![]() $\langle X \setminus \{x\} \rangle \leqslant M_x$
and
$\langle X \setminus \{x\} \rangle \leqslant M_x$
and
![]() $\langle X \setminus \{y\} \rangle \leqslant M_x$
, so
$\langle X \setminus \{y\} \rangle \leqslant M_x$
, so
![]() $G = \langle X \rangle \leqslant M_x$
, which is impossible.
$G = \langle X \rangle \leqslant M_x$
, which is impossible.
First, assume that for all
![]() $x \in X$
the maximal subgroup
$x \in X$
the maximal subgroup
![]() $M_x$
contains
$M_x$
contains
![]() $\mathrm {soc}(G)$
or has type (I*), (II), (III) or (V). For a contradiction, suppose that
$\mathrm {soc}(G)$
or has type (I*), (II), (III) or (V). For a contradiction, suppose that
![]() $|X|> \alpha (r+\omega (f))^\beta $
. This means that
$|X|> \alpha (r+\omega (f))^\beta $
. This means that
 $$ \begin{gather*} |X|> \alpha(r+\omega(f))^\beta \geqslant 100A(r+\omega(f))^{B+2} \geqslant (Ar^B + \omega(f)) \cdot 100(r+\omega(f))^2 \\ \geqslant (Ar^B + \omega(f)) \cdot (100r + (r+1)(\omega(f)+2)) + (2r + \omega(f) + 10). \end{gather*} $$
$$ \begin{gather*} |X|> \alpha(r+\omega(f))^\beta \geqslant 100A(r+\omega(f))^{B+2} \geqslant (Ar^B + \omega(f)) \cdot 100(r+\omega(f))^2 \\ \geqslant (Ar^B + \omega(f)) \cdot (100r + (r+1)(\omega(f)+2)) + (2r + \omega(f) + 10). \end{gather*} $$
By Proposition 2.4(i),
![]() $\mathrm {soc}(G) \leqslant M_x$
for at most
$\mathrm {soc}(G) \leqslant M_x$
for at most
![]() $2r + \omega (f) + 10$
elements x of X. Therefore,
$2r + \omega (f) + 10$
elements x of X. Therefore,
![]() $M_x$
is core-free for strictly greater than
$M_x$
is core-free for strictly greater than
![]() $(Ar^B + \omega (f)) \cdot (100r + (r+1)(\omega (f)+2))$
elements x of X. Now, Proposition 2.4(ii)–(iii) together with the pigeonhole principle implies that there exists a core-free maximal subgroup M of G and a subset
$(Ar^B + \omega (f)) \cdot (100r + (r+1)(\omega (f)+2))$
elements x of X. Now, Proposition 2.4(ii)–(iii) together with the pigeonhole principle implies that there exists a core-free maximal subgroup M of G and a subset
![]() $Y \subseteq X$
such that
$Y \subseteq X$
such that
![]() $|Y|> Ar^B + \omega (f)$
and for all
$|Y|> Ar^B + \omega (f)$
and for all
![]() $y \in Y$
there exists
$y \in Y$
there exists
![]() $g_y \in G$
such that
$g_y \in G$
such that
![]() $M_y = M^{g_y}$
.
$M_y = M^{g_y}$
.
We claim that
![]() $\bigcap _{y \in Y} M^{g_y} < \bigcap _{y \in Y \setminus \{y_0\}} M^{g_y}$
for all
$\bigcap _{y \in Y} M^{g_y} < \bigcap _{y \in Y \setminus \{y_0\}} M^{g_y}$
for all
![]() $y_0 \in Y$
. To see this, it suffices to fix
$y_0 \in Y$
. To see this, it suffices to fix
![]() $y_0 \in Y$
and show that
$y_0 \in Y$
and show that
![]() $\bigcap _{y \in Y \setminus \{y_0\}} M^{g_y} \nleqslant M^{g_{y_0}}$
. For a contradiction, suppose otherwise. First, note that
$\bigcap _{y \in Y \setminus \{y_0\}} M^{g_y} \nleqslant M^{g_{y_0}}$
. For a contradiction, suppose otherwise. First, note that
![]() $\langle X \setminus \{y_0\} \rangle = H_{y_0} \leqslant M_{y_0} = M^{g_{y_0}}$
, Second note that for all
$\langle X \setminus \{y_0\} \rangle = H_{y_0} \leqslant M_{y_0} = M^{g_{y_0}}$
, Second note that for all
![]() $y \in Y \setminus \{y_0\}$
we have
$y \in Y \setminus \{y_0\}$
we have
![]() $y_0 \in \langle X \setminus (Y \setminus \{y_0\}) \rangle \leqslant \langle X \setminus \{y\} \rangle = H_y \leqslant M_y = M^{g_y}$
, so
$y_0 \in \langle X \setminus (Y \setminus \{y_0\}) \rangle \leqslant \langle X \setminus \{y\} \rangle = H_y \leqslant M_y = M^{g_y}$
, so
![]() $y_0 \in \bigcap _{y \in Y \setminus \{y_0\}} M^{g_y}$
. Therefore, under the supposition that
$y_0 \in \bigcap _{y \in Y \setminus \{y_0\}} M^{g_y}$
. Therefore, under the supposition that
![]() $\bigcap _{y \in Y \setminus \{y_0\}} M^{g_y} \leqslant M^{g_{y_0}}$
, we deduce that
$\bigcap _{y \in Y \setminus \{y_0\}} M^{g_y} \leqslant M^{g_{y_0}}$
, we deduce that
![]() $G = \langle X \rangle \leqslant M^{g_{y_0}}$
, which is absurd. This establishes the claim.
$G = \langle X \rangle \leqslant M^{g_{y_0}}$
, which is absurd. This establishes the claim.
This means that
![]() $\{ Mg_y \mid y \in Y \}$
is an independent set for the action of G on
$\{ Mg_y \mid y \in Y \}$
is an independent set for the action of G on
![]() $G/M$
, so Theorem 3 implies that
$G/M$
, so Theorem 3 implies that
![]() $|Y| \leqslant Ar^B + \omega (f)$
(see (ii) above), but this directly contradicts the fact that
$|Y| \leqslant Ar^B + \omega (f)$
(see (ii) above), but this directly contradicts the fact that
![]() $|Y|> Ar^B + \omega (f)$
. Therefore, we deduce that
$|Y|> Ar^B + \omega (f)$
. Therefore, we deduce that
![]() $|X| \leqslant \alpha (r+\omega (f))^\beta $
.
$|X| \leqslant \alpha (r+\omega (f))^\beta $
.
Next, assume that there exists
![]() $x \in X$
such that
$x \in X$
such that
![]() $M_x$
has type (IV*). We clearly have the inequalities
$M_x$
has type (IV*). We clearly have the inequalities
![]() $|X| \leqslant m(H_x) + 1 \leqslant \ell (H_x) + 1 \leqslant \ell (M_x) + 1$
. Proposition 2.3 implies that
$|X| \leqslant m(H_x) + 1 \leqslant \ell (H_x) + 1 \leqslant \ell (M_x) + 1$
. Proposition 2.3 implies that
![]() $\ell (M_x) \leqslant Cr \leqslant \alpha r$
(see (i) above), so
$\ell (M_x) \leqslant Cr \leqslant \alpha r$
(see (i) above), so
![]() $|X| \leqslant \alpha r+1 \leqslant \alpha (r+\omega (f))^\beta $
.
$|X| \leqslant \alpha r+1 \leqslant \alpha (r+\omega (f))^\beta $
.
We now pause to observe that we have proved equation (3.1) when
![]() $\mathrm {soc}(G) = \mathrm {PSL}_2(p^f)$
since in this case the (I) coincides with (I*) and (IV) coincides with (IV*).
$\mathrm {soc}(G) = \mathrm {PSL}_2(p^f)$
since in this case the (I) coincides with (I*) and (IV) coincides with (IV*).
Having established the result in the base case where the rank r is
![]() $1$
, we now complete the proof by induction. Suppose that
$1$
, we now complete the proof by induction. Suppose that
![]() $r = s> 1$
and that equation (3.1) holds for all groups with
$r = s> 1$
and that equation (3.1) holds for all groups with
![]() $r < s$
.
$r < s$
.
By Proposition 2.2, it remains to assume that G is classical and
![]() $H_x$
is an almost simple group of Lie type defined over
$H_x$
is an almost simple group of Lie type defined over
![]() $\mathbb {F}_{p^e} \subseteq \mathbb {F}_{p^f}$
such that
$\mathbb {F}_{p^e} \subseteq \mathbb {F}_{p^f}$
such that
![]() $\mathrm {rank}(M_x) < r$
. Now, by induction,
$\mathrm {rank}(M_x) < r$
. Now, by induction,
Therefore, in all cases
![]() $|X| \leqslant \alpha (r+\omega (f))^\beta $
, as desired.
$|X| \leqslant \alpha (r+\omega (f))^\beta $
, as desired.
We next show that, up to improving
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
, the bound in Theorem 2 is best possible.
$\beta $
, the bound in Theorem 2 is best possible.
Proposition 3.2. Let G be a finite simple group of Lie type of rank r over
![]() $\mathbb {F}_{p^f}$
, where p is prime. Then
$\mathbb {F}_{p^f}$
, where p is prime. Then
![]() $m(G) \geqslant 2r + \omega (f)$
.
$m(G) \geqslant 2r + \omega (f)$
.
Proof. Let B be a Borel subgroup of G containing a maximal torus T, let
![]() $\Phi $
be the corresponding root system of G and let
$\Phi $
be the corresponding root system of G and let
![]() $\Delta = \{ \alpha _1, \dots , \alpha _r \}$
be a set of simple roots. We will now construct a minimal generating set for G. To refer to elements of G, we will use the standard Lie theoretic notation
$\Delta = \{ \alpha _1, \dots , \alpha _r \}$
be a set of simple roots. We will now construct a minimal generating set for G. To refer to elements of G, we will use the standard Lie theoretic notation
![]() $x_\alpha (t)$
and
$x_\alpha (t)$
and
![]() $h_\alpha (t)$
; see [Reference Gorenstein, Lyons and Solomon13, Theorem 1.12.1], for example.
$h_\alpha (t)$
; see [Reference Gorenstein, Lyons and Solomon13, Theorem 1.12.1], for example.
For
![]() $1 \leqslant i \leqslant r$
, let
$1 \leqslant i \leqslant r$
, let
![]() $x_i$
and
$x_i$
and
![]() $y_i$
be the root elements
$y_i$
be the root elements
![]() $x_{\alpha _i}(1)$
and
$x_{\alpha _i}(1)$
and
![]() $x_{-\alpha _i}(1)$
, respectively. Write
$x_{-\alpha _i}(1)$
, respectively. Write
![]() $f = e_1^{a_1} \cdots e_k^{a_k}$
, where
$f = e_1^{a_1} \cdots e_k^{a_k}$
, where
![]() $e_1, \dots , e_k$
are the distinct prime divisors of f (so
$e_1, \dots , e_k$
are the distinct prime divisors of f (so
![]() $k = \omega (f)$
). For
$k = \omega (f)$
). For
![]() $1 \leqslant i \leqslant k$
, let
$1 \leqslant i \leqslant k$
, let
![]() $f_i = e_i^{a_i}$
, let
$f_i = e_i^{a_i}$
, let
![]() $\lambda _i$
be a primitive element of the subfield
$\lambda _i$
be a primitive element of the subfield
![]() $\mathbb {F}_{p^{f_i}}$
and let
$\mathbb {F}_{p^{f_i}}$
and let
![]() $z_i = h_{\alpha _1}(\lambda _i)$
.
$z_i = h_{\alpha _1}(\lambda _i)$
.
We claim that
![]() $X = \{ x_1, \dots , x_r, y_1, \dots , y_r, z_1, \dots , z_k \}$
is a minimal generating set for G (since
$X = \{ x_1, \dots , x_r, y_1, \dots , y_r, z_1, \dots , z_k \}$
is a minimal generating set for G (since
![]() $|X| = 2r+\omega (f)$
this establishes the result). The fact that X generates G follows from [Reference Gorenstein, Lyons and Solomon13, Theorem 1.12.1] and [Reference Malle and Testerman25, Corollary 24.2]. To see that X is minimal, note that for all
$|X| = 2r+\omega (f)$
this establishes the result). The fact that X generates G follows from [Reference Gorenstein, Lyons and Solomon13, Theorem 1.12.1] and [Reference Malle and Testerman25, Corollary 24.2]. To see that X is minimal, note that for all
![]() $1 \leqslant i \leqslant k$
, the set
$1 \leqslant i \leqslant k$
, the set
![]() $X \setminus \{z_i\}$
is contained in the subfield subgroup defined over the subfield
$X \setminus \{z_i\}$
is contained in the subfield subgroup defined over the subfield
![]() $\mathbb {F}_{p^{f/e_i}}$
, and for all
$\mathbb {F}_{p^{f/e_i}}$
, and for all
![]() $1 \leqslant i \leqslant r$
, both of the sets
$1 \leqslant i \leqslant r$
, both of the sets
![]() $X \setminus \{x_i\}$
and
$X \setminus \{x_i\}$
and
![]() $X \setminus \{y_i\}$
are contained in parabolic subgroups of type
$X \setminus \{y_i\}$
are contained in parabolic subgroups of type
![]() $P_i$
(corresponding to deleting node i from the Dynkin diagram of
$P_i$
(corresponding to deleting node i from the Dynkin diagram of
![]() $\Phi $
).
$\Phi $
).
Example 3.3. To elucidate the proof of Proposition 3.2, let us give an explicit description of the minimal generating set when
![]() $G = \mathrm {PSL}_3(q)$
and
$G = \mathrm {PSL}_3(q)$
and
![]() $q = p^{f_1f_2}$
for distinct primes
$q = p^{f_1f_2}$
for distinct primes
![]() $f_1$
and
$f_1$
and
![]() $f_2$
. Let
$f_2$
. Let
![]() $\lambda _1$
and
$\lambda _1$
and
![]() $\lambda _2$
be primitive elements of
$\lambda _2$
be primitive elements of
![]() $\mathbb {F}_{p^{f_1}}$
and
$\mathbb {F}_{p^{f_1}}$
and
![]() $\mathbb {F}_{p^{f_2}}$
, respectively. Then we obtain a minimal generating set
$\mathbb {F}_{p^{f_2}}$
, respectively. Then we obtain a minimal generating set
![]() $\{x_1,x_2,y_1,y_2,z_1,z_2\}$
, where
$\{x_1,x_2,y_1,y_2,z_1,z_2\}$
, where
 $$ \begin{gather*} x_1 = \left( \begin{array}{ccc} 1 & 1 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array} \right), \quad x_2 = \left( \begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 1 \\ 0 & 0 & 1 \end{array} \right), \quad y_1 = \left( \begin{array}{ccc} 1 & 0 & 0 \\ 1 & 1 & 0 \\ 0 & 0 & 1 \end{array} \right), \quad y_2 = \left( \begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 1 & 1 \end{array} \right) \\[5pt] z_1 = \left( \begin{array}{ccc} \lambda_1 & 0 & 0 \\ 0 & \lambda_1^{-1} & 0 \\ 0 & 0 & 1 \end{array} \right), \quad z_2 = \left( \begin{array}{ccc} \lambda_2 & 0 & 0 \\ 0 & \lambda_2^{-1} & 0 \\ 0 & 0 & 1 \end{array} \right). \end{gather*} $$
$$ \begin{gather*} x_1 = \left( \begin{array}{ccc} 1 & 1 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array} \right), \quad x_2 = \left( \begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 1 \\ 0 & 0 & 1 \end{array} \right), \quad y_1 = \left( \begin{array}{ccc} 1 & 0 & 0 \\ 1 & 1 & 0 \\ 0 & 0 & 1 \end{array} \right), \quad y_2 = \left( \begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 1 & 1 \end{array} \right) \\[5pt] z_1 = \left( \begin{array}{ccc} \lambda_1 & 0 & 0 \\ 0 & \lambda_1^{-1} & 0 \\ 0 & 0 & 1 \end{array} \right), \quad z_2 = \left( \begin{array}{ccc} \lambda_2 & 0 & 0 \\ 0 & \lambda_2^{-1} & 0 \\ 0 & 0 & 1 \end{array} \right). \end{gather*} $$
3.3 Minimal generating sets for an arbitrary finite group
We now use Theorem 2 to prove Theorem 1. We first require the following reduction theorem, which was proved by Lucchini, Moscatiello and Spiga [Reference Lucchini, Moscatiello and Spiga24, Theorem 1.4].
Theorem 3.4. Let
![]() $a \geqslant 1$
and
$a \geqslant 1$
and
![]() $b \geqslant 2$
. Let G be a finite group. Assume that every composition factor
$b \geqslant 2$
. Let G be a finite group. Assume that every composition factor
![]() $S_0$
of G and every almost simple group S with socle
$S_0$
of G and every almost simple group S with socle
![]() $S_0$
satisfies
$S_0$
satisfies
![]() $m(S)-m(S/S_0) \leqslant a \cdot \omega (|S_0|)^b$
. Then
$m(S)-m(S/S_0) \leqslant a \cdot \omega (|S_0|)^b$
. Then
![]() $m(G) \leqslant a \cdot \delta (G)^b$
.
$m(G) \leqslant a \cdot \delta (G)^b$
.
We have focused on almost simple groups of Lie type since otherwise the required result follows from existing work in the literature as the following theorem highlights (this is noted in [Reference Lucchini, Moscatiello and Spiga24, Lemma 4.5] without an explicit constant).
Theorem 3.5. There exists a constant
![]() $\gamma> 0$
such that if G is an almost simple group that is not a group of Lie type, then
$\gamma> 0$
such that if G is an almost simple group that is not a group of Lie type, then
![]() $m(G) \leqslant \gamma \cdot \omega (|\mathrm {soc}(G)|)^2$
. Moreover, this is true with
$m(G) \leqslant \gamma \cdot \omega (|\mathrm {soc}(G)|)^2$
. Moreover, this is true with
![]() $\gamma = 52$
.
$\gamma = 52$
.
Proof. Let
![]() $\gamma = 52$
. If
$\gamma = 52$
. If
![]() $\mathrm {soc}(G)$
is sporadic, then
$\mathrm {soc}(G)$
is sporadic, then
![]() $m(G) \leqslant \ell (G) \leqslant 52$
(see [Reference Cameron, Solomon and Turull6, Tables III and IV]), and it is easy to check that the same bound holds when
$m(G) \leqslant \ell (G) \leqslant 52$
(see [Reference Cameron, Solomon and Turull6, Tables III and IV]), and it is easy to check that the same bound holds when
![]() $\mathrm {soc}(G)$
is
$\mathrm {soc}(G)$
is
![]() $A_6$
or
$A_6$
or
![]() ${}^2F_4(2)'$
.
${}^2F_4(2)'$
.
We can now assume that
![]() $\mathrm {soc}(G) = A_n$
for
$\mathrm {soc}(G) = A_n$
for
![]() $n \neq 6$
. In this case, G is
$n \neq 6$
. In this case, G is
![]() $A_n$
or
$A_n$
or
![]() $S_n$
and Whiston proved that
$S_n$
and Whiston proved that
![]() $m(G)$
is
$m(G)$
is
![]() $n-2$
or
$n-2$
or
![]() $n-1$
, respectively [Reference Whiston29]. If
$n-1$
, respectively [Reference Whiston29]. If
![]() $n \leqslant 53$
, then
$n \leqslant 53$
, then
![]() $m(G) \leqslant n-1 \leqslant 52$
. Otherwise, by [Reference Rosser and Schoenfeld26, Corollary 1] we know that
$m(G) \leqslant n-1 \leqslant 52$
. Otherwise, by [Reference Rosser and Schoenfeld26, Corollary 1] we know that
![]() $\pi (n)> n/\log {n}$
, where
$\pi (n)> n/\log {n}$
, where
![]() $\pi $
is the prime-counting function and
$\pi $
is the prime-counting function and
![]() $\log $
is the natural logarithm. Noting that
$\log $
is the natural logarithm. Noting that
![]() $\log {n} < \sqrt {n}$
, these bounds give
$\log {n} < \sqrt {n}$
, these bounds give
The following lemma relates Theorems 2 and 3.4 for groups of Lie type.
Lemma 3.6. Let G be an almost simple group of Lie type of rank r over
![]() $\mathbb {F}_{p^f}$
(where p is prime). Then
$\mathbb {F}_{p^f}$
(where p is prime). Then
Proof. It is easy to check that
![]() $|\mathrm {soc}(G)|$
is divisible by
$|\mathrm {soc}(G)|$
is divisible by
![]() $p^{fd_1}-1$
,
$p^{fd_1}-1$
,
![]() $p^{fd_2}-1$
, …
$p^{fd_2}-1$
, …
![]() $p^{fd_k} -1$
for some
$p^{fd_k} -1$
for some
![]() $d_1 < d_2 < \dots < d_k$
with
$d_1 < d_2 < \dots < d_k$
with
![]() $k \geqslant \max (1,\frac {1}{2}(r-1))$
. Moreover, if
$k \geqslant \max (1,\frac {1}{2}(r-1))$
. Moreover, if
![]() $e_1, \dots , e_l$
are the distinct prime divisors of f, then
$e_1, \dots , e_l$
are the distinct prime divisors of f, then
![]() $|\mathrm {soc}(G)|$
is divisible by
$|\mathrm {soc}(G)|$
is divisible by
![]() $p-1$
,
$p-1$
,
![]() $(p^{e_1}-1)/(p-1)$
,
$(p^{e_1}-1)/(p-1)$
,
![]() $(p^{e_1 e_2}-1)/(p-1)$
…,
$(p^{e_1 e_2}-1)/(p-1)$
…,
![]() $(p^{e_1 e_2 \dots e_l}-1)/(p-1)$
. Note that
$(p^{e_1 e_2 \dots e_l}-1)/(p-1)$
. Note that
![]() $1 < e_1 < e_1e_2 < \dots < e_1e_2 \dots e_l < fd_2 < fd_3 \dots < fd_k$
. By Zsigmondy’s theorem [Reference Zsigmondy32], for all but at most one
$1 < e_1 < e_1e_2 < \dots < e_1e_2 \dots e_l < fd_2 < fd_3 \dots < fd_k$
. By Zsigmondy’s theorem [Reference Zsigmondy32], for all but at most one
![]() $i \in \{1, e_1, \dots , e_1e_2 \dots e_l, fd_2, fd_3, \dots , fd_k \}$
we may fix a primitive prime divisor of
$i \in \{1, e_1, \dots , e_1e_2 \dots e_l, fd_2, fd_3, \dots , fd_k \}$
we may fix a primitive prime divisor of
![]() $p^i-1$
. Noting that
$p^i-1$
. Noting that
![]() $|\mathrm {soc}(G)|$
is also divisible by p, we deduce that
$|\mathrm {soc}(G)|$
is also divisible by p, we deduce that
![]() $\omega (|\mathrm {soc}(G)|) \geqslant \max (1,\frac {1}{2}(r-1)) + \omega (f)$
.
$\omega (|\mathrm {soc}(G)|) \geqslant \max (1,\frac {1}{2}(r-1)) + \omega (f)$
.
We can now prove Theorem 1.
Proof of Theorem 1.
Let
![]() $\alpha , \beta , \gamma> 0$
be constants satisfying Theorems 2 and 3.5. Let us define
$\alpha , \beta , \gamma> 0$
be constants satisfying Theorems 2 and 3.5. Let us define
![]() $a = \max \{\alpha \cdot 3^\beta , \gamma \}$
and
$a = \max \{\alpha \cdot 3^\beta , \gamma \}$
and
![]() $b = \max \{\beta ,2\}$
(note that
$b = \max \{\beta ,2\}$
(note that
![]() $b=10$
is a valid choice here since
$b=10$
is a valid choice here since
![]() $\beta =10$
is a valid choice in Theorem 2, and using
$\beta =10$
is a valid choice in Theorem 2, and using
![]() $\alpha =10^5$
and
$\alpha =10^5$
and
![]() $\gamma =52$
gives
$\gamma =52$
gives
![]() $a < 10^{10}$
).
$a < 10^{10}$
).
Let G be a finite group, let
![]() $S_0$
be a composition factor of G and let S be an almost simple group with socle
$S_0$
be a composition factor of G and let S be an almost simple group with socle
![]() $S_0$
. First assume that
$S_0$
. First assume that
![]() $S_0$
is alternating, sporadic or the Tits group. Then Theorem 3.5 implies that
$S_0$
is alternating, sporadic or the Tits group. Then Theorem 3.5 implies that
![]() $m(S) \leqslant \gamma \cdot \omega (|S_0|)^2$
. Now, assume that
$m(S) \leqslant \gamma \cdot \omega (|S_0|)^2$
. Now, assume that
![]() $S_0$
is finite simple group of Lie type of rank r over
$S_0$
is finite simple group of Lie type of rank r over
![]() $\mathbb {F}_{p^f}$
, where p is prime. Then Theorem 2 gives us the bound
$\mathbb {F}_{p^f}$
, where p is prime. Then Theorem 2 gives us the bound
![]() $m(S) \leqslant \alpha (r+\omega (f))^\beta $
. By Lemma 3.6,
$m(S) \leqslant \alpha (r+\omega (f))^\beta $
. By Lemma 3.6,
![]() $\omega (|S_0|) \geqslant \max (1,\frac {1}{2}(r-1))+\omega (f) \geqslant \frac {1}{3}(r+\omega (f))$
, so
$\omega (|S_0|) \geqslant \max (1,\frac {1}{2}(r-1))+\omega (f) \geqslant \frac {1}{3}(r+\omega (f))$
, so
![]() $m(S) \leqslant \alpha \cdot 3^\beta \cdot \omega (|S_0|)^\beta $
. Therefore, in both cases,
$m(S) \leqslant \alpha \cdot 3^\beta \cdot \omega (|S_0|)^\beta $
. Therefore, in both cases,
![]() $m(S) \leqslant a \cdot \omega (|S_0|)^b$
. By Theorem 3.4, this establishes that
$m(S) \leqslant a \cdot \omega (|S_0|)^b$
. By Theorem 3.4, this establishes that
![]() $m(G) \leqslant a \cdot \delta (G)^b$
.
$m(G) \leqslant a \cdot \delta (G)^b$
.
Acknowledgments
The author thanks Andrea Lucchini for introducing him to this topic, Nick Gill and Martin Liebeck for information in advance of [Reference Gill and Liebeck10], Colva Roney-Dougal for several influential conversations, particularly concerning Section 3.1, and the anonymous referee for useful comments.
Competing interest
The authors have no competing interest to declare.
Financial support
The author is a Leverhulme Early Career Fellow (ECF-2022-154), and he thanks the Leverhulme Trust for their financial support.