1 Introduction
Let
![]() $E $
be a CM field, V a hermitian space over E of signature
$E $
be a CM field, V a hermitian space over E of signature
![]() $(n,1), (n+1,0),.. . ,(n+1,0)$
, and X a Shimura variety for
$(n,1), (n+1,0),.. . ,(n+1,0)$
, and X a Shimura variety for
![]() $U(V)$
. Let F be the maximal totally real subfield and
$U(V)$
. Let F be the maximal totally real subfield and
![]() $F_{>0}$
the set of totally positive elements of F. For
$F_{>0}$
the set of totally positive elements of F. For
![]() $t \in F_{>0}$
, we have a special divisor
$t \in F_{>0}$
, we have a special divisor
![]() $Z_t$
on X, following Kudla’s work [Reference KudlaKud97a] for orthogonal Shimura varieties. Let
$Z_t$
on X, following Kudla’s work [Reference KudlaKud97a] for orthogonal Shimura varieties. Let
![]() $[ Z_t]$
be the class of
$[ Z_t]$
be the class of
![]() $Z_t$
in the Chow group
$Z_t$
in the Chow group
![]() ${\mathrm {Ch}}^1(X)_{\mathbb {C}}$
of divisors on X with
${\mathrm {Ch}}^1(X)_{\mathbb {C}}$
of divisors on X with
![]() ${\mathbb {C}}$
-coefficients. By Liu [Reference LiuLiu11a], the generating series
${\mathbb {C}}$
-coefficients. By Liu [Reference LiuLiu11a], the generating series
with a suitable constant term, is a
![]() ${\mathrm {Ch}}^1(X)_{\mathbb {C}}$
-valued holomorphic modular form. Here,
${\mathrm {Ch}}^1(X)_{\mathbb {C}}$
-valued holomorphic modular form. Here,
![]() $q=\prod _{k=1}^{[F:{\mathbb {Q}}]} e^{2\pi i\tau _k}$
with
$q=\prod _{k=1}^{[F:{\mathbb {Q}}]} e^{2\pi i\tau _k}$
with
![]() $\tau =(\tau _k )_{k=1}^{[F:{\mathbb {Q}}]}\in {\mathcal {H}}^{[F:{\mathbb {Q}}]}$
, where
$\tau =(\tau _k )_{k=1}^{[F:{\mathbb {Q}}]}\in {\mathcal {H}}^{[F:{\mathbb {Q}}]}$
, where
![]() ${\mathcal {H}}$
is the usual upper half plane. This is an analog of the theorem of Borcherds [Reference BorcherdsBor99], Yuan, S. Zhang and W. Zhang [Reference Yuan, Zhang and ZhangYZZ09] for orthogonal Shimura varieties, which was originally conjectured by Kudla [Reference KudlaKud97a]. In [Reference KudlaKud02, Reference KudlaKud03, Reference KudlaKud04], Kudla also raised the problem of finding (canonical) arithmetic extensions of special divisors on integral models of Shimura varieties to obtain a modular generating series, which is crucial for Kudla’s program on arithmetic theta lifting.
${\mathcal {H}}$
is the usual upper half plane. This is an analog of the theorem of Borcherds [Reference BorcherdsBor99], Yuan, S. Zhang and W. Zhang [Reference Yuan, Zhang and ZhangYZZ09] for orthogonal Shimura varieties, which was originally conjectured by Kudla [Reference KudlaKud97a]. In [Reference KudlaKud02, Reference KudlaKud03, Reference KudlaKud04], Kudla also raised the problem of finding (canonical) arithmetic extensions of special divisors on integral models of Shimura varieties to obtain a modular generating series, which is crucial for Kudla’s program on arithmetic theta lifting.
The main result of this paper provides a solution to Kudla’s modularity problem in the case that X is proper with arbitrary level structures at split places and certain lattice level structures at nonsplit places. The arithmetic extensions are defined using S. Zhang’s theory of admissible arithmetic divisors. Slightly more explicitly, we construct a regular integral model
![]() ${\mathcal {X}}$
of X proper flat over
${\mathcal {X}}$
of X proper flat over
![]() ${\mathcal {O}}_E$
. An admissible arithmetic divisor on
${\mathcal {O}}_E$
. An admissible arithmetic divisor on
![]() ${\mathcal {X}}$
is an analog of an admissible Green function (i.e., one with harmonic curvature). Consider the normalized admissible extension
${\mathcal {X}}$
is an analog of an admissible Green function (i.e., one with harmonic curvature). Consider the normalized admissible extension
![]() $ Z_t^{\overline {\mathcal {L}}}$
of
$ Z_t^{\overline {\mathcal {L}}}$
of
![]() $Z_t$
, which is the Zariski closure at every finite place of E where the model is smooth. Let
$Z_t$
, which is the Zariski closure at every finite place of E where the model is smooth. Let
![]() $[ Z_t^{\overline {\mathcal {L}}}]$
be its class in the arithmetic Chow group. Then the generating series
$[ Z_t^{\overline {\mathcal {L}}}]$
be its class in the arithmetic Chow group. Then the generating series
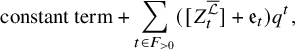 $$ \begin{align} \text{constant term}+\sum_{t \in F_{>0}}([ Z_t^{\overline{\mathcal{L}}}]+{\mathfrak{e}}_t) q^t, \end{align} $$
$$ \begin{align} \text{constant term}+\sum_{t \in F_{>0}}([ Z_t^{\overline{\mathcal{L}}}]+{\mathfrak{e}}_t) q^t, \end{align} $$
with a suitable constant term, is a holomorphic modular form. Here,
![]() $ {\mathfrak {e}}_t $
is formed using coefficients of an explicit Eisenstein series and its derivative.
$ {\mathfrak {e}}_t $
is formed using coefficients of an explicit Eisenstein series and its derivative.
Previous to our work, solutions to Kudla’s modularity problem were obtained using different methods by Kudla, Rapoport and Yang [Reference KudlaKud03] [Reference Kudla, Rapoport and YangKRY06] for quaternionic Shimura curves, by Bruinier, Burgos Gil, and Kühn [Reference Bruinier, Burgos Gil and KühnBBGK07] for Hilbert modular surfaces, over
![]() ${\mathbb {Q}}$
with minimal level structures, by Howard and Madapusi Pera [Reference Howard and PeraHMP20] for orthogonal Shimura varieties over
${\mathbb {Q}}$
with minimal level structures, by Howard and Madapusi Pera [Reference Howard and PeraHMP20] for orthogonal Shimura varieties over
![]() ${\mathbb {Q}}$
, and by Bruinier, Howard, Kudla, Rapoport and Yang [Reference Bruinier, Howard, Kudla, Rapoport and YangBHK+20a] for unitary Shimura varieties over imaginary quadratic fields, with self-dual lattice level structures. Compared to these results, we expect that the greater generality of the level structures in our result could be more useful for some purposes – for example, to approach modularity in higher codimensions following the inductive process in [Reference Yuan, Zhang and ZhangYZZ09] for the generic fibers.
${\mathbb {Q}}$
, and by Bruinier, Howard, Kudla, Rapoport and Yang [Reference Bruinier, Howard, Kudla, Rapoport and YangBHK+20a] for unitary Shimura varieties over imaginary quadratic fields, with self-dual lattice level structures. Compared to these results, we expect that the greater generality of the level structures in our result could be more useful for some purposes – for example, to approach modularity in higher codimensions following the inductive process in [Reference Yuan, Zhang and ZhangYZZ09] for the generic fibers.
In the other direction, S. Zhang [Reference ZhangZha20] introduced the notion of
![]() $\mathsf {L}$
-liftings of divisor classes (on general polarized arithmetic varieties), and then deduced a solution to Kudla’s modularity problem directly from the modularity results for the generic fibers in the first paragraph, regardless of level structures. The
$\mathsf {L}$
-liftings of divisor classes (on general polarized arithmetic varieties), and then deduced a solution to Kudla’s modularity problem directly from the modularity results for the generic fibers in the first paragraph, regardless of level structures. The
![]() $\mathsf {L}$
-lifting of a divisor class is also admissible but ‘normalized’ in the level of arithmetic divisor classes using the Faltings heights. Our approach is an explicit alternative of S. Zhang’s. In some applications, an explicit modular generating series as our (1.2) is necessary. For example, W. Zhang’s proof of the arithmetic fundamental lemma [Reference ZhangZha21a] used the explicit result of [Reference Bruinier, Howard, Kudla, Rapoport and YangBHK+20a].
$\mathsf {L}$
-lifting of a divisor class is also admissible but ‘normalized’ in the level of arithmetic divisor classes using the Faltings heights. Our approach is an explicit alternative of S. Zhang’s. In some applications, an explicit modular generating series as our (1.2) is necessary. For example, W. Zhang’s proof of the arithmetic fundamental lemma [Reference ZhangZha21a] used the explicit result of [Reference Bruinier, Howard, Kudla, Rapoport and YangBHK+20a].
The main ingredient in the proof of our main result is an arithmetic mixed Siegel-Weil formula, which identifies the arithmetic intersection between the generating series (1.2) with a CM 1-cycle on
![]() ${\mathcal {X}}$
(associated to a 1-dimensional hermitian subspace of V) and an explicit modular form constructed from theta series and (derivatives of) Eisenstein series.
${\mathcal {X}}$
(associated to a 1-dimensional hermitian subspace of V) and an explicit modular form constructed from theta series and (derivatives of) Eisenstein series.
Arithmetic mixed Siegel-Weil formulas appeared in the literature in different contexts. The first one appeared in the work of Gross and Zagier [Reference Gross and ZagierGZ86, p 233, (9.3)] for generating series of Hecke operators on the square of a modular curve, and implies their celebrated formula relating heights of heegner points and derivatives of L-functions. This arithmetic mixed Siegel-Weil formula was partially generalized to quaternionic Shimura curves over totally real fields in the work of Yuan, S. Zhang and W. Zhang [Reference Yuan, Zhang and ZhangYZZ13, 1.5.6] on the general Gross-Zagier formula. For certain orthogonal Shimura varieties over
![]() ${\mathbb {Q}}$
, an arithmetic mixed Siegel-Weil formula was conjectured by Bruinier and Yang [Reference Bruinier and YangBY09, Conjecture 1.3]. Its analog for unitary Shimura varieties over imaginary quadratic fields with certain self-dual lattice level structures was proved by Bruinier, Howard and Yang [Reference Bruinier, Howard and YangBHY15, Theorem C].
${\mathbb {Q}}$
, an arithmetic mixed Siegel-Weil formula was conjectured by Bruinier and Yang [Reference Bruinier and YangBY09, Conjecture 1.3]. Its analog for unitary Shimura varieties over imaginary quadratic fields with certain self-dual lattice level structures was proved by Bruinier, Howard and Yang [Reference Bruinier, Howard and YangBHY15, Theorem C].
In the rest of this introduction, we first state our main result in more detail. Then we discuss its proof. Finally, we mention two non-holomorphic modular variants of (1.2).
1.1 Main result
To state our main result, we need some preliminaries.
1.1.1 Admissible divisors
Let E be a number field,
![]() ${\mathcal {X}}$
a regular scheme (or more generally Deligne-Mumford stack) proper flat over
${\mathcal {X}}$
a regular scheme (or more generally Deligne-Mumford stack) proper flat over
![]() $\operatorname {\mathrm {Spec}} {\mathcal {O}}_E$
and
$\operatorname {\mathrm {Spec}} {\mathcal {O}}_E$
and
![]() $\overline {\mathcal {L}}=({\mathcal {L}},\|\cdot \|)$
an ample hermitian line bundle on
$\overline {\mathcal {L}}=({\mathcal {L}},\|\cdot \|)$
an ample hermitian line bundle on
![]() ${\mathcal {X}}$
. At each infinite place v of E, equip the complex manifold
${\mathcal {X}}$
. At each infinite place v of E, equip the complex manifold
![]() $ {\mathcal {X}}_{E_v} $
with the Kähler form that is the curvature form
$ {\mathcal {X}}_{E_v} $
with the Kähler form that is the curvature form
![]() ${\mathrm {curv}}(\overline {\mathcal {L}}_{E_v})$
. First, a Green function is admissible (introduced by Gillet and Soulé [Reference Gillet and SouléGS90, 5.1] following Arakelov [Reference ArakelovAra74]) if its curvature form
${\mathrm {curv}}(\overline {\mathcal {L}}_{E_v})$
. First, a Green function is admissible (introduced by Gillet and Soulé [Reference Gillet and SouléGS90, 5.1] following Arakelov [Reference ArakelovAra74]) if its curvature form
![]() $\alpha $
is harmonic; equivalently, on each connected component of
$\alpha $
is harmonic; equivalently, on each connected component of
![]() ${\mathcal {X}}_{E_v}$
,
${\mathcal {X}}_{E_v}$
,
![]() ${\mathrm {curv}}(\overline {\mathcal {L}}_{E_v})^{n-1}\wedge \alpha $
is proportional to
${\mathrm {curv}}(\overline {\mathcal {L}}_{E_v})^{n-1}\wedge \alpha $
is proportional to
![]() ${\mathrm {curv}}(\overline {\mathcal {L}}_{E_v})^{n}$
, where
${\mathrm {curv}}(\overline {\mathcal {L}}_{E_v})^{n}$
, where
![]() $n=\dim {\mathcal {X}}_{E_v}$
. It is further normalized if on each connected component of
$n=\dim {\mathcal {X}}_{E_v}$
. It is further normalized if on each connected component of
![]() ${\mathcal {X}}_{E_v}$
, its pairing with (i.e., integration against)
${\mathcal {X}}_{E_v}$
, its pairing with (i.e., integration against)
![]() ${\mathrm {curv}}(\overline {\mathcal {L}}_{E_v})^{n}$
is 0. Second, at each finite place v, a divisor Y on
${\mathrm {curv}}(\overline {\mathcal {L}}_{E_v})^{n}$
is 0. Second, at each finite place v, a divisor Y on
![]() ${\mathcal {X}}_{ {\mathcal {O}}_{E_v}}$
is admissible if it has ‘harmonic curvature’ with respect to
${\mathcal {X}}_{ {\mathcal {O}}_{E_v}}$
is admissible if it has ‘harmonic curvature’ with respect to
![]() $\overline {\mathcal {L}}_{ {\mathcal {O}}_{E_v}}$
, in the sense that on each connected component of
$\overline {\mathcal {L}}_{ {\mathcal {O}}_{E_v}}$
, in the sense that on each connected component of
![]() ${\mathcal {X}}_{{\mathcal {O}}_{E_v}}$
, the linear form on the space of vertical divisors defined by intersecting with
${\mathcal {X}}_{{\mathcal {O}}_{E_v}}$
, the linear form on the space of vertical divisors defined by intersecting with
![]() $Y\cdot c_1( {\mathcal {L}}_{ {\mathcal {O}}_{E_v}})^{n-1}$
is proportional to the linear form defined by intersecting with
$Y\cdot c_1( {\mathcal {L}}_{ {\mathcal {O}}_{E_v}})^{n-1}$
is proportional to the linear form defined by intersecting with
![]() $ c_1( {\mathcal {L}}_{ {\mathcal {O}}_{E_v}})^{n}$
. We further call Y normalized if its vertical part has intersection pairing 0 with
$ c_1( {\mathcal {L}}_{ {\mathcal {O}}_{E_v}})^{n}$
. We further call Y normalized if its vertical part has intersection pairing 0 with
![]() $c_1({\mathcal {L}})^{n}$
. Finally, an arithmetic divisor on
$c_1({\mathcal {L}})^{n}$
. Finally, an arithmetic divisor on
![]() ${\mathcal {X}}$
is (normalized) admissible if it is (normalized) admissible at every finite place and its Green function is (normalized) admissible. For a divisor Z on
${\mathcal {X}}$
is (normalized) admissible if it is (normalized) admissible at every finite place and its Green function is (normalized) admissible. For a divisor Z on
![]() ${\mathcal {X}}_E $
, we have the unique normalized admissible extension
${\mathcal {X}}_E $
, we have the unique normalized admissible extension
![]() $Z^{\overline {\mathcal {L}}}$
on
$Z^{\overline {\mathcal {L}}}$
on
![]() ${\mathcal {X}}$
(called the Arakelov lifting of Z in [Reference ZhangZha20]).
${\mathcal {X}}$
(called the Arakelov lifting of Z in [Reference ZhangZha20]).
Let
![]() $\widehat {\mathrm {Ch}}_{{\overline {\mathcal {L}}},{\mathbb {C}}} ^1({\mathcal {X}}) $
be the space of admissible arithmetic divisors with
$\widehat {\mathrm {Ch}}_{{\overline {\mathcal {L}}},{\mathbb {C}}} ^1({\mathcal {X}}) $
be the space of admissible arithmetic divisors with
![]() ${\mathbb {C}}$
-coefficients, modulo the
${\mathbb {C}}$
-coefficients, modulo the
![]() ${\mathbb {C}}$
-span of the principal ones. If
${\mathbb {C}}$
-span of the principal ones. If
![]() ${\mathcal {X}}$
is connected, then the natural map
${\mathcal {X}}$
is connected, then the natural map
is surjective and has a 1-dimensional kernel. It is the pullback of
![]() $ \widehat {\mathrm {Ch}}_{\mathbb {C}}^1\left ( \operatorname {\mathrm {Spec}} {\mathcal {O}}_{E} \right ){\ \simeq \ } {\mathbb {C}}$
, where the isomorphism is by taking degrees. Then the
$ \widehat {\mathrm {Ch}}_{\mathbb {C}}^1\left ( \operatorname {\mathrm {Spec}} {\mathcal {O}}_{E} \right ){\ \simeq \ } {\mathbb {C}}$
, where the isomorphism is by taking degrees. Then the
![]() ${\mathfrak {e}}_t\in {\mathbb {C}}\subset \widehat {\mathrm {Ch}}_{{\overline {\mathcal {L}}},{\mathbb {C}}}^1({\mathcal {X}})$
in (1.2) is understood in this way.
${\mathfrak {e}}_t\in {\mathbb {C}}\subset \widehat {\mathrm {Ch}}_{{\overline {\mathcal {L}}},{\mathbb {C}}}^1({\mathcal {X}})$
in (1.2) is understood in this way.
1.1.2 Shimura varieties and integral models
Let
![]() $V({\mathbb {A}}_E^\infty )$
be the space of finite adelic points of V. For an open compact subgroup
$V({\mathbb {A}}_E^\infty )$
be the space of finite adelic points of V. For an open compact subgroup
![]() $K\subset U(V({\mathbb {A}}_E^\infty ))$
, we have a
$K\subset U(V({\mathbb {A}}_E^\infty ))$
, we have a
![]() $U(V)$
-Shimura variety
$U(V)$
-Shimura variety
![]() ${\mathrm {Sh}}(V)_K$
(which could be stacky) of level K defined over E. We assume that
${\mathrm {Sh}}(V)_K$
(which could be stacky) of level K defined over E. We assume that
![]() ${\mathrm {Sh}}(V)_K$
is proper; equivalently,
${\mathrm {Sh}}(V)_K$
is proper; equivalently,
![]() $F\neq {\mathbb {Q}}$
or
$F\neq {\mathbb {Q}}$
or
![]() $F={\mathbb {Q}},n=1$
and
$F={\mathbb {Q}},n=1$
and
![]() $V $
is nonsplit at some finite place.
$V $
is nonsplit at some finite place.
Let
![]() $\Lambda \subset V({\mathbb {A}}_E^\infty )$
be a hermitian lattice with stabilizer
$\Lambda \subset V({\mathbb {A}}_E^\infty )$
be a hermitian lattice with stabilizer
![]() $K_\Lambda \subset U(V({\mathbb {A}}_E^\infty ))$
. Let
$K_\Lambda \subset U(V({\mathbb {A}}_E^\infty ))$
. Let
![]() $K\subset K_\Lambda $
such that
$K\subset K_\Lambda $
such that
![]() $K_v=K_{\Lambda ,v}$
for v nonsplit in E. We construct a regular integral model
$K_v=K_{\Lambda ,v}$
for v nonsplit in E. We construct a regular integral model
![]() ${\mathcal {X}}_E$
of
${\mathcal {X}}_E$
of
![]() ${\mathrm {Sh}}(V)_K$
proper flat over
${\mathrm {Sh}}(V)_K$
proper flat over
![]() ${\mathcal {O}}_E$
under some conditions on
${\mathcal {O}}_E$
under some conditions on
![]() $E,F,\Lambda $
(Theorem 4.4.4). Our construction is largely suggested by Liu.
$E,F,\Lambda $
(Theorem 4.4.4). Our construction is largely suggested by Liu.
We have two constructions according to different conditions on
![]() $E,F$
. First, assume that
$E,F$
. First, assume that
![]() $E/{\mathbb {Q}}$
is tamely ramified. We have the normalization in
$E/{\mathbb {Q}}$
is tamely ramified. We have the normalization in
![]() ${\mathrm {Sh}}(V)_K$
of the flat model of
${\mathrm {Sh}}(V)_K$
of the flat model of
![]() ${\mathrm {Sh}}(V)_{K_\Lambda }$
of Kisin [Reference KisinKis10], Kisin and Pappas [Reference Kisin and PappasKP18] over
${\mathrm {Sh}}(V)_{K_\Lambda }$
of Kisin [Reference KisinKis10], Kisin and Pappas [Reference Kisin and PappasKP18] over
![]() ${\mathcal {O}}_{E,(v)}$
, for every finite place v. We want to show their regularity and glue them to obtain a regular integral model
${\mathcal {O}}_{E,(v)}$
, for every finite place v. We want to show their regularity and glue them to obtain a regular integral model
![]() ${\mathcal {X}}_K$
over
${\mathcal {X}}_K$
over
![]() ${\mathcal {O}}_E$
. For this purpose, we use a certain regular PEL moduli space for a group closely related to
${\mathcal {O}}_E$
. For this purpose, we use a certain regular PEL moduli space for a group closely related to
![]() $U(V)$
over the ring of integers of a reflex field
$U(V)$
over the ring of integers of a reflex field
![]() $E'/E$
, constructed by Rapoport, Smithling and W. Zhang [Reference Rapoport, Smithling and ZhangRSZ20]. Expectably, the moduli space and our integral models are closely related, as shown by Xu in Appendix B (the proof for the general level at split places was suggested by Liu). Second, replacing the tameness assumption by the assumption that
$E'/E$
, constructed by Rapoport, Smithling and W. Zhang [Reference Rapoport, Smithling and ZhangRSZ20]. Expectably, the moduli space and our integral models are closely related, as shown by Xu in Appendix B (the proof for the general level at split places was suggested by Liu). Second, replacing the tameness assumption by the assumption that
![]() $E/{\mathbb {Q}}$
is Galois or
$E/{\mathbb {Q}}$
is Galois or
![]() $E $
is the composition of F with some imaginary quadratic field, which implies that
$E $
is the composition of F with some imaginary quadratic field, which implies that
![]() $E'=E$
, we can construct a regular integral model over
$E'=E$
, we can construct a regular integral model over
![]() ${\mathcal {O}}_{E,(v)}$
from the above moduli space, following [Reference Liu, Tian, Xiao, Zhang and ZhuLTX+22]. Moreover, if both the tameness assumption and the replacement hold, the two constructions give the same model.
${\mathcal {O}}_{E,(v)}$
from the above moduli space, following [Reference Liu, Tian, Xiao, Zhang and ZhuLTX+22]. Moreover, if both the tameness assumption and the replacement hold, the two constructions give the same model.
We remark that by our choice of
![]() $\Lambda $
,
$\Lambda $
,
![]() ${\mathcal {X}}_{K_\Lambda }$
is smooth over
${\mathcal {X}}_{K_\Lambda }$
is smooth over
![]() ${\mathcal {O}}_E$
so that the finite part of the normalized admissible extension of a divisor on
${\mathcal {O}}_E$
so that the finite part of the normalized admissible extension of a divisor on
![]() ${\mathrm {Sh}}(V)_{K_\Lambda }$
is the Zariski closure on
${\mathrm {Sh}}(V)_{K_\Lambda }$
is the Zariski closure on
![]() ${\mathcal {X}}_{K_\Lambda }$
.
${\mathcal {X}}_{K_\Lambda }$
.
1.1.3 Hodge bundles and CM cycles
Let
![]() ${\mathcal {L}}_{K_\Lambda }$
be an arbitrarily line bundle on
${\mathcal {L}}_{K_\Lambda }$
be an arbitrarily line bundle on
![]() ${\mathcal {X}}_{K_\Lambda }$
extending the Hodge (line) bundle on
${\mathcal {X}}_{K_\Lambda }$
extending the Hodge (line) bundle on
![]() ${\mathrm {Sh}}(V)_{K_\Lambda }$
. Let
${\mathrm {Sh}}(V)_{K_\Lambda }$
. Let
![]() ${\mathcal {L}}_K$
, denoted by
${\mathcal {L}}_K$
, denoted by
![]() ${\mathcal {L}}$
if K is clear from the context, be the pullback of
${\mathcal {L}}$
if K is clear from the context, be the pullback of
![]() ${\mathcal {L}}_{K_\Lambda }$
to
${\mathcal {L}}_{K_\Lambda }$
to
![]() ${\mathcal {X}}_K$
. Let
${\mathcal {X}}_K$
. Let
![]() $\overline {\mathcal {L}}=({\mathcal {L}},\|\cdot \|)$
, where
$\overline {\mathcal {L}}=({\mathcal {L}},\|\cdot \|)$
, where
![]() $\|\cdot \|$
is the descent of the natural hermitian metric on the hermitian symmetric domain uniformizing
$\|\cdot \|$
is the descent of the natural hermitian metric on the hermitian symmetric domain uniformizing
![]() ${\mathrm {Sh}}(V)_K$
. It is compatible under pullbacks as K shrinks. Changing
${\mathrm {Sh}}(V)_K$
. It is compatible under pullbacks as K shrinks. Changing
![]() $\overline {\mathcal {L}}$
,
$\overline {\mathcal {L}}$
,
![]() $c_1(\overline {\mathcal {L}})\in \widehat {\mathrm {Ch}}_{\mathbb {C}}^1\left ( {\mathcal {X}} \right )$
changes by an element in the pullback of
$c_1(\overline {\mathcal {L}})\in \widehat {\mathrm {Ch}}_{\mathbb {C}}^1\left ( {\mathcal {X}} \right )$
changes by an element in the pullback of
![]() $ \widehat {\mathrm {Ch}}_{\mathbb {C}}^1\left ( \operatorname {\mathrm {Spec}} {\mathcal {O}}_{E}\right ) $
. (It is a special feature due to the smoothness of
$ \widehat {\mathrm {Ch}}_{\mathbb {C}}^1\left ( \operatorname {\mathrm {Spec}} {\mathcal {O}}_{E}\right ) $
. (It is a special feature due to the smoothness of
![]() ${\mathcal {X}}_{K_\Lambda }$
over
${\mathcal {X}}_{K_\Lambda }$
over
![]() ${\mathcal {O}}_E$
.) In particular, changing
${\mathcal {O}}_E$
.) In particular, changing
![]() $\overline {\mathcal {L}}$
will not change the generating series (1.2). However, this fact does not play a role in our proof.
$\overline {\mathcal {L}}$
will not change the generating series (1.2). However, this fact does not play a role in our proof.
For a 1-dimensional hermitian subspace
![]() $ W\subset V$
, we have an associated 0-dimensional Shimura subvariety of
$ W\subset V$
, we have an associated 0-dimensional Shimura subvariety of
![]() ${\mathrm {Sh}}(V)$
. On
${\mathrm {Sh}}(V)$
. On
![]() ${\mathcal {X}}_{K_\Lambda }$
, let the 1-cycle
${\mathcal {X}}_{K_\Lambda }$
, let the 1-cycle
![]() ${\mathcal {P}}_{K_\Lambda }$
be its Zariski closure, divided by the degree of its genetic fiber (so that
${\mathcal {P}}_{K_\Lambda }$
be its Zariski closure, divided by the degree of its genetic fiber (so that
![]() $\deg {\mathcal {P}}_{K_\Lambda ,E}=1$
). Then
$\deg {\mathcal {P}}_{K_\Lambda ,E}=1$
). Then
![]() ${\mathcal {P}}_{K_\Lambda }$
is independent of the choice of this subspace (Proposition 5.1.9). We do not need CM cycles at other levels.
${\mathcal {P}}_{K_\Lambda }$
is independent of the choice of this subspace (Proposition 5.1.9). We do not need CM cycles at other levels.
1.1.4 Generating series
We start with the non-constant terms of the generating series (1.2).
For
![]() $x\in {\mathbb {V}}^{\infty }$
with norm in
$x\in {\mathbb {V}}^{\infty }$
with norm in
![]() $ F_{>0}$
, the orthogonal complement of
$ F_{>0}$
, the orthogonal complement of
![]() ${\mathbb {A}}_E ^\infty x $
in
${\mathbb {A}}_E ^\infty x $
in
![]() ${\mathbb {V}}^\infty $
defines a (shifted) unitary Shimura subvariety
${\mathbb {V}}^\infty $
defines a (shifted) unitary Shimura subvariety
![]() $Z(x)_K$
of
$Z(x)_K$
of
![]() ${\mathrm {Sh}}(V)_K$
of codimension 1. For
${\mathrm {Sh}}(V)_K$
of codimension 1. For
![]() $t\in F_{>0}$
and a Schwartz function
$t\in F_{>0}$
and a Schwartz function
![]() $\phi $
on
$\phi $
on
![]() $V({\mathbb {A}}_E^\infty )$
invariant by K, the weighted special divisor is
$V({\mathbb {A}}_E^\infty )$
invariant by K, the weighted special divisor is
It is compatible under pullbacks as K shrinks.
Now we define
![]() ${\mathfrak {e}}_t$
. Let
${\mathfrak {e}}_t$
. Let
![]() $E(s,\tau )$
be the Siegel-Eisenstein series on
$E(s,\tau )$
be the Siegel-Eisenstein series on
![]() ${\mathcal {H}}^{[F:{\mathbb {Q}}]}$
associated to
${\mathcal {H}}^{[F:{\mathbb {Q}}]}$
associated to
![]() $\phi $
. Its t-th Whittaker function
$\phi $
. Its t-th Whittaker function
![]() $E_t(s,\tau )$
has a decomposition
$E_t(s,\tau )$
has a decomposition
into the infinite component and the finite component. Here, we choose the s-variable so that
![]() $E(0,\tau )$
is holomorphic of weight
$E(0,\tau )$
is holomorphic of weight
![]() $n+1$
, equivalently, the infinite component
$n+1$
, equivalently, the infinite component
![]() $W_{\infty ,t} (0, \tau )$
is a multiple of
$W_{\infty ,t} (0, \tau )$
is a multiple of
![]() $q^t$
. (Note that
$q^t$
. (Note that
![]() $s=0$
is the critical point for the Siegel-Weil formula, but not the center for the functional equation.) The t-th Fourier coefficient of
$s=0$
is the critical point for the Siegel-Weil formula, but not the center for the functional equation.) The t-th Fourier coefficient of
![]() $E(0,\tau )$
is
$E(0,\tau )$
is
![]() $\frac {E_t(0,\tau )} {q^t}$
. Define
$\frac {E_t(0,\tau )} {q^t}$
. Define
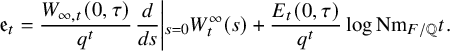 $$ \begin{align}{\mathfrak{e}}_t=\frac{ W_{\infty,t} (0, \tau ) } {q^t}\left.\frac{d}{ds}\right|{}_{s=0}W^\infty_{t} (s )+\frac{E_t(0,\tau) } {q^t}\log {\mathrm{Nm}}_{F/{\mathbb{Q}}}t.\end{align} $$
$$ \begin{align}{\mathfrak{e}}_t=\frac{ W_{\infty,t} (0, \tau ) } {q^t}\left.\frac{d}{ds}\right|{}_{s=0}W^\infty_{t} (s )+\frac{E_t(0,\tau) } {q^t}\log {\mathrm{Nm}}_{F/{\mathbb{Q}}}t.\end{align} $$
Then
![]() ${\mathfrak {e}}_t$
is independent of
${\mathfrak {e}}_t$
is independent of
![]() $\tau $
.
$\tau $
.
We introduce a number that will appear in the constant term of the generating series. Let
where
![]() ${\mathrm {Disc}}_E\in {\mathbb {Z}}$
is the discriminant of
${\mathrm {Disc}}_E\in {\mathbb {Z}}$
is the discriminant of
![]() $E/{\mathbb {Q}}$
, and
$E/{\mathbb {Q}}$
, and
![]() ${\mathfrak {b}} =-({1+\log 4})$
when
${\mathfrak {b}} =-({1+\log 4})$
when
![]() $ n=1$
and more complicated in general. See (3.30) and the remarking following it. We hope to compute the Faltings height
$ n=1$
and more complicated in general. See (3.30) and the remarking following it. We hope to compute the Faltings height
![]() $c_1(\overline {\mathcal {L}}_{K_\Lambda })\cdot {\mathcal {P}}_{ K_\Lambda }$
based on [Reference YuanYZ18] in a future work. And we expect cancellation among the terms defining
$c_1(\overline {\mathcal {L}}_{K_\Lambda })\cdot {\mathcal {P}}_{ K_\Lambda }$
based on [Reference YuanYZ18] in a future work. And we expect cancellation among the terms defining
![]() ${\mathfrak {a}}$
so that the definition of
${\mathfrak {a}}$
so that the definition of
![]() ${\mathfrak {a}}$
will be elementary and transparent.
${\mathfrak {a}}$
will be elementary and transparent.
Theorem 1.1.1 (Theorem 4.4.21, (4.28)).
If
![]() $\phi _v=1_{\Lambda _v}$
at ramified places, the generating series (1.2) with the constant term being
$\phi _v=1_{\Lambda _v}$
at ramified places, the generating series (1.2) with the constant term being
![]() $\phi (0)\left ( c_1(\overline {\mathcal {L}}^\vee )+{\mathfrak {a}}\right )$
is a holomorphic modular form on
$\phi (0)\left ( c_1(\overline {\mathcal {L}}^\vee )+{\mathfrak {a}}\right )$
is a holomorphic modular form on
![]() ${\mathcal {H}}^{[F:{\mathbb {Q}}]}$
of parallel weight
${\mathcal {H}}^{[F:{\mathbb {Q}}]}$
of parallel weight
![]() $n+1$
valued in
$n+1$
valued in
![]() $\widehat {\mathrm {Ch}}^{1}_{{\overline {\mathcal {L}}},{\mathbb {C}}}( {\mathcal {X}}_K)$
. Here, we understand
$\widehat {\mathrm {Ch}}^{1}_{{\overline {\mathcal {L}}},{\mathbb {C}}}( {\mathcal {X}}_K)$
. Here, we understand
![]() ${\mathfrak {a}},{\mathfrak {e}}_t\in {\mathbb {C}}\subset \widehat {\mathrm {Ch}}_{{\overline {\mathcal {L}}},{\mathbb {C}}}^1({\mathcal {X}}_K)$
as discussed below (1.3).
${\mathfrak {a}},{\mathfrak {e}}_t\in {\mathbb {C}}\subset \widehat {\mathrm {Ch}}_{{\overline {\mathcal {L}}},{\mathbb {C}}}^1({\mathcal {X}}_K)$
as discussed below (1.3).
Since the formation of normalized admissible extension is compatible under flat pullbacks, the generating series (1.2) is compatible under pullbacks as K shrinks.
We note that the sum of the normalized admissible Green function for
![]() $Z_t$
and
$Z_t$
and
![]() ${\mathfrak {e}}_t$
recovers the Bruinier-Borcherds Green function used by Bruinier, Howard, Kudla, Rapoport and Yang [Reference Bruinier, Howard, Kudla, Rapoport and YangBHK+20a] for
${\mathfrak {e}}_t$
recovers the Bruinier-Borcherds Green function used by Bruinier, Howard, Kudla, Rapoport and Yang [Reference Bruinier, Howard, Kudla, Rapoport and YangBHK+20a] for
![]() $F={\mathbb {Q}}$
, so that Theorem 1.1.1 is an analog of [Reference Bruinier, Howard, Kudla, Rapoport and YangBHK+20a, Theorem B]. Though the Bruinier-Borcherds construction can not be directly extended to a general F (as explained to us by Bruinier), our construction could be considered as an alternative generalization.
$F={\mathbb {Q}}$
, so that Theorem 1.1.1 is an analog of [Reference Bruinier, Howard, Kudla, Rapoport and YangBHK+20a, Theorem B]. Though the Bruinier-Borcherds construction can not be directly extended to a general F (as explained to us by Bruinier), our construction could be considered as an alternative generalization.
1.2 Sketch of the proof
Now we discuss the proof of Theorem 1.1.1. By the 1-dimensionality of the kernel of (1.3) and the modularity of the generic fiber of the generating series (1.2) (i.e., the generating series (1.1)), the modularity of (1.2) is equivalent to the modularity of the generating series of arithmetic intersection numbers between
![]() $[Z_t^{\overline {\mathcal {L}}}]+{\mathfrak {e}}_t $
’s and a 1-cycle on
$[Z_t^{\overline {\mathcal {L}}}]+{\mathfrak {e}}_t $
’s and a 1-cycle on
![]() ${\mathcal {X}}_K$
whose generic fiber has nonzero degree. (A similar strategy was used in [Reference KudlaKud03, Reference Kudla, Rapoport and YangKRY06].)
${\mathcal {X}}_K$
whose generic fiber has nonzero degree. (A similar strategy was used in [Reference KudlaKud03, Reference Kudla, Rapoport and YangKRY06].)
Assume that
![]() $K=K_\Lambda $
for simplicity and let us take the 1-cycle to be
$K=K_\Lambda $
for simplicity and let us take the 1-cycle to be
![]() ${\mathcal {P}}_{K_\Lambda }$
. Then this generating series of arithmetic intersection numbers
${\mathcal {P}}_{K_\Lambda }$
. Then this generating series of arithmetic intersection numbers
![]() $ \left ( [Z_t^{\overline {\mathcal {L}}}]+{\mathfrak {e}}_t\right )\cdot {\mathcal {P}}_{K_\Lambda }$
is the arithmetic analog of the integration of a theta series of
$ \left ( [Z_t^{\overline {\mathcal {L}}}]+{\mathfrak {e}}_t\right )\cdot {\mathcal {P}}_{K_\Lambda }$
is the arithmetic analog of the integration of a theta series of
![]() $U(1,1)\times U(V) $
along
$U(1,1)\times U(V) $
along
![]() $U(W)\backslash U(W({\mathbb {A}}_E))$
, where
$U(W)\backslash U(W({\mathbb {A}}_E))$
, where
![]() $W\subset V$
is the 1-dimensional hermitian subspace defining
$W\subset V$
is the 1-dimensional hermitian subspace defining
![]() ${\mathcal {P}}_{K_\Lambda }$
. By the Siegel-Weil formula for
${\mathcal {P}}_{K_\Lambda }$
. By the Siegel-Weil formula for
![]() $U(1,1)\times U(W) $
, this integration is a theta-Eisenstein series (i.e., a linear combination of products of theta series and Eisenstein series).Footnote
1
$U(1,1)\times U(W) $
, this integration is a theta-Eisenstein series (i.e., a linear combination of products of theta series and Eisenstein series).Footnote
1
Let
![]() ${\theta E}(s,\tau )$
be the theta-Eisenstein series associated to
${\theta E}(s,\tau )$
be the theta-Eisenstein series associated to
![]() $\phi $
and let
$\phi $
and let
![]() ${\theta E}_{t}(s,\tau )$
be its t-th Whittaker coefficient. We study the holomorphic projections of
${\theta E}_{t}(s,\tau )$
be its t-th Whittaker coefficient. We study the holomorphic projections of
![]() ${\theta E}'(0,\tau )$
in order to match the above generating series of arithmetic intersection numbers, which is supposed to be holomorphic in view of our goal (Theorem 1.1.1). A priori, there are two holomorphic projections. One is the projection of
${\theta E}'(0,\tau )$
in order to match the above generating series of arithmetic intersection numbers, which is supposed to be holomorphic in view of our goal (Theorem 1.1.1). A priori, there are two holomorphic projections. One is the projection of
![]() ${\theta E}'(0,\tau )$
to the space of holomorphic cusp forms, which we call ‘cuspidal holomorphic projection’ and denote by
${\theta E}'(0,\tau )$
to the space of holomorphic cusp forms, which we call ‘cuspidal holomorphic projection’ and denote by
![]() ${\theta E}^{\prime }_{{\mathrm {chol}}}(0,\tau )$
. Let
${\theta E}^{\prime }_{{\mathrm {chol}}}(0,\tau )$
. Let
![]() ${\theta E}^{\prime }_{{\mathrm {chol}},t}(0,\tau )$
be its t-th Whittaker coefficient. The other is for
${\theta E}^{\prime }_{{\mathrm {chol}},t}(0,\tau )$
be its t-th Whittaker coefficient. The other is for
![]() ${\theta E}_{t}'(0,\tau )$
and purely at infinite places, which we call ‘quasi-holomorphic projection’ following [Reference Yuan, Zhang and ZhangYZZ13] and denote by
${\theta E}_{t}'(0,\tau )$
and purely at infinite places, which we call ‘quasi-holomorphic projection’ following [Reference Yuan, Zhang and ZhangYZZ13] and denote by
![]() ${\theta E}_{t,{\mathrm {qhol}}}'(0,\tau )$
. However, neither of them could be the desired match, since
${\theta E}_{t,{\mathrm {qhol}}}'(0,\tau )$
. However, neither of them could be the desired match, since
![]() ${\theta E}^{\prime }_{{\mathrm {chol}}}(0,\tau )$
has no constant term and
${\theta E}^{\prime }_{{\mathrm {chol}}}(0,\tau )$
has no constant term and
![]() ${\theta E}_{t,{\mathrm {qhol}}}'(0,\tau )$
is (in general) not the t-th Whittaker coefficient of a modular form. Thus, we compute their difference and find that
${\theta E}_{t,{\mathrm {qhol}}}'(0,\tau )$
is (in general) not the t-th Whittaker coefficient of a modular form. Thus, we compute their difference and find that
![]() ${\theta E}_{t,{\mathrm {qhol}}}'(0,\tau )-{\theta E}^{\prime }_{{\mathrm {chol}},t}(0,\tau )$
is the sum of
${\theta E}_{t,{\mathrm {qhol}}}'(0,\tau )-{\theta E}^{\prime }_{{\mathrm {chol}},t}(0,\tau )$
is the sum of
![]() $2{\mathfrak {e}}_t q^t$
and the t-th Whittaker coefficient of a holomorphic Eisenstein series. See (3.31). In the case
$2{\mathfrak {e}}_t q^t$
and the t-th Whittaker coefficient of a holomorphic Eisenstein series. See (3.31). In the case
![]() $n=1$
, the computations of holomorphic projections have their roots in [Reference Gross and ZagierGZ86]. The strategy we follow is outlined in [Reference Yuan, Zhang and ZhangYZZ13, 6.4.3], and the explicit computation was done by Yuan [Reference YuanYua22]. We largely follow [Reference YuanYua22].
$n=1$
, the computations of holomorphic projections have their roots in [Reference Gross and ZagierGZ86]. The strategy we follow is outlined in [Reference Yuan, Zhang and ZhangYZZ13, 6.4.3], and the explicit computation was done by Yuan [Reference YuanYua22]. We largely follow [Reference YuanYua22].
Let f be the sum of
![]() $-\frac {1}{2}{\theta E}^{\prime }_{{\mathrm {chol}}}(0,\tau )$
and the negative of the holomorphic Eisenstein series in the last sentence. Then f is a holomorphic modular form on
$-\frac {1}{2}{\theta E}^{\prime }_{{\mathrm {chol}}}(0,\tau )$
and the negative of the holomorphic Eisenstein series in the last sentence. Then f is a holomorphic modular form on
![]() ${\mathcal {H}}^{[F:{\mathbb {Q}}]}$
of parallel weight
${\mathcal {H}}^{[F:{\mathbb {Q}}]}$
of parallel weight
![]() $n+1$
. The t-th Whittaker coefficient of f is
$n+1$
. The t-th Whittaker coefficient of f is
![]() $ -\frac {1}{2}\frac {{\theta E}_{t,{\mathrm {qhol}}}'(0,\tau ) }{q^t}+{\mathfrak {e}}_t $
.
$ -\frac {1}{2}\frac {{\theta E}_{t,{\mathrm {qhol}}}'(0,\tau ) }{q^t}+{\mathfrak {e}}_t $
.
In 5.2.1, we define some explicit Schwartz functions
![]() $\phi _v'$
, for every ramified place v, which are ‘error functions’ due to ramification. Let g be sum of the theta-Eisenstein series associated to
$\phi _v'$
, for every ramified place v, which are ‘error functions’ due to ramification. Let g be sum of the theta-Eisenstein series associated to
![]() $\phi ^v\phi _v'$
’s. The following is our arithmetic mixed Siegel-Weil formula (Theorem 5.2.5) in the case
$\phi ^v\phi _v'$
’s. The following is our arithmetic mixed Siegel-Weil formula (Theorem 5.2.5) in the case
![]() $K=K_\Lambda $
.
$K=K_\Lambda $
.
Theorem 1.2.1. Assume that
![]() $\phi _v=1_{\Lambda _v}$
for v nonsplit in E. The arithmetic intersection number
$\phi _v=1_{\Lambda _v}$
for v nonsplit in E. The arithmetic intersection number
![]() $ \left ( [Z_t^{\overline {\mathcal {L}}}]+{\mathfrak {e}}_t\right )\cdot {\mathcal {P}}_{K_\Lambda }$
is the t-th Fourier coefficient of
$ \left ( [Z_t^{\overline {\mathcal {L}}}]+{\mathfrak {e}}_t\right )\cdot {\mathcal {P}}_{K_\Lambda }$
is the t-th Fourier coefficient of
![]() $f-g-\frac {1}{n}E(0,\tau )$
.
$f-g-\frac {1}{n}E(0,\tau )$
.
In Theorem 5.2.5 for a general K, we use the pullback of
![]() ${\mathcal {P}}_{K_\Lambda }$
to
${\mathcal {P}}_{K_\Lambda }$
to
![]() ${\mathcal {X}}_K$
, instead of natural CM cycles on
${\mathcal {X}}_K$
, instead of natural CM cycles on
![]() ${\mathcal {X}}_K$
, to simplify certain local computations. See Remark 5.2.6.
${\mathcal {X}}_K$
, to simplify certain local computations. See Remark 5.2.6.
We remind the reader that in Theorem 5.2.5, we actually use the automorphic Green function for
![]() $Z_t$
constructed by Bruinier [Reference BruinierBru02, Reference BruinierBru12] and Oda and Tsuzuki [Reference Oda and TsuzukiOT03] (for
$Z_t$
constructed by Bruinier [Reference BruinierBru02, Reference BruinierBru12] and Oda and Tsuzuki [Reference Oda and TsuzukiOT03] (for
![]() $n=1$
and
$n=1$
and
![]() $F={\mathbb {Q}}$
, it was well known and used by Gross and Zagier [Reference Gross and ZagierGZ86]). Its difference with the normalized admissible Green function is
$F={\mathbb {Q}}$
, it was well known and used by Gross and Zagier [Reference Gross and ZagierGZ86]). Its difference with the normalized admissible Green function is
![]() $\frac {1}{n}E_t(0,\tau )$
by Lemma 4.2.4 and the remark following it.
$\frac {1}{n}E_t(0,\tau )$
by Lemma 4.2.4 and the remark following it.
Let us remark on the innovation in proving the arithmetic mixed Siegel-Weil formula. We consider the difference of two CM cycles. The generic fiber of the difference has degree 0. Then the generating series of arithmetic intersection numbers is modular by the admissibility. (A similar observation was used in [Reference Mihatsch and ZhangMZ21] to generalize the arithmetic fundamental lemma. See also [Reference ZhangZha21b].) This modularity enables us to ‘switch CM cycles’ and thus avoid computing improper intersections directly. This idea is inspired by [Reference Yuan, Zhang and ZhangYZZ13] and [Reference ZhangZha21a].
1.3 Non-holomorphic variants
We obtain a non-holomorphic modular variant of the generating series (1.2), where the sum of the normalized admissible Green function for
![]() $Z_t$
and
$Z_t$
and
![]() ${\mathfrak {e}}_t$
is replaced by Kudla’s Green function [Reference KudlaKud97b]. See Theorem 4.4.24. This is an analog of [Reference Kudla, Rapoport and YangKRY06, Theorem A] [Reference Bruinier, Howard, Kudla, Rapoport and YangBHK+20a, Theorem 7.4.1]. Theorem 4.4.24 follows from Theorem 1.1.1, and the modularity of the differences between the generating series of two kinds of Green functions (Theorem 4.2.10). The latter (Theorem 4.2.10) is an analog of the main result of Ehlen and Sankaran [Reference Ehlen and SankaranES18] for
${\mathfrak {e}}_t$
is replaced by Kudla’s Green function [Reference KudlaKud97b]. See Theorem 4.4.24. This is an analog of [Reference Kudla, Rapoport and YangKRY06, Theorem A] [Reference Bruinier, Howard, Kudla, Rapoport and YangBHK+20a, Theorem 7.4.1]. Theorem 4.4.24 follows from Theorem 1.1.1, and the modularity of the differences between the generating series of two kinds of Green functions (Theorem 4.2.10). The latter (Theorem 4.2.10) is an analog of the main result of Ehlen and Sankaran [Reference Ehlen and SankaranES18] for
![]() $F={\mathbb {Q}}$
.
$F={\mathbb {Q}}$
.
Note that Kudla’s Green function is not admissible. We also obtain a non-holomorphic modular generating series with admissible Green functions (Theorem 4.4.21, (4.29)). This has not appeared in the literature yet, as far as we know.
2 Some notations and conventions
2.1
For a number field F, let
![]() ${\mathbb {A}}_F$
be the ring of adeles of F and
${\mathbb {A}}_F$
be the ring of adeles of F and
![]() ${\mathbb {A}}_F^\infty $
the ring of finite adeles of F. For a finite place v of a number field F, let
${\mathbb {A}}_F^\infty $
the ring of finite adeles of F. For a finite place v of a number field F, let
![]() $\varpi _{F_v}$
be a uniformizer of
$\varpi _{F_v}$
be a uniformizer of
![]() $F_v$
. Let
$F_v$
. Let
![]() $q_{F_v}$
be the cardinality of
$q_{F_v}$
be the cardinality of
![]() ${\mathcal {O}}_{F_v}/\varpi _{F_v}$
. The discrete valuation is
${\mathcal {O}}_{F_v}/\varpi _{F_v}$
. The discrete valuation is
![]() $v(\varpi _{F_v})=1$
and the absolute value
$v(\varpi _{F_v})=1$
and the absolute value
![]() $| \cdot |_{F_v}$
is
$| \cdot |_{F_v}$
is
![]() $|\varpi _v|_{F_v}=q_{F_v}^{-1}$
. For an infinite place, v is understood as a pair of complex embeddings. If v is real, the absolute value
$|\varpi _v|_{F_v}=q_{F_v}^{-1}$
. For an infinite place, v is understood as a pair of complex embeddings. If v is real, the absolute value
![]() $| \cdot |_{F_v}$
is the usual one; if v is complex, the absolute value
$| \cdot |_{F_v}$
is the usual one; if v is complex, the absolute value
![]() $| \cdot |_{F_v}$
is the square of the usual one. Their product is
$| \cdot |_{F_v}$
is the square of the usual one. Their product is
![]() $|\cdot |_{{\mathbb {A}}_F}$
. The symbol
$|\cdot |_{{\mathbb {A}}_F}$
. The symbol
![]() $|\cdot |$
without a subscript means the usual real or complex absolute value.
$|\cdot |$
without a subscript means the usual real or complex absolute value.
Below in this paper,
![]() $E/F$
is always a CM extension. Let
$E/F$
is always a CM extension. Let
![]() $\infty $
be the set of infinite places of F. Let
$\infty $
be the set of infinite places of F. Let
![]() $F_{>0}\subset F$
be the subset of totally positive elements. For a place v of F,
$F_{>0}\subset F$
be the subset of totally positive elements. For a place v of F,
![]() $E_v$
is understood as
$E_v$
is understood as
![]() $E\otimes _F F_v$
. The nontrivial Galois action will be denoted by
$E\otimes _F F_v$
. The nontrivial Galois action will be denoted by
![]() $x\mapsto \overline x$
, and the norm map
$x\mapsto \overline x$
, and the norm map
![]() ${\mathrm {Nm}}_{E/F}$
or its local version is abbreviated as
${\mathrm {Nm}}_{E/F}$
or its local version is abbreviated as
![]() ${\mathrm {Nm}}$
. Let
${\mathrm {Nm}}$
. Let
![]() $\eta $
be the associated quadratic Hecke character of
$\eta $
be the associated quadratic Hecke character of
![]() $ F^\times \backslash {\mathbb {A}}_F^\times $
via the class field theory.
$ F^\times \backslash {\mathbb {A}}_F^\times $
via the class field theory.
For a set of place S of F and a decomposable adelic object X over
![]() ${\mathbb {A}}_F$
, we use
${\mathbb {A}}_F$
, we use
![]() $X_S$
(resp.
$X_S$
(resp.
![]() $X^S$
) to denote the S-component (resp. component away from S) of X if the decomposition of X into the product of
$X^S$
) to denote the S-component (resp. component away from S) of X if the decomposition of X into the product of
![]() $X_S$
and
$X_S$
and
![]() $X^S$
is clear from the context. For example,
$X^S$
is clear from the context. For example,
![]() ${\mathbb {A}}_F={\mathbb {A}}_{F,S}{\mathbb {A}}_{F}^S$
and
${\mathbb {A}}_F={\mathbb {A}}_{F,S}{\mathbb {A}}_{F}^S$
and
![]() ${\mathbb {A}}_E={\mathbb {A}}_{E,S}{\mathbb {A}}_{E}^S$
by regarding
${\mathbb {A}}_E={\mathbb {A}}_{E,S}{\mathbb {A}}_{E}^S$
by regarding
![]() ${\mathbb {A}}_E$
as over
${\mathbb {A}}_E$
as over
![]() ${\mathbb {A}}_F$
. Here is another example which is ubiquitous in the paper: a function
${\mathbb {A}}_F$
. Here is another example which is ubiquitous in the paper: a function
![]() $\phi $
on the space of
$\phi $
on the space of
![]() ${\mathbb {A}}_{F}$
-points of an algebraic group over F that can be decomposed as
${\mathbb {A}}_{F}$
-points of an algebraic group over F that can be decomposed as
![]() $\phi =\phi _S\otimes \phi ^S$
, where
$\phi =\phi _S\otimes \phi ^S$
, where
![]() $\phi _S$
(resp.
$\phi _S$
(resp.
![]() $\phi ^S$
) is a function on the set of
$\phi ^S$
) is a function on the set of
![]() ${\mathbb {A}}_{F,S}$
-points (resp.
${\mathbb {A}}_{F,S}$
-points (resp.
![]() ${\mathbb {A}}_{F}^{S}$
-points) of the group. Note that such a decomposition of
${\mathbb {A}}_{F}^{S}$
-points) of the group. Note that such a decomposition of
![]() $\phi $
is not unique. By using these notations, we understand that we have fixed such a decomposition. See 2.3 for an example. If
$\phi $
is not unique. By using these notations, we understand that we have fixed such a decomposition. See 2.3 for an example. If
![]() $S=\{v\}$
, we write
$S=\{v\}$
, we write
![]() $X_v$
(resp.
$X_v$
(resp.
![]() $X^v$
) for
$X^v$
) for
![]() $X_S$
(resp.
$X_S$
(resp.
![]() $X^S$
).
$X^S$
).
2.2
All hermitian spaces are assumed to be nondegenerate. We always use
![]() $\langle {\cdot ,\cdot } \rangle $
to denote a hermitian pairing and
$\langle {\cdot ,\cdot } \rangle $
to denote a hermitian pairing and
![]() $q(x)=\langle {x,x} \rangle $
the hermitian norm if the underlying hermitian space (over E,
$q(x)=\langle {x,x} \rangle $
the hermitian norm if the underlying hermitian space (over E,
![]() $E_v$
or
$E_v$
or
![]() ${\mathbb {A}}_E$
) is indicated in the context. For a hermitian space V over E, we use V to denote
${\mathbb {A}}_E$
) is indicated in the context. For a hermitian space V over E, we use V to denote
![]() $V(E)$
to lighten the notation if there is no confusion. For
$V(E)$
to lighten the notation if there is no confusion. For
![]() $t\in F$
, let
$t\in F$
, let
![]() $V^t=\{v\in V:q(v)=t\}.$
The same notation applies to a local or adelic hermitian space. We use
$V^t=\{v\in V:q(v)=t\}.$
The same notation applies to a local or adelic hermitian space. We use
![]() $U(V)$
for both the algebraic group
$U(V)$
for both the algebraic group
![]() $U(V)$
and its group of F-points. Define
$U(V)$
and its group of F-points. Define
A hermitian space
![]() ${\mathbb {V}}/{\mathbb {A}}_E$
is called coherent (resp. incoherent) if its determinant belongs (resp. does not belong) to
${\mathbb {V}}/{\mathbb {A}}_E$
is called coherent (resp. incoherent) if its determinant belongs (resp. does not belong) to
![]() $ F^\times {\mathrm {Nm}} ( {\mathbb {A}}_E^\times )$
; equivalently,
$ F^\times {\mathrm {Nm}} ( {\mathbb {A}}_E^\times )$
; equivalently,
![]() ${\mathbb {V}}{\ \simeq \ } V({\mathbb {A}}_E)$
for some (resp. no) hermitian space
${\mathbb {V}}{\ \simeq \ } V({\mathbb {A}}_E)$
for some (resp. no) hermitian space
![]() $V/E$
. If
$V/E$
. If
![]() ${\mathbb {V}}$
is incoherent of dimension
${\mathbb {V}}$
is incoherent of dimension
![]() $1$
, for a place v of F nonsplit in E, there is a unique hermitian space
$1$
, for a place v of F nonsplit in E, there is a unique hermitian space
![]() $V/E$
such
$V/E$
such
![]() $V({\mathbb {A}}_E^v){\ \simeq \ } {\mathbb {V}}^v$
. We call V the v-nearby hermitian space of
$V({\mathbb {A}}_E^v){\ \simeq \ } {\mathbb {V}}^v$
. We call V the v-nearby hermitian space of
![]() ${\mathbb {W}}$
.
${\mathbb {W}}$
.
2.3
Let
![]() ${\mathcal {S}}({\mathbb {V}})$
be the space of
${\mathcal {S}}({\mathbb {V}})$
be the space of
![]() ${\mathbb {C}}$
-valued Schwartz functions. For
${\mathbb {C}}$
-valued Schwartz functions. For
![]() $v\in \infty $
such that
$v\in \infty $
such that
![]() ${\mathbb {V}}(E_v)$
is positive definite, the standard Gaussian function on
${\mathbb {V}}(E_v)$
is positive definite, the standard Gaussian function on
![]() ${\mathbb {V}}_\infty $
is
${\mathbb {V}}_\infty $
is
![]() $e^{-2\pi {q(x)}}\in {\mathcal {S}}({\mathbb {V}}(E_v)) $
. If a hermitian space
$e^{-2\pi {q(x)}}\in {\mathcal {S}}({\mathbb {V}}(E_v)) $
. If a hermitian space
![]() ${\mathbb {V}}/{\mathbb {A}}_E$
is totally positive-definite, let
${\mathbb {V}}/{\mathbb {A}}_E$
is totally positive-definite, let
be the subspace of functions of the form
![]() $\phi = \phi _\infty \otimes \phi ^\infty $
, where
$\phi = \phi _\infty \otimes \phi ^\infty $
, where
![]() $\phi _\infty $
is the pure tensor of standard Gaussian functions over all infinite places and
$\phi _\infty $
is the pure tensor of standard Gaussian functions over all infinite places and
![]() $ \phi ^\infty \in {\mathcal {S}}({\mathbb {V}} ^\infty ) $
taking values in
$ \phi ^\infty \in {\mathcal {S}}({\mathbb {V}} ^\infty ) $
taking values in
![]() ${\mathbb {C}}$
. For
${\mathbb {C}}$
. For
![]() $\phi \in {\mathcal {S}}({\mathbb {V}} ^\infty ) $
, we always fix such a decomposition.
$\phi \in {\mathcal {S}}({\mathbb {V}} ^\infty ) $
, we always fix such a decomposition.
2.4
Fix the additive character of
![]() $F\backslash {\mathbb {A}}_F$
to be
$F\backslash {\mathbb {A}}_F$
to be
![]() $\psi :=\psi _{\mathbb {Q}}\circ {\mathrm {Tr}}_{F/ {\mathbb {Q}}} $
, where
$\psi :=\psi _{\mathbb {Q}}\circ {\mathrm {Tr}}_{F/ {\mathbb {Q}}} $
, where
![]() $\psi _{\mathbb {Q}}$
is the unique additive character of
$\psi _{\mathbb {Q}}$
is the unique additive character of
![]() ${\mathbb {Q}}\backslash {\mathbb {A}}_{\mathbb {Q}}$
such that
${\mathbb {Q}}\backslash {\mathbb {A}}_{\mathbb {Q}}$
such that
![]() $\psi _{{\mathbb {Q}},\infty }(x)=e^{2\pi ix}$
. The additive character of
$\psi _{{\mathbb {Q}},\infty }(x)=e^{2\pi ix}$
. The additive character of
![]() ${\mathbb {A}}_E$
is
${\mathbb {A}}_E$
is
![]() $\psi _{E}:=\psi \circ {\mathrm {Tr}}_{E/ F} $
. For
$\psi _{E}:=\psi \circ {\mathrm {Tr}}_{E/ F} $
. For
![]() $ t\in {\mathbb {A}}_F $
(we in fact only use
$ t\in {\mathbb {A}}_F $
(we in fact only use
![]() $t\in F$
), let
$t\in F$
), let
![]() $\psi _{t}(b)=\psi (tb) .$
For a place v of F and
$\psi _{t}(b)=\psi (tb) .$
For a place v of F and
![]() $t\in F_v$
, Let
$t\in F_v$
, Let
![]() $\psi _{v,t}(b)=\psi _v (tb) .$
Then
$\psi _{v,t}(b)=\psi _v (tb) .$
Then
![]() $\psi _{v,t}=\psi _{v,t_v}$
for
$\psi _{v,t}=\psi _{v,t_v}$
for
![]() $ t\in {\mathbb {A}}_F $
.
$ t\in {\mathbb {A}}_F $
.
Fix the self-dual Haar measures for
![]() $F_v$
and
$F_v$
and
![]() $E_v$
. Then
$E_v$
. Then
are the induced Haar measures on
![]() $F_v^\times $
and
$F_v^\times $
and
![]() $E_v^\times $
. The subscripts will be omitted later in the paper. They induce the quotient measure on
$E_v^\times $
. The subscripts will be omitted later in the paper. They induce the quotient measure on
![]() $E_v^\times /F_v^\times {\ \simeq \ } U(1)({F_v})$
.
$E_v^\times /F_v^\times {\ \simeq \ } U(1)({F_v})$
.
For
![]() $\phi \in {\mathcal {S}}({\mathbb {V}}(E_v))$
, the Fourier transform of
$\phi \in {\mathcal {S}}({\mathbb {V}}(E_v))$
, the Fourier transform of
![]() $\phi $
(with respect to
$\phi $
(with respect to
![]() $\psi $
and a Haar measure) is
$\psi $
and a Haar measure) is
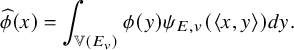 $$ \begin{align*}\widehat \phi(x)=\int_{{\mathbb{V}}(E_v)}\phi(y)\psi_{E,v}(\langle {x,y} \rangle) dy.\end{align*} $$
$$ \begin{align*}\widehat \phi(x)=\int_{{\mathbb{V}}(E_v)}\phi(y)\psi_{E,v}(\langle {x,y} \rangle) dy.\end{align*} $$
We fix the self-dual Haar measure on
![]() ${\mathbb {V}}(E_v)$
.
${\mathbb {V}}(E_v)$
.
2.5
Let
![]() $G=U(1,1) $
be the unitary group over F of the standard skew-hermitian space over E of dimension
$G=U(1,1) $
be the unitary group over F of the standard skew-hermitian space over E of dimension
![]() $2$
; that is, the skew-hermitian form is given by the matrix
$2$
; that is, the skew-hermitian form is given by the matrix
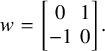 $$ \begin{align*}w= \begin{bmatrix}0&1\\ -1&0\end{bmatrix}. \end{align*} $$
$$ \begin{align*}w= \begin{bmatrix}0&1\\ -1&0\end{bmatrix}. \end{align*} $$
Then
![]() $w\in G(F)$
. We use
$w\in G(F)$
. We use
![]() $w_v$
to denote the same matrix in
$w_v$
to denote the same matrix in
![]() $G(F_v)$
$G(F_v)$
For
![]() $b\in {\mathbb {G}}_{a,F}$
, let
$b\in {\mathbb {G}}_{a,F}$
, let
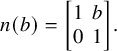 $$ \begin{align*}n(b) = \begin{bmatrix}1&b\\ 0&1\end{bmatrix}.\end{align*} $$
$$ \begin{align*}n(b) = \begin{bmatrix}1&b\\ 0&1\end{bmatrix}.\end{align*} $$
For
![]() $a\in {\mathrm {Res}}_{E/F}{\mathbb {G}}_{m,E} $
, let
$a\in {\mathrm {Res}}_{E/F}{\mathbb {G}}_{m,E} $
, let
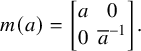 $$ \begin{align*}m(a) = \begin{bmatrix}a&0\\ 0&\overline a ^{-1} \end{bmatrix}.\end{align*} $$
$$ \begin{align*}m(a) = \begin{bmatrix}a&0\\ 0&\overline a ^{-1} \end{bmatrix}.\end{align*} $$
Let
![]() $N=\{n(b):b \in {\mathbb {G}}_{a,F}\}\subset G$
,
$N=\{n(b):b \in {\mathbb {G}}_{a,F}\}\subset G$
,
![]() $M=\{m(a):a \in {\mathrm {Res}}_{E/F}{\mathbb {G}}_{m,E} \}\subset G,$
and
$M=\{m(a):a \in {\mathrm {Res}}_{E/F}{\mathbb {G}}_{m,E} \}\subset G,$
and
![]() $P=MN$
the subgroup of upper triangular matrices. Then G is generated P and w. The isomorphism
$P=MN$
the subgroup of upper triangular matrices. Then G is generated P and w. The isomorphism
![]() $N{\ \simeq \ } {\mathbb {G}}_{a,F}$
induces an additive character and a Haar measure on
$N{\ \simeq \ } {\mathbb {G}}_{a,F}$
induces an additive character and a Haar measure on
![]() $N({\mathbb {A}}_F)$
which we fix in this paper.
$N({\mathbb {A}}_F)$
which we fix in this paper.
Let
![]() $K^{\max }_v$
be the intersection of
$K^{\max }_v$
be the intersection of
![]() $G(F_v) $
with the standard maximal compact subgroup
$G(F_v) $
with the standard maximal compact subgroup
![]() ${\mathrm {GL}}_{2}(E_v)$
. Then
${\mathrm {GL}}_{2}(E_v)$
. Then
![]() $K^{\max }_v$
is a maximal compact subgroup of
$K^{\max }_v$
is a maximal compact subgroup of
![]() $G(F_v) $
. For
$G(F_v) $
. For
![]() $v\in \infty $
,
$v\in \infty $
,
![]() $K^{\max }_v$
is the group of matrices
$K^{\max }_v$
is the group of matrices
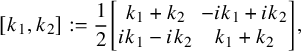 $$ \begin{align*}[k_1,k_2]:=\frac{1}{2}\begin{bmatrix}k_1+k_2&-ik_1+ik_2\\ ik_1-ik_2&k_1+k_2\end{bmatrix},\end{align*} $$
$$ \begin{align*}[k_1,k_2]:=\frac{1}{2}\begin{bmatrix}k_1+k_2&-ik_1+ik_2\\ ik_1-ik_2&k_1+k_2\end{bmatrix},\end{align*} $$
where
![]() $k_1,k_2\in E_v$
are of norm 1. We have the Iwasawa decomposition
$k_1,k_2\in E_v$
are of norm 1. We have the Iwasawa decomposition
2.6
For a place v of F, the local modulus character of
![]() $G(F_v) $
is given by
$G(F_v) $
is given by
if
![]() $g=n(b)m(a)k$
with
$g=n(b)m(a)k$
with
![]() $k\in K^{\max }_v$
under the Iwasawa decomposition. The global modulus character
$k\in K^{\max }_v$
under the Iwasawa decomposition. The global modulus character
![]() $\delta $
of
$\delta $
of
![]() $G({\mathbb {A}}_F) $
is the product of the local ones. Since we will use results in [Reference YuanYZ18, Reference Yuan, Zhang and ZhangYZZ13], where the subgroup
$G({\mathbb {A}}_F) $
is the product of the local ones. Since we will use results in [Reference YuanYZ18, Reference Yuan, Zhang and ZhangYZZ13], where the subgroup
![]() ${\mathrm {SL}}_2 \subset G $
is used, we remind the reader that our modulus character, when restricted to
${\mathrm {SL}}_2 \subset G $
is used, we remind the reader that our modulus character, when restricted to
![]() ${\mathrm {SL}}_2(F_v)\subset G(F_v)$
, is the square of the one in loc. cit..
${\mathrm {SL}}_2(F_v)\subset G(F_v)$
, is the square of the one in loc. cit..
2.7
For
![]() ${\mathfrak {w}}=({\mathfrak {w}}_v)_{v\in \infty }$
, where
${\mathfrak {w}}=({\mathfrak {w}}_v)_{v\in \infty }$
, where
![]() ${\mathfrak {w}}_v$
is a pair of integers, let
${\mathfrak {w}}_v$
is a pair of integers, let
![]() $ {\mathcal {A}} (G,{\mathfrak {w}}) $
be the space of smooth automorphic forms for G of weight
$ {\mathcal {A}} (G,{\mathfrak {w}}) $
be the space of smooth automorphic forms for G of weight
![]() ${\mathfrak {w}}$
. Let
${\mathfrak {w}}$
. Let
![]() ${\mathcal {A}}_{{\mathrm {hol}}}(G,{\mathfrak {w}})$
be the subspace of holomorphic automorphic forms. A characterization is as follows. For
${\mathcal {A}}_{{\mathrm {hol}}}(G,{\mathfrak {w}})$
be the subspace of holomorphic automorphic forms. A characterization is as follows. For
![]() $v\in \infty $
,
$v\in \infty $
,
![]() $t\in F_{v, \geq 0}$
and a pair of integers
$t\in F_{v, \geq 0}$
and a pair of integers
![]() $(w_1,w_2) $
, the standard holomorphic
$(w_1,w_2) $
, the standard holomorphic
![]() $\psi _{v,t}$
-Whittaker function on
$\psi _{v,t}$
-Whittaker function on
![]() $G(F_v)$
of weight
$G(F_v)$
of weight
![]() $(w_1,w_2)$
is
$(w_1,w_2)$
is
for
![]() $g=n(b)m(a)[k_1,k_2]$
under the Iwasawa decomposition. For
$g=n(b)m(a)[k_1,k_2]$
under the Iwasawa decomposition. For
![]() $t\in {\mathbb {A}}_{F,\infty }$
, let
$t\in {\mathbb {A}}_{F,\infty }$
, let
An automorphic form f on
![]() $G({\mathbb {A}}_F)$
is holomorphic of weight
$G({\mathbb {A}}_F)$
is holomorphic of weight
![]() ${\mathfrak {w}}$
if for
${\mathfrak {w}}$
if for
![]() $t\in F_{>0}\cup \{0\}$
, its
$t\in F_{>0}\cup \{0\}$
, its
![]() $\psi _t$
-Whittaker function is a tensor of the finite and infinite component:
$\psi _t$
-Whittaker function is a tensor of the finite and infinite component:
![]() $f_t= f_t^\infty \otimes W^{{\mathfrak {w}}}_{\infty , t}$
, and for other
$f_t= f_t^\infty \otimes W^{{\mathfrak {w}}}_{\infty , t}$
, and for other
![]() $t\in F$
, its
$t\in F$
, its
![]() $\psi _t$
-Whittaker function is 0. In this case, we call the locally constant function
$\psi _t$
-Whittaker function is 0. In this case, we call the locally constant function
![]() $f_t^\infty $
on
$f_t^\infty $
on
![]() $G({\mathbb {A}}_F^\infty )$
the t-th Fourier coefficient of f. (Then
$G({\mathbb {A}}_F^\infty )$
the t-th Fourier coefficient of f. (Then
![]() $f_t^\infty (1)$
is the t-th Fourier coefficient in the sense of classical modular forms.)
$f_t^\infty (1)$
is the t-th Fourier coefficient in the sense of classical modular forms.)
For a subfield
![]() $C\subset {\mathbb {C}}$
, let
$C\subset {\mathbb {C}}$
, let
be the C-subspace of automorphic forms f whose Fourier coefficients take values in C. (In the sense of classical modular forms, it means that the coefficients of the q-expansion of f along all cusps are in C.) Taking Fourier coefficients defines an embedding of C-vector spaces
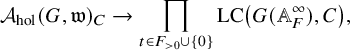 $$ \begin{align*}{\mathcal{A}}_{{\mathrm{hol}}}(G,{\mathfrak{w}})_{C}\to \prod_{t\in {F_{>0}}\cup\{0\}} {\mathrm{LC}}\left( G({\mathbb {A}}_F^\infty), C\right),\end{align*} $$
$$ \begin{align*}{\mathcal{A}}_{{\mathrm{hol}}}(G,{\mathfrak{w}})_{C}\to \prod_{t\in {F_{>0}}\cup\{0\}} {\mathrm{LC}}\left( G({\mathbb {A}}_F^\infty), C\right),\end{align*} $$
where
![]() ${\mathrm {LC}}\left ( G({\mathbb {A}}_F^\infty ), C\right )$
means locally constant functions on
${\mathrm {LC}}\left ( G({\mathbb {A}}_F^\infty ), C\right )$
means locally constant functions on
![]() $G({\mathbb {A}}_F^\infty )$
valued in
$G({\mathbb {A}}_F^\infty )$
valued in
![]() $ C$
. For a C-vector space X, we have the induced embedding
$ C$
. For a C-vector space X, we have the induced embedding
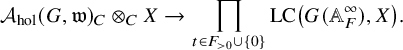 $$ \begin{align*}{\mathcal{A}}_{{\mathrm{hol}}}(G,{\mathfrak{w}})_{C}\otimes_C X \to \prod_{t\in {F_{>0}}\cup\{0\}} {\mathrm{LC}}\left( G({\mathbb {A}}_F^\infty), X\right).\end{align*} $$
$$ \begin{align*}{\mathcal{A}}_{{\mathrm{hol}}}(G,{\mathfrak{w}})_{C}\otimes_C X \to \prod_{t\in {F_{>0}}\cup\{0\}} {\mathrm{LC}}\left( G({\mathbb {A}}_F^\infty), X\right).\end{align*} $$
Define the t-th Fourier coefficient of an element in
![]() ${\mathcal {A}}_{{\mathrm {hol}}}(G,{\mathfrak {w}})_{C}\otimes _C X$
to be the t-th component of its image.
${\mathcal {A}}_{{\mathrm {hol}}}(G,{\mathfrak {w}})_{C}\otimes _C X$
to be the t-th component of its image.
2.8
Let
![]() ${\mathbb {V}}/{\mathbb {A}}_E$
be a hermitian space. For a character
${\mathbb {V}}/{\mathbb {A}}_E$
be a hermitian space. For a character
![]() $\chi _{_{\mathbb {W}}}$
of
$\chi _{_{\mathbb {W}}}$
of
![]() $E^\times \backslash {\mathbb {A}}_E^\times $
such that
$E^\times \backslash {\mathbb {A}}_E^\times $
such that
![]() $\chi _{_{\mathbb {V}},v}|_{ F_v^\times }=\eta _v^{\dim {\mathbb {V}}}$
for every place v of F, the Weil representation
$\chi _{_{\mathbb {V}},v}|_{ F_v^\times }=\eta _v^{\dim {\mathbb {V}}}$
for every place v of F, the Weil representation
![]() $\omega =\omega _{_{\mathbb {V}}}$
on
$\omega =\omega _{_{\mathbb {V}}}$
on
![]() ${\mathcal {S}}( {{\mathbb {V}}})$
is the restricted tensor product of local Weil representations of
${\mathcal {S}}( {{\mathbb {V}}})$
is the restricted tensor product of local Weil representations of
![]() $G(F_v)\times U({{\mathbb {V}}(E_v)})$
on
$G(F_v)\times U({{\mathbb {V}}(E_v)})$
on
![]() ${\mathcal {S}}({{\mathbb {V}}(E_v)})$
. The local Weil representation (which we still denote by
${\mathcal {S}}({{\mathbb {V}}(E_v)})$
. The local Weil representation (which we still denote by
![]() $ \omega $
instead of
$ \omega $
instead of
![]() $ \omega _v$
if the meaning is clear from the context) of
$ \omega _v$
if the meaning is clear from the context) of
![]() $G(F_v)$
is defined as follows: for
$G(F_v)$
is defined as follows: for
![]() $\phi \in {\mathcal {S}}( {{\mathbb {V}}(E_v)}) $
,
$\phi \in {\mathcal {S}}( {{\mathbb {V}}(E_v)}) $
,
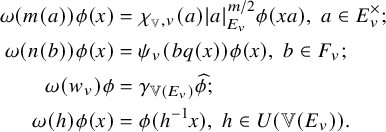 $$ \begin{align*} \omega (m(a))\phi(x)&=\chi_{_{\mathbb{V}},v}( a)| a|_{E_v}^{m/2}\phi(xa),\ a\in E_v^\times;\\ \omega (n(b))\phi(x)&=\psi_v\left( bq(x)\right) \phi(x),\ b\in F_v;\\ \omega (w_v)\phi&=\gamma_{{\mathbb{V}}(E_v)}\widehat \phi ;\\ \omega (h)\phi(x)&= \phi(h^{-1}x),\ h\in U({{\mathbb{V}}(E_v)}). \end{align*} $$
$$ \begin{align*} \omega (m(a))\phi(x)&=\chi_{_{\mathbb{V}},v}( a)| a|_{E_v}^{m/2}\phi(xa),\ a\in E_v^\times;\\ \omega (n(b))\phi(x)&=\psi_v\left( bq(x)\right) \phi(x),\ b\in F_v;\\ \omega (w_v)\phi&=\gamma_{{\mathbb{V}}(E_v)}\widehat \phi ;\\ \omega (h)\phi(x)&= \phi(h^{-1}x),\ h\in U({{\mathbb{V}}(E_v)}). \end{align*} $$
Here,
![]() $\gamma _{{\mathbb {V}}(E_v)}$
is the Weil index associated to
$\gamma _{{\mathbb {V}}(E_v)}$
is the Weil index associated to
![]() $\psi _v$
and
$\psi _v$
and
![]() ${{\mathbb {V}}(E_v)}$
.
${{\mathbb {V}}(E_v)}$
.
2.9
For
![]() $v\in \infty $
, define
$v\in \infty $
, define
![]() ${\mathfrak {k}}^{\chi _{_{\mathbb {V}},v}}$
to be the unique integer such that
${\mathfrak {k}}^{\chi _{_{\mathbb {V}},v}}$
to be the unique integer such that
for
![]() $z\in E_v$
of norm 1. Define
$z\in E_v$
of norm 1. Define
![]() ${\mathfrak {w}}_{\chi _{_{\mathbb {V}}}}=({\mathfrak {w}}_{\chi _{_{\mathbb {V}}},v})_{v\in \infty }$
, where
${\mathfrak {w}}_{\chi _{_{\mathbb {V}}}}=({\mathfrak {w}}_{\chi _{_{\mathbb {V}}},v})_{v\in \infty }$
, where
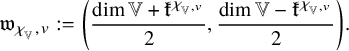 $$ \begin{align*} {\mathfrak{w}}_{\chi_{_{\mathbb{V}}},v}:=\left( \frac{\dim {\mathbb{V}}+{\mathfrak{k}}^{\chi_{_{\mathbb{V}},v}}}{2}, \frac{\dim {\mathbb{V}}-{\mathfrak{k}}^{\chi_{_{\mathbb{V}},v}}}{2}\right). \end{align*} $$
$$ \begin{align*} {\mathfrak{w}}_{\chi_{_{\mathbb{V}}},v}:=\left( \frac{\dim {\mathbb{V}}+{\mathfrak{k}}^{\chi_{_{\mathbb{V}},v}}}{2}, \frac{\dim {\mathbb{V}}-{\mathfrak{k}}^{\chi_{_{\mathbb{V}},v}}}{2}\right). \end{align*} $$
3 Theta-Eisenstein series
First, we recall basic knowledge about Eisenstein series and theta series. Then we set up basic properties of theta-Eisenstein series (i.e., linear combinations of products of theta series and Eisenstein series). Finally, we study two kinds of holomorphic projections of theta-Eisenstein series. The origin of theta-Eisenstein series is in the work of Gross and Zagier[Reference Gross and ZagierGZ86]. We largely follow the works of Yuan, S. Zhang and W. Zhang [Reference YuanYua22, Reference YuanYZ18, Reference Yuan, Zhang and ZhangYZZ13].
3.1 Eisenstein series and theta series
Let
![]() ${\mathbb {W}}$
be a hermitian space over
${\mathbb {W}}$
be a hermitian space over
![]() $ {\mathbb {A}}_E$
(with respect to the extension
$ {\mathbb {A}}_E$
(with respect to the extension
![]() $E/F$
). Let
$E/F$
). Let
![]() $\chi _{_{\mathbb {W}}}$
be a character of
$\chi _{_{\mathbb {W}}}$
be a character of
![]() $E^\times \backslash {\mathbb {A}}_E^\times $
such that
$E^\times \backslash {\mathbb {A}}_E^\times $
such that
![]() $\chi _{_{\mathbb {V}}}|_{{\mathbb {A}}_F^\times }=\eta $
. We have the Weil representation
$\chi _{_{\mathbb {V}}}|_{{\mathbb {A}}_F^\times }=\eta $
. We have the Weil representation
![]() $\omega _{_{\mathbb {W}}}$
, which we simply denote by
$\omega _{_{\mathbb {W}}}$
, which we simply denote by
![]() $\omega $
.
$\omega $
.
3.1.1 Local Whittaker integrals
Let v be a place of F. For
![]() $t\in F_v$
,
$t\in F_v$
,
![]() $\phi \in {\mathcal {S}}( {\mathbb {W}}_v )$
and
$\phi \in {\mathcal {S}}( {\mathbb {W}}_v )$
and
![]() $g\in G(F_v)$
, define the Whittaker integral
$g\in G(F_v)$
, define the Whittaker integral
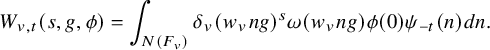 $$ \begin{align} W_{v,t} (s, g, \phi) =\int_{N(F_v) } \delta_v(w_vng)^{s }\omega (w_vng) \phi(0) \psi_{-t}(n) dn. \end{align} $$
$$ \begin{align} W_{v,t} (s, g, \phi) =\int_{N(F_v) } \delta_v(w_vng)^{s }\omega (w_vng) \phi(0) \psi_{-t}(n) dn. \end{align} $$
We immediately have the following equations:
Since
![]() $wn(b)m(a)=m(\overline a^{-1})wn(b{\mathrm {Nm}}(a)^{-1})$
,
$wn(b)m(a)=m(\overline a^{-1})wn(b{\mathrm {Nm}}(a)^{-1})$
,
![]() $ m(\overline a^{-1})n(b)=n(b')m(\overline a^{-1})$
for some
$ m(\overline a^{-1})n(b)=n(b')m(\overline a^{-1})$
for some
![]() $b'$
, and
$b'$
, and
![]() $\chi _{_{\mathbb {W}},v}({\mathrm {Nm}}(a))=1$
, a direct computation gives
$\chi _{_{\mathbb {W}},v}({\mathrm {Nm}}(a))=1$
, a direct computation gives
Lemma 3.1.1 [Reference IchinoIch04, Proposition 6.2][Reference Yuan, Zhang and ZhangYZZ13, Proposition 2.7 (2)].
Let
![]() $t\neq 0$
.
$t\neq 0$
.
(1) The set
![]() $ {\mathbb {W}}_v^t$
is either empty or consists of one orbit of
$ {\mathbb {W}}_v^t$
is either empty or consists of one orbit of
![]() $U( {\mathbb {W}}_v)$
.
$U( {\mathbb {W}}_v)$
.
(2) If
![]() $ {\mathbb {W}}_v^t$
is empty, then
$ {\mathbb {W}}_v^t$
is empty, then
![]() $W_{v,t}(0,g,\phi )=0$
. Otherwise, for
$W_{v,t}(0,g,\phi )=0$
. Otherwise, for
![]() $x\in {\mathbb {W}}_v^t$
, we have
$x\in {\mathbb {W}}_v^t$
, we have
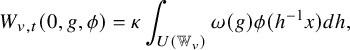 $$ \begin{align*}W_{v,t}(0,g,\phi)= \kappa \int_{ U( {\mathbb{W}}_v)}\omega(g)\phi(h^{-1} x)dh ,\end{align*} $$
$$ \begin{align*}W_{v,t}(0,g,\phi)= \kappa \int_{ U( {\mathbb{W}}_v)}\omega(g)\phi(h^{-1} x)dh ,\end{align*} $$
for a nonzero constant
![]() $\kappa $
.
$\kappa $
.
(3) If
![]() $\dim {\mathbb {W}}=1$
, with the measure fixed in 2.4,
$\dim {\mathbb {W}}=1$
, with the measure fixed in 2.4,
![]() $\kappa =\frac {\gamma _{{\mathbb {W}}_v}}{L(1,\eta _v)}$
.
$\kappa =\frac {\gamma _{{\mathbb {W}}_v}}{L(1,\eta _v)}$
.
Assume
![]() $\dim {\mathbb {W}}=1$
.
$\dim {\mathbb {W}}=1$
.
Lemma 3.1.2. Assume that v is a finite place and
![]() $\phi (0)=0$
. Then for t small enough,
$\phi (0)=0$
. Then for t small enough,
![]() $W_{v,t} (s, g, \phi )=W_{v,0} (s, g, \phi )$
and is a holomorphic function.
$W_{v,t} (s, g, \phi )=W_{v,0} (s, g, \phi )$
and is a holomorphic function.
Proof. The proof is by the reasoning as the proof of [Reference QiuQiu21, Lemma 4.2.4 (2)]
We define the following normalization (following [Reference Yuan, Zhang and ZhangYZZ13, 6.1.1]):
For
![]() $t=0$
,
$t=0$
,
![]() $W_{v,t} (s, g, \phi ) $
has a possible pole at
$W_{v,t} (s, g, \phi ) $
has a possible pole at
![]() $s=0$
. And we take a different normalization (following [Reference Yuan, Zhang and ZhangYZZ13, 6.1.1], and taking care of the difference between the modulus characters mentioned in 2.6),
$s=0$
. And we take a different normalization (following [Reference Yuan, Zhang and ZhangYZZ13, 6.1.1], and taking care of the difference between the modulus characters mentioned in 2.6),
Here, if v is a finite place,
![]() ${\mathrm {Diff}}_v$
is the different of
${\mathrm {Diff}}_v$
is the different of
![]() $F_v/{\mathbb {Q}}_v$
and
$F_v/{\mathbb {Q}}_v$
and
![]() ${\mathrm {Disc}}_v$
is the discriminant of
${\mathrm {Disc}}_v$
is the discriminant of
![]() $E_v/F_v$
, and if
$E_v/F_v$
, and if
![]() $v\in \infty $
,
$v\in \infty $
,
![]() ${\mathrm {Diff}}_{v}={\mathrm {Disc}}_v=1$
.
${\mathrm {Diff}}_{v}={\mathrm {Disc}}_v=1$
.
Lemma 3.1.3.
(1) There is an analytic continuation of
![]() $ W^\circ _0(s,g,\phi )$
to
$ W^\circ _0(s,g,\phi )$
to
![]() ${\mathbb {C}}$
such that
${\mathbb {C}}$
such that
![]() $ W^\circ _0(0,g,\phi )=\omega (g)\phi (0)$
.
$ W^\circ _0(0,g,\phi )=\omega (g)\phi (0)$
.
(2) If
![]() $E_v/{\mathbb {Q}}_{v}$
is unramified where
$E_v/{\mathbb {Q}}_{v}$
is unramified where
![]() ${\mathbb {W}}_v=E_v$
with
${\mathbb {W}}_v=E_v$
with
![]() $q={\mathrm {Nm}}$
, and
$q={\mathrm {Nm}}$
, and
![]() $\phi =1_{{\mathcal {O}}_{E_v}}$
, then
$\phi =1_{{\mathcal {O}}_{E_v}}$
, then
![]() $ W^\circ _0(s,g,\phi )=\delta _v(g)^{-s}\omega (g)\phi (0).$
$ W^\circ _0(s,g,\phi )=\delta _v(g)^{-s}\omega (g)\phi (0).$
(3) If
![]() $v\in \infty $
and
$v\in \infty $
and
![]() $\phi $
is the standard Gaussian function, then
$\phi $
is the standard Gaussian function, then
![]() $ W^\circ _0(s,g,\phi )=\delta _v(g)^{-s}\omega (g)\phi (0).$
$ W^\circ _0(s,g,\phi )=\delta _v(g)^{-s}\omega (g)\phi (0).$
Proof. (1) follows from [Reference Yuan, Zhang and ZhangYZZ13, Proposition 6.1]. (2) follows from [Reference TanTan99, Proposition 2.1]. (3) follows from [Reference YuanYZ18, Lemma 7.6 (1)] (or its proof).
3.1.2 Siegel-Eisenstein series
Now we come back to a general
![]() ${\mathbb {W}}$
. For
${\mathbb {W}}$
. For
![]() $\phi \in {\mathcal {S}}({\mathbb {W}})$
, we have a Siegel-Eisenstein series of G:
$\phi \in {\mathcal {S}}({\mathbb {W}})$
, we have a Siegel-Eisenstein series of G:
 $$ \begin{align}E(s,g,\phi)=\sum_{\gamma\in P(F)\backslash G(F)}\delta (\gamma g)^{s } \omega (\gamma g)\phi (0), \end{align} $$
$$ \begin{align}E(s,g,\phi)=\sum_{\gamma\in P(F)\backslash G(F)}\delta (\gamma g)^{s } \omega (\gamma g)\phi (0), \end{align} $$
which is absolutely convergent if
![]() ${\mathrm {Re}} s>1-\dim {\mathbb {W}}/2$
and has a meromorphic continuation to the entire complex plane [Reference TanTan99]. Moreover, it is holomorphic at
${\mathrm {Re}} s>1-\dim {\mathbb {W}}/2$
and has a meromorphic continuation to the entire complex plane [Reference TanTan99]. Moreover, it is holomorphic at
![]() $s=0$
[Reference TanTan99, Proposition 4.1].
$s=0$
[Reference TanTan99, Proposition 4.1].
Let
![]() $E_t(s,g,\phi )$
be the
$E_t(s,g,\phi )$
be the
![]() $\psi _t$
-Whittaker function of
$\psi _t$
-Whittaker function of
![]() $E(s,g,\phi )$
. Let
$E(s,g,\phi )$
. Let
![]() $W_{t} (s, g, \phi )$
be the global counterpart of the Whittaker integral (3.1) so that if
$W_{t} (s, g, \phi )$
be the global counterpart of the Whittaker integral (3.1) so that if
![]() $\phi $
is a pure tensor, then
$\phi $
is a pure tensor, then
![]() $W_{t} (s, g, \phi )$
is the product of
$W_{t} (s, g, \phi )$
is the product of
![]() $W_{v,t} (s, g_v, \phi _v)$
over all places of F. By the non-vanishing of
$W_{v,t} (s, g_v, \phi _v)$
over all places of F. By the non-vanishing of
![]() $L(1,\eta )$
and Lemma 3.1.3,
$L(1,\eta )$
and Lemma 3.1.3,
![]() $W_{0} (s, g, \phi )$
has a meromorphic continuation to the entire complex plane, which is holomorphic at
$W_{0} (s, g, \phi )$
has a meromorphic continuation to the entire complex plane, which is holomorphic at
![]() $s=0$
. Then we have
$s=0$
. Then we have
By Lemma 3.1.1 (2) and (3.8), for
![]() $h\in U({\mathbb {W}})$
, we have
$h\in U({\mathbb {W}})$
, we have
For
![]() $t\neq 0$
and a pure tensor
$t\neq 0$
and a pure tensor
![]() $\phi $
, define
$\phi $
, define
Extend the definition to all Schwartz functions by linearity. Then
3.1.3 Coherent case: Siegel-Weil formula
Assume that
![]() ${\mathbb {W}}=W({\mathbb {A}}_E)$
is coherent. For
${\mathbb {W}}=W({\mathbb {A}}_E)$
is coherent. For
![]() $\phi \in {\mathcal {S}}(W ({\mathbb {A}}_E))$
and
$\phi \in {\mathcal {S}}(W ({\mathbb {A}}_E))$
and
![]() $(g,h)\in G({\mathbb {A}}_F ) \times U({\mathbb {W}} ) $
, we define a theta series, which is absolutely convergent:
$(g,h)\in G({\mathbb {A}}_F ) \times U({\mathbb {W}} ) $
, we define a theta series, which is absolutely convergent:
Then
![]() $ \theta (g,h,\phi )$
is smooth, slowly increasing and
$ \theta (g,h,\phi )$
is smooth, slowly increasing and
![]() $ G(F)\times U(W) $
-invariant.
$ G(F)\times U(W) $
-invariant.
Assume that W is anisotropic. Then
![]() $E(s,g,\phi )$
is holomorphic at
$E(s,g,\phi )$
is holomorphic at
![]() $s=0$
, and the following equation is a special case of the regularized Siegel-Weil formula [Reference IchinoIch04, Theorem 4.2]:
$s=0$
, and the following equation is a special case of the regularized Siegel-Weil formula [Reference IchinoIch04, Theorem 4.2]:
where
![]() $\kappa =2$
if
$\kappa =2$
if
![]() $ \dim W=1$
and
$ \dim W=1$
and
![]() $\kappa =1$
if
$\kappa =1$
if
![]() $ \dim W>1$
.
$ \dim W>1$
.
3.1.4 Incoherent case: derivative
Assume that
![]() ${\mathbb {W}}$
is incoherent. By Lemma 3.1.1 (1), for
${\mathbb {W}}$
is incoherent. By Lemma 3.1.1 (1), for
![]() $t\neq 0$
, the summand in (3.12) corresponding to v is nonzero only if t is represented by
$t\neq 0$
, the summand in (3.12) corresponding to v is nonzero only if t is represented by
![]() ${\mathbb {W}}^v$
. By the incoherence,
${\mathbb {W}}^v$
. By the incoherence,
![]() ${\mathbb {W}}_v$
does not represent t. In particular, we have the following lemma.
${\mathbb {W}}_v$
does not represent t. In particular, we have the following lemma.
Lemma 3.1.4. For v split in E, the summand in (3.12) corresponding v is
![]() $0$
.
$0$
.
Assume that
![]() $\dim {\mathbb {W}}=1$
. Assume that
$\dim {\mathbb {W}}=1$
. Assume that
![]() $\phi $
is a pure tensor.
$\phi $
is a pure tensor.
First, assume that
![]() $t\neq 0$
. By the product formula for Hasse invariant and the Hasse principle, if t is represented by
$t\neq 0$
. By the product formula for Hasse invariant and the Hasse principle, if t is represented by
![]() ${\mathbb {W}}^v$
, then v is nonsplit in E and t is represented by the v-nearby hermitian space W of
${\mathbb {W}}^v$
, then v is nonsplit in E and t is represented by the v-nearby hermitian space W of
![]() ${\mathbb {W}}$
. See 2.2. By Lemma 3.1.1 (2) and Lemma 3.1.4, we have
${\mathbb {W}}$
. See 2.2. By Lemma 3.1.1 (2) and Lemma 3.1.4, we have
for
![]() $h\in U({\mathbb {W}}_v)$
, where v is split in E.
$h\in U({\mathbb {W}}_v)$
, where v is split in E.
Now we consider the constant term. Let
where
![]() ${\mathrm {Disc}}_E,{\mathrm {Disc}}_F\in {\mathbb {Z}}$
are the discriminants of E and F over
${\mathrm {Disc}}_E,{\mathrm {Disc}}_F\in {\mathbb {Z}}$
are the discriminants of E and F over
![]() ${\mathbb {Q}}$
. By [Reference YuanYZ18, p 586] (note the difference by
${\mathbb {Q}}$
. By [Reference YuanYZ18, p 586] (note the difference by
![]() $2$
between the s-variables in the L-factors in loc. cit. and (3.6)),
$2$
between the s-variables in the L-factors in loc. cit. and (3.6)),
3.2 Theta-Eisenstein series
From now on, always assume
![]() $\dim {\mathbb {W}}=1$
.
$\dim {\mathbb {W}}=1$
.
3.2.1 Definition
Let
![]() $V^\sharp /E$
be a hermitian space of dimension
$V^\sharp /E$
be a hermitian space of dimension
![]() $n>0$
. Let
$n>0$
. Let
![]() $\chi _{V^\sharp }$
be a character of
$\chi _{V^\sharp }$
be a character of
![]() $E^\times \backslash {\mathbb {A}}_E^\times $
such that
$E^\times \backslash {\mathbb {A}}_E^\times $
such that
![]() $\chi _{V^\sharp }|_{{\mathbb {A}}_F^\times }=\eta ^{n}$
. Let
$\chi _{V^\sharp }|_{{\mathbb {A}}_F^\times }=\eta ^{n}$
. Let
![]() ${\mathbb {V}}= {\mathbb {W}}\oplus V^\sharp ({\mathbb {A}}_E)$
be the orthogonal direct sum and
${\mathbb {V}}= {\mathbb {W}}\oplus V^\sharp ({\mathbb {A}}_E)$
be the orthogonal direct sum and
![]() $\chi _{\mathbb {V}}=\chi _{_{\mathbb {W}}}\chi _{V^\sharp }$
. We have the corresponding Weil representations. Below, we shall use
$\chi _{\mathbb {V}}=\chi _{_{\mathbb {W}}}\chi _{V^\sharp }$
. We have the corresponding Weil representations. Below, we shall use
![]() $\omega $
to denote a Weil representation if the hermitian space is indicated in the context – for example, by the function that it acts on.
$\omega $
to denote a Weil representation if the hermitian space is indicated in the context – for example, by the function that it acts on.
For
![]() $ \phi \in {\mathcal {S}}\left ( {\mathbb {V}}\right )$
, we define a theta-Eisenstein series
$ \phi \in {\mathcal {S}}\left ( {\mathbb {V}}\right )$
, we define a theta-Eisenstein series
![]() $ {\theta E}(s,g,\phi )$
on G associated the to the orthogonal decomposition
$ {\theta E}(s,g,\phi )$
on G associated the to the orthogonal decomposition
![]() ${\mathbb {V}}= {\mathbb {W}}\oplus V^\sharp ({\mathbb {A}}_E)$
:
${\mathbb {V}}= {\mathbb {W}}\oplus V^\sharp ({\mathbb {A}}_E)$
:
 $$ \begin{align} {\theta E} (s,g,\phi)= \sum_{\gamma\in P(F)\backslash G(F)}\delta (\gamma g)^{s } \sum_{x\in V^\sharp{{}}} \omega (\gamma g)\phi ((0,x)). \end{align} $$
$$ \begin{align} {\theta E} (s,g,\phi)= \sum_{\gamma\in P(F)\backslash G(F)}\delta (\gamma g)^{s } \sum_{x\in V^\sharp{{}}} \omega (\gamma g)\phi ((0,x)). \end{align} $$
If
![]() $\phi =\phi _1\otimes \phi _2$
with
$\phi =\phi _1\otimes \phi _2$
with
![]() $\phi _1\in {\mathcal {S}}\left ( {\mathbb {W}}\right )$
and
$\phi _1\in {\mathcal {S}}\left ( {\mathbb {W}}\right )$
and
![]() $\phi _2\in {\mathcal {S}}\left ( V^\sharp ({\mathbb {A}}_E)\right )$
, then
$\phi _2\in {\mathcal {S}}\left ( V^\sharp ({\mathbb {A}}_E)\right )$
, then
For
![]() $t\in F$
, let
$t\in F$
, let
![]() ${\theta E} _t (s,g,\phi )$
be the
${\theta E} _t (s,g,\phi )$
be the
![]() $\psi _t$
-Whittaker function of
$\psi _t$
-Whittaker function of
![]() ${\theta E} (s,g,\phi )$
.
${\theta E} (s,g,\phi )$
.
3.2.2 Coherent case
Assume that
![]() ${\mathbb {W}}=W({\mathbb {A}}_E)$
is coherent. The regularized Siegel-Weil formula (3.13) immediately implies the following ‘mixed Siegel-Weil formula’:
${\mathbb {W}}=W({\mathbb {A}}_E)$
is coherent. The regularized Siegel-Weil formula (3.13) immediately implies the following ‘mixed Siegel-Weil formula’:
(We will prove an arithmetic analog of (3.19) for
![]() ${\mathbb {W}}$
being incoherent in 5.2.) Then for
${\mathbb {W}}$
being incoherent in 5.2.) Then for
![]() $t\in F$
,
$t\in F$
,
 $$ \begin{align} {\theta E}_{t} (0,g,\phi) = \frac{2}{ {\mathrm{Vol}}([U(W)]) } \int_{ [U(W)]}\sum_{x\in V ^t } \omega(g)\phi(h^{-1} x)dh. \end{align} $$
$$ \begin{align} {\theta E}_{t} (0,g,\phi) = \frac{2}{ {\mathrm{Vol}}([U(W)]) } \int_{ [U(W)]}\sum_{x\in V ^t } \omega(g)\phi(h^{-1} x)dh. \end{align} $$
For
![]() $\phi $
invariant by
$\phi $
invariant by
![]() $U(W(E_v)), v\in \infty $
, the integration in (3.20) is a finite sum.
$U(W(E_v)), v\in \infty $
, the integration in (3.20) is a finite sum.
Lemma 3.2.1. Let
![]() $t\in F_{>0}$
and
$t\in F_{>0}$
and
![]() $\phi $
a pure tensor. Let u be a finite place of F,
$\phi $
a pure tensor. Let u be a finite place of F,
![]() $O\subset {\mathbb {V}}_u$
an open compact neighborhood of
$O\subset {\mathbb {V}}_u$
an open compact neighborhood of
![]() $0$
and
$0$
and
![]() $\phi ^O= \phi ^u\otimes (\phi _u 1_{{\mathbb {V}}_u-O})$
. Given
$\phi ^O= \phi ^u\otimes (\phi _u 1_{{\mathbb {V}}_u-O})$
. Given
![]() $g\in G({\mathbb {A}}_F^{u })P(F_u)$
, for O small enough, we have
$g\in G({\mathbb {A}}_F^{u })P(F_u)$
, for O small enough, we have
![]() $ {\theta E} _t (0,g,\phi ) = {\theta E} _t (0,g,\phi ^O) .$
$ {\theta E} _t (0,g,\phi ) = {\theta E} _t (0,g,\phi ^O) .$
Proof. Write
![]() $g_u=m(a)n(b)$
, where
$g_u=m(a)n(b)$
, where
![]() $a\in E_u^\times $
. See 2.5. Then
$a\in E_u^\times $
. See 2.5. Then
![]() $\{a h_u^{-1}x:x\in V^t,h\in U({\mathbb {V}})\}\subset {\mathbb {V}}_u^{a^2t} $
. The latter is closed in
$\{a h_u^{-1}x:x\in V^t,h\in U({\mathbb {V}})\}\subset {\mathbb {V}}_u^{a^2t} $
. The latter is closed in
![]() ${\mathbb {V}}_u$
and does not contain 0. Thus,
${\mathbb {V}}_u$
and does not contain 0. Thus,
![]() $O\cap \{ah_u^{-1}x:x\in V^t,h\in U({\mathbb {V}})\}=\emptyset $
if O is small enough. Then the lemma follows from (3.20), the remark below it, and the definition of the Weil representation in 2.8.
$O\cap \{ah_u^{-1}x:x\in V^t,h\in U({\mathbb {V}})\}=\emptyset $
if O is small enough. Then the lemma follows from (3.20), the remark below it, and the definition of the Weil representation in 2.8.
3.2.3 Incoherent case
Assume that
![]() ${\mathbb {W}}$
is incoherent.
${\mathbb {W}}$
is incoherent.
For a place v of F nonsplit in E, let W be the v-nearby hermitian space of
![]() ${\mathbb {W}}$
. For
${\mathbb {W}}$
. For
![]() $\phi =\phi _{1}\otimes \phi _{2}$
with
$\phi =\phi _{1}\otimes \phi _{2}$
with
![]() $\phi _{1}\in {\mathcal {S}}\left ( {\mathbb {W}}_v \right )$
,
$\phi _{1}\in {\mathcal {S}}\left ( {\mathbb {W}}_v \right )$
,
![]() $\phi _2\in {\mathcal {S}}\left ( V^\sharp (E_v)\right )$
and
$\phi _2\in {\mathcal {S}}\left ( V^\sharp (E_v)\right )$
and
![]() $x=(x_1,x_2)\in V:= W(E_v)\oplus V^\sharp (E_v)$
with
$x=(x_1,x_2)\in V:= W(E_v)\oplus V^\sharp (E_v)$
with
![]() $ x_1\neq 0,$
let
$ x_1\neq 0,$
let
This is a local analog of (3.18). Extend this definition to
![]() $ {\mathcal {S}}\left ( {\mathbb {W}}_v \right )\otimes {\mathcal {S}}\left ( V^\sharp (E_v)\right )\subset {\mathcal {S}}\left ( {\mathbb {V}}(E_v) \right )$
by linearity. The inclusion is an equality unless
$ {\mathcal {S}}\left ( {\mathbb {W}}_v \right )\otimes {\mathcal {S}}\left ( V^\sharp (E_v)\right )\subset {\mathcal {S}}\left ( {\mathbb {V}}(E_v) \right )$
by linearity. The inclusion is an equality unless
![]() $v\in \infty $
. However, this subspace is enough for our purpose. (Besides, there is another definition of
$v\in \infty $
. However, this subspace is enough for our purpose. (Besides, there is another definition of
![]() ${W\theta }_{v,x}$
for the whole
${W\theta }_{v,x}$
for the whole
![]() $ {\mathcal {S}}\left ( {\mathbb {V}}(E_v) \right )$
. We will not need it.) For v nonsplit in E and
$ {\mathcal {S}}\left ( {\mathbb {V}}(E_v) \right )$
. We will not need it.) For v nonsplit in E and
![]() $t\neq 0$
, define
$t\neq 0$
, define
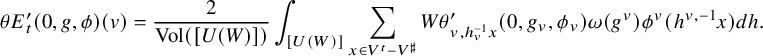 $$ \begin{align} {\theta E}^{\prime}_{t} (0,g,\phi) (v) = \frac{2}{ {\mathrm{Vol}}([U(W)]) } \int_{ [U(W)]}\sum_{x\in V ^t -V^\sharp } {W\theta}_{v,h_v^{-1}x} '(0, g_v, \phi_v) \omega(g^v)\phi^v(h^{v,-1} x)dh. \end{align} $$
$$ \begin{align} {\theta E}^{\prime}_{t} (0,g,\phi) (v) = \frac{2}{ {\mathrm{Vol}}([U(W)]) } \int_{ [U(W)]}\sum_{x\in V ^t -V^\sharp } {W\theta}_{v,h_v^{-1}x} '(0, g_v, \phi_v) \omega(g^v)\phi^v(h^{v,-1} x)dh. \end{align} $$
Note that the analog of (3.12) does not hold.
We study
![]() ${W\theta }_{v,x} '(0,g,\phi )$
following [Reference Yuan, Zhang and ZhangYZZ13]. Indeed, the computation is only on the Eisenstein (i.e., Whittaker) part. We remind the reader of the difference between the modulus characters mentioned in 2.6. By (3.3), (3.4) and Lemma 3.1.1, we have the following lemma, which says that under the action of
${W\theta }_{v,x} '(0,g,\phi )$
following [Reference Yuan, Zhang and ZhangYZZ13]. Indeed, the computation is only on the Eisenstein (i.e., Whittaker) part. We remind the reader of the difference between the modulus characters mentioned in 2.6. By (3.3), (3.4) and Lemma 3.1.1, we have the following lemma, which says that under the action of
![]() $P(F_v)$
,
$P(F_v)$
,
![]() ${W\theta }_{v,x} '(s_0, g , \phi )$
behaves in the same was as the Weil representation.
${W\theta }_{v,x} '(s_0, g , \phi )$
behaves in the same was as the Weil representation.
Lemma 3.2.2 [Reference Yuan, Zhang and ZhangYZZ13, Lemma 6.6].
The following relations hold:
Corollary 3.2.3. For
![]() $a\in E^\times $
,
$a\in E^\times $
,
![]() ${\theta E}^{\prime }_{t} (0,m(a)g,\phi ) (v)={\theta E}^{\prime }_{a^2t} (0,g,\phi ) (v)$
.
${\theta E}^{\prime }_{t} (0,m(a)g,\phi ) (v)={\theta E}^{\prime }_{a^2t} (0,g,\phi ) (v)$
.
3.3 Holomorphic projections
We define quasi-holomorphic projection and cuspidal holomorphic projection, and compare them for theta-Eisenstein series (Lemma 3.3.3). After imposing Gaussian condition at infinite places in 3.3.4, we make the comparison more explicit in (3.31). Finally, after imposing the incoherence condition, we explicitly compute the quasi-holomorphic projection (Proposition 3.3.13).
3.3.1 Definitions
For
![]() $v\in \infty $
, let
$v\in \infty $
, let
![]() ${\mathfrak {w}}_v$
be a pair of integers whose sum
${\mathfrak {w}}_v$
be a pair of integers whose sum
![]() $|{\mathfrak {w}}_v|$
is
$|{\mathfrak {w}}_v|$
is
![]() $\geq 2$
. For
$\geq 2$
. For
![]() $t\in F_{v,>0}$
, let
$t\in F_{v,>0}$
, let
![]() $W^{{\mathfrak {w}}_v}_{v, t}$
be the standard holomorphic Whittaker function of weight
$W^{{\mathfrak {w}}_v}_{v, t}$
be the standard holomorphic Whittaker function of weight
![]() ${\mathfrak {w}}_v$
as in 2.7. Then
${\mathfrak {w}}_v$
as in 2.7. Then
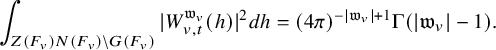 $$ \begin{align*}\int_{Z(F_v)N(F_v)\backslash G(F_v)} |W^{{\mathfrak{w}}_v}_{v, t}(h)|^2 dh=(4\pi)^{-|{\mathfrak{w}}_v|+1}\Gamma(|{\mathfrak{w}}_v|-1).\end{align*} $$
$$ \begin{align*}\int_{Z(F_v)N(F_v)\backslash G(F_v)} |W^{{\mathfrak{w}}_v}_{v, t}(h)|^2 dh=(4\pi)^{-|{\mathfrak{w}}_v|+1}\Gamma(|{\mathfrak{w}}_v|-1).\end{align*} $$
For
![]() $t\in F_{v,>0}$
, a
$t\in F_{v,>0}$
, a
![]() $\psi _{v,t}$
-Whittaker function W on
$\psi _{v,t}$
-Whittaker function W on
![]() $G(F_v)$
, and
$G(F_v)$
, and
![]() $g\in G(F_v)$
, define
$g\in G(F_v)$
, define
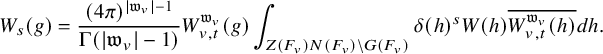 $$ \begin{align*}W_s(g)=\frac{(4\pi)^{|{\mathfrak{w}}_v|-1}}{\Gamma(|{\mathfrak{w}}_v|-1)} W^{{\mathfrak{w}}_v}_{v, t}(g) \int_{Z(F_v)N(F_v)\backslash G(F_v)}\delta(h)^sW(h) \overline{W^{{\mathfrak{w}}_v}_{v, t}(h)} dh.\end{align*} $$
$$ \begin{align*}W_s(g)=\frac{(4\pi)^{|{\mathfrak{w}}_v|-1}}{\Gamma(|{\mathfrak{w}}_v|-1)} W^{{\mathfrak{w}}_v}_{v, t}(g) \int_{Z(F_v)N(F_v)\backslash G(F_v)}\delta(h)^sW(h) \overline{W^{{\mathfrak{w}}_v}_{v, t}(h)} dh.\end{align*} $$
If
![]() $W_{s}$
has a meromorphic continuation to
$W_{s}$
has a meromorphic continuation to
![]() $s=0$
, define the quasi-holomorphic projection
$s=0$
, define the quasi-holomorphic projection
of W of weight
![]() ${\mathfrak {w}}_v$
. Here,
${\mathfrak {w}}_v$
. Here,
![]() $\widetilde {\lim \limits _{s\to 0}}$
denotes the constant term at
$\widetilde {\lim \limits _{s\to 0}}$
denotes the constant term at
![]() $s=0$
.
$s=0$
.
Let
![]() ${\mathfrak {w}}=({\mathfrak {w}}_v)_{v\in \infty }$
, where
${\mathfrak {w}}=({\mathfrak {w}}_v)_{v\in \infty }$
, where
![]() ${\mathfrak {w}}_v$
is a pair of integers. For a continuous function
${\mathfrak {w}}_v$
is a pair of integers. For a continuous function
![]() $f:N(F)\backslash G({\mathbb {A}}_F)\to {\mathbb {C}}$
with
$f:N(F)\backslash G({\mathbb {A}}_F)\to {\mathbb {C}}$
with
![]() $\psi _t$
-Whittaker function
$\psi _t$
-Whittaker function
![]() $f_t$
for
$f_t$
for
![]() $t\in F_{>0}$
, let
$t\in F_{>0}$
, let
![]() $f_{t,{\mathrm {qhol}}}$
be the quasi-holomorphic projection of
$f_{t,{\mathrm {qhol}}}$
be the quasi-holomorphic projection of
![]() $f_t$
of weight
$f_t$
of weight
![]() ${\mathfrak {w}}$
at all infinite places (if it is well defined).
${\mathfrak {w}}$
at all infinite places (if it is well defined).
For an automorphic form f on
![]() $G({\mathbb {A}}_F)$
, the cuspidal holomorphic projection
$G({\mathbb {A}}_F)$
, the cuspidal holomorphic projection
![]() $f_{{\mathrm {chol}}}$
of weight
$f_{{\mathrm {chol}}}$
of weight
![]() ${\mathfrak {w}}$
of f is the
${\mathfrak {w}}$
of f is the
![]() $L^2$
-orthogonal projection of f to the subspace
$L^2$
-orthogonal projection of f to the subspace
![]() ${\mathcal {A}}_{{\mathrm {hol}}}(G,{\mathfrak {w}})$
of cusp forms – that is, for every cusp form
${\mathcal {A}}_{{\mathrm {hol}}}(G,{\mathfrak {w}})$
of cusp forms – that is, for every cusp form
![]() $\phi \in {\mathcal {A}}_{{\mathrm {hol}}}(G,{\mathfrak {w}})$
, the Petersson inner product
$\phi \in {\mathcal {A}}_{{\mathrm {hol}}}(G,{\mathfrak {w}})$
, the Petersson inner product
![]() $\langle {f,\phi } \rangle $
equals
$\langle {f,\phi } \rangle $
equals
![]() $\langle {f_{{\mathrm {chol}}},\phi } \rangle $
.
$\langle {f_{{\mathrm {chol}}},\phi } \rangle $
.
Lemma 3.3.1 [Reference LiuLiu11b, Proposition 6.2][Reference Yuan, Zhang and ZhangYZZ13, Proposition 6.12].
Assume that there exists
![]() $\epsilon>0$
such that for
$\epsilon>0$
such that for
![]() $v\in \infty $
and
$v\in \infty $
and
![]() $a \in E_v^\times $
with
$a \in E_v^\times $
with
![]() $|a|_{E_v}\to \infty $
, we have
$|a|_{E_v}\to \infty $
, we have
where
![]() $m(a)$
is as in 2.5. Then for
$m(a)$
is as in 2.5. Then for
![]() $t\in F_{>0}$
,
$t\in F_{>0}$
,
![]() $f_{t,{\mathrm {qhol}}}$
is well defined and
$f_{t,{\mathrm {qhol}}}$
is well defined and
![]() $f_{t,{\mathrm {qhol}}}=f_{{\mathrm {chol}},t}$
.
$f_{t,{\mathrm {qhol}}}=f_{{\mathrm {chol}},t}$
.
3.3.2 Holomorphic projections of
 ${\theta E} ' (0,g,\phi )$
${\theta E} ' (0,g,\phi )$
Let
![]() ${\mathfrak {w}}={\mathfrak {w}}_{\chi _{_{\mathbb {V}}}}$
be as in 2.9. Then
${\mathfrak {w}}={\mathfrak {w}}_{\chi _{_{\mathbb {V}}}}$
be as in 2.9. Then
![]() $|{\mathfrak {w}}_v|=n+1$
. Holomorphic projections below are of weight
$|{\mathfrak {w}}_v|=n+1$
. Holomorphic projections below are of weight
![]() ${\mathfrak {w}}$
. Retrieve the notations in 3.2.1. Let
${\mathfrak {w}}$
. Retrieve the notations in 3.2.1. Let
![]() ${\theta E}^{\prime }_{{\mathrm {chol}}}(0,g,\phi )$
be the cuspidal holomorphic projection of the derivative
${\theta E}^{\prime }_{{\mathrm {chol}}}(0,g,\phi )$
be the cuspidal holomorphic projection of the derivative
![]() ${\theta E}'(0,g,\phi )$
. For
${\theta E}'(0,g,\phi )$
. For
![]() $t\in F_{>0}$
, let
$t\in F_{>0}$
, let
![]() ${\theta E}^{\prime }_{{\mathrm {chol}},t}(0,g,\phi )$
be its
${\theta E}^{\prime }_{{\mathrm {chol}},t}(0,g,\phi )$
be its
![]() $\psi _t$
-Whittaker function. Let
$\psi _t$
-Whittaker function. Let
![]() ${\theta E}_t(s,g,\phi )$
be the
${\theta E}_t(s,g,\phi )$
be the
![]() $\psi _t$
-Whittaker function of
$\psi _t$
-Whittaker function of
![]() ${\theta E}(s,g,\phi )$
. Let
${\theta E}(s,g,\phi )$
. Let
![]() ${\theta E}_{t,{\mathrm {qhol}}}'(0,g,\phi )$
be the quasi-holomorphic projection of
${\theta E}_{t,{\mathrm {qhol}}}'(0,g,\phi )$
be the quasi-holomorphic projection of
![]() $ {\theta E}_t'(0,g,\phi )$
if it is well defined. The difference between
$ {\theta E}_t'(0,g,\phi )$
if it is well defined. The difference between
![]() ${\theta E}^{\prime }_{{\mathrm {chol}},t}(0,g,\phi )$
and
${\theta E}^{\prime }_{{\mathrm {chol}},t}(0,g,\phi )$
and
![]() ${\theta E}_{t,{\mathrm {qhol}}}'(0,g,\phi )$
is given as follows.
${\theta E}_{t,{\mathrm {qhol}}}'(0,g,\phi )$
is given as follows.
For
![]() $\phi =\phi _1\otimes \phi _2\in \overline {\mathcal {S}}\left ( {\mathbb {V}}\right )$
with
$\phi =\phi _1\otimes \phi _2\in \overline {\mathcal {S}}\left ( {\mathbb {V}}\right )$
with
![]() $\phi _1\in {\mathcal {S}}\left ( {\mathbb {W}}\right )$
and
$\phi _1\in {\mathcal {S}}\left ( {\mathbb {W}}\right )$
and
![]() $\phi _2\in \overline {\mathcal {S}}\left ( V^\sharp ({\mathbb {A}}_E)\right )$
, define
$\phi _2\in \overline {\mathcal {S}}\left ( V^\sharp ({\mathbb {A}}_E)\right )$
, define
which is the product of
![]() $E_0(s,g,\phi _1)$
and the constant term of
$E_0(s,g,\phi _1)$
and the constant term of
![]() $\theta (g,\phi _2)$
. See (3.9). The definition extends to general
$\theta (g,\phi _2)$
. See (3.9). The definition extends to general
![]() $\phi \in {\mathcal {S}}\left ( {\mathbb {V}}\right )$
by linearity. By (3.3) and (3.4), we can define an Eisenstein series
$\phi \in {\mathcal {S}}\left ( {\mathbb {V}}\right )$
by linearity. By (3.3) and (3.4), we can define an Eisenstein series
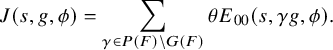 $$ \begin{align*}J(s,g,\phi)=\sum_{\gamma\in P(F)\backslash G(F)}{\theta E}_{00}(s,\gamma g,\phi). \end{align*} $$
$$ \begin{align*}J(s,g,\phi)=\sum_{\gamma\in P(F)\backslash G(F)}{\theta E}_{00}(s,\gamma g,\phi). \end{align*} $$
For
![]() $t\in F_{>0}$
, let
$t\in F_{>0}$
, let
![]() $J_t(s,g,\phi )$
be its
$J_t(s,g,\phi )$
be its
![]() $\psi _t$
-Whittaker function. Let
$\psi _t$
-Whittaker function. Let
![]() $J_{t,{\mathrm {qhol}}}'(0,g,\phi )$
be the quasi-holomorphic projection of the derivative
$J_{t,{\mathrm {qhol}}}'(0,g,\phi )$
be the quasi-holomorphic projection of the derivative
![]() $J_t'(0,g,\phi )$
if it is well defined.
$J_t'(0,g,\phi )$
if it is well defined.
Remark 3.3.2. In the notations of [Reference TanTan99],
![]() $\delta (g)^s \omega (g)\phi (0)$
is in the degenerate principal series
$\delta (g)^s \omega (g)\phi (0)$
is in the degenerate principal series
![]() $I(n/2+s,\chi _{_{\mathbb {V}}})$
, while
$I(n/2+s,\chi _{_{\mathbb {V}}})$
, while
![]() $W_0(s,g,\phi _1) \omega (g)\phi _2(0)$
is in
$W_0(s,g,\phi _1) \omega (g)\phi _2(0)$
is in
![]() $I(n/2-s,\chi _{_{\mathbb {V}}})$
by (3.3) and (3.4).
$I(n/2-s,\chi _{_{\mathbb {V}}})$
by (3.3) and (3.4).
Lemma 3.3.3. If one of
![]() $ {\theta E}_{t,{\mathrm {qhol}}}'(0,g,\phi )$
and
$ {\theta E}_{t,{\mathrm {qhol}}}'(0,g,\phi )$
and
![]() $J_{t,{\mathrm {qhol}}}'(0,g,\phi )$
is well defined, then so is the other one. In this case,
$J_{t,{\mathrm {qhol}}}'(0,g,\phi )$
is well defined, then so is the other one. In this case,
![]() ${\theta E}^{\prime }_{{\mathrm {chol}},t}(0,g,\phi )={\theta E}_{t,{\mathrm {qhol}}}'(0,g,\phi )-J_{t,{\mathrm {qhol}}}'(0,g,\phi )$
.
${\theta E}^{\prime }_{{\mathrm {chol}},t}(0,g,\phi )={\theta E}_{t,{\mathrm {qhol}}}'(0,g,\phi )-J_{t,{\mathrm {qhol}}}'(0,g,\phi )$
.
Proof. By the same proof of [Reference Yuan, Zhang and ZhangYZZ13, Lemma 6.13],
![]() ${\theta E}' (0,m(a)g,\phi )-{\theta E}_{00}'(0,m(a)g,\phi )$
is exponentially decay, and
${\theta E}' (0,m(a)g,\phi )-{\theta E}_{00}'(0,m(a)g,\phi )$
is exponentially decay, and
![]() $J' (0,m(a)g,\phi )-{\theta E}_{00}'(0,m(a)g,\phi )$
is exponentially decay up to the derivative at
$J' (0,m(a)g,\phi )-{\theta E}_{00}'(0,m(a)g,\phi )$
is exponentially decay up to the derivative at
![]() $s=0$
of the intertwining part of the constant term. The intertwining part of the constant term lies in
$s=0$
of the intertwining part of the constant term. The intertwining part of the constant term lies in
![]() $I(-n/2\pm s,\chi _{_{\mathbb {V}}})$
so that its derivative at
$I(-n/2\pm s,\chi _{_{\mathbb {V}}})$
so that its derivative at
![]() $s=0$
has growth rate
$s=0$
has growth rate
![]() $O_g\left (|a | _{E_v}^{-n/2+1/2+\epsilon } \right )$
(in the notations in Lemma 3.3.1). In particular, both differences satisfy the growth condition in Lemma 3.3.1. Thus,
$O_g\left (|a | _{E_v}^{-n/2+1/2+\epsilon } \right )$
(in the notations in Lemma 3.3.1). In particular, both differences satisfy the growth condition in Lemma 3.3.1. Thus,
![]() ${\theta E}' (0,g,\phi )- J' (0,g,\phi ) $
satisfies the growth condition in Lemma 3.3.1. Since the cuspidal holomorphic projection of the Eisenstein series
${\theta E}' (0,g,\phi )- J' (0,g,\phi ) $
satisfies the growth condition in Lemma 3.3.1. Since the cuspidal holomorphic projection of the Eisenstein series
![]() $J(s,g,\phi )$
is
$J(s,g,\phi )$
is
![]() $0$
, the lemma follows.
$0$
, the lemma follows.
3.3.3 A new Eisenstein series
We introduce a new Eisenstein series in order to compute
![]() $J'(0,g,\phi )$
. For
$J'(0,g,\phi )$
. For
![]() $\phi _v=\phi _{v,1}\otimes \phi _{2,v}\in {\mathcal {S}}\left ( {\mathbb {V}}(E_v)\right )$
with
$\phi _v=\phi _{v,1}\otimes \phi _{2,v}\in {\mathcal {S}}\left ( {\mathbb {V}}(E_v)\right )$
with
![]() $\phi _{v,1}\in {\mathcal {S}}\left ( {\mathbb {W}}_v\right )$
and
$\phi _{v,1}\in {\mathcal {S}}\left ( {\mathbb {W}}_v\right )$
and
![]() $\phi _{2,v}\in {\mathcal {S}}\left ( V^\sharp (E_v)\right )$
, define a function on
$\phi _{2,v}\in {\mathcal {S}}\left ( V^\sharp (E_v)\right )$
, define a function on
![]() $G(F_v)\times V^\sharp (E_v)$
:
$G(F_v)\times V^\sharp (E_v)$
:
For the moment, we only need
Extend this definition to the whole
![]() $ {\mathcal {S}}\left ( {\mathbb {V}}(E_v)\right )$
linearly.
$ {\mathcal {S}}\left ( {\mathbb {V}}(E_v)\right )$
linearly.
By (3.3), (3.4) and Lemma 3.1.3 (1), a direct computation shows the following lemma.
Lemma 3.3.4. The function
![]() $c(g,\phi _v)$
on
$c(g,\phi _v)$
on
![]() $G(F_v)$
is in the same principal series as
$G(F_v)$
is in the same principal series as
![]() $ \omega (g)\phi _v(0)$
; that is,
$ \omega (g)\phi _v(0)$
; that is,
(1)
![]() $c(m(a) g , \phi _v )= \chi _{_{\mathbb {V}},v} (a)|\det a|_{E_v }^{\dim {\mathbb {V}}/2} c(g,\phi _v)$
for
$c(m(a) g , \phi _v )= \chi _{_{\mathbb {V}},v} (a)|\det a|_{E_v }^{\dim {\mathbb {V}}/2} c(g,\phi _v)$
for
![]() $ a\in E_v^\times $
;
$ a\in E_v^\times $
;
(2)
![]() $c(n(b) g , \phi _v )= c(g,\phi _v)$
for
$c(n(b) g , \phi _v )= c(g,\phi _v)$
for
![]() $ b\in F_v$
.
$ b\in F_v$
.
Thus, we can define the following Eisenstein series in the case that
![]() $\phi $
is a pure tensor:
$\phi $
is a pure tensor:
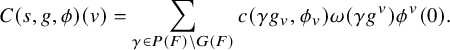 $$ \begin{align*}C(s,g,\phi)(v)=\sum_{\gamma\in P(F)\backslash G(F)}c(\gamma g_v,\phi_v) \omega(\gamma g^v)\phi^v(0).\end{align*} $$
$$ \begin{align*}C(s,g,\phi)(v)=\sum_{\gamma\in P(F)\backslash G(F)}c(\gamma g_v,\phi_v) \omega(\gamma g^v)\phi^v(0).\end{align*} $$
Lemma 3.3.5. For all but finitely many finite places,
![]() $c(g,\phi _v)=0$
for all g.
$c(g,\phi _v)=0$
for all g.
Proof. If
![]() $v\in \infty $
, by Lemma 3.1.3 (3) which says
$v\in \infty $
, by Lemma 3.1.3 (3) which says
![]() $ W^\circ _0(s,g,\phi )=\delta _v(g)^{-s}\omega (g)\phi (0),$
we clearly have
$ W^\circ _0(s,g,\phi )=\delta _v(g)^{-s}\omega (g)\phi (0),$
we clearly have
![]() $c(g,\phi _v) = 0$
. The same is true if
$c(g,\phi _v) = 0$
. The same is true if
![]() $E_v/{\mathbb {Q}}_{v}$
is unramified and
$E_v/{\mathbb {Q}}_{v}$
is unramified and
![]() $\phi =1_{{\mathcal {O}}_{E_v}}$
by Lemma 3.1.3 (2). These cases cover all but finitely many finite places.
$\phi =1_{{\mathcal {O}}_{E_v}}$
by Lemma 3.1.3 (2). These cases cover all but finitely many finite places.
Let
where the sum is over these finite places of F. Let
![]() $C_t(s,g,\phi )$
be the
$C_t(s,g,\phi )$
be the
![]() $\psi _t$
-Whittaker function of
$\psi _t$
-Whittaker function of
![]() $C(0,g,\phi )$
. The definitions can be obviously extended to the whole
$C(0,g,\phi )$
. The definitions can be obviously extended to the whole
![]() $ {\mathcal {S}}\left ( {\mathbb {V}}\right )$
by linearity.
$ {\mathcal {S}}\left ( {\mathbb {V}}\right )$
by linearity.
By (3.16), a direct computation shows that
3.3.4 Gaussian functions and holomorphy
Below in this section, assume that
![]() ${\mathbb {V}} $
is totally positive definite and
${\mathbb {V}} $
is totally positive definite and
![]() $\phi = \phi _\infty \otimes \phi ^\infty \in \overline {\mathcal {S}}\left ( {\mathbb {V}}\right )$
. (So
$\phi = \phi _\infty \otimes \phi ^\infty \in \overline {\mathcal {S}}\left ( {\mathbb {V}}\right )$
. (So
![]() $ \phi _\infty $
is Gaussian. See 2.3.) Let
$ \phi _\infty $
is Gaussian. See 2.3.) Let
![]() $v\in \infty .$
Then
$v\in \infty .$
Then
for
![]() $[k_1,k_2]\in K_v^{\max }$
as in 2.5 if
$[k_1,k_2]\in K_v^{\max }$
as in 2.5 if
![]() ${\mathfrak {w}}_v=(w_1,w_2)$
. (Indeed, first check (3.26) for
${\mathfrak {w}}_v=(w_1,w_2)$
. (Indeed, first check (3.26) for
![]() $g=w_v$
and
$g=w_v$
and
![]() $g\in K_v^{\max }$
being diagonal, then for
$g\in K_v^{\max }$
being diagonal, then for
![]() $g\in K_v^{\max }$
being anti-diagonal, and finally for general
$g\in K_v^{\max }$
being anti-diagonal, and finally for general
![]() $g\in K_v^{\max }$
.) Then by the Iwasawa decomposition, it is easy to check that for
$g\in K_v^{\max }$
.) Then by the Iwasawa decomposition, it is easy to check that for
![]() $g\in G(F_v), x\in {\mathbb {V}}(E_v)$
,
$g\in G(F_v), x\in {\mathbb {V}}(E_v)$
,
By (3.2) combined with (3.25), (3.3) and (3.4),
![]() $W_{v,t} (0, \cdot , \phi _v)$
is a multiple of
$W_{v,t} (0, \cdot , \phi _v)$
is a multiple of
![]() $ W^{{\mathfrak {w}}_v}_{v, t} $
. Then by [Reference Yuan, Zhang and ZhangYZZ13, Proposition 2.11 (2) (4)], we have
$ W^{{\mathfrak {w}}_v}_{v, t} $
. Then by [Reference Yuan, Zhang and ZhangYZZ13, Proposition 2.11 (2) (4)], we have
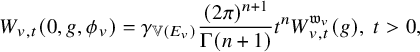 $$ \begin{align} W_{v,t} (0, g, \phi_v) &=\gamma_{{\mathbb{V}}(E_v)} \frac{(2\pi)^{n+1}}{\Gamma(n+1)} t^n W^{{\mathfrak{w}}_v}_{v, t}(g), \ t>0, \end{align} $$
$$ \begin{align} W_{v,t} (0, g, \phi_v) &=\gamma_{{\mathbb{V}}(E_v)} \frac{(2\pi)^{n+1}}{\Gamma(n+1)} t^n W^{{\mathfrak{w}}_v}_{v, t}(g), \ t>0, \end{align} $$
Lemma 3.3.6. Both
![]() $E(0,g,\phi )$
and
$E(0,g,\phi )$
and
![]() $C(0,g,\phi )$
are holomorphic of weight
$C(0,g,\phi )$
are holomorphic of weight
![]() ${\mathfrak {w}}$
.
${\mathfrak {w}}$
.
Proof. For
![]() $E(0,g,\phi )$
, use (3.8), (3.9), (3.26), (3.27) and (3.28). For
$E(0,g,\phi )$
, use (3.8), (3.9), (3.26), (3.27) and (3.28). For
![]() $C(0,g,\phi )$
, by Lemma 3.1.3 (3),
$C(0,g,\phi )$
, by Lemma 3.1.3 (3),
![]() $c(g,\phi _v)=0$
for
$c(g,\phi _v)=0$
for
![]() $v\in \infty $
. Thus,
$v\in \infty $
. Thus,
![]() $C(s,g,\phi )(v)=0$
for
$C(s,g,\phi )(v)=0$
for
![]() $v\in \infty $
. The rest of the proof is the same as the proof for
$v\in \infty $
. The rest of the proof is the same as the proof for
![]() $E(0,g,\phi )$
.
$E(0,g,\phi )$
.
For
![]() $t\in F^\times $
, let
$t\in F^\times $
, let
![]() $ E_t'(0,g,\phi )(v)$
be as in (3.11) so that we have the decomposition (3.12). Let
$ E_t'(0,g,\phi )(v)$
be as in (3.11) so that we have the decomposition (3.12). Let
By (3.27) and (3.28), if
![]() $t\in F_{>0}$
, then
$t\in F_{>0}$
, then
![]() $E^{\prime }_{t,{\mathrm {f}}}(0,g,\phi )$
is a multiple of
$E^{\prime }_{t,{\mathrm {f}}}(0,g,\phi )$
is a multiple of
![]() $W^{{\mathfrak {w}}}_{\infty , t}(g_\infty )$
; otherwise,
$W^{{\mathfrak {w}}}_{\infty , t}(g_\infty )$
; otherwise,
![]() $E^{\prime }_{t,{\mathrm {f}}}(0,g,\phi )=0$
. We call
$E^{\prime }_{t,{\mathrm {f}}}(0,g,\phi )=0$
. We call
![]() $E^{\prime }_{t,{\mathrm {f}}}(0,g,\phi )$
the holomorphic part of the Whittaker function
$E^{\prime }_{t,{\mathrm {f}}}(0,g,\phi )$
the holomorphic part of the Whittaker function
![]() $E_t'(0,g,\phi )$
.
$E_t'(0,g,\phi )$
.
3.3.5 Properties of Eisenstein series
We list some properties of the above Eisenstein series for later use. The reader may skip these properties for the moment.
By [Reference YuanYZ18, Lemma 7.6 (2)] (or its proof) and taking care of the difference between the modulus characters mentioned in 2.6, we have the following lemma.
Lemma 3.3.7. Let
![]() $E_v/F_v$
be split,
$E_v/F_v$
be split,
![]() ${\mathbb {W}}_v=E_v$
and
${\mathbb {W}}_v=E_v$
and
![]() $q={\mathrm {Nm}}$
. Assume
$q={\mathrm {Nm}}$
. Assume
![]() $\phi _v=\phi _{v,1}\otimes \phi _{v,2}$
, where
$\phi _v=\phi _{v,1}\otimes \phi _{v,2}$
, where
![]() $\phi _{v,1}=1_{{\mathcal {O}}_{E_v}}$
and
$\phi _{v,1}=1_{{\mathcal {O}}_{E_v}}$
and
![]() $\phi _{v,2}\in {\mathcal {S}}\left ( V^\sharp (E_v)\right )$
. Then
$\phi _{v,2}\in {\mathcal {S}}\left ( V^\sharp (E_v)\right )$
. Then
![]() $c(1,\phi _v) =2 \log |{\mathrm {Diff}}_{v}|_v \phi _v(0),$
where
$c(1,\phi _v) =2 \log |{\mathrm {Diff}}_{v}|_v \phi _v(0),$
where
![]() ${\mathrm {Diff}}_{v}$
is the different of
${\mathrm {Diff}}_{v}$
is the different of
![]() $F_v/{\mathbb {Q}}_{v}$
.
$F_v/{\mathbb {Q}}_{v}$
.
We omit the routine proof of the following analog of (3.2).
Lemma 3.3.8. For a place v of F and
![]() $k\in K^{\max }_v$
, we have
$k\in K^{\max }_v$
, we have
![]() $E(s,g,\omega (k)\phi )=E(s,gk,\phi )$
. The same relation holds for
$E(s,g,\omega (k)\phi )=E(s,gk,\phi )$
. The same relation holds for
![]() $C(s,g,\phi )$
,
$C(s,g,\phi )$
,
![]() ${\theta E}(s,g,\phi ) $
,
${\theta E}(s,g,\phi ) $
,
![]() ${\theta E}^{\prime }_{{\mathrm {chol}}}(0,g,\phi ),$
and their t-th Whittaker/Fourier coefficients, and
${\theta E}^{\prime }_{{\mathrm {chol}}}(0,g,\phi ),$
and their t-th Whittaker/Fourier coefficients, and
![]() $E^{\prime }_{t}(0,g,\phi ) (v)$
(thus,
$E^{\prime }_{t}(0,g,\phi ) (v)$
(thus,
![]() $E^{\prime }_{t,{\mathrm {f}}}(0,g,\phi )$
) for
$E^{\prime }_{t,{\mathrm {f}}}(0,g,\phi )$
) for
![]() $t\in F^\times $
.
$t\in F^\times $
.
Lemma 3.3.9.
(1) We have
![]() $E_0(0,g,\phi )= \omega ( g)\phi (0)$
.
$E_0(0,g,\phi )= \omega ( g)\phi (0)$
.
(2) If, moreover,
![]() ${\mathbb {V}}$
is incoherent, then for a finite place v,
${\mathbb {V}}$
is incoherent, then for a finite place v,
![]() $C_0(0,g,\phi )(v)= c(g_v,\phi _v)\omega ( g^v)\phi ^v (0)$
.
$C_0(0,g,\phi )(v)= c(g_v,\phi _v)\omega ( g^v)\phi ^v (0)$
.
(3) In (2), assume that
![]() $\phi _{{{v}}}$
is supported outside
$\phi _{{{v}}}$
is supported outside
![]() $V^\sharp (E_{v})$
for v in a set S of two places of F and
$V^\sharp (E_{v})$
for v in a set S of two places of F and
![]() $g\in P ({\mathbb {A}}_{F,S })G({\mathbb {A}}_F^{S })$
. Then
$g\in P ({\mathbb {A}}_{F,S })G({\mathbb {A}}_F^{S })$
. Then
![]() $E_0(0,g,\phi )=0$
and
$E_0(0,g,\phi )=0$
and
![]() $C_0(0,g,\phi )=0$
.
$C_0(0,g,\phi )=0$
.
Proof. (1) If
![]() $F={\mathbb {Q}},n=1$
and
$F={\mathbb {Q}},n=1$
and
![]() ${\mathbb {V}}^\infty $
is not split at some finite place, it is proved in [Reference Yuan, Zhang and ZhangYZZ13, Proposition 2.9 (3)]. If
${\mathbb {V}}^\infty $
is not split at some finite place, it is proved in [Reference Yuan, Zhang and ZhangYZZ13, Proposition 2.9 (3)]. If
![]() $F\neq {\mathbb {Q}}$
so that we have at least 2 infinite places, its proof is similar to the one in [Reference Yuan, Zhang and ZhangYZZ13, Proposition 2.9 (3)] by using (3.9) and (3.28) (for
$F\neq {\mathbb {Q}}$
so that we have at least 2 infinite places, its proof is similar to the one in [Reference Yuan, Zhang and ZhangYZZ13, Proposition 2.9 (3)] by using (3.9) and (3.28) (for
![]() $t=0$
).
$t=0$
).
(2) The proof is similar, with the fact that
![]() ${\mathbb {V}}$
is not split at (at least) 2 places outside v by the incoherence. See also [Reference YuanYua22, p 65-66].
${\mathbb {V}}$
is not split at (at least) 2 places outside v by the incoherence. See also [Reference YuanYua22, p 65-66].
(3) follows from (1)(2) directly.
3.3.6 Compute
 $J_{t,{\mathrm {qhol}}}'(0,g,\phi )$
$J_{t,{\mathrm {qhol}}}'(0,g,\phi )$
Let
![]() $t\in F_{>0}$
. For
$t\in F_{>0}$
. For
![]() $v\in \infty $
, let
$v\in \infty $
, let
![]() $E_{t,{\mathrm {qhol}}}'(0,g,\phi )(v)$
be the quasi-holomorphic projection of
$E_{t,{\mathrm {qhol}}}'(0,g,\phi )(v)$
be the quasi-holomorphic projection of
![]() $ E_t'(0,g,\phi )(v)$
. By (3.24), Lemma 3.3.6 and the discussion below it, to compute
$ E_t'(0,g,\phi )(v)$
. By (3.24), Lemma 3.3.6 and the discussion below it, to compute
![]() $J_{t,{\mathrm {qhol}}}'(0,g,\phi )$
, we only need to compute
$J_{t,{\mathrm {qhol}}}'(0,g,\phi )$
, we only need to compute
![]() $E_{t,{\mathrm {qhol}}}'(0,g,\phi )(v)$
.
$E_{t,{\mathrm {qhol}}}'(0,g,\phi )(v)$
.
Consider the quasi-holomorphic projection
![]() $W_{v,t,{\mathrm {qhol}}}' (0, g, \phi _v)$
of
$W_{v,t,{\mathrm {qhol}}}' (0, g, \phi _v)$
of
![]() $W_{v,t}' (0, g, \phi _v)$
. By definition, it is a multiple of
$W_{v,t}' (0, g, \phi _v)$
. By definition, it is a multiple of
![]() $W^{{\mathfrak {w}}_v}_{v, t}(g)$
. Then by (3.27),
$W^{{\mathfrak {w}}_v}_{v, t}(g)$
. Then by (3.27),
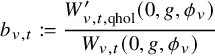 $$ \begin{align*}b_{v,t}: = \frac{W_{v,t,{\mathrm{qhol}}}' (0, g, \phi_v)}{ W_{v,t} (0, g, \phi_v)} \end{align*} $$
$$ \begin{align*}b_{v,t}: = \frac{W_{v,t,{\mathrm{qhol}}}' (0, g, \phi_v)}{ W_{v,t} (0, g, \phi_v)} \end{align*} $$
is a well defined constant
![]() $b_{v,t}$
. We define
$b_{v,t}$
. We define
Remark 3.3.10. The constant
![]() ${{\mathfrak {b}}}$
can be explicitly computed using [Reference Yuan, Zhang and ZhangYZZ13, Proposition 2.11] and [Reference YuanYua22, Lemma 3.3] in principle. For example, if
${{\mathfrak {b}}}$
can be explicitly computed using [Reference Yuan, Zhang and ZhangYZZ13, Proposition 2.11] and [Reference YuanYua22, Lemma 3.3] in principle. For example, if
![]() $ n=1$
, then
$ n=1$
, then
![]() ${\mathfrak {b}} =-({1+\log 4})$
. (This is twice of the corresponding number in [Reference YuanYua22, Lemma 3.3 (2)] due to the difference between the modulus characters mentioned in 2.6.) It is more complicated in general. The full computation could be tedious, and the result in a previous version of our paper actually contains a mistake. (Fortunately, we will not need the explict number of
${\mathfrak {b}} =-({1+\log 4})$
. (This is twice of the corresponding number in [Reference YuanYua22, Lemma 3.3 (2)] due to the difference between the modulus characters mentioned in 2.6.) It is more complicated in general. The full computation could be tedious, and the result in a previous version of our paper actually contains a mistake. (Fortunately, we will not need the explict number of
![]() ${\mathfrak {b}}$
.) Ziqi Guo (student of Yuan, author of [Reference YuanYua22]) pointed this out to us and informed us that he will give full details on this in his upcoming work.
${\mathfrak {b}}$
.) Ziqi Guo (student of Yuan, author of [Reference YuanYua22]) pointed this out to us and informed us that he will give full details on this in his upcoming work.
Lemma 3.3.11. We have
![]() $b_{v,t}=b_{v,1}+\log | t|_v$
and
$b_{v,t}=b_{v,1}+\log | t|_v$
and
![]() $b_{v,1}$
is independent of v.
$b_{v,1}$
is independent of v.
Proof. The lemma follows direct computations with the following ingredients. For the equation, use (3.4) and (3.27). Note that the dependence on v is on the weight
![]() ${\mathfrak {w}}_v$
. We use (3.2) and (3.26) for
${\mathfrak {w}}_v$
. We use (3.2) and (3.26) for
![]() $g\in K_v^{\max }$
.
$g\in K_v^{\max }$
.
Then
![]() $E_{t,{\mathrm {qhol}}}'(0,g,\phi )(v)=({{\mathfrak {b}}} + \log |t|_v) E_t(0,g,\phi ). $
Since both
$E_{t,{\mathrm {qhol}}}'(0,g,\phi )(v)=({{\mathfrak {b}}} + \log |t|_v) E_t(0,g,\phi ). $
Since both
![]() $E(0,g,\phi )$
and
$E(0,g,\phi )$
and
![]() $C(0,g,\phi )$
in (3.24) are holomorphic of weight
$C(0,g,\phi )$
in (3.24) are holomorphic of weight
![]() ${\mathfrak {w}}$
, we have
${\mathfrak {w}}$
, we have
Combined with Lemma 3.3.3, we have
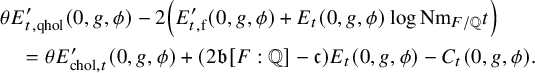 $$ \begin{align} \begin{aligned} &{\theta E}_{t,{\mathrm{qhol}}}^{\prime}(0,g,\phi)-2\left( E^{\prime}_{t,{\mathrm{f}}}(0,g,\phi) +E_t(0,g,\phi) \log {\mathrm{Nm}}_{F/{\mathbb{Q}}}t\right)\\& \quad ={\theta E}^{\prime}_{{\mathrm{chol}},t}(0,g,\phi) +( 2{{\mathfrak{b}}}[F:{\mathbb{Q}}]-{{\mathfrak{c}}})E_t(0,g,\phi)-C_t(0,g,\phi). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &{\theta E}_{t,{\mathrm{qhol}}}^{\prime}(0,g,\phi)-2\left( E^{\prime}_{t,{\mathrm{f}}}(0,g,\phi) +E_t(0,g,\phi) \log {\mathrm{Nm}}_{F/{\mathbb{Q}}}t\right)\\& \quad ={\theta E}^{\prime}_{{\mathrm{chol}},t}(0,g,\phi) +( 2{{\mathfrak{b}}}[F:{\mathbb{Q}}]-{{\mathfrak{c}}})E_t(0,g,\phi)-C_t(0,g,\phi). \end{aligned} \end{align} $$
3.3.7 Quasi-holomorphic projection of
 ${\theta E} ' _t (0,g,\phi )$
${\theta E} ' _t (0,g,\phi )$
Assume that
![]() ${\mathbb {W}}/{\mathbb {E}}$
is incoherent. For
${\mathbb {W}}/{\mathbb {E}}$
is incoherent. For
![]() $v\in \infty $
and W the v-nearby hermitian space of
$v\in \infty $
and W the v-nearby hermitian space of
![]() ${\mathbb {W}}$
, let
${\mathbb {W}}$
, let
![]() $V=W\oplus V^\sharp $
. For
$V=W\oplus V^\sharp $
. For
![]() $x\in V(E_v)-V^\sharp (E_v)$
, define
$x\in V(E_v)-V^\sharp (E_v)$
, define
where
![]() $x_1$
is the projection of x to
$x_1$
is the projection of x to
![]() $W(E_v)$
(so that
$W(E_v)$
(so that
![]() $x_1\neq 0$
), and
$x_1\neq 0$
), and
(For
![]() $s \in {\mathbb {C}}$
with
$s \in {\mathbb {C}}$
with
![]() $ {\mathrm {Re}} s>-n$
,
$ {\mathrm {Re}} s>-n$
,
![]() $P_s(t)$
converges absolutely.) Define
$P_s(t)$
converges absolutely.) Define
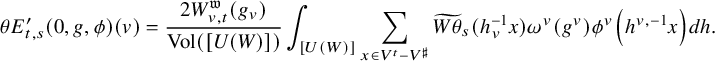 $$ \begin{align} {\theta E}^{\prime}_{t,s} (0,g,\phi)(v) = \frac{2 W^{\mathfrak{w}}_{v,t}(g_v) }{ {\mathrm{Vol}}([U(W)]) } \int_{ [U(W)]}\sum_{x\in V {{}} ^t -V^\sharp} \widetilde{W\theta}_{s} (h_v^{-1}x) \omega^v(g^v)\phi^v \left( h^{v,-1} x\right) dh. \end{align} $$
$$ \begin{align} {\theta E}^{\prime}_{t,s} (0,g,\phi)(v) = \frac{2 W^{\mathfrak{w}}_{v,t}(g_v) }{ {\mathrm{Vol}}([U(W)]) } \int_{ [U(W)]}\sum_{x\in V {{}} ^t -V^\sharp} \widetilde{W\theta}_{s} (h_v^{-1}x) \omega^v(g^v)\phi^v \left( h^{v,-1} x\right) dh. \end{align} $$
Lemma 3.3.12. For
![]() $s\in {\mathbb {C}}$
with
$s\in {\mathbb {C}}$
with
![]() ${\mathrm {Re}} s>0$
, (3.33) converges absolutely and
${\mathrm {Re}} s>0$
, (3.33) converges absolutely and
![]() ${\theta E}^{\prime }_{t,s} (0,g,\phi )(v)$
is holomorphic on s. Moreover,
${\theta E}^{\prime }_{t,s} (0,g,\phi )(v)$
is holomorphic on s. Moreover,
![]() $ {\theta E}^{\prime }_{t,s} (0,g,\phi )(v)$
admits a meromorphic continuation to
$ {\theta E}^{\prime }_{t,s} (0,g,\phi )(v)$
admits a meromorphic continuation to
![]() $\{s\in {\mathbb {C}}, {\mathrm {Re}} s>-1\}$
with at most a simple pole at
$\{s\in {\mathbb {C}}, {\mathrm {Re}} s>-1\}$
with at most a simple pole at
![]() $s=0$
.
$s=0$
.
Then the constant term
![]() $\widetilde {\lim \limits _{s\to 0}}{\theta E}^{\prime }_{t,s} (0,g,\phi )(v)$
of
$\widetilde {\lim \limits _{s\to 0}}{\theta E}^{\prime }_{t,s} (0,g,\phi )(v)$
of
![]() $ {\theta E}^{\prime }_{t,s} (0,g,\phi )(v)$
at
$ {\theta E}^{\prime }_{t,s} (0,g,\phi )(v)$
at
![]() $s=0$
is well defined (and used in the following proposition). We will prove Lemma 3.3.12 after Lemma 6.1.10, by comparing
$s=0$
is well defined (and used in the following proposition). We will prove Lemma 3.3.12 after Lemma 6.1.10, by comparing
![]() ${\theta E}^{\prime }_{t,s} (0,g,\phi )(v)$
to a Green function with s-variable, which has a meromorphic continuation.
${\theta E}^{\prime }_{t,s} (0,g,\phi )(v)$
to a Green function with s-variable, which has a meromorphic continuation.
Proposition 3.3.13. Let
![]() $t\in F_{>0}$
and let
$t\in F_{>0}$
and let
![]() $\phi \in \overline {\mathcal {S}}({\mathbb {V}})$
be a pure tensor.
$\phi \in \overline {\mathcal {S}}({\mathbb {V}})$
be a pure tensor.
(1) We have
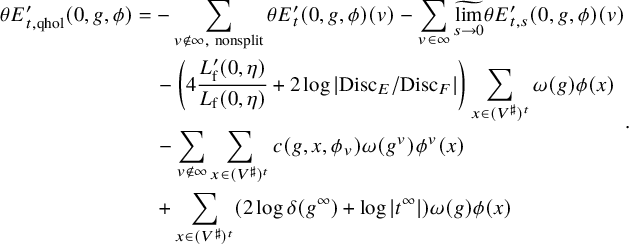 $$ \begin{align} \begin{aligned} {\theta E}_{t,{\mathrm{qhol}}}'(0,g,\phi) &=-\sum_{v \not\in \infty,\ \text{nonsplit}}{\theta E}^{\prime}_t (0,g,\phi)(v)-\sum_{v\in \infty}\widetilde{\lim _{s\to 0}}{\theta E}^{\prime}_{t,s} (0,g,\phi)(v)\\& \quad -\left( 4\frac{L_{\mathrm{f}}'(0,\eta)}{L_{\mathrm{f}}(0,\eta)}+2\log |{\mathrm{Disc}}_E/{\mathrm{Disc}}_F|\right)\sum_{x\in (V^\sharp)^t}\omega(g)\phi(x)\\& \quad -\sum_{v\not\in \infty}\sum_{x\in (V^\sharp)^t}c(g,x,\phi_v)\omega(g^v)\phi^v(x)\\& \quad +\sum_{x\in (V^\sharp)^t}(2\log \delta(g^\infty)+\log|t^\infty|)\omega(g)\phi(x)\end{aligned}. \end{align} $$
$$ \begin{align} \begin{aligned} {\theta E}_{t,{\mathrm{qhol}}}'(0,g,\phi) &=-\sum_{v \not\in \infty,\ \text{nonsplit}}{\theta E}^{\prime}_t (0,g,\phi)(v)-\sum_{v\in \infty}\widetilde{\lim _{s\to 0}}{\theta E}^{\prime}_{t,s} (0,g,\phi)(v)\\& \quad -\left( 4\frac{L_{\mathrm{f}}'(0,\eta)}{L_{\mathrm{f}}(0,\eta)}+2\log |{\mathrm{Disc}}_E/{\mathrm{Disc}}_F|\right)\sum_{x\in (V^\sharp)^t}\omega(g)\phi(x)\\& \quad -\sum_{v\not\in \infty}\sum_{x\in (V^\sharp)^t}c(g,x,\phi_v)\omega(g^v)\phi^v(x)\\& \quad +\sum_{x\in (V^\sharp)^t}(2\log \delta(g^\infty)+\log|t^\infty|)\omega(g)\phi(x)\end{aligned}. \end{align} $$
Here,
![]() $L_{\mathrm {f}}(s,\eta )$
is the finite part of
$L_{\mathrm {f}}(s,\eta )$
is the finite part of
![]() $L(s,\eta )$
.
$L(s,\eta )$
.
(2) Assume that
![]() $\phi _{{{v}}}$
is supported outside
$\phi _{{{v}}}$
is supported outside
![]() $V^\sharp (E_{v})$
for v in a set S of two places of F and
$V^\sharp (E_{v})$
for v in a set S of two places of F and
![]() $g\in P ({\mathbb {A}}_{F,S })G({\mathbb {A}}_F^{S })$
. Then we have
$g\in P ({\mathbb {A}}_{F,S })G({\mathbb {A}}_F^{S })$
. Then we have
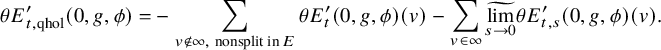 $$ \begin{align} {\theta E}_{t,{\mathrm{qhol}}}'(0,g,\phi) =&-\sum_{v \not\in \infty, \ \text{nonsplit in }E}{\theta E}^{\prime}_t (0,g,\phi)(v)-\sum_{v\in \infty}\widetilde{\lim _{s\to 0}}{\theta E}^{\prime}_{t,s} (0,g,\phi)(v). \end{align} $$
$$ \begin{align} {\theta E}_{t,{\mathrm{qhol}}}'(0,g,\phi) =&-\sum_{v \not\in \infty, \ \text{nonsplit in }E}{\theta E}^{\prime}_t (0,g,\phi)(v)-\sum_{v\in \infty}\widetilde{\lim _{s\to 0}}{\theta E}^{\prime}_{t,s} (0,g,\phi)(v). \end{align} $$
Proof. The proof of (1) is almost identical with [Reference YuanYZ18, Theorem 7.2] and is omitted. (Note that [Reference YuanYZ18, Assumption 7.1] in [Reference YuanYZ18, Theorem 7.2] is only used to identify the quasi-holomorphic projection with the cuspidal holomorphic projection and does not play a role in computing the quasi-holomorphic projection). (2) follows from (1) immediately.
Lemma 3.3.14. Let
![]() $t\in F_{>0}$
and let
$t\in F_{>0}$
and let
![]() $\phi $
be a pure tensor such that
$\phi $
be a pure tensor such that
![]() $\phi ^\infty $
is
$\phi ^\infty $
is
![]() ${\overline {\mathbb {Q}}}$
-valued. Let u be a finite place of F of residue characteristic p. Let
${\overline {\mathbb {Q}}}$
-valued. Let u be a finite place of F of residue characteristic p. Let
![]() $O\subset {\mathbb {V}}_u$
be an open compact neighborhood of
$O\subset {\mathbb {V}}_u$
be an open compact neighborhood of
![]() $0$
and
$0$
and
![]() $\phi ^O= \phi ^u\otimes (\phi _u 1_{{\mathbb {V}}_u-O})$
. Given
$\phi ^O= \phi ^u\otimes (\phi _u 1_{{\mathbb {V}}_u-O})$
. Given
![]() $g\in G({\mathbb {A}}_F^{u })P(F_u)$
, for O small enough, we have
$g\in G({\mathbb {A}}_F^{u })P(F_u)$
, for O small enough, we have
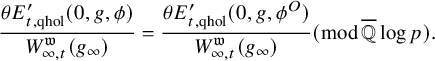 $$ \begin{align*}\frac{{\theta E}_{t,{\mathrm{qhol}}}'(0,g,\phi)}{W^{{\mathfrak{w}}}_{\infty, t}(g_\infty)}= \frac{{\theta E} ^{\prime}_{t,{\mathrm{qhol}}} (0,g,\phi^O)} {W^{{\mathfrak{w}}}_{\infty, t}(g_\infty)}(\operatorname{\mathrm{mod}}\overline{{\mathbb{Q}}}\log p).\end{align*} $$
$$ \begin{align*}\frac{{\theta E}_{t,{\mathrm{qhol}}}'(0,g,\phi)}{W^{{\mathfrak{w}}}_{\infty, t}(g_\infty)}= \frac{{\theta E} ^{\prime}_{t,{\mathrm{qhol}}} (0,g,\phi^O)} {W^{{\mathfrak{w}}}_{\infty, t}(g_\infty)}(\operatorname{\mathrm{mod}}\overline{{\mathbb{Q}}}\log p).\end{align*} $$
Proof. The proof is similar to the one of Lemma 3.2.1, except that we further need (3.22), (3.26), (3.33) and (3.34).
By (3.34), using (3.22) and (3.33), for
![]() $h\in U({\mathbb {W}}_v)$
where v is split in E,
$h\in U({\mathbb {W}}_v)$
where v is split in E,
4 Special divisors
This section is about special divisors on unitary Shimura varieties. It consists of 4.1-4.4. First, we define their generating series which are modular. Second, we introduce their Green functions and show the modularity of the differences between the generating series of different kinds of Green functions. Third, we raise two modularity problems for their admissible extensions on integral models. Finally, we propose a precise conjecture and state our modularity theorems.
4.1 Generating series
Let
![]() ${\mathbb {V}} $
be a totally positive-definite incoherent hermitian space over
${\mathbb {V}} $
be a totally positive-definite incoherent hermitian space over
![]() ${\mathbb {A}}_E$
(with respect to the extension
${\mathbb {A}}_E$
(with respect to the extension
![]() $E/F$
) of dimension
$E/F$
) of dimension
![]() $n+1$
where
$n+1$
where
![]() $n>0$
. Fix an infinite place
$n>0$
. Fix an infinite place
![]() $v_0 \in \infty $
of F. Let
$v_0 \in \infty $
of F. Let
![]() $V_0$
be the unique hermitian space over E such that
$V_0$
be the unique hermitian space over E such that
![]() $V_0({\mathbb {A}}_E^v){\ \simeq \ } {\mathbb {V}}^v$
and
$V_0({\mathbb {A}}_E^v){\ \simeq \ } {\mathbb {V}}^v$
and
![]() $V_0(E_v)$
is of signature
$V_0(E_v)$
is of signature
![]() $(n,1)$
. For an open compact subgroup K of
$(n,1)$
. For an open compact subgroup K of
![]() $U({\mathbb {V}}^\infty )$
, let
$U({\mathbb {V}}^\infty )$
, let
![]() ${\mathrm {Sh}}({\mathbb {V}})_K$
be the n-dimensional smooth unitary Shimura variety associated to
${\mathrm {Sh}}({\mathbb {V}})_K$
be the n-dimensional smooth unitary Shimura variety associated to
![]() $U(V_0)$
of level K over E (see [Reference Liu, Tian, Xiao, Zhang and ZhuLTX+22, 3.2]), which we allow to be a Deligne-Mumford stack. (It is expected that
$U(V_0)$
of level K over E (see [Reference Liu, Tian, Xiao, Zhang and ZhuLTX+22, 3.2]), which we allow to be a Deligne-Mumford stack. (It is expected that
![]() ${\mathrm {Sh}}({\mathbb {V}})_K$
does not depend on the choice of
${\mathrm {Sh}}({\mathbb {V}})_K$
does not depend on the choice of
![]() $v_0$
. See [Reference Li and LiuLL21, Remark 1.2].) See (4.4) for its usual complex uniformization.
$v_0$
. See [Reference Li and LiuLL21, Remark 1.2].) See (4.4) for its usual complex uniformization.
-
• From now on, we always assume that
 ${\mathrm {Sh}}({\mathbb {V}})_K$
is proper.
${\mathrm {Sh}}({\mathbb {V}})_K$
is proper.
Equivalently,
![]() $F\neq {\mathbb {Q}}$
, or
$F\neq {\mathbb {Q}}$
, or
![]() $F={\mathbb {Q}},n=1$
and
$F={\mathbb {Q}},n=1$
and
![]() ${\mathbb {V}}^\infty $
is not split at some finite place.
${\mathbb {V}}^\infty $
is not split at some finite place.
4.1.1 Simple special divisors
Let
![]() ${\mathbb {V}}^{\infty }_{>0}\subset {\mathbb {V}}^{\infty }$
be the subset of x’s such that
${\mathbb {V}}^{\infty }_{>0}\subset {\mathbb {V}}^{\infty }$
be the subset of x’s such that
![]() ${q(x)}\in F_{>0}$
. For
${q(x)}\in F_{>0}$
. For
![]() $x\in {\mathbb {V}}^{\infty }_{>0}$
, let
$x\in {\mathbb {V}}^{\infty }_{>0}$
, let
![]() $ x^\perp $
be the orthogonal complement of
$ x^\perp $
be the orthogonal complement of
![]() ${\mathbb {A}}_E ^\infty x $
in
${\mathbb {A}}_E ^\infty x $
in
![]() ${\mathbb {V}}^\infty $
. Regard
${\mathbb {V}}^\infty $
. Regard
![]() $U\left ( x^{\perp } \right )$
as a subgroup of
$U\left ( x^{\perp } \right )$
as a subgroup of
![]() $U({\mathbb {V}}^\infty )$
. Then we have a finite morphism
$U({\mathbb {V}}^\infty )$
. Then we have a finite morphism
explicated in [Reference KudlaKud97a, (2.4)] and [Reference Li and LiuLL21, Definition 4.1]. The proper pushforward defines a divisor
![]() $Z(x)_K $
on
$Z(x)_K $
on
![]() ${\mathrm {Sh}}({\mathbb {V}})_K$
that is called a simple special divisor. The following observation is trivial.
${\mathrm {Sh}}({\mathbb {V}})_K$
that is called a simple special divisor. The following observation is trivial.
Lemma 4.1.1. We have
![]() $Z(x)_K=Z(kxa)_K$
for every
$Z(x)_K=Z(kxa)_K$
for every
![]() $a\in E^\times , k\in K$
.
$a\in E^\times , k\in K$
.
Let
![]() $L_K$
be the Hodge line bundle on
$L_K$
be the Hodge line bundle on
![]() ${\mathrm {Sh}}({\mathbb {V}})_K$
. See 4.2.1 for the description in terms of the complex uniformization of
${\mathrm {Sh}}({\mathbb {V}})_K$
. See 4.2.1 for the description in terms of the complex uniformization of
![]() ${\mathrm {Sh}}({\mathbb {V}})_K$
. Let
${\mathrm {Sh}}({\mathbb {V}})_K$
. Let
![]() $c_1(L_K^\vee )$
be the first Chern class of the dual of
$c_1(L_K^\vee )$
be the first Chern class of the dual of
![]() $ L_K$
, and
$ L_K$
, and
![]() $[Z(x)_K]\in {\mathrm {Ch}}^{1}({\mathrm {Sh}}({\mathbb {V}})_K) $
the class of
$[Z(x)_K]\in {\mathrm {Ch}}^{1}({\mathrm {Sh}}({\mathbb {V}})_K) $
the class of
![]() $Z(x)_K$
. For
$Z(x)_K$
. For
![]() $ \phi \in \overline {\mathcal {S}}\left ( {\mathbb {V}} \right )^{K}$
the subspace of K-invariant functions, define a formal generating series of divisor classes:
$ \phi \in \overline {\mathcal {S}}\left ( {\mathbb {V}} \right )^{K}$
the subspace of K-invariant functions, define a formal generating series of divisor classes:
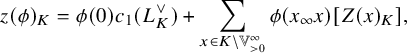 $$ \begin{align*}z(\phi)_K=\phi(0)c_1(L_K^\vee)+\sum_{x\in K\backslash {\mathbb{V}}^{ \infty}_{>0}}\phi( x_\infty x) [Z(x)_K] , \end{align*} $$
$$ \begin{align*}z(\phi)_K=\phi(0)c_1(L_K^\vee)+\sum_{x\in K\backslash {\mathbb{V}}^{ \infty}_{>0}}\phi( x_\infty x) [Z(x)_K] , \end{align*} $$
where
![]() $ x_\infty \in {\mathbb {V}}_\infty $
such that
$ x_\infty \in {\mathbb {V}}_\infty $
such that
![]() $q(x_\infty )={q(x)}\in F_{>0}$
.
$q(x_\infty )={q(x)}\in F_{>0}$
.
Let
![]() ${\mathfrak {w}}={\mathfrak {w}}_{\chi _{_{\mathbb {V}}}}$
which is defined in 2.9.
${\mathfrak {w}}={\mathfrak {w}}_{\chi _{_{\mathbb {V}}}}$
which is defined in 2.9.
Theorem 4.1.2 [Reference LiuLiu11a, Theorem 3.5].
For every
![]() $ \phi \in \overline {\mathcal {S}}\left ( {\mathbb {V}} \right )^{K} $
, we have
$ \phi \in \overline {\mathcal {S}}\left ( {\mathbb {V}} \right )^{K} $
, we have
Note that
![]() $ \dim {\mathrm {Ch}}^{1}({\mathrm {Sh}}({\mathbb {V}})_K)_{{\mathbb {C}}} <\infty .$
$ \dim {\mathrm {Ch}}^{1}({\mathrm {Sh}}({\mathbb {V}})_K)_{{\mathbb {C}}} <\infty .$
4.1.2 Weighted special divisors
For
![]() $\phi \in \overline {\mathcal {S}}\left ( {\mathbb {V}} \right )^{K}$
and
$\phi \in \overline {\mathcal {S}}\left ( {\mathbb {V}} \right )^{K}$
and
![]() $t\in F_{>0}$
, define the weighted special divisor
$t\in F_{>0}$
, define the weighted special divisor
which is a finite sum. Lemma 4.1.1 implies the following lemma.
Lemma 4.1.3. For every
![]() $a\in E^\times $
,
$a\in E^\times $
,
![]() $Z_t(\phi )_K=Z_{a^2t}(\omega (a)\phi )_K.$
$Z_t(\phi )_K=Z_{a^2t}(\omega (a)\phi )_K.$
Let
![]() $\phi = \phi _\infty \otimes \phi ^\infty $
be as in 2.3. We define another weighted special divisor
$\phi = \phi _\infty \otimes \phi ^\infty $
be as in 2.3. We define another weighted special divisor
By (3.26), for
![]() $g\in G({\mathbb {A}}_F)$
, we have
$g\in G({\mathbb {A}}_F)$
, we have
Then
![]() $[Z_t\left ( \omega (\cdot )\phi ^\infty \right )_K] $
is the t-th Fourier coefficient of
$[Z_t\left ( \omega (\cdot )\phi ^\infty \right )_K] $
is the t-th Fourier coefficient of
![]() $z\left (\omega (\cdot )\phi \right )_K$
. See 2.7.
$z\left (\omega (\cdot )\phi \right )_K$
. See 2.7.
Lemma 4.1.4. Let
![]() $\phi \in \overline {\mathcal {S}}\left ( {\mathbb {V}} \right ) $
be a pure tensor. Let u be a finite place of F,
$\phi \in \overline {\mathcal {S}}\left ( {\mathbb {V}} \right ) $
be a pure tensor. Let u be a finite place of F,
![]() $O\subset {\mathbb {V}}_u$
an open compact neighborhood of
$O\subset {\mathbb {V}}_u$
an open compact neighborhood of
![]() $0$
and
$0$
and
![]() $\phi ^O=\phi ^u\otimes (\phi _u 1_{{\mathbb {V}}_u-O})$
. Given
$\phi ^O=\phi ^u\otimes (\phi _u 1_{{\mathbb {V}}_u-O})$
. Given
![]() $g\in G({\mathbb {A}}_F^{u })P(F_u)$
, for O small enough, if K fixes
$g\in G({\mathbb {A}}_F^{u })P(F_u)$
, for O small enough, if K fixes
![]() $\phi ^O$
, then
$\phi ^O$
, then
![]() $ Z_t(\omega (g)\phi ) _K= Z_t(\omega (g)\phi ^O) _K.$
$ Z_t(\omega (g)\phi ) _K= Z_t(\omega (g)\phi ^O) _K.$
Proof. The lemma is an analog to Lemma 3.2.1, and the proof is also similar. We record the proof for the reader’s convenience. Write
![]() $g_u=m(a)n(b)$
, where
$g_u=m(a)n(b)$
, where
![]() $a\in E_u^\times $
. See 2.5. Then
$a\in E_u^\times $
. See 2.5. Then
![]() $\{a x:x\in {\mathbb {V}}_u^t\}\subset {\mathbb {V}}_u^{a^2t} $
. The latter is closed in
$\{a x:x\in {\mathbb {V}}_u^t\}\subset {\mathbb {V}}_u^{a^2t} $
. The latter is closed in
![]() ${\mathbb {V}}_u$
and does not contain 0. Thus,
${\mathbb {V}}_u$
and does not contain 0. Thus,
![]() $O\cap \{ax:x\in {\mathbb {V}}_u^t\}=\emptyset $
if O is small enough. Then the lemma follows from the definition of
$O\cap \{ax:x\in {\mathbb {V}}_u^t\}=\emptyset $
if O is small enough. Then the lemma follows from the definition of
![]() $ Z_t(\omega (g)\phi ) _K$
and the Weil representation formula in 2.8.
$ Z_t(\omega (g)\phi ) _K$
and the Weil representation formula in 2.8.
4.1.3 Change level
For
![]() $K\subset K'$
, let
$K\subset K'$
, let
![]() $\pi _{_K,_{K'}}:{\mathrm {Sh}}({\mathbb {V}})_{K}\to {\mathrm {Sh}}({\mathbb {V}})_{K'}$
be the natural projection.
$\pi _{_K,_{K'}}:{\mathrm {Sh}}({\mathbb {V}})_{K}\to {\mathrm {Sh}}({\mathbb {V}})_{K'}$
be the natural projection.
Lemma 4.1.5 [Reference KudlaKud97a, PROPOSITION 5.10][Reference LiuLiu11a, Corollary 3.4].
We have
![]() $\pi _{_K,_{K'}}^{*}Z_t(\phi )_{K'}=Z_t(\phi )_K$
and
$\pi _{_K,_{K'}}^{*}Z_t(\phi )_{K'}=Z_t(\phi )_K$
and
![]() $\pi _{_K,_{K'}}^{*}L_{K '}=L_K$
. In particular,
$\pi _{_K,_{K'}}^{*}L_{K '}=L_K$
. In particular,
![]() $\pi _{_K,_{K'}}^{*}z(\phi )_{K'}=z(\phi )_K$
.
$\pi _{_K,_{K'}}^{*}z(\phi )_{K'}=z(\phi )_K$
.
Remark 4.1.6. We have
![]() $\pi _{_K,_{K'},*}Z(x)_K =d(x) Z(x)_{K'}$
where
$\pi _{_K,_{K'},*}Z(x)_K =d(x) Z(x)_{K'}$
where
![]() $d(x)$
is the degree of
$d(x)$
is the degree of
![]() $Z(x)_K$
over
$Z(x)_K$
over
![]() $Z(x)_{K'}$
. It is easy to check that
$Z(x)_{K'}$
. It is easy to check that
![]() $d(x)$
is not constant near 0. In particular, it does not extend to a smooth function on
$d(x)$
is not constant near 0. In particular, it does not extend to a smooth function on
![]() ${\mathbb {V}}^\infty $
. Thus, for a general
${\mathbb {V}}^\infty $
. Thus, for a general
![]() $\phi $
, there seems no
$\phi $
, there seems no
![]() $\phi '\in \overline {\mathcal {S}}\left ( {\mathbb {V}} \right )^{K'}$
such that
$\phi '\in \overline {\mathcal {S}}\left ( {\mathbb {V}} \right )^{K'}$
such that
![]() $\pi _{_K,_{K'},*}Z_t(\phi )_{K}$
is of the form
$\pi _{_K,_{K'},*}Z_t(\phi )_{K}$
is of the form
![]() $Z_t(\phi ')_{K'}$
for every t.
$Z_t(\phi ')_{K'}$
for every t.
Below, let
![]() $L=L_K$
,
$L=L_K$
,
![]() $Z(x)=Z(x)_K$
,
$Z(x)=Z(x)_K$
,
![]() $Z_t(\phi )=Z_t(\phi )_K$
and
$Z_t(\phi )=Z_t(\phi )_K$
and
![]() $z(\phi )=z(\phi )_K$
for simplicity if K is clear from the context.
$z(\phi )=z(\phi )_K$
for simplicity if K is clear from the context.
4.2 Green functions
We use complex uniformization to defined automorphic Green functions for special divisors. They are admissible. We compare them with the normalized admissible Green functions and show the modularity of the differences between their generating series. Then we recall Kudla’s Green functions and prove the modularity of the differences between the generating series of normalized admissible Green functions and Kudla’s Green functions.
4.2.1 Complex uniformization
For nonnegative integers
![]() $p,q$
, let
$p,q$
, let
![]() ${\mathbb {C}}^{p,q}$
be the
${\mathbb {C}}^{p,q}$
be the
![]() $p+q$
dimensional hermitian space associated to the hermitian matrix
$p+q$
dimensional hermitian space associated to the hermitian matrix
![]() ${\mathrm {diag}}(-1_p,1_q)$
. Let
${\mathrm {diag}}(-1_p,1_q)$
. Let
![]() $U\left ({\mathbb {C}}^{1,n}\right )$
be the unitary group of
$U\left ({\mathbb {C}}^{1,n}\right )$
be the unitary group of
![]() ${\mathbb {C}}^{1,n}$
(so of signature
${\mathbb {C}}^{1,n}$
(so of signature
![]() $(n,1)$
in the usual convention). Let
$(n,1)$
in the usual convention). Let
![]() ${\mathbb {B}}_n$
be the complex open unit ball of dimension n. Embed
${\mathbb {B}}_n$
be the complex open unit ball of dimension n. Embed
![]() ${\mathbb {B}}_n$
in
${\mathbb {B}}_n$
in
![]() ${\mathbb {P}}({\mathbb {C}}^{1,n})$
as the set of negative lines as follows:
${\mathbb {P}}({\mathbb {C}}^{1,n})$
as the set of negative lines as follows:
![]() $[z_1,\ldots ,z_n]\in {\mathbb {B}}_{n}$
, where
$[z_1,\ldots ,z_n]\in {\mathbb {B}}_{n}$
, where
![]() $\sum _{i=1}^{n}|z_i|^2<1$
, is the line containing the vector
$\sum _{i=1}^{n}|z_i|^2<1$
, is the line containing the vector
![]() $(1,z_1\ldots ,z_n) $
. Then
$(1,z_1\ldots ,z_n) $
. Then
![]() $U\left ({\mathbb {C}}^{1,n}\right )$
acts on
$U\left ({\mathbb {C}}^{1,n}\right )$
acts on
![]() ${\mathbb {B}}_n$
naturally and transitively. Let
${\mathbb {B}}_n$
naturally and transitively. Let
![]() $\Omega $
be the tautological bundle of negative lines on
$\Omega $
be the tautological bundle of negative lines on
![]() ${\mathbb {B}}_n$
, and
${\mathbb {B}}_n$
, and
![]() $\overline \Omega $
the hermitian line bundle with the metric induced from the negative of the hermitian form. The Chern form of
$\overline \Omega $
the hermitian line bundle with the metric induced from the negative of the hermitian form. The Chern form of
![]() $\overline \Omega $
is a
$\overline \Omega $
is a
![]() $U\left ({\mathbb {C}}^{1,n}\right )$
-invariant Kähler form
$U\left ({\mathbb {C}}^{1,n}\right )$
-invariant Kähler form
 $$ \begin{align}c_1(\overline\Omega)= \frac{1}{2\pi i } \partial \bar\partial \log (1-\sum_{i=1}^{n}|z_i|^2).\end{align} $$
$$ \begin{align}c_1(\overline\Omega)= \frac{1}{2\pi i } \partial \bar\partial \log (1-\sum_{i=1}^{n}|z_i|^2).\end{align} $$
For an arithmetic subgroup
![]() $\Gamma \subset U({\mathbb {C}}^{1,n})$
, on (the orbifold)
$\Gamma \subset U({\mathbb {C}}^{1,n})$
, on (the orbifold)
![]() $\Gamma \backslash {\mathbb {B}}_n $
, we have the descent
$\Gamma \backslash {\mathbb {B}}_n $
, we have the descent
![]() $\overline \Omega _\Gamma $
of
$\overline \Omega _\Gamma $
of
![]() $\overline \Omega $
whose (orbifold) Chern curvature form is the descent of
$\overline \Omega $
whose (orbifold) Chern curvature form is the descent of
![]() $c_1(\overline \Omega )$
. Define the degree
$c_1(\overline \Omega )$
. Define the degree
If
![]() $\Gamma \backslash {\mathbb {B}}_n$
is compact, this degree is the usual degree via intersection theory.
$\Gamma \backslash {\mathbb {B}}_n$
is compact, this degree is the usual degree via intersection theory.
For
![]() $x\in {\mathbb {C}}^{1,n}$
, let
$x\in {\mathbb {C}}^{1,n}$
, let
![]() ${\mathbb {B}}_x\subset {\mathbb {B}}_n$
be the subset of negative lines perpendicular to x. Later, we will use the following function on
${\mathbb {B}}_x\subset {\mathbb {B}}_n$
be the subset of negative lines perpendicular to x. Later, we will use the following function on
![]() ${\mathbb {B}}_n $
measuring ‘the distance to
${\mathbb {B}}_n $
measuring ‘the distance to
![]() ${\mathbb {B}}_x$
’:
${\mathbb {B}}_x$
’:
 $$ \begin{align*}R_x(z)=-\frac{|\langle {x,\widetilde z} \rangle|^2}{\langle {\widetilde z,\widetilde z} \rangle},\end{align*} $$
$$ \begin{align*}R_x(z)=-\frac{|\langle {x,\widetilde z} \rangle|^2}{\langle {\widetilde z,\widetilde z} \rangle},\end{align*} $$
where
![]() $\widetilde z $
is a nonzero vector contained in the line z. In particular,
$\widetilde z $
is a nonzero vector contained in the line z. In particular,
![]() $R_x>0$
outside
$R_x>0$
outside
![]() ${\mathbb {B}}_x$
. If
${\mathbb {B}}_x$
. If
![]() $q(x)<0$
, then
$q(x)<0$
, then
![]() $x^\perp $
is of signature
$x^\perp $
is of signature
![]() $(n,0)$
so that
$(n,0)$
so that
![]() ${\mathbb {B}}_x=\emptyset $
. Below, until 4.2.3, assume
${\mathbb {B}}_x=\emptyset $
. Below, until 4.2.3, assume
![]() ${q(x)}>0$
. Then
${q(x)}>0$
. Then
![]() $x^\perp $
is of signature
$x^\perp $
is of signature
![]() $(n-1,1)$
. So
$(n-1,1)$
. So
![]() ${\mathbb {B}}_x$
is a complex unit ball of dimension
${\mathbb {B}}_x$
is a complex unit ball of dimension
![]() $n-1$
. Assume that
$n-1$
. Assume that
![]() $\Gamma \cap U (x^\perp )$
is an arithmetic subgroup of
$\Gamma \cap U (x^\perp )$
is an arithmetic subgroup of
![]() $U (x^\perp )$
. Let
$U (x^\perp )$
. Let
![]() $C(x,\Gamma )$
be the pushforward of the fundamental cycle by
$C(x,\Gamma )$
be the pushforward of the fundamental cycle by
Define
Now we can uniformize Shimura varieties and special divisors. Let v be an infinite place of F. Let V be the unique hermitian space over E such that
![]() $V({\mathbb {A}}_E^v){\ \simeq \ } {\mathbb {V}}^v$
and
$V({\mathbb {A}}_E^v){\ \simeq \ } {\mathbb {V}}^v$
and
![]() $V(E_v){\ \simeq \ } {\mathbb {C}}^{1,n}$
. By [Reference Li and LiuLL21, Lemma 5.5], we have the complex uniformization:
$V(E_v){\ \simeq \ } {\mathbb {C}}^{1,n}$
. By [Reference Li and LiuLL21, Lemma 5.5], we have the complex uniformization:
Then the Hodge bundle
![]() $L_{E_v}$
is the descent of
$L_{E_v}$
is the descent of
![]() $\Omega \times 1_{U({\mathbb {V}}^\infty )/K}$
. Let
$\Omega \times 1_{U({\mathbb {V}}^\infty )/K}$
. Let
![]() $\overline {L}_{E_v}$
be the descent of
$\overline {L}_{E_v}$
be the descent of
![]() $\overline \Omega \times 1_{U({\mathbb {V}}^\infty )/K}$
. Let
$\overline \Omega \times 1_{U({\mathbb {V}}^\infty )/K}$
. Let
![]() $h_1,.. .,h_m$
be a set of representatives of
$h_1,.. .,h_m$
be a set of representatives of
![]() $U(V)\backslash U({\mathbb {V}}^\infty )/K$
. Let
$U(V)\backslash U({\mathbb {V}}^\infty )/K$
. Let
![]() $\Gamma _{h_j}=U(V)\cap h_jKh_j^{-1}$
. Then (4.4) decomposes as the disjoint union of
$\Gamma _{h_j}=U(V)\cap h_jKh_j^{-1}$
. Then (4.4) decomposes as the disjoint union of
![]() $\Gamma _{h_j} \backslash {\mathbb {B}}_n$
’s. Then for
$\Gamma _{h_j} \backslash {\mathbb {B}}_n$
’s. Then for
![]() $t\in F_{>0}$
, we have (see [Reference KudlaKud97a, PROPOSITION 5.4])
$t\in F_{>0}$
, we have (see [Reference KudlaKud97a, PROPOSITION 5.4])
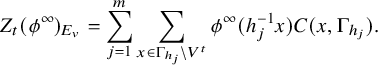 $$ \begin{align} Z_t(\phi^\infty)_{E_v}=\sum_{j=1}^m\sum_{x\in \Gamma_{h_j}\backslash V^t} \phi^\infty(h_j^{-1}x)C(x,\Gamma_{h_j}).\end{align} $$
$$ \begin{align} Z_t(\phi^\infty)_{E_v}=\sum_{j=1}^m\sum_{x\in \Gamma_{h_j}\backslash V^t} \phi^\infty(h_j^{-1}x)C(x,\Gamma_{h_j}).\end{align} $$
4.2.2 Admissible Green functions
Admissible Green functions are Green functions with harmonic curvatures. See Appendix A.3. Admissible Green functions for special divisors are constructed by Bruinier [Reference BruinierBru02, Reference BruinierBru12], Oda and Tsuzuki [Reference Oda and TsuzukiOT03]. For
![]() $F={\mathbb {Q}}$
and
$F={\mathbb {Q}}$
and
![]() $n=1$
, it appeared in the work of Gross and Zagier [Reference Gross and ZagierGZ86] for
$n=1$
, it appeared in the work of Gross and Zagier [Reference Gross and ZagierGZ86] for
![]() $n=1$
. We learned the following explicit computation from S. Zhang.
$n=1$
. We learned the following explicit computation from S. Zhang.
First, we start by working on
![]() ${\mathbb {B}}_n$
. Let
${\mathbb {B}}_n$
. Let
![]() $x_0=(0,\ldots ,0,1)\in {\mathbb {C}}^{1,n}$
. Then
$x_0=(0,\ldots ,0,1)\in {\mathbb {C}}^{1,n}$
. Then
![]() ${\mathbb {B}}_{x_0}\subset {\mathbb {B}}_n$
consists of points
${\mathbb {B}}_{x_0}\subset {\mathbb {B}}_n$
consists of points
![]() $ (z_1,\ldots ,z_{n-1},0) $
’s. We want a
$ (z_1,\ldots ,z_{n-1},0) $
’s. We want a
![]() $U\left ( x_0 ^\perp \right )$
-invariant smooth function G on
$U\left ( x_0 ^\perp \right )$
-invariant smooth function G on
![]() ${\mathbb {B}}_n-{\mathbb {B}}_{x_0}$
such that
${\mathbb {B}}_n-{\mathbb {B}}_{x_0}$
such that
![]() $G(z_1,\ldots ,z_n)+\log |z_n|^2 $
extends smoothly to
$G(z_1,\ldots ,z_n)+\log |z_n|^2 $
extends smoothly to
![]() ${\mathbb {B}}_n$
,
${\mathbb {B}}_n$
,
![]() $\lim _{|z|\to 1}G(z) =0,$
and G is a solution of the following Laplacian equation:
$\lim _{|z|\to 1}G(z) =0,$
and G is a solution of the following Laplacian equation:
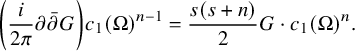 $$ \begin{align}\left(\frac{i }{2\pi } \partial \bar\partial G \right) {c_1(\Omega)}^{n-1}=\frac{s(s+n) }{2}G \cdot {c_1(\Omega)}^{n} .\end{align} $$
$$ \begin{align}\left(\frac{i }{2\pi } \partial \bar\partial G \right) {c_1(\Omega)}^{n-1}=\frac{s(s+n) }{2}G \cdot {c_1(\Omega)}^{n} .\end{align} $$
The quotient of
![]() ${\mathbb {B}}_n-{\mathbb {B}}_{x_0}$
by
${\mathbb {B}}_n-{\mathbb {B}}_{x_0}$
by
![]() $U\left ( x_0 ^\perp \right )$
is isomorphic to
$U\left ( x_0 ^\perp \right )$
is isomorphic to
![]() $(1,\infty )$
via
$(1,\infty )$
via
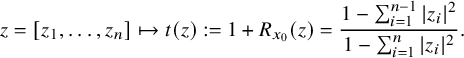 $$ \begin{align*}z=[z_1,\ldots,z_n]\mapsto t(z):= 1+ R_{ x_0 }\left( z\right)=\frac{1-\sum_{i=1}^{n-1}|z_i|^2}{1-\sum_{i=1}^{n}|z_i|^2} .\end{align*} $$
$$ \begin{align*}z=[z_1,\ldots,z_n]\mapsto t(z):= 1+ R_{ x_0 }\left( z\right)=\frac{1-\sum_{i=1}^{n-1}|z_i|^2}{1-\sum_{i=1}^{n}|z_i|^2} .\end{align*} $$
Thus, we look for
![]() $G=Q(t(z))$
, where Q is a smooth function on
$G=Q(t(z))$
, where Q is a smooth function on
![]() $(1,\infty )$
such that
$(1,\infty )$
such that
![]() $ Q(t)+ \log ( t-1) $
extends to a smooth function on
$ Q(t)+ \log ( t-1) $
extends to a smooth function on
![]() ${\mathbb {R}}$
. By (4.3) and the
${\mathbb {R}}$
. By (4.3) and the
![]() $U\left ( x_0 ^\perp \right )$
-invariance, (4.6) is reduced to the following hypergeometric differential equation
$U\left ( x_0 ^\perp \right )$
-invariance, (4.6) is reduced to the following hypergeometric differential equation
For
![]() ${\mathrm {Re}} s>-1$
, there is a unique solution
${\mathrm {Re}} s>-1$
, there is a unique solution
![]() $Q_s$
such that
$Q_s$
such that
![]() $Q_s(t)+\log (t-1)$
extends to a smooth function on
$Q_s(t)+\log (t-1)$
extends to a smooth function on
![]() ${\mathbb {R}}$
and
${\mathbb {R}}$
and
![]() $\lim _ {t\to \infty }Q_s(t)=0$
:
$\lim _ {t\to \infty }Q_s(t)=0$
:
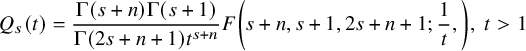 $$ \begin{align} Q_s(t)=\frac{\Gamma(s+n)\Gamma(s+1)}{\Gamma(2s+n+1)t^{s+n}} F\left( s+n,s+1,2s+n+1;\frac{1}{t},\right), \ t>1\end{align} $$
$$ \begin{align} Q_s(t)=\frac{\Gamma(s+n)\Gamma(s+1)}{\Gamma(2s+n+1)t^{s+n}} F\left( s+n,s+1,2s+n+1;\frac{1}{t},\right), \ t>1\end{align} $$
where F is the hypergeometric function. (See also [Reference Oda and TsuzukiOT03, 2.5.3]. When
![]() $n=1$
, our
$n=1$
, our
![]() $Q_s$
is the Legendre function of the second kind in [Reference Gross and ZagierGZ86, 238] up to shifting s by 1).
$Q_s$
is the Legendre function of the second kind in [Reference Gross and ZagierGZ86, 238] up to shifting s by 1).
For a general x with
![]() $q(x)>0$
, we have the following Green function for
$q(x)>0$
, we have the following Green function for
![]() ${\mathbb {B}}_x$
:
${\mathbb {B}}_x$
:
We will need the following explicit formula later: if
![]() $ x=(x_1,x_2)\in {\mathbb {C}}^{1,n}= {\mathbb {C}}^{1,0}\oplus {\mathbb {C}}^{0,n} $
, then
$ x=(x_1,x_2)\in {\mathbb {C}}^{1,n}= {\mathbb {C}}^{1,0}\oplus {\mathbb {C}}^{0,n} $
, then
Second, we define Green functions for
![]() $ C( x ,\Gamma )$
on arithmetic quotient of
$ C( x ,\Gamma )$
on arithmetic quotient of
![]() ${\mathbb {B}}_n.$
Let
${\mathbb {B}}_n.$
Let
![]() $\Gamma $
be an arithmetic subgroup of
$\Gamma $
be an arithmetic subgroup of
![]() $U\left ({\mathbb {C}}^{1,n}\right )$
. Let
$U\left ({\mathbb {C}}^{1,n}\right )$
. Let
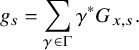 $$ \begin{align*}g_s=\sum_{\gamma\in \Gamma}\gamma^{*}G_{ x ,s}.\end{align*} $$
$$ \begin{align*}g_s=\sum_{\gamma\in \Gamma}\gamma^{*}G_{ x ,s}.\end{align*} $$
Lemma 4.2.1 [Reference Oda and TsuzukiOT03, Proposition 3.1.1, Remark 3.1.1, Remark 3.2.1].
For
![]() $s \in {\mathbb {C}}$
with
$s \in {\mathbb {C}}$
with
![]() ${\mathrm {Re}} s>0$
, the sum
${\mathrm {Re}} s>0$
, the sum
![]() $g_s$
converges absolutely and defines a smooth function on
$g_s$
converges absolutely and defines a smooth function on
![]() $ \Gamma \backslash {\mathbb {B}}_{n}-C( x ,\Gamma )$
. Moreover,
$ \Gamma \backslash {\mathbb {B}}_{n}-C( x ,\Gamma )$
. Moreover,
![]() $g_s$
is holomorphic on s.
$g_s$
is holomorphic on s.
It is easy to see that
![]() $g_s$
with
$g_s$
with
![]() ${\mathrm {Re}} s>0$
is a Green function for
${\mathrm {Re}} s>0$
is a Green function for
![]() $ C( x ,\Gamma )$
.
$ C( x ,\Gamma )$
.
Theorem 4.2.2 [Reference Oda and TsuzukiOT03, Theorem 7.8.1].
(1) There is a meromorphic continuation of
![]() $g_s$
to
$g_s$
to
![]() $s\in {\mathbb {C}}$
with a simple pole at
$s\in {\mathbb {C}}$
with a simple pole at
![]() $s=0$
and residue
$s=0$
and residue
![]() $-\frac {\deg _{\overline \Omega _\Gamma }(C( x ,\Gamma ))}{\deg (\overline \Omega _ \Gamma )}$
.
$-\frac {\deg _{\overline \Omega _\Gamma }(C( x ,\Gamma ))}{\deg (\overline \Omega _ \Gamma )}$
.
(2) The function
![]() $\widetilde {\lim \limits _{s\to 0}} g_s$
is an admissible Green function for
$\widetilde {\lim \limits _{s\to 0}} g_s$
is an admissible Green function for
![]() $ C( x ,\Gamma )$
.
$ C( x ,\Gamma )$
.
Recall that
![]() $\widetilde {\lim \limits _{s\to 0}}$
denotes taking the constant term at
$\widetilde {\lim \limits _{s\to 0}}$
denotes taking the constant term at
![]() $s=0$
.
$s=0$
.
Remark 4.2.3. (1) We read the residue
![]() $\kappa $
in [Reference Oda and TsuzukiOT03, Theorem 7.8.1 (3)] as follows. Beside the obvious differences between the choices of Green function here and in [Reference Oda and TsuzukiOT03] (more precisely, s-variables and signs), the Kähler form and ‘volume form’ here and in [Reference Oda and TsuzukiOT03] are different. First, the Kähler form on the bottom of [Reference Oda and TsuzukiOT03, 514] is
$\kappa $
in [Reference Oda and TsuzukiOT03, Theorem 7.8.1 (3)] as follows. Beside the obvious differences between the choices of Green function here and in [Reference Oda and TsuzukiOT03] (more precisely, s-variables and signs), the Kähler form and ‘volume form’ here and in [Reference Oda and TsuzukiOT03] are different. First, the Kähler form on the bottom of [Reference Oda and TsuzukiOT03, 514] is
![]() $\pi c_1(\overline \Omega )$
in our notation. Second, [Reference Oda and TsuzukiOT03, Theorem 7.8.1 (3)] uses volumes to express the residue, while we use degrees of line bundles to express the residue. The volume form for
$\pi c_1(\overline \Omega )$
in our notation. Second, [Reference Oda and TsuzukiOT03, Theorem 7.8.1 (3)] uses volumes to express the residue, while we use degrees of line bundles to express the residue. The volume form for
![]() $ {\mathbb {B}}_n$
on the top of [Reference Oda and TsuzukiOT03, 515] is
$ {\mathbb {B}}_n$
on the top of [Reference Oda and TsuzukiOT03, 515] is
![]() $\frac {\pi ^n}{n!}c_1(\overline \Omega )^n$
in our notation. Third, there is a
$\frac {\pi ^n}{n!}c_1(\overline \Omega )^n$
in our notation. Third, there is a
![]() $\pi $
missing in (the numerator of) the residue
$\pi $
missing in (the numerator of) the residue
![]() $\kappa $
in [Reference Oda and TsuzukiOT03, Theorem 7.8.1 (3)]. It should be easy to spot from [Reference Oda and TsuzukiOT03, Proposition 3.1.2, Lemma 7.2.2].
$\kappa $
in [Reference Oda and TsuzukiOT03, Theorem 7.8.1 (3)]. It should be easy to spot from [Reference Oda and TsuzukiOT03, Proposition 3.1.2, Lemma 7.2.2].
(2) When
![]() $n=1$
and
$n=1$
and
![]() $\Gamma ={\mathrm {SL}}_2({\mathbb {Z}})$
via
$\Gamma ={\mathrm {SL}}_2({\mathbb {Z}})$
via
![]() ${\mathrm {SU}}({\mathbb {C}}^{1,1}){\ \simeq \ } {\mathrm {SL}}_2({\mathbb {R}})$
, we have
${\mathrm {SU}}({\mathbb {C}}^{1,1}){\ \simeq \ } {\mathrm {SL}}_2({\mathbb {R}})$
, we have
![]() $\deg (\overline \Omega _ \Gamma )=\frac {1}{12}$
. See [Reference KühnK01, 4.10]. Thus, for
$\deg (\overline \Omega _ \Gamma )=\frac {1}{12}$
. See [Reference KühnK01, 4.10]. Thus, for
![]() $\Gamma _0(N)$
a standard congruence subgroup of
$\Gamma _0(N)$
a standard congruence subgroup of
![]() $\Gamma $
, Theorem 4.2.2 (1) coincides with the residue
$\Gamma $
, Theorem 4.2.2 (1) coincides with the residue
![]() $\frac {-12}{[\Gamma :\Gamma _0(N)]}$
in [Reference Gross and ZagierGZ86, p 239, (2.13)]. Theorem 4.2.2 (1) is not used in any other place of the paper.
$\frac {-12}{[\Gamma :\Gamma _0(N)]}$
in [Reference Gross and ZagierGZ86, p 239, (2.13)]. Theorem 4.2.2 (1) is not used in any other place of the paper.
By [Reference Oda and TsuzukiOT03, Proposition 3.1.2] and taking care of the differences in the remark, we have
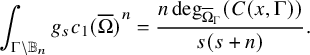 $$ \begin{align*}\int_{\Gamma\backslash {\mathbb{B}}_n} g_s {c_1(\overline \Omega)}^n=\frac{n\deg_{\overline\Omega_\Gamma}(C( x ,\Gamma))}{s(s+n)}.\end{align*} $$
$$ \begin{align*}\int_{\Gamma\backslash {\mathbb{B}}_n} g_s {c_1(\overline \Omega)}^n=\frac{n\deg_{\overline\Omega_\Gamma}(C( x ,\Gamma))}{s(s+n)}.\end{align*} $$
Thus,
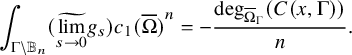 $$ \begin{align} \int_{\Gamma\backslash {\mathbb{B}}_n}(\widetilde{\lim\limits _{s\to 0}}g_s ) {c_1(\overline \Omega)}^n=-\frac{\deg_{\overline\Omega_\Gamma}(C( x ,\Gamma))}{n}. \end{align} $$
$$ \begin{align} \int_{\Gamma\backslash {\mathbb{B}}_n}(\widetilde{\lim\limits _{s\to 0}}g_s ) {c_1(\overline \Omega)}^n=-\frac{\deg_{\overline\Omega_\Gamma}(C( x ,\Gamma))}{n}. \end{align} $$
Finally, we define Green functions for
![]() $Z_t(\phi )$
,
$Z_t(\phi )$
,
![]() $t\in F_{>0}$
. Let
$t\in F_{>0}$
. Let
![]() $v\in \infty $
and V as in 4.2.1. For
$v\in \infty $
and V as in 4.2.1. For
![]() $s \in {\mathbb {C}}$
with
$s \in {\mathbb {C}}$
with
![]() ${\mathrm {Re}} s> 0$
, consider the following formal sum for
${\mathrm {Re}} s> 0$
, consider the following formal sum for
![]() $(z,h)\in {\mathbb {B}}_n \times U({\mathbb {V}}^\infty )$
:
$(z,h)\in {\mathbb {B}}_n \times U({\mathbb {V}}^\infty )$
:
By (4.5) and Lemma 4.2.1, if
![]() $(z,h)$
is not over
$(z,h)$
is not over
![]() $Z_t(\phi ^\infty )_{E_v}$
via (4.4), the formal sum is defined and absolutely convergent. Thus,
$Z_t(\phi ^\infty )_{E_v}$
via (4.4), the formal sum is defined and absolutely convergent. Thus,
![]() $ {\mathcal {G}}_{Z_t(\phi ^\infty )_{E_v},s}$
descends to
$ {\mathcal {G}}_{Z_t(\phi ^\infty )_{E_v},s}$
descends to
![]() ${\mathrm {Sh}}({\mathbb {V}})_{K,E_v}-Z_t(\phi ^\infty )_{E_v} $
via (4.4), which we still denote by
${\mathrm {Sh}}({\mathbb {V}})_{K,E_v}-Z_t(\phi ^\infty )_{E_v} $
via (4.4), which we still denote by
![]() ${\mathcal {G}}_{Z_t(\phi ^\infty )_{E_v},s}$
. By (4.5) and Theorem 4.2.2,
${\mathcal {G}}_{Z_t(\phi ^\infty )_{E_v},s}$
. By (4.5) and Theorem 4.2.2,
![]() ${\mathcal {G}}_{Z_t(\phi ^\infty )_{E_v},s} $
is a Green function for
${\mathcal {G}}_{Z_t(\phi ^\infty )_{E_v},s} $
is a Green function for
![]() $Z_t(\phi ^\infty )_{E_v}$
. For
$Z_t(\phi ^\infty )_{E_v}$
. For
![]() $g\in G({\mathbb {A}}_F)$
, let
$g\in G({\mathbb {A}}_F)$
, let
which is a Green function for
![]() $Z_t(\omega (g)\phi )_{E_v}$
by (4.2). Define the automorphic Green functions for
$Z_t(\omega (g)\phi )_{E_v}$
by (4.2). Define the automorphic Green functions for
![]() $Z_t(\phi ^\infty )_{E_v}$
and
$Z_t(\phi ^\infty )_{E_v}$
and
![]() $Z_t(\omega (g)\phi )_{E_v}$
to be
$Z_t(\omega (g)\phi )_{E_v}$
to be
respectively, which are admissible by Theorem 4.2.2.
Let
![]() $ {\mathcal {G}}^{\overline L_{E_v}}_{Z_t(\phi )_{E_v}}$
be the normalized admissible Green function for
$ {\mathcal {G}}^{\overline L_{E_v}}_{Z_t(\phi )_{E_v}}$
be the normalized admissible Green function for
![]() $Z_t(\phi )_{E_v}$
with respect to
$Z_t(\phi )_{E_v}$
with respect to
![]() $\overline L_{E_v}$
as in Definition A.3.3. In particular, its integration against
$\overline L_{E_v}$
as in Definition A.3.3. In particular, its integration against
![]() $c_1(\overline L_{E_v})^{n}$
is 0.
$c_1(\overline L_{E_v})^{n}$
is 0.
Lemma 4.2.4. (1) We have
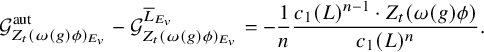 $$ \begin{align*}{\mathcal{G}}^{{\mathrm{aut}}}_{Z_t(\omega(g)\phi)_{E_v}}- {\mathcal{G}}^{\overline L_{E_v}}_{Z_t(\omega(g)\phi)_{E_v}}=-\frac{1}{n} \frac{c_1(L)^{n-1}\cdot Z_t(\omega(g)\phi) }{c_1(L)^{n} }.\end{align*} $$
$$ \begin{align*}{\mathcal{G}}^{{\mathrm{aut}}}_{Z_t(\omega(g)\phi)_{E_v}}- {\mathcal{G}}^{\overline L_{E_v}}_{Z_t(\omega(g)\phi)_{E_v}}=-\frac{1}{n} \frac{c_1(L)^{n-1}\cdot Z_t(\omega(g)\phi) }{c_1(L)^{n} }.\end{align*} $$
Both sides are independent of K.
(2) We have
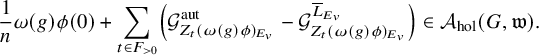 $$ \begin{align*}\frac{1}{n}\omega(g)\phi(0)+\sum_{t\in F_{>0}} \left( {\mathcal{G}}^{{\mathrm{aut}}}_{Z_t(\omega(g)\phi)_{E_v}}- {\mathcal{G}}^{\overline L_{E_v}}_{Z_t(\omega(g)\phi)_{E_v}}\right)\in {\mathcal{A}}_{{\mathrm{hol}}}(G,{\mathfrak{w}}).\end{align*} $$
$$ \begin{align*}\frac{1}{n}\omega(g)\phi(0)+\sum_{t\in F_{>0}} \left( {\mathcal{G}}^{{\mathrm{aut}}}_{Z_t(\omega(g)\phi)_{E_v}}- {\mathcal{G}}^{\overline L_{E_v}}_{Z_t(\omega(g)\phi)_{E_v}}\right)\in {\mathcal{A}}_{{\mathrm{hol}}}(G,{\mathfrak{w}}).\end{align*} $$
Proof. The equation in (1) follows from (4.9) and the independence of the right-hand side follows from the projection formula. (2) follows from Theorem 4.1.2.
Remark 4.2.5. The automorphic form in Lemma 4.2.4 (2) can be made explicit:
This is a geometric version of the Siegel-Weil formula (3.13). It is stated in [Reference KudlaKud97a, COROLLARY 10.5] for the orthogonal case; the proof carries over to the unitary case.
4.2.3 Kudla’s Green function
We recall Kudla’s Green functions for special divisors [Reference KudlaKud97b], following [Reference LiuLiu11a, 4C] in the unitary case. We consider simple special divisors
![]() $Z(x)$
’s, instead of weight special divisors
$Z(x)$
’s, instead of weight special divisors
![]() $Z_t(\phi )$
’s. We extend the definition of special divisors as follows. For
$Z_t(\phi )$
’s. We extend the definition of special divisors as follows. For
![]() $x\in {\mathbb {V}}^{\infty } $
such that
$x\in {\mathbb {V}}^{\infty } $
such that
![]() ${q(x)}\in F ^\times -F_{>0}$
, let
${q(x)}\in F ^\times -F_{>0}$
, let
![]() $Z(x)= 0$
.
$Z(x)= 0$
.
First, we work on
![]() ${\mathbb {B}}_n$
. For
${\mathbb {B}}_n$
. For
![]() $v\in \infty $
, V as in the end of 4.2.1 with respect to v,
$v\in \infty $
, V as in the end of 4.2.1 with respect to v,
![]() $g\in G(F_v)$
and
$g\in G(F_v)$
and
![]() $x\in V$
, define
$x\in V$
, define
where the exponential integral
![]() ${\mathrm {Ei}}(t)=\int _{-\infty }^t\frac {e^s}{s}ds$
on
${\mathrm {Ei}}(t)=\int _{-\infty }^t\frac {e^s}{s}ds$
on
![]() $t\in (-\infty ,0)$
has a log-singularity at 0. If
$t\in (-\infty ,0)$
has a log-singularity at 0. If
![]() $q(x)\neq 0$
so that
$q(x)\neq 0$
so that
![]() ${\mathbb {B}}_x$
is either empty or a complex unit ball of dimension
${\mathbb {B}}_x$
is either empty or a complex unit ball of dimension
![]() $n-1$
,
$n-1$
,
![]() $G^{\mathrm {Kud}}(x,g)$
is a Green function for
$G^{\mathrm {Kud}}(x,g)$
is a Green function for
![]() ${\mathbb {B}}_x$
. If
${\mathbb {B}}_x$
. If
![]() $q(x)<0$
, equivalently
$q(x)<0$
, equivalently
![]() ${\mathbb {B}}_x$
is empty, then
${\mathbb {B}}_x$
is empty, then
![]() $G^{\mathrm {Kud}}$
is smooth.
$G^{\mathrm {Kud}}$
is smooth.
Now we work on
![]() ${\mathrm {Sh}}({\mathbb {V}})_K$
. Let
${\mathrm {Sh}}({\mathbb {V}})_K$
. Let
![]() $x\in {\mathbb {V}}^\infty $
with
$x\in {\mathbb {V}}^\infty $
with
![]() $q(x)\in F^\times $
. For
$q(x)\in F^\times $
. For
![]() $v\in \infty $
, if
$v\in \infty $
, if
![]() $u(q(x))>0$
for every
$u(q(x))>0$
for every
![]() $u\in \infty -\{v\}$
, by the Hasse-Minkowski theorem and Witt’s theorem, there exists
$u\in \infty -\{v\}$
, by the Hasse-Minkowski theorem and Witt’s theorem, there exists
![]() $h\in U({\mathbb {V}}^\infty )$
and
$h\in U({\mathbb {V}}^\infty )$
and
![]() $x^{(v)}\in V-\{0\}$
, where V is as in the last paragraph, such that
$x^{(v)}\in V-\{0\}$
, where V is as in the last paragraph, such that
![]() $ x=h^{-1}x^{(v)}$
. Define
$ x=h^{-1}x^{(v)}$
. Define
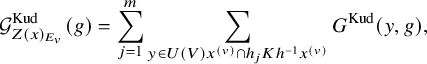 $$ \begin{align}{\mathcal{G}}^{\mathrm{Kud}}_{Z( x)_{E_v}}(g)=\sum_{j=1}^m\sum_{y\in U(V)x^{(v)}\cap h_jK h^{-1}x^{(v)}} G^{\mathrm{Kud}}(y,g) ,\end{align} $$
$$ \begin{align}{\mathcal{G}}^{\mathrm{Kud}}_{Z( x)_{E_v}}(g)=\sum_{j=1}^m\sum_{y\in U(V)x^{(v)}\cap h_jK h^{-1}x^{(v)}} G^{\mathrm{Kud}}(y,g) ,\end{align} $$
where
![]() $h_1,.. .,h_m$
is a set of representatives of
$h_1,.. .,h_m$
is a set of representatives of
![]() $U(V)\backslash U({\mathbb {V}}^\infty )/K$
. By the decomposition analogous to (4.5) (see the second equation on [Reference KudlaKud97a, p 56]) and [Reference LiuLiu11a, Proposition 4.9]),
$U(V)\backslash U({\mathbb {V}}^\infty )/K$
. By the decomposition analogous to (4.5) (see the second equation on [Reference KudlaKud97a, p 56]) and [Reference LiuLiu11a, Proposition 4.9]),
![]() ${\mathcal {G}}^{\mathrm {Kud}}_{Z( x)_{E_v}}(g)$
is absolutely convergent and descends to
${\mathcal {G}}^{\mathrm {Kud}}_{Z( x)_{E_v}}(g)$
is absolutely convergent and descends to
![]() ${\mathrm {Sh}}({\mathbb {V}})_{K,E_v}$
via (4.4). And it is a Green function for
${\mathrm {Sh}}({\mathbb {V}})_{K,E_v}$
via (4.4). And it is a Green function for
![]() $Z(x)_{E_v}$
.
$Z(x)_{E_v}$
.
Besides Kudla’s Green functions, we will need their projections to the constant function
![]() $1$
to modify the normalized Green function. See 4.4.3.
$1$
to modify the normalized Green function. See 4.4.3.
Definition 4.2.6. For
![]() $x\in {\mathbb {V}}^\infty $
with
$x\in {\mathbb {V}}^\infty $
with
![]() $q(x)\in F^\times $
,
$q(x)\in F^\times $
,
![]() $g\in G({\mathbb {A}}_{F,\infty })$
and
$g\in G({\mathbb {A}}_{F,\infty })$
and
![]() $v\in \infty $
, let
$v\in \infty $
, let
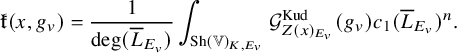 $$ \begin{align*}{\mathfrak{k}}(x,g_v)=\frac{1}{\deg (\overline{L}_{E_v})}\int_{{\mathrm{Sh}}({\mathbb{V}})_{K,E_v} }{\mathcal{G}}^{\mathrm{Kud}}_{Z(x)_{E_v}}(g_v) c_1(\overline{L}_{E_v})^n.\end{align*} $$
$$ \begin{align*}{\mathfrak{k}}(x,g_v)=\frac{1}{\deg (\overline{L}_{E_v})}\int_{{\mathrm{Sh}}({\mathbb{V}})_{K,E_v} }{\mathcal{G}}^{\mathrm{Kud}}_{Z(x)_{E_v}}(g_v) c_1(\overline{L}_{E_v})^n.\end{align*} $$
Note that if
![]() $u(q(x))<0$
for some
$u(q(x))<0$
for some
![]() $u\in \infty -\{v\}$
, then
$u\in \infty -\{v\}$
, then
![]() ${\mathcal {G}}^{\mathrm {Kud}}_{Z(x)_{E_v}}(g)=0$
. Thus, if
${\mathcal {G}}^{\mathrm {Kud}}_{Z(x)_{E_v}}(g)=0$
. Thus, if
![]() $q(x) $
is negative at more than one infinite places, then
$q(x) $
is negative at more than one infinite places, then
![]() ${\mathcal {G}}^{\mathrm {Kud}}_{Z(x)_{E_v}}(g)=0$
and
${\mathcal {G}}^{\mathrm {Kud}}_{Z(x)_{E_v}}(g)=0$
and
![]() $ {\mathfrak {k}}(x,g_v ) =0$
for every
$ {\mathfrak {k}}(x,g_v ) =0$
for every
![]() $v\in \infty $
.
$v\in \infty $
.
The following can be read from [Reference Garcia and SankaranGS19, (1.12), Theorem 1.2, (1.18), (1.19), Proposition 5.9].
Theorem 4.2.7. Let
![]() $ E_t'(0,g,\phi )(v)$
be as in (3.11). For
$ E_t'(0,g,\phi )(v)$
be as in (3.11). For
![]() $t\in F_{>0}$
and
$t\in F_{>0}$
and
![]() $v\in \infty $
, we have
$v\in \infty $
, we have
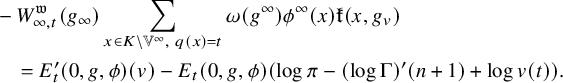 $$ \begin{align*} &-W^{{\mathfrak{w}}}_{\infty, t}(g_\infty) \sum_{x\in K\backslash {\mathbb{V}}^{ \infty}, \ q(x)=t}\omega(g^\infty)\phi^\infty ( x) {\mathfrak{k}}(x,g_v)\\& \quad = E' _t(0,g,\phi)(v) -E_t(0,g,\phi) \left( \log \pi-(\log\Gamma)'(n+1) + \log v(t)\right). \end{align*} $$
$$ \begin{align*} &-W^{{\mathfrak{w}}}_{\infty, t}(g_\infty) \sum_{x\in K\backslash {\mathbb{V}}^{ \infty}, \ q(x)=t}\omega(g^\infty)\phi^\infty ( x) {\mathfrak{k}}(x,g_v)\\& \quad = E' _t(0,g,\phi)(v) -E_t(0,g,\phi) \left( \log \pi-(\log\Gamma)'(n+1) + \log v(t)\right). \end{align*} $$
For
![]() $t\in F^\times $
with
$t\in F^\times $
with
![]() $v(t)<0$
for exactly one infinite place v, we have
$v(t)<0$
for exactly one infinite place v, we have
And for
![]() $t=0$
, we have
$t=0$
, we have
We remind the reader that
![]() $\infty $
is the set of infinite places of F. And our formulas differ from [Reference Garcia and SankaranGS19] by a factor
$\infty $
is the set of infinite places of F. And our formulas differ from [Reference Garcia and SankaranGS19] by a factor
![]() $1/2$
since in loc. cit., the authors use the set of infinite places of E.
$1/2$
since in loc. cit., the authors use the set of infinite places of E.
4.2.4 Modularity of difference of Green functions
We need a more general notion of modular forms.
Definition 4.2.8. Let V be a topological
![]() ${\mathbb {C}}$
-vector space and
${\mathbb {C}}$
-vector space and
![]() $V^{*}$
the continuous dual. Let
$V^{*}$
the continuous dual. Let
![]() $ {\mathcal {A}}(G,{\mathfrak {w}}, V) $
be the space of smooth V-valued function f on
$ {\mathcal {A}}(G,{\mathfrak {w}}, V) $
be the space of smooth V-valued function f on
![]() $G({\mathbb {A}})$
such that for every
$G({\mathbb {A}})$
such that for every
![]() $l\in V^{*}$
, we have
$l\in V^{*}$
, we have
![]() $l\circ f\in {\mathcal {A}}(G,{\mathfrak {w}}).$
$l\circ f\in {\mathcal {A}}(G,{\mathfrak {w}}).$
Remark 4.2.9. Note that
![]() $l\circ f$
is automatically smooth.
$l\circ f$
is automatically smooth.
Clearly, if V is the topological direct sum of
![]() $V_1, V_2$
and
$V_1, V_2$
and
![]() $f_i\in {\mathcal {A}}(G,{\mathfrak {w}}, V_i) $
, then
$f_i\in {\mathcal {A}}(G,{\mathfrak {w}}, V_i) $
, then
![]() $f_1+f_2\in {\mathcal {A}}(G,{\mathfrak {w}}, V) $
.
$f_1+f_2\in {\mathcal {A}}(G,{\mathfrak {w}}, V) $
.
Now we define the formal generating series of Green functions. Recall that
![]() $\infty $
is the set of infinite places of F, of cardinality
$\infty $
is the set of infinite places of F, of cardinality
![]() $[F:{\mathbb {Q}}]$
. Let
$[F:{\mathbb {Q}}]$
. Let
which is the product of
![]() $[F:{\mathbb {Q}}]$
many copies of
$[F:{\mathbb {Q}}]$
many copies of
![]() ${\mathbb {C}}$
. Then
${\mathbb {C}}$
. Then
is the (disconnected) complex manifold that is the disjoint union of all base changes of
![]() ${\mathrm {Sh}}({\mathbb {V}})_{K}$
to
${\mathrm {Sh}}({\mathbb {V}})_{K}$
to
![]() $E_v$
’s (each base change itself may not be connected either!).
$E_v$
’s (each base change itself may not be connected either!).
Let
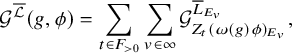 $$ \begin{align*}{\mathcal{G}}^{{\overline{\mathcal{L}}}}(g,\phi)=\sum_{t\in F_{>0}} \sum_{v\in \infty} {\mathcal{G}}^{\overline L_{E_v}}_{Z_t(\omega(g)\phi)_{E_v}},\end{align*} $$
$$ \begin{align*}{\mathcal{G}}^{{\overline{\mathcal{L}}}}(g,\phi)=\sum_{t\in F_{>0}} \sum_{v\in \infty} {\mathcal{G}}^{\overline L_{E_v}}_{Z_t(\omega(g)\phi)_{E_v}},\end{align*} $$
which are formal generating series of smooth functions on
![]() ${\mathrm {Sh}}({\mathbb {V}})_{K,E_\infty }$
with logarithmic singularities along the same formal generating series of special divisors. Then
${\mathrm {Sh}}({\mathbb {V}})_{K,E_\infty }$
with logarithmic singularities along the same formal generating series of special divisors. Then
![]() $ {\mathcal {G}}^{{\overline {\mathcal {L}}}}(g,\phi )- {\mathcal {G}}^{\mathrm {Kud}}(g,\phi )$
is a formal generating series valued in
$ {\mathcal {G}}^{{\overline {\mathcal {L}}}}(g,\phi )- {\mathcal {G}}^{\mathrm {Kud}}(g,\phi )$
is a formal generating series valued in
![]() ${C^\infty }({\mathrm {Sh}}({\mathbb {V}})_{K,E_\infty }),$
the space of smooth
${C^\infty }({\mathrm {Sh}}({\mathbb {V}})_{K,E_\infty }),$
the space of smooth
![]() ${\mathbb {C}}$
-valued functions on
${\mathbb {C}}$
-valued functions on
![]() ${\mathrm {Sh}}({\mathbb {V}})_{K,E_\infty }$
.
${\mathrm {Sh}}({\mathbb {V}})_{K,E_\infty }$
.
Let
![]() $E_1:={\mathcal {O}}_{{\mathrm {Sh}}({\mathbb {V}})_{K}}\left ( {\mathrm {Sh}}({\mathbb {V}})_{K}\right )$
, which is a finite field extension of E (since
$E_1:={\mathcal {O}}_{{\mathrm {Sh}}({\mathbb {V}})_{K}}\left ( {\mathrm {Sh}}({\mathbb {V}})_{K}\right )$
, which is a finite field extension of E (since
![]() ${\mathrm {Sh}}({\mathbb {V}})_{K}$
is connected). Then we have a morphism
${\mathrm {Sh}}({\mathbb {V}})_{K}$
is connected). Then we have a morphism
![]() ${\mathrm {Sh}}({\mathbb {V}})_{K }\to \operatorname {\mathrm {Spec}} E_1$
. By Stein factorization,
${\mathrm {Sh}}({\mathbb {V}})_{K }\to \operatorname {\mathrm {Spec}} E_1$
. By Stein factorization,
![]() ${\mathrm {Sh}}({\mathbb {V}})_{K }$
, as a variety over
${\mathrm {Sh}}({\mathbb {V}})_{K }$
, as a variety over
![]() $E_1$
, is geometrically connected. So the connected components of
$E_1$
, is geometrically connected. So the connected components of
![]() ${\mathrm {Sh}}({\mathbb {V}})_{K,E_\infty } ={\mathrm {Sh}}({\mathbb {V}})_{K}\otimes _{\mathbb {Q}}{\mathbb {R}} $
are exactly indexed by the underlying set of
${\mathrm {Sh}}({\mathbb {V}})_{K,E_\infty } ={\mathrm {Sh}}({\mathbb {V}})_{K}\otimes _{\mathbb {Q}}{\mathbb {R}} $
are exactly indexed by the underlying set of
![]() $\operatorname {\mathrm {Spec}} E_1\otimes _{\mathbb {Q}}{\mathbb {R}}$
, equivalently, the set of conjugate pairs of infinite places of
$\operatorname {\mathrm {Spec}} E_1\otimes _{\mathbb {Q}}{\mathbb {R}}$
, equivalently, the set of conjugate pairs of infinite places of
![]() $E_1$
(which, as a finite field extension of the CM field E, has only complex embeddings but no real embeddings). Let
$E_1$
(which, as a finite field extension of the CM field E, has only complex embeddings but no real embeddings). Let
![]() $ {\mathrm {LC}}({\mathrm {Sh}}({\mathbb {V}})_{K,E_\infty })$
be the space of locally constant functions on
$ {\mathrm {LC}}({\mathrm {Sh}}({\mathbb {V}})_{K,E_\infty })$
be the space of locally constant functions on
![]() ${\mathrm {Sh}}({\mathbb {V}})_{K,E_\infty }$
. Then we have the canonical isomorphism from
${\mathrm {Sh}}({\mathbb {V}})_{K,E_\infty }$
. Then we have the canonical isomorphism from
![]() $ {\mathrm {LC}}({\mathrm {Sh}}({\mathbb {V}})_{K,E_\infty })$
to the product copies of
$ {\mathrm {LC}}({\mathrm {Sh}}({\mathbb {V}})_{K,E_\infty })$
to the product copies of
![]() ${\mathbb {C}}$
indexed by the set of conjugate pairs of infinite places of
${\mathbb {C}}$
indexed by the set of conjugate pairs of infinite places of
![]() $E_1$
. Now we can embed
$E_1$
. Now we can embed
![]() $ {\mathcal {O}}_{E_1}^\times $
in
$ {\mathcal {O}}_{E_1}^\times $
in
![]() ${\mathrm {LC}}({\mathrm {Sh}}({\mathbb {V}})_{K,E_\infty })$
via this isomorphism and the Dirichlet regulator map, so that the
${\mathrm {LC}}({\mathrm {Sh}}({\mathbb {V}})_{K,E_\infty })$
via this isomorphism and the Dirichlet regulator map, so that the
![]() ${\mathbb {C}}$
-span of the image of
${\mathbb {C}}$
-span of the image of
![]() $ {\mathcal {O}}_{E_1}^\times $
, denoted by
$ {\mathcal {O}}_{E_1}^\times $
, denoted by
![]() ${\mathbb {C}} {\mathcal {O}}_{E_1}^\times $
is of codimension 1 in
${\mathbb {C}} {\mathcal {O}}_{E_1}^\times $
is of codimension 1 in
![]() $ {\mathrm {LC}}({\mathrm {Sh}}({\mathbb {V}})_{K,E_\infty })$
by Dirichlet’s unit theorem. Let
$ {\mathrm {LC}}({\mathrm {Sh}}({\mathbb {V}})_{K,E_\infty })$
by Dirichlet’s unit theorem. Let
![]() ${\mathbb {C}} {\mathcal {O}}_{E_1}^\times $
be this span. Let
${\mathbb {C}} {\mathcal {O}}_{E_1}^\times $
be this span. Let
Equip
![]() $\overline {C^\infty }({\mathrm {Sh}}({\mathbb {V}})_{K,E_\infty }) $
with the quotient of the
$\overline {C^\infty }({\mathrm {Sh}}({\mathbb {V}})_{K,E_\infty }) $
with the quotient of the
![]() $L^\infty $
-topology. Define an embedding
$L^\infty $
-topology. Define an embedding
by mapping
![]() $a\in {\mathbb {C}}$
to the constant function a on
$a\in {\mathbb {C}}$
to the constant function a on
![]() ${\mathrm {Sh}}({\mathbb {V}})_{K,E_v}$
for some
${\mathrm {Sh}}({\mathbb {V}})_{K,E_v}$
for some
![]() $v\in \infty $
(rather than
$v\in \infty $
(rather than
![]() ${\mathrm {Sh}}({\mathbb {V}})_{K,E_{1,w}}$
for some infinite place w of
${\mathrm {Sh}}({\mathbb {V}})_{K,E_{1,w}}$
for some infinite place w of
![]() $E_1$
). Below, by a complex number in
$E_1$
). Below, by a complex number in
![]() $ \overline {C^\infty }({\mathrm {Sh}}({\mathbb {V}})_{K,E_\infty }) $
, we understand it as the image by (4.13).
$ \overline {C^\infty }({\mathrm {Sh}}({\mathbb {V}})_{K,E_\infty }) $
, we understand it as the image by (4.13).
Theorem 4.2.10. Let
![]() $E^{\prime }_{t,{\mathrm {f}}}(0,g,\phi )$
be as in (3.29). For
$E^{\prime }_{t,{\mathrm {f}}}(0,g,\phi )$
be as in (3.29). For
![]() $g\in G({\mathbb {A}})$
, the generating series of
$g\in G({\mathbb {A}})$
, the generating series of
![]() $\overline {C^\infty }({\mathrm {Sh}}({\mathbb {V}})_{K,E_\infty }) $
-valued functions on
$\overline {C^\infty }({\mathrm {Sh}}({\mathbb {V}})_{K,E_\infty }) $
-valued functions on
![]() $G({\mathbb {A}})$
$G({\mathbb {A}})$
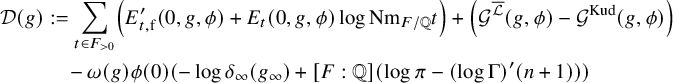 $$ \begin{align*} {\mathcal{D}}(g)&:= \sum_{t\in F_{>0}}\left( E^{\prime}_{t,{\mathrm{f}}}(0,g,\phi) +E_t(0,g,\phi ) \log {\mathrm{Nm}}_{F/{\mathbb{Q}}}t\right) + \left( {\mathcal{G}}^{{\overline{\mathcal{L}}}}(g,\phi)- {\mathcal{G}}^{\mathrm{Kud}}(g,\phi) \right) \\& \quad - \omega(g)\phi (0 ) \left( -\log \delta_\infty(g_\infty)+ [F:{\mathbb{Q}}]\left( \log \pi-(\log\Gamma)'(n+1)\right)\right) \end{align*} $$
$$ \begin{align*} {\mathcal{D}}(g)&:= \sum_{t\in F_{>0}}\left( E^{\prime}_{t,{\mathrm{f}}}(0,g,\phi) +E_t(0,g,\phi ) \log {\mathrm{Nm}}_{F/{\mathbb{Q}}}t\right) + \left( {\mathcal{G}}^{{\overline{\mathcal{L}}}}(g,\phi)- {\mathcal{G}}^{\mathrm{Kud}}(g,\phi) \right) \\& \quad - \omega(g)\phi (0 ) \left( -\log \delta_\infty(g_\infty)+ [F:{\mathbb{Q}}]\left( \log \pi-(\log\Gamma)'(n+1)\right)\right) \end{align*} $$
pointwise converges to an element in
![]() $ {\mathcal {A}}\left ( G,{\mathfrak {w}}, \overline {C^\infty }({\mathrm {Sh}}({\mathbb {V}})_{K,E_\infty })\right ) .$
$ {\mathcal {A}}\left ( G,{\mathfrak {w}}, \overline {C^\infty }({\mathrm {Sh}}({\mathbb {V}})_{K,E_\infty })\right ) .$
Remark 4.2.11. (1) It might be interesting to study whether Theorem 4.2.10 still holds if we put Fréchet topology on
![]() $\overline {C^\infty }({\mathrm {Sh}}({\mathbb {V}})_{K,E_\infty })$
, and if we require stronger convergence.
$\overline {C^\infty }({\mathrm {Sh}}({\mathbb {V}})_{K,E_\infty })$
, and if we require stronger convergence.
(2) Theorem 4.2.10 is a strengthened analog of the main result of Ehlen and Sankaran [Reference Ehlen and SankaranES18], which is for
![]() $F={\mathbb {Q}}$
.
$F={\mathbb {Q}}$
.
Proof. We follow [Reference Kudla, Rapoport and YangKRY06] and [Reference Mihatsch and ZhangMZ21]. Let
![]() $C^\infty ({\mathrm {Sh}}({\mathbb {V}})_{K,E_\infty })^\circ $
be the
$C^\infty ({\mathrm {Sh}}({\mathbb {V}})_{K,E_\infty })^\circ $
be the
![]() $L^2$
-orthogonal complement of
$L^2$
-orthogonal complement of
![]() ${\mathrm {LC}}({\mathrm {Sh}}({\mathbb {V}})_{K,E_\infty })$
in
${\mathrm {LC}}({\mathrm {Sh}}({\mathbb {V}})_{K,E_\infty })$
in
![]() $C^\infty ({\mathrm {Sh}}({\mathbb {V}})_{K,E_\infty })$
, endowed with
$C^\infty ({\mathrm {Sh}}({\mathbb {V}})_{K,E_\infty })$
, endowed with
![]() $L^\infty $
-topology. Then
$L^\infty $
-topology. Then
![]() $\overline {C^\infty }({\mathrm {Sh}}({\mathbb {V}})_{K,E_\infty }) $
is the topological direct sum of
$\overline {C^\infty }({\mathrm {Sh}}({\mathbb {V}})_{K,E_\infty }) $
is the topological direct sum of
![]() $C^\infty ({\mathrm {Sh}}({\mathbb {V}})_{K,E_\infty })^\circ $
and
$C^\infty ({\mathrm {Sh}}({\mathbb {V}})_{K,E_\infty })^\circ $
and
![]() $ {\mathrm {LC}}({\mathrm {Sh}}({\mathbb {V}})_{K,E_\infty }) /{\mathbb {C}} {\mathcal {O}}_{E_1}^\times $
.
$ {\mathrm {LC}}({\mathrm {Sh}}({\mathbb {V}})_{K,E_\infty }) /{\mathbb {C}} {\mathcal {O}}_{E_1}^\times $
.
Let the generating series
![]() ${\mathcal {D}}^\circ $
be the projection of
${\mathcal {D}}^\circ $
be the projection of
![]() ${\mathcal {D}}$
to
${\mathcal {D}}$
to
![]() $C^\infty ({\mathrm {Sh}}({\mathbb {V}})_{K,E_\infty })^\circ $
. By [Reference Mihatsch and ZhangMZ21, Lemma 3.8]Footnote
2
and the same argument in the proof [Reference Kudla, Rapoport and YangKRY06, Theorem 4.4.4],Footnote
3
for every
$C^\infty ({\mathrm {Sh}}({\mathbb {V}})_{K,E_\infty })^\circ $
. By [Reference Mihatsch and ZhangMZ21, Lemma 3.8]Footnote
2
and the same argument in the proof [Reference Kudla, Rapoport and YangKRY06, Theorem 4.4.4],Footnote
3
for every
![]() $g\in G({\mathbb {A}})$
,
$g\in G({\mathbb {A}})$
,
![]() ${\mathcal {D}}^\circ (g)$
converges in
${\mathcal {D}}^\circ (g)$
converges in
![]() $L^\infty \left ({\mathrm {Sh}}({\mathbb {V}})_{K,E_\infty }\right ) $
. Particularly,
$L^\infty \left ({\mathrm {Sh}}({\mathbb {V}})_{K,E_\infty }\right ) $
. Particularly,
![]() ${\mathcal {D}}^\circ (g)$
converges in
${\mathcal {D}}^\circ (g)$
converges in
![]() $L^2\left ({\mathrm {Sh}}({\mathbb {V}})_{K,E_\infty }\right )$
since
$L^2\left ({\mathrm {Sh}}({\mathbb {V}})_{K,E_\infty }\right )$
since
![]() ${\mathrm {Sh}}({\mathbb {V}})_{K,E_\infty }$
is compact. So we can consider
${\mathrm {Sh}}({\mathbb {V}})_{K,E_\infty }$
is compact. So we can consider
![]() ${\mathcal {D}}^\circ $
(identified as its limit) as a function on
${\mathcal {D}}^\circ $
(identified as its limit) as a function on
![]() $G({\mathbb {A}}) \times {\mathrm {Sh}}({\mathbb {V}})_{K,E_\infty }$
. Then by the argument in the proof of [Reference Mihatsch and ZhangMZ21, Theorem 3.9],
$G({\mathbb {A}}) \times {\mathrm {Sh}}({\mathbb {V}})_{K,E_\infty }$
. Then by the argument in the proof of [Reference Mihatsch and ZhangMZ21, Theorem 3.9],
![]() ${\mathcal {D}}^\circ \in C^\infty \left ( G({\mathbb {A}}) \times {\mathrm {Sh}}({\mathbb {V}})_{K,E_\infty }\right )$
. Also note that for every
${\mathcal {D}}^\circ \in C^\infty \left ( G({\mathbb {A}}) \times {\mathrm {Sh}}({\mathbb {V}})_{K,E_\infty }\right )$
. Also note that for every
![]() $g\in G({\mathbb {A}})$
,
$g\in G({\mathbb {A}})$
,
![]() ${\mathcal {D}}^\circ (g)\in C^\infty \left ( {\mathrm {Sh}}({\mathbb {V}})_{K,E_\infty }\right )^\circ $
. Thus,
${\mathcal {D}}^\circ (g)\in C^\infty \left ( {\mathrm {Sh}}({\mathbb {V}})_{K,E_\infty }\right )^\circ $
. Thus,
![]() ${\mathcal {D}}^\circ $
is a smooth
${\mathcal {D}}^\circ $
is a smooth
![]() $C^\infty \left ( {\mathrm {Sh}}({\mathbb {V}})_{K,E_\infty }\right )^\circ $
-valued function on
$C^\infty \left ( {\mathrm {Sh}}({\mathbb {V}})_{K,E_\infty }\right )^\circ $
-valued function on
![]() $G({\mathbb {A}})$
. See [Reference TrévesTré67, Theorem 40.1 and Corollary]. Then the argument in the proof of either [Reference Kudla, Rapoport and YangKRY06, Theorem 4.4.4] or [Reference Mihatsch and ZhangMZ21, Theorem 3.9] shows that
$G({\mathbb {A}})$
. See [Reference TrévesTré67, Theorem 40.1 and Corollary]. Then the argument in the proof of either [Reference Kudla, Rapoport and YangKRY06, Theorem 4.4.4] or [Reference Mihatsch and ZhangMZ21, Theorem 3.9] shows that
![]() ${\mathcal {D}}^\circ \in {\mathcal {A}}\left ( G,{\mathfrak {w}}, \overline {C^\infty }({\mathrm {Sh}}({\mathbb {V}})_{K,E_\infty })^\circ \right ) .$
${\mathcal {D}}^\circ \in {\mathcal {A}}\left ( G,{\mathfrak {w}}, \overline {C^\infty }({\mathrm {Sh}}({\mathbb {V}})_{K,E_\infty })^\circ \right ) .$
Consider the projection from
![]() $\overline {C^\infty }({\mathrm {Sh}}({\mathbb {V}})_{K,E_\infty }) $
to
$\overline {C^\infty }({\mathrm {Sh}}({\mathbb {V}})_{K,E_\infty }) $
to
![]() $ {\mathrm {LC}}({\mathrm {Sh}}({\mathbb {V}})_{K,E_\infty }) /{\mathbb {C}} {\mathcal {O}}_{E_1}^\times {\ \simeq \ } {\mathbb {C}}$
– that is,
$ {\mathrm {LC}}({\mathrm {Sh}}({\mathbb {V}})_{K,E_\infty }) /{\mathbb {C}} {\mathcal {O}}_{E_1}^\times {\ \simeq \ } {\mathbb {C}}$
– that is,
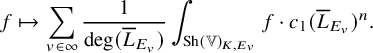 $$ \begin{align*}f\mapsto \sum_{v\in \infty}\frac{1}{\deg (\overline{L}_{E_v})}\int_{{\mathrm{Sh}}({\mathbb{V}})_{K,E_v} } f\cdot c_1(\overline{L}_{E_v})^n. \end{align*} $$
$$ \begin{align*}f\mapsto \sum_{v\in \infty}\frac{1}{\deg (\overline{L}_{E_v})}\int_{{\mathrm{Sh}}({\mathbb{V}})_{K,E_v} } f\cdot c_1(\overline{L}_{E_v})^n. \end{align*} $$
By Theorem 4.2.7 and that
![]() $E_0(0,g,\phi )= \omega ( g)\phi (0)$
(see Lemma 3.3.9 (1)), the projection of
$E_0(0,g,\phi )= \omega ( g)\phi (0)$
(see Lemma 3.3.9 (1)), the projection of
![]() ${\mathcal {D}}$
(defined on each of its terms) pointwise converges to an element in
${\mathcal {D}}$
(defined on each of its terms) pointwise converges to an element in
![]() $ {\mathcal {A}}\left ( G,{\mathfrak {w}} \right ).$
Since
$ {\mathcal {A}}\left ( G,{\mathfrak {w}} \right ).$
Since
![]() ${\mathcal {D}}$
is the sum of this projection and
${\mathcal {D}}$
is the sum of this projection and
![]() ${\mathcal {D}}^\circ $
, the theorem follows.
${\mathcal {D}}^\circ $
, the theorem follows.
4.3 Modularity problems
We will raise two modularity problems for admissible extensions of special divisors. Before that, we recall some notions and Kudla’s modularity problem.
4.3.1 Preliminaries
A (regular) integral model of
![]() ${\mathrm {Sh}}({\mathbb {V}})_{K}$
over an integral domain R with fraction field E is a (regular) Deligne-Mumford stack proper flat over
${\mathrm {Sh}}({\mathbb {V}})_{K}$
over an integral domain R with fraction field E is a (regular) Deligne-Mumford stack proper flat over
![]() $\operatorname {\mathrm {Spec}} R$
with a fixed isomorphism of its generic fiber to
$\operatorname {\mathrm {Spec}} R$
with a fixed isomorphism of its generic fiber to
![]() $ {\mathrm {Sh}}({\mathbb {V}})_{K }.$
An isomorphism between integral models is an isomorphism over
$ {\mathrm {Sh}}({\mathbb {V}})_{K }.$
An isomorphism between integral models is an isomorphism over
![]() $\operatorname {\mathrm {Spec}} R$
that respects the fixed isomorphisms to
$\operatorname {\mathrm {Spec}} R$
that respects the fixed isomorphisms to
![]() $ {\mathrm {Sh}}({\mathbb {V}})_{K }.$
$ {\mathrm {Sh}}({\mathbb {V}})_{K }.$
Let
![]() ${\mathcal {X}}_K$
be a regular integral model of
${\mathcal {X}}_K$
be a regular integral model of
![]() ${\mathrm {Sh}}({\mathbb {V}})_{K}$
over
${\mathrm {Sh}}({\mathbb {V}})_{K}$
over
![]() $\operatorname {\mathrm {Spec}} {\mathcal {O}}_E$
. Let
$\operatorname {\mathrm {Spec}} {\mathcal {O}}_E$
. Let
![]() $\widehat {\mathrm {Ch}}^1_{{\mathbb {C}}}({\mathcal {X}}_K) $
be the Chow group of arithmetic divisors with
$\widehat {\mathrm {Ch}}^1_{{\mathbb {C}}}({\mathcal {X}}_K) $
be the Chow group of arithmetic divisors with
![]() ${\mathbb {C}}$
-coefficients. See Definition A.3.4. In particular, we have an isomorphism
${\mathbb {C}}$
-coefficients. See Definition A.3.4. In particular, we have an isomorphism
by taking degrees (see Remark A.3.5), and an arithmetic intersection pairing
See Appendix A.4. Here, we recall that
![]() $Z_1({\mathcal {X}}_K)$
is the group of 1-cycles on
$Z_1({\mathcal {X}}_K)$
is the group of 1-cycles on
![]() ${\mathcal {X}}_K$
.
${\mathcal {X}}_K$
.
Let
![]() $ {\mathcal {L}}= {\mathcal {L}}_K$
be an extension of
$ {\mathcal {L}}= {\mathcal {L}}_K$
be an extension of
![]() $L=L_K $
to
$L=L_K $
to
![]() ${\mathcal {X}}_K$
, which we allow to be a line bundle. Let
${\mathcal {X}}_K$
, which we allow to be a line bundle. Let
![]() $ \overline {\mathcal {L}} $
be
$ \overline {\mathcal {L}} $
be
![]() ${\mathcal {L}}$
equipped with a hermitian metric. Let
${\mathcal {L}}$
equipped with a hermitian metric. Let
![]() $c_1(\overline {\mathcal {L}}^\vee )\in \widehat {\mathrm {Ch}}^{1}_{{\mathbb {C}}}({\mathcal {X}}_K) $
be the first arithmetic Chern class of the dual of
$c_1(\overline {\mathcal {L}}^\vee )\in \widehat {\mathrm {Ch}}^{1}_{{\mathbb {C}}}({\mathcal {X}}_K) $
be the first arithmetic Chern class of the dual of
![]() $\overline {\mathcal {L}}$
. See Example A.3.7.
$\overline {\mathcal {L}}$
. See Example A.3.7.
4.3.2 Kudla’s problem
We consider the following modularity problem of Kudla [Reference KudlaKud02, Reference KudlaKud03, Reference KudlaKud04]: find an arithmetic divisor
![]() $\widehat {\mathcal {Z}}(x)$
on
$\widehat {\mathcal {Z}}(x)$
on
![]() ${\mathcal {X}}$
extending
${\mathcal {X}}$
extending
![]() $Z(x)$
, explicitly and canonically, such that
$Z(x)$
, explicitly and canonically, such that
 $$ \begin{align*} \omega(g)\phi(0)c_1(\overline {\mathcal{L}}^\vee)+\sum_{x\in K\backslash {\mathbb{V}}^{ \infty}_{>0}} \omega(g)\phi( x_\infty x) \widehat {\mathcal{Z}}(x) ,\\[-20pt] \end{align*} $$
$$ \begin{align*} \omega(g)\phi(0)c_1(\overline {\mathcal{L}}^\vee)+\sum_{x\in K\backslash {\mathbb{V}}^{ \infty}_{>0}} \omega(g)\phi( x_\infty x) \widehat {\mathcal{Z}}(x) ,\\[-20pt] \end{align*} $$
where
![]() $ x_\infty \in {\mathbb {V}}_\infty $
such that
$ x_\infty \in {\mathbb {V}}_\infty $
such that
![]() $q(x_\infty )={q(x)}\in F_{>0}$
lies in
$q(x_\infty )={q(x)}\in F_{>0}$
lies in
![]() $ {\mathcal {A}}_{{\mathrm {hol}}}(G,{\mathfrak {w}}) \otimes \widehat {\mathrm {Ch}}^{1}_{{\mathbb {C}}}({\mathcal {X}}_K) $
. The existence of such
$ {\mathcal {A}}_{{\mathrm {hol}}}(G,{\mathfrak {w}}) \otimes \widehat {\mathrm {Ch}}^{1}_{{\mathbb {C}}}({\mathcal {X}}_K) $
. The existence of such
![]() $\widehat {\mathcal {Z}}(x)$
is obvious, by choosing a section of the natural surjection
$\widehat {\mathcal {Z}}(x)$
is obvious, by choosing a section of the natural surjection
![]() $\widehat {\mathrm {Ch}}^1_{{\mathbb {C}}}({\mathcal {X}}_K)\to {\mathrm {Ch}}^1({\mathrm {Sh}}({\mathbb {V}})_K)_{\mathbb {C}}$
. However, it is only defined at the level of divisor classes, and not explicit.
$\widehat {\mathrm {Ch}}^1_{{\mathbb {C}}}({\mathcal {X}}_K)\to {\mathrm {Ch}}^1({\mathrm {Sh}}({\mathbb {V}})_K)_{\mathbb {C}}$
. However, it is only defined at the level of divisor classes, and not explicit.
4.3.3 Admissible extensions
We consider the above modularity problem for admissible extensions. In particular, we assume Assumption A.1.1 for
![]() ${\mathcal {X}}_K$
. (Also recall that
${\mathcal {X}}_K$
. (Also recall that
![]() ${\mathcal {X}}_K$
is connected, as
${\mathcal {X}}_K$
is connected, as
![]() ${\mathrm {Sh}}({\mathbb {V}})_K$
is.) Assume that
${\mathrm {Sh}}({\mathbb {V}})_K$
is.) Assume that
![]() $ {\mathcal {L}}$
is ample. Let
$ {\mathcal {L}}$
is ample. Let
![]() $ \widehat {\mathrm {Ch}}^{1}_{{\overline {\mathcal {L}}},{\mathbb {C}}}({\mathcal {X}}_K) \subset \widehat {\mathrm {Ch}}^1_{\mathbb {C}}({\mathcal {X}}_K)$
be the subgroup of arithmetic divisors that are admissible with respect to
$ \widehat {\mathrm {Ch}}^{1}_{{\overline {\mathcal {L}}},{\mathbb {C}}}({\mathcal {X}}_K) \subset \widehat {\mathrm {Ch}}^1_{\mathbb {C}}({\mathcal {X}}_K)$
be the subgroup of arithmetic divisors that are admissible with respect to
![]() $\overline {\mathcal {L}}$
. See Definition A.3.4. By Lemma A.3.6, the natural map
$\overline {\mathcal {L}}$
. See Definition A.3.4. By Lemma A.3.6, the natural map
is surjective, and the kernel is the image of the pullback
In particular,
![]() $ \widehat {\mathrm {Ch}}^{1}_{{\overline {\mathcal {L}}},{\mathbb {C}}}({\mathcal {X}}_K) $
is finite dimensional.
$ \widehat {\mathrm {Ch}}^{1}_{{\overline {\mathcal {L}}},{\mathbb {C}}}({\mathcal {X}}_K) $
is finite dimensional.
Definition 4.3.1. Define an embedding
![]() $ {\mathbb {C}}\hookrightarrow \widehat {\mathrm {Ch}}^1_{{\overline {\mathcal {L}}},{\mathbb {C}}}({\mathcal {X}}_K) $
as the composition of the inverse
$ {\mathbb {C}}\hookrightarrow \widehat {\mathrm {Ch}}^1_{{\overline {\mathcal {L}}},{\mathbb {C}}}({\mathcal {X}}_K) $
as the composition of the inverse
![]() $\deg ^{-1}: {\mathbb {C}}{\ \simeq \ } \widehat {\mathrm {Ch}}^1_{{\mathbb {C}}}\left ( \operatorname {\mathrm {Spec}} {\mathcal {O}}_{E} \right )$
of taking degree and (4.15). Below, by a complex number in
$\deg ^{-1}: {\mathbb {C}}{\ \simeq \ } \widehat {\mathrm {Ch}}^1_{{\mathbb {C}}}\left ( \operatorname {\mathrm {Spec}} {\mathcal {O}}_{E} \right )$
of taking degree and (4.15). Below, by a complex number in
![]() $\widehat {\mathrm {Ch}}^1_{{\overline {\mathcal {L}}},{\mathbb {C}}}({\mathcal {X}}_K)$
, we understand it as the image by this embedding.
$\widehat {\mathrm {Ch}}^1_{{\overline {\mathcal {L}}},{\mathbb {C}}}({\mathcal {X}}_K)$
, we understand it as the image by this embedding.
Remark 4.3.2. The intersection
![]() $ \widehat {\mathrm {Ch}}^1_{{\overline {\mathcal {L}}},{\mathbb {C}}}({\mathcal {X}}_K)\cap \overline {C^\infty }({\mathrm {Sh}}({\mathbb {V}})_{K,E_\infty }) $
in
$ \widehat {\mathrm {Ch}}^1_{{\overline {\mathcal {L}}},{\mathbb {C}}}({\mathcal {X}}_K)\cap \overline {C^\infty }({\mathrm {Sh}}({\mathbb {V}})_{K,E_\infty }) $
in
![]() $ \widehat {\mathrm {Ch}}_{\mathbb {C}}({\mathcal {X}}_K) $
is
$ \widehat {\mathrm {Ch}}_{\mathbb {C}}({\mathcal {X}}_K) $
is
![]() ${\mathbb {C}}$
, where
${\mathbb {C}}$
, where
![]() ${\mathbb {C}}$
is in
${\mathbb {C}}$
is in
![]() $\overline {C^\infty }({\mathrm {Sh}}({\mathbb {V}})_{K,E_\infty })$
via (4.13).
$\overline {C^\infty }({\mathrm {Sh}}({\mathbb {V}})_{K,E_\infty })$
via (4.13).
Let
![]() ${\widehat {Z}}^1_{{\overline {\mathcal {L}}},{\mathbb {C}}}({\mathcal {X}}_K)$
the group of admissible arithmetic divisors. See Definition A.3.1. For a divisor Z on
${\widehat {Z}}^1_{{\overline {\mathcal {L}}},{\mathbb {C}}}({\mathcal {X}}_K)$
the group of admissible arithmetic divisors. See Definition A.3.1. For a divisor Z on
![]() ${\mathrm {Sh}}({\mathbb {V}})_{K}{\ \simeq \ } {\mathcal {X}}_{K,E}$
, let
${\mathrm {Sh}}({\mathbb {V}})_{K}{\ \simeq \ } {\mathcal {X}}_{K,E}$
, let
be the normalized admissible extension of Z with respect to
![]() $\overline {\mathcal {L}}$
. See Definition A.3.3. Let
$\overline {\mathcal {L}}$
. See Definition A.3.3. Let
![]() $[ Z(x)^{\overline {\mathcal {L}}}] $
be its class in
$[ Z(x)^{\overline {\mathcal {L}}}] $
be its class in
![]() $\widehat {\mathrm {Ch}}^1_{{\overline {\mathcal {L}}},{\mathbb {C}}}({\mathcal {X}}_K)$
. Then a preiamge of
$\widehat {\mathrm {Ch}}^1_{{\overline {\mathcal {L}}},{\mathbb {C}}}({\mathcal {X}}_K)$
. Then a preiamge of
![]() $[ Z(x)] $
via (4.14) is of the form
$[ Z(x)] $
via (4.14) is of the form
![]() $[ Z(x)^{\overline {\mathcal {L}}}] +e(x)$
for some
$[ Z(x)^{\overline {\mathcal {L}}}] +e(x)$
for some
![]() $e(x)\in {\mathbb {C}}$
. Note that
$e(x)\in {\mathbb {C}}$
. Note that
![]() $c_1(\overline {\mathcal {L}}^\vee )\in \widehat {\mathrm {Ch}}^{1}_{{\overline {\mathcal {L}}},{\mathbb {C}}}({\mathcal {X}}_K) $
. See Example A.3.7.
$c_1(\overline {\mathcal {L}}^\vee )\in \widehat {\mathrm {Ch}}^{1}_{{\overline {\mathcal {L}}},{\mathbb {C}}}({\mathcal {X}}_K) $
. See Example A.3.7.
Problem 4.3.3. Find
![]() $a\in {\mathbb {C}}$
and
$a\in {\mathbb {C}}$
and
![]() $e=\{e(x) \in {\mathbb {C}}\}_{x\in K\backslash {\mathbb {V}}^{ \infty }_{>0}}$
explicitly such that for every
$e=\{e(x) \in {\mathbb {C}}\}_{x\in K\backslash {\mathbb {V}}^{ \infty }_{>0}}$
explicitly such that for every
![]() $\phi \in \overline {\mathcal {S}}\left ( {\mathbb {V}} \right )^{K}$
, the generating series
$\phi \in \overline {\mathcal {S}}\left ( {\mathbb {V}} \right )^{K}$
, the generating series
 $$ \begin{align}z(\omega(g)\phi)_{e,a} ^{\overline{\mathcal{L}}}:=\omega(g)\phi(0)\left( c_1(\overline {\mathcal{L}}^\vee)+a\right)+\sum_{x\in K\backslash {\mathbb{V}}^{ \infty}_{>0}}\omega(g)\phi( x_\infty x) \left([ Z(x)^{\overline{\mathcal{L}}}]+e(x)\right), \end{align} $$
$$ \begin{align}z(\omega(g)\phi)_{e,a} ^{\overline{\mathcal{L}}}:=\omega(g)\phi(0)\left( c_1(\overline {\mathcal{L}}^\vee)+a\right)+\sum_{x\in K\backslash {\mathbb{V}}^{ \infty}_{>0}}\omega(g)\phi( x_\infty x) \left([ Z(x)^{\overline{\mathcal{L}}}]+e(x)\right), \end{align} $$
where
![]() $ x_\infty \in {\mathbb {V}}_\infty $
such that
$ x_\infty \in {\mathbb {V}}_\infty $
such that
![]() $q(x_\infty )={q(x)}\in F_{>0}$
, lies in
$q(x_\infty )={q(x)}\in F_{>0}$
, lies in
![]() $ {\mathcal {A}}_{{\mathrm {hol}}}(G,{\mathfrak {w}}) \otimes \widehat {\mathrm {Ch}}^{1}_{{\overline {\mathcal {L}}},{\mathbb {C}}}({\mathcal {X}}_K) $
. Moreover,
$ {\mathcal {A}}_{{\mathrm {hol}}}(G,{\mathfrak {w}}) \otimes \widehat {\mathrm {Ch}}^{1}_{{\overline {\mathcal {L}}},{\mathbb {C}}}({\mathcal {X}}_K) $
. Moreover,
![]() $e(x)$
should to be naturally decomposed into a sum of ‘local components’ such that the v-component should be 0 at all but finitely many places and
$e(x)$
should to be naturally decomposed into a sum of ‘local components’ such that the v-component should be 0 at all but finitely many places and
![]() $\infty $
-component should be independent of the choice of the regular integral model.
$\infty $
-component should be independent of the choice of the regular integral model.
In other words, we want a modular generating series by modifying each
![]() $[Z(x)^{\overline {\mathcal {L}}}]$
by an explicit constant once for all
$[Z(x)^{\overline {\mathcal {L}}}]$
by an explicit constant once for all
![]() $\phi $
. A weaker statement is to allow the modification to depend on
$\phi $
. A weaker statement is to allow the modification to depend on
![]() $g,\phi $
.
$g,\phi $
.
Problem 4.3.4. Find
![]() $a\in {\mathbb {C}}$
and a smooth function
$a\in {\mathbb {C}}$
and a smooth function
![]() $e_t(g,\phi )$
on
$e_t(g,\phi )$
on
![]() $G({\mathbb {A}}_F)$
for
$G({\mathbb {A}}_F)$
for
![]() $\phi \in \overline {\mathcal {S}}\left ( {\mathbb {V}} \right )^{K}$
explicitly such that the generating series
$\phi \in \overline {\mathcal {S}}\left ( {\mathbb {V}} \right )^{K}$
explicitly such that the generating series
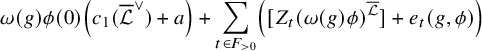 $$ \begin{align}\omega(g)\phi(0)\left( c_1(\overline {\mathcal{L}}^\vee)+a\right) + \sum_{t\in F_{>0}}\left( [Z_t( \omega(g)\phi )^{\overline{\mathcal{L}}}]+ e_t(g,\phi)\right) \end{align} $$
$$ \begin{align}\omega(g)\phi(0)\left( c_1(\overline {\mathcal{L}}^\vee)+a\right) + \sum_{t\in F_{>0}}\left( [Z_t( \omega(g)\phi )^{\overline{\mathcal{L}}}]+ e_t(g,\phi)\right) \end{align} $$
lies in
![]() $ {\mathcal {A}}_{{\mathrm {hol}}}(G,{\mathfrak {w}}) \otimes \widehat {\mathrm {Ch}}^{1}_{{\overline {\mathcal {L}}},{\mathbb {C}}}({\mathcal {X}}_K) $
. Moreover,
$ {\mathcal {A}}_{{\mathrm {hol}}}(G,{\mathfrak {w}}) \otimes \widehat {\mathrm {Ch}}^{1}_{{\overline {\mathcal {L}}},{\mathbb {C}}}({\mathcal {X}}_K) $
. Moreover,
![]() $e_t(g,\phi )$
should to be naturally decomposed into a sum of ‘local components’ such that the v-component should be 0 at all but finitely many places and
$e_t(g,\phi )$
should to be naturally decomposed into a sum of ‘local components’ such that the v-component should be 0 at all but finitely many places and
![]() $\infty $
-component should be independent of the choice of the regular integral model.
$\infty $
-component should be independent of the choice of the regular integral model.
Remark 4.3.5. In (4.17) and (4.18), one may replace
![]() $\omega (g)\phi (0)\left ( c_1(\overline {\mathcal {L}}^\vee )+a\right )$
by
$\omega (g)\phi (0)\left ( c_1(\overline {\mathcal {L}}^\vee )+a\right )$
by
![]() $\omega (g)\phi (0)c_1(\overline {\mathcal {L}}^\vee )$
by adding a suitable multiple of the degree of
$\omega (g)\phi (0)c_1(\overline {\mathcal {L}}^\vee )$
by adding a suitable multiple of the degree of
![]() $z\left (\omega (g)\phi \right )$
, which is modular by Theorem 4.1.2 and can be made explicit by (4.11). However, we keep the freedom to have ‘a’ to get the decomposition of
$z\left (\omega (g)\phi \right )$
, which is modular by Theorem 4.1.2 and can be made explicit by (4.11). However, we keep the freedom to have ‘a’ to get the decomposition of
![]() $e_t(g,\phi )$
as we will see in Section 4.4.
$e_t(g,\phi )$
as we will see in Section 4.4.
By Theorem 4.1.2 and Lemma A.3.6 (1), we immediately have the following lemma.
Lemma 4.3.6. For
![]() ${\mathcal {P}}\in Z_1({\mathcal {X}}_K )_{\mathbb {C}}$
such that
${\mathcal {P}}\in Z_1({\mathcal {X}}_K )_{\mathbb {C}}$
such that
![]() $\deg {\mathcal {P}}_E=0$
,
$\deg {\mathcal {P}}_E=0$
,
Remark 4.3.7. (1) This lemma is called almost modularity in [Reference Mihatsch and ZhangMZ21, Theorem 4.3].
(2) In the case that
![]() $K=K_{\Lambda }$
with a different
$K=K_{\Lambda }$
with a different
![]() $\Lambda $
, for Kudla-Rapoport arithmetic divisors and
$\Lambda $
, for Kudla-Rapoport arithmetic divisors and
![]() ${\mathcal {P}}\in Z_1({\mathcal {X}}_K )_{\mathbb {C}}$
with
${\mathcal {P}}\in Z_1({\mathcal {X}}_K )_{\mathbb {C}}$
with
![]() ${\mathcal {P}}_E=0$
, the analogous statement is proved in [Reference ZhangZha21b, Theorem 14.6].
${\mathcal {P}}_E=0$
, the analogous statement is proved in [Reference ZhangZha21b, Theorem 14.6].
When
![]() $\deg {\mathcal {P}}_E\neq 0$
, the truth of (4.19) is in fact equivalent to the modularity of
$\deg {\mathcal {P}}_E\neq 0$
, the truth of (4.19) is in fact equivalent to the modularity of
![]() $ z\left (\omega (g)\phi \right )_{e,a}^{\overline {\mathcal {L}}}$
by Lemma 4.3.8 below. We will not use exactly this ‘numerical criterion’, but use Lemma 4.3.8 in a more sophisticated way to prove our modularity results in 5.2.4.
$ z\left (\omega (g)\phi \right )_{e,a}^{\overline {\mathcal {L}}}$
by Lemma 4.3.8 below. We will not use exactly this ‘numerical criterion’, but use Lemma 4.3.8 in a more sophisticated way to prove our modularity results in 5.2.4.
Lemma 4.3.8. Let X be a
![]() ${\mathbb {C}}$
-vector space,
${\mathbb {C}}$
-vector space,
![]() $x\in X$
nonzero, and l a linear form on X such that
$x\in X$
nonzero, and l a linear form on X such that
![]() $l(x)=1$
. Let f be a formal generating series of functions on
$l(x)=1$
. Let f be a formal generating series of functions on
![]() $G({\mathbb {A}})$
valued in X and
$G({\mathbb {A}})$
valued in X and
![]() $\overline f$
the corresponding formal generating series of functions on
$\overline f$
the corresponding formal generating series of functions on
![]() $G({\mathbb {A}})$
valued in
$G({\mathbb {A}})$
valued in
![]() $X/{\mathbb {C}} x$
. Assume that
$X/{\mathbb {C}} x$
. Assume that
![]() $\overline f\in {\mathcal {A}}(G,{\mathfrak {w}}) \otimes X/{\mathbb {C}} x$
. Then
$\overline f\in {\mathcal {A}}(G,{\mathfrak {w}}) \otimes X/{\mathbb {C}} x$
. Then
![]() $ f\in {\mathcal {A}}(G,{\mathfrak {w}}) \otimes X $
if and only if
$ f\in {\mathcal {A}}(G,{\mathfrak {w}}) \otimes X $
if and only if
![]() $l\circ f\in {\mathcal {A}}(G,{\mathfrak {w}}). $
$l\circ f\in {\mathcal {A}}(G,{\mathfrak {w}}). $
Proof. Define a section
![]() ${\mathfrak {s}}$
of the projection
${\mathfrak {s}}$
of the projection
![]() $X\to X/{\mathbb {C}} x$
by
$X\to X/{\mathbb {C}} x$
by
![]() ${\mathfrak {s}}:z\mapsto s(z)- l\left ( s(z)\right ) \cdot x,$
where s is any section (and
${\mathfrak {s}}:z\mapsto s(z)- l\left ( s(z)\right ) \cdot x,$
where s is any section (and
![]() ${\mathfrak {s}}$
is independent of the choice of s). Then
${\mathfrak {s}}$
is independent of the choice of s). Then
![]() $ f= {\mathfrak {s}}(\overline f)+ \left ( l\circ f \right ) \cdot x $
, and the lemma follows.
$ f= {\mathfrak {s}}(\overline f)+ \left ( l\circ f \right ) \cdot x $
, and the lemma follows.
4.4 Conjecture and theorems
First, we define specific integral models. Then we define explicit admissible extensions. Then we will propose a precise conjecture. Finally, we state our modularity theorems.
4.4.1 Integral models
Let us at first set up some notations and assumptions that are needed to construct our integral models. For a finite place v of F and an
![]() ${\mathcal {O}}_{E_v}$
-lattice
${\mathcal {O}}_{E_v}$
-lattice
![]() ${\Lambda _v}$
of
${\Lambda _v}$
of
![]() ${\mathbb {V}}(E_v)$
, the dual lattice is defined as
${\mathbb {V}}(E_v)$
, the dual lattice is defined as
![]() $\Lambda _v^\vee =\{x\in {\mathbb {V}}(E_v):\langle {x,{\Lambda _v}} \rangle \subset {\mathcal {O}}_{E_v}\}$
. Then
$\Lambda _v^\vee =\{x\in {\mathbb {V}}(E_v):\langle {x,{\Lambda _v}} \rangle \subset {\mathcal {O}}_{E_v}\}$
. Then
![]() ${\Lambda _v}$
is called
${\Lambda _v}$
is called
-
• self-dual if
 ${\Lambda _v}=\Lambda _v^\vee $
;
${\Lambda _v}=\Lambda _v^\vee $
; -
•
 $\varpi _{E_v}$
-modular if
$\varpi _{E_v}$
-modular if
 $ \Lambda _v^\vee =\varpi _{E_v}^{-1}{\Lambda _v}$
;
$ \Lambda _v^\vee =\varpi _{E_v}^{-1}{\Lambda _v}$
; -
• almost
 $\varpi _{E_v}$
-modular if
$\varpi _{E_v}$
-modular if
 $ \Lambda _v^\vee \subset \varpi _E^{-1}{\Lambda _v}$
and the inclusion is of colength 1.
$ \Lambda _v^\vee \subset \varpi _E^{-1}{\Lambda _v}$
and the inclusion is of colength 1.
Assume the following assumption in the rest of the paper.
Assumption 4.4.1. (1) At least one of the following three conditions hold:
-
(1.a) every finite place of E is at most tamely ramified over
 $ {\mathbb {Q}}$
;
$ {\mathbb {Q}}$
; -
(1.b)
 $E/{\mathbb {Q}}$
is Galois;
$E/{\mathbb {Q}}$
is Galois; -
(1.c)
 $E $
is the composition of F with some imaginary quadratic field.
$E $
is the composition of F with some imaginary quadratic field.
(2) Every finite place v of F ramified over
![]() $ {\mathbb {Q}}$
or of residue characteristic 2 is unramified in E.
$ {\mathbb {Q}}$
or of residue characteristic 2 is unramified in E.
(3) At every finite place v of F inert in E, there is a self-dual lattice
![]() $\Lambda _v$
in
$\Lambda _v$
in
![]() ${\mathbb {V}}(E_v)$
.
${\mathbb {V}}(E_v)$
.
(4) At every finite place v of F ramified in E, there is a
![]() $\pi _v$
-modular (resp. almost
$\pi _v$
-modular (resp. almost
![]() $\pi _v$
-modular) lattice
$\pi _v$
-modular) lattice
![]() $\Lambda _v$
in
$\Lambda _v$
in
![]() ${\mathbb {V}}(E_v)$
if n is odd (resp. n is even).
${\mathbb {V}}(E_v)$
if n is odd (resp. n is even).
We will classify
![]() ${\mathbb {V}}$
containing such
${\mathbb {V}}$
containing such
![]() $\Lambda $
in Remark 5.1.2 below.
$\Lambda $
in Remark 5.1.2 below.
At every place v split in E, let
![]() $\Lambda _v$
be a self-dual lattice in
$\Lambda _v$
be a self-dual lattice in
![]() ${\mathbb {V}}(E_v)$
. Let
${\mathbb {V}}(E_v)$
. Let
Let
![]() $K_\Lambda \subset U({\mathbb {V}}^\infty )$
be the stabilizer of
$K_\Lambda \subset U({\mathbb {V}}^\infty )$
be the stabilizer of
![]() $\Lambda $
.
$\Lambda $
.
Definition 4.4.2. Let
![]() ${{\widetilde K_\Lambda }}$
be the directed poset of compact open subgroups
${{\widetilde K_\Lambda }}$
be the directed poset of compact open subgroups
![]() $K\subset K_\Lambda $
, under the inclusion relation, such that for a finite place v of F,
$K\subset K_\Lambda $
, under the inclusion relation, such that for a finite place v of F,
-
(1) if
 $v $
is non-split in E, then
$v $
is non-split in E, then
 $K_v=K_{\Lambda ,v}$
;
$K_v=K_{\Lambda ,v}$
; -
(2) if
 $v $
is split in E, then
$v $
is split in E, then
 $K_v$
is a principal congruence subgroup of
$K_v$
is a principal congruence subgroup of
 $K_{\Lambda ,v}$
.
$K_{\Lambda ,v}$
.
Under Assumption 4.4.1 (1.a), for
![]() $K\in {{\widetilde K_\Lambda }}$
and a finite place v of E, we have an integral model
$K\in {{\widetilde K_\Lambda }}$
and a finite place v of E, we have an integral model
![]() $\mathscr {S}_v$
of
$\mathscr {S}_v$
of
![]() ${\mathrm {Sh}}({\mathbb {V}})_{K}$
over
${\mathrm {Sh}}({\mathbb {V}})_{K}$
over
![]() $\operatorname {\mathrm {Spec}} {\mathcal {O}}_{E,(v)}$
, as constructed in (B.2.11), B.2.25 and B.2.28. (Note that we can always choose a CM type satisfying the matching condition (B.2.20).) We remind the reader of the differences between the notations on the fields here and in Appendix B.
$\operatorname {\mathrm {Spec}} {\mathcal {O}}_{E,(v)}$
, as constructed in (B.2.11), B.2.25 and B.2.28. (Note that we can always choose a CM type satisfying the matching condition (B.2.20).) We remind the reader of the differences between the notations on the fields here and in Appendix B.
Lemma 4.4.3.
(1) The integral model
![]() $\mathscr {S}_v$
is regular.
$\mathscr {S}_v$
is regular.
(2) If
![]() $K= {K_{\Lambda }}$
, there is an ample
$K= {K_{\Lambda }}$
, there is an ample
![]() ${\mathbb {Q}}$
-line bundle
${\mathbb {Q}}$
-line bundle
![]() $\mathscr {P}_v$
on
$\mathscr {P}_v$
on
![]() $\mathscr {S}_v$
extending
$\mathscr {S}_v$
extending
![]() $L_{K_\Lambda }$
.
$L_{K_\Lambda }$
.
Proof. (1) We apply B.2.26. We use M to denote the reflex field in B.2.26, which is defined in (B.1.15) (and denoted by E there), to avoid confusion. We use N to denote the field extension of the reflex field in B.2.26 (denoted by L there). By the finite étaleness of the moduli space of relative dimenison 0 as in B.1.23, we may choose
![]() $N/M$
to be unramified at
$N/M$
to be unramified at
![]() $\nu $
[Reference ProjectSta18, Tag 04GL]. Then by [Reference Rapoport, Smithling and ZhangRSZ20] and B.2.26,
$\nu $
[Reference ProjectSta18, Tag 04GL]. Then by [Reference Rapoport, Smithling and ZhangRSZ20] and B.2.26,
![]() $\mathscr {S}_{v,{\mathcal {O}}_{N,(\nu )}}$
is regular for a place
$\mathscr {S}_{v,{\mathcal {O}}_{N,(\nu )}}$
is regular for a place
![]() $\nu $
of N over v. By the descent of regularity under faithfully flat morphism [Reference ProjectSta18, Tag 033D], the lemma follows.
$\nu $
of N over v. By the descent of regularity under faithfully flat morphism [Reference ProjectSta18, Tag 033D], the lemma follows.
(2) Let
![]() $N/E$
be a finite Galois extension such that v is unramified in N and every connected component of
$N/E$
be a finite Galois extension such that v is unramified in N and every connected component of
![]() $\mathscr {S}_{v,{\mathcal {O}}_{N,(v)}}$
is geometrically connected. By its construction (B.2.11), every connected component is a quotient of a connected component of an integral model of Hodge type over
$\mathscr {S}_{v,{\mathcal {O}}_{N,(v)}}$
is geometrically connected. By its construction (B.2.11), every connected component is a quotient of a connected component of an integral model of Hodge type over
![]() ${\mathcal {O}}_{N,(v)}$
by a finite group action. The integral model of Hodge type is a closed subscheme of the integral Siegel moduli space [Reference XuXu21, Reference XuXu25], on which we have a well-known ample Hodge line bundle. The restriction is an ample line bundle on each geometrically connected component of the integral model of Hodge type. Taking norm along the quotient map by the finite group action, we get an an ample line bundle on every component of
${\mathcal {O}}_{N,(v)}$
by a finite group action. The integral model of Hodge type is a closed subscheme of the integral Siegel moduli space [Reference XuXu21, Reference XuXu25], on which we have a well-known ample Hodge line bundle. The restriction is an ample line bundle on each geometrically connected component of the integral model of Hodge type. Taking norm along the quotient map by the finite group action, we get an an ample line bundle on every component of
![]() $\mathscr {S}_{v,{\mathcal {O}}_{N,(v)}}$
. See [Reference Bosch, Lütkebohmert and RaynaudBLR90, Section 6, Theorem 7 and Example B] and [Reference VistoliVis04] for the stack case. Then taking norm map along the quotient map by the
$\mathscr {S}_{v,{\mathcal {O}}_{N,(v)}}$
. See [Reference Bosch, Lütkebohmert and RaynaudBLR90, Section 6, Theorem 7 and Example B] and [Reference VistoliVis04] for the stack case. Then taking norm map along the quotient map by the
![]() ${\mathrm {Gal}}(N/E)$
, we have an ample line bundle
${\mathrm {Gal}}(N/E)$
, we have an ample line bundle
![]() $\mathscr {P}'$
on
$\mathscr {P}'$
on
![]() $\mathscr {S}_{v}$
. Dividing
$\mathscr {S}_{v}$
. Dividing
![]() $\mathscr {P}'$
by the product of the order of the finite group and
$\mathscr {P}'$
by the product of the order of the finite group and
![]() $[N:E]$
, we get the desired ample line bundle on
$[N:E]$
, we get the desired ample line bundle on
![]() $\mathscr {S}_{v}$
.
$\mathscr {S}_{v}$
.
Under Assumption 4.4.1 (1.b) or (1.c), the reflex field (B.1.15), in our notations, is E. For
![]() $K\in {{\widetilde K_\Lambda }}$
and a finite place v of E, both sides of the morphism (B.1.30) (and the generalizations as in B.2.17 or B.2.28) are equipped with a natural action of the finite group
$K\in {{\widetilde K_\Lambda }}$
and a finite place v of E, both sides of the morphism (B.1.30) (and the generalizations as in B.2.17 or B.2.28) are equipped with a natural action of the finite group
![]() $Z^{{\mathbb {Q}}}\left ( {\mathbb {A}}_{\mathbb {Q}}^{\{p\}\cup \infty } \right )/Z^{{\mathbb {Q}}}({\mathbb {Z}}_{(p)})K_{Z^{{\mathbb {Q}}}}^p $
compatible with the morphism. See [Reference Liu, Tian, Xiao, Zhang and ZhuLTX+22, Definition 4.2.2]. Moreover, taking quotients by this finite group, we get a new morphism whose target is isomorphic to
$Z^{{\mathbb {Q}}}\left ( {\mathbb {A}}_{\mathbb {Q}}^{\{p\}\cup \infty } \right )/Z^{{\mathbb {Q}}}({\mathbb {Z}}_{(p)})K_{Z^{{\mathbb {Q}}}}^p $
compatible with the morphism. See [Reference Liu, Tian, Xiao, Zhang and ZhuLTX+22, Definition 4.2.2]. Moreover, taking quotients by this finite group, we get a new morphism whose target is isomorphic to
![]() $\operatorname {\mathrm {Spec}} {\mathcal {O}}_{E,(v)}$
. Then the source of the new morphism is an integral model of
$\operatorname {\mathrm {Spec}} {\mathcal {O}}_{E,(v)}$
. Then the source of the new morphism is an integral model of
![]() ${\mathrm {Sh}}({\mathbb {V}})_{K}$
over
${\mathrm {Sh}}({\mathbb {V}})_{K}$
over
![]() $\operatorname {\mathrm {Spec}} {\mathcal {O}}_{E,(v)}$
, whose regularity is assured by [Reference Rapoport, Smithling and ZhangRSZ20] and faithfully flat descent of regularity. We also denote this integral model by
$\operatorname {\mathrm {Spec}} {\mathcal {O}}_{E,(v)}$
, whose regularity is assured by [Reference Rapoport, Smithling and ZhangRSZ20] and faithfully flat descent of regularity. We also denote this integral model by
![]() $\mathscr {S}_v$
. Moreover, if Assumption 4.4.1 (1.a) also holds, then the construction here and in Lemma 4.4.3 coincides, by B.2.26.
$\mathscr {S}_v$
. Moreover, if Assumption 4.4.1 (1.a) also holds, then the construction here and in Lemma 4.4.3 coincides, by B.2.26.
We want to glue these models to obtain a regular integral model of
![]() ${\mathrm {Sh}}({\mathbb {V}})_{K}$
over
${\mathrm {Sh}}({\mathbb {V}})_{K}$
over
![]() $\operatorname {\mathrm {Spec}} {\mathcal {O}}_{E}$
.
$\operatorname {\mathrm {Spec}} {\mathcal {O}}_{E}$
.
Theorem 4.4.4. Assume Assumption 4.4.1.
(1) For
![]() $K\in {{\widetilde K_\Lambda }}$
, there is a regular integral model
$K\in {{\widetilde K_\Lambda }}$
, there is a regular integral model
![]() ${\mathcal {X}}_K$
of
${\mathcal {X}}_K$
of
![]() ${\mathrm {Sh}}({\mathbb {V}})_{K}$
over
${\mathrm {Sh}}({\mathbb {V}})_{K}$
over
![]() $\operatorname {\mathrm {Spec}} {\mathcal {O}}_{E}$
such that
$\operatorname {\mathrm {Spec}} {\mathcal {O}}_{E}$
such that
![]() ${\mathcal {X}}_{K, {\mathcal {O}}_{E,(v)}}{\ \simeq \ } \mathscr {S}_v$
as integral models. See 4.3.2. Moreover, Assumption A.1.1 holds for
${\mathcal {X}}_{K, {\mathcal {O}}_{E,(v)}}{\ \simeq \ } \mathscr {S}_v$
as integral models. See 4.3.2. Moreover, Assumption A.1.1 holds for
![]() ${\mathcal {X}}_K$
.
${\mathcal {X}}_K$
.
(2) For
![]() $K\subset K'$
in
$K\subset K'$
in
![]() ${{\widetilde K_\Lambda }}$
, there is a unique finite flat morphism
${{\widetilde K_\Lambda }}$
, there is a unique finite flat morphism
![]() $\pi _{K,K' }:{\mathcal {X}}_{K }\to {\mathcal {X}}_{K' }$
extending the natural morphism
$\pi _{K,K' }:{\mathcal {X}}_{K }\to {\mathcal {X}}_{K' }$
extending the natural morphism
![]() ${\mathrm {Sh}}({\mathbb {V}})_{K }\to {\mathrm {Sh}}({\mathbb {V}})_{K' }$
.
${\mathrm {Sh}}({\mathbb {V}})_{K }\to {\mathrm {Sh}}({\mathbb {V}})_{K' }$
.
(3) Regard
![]() ${\mathcal {X}}_{K }$
as an
${\mathcal {X}}_{K }$
as an
![]() $ {\mathcal {X}}_{K_{\Lambda } }$
-scheme and
$ {\mathcal {X}}_{K_{\Lambda } }$
-scheme and
![]() ${\mathrm {Sh}}({\mathbb {V}})_{K }$
as an
${\mathrm {Sh}}({\mathbb {V}})_{K }$
as an
![]() $ {\mathrm {Sh}}({\mathbb {V}})_{K_{\Lambda } }$
-scheme via
$ {\mathrm {Sh}}({\mathbb {V}})_{K_{\Lambda } }$
-scheme via
![]() $\pi _{K,K' }$
. There is a unique action of
$\pi _{K,K' }$
. There is a unique action of
![]() $K_\Lambda /K$
(note that K is normal in
$K_\Lambda /K$
(note that K is normal in
![]() $K_{\Lambda }$
) on the
$K_{\Lambda }$
) on the
![]() $ {\mathcal {X}}_{K_{\Lambda } }$
-scheme
$ {\mathcal {X}}_{K_{\Lambda } }$
-scheme
![]() ${\mathcal {X}}_{K }$
extending the standard action of
${\mathcal {X}}_{K }$
extending the standard action of
![]() $K_\Lambda /K$
on the
$K_\Lambda /K$
on the
![]() $ {\mathrm {Sh}}({\mathbb {V}})_{K_{\Lambda } }$
-scheme
$ {\mathrm {Sh}}({\mathbb {V}})_{K_{\Lambda } }$
-scheme
![]() ${\mathrm {Sh}}({\mathbb {V}})_{K }$
by ‘right translation’.
${\mathrm {Sh}}({\mathbb {V}})_{K }$
by ‘right translation’.
Proof. The construction of
![]() ${\mathcal {X}}_K$
is as follows. Continue to use the notation M in the proof of Lemma 4.4.3. First, consider the analog of the morphism (B.1.30) over
${\mathcal {X}}_K$
is as follows. Continue to use the notation M in the proof of Lemma 4.4.3. First, consider the analog of the morphism (B.1.30) over
![]() ${\mathcal {O}}_M[R^{-1}]$
, where R is a finite set of finite places of
${\mathcal {O}}_M[R^{-1}]$
, where R is a finite set of finite places of
![]() $ {\mathbb {Q}}$
such that
$ {\mathbb {Q}}$
such that
![]() $K_v=K_{\Lambda ,v}$
for v not over R (in particular, we do not need the generalizations as in B.2.17 or B.2.28). See, for example, [Reference Rapoport, Smithling and ZhangRSZ20, 5.1] with extra level structures over R (similar to (B.1.29)). Denote this morphism by
$K_v=K_{\Lambda ,v}$
for v not over R (in particular, we do not need the generalizations as in B.2.17 or B.2.28). See, for example, [Reference Rapoport, Smithling and ZhangRSZ20, 5.1] with extra level structures over R (similar to (B.1.29)). Denote this morphism by
![]() ${\mathcal {M}}\to {\mathcal {M}}_0$
. We use Galois descent to construct a model of
${\mathcal {M}}\to {\mathcal {M}}_0$
. We use Galois descent to construct a model of
![]() ${\mathrm {Sh}}({\mathbb {V}})_K$
outside finitely many finite places. Let
${\mathrm {Sh}}({\mathbb {V}})_K$
outside finitely many finite places. Let
![]() $N/M$
be a finite extension, Galois over E, such that the base change of
$N/M$
be a finite extension, Galois over E, such that the base change of
![]() ${\mathcal {M}}_0$
to
${\mathcal {M}}_0$
to
![]() $\operatorname {\mathrm {Spec}} {\mathcal {O}}_{N}[R^{-1}]$
is a finite disjoint union of
$\operatorname {\mathrm {Spec}} {\mathcal {O}}_{N}[R^{-1}]$
is a finite disjoint union of
![]() $\operatorname {\mathrm {Spec}} {\mathcal {O}}_{N}[R^{-1}]$
. Let
$\operatorname {\mathrm {Spec}} {\mathcal {O}}_{N}[R^{-1}]$
. Let
![]() $S\supset R$
be a finite set of finite places of
$S\supset R$
be a finite set of finite places of
![]() ${\mathbb {Q}}$
such that
${\mathbb {Q}}$
such that
![]() $\operatorname {\mathrm {Spec}} {\mathcal {O}}_{N}[S^{-1}]\to \operatorname {\mathrm {Spec}} {\mathcal {O}}_{E}[S^{-1}] $
is unramified. Then the fiber of
$\operatorname {\mathrm {Spec}} {\mathcal {O}}_{N}[S^{-1}]\to \operatorname {\mathrm {Spec}} {\mathcal {O}}_{E}[S^{-1}] $
is unramified. Then the fiber of
![]() ${\mathcal {M}}_{{\mathcal {O}}_{N}[S^{-1}]}\to {\mathcal {M}}_{0,{\mathcal {O}}_{N}[S^{-1}]}$
over a chosen
${\mathcal {M}}_{{\mathcal {O}}_{N}[S^{-1}]}\to {\mathcal {M}}_{0,{\mathcal {O}}_{N}[S^{-1}]}$
over a chosen
![]() $\operatorname {\mathrm {Spec}} {\mathcal {O}}_{N}[S^{-1}]$
is a regular Deligne-Mumford stack
$\operatorname {\mathrm {Spec}} {\mathcal {O}}_{N}[S^{-1}]$
is a regular Deligne-Mumford stack
![]() ${\mathcal {M}}^S$
proper over
${\mathcal {M}}^S$
proper over
![]() $ \operatorname {\mathrm {Spec}} {\mathcal {O}}_{N}[S^{-1}]$
with generic fiber
$ \operatorname {\mathrm {Spec}} {\mathcal {O}}_{N}[S^{-1}]$
with generic fiber
![]() ${\mathrm {Sh}}({\mathbb {V}})_{K,N}$
. By Zariski’s main theorem (for stacks which easily follows from the scheme version), after possibly enlarging S, we may assume that the action of the finite group
${\mathrm {Sh}}({\mathbb {V}})_{K,N}$
. By Zariski’s main theorem (for stacks which easily follows from the scheme version), after possibly enlarging S, we may assume that the action of the finite group
![]() ${\mathrm {Gal}}(N/E)$
on
${\mathrm {Gal}}(N/E)$
on
![]() ${\mathrm {Sh}}({\mathbb {V}})_{K,N}$
extends to an action on
${\mathrm {Sh}}({\mathbb {V}})_{K,N}$
extends to an action on
![]() ${\mathcal {M}}^S$
. By [Reference Bosch, Lütkebohmert and RaynaudBLR90, Section 6, Example] (and [Reference VistoliVis04] for the stack case), after possibly enlarging S,
${\mathcal {M}}^S$
. By [Reference Bosch, Lütkebohmert and RaynaudBLR90, Section 6, Example] (and [Reference VistoliVis04] for the stack case), after possibly enlarging S,
![]() ${\mathcal {M}}^S$
descends to
${\mathcal {M}}^S$
descends to
![]() $\operatorname {\mathrm {Spec}} {\mathcal {O}}_{E}[S^{-1}]$
. Let
$\operatorname {\mathrm {Spec}} {\mathcal {O}}_{E}[S^{-1}]$
. Let
![]() ${\mathcal {Y}} ^S$
be the resulted Deligne-Mumford stack. By construction and B.2.26, we have
${\mathcal {Y}} ^S$
be the resulted Deligne-Mumford stack. By construction and B.2.26, we have
![]() ${\mathcal {Y}} ^S_{{\mathcal {O}}_{E,(v)}}{\ \simeq \ } \mathscr {S}_v$
for
${\mathcal {Y}} ^S_{{\mathcal {O}}_{E,(v)}}{\ \simeq \ } \mathscr {S}_v$
for
![]() $v\not \in S$
. Now, let
$v\not \in S$
. Now, let
![]() ${\mathcal {X}}_K$
be the glueing of
${\mathcal {X}}_K$
be the glueing of
![]() ${\mathcal {Y}}^S$
and
${\mathcal {Y}}^S$
and
![]() $\mathscr {S}_v$
with
$\mathscr {S}_v$
with
![]() $v\in S$
. Then
$v\in S$
. Then
![]() ${\mathcal {X}}_{K, {\mathcal {O}}_{E,(v)}}{\ \simeq \ } \mathscr {S}_v$
for every finite place v.
${\mathcal {X}}_{K, {\mathcal {O}}_{E,(v)}}{\ \simeq \ } \mathscr {S}_v$
for every finite place v.
We check Assumption A.1.1. For
![]() $K'\subset K$
small enough with
$K'\subset K$
small enough with
![]() $K^{\prime S}=K^S$
, the resulted Deligne-Mumford stack
$K^{\prime S}=K^S$
, the resulted Deligne-Mumford stack
![]() ${\mathcal {Y}}^{\prime S}$
is representable by [Reference Rapoport, Smithling and ZhangRSZ20, 5.2]. Note that
${\mathcal {Y}}^{\prime S}$
is representable by [Reference Rapoport, Smithling and ZhangRSZ20, 5.2]. Note that
![]() $\operatorname {\mathrm {Spec}} {\mathcal {O}}_{N}[S^{-1}]\to \operatorname {\mathrm {Spec}} {\mathcal {O}}_{E}[S^{-1}] $
is unramified (so finite étale). Then Assumption A.1.1 (1) holds (with the current S) by construction. Similarly, Assumption A.1.1 (2) holds.
$\operatorname {\mathrm {Spec}} {\mathcal {O}}_{N}[S^{-1}]\to \operatorname {\mathrm {Spec}} {\mathcal {O}}_{E}[S^{-1}] $
is unramified (so finite étale). Then Assumption A.1.1 (1) holds (with the current S) by construction. Similarly, Assumption A.1.1 (2) holds.
The uniqueness in (2) and (3) follows from the separatedness of the models. The existence follows from the construction and corresponding properties of the PEL type integral models in [Reference Rapoport, Smithling and ZhangRSZ20, Theorem 5.4]. We omit the details.
Remark 4.4.5. If we drop condition (2) in Definition 4.4.2 on K, Theorem 4.4.4 (1)(2) still holds. Indeed, to construct
![]() ${\mathcal {X}}_K$
, choose
${\mathcal {X}}_K$
, choose
![]() $K_1\in \widetilde K_\Lambda $
such that
$K_1\in \widetilde K_\Lambda $
such that
![]() $K_1\subset K$
. Let
$K_1\subset K$
. Let
![]() ${\mathcal {X}}_K$
be the quotient of
${\mathcal {X}}_K$
be the quotient of
![]() ${\mathcal {X}}_{K_1}$
by
${\mathcal {X}}_{K_1}$
by
![]() $K/K_1$
where is the action is Theorem 4.4.4 (3).
$K/K_1$
where is the action is Theorem 4.4.4 (3).
By [Reference Rapoport, Smithling and ZhangRSZ20, Theorem 5.2] and our construction, we deduce the following lemma.
Lemma 4.4.6. If
![]() $K_v=K_{\Lambda ,v}$
, then
$K_v=K_{\Lambda ,v}$
, then
![]() ${\mathcal {X}}_{K,{\mathcal {O}}_{E}, (v)}$
is smooth over
${\mathcal {X}}_{K,{\mathcal {O}}_{E}, (v)}$
is smooth over
![]() $\operatorname {\mathrm {Spec}} {\mathcal {O}}_{{E}, (v)}$
.
$\operatorname {\mathrm {Spec}} {\mathcal {O}}_{{E}, (v)}$
.
Remark 4.4.7. We may relax Assumption 4.4.1 (3) by allowing
![]() $\Lambda _v$
to be almost self-dual. See B.2.28. Then Lemma 4.4.3 still holds. However, Lemma 4.4.6 does not hold any more.
$\Lambda _v$
to be almost self-dual. See B.2.28. Then Lemma 4.4.3 still holds. However, Lemma 4.4.6 does not hold any more.
Corollary 4.4.8. A
![]() ${\mathbb {Q}}$
-line bundle (in particular a line bundle)
${\mathbb {Q}}$
-line bundle (in particular a line bundle)
![]() ${\mathcal {L}}_{K_{\Lambda }}$
on
${\mathcal {L}}_{K_{\Lambda }}$
on
![]() ${\mathcal {X}}_{K_{\Lambda }}$
extending
${\mathcal {X}}_{K_{\Lambda }}$
extending
![]() $L_{K_{\Lambda }}$
is ample. Moreover, it is unique as a
$L_{K_{\Lambda }}$
is ample. Moreover, it is unique as a
![]() ${\mathbb {Q}}$
-line bundle.
${\mathbb {Q}}$
-line bundle.
Proof. By Lemma 4.4.6, the corresponding divisors of two different extensions differ by a
![]() ${\mathbb {Q}}$
-linear combination of special fibers of
${\mathbb {Q}}$
-linear combination of special fibers of
![]() ${\mathcal {X}}_{K_{\Lambda }}$
, which is 0 in
${\mathcal {X}}_{K_{\Lambda }}$
, which is 0 in
![]() ${\mathrm {Ch}}^1\left ( {\mathcal {X}}_{K_{\Lambda }}\right )_{\mathbb {Q}}$
. The uniqueness follows. Now the ampleness follows from Lemma 4.4.3 (2).
${\mathrm {Ch}}^1\left ( {\mathcal {X}}_{K_{\Lambda }}\right )_{\mathbb {Q}}$
. The uniqueness follows. Now the ampleness follows from Lemma 4.4.3 (2).
Below, by a line bundle, we mean a
![]() ${\mathbb {Q}}$
-line bundle.
${\mathbb {Q}}$
-line bundle.
4.4.2 Admissible extensions
We want to define admissible extensions that are compatible as the level changes. So we consider a system of integral models.
Definition 4.4.9. (1) Let
![]() $\widetilde {\mathcal {X}}$
be the system
$\widetilde {\mathcal {X}}$
be the system
![]() $\{{\mathcal {X}}_K\}_{K\in {{\widetilde K_\Lambda }}}$
of integral models with transition morphisms
$\{{\mathcal {X}}_K\}_{K\in {{\widetilde K_\Lambda }}}$
of integral models with transition morphisms
![]() $\pi _{_K,_{K'}}$
as in Theorem 4.4.4 (1)(2).
$\pi _{_K,_{K'}}$
as in Theorem 4.4.4 (1)(2).
(2) For
![]() $h\in K_\Lambda $
, define the ‘right translation by h’ automorphism on
$h\in K_\Lambda $
, define the ‘right translation by h’ automorphism on
![]() ${\mathcal {X}}_K$
to be the action of h as in Theorem 4.4.4 (3).
${\mathcal {X}}_K$
to be the action of h as in Theorem 4.4.4 (3).
(3) Fix an arbitrarily (
![]() ${\mathbb {Q}}$
-)line bundle
${\mathbb {Q}}$
-)line bundle
![]() ${\mathcal {L}}_{K_{\Lambda }}$
on
${\mathcal {L}}_{K_{\Lambda }}$
on
![]() ${\mathcal {X}}_{K_\Lambda }$
extending
${\mathcal {X}}_{K_\Lambda }$
extending
![]() $L_{K_{\Lambda }}.$
Let
$L_{K_{\Lambda }}.$
Let
![]() $ {\mathcal {L}}_K=\pi _{_K,{_K}_{\Lambda }}^{*} {\mathcal {L}}_{K_{\Lambda }}$
.
$ {\mathcal {L}}_K=\pi _{_K,{_K}_{\Lambda }}^{*} {\mathcal {L}}_{K_{\Lambda }}$
.
We use
![]() ${\mathcal {L}}$
to denote the compatible-under-pullback system
${\mathcal {L}}$
to denote the compatible-under-pullback system
![]() $\{{\mathcal {L}}_K\}_{K\in {{\widetilde K_\Lambda }}}$
of ample line bundles on
$\{{\mathcal {L}}_K\}_{K\in {{\widetilde K_\Lambda }}}$
of ample line bundles on
![]() $\widetilde {\mathcal {X}}=\{{\mathcal {X}}_K\}_{K\in {{\widetilde K_\Lambda }}}$
. The ampleness follows from the ampleness of
$\widetilde {\mathcal {X}}=\{{\mathcal {X}}_K\}_{K\in {{\widetilde K_\Lambda }}}$
. The ampleness follows from the ampleness of
![]() ${\mathcal {L}}_{K_{\Lambda }}$
and finiteness of
${\mathcal {L}}_{K_{\Lambda }}$
and finiteness of
![]() $\pi _{_K,{_K}_{\Lambda }}$
. While using
$\pi _{_K,{_K}_{\Lambda }}$
. While using
![]() ${\mathcal {L}}$
for
${\mathcal {L}}$
for
![]() ${\mathcal {X}}_K$
, we mean
${\mathcal {X}}_K$
, we mean
![]() ${\mathcal {L}}_K$
so that it has the same meaning as before (we previously used
${\mathcal {L}}_K$
so that it has the same meaning as before (we previously used
![]() ${\mathcal {L}}$
as the abbreviation of
${\mathcal {L}}$
as the abbreviation of
![]() ${\mathcal {L}}_K$
). Let
${\mathcal {L}}_K$
). Let
![]() $\overline {\mathcal {L}}_K$
be the corresponding hermitian line bundle with the hermitian metric as in 4.2.1, and define
$\overline {\mathcal {L}}_K$
be the corresponding hermitian line bundle with the hermitian metric as in 4.2.1, and define
![]() $\overline {\mathcal {L}}$
accordingly.
$\overline {\mathcal {L}}$
accordingly.
By Proposition A.3.8 – that is, the compatibility of the formation of admissible (Chow) cycles under flat pullback – we can define the direct limit group of admissible arithmetic divisors along the directed poset
![]() ${\widetilde K_\Lambda }$
${\widetilde K_\Lambda }$
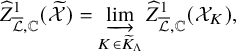 $$ \begin{align}\widehat Z^{1}_{{\overline{\mathcal{L}}},{\mathbb{C}}}(\widetilde{\mathcal{X}})=\varinjlim_{K\in {{\widetilde K_\Lambda}}}\widehat Z^{1}_{{\overline{\mathcal{L}}},{\mathbb{C}}}({\mathcal{X}}_K) ,\end{align} $$
$$ \begin{align}\widehat Z^{1}_{{\overline{\mathcal{L}}},{\mathbb{C}}}(\widetilde{\mathcal{X}})=\varinjlim_{K\in {{\widetilde K_\Lambda}}}\widehat Z^{1}_{{\overline{\mathcal{L}}},{\mathbb{C}}}({\mathcal{X}}_K) ,\end{align} $$
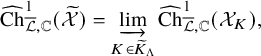 $$ \begin{align}\widehat{\mathrm{Ch}}^{1}_{{\overline{\mathcal{L}}},{\mathbb{C}}}(\widetilde{\mathcal{X}})=\varinjlim_{K\in {{\widetilde K_\Lambda}}}\widehat{\mathrm{Ch}}^{1}_{{\overline{\mathcal{L}}},{\mathbb{C}}}({\mathcal{X}}_K), \end{align} $$
$$ \begin{align}\widehat{\mathrm{Ch}}^{1}_{{\overline{\mathcal{L}}},{\mathbb{C}}}(\widetilde{\mathcal{X}})=\varinjlim_{K\in {{\widetilde K_\Lambda}}}\widehat{\mathrm{Ch}}^{1}_{{\overline{\mathcal{L}}},{\mathbb{C}}}({\mathcal{X}}_K), \end{align} $$
where the transition maps are
![]() $\pi _{_K,_{K'}}^{*}$
’s. By the projection formula (which gives that the composition of pullback by pushforward is the multiplication by the degree of the finite flat morphism), the natural maps
$\pi _{_K,_{K'}}^{*}$
’s. By the projection formula (which gives that the composition of pullback by pushforward is the multiplication by the degree of the finite flat morphism), the natural maps
are injective and we understand the formers as subspaces of the latters, respectively. The embeddings
![]() $ {\mathbb {C}}\hookrightarrow \widehat {\mathrm {Ch}}^1_{{\overline {\mathcal {L}}},{\mathbb {C}}}({\mathcal {X}}_K)$
(Definition 4.3.1) are then the same embedding
$ {\mathbb {C}}\hookrightarrow \widehat {\mathrm {Ch}}^1_{{\overline {\mathcal {L}}},{\mathbb {C}}}({\mathcal {X}}_K)$
(Definition 4.3.1) are then the same embedding
Remark 4.4.10. If we drop condition (2) in Definition 4.4.2 as in Remark 4.4.10, (4.20)–(4.22) do not change.
Definition 4.4.11. Let
![]() $\overline {\mathcal {S}}\left ( {\mathbb {V}} \right ) ^{{{\widetilde K_\Lambda }}}\subset \overline {\mathcal {S}}\left ( {\mathbb {V}} \right ) $
consist of functions invariant by some
$\overline {\mathcal {S}}\left ( {\mathbb {V}} \right ) ^{{{\widetilde K_\Lambda }}}\subset \overline {\mathcal {S}}\left ( {\mathbb {V}} \right ) $
consist of functions invariant by some
![]() $K\in {{{\widetilde K_\Lambda }}}$
.
$K\in {{{\widetilde K_\Lambda }}}$
.
For
![]() $t\in F_{>0}$
,
$t\in F_{>0}$
,
![]() $\phi \in \overline {\mathcal {S}}\left ( {\mathbb {V}} \right ) ^{{{\widetilde K_\Lambda }}}$
and
$\phi \in \overline {\mathcal {S}}\left ( {\mathbb {V}} \right ) ^{{{\widetilde K_\Lambda }}}$
and
![]() $K\in {{\widetilde K_\Lambda }}$
stabilizing
$K\in {{\widetilde K_\Lambda }}$
stabilizing
![]() $\phi $
, consider the normalized admissible extension
$\phi $
, consider the normalized admissible extension
![]() $ Z_t( \omega (g)\phi )_K^{\overline {\mathcal {L}}} $
of
$ Z_t( \omega (g)\phi )_K^{\overline {\mathcal {L}}} $
of
![]() $ Z_t( \omega (g)\phi )_K$
(as in (4.16)). By Lemma 4.1.5 and Proposition A.3.8,
$ Z_t( \omega (g)\phi )_K$
(as in (4.16)). By Lemma 4.1.5 and Proposition A.3.8,
is independent of K. And by definition,
is independent of K.
For
![]() $h\in K_\Lambda $
, the ‘right translation by h’ in
$h\in K_\Lambda $
, the ‘right translation by h’ in
![]() ${\mathrm {Aut}}\left ( {\mathcal {X}}_{K}/{\mathcal {X}}_{K_{\Lambda } }\right )$
fixes
${\mathrm {Aut}}\left ( {\mathcal {X}}_{K}/{\mathcal {X}}_{K_{\Lambda } }\right )$
fixes
![]() ${\mathcal {L}}_K$
by definition. Thus, it induces an automorphism on
${\mathcal {L}}_K$
by definition. Thus, it induces an automorphism on
![]() $\widehat Z^{1}_{{\overline {\mathcal {L}}},{\mathbb {C}}}(\widetilde {\mathcal {X}})$
and
$\widehat Z^{1}_{{\overline {\mathcal {L}}},{\mathbb {C}}}(\widetilde {\mathcal {X}})$
and
![]() $ \widehat {\mathrm {Ch}}^{1}_{{\overline {\mathcal {L}}},{\mathbb {C}}}(\widetilde {\mathcal {X}}) $
. Since it sends
$ \widehat {\mathrm {Ch}}^{1}_{{\overline {\mathcal {L}}},{\mathbb {C}}}(\widetilde {\mathcal {X}}) $
. Since it sends
![]() $Z_t(g ,\phi ) $
to
$Z_t(g ,\phi ) $
to
![]() $Z_t(g ,\omega (h)\phi ) $
, by Proposition A.3.8, we have the following lemma.
$Z_t(g ,\omega (h)\phi ) $
, by Proposition A.3.8, we have the following lemma.
Lemma 4.4.12. The ‘right translation by h’ automorphism is the identity map on the image of
![]() $ {\mathbb {C}}\hookrightarrow \widehat {\mathrm {Ch}}^{1}_{{\overline {\mathcal {L}}},{\mathbb {C}}}(\widetilde {\mathcal {X}})$
, fixes
$ {\mathbb {C}}\hookrightarrow \widehat {\mathrm {Ch}}^{1}_{{\overline {\mathcal {L}}},{\mathbb {C}}}(\widetilde {\mathcal {X}})$
, fixes
![]() $c_1(\overline {\mathcal {L}}^\vee ) $
, and sends
$c_1(\overline {\mathcal {L}}^\vee ) $
, and sends
![]() $Z_t(g ,\phi ) ^{\overline {\mathcal {L}}}$
to
$Z_t(g ,\phi ) ^{\overline {\mathcal {L}}}$
to
![]() $Z_t(g ,\omega (h)\phi ) ^{\overline {\mathcal {L}}}$
.
$Z_t(g ,\omega (h)\phi ) ^{\overline {\mathcal {L}}}$
.
4.4.3 Conjecture
We define generating series of admissible arithmetic divisors in two ways, essentially by choosing different Green functions. (In fact, there will be a third one in 5.2.2.) The first (resp. second) definition is made toward Problem 4.3.4 (resp. Problem 4.3.3).
Recall the holomorphic part
![]() $E^{\prime }_{t,{\mathrm {f}}}(0,g,\phi )$
of the derivative of
$E^{\prime }_{t,{\mathrm {f}}}(0,g,\phi )$
of the derivative of
![]() $E_t(s,g,\phi )$
at
$E_t(s,g,\phi )$
at
![]() $s=0$
. See (3.29).
$s=0$
. See (3.29).
Definition 4.4.13. For
![]() $\phi \in \overline {\mathcal {S}}\left ( {\mathbb {V}} \right )^{{{\widetilde K_\Lambda }}}$
,
$\phi \in \overline {\mathcal {S}}\left ( {\mathbb {V}} \right )^{{{\widetilde K_\Lambda }}}$
,
![]() $t\in F_{>0}$
and
$t\in F_{>0}$
and
![]() $g\in G({\mathbb {A}}_F )$
, let
$g\in G({\mathbb {A}}_F )$
, let
For
![]() $a\in {\mathbb {C}}$
and
$a\in {\mathbb {C}}$
and
![]() $g\in G({\mathbb {A}}_F)$
, let
$g\in G({\mathbb {A}}_F)$
, let
Remark 4.4.14. (1) We rewrite the definition of
![]() $z_t(g, \phi )_{{\mathfrak {e}}}^{{\overline {\mathcal {L}}}}$
as follows, which is closer to the notation ‘
$z_t(g, \phi )_{{\mathfrak {e}}}^{{\overline {\mathcal {L}}}}$
as follows, which is closer to the notation ‘
![]() $\left ( [ Z_t^{\overline {\mathcal {L}}}]+{\mathfrak {e}}_t\right ) q^t $
’ in (1.2). For
$\left ( [ Z_t^{\overline {\mathcal {L}}}]+{\mathfrak {e}}_t\right ) q^t $
’ in (1.2). For
![]() $t\in F_{>0}$
, we have the t-th Fourier coefficient
$t\in F_{>0}$
, we have the t-th Fourier coefficient
![]() $ \frac {E_t(0,g,\phi )} {W^{{\mathfrak {w}}}_{\infty , t}(1)}$
,
$ \frac {E_t(0,g,\phi )} {W^{{\mathfrak {w}}}_{\infty , t}(1)}$
,
![]() $g\in G({\mathbb {A}}_F^\infty ),$
of
$g\in G({\mathbb {A}}_F^\infty ),$
of
![]() $E(0,g,\phi )$
. See 2.7. We similarly and formally consider
$E(0,g,\phi )$
. See 2.7. We similarly and formally consider
![]() $ \frac {E^{\prime }_{t,{\mathrm {f}}}(0,g,\phi ) } {W^{{\mathfrak {w}}}_{\infty , t}(1)},\ g\in G({\mathbb {A}}_F^\infty )$
as the ‘t-th Fourier coefficient’ of
$ \frac {E^{\prime }_{t,{\mathrm {f}}}(0,g,\phi ) } {W^{{\mathfrak {w}}}_{\infty , t}(1)},\ g\in G({\mathbb {A}}_F^\infty )$
as the ‘t-th Fourier coefficient’ of
![]() $E^{\prime }_{t,{\mathrm {f}}}(0,g,\phi )$
. Let
$E^{\prime }_{t,{\mathrm {f}}}(0,g,\phi )$
. Let
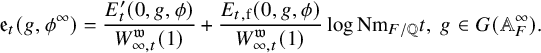 $$ \begin{align} {\mathfrak{e}}_t(g , \phi^\infty)= \frac{E^{\prime}_t(0,g,\phi)} {W^{{\mathfrak{w}}}_{\infty, t}(1)}+\frac{E_{t,{\mathrm{f}}}(0,g,\phi) } {W^{{\mathfrak{w}}}_{\infty, t}(1)}\log {\mathrm{Nm}}_{F/{\mathbb{Q}}}t,\ g\in G({\mathbb {A}}_F^\infty).\end{align} $$
$$ \begin{align} {\mathfrak{e}}_t(g , \phi^\infty)= \frac{E^{\prime}_t(0,g,\phi)} {W^{{\mathfrak{w}}}_{\infty, t}(1)}+\frac{E_{t,{\mathrm{f}}}(0,g,\phi) } {W^{{\mathfrak{w}}}_{\infty, t}(1)}\log {\mathrm{Nm}}_{F/{\mathbb{Q}}}t,\ g\in G({\mathbb {A}}_F^\infty).\end{align} $$
Then
![]() $ {\mathfrak {e}}_t(1 ,\phi ^\infty )$
is the constant
$ {\mathfrak {e}}_t(1 ,\phi ^\infty )$
is the constant
![]() ${\mathfrak {e}}_t $
in (1.4). And we can rewrite
${\mathfrak {e}}_t $
in (1.4). And we can rewrite
(2) We also expect that the (proposed) infinite component of
![]() $e_t(g,\phi )$
in Problem 4.3.4 is
$e_t(g,\phi )$
in Problem 4.3.4 is
![]() $ E^{\prime }_{t,{\mathrm {f}}}(0,g,\phi ) +E_t(0,g,\phi ) \log {\mathrm {Nm}}_{F/{\mathbb {Q}}}t$
for any unitary Shimura variety. In particular, in the situation of this section, the v-component is 0 for every finite place v. It is related to Lemma 4.4.6. (The smoothness is ‘exotic’ at places where
$ E^{\prime }_{t,{\mathrm {f}}}(0,g,\phi ) +E_t(0,g,\phi ) \log {\mathrm {Nm}}_{F/{\mathbb {Q}}}t$
for any unitary Shimura variety. In particular, in the situation of this section, the v-component is 0 for every finite place v. It is related to Lemma 4.4.6. (The smoothness is ‘exotic’ at places where
![]() $E/F$
is ramified.)
$E/F$
is ramified.)
By (3.10), (3.14) and Lemma 4.4.12, we have the following lemma.
Lemma 4.4.15. For
![]() $h\in K_{\Lambda }$
, the ‘’right translation by h’ automorphism on
$h\in K_{\Lambda }$
, the ‘’right translation by h’ automorphism on
![]() ${\mathcal {X}}_{K}$
sends
${\mathcal {X}}_{K}$
sends
![]() $z(g, \phi )_{{\mathfrak {e}},a}^{{\overline {\mathcal {L}}}}$
to
$z(g, \phi )_{{\mathfrak {e}},a}^{{\overline {\mathcal {L}}}}$
to
![]() $z(g, \omega (h)\phi )_{{\mathfrak {e}},a}^{{\overline {\mathcal {L}}}}$
.
$z(g, \omega (h)\phi )_{{\mathfrak {e}},a}^{{\overline {\mathcal {L}}}}$
.
Now we specify the correct constant a to be used in
![]() $z(g, \phi )_{{\mathfrak {e}},a}^{{\overline {\mathcal {L}}}}$
. Let
$z(g, \phi )_{{\mathfrak {e}},a}^{{\overline {\mathcal {L}}}}$
. Let
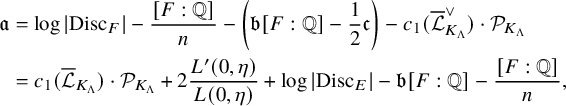 $$ \begin{align}{\mathfrak{a}}&= \log|{\mathrm{Disc}}_F| -\frac{[F:{\mathbb{Q}}]}{n}- \left( {{\mathfrak{b}}}[F:{\mathbb{Q}}]-\frac{1}{2}{{\mathfrak{c}}}\right) -c_1(\overline {\mathcal{L}}_{K_\Lambda}^\vee)\cdot {\mathcal{P}}_{ K_\Lambda} \\ &=c_1(\overline {\mathcal{L}}_{K_\Lambda})\cdot {\mathcal{P}}_{ K_\Lambda} +2\frac{L'(0,\eta)}{L(0,\eta)}+ \log|{\mathrm{Disc}}_E|- {{\mathfrak{b}}}[F:{\mathbb{Q}}]- \frac{[F:{\mathbb{Q}}]}{n}\nonumber,\end{align} $$
$$ \begin{align}{\mathfrak{a}}&= \log|{\mathrm{Disc}}_F| -\frac{[F:{\mathbb{Q}}]}{n}- \left( {{\mathfrak{b}}}[F:{\mathbb{Q}}]-\frac{1}{2}{{\mathfrak{c}}}\right) -c_1(\overline {\mathcal{L}}_{K_\Lambda}^\vee)\cdot {\mathcal{P}}_{ K_\Lambda} \\ &=c_1(\overline {\mathcal{L}}_{K_\Lambda})\cdot {\mathcal{P}}_{ K_\Lambda} +2\frac{L'(0,\eta)}{L(0,\eta)}+ \log|{\mathrm{Disc}}_E|- {{\mathfrak{b}}}[F:{\mathbb{Q}}]- \frac{[F:{\mathbb{Q}}]}{n}\nonumber,\end{align} $$
where
![]() ${\mathfrak {b}}$
is as in (3.30),
${\mathfrak {b}}$
is as in (3.30),
![]() ${\mathfrak {c}}$
is as in (3.15),
${\mathfrak {c}}$
is as in (3.15),
![]() ${\mathrm {Disc}}_F$
is the discriminant of
${\mathrm {Disc}}_F$
is the discriminant of
![]() $F/ {\mathbb {Q}}$
, and
$F/ {\mathbb {Q}}$
, and
![]() ${\mathcal {P}}_{K_\Lambda }\in Z^1({\mathcal {X}}_{K_\Lambda })$
is a CM cycle to be precisely defined in Definition 5.1.10.
${\mathcal {P}}_{K_\Lambda }\in Z^1({\mathcal {X}}_{K_\Lambda })$
is a CM cycle to be precisely defined in Definition 5.1.10.
Remark 4.4.16. (1) The definition of
![]() ${\mathfrak {a}}$
is rather complicated. The reader may skip it for the moment.
${\mathfrak {a}}$
is rather complicated. The reader may skip it for the moment.
(2) Looking at [Reference YuanYZ18, Theorem 1.7] and [Reference YuanYZ18, p 590], one can deduce cancellation between the terms in the definition of
![]() ${\mathfrak {a}}$
if one can, expectably, relate the Shimura varieties here and in loc. cit..
${\mathfrak {a}}$
if one can, expectably, relate the Shimura varieties here and in loc. cit..
Conjecture 4.4.17. Assume Assumption 4.4.1. Let
![]() $ \phi \in \overline {\mathcal {S}}\left ( {\mathbb {V}} \right ) ^{{{\widetilde K_\Lambda }}}$
. For
$ \phi \in \overline {\mathcal {S}}\left ( {\mathbb {V}} \right ) ^{{{\widetilde K_\Lambda }}}$
. For
![]() $g\in G({\mathbb {A}})$
, we have
$g\in G({\mathbb {A}})$
, we have
For the second definition, we modify the normalized admissible extensions of special divisors
![]() $Z(x)$
’s instead of weighted special divisors
$Z(x)$
’s instead of weighted special divisors
![]() $Z_t( \omega (g)\phi )^{\overline {\mathcal {L}}}$
. Unfortunately, the modification does not only depend on x, and the result generating series is not holomorphic.
$Z_t( \omega (g)\phi )^{\overline {\mathcal {L}}}$
. Unfortunately, the modification does not only depend on x, and the result generating series is not holomorphic.
Definition 4.4.18. For
![]() $x\in {\mathbb {V}}^\infty $
with
$x\in {\mathbb {V}}^\infty $
with
![]() $q(x)\in F^\times $
,
$q(x)\in F^\times $
,
![]() $g\in G({\mathbb {A}}_{F,\infty })$
and
$g\in G({\mathbb {A}}_{F,\infty })$
and
![]() $K\in {{\widetilde K_\Lambda }}$
, let
$K\in {{\widetilde K_\Lambda }}$
, let
![]() $ Z(x)^{\mathcal {L}} $
be the divisor on
$ Z(x)^{\mathcal {L}} $
be the divisor on
![]() ${\mathcal {X}}_K$
that is the normalized admissible extension of
${\mathcal {X}}_K$
that is the normalized admissible extension of
![]() $Z(x)$
with respect to
$Z(x)$
with respect to
![]() ${\mathcal {L}}$
, and
${\mathcal {L}}$
, and
![]() $ {\mathcal {G}}_{Z(x)_{E_v}}^{\overline L_{E_v}}$
the normalized admissible Green function for
$ {\mathcal {G}}_{Z(x)_{E_v}}^{\overline L_{E_v}}$
the normalized admissible Green function for
![]() $Z(x)_{E_v}$
with respect to
$Z(x)_{E_v}$
with respect to
![]() $\overline L_{E_v}$
. Let
$\overline L_{E_v}$
. Let
Here,
![]() $ {\mathfrak {k}}(x,g_v)$
is defined in Definition 4.2.6. For
$ {\mathfrak {k}}(x,g_v)$
is defined in Definition 4.2.6. For
![]() $\phi \in \overline {\mathcal {S}}\left ( {\mathbb {V}} \right )^{K}$
,
$\phi \in \overline {\mathcal {S}}\left ( {\mathbb {V}} \right )^{K}$
,
![]() $a\in {\mathbb {C}}$
and
$a\in {\mathbb {C}}$
and
![]() $g\in G({\mathbb {A}}_F)$
, let
$g\in G({\mathbb {A}}_F)$
, let
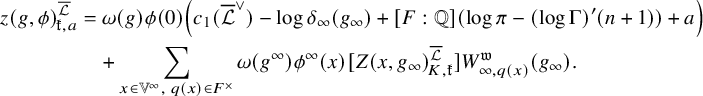 $$ \begin{align*} z(g, \phi)_{{\mathfrak{k}},a}^{{\overline{\mathcal{L}}}}&=\omega(g )\phi(0)\left( c_1(\overline {\mathcal{L}}^\vee)-\log \delta_\infty(g_\infty)+ [F:{\mathbb{Q}}]\left( \log \pi-(\log\Gamma)'(n+1)\right)+a\right)\\& \quad +\sum_{x\in {\mathbb{V}}^\infty,\ q(x)\in F^\times} \omega(g^\infty)\phi^\infty ( x) [Z(x,g_\infty)_{K,{\mathfrak{k}}}^{\overline{\mathcal{L}}}] W^{{\mathfrak{w}}}_{\infty, q(x)}(g_\infty). \end{align*} $$
$$ \begin{align*} z(g, \phi)_{{\mathfrak{k}},a}^{{\overline{\mathcal{L}}}}&=\omega(g )\phi(0)\left( c_1(\overline {\mathcal{L}}^\vee)-\log \delta_\infty(g_\infty)+ [F:{\mathbb{Q}}]\left( \log \pi-(\log\Gamma)'(n+1)\right)+a\right)\\& \quad +\sum_{x\in {\mathbb{V}}^\infty,\ q(x)\in F^\times} \omega(g^\infty)\phi^\infty ( x) [Z(x,g_\infty)_{K,{\mathfrak{k}}}^{\overline{\mathcal{L}}}] W^{{\mathfrak{w}}}_{\infty, q(x)}(g_\infty). \end{align*} $$
Though
![]() $Z(x,g)_{K,{\mathfrak {k}}}^{\overline {\mathcal {L}}}$
, as an element in
$Z(x,g)_{K,{\mathfrak {k}}}^{\overline {\mathcal {L}}}$
, as an element in
![]() $\widehat Z^1_{{\overline {\mathcal {L}}},{\mathbb {C}}}(\widetilde {\mathcal {X}}) $
, depends on K,
$\widehat Z^1_{{\overline {\mathcal {L}}},{\mathbb {C}}}(\widetilde {\mathcal {X}}) $
, depends on K,
![]() $z(g, \phi )_{{\mathfrak {k}},a}^{{\overline {\mathcal {L}}}}$
does not. Indeed, by Lemma 3.3.9 (1),
$z(g, \phi )_{{\mathfrak {k}},a}^{{\overline {\mathcal {L}}}}$
does not. Indeed, by Lemma 3.3.9 (1),
![]() $E_0(0,g,\phi )= \omega ( g)\phi (0)$
. Then by Theorem 4.2.7, we have
$E_0(0,g,\phi )= \omega ( g)\phi (0)$
. Then by Theorem 4.2.7, we have
Then since
![]() $z(g, \phi )_{{\mathfrak {e}},a }^{{\overline {\mathcal {L}}}}$
does not depend on K, neither does
$z(g, \phi )_{{\mathfrak {e}},a }^{{\overline {\mathcal {L}}}}$
does not depend on K, neither does
![]() $z(g, \phi )_{{\mathfrak {k}},a }^{{\overline {\mathcal {L}}}}$
.
$z(g, \phi )_{{\mathfrak {k}},a }^{{\overline {\mathcal {L}}}}$
.
The above reasoning also shows that (4.26) is equivalent to
4.4.4 Modularity theorems
We need some notations to state our theorems. Let
![]() ${\mathfrak {Ram}}$
be the set of finite places of F nonsplit in E, that are ramified in E or over
${\mathfrak {Ram}}$
be the set of finite places of F nonsplit in E, that are ramified in E or over
![]() ${\mathbb {Q}}$
. Let
${\mathbb {Q}}$
. Let
Let
be the span of pure tensors
![]() $\phi $
such that for every finite place v of F nonsplit in E,
$\phi $
such that for every finite place v of F nonsplit in E,
![]() $\phi _v=\omega (g)1_{\Lambda _v}$
for some
$\phi _v=\omega (g)1_{\Lambda _v}$
for some
![]() $g\in {\mathbb {G}}_v$
. In particular, we have no condition for
$g\in {\mathbb {G}}_v$
. In particular, we have no condition for
![]() $\phi \in \overline {\mathcal {S}}\left ( {\mathbb {V}} \right ) ^{{{\widetilde K_\Lambda }}}_{\mathfrak {Ram}}$
over split places. The following proposition and remark further show that we have no condition for
$\phi \in \overline {\mathcal {S}}\left ( {\mathbb {V}} \right ) ^{{{\widetilde K_\Lambda }}}_{\mathfrak {Ram}}$
over split places. The following proposition and remark further show that we have no condition for
![]() $\phi $
outside
$\phi $
outside
![]() ${\mathfrak {Ram}}$
.
${\mathfrak {Ram}}$
.
Proposition 4.4.19. For a finite place v of F inert in E (so that
![]() $\Lambda _v$
is self-dual by Assumption 4.4.1) such that
$\Lambda _v$
is self-dual by Assumption 4.4.1) such that
![]() $\chi _{_{\mathbb {V}},v}$
is unramified, the span of
$\chi _{_{\mathbb {V}},v}$
is unramified, the span of
![]() $ \{\omega (g)1_{\Lambda _v}, g\in G(F_v)\}$
is
$ \{\omega (g)1_{\Lambda _v}, g\in G(F_v)\}$
is
![]() ${\mathcal {S}}({\mathbb {V}}(E_v))^{K_{\Lambda ,v}}$
.
${\mathcal {S}}({\mathbb {V}}(E_v))^{K_{\Lambda ,v}}$
.
Proof. If v has residue characteristic
![]() $\neq 2$
, this is a special case of [Reference HoweHow79, Theorem 10.2]. In general, let
$\neq 2$
, this is a special case of [Reference HoweHow79, Theorem 10.2]. In general, let
![]() $K^{\max }_v\subset G(F_v)$
be as in (2.5). Embedding
$K^{\max }_v\subset G(F_v)$
be as in (2.5). Embedding
![]() ${\mathcal {S}}({\mathbb {V}}(E_v))^{K_{\Lambda ,v}\times K^{\max }_v}$
in an induced representation as [Reference RallisRal82, (3.1)]. It is routine to show that
${\mathcal {S}}({\mathbb {V}}(E_v))^{K_{\Lambda ,v}\times K^{\max }_v}$
in an induced representation as [Reference RallisRal82, (3.1)]. It is routine to show that
![]() ${\mathcal {S}}({\mathbb {V}}(E_v))^{K_{\Lambda ,v}\times K^{\max }_v}$
is generated by
${\mathcal {S}}({\mathbb {V}}(E_v))^{K_{\Lambda ,v}\times K^{\max }_v}$
is generated by
![]() $1_{\Lambda _v}$
as a module over the Hecke algebra of bi-
$1_{\Lambda _v}$
as a module over the Hecke algebra of bi-
![]() $K^{\max }_v$
-invariant Schwartz functions on
$K^{\max }_v$
-invariant Schwartz functions on
![]() $G(F_v)$
. Then the proposition follows from Kudla’s supercuspidal support theorem for big theta lift. See [Reference Gan and IchinoGI14, Proposition 5.2]
$G(F_v)$
. Then the proposition follows from Kudla’s supercuspidal support theorem for big theta lift. See [Reference Gan and IchinoGI14, Proposition 5.2]
Remark 4.4.20. We may choose
![]() $\chi _{_{\mathbb {V}}}$
such
$\chi _{_{\mathbb {V}}}$
such
![]() $\chi _{_{\mathbb {V}},v}$
is unramified if v is inert in E.
$\chi _{_{\mathbb {V}},v}$
is unramified if v is inert in E.
Let
![]() $ {\mathcal {A}}_{{\mathrm {hol}}}\left ( {\mathbb {G}},{\mathfrak {w}}\right ) $
and
$ {\mathcal {A}}_{{\mathrm {hol}}}\left ( {\mathbb {G}},{\mathfrak {w}}\right ) $
and
![]() $ {\mathcal {A}} \left ( {\mathbb {G}},{\mathfrak {w}}\right ) $
be the restrictions of
$ {\mathcal {A}} \left ( {\mathbb {G}},{\mathfrak {w}}\right ) $
be the restrictions of
![]() $ {\mathcal {A}}_{{\mathrm {hol}}}(G,{\mathfrak {w}})$
and
$ {\mathcal {A}}_{{\mathrm {hol}}}(G,{\mathfrak {w}})$
and
![]() $ {\mathcal {A}} (G,{\mathfrak {w}})$
to
$ {\mathcal {A}} (G,{\mathfrak {w}})$
to
![]() ${\mathbb {G}}$
, respectively.
${\mathbb {G}}$
, respectively.
Theorem 4.4.21. Assume Assumption 4.4.1. Let
![]() $\phi \in \overline {\mathcal {S}}\left ( {\mathbb {V}} \right ) ^{{{\widetilde K_\Lambda }}}_{\mathfrak {Ram}} $
. For
$\phi \in \overline {\mathcal {S}}\left ( {\mathbb {V}} \right ) ^{{{\widetilde K_\Lambda }}}_{\mathfrak {Ram}} $
. For
![]() $g\in {\mathbb {G}}$
, we have
$g\in {\mathbb {G}}$
, we have
and
In fact, by (4.27), (4.28) and (4.29) are equivalent. Theorem 4.4.21 will be proved in 5.2.4.
Remark 4.4.22. (1) The restriction of (4.28) to
![]() $g\in G({\mathbb {A}}_\infty )\subset {\mathbb {G}}$
gives Theorem 1.1.1, with a less strict condition on
$g\in G({\mathbb {A}}_\infty )\subset {\mathbb {G}}$
gives Theorem 1.1.1, with a less strict condition on
![]() $\phi _v$
,
$\phi _v$
,
![]() $v\in {\mathfrak {Ram}}$
. Remark 4.4.10 allows
$v\in {\mathfrak {Ram}}$
. Remark 4.4.10 allows
![]() $K_v$
to be arbitrary for v split in E.
$K_v$
to be arbitrary for v split in E.
(2) By the density of
![]() ${\mathbb {G}}\subset G(F)\backslash G({\mathbb {A}}_F)$
, the restriction gives
${\mathbb {G}}\subset G(F)\backslash G({\mathbb {A}}_F)$
, the restriction gives
In particular,
![]() $ z(g, \phi )_{{\mathfrak {e}},{\mathfrak {a}}}^{{\overline {\mathcal {L}}}}$
with
$ z(g, \phi )_{{\mathfrak {e}},{\mathfrak {a}}}^{{\overline {\mathcal {L}}}}$
with
![]() $ g\in {\mathbb {G}}$
extends uniquely to an element in
$ g\in {\mathbb {G}}$
extends uniquely to an element in
![]() $ {\mathcal {A}}_{{\mathrm {hol}}}\left ( G,{\mathfrak {w}}\right )\otimes \widehat {\mathrm {Ch}}^{1}_{{\overline {\mathcal {L}}},{\mathbb {C}}}(\widetilde {\mathcal {X}})$
. Conjecture 4.4.17 predicts that this extension is
$ {\mathcal {A}}_{{\mathrm {hol}}}\left ( G,{\mathfrak {w}}\right )\otimes \widehat {\mathrm {Ch}}^{1}_{{\overline {\mathcal {L}}},{\mathbb {C}}}(\widetilde {\mathcal {X}})$
. Conjecture 4.4.17 predicts that this extension is
![]() $ z(g, \phi )_{{\mathfrak {e}},{\mathfrak {a}}}^{{\overline {\mathcal {L}}}}$
with
$ z(g, \phi )_{{\mathfrak {e}},{\mathfrak {a}}}^{{\overline {\mathcal {L}}}}$
with
![]() $ g\in G({\mathbb {A}})$
. However, it seems not trivial to check this prediction. The same discussion applies to
$ g\in G({\mathbb {A}})$
. However, it seems not trivial to check this prediction. The same discussion applies to
![]() $z(g, \phi )_{{\mathfrak {k}},{\mathfrak {a}} }^{{\overline {\mathcal {L}}}}$
.
$z(g, \phi )_{{\mathfrak {k}},{\mathfrak {a}} }^{{\overline {\mathcal {L}}}}$
.
Definition 4.4.23. For
![]() $x\in {\mathbb {V}}^\infty $
with
$x\in {\mathbb {V}}^\infty $
with
![]() $q(x)\in F^\times $
and
$q(x)\in F^\times $
and
![]() $g\in G({\mathbb {A}}_{F,\infty })$
, let
$g\in G({\mathbb {A}}_{F,\infty })$
, let
Here, Kudla’s Green function
![]() $ {\mathcal {G}}_{Z(x)_{E_v}}^{\mathrm {Kud}}$
is defined in (4.12).
$ {\mathcal {G}}_{Z(x)_{E_v}}^{\mathrm {Kud}}$
is defined in (4.12).
For
![]() $\phi \in \overline {\mathcal {S}}\left ( {\mathbb {V}} \right )^{K}$
,
$\phi \in \overline {\mathcal {S}}\left ( {\mathbb {V}} \right )^{K}$
,
![]() $a\in {\mathbb {C}}$
and
$a\in {\mathbb {C}}$
and
![]() $g\in G({\mathbb {A}}_F)$
, let
$g\in G({\mathbb {A}}_F)$
, let
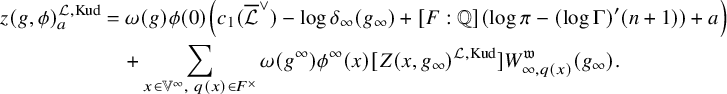 $$ \begin{align*} z(g, \phi)_{ a}^{{\mathcal{L}},\mathrm{Kud}}&=\omega(g )\phi(0)\left( c_1(\overline {\mathcal{L}}^\vee)-\log \delta_\infty(g_\infty)+ [F:{\mathbb{Q}}]\left( \log \pi-(\log\Gamma)'(n+1)\right)+a\right)\\&\quad +\sum_{x\in {\mathbb{V}}^\infty,\ q(x)\in F^\times} \omega(g^\infty)\phi^\infty ( x) [Z(x,g_\infty) ^{{\mathcal{L}},\mathrm{Kud}}] W^{{\mathfrak{w}}}_{\infty, q(x)}(g_\infty). \end{align*} $$
$$ \begin{align*} z(g, \phi)_{ a}^{{\mathcal{L}},\mathrm{Kud}}&=\omega(g )\phi(0)\left( c_1(\overline {\mathcal{L}}^\vee)-\log \delta_\infty(g_\infty)+ [F:{\mathbb{Q}}]\left( \log \pi-(\log\Gamma)'(n+1)\right)+a\right)\\&\quad +\sum_{x\in {\mathbb{V}}^\infty,\ q(x)\in F^\times} \omega(g^\infty)\phi^\infty ( x) [Z(x,g_\infty) ^{{\mathcal{L}},\mathrm{Kud}}] W^{{\mathfrak{w}}}_{\infty, q(x)}(g_\infty). \end{align*} $$
It is directly to check that
![]() $z(g, \phi )_{a}^{{\mathcal {L}},\mathrm {Kud}}$
is compatible under pullbacks by
$z(g, \phi )_{a}^{{\mathcal {L}},\mathrm {Kud}}$
is compatible under pullbacks by
![]() $\pi _{_K,_{K'}}$
’s.
$\pi _{_K,_{K'}}$
’s.
Define the topology on
![]() $\widehat {\mathrm {Ch}}^{1}_{{\mathbb {C}}}({\mathcal {X}}_K)$
as follows. Let
$\widehat {\mathrm {Ch}}^{1}_{{\mathbb {C}}}({\mathcal {X}}_K)$
as follows. Let
![]() $C^\infty ({\mathrm {Sh}}({\mathbb {V}})_{K,E_\infty })^\circ $
be the
$C^\infty ({\mathrm {Sh}}({\mathbb {V}})_{K,E_\infty })^\circ $
be the
![]() $L^2$
-orthogonal complement of
$L^2$
-orthogonal complement of
![]() ${\mathrm {LC}}({\mathrm {Sh}}({\mathbb {V}})_{K,E_\infty })$
in
${\mathrm {LC}}({\mathrm {Sh}}({\mathbb {V}})_{K,E_\infty })$
in
![]() $C^\infty ({\mathrm {Sh}}({\mathbb {V}})_{K,E_\infty })$
, endowed with
$C^\infty ({\mathrm {Sh}}({\mathbb {V}})_{K,E_\infty })$
, endowed with
![]() $L^\infty $
-topology. Then
$L^\infty $
-topology. Then
![]() $\widehat {\mathrm {Ch}}^{1}_{{\mathbb {C}}}({\mathcal {X}}_K)$
is the direct sum of
$\widehat {\mathrm {Ch}}^{1}_{{\mathbb {C}}}({\mathcal {X}}_K)$
is the direct sum of
![]() $C^\infty ({\mathrm {Sh}}({\mathbb {V}})_{K,E_\infty })^\circ $
and the finite dimensional subspace of cycles with harmonic curvatures at
$C^\infty ({\mathrm {Sh}}({\mathbb {V}})_{K,E_\infty })^\circ $
and the finite dimensional subspace of cycles with harmonic curvatures at
![]() $\infty $
. Endow
$\infty $
. Endow
![]() $\widehat {\mathrm {Ch}}^{1}_{{\mathbb {C}}}({\mathcal {X}}_K)$
with the direct sum topology. Let
$\widehat {\mathrm {Ch}}^{1}_{{\mathbb {C}}}({\mathcal {X}}_K)$
with the direct sum topology. Let
![]() $ {\mathcal {A}} \left ( {\mathbb {G}},{\mathfrak {w}},\widehat {\mathrm {Ch}}^{1}_{{\mathbb {C}}}({\mathcal {X}}_K)\right )$
be the restrictions of
$ {\mathcal {A}} \left ( {\mathbb {G}},{\mathfrak {w}},\widehat {\mathrm {Ch}}^{1}_{{\mathbb {C}}}({\mathcal {X}}_K)\right )$
be the restrictions of
![]() $ {\mathcal {A}} \left ( G,{\mathfrak {w}},\widehat {\mathrm {Ch}}^{1}_{{\mathbb {C}}}({\mathcal {X}}_K)\right )$
to
$ {\mathcal {A}} \left ( G,{\mathfrak {w}},\widehat {\mathrm {Ch}}^{1}_{{\mathbb {C}}}({\mathcal {X}}_K)\right )$
to
![]() ${\mathbb {G}}$
.
${\mathbb {G}}$
.
Theorem 4.2.10 and (4.28) of Theorem 4.4.21 imply the following theorem.
Theorem 4.4.24. Let
![]() $\phi \in \overline {\mathcal {S}}\left ( {\mathbb {V}} \right ) ^{K}_{\mathfrak {Ram}} $
, where
$\phi \in \overline {\mathcal {S}}\left ( {\mathbb {V}} \right ) ^{K}_{\mathfrak {Ram}} $
, where
![]() $K\in {{\widetilde K_\Lambda }}$
. The generating series
$K\in {{\widetilde K_\Lambda }}$
. The generating series
![]() $z(g, \phi )_{ {\mathfrak {a}}}^{{\mathcal {L}},\mathrm {Kud}}$
of
$z(g, \phi )_{ {\mathfrak {a}}}^{{\mathcal {L}},\mathrm {Kud}}$
of
![]() $\widehat {\mathrm {Ch}}^{1}_{{\mathbb {C}}}({\mathcal {X}}_K)$
-valued functions on
$\widehat {\mathrm {Ch}}^{1}_{{\mathbb {C}}}({\mathcal {X}}_K)$
-valued functions on
![]() ${\mathbb {G}}$
pointwise converges to an element in
${\mathbb {G}}$
pointwise converges to an element in
![]() $ {\mathcal {A}} \left ( {\mathbb {G}},{\mathfrak {w}},\widehat {\mathrm {Ch}}^{1}_{{\mathbb {C}}}({\mathcal {X}}_K)\right ).$
$ {\mathcal {A}} \left ( {\mathbb {G}},{\mathfrak {w}},\widehat {\mathrm {Ch}}^{1}_{{\mathbb {C}}}({\mathcal {X}}_K)\right ).$
5 Arithmetic mixed Siegel-Weil formula
In this section, we prove our modularity theorem (Theorem 4.4.21) above using an arithmetic analog of the mixed Siegel-Weil formula (3.19). First, we define CM cycles. Then, we state the formula and use this formula to prove Theorem 4.4.21. We end this section by discussing some possible future generalizations and applications of our results. We continue to use notations and assumptions in 4.4.
5.1 CM cycles
In this subsection, we define an orthogonal decomposition
where
![]() ${\mathbb {W}}$
is an incoherent hermitian space over
${\mathbb {W}}$
is an incoherent hermitian space over
![]() ${\mathbb {A}}_E$
of dimension 1, and
${\mathbb {A}}_E$
of dimension 1, and
![]() $V^\sharp $
is a hermitian space over E of dimension n. Then we define a CM cycle
$V^\sharp $
is a hermitian space over E of dimension n. Then we define a CM cycle
associated to the 0-dimensional Shimura variety for
![]() ${\mathbb {W}}$
, normalized to be of generic degree 1.
${\mathbb {W}}$
, normalized to be of generic degree 1.
5.1.1 Lattices at unramified places
For a finite place v of F unramified in E, by [Reference JacobowitzJac62, Section 7], there exists
![]() $e_v^{(0)},\ldots ,e_v^{(n)}\in \Lambda _v$
of unit norms, such that
$e_v^{(0)},\ldots ,e_v^{(n)}\in \Lambda _v$
of unit norms, such that
![]() $\Lambda _v$
is their orthogonal direct sum.
$\Lambda _v$
is their orthogonal direct sum.
5.1.2 Lattices at ramified places
Let
![]() ${\mathfrak {Ram}}_{E/F}$
be the set of finite places of F ramified in E. For
${\mathfrak {Ram}}_{E/F}$
be the set of finite places of F ramified in E. For
![]() $v\in {\mathfrak {Ram}}_{E/F}$
, let
$v\in {\mathfrak {Ram}}_{E/F}$
, let
![]() ${\mathbb {M}}_v$
be the
${\mathbb {M}}_v$
be the
![]() $ {\mathcal {O}}_{E_v}$
-lattice of rank 2 with an isotropic basis
$ {\mathcal {O}}_{E_v}$
-lattice of rank 2 with an isotropic basis
![]() $\{X,Y\}$
such that
$\{X,Y\}$
such that
![]() $\langle {X,Y} \rangle =\varpi _{E_v}$
. Then
$\langle {X,Y} \rangle =\varpi _{E_v}$
. Then
![]() ${\mathbb {M}}_v$
is a
${\mathbb {M}}_v$
is a
![]() $\varpi _{E_v}$
-modular lattice in
$\varpi _{E_v}$
-modular lattice in
![]() ${\mathbb {M}}_v\otimes {E_v}$
, and its determinant with respect to this basis is
${\mathbb {M}}_v\otimes {E_v}$
, and its determinant with respect to this basis is
![]() $-{\mathrm {Nm}}(\varpi _{E_v})$
. The hermitian space
$-{\mathrm {Nm}}(\varpi _{E_v})$
. The hermitian space
![]() ${\mathbb {M}}_v\otimes {E_v}$
has determinant
${\mathbb {M}}_v\otimes {E_v}$
has determinant
![]() $-1\in F_v^\times /{\mathrm {Nm}}( {E_v^\times })$
. In the other direction, starting with a 2-dimensional hermitian space H over
$-1\in F_v^\times /{\mathrm {Nm}}( {E_v^\times })$
. In the other direction, starting with a 2-dimensional hermitian space H over
![]() $E_v$
of determinant
$E_v$
of determinant
![]() $-1\in F_v^\times /{\mathrm {Nm}}( {E_v^\times })$
, let
$-1\in F_v^\times /{\mathrm {Nm}}( {E_v^\times })$
, let
![]() $e_v^{(0)},e_v^{(1)}\in H$
be orthogonal such that
$e_v^{(0)},e_v^{(1)}\in H$
be orthogonal such that
![]() $q\left ( e_v^{(0)}\right ), q\left ( e_v^{(1)}\right )\in {\mathcal {O}}_{F_v}^\times .$
Then one can choose
$q\left ( e_v^{(0)}\right ), q\left ( e_v^{(1)}\right )\in {\mathcal {O}}_{F_v}^\times .$
Then one can choose
![]() ${\mathbb {M}}_v\subset {\mathcal {O}}_{E_v}e_v^{(0)}\oplus {\mathcal {O}}_{E_v}e_v^{(1)}$
to be the preimage of one of the two isotropic lines in
${\mathbb {M}}_v\subset {\mathcal {O}}_{E_v}e_v^{(0)}\oplus {\mathcal {O}}_{E_v}e_v^{(1)}$
to be the preimage of one of the two isotropic lines in
![]() $( {\mathcal {O}}_{E_v}e_v^{(0)}\oplus {\mathcal {O}}_{E_v}e_v^{(1)})/\varpi _{E_v}.$
In particular, one easily sees that
$( {\mathcal {O}}_{E_v}e_v^{(0)}\oplus {\mathcal {O}}_{E_v}e_v^{(1)})/\varpi _{E_v}.$
In particular, one easily sees that
and
These two relations will only be used in the proof of Lemma 5.2.3.
Recall that for
![]() $v\in {\mathfrak {Ram}}_{E/F}$
,
$v\in {\mathfrak {Ram}}_{E/F}$
,
![]() $v\nmid 2$
by Assumption 4.4.1 (1), and
$v\nmid 2$
by Assumption 4.4.1 (1), and
![]() $\Lambda _v$
is (almost)
$\Lambda _v$
is (almost)
![]() $\varpi _{E_v}$
-modular as in Assumption 4.4.1 (4). Recall that the rank of
$\varpi _{E_v}$
-modular as in Assumption 4.4.1 (4). Recall that the rank of
![]() $\Lambda _v$
is
$\Lambda _v$
is
![]() $n+1$
.
$n+1$
.
Lemma 5.1.1 [Reference JacobowitzJac62, Section 8].
(1) If n is odd, then
![]() $\Lambda _v{\ \simeq \ } {\mathbb {M}}_v^{\oplus (n+1)/2}$
.
$\Lambda _v{\ \simeq \ } {\mathbb {M}}_v^{\oplus (n+1)/2}$
.
(2) If n is even, then
![]() $\Lambda _v$
is the orthogonal direct sum of
$\Lambda _v$
is the orthogonal direct sum of
![]() $n/2$
-copies of
$n/2$
-copies of
![]() ${\mathbb {M}}_v$
and a rank-1 hermitian
${\mathbb {M}}_v$
and a rank-1 hermitian
![]() ${\mathcal {O}}_{E_v}$
-module with determinant in
${\mathcal {O}}_{E_v}$
-module with determinant in
![]() ${\mathcal {O}}_{F_v}^\times $
.
${\mathcal {O}}_{F_v}^\times $
.
5.1.3 CM cycles
For a finite place
![]() $v\not \in {\mathfrak {Ram}}_{E/F}$
, let
$v\not \in {\mathfrak {Ram}}_{E/F}$
, let
![]() $e_v^{(0)}$
be as in 5.1.1. For
$e_v^{(0)}$
be as in 5.1.1. For
![]() $v \in {\mathfrak {Ram}}_{E/F}$
, let
$v \in {\mathfrak {Ram}}_{E/F}$
, let
![]() $\Lambda _{v,1}\subset \Lambda _v$
be a copy of
$\Lambda _{v,1}\subset \Lambda _v$
be a copy of
![]() ${\mathbb {M}}_v$
. See Lemma 5.1.1. Let
${\mathbb {M}}_v$
. See Lemma 5.1.1. Let
![]() $e_v^{(0)}\in E_v \Lambda _{v,1}$
such that
$e_v^{(0)}\in E_v \Lambda _{v,1}$
such that
Let
![]() ${\mathbb {W}}$
be the restricted tensor product of
${\mathbb {W}}$
be the restricted tensor product of
![]() $E_v e_{v}^{(0)}$
, for every
$E_v e_{v}^{(0)}$
, for every
![]() $v\not \in \infty $
, and a
$v\not \in \infty $
, and a
![]() $1$
-dimensional subspace of
$1$
-dimensional subspace of
![]() ${\mathbb {V}}(E_v)$
, for every
${\mathbb {V}}(E_v)$
, for every
![]() $v\in \infty $
. Note that since
$v\in \infty $
. Note that since
![]() ${\mathbb {W}}$
is incoherent. The orthogonal complement of
${\mathbb {W}}$
is incoherent. The orthogonal complement of
![]() ${\mathbb {W}}$
in
${\mathbb {W}}$
in
![]() ${\mathbb {V}}$
is coherent of dimension n. We denote the corresponding hermitian space over E by
${\mathbb {V}}$
is coherent of dimension n. We denote the corresponding hermitian space over E by
![]() $V^\sharp $
. This gives (5.1).
$V^\sharp $
. This gives (5.1).
Let
![]() $K_{{\mathbb {W}}}= K\cap U({\mathbb {W}}^\infty )$
. The morphism
$K_{{\mathbb {W}}}= K\cap U({\mathbb {W}}^\infty )$
. The morphism
![]() ${\mathrm {Sh}}({\mathbb {W}})_{K_{\mathbb {W}}}\to {\mathrm {Sh}}({\mathbb {V}})_{K}$
, analogous to (4.1), defines a zero cycle on
${\mathrm {Sh}}({\mathbb {W}})_{K_{\mathbb {W}}}\to {\mathrm {Sh}}({\mathbb {V}})_{K}$
, analogous to (4.1), defines a zero cycle on
![]() ${\mathrm {Sh}}({\mathbb {V}})_{K}$
. (Indeed, this is a ‘simple special zero cycle’ compared with 4.1.1.)
${\mathrm {Sh}}({\mathbb {V}})_{K}$
. (Indeed, this is a ‘simple special zero cycle’ compared with 4.1.1.)
Definition 5.1.3. Let
![]() $d_{{\mathbb {W}},K} $
be the degree of this zero cycle. Let
$d_{{\mathbb {W}},K} $
be the degree of this zero cycle. Let
![]() $ {\mathcal {P}}_{{\mathbb {W}},K}\in Z_1({\mathcal {X}}_K)_{\mathbb {Q}}$
be
$ {\mathcal {P}}_{{\mathbb {W}},K}\in Z_1({\mathcal {X}}_K)_{\mathbb {Q}}$
be
![]() $1/ d_{{\mathbb {W}},K}$
times the Zariski closure of this cycle.
$1/ d_{{\mathbb {W}},K}$
times the Zariski closure of this cycle.
Recall that K is normal in
![]() $K_{\Lambda }$
(Definition 4.4.2), and for
$K_{\Lambda }$
(Definition 4.4.2), and for
![]() $h\in K_\Lambda $
, there is the ‘right translation by h’ automorphism on
$h\in K_\Lambda $
, there is the ‘right translation by h’ automorphism on
![]() ${\mathcal {X}}_{K}$
(Definition 4.4.9 (3)).
${\mathcal {X}}_{K}$
(Definition 4.4.9 (3)).
Lemma 5.1.4. The ‘right translation by h’ automorphism on
![]() ${\mathcal {X}}_{K}$
sends
${\mathcal {X}}_{K}$
sends
![]() $ {\mathcal {P}}_{{\mathbb {W}},K}$
to
$ {\mathcal {P}}_{{\mathbb {W}},K}$
to
![]() $ {\mathcal {P}}_{h{\mathbb {W}},K}$
.
$ {\mathcal {P}}_{h{\mathbb {W}},K}$
.
Proof. When restricted to the generic fiber, the proof goes in the same way as [Reference KudlaKud97a, LEMMA 2.2 (iv)]. Taking Zariski closure, we get the lemma.
In particular, for
![]() $k\in K$
,
$k\in K$
,
![]() $d_{{\mathbb {W}},K} =d_{k {\mathbb {W}},K},$
and
$d_{{\mathbb {W}},K} =d_{k {\mathbb {W}},K},$
and
![]() $ {\mathcal {P}}_{{\mathbb {W}},K} ={\mathcal {P}}_{k {\mathbb {W}},K}. $
Then by the flatness of
$ {\mathcal {P}}_{{\mathbb {W}},K} ={\mathcal {P}}_{k {\mathbb {W}},K}. $
Then by the flatness of
![]() $\pi _{_K,_{K'}}$
(and the commutativity of taking Zariski closure and flat pullback) and [Reference LiuLiu11a, Proposition 3.2],
$\pi _{_K,_{K'}}$
(and the commutativity of taking Zariski closure and flat pullback) and [Reference LiuLiu11a, Proposition 3.2],
 $$ \begin{align} \pi_{_K,_{K'}}^{*}{\mathcal{P}}_{{\mathbb{W}},K'}=\sum _{k\in (U({\mathbb{W}})\cap K')\backslash K'/K} \frac{d_{k^{-1}{\mathbb{W}},K}}{ d_{{\mathbb{W}},K'}}{\mathcal{P}}_{k^{-1}{\mathbb{W}},K}, \end{align} $$
$$ \begin{align} \pi_{_K,_{K'}}^{*}{\mathcal{P}}_{{\mathbb{W}},K'}=\sum _{k\in (U({\mathbb{W}})\cap K')\backslash K'/K} \frac{d_{k^{-1}{\mathbb{W}},K}}{ d_{{\mathbb{W}},K'}}{\mathcal{P}}_{k^{-1}{\mathbb{W}},K}, \end{align} $$
where each summand is independent of the choice of the representatives k. We shall later abbreviate
![]() $(U({\mathbb {W}})\cap K')\backslash K'/K$
as
$(U({\mathbb {W}})\cap K')\backslash K'/K$
as
![]() $U({\mathbb {W}})\backslash K'/K$
.
$U({\mathbb {W}})\backslash K'/K$
.
5.1.4 Another description
We will give another description of
![]() ${\mathcal {P}}_{{\mathbb {W}},K}$
that shows the independence of
${\mathcal {P}}_{{\mathbb {W}},K}$
that shows the independence of
![]() ${\mathcal {P}}_{{\mathbb {W}},K_\Lambda }$
on
${\mathcal {P}}_{{\mathbb {W}},K_\Lambda }$
on
![]() ${\mathbb {W}}$
. (It will also be used in 6.1.2 to compute intersection numbers.) Before that, we introduce new lattices, open compact subgroups and Shimura varieties.
${\mathbb {W}}$
. (It will also be used in 6.1.2 to compute intersection numbers.) Before that, we introduce new lattices, open compact subgroups and Shimura varieties.
For
![]() $v\in {\mathfrak {Ram}}_{E/F}$
, let
$v\in {\mathfrak {Ram}}_{E/F}$
, let
![]() $e_v^{(1)}\in \Lambda _{v,1}$
be orthogonal to
$e_v^{(1)}\in \Lambda _{v,1}$
be orthogonal to
![]() $e_v^{(0)}$
such that
$e_v^{(0)}$
such that
![]() $ q\left ( e_v^{(1)}\right )\in {\mathcal {O}}_{F_v}^\times ,$
and let
$ q\left ( e_v^{(1)}\right )\in {\mathcal {O}}_{F_v}^\times ,$
and let
![]() $\Lambda _{v,1}^\perp \subset \Lambda _v$
be the orthogonal complement of
$\Lambda _{v,1}^\perp \subset \Lambda _v$
be the orthogonal complement of
![]() $\Lambda _{v,1}$
. Then we have
$\Lambda _{v,1}$
. Then we have
where each inclusion is of colength 1, and
![]() $\Lambda _v=\Lambda _{v,1}\oplus \Lambda _{v,1}^\perp .$
$\Lambda _v=\Lambda _{v,1}\oplus \Lambda _{v,1}^\perp .$
Let
![]() $K_v^\dagger \subset U({\mathbb {V}}_{v})$
be the stabilizer of
$K_v^\dagger \subset U({\mathbb {V}}_{v})$
be the stabilizer of
![]() ${\mathcal {O}}_{E_v}e_v^{(0)}\oplus {\mathcal {O}}_{E_v}e_v^{(1)}\oplus \Lambda _{v,1}^\perp $
, and
${\mathcal {O}}_{E_v}e_v^{(0)}\oplus {\mathcal {O}}_{E_v}e_v^{(1)}\oplus \Lambda _{v,1}^\perp $
, and
![]() $K^\dagger =K_v^\dagger \prod _{u\neq v}K_u$
.
$K^\dagger =K_v^\dagger \prod _{u\neq v}K_u$
.
Lemma 5.1.5. We have
![]() $[K_v^\dagger :K_v^\dagger \cap K_v]=2$
.
$[K_v^\dagger :K_v^\dagger \cap K_v]=2$
.
Proof. The index is the cardinality of the isotropic lines in
![]() $\left ({\mathcal {O}}_{E_v}e_v^{(0)}\oplus {\mathcal {O}}_{E_v}e_v^{(1)}\right ) /\varpi _{E_v}$
, which is 2.
$\left ({\mathcal {O}}_{E_v}e_v^{(0)}\oplus {\mathcal {O}}_{E_v}e_v^{(1)}\right ) /\varpi _{E_v}$
, which is 2.
Let
![]() $K_{{\mathbb {W}},v}^{(0)}\subset U({\mathbb {W}}_v)$
be the stabilizer of
$K_{{\mathbb {W}},v}^{(0)}\subset U({\mathbb {W}}_v)$
be the stabilizer of
![]() ${\mathcal {O}}_{E_v}e_v^{(0)}$
, that is,
${\mathcal {O}}_{E_v}e_v^{(0)}$
, that is,
![]() $K_{{\mathbb {W}},v}^{(0)}=U({\mathbb {W}}_v)$
, and
$K_{{\mathbb {W}},v}^{(0)}=U({\mathbb {W}}_v)$
, and
![]() $K_{\mathbb {W}}^{(0)}=K_{{\mathbb {W}},v}^{(0)} \prod _{u\neq v }K_{{\mathbb {W}},u}$
. Then we have a diagram of morphisms of Shimura varieties
$K_{\mathbb {W}}^{(0)}=K_{{\mathbb {W}},v}^{(0)} \prod _{u\neq v }K_{{\mathbb {W}},u}$
. Then we have a diagram of morphisms of Shimura varieties
Applying pushfoward, pullback and pushfoward along the diagram (5.5) to the fundamental cycle of
![]() ${\mathrm {Sh}}({\mathbb {W}})_{K_{\mathbb {W}}^{(0)}}$
, we obtain a zero cycle on
${\mathrm {Sh}}({\mathbb {W}})_{K_{\mathbb {W}}^{(0)}}$
, we obtain a zero cycle on
![]() ${\mathrm {Sh}}({\mathbb {V}})_{K}$
. Divide it by its degree to obtain a zero cycle of degree 1.
${\mathrm {Sh}}({\mathbb {V}})_{K}$
. Divide it by its degree to obtain a zero cycle of degree 1.
Lemma 5.1.6. The Zariski closure of this degree 1 zero cycle is
![]() ${\mathcal {P}}_{{\mathbb {W}},K}$
.
${\mathcal {P}}_{{\mathbb {W}},K}$
.
Proof. By Lemma 5.1.5,
![]() $[K^\dagger :K^\dagger \cap K]=2$
. Since
$[K^\dagger :K^\dagger \cap K]=2$
. Since
![]() $K_{{\mathbb {W}},v}^{(0)}\not \subset K$
,
$K_{{\mathbb {W}},v}^{(0)}\not \subset K$
,
![]() $K_{{\mathbb {W}},v}^{(0)} (K^\dagger \cap K) =K^\dagger $
. Then the fiber product of the first two morphisms in (5.5) is
$K_{{\mathbb {W}},v}^{(0)} (K^\dagger \cap K) =K^\dagger $
. Then the fiber product of the first two morphisms in (5.5) is
![]() ${\mathrm {Sh}}({\mathbb {W}})_{ (K^\dagger \cap K)\cap U({\mathbb {W}}^\infty ) }$
(an analog of (5.4)). The natural morphism
${\mathrm {Sh}}({\mathbb {W}})_{ (K^\dagger \cap K)\cap U({\mathbb {W}}^\infty ) }$
(an analog of (5.4)). The natural morphism
![]() ${\mathrm {Sh}}({\mathbb {W}})_{ (K^\dagger \cap K) \cap U({\mathbb {W}}^\infty ) } \to {\mathrm {Sh}}({\mathbb {V}})_{ K }$
factors through
${\mathrm {Sh}}({\mathbb {W}})_{ (K^\dagger \cap K) \cap U({\mathbb {W}}^\infty ) } \to {\mathrm {Sh}}({\mathbb {V}})_{ K }$
factors through
![]() ${\mathrm {Sh}}({\mathbb {W}})_{ K_{\mathbb {W}}}$
. The lemma follows.
${\mathrm {Sh}}({\mathbb {W}})_{ K_{\mathbb {W}}}$
. The lemma follows.
Remark 5.1.7. One may define
![]() ${\mathcal {P}}_{{\mathbb {W}},K}$
via a diagram of integral models similar to (5.5), as in [Reference Rapoport, Smithling and ZhangRSZ20, (4.30)].
${\mathcal {P}}_{{\mathbb {W}},K}$
via a diagram of integral models similar to (5.5), as in [Reference Rapoport, Smithling and ZhangRSZ20, (4.30)].
Lemma 5.1.8. Let
![]() $h\in U(E_v \Lambda _{v,1})\times \{1_{E_v\Lambda _{v,1}^\perp }\}\subset U({\mathbb {V}}(E_v))$
such that
$h\in U(E_v \Lambda _{v,1})\times \{1_{E_v\Lambda _{v,1}^\perp }\}\subset U({\mathbb {V}}(E_v))$
such that
![]() $\Lambda _{v,1}\subset h\left ( {\mathcal {O}}_{E_v} e_v^{(0)}\oplus {\mathcal {O}}_{E_v} e_v^{(1)}\right )$
and is the preimage of one of the two isotropic lines in the reduction modulo
$\Lambda _{v,1}\subset h\left ( {\mathcal {O}}_{E_v} e_v^{(0)}\oplus {\mathcal {O}}_{E_v} e_v^{(1)}\right )$
and is the preimage of one of the two isotropic lines in the reduction modulo
![]() $\varpi _{E_v}$
. Then
$\varpi _{E_v}$
. Then
![]() $h\in K_v^\dagger $
.
$h\in K_v^\dagger $
.
Proof. Let
![]() $K^c=K^\dagger \backslash K$
. The two preimages of the two isotropic lines in the reduction of
$K^c=K^\dagger \backslash K$
. The two preimages of the two isotropic lines in the reduction of
![]() $h\left ( {\mathcal {O}}_{E_v} e_v^{(0)}\oplus {\mathcal {O}}_{E_v} e_v^{(1)}\right )$
are
$h\left ( {\mathcal {O}}_{E_v} e_v^{(0)}\oplus {\mathcal {O}}_{E_v} e_v^{(1)}\right )$
are
![]() $h \Lambda _{v,1}$
and
$h \Lambda _{v,1}$
and
![]() $hK^c \Lambda _{v,1}$
. Then either
$hK^c \Lambda _{v,1}$
. Then either
![]() $h \Lambda _{v,1}=\Lambda _{v,1}$
or
$h \Lambda _{v,1}=\Lambda _{v,1}$
or
![]() $hK^c \Lambda _{v,1}= \Lambda _{v,1}$
. Each implies
$hK^c \Lambda _{v,1}= \Lambda _{v,1}$
. Each implies
![]() $h\in K_v^\dagger $
.
$h\in K_v^\dagger $
.
Proposition 5.1.9. The CM cycle
![]() ${\mathcal {P}}_{{\mathbb {W}},K_\Lambda }$
does not depend on the choice of
${\mathcal {P}}_{{\mathbb {W}},K_\Lambda }$
does not depend on the choice of
![]() ${\mathbb {W}}$
.
${\mathbb {W}}$
.
Proof. To define
![]() ${\mathcal {P}}_{{\mathbb {W}},K_\Lambda }$
, we specify
${\mathcal {P}}_{{\mathbb {W}},K_\Lambda }$
, we specify
![]() $e_v^{(0)}\in {\mathbb {W}}$
as in 5.1.3. For
$e_v^{(0)}\in {\mathbb {W}}$
as in 5.1.3. For
![]() $v\not \in {\mathfrak {Ram}}_{E/F}$
, the choices of
$v\not \in {\mathfrak {Ram}}_{E/F}$
, the choices of
![]() $e_v^{(0)}$
differ by
$e_v^{(0)}$
differ by
![]() $K_{\Lambda ,v}$
actions, which do not change
$K_{\Lambda ,v}$
actions, which do not change
![]() ${\mathcal {P}}_{{\mathbb {W}},K_\Lambda }$
by Lemma 5.1.4. For
${\mathcal {P}}_{{\mathbb {W}},K_\Lambda }$
by Lemma 5.1.4. For
![]() $v \in {\mathfrak {Ram}}_{E/F}$
, the choices of
$v \in {\mathfrak {Ram}}_{E/F}$
, the choices of
![]() $\Lambda _{v,1}$
differ by
$\Lambda _{v,1}$
differ by
![]() $K_{\Lambda ,v}$
actions. See Lemma 5.1.1. By Lemma 5.1.8, we only need to show that
$K_{\Lambda ,v}$
actions. See Lemma 5.1.1. By Lemma 5.1.8, we only need to show that
![]() ${\mathcal {P}}_{{\mathbb {W}},K_\Lambda }= {\mathcal {P}}_{h{\mathbb {W}},K_\Lambda }$
for
${\mathcal {P}}_{{\mathbb {W}},K_\Lambda }= {\mathcal {P}}_{h{\mathbb {W}},K_\Lambda }$
for
![]() $h\in K_v^\dagger $
, where
$h\in K_v^\dagger $
, where
![]() $v\in {\mathfrak {Ram}}_{E/F}$
. We use Lemma 5.1.6. The pushforward of the fundamental cycle of
$v\in {\mathfrak {Ram}}_{E/F}$
. We use Lemma 5.1.6. The pushforward of the fundamental cycle of
![]() ${\mathrm {Sh}}({\mathbb {W}})_{K_{\mathbb {W}}^{(0)}}$
by the first map in (5.5) is the same as the one obtained by replacing
${\mathrm {Sh}}({\mathbb {W}})_{K_{\mathbb {W}}^{(0)}}$
by the first map in (5.5) is the same as the one obtained by replacing
![]() ${\mathbb {W}}$
by
${\mathbb {W}}$
by
![]() $h{\mathbb {W}}$
, by the analog of Lemma 5.1.4 (on the generic fiber).
$h{\mathbb {W}}$
, by the analog of Lemma 5.1.4 (on the generic fiber).
Definition 5.1.10. We denote
![]() ${\mathcal {P}}_{{\mathbb {W}},K_\Lambda }$
by
${\mathcal {P}}_{{\mathbb {W}},K_\Lambda }$
by
![]() ${\mathcal {P}}_{K_\Lambda }$
.
${\mathcal {P}}_{K_\Lambda }$
.
This definition is only used in (4.25). Later, we will still use
![]() ${\mathcal {P}}_{{\mathbb {W}},K_\Lambda }$
for the uniformity of the notation as the level changes. (For
${\mathcal {P}}_{{\mathbb {W}},K_\Lambda }$
for the uniformity of the notation as the level changes. (For
![]() $K\neq K_\Lambda $
,
$K\neq K_\Lambda $
,
![]() ${\mathcal {P}}_{{\mathbb {W}},K}$
depends on the choice of
${\mathcal {P}}_{{\mathbb {W}},K}$
depends on the choice of
![]() ${\mathbb {W}}$
.)
${\mathbb {W}}$
.)
5.2 Formula
The arithmetic mixed Siegel-Weil formula compares the generating series of arithmetic intersection numbers between arithmetic special divisors and CM 1-cycles on the integral models with an explicit automorphic form. We use this formula to prove our main theorem Theorem 4.4.21.
5.2.1 Error functions
Both sides of the arithmetic mixed Siegel-Weil formula will have decompositions into local components (we will see in the proof in Section 6). We define some functions measuring the difference between these local components, and they will appear in the explicit automorphic form.
For a place v of F nonsplit in E, let W be the v-nearby hermitian space of
![]() ${\mathbb {W}}$
. See 2.2. Define the orthogonal direct sum
${\mathbb {W}}$
. See 2.2. Define the orthogonal direct sum
Then we have isomorpisms
and similar isomorphisms for W and
![]() ${\mathbb {W}}$
. Consider
${\mathbb {W}}$
. Consider
Let
![]() $\Lambda _v^\sharp \subset {\mathbb {W}}_v$
be the orthogonal complement of
$\Lambda _v^\sharp \subset {\mathbb {W}}_v$
be the orthogonal complement of
![]() ${\mathcal {O}}_{E_v}e_v^{(0)}$
in
${\mathcal {O}}_{E_v}e_v^{(0)}$
in
![]() $\Lambda _v$
. For
$\Lambda _v$
. For
![]() $x=(x_1,x_2)\in V(E_v)-V^\sharp (E_v) ,$
let
$x=(x_1,x_2)\in V(E_v)-V^\sharp (E_v) ,$
let
where the smooth function
![]() ${W\theta }_{v,x} '(0, 1, \phi _v)$
on
${W\theta }_{v,x} '(0, 1, \phi _v)$
on
![]() $V(E_v)-V^\sharp (E_v)$
is as in (3.21).
$V(E_v)-V^\sharp (E_v)$
is as in (3.21).
Note that
![]() $\Lambda _v={\mathcal {O}}_{E_v}e_v^{(0)}\oplus \Lambda _v^\sharp $
. So the computation for
$\Lambda _v={\mathcal {O}}_{E_v}e_v^{(0)}\oplus \Lambda _v^\sharp $
. So the computation for
![]() $\phi _v'(x)$
is only on the component
$\phi _v'(x)$
is only on the component
![]() ${\mathcal {O}}_{E_v}e_v^{(0)}$
, and we can apply computations in [Reference YuanYZ18, Reference Yuan, Zhang and ZhangYZZ13].
${\mathcal {O}}_{E_v}e_v^{(0)}$
, and we can apply computations in [Reference YuanYZ18, Reference Yuan, Zhang and ZhangYZZ13].
Lemma 5.2.1 [Reference Yuan, Zhang and ZhangYZZ13, Proposition 6.8].
Assume that
![]() $v\not \in {\mathfrak {Ram}}$
. Then
$v\not \in {\mathfrak {Ram}}$
. Then
![]() $\phi _v'=0$
.
$\phi _v'=0$
.
Let
![]() $c(g,\phi _v)$
be as below (3.23). Recall that
$c(g,\phi _v)$
be as below (3.23). Recall that
![]() ${\mathrm {Diff}}_{v}$
is the different of
${\mathrm {Diff}}_{v}$
is the different of
![]() $F_v$
over
$F_v$
over
![]() ${\mathbb {Q}}_{v}$
.
${\mathbb {Q}}_{v}$
.
Lemma 5.2.2 [Reference YuanYZ18, Lemma 9.2].
Assume that
![]() $v\in {\mathfrak {Ram}}-{\mathfrak {Ram}}_{E/F}$
. Then
$v\in {\mathfrak {Ram}}-{\mathfrak {Ram}}_{E/F}$
. Then
![]() $\phi _v'$
extends to a Schwartz function on
$\phi _v'$
extends to a Schwartz function on
![]() $ V(E_v)$
such that
$ V(E_v)$
such that
![]() $c(1,\phi _v)-2\phi _v'(0)=2\log |{\mathrm {Diff}}_{v}|_{v}$
.
$c(1,\phi _v)-2\phi _v'(0)=2\log |{\mathrm {Diff}}_{v}|_{v}$
.
For
![]() $v \in {\mathfrak {Ram}}_{E/F}$
, as in 5.1.4, we have
$v \in {\mathfrak {Ram}}_{E/F}$
, as in 5.1.4, we have
and
![]() $\Lambda _v=\Lambda _{v,1}\oplus \Lambda _{v,1}^\perp $
. For
$\Lambda _v=\Lambda _{v,1}\oplus \Lambda _{v,1}^\perp $
. For
![]() $x=(x_1,x_2)\in V(E_v)-V^\sharp (E_v) ,$
let
$x=(x_1,x_2)\in V(E_v)-V^\sharp (E_v) ,$
let
Lemma 5.2.3. Assume that
![]() $v\in {\mathfrak {Ram}}_{E/F}$
. Then
$v\in {\mathfrak {Ram}}_{E/F}$
. Then
![]() $\phi _v'$
extends to a Schwartz function on
$\phi _v'$
extends to a Schwartz function on
![]() $ V(E_v)$
such that
$ V(E_v)$
such that
![]() $c(1,\phi _v)-2\phi _v'(0)=2 \log |{\mathrm {Diff}}_v|_{F_v} $
.
$c(1,\phi _v)-2\phi _v'(0)=2 \log |{\mathrm {Diff}}_v|_{F_v} $
.
Proof. The computation for
![]() $\phi _v'(x)$
is indeed only on the component
$\phi _v'(x)$
is indeed only on the component
![]() $\Lambda _{v,1}$
of
$\Lambda _{v,1}$
of
![]() $\Lambda _v$
. For simplicity, we assume that
$\Lambda _v$
. For simplicity, we assume that
![]() $n=2$
so that we do not have the component
$n=2$
so that we do not have the component
![]() $ \Lambda _{v,1}^\perp $
.
$ \Lambda _{v,1}^\perp $
.
Consider a larger lattice
![]() $A={\mathcal {O}}_{E_v}e_v^{(0)}\oplus {\mathcal {O}}_{E_v}e_v^{(1)}$
. For
$A={\mathcal {O}}_{E_v}e_v^{(0)}\oplus {\mathcal {O}}_{E_v}e_v^{(1)}$
. For
![]() $x=(x_1,x_2)\in V(E_v)-V^\sharp (E_v) ,$
let
$x=(x_1,x_2)\in V(E_v)-V^\sharp (E_v) ,$
let
By [Reference YuanYZ18, Lemma 9.2],
![]() $ \varphi $
extends to a Schwartz function on
$ \varphi $
extends to a Schwartz function on
![]() $ V(E_v)$
such that
$ V(E_v)$
such that
![]() $c(1,1_{A})-2 \varphi (0)=2\log |{\mathrm {Diff}}_v|_{F_v}$
. It is enough to extend
$c(1,1_{A})-2 \varphi (0)=2\log |{\mathrm {Diff}}_v|_{F_v}$
. It is enough to extend
![]() $\varphi (x) 1_{{ \varpi _{E_v}{\mathcal {O}}_{E_v} e_v^{(1)} } } (x_2)-\phi _v'(x)$
to a Schwartz function on
$\varphi (x) 1_{{ \varpi _{E_v}{\mathcal {O}}_{E_v} e_v^{(1)} } } (x_2)-\phi _v'(x)$
to a Schwartz function on
![]() $ V(E_v)$
, and show that the twice of its value at
$ V(E_v)$
, and show that the twice of its value at
![]() $0$
is
$0$
is
![]() $c(1,1_{A})-c(1,\phi _v) $
. First,
$c(1,1_{A})-c(1,\phi _v) $
. First,
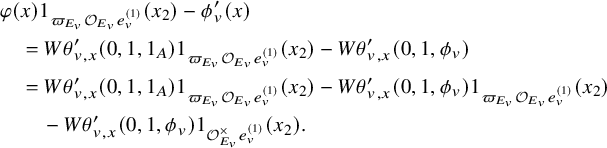 $$ \begin{align*} &\varphi(x) 1_{{ \varpi_{E_v}{\mathcal{O}}_{E_v} e_v^{(1)} } } (x_2)-\phi_v'(x)\\& \quad = {W\theta}_{v,x} '(0, 1, 1_{A}) 1_{{ \varpi_{E_v}{\mathcal{O}}_{E_v} e_v^{(1)} } } (x_2)- {W\theta}_{v,x} '(0, 1, \phi_v)\\& \quad ={W\theta}_{v,x} '(0, 1, 1_{A}) 1_{{ \varpi_{E_v}{\mathcal{O}}_{E_v} e_v^{(1)} } } (x_2)- {W\theta}_{v,x} '(0, 1, \phi_v)1_{{ \varpi_{E_v}{\mathcal{O}}_{E_v} e_v^{(1)} } } (x_2) \\& \qquad -{W\theta}_{v,x} '(0, 1, \phi_v)1_{{ {\mathcal{O}}_{E_v}^\times e_v^{(1)} } } (x_2). \end{align*} $$
$$ \begin{align*} &\varphi(x) 1_{{ \varpi_{E_v}{\mathcal{O}}_{E_v} e_v^{(1)} } } (x_2)-\phi_v'(x)\\& \quad = {W\theta}_{v,x} '(0, 1, 1_{A}) 1_{{ \varpi_{E_v}{\mathcal{O}}_{E_v} e_v^{(1)} } } (x_2)- {W\theta}_{v,x} '(0, 1, \phi_v)\\& \quad ={W\theta}_{v,x} '(0, 1, 1_{A}) 1_{{ \varpi_{E_v}{\mathcal{O}}_{E_v} e_v^{(1)} } } (x_2)- {W\theta}_{v,x} '(0, 1, \phi_v)1_{{ \varpi_{E_v}{\mathcal{O}}_{E_v} e_v^{(1)} } } (x_2) \\& \qquad -{W\theta}_{v,x} '(0, 1, \phi_v)1_{{ {\mathcal{O}}_{E_v}^\times e_v^{(1)} } } (x_2). \end{align*} $$
By Lemma 3.1.2 and (5.3),
![]() ${W\theta }_{v,x} '(0, 1, \phi _v)1_{{ {\mathcal {O}}_{E_v}^\times e_v^{(1)} } } (x_2)$
extends to a Schwartz function on
${W\theta }_{v,x} '(0, 1, \phi _v)1_{{ {\mathcal {O}}_{E_v}^\times e_v^{(1)} } } (x_2)$
extends to a Schwartz function on
![]() $ V(E_v)$
. It is supported on
$ V(E_v)$
. It is supported on
![]() $\{x_2\in {\mathcal {O}}_{E_v}^\times e_v^{(1)}\} $
so that its value at 0 is 0. By (3.5), (3.21) and (5.2),
$\{x_2\in {\mathcal {O}}_{E_v}^\times e_v^{(1)}\} $
so that its value at 0 is 0. By (3.5), (3.21) and (5.2),
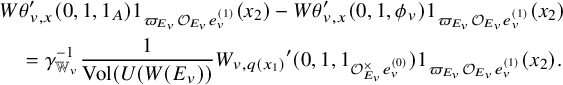 $$ \begin{align} & {W\theta}_{v,x} '(0, 1, 1_{A}) 1_{{ \varpi_{E_v}{\mathcal{O}}_{E_v} e_v^{(1)} } } (x_2)- {W\theta}_{v,x} '(0, 1, \phi_v)1_{{ \varpi_{E_v}{\mathcal{O}}_{E_v} e_v^{(1)} } } (x_2)\\& \quad = \gamma_{{\mathbb{W}}_v}^{-1}\frac{1}{ {\mathrm{Vol}}(U(W(E_v))} { W_{v,q(x_1)}}'(0,1,1_{ {\mathcal{O}}_{E_v}^\times e_v^{(0)}}) 1_{{ \varpi_{E_v}{\mathcal{O}}_{E_v} e_v^{(1)} } } (x_2).\nonumber \end{align} $$
$$ \begin{align} & {W\theta}_{v,x} '(0, 1, 1_{A}) 1_{{ \varpi_{E_v}{\mathcal{O}}_{E_v} e_v^{(1)} } } (x_2)- {W\theta}_{v,x} '(0, 1, \phi_v)1_{{ \varpi_{E_v}{\mathcal{O}}_{E_v} e_v^{(1)} } } (x_2)\\& \quad = \gamma_{{\mathbb{W}}_v}^{-1}\frac{1}{ {\mathrm{Vol}}(U(W(E_v))} { W_{v,q(x_1)}}'(0,1,1_{ {\mathcal{O}}_{E_v}^\times e_v^{(0)}}) 1_{{ \varpi_{E_v}{\mathcal{O}}_{E_v} e_v^{(1)} } } (x_2).\nonumber \end{align} $$
Here, we used that
![]() $L(s,\eta _v)=1$
due to the ramification of v in E. By Lemma 3.1.2, (5.8) extends to a Schwartz function on
$L(s,\eta _v)=1$
due to the ramification of v in E. By Lemma 3.1.2, (5.8) extends to a Schwartz function on
![]() $ V(E_v)$
.
$ V(E_v)$
.
Second, by a direct computation using (3.6), Lemma 3.1.2 and (5.2), we have
By [Reference Yuan, Zhang and ZhangYZZ13, p 23], which says
![]() ${\mathrm {Vol}}(U(W(E_v))=2|{\mathrm {Diff}}_v{\mathrm {Disc}}_v|_{F_v}^{1/2} $
, the lemma follows.
${\mathrm {Vol}}(U(W(E_v))=2|{\mathrm {Diff}}_v{\mathrm {Disc}}_v|_{F_v}^{1/2} $
, the lemma follows.
5.2.2 Generating series with automorphic Green functions
For
![]() $t\in F_{>0}$
, let
$t\in F_{>0}$
, let
![]() $Z_t(\phi )^{{\mathcal {L}},{\mathrm {aut}}}\in \widehat Z^{1}_{{\overline {\mathcal {L}}},{\mathbb {C}}}( {\mathcal {X}}_K)$
be the admissible extension of
$Z_t(\phi )^{{\mathcal {L}},{\mathrm {aut}}}\in \widehat Z^{1}_{{\overline {\mathcal {L}}},{\mathbb {C}}}( {\mathcal {X}}_K)$
be the admissible extension of
![]() $Z_t(\phi ) $
that is normalized at all finite places with respect to
$Z_t(\phi ) $
that is normalized at all finite places with respect to
![]() ${\mathcal {L}}$
and equals the automorphic Green function (4.10) at all infinite places. Comparing with (4.23), by Lemma 4.2.4 (1),
${\mathcal {L}}$
and equals the automorphic Green function (4.10) at all infinite places. Comparing with (4.23), by Lemma 4.2.4 (1),
only depends on
![]() $\phi $
, but not on K. For
$\phi $
, but not on K. For
![]() $g\in G({\mathbb {A}}_F )$
and
$g\in G({\mathbb {A}}_F )$
and
![]() $a\in {\mathbb {C}}$
, define
$a\in {\mathbb {C}}$
, define
![]() $z_t(g, \phi )_{{\mathfrak {e}}}^{{\mathcal {L}},{\mathrm {aut}}}$
(resp.
$z_t(g, \phi )_{{\mathfrak {e}}}^{{\mathcal {L}},{\mathrm {aut}}}$
(resp.
![]() $z(g, \phi )_{{\mathfrak {e}},a}^{{\mathcal {L}},{\mathrm {aut}}}$
) by the formula defining
$z(g, \phi )_{{\mathfrak {e}},a}^{{\mathcal {L}},{\mathrm {aut}}}$
) by the formula defining
![]() $z_t(g, \phi )_{{\mathfrak {e}}}^{{\overline {\mathcal {L}}}}$
(resp.
$z_t(g, \phi )_{{\mathfrak {e}}}^{{\overline {\mathcal {L}}}}$
(resp.
![]() $z(g, \phi )_{{\mathfrak {e}},a}^{{\overline {\mathcal {L}}}}$
) in Definition 4.4.13, replacing
$z(g, \phi )_{{\mathfrak {e}},a}^{{\overline {\mathcal {L}}}}$
) in Definition 4.4.13, replacing
![]() $Z_t(\phi )^{\overline {\mathcal {L}}}$
by
$Z_t(\phi )^{\overline {\mathcal {L}}}$
by
![]() $Z_t(\phi )^{{\mathcal {L}},{\mathrm {aut}}}$
. By Lemma 4.2.4 (2), (4.26) is equivalent to
$Z_t(\phi )^{{\mathcal {L}},{\mathrm {aut}}}$
. By Lemma 4.2.4 (2), (4.26) is equivalent to
Formally define the ‘t-th Fourier coefficient’ (and compare with Remark 4.4.14 (1))
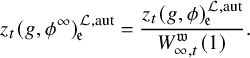 $$ \begin{align*}z_t(g, \phi^\infty)_{\mathfrak{e}}^{{\mathcal{L}},{\mathrm{aut}}}=\frac{z_t(g, \phi)_{\mathfrak{e}}^{{\mathcal{L}},{\mathrm{aut}}}}{W^{{\mathfrak{w}}}_{\infty, t}(1)}.\end{align*} $$
$$ \begin{align*}z_t(g, \phi^\infty)_{\mathfrak{e}}^{{\mathcal{L}},{\mathrm{aut}}}=\frac{z_t(g, \phi)_{\mathfrak{e}}^{{\mathcal{L}},{\mathrm{aut}}}}{W^{{\mathfrak{w}}}_{\infty, t}(1)}.\end{align*} $$
5.2.3 Arithmetic mixed Siegel-Weil formula
Let
![]() $\phi \in \overline {\mathcal {S}}\left ( {\mathbb {V}} \right ) ^{{{\widetilde K_\Lambda }}}$
. See Definition 4.4.11. Assume that
$\phi \in \overline {\mathcal {S}}\left ( {\mathbb {V}} \right ) ^{{{\widetilde K_\Lambda }}}$
. See Definition 4.4.11. Assume that
![]() $\phi $
is a pure tensor for simplicity. Define the automorphic form to appear in the formula as follows. For
$\phi $
is a pure tensor for simplicity. Define the automorphic form to appear in the formula as follows. For
![]() $K\in {{\widetilde K_\Lambda }}$
stabilizing
$K\in {{\widetilde K_\Lambda }}$
stabilizing
![]() $\phi $
, and
$\phi $
, and
![]() $K'\in {{\widetilde K_\Lambda }}$
containing K, let
$K'\in {{\widetilde K_\Lambda }}$
containing K, let
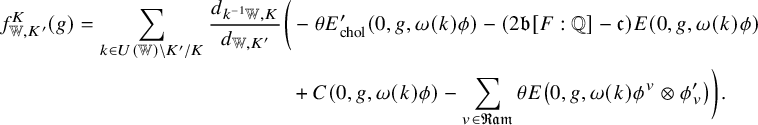 $$ \begin{align} \begin{aligned} f_{{\mathbb{W}},K'}^K(g)= \sum _{k\in U({\mathbb{W}})\backslash K' /K } \frac{d_{k^{-1}{\mathbb{W}},K}}{ d_{{\mathbb{W}},K'}} \bigg(&-{\theta E}^{\prime}_{{\mathrm{chol}}}(0,g,\omega(k)\phi)-( 2{{\mathfrak{b}}}[F:{\mathbb{Q}}] -{{\mathfrak{c}}})E(0,g,\omega(k)\phi) \\ &+C(0,g,\omega(k)\phi)- \sum_{v\in {{\mathfrak{Ram}}}} {\theta E} \left(0,g,\omega(k)\phi^{v}\otimes\phi_v'\right)\bigg). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} f_{{\mathbb{W}},K'}^K(g)= \sum _{k\in U({\mathbb{W}})\backslash K' /K } \frac{d_{k^{-1}{\mathbb{W}},K}}{ d_{{\mathbb{W}},K'}} \bigg(&-{\theta E}^{\prime}_{{\mathrm{chol}}}(0,g,\omega(k)\phi)-( 2{{\mathfrak{b}}}[F:{\mathbb{Q}}] -{{\mathfrak{c}}})E(0,g,\omega(k)\phi) \\ &+C(0,g,\omega(k)\phi)- \sum_{v\in {{\mathfrak{Ram}}}} {\theta E} \left(0,g,\omega(k)\phi^{v}\otimes\phi_v'\right)\bigg). \end{aligned} \end{align} $$
Here, the index set and coefficients are the ones in (5.4). We choose a representative k such that
![]() $k_v=1$
if
$k_v=1$
if
![]() $K_v=K^{\prime }_v$
. In particular,
$K_v=K^{\prime }_v$
. In particular,
![]() $\omega (k)(\phi ^{v}\otimes \phi _v')=\left ( \omega (k)\phi ^{v}\right )\otimes \phi _v'$
for v nonsplit in E, which is what we wrote
$\omega (k)(\phi ^{v}\otimes \phi _v')=\left ( \omega (k)\phi ^{v}\right )\otimes \phi _v'$
for v nonsplit in E, which is what we wrote
![]() $\omega (k)\phi ^{v}\otimes \phi _v'$
for. Inside the bracket, we have 4 automorphic forms in
$\omega (k)\phi ^{v}\otimes \phi _v'$
for. Inside the bracket, we have 4 automorphic forms in
![]() ${\mathcal {A}}_{{\mathrm {hol}}}(G,{\mathfrak {w}})$
. Here, we use the orthogonal decomposition
${\mathcal {A}}_{{\mathrm {hol}}}(G,{\mathfrak {w}})$
. Here, we use the orthogonal decomposition
![]() ${\mathbb {V}}={\mathbb {W}}\oplus V^\sharp ({\mathbb {A}}_E)$
to define
${\mathbb {V}}={\mathbb {W}}\oplus V^\sharp ({\mathbb {A}}_E)$
to define
![]() ${\theta E}^{\prime }_{{\mathrm {chol}}}(\dots )$
and
${\theta E}^{\prime }_{{\mathrm {chol}}}(\dots )$
and
![]() $C(\dots )$
, and for a given
$C(\dots )$
, and for a given
![]() $v\in {\mathfrak {Ram}}$
, we use the orthogonal decomposition
$v\in {\mathfrak {Ram}}$
, we use the orthogonal decomposition
![]() $ V=W\oplus V^\sharp $
as in (5.6) to define
$ V=W\oplus V^\sharp $
as in (5.6) to define
![]() $ {\theta E} \left (\dots \right )$
. See 3.2.1, 3.3.1 and 3.3.3 for their definitions. In particular,
$ {\theta E} \left (\dots \right )$
. See 3.2.1, 3.3.1 and 3.3.3 for their definitions. In particular,
![]() $f_{{\mathbb {W}},K'}^K\in {\mathcal {A}}_{{\mathrm {hol}}}(G,{\mathfrak {w}})$
. Finally, the constant
$f_{{\mathbb {W}},K'}^K\in {\mathcal {A}}_{{\mathrm {hol}}}(G,{\mathfrak {w}})$
. Finally, the constant
![]() ${\mathfrak {b}}$
is as in (3.30),
${\mathfrak {b}}$
is as in (3.30),
![]() ${\mathfrak {c}}$
is as in (3.15) and the term
${\mathfrak {c}}$
is as in (3.15) and the term
![]() $2{{\mathfrak {b}}}[F:{\mathbb {Q}}] -{{\mathfrak {c}}}$
appears in both (3.31) and (4.25).
$2{{\mathfrak {b}}}[F:{\mathbb {Q}}] -{{\mathfrak {c}}}$
appears in both (3.31) and (4.25).
Remark 5.2.4. The bracketed automorphic form indexed by
![]() $k\in U({\mathbb {W}})\backslash K' /K$
on the right-hand side of (5.9) is independent of the choice of k. Indeed, the 4th automorphic form
$k\in U({\mathbb {W}})\backslash K' /K$
on the right-hand side of (5.9) is independent of the choice of k. Indeed, the 4th automorphic form
![]() $ {\theta E} \left (0,g,\omega (k)\phi ^{v}\otimes \phi _v'\right ) $
is independent of the choice of k, by the
$ {\theta E} \left (0,g,\omega (k)\phi ^{v}\otimes \phi _v'\right ) $
is independent of the choice of k, by the
![]() $K^v$
-invariance of
$K^v$
-invariance of
![]() $\phi ^v$
and the mixed Siegel-Weil formula (3.19). By (3.31), for
$\phi ^v$
and the mixed Siegel-Weil formula (3.19). By (3.31), for
![]() $t\in F_{>0}$
, the
$t\in F_{>0}$
, the
![]() $\psi _t$
-Whittaker function of the rest 3 terms becomes
$\psi _t$
-Whittaker function of the rest 3 terms becomes
Then the independence of the choice of k follows from (3.10), (3.14) and (3.36). Then the independence of the choice of k follows from the automorphy.
Theorem 5.2.5. Let
![]() $\phi \in \overline {\mathcal {S}}\left ( {\mathbb {V}} \right ) ^{{{\widetilde K_\Lambda }}}$
be a pure tensor such that
$\phi \in \overline {\mathcal {S}}\left ( {\mathbb {V}} \right ) ^{{{\widetilde K_\Lambda }}}$
be a pure tensor such that
![]() $\phi _v=1_{\Lambda _v}$
for every finite place v of F nonsplit in E. Let
$\phi _v=1_{\Lambda _v}$
for every finite place v of F nonsplit in E. Let
![]() $K\in {{\widetilde K_\Lambda }}$
stabilize
$K\in {{\widetilde K_\Lambda }}$
stabilize
![]() $\phi $
. For
$\phi $
. For
![]() $t\in F_{>0}$
and
$t\in F_{>0}$
and
![]() $g\in P\left ({\mathbb {A}}_{F,{{\mathfrak {Ram}}} }\right ) G\left ({\mathbb {A}}_F^{{{\mathfrak {Ram}}} \cup \infty }\right ) $
, we have
$g\in P\left ({\mathbb {A}}_{F,{{\mathfrak {Ram}}} }\right ) G\left ({\mathbb {A}}_F^{{{\mathfrak {Ram}}} \cup \infty }\right ) $
, we have
where the arithmetic intersection on the left-hand side is taken on
![]() ${\mathcal {X}}_K$
, and
${\mathcal {X}}_K$
, and
![]() $ f_{{\mathbb {W}},{K_\Lambda },t}^{K,\infty }$
is the t-th Fourier coefficient of
$ f_{{\mathbb {W}},{K_\Lambda },t}^{K,\infty }$
is the t-th Fourier coefficient of
![]() $f_{{\mathbb {W}},{K_\Lambda }}^K$
. See 2.7.
$f_{{\mathbb {W}},{K_\Lambda }}^K$
. See 2.7.
Theorem 5.2.5 will be proved in (the end of) Section 6.
Remark 5.2.6. (1) By the projection formula, given
![]() $\phi $
and
$\phi $
and
![]() $K'$
, the truth of (5.10) does not depend on the choice of K (stabilizing the given
$K'$
, the truth of (5.10) does not depend on the choice of K (stabilizing the given
![]() $\phi $
).
$\phi $
).
(2) We use
![]() $\pi _{_K,_{K'}}^{*}{\mathcal {P}}_{{\mathbb {W}},K'} $
with
$\pi _{_K,_{K'}}^{*}{\mathcal {P}}_{{\mathbb {W}},K'} $
with
![]() $K'=K_{\Lambda }$
, instead of the more natural CM cycle
$K'=K_{\Lambda }$
, instead of the more natural CM cycle
![]() ${\mathcal {P}}_{{\mathbb {W}},K}$
(i.e.,
${\mathcal {P}}_{{\mathbb {W}},K}$
(i.e.,
![]() $K'=K$
), in order to apply Corollary A.2.6 to avoid computing normalized admissible extensions. (One may expect to reduce the whole Theorem 5.2.5 to the level
$K'=K$
), in order to apply Corollary A.2.6 to avoid computing normalized admissible extensions. (One may expect to reduce the whole Theorem 5.2.5 to the level
![]() $K_\Lambda $
by the projection formula. However, this is not possible due to Remark 4.1.6.)
$K_\Lambda $
by the projection formula. However, this is not possible due to Remark 4.1.6.)
(3) We can also consider Theorem 5.2.5 for
![]() $K'=K$
. Taking advantage of Theorem 4.4.21, the only difficulty in proving Theorem 5.2.5 for
$K'=K$
. Taking advantage of Theorem 4.4.21, the only difficulty in proving Theorem 5.2.5 for
![]() $K'=K$
is computing normalized admissible extensions at split place. By considering admissible 1-cycles, the difficulty could be solved as in [Reference Yuan, Zhang and ZhangYZZ13, 8.5.1]. Note that we do not need Assumption 5.4 in loc. cit. Rather we will get an extra Eisenstein series.
$K'=K$
is computing normalized admissible extensions at split place. By considering admissible 1-cycles, the difficulty could be solved as in [Reference Yuan, Zhang and ZhangYZZ13, 8.5.1]. Note that we do not need Assumption 5.4 in loc. cit. Rather we will get an extra Eisenstein series.
5.2.4 Proof of Theorem 4.4.21
Assuming Theorem 5.2.5, we prove Theorem 4.4.21 as follows. Recall that as we have discussed immediately after Theorem 4.4.21, that (4.28) and (4.29) of Theorem 4.4.21 are equivalent. We will prove (4.28), assuming that
![]() $\phi $
is a pure tensor such that
$\phi $
is a pure tensor such that
![]() $\phi _{v}=1_{\Lambda _v} $
for every finite place v nonsplit in E (so that Theorem 5.2.5 applies to
$\phi _{v}=1_{\Lambda _v} $
for every finite place v nonsplit in E (so that Theorem 5.2.5 applies to
![]() $\phi $
). So (4.29) holds. It follows from Definition 4.4.18 that (4.29) holds for
$\phi $
). So (4.29) holds. It follows from Definition 4.4.18 that (4.29) holds for
![]() $ \omega (g)\phi $
with
$ \omega (g)\phi $
with
![]() $g\in {\mathbb {G}}^\infty $
. Thus, Theorem 4.4.21 holds by the definition of
$g\in {\mathbb {G}}^\infty $
. Thus, Theorem 4.4.21 holds by the definition of
![]() $ \overline {\mathcal {S}}\left ( {\mathbb {V}} \right ) ^{{{\widetilde K_\Lambda }}}_{\mathfrak {Ram}}$
above it.
$ \overline {\mathcal {S}}\left ( {\mathbb {V}} \right ) ^{{{\widetilde K_\Lambda }}}_{\mathfrak {Ram}}$
above it.
So now we assume that
![]() $\phi $
is a pure tensor such that
$\phi $
is a pure tensor such that
![]() $\phi _{v}=1_{\Lambda _v} $
for every finite place v nonsplit in E and want to prove (4.28); that is,
$\phi _{v}=1_{\Lambda _v} $
for every finite place v nonsplit in E and want to prove (4.28); that is,
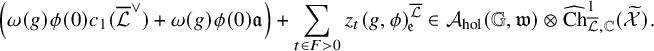 $$ \begin{align} \left(\omega(g )\phi(0) c_1(\overline {\mathcal{L}}^\vee)+ \omega(g)\phi(0) {\mathfrak{a}} \right)+\sum_{t\in {F>0}}z_t(g ,\phi )_{\mathfrak{e}}^{\overline{\mathcal{L}}} \in {\mathcal{A}}_{{\mathrm{hol}}}({\mathbb{G}},{\mathfrak{w}}) \otimes\widehat {\mathrm{Ch}}^{1}_{{\overline{\mathcal{L}}},{\mathbb{C}}}(\widetilde{\mathcal{X}}). \end{align} $$
$$ \begin{align} \left(\omega(g )\phi(0) c_1(\overline {\mathcal{L}}^\vee)+ \omega(g)\phi(0) {\mathfrak{a}} \right)+\sum_{t\in {F>0}}z_t(g ,\phi )_{\mathfrak{e}}^{\overline{\mathcal{L}}} \in {\mathcal{A}}_{{\mathrm{hol}}}({\mathbb{G}},{\mathfrak{w}}) \otimes\widehat {\mathrm{Ch}}^{1}_{{\overline{\mathcal{L}}},{\mathbb{C}}}(\widetilde{\mathcal{X}}). \end{align} $$
Let
![]() $K\in \widetilde K_\Lambda $
such that
$K\in \widetilde K_\Lambda $
such that
![]() $\phi $
is K-invariant. Let
$\phi $
is K-invariant. Let
![]() $ f_{{\mathbb {W}},K_\Lambda ,0}^{K} $
be the
$ f_{{\mathbb {W}},K_\Lambda ,0}^{K} $
be the
![]() $0$
-th Whittaker coefficient of
$0$
-th Whittaker coefficient of
![]() $f_{{\mathbb {W}},K_\Lambda }^{K}$
. Let
$f_{{\mathbb {W}},K_\Lambda }^{K}$
. Let
![]() $ A(\cdot , \phi )_K$
be the
$ A(\cdot , \phi )_K$
be the
![]() ${\mathbb {C}}$
-valued function on
${\mathbb {C}}$
-valued function on
![]() $G({\mathbb {A}})$
, understood as valued
$G({\mathbb {A}})$
, understood as valued
![]() $\widehat {\mathrm {Ch}}^{1}_{{\overline {\mathcal {L}}},{\mathbb {C}}}(\widetilde {\mathcal {X}})$
via
$\widehat {\mathrm {Ch}}^{1}_{{\overline {\mathcal {L}}},{\mathbb {C}}}(\widetilde {\mathcal {X}})$
via
![]() $ {\mathbb {C}}\hookrightarrow \widehat {\mathrm {Ch}}^{1}_{{\overline {\mathcal {L}}},{\mathbb {C}}}(\widetilde {\mathcal {X}})$
as in (4.22), defined by
$ {\mathbb {C}}\hookrightarrow \widehat {\mathrm {Ch}}^{1}_{{\overline {\mathcal {L}}},{\mathbb {C}}}(\widetilde {\mathcal {X}})$
as in (4.22), defined by
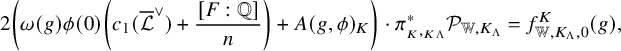 $$ \begin{align*} 2 \left( \omega(g )\phi(0) \left( c_1(\overline {\mathcal{L}}^\vee)+\frac{[F:{\mathbb{Q}}]}{n}\right) + A(g,\phi) _K\right) \cdot \pi_{_K,{_K}_{\Lambda}}^{*}{\mathcal{P}}_{{\mathbb{W}},K_\Lambda} = f_{{\mathbb{W}},K_\Lambda,0}^{K}(g), \end{align*} $$
$$ \begin{align*} 2 \left( \omega(g )\phi(0) \left( c_1(\overline {\mathcal{L}}^\vee)+\frac{[F:{\mathbb{Q}}]}{n}\right) + A(g,\phi) _K\right) \cdot \pi_{_K,{_K}_{\Lambda}}^{*}{\mathcal{P}}_{{\mathbb{W}},K_\Lambda} = f_{{\mathbb{W}},K_\Lambda,0}^{K}(g), \end{align*} $$
that is,
 $$ \begin{align} A(g,\phi) _K = \frac{1}{2\deg \pi_{_K,{_K}_{\Lambda}} }\left( f_{{\mathbb{W}},K_\Lambda,0}^{K}(g)- 2 \omega(g )\phi(0) \left( c_1(\overline {\mathcal{L}}^\vee)+\frac{[F:{\mathbb{Q}}]}{n}\right) \cdot \pi_{_K,{_K}_{\Lambda}}^{*}{\mathcal{P}}_{{\mathbb{W}},K_\Lambda} \right). \end{align} $$
$$ \begin{align} A(g,\phi) _K = \frac{1}{2\deg \pi_{_K,{_K}_{\Lambda}} }\left( f_{{\mathbb{W}},K_\Lambda,0}^{K}(g)- 2 \omega(g )\phi(0) \left( c_1(\overline {\mathcal{L}}^\vee)+\frac{[F:{\mathbb{Q}}]}{n}\right) \cdot \pi_{_K,{_K}_{\Lambda}}^{*}{\mathcal{P}}_{{\mathbb{W}},K_\Lambda} \right). \end{align} $$
By Lemma 4.3.8 (with G and
![]() $G({\mathbb {A}})$
replaced by
$G({\mathbb {A}})$
replaced by
![]() ${\mathbb {G}}$
) and Theorem 5.2.5,
${\mathbb {G}}$
) and Theorem 5.2.5,
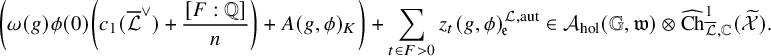 $$ \begin{align*} \left(\omega(g )\phi(0) \left( c_1(\overline {\mathcal{L}}^\vee)+\frac{[F:{\mathbb{Q}}]}{n}\right) + A(g,\phi)_K \right)+\sum_{t\in {F>0}}z_t(g ,\phi )_{\mathfrak{e}}^{{\mathcal{L}},{\mathrm{aut}}} \in {\mathcal{A}}_{{\mathrm{hol}}}({\mathbb{G}},{\mathfrak{w}}) \otimes\widehat {\mathrm{Ch}}^{1}_{{\overline{\mathcal{L}}},{\mathbb{C}}}(\widetilde{\mathcal{X}}). \end{align*} $$
$$ \begin{align*} \left(\omega(g )\phi(0) \left( c_1(\overline {\mathcal{L}}^\vee)+\frac{[F:{\mathbb{Q}}]}{n}\right) + A(g,\phi)_K \right)+\sum_{t\in {F>0}}z_t(g ,\phi )_{\mathfrak{e}}^{{\mathcal{L}},{\mathrm{aut}}} \in {\mathcal{A}}_{{\mathrm{hol}}}({\mathbb{G}},{\mathfrak{w}}) \otimes\widehat {\mathrm{Ch}}^{1}_{{\overline{\mathcal{L}}},{\mathbb{C}}}(\widetilde{\mathcal{X}}). \end{align*} $$
Then by Lemma 4.2.4 (2), we have
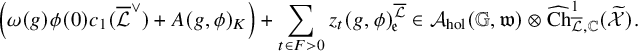 $$ \begin{align} \left(\omega(g )\phi(0) c_1(\overline {\mathcal{L}}^\vee)+ A(g,\phi)_K \right)+\sum_{t\in {F>0}}z_t(g ,\phi )_{\mathfrak{e}}^{\overline{\mathcal{L}}} \in {\mathcal{A}}_{{\mathrm{hol}}}({\mathbb{G}},{\mathfrak{w}}) \otimes\widehat {\mathrm{Ch}}^{1}_{{\overline{\mathcal{L}}},{\mathbb{C}}}(\widetilde{\mathcal{X}}). \end{align} $$
$$ \begin{align} \left(\omega(g )\phi(0) c_1(\overline {\mathcal{L}}^\vee)+ A(g,\phi)_K \right)+\sum_{t\in {F>0}}z_t(g ,\phi )_{\mathfrak{e}}^{\overline{\mathcal{L}}} \in {\mathcal{A}}_{{\mathrm{hol}}}({\mathbb{G}},{\mathfrak{w}}) \otimes\widehat {\mathrm{Ch}}^{1}_{{\overline{\mathcal{L}}},{\mathbb{C}}}(\widetilde{\mathcal{X}}). \end{align} $$
Thus, (5.11) is reduced to the following lemma, whose proof requires some preparations.
Lemma 5.2.7. We have
![]() $ A(g, \phi )_K = \omega (g)\phi (0) {\mathfrak {a}}.$
$ A(g, \phi )_K = \omega (g)\phi (0) {\mathfrak {a}}.$
To determine
![]() $ A(g, \phi )_K$
, one a priori needs to compute
$ A(g, \phi )_K$
, one a priori needs to compute
![]() $ f_{{\mathbb {W}},K_\Lambda ,0}^{K}(g) $
, which could be complicated. Indeed, by (3.20) for
$ f_{{\mathbb {W}},K_\Lambda ,0}^{K}(g) $
, which could be complicated. Indeed, by (3.20) for
![]() $t=0$
and Lemma 3.3.9 (1) (2), we have
$t=0$
and Lemma 3.3.9 (1) (2), we have
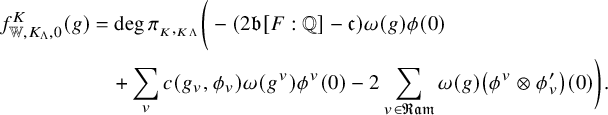 $$ \begin{align} \begin{aligned} f_{{\mathbb{W}},K_\Lambda,0}^{K}(g) & = \deg \pi_{_K,{_K}_{\Lambda}} \bigg(-( 2{{\mathfrak{b}}}[F:{\mathbb{Q}}] -{{\mathfrak{c}}}) \omega ( g)\phi (0) \\&\quad +\sum_{v }c(g_v,\phi_v)\omega ( g^v)\phi^v (0) - 2\sum_{v\in {{\mathfrak{Ram}}}} \omega(g) \left( \phi^{v}\otimes\phi_v'\right) (0) \bigg). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} f_{{\mathbb{W}},K_\Lambda,0}^{K}(g) & = \deg \pi_{_K,{_K}_{\Lambda}} \bigg(-( 2{{\mathfrak{b}}}[F:{\mathbb{Q}}] -{{\mathfrak{c}}}) \omega ( g)\phi (0) \\&\quad +\sum_{v }c(g_v,\phi_v)\omega ( g^v)\phi^v (0) - 2\sum_{v\in {{\mathfrak{Ram}}}} \omega(g) \left( \phi^{v}\otimes\phi_v'\right) (0) \bigg). \end{aligned} \end{align} $$
The terms in the second line cause the complicatedness.
We take a different approach. We study the invariance properties of
![]() $ A(g, \phi )_K$
. We need a notation. Let
$ A(g, \phi )_K$
. We need a notation. Let
![]() $W_0({\mathbb {G}})$
be the space of
$W_0({\mathbb {G}})$
be the space of
![]() $\psi _0$
-Whittaker functions on
$\psi _0$
-Whittaker functions on
![]() ${\mathbb {G}}$
(i.e., smooth
${\mathbb {G}}$
(i.e., smooth
![]() ${\mathbb {C}}$
-valued functions f such that
${\mathbb {C}}$
-valued functions f such that
![]() $f(ng)=f(g) $
for
$f(ng)=f(g) $
for
![]() $ n\in N({\mathbb {A}})).$
Then
$ n\in N({\mathbb {A}})).$
Then
By (5.14) and Lemma 3.3.4 (2), we have
![]() $ f_{{\mathbb {W}},K_\Lambda ,0}^{K} \in W_0 ({\mathbb {G}})$
. Then by (5.12), we have
$ f_{{\mathbb {W}},K_\Lambda ,0}^{K} \in W_0 ({\mathbb {G}})$
. Then by (5.12), we have
![]() $A(g, \phi )_K\in W_0({\mathbb {G}}).$
For
$A(g, \phi )_K\in W_0({\mathbb {G}}).$
For
![]() $K'\in \widetilde K_\Lambda $
such that
$K'\in \widetilde K_\Lambda $
such that
![]() $\phi $
is
$\phi $
is
![]() $K'$
-invariant, by (5.13),
$K'$
-invariant, by (5.13),
![]() $A(g,\phi )_K-A(g,\phi )_{K'}\in {\mathcal {A}}_{{\mathrm {hol}}}({\mathbb {G}},{\mathfrak {w}})$
. Thus, by (5.15),
$A(g,\phi )_K-A(g,\phi )_{K'}\in {\mathcal {A}}_{{\mathrm {hol}}}({\mathbb {G}},{\mathfrak {w}})$
. Thus, by (5.15),
![]() $A(g,\phi )_K$
does not depend on K. Let us denote
$A(g,\phi )_K$
does not depend on K. Let us denote
![]() $A(g,\phi )_K$
by
$A(g,\phi )_K$
by
![]() $ A(g, \phi )$
.
$ A(g, \phi )$
.
Lemma 5.2.8.
(1) For
![]() $g'\in {\mathbb {G}}^\infty $
,
$g'\in {\mathbb {G}}^\infty $
,
![]() $ A(gg', \phi )=A(g ,\omega (g')\phi )$
.
$ A(gg', \phi )=A(g ,\omega (g')\phi )$
.
(2) For
![]() $h\in K_{\Lambda }$
,
$h\in K_{\Lambda }$
,
![]() $ A(g,\omega (h)\phi )=A(g,\phi )$
.
$ A(g,\omega (h)\phi )=A(g,\phi )$
.
Proof. (1) Since
![]() $ A(g,\phi ), \omega (g )\phi (0)\in W_0({\mathbb {G}})$
,
$ A(g,\phi ), \omega (g )\phi (0)\in W_0({\mathbb {G}})$
,
Claim:
 $$ \begin{align} B(g,\phi)+\sum_{x\in {\mathbb{V}}^\infty,\ q(x)\in F^\times} \omega(g^\infty)\phi^\infty ( x) [Z(x,g_\infty)_{\mathfrak{t}}^{\overline{\mathcal{L}}}] W^{{\mathfrak{w}}}_{\infty, q(x)}(g_\infty) \in {\mathcal{A}} ({\mathbb{G}},{\mathfrak{w}}) \otimes\widehat {\mathrm{Ch}}^{1}_{{\overline{\mathcal{L}}},{\mathbb{C}}}(\widetilde{\mathcal{X}}). \end{align} $$
$$ \begin{align} B(g,\phi)+\sum_{x\in {\mathbb{V}}^\infty,\ q(x)\in F^\times} \omega(g^\infty)\phi^\infty ( x) [Z(x,g_\infty)_{\mathfrak{t}}^{\overline{\mathcal{L}}}] W^{{\mathfrak{w}}}_{\infty, q(x)}(g_\infty) \in {\mathcal{A}} ({\mathbb{G}},{\mathfrak{w}}) \otimes\widehat {\mathrm{Ch}}^{1}_{{\overline{\mathcal{L}}},{\mathbb{C}}}(\widetilde{\mathcal{X}}). \end{align} $$
Indeed, by Theorem 4.2.7, the difference between the generating series in (5.13) and (5.16) equals
(This is the analog of (4.27).) Then the claim follows from (5.13).
Now we prove (1). Apply (5.16) in two ways: first, replace
![]() $\phi $
by
$\phi $
by
![]() $\omega (g')\phi $
and call the resulted series
$\omega (g')\phi $
and call the resulted series
![]() $S_1$
; second, replace g by
$S_1$
; second, replace g by
![]() $gg'$
and call the resulted series
$gg'$
and call the resulted series
![]() $S_2$
. Then
$S_2$
. Then
![]() $S_1,S_2\in {\mathcal {A}} ({\mathbb {G}},{\mathfrak {w}}) \otimes \widehat {\mathrm {Ch}}^{1}_{{\overline {\mathcal {L}}},{\mathbb {C}}}(\widetilde {\mathcal {X}}) $
. So
$S_1,S_2\in {\mathcal {A}} ({\mathbb {G}},{\mathfrak {w}}) \otimes \widehat {\mathrm {Ch}}^{1}_{{\overline {\mathcal {L}}},{\mathbb {C}}}(\widetilde {\mathcal {X}}) $
. So
Thus, it must be 0 by (5.15). This gives (1).
(2) By Lemma 4.4.12, after the ‘right translation by h’, (5.13) becomes
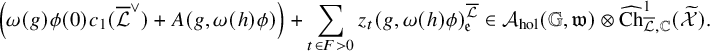 $$ \begin{align*} \left(\omega(g ) \phi(0) c_1(\overline {\mathcal{L}}^\vee)+ A(g,\omega(h)\phi) \right)+\sum_{t\in {F>0}}z_t(g ,\omega(h)\phi )_{\mathfrak{e}}^{\overline{\mathcal{L}}} \in {\mathcal{A}}_{{\mathrm{hol}}}({\mathbb{G}},{\mathfrak{w}}) \otimes\widehat {\mathrm{Ch}}^{1}_{{\overline{\mathcal{L}}},{\mathbb{C}}}(\widetilde{\mathcal{X}}). \end{align*} $$
$$ \begin{align*} \left(\omega(g ) \phi(0) c_1(\overline {\mathcal{L}}^\vee)+ A(g,\omega(h)\phi) \right)+\sum_{t\in {F>0}}z_t(g ,\omega(h)\phi )_{\mathfrak{e}}^{\overline{\mathcal{L}}} \in {\mathcal{A}}_{{\mathrm{hol}}}({\mathbb{G}},{\mathfrak{w}}) \otimes\widehat {\mathrm{Ch}}^{1}_{{\overline{\mathcal{L}}},{\mathbb{C}}}(\widetilde{\mathcal{X}}). \end{align*} $$
(This is similar to Lemma 4.4.15.) Since (5.13) holds with
![]() $\phi $
replaced by
$\phi $
replaced by
![]() $\omega (h) \phi $
, taking the difference, we have
$\omega (h) \phi $
, taking the difference, we have
![]() $ A(g,\omega (h)\phi )-A(g,\phi )\in {\mathcal {A}}_{{\mathrm {hol}}}({\mathbb {G}},{\mathfrak {w}})$
. It is 0 by (5.15).
$ A(g,\omega (h)\phi )-A(g,\phi )\in {\mathcal {A}}_{{\mathrm {hol}}}({\mathbb {G}},{\mathfrak {w}})$
. It is 0 by (5.15).
To prove Lemma 5.2.7, we need a final ingredient, whose proof is easy and left to the reader.
Lemma 5.2.9. For v split in E, identify
![]() ${\mathbb {W}}_v=E_v $
and
${\mathbb {W}}_v=E_v $
and
![]() $K_{\Lambda ,v}\cap U({\mathbb {W}}_v)={\mathcal {O}}_{E_v}^\times $
. Then
$K_{\Lambda ,v}\cap U({\mathbb {W}}_v)={\mathcal {O}}_{E_v}^\times $
. Then
![]() ${\mathcal {S}}({\mathbb {W}}_v)^{K_{\Lambda ,v}\cap U({\mathbb {W}}_v)}$
is spanned by
${\mathcal {S}}({\mathbb {W}}_v)^{K_{\Lambda ,v}\cap U({\mathbb {W}}_v)}$
is spanned by
![]() $f_a$
’s, where
$f_a$
’s, where
![]() $f_a(x):= 1_{{\mathcal {O}}_{E_v}}( xa), a\in E_v^\times $
.
$f_a(x):= 1_{{\mathcal {O}}_{E_v}}( xa), a\in E_v^\times $
.
Proof of Lemma 5.2.7.
We have some reduction steps about
![]() $\phi $
. By Lemma 5.2.8 (2), we may assume that
$\phi $
. By Lemma 5.2.8 (2), we may assume that
![]() $\phi $
is
$\phi $
is
![]() $K_\Lambda $
-invariant. In particular, for v split in E,
$K_\Lambda $
-invariant. In particular, for v split in E,
![]() $\phi _v$
is
$\phi _v$
is
![]() $K_{\Lambda ,v}\cap U({\mathbb {W}}_v)$
-invariant. Identify
$K_{\Lambda ,v}\cap U({\mathbb {W}}_v)$
-invariant. Identify
![]() ${\mathbb {W}}_v=E_v$
and
${\mathbb {W}}_v=E_v$
and
![]() $q={\mathrm {Nm}}$
. By Lemma 5.2.8 (1), Lemma 5.2.9 and the first Weil representation formula in 2.8, we may further assume that
$q={\mathrm {Nm}}$
. By Lemma 5.2.8 (1), Lemma 5.2.9 and the first Weil representation formula in 2.8, we may further assume that
![]() $\phi _v=\phi _{v,1}\otimes \phi _{v,2}$
where
$\phi _v=\phi _{v,1}\otimes \phi _{v,2}$
where
![]() $\phi _{v,1}=1_{{\mathcal {O}}_{E_v}}$
and
$\phi _{v,1}=1_{{\mathcal {O}}_{E_v}}$
and
![]() $\phi _{v,2}\in {\mathcal {S}}\left ( V^\sharp (E_v)\right )$
(recall that
$\phi _{v,2}\in {\mathcal {S}}\left ( V^\sharp (E_v)\right )$
(recall that
![]() $V^\sharp (E_v)$
is the orthogonal complement of
$V^\sharp (E_v)$
is the orthogonal complement of
![]() ${\mathbb {W}}_v$
).
${\mathbb {W}}_v$
).
Now we look at
![]() $f_{{\mathbb {W}},K_\Lambda ,0}^{K}(g)$
given by (5.14). By the definition (3.23) and Lemma 3.1.3 (2) (3),
$f_{{\mathbb {W}},K_\Lambda ,0}^{K}(g)$
given by (5.14). By the definition (3.23) and Lemma 3.1.3 (2) (3),
![]() $c(g_v,\phi _v)=0$
unless
$c(g_v,\phi _v)=0$
unless
![]() $v\in {\mathfrak {Ram}}$
or v split in E (by the same argument as in Lemma 3.3.4). By Lemma 5.2.8 (1), we may assume
$v\in {\mathfrak {Ram}}$
or v split in E (by the same argument as in Lemma 3.3.4). By Lemma 5.2.8 (1), we may assume
![]() $g^\infty =1$
. Then by Lemma 3.3.7, Lemma 5.2.2, Lemma 5.2.3,
$g^\infty =1$
. Then by Lemma 3.3.7, Lemma 5.2.2, Lemma 5.2.3,
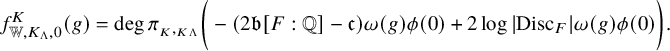 $$ \begin{align*} f_{{\mathbb{W}},K_\Lambda,0}^{K}(g) =\deg \pi_{_K,{_K}_{\Lambda}} \bigg(-( 2{{\mathfrak{b}}}[F:{\mathbb{Q}}] -{{\mathfrak{c}}}) \omega ( g)\phi (0) +2\log|{\mathrm{Disc}}_F| \omega ( g)\phi (0) \bigg). \end{align*} $$
$$ \begin{align*} f_{{\mathbb{W}},K_\Lambda,0}^{K}(g) =\deg \pi_{_K,{_K}_{\Lambda}} \bigg(-( 2{{\mathfrak{b}}}[F:{\mathbb{Q}}] -{{\mathfrak{c}}}) \omega ( g)\phi (0) +2\log|{\mathrm{Disc}}_F| \omega ( g)\phi (0) \bigg). \end{align*} $$
Since
![]() $c_1(\overline {\mathcal {L}}_{K }^\vee )=\pi _{_K,{_K}_{\Lambda }}^{*}{\mathcal {L}}_{K_\Lambda }^\vee $
, by the projection formula,
$c_1(\overline {\mathcal {L}}_{K }^\vee )=\pi _{_K,{_K}_{\Lambda }}^{*}{\mathcal {L}}_{K_\Lambda }^\vee $
, by the projection formula,
Now by the definition of
![]() $ A(g, \phi )_K$
in (5.12) and the definition of
$ A(g, \phi )_K$
in (5.12) and the definition of
![]() ${\mathfrak {a}}$
in the first line of (4.25), the lemma follows.
${\mathfrak {a}}$
in the first line of (4.25), the lemma follows.
5.3 Generalizations and applications
5.3.1 Higher codimensions
Based on their modularity result for generating series of special divisors, Yuan, S. Zhang and W. Zhang [Reference Yuan, Zhang and ZhangYZZ09] proved the modularity for higher-codimensional special cycles inductively, assuming the convergence. One would like to mimic their proof in the arithmetic situation. Then one needs a modularity theorem for divisors with general level structures and test functions, even if the given test function is very good. Thus, the generality of our results is necessary toward modularity in the arithmetic situation in higher codimensions.
In the codimension n case (i.e., for arithmetic 1-cycles), S. Zhang’s theory of admissible cycles is unconditional modulo vertical 1-cycles that are numerically trivial [Reference ZhangZha20]. Then the method in the current paper is still applicable to approach the modularity in the arithmetic situation.
5.3.2 Almost-self dual lattice
There is another lattice level structure at a finite place considered in [Reference Rapoport, Smithling and ZhangRSZ20], defined by an almost-self dual lattice. The integral model is not smooth, but is explicitly described in [Reference Liu, Tian, Xiao, Zhang and ZhuLTX+22]. We hope to include this level structure in a future work. In fact, if we also use admissible 1-cycles, our approach combined with a recent result of Z. Zhang [Reference ZhangZha21b, Theorem 14.6] is already applicable to prove the analog of Theorem 4.4.21, after replacing normalized admissible extensions of special divisors by the ‘admissible projections’ of the Kudla-Rapoport divisors at these new places (provided that they can also be suitably defined on our models). However, the difference between two extensions is not clear so far.
5.3.3 Faltings heights of Shimura varieties and Arithmetic Siegel-Weil formula
Following Kudla [Reference KudlaKud03, Reference KudlaKud04], we propose the arithmetic analog of the geometric Siegel Weil formula (4.11).
Problem 5.3.1. Match
![]() $c_1(\overline {\mathcal {L}})^n\cdot z(g, \phi )_{ {\mathfrak {a}}}^{{\mathcal {L}},\mathrm {Kud}}$
with a linear combination of
$c_1(\overline {\mathcal {L}})^n\cdot z(g, \phi )_{ {\mathfrak {a}}}^{{\mathcal {L}},\mathrm {Kud}}$
with a linear combination of
![]() $E(0,g, \phi )$
and
$E(0,g, \phi )$
and
![]() $ E'(0,g, \phi )$
(possibly up to some error terms).
$ E'(0,g, \phi )$
(possibly up to some error terms).
The modularity of
![]() $z(g, \phi )_{ {\mathfrak {a}}}^{{\mathcal {L}},\mathrm {Kud}}$
helps to attack this problem as follows. The constant term of
$z(g, \phi )_{ {\mathfrak {a}}}^{{\mathcal {L}},\mathrm {Kud}}$
helps to attack this problem as follows. The constant term of
![]() $c_1(\overline {\mathcal {L}})^n\cdot z(g, \phi )_{ {\mathfrak {a}}}^{{\mathcal {L}},\mathrm {Kud}}$
is indeed the Faltings height of
$c_1(\overline {\mathcal {L}})^n\cdot z(g, \phi )_{ {\mathfrak {a}}}^{{\mathcal {L}},\mathrm {Kud}}$
is indeed the Faltings height of
![]() ${\mathcal {X}}_{K}$
itself, while the non-constant terms are given by Faltings heights of Shimura subvarieties with the numbers in Definition 4.2.6. (Here, by the Faltings height of
${\mathcal {X}}_{K}$
itself, while the non-constant terms are given by Faltings heights of Shimura subvarieties with the numbers in Definition 4.2.6. (Here, by the Faltings height of
![]() ${\mathcal {X}}$
, we mean
${\mathcal {X}}$
, we mean
![]() $ \deg c_1(\overline {\mathcal {L}})^{n+1}$
.) There is clearly an inductive scheme to compute the Faltings heights/attack arithmetic Siegel-Weil formula, by applying the modularity of the generating series. Moreover, we only need to compute enough terms. This might enable us to avoid dealing with Shimura subvarieties of general level structures from the inductive steps. We can also use
$ \deg c_1(\overline {\mathcal {L}})^{n+1}$
.) There is clearly an inductive scheme to compute the Faltings heights/attack arithmetic Siegel-Weil formula, by applying the modularity of the generating series. Moreover, we only need to compute enough terms. This might enable us to avoid dealing with Shimura subvarieties of general level structures from the inductive steps. We can also use
![]() $ z(g, \phi )_{{\mathfrak {k}},{\mathfrak {a}} }^{{\overline {\mathcal {L}}}}$
to attack Problem 5.3.1, since by a direct computation,
$ z(g, \phi )_{{\mathfrak {k}},{\mathfrak {a}} }^{{\overline {\mathcal {L}}}}$
to attack Problem 5.3.1, since by a direct computation,
For quaternionic Shimura curves, Faltings heights are computed in [Reference Kudla, Rapoport and YangKRY06] [Reference YuanYua22]. For unitary Shimura varieties, in the case
![]() $F={\mathbb {Q}}$
, the Faltings height of
$F={\mathbb {Q}}$
, the Faltings height of
![]() ${\mathcal {X}}_{K_\Lambda }$
(for a different lattice
${\mathcal {X}}_{K_\Lambda }$
(for a different lattice
![]() $\Lambda $
) was computed in [Reference Bruinier and HowardBH21] using Borcherds’ theory. See [Reference Bruinier and HowardBH21] for other related results.
$\Lambda $
) was computed in [Reference Bruinier and HowardBH21] using Borcherds’ theory. See [Reference Bruinier and HowardBH21] for other related results.
5.3.4 Arithmetic theta lifting and Gross-Zagier type formula
Consider the Petersson inner product between the modular generating series of special divisors on the generic fiber and a cusp form f of G [Reference KudlaKud03, Reference KudlaKud04]. When
![]() $n=1$
, it is cohomological trivial and its Beilinson-Bloch height was studied in [Reference LiuLiu11a, Reference LiuLiu11b]. However, when
$n=1$
, it is cohomological trivial and its Beilinson-Bloch height was studied in [Reference LiuLiu11a, Reference LiuLiu11b]. However, when
![]() $n>1$
, the Picard group of
$n>1$
, the Picard group of
![]() ${\mathrm {Sh}}({\mathbb {V}})_K$
is CM by [Reference Murty and RamakrishnanMR92], so that the inner product is 0 in most cases after cohomological trivialization. Thus, it is necessary to consider arithmetic intersection pairing on an integral model (without cohomological trivialization).
${\mathrm {Sh}}({\mathbb {V}})_K$
is CM by [Reference Murty and RamakrishnanMR92], so that the inner product is 0 in most cases after cohomological trivialization. Thus, it is necessary to consider arithmetic intersection pairing on an integral model (without cohomological trivialization).
The arithmetic intersection pairing with our CM 1-cycle as in Theorem 5.2.5 is simply the Petersson inner product between (5.9) and f. Such a pairing appeared in the work of Gross and Zagier [Reference Gross and ZagierGZ86] and leads to their celebrated formula. We hope to get a Gross-Zagier type formula. In the case
![]() $F={\mathbb {Q}}$
and
$F={\mathbb {Q}}$
and
![]() $\phi ^\infty =1_{\Lambda }$
(for a different
$\phi ^\infty =1_{\Lambda }$
(for a different
![]() $\Lambda $
), a Gross-Zagier type formula was obtained in [Reference Bruinier, Howard and YangBHY15] and [Reference Bruinier, Howard, Kudla, Rapoport and YangBHK+20b]. See also [Reference Bruinier and YangBY09]. For general F and test functions as in our case, a general theory of Shimura-type integrals is to be developed.
$\Lambda $
), a Gross-Zagier type formula was obtained in [Reference Bruinier, Howard and YangBHY15] and [Reference Bruinier, Howard, Kudla, Rapoport and YangBHK+20b]. See also [Reference Bruinier and YangBY09]. For general F and test functions as in our case, a general theory of Shimura-type integrals is to be developed.
6 Intersections
In this section, we prove the arithmetic mixed Siegel-Weil formula (Theorem 5.2.5). First, we prove local analogs of the formula, under some regularity assumption which forces improper intersections to disappear. Then, to prove Theorem 5.2.5, we use a global argument involving admissibility of our arithmetic divisors and modularity on the generic fiber (more precisely, Lemma 4.3.6).
6.1 Proper intersections
In order to state the local analogs of the Arithmetic mixed Siegel-Weil formula (Proposition 6.1.4), we need some preliminaries.
We use the CM cycles in 5.1, as well as the notations there – in particular, the orthogonal decomposition
![]() ${\mathbb {V}}={\mathbb {W}}\oplus V^\sharp ({\mathbb {A}}_E). $
${\mathbb {V}}={\mathbb {W}}\oplus V^\sharp ({\mathbb {A}}_E). $
Definition 6.1.1. For a finite place v of F, a Schwartz function on
![]() ${\mathbb {V}}(E_v)$
is
${\mathbb {V}}(E_v)$
is
![]() ${\mathbb {W}}_v$
-regular if it is supported outside the orthogonal complement
${\mathbb {W}}_v$
-regular if it is supported outside the orthogonal complement
![]() ${\mathbb {W}}_v^\perp =V^\sharp (E_{v})$
.
${\mathbb {W}}_v^\perp =V^\sharp (E_{v})$
.
Let
![]() $\phi \in \overline {\mathcal {S}}\left ( {\mathbb {V}} \right ) $
be a pure tensor such that
$\phi \in \overline {\mathcal {S}}\left ( {\mathbb {V}} \right ) $
be a pure tensor such that
![]() $\phi _v=1_{\Lambda _v}$
for every finite place v nonsplit in E. Let
$\phi _v=1_{\Lambda _v}$
for every finite place v nonsplit in E. Let
![]() $K\in \widetilde K_\Lambda $
such that
$K\in \widetilde K_\Lambda $
such that
![]() $\phi $
is K-invariant.
$\phi $
is K-invariant.
We assume the following assumption throughout this subsection.
Assumption 6.1.2. There is a nonempty set R of places of F such that
![]() $\phi _v$
is
$\phi _v$
is
![]() ${\mathbb {W}}_v$
-regular for
${\mathbb {W}}_v$
-regular for
![]() $v\in R$
.
$v\in R$
.
Since
![]() $\phi _v=1_{\Lambda _v}$
for every finite place v nonsplit in E, R necessarily contains only places split in E.
$\phi _v=1_{\Lambda _v}$
for every finite place v nonsplit in E, R necessarily contains only places split in E.
As we have seen in the proof of Lemma 4.4.3, for a finite place v of E, there exists a finite unramified extension
![]() $N/E_v$
such that
$N/E_v$
such that
![]() ${\mathcal {X}}_{K ,{\mathcal {O}}_{N}} $
is (part of) a PEL moduli space, and the supersingular locus is thus defined and obviously independent of the choice of N. Let
${\mathcal {X}}_{K ,{\mathcal {O}}_{N}} $
is (part of) a PEL moduli space, and the supersingular locus is thus defined and obviously independent of the choice of N. Let
![]() $t\in F_{>0}$
.
$t\in F_{>0}$
.
Lemma 6.1.3. For
![]() $g\in P \left ({\mathbb {A}}_{F,R }\right ) G\left ( {\mathbb {A}}_F^{R }\right )$
, the supports of the Zariski closure of
$g\in P \left ({\mathbb {A}}_{F,R }\right ) G\left ( {\mathbb {A}}_F^{R }\right )$
, the supports of the Zariski closure of
![]() $ Z_t(\omega (g)\phi )^{\mathrm {zar}} $
and
$ Z_t(\omega (g)\phi )^{\mathrm {zar}} $
and
![]() $ {\mathcal {P}}_{{\mathbb {W}},K }$
on
$ {\mathcal {P}}_{{\mathbb {W}},K }$
on
![]() ${\mathcal {X}}_{K } $
only intersect on the supersingular loci at finite places of E nonsplit over F.
${\mathcal {X}}_{K } $
only intersect on the supersingular loci at finite places of E nonsplit over F.
Proof. The regularity of
![]() $\phi $
at R is preserved by the action of
$\phi $
at R is preserved by the action of
![]() $P \left ({\mathbb {A}}_{F,R }\right )$
on
$P \left ({\mathbb {A}}_{F,R }\right )$
on
![]() $\phi $
. By the regularity of
$\phi $
. By the regularity of
![]() $\omega (g)\phi $
, the lemma follows from the same proof as [Reference Kudla and RapoportKR14, Lemma 2.21]. Or one may reduce the lemma to (the version over a general CM field of) [Reference Kudla and RapoportKR14, Lemma 2.21] as follows. Choose n vectors
$\omega (g)\phi $
, the lemma follows from the same proof as [Reference Kudla and RapoportKR14, Lemma 2.21]. Or one may reduce the lemma to (the version over a general CM field of) [Reference Kudla and RapoportKR14, Lemma 2.21] as follows. Choose n vectors
![]() $x_1,\ldots ,x_n$
spanning
$x_1,\ldots ,x_n$
spanning
![]() $V^\sharp $
. Then
$V^\sharp $
. Then
![]() $ {\mathcal {P}}_{{\mathbb {W}},K ,E }\subset Z(x_1)\cap \ldots \cap Z(x_n)$
. Since
$ {\mathcal {P}}_{{\mathbb {W}},K ,E }\subset Z(x_1)\cap \ldots \cap Z(x_n)$
. Since
![]() $ Z_t(\omega (g)\phi ) $
is a finite sum of
$ Z_t(\omega (g)\phi ) $
is a finite sum of
![]() $Z(x)$
’s with
$Z(x)$
’s with
![]() $x $
outside
$x $
outside
![]() $V^\sharp ({\mathbb {A}}_E) $
, [Reference Kudla and RapoportKR14, Lemma 2.21] applies.
$V^\sharp ({\mathbb {A}}_E) $
, [Reference Kudla and RapoportKR14, Lemma 2.21] applies.
For
![]() $k\in U({\mathbb {V}}^{\infty \cup R})$
, that is,
$k\in U({\mathbb {V}}^{\infty \cup R})$
, that is,
![]() $k_v=1$
for
$k_v=1$
for
![]() $v\in R$
. Then
$v\in R$
. Then
![]() ${\mathbb {W}}_v=(k{\mathbb {W}})_v$
and
${\mathbb {W}}_v=(k{\mathbb {W}})_v$
and
![]() $\phi _v$
is
$\phi _v$
is
![]() $(k{\mathbb {W}})_v$
-regular. By Lemma 6.1.3, the intersection number
$(k{\mathbb {W}})_v$
-regular. By Lemma 6.1.3, the intersection number
![]() $\left ( Z_t(\omega (g) \phi ) ^{\mathrm {zar}} \cdot {\mathcal {P}}_{k^{-1}{\mathbb {W}},K} \right )_{{\mathcal {X}}_{K,{\mathcal {O}}_{E_v}}}$
of the restrictions of the cycles to
$\left ( Z_t(\omega (g) \phi ) ^{\mathrm {zar}} \cdot {\mathcal {P}}_{k^{-1}{\mathbb {W}},K} \right )_{{\mathcal {X}}_{K,{\mathcal {O}}_{E_v}}}$
of the restrictions of the cycles to
![]() ${\mathcal {X}}_{K,{\mathcal {O}}_{E_v}}$
is well defined as in (A.1).
${\mathcal {X}}_{K,{\mathcal {O}}_{E_v}}$
is well defined as in (A.1).
Proposition 6.1.4. Recall the set
![]() ${\mathfrak {Ram}}$
of finite places of F nonsplit in E, and ramified in E or over
${\mathfrak {Ram}}$
of finite places of F nonsplit in E, and ramified in E or over
![]() ${\mathbb {Q}}$
. Let
${\mathbb {Q}}$
. Let
![]() $g\in P\left ({\mathbb {A}}_{F,{\mathfrak {Ram}}\cup R}\right ) G\left ({\mathbb {A}}_F^{{\mathfrak {Ram}}\cup R}\right ) $
. Let v be a place of F nonsplit in E and
$g\in P\left ({\mathbb {A}}_{F,{\mathfrak {Ram}}\cup R}\right ) G\left ({\mathbb {A}}_F^{{\mathfrak {Ram}}\cup R}\right ) $
. Let v be a place of F nonsplit in E and
![]() $k\in U({\mathbb {V}}^{\infty \cup R\cup \{v\}})$
. For
$k\in U({\mathbb {V}}^{\infty \cup R\cup \{v\}})$
. For
![]() $v\not \in {\mathfrak {Ram}}\cup \infty $
, resp.
$v\not \in {\mathfrak {Ram}}\cup \infty $
, resp.
![]() $v\in {\mathfrak {Ram}} $
, resp.
$v\in {\mathfrak {Ram}} $
, resp.
![]() $v\in \infty $
, we respectively have
$v\in \infty $
, we respectively have
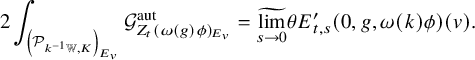 $$ \begin{align} 2 \int_{\left({\mathcal{P}}_{k^{-1}{\mathbb{W}},K}\right)_{E_v}} {\mathcal{G}}_{Z_t(\omega(g)\phi) _{E_v}}^{\mathrm{aut}} = \widetilde{\lim _{s\to 0}}{\theta E}^{\prime}_{t,s} (0,g,\omega(k)\phi)(v). \end{align} $$
$$ \begin{align} 2 \int_{\left({\mathcal{P}}_{k^{-1}{\mathbb{W}},K}\right)_{E_v}} {\mathcal{G}}_{Z_t(\omega(g)\phi) _{E_v}}^{\mathrm{aut}} = \widetilde{\lim _{s\to 0}}{\theta E}^{\prime}_{t,s} (0,g,\omega(k)\phi)(v). \end{align} $$
We will prove Proposition 6.1.4 for
![]() $k=1$
, in Proposition 6.1.6 (
$k=1$
, in Proposition 6.1.6 (
![]() $v\not \in {\mathfrak {Ram}}\cup \infty $
), Proposition 6.1.7 and Proposition 6.1.9 (
$v\not \in {\mathfrak {Ram}}\cup \infty $
), Proposition 6.1.7 and Proposition 6.1.9 (
![]() $v\in {\mathfrak {Ram}} $
), Proposition 6.1.11 (
$v\in {\mathfrak {Ram}} $
), Proposition 6.1.11 (
![]() $v\in \infty $
). The proof for the general k is the same, except one needs to keep track of k. For simplicity, let
$v\in \infty $
). The proof for the general k is the same, except one needs to keep track of k. For simplicity, let
We prepare more notations for later computations. For a finite place v of F nonsplit in E, let
![]() $E_v^{\mathrm {ur}}$
be the complete maximal unramified extension of
$E_v^{\mathrm {ur}}$
be the complete maximal unramified extension of
![]() $E_v$
. Let
$E_v$
. Let
![]() ${\mathbb {E}}$
be the unique formal
${\mathbb {E}}$
be the unique formal
![]() ${\mathcal {O}}_{F_v}$
-module of relative height
${\mathcal {O}}_{F_v}$
-module of relative height
![]() $2$
and dimension 1 over
$2$
and dimension 1 over
![]() $\operatorname {\mathrm {Spec}} E_v^{\mathrm {ur}}/\varpi _{E_v}$
. The endomorphism ring of
$\operatorname {\mathrm {Spec}} E_v^{\mathrm {ur}}/\varpi _{E_v}$
. The endomorphism ring of
![]() ${\mathbb {E}}$
is the maximal order of the unique division quaternion algebra B over
${\mathbb {E}}$
is the maximal order of the unique division quaternion algebra B over
![]() $F_v $
. Fixing an embedding
$F_v $
. Fixing an embedding
![]() $\iota : E_v \hookrightarrow B$
such that
$\iota : E_v \hookrightarrow B$
such that
![]() $\iota ( {\mathcal {O}}_{E_v})$
is in the maximal order of B. Then
$\iota ( {\mathcal {O}}_{E_v})$
is in the maximal order of B. Then
![]() ${\mathbb {E}}$
becomes a formal
${\mathbb {E}}$
becomes a formal
![]() ${\mathcal {O}}_{E_v}$
-module of relative height
${\mathcal {O}}_{E_v}$
-module of relative height
![]() $1$
and dimension 1, which we still donote by
$1$
and dimension 1, which we still donote by
![]() ${\mathbb {E}}$
. Let
${\mathbb {E}}$
. Let
![]() $\overline \iota $
be
$\overline \iota $
be
![]() $\iota $
precomposed with the nontrivial
$\iota $
precomposed with the nontrivial
![]() ${\mathrm {Gal}}(E_v/{F_v})$
-conjugation. It produces another
${\mathrm {Gal}}(E_v/{F_v})$
-conjugation. It produces another
![]() ${\mathcal {O}}_{E_v}$
-module
${\mathcal {O}}_{E_v}$
-module
![]() $\overline {\mathbb {E}}$
. Fix an
$\overline {\mathbb {E}}$
. Fix an
![]() ${\mathcal {O}}_{F_v}$
-linear principal polarization
${\mathcal {O}}_{F_v}$
-linear principal polarization
![]() $\lambda _{{\mathbb {E}}}$
on
$\lambda _{{\mathbb {E}}}$
on
![]() ${\mathbb {E}}$
. Let
${\mathbb {E}}$
. Let
![]() ${\mathcal {E}}$
and
${\mathcal {E}}$
and
![]() $\overline {\mathcal {E}}$
be the canonical liftings of
$\overline {\mathcal {E}}$
be the canonical liftings of
![]() ${\mathbb {E}}$
and
${\mathbb {E}}$
and
![]() $\overline {\mathbb {E}}$
respectively, as
$\overline {\mathbb {E}}$
respectively, as
![]() ${\mathcal {O}}_{E_v}$
-modules. They are isomorphic as formal
${\mathcal {O}}_{E_v}$
-modules. They are isomorphic as formal
![]() ${\mathcal {O}}_{F_v}$
-modules, and equipped with a unique
${\mathcal {O}}_{F_v}$
-modules, and equipped with a unique
![]() ${\mathcal {O}}_{F_v}$
-linear principal polarization
${\mathcal {O}}_{F_v}$
-linear principal polarization
![]() $\lambda _{\mathcal {E}}$
lifting
$\lambda _{\mathcal {E}}$
lifting
![]() $\lambda _{{\mathbb {E}}}$
.
$\lambda _{{\mathbb {E}}}$
.
6.1.1 Finite places of F inert in E
For such a v,
![]() $\Lambda _v$
is self-dual.
$\Lambda _v$
is self-dual.
Before we can compute the intersection number, we need to uniformize the integral model, CM cycle and special divisors using Rapoport-Zink spaces.
For a nonnegative integer m, let
![]() ${\mathcal {N}}_m $
be the unramified relative unitary Rapoport-Zink space of signature
${\mathcal {N}}_m $
be the unramified relative unitary Rapoport-Zink space of signature
![]() $(m,1)$
[Reference Kudla and RapoportKR11] [Reference Li and ZhangLZ21, 2.1] over
$(m,1)$
[Reference Kudla and RapoportKR11] [Reference Li and ZhangLZ21, 2.1] over
![]() $\operatorname {\mathrm {Spf}} {\mathcal {O}}_{E_v^{\mathrm {ur}}}$
. It is the deformation space of the polarized hermitian
$\operatorname {\mathrm {Spf}} {\mathcal {O}}_{E_v^{\mathrm {ur}}}$
. It is the deformation space of the polarized hermitian
![]() ${\mathcal {O}}_{E_v}$
-module
${\mathcal {O}}_{E_v}$
-module
![]() ${\mathbb {X}}_m:=\overline {\mathbb {E}}\times {\mathbb {E}}^m$
with the product polarization
${\mathbb {X}}_m:=\overline {\mathbb {E}}\times {\mathbb {E}}^m$
with the product polarization
![]() $\lambda _m$
. It is formally smooth of relative dimension m. The space
$\lambda _m$
. It is formally smooth of relative dimension m. The space
![]() ${\mathrm {Hom}}_{{\mathcal {O}}_{E_v}}({\mathbb {E}},{\mathbb {X}}_m)_{{\mathbb {Q}}}$
carries a natural hermitian pairing
${\mathrm {Hom}}_{{\mathcal {O}}_{E_v}}({\mathbb {E}},{\mathbb {X}}_m)_{{\mathbb {Q}}}$
carries a natural hermitian pairing
For
![]() $m=n$
, we let
$m=n$
, we let
![]() ${\mathcal {N}}={\mathcal {N}}_n$
. By [Reference Li and ZhangLZ21, 2.2], we have
${\mathcal {N}}={\mathcal {N}}_n$
. By [Reference Li and ZhangLZ21, 2.2], we have
![]() ${\mathrm {Hom}}_{{\mathcal {O}}_{E_v}}({\mathbb {E}},{\mathbb {X}}_n)_{{\mathbb {Q}}}{\ \simeq \ } V(E_v).$
And
${\mathrm {Hom}}_{{\mathcal {O}}_{E_v}}({\mathbb {E}},{\mathbb {X}}_n)_{{\mathbb {Q}}}{\ \simeq \ } V(E_v).$
And
![]() $U(V(E_v))$
is isomorphic to the group of
$U(V(E_v))$
is isomorphic to the group of
![]() ${\mathcal {O}}_{E_v}$
-linear self-quasi-isogenies of
${\mathcal {O}}_{E_v}$
-linear self-quasi-isogenies of
![]() ${\mathbb {X}}_n$
preserving
${\mathbb {X}}_n$
preserving
![]() $\lambda _n$
[Reference Rapoport, Smithling and ZhangRSZ18, (4.3)]. In particular,
$\lambda _n$
[Reference Rapoport, Smithling and ZhangRSZ18, (4.3)]. In particular,
![]() $U(V(E_v))$
acts on
$U(V(E_v))$
acts on
![]() ${\mathcal {N}}$
. For every
${\mathcal {N}}$
. For every
![]() $x\in V(E_v)-\{0\} $
, we have the Kudla-Rapoport divisor
$x\in V(E_v)-\{0\} $
, we have the Kudla-Rapoport divisor
![]() ${\mathcal {Z}}(x)$
on
${\mathcal {Z}}(x)$
on
![]() $ {\mathcal {N}} $
[Reference Kudla and RapoportKR11] [Reference Li and ZhangLZ21, 2.3] that is the locus where x lifts to a quasi-isogeny. It is a (possibly empty) relative Cartier divisor. See [Reference Kudla and RapoportKR11, Proposition 3.5], which is only stated for
$ {\mathcal {N}} $
[Reference Kudla and RapoportKR11] [Reference Li and ZhangLZ21, 2.3] that is the locus where x lifts to a quasi-isogeny. It is a (possibly empty) relative Cartier divisor. See [Reference Kudla and RapoportKR11, Proposition 3.5], which is only stated for
![]() $F_v={\mathbb {Q}}_p$
but holds in the general case.
$F_v={\mathbb {Q}}_p$
but holds in the general case.
Let
![]() $\widehat {{\mathcal {X}}_{K, {\mathcal {O}}_{E_v^{\mathrm {ur}}}}^{ss}} $
be the formal completion of
$\widehat {{\mathcal {X}}_{K, {\mathcal {O}}_{E_v^{\mathrm {ur}}}}^{ss}} $
be the formal completion of
![]() ${\mathcal {X}}_{K, {\mathcal {O}}_{E_v^{\mathrm {ur}}}}$
along the supersingular locus. Then we have the following formal uniformization [Reference Li and ZhangLZ21, 13.1]:
${\mathcal {X}}_{K, {\mathcal {O}}_{E_v^{\mathrm {ur}}}}$
along the supersingular locus. Then we have the following formal uniformization [Reference Li and ZhangLZ21, 13.1]:
For
![]() $x\in V(E_v)-\{0\} $
and
$x\in V(E_v)-\{0\} $
and
![]() $h\in U\left ( {\mathbb {V}}^{\infty ,v}\right )$
, we have a relative cartier divisor
$h\in U\left ( {\mathbb {V}}^{\infty ,v}\right )$
, we have a relative cartier divisor
![]() $[{\mathcal {Z}}(x),h]$
of
$[{\mathcal {Z}}(x),h]$
of
![]() $\widehat {{\mathcal {X}}_{K, {\mathcal {O}}_{E_v^{\mathrm {ur}}}}^{ss}} $
.
$\widehat {{\mathcal {X}}_{K, {\mathcal {O}}_{E_v^{\mathrm {ur}}}}^{ss}} $
.
The Rapoport-Zink space
![]() ${\mathcal {N}}_0 $
is naturally a closed formal subscheme of
${\mathcal {N}}_0 $
is naturally a closed formal subscheme of
![]() ${\mathcal {N}}$
by adding canonical liftings; that is, the morphism
${\mathcal {N}}$
by adding canonical liftings; that is, the morphism
![]() ${\mathcal {N}}_0\to {\mathcal {N}}$
is given by
${\mathcal {N}}_0\to {\mathcal {N}}$
is given by
![]() $X\mapsto X\times {\mathcal {E}}^n$
. The subspace
$X\mapsto X\times {\mathcal {E}}^n$
. The subspace
becomes the subspace
![]() $W(E_v)$
of
$W(E_v)$
of
![]() $V(E_v)$
, and the subgroup
$V(E_v)$
, and the subgroup
![]() $U(W(E_v))$
stabilizes
$U(W(E_v))$
stabilizes
![]() ${\mathcal {N}}_0$
. We have
${\mathcal {N}}_0$
. We have
where
![]() $d_{{\mathbb {W}},K} $
is the degree of the fundamental cycle of
$d_{{\mathbb {W}},K} $
is the degree of the fundamental cycle of
![]() ${\mathrm {Sh}}({\mathbb {W}})_{K_{\mathbb {W}}}$
. See Definition 5.1.3), and the right-hand side is defined using the formal uniformization (6.5) of
${\mathrm {Sh}}({\mathbb {W}})_{K_{\mathbb {W}}}$
. See Definition 5.1.3), and the right-hand side is defined using the formal uniformization (6.5) of
![]() $\widehat {{\mathcal {X}}_{K, {\mathcal {O}}_{E_v^{\mathrm {ur}}}}^{ss}}$
with
$\widehat {{\mathcal {X}}_{K, {\mathcal {O}}_{E_v^{\mathrm {ur}}}}^{ss}}$
with
![]() ${\mathcal {N}}_{0}$
understood as a 1-cycle on
${\mathcal {N}}_{0}$
understood as a 1-cycle on
![]() ${\mathcal {N}}$
.
${\mathcal {N}}$
.
Recall that
![]() $V^t$
is the subset of
$V^t$
is the subset of
![]() $V(E)$
of elements of norm t.
$V(E)$
of elements of norm t.
Proposition 6.1.5. Under the formal uniformization (6.5) of
![]() $\widehat {{\mathcal {X}}_{K, {\mathcal {O}}_{E_v^{\mathrm {ur}}}}^{ss}}$
, for
$\widehat {{\mathcal {X}}_{K, {\mathcal {O}}_{E_v^{\mathrm {ur}}}}^{ss}}$
, for
![]() $g\in G({\mathbb {A}}_F^{ v})$
, we have
$g\in G({\mathbb {A}}_F^{ v})$
, we have
Proof. This follows from [Reference Li and LiuLL21, (8.3)] and the flatness of
![]() ${\mathcal {Z}}(x)$
.
${\mathcal {Z}}(x)$
.
Let
![]() $ \left ({\mathcal {Z}}(x)\cdot {\mathcal {N}}_0\right )_{{\mathcal {N}}}$
be the Euler-Poincaré characteristic of the derived tensor product
$ \left ({\mathcal {Z}}(x)\cdot {\mathcal {N}}_0\right )_{{\mathcal {N}}}$
be the Euler-Poincaré characteristic of the derived tensor product
![]() ${\mathcal {O}}_{{\mathcal {Z}}(x) }\otimes ^{\mathbb {L}} {\mathcal {O}}_{{\mathcal {N}}_0}$
. Since
${\mathcal {O}}_{{\mathcal {Z}}(x) }\otimes ^{\mathbb {L}} {\mathcal {O}}_{{\mathcal {N}}_0}$
. Since
![]() $h\in U(W(E_v))$
stabilizes
$h\in U(W(E_v))$
stabilizes
![]() ${\mathcal {N}}_0$
,
${\mathcal {N}}_0$
,
![]() $\left ({\mathcal {Z}}(x)\cdot {\mathcal {N}}_0\right )_{{\mathcal {N}}}= \left ({\mathcal {Z}}(hx)\cdot {\mathcal {N}}_0\right )_{{\mathcal {N}}}$
. By Lemma 6.1.3, (6.6), Proposition 6.1.5 and a direct computation, for
$\left ({\mathcal {Z}}(x)\cdot {\mathcal {N}}_0\right )_{{\mathcal {N}}}= \left ({\mathcal {Z}}(hx)\cdot {\mathcal {N}}_0\right )_{{\mathcal {N}}}$
. By Lemma 6.1.3, (6.6), Proposition 6.1.5 and a direct computation, for
![]() $g\in P ({\mathbb {A}}_{F,R\cup \{v\}})G({\mathbb {A}}_F^{ R\cup \{v\}})$
,
$g\in P ({\mathbb {A}}_{F,R\cup \{v\}})G({\mathbb {A}}_F^{ R\cup \{v\}})$
,
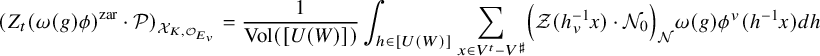 $$ \begin{align} \left( {Z_t( \omega(g)\phi)}^{\mathrm{zar}}\cdot {\mathcal{P}} \right)_{{\mathcal{X}}_{K,{\mathcal{O}}_{E_v}} } =\frac{1}{{\mathrm{Vol}}([U(W)])} \int_{ h\in [U(W)]} \sum_{x\in V^t-V^\sharp} \left({\mathcal{Z}}(h_v^{-1}x) \cdot{\mathcal{N}}_0\right)_{{\mathcal{N}}} \omega(g) \phi^v(h^{-1} x) dh \end{align} $$
$$ \begin{align} \left( {Z_t( \omega(g)\phi)}^{\mathrm{zar}}\cdot {\mathcal{P}} \right)_{{\mathcal{X}}_{K,{\mathcal{O}}_{E_v}} } =\frac{1}{{\mathrm{Vol}}([U(W)])} \int_{ h\in [U(W)]} \sum_{x\in V^t-V^\sharp} \left({\mathcal{Z}}(h_v^{-1}x) \cdot{\mathcal{N}}_0\right)_{{\mathcal{N}}} \omega(g) \phi^v(h^{-1} x) dh \end{align} $$
Proposition 6.1.6. If v is unramified over
![]() ${\mathbb {Q}}$
, for
${\mathbb {Q}}$
, for
![]() $g\in P ({\mathbb {A}}_{F,R})G({\mathbb {A}}_F^{ R})$
and
$g\in P ({\mathbb {A}}_{F,R})G({\mathbb {A}}_F^{ R})$
and
![]() $k=1$
, (6.1) holds.
$k=1$
, (6.1) holds.
Proof. First, we compute
![]() $ \left ( {\mathcal {Z}}(x)\cdot {\mathcal {N}}_0\right )_{{\mathcal {N}}}$
(i.e., we need to compute the length of the locus on
$ \left ( {\mathcal {Z}}(x)\cdot {\mathcal {N}}_0\right )_{{\mathcal {N}}}$
(i.e., we need to compute the length of the locus on
![]() ${\mathcal {N}}_0$
to which x lifts). Recall that
${\mathcal {N}}_0$
to which x lifts). Recall that
![]() $\Lambda _v^\sharp \subset {\mathbb {V}}(E_v)$
is the orthogonal complement of
$\Lambda _v^\sharp \subset {\mathbb {V}}(E_v)$
is the orthogonal complement of
![]() ${\mathcal {O}}_{E_v}e_v^{(0)}$
in
${\mathcal {O}}_{E_v}e_v^{(0)}$
in
![]() $\Lambda _v$
. Under the isomorphism
$\Lambda _v$
. Under the isomorphism
![]() ${\mathrm {Hom}}_{{\mathcal {O}}_{E_v}}({\mathbb {E}},{\mathbb {X}}_n)_{{\mathbb {Q}}}{\ \simeq \ } V(E_v)$
, the image of
${\mathrm {Hom}}_{{\mathcal {O}}_{E_v}}({\mathbb {E}},{\mathbb {X}}_n)_{{\mathbb {Q}}}{\ \simeq \ } V(E_v)$
, the image of
![]() ${\mathrm {Hom}}_{{\mathcal {O}}_{E_v}}({\mathbb {E}}, {\mathbb {E}}^n)$
is
${\mathrm {Hom}}_{{\mathcal {O}}_{E_v}}({\mathbb {E}}, {\mathbb {E}}^n)$
is
![]() $\Lambda _v^\sharp $
. Then for
$\Lambda _v^\sharp $
. Then for
![]() $ x=(x_1,x_2)\in W(E_v)\oplus V^\sharp (E_v) $
with
$ x=(x_1,x_2)\in W(E_v)\oplus V^\sharp (E_v) $
with
![]() $x_1\neq 0$
, if it lifts, then
$x_1\neq 0$
, if it lifts, then
![]() $x_2\in \Lambda _v^\sharp $
. Moreover, by Gross’ result on canonical lifting [Reference GrossGro86, Proposition3.3], we have
$x_2\in \Lambda _v^\sharp $
. Moreover, by Gross’ result on canonical lifting [Reference GrossGro86, Proposition3.3], we have
Second, if
![]() $g_v= 1$
, express the left-hand side of (6.1) by (6.8) and (6.9). Compare it with the expression of the right-hand side of (6.1) given by (3.22). By Lemma 5.2.1, (6.1) follows.
$g_v= 1$
, express the left-hand side of (6.1) by (6.8) and (6.9). Compare it with the expression of the right-hand side of (6.1) given by (3.22). By Lemma 5.2.1, (6.1) follows.
Finally, we reduce the general case to the case
![]() $g_v=1$
in two reduction steps. (I) We claim the following: replacing
$g_v=1$
in two reduction steps. (I) We claim the following: replacing
![]() $g_v$
by
$g_v$
by
![]() $g_vn(b_v)$
for
$g_vn(b_v)$
for
![]() $b_v\in F_v$
or by
$b_v\in F_v$
or by
![]() $g_vk_v $
for
$g_vk_v $
for
![]() $k_v\in K_v^{\max }$
(see 2.5), both sides of (6.1) are multiplied by the same constant. Indeed, for the left-hand side of (6.1), we directly use the definition of the Weil representation. For the right-hand side, besides the definition, we further need (3.2) and Lemma 3.2.2. (II), By Corollary 3.2.3 and Lemma 4.1.3, we can replace g by
$k_v\in K_v^{\max }$
(see 2.5), both sides of (6.1) are multiplied by the same constant. Indeed, for the left-hand side of (6.1), we directly use the definition of the Weil representation. For the right-hand side, besides the definition, we further need (3.2) and Lemma 3.2.2. (II), By Corollary 3.2.3 and Lemma 4.1.3, we can replace g by
![]() $m(a)g$
for some
$m(a)g$
for some
![]() $a\in E^\times $
. By the Iwasawa decomposition, the fact that
$a\in E^\times $
. By the Iwasawa decomposition, the fact that
![]() $E_v^\times =E^\times {\mathcal {O}}_{E_v}^\times $
, and the claim in the first reduction step, we may assume that
$E_v^\times =E^\times {\mathcal {O}}_{E_v}^\times $
, and the claim in the first reduction step, we may assume that
![]() $g_v= 1$
. The proposition is proved.
$g_v= 1$
. The proposition is proved.
Proposition 6.1.7. If v is ramified over
![]() ${\mathbb {Q}}$
, for
${\mathbb {Q}}$
, for
![]() $g\in P ({\mathbb {A}}_{F,R\cup \{v\}})G({\mathbb {A}}_F^{ R\cup \{v\}})$
, (6.2) holds.
$g\in P ({\mathbb {A}}_{F,R\cup \{v\}})G({\mathbb {A}}_F^{ R\cup \{v\}})$
, (6.2) holds.
Proof. The proof is the same with the proof of Proposition 6.1.6 with the following exceptions:
-
• in the claim in the reduction step (I), remove ‘or by
 $g_vk_v $
for
$g_vk_v $
for
 $k_v\in K_v^{\max }$
’;
$k_v\in K_v^{\max }$
’; -
• in the reduction step (II), ‘Corollary 3.2.3’ should be replaced by ‘Corollary 3.2.3 and that
 $ {\theta E} \left (0,m(a)g,\phi ^{v}\otimes \phi _v'\right )= {\theta E} \left (0,g,\phi ^{v}\otimes \phi _v'\right ) $
for
$ {\theta E} \left (0,m(a)g,\phi ^{v}\otimes \phi _v'\right )= {\theta E} \left (0,g,\phi ^{v}\otimes \phi _v'\right ) $
for
 $a\in E^\times $
’.
$a\in E^\times $
’.
6.1.2 Finite places of F ramified in E
For such a v,
![]() $\Lambda _v$
is a
$\Lambda _v$
is a
![]() $\pi _v$
-modular or almost
$\pi _v$
-modular or almost
![]() $\pi _v$
-modular lattice. This case is more complicated.
$\pi _v$
-modular lattice. This case is more complicated.
We still need formal uniformization using Rapoport-Zink spaces. For a nonnegative integer m, let
![]() ${\mathcal {N}}_m$
be the exotic smooth relative unitary Rapoport-Zink space of signature
${\mathcal {N}}_m$
be the exotic smooth relative unitary Rapoport-Zink space of signature
![]() $(m,1)$
over
$(m,1)$
over
![]() $\operatorname {\mathrm {Spf}} {\mathcal {O}}_{E_v^{\mathrm {ur}}}$
. See [Reference Rapoport, Smithling and ZhangRSZ18, Section 6,7], [Reference Rapoport, Smithling and ZhangRSZ17, 3.5] and [Reference Li and LiuLL22, 2.1]. It will also be specified below. It is formally smooth over
$\operatorname {\mathrm {Spf}} {\mathcal {O}}_{E_v^{\mathrm {ur}}}$
. See [Reference Rapoport, Smithling and ZhangRSZ18, Section 6,7], [Reference Rapoport, Smithling and ZhangRSZ17, 3.5] and [Reference Li and LiuLL22, 2.1]. It will also be specified below. It is formally smooth over
![]() $\operatorname {\mathrm {Spf}} {\mathcal {O}}_{E_v^{\mathrm {ur}}}$
of relative dimension m. (Note that the case
$\operatorname {\mathrm {Spf}} {\mathcal {O}}_{E_v^{\mathrm {ur}}}$
of relative dimension m. (Note that the case
![]() $m=0$
is not covered in either [Reference Rapoport, Smithling and ZhangRSZ17] or [Reference Li and LiuLL22], but is specifically indicated in [Reference Rapoport, Smithling and ZhangRSZ18, Example 7.2].) Let
$m=0$
is not covered in either [Reference Rapoport, Smithling and ZhangRSZ17] or [Reference Li and LiuLL22], but is specifically indicated in [Reference Rapoport, Smithling and ZhangRSZ18, Example 7.2].) Let
![]() ${\mathcal {N}}={\mathcal {N}}_n$
. We will use
${\mathcal {N}}={\mathcal {N}}_n$
. We will use
![]() ${\mathcal {N}} $
for the formal uniformization of
${\mathcal {N}} $
for the formal uniformization of
![]() ${\mathcal {X}}_K$
. The analog of the formal uniformization (6.6) of
${\mathcal {X}}_K$
. The analog of the formal uniformization (6.6) of
![]() ${\mathcal {P}}$
using
${\mathcal {P}}$
using
![]() ${\mathcal {N}}_0$
is more subtle: we will use
${\mathcal {N}}_0$
is more subtle: we will use
![]() ${\mathcal {N}}_1$
to define morphisms
${\mathcal {N}}_1$
to define morphisms
![]() ${\mathcal {N}}_0\to {\mathcal {N}}_1\to {\mathcal {N}}$
, which will lead us to the formal uniformization (6.11) of
${\mathcal {N}}_0\to {\mathcal {N}}_1\to {\mathcal {N}}$
, which will lead us to the formal uniformization (6.11) of
![]() ${\mathcal {P}}$
.
${\mathcal {P}}$
.
Remark 6.1.8. The reason for this subtlety might be explained as follows. Recall that the construction of
![]() ${\mathcal {P}}$
requires an additional rank 2 sub-lattice
${\mathcal {P}}$
requires an additional rank 2 sub-lattice
![]() $\Lambda _{v,1}$
as in 5.1.3 at each finite place, which is a direct summand of
$\Lambda _{v,1}$
as in 5.1.3 at each finite place, which is a direct summand of
![]() $\Lambda _v$
. And
$\Lambda _v$
. And
![]() $E_v\Lambda _{v,1}$
contains a distinguished vector
$E_v\Lambda _{v,1}$
contains a distinguished vector
![]() $e_v^{(0)}$
of unit norm. One might consider
$e_v^{(0)}$
of unit norm. One might consider
![]() ${\mathcal {O}}_{E_v}e_v^{(0)}\subset E_v\Lambda _{v,1}$
and
${\mathcal {O}}_{E_v}e_v^{(0)}\subset E_v\Lambda _{v,1}$
and
![]() $ \Lambda _{v,1}\subset \Lambda _v$
as being parallel to the morphisms
$ \Lambda _{v,1}\subset \Lambda _v$
as being parallel to the morphisms
![]() ${\mathcal {N}}_0\to {\mathcal {N}}_1$
and
${\mathcal {N}}_0\to {\mathcal {N}}_1$
and
![]() ${\mathcal {N}}_1\to {\mathcal {N}}$
. Note that
${\mathcal {N}}_1\to {\mathcal {N}}$
. Note that
![]() ${\mathcal {O}}_{E_v}e_v^{(0)}$
is not contained in
${\mathcal {O}}_{E_v}e_v^{(0)}$
is not contained in
![]() $\Lambda _{v,1}$
( or
$\Lambda _{v,1}$
( or
![]() $\Lambda _v$
). This makes it nontrivial to define a morphism
$\Lambda _v$
). This makes it nontrivial to define a morphism
![]() ${\mathcal {N}}_0\to {\mathcal {N}}_1$
or
${\mathcal {N}}_0\to {\mathcal {N}}_1$
or
![]() ${\mathcal {N}}_0\to {\mathcal {N}}$
. See also [Reference Rapoport, Smithling and ZhangRSZ18, Remark 12.3]. The morphism
${\mathcal {N}}_0\to {\mathcal {N}}$
. See also [Reference Rapoport, Smithling and ZhangRSZ18, Remark 12.3]. The morphism
![]() ${\mathcal {N}}_0\to {\mathcal {N}}_1$
we use is given by [Reference Rapoport, Smithling and ZhangRSZ18, Section 12].
${\mathcal {N}}_0\to {\mathcal {N}}_1$
we use is given by [Reference Rapoport, Smithling and ZhangRSZ18, Section 12].
We have 6 steps before the main result Proposition 6.1.9 of this 6.1.2.
First, we specify
![]() ${\mathcal {N}}_1$
,
${\mathcal {N}}_1$
,
![]() ${\mathcal {N}}$
and
${\mathcal {N}}$
and
![]() ${\mathcal {N}}_1\to {\mathcal {N}}$
. Assume that
${\mathcal {N}}_1\to {\mathcal {N}}$
. Assume that
![]() $\varpi _{E_v}^2=\varpi _{F_v}$
. The framing object
$\varpi _{E_v}^2=\varpi _{F_v}$
. The framing object
![]() ${\mathbb {X}}_1$
for the deformation space
${\mathbb {X}}_1$
for the deformation space
![]() ${\mathcal {N}}_1$
is the Serre tensor
${\mathcal {N}}_1$
is the Serre tensor
![]() ${\mathcal {O}}_{E_v}\otimes _{{\mathcal {O}}_{F_v}}\overline {\mathbb {E}}$
, which is the conjugate of the framing object [Reference Rapoport, Smithling and ZhangRSZ17, (3.5)], with the polarization conjugate to the one in [Reference Rapoport, Smithling and ZhangRSZ17, (3.6)]. In the case that n is odd (the case of Lemma 5.1.1 (1)), the framing object for
${\mathcal {O}}_{E_v}\otimes _{{\mathcal {O}}_{F_v}}\overline {\mathbb {E}}$
, which is the conjugate of the framing object [Reference Rapoport, Smithling and ZhangRSZ17, (3.5)], with the polarization conjugate to the one in [Reference Rapoport, Smithling and ZhangRSZ17, (3.6)]. In the case that n is odd (the case of Lemma 5.1.1 (1)), the framing object for
![]() ${\mathcal {N}}$
is
${\mathcal {N}}$
is
![]() ${\mathbb {X}}_n:={\mathbb {X}}_1\times ({\mathbb {E}}^2)^{(n-1)/2}$
with the product polarization
${\mathbb {X}}_n:={\mathbb {X}}_1\times ({\mathbb {E}}^2)^{(n-1)/2}$
with the product polarization
![]() $\lambda _n$
, where the polarization on
$\lambda _n$
, where the polarization on
![]() ${\mathbb {E}}^2$
is given by
${\mathbb {E}}^2$
is given by
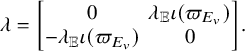 $$ \begin{align} \lambda = \begin{bmatrix}0&\lambda_{{\mathbb{E}}}\iota(\varpi_{E_v})\\ -\lambda_{{\mathbb{E}}}\iota(\varpi_{E_v})&0\end{bmatrix}.\end{align} $$
$$ \begin{align} \lambda = \begin{bmatrix}0&\lambda_{{\mathbb{E}}}\iota(\varpi_{E_v})\\ -\lambda_{{\mathbb{E}}}\iota(\varpi_{E_v})&0\end{bmatrix}.\end{align} $$
In the same way, we have a polarization
![]() $\widetilde {\lambda } $
on
$\widetilde {\lambda } $
on
![]() ${\mathcal {E}}^2$
using
${\mathcal {E}}^2$
using
![]() $\lambda _{\mathcal {E}}$
. This gives us a morphism
$\lambda _{\mathcal {E}}$
. This gives us a morphism
![]() ${\mathcal {N}}_1\to {\mathcal {N}}$
by
${\mathcal {N}}_1\to {\mathcal {N}}$
by
![]() $X\mapsto X\times ({\mathcal {E}}^2)^{(n-1)/2}$
with the polarization
$X\mapsto X\times ({\mathcal {E}}^2)^{(n-1)/2}$
with the polarization
![]() $\widetilde {\lambda } $
on each of
$\widetilde {\lambda } $
on each of
![]() ${\mathcal {E}}^2$
. In the case that n is even (the case of Lemma 5.1.1 (2)), the framing object for
${\mathcal {E}}^2$
. In the case that n is even (the case of Lemma 5.1.1 (2)), the framing object for
![]() ${\mathcal {N}}$
is
${\mathcal {N}}$
is
![]() ${\mathbb {X}}_n:={\mathbb {X}}_1\times ({\mathbb {E}}^2)^{(n-2)/2} \times {\mathbb {E}}$
where the polarization
${\mathbb {X}}_n:={\mathbb {X}}_1\times ({\mathbb {E}}^2)^{(n-2)/2} \times {\mathbb {E}}$
where the polarization
![]() $\lambda _{{\mathbb {E}}}'$
on the last component is a multiple of
$\lambda _{{\mathbb {E}}}'$
on the last component is a multiple of
![]() $\lambda _{{\mathbb {E}}}$
so that the induced hermitian pairing on
$\lambda _{{\mathbb {E}}}$
so that the induced hermitian pairing on
![]() ${\mathrm {Hom}}({\mathbb {E}},{\mathbb {E}})_{{\mathbb {Q}}}$
(defined as in (6.4)) has determinant
${\mathrm {Hom}}({\mathbb {E}},{\mathbb {E}})_{{\mathbb {Q}}}$
(defined as in (6.4)) has determinant
![]() $q(e_v)$
as in Lemma 5.1.1 (2). This gives us a morphism
$q(e_v)$
as in Lemma 5.1.1 (2). This gives us a morphism
![]() ${\mathcal {N}}_1\to {\mathcal {N}}$
by
${\mathcal {N}}_1\to {\mathcal {N}}$
by
![]() $X\mapsto X\times ({\mathcal {E}}^2)^{(n-1)/2}\times {\mathcal {E}}$
with the unique lifting of
$X\mapsto X\times ({\mathcal {E}}^2)^{(n-1)/2}\times {\mathcal {E}}$
with the unique lifting of
![]() $\lambda _{{\mathbb {E}}}'$
on the last component
$\lambda _{{\mathbb {E}}}'$
on the last component
![]() ${\mathcal {E}}$
.
${\mathcal {E}}$
.
Second, the uniformizations of
![]() $\widehat {{\mathcal {X}}_{K, {\mathcal {O}}_{E_v^{\mathrm {ur}}}}^{ss}}$
and
$\widehat {{\mathcal {X}}_{K, {\mathcal {O}}_{E_v^{\mathrm {ur}}}}^{ss}}$
and
![]() $Z_t(\phi )^{\mathrm {zar}}$
are as follows. By [Reference Rapoport, Smithling and ZhangRSZ17, (3.10)],
$Z_t(\phi )^{\mathrm {zar}}$
are as follows. By [Reference Rapoport, Smithling and ZhangRSZ17, (3.10)],
![]() $V(E_v){\ \simeq \ } {\mathrm {Hom}}_{{\mathcal {O}}_{E_v}}({\mathbb {E}},{\mathbb {X}}_n)_{{\mathbb {Q}}} $
and
$V(E_v){\ \simeq \ } {\mathrm {Hom}}_{{\mathcal {O}}_{E_v}}({\mathbb {E}},{\mathbb {X}}_n)_{{\mathbb {Q}}} $
and
![]() $U(V(E_v))$
is isomorphic to the group of
$U(V(E_v))$
is isomorphic to the group of
![]() ${\mathcal {O}}_{E_v}$
-linear self-quasi-isogenies of
${\mathcal {O}}_{E_v}$
-linear self-quasi-isogenies of
![]() ${\mathbb {X}}_n$
preserving
${\mathbb {X}}_n$
preserving
![]() $\lambda _n$
. In particular,
$\lambda _n$
. In particular,
![]() $U(V)$
acts on
$U(V)$
acts on
![]() ${\mathcal {N}}$
. The analog of the formal uniformization (6.5) of
${\mathcal {N}}$
. The analog of the formal uniformization (6.5) of
![]() $\widehat {{\mathcal {X}}_{K, {\mathcal {O}}_{E_v^{\mathrm {ur}}}}^{ss}}$
holds by [Reference Li and LiuLL22, (4.9)]. For every
$\widehat {{\mathcal {X}}_{K, {\mathcal {O}}_{E_v^{\mathrm {ur}}}}^{ss}}$
holds by [Reference Li and LiuLL22, (4.9)]. For every
![]() $x\in V(E_v)-\{0\} $
, we have the Kudla-Rapoport divisor
$x\in V(E_v)-\{0\} $
, we have the Kudla-Rapoport divisor
![]() ${\mathcal {Z}}(x)$
on
${\mathcal {Z}}(x)$
on
![]() $ {\mathcal {N}} $
, which is a (possibly empty) relative Cartier divisor [Reference Li and LiuLL22, Lemma 2.41]. The analog of Proposition 6.1.5 holds by [Reference Li and LiuLL22, Proposition 4.29] combined with the argument in the proof of Proposition 6.1.5. Though [Reference Li and LiuLL22] only uses even dimensional hermitian spaces, the specific results that we cite hold in the general case by the same proof.
$ {\mathcal {N}} $
, which is a (possibly empty) relative Cartier divisor [Reference Li and LiuLL22, Lemma 2.41]. The analog of Proposition 6.1.5 holds by [Reference Li and LiuLL22, Proposition 4.29] combined with the argument in the proof of Proposition 6.1.5. Though [Reference Li and LiuLL22] only uses even dimensional hermitian spaces, the specific results that we cite hold in the general case by the same proof.
Third, we recall the morphisms
![]() ${\mathcal {N}}_0\to {\mathcal {N}}_1$
defined in [Reference Rapoport, Smithling and ZhangRSZ18, Section 12]. This is rather complicated for general
${\mathcal {N}}_0\to {\mathcal {N}}_1$
defined in [Reference Rapoport, Smithling and ZhangRSZ18, Section 12]. This is rather complicated for general
![]() ${\mathcal {N}}_{2m}\to {\mathcal {N}}_{2m+1}$
. Fortunately, in our case, we have the following convenient description. By [Reference Rapoport, Smithling and ZhangRSZ18, Example 12.2],
${\mathcal {N}}_{2m}\to {\mathcal {N}}_{2m+1}$
. Fortunately, in our case, we have the following convenient description. By [Reference Rapoport, Smithling and ZhangRSZ18, Example 12.2],
![]() $ {\mathcal {N}}_1$
is isomorphic to the disjoint union of two copies of the Lubin-Tate deformation space for the formal
$ {\mathcal {N}}_1$
is isomorphic to the disjoint union of two copies of the Lubin-Tate deformation space for the formal
![]() ${\mathcal {O}}_{F_v}$
-module
${\mathcal {O}}_{F_v}$
-module
![]() ${\mathbb {E}}$
. We write
${\mathbb {E}}$
. We write
![]() ${\mathcal {N}}_1={\mathcal {N}}_1^+\coprod {\mathcal {N}}_1^{-}$
. Recall that B is the unique division quaternion algebra over
${\mathcal {N}}_1={\mathcal {N}}_1^+\coprod {\mathcal {N}}_1^{-}$
. Recall that B is the unique division quaternion algebra over
![]() $F_v $
, and its maximal order
$F_v $
, and its maximal order
![]() ${\mathcal {O}}_B$
is the endomorphism ring of
${\mathcal {O}}_B$
is the endomorphism ring of
![]() ${\mathbb {E}}$
. For
${\mathbb {E}}$
. For
![]() $c\in B^\times $
, we have two closed embeddings (moduli of the canonical lifting)
$c\in B^\times $
, we have two closed embeddings (moduli of the canonical lifting)
![]() ${\mathcal {N}}_0\to {\mathcal {N}}_1^{\pm }$
associated to
${\mathcal {N}}_0\to {\mathcal {N}}_1^{\pm }$
associated to
![]() $c\iota c^{-1}:E_v\hookrightarrow B$
. Let
$c\iota c^{-1}:E_v\hookrightarrow B$
. Let
![]() ${\mathcal {N}}_0^{c,\pm }$
be the union of the images.
${\mathcal {N}}_0^{c,\pm }$
be the union of the images.
Fourth, we need to specify c so that we can use
![]() ${\mathcal {N}}_0^{c,\pm }$
to uniformize
${\mathcal {N}}_0^{c,\pm }$
to uniformize
![]() ${\mathcal {P}}$
. See (6.11) below. Let
${\mathcal {P}}$
. See (6.11) below. Let
![]() $e_v^{(1)}$
be as in 5.1.4. Then
$e_v^{(1)}$
be as in 5.1.4. Then
where the middle is the adjunction isomorphism, and the last isomorphism is compatible with
![]() ${\mathrm {Hom}}_{{\mathcal {O}}_{E_v}}({\mathbb {E}},{\mathbb {X}}_n)_{{\mathbb {Q}}}{\ \simeq \ } V(E_v)$
. And the hermitian form on
${\mathrm {Hom}}_{{\mathcal {O}}_{E_v}}({\mathbb {E}},{\mathbb {X}}_n)_{{\mathbb {Q}}}{\ \simeq \ } V(E_v)$
. And the hermitian form on
![]() $W(E_v)\oplus E_v e_v^{(1)}$
corresponds to
$W(E_v)\oplus E_v e_v^{(1)}$
corresponds to
![]() $-2\varpi _{F_v}{\mathrm {Nm}}_B $
(see the proof of [Reference Rapoport, Smithling and ZhangRSZ17, Lemma 3.5]), where
$-2\varpi _{F_v}{\mathrm {Nm}}_B $
(see the proof of [Reference Rapoport, Smithling and ZhangRSZ17, Lemma 3.5]), where
![]() ${\mathrm {Nm}}_B$
is the reduced norm on B. Let c correspond to
${\mathrm {Nm}}_B$
is the reduced norm on B. Let c correspond to
![]() $\varpi _{E_v} e_v^{(1)}$
. Since
$\varpi _{E_v} e_v^{(1)}$
. Since
![]() $q\left ( e_v^{(1)}\right )\in {\mathcal {O}}_{F_v}^\times $
(see 5.1.2),
$q\left ( e_v^{(1)}\right )\in {\mathcal {O}}_{F_v}^\times $
(see 5.1.2),
![]() $c\in {\mathcal {O}}_B^\times $
(note that
$c\in {\mathcal {O}}_B^\times $
(note that
![]() $v\nmid 2$
here).
$v\nmid 2$
here).
Fifth, we uniformize
![]() ${\mathcal {P}}$
. By Lemma 5.1.6, we have another description of
${\mathcal {P}}$
. By Lemma 5.1.6, we have another description of
![]() ${\mathcal {P}}$
via the diagram (5.5) of morphisms of Shimura varieties. See also Remark 5.1.7. Comparing it with the moduli interpretation of
${\mathcal {P}}$
via the diagram (5.5) of morphisms of Shimura varieties. See also Remark 5.1.7. Comparing it with the moduli interpretation of
![]() ${\mathcal {N}}_0\to {\mathcal {N}}_1$
in [Reference Rapoport, Smithling and ZhangRSZ18, Proposition 12.1], we have the following analog of (6.6):
${\mathcal {N}}_0\to {\mathcal {N}}_1$
in [Reference Rapoport, Smithling and ZhangRSZ18, Proposition 12.1], we have the following analog of (6.6):
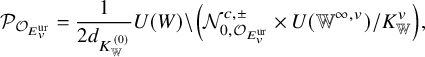 $$ \begin{align} {\mathcal{P}}_{{\mathcal{O}}_{E_v^{\mathrm{ur}}}} =\frac{1}{2d_{K_{\mathbb{W}}^{(0)}}} U(W) \backslash \left( {\mathcal{N}}_{0,{\mathcal{O}}_{E_v^{\mathrm{ur}}}}^{c,\pm}\times U \left( {\mathbb{W}}^{\infty,v}\right)/ K_{\mathbb{W}}^v\right), \end{align} $$
$$ \begin{align} {\mathcal{P}}_{{\mathcal{O}}_{E_v^{\mathrm{ur}}}} =\frac{1}{2d_{K_{\mathbb{W}}^{(0)}}} U(W) \backslash \left( {\mathcal{N}}_{0,{\mathcal{O}}_{E_v^{\mathrm{ur}}}}^{c,\pm}\times U \left( {\mathbb{W}}^{\infty,v}\right)/ K_{\mathbb{W}}^v\right), \end{align} $$
where
![]() $d_{K_{\mathbb {W}}^{(0)}} $
is the degree of the fundamental cycle of
$d_{K_{\mathbb {W}}^{(0)}} $
is the degree of the fundamental cycle of
![]() ${\mathrm {Sh}}({\mathbb {W}})_{K_{\mathbb {W}}^{(0)}}$
. See (5.5). Here, the extra factor 2 comes from Lemma 5.1.5.
${\mathrm {Sh}}({\mathbb {W}})_{K_{\mathbb {W}}^{(0)}}$
. See (5.5). Here, the extra factor 2 comes from Lemma 5.1.5.
Finally, we compute
![]() $ \left ( {\mathcal {Z}}(x)\cdot {\mathcal {N}}_{0}^{c,\pm }\right )_{{\mathcal {N}}}$
. Since
$ \left ( {\mathcal {Z}}(x)\cdot {\mathcal {N}}_{0}^{c,\pm }\right )_{{\mathcal {N}}}$
. Since
![]() $c\in {\mathcal {O}}_B^\times $
, by [Reference Rapoport, Smithling and ZhangRSZ17, Lemma 6.5, Proposition 7.1],
$c\in {\mathcal {O}}_B^\times $
, by [Reference Rapoport, Smithling and ZhangRSZ17, Lemma 6.5, Proposition 7.1],
Here,
![]() ${\mathcal {Y}}\left (\varpi _{E_v}e_v^{(1)}\right )$
is the Kudla-Rapoport divisor on
${\mathcal {Y}}\left (\varpi _{E_v}e_v^{(1)}\right )$
is the Kudla-Rapoport divisor on
![]() ${\mathcal {N}}_1$
, where
${\mathcal {N}}_1$
, where
![]() $\varpi _{E_v}e_v^{(1)}$
lifts. Let
$\varpi _{E_v}e_v^{(1)}$
lifts. Let
![]() ${\mathbb {X}}^\perp $
be the direct complement of
${\mathbb {X}}^\perp $
be the direct complement of
![]() ${\mathbb {X}}_1$
in
${\mathbb {X}}_1$
in
![]() ${\mathbb {X}}_n$
, that is,
${\mathbb {X}}_n$
, that is,
![]() ${\mathbb {X}}^\perp =({\mathbb {E}}^2)^{(n-1)/2}$
if n is odd, and
${\mathbb {X}}^\perp =({\mathbb {E}}^2)^{(n-1)/2}$
if n is odd, and
![]() ${\mathbb {X}}^\perp =({\mathbb {E}}^2)^{(n-2)/2} \times {\mathbb {E}}$
is n is even. Let
${\mathbb {X}}^\perp =({\mathbb {E}}^2)^{(n-2)/2} \times {\mathbb {E}}$
is n is even. Let
![]() $ \Lambda _{v,1}^\perp $
be as in 5.1.4. By Lemma 5.1.1 and (6.10),
$ \Lambda _{v,1}^\perp $
be as in 5.1.4. By Lemma 5.1.1 and (6.10),
corresponds to
![]() $\Lambda _v^\perp $
. Then (similar to the deduction of (6.9)) by (6.12) and Gross’ result on canonical lifting [Reference GrossGro86, Proposition 3.3], we have
$\Lambda _v^\perp $
. Then (similar to the deduction of (6.9)) by (6.12) and Gross’ result on canonical lifting [Reference GrossGro86, Proposition 3.3], we have
for
![]() $ x=(x_1,x_2)\in W(E_v)\oplus V^\sharp (E_v) $
with
$ x=(x_1,x_2)\in W(E_v)\oplus V^\sharp (E_v) $
with
![]() $x_1\neq 0$
. Here, the extra factor 2 comes from that
$x_1\neq 0$
. Here, the extra factor 2 comes from that
![]() ${\mathcal {N}}_0^{c,\pm }$
has 2 components.
${\mathcal {N}}_0^{c,\pm }$
has 2 components.
Proposition 6.1.9. Assume that
![]() $g\in P ({\mathbb {A}}_{F,R\cup \{v\}})G({\mathbb {A}}_F^{ R\cup \{v\}})$
and
$g\in P ({\mathbb {A}}_{F,R\cup \{v\}})G({\mathbb {A}}_F^{ R\cup \{v\}})$
and
![]() $k=1$
. Then (6.2) holds.
$k=1$
. Then (6.2) holds.
Proof. As an analog of (6.8), we have
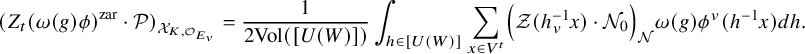 $$ \begin{align*}\left( {Z_t(\omega(g) \phi)}^{\mathrm{zar}}\cdot {\mathcal{P}} \right)_{{\mathcal{X}}_{K,{\mathcal{O}}_{E_v}} } =\frac{1}{2{\mathrm{Vol}}([U(W)])} \int_{ h\in [U(W)]} \sum_{x\in V^t} \left({\mathcal{Z}}(h_v^{-1}x) \cdot{\mathcal{N}}_0\right)_{{\mathcal{N}}}\omega(g) \phi^v(h^{-1} x) dh. \end{align*} $$
$$ \begin{align*}\left( {Z_t(\omega(g) \phi)}^{\mathrm{zar}}\cdot {\mathcal{P}} \right)_{{\mathcal{X}}_{K,{\mathcal{O}}_{E_v}} } =\frac{1}{2{\mathrm{Vol}}([U(W)])} \int_{ h\in [U(W)]} \sum_{x\in V^t} \left({\mathcal{Z}}(h_v^{-1}x) \cdot{\mathcal{N}}_0\right)_{{\mathcal{N}}}\omega(g) \phi^v(h^{-1} x) dh. \end{align*} $$
The rest of the proof is the same as the proof of Proposition 6.1.7, after replacing Lemma 5.2.2 by Lemma 5.2.3.
6.1.3 Infinite places of F
Let
![]() $v\in \infty $
. Under the complex uniformization (4.4) of
$v\in \infty $
. Under the complex uniformization (4.4) of
![]() $ {\mathrm {Sh}}({\mathbb {V}})_{K,E_v}$
,
$ {\mathrm {Sh}}({\mathbb {V}})_{K,E_v}$
,
where
![]() $o:=[0,.. .,0]\in {\mathbb {B}}_n$
, and
$o:=[0,.. .,0]\in {\mathbb {B}}_n$
, and
![]() $d_{{\mathbb {W}},K} $
is the degree of the fundamental cycle of
$d_{{\mathbb {W}},K} $
is the degree of the fundamental cycle of
![]() ${\mathrm {Sh}}({\mathbb {W}})_{K_{\mathbb {W}}}$
. For
${\mathrm {Sh}}({\mathbb {W}})_{K_{\mathbb {W}}}$
. For
![]() $g\in P ({\mathbb {A}}_{F,R})G({\mathbb {A}}_F^{ R})$
, by the definition of
$g\in P ({\mathbb {A}}_{F,R})G({\mathbb {A}}_F^{ R})$
, by the definition of
![]() ${\mathcal {G}}_{Z_t( \cdot )_{E_v},s}$
(above (4.10)), a direct computation gives
${\mathcal {G}}_{Z_t( \cdot )_{E_v},s}$
(above (4.10)), a direct computation gives
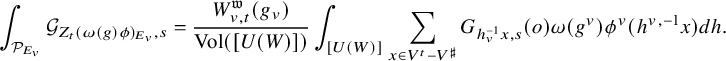 $$ \begin{align} \int_{{\mathcal{P}} _{E_v}}{\mathcal{G}}_{Z_t(\omega(g) \phi)_{E_v},s} =\frac{ W^{\mathfrak{w}}_{v,t}(g_v) }{ {\mathrm{Vol}}([U(W)]) } \int_{ [U(W)]} \sum_{x\in V^t-V^\sharp } G_{h_v^{-1}x,s}(o) \omega(g^v) \phi ^{ v}( h^{v,-1} x)dh. \end{align} $$
$$ \begin{align} \int_{{\mathcal{P}} _{E_v}}{\mathcal{G}}_{Z_t(\omega(g) \phi)_{E_v},s} =\frac{ W^{\mathfrak{w}}_{v,t}(g_v) }{ {\mathrm{Vol}}([U(W)]) } \int_{ [U(W)]} \sum_{x\in V^t-V^\sharp } G_{h_v^{-1}x,s}(o) \omega(g^v) \phi ^{ v}( h^{v,-1} x)dh. \end{align} $$
Now we compare the inner sums in (3.33) and (6.14). Recall the involved functions
![]() $P_s$
and
$P_s$
and
![]() $Q_s$
. See (3.32) and (4.7), respectively. From (3.32), we have
$Q_s$
. See (3.32) and (4.7), respectively. From (3.32), we have
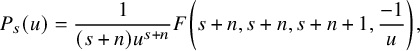 $$ \begin{align*}P_s(u)=\frac{1}{(s+n)u^{s+n}} F\left( s+n, s+n, s+n+1, \frac{-1}{u}\right),\end{align*} $$
$$ \begin{align*}P_s(u)=\frac{1}{(s+n)u^{s+n}} F\left( s+n, s+n, s+n+1, \frac{-1}{u}\right),\end{align*} $$
where F is the hypergeometric function. In particular,
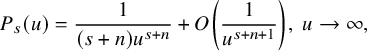 $$ \begin{align} P_s(u)=\frac{1}{(s+n)u^{s+n}}+O\left( \frac{1}{u^{s+n+1}}\right) , \ u\to \infty,\end{align} $$
$$ \begin{align} P_s(u)=\frac{1}{(s+n)u^{s+n}}+O\left( \frac{1}{u^{s+n+1}}\right) , \ u\to \infty,\end{align} $$
where the constant for
![]() $O(\cdot )$
is uniform near
$O(\cdot )$
is uniform near
![]() $s=0$
. We also have
$s=0$
. We also have
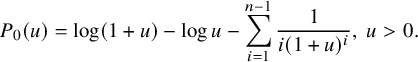 $$ \begin{align} P_0(u)=\log(1+u)-\log u-\sum_{i=1}^{n-1}\frac{1}{i(1+u)^i},\ u>0.\end{align} $$
$$ \begin{align} P_0(u)=\log(1+u)-\log u-\sum_{i=1}^{n-1}\frac{1}{i(1+u)^i},\ u>0.\end{align} $$
From (4.7), we have
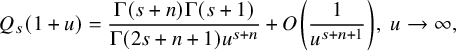 $$ \begin{align} Q_s(1+u)= \frac{\Gamma(s+n)\Gamma(s+1)}{\Gamma(2s+n+1)u^{s+n}} +O\left( \frac{1}{u^{s+n+1}}\right) , \ u\to \infty,\end{align} $$
$$ \begin{align} Q_s(1+u)= \frac{\Gamma(s+n)\Gamma(s+1)}{\Gamma(2s+n+1)u^{s+n}} +O\left( \frac{1}{u^{s+n+1}}\right) , \ u\to \infty,\end{align} $$
where the constant for
![]() $O(\cdot )$
is uniform near
$O(\cdot )$
is uniform near
![]() $s=0$
. We also have
$s=0$
. We also have
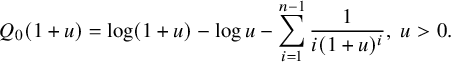 $$ \begin{align} Q_0(1+u)=\log(1+u)-\log u-\sum_{i=1}^{n-1}\frac{1}{i(1+u)^i},\ u>0.\end{align} $$
$$ \begin{align} Q_0(1+u)=\log(1+u)-\log u-\sum_{i=1}^{n-1}\frac{1}{i(1+u)^i},\ u>0.\end{align} $$
Lemma 6.1.10. For
![]() $s_0>-1$
, on
$s_0>-1$
, on
![]() $\{s\in {\mathbb {C}},{\mathrm {Re}} s>s_0\}$
, the sum
$\{s\in {\mathbb {C}},{\mathrm {Re}} s>s_0\}$
, the sum
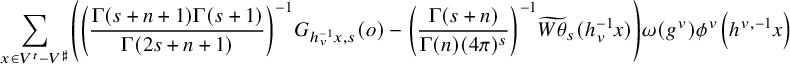 $$ \begin{align*} \sum_{x\in V {{}} ^t-V^\sharp }\left( \left(\frac{\Gamma(s+n+1)\Gamma(s+1)}{\Gamma(2s+n+1) }\right)^{-1}G_{h_v^{-1}x,s}(o)- \left( \frac{\Gamma(s+n)}{\Gamma(n) (4\pi)^{s}}\right)^{-1} \widetilde{W\theta}_{s} (h_v^{-1}x)\right) \omega(g^v) \phi^v \left( h^{v,-1} x\right) \end{align*} $$
$$ \begin{align*} \sum_{x\in V {{}} ^t-V^\sharp }\left( \left(\frac{\Gamma(s+n+1)\Gamma(s+1)}{\Gamma(2s+n+1) }\right)^{-1}G_{h_v^{-1}x,s}(o)- \left( \frac{\Gamma(s+n)}{\Gamma(n) (4\pi)^{s}}\right)^{-1} \widetilde{W\theta}_{s} (h_v^{-1}x)\right) \omega(g^v) \phi^v \left( h^{v,-1} x\right) \end{align*} $$
converges uniformly and absolutely. And its value at
![]() $s=0$
is 0.
$s=0$
is 0.
Proof. We compare the sum in the lemma with the sum in (6.14), which is absolutely convergent by Lemma 4.2.1. By (6.15) and (6.17), the sum in the lemma for s is dominated by a multiple of the sum in (6.14) with s replaced by
![]() $s+1$
. The convergence in the lemma follows. By (6.16) and (6.18), the value at
$s+1$
. The convergence in the lemma follows. By (6.16) and (6.18), the value at
![]() $s=0$
is 0.
$s=0$
is 0.
By Theorem 4.2.2, the integration on the right-hand side of (6.14) admits a meromorphic continuation to s around 0 with a simple pole at
![]() $s=0$
.
$s=0$
.
Proof of Lemma 3.3.12.
For this moment, we consider a general
![]() $ \phi \in \overline {\mathcal {S}}({\mathbb {V}}) $
(without any regularity assumption). The above discussion still holds replacing
$ \phi \in \overline {\mathcal {S}}({\mathbb {V}}) $
(without any regularity assumption). The above discussion still holds replacing
![]() $Z_t(\phi )$
by
$Z_t(\phi )$
by
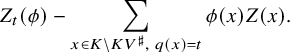 $$ \begin{align*}Z_t(\phi)-\sum_{x\in K\backslash K V^\sharp, \ q(x)=t}\phi ( x) Z(x). \end{align*} $$
$$ \begin{align*}Z_t(\phi)-\sum_{x\in K\backslash K V^\sharp, \ q(x)=t}\phi ( x) Z(x). \end{align*} $$
Then Lemma 3.3.12 follows from (6.14) and the first part of Lemma 6.1.10.
Recall the definition of
![]() ${\mathcal {G}}_{Z_t( \cdot ) _{E_v}}^{\mathrm {aut}}$
in (4.10). Then
${\mathcal {G}}_{Z_t( \cdot ) _{E_v}}^{\mathrm {aut}}$
in (4.10). Then
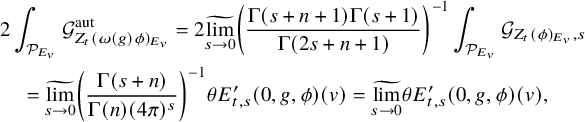 $$ \begin{align*} &2\int_{{\mathcal{P}} _{E_v}}{\mathcal{G}}_{Z_t( \omega(g)\phi) _{E_v}}^{\mathrm{aut}} = 2\widetilde{\lim\limits _{s\to 0}} \left(\frac{\Gamma(s+n+1)\Gamma(s+1)}{\Gamma(2s+n+1) }\right)^{-1} \int_{{\mathcal{P}} _{E_v}}{\mathcal{G}}_{Z_t( \phi)_{E_v},s}\\& \quad = \widetilde{\lim _{s\to 0}}\left( \frac{\Gamma(s+n)}{\Gamma(n) (4\pi)^{s}}\right)^{-1}{\theta E}^{\prime}_{t,s} (0,g,\phi)(v) =\widetilde{\lim _{s\to 0}}{\theta E}^{\prime}_{t,s} (0,g,\phi)(v),\end{align*} $$
$$ \begin{align*} &2\int_{{\mathcal{P}} _{E_v}}{\mathcal{G}}_{Z_t( \omega(g)\phi) _{E_v}}^{\mathrm{aut}} = 2\widetilde{\lim\limits _{s\to 0}} \left(\frac{\Gamma(s+n+1)\Gamma(s+1)}{\Gamma(2s+n+1) }\right)^{-1} \int_{{\mathcal{P}} _{E_v}}{\mathcal{G}}_{Z_t( \phi)_{E_v},s}\\& \quad = \widetilde{\lim _{s\to 0}}\left( \frac{\Gamma(s+n)}{\Gamma(n) (4\pi)^{s}}\right)^{-1}{\theta E}^{\prime}_{t,s} (0,g,\phi)(v) =\widetilde{\lim _{s\to 0}}{\theta E}^{\prime}_{t,s} (0,g,\phi)(v),\end{align*} $$
where both multipliers
![]() $(\cdot )^{-1}$
go to 1 as
$(\cdot )^{-1}$
go to 1 as
![]() $s\to 0$
(this gives the first and third ‘=’), and the second ‘=’ follows from Lemma 6.1.10. Thus, we have proved the following proposition.
$s\to 0$
(this gives the first and third ‘=’), and the second ‘=’ follows from Lemma 6.1.10. Thus, we have proved the following proposition.
Proposition 6.1.11. For
![]() $g\in P ({\mathbb {A}}_{F,R})G({\mathbb {A}}_F^{ R})$
, (6.3) holds for v.
$g\in P ({\mathbb {A}}_{F,R})G({\mathbb {A}}_F^{ R})$
, (6.3) holds for v.
6.2 Improper intersections
In this subsection, we prove the arithmetic mixed Siegel-Weil formula (Theorem 5.2.5). The proof starts in 6.2.1. Before that, let us discuss the strategy.
Lemma 6.2.1. Let
![]() $Y=X\oplus X'$
be the orthogonal direct sum of two non-degenerate quadratic spaces over a non-archimedean local field of characteristic
$Y=X\oplus X'$
be the orthogonal direct sum of two non-degenerate quadratic spaces over a non-archimedean local field of characteristic
![]() $\neq 2$
. Let
$\neq 2$
. Let
![]() $\widehat {\mathcal {S}}(Y- X')_{\overline {\mathbb {Q}}}$
be the space of the Fourier transforms of functions in the space
$\widehat {\mathcal {S}}(Y- X')_{\overline {\mathbb {Q}}}$
be the space of the Fourier transforms of functions in the space
![]() ${\mathcal {S}}(Y- X')_{\overline {\mathbb {Q}}}$
of
${\mathcal {S}}(Y- X')_{\overline {\mathbb {Q}}}$
of
![]() $\overline {\mathbb {Q}}$
-valued Schwartz functions on Y supported on
$\overline {\mathbb {Q}}$
-valued Schwartz functions on Y supported on
![]() $Y-X'$
(the Fourier transforms are clearly also
$Y-X'$
(the Fourier transforms are clearly also
![]() $\overline {\mathbb {Q}}$
-valued). Then
$\overline {\mathbb {Q}}$
-valued). Then
Proof. Since Fourier transform respects orthogonal direct sum, one may assume that
![]() $X'=\{0\}$
. Then the lemma is well known and also easy to check directly.
$X'=\{0\}$
. Then the lemma is well known and also easy to check directly.
We will use the following notation. For a finite set
![]() $S $
of finite places of F, let
$S $
of finite places of F, let
The main difficulty in proving Theorem 5.2.5 is from improper-intersections. However, if we choose a
![]() $\overline {\mathbb {Q}}$
-valued pure tensor
$\overline {\mathbb {Q}}$
-valued pure tensor
![]() $\phi $
that is
$\phi $
that is
![]() ${\mathbb {W}}_v$
-regular at some places v in S, we can prove a
${\mathbb {W}}_v$
-regular at some places v in S, we can prove a
![]() $\operatorname {\mathrm {mod}} \overline {\mathbb {Q}}\log S$
-version of Theorem 5.2.5 for
$\operatorname {\mathrm {mod}} \overline {\mathbb {Q}}\log S$
-version of Theorem 5.2.5 for
![]() $\phi $
, see Lemma 6.2.3. Note that both the CM cycle and the regularity assumption are associated to
$\phi $
, see Lemma 6.2.3. Note that both the CM cycle and the regularity assumption are associated to
![]() ${\mathbb {W}}$
. The same result holds if we replace
${\mathbb {W}}$
. The same result holds if we replace
![]() ${\mathbb {W}}$
by some
${\mathbb {W}}$
by some
![]() ${\mathbb {W}}'$
(and use the corresponding CM cycle and regularity assumption). Accordingly, we make Table 1.
${\mathbb {W}}'$
(and use the corresponding CM cycle and regularity assumption). Accordingly, we make Table 1.
The table displays the
![]() $\operatorname {\mathrm {mod}} \overline {\mathbb {Q}}\log S$
-version of Theorem 5.2.5 under different conditions. The second row indicates that we consider the CM cycle associated to
$\operatorname {\mathrm {mod}} \overline {\mathbb {Q}}\log S$
-version of Theorem 5.2.5 under different conditions. The second row indicates that we consider the CM cycle associated to
![]() ${\mathbb {W}}$
or
${\mathbb {W}}$
or
![]() ${\mathbb {W}}'$
. The second column indicates that we impose the regularity assumption on
${\mathbb {W}}'$
. The second column indicates that we impose the regularity assumption on
![]() $\phi $
associated to
$\phi $
associated to
![]() ${\mathbb {W}}$
or
${\mathbb {W}}$
or
![]() ${\mathbb {W}}'$
, or no regularity assumption. Then a cell indexed by them indicates the
${\mathbb {W}}'$
, or no regularity assumption. Then a cell indexed by them indicates the
![]() $\operatorname {\mathrm {mod}} \overline {\mathbb {Q}}\log S$
-version of Theorem 5.2.5 for the corresponding CM cycle under the corresponding regularity assumption on
$\operatorname {\mathrm {mod}} \overline {\mathbb {Q}}\log S$
-version of Theorem 5.2.5 for the corresponding CM cycle under the corresponding regularity assumption on
![]() $\phi $
.
$\phi $
.
Lemma 6.2.3 gives the cell L of Table 1. Replacing
![]() ${\mathbb {W}}$
by
${\mathbb {W}}$
by
![]() ${\mathbb {W}}'$
, we get L
${\mathbb {W}}'$
, we get L
![]() $'$
.
$'$
.
We want to arrive at the cell C (proved in Corollary 6.2.9), the
![]() $\operatorname {\mathrm {mod}} \overline {\mathbb {Q}}\log S$
-version of Theorem 5.2.5 for the general
$\operatorname {\mathrm {mod}} \overline {\mathbb {Q}}\log S$
-version of Theorem 5.2.5 for the general
![]() $\phi $
. We use the cell B the bridge from L to C. The relation between this cell B and L
$\phi $
. We use the cell B the bridge from L to C. The relation between this cell B and L
![]() $'$
is the ‘switch CM cycles’ indicated in the last paragraph above 1.3. The relation between B and L could be considered as ‘switch regularity assumptions’.
$'$
is the ‘switch CM cycles’ indicated in the last paragraph above 1.3. The relation between B and L could be considered as ‘switch regularity assumptions’.
Instead of considering this cell B directly, we consider the generating series of arithmetic intersection numbers with the difference of the two CM cycles, which is modular by Lemma 4.3.6. Then using Lemma 6.2.1, we prove the
![]() $\operatorname {\mathrm {mod}} \overline {\mathbb {Q}}\log S$
-version of Theorem 5.2.5 for the general
$\operatorname {\mathrm {mod}} \overline {\mathbb {Q}}\log S$
-version of Theorem 5.2.5 for the general
![]() $\phi $
, after replacing the CM cycle by the difference. See Proposition 6.2.5. This gives P of Table 2. Then the combination of L
$\phi $
, after replacing the CM cycle by the difference. See Proposition 6.2.5. This gives P of Table 2. Then the combination of L
![]() $'$
and P/
$'$
and P/
![]() ${\mathbb {W}}'$
proves the cell B. Here, P/
${\mathbb {W}}'$
proves the cell B. Here, P/
![]() ${\mathbb {W}}'$
is the special case of P under the extra regularity assumption associated to
${\mathbb {W}}'$
is the special case of P under the extra regularity assumption associated to
![]() ${\mathbb {W}}'$
.
${\mathbb {W}}'$
.
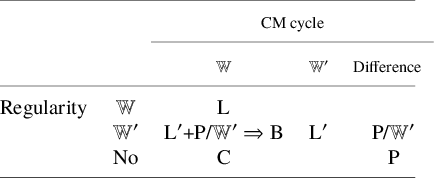
We need to remove ‘
![]() $(\operatorname {\mathrm {mod}} \overline {\mathbb {Q}}\log S)$
’. We will use the following theorem. It is a corollary of Baker’s celebrated theorem on transcendence of logarithms of algebraic numbers (see [Reference WaldschmidtWal03, Theorem 1.1]), and the fact that logarithms of prime numbers are
$(\operatorname {\mathrm {mod}} \overline {\mathbb {Q}}\log S)$
’. We will use the following theorem. It is a corollary of Baker’s celebrated theorem on transcendence of logarithms of algebraic numbers (see [Reference WaldschmidtWal03, Theorem 1.1]), and the fact that logarithms of prime numbers are
![]() ${\mathbb {Q}}$
-linearly independent.
${\mathbb {Q}}$
-linearly independent.
Theorem 6.2.2. Let
![]() $p_1,\ldots ,p_m$
be distinct prime numbers, then
$p_1,\ldots ,p_m$
be distinct prime numbers, then
![]() $\log p_1,\ldots ,\log p_m$
are
$\log p_1,\ldots ,\log p_m$
are
![]() $ \overline {\mathbb {Q}}$
-linearly independent.
$ \overline {\mathbb {Q}}$
-linearly independent.
6.2.1 Set-up
We need the following convenient notation. For a set T of finite places of F, let
For example,
![]() $ {\mathbb {G}}_{ \emptyset }=G\left ({\mathbb {A}}_F^{{{\mathfrak {Ram}}} \cup \infty }\right ) P\left ({\mathbb {A}}_{F,{{\mathfrak {Ram}}}}\right ) $
is the group appearing in Theorem 5.2.5.
$ {\mathbb {G}}_{ \emptyset }=G\left ({\mathbb {A}}_F^{{{\mathfrak {Ram}}} \cup \infty }\right ) P\left ({\mathbb {A}}_{F,{{\mathfrak {Ram}}}}\right ) $
is the group appearing in Theorem 5.2.5.
Below, let
![]() $\phi \in \overline {\mathcal {S}}\left ( {\mathbb {V}} \right ) ^{{{\widetilde K_\Lambda }}}$
be a pure tensor such that
$\phi \in \overline {\mathcal {S}}\left ( {\mathbb {V}} \right ) ^{{{\widetilde K_\Lambda }}}$
be a pure tensor such that
![]() $\phi ^\infty $
is
$\phi ^\infty $
is
![]() $\overline {\mathbb {Q}}$
-valued and
$\overline {\mathbb {Q}}$
-valued and
![]() $\phi _v=1_{\Lambda _v}$
for every finite place v of F nonsplit in E. Let
$\phi _v=1_{\Lambda _v}$
for every finite place v of F nonsplit in E. Let
![]() $K\in {{\widetilde K_\Lambda }}$
stabilize
$K\in {{\widetilde K_\Lambda }}$
stabilize
![]() $\phi $
. Let S be a set of finite places of F, and
$\phi $
. Let S be a set of finite places of F, and
![]() $K'=K_S K_\Lambda ^S$
. Let
$K'=K_S K_\Lambda ^S$
. Let
Let
![]() $f_{{\mathbb {W}}}=f_{{\mathbb {W}},K'}^K$
be defined as in (5.9). We remind the reader that we will use other incoherent hermitian spaces
$f_{{\mathbb {W}}}=f_{{\mathbb {W}},K'}^K$
be defined as in (5.9). We remind the reader that we will use other incoherent hermitian spaces
![]() ${\mathbb {W}}'$
over
${\mathbb {W}}'$
over
![]() ${\mathbb {A}}_E$
of dimension 1. These notations apply to
${\mathbb {A}}_E$
of dimension 1. These notations apply to
![]() ${\mathbb {W}}'$
in the same way.
${\mathbb {W}}'$
in the same way.
Let
![]() $t\in F_{>0}$
. Our goal is to prove that for
$t\in F_{>0}$
. Our goal is to prove that for
![]() $g\in {\mathbb {G}}_{ \emptyset } $
and a suitable set S of finite places of F,
$g\in {\mathbb {G}}_{ \emptyset } $
and a suitable set S of finite places of F,
We also introduce an equation equivalent to (6.20), and both will play roles in the proof of Theorem 5.2.5. The
![]() $\psi _t$
-Whittaker function of the right-hand side of (5.9) (which is the definition of
$\psi _t$
-Whittaker function of the right-hand side of (5.9) (which is the definition of
![]() $f_{{\mathbb {W}}}$
), coincides with the right-hand side of (3.31) up to the last term. Comparing the definition of
$f_{{\mathbb {W}}}$
), coincides with the right-hand side of (3.31) up to the last term. Comparing the definition of
![]() $z_t(g, \phi )_{\mathfrak {e}}^{{\mathcal {L}},{\mathrm {aut}}}$
with the left-hand side of (3.31), (6.20) is equivalent to the following equation:
$z_t(g, \phi )_{\mathfrak {e}}^{{\mathcal {L}},{\mathrm {aut}}}$
with the left-hand side of (3.31), (6.20) is equivalent to the following equation:
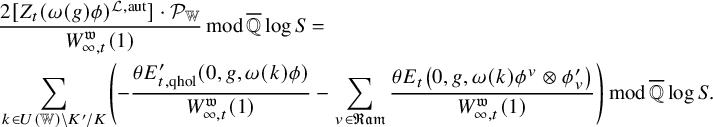 $$ \begin{align} \begin{aligned} & \frac{2 [Z_t(\omega(g) \phi ) ^{{\mathcal{L}},{\mathrm{aut}}}] \cdot {\mathcal{P}} _{\mathbb{W}}}{W^{{\mathfrak{w}}}_{\infty, t}(1)}\operatorname{\mathrm{mod}}\overline{\mathbb{Q}}\log {{S}} = \\ &\sum _{k\in U({\mathbb{W}})\backslash K'/K} \left(- \frac{{\theta E}_{t,{\mathrm{qhol}}}'(0,g,\omega(k)\phi)}{W^{{\mathfrak{w}}}_{\infty, t}(1)}-\sum_{v\in {{\mathfrak{Ram}}}} \frac{ {\theta E} _t \left(0,g,\omega(k)\phi^{v}\otimes \phi_v'\right)}{W^{{\mathfrak{w}}}_{\infty, t}(1)}\right) \operatorname{\mathrm{mod}}\overline{\mathbb{Q}}\log {{S}}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} & \frac{2 [Z_t(\omega(g) \phi ) ^{{\mathcal{L}},{\mathrm{aut}}}] \cdot {\mathcal{P}} _{\mathbb{W}}}{W^{{\mathfrak{w}}}_{\infty, t}(1)}\operatorname{\mathrm{mod}}\overline{\mathbb{Q}}\log {{S}} = \\ &\sum _{k\in U({\mathbb{W}})\backslash K'/K} \left(- \frac{{\theta E}_{t,{\mathrm{qhol}}}'(0,g,\omega(k)\phi)}{W^{{\mathfrak{w}}}_{\infty, t}(1)}-\sum_{v\in {{\mathfrak{Ram}}}} \frac{ {\theta E} _t \left(0,g,\omega(k)\phi^{v}\otimes \phi_v'\right)}{W^{{\mathfrak{w}}}_{\infty, t}(1)}\right) \operatorname{\mathrm{mod}}\overline{\mathbb{Q}}\log {{S}}. \end{aligned} \end{align} $$
6.2.2 Regular test functions
We use Assumption 6.1.2 on regularity here.
Lemma 6.2.3. Assume that S contains a nonempty subset R such that
![]() $\phi _v$
is
$\phi _v$
is
![]() ${\mathbb {W}}_v$
-regular for
${\mathbb {W}}_v$
-regular for
![]() $v\in R$
(i.e., Assumption 6.1.2 holds). Then for
$v\in R$
(i.e., Assumption 6.1.2 holds). Then for
![]() $g\in {\mathbb {G}}_{R}$
, (6.20) holds. Equivalently, (6.21) holds.
$g\in {\mathbb {G}}_{R}$
, (6.20) holds. Equivalently, (6.21) holds.
Remark 6.2.4. The statement in Lemma 6.2.3 becomes more transparent if
![]() $S=R$
. However, we need the flexibility to vary such R in S later.
$S=R$
. However, we need the flexibility to vary such R in S later.
Proof. Recall (5.4),
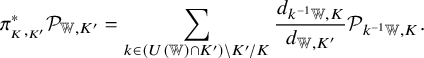 $$ \begin{align*} \pi_{_K,_{K'}}^{*}{\mathcal{P}}_{{\mathbb{W}},K'}=\sum _{k\in (U({\mathbb{W}})\cap K')\backslash K'/K} \frac{d_{k^{-1}{\mathbb{W}},K}}{ d_{{\mathbb{W}},K'}}{\mathcal{P}}_{k^{-1}{\mathbb{W}},K}. \end{align*} $$
$$ \begin{align*} \pi_{_K,_{K'}}^{*}{\mathcal{P}}_{{\mathbb{W}},K'}=\sum _{k\in (U({\mathbb{W}})\cap K')\backslash K'/K} \frac{d_{k^{-1}{\mathbb{W}},K}}{ d_{{\mathbb{W}},K'}}{\mathcal{P}}_{k^{-1}{\mathbb{W}},K}. \end{align*} $$
Here, we choose k such that
![]() $k_v=1$
for
$k_v=1$
for
![]() $v\in S$
or nonsplit in E. (This is possible since
$v\in S$
or nonsplit in E. (This is possible since
![]() $K'=K_S K_\Lambda ^S$
and
$K'=K_S K_\Lambda ^S$
and
![]() $K_v=K_{\Lambda ,v}$
for v nonsplit in E.) Then Assumption 6.1.2 still holds with
$K_v=K_{\Lambda ,v}$
for v nonsplit in E.) Then Assumption 6.1.2 still holds with
![]() ${\mathbb {W}}$
replaced by
${\mathbb {W}}$
replaced by
![]() $k^{-1}{\mathbb {W}}$
. So by Lemma 6.1.3,
$k^{-1}{\mathbb {W}}$
. So by Lemma 6.1.3,
![]() $Z_t(\omega (g) \phi ^\infty ) $
and
$Z_t(\omega (g) \phi ^\infty ) $
and
![]() ${\mathcal {P}}_{k^{-1}{\mathbb {W}},K}$
do not meet on the generic fiber. Then by Lemma 4.4.6, we can apply Corollary A.2.6 at finite places
${\mathcal {P}}_{k^{-1}{\mathbb {W}},K}$
do not meet on the generic fiber. Then by Lemma 4.4.6, we can apply Corollary A.2.6 at finite places
![]() $v\not \in S$
(nothing happens if
$v\not \in S$
(nothing happens if
![]() $K_v=K_{\Lambda ,v}$
). Then we have
$K_v=K_{\Lambda ,v}$
). Then we have
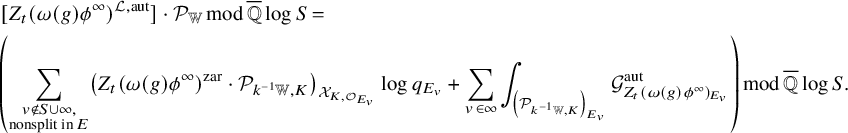 $$ \begin{align*} \begin{aligned} & [Z_t(\omega(g) \phi^\infty) ^{{\mathcal{L}},{\mathrm{aut}}}] \cdot {\mathcal{P}}_{{\mathbb{W}}} \operatorname{\mathrm{mod}}\overline{{\mathbb{Q}}}\log S =\\ & \left( \sum_{\substack{v\not\in S\cup\infty,\\ \text{nonsplit in }E}}\left( Z_t(\omega(g) \phi^\infty) ^{\mathrm{zar}} \cdot {\mathcal{P}}_{k^{-1}{\mathbb{W}},K} \right)_{{\mathcal{X}}_{K,{\mathcal{O}}_{E_v}}}\log q_{E_v} +\sum_{v\in \infty } \int_{\left( {\mathcal{P}}_{k^{-1}{\mathbb{W}},K}\right)_{E_v} }{\mathcal{G}}_{Z_t(\omega(g)\phi^\infty) _{E_v}}^{\mathrm{aut}} \right) \operatorname{\mathrm{mod}}\overline{{\mathbb{Q}}}\log S. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} & [Z_t(\omega(g) \phi^\infty) ^{{\mathcal{L}},{\mathrm{aut}}}] \cdot {\mathcal{P}}_{{\mathbb{W}}} \operatorname{\mathrm{mod}}\overline{{\mathbb{Q}}}\log S =\\ & \left( \sum_{\substack{v\not\in S\cup\infty,\\ \text{nonsplit in }E}}\left( Z_t(\omega(g) \phi^\infty) ^{\mathrm{zar}} \cdot {\mathcal{P}}_{k^{-1}{\mathbb{W}},K} \right)_{{\mathcal{X}}_{K,{\mathcal{O}}_{E_v}}}\log q_{E_v} +\sum_{v\in \infty } \int_{\left( {\mathcal{P}}_{k^{-1}{\mathbb{W}},K}\right)_{E_v} }{\mathcal{G}}_{Z_t(\omega(g)\phi^\infty) _{E_v}}^{\mathrm{aut}} \right) \operatorname{\mathrm{mod}}\overline{{\mathbb{Q}}}\log S. \end{aligned} \end{align*} $$
Comparing this equation with (3.35), (6.21) is implied by Proposition 6.1.4.
6.2.3 CM cycles of degree 0
Let
![]() ${\mathbb {W}}'$
be another incoherent hermitian subspace of
${\mathbb {W}}'$
be another incoherent hermitian subspace of
![]() ${\mathbb {W}}$
and
${\mathbb {W}}$
and
![]() ${\mathcal {P}}_{{\mathbb {W}}'}$
the CM cycle defined accordingly as in 5.1. Since the automorphic Green function is admissible and
${\mathcal {P}}_{{\mathbb {W}}'}$
the CM cycle defined accordingly as in 5.1. Since the automorphic Green function is admissible and
![]() $ {\mathcal {P}}_{{\mathbb {W}} ,E}-{\mathcal {P}}_{{\mathbb {W}}',E} $
has degree 0, by Lemma 4.3.6,
$ {\mathcal {P}}_{{\mathbb {W}} ,E}-{\mathcal {P}}_{{\mathbb {W}}',E} $
has degree 0, by Lemma 4.3.6,
Moreover, (6.22) is independent of the choice of a. We abbreviate
![]() $z(g, \phi )_{{\mathfrak {e}},a}^{{\overline {\mathcal {L}}}}$
to
$z(g, \phi )_{{\mathfrak {e}},a}^{{\overline {\mathcal {L}}}}$
to
![]() $z(g, \phi )_{{\mathfrak {e}}}^{{\overline {\mathcal {L}}}}$
. The 0-th Fourier coefficient of (6.22) is 0. Indeed, by Lemma 4.4.12, the action of
$z(g, \phi )_{{\mathfrak {e}}}^{{\overline {\mathcal {L}}}}$
. The 0-th Fourier coefficient of (6.22) is 0. Indeed, by Lemma 4.4.12, the action of
![]() $K_\Lambda $
on
$K_\Lambda $
on
![]() $ \widehat {\mathrm {Ch}}^{1}_{{\overline {\mathcal {L}}},{\mathbb {C}}}(\widetilde {\mathcal {X}})$
fixes
$ \widehat {\mathrm {Ch}}^{1}_{{\overline {\mathcal {L}}},{\mathbb {C}}}(\widetilde {\mathcal {X}})$
fixes
![]() $c_1(\overline {\mathcal {L}}_K^\vee )$
. The vanishing of the 0-th Fourier coefficient follows from Lemma 5.1.4.
$c_1(\overline {\mathcal {L}}_K^\vee )$
. The vanishing of the 0-th Fourier coefficient follows from Lemma 5.1.4.
Proposition 6.2.5. Assume that the cardinality of S is at least 2. Given
![]() $\phi $
as in 6.2.1, if
$\phi $
as in 6.2.1, if
![]() $K_S$
is small enough (depending on
$K_S$
is small enough (depending on
![]() $\phi _S$
), then for all
$\phi _S$
), then for all
![]() $g\in G({\mathbb {A}}_{F}^\infty )$
,
$g\in G({\mathbb {A}}_{F}^\infty )$
,
Proof. For
![]() $G^{\mathrm {der}}=SU(1,1)$
,
$G^{\mathrm {der}}=SU(1,1)$
,
![]() $G(F_v)=G^{\mathrm {der}}(F_v) K^{\max }_v$
. By Lemma 3.3.8, it is enough to prove (6.23) for
$G(F_v)=G^{\mathrm {der}}(F_v) K^{\max }_v$
. By Lemma 3.3.8, it is enough to prove (6.23) for
![]() $g\in G^{\mathrm {der}}({\mathbb {A}}_F) $
.
$g\in G^{\mathrm {der}}({\mathbb {A}}_F) $
.
We need a lemma whose statement requires some more notations. Since
![]() $G^{\mathrm {der}} {\ \simeq \ } {\mathrm {SL}}_{2,F}$
, by the q-expansion principle for
$G^{\mathrm {der}} {\ \simeq \ } {\mathrm {SL}}_{2,F}$
, by the q-expansion principle for
![]() ${\mathrm {SL}}_{2,F}$
[Reference ChaiCha90], we have
${\mathrm {SL}}_{2,F}$
[Reference ChaiCha90], we have
Here,
![]() ${\mathcal {A}}_{{\mathrm {hol}}}(G^{\mathrm {der}},{\mathfrak {w}})_{\overline {\mathbb {Q}}}$
is as in 2.7 with G replaced by
${\mathcal {A}}_{{\mathrm {hol}}}(G^{\mathrm {der}},{\mathfrak {w}})_{\overline {\mathbb {Q}}}$
is as in 2.7 with G replaced by
![]() $G^{\mathrm {der}}$
, and
$G^{\mathrm {der}}$
, and
![]() ${\mathfrak {w}}$
is understood as the restriction of
${\mathfrak {w}}$
is understood as the restriction of
![]() ${\mathfrak {w}}$
to
${\mathfrak {w}}$
to
![]() $G^{\mathrm {der}}(F_\infty )\cap K^{\max }_v$
for
$G^{\mathrm {der}}(F_\infty )\cap K^{\max }_v$
for
![]() $v\in \infty $
. Thus, we have Fourier coefficients as in 2.7. For
$v\in \infty $
. Thus, we have Fourier coefficients as in 2.7. For
![]() $f\in {\mathcal {A}}_{{\mathrm {hol}}}(G^{\mathrm {der}},{\mathfrak {w}})$
, let
$f\in {\mathcal {A}}_{{\mathrm {hol}}}(G^{\mathrm {der}},{\mathfrak {w}})$
, let
![]() $[f ]$
be its image in
$[f ]$
be its image in
![]() $ {\mathcal {A}}_{{\mathrm {hol}}}(G^{\mathrm {der}},{\mathfrak {w}})_{\overline {\mathbb {Q}}}\otimes _{\overline {\mathbb {Q}}} {\mathbb {C}}/ \overline {\mathbb {Q}}\log {{S}} $
. Then the
$ {\mathcal {A}}_{{\mathrm {hol}}}(G^{\mathrm {der}},{\mathfrak {w}})_{\overline {\mathbb {Q}}}\otimes _{\overline {\mathbb {Q}}} {\mathbb {C}}/ \overline {\mathbb {Q}}\log {{S}} $
. Then the
![]() $ {\mathbb {C}}/ \overline {\mathbb {Q}}\log {{S}}$
-valued locally constant function
$ {\mathbb {C}}/ \overline {\mathbb {Q}}\log {{S}}$
-valued locally constant function
![]() $f_t^\infty \operatorname {\mathrm {mod}}\overline {\mathbb {Q}}\log {{S}}$
on
$f_t^\infty \operatorname {\mathrm {mod}}\overline {\mathbb {Q}}\log {{S}}$
on
![]() $G^{\mathrm {der}}({\mathbb {A}}_F^\infty )$
coincides with the t-th Fourier coefficient of
$G^{\mathrm {der}}({\mathbb {A}}_F^\infty )$
coincides with the t-th Fourier coefficient of
![]() $[f ]$
.
$[f ]$
.
Lemma 6.2.6. Assume that
![]() $\phi _R$
is
$\phi _R$
is
![]() ${\mathbb {W}}_R$
-regular, where
${\mathbb {W}}_R$
-regular, where
![]() $R\subset S$
consists of a single element, and
$R\subset S$
consists of a single element, and
![]() $\phi _{R'}$
is
$\phi _{R'}$
is
![]() ${\mathbb {W}}^{\prime }_{R'}$
-regular, where
${\mathbb {W}}^{\prime }_{R'}$
-regular, where
![]() $R' \subset S\backslash R$
consists of a single element. Then we have the following equality in
$R' \subset S\backslash R$
consists of a single element. Then we have the following equality in
![]() $ {\mathcal {A}}_{{\mathrm {hol}}}(G^{\mathrm {der}},{\mathfrak {w}})_{\overline {\mathbb {Q}}}\otimes _{\overline {\mathbb {Q}}} {\mathbb {C}}/ \overline {\mathbb {Q}}\log {{S}} $
after restriction from G to
$ {\mathcal {A}}_{{\mathrm {hol}}}(G^{\mathrm {der}},{\mathfrak {w}})_{\overline {\mathbb {Q}}}\otimes _{\overline {\mathbb {Q}}} {\mathbb {C}}/ \overline {\mathbb {Q}}\log {{S}} $
after restriction from G to
![]() $G^{\mathrm {der}}$
:
$G^{\mathrm {der}}$
:
Proof. Consider the difference
of the two sides of (6.24), before passing to
![]() ${\mathcal {A}}_{{\mathrm {hol}}}(G^{\mathrm {der}},{\mathfrak {w}})_{\overline {\mathbb {Q}}}\otimes _{\overline {\mathbb {Q}}} {\mathbb {C}}/ \overline {\mathbb {Q}}\log {{S}} $
. By the cuspidality of (6.22) and Lemma 3.3.9 (3), the
${\mathcal {A}}_{{\mathrm {hol}}}(G^{\mathrm {der}},{\mathfrak {w}})_{\overline {\mathbb {Q}}}\otimes _{\overline {\mathbb {Q}}} {\mathbb {C}}/ \overline {\mathbb {Q}}\log {{S}} $
. By the cuspidality of (6.22) and Lemma 3.3.9 (3), the
![]() $0$
-th Fourier coefficient
$0$
-th Fourier coefficient
![]() $ f_0^\infty (g) =0$
for
$ f_0^\infty (g) =0$
for
![]() $g\in {\mathbb {G}}_{\{v_1,v_2\}} .$
Write
$g\in {\mathbb {G}}_{\{v_1,v_2\}} .$
Write
as a finite sum, where
![]() $f_i\in {\mathcal {A}}_{{\mathrm {hol}}}(G^{\mathrm {der}},{\mathfrak {w}})_{\overline {\mathbb {Q}}}$
and
$f_i\in {\mathcal {A}}_{{\mathrm {hol}}}(G^{\mathrm {der}},{\mathfrak {w}})_{\overline {\mathbb {Q}}}$
and
![]() $a_i\in {\mathbb {C}}/ \overline {\mathbb {Q}}\log {{S}}$
are
$a_i\in {\mathbb {C}}/ \overline {\mathbb {Q}}\log {{S}}$
are
![]() $\overline {{\mathbb {Q}}}$
-linearly independent. Then for
$\overline {{\mathbb {Q}}}$
-linearly independent. Then for
![]() $t\in F_{>0}\cup \{0\}$
, the t-th Fourier coefficient of (6.25) is
$t\in F_{>0}\cup \{0\}$
, the t-th Fourier coefficient of (6.25) is
![]() $\sum _{i} f_{i,t}^\infty a_i $
. For
$\sum _{i} f_{i,t}^\infty a_i $
. For
![]() $g\in {\mathbb {G}}_{R\cup R'} \cap G^{\mathrm {der}}({\mathbb {A}}_F)$
,
$g\in {\mathbb {G}}_{R\cup R'} \cap G^{\mathrm {der}}({\mathbb {A}}_F)$
,
![]() $\sum _{i} f_{i,t}^\infty (g) a_i=0 $
for
$\sum _{i} f_{i,t}^\infty (g) a_i=0 $
for
![]() $t\in F_{>0}$
by Lemma 6.2.3 (applied to
$t\in F_{>0}$
by Lemma 6.2.3 (applied to
![]() ${\mathbb {W}},{\mathbb {W}}'$
respectively), and also for
${\mathbb {W}},{\mathbb {W}}'$
respectively), and also for
![]() $t=0$
by the above discussion for the constant term. Thus,
$t=0$
by the above discussion for the constant term. Thus,
![]() $f_{i,t}^\infty (g)=0$
by the
$f_{i,t}^\infty (g)=0$
by the
![]() $\overline {{\mathbb {Q}}}$
-linear independence of
$\overline {{\mathbb {Q}}}$
-linear independence of
![]() $a_i$
’s. So
$a_i$
’s. So
![]() $f_i(g)=0$
. By the density of
$f_i(g)=0$
. By the density of
![]() ${\mathbb {G}}_{R\cup R'} \cap G^{\mathrm {der}}({\mathbb {A}}_F) $
in
${\mathbb {G}}_{R\cup R'} \cap G^{\mathrm {der}}({\mathbb {A}}_F) $
in
![]() $G^{\mathrm {der}}(F)\backslash G^{\mathrm {der}}({\mathbb {A}}_F)$
,
$G^{\mathrm {der}}(F)\backslash G^{\mathrm {der}}({\mathbb {A}}_F)$
,
![]() $f_i(g)=0$
for
$f_i(g)=0$
for
![]() $G^{\mathrm {der}}({\mathbb {A}}_F)$
. So (6.24) holds.
$G^{\mathrm {der}}({\mathbb {A}}_F)$
. So (6.24) holds.
Remark 6.2.7. The density argument can not be applied directly to
![]() $[f|_{G^{\mathrm {der}}({\mathbb {A}}_F)}].$
$[f|_{G^{\mathrm {der}}({\mathbb {A}}_F)}].$
Now we continue the proof of the proposition. Recall that
![]() $w_{v} \in G^{\mathrm {der}}(F_{v})\subset G(F_{v})$
as in 2.5 acts on
$w_{v} \in G^{\mathrm {der}}(F_{v})\subset G(F_{v})$
as in 2.5 acts on
![]() ${\mathcal {S}}({\mathbb {V}}_{v}) $
by Fourier transform (multiplied by the Weil index) via the Weil representation
${\mathcal {S}}({\mathbb {V}}_{v}) $
by Fourier transform (multiplied by the Weil index) via the Weil representation
![]() $\omega $
. See 2.8. By Lemma 6.2.1, for a finite place v of F, there exists a
$\omega $
. See 2.8. By Lemma 6.2.1, for a finite place v of F, there exists a
![]() ${\mathbb {W}}_v$
-regular Schwartz function
${\mathbb {W}}_v$
-regular Schwartz function
![]() $\Phi _{{{v}}} $
on
$\Phi _{{{v}}} $
on
![]() ${\mathbb {V}}(E_v)$
such that
${\mathbb {V}}(E_v)$
such that
![]() $\phi _{{{v}}}= \Phi _{{{v}}}+\omega (w_{v}) \Phi _{{{v}}}.$
Choose
$\phi _{{{v}}}= \Phi _{{{v}}}+\omega (w_{v}) \Phi _{{{v}}}.$
Choose
![]() $K_R , K_{ R'}$
small enough to stabilize
$K_R , K_{ R'}$
small enough to stabilize
![]() $ \Phi _{{R}}, \Phi _{{R'}}$
. By Lemma 6.2.6, (6.23) with
$ \Phi _{{R}}, \Phi _{{R'}}$
. By Lemma 6.2.6, (6.23) with
![]() $\phi _{{R}},\phi _{{R'}}$
replaced by
$\phi _{{R}},\phi _{{R'}}$
replaced by
![]() $\Phi _{{R}},\Phi _{{R'}}$
holds for
$\Phi _{{R}},\Phi _{{R'}}$
holds for
![]() $g\in G^{\mathrm {der}}({\mathbb {A}}_F) $
, and thus, it holds for
$g\in G^{\mathrm {der}}({\mathbb {A}}_F) $
, and thus, it holds for
![]() $gw_{R},gw_{R'},gw_{R}w_{R'}\in G^{\mathrm {der}}({\mathbb {A}}_F) $
replacing g as well. Then by Lemma 3.3.8, (6.23) with one or both of
$gw_{R},gw_{R'},gw_{R}w_{R'}\in G^{\mathrm {der}}({\mathbb {A}}_F) $
replacing g as well. Then by Lemma 3.3.8, (6.23) with one or both of
![]() $\phi _{{R}},\phi _{{R'}}$
replaced by
$\phi _{{R}},\phi _{{R'}}$
replaced by
![]() $ \omega (w_{R}) \Phi _{{R}},\omega (w_{R'}) \Phi _{{R'}}$
respectively holds for
$ \omega (w_{R}) \Phi _{{R}},\omega (w_{R'}) \Phi _{{R'}}$
respectively holds for
![]() $g\in G^{\mathrm {der}}({\mathbb {A}}_F) $
. Thus, including (6.23), we have four equations in total. Taking their sum, we have (6.23) for the original
$g\in G^{\mathrm {der}}({\mathbb {A}}_F) $
. Thus, including (6.23), we have four equations in total. Taking their sum, we have (6.23) for the original
![]() $\phi $
and
$\phi $
and
![]() $g\in G^{\mathrm {der}}({\mathbb {A}}_F) $
.
$g\in G^{\mathrm {der}}({\mathbb {A}}_F) $
.
6.2.4 Remove regularity and log S
Lemma 6.2.8. Assume that the cardinality of S is at least 2. Assume that
![]() $R\subset S$
consists of a single element and
$R\subset S$
consists of a single element and
![]() $\phi _R$
is
$\phi _R$
is
![]() ${\mathbb {W}}^{\prime }_R$
-regular. If
${\mathbb {W}}^{\prime }_R$
-regular. If
![]() $K_S$
is small enough (depending on
$K_S$
is small enough (depending on
![]() $\phi _S$
), then for
$\phi _S$
), then for
![]() $g\in {\mathbb {G}}_{R} $
, (6.20) holds (literally, for
$g\in {\mathbb {G}}_{R} $
, (6.20) holds (literally, for
![]() ${\mathbb {W}}$
rather than
${\mathbb {W}}$
rather than
![]() ${\mathbb {W}}'$
). Equivalently, (6.21) holds.
${\mathbb {W}}'$
). Equivalently, (6.21) holds.
Proof. By Lemma 6.2.3 (with
![]() ${\mathbb {W}}$
replaced by
${\mathbb {W}}$
replaced by
![]() ${{\mathbb {W}}'}$
), for
${{\mathbb {W}}'}$
), for
![]() $g\in {\mathbb {G}}_R $
, we have
$g\in {\mathbb {G}}_R $
, we have
Taking the difference between (6.23) and (6.26), (6.20) follows for
![]() $g\in {\mathbb {G}}_{ R} $
.
$g\in {\mathbb {G}}_{ R} $
.
Corollary 6.2.9. If K is small enough, then for
![]() $g\in {\mathbb {G}}_{\emptyset } $
, (6.20) holds.
$g\in {\mathbb {G}}_{\emptyset } $
, (6.20) holds.
Proof. We prove (6.21), which is equivalent to (6.20). Let
![]() $R\subset S$
consist of a single element. By Lemma 3.3.8 and the Iwasawa decomposition, it is enough to prove (6.21) for
$R\subset S$
consist of a single element. By Lemma 3.3.8 and the Iwasawa decomposition, it is enough to prove (6.21) for
![]() $g\in {\mathbb {G}}_{R}$
. Then by Lemma 3.2.1, Lemma 3.3.14 and Lemma 4.1.4, we may assume that
$g\in {\mathbb {G}}_{R}$
. Then by Lemma 3.2.1, Lemma 3.3.14 and Lemma 4.1.4, we may assume that
![]() $\phi _{R}(0)=0$
. Such a
$\phi _{R}(0)=0$
. Such a
![]() $\phi _{R}$
can be written as a sum of
$\phi _{R}$
can be written as a sum of
![]() ${\mathbb {W}}^{\prime }_{R}$
-regular functions for finitely many
${\mathbb {W}}^{\prime }_{R}$
-regular functions for finitely many
![]() ${\mathbb {W}}'$
’s (in fact, only depending on
${\mathbb {W}}'$
’s (in fact, only depending on
![]() ${\mathbb {W}}^{\prime }_{R}$
). Since (6.21) is linear on
${\mathbb {W}}^{\prime }_{R}$
). Since (6.21) is linear on
![]() $\phi _{R}$
, the corollary follows from Lemma 6.2.8 with
$\phi _{R}$
, the corollary follows from Lemma 6.2.8 with
![]() ${\mathbb {W}}^{\prime R} ={\mathbb {W}}^R$
and
${\mathbb {W}}^{\prime R} ={\mathbb {W}}^R$
and
![]() ${\mathbb {W}}^{\prime }_{R}$
varying.
${\mathbb {W}}^{\prime }_{R}$
varying.
Proof of Theorem 5.2.5.
We may assume that
![]() $\phi ^\infty $
is
$\phi ^\infty $
is
![]() $\overline {\mathbb {Q}}$
-valued. It is enough to prove (5.10) modulo
$\overline {\mathbb {Q}}$
-valued. It is enough to prove (5.10) modulo
![]() $\overline {\mathbb {Q}}\log {{S}}$
. Indeed, choosing another set
$\overline {\mathbb {Q}}\log {{S}}$
. Indeed, choosing another set
![]() $S'$
of 4 places split in E modulo
$S'$
of 4 places split in E modulo
![]() $\overline {\mathbb {Q}}\log {{S'}}$
and requiring S and
$\overline {\mathbb {Q}}\log {{S'}}$
and requiring S and
![]() $S'$
to have no same residue characteristics, then (5.10) follows from Theorem 6.2.2 (i.e., the
$S'$
to have no same residue characteristics, then (5.10) follows from Theorem 6.2.2 (i.e., the
![]() $\overline {{\mathbb {Q}}}$
-linear independence of
$\overline {{\mathbb {Q}}}$
-linear independence of
![]() $\log p$
’s).
$\log p$
’s).
Now we prove (5.10) modulo
![]() $\overline {\mathbb {Q}}\log {{S}}$
by decomposing it into equations established in Corollary 6.2.9 for
$\overline {\mathbb {Q}}\log {{S}}$
by decomposing it into equations established in Corollary 6.2.9 for
![]() $l^{-1}{\mathbb {W}}$
’s where
$l^{-1}{\mathbb {W}}$
’s where
![]() $l\in U({\mathbb {W}})\backslash K_\Lambda / K'$
(instead of a single
$l\in U({\mathbb {W}})\backslash K_\Lambda / K'$
(instead of a single
![]() ${\mathbb {W}}$
, and the double coset is clarified below (5.4)). Note that by Remark 5.2.6, we may shrink K freely. For the left-hand side of (5.10), that is,
${\mathbb {W}}$
, and the double coset is clarified below (5.4)). Note that by Remark 5.2.6, we may shrink K freely. For the left-hand side of (5.10), that is,
![]() $2 z_t(g, \phi ^\infty )_{\mathfrak {e}}^{{\mathcal {L}},{\mathrm {aut}}}\cdot \pi _{_K,{_K}_{\Lambda }}^{*}{\mathcal {P}}_{{\mathbb {W}},{K_\Lambda }}$
, by (5.4), we have
$2 z_t(g, \phi ^\infty )_{\mathfrak {e}}^{{\mathcal {L}},{\mathrm {aut}}}\cdot \pi _{_K,{_K}_{\Lambda }}^{*}{\mathcal {P}}_{{\mathbb {W}},{K_\Lambda }}$
, by (5.4), we have
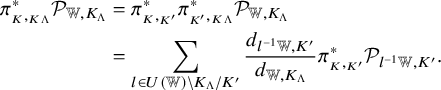 $$ \begin{align} \begin{aligned}\pi_{_K,{_K}_{\Lambda}}^{*}{\mathcal{P}}_{{\mathbb{W}},K_{\Lambda}} &=\pi_{_K,_{K'}}^{*} \pi_{_{K'},{_K}_{\Lambda}}^{*}{\mathcal{P}}_{{\mathbb{W}},K_{\Lambda}} \\ &=\sum_{l\in U({\mathbb{W}})\backslash K_\Lambda/ K'}\frac{d_{l^{-1}{\mathbb{W}},K'}}{ d_{{\mathbb{W}},K_{\Lambda}}}\pi_{_K,_{K'}}^{*} {\mathcal{P}}_{l^{-1}{\mathbb{W}},K'}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned}\pi_{_K,{_K}_{\Lambda}}^{*}{\mathcal{P}}_{{\mathbb{W}},K_{\Lambda}} &=\pi_{_K,_{K'}}^{*} \pi_{_{K'},{_K}_{\Lambda}}^{*}{\mathcal{P}}_{{\mathbb{W}},K_{\Lambda}} \\ &=\sum_{l\in U({\mathbb{W}})\backslash K_\Lambda/ K'}\frac{d_{l^{-1}{\mathbb{W}},K'}}{ d_{{\mathbb{W}},K_{\Lambda}}}\pi_{_K,_{K'}}^{*} {\mathcal{P}}_{l^{-1}{\mathbb{W}},K'}. \end{aligned} \end{align} $$
Now we consider the right-hand side of (5.10); that is,
![]() $ f_{{\mathbb {W}},{K_\Lambda },t}^{K,\infty }(g) $
. We choose l such that
$ f_{{\mathbb {W}},{K_\Lambda },t}^{K,\infty }(g) $
. We choose l such that
![]() $l_v=1$
for
$l_v=1$
for
![]() $v\not \in S$
(this is possible since
$v\not \in S$
(this is possible since
![]() $K'=K_S K_\Lambda ^S$
). In particular,
$K'=K_S K_\Lambda ^S$
). In particular,
![]() $(l{\mathbb {W}})_v={\mathbb {W}}_v$
for
$(l{\mathbb {W}})_v={\mathbb {W}}_v$
for
![]() $v\in {\mathfrak {Ram}}$
so that
$v\in {\mathfrak {Ram}}$
so that
![]() $\phi _v'$
defined in (5.7) in terms of
$\phi _v'$
defined in (5.7) in terms of
![]() ${\mathbb {W}}_v$
is the same as that defined in (5.7) in terms of
${\mathbb {W}}_v$
is the same as that defined in (5.7) in terms of
![]() $(l{\mathbb {W}})_v$
. By the coset decomposition
$(l{\mathbb {W}})_v$
. By the coset decomposition
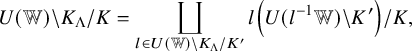 $$ \begin{align*}U({\mathbb{W}})\backslash K_\Lambda/ K =\coprod_{l\in U({\mathbb{W}})\backslash K_\Lambda/ K'} l\left( U({l^{-1}{\mathbb{W}}})\backslash K'\right)/ K ,\end{align*} $$
$$ \begin{align*}U({\mathbb{W}})\backslash K_\Lambda/ K =\coprod_{l\in U({\mathbb{W}})\backslash K_\Lambda/ K'} l\left( U({l^{-1}{\mathbb{W}}})\backslash K'\right)/ K ,\end{align*} $$
and
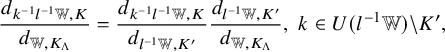 $$ \begin{align*}\frac{d_{k^{-1}l^{-1}{\mathbb{W}},K}}{ d_{{\mathbb{W}},K_\Lambda}} = \frac{d_{k^{-1}l^{-1}{\mathbb{W}},K}}{ d_{ l^{-1}{\mathbb{W}},K'}} \frac{d_{l^{-1}{\mathbb{W}},K'}}{ d_{{\mathbb{W}},K_\Lambda}},\ k\in U({l^{-1}{\mathbb{W}}})\backslash K',\end{align*} $$
$$ \begin{align*}\frac{d_{k^{-1}l^{-1}{\mathbb{W}},K}}{ d_{{\mathbb{W}},K_\Lambda}} = \frac{d_{k^{-1}l^{-1}{\mathbb{W}},K}}{ d_{ l^{-1}{\mathbb{W}},K'}} \frac{d_{l^{-1}{\mathbb{W}},K'}}{ d_{{\mathbb{W}},K_\Lambda}},\ k\in U({l^{-1}{\mathbb{W}}})\backslash K',\end{align*} $$
we deduce from the definition (5.9) of
![]() $ f_{{\mathbb {W}},{K_\Lambda }}^{K} $
that
$ f_{{\mathbb {W}},{K_\Lambda }}^{K} $
that
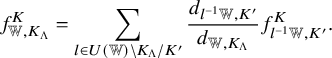 $$ \begin{align} f_{{\mathbb{W}},K_\Lambda}^K =\sum_{l\in U({\mathbb{W}})\backslash K_\Lambda/ K'} \frac{d_{l^{-1}{\mathbb{W}},K'}}{ d_{{\mathbb{W}},K_{\Lambda}}}f_{l^{-1}{\mathbb{W}},K'}^K. \end{align} $$
$$ \begin{align} f_{{\mathbb{W}},K_\Lambda}^K =\sum_{l\in U({\mathbb{W}})\backslash K_\Lambda/ K'} \frac{d_{l^{-1}{\mathbb{W}},K'}}{ d_{{\mathbb{W}},K_{\Lambda}}}f_{l^{-1}{\mathbb{W}},K'}^K. \end{align} $$
By Corollary 6.2.9, (6.27) and (6.28) imply (5.10) modulo
![]() $\overline {\mathbb {Q}}\log {{S}}$
.
$\overline {\mathbb {Q}}\log {{S}}$
.
A Admissible divisors
We recall S. Zhang’s theory of admissible cycles on a polarized arithmetic variety [Reference ZhangZha20]. They are cycles with ‘harmonic curvatures’. We only consider admissible divisors [Reference ZhangZha20, 2.5, Admissible cycles]. In particular, for a divisor on the generic fiber, we have its admissible extensions. With an extra local condition, we have the normalized admissible extension. The functoriality of (normalized) admissibile cycles under flat morphisms is important for us.
It is worth mentioning that while the normalized admissible extension is defined purely locally and at the level of divisors, a global lifting of a divisors class on the generic fiber is defined (and it is called
![]() $\mathsf {L}$
-lifting) in [Reference ZhangZha20, Corollary 2.5.7]. It is an admissible extension [Reference ZhangZha20, Corollary 2.5.7 (1)] with vanishing Faltings height [Reference ZhangZha20, Corollary 2.5.7 (2)]. They will not be further discussed in this appendix, and are not needed in this paper.
$\mathsf {L}$
-lifting) in [Reference ZhangZha20, Corollary 2.5.7]. It is an admissible extension [Reference ZhangZha20, Corollary 2.5.7 (1)] with vanishing Faltings height [Reference ZhangZha20, Corollary 2.5.7 (2)]. They will not be further discussed in this appendix, and are not needed in this paper.
A.1 Deligne-Mumford stacks over a Dedekind domain
Let
![]() ${\mathcal {O}}$
be a Dedekind domain. Let
${\mathcal {O}}$
be a Dedekind domain. Let
![]() ${\mathcal {M}}$
be a connected regular Deligne-Mumford stack proper flat over
${\mathcal {M}}$
be a connected regular Deligne-Mumford stack proper flat over
![]() $\operatorname {\mathrm {Spec}} {\mathcal {O}}$
of relative dimension n. Let M be its generic fiber. Definitions of cycles, rational equivalence, proper pushforward and flat pullback for (Chow) cycles are applicable to Deligne-Mumford stacks over
$\operatorname {\mathrm {Spec}} {\mathcal {O}}$
of relative dimension n. Let M be its generic fiber. Definitions of cycles, rational equivalence, proper pushforward and flat pullback for (Chow) cycles are applicable to Deligne-Mumford stacks over
![]() $\operatorname {\mathrm {Spec}} {\mathcal {O}}$
. See [Reference GilletGil09]. Let
$\operatorname {\mathrm {Spec}} {\mathcal {O}}$
. See [Reference GilletGil09]. Let
![]() $Z^{*}(M)$
(resp.
$Z^{*}(M)$
(resp.
![]() $Z^{*}({\mathcal {M}})$
) be the graded
$Z^{*}({\mathcal {M}})$
) be the graded
![]() ${\mathbb {Q}}$
-vector space of cycles on M (resp.
${\mathbb {Q}}$
-vector space of cycles on M (resp.
![]() $ {\mathcal {M}}$
) with
$ {\mathcal {M}}$
) with
![]() ${\mathbb {Q}}$
-coefficients. Let
${\mathbb {Q}}$
-coefficients. Let
![]() ${\mathrm {Ch}}^{*}(M)$
and
${\mathrm {Ch}}^{*}(M)$
and
![]() ${\mathrm {Ch}}^{*}({\mathcal {M}})$
be the
${\mathrm {Ch}}^{*}({\mathcal {M}})$
be the
![]() ${\mathbb {Q}}$
-vector spaces of Chow cycles.
${\mathbb {Q}}$
-vector spaces of Chow cycles.
We shall only work under the following convenient assumption, which simplifies the local intersection theory. For every closed point
![]() $s\in \operatorname {\mathrm {Spec}} {\mathcal {O}}$
, let
$s\in \operatorname {\mathrm {Spec}} {\mathcal {O}}$
, let
![]() ${\mathcal {O}}_s$
be the completed local ring.
${\mathcal {O}}_s$
be the completed local ring.
Assumption A.1.1. (1) There is a finite subset
![]() $S\subset \operatorname {\mathrm {Spec}} {\mathcal {O}}$
, a regular scheme
$S\subset \operatorname {\mathrm {Spec}} {\mathcal {O}}$
, a regular scheme
![]() $\widetilde {\mathcal {M}}$
proper flat over
$\widetilde {\mathcal {M}}$
proper flat over
![]() $\operatorname {\mathrm {Spec}} {\mathcal {O}}-S$
and a finite étale morphism
$\operatorname {\mathrm {Spec}} {\mathcal {O}}-S$
and a finite étale morphism
![]() $\pi :\widetilde {\mathcal {M}}\to {\mathcal {M}}|_{\operatorname {\mathrm {Spec}} {\mathcal {O}}-S}$
over
$\pi :\widetilde {\mathcal {M}}\to {\mathcal {M}}|_{\operatorname {\mathrm {Spec}} {\mathcal {O}}-S}$
over
![]() $\operatorname {\mathrm {Spec}} {\mathcal {O}}-S$
.
$\operatorname {\mathrm {Spec}} {\mathcal {O}}-S$
.
(2) For every
![]() $s\in S$
, there is a regular scheme
$s\in S$
, there is a regular scheme
![]() $\widetilde {\mathcal {M}}$
proper flat over
$\widetilde {\mathcal {M}}$
proper flat over
![]() $\operatorname {\mathrm {Spec}} {\mathcal {O}}_s$
and a finite étale morphism
$\operatorname {\mathrm {Spec}} {\mathcal {O}}_s$
and a finite étale morphism
![]() $\pi :\widetilde {\mathcal {M}}\to {\mathcal {M}}_{\operatorname {\mathrm {Spec}} {\mathcal {O}}_s}$
over
$\pi :\widetilde {\mathcal {M}}\to {\mathcal {M}}_{\operatorname {\mathrm {Spec}} {\mathcal {O}}_s}$
over
![]() $\operatorname {\mathrm {Spec}} {\mathcal {O}}_s$
.
$\operatorname {\mathrm {Spec}} {\mathcal {O}}_s$
.
In either case (1) or (2), we call
![]() $\widetilde {\mathcal {M}}$
a covering of
$\widetilde {\mathcal {M}}$
a covering of
![]() $ {\mathcal {M}}|_{\operatorname {\mathrm {Spec}} {\mathcal {O}}-S}$
or
$ {\mathcal {M}}|_{\operatorname {\mathrm {Spec}} {\mathcal {O}}-S}$
or
![]() $ {\mathcal {M}}_{\operatorname {\mathrm {Spec}} {\mathcal {O}}_s}$
. For another covering
$ {\mathcal {M}}_{\operatorname {\mathrm {Spec}} {\mathcal {O}}_s}$
. For another covering
![]() $\widetilde {\mathcal {M}}'$
, the fiber product is regular and proper flat over
$\widetilde {\mathcal {M}}'$
, the fiber product is regular and proper flat over
![]() $\operatorname {\mathrm {Spec}} {\mathcal {O}}-S$
or
$\operatorname {\mathrm {Spec}} {\mathcal {O}}-S$
or
![]() $\operatorname {\mathrm {Spec}} {\mathcal {O}}_s$
, making a third covering.
$\operatorname {\mathrm {Spec}} {\mathcal {O}}_s$
, making a third covering.
A line bundle
![]() ${\mathcal {L}}$
on
${\mathcal {L}}$
on
![]() ${\mathcal {M}}$
is ample if in both cases (1) and (2), its pullback to some covering is ample. And it is relatively positive if
${\mathcal {M}}$
is ample if in both cases (1) and (2), its pullback to some covering is ample. And it is relatively positive if
![]() $ \deg {\mathcal {L}}|_ C> 0$
for every closed curve (1-dimensional closed substack) C in every special fiber of
$ \deg {\mathcal {L}}|_ C> 0$
for every closed curve (1-dimensional closed substack) C in every special fiber of
![]() ${\mathcal {M}}$
. It is routine to check that the definition does not depend on the choice of covering by making a third covering. The following notions, which are used in the whole paper, are also defined via coverings: intersection number, Chern class and Zariski closure.
${\mathcal {M}}$
. It is routine to check that the definition does not depend on the choice of covering by making a third covering. The following notions, which are used in the whole paper, are also defined via coverings: intersection number, Chern class and Zariski closure.
A.2 Local cycles
Assume that
![]() ${\mathcal {O}}$
is a completed local ring (so a DVR). Let s be the unique closed point of
${\mathcal {O}}$
is a completed local ring (so a DVR). Let s be the unique closed point of
![]() $\operatorname {\mathrm {Spec}} {\mathcal {O}}$
. We will use two intersection pairings. First, for
$\operatorname {\mathrm {Spec}} {\mathcal {O}}$
. We will use two intersection pairings. First, for
![]() $X\in Z ^i({\mathcal {M}} )$
and
$X\in Z ^i({\mathcal {M}} )$
and
![]() $Y\in Z^{n+1-i}({\mathcal {M}} )$
with disjoint supports on M, define
$Y\in Z^{n+1-i}({\mathcal {M}} )$
with disjoint supports on M, define
where
![]() $\pi $
is a covering morphism and the latter intersection number is a usual one, defined either using Serre’s
$\pi $
is a covering morphism and the latter intersection number is a usual one, defined either using Serre’s
![]() ${\mathrm {Tor}}$
-formula (equivalently rephrased as the Euler-Poincaré characteristic of the derived tensor product
${\mathrm {Tor}}$
-formula (equivalently rephrased as the Euler-Poincaré characteristic of the derived tensor product
![]() ${\mathcal {O}}_{\pi ^{*}(X)}\bigotimes ^{\mathbb {L}} {\mathcal {O}}_{\pi ^{*}(Y)}$
([Reference Gillet and SouléGS90, 4.3.8 (iv)]), or as a cohomological pairing.
${\mathcal {O}}_{\pi ^{*}(X)}\bigotimes ^{\mathbb {L}} {\mathcal {O}}_{\pi ^{*}(Y)}$
([Reference Gillet and SouléGS90, 4.3.8 (iv)]), or as a cohomological pairing.
Second, let
![]() ${\mathcal {M}}_s$
be the special fiber of
${\mathcal {M}}_s$
be the special fiber of
![]() ${\mathcal {M}}$
and
${\mathcal {M}}$
and
![]() $Z_s^1({\mathcal {M}} )\subset Z^1({\mathcal {M}})$
the subspace of divisors supported on
$Z_s^1({\mathcal {M}} )\subset Z^1({\mathcal {M}})$
the subspace of divisors supported on
![]() ${\mathcal {M}}_s$
. We use the intersection pairing between
${\mathcal {M}}_s$
. We use the intersection pairing between
![]() $ Z_s^1({\mathcal {M}} )$
and an n-tuple of
$ Z_s^1({\mathcal {M}} )$
and an n-tuple of
![]() ${\mathbb {Q}}$
-Cartier divisors as in [Reference FultonFul84, Example 6.5.1] (defined using a covering as in (A.1)):
${\mathbb {Q}}$
-Cartier divisors as in [Reference FultonFul84, Example 6.5.1] (defined using a covering as in (A.1)):
It only depends on the rational equivalence classes of the Cartier divisors. (In particular, by fixing
![]() $n-1$
rational equivalence classes of Cartier divisors, we get a pairing between
$n-1$
rational equivalence classes of Cartier divisors, we get a pairing between
![]() $Z_s^1({\mathcal {M}} )$
and
$Z_s^1({\mathcal {M}} )$
and
![]() $ Z^{1}({\mathcal {M}} )$
. This view point might be helpful.) In this subsection, we will use this second intersection pairing until Corollary A.2.6.
$ Z^{1}({\mathcal {M}} )$
. This view point might be helpful.) In this subsection, we will use this second intersection pairing until Corollary A.2.6.
Let
![]() ${\mathcal {L}}$
be a line bundle on
${\mathcal {L}}$
be a line bundle on
![]() ${\mathcal {M}}$
. Let
${\mathcal {M}}$
. Let
![]() $B^1_{\mathcal {L}}({\mathcal {M}})\subset Z_s^{1}( {{\mathcal {M}} }$
be the kernel of the linear form
$B^1_{\mathcal {L}}({\mathcal {M}})\subset Z_s^{1}( {{\mathcal {M}} }$
be the kernel of the linear form
![]() $Z_s^{1}( {{\mathcal {M}} }) \to {\mathbb {Q}}$
defined by intersection with
$Z_s^{1}( {{\mathcal {M}} }) \to {\mathbb {Q}}$
defined by intersection with
![]() $ c_1({\mathcal {L}})^{n}$
. Assume that the generic fiber of
$ c_1({\mathcal {L}})^{n}$
. Assume that the generic fiber of
![]() ${\mathcal {L}} $
is ample and
${\mathcal {L}} $
is ample and
![]() ${\mathcal {L}}$
is relatively positive. The local index theorem [Reference ZhangZha20, Lemma 2.5.1] (see also [Reference Yuan and ZhangYZ17]) implies the following lemma.
${\mathcal {L}}$
is relatively positive. The local index theorem [Reference ZhangZha20, Lemma 2.5.1] (see also [Reference Yuan and ZhangYZ17]) implies the following lemma.
Lemma A.2.1. The pairing
![]() $(X,Y)\mapsto X\cdot c_1({\mathcal {L}})^{n-1} \cdot Y$
on
$(X,Y)\mapsto X\cdot c_1({\mathcal {L}})^{n-1} \cdot Y$
on
![]() $B_{\mathcal {L}}^1({\mathcal {M}})$
is negative definite.
$B_{\mathcal {L}}^1({\mathcal {M}})$
is negative definite.
Let
![]() $Z_{\mathcal {L}}^1({\mathcal {M}} )$
be the orthogonal complement of
$Z_{\mathcal {L}}^1({\mathcal {M}} )$
be the orthogonal complement of
![]() $B_{\mathcal {L}}^1({\mathcal {M}})$
under the pairing
$B_{\mathcal {L}}^1({\mathcal {M}})$
under the pairing
![]() $X\cdot c_1({\mathcal {L}})^{n-1} \cdot Y$
; that is,
$X\cdot c_1({\mathcal {L}})^{n-1} \cdot Y$
; that is,
Then by definition, we have a decomposition
and an exact sequence
For a prime cycle X on M, let
![]() $X^{\mathrm {zar}}$
be its Zariski closure on
$X^{\mathrm {zar}}$
be its Zariski closure on
![]() ${\mathcal {M}}$
. Extend the definition by linearity.
${\mathcal {M}}$
. Extend the definition by linearity.
Definition A.2.2. (1) We call
![]() $Z_{\mathcal {L}}^1({\mathcal {M}} )$
the space of admissible divisors with respect to
$Z_{\mathcal {L}}^1({\mathcal {M}} )$
the space of admissible divisors with respect to
![]() ${\mathcal {L}}$
.
${\mathcal {L}}$
.
(2) For
![]() $X\in Z^1(M)$
, an admissible extension with respect to
$X\in Z^1(M)$
, an admissible extension with respect to
![]() ${\mathcal {L}}$
is an element in its preimage by
${\mathcal {L}}$
is an element in its preimage by
![]() $ Z_{\mathcal {L}}^1({\mathcal {M}} )\to Z^1(M)$
. Define the normalized admissible extension
$ Z_{\mathcal {L}}^1({\mathcal {M}} )\to Z^1(M)$
. Define the normalized admissible extension
![]() $X^{\mathcal {L}}$
of X with respect to
$X^{\mathcal {L}}$
of X with respect to
![]() ${\mathcal {L}}$
to be the projection of
${\mathcal {L}}$
to be the projection of
![]() $X^{\mathrm {zar}}$
to
$X^{\mathrm {zar}}$
to
![]() $Z_{\mathcal {L}}^1({\mathcal {M}} )$
in (A.2).
$Z_{\mathcal {L}}^1({\mathcal {M}} )$
in (A.2).
Remark A.2.3. In terms of [Reference ZhangZha20, Corollary 2.5.7 (1)],
![]() $Z_{\mathcal {L}}^1({\mathcal {M}} )\subset Z ^1({\mathcal {M}} )$
is the subspace of cycles X with ‘harmonic curvatures’ (compare with Remark A.3.2 (3)); that is, the element in
$Z_{\mathcal {L}}^1({\mathcal {M}} )\subset Z ^1({\mathcal {M}} )$
is the subspace of cycles X with ‘harmonic curvatures’ (compare with Remark A.3.2 (3)); that is, the element in
![]() $ {\mathrm {Hom}}_{\mathbb {Q}}\left ( Z_s^{1}({\mathcal {M}} ),{\mathbb {Q}}\right )$
defined by intersection with
$ {\mathrm {Hom}}_{\mathbb {Q}}\left ( Z_s^{1}({\mathcal {M}} ),{\mathbb {Q}}\right )$
defined by intersection with
![]() $ X \cdot c_1({\mathcal {L}})^{n-1} $
is a multiple of the one defined by intersection with
$ X \cdot c_1({\mathcal {L}})^{n-1} $
is a multiple of the one defined by intersection with
![]() $ c_1({\mathcal {L}})^{n} $
.
$ c_1({\mathcal {L}})^{n} $
.
Then by definition, we have the following lemma.
Lemma A.2.4. Assume that
![]() ${\mathcal {M}}$
is smooth over
${\mathcal {M}}$
is smooth over
![]() $\operatorname {\mathrm {Spec}} {\mathcal {O}}$
. Then
$\operatorname {\mathrm {Spec}} {\mathcal {O}}$
. Then
![]() $B_{\mathcal {L}}^1({\mathcal {M}})=0$
. In particular, for
$B_{\mathcal {L}}^1({\mathcal {M}})=0$
. In particular, for
![]() $X\in Z^1(M)$
,
$X\in Z^1(M)$
,
![]() $X^{\mathrm {zar}}$
is the normalized admissible extension.
$X^{\mathrm {zar}}$
is the normalized admissible extension.
By the projection formula (and the commutativity of taking Zariski closure and closed pushforward/flat pullback), we easily deduce the following lemma.
Lemma A.2.5. Let
![]() ${\mathcal {M}}'$
be a regular Deligne-Mumford stack and
${\mathcal {M}}'$
be a regular Deligne-Mumford stack and
![]() $ f: {\mathcal {M}}'\to {\mathcal {M}}$
a finite flat morphism. Let
$ f: {\mathcal {M}}'\to {\mathcal {M}}$
a finite flat morphism. Let
![]() ${\mathcal {L}}'$
be the pullback of
${\mathcal {L}}'$
be the pullback of
![]() ${\mathcal {L}}$
to
${\mathcal {L}}$
to
![]() ${\mathcal {M}}'$
. Consider
${\mathcal {M}}'$
. Consider
![]() ${\mathcal {M}}'$
as a Deligne-Mumford stack over
${\mathcal {M}}'$
as a Deligne-Mumford stack over
![]() $\operatorname {\mathrm {Spec}} {\mathcal {O}}$
via f and
$\operatorname {\mathrm {Spec}} {\mathcal {O}}$
via f and
![]() ${\mathcal {M}}$
. Then
${\mathcal {M}}$
. Then
![]() $f^{*}\left ( B_{\mathcal {L}}^1({\mathcal {M}})\right )\subset B_{{\mathcal {L}}'}^1({\mathcal {M}}') $
,
$f^{*}\left ( B_{\mathcal {L}}^1({\mathcal {M}})\right )\subset B_{{\mathcal {L}}'}^1({\mathcal {M}}') $
,
![]() $f_*\left ( B_{{\mathcal {L}}'}^1({\mathcal {M}}')\right )= B_{{\mathcal {L}}}^1({\mathcal {M}}) $
,
$f_*\left ( B_{{\mathcal {L}}'}^1({\mathcal {M}}')\right )= B_{{\mathcal {L}}}^1({\mathcal {M}}) $
,
![]() $f^{*}\left ( Z_{\mathcal {L}}^1({\mathcal {M}})\right )\subset Z_{{\mathcal {L}}'}^1({\mathcal {M}}') $
and
$f^{*}\left ( Z_{\mathcal {L}}^1({\mathcal {M}})\right )\subset Z_{{\mathcal {L}}'}^1({\mathcal {M}}') $
and
![]() $f_*\left ( Z_{{\mathcal {L}}'}^1({\mathcal {M}}')\right )= Z_{{\mathcal {L}}}^1({\mathcal {M}}) .$
In particular, the decomposition (A.2) and the formation of normalized admissible extension are preserved under pullback and pushforward by f.
$f_*\left ( Z_{{\mathcal {L}}'}^1({\mathcal {M}}')\right )= Z_{{\mathcal {L}}}^1({\mathcal {M}}) .$
In particular, the decomposition (A.2) and the formation of normalized admissible extension are preserved under pullback and pushforward by f.
Corollary A.2.6. In Lemma A.2.5 with f finite, let
![]() $M'$
be the generic fiber of
$M'$
be the generic fiber of
![]() ${\mathcal {M}}'$
and assume that
${\mathcal {M}}'$
and assume that
![]() ${\mathcal {M}}\to \operatorname {\mathrm {Spec}} {\mathcal {O}}$
is smooth. Let
${\mathcal {M}}\to \operatorname {\mathrm {Spec}} {\mathcal {O}}$
is smooth. Let
![]() $X\in Z^1(M')$
and
$X\in Z^1(M')$
and
![]() $Y\in Z^{n}({\mathcal {M}})$
such that X and
$Y\in Z^{n}({\mathcal {M}})$
such that X and
![]() $f^{*}(Y)$
have disjoint supports. Then we have
$f^{*}(Y)$
have disjoint supports. Then we have
![]() $X^{\mathcal {L}}\cdot f^{*}(Y)=X^{\mathrm {zar}}\cdot f^{*}(Y)$
.
$X^{\mathcal {L}}\cdot f^{*}(Y)=X^{\mathrm {zar}}\cdot f^{*}(Y)$
.
A.3 Admissible arithmetic Chow group of divisors
Now let
![]() ${\mathcal {O}}$
be the ring of integers of a number field. In particular,
${\mathcal {O}}$
be the ring of integers of a number field. In particular,
![]() ${\mathcal {M}}_{\mathbb {C}}:={\mathcal {M}} \otimes _{\mathbb {Z}} {\mathbb {C}}=M\otimes _{\mathbb {Q}}{\mathbb {C}}$
is a complex orbifold. Let
${\mathcal {M}}_{\mathbb {C}}:={\mathcal {M}} \otimes _{\mathbb {Z}} {\mathbb {C}}=M\otimes _{\mathbb {Q}}{\mathbb {C}}$
is a complex orbifold. Let
![]() $\overline {\mathcal {L}}=({\mathcal {L}},\|\cdot \|)$
be a hermitian line bundle on
$\overline {\mathcal {L}}=({\mathcal {L}},\|\cdot \|)$
be a hermitian line bundle on
![]() ${\mathcal {M}}$
such that the generic fiber of
${\mathcal {M}}$
such that the generic fiber of
![]() ${\mathcal {L}} $
is ample,
${\mathcal {L}} $
is ample,
![]() ${\mathcal {L}}$
is relatively positive, and the hermitian metric
${\mathcal {L}}$
is relatively positive, and the hermitian metric
![]() $\|\cdot \|$
is invariant under the involution induced by complex conjugation. See [Reference Gillet and SouléGS90, 3.1.2]. In particular, endowing
$\|\cdot \|$
is invariant under the involution induced by complex conjugation. See [Reference Gillet and SouléGS90, 3.1.2]. In particular, endowing
![]() ${\mathcal {M}}_{\mathbb {C}} $
with the Chern curvature form
${\mathcal {M}}_{\mathbb {C}} $
with the Chern curvature form
![]() ${\mathrm {curv}}\left ( \overline {\mathcal {L}}_{\mathbb {C}}\right )$
, it is a smooth Kähler orbifold.
${\mathrm {curv}}\left ( \overline {\mathcal {L}}_{\mathbb {C}}\right )$
, it is a smooth Kähler orbifold.
Definition A.3.1. (1) The group
![]() ${\widehat {Z}}^1_{{\overline {\mathcal {L}}},{\mathbb {C}}}({\mathcal {M}})$
of admissible (with respect to
${\widehat {Z}}^1_{{\overline {\mathcal {L}}},{\mathbb {C}}}({\mathcal {M}})$
of admissible (with respect to
![]() $\overline {\mathcal {L}}$
) arithmetic divisors on
$\overline {\mathcal {L}}$
) arithmetic divisors on
![]() ${\mathcal {M}}$
with
${\mathcal {M}}$
with
![]() ${\mathbb {C}}$
-coefficients is the
${\mathbb {C}}$
-coefficients is the
![]() ${\mathbb {C}}$
-vector space of pairs
${\mathbb {C}}$
-vector space of pairs
![]() $(X,g)$
where
$(X,g)$
where
-
•
 $X\in Z^1({\mathcal {M}}) _{\mathbb {C}} $
such that for every closed point
$X\in Z^1({\mathcal {M}}) _{\mathbb {C}} $
such that for every closed point
 $s\in \operatorname {\mathrm {Spec}} {\mathcal {O}}$
, the restriction of X to
$s\in \operatorname {\mathrm {Spec}} {\mathcal {O}}$
, the restriction of X to
 $ {\mathcal {M}}_{{\mathcal {O}}_s} $
is contained in
$ {\mathcal {M}}_{{\mathcal {O}}_s} $
is contained in
 $Z^1_{{\mathcal {L}}_{{\mathcal {O}}_s} }\left ( {\mathcal {M}}_{{\mathcal {O}}_s}\right )_{\mathbb {C}}$
,
$Z^1_{{\mathcal {L}}_{{\mathcal {O}}_s} }\left ( {\mathcal {M}}_{{\mathcal {O}}_s}\right )_{\mathbb {C}}$
, -
• g is a Green function for
 $ X_ {\mathbb {C}}$
on
$ X_ {\mathbb {C}}$
on
 ${\mathcal {M}}_{\mathbb {C}}$
, admissible with respect to
${\mathcal {M}}_{\mathbb {C}}$
, admissible with respect to
 $\overline {\mathcal {L}}_{\mathbb {C}}$
, and invariant under the involution induced by complex conjugation. Here, admissibility means that the curvature form
$\overline {\mathcal {L}}_{\mathbb {C}}$
, and invariant under the involution induced by complex conjugation. Here, admissibility means that the curvature form
 $ \delta _{X}+\frac {i }{2\pi }\partial \bar \partial g$
is harmonic.
$ \delta _{X}+\frac {i }{2\pi }\partial \bar \partial g$
is harmonic.
(2) For
![]() $X\in Z^1(M)_{\mathbb {C}}$
, an admissible extension of X with respect to
$X\in Z^1(M)_{\mathbb {C}}$
, an admissible extension of X with respect to
![]() $\overline {\mathcal {L}}$
is an element in the preimage of X by the natural surjection
$\overline {\mathcal {L}}$
is an element in the preimage of X by the natural surjection
![]() ${\widehat {Z}}^1_{{\overline {\mathcal {L}}},{\mathbb {C}}}({\mathcal {M}}) \to Z^1(M)_{\mathbb {C}}$
.
${\widehat {Z}}^1_{{\overline {\mathcal {L}}},{\mathbb {C}}}({\mathcal {M}}) \to Z^1(M)_{\mathbb {C}}$
.
Remark A.3.2. (1) A Green current on Deligne-Mumford stacks is defined in [Reference GilletGil09, Section 1]. In our situation, a Green function is simply an orbifold function whose pullback to the finite étale cover by a smooth variety is a usual Green function.
(2) Admissible Green functions for
![]() $X_{\mathbb {C}}$
always exists and are the same modulo locally constant functions, and (A.3) is the non-archimedean analog of this fact.
$X_{\mathbb {C}}$
always exists and are the same modulo locally constant functions, and (A.3) is the non-archimedean analog of this fact.
(3) By [Reference ZhangZha20, 2.2], a closed
![]() $(1,1)$
-form
$(1,1)$
-form
![]() $\alpha $
is harmonic if and and only if on each connected component of
$\alpha $
is harmonic if and and only if on each connected component of
![]() ${\mathcal {M}}_{\mathbb {C}}$
,
${\mathcal {M}}_{\mathbb {C}}$
,
![]() $ \alpha \wedge {\mathrm {curv}}\left ( \overline {\mathcal {L}}_{\mathbb {C}}\right ) ^{n-1} $
is a constant multiple of
$ \alpha \wedge {\mathrm {curv}}\left ( \overline {\mathcal {L}}_{\mathbb {C}}\right ) ^{n-1} $
is a constant multiple of
![]() $ {\mathrm {curv}}\left ( \overline {\mathcal {L}}_{\mathbb {C}}\right ) ^{n}.$
$ {\mathrm {curv}}\left ( \overline {\mathcal {L}}_{\mathbb {C}}\right ) ^{n}.$
Definition A.3.3. (1) An admissible Green function is normalized with respect to
![]() $\overline {\mathcal {L}}_{\mathbb {C}}$
if it has vanishing harmonic projection; that is, on each connected component of
$\overline {\mathcal {L}}_{\mathbb {C}}$
if it has vanishing harmonic projection; that is, on each connected component of
![]() ${\mathcal {M}}_{\mathbb {C}}$
, its integration against
${\mathcal {M}}_{\mathbb {C}}$
, its integration against
![]() ${\mathrm {curv}}(\overline {\mathcal {L}}_{\mathbb {C}})^{n}$
is 0.
${\mathrm {curv}}(\overline {\mathcal {L}}_{\mathbb {C}})^{n}$
is 0.
(2) An element in
![]() ${\widehat {Z}}^1_{{\overline {\mathcal {L}}},{\mathbb {C}}}({\mathcal {M}})$
is normalized with respect to
${\widehat {Z}}^1_{{\overline {\mathcal {L}}},{\mathbb {C}}}({\mathcal {M}})$
is normalized with respect to
![]() $\overline {\mathcal {L}}$
if it is normalized at every place. For
$\overline {\mathcal {L}}$
if it is normalized at every place. For
![]() $X\in Z^1(M)_{{\mathbb {C}}}$
, let
$X\in Z^1(M)_{{\mathbb {C}}}$
, let
![]() $X^{\overline {\mathcal {L}}}\in {\widehat {Z}}^1_{{\overline {\mathcal {L}}},{\mathbb {C}}}({\mathcal {M}}) $
be its normalized admissible extension with respect to
$X^{\overline {\mathcal {L}}}\in {\widehat {Z}}^1_{{\overline {\mathcal {L}}},{\mathbb {C}}}({\mathcal {M}}) $
be its normalized admissible extension with respect to
![]() $\overline {\mathcal {L}}$
.
$\overline {\mathcal {L}}$
.
Then the normalized admissible extension of a divisor on M exists and is unique.
For every nonzero rational function f on M,
![]() $({\mathrm {div}}(f),-\log |f|^2)$
is contained in
$({\mathrm {div}}(f),-\log |f|^2)$
is contained in
![]() ${\widehat {Z}}^1_{{\overline {\mathcal {L}}},{\mathbb {C}}}({\mathcal {M}})$
.
${\widehat {Z}}^1_{{\overline {\mathcal {L}}},{\mathbb {C}}}({\mathcal {M}})$
.
Definition A.3.4. (1) Let
![]() $\widehat {\mathrm {Ch}}^1_{{\mathbb {C}}}({\mathcal {M}}) $
be the quotient of the space of arithmetic divisors with
$\widehat {\mathrm {Ch}}^1_{{\mathbb {C}}}({\mathcal {M}}) $
be the quotient of the space of arithmetic divisors with
![]() ${\mathbb {C}}$
-coefficients by the
${\mathbb {C}}$
-coefficients by the
![]() ${\mathbb {C}}$
-span of
${\mathbb {C}}$
-span of
![]() $({\mathrm {div}}(f),-\log |f|^2)$
’s for all nonzero rational functions.
$({\mathrm {div}}(f),-\log |f|^2)$
’s for all nonzero rational functions.
(2) Let
![]() $\widehat {\mathrm {Ch}}_{{\overline {\mathcal {L}}},{\mathbb {C}}}^1({\mathcal {M}}) $
be the quotient of
$\widehat {\mathrm {Ch}}_{{\overline {\mathcal {L}}},{\mathbb {C}}}^1({\mathcal {M}}) $
be the quotient of
![]() ${\widehat {Z}}^1_{{\overline {\mathcal {L}}},{\mathbb {C}}}({\mathcal {M}})$
by the
${\widehat {Z}}^1_{{\overline {\mathcal {L}}},{\mathbb {C}}}({\mathcal {M}})$
by the
![]() ${\mathbb {C}}$
-span of
${\mathbb {C}}$
-span of
![]() $({\mathrm {div}}(f),-\log |f|^2)$
’s.
$({\mathrm {div}}(f),-\log |f|^2)$
’s.
Remark A.3.5. Let
![]() $ \widehat {\mathrm {Ch}}^{1}({\mathcal {M}})$
be the Chow group of arithmetic divisors with
$ \widehat {\mathrm {Ch}}^{1}({\mathcal {M}})$
be the Chow group of arithmetic divisors with
![]() ${\mathbb {Z}}$
-coefficients defined by Gillet and Soulé [Reference Gillet and SouléGS90] for schemes, which is extended to the stacky case in [Reference GilletGil09]. Then
${\mathbb {Z}}$
-coefficients defined by Gillet and Soulé [Reference Gillet and SouléGS90] for schemes, which is extended to the stacky case in [Reference GilletGil09]. Then
![]() $\widehat {\mathrm {Ch}}^1_{{\mathbb {C}}}({\mathcal {M}}) $
is the quotient of
$\widehat {\mathrm {Ch}}^1_{{\mathbb {C}}}({\mathcal {M}}) $
is the quotient of
![]() $\widehat {\mathrm {Ch}}^1({\mathcal {M}}) _{{\mathbb {C}}}$
by the pullback of the kernel of the degree map
$\widehat {\mathrm {Ch}}^1({\mathcal {M}}) _{{\mathbb {C}}}$
by the pullback of the kernel of the degree map
![]() $ \widehat {\mathrm {Ch}}^1\left ( \operatorname {\mathrm {Spec}} {\mathcal {O}} \right )_{{\mathbb {C}}}\to {\mathbb {C}}$
. In particular, we have an isomorphism
$ \widehat {\mathrm {Ch}}^1\left ( \operatorname {\mathrm {Spec}} {\mathcal {O}} \right )_{{\mathbb {C}}}\to {\mathbb {C}}$
. In particular, we have an isomorphism
![]() $ \widehat {\mathrm {Ch}}^1_{{\mathbb {C}}}\left ( \operatorname {\mathrm {Spec}} {\mathcal {O}} \right ){\ \simeq \ } {\mathbb {C}}$
by taking degrees.
$ \widehat {\mathrm {Ch}}^1_{{\mathbb {C}}}\left ( \operatorname {\mathrm {Spec}} {\mathcal {O}} \right ){\ \simeq \ } {\mathbb {C}}$
by taking degrees.
Lemma A.3.6. (1) The natural map
![]() $\widehat {\mathrm {Ch}}^1_{{\overline {\mathcal {L}}},{\mathbb {C}}}({\mathcal {M}}) \to {\mathrm {Ch}}^1(M) _{\mathbb {C}}$
is surjective. Its kernel is generated by connected components of special fibers of
$\widehat {\mathrm {Ch}}^1_{{\overline {\mathcal {L}}},{\mathbb {C}}}({\mathcal {M}}) \to {\mathrm {Ch}}^1(M) _{\mathbb {C}}$
is surjective. Its kernel is generated by connected components of special fibers of
![]() ${\mathcal {M}}$
at all finite places and locally constant functions on
${\mathcal {M}}$
at all finite places and locally constant functions on
![]() ${\mathcal {M}}_{\mathbb {C}}$
.
${\mathcal {M}}_{\mathbb {C}}$
.
(2) Assume that
![]() ${\mathcal {M}}$
is connected. Then the kernel of
${\mathcal {M}}$
is connected. Then the kernel of
![]() $\widehat {\mathrm {Ch}}^1_{{\overline {\mathcal {L}}},{\mathbb {C}}}({\mathcal {M}})\to {\mathrm {Ch}}^1(M)_{\mathbb {C}}$
is 1-dimensional, and is the pullback of
$\widehat {\mathrm {Ch}}^1_{{\overline {\mathcal {L}}},{\mathbb {C}}}({\mathcal {M}})\to {\mathrm {Ch}}^1(M)_{\mathbb {C}}$
is 1-dimensional, and is the pullback of
![]() $\widehat {\mathrm {Ch}}^1_{{\mathbb {C}}}\left ( \operatorname {\mathrm {Spec}} {\mathcal {O}}\right )$
.
$\widehat {\mathrm {Ch}}^1_{{\mathbb {C}}}\left ( \operatorname {\mathrm {Spec}} {\mathcal {O}}\right )$
.
Proof. By (A.3) and Remark A.3.2 (2), (1) holds. If
![]() ${\mathcal {M}}$
is connected, then
${\mathcal {M}}$
is connected, then
![]() $E_1:={\mathcal {O}}_M(M)$
is a finite field extension of the fraction field of
$E_1:={\mathcal {O}}_M(M)$
is a finite field extension of the fraction field of
![]() ${\mathcal {O}}$
. Then
${\mathcal {O}}$
. Then
![]() ${\mathcal {M}}$
over
${\mathcal {M}}$
over
![]() $\operatorname {\mathrm {Spec}} {\mathcal {O}}_{E_1}$
has geometrically connected fibers by Stein factorization. By (1), the kernel is the pullback of
$\operatorname {\mathrm {Spec}} {\mathcal {O}}_{E_1}$
has geometrically connected fibers by Stein factorization. By (1), the kernel is the pullback of
![]() $\widehat {\mathrm {Ch}}^1_{{\mathbb {C}}}\left ( \operatorname {\mathrm {Spec}} {\mathcal {O}}_{E_1}\right ) $
, which is 1-dimensional by the finiteness of the class number of
$\widehat {\mathrm {Ch}}^1_{{\mathbb {C}}}\left ( \operatorname {\mathrm {Spec}} {\mathcal {O}}_{E_1}\right ) $
, which is 1-dimensional by the finiteness of the class number of
![]() $E_1$
and Dirichlet’s unit theorem. See [Reference Gillet and SouléGS90, 3.4.3]. And it equals the pullback of
$E_1$
and Dirichlet’s unit theorem. See [Reference Gillet and SouléGS90, 3.4.3]. And it equals the pullback of
![]() $\widehat {\mathrm {Ch}}^1_{{\mathbb {C}}}\left ( \operatorname {\mathrm {Spec}} {\mathcal {O}}\right )$
.
$\widehat {\mathrm {Ch}}^1_{{\mathbb {C}}}\left ( \operatorname {\mathrm {Spec}} {\mathcal {O}}\right )$
.
Example A.3.7. The arithmetic first Chern class
![]() $c_1(\overline {\mathcal {L}})$
of
$c_1(\overline {\mathcal {L}})$
of
![]() $\overline {\mathcal {L}}$
is the class of
$\overline {\mathcal {L}}$
is the class of
![]() $ ({\mathrm {div}}(s),-\log \|s\| ^2)$
for a nonzero rational section s. By Remark A.2.3 (or one may follow our definition), one immediately sees that
$ ({\mathrm {div}}(s),-\log \|s\| ^2)$
for a nonzero rational section s. By Remark A.2.3 (or one may follow our definition), one immediately sees that
![]() ${\mathrm {div}}(s)$
has ‘harmonic curvature’ at every finite place. The curvature form of
${\mathrm {div}}(s)$
has ‘harmonic curvature’ at every finite place. The curvature form of
![]() $-\log \|s\| ^2$
is by definition the Kähler form. So
$-\log \|s\| ^2$
is by definition the Kähler form. So
![]() $c_1(\overline {\mathcal {L}})\in \widehat {\mathrm {Ch}}^1_{{\mathbb {C}},{\overline {\mathcal {L}}}}({\mathcal {M}})$
.
$c_1(\overline {\mathcal {L}})\in \widehat {\mathrm {Ch}}^1_{{\mathbb {C}},{\overline {\mathcal {L}}}}({\mathcal {M}})$
.
Now we consider the functoriality. By Lemma A.2.5, we have the following proposition.
Proposition A.3.8. Let
![]() ${\mathcal {M}}'$
be a regular Deligne-Mumford stack and
${\mathcal {M}}'$
be a regular Deligne-Mumford stack and
![]() $ f: {\mathcal {M}}'\to {\mathcal {M}}$
a finite flat morphism over
$ f: {\mathcal {M}}'\to {\mathcal {M}}$
a finite flat morphism over
![]() $\operatorname {\mathrm {Spec}} {\mathcal {O}}$
, such that the restriction of f to the generic fibers is finite étale. Let
$\operatorname {\mathrm {Spec}} {\mathcal {O}}$
, such that the restriction of f to the generic fibers is finite étale. Let
![]() ${\mathcal {L}}'$
be the pullback of
${\mathcal {L}}'$
be the pullback of
![]() ${\mathcal {L}}$
to
${\mathcal {L}}$
to
![]() ${\mathcal {M}}'$
. Consider
${\mathcal {M}}'$
. Consider
![]() ${\mathcal {M}}'$
as a Deligne-Mumford stack over
${\mathcal {M}}'$
as a Deligne-Mumford stack over
![]() $\operatorname {\mathrm {Spec}} {\mathcal {O}}$
via f and
$\operatorname {\mathrm {Spec}} {\mathcal {O}}$
via f and
![]() ${\mathcal {M}}$
. Then the formation of
${\mathcal {M}}$
. Then the formation of
![]() ${\widehat {Z}}^1_{{\mathbb {C}},{\overline {\mathcal {L}}}}({\mathcal {M}})$
,
${\widehat {Z}}^1_{{\mathbb {C}},{\overline {\mathcal {L}}}}({\mathcal {M}})$
,
![]() $\widehat {\mathrm {Ch}}^1_{{\mathbb {C}},{\overline {\mathcal {L}}}}({\mathcal {M}}) $
and normalized admissible extension with respect to
$\widehat {\mathrm {Ch}}^1_{{\mathbb {C}},{\overline {\mathcal {L}}}}({\mathcal {M}}) $
and normalized admissible extension with respect to
![]() $\overline {\mathcal {L}}$
is preserved under pullback and pushforward by f.
$\overline {\mathcal {L}}$
is preserved under pullback and pushforward by f.
A.4 Arithmetic intersection pairing
Let
![]() $Z_1({\mathcal {M}})_{\mathbb {C}}$
be the group of 1-cycles on
$Z_1({\mathcal {M}})_{\mathbb {C}}$
be the group of 1-cycles on
![]() ${\mathcal {M}}$
. We define an arithmetic intersection pairing following [Reference Bost, Gillet and SouléBGS94, 2.3.1]:
${\mathcal {M}}$
. We define an arithmetic intersection pairing following [Reference Bost, Gillet and SouléBGS94, 2.3.1]:
We reduce the pairing to the arithmetic intersection pairing between
![]() $\widehat {\mathrm {Ch}}^1 ({\mathcal {M}}) _{{\mathbb {C}}}$
and
$\widehat {\mathrm {Ch}}^1 ({\mathcal {M}}) _{{\mathbb {C}}}$
and
![]() $\widehat {\mathrm {Ch}}^n ({\mathcal {M}}) _{{\mathbb {C}}}$
, which is defined in [Reference GilletGil09] for general Deligne-Mumford stacks (without Assumption A.1.1). Let
$\widehat {\mathrm {Ch}}^n ({\mathcal {M}}) _{{\mathbb {C}}}$
, which is defined in [Reference GilletGil09] for general Deligne-Mumford stacks (without Assumption A.1.1). Let
![]() $\omega ({\widehat x})$
be the curvature form of
$\omega ({\widehat x})$
be the curvature form of
![]() $\widehat x$
, which is a smooth
$\widehat x$
, which is a smooth
![]() $(1,1)$
form on the orbifold
$(1,1)$
form on the orbifold
![]() $M_{{\mathbb {C}}}$
independent of the choice of a representative of
$M_{{\mathbb {C}}}$
independent of the choice of a representative of
![]() $\widehat x$
. Choose
$\widehat x$
. Choose
![]() $\widehat y=(Y,g_Y)\in \widehat {\mathrm {Ch}}^n_{{\mathbb {C}}}({\mathcal {M}})$
. Then
$\widehat y=(Y,g_Y)\in \widehat {\mathrm {Ch}}^n_{{\mathbb {C}}}({\mathcal {M}})$
. Then
![]() $ \widehat x\cdot Y$
is the arithmetic intersection number
$ \widehat x\cdot Y$
is the arithmetic intersection number
![]() $\widehat x\cdot \widehat y $
minus
$\widehat x\cdot \widehat y $
minus
![]() $\int _{{\mathcal {M}}_{\mathbb {C}}}\omega ({\widehat x}) g_Y$
.
$\int _{{\mathcal {M}}_{\mathbb {C}}}\omega ({\widehat x}) g_Y$
.
Now assume Assumption A.1.1 and that
![]() $(X,g_X)$
is a representative of
$(X,g_X)$
is a representative of
![]() $\widehat x$
such that
$\widehat x$
such that
![]() $X\cap Y$
is empty on the generic fiber of
$X\cap Y$
is empty on the generic fiber of
![]() ${\mathcal {M}}$
. Then
${\mathcal {M}}$
. Then
![]() $ \widehat x\cdot Y $
is the sum of the intersection numbers of the restrictions of X and Y to
$ \widehat x\cdot Y $
is the sum of the intersection numbers of the restrictions of X and Y to
![]() ${\mathcal {M}}_{{\mathcal {O}}_s}$
over all closed points
${\mathcal {M}}_{{\mathcal {O}}_s}$
over all closed points
![]() $s\in \operatorname {\mathrm {Spec}} {\mathcal {O}}$
defined in (A.1), and
$s\in \operatorname {\mathrm {Spec}} {\mathcal {O}}$
defined in (A.1), and
![]() $\int _{Y_{\mathbb {C}}}g_X$
.
$\int _{Y_{\mathbb {C}}}g_X$
.
The pullback of the kernel of the degree map
![]() $ \widehat {\mathrm {Ch}}^1\left ( \operatorname {\mathrm {Spec}} {\mathcal {O}} \right )_{{\mathbb {C}}}\to {\mathbb {C}}$
to
$ \widehat {\mathrm {Ch}}^1\left ( \operatorname {\mathrm {Spec}} {\mathcal {O}} \right )_{{\mathbb {C}}}\to {\mathbb {C}}$
to
![]() $\widehat {\mathrm {Ch}}^1({\mathcal {M}})_{{\mathbb {C}}}$
is annihilated by the arithmetic intersection pairing with
$\widehat {\mathrm {Ch}}^1({\mathcal {M}})_{{\mathbb {C}}}$
is annihilated by the arithmetic intersection pairing with
![]() $Z_1({\mathcal {M}})_{\mathbb {C}}$
. By Remark A.3.5, the above arithmetic intersection pairing factors through an arithmetic intersection pairing
$Z_1({\mathcal {M}})_{\mathbb {C}}$
. By Remark A.3.5, the above arithmetic intersection pairing factors through an arithmetic intersection pairing
Similar to Corollary A.2.6, Proposition A.3.8 implies the following result.
Corollary A.4.1. In Proposition A.3.8, let
![]() $M'$
be the generic fiber of
$M'$
be the generic fiber of
![]() ${\mathcal {M}}'$
and assume that
${\mathcal {M}}'$
and assume that
![]() ${\mathcal {M}}\to \operatorname {\mathrm {Spec}} {\mathcal {O}}_E$
is smooth. Then for
${\mathcal {M}}\to \operatorname {\mathrm {Spec}} {\mathcal {O}}_E$
is smooth. Then for
![]() $X\in Z^1(M')_{{\mathbb {C}}}$
and
$X\in Z^1(M')_{{\mathbb {C}}}$
and
![]() $Y\in Z^{n}_{{\mathbb {C}}}({\mathcal {M}})$
, we have
$Y\in Z^{n}_{{\mathbb {C}}}({\mathcal {M}})$
, we have
where
![]() $g_{X}^{\overline {\mathcal {L}}}$
is the normalized admissible Green function for X.
$g_{X}^{\overline {\mathcal {L}}}$
is the normalized admissible Green function for X.
B A comparison of the ‘closure’ model with Rapoport–Smithling–Zhang model (appendix by Yujie Xu)
B.1 Preliminaries
B.1.1
Let F be a CM field and
![]() $F_0$
its maximal totally real subfield of index
$F_0$
its maximal totally real subfield of index
![]() $2$
. Let
$2$
. Let
![]() $a\mapsto \overline {a}$
be the nontrivial automorphism of
$a\mapsto \overline {a}$
be the nontrivial automorphism of
![]() $F/F_0$
. We fix a presentation
$F/F_0$
. We fix a presentation
![]() $F=F_0(\sqrt {\Delta })$
for some totally negative element
$F=F_0(\sqrt {\Delta })$
for some totally negative element
![]() $\Delta \in F_0$
. Let
$\Delta \in F_0$
. Let
![]() $\Phi $
denote the CM type for F determined by
$\Phi $
denote the CM type for F determined by
![]() $\sqrt {\Delta }$
; that is,
$\sqrt {\Delta }$
; that is,
Let W be a non-degenerate
![]() $F/F_0$
-hermitian space of dimension
$F/F_0$
-hermitian space of dimension
![]() $n\geq 2$
. Let
$n\geq 2$
. Let
As in [Reference Rapoport, Smithling and ZhangRSZ20,
![]() $\S$
2.1], we use the symbol c to denote the similitude factor of a point on a unitary similitude group. We consider the following algebraic groups over
$\S$
2.1], we use the symbol c to denote the similitude factor of a point on a unitary similitude group. We consider the following algebraic groups over
![]() $\mathbb {Q}$
:
$\mathbb {Q}$
:
Note that
![]() $Z^{\mathbb {Q}}$
is naturally a central subgroup of
$Z^{\mathbb {Q}}$
is naturally a central subgroup of
![]() $G^{\mathbb {Q}}$
, and we have the following product decompositions
$G^{\mathbb {Q}}$
, and we have the following product decompositions
B.1.8
From now on, we assume, moreover, that the hermitian space W has the following signatures at the archimedean places of
![]() $F_0$
: for a distinguished element
$F_0$
: for a distinguished element
![]() $\varphi _0\in \Phi $
, the signature of
$\varphi _0\in \Phi $
, the signature of
![]() $W_{\varphi _0}$
is
$W_{\varphi _0}$
is
![]() $(1,n-1)$
; and for all other
$(1,n-1)$
; and for all other
![]() $\varphi \in \Phi $
, the signature of
$\varphi \in \Phi $
, the signature of
![]() $W_{\varphi }$
is
$W_{\varphi }$
is
![]() $(0,n)$
. In order to define a Shimura datum
$(0,n)$
. In order to define a Shimura datum
![]() $(G^{\mathbb {Q}},\{h_{G^{\mathbb {Q}}}\})$
, by the canonical inclusions
$(G^{\mathbb {Q}},\{h_{G^{\mathbb {Q}}}\})$
, by the canonical inclusions
![]() $G_{\mathbb {R}}^{\mathbb {Q}}\subset \prod \limits _{\varphi \in \Phi }\operatorname {GU}(W_{\varphi })$
, it suffices to define the components
$G_{\mathbb {R}}^{\mathbb {Q}}\subset \prod \limits _{\varphi \in \Phi }\operatorname {GU}(W_{\varphi })$
, it suffices to define the components
![]() $h_{G^{\mathbb {Q}},\varphi }$
of
$h_{G^{\mathbb {Q}},\varphi }$
of
![]() $h_{G^{\mathbb {Q}}}$
. Consider the matrices
$h_{G^{\mathbb {Q}}}$
. Consider the matrices
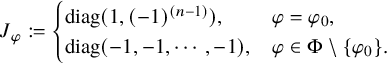 $$ \begin{align} J_{\varphi}:=\begin{cases}\mathrm{diag}(1,(-1)^{(n-1)}),&\varphi=\varphi_0,\\ \mathrm{diag}(-1,-1,\cdots,-1), &\varphi\in\Phi\setminus\{\varphi _0\}.\end{cases} \end{align} $$
$$ \begin{align} J_{\varphi}:=\begin{cases}\mathrm{diag}(1,(-1)^{(n-1)}),&\varphi=\varphi_0,\\ \mathrm{diag}(-1,-1,\cdots,-1), &\varphi\in\Phi\setminus\{\varphi _0\}.\end{cases} \end{align} $$
We also choose bases
![]() $W_{\varphi }\ \simeq \ \mathbb {C}^n$
such that the hermitian form on
$W_{\varphi }\ \simeq \ \mathbb {C}^n$
such that the hermitian form on
![]() $W_{\varphi }$
is given by
$W_{\varphi }$
is given by
![]() $J_{\varphi }$
. Consider the
$J_{\varphi }$
. Consider the
![]() $\mathbb {R}$
-algebra homomorphisms
$\mathbb {R}$
-algebra homomorphisms
which induce our desired component maps
![]() $h_{G^{\mathbb {Q}},\varphi }:\mathbb {C}^{\times }\to \operatorname {GU}(W_{\varphi })(\mathbb {R})$
. This gives us our desired Shimura datum
$h_{G^{\mathbb {Q}},\varphi }:\mathbb {C}^{\times }\to \operatorname {GU}(W_{\varphi })(\mathbb {R})$
. This gives us our desired Shimura datum
![]() $(G^{\mathbb {Q}},\{h_{G^{\mathbb {Q}}}\})$
.
$(G^{\mathbb {Q}},\{h_{G^{\mathbb {Q}}}\})$
.
B.1.11
For the group
![]() $Z^{\mathbb {Q}}$
defined in B.1.4, the CM type
$Z^{\mathbb {Q}}$
defined in B.1.4, the CM type
![]() $\Phi $
induces an identification
$\Phi $
induces an identification
which allows us to define
![]() $h_{Z^{\mathbb {Q}}}:\mathbb {C}^{\times }\to Z^{\mathbb {Q}}(\mathbb {R})$
as the diagonal embedding (via the identification B.1.12) precomposed with complex conjugation. This gives us a Shimura datum
$h_{Z^{\mathbb {Q}}}:\mathbb {C}^{\times }\to Z^{\mathbb {Q}}(\mathbb {R})$
as the diagonal embedding (via the identification B.1.12) precomposed with complex conjugation. This gives us a Shimura datum
![]() $(Z^{\mathbb {Q}},\{h_{Z^{\mathbb {Q}}}\})$
with reflex field
$(Z^{\mathbb {Q}},\{h_{Z^{\mathbb {Q}}}\})$
with reflex field
which is the reflex field for the CM type
![]() $\Phi $
. Recall that this can be computed as the fixed field in
$\Phi $
. Recall that this can be computed as the fixed field in
![]() $\mathbb {C}$
of the group
$\mathbb {C}$
of the group
![]() $\{\sigma \in {\mathrm {Aut}}(\mathbb {C})=|\sigma \circ \Phi =\Phi \}$
.
$\{\sigma \in {\mathrm {Aut}}(\mathbb {C})=|\sigma \circ \Phi =\Phi \}$
.
For the group
![]() $\widetilde {G}$
defined in B.1.6, we consider the map
$\widetilde {G}$
defined in B.1.6, we consider the map
which gives us a Shimura datum
![]() $(\widetilde {G},\{h_{\widetilde {G}}\})$
. Let
$(\widetilde {G},\{h_{\widetilde {G}}\})$
. Let
be the reflex field for
![]() $(\widetilde {G},\{h_{\widetilde {G}}\})$
, by definition it is computed via
$(\widetilde {G},\{h_{\widetilde {G}}\})$
, by definition it is computed via
Note that E is the compositum of
![]() $E_{\Phi }$
(as in B.1.13) and F. By [Reference DeligneDel71], we have canonical models
$E_{\Phi }$
(as in B.1.13) and F. By [Reference DeligneDel71], we have canonical models
![]() ${\mathrm {Sh}}_{K_{\widetilde {G}}}(\widetilde {G},\{h_{\widetilde {G}}\})$
over E, for compact open subgroups
${\mathrm {Sh}}_{K_{\widetilde {G}}}(\widetilde {G},\{h_{\widetilde {G}}\})$
over E, for compact open subgroups
![]() $K_{\widetilde {G}}\subset \widetilde {G}(\mathbb {A}_f)$
. By [Reference KisinKis10] (resp. [Reference Kisin and PappasKP18] depending on the level structure), we have integral models
$K_{\widetilde {G}}\subset \widetilde {G}(\mathbb {A}_f)$
. By [Reference KisinKis10] (resp. [Reference Kisin and PappasKP18] depending on the level structure), we have integral models
![]() $\mathscr {S}_{K_{\widetilde {G}}}(\widetilde {G},\{h_{\widetilde {G}}\})$
over
$\mathscr {S}_{K_{\widetilde {G}}}(\widetilde {G},\{h_{\widetilde {G}}\})$
over
![]() $\mathcal {O}_{E,(v)}$
.
$\mathcal {O}_{E,(v)}$
.
B.1.17
We introduce a Shimura datum
![]() $(G,\{h_G\})$
. Let
$(G,\{h_G\})$
. Let
![]() $h_G$
be the map
$h_G$
be the map
defined by composing
![]() $h_{\widetilde {G}}$
(from B.1.14) with the projection onto the second factor in the map B.1.7. The reflex field for
$h_{\widetilde {G}}$
(from B.1.14) with the projection onto the second factor in the map B.1.7. The reflex field for
![]() $(G,\{h_G\})$
is F, embedded into
$(G,\{h_G\})$
is F, embedded into
![]() $\mathbb {C}$
via
$\mathbb {C}$
via
![]() $\varphi _0$
.
$\varphi _0$
.
Moreover, the decomposition in B.1.7 induces a decomposition of Shimura data
Let
![]() $K_{\widetilde {G}}$
be decomposed via B.1.7 into
$K_{\widetilde {G}}$
be decomposed via B.1.7 into
The natural projections in B.1.19 then induce morphisms of Shimura varieties
Note that the Shimura variety
![]() ${\mathrm {Sh}}_{K_G}(G,\{h_G\})$
, which originally appeared in [Reference Gan, Gross and PrasadGGP12], is not of PEL type. However, it is of abelian type, and we have an integral model
${\mathrm {Sh}}_{K_G}(G,\{h_G\})$
, which originally appeared in [Reference Gan, Gross and PrasadGGP12], is not of PEL type. However, it is of abelian type, and we have an integral model
![]() $\mathscr {S}_{K_G}(G,\{h_G\})$
defined over
$\mathscr {S}_{K_G}(G,\{h_G\})$
defined over
![]() $\mathcal {O}_{F,(\nu )}$
by [Reference KisinKis10] (resp. [Reference Kisin and PappasKP18] depending on the level structureFootnote
4
).
$\mathcal {O}_{F,(\nu )}$
by [Reference KisinKis10] (resp. [Reference Kisin and PappasKP18] depending on the level structureFootnote
4
).
B.1.23
Let
![]() $\nu |p$
be a place of E. Let
$\nu |p$
be a place of E. Let
![]() $\mathcal {M}_0$
be the moduli functor which associates to each locally Noetherian
$\mathcal {M}_0$
be the moduli functor which associates to each locally Noetherian
![]() $\mathcal {O}_{E,\nu }$
-scheme S the groupoid of tuples
$\mathcal {O}_{E,\nu }$
-scheme S the groupoid of tuples
![]() $\mathcal {M}_0(S):=(A_0,\lambda _0,\iota _0 )$
where
$\mathcal {M}_0(S):=(A_0,\lambda _0,\iota _0 )$
where
-
(i)
 $A_0$
is an abelian scheme over S;
$A_0$
is an abelian scheme over S; -
(ii)
 $\iota _0: \mathcal {O}_F\to {\mathrm {End}}_S(A_0)$
is an
$\iota _0: \mathcal {O}_F\to {\mathrm {End}}_S(A_0)$
is an
 $\mathcal {O}_F$
-endomorphism structure on
$\mathcal {O}_F$
-endomorphism structure on
 $A_0$
satisfying the Kottwitz condition of signature
$A_0$
satisfying the Kottwitz condition of signature
 $((0,1)_{\varphi \in \Phi })$
; that is,
$((0,1)_{\varphi \in \Phi })$
; that is,  $$\begin{align*}{\mathrm{Char}}(\iota_0(a)|{\mathrm{Lie}} A_0)=\prod\limits_{\varphi\in\Phi}(T-\overline{\varphi}(a))\quad\text{ for all }a\in \mathcal{O}_F;\end{align*}$$
$$\begin{align*}{\mathrm{Char}}(\iota_0(a)|{\mathrm{Lie}} A_0)=\prod\limits_{\varphi\in\Phi}(T-\overline{\varphi}(a))\quad\text{ for all }a\in \mathcal{O}_F;\end{align*}$$
-
(iii)
 $\lambda _0$
is a principal polarization of
$\lambda _0$
is a principal polarization of
 $A_0$
such that the associated Rosati involution induces the nontrivial Galois automorphism of
$A_0$
such that the associated Rosati involution induces the nontrivial Galois automorphism of
 $F/F_0$
on
$F/F_0$
on
 $\mathcal {O}_F$
via
$\mathcal {O}_F$
via
 $\iota _0$
.
$\iota _0$
.
Then
![]() $\mathcal {M}_0$
is representable by a Deligne-Mumford stack
$\mathcal {M}_0$
is representable by a Deligne-Mumford stack
![]() $\mathcal {M}_0$
finite étale over
$\mathcal {M}_0$
finite étale over
![]() $\operatorname {\mathrm {Spec}}\mathcal {O}_{E,\nu }$
. Moreover, we assume
$\operatorname {\mathrm {Spec}}\mathcal {O}_{E,\nu }$
. Moreover, we assume
![]() $K^p$
is small enough, so that
$K^p$
is small enough, so that
![]() $\mathcal {M}_0$
is nonempty. We shall assume throughout the rest of this appendix that
$\mathcal {M}_0$
is nonempty. We shall assume throughout the rest of this appendix that
![]() $\mathcal {M}_0$
is nonempty.
$\mathcal {M}_0$
is nonempty.
Lemma B.1.24 [Reference Rapoport, Smithling and ZhangRSZ20, Lemma 3.4].
The stack
![]() $\mathcal {M}_0$
admits the following decompositon into open and closed substacksFootnote
5
:
$\mathcal {M}_0$
admits the following decompositon into open and closed substacksFootnote
5
:
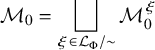 $$ \begin{align} \mathcal{M}_0=\bigsqcup\limits_{\xi\in\mathcal{L}_{\Phi}/\sim}\mathcal{M}_0^{\xi} \end{align} $$
$$ \begin{align} \mathcal{M}_0=\bigsqcup\limits_{\xi\in\mathcal{L}_{\Phi}/\sim}\mathcal{M}_0^{\xi} \end{align} $$
such that the generic fiber of
![]() $\mathcal {M}_0^{\xi }$
is canonically isomorphic to
$\mathcal {M}_0^{\xi }$
is canonically isomorphic to
![]() $ {\mathrm {Sh}}_{K_{Z^{\mathbb {Q}}}}(Z^{\mathbb {Q}},\{h_{Z^{\mathbb {Q}}}\})_E$
.
$ {\mathrm {Sh}}_{K_{Z^{\mathbb {Q}}}}(Z^{\mathbb {Q}},\{h_{Z^{\mathbb {Q}}}\})_E$
.
B.1.26
Let
![]() $F_{0,v}$
be the v-adic completion of
$F_{0,v}$
be the v-adic completion of
![]() $F_0$
, and we set
$F_0$
, and we set
![]() $F_v:=F\otimes _{F_0}F_{0,v}$
. Suppose for now that the place
$F_v:=F\otimes _{F_0}F_{0,v}$
. Suppose for now that the place
![]() $v_0$
of
$v_0$
of
![]() $F_0$
is unramified over p, and that
$F_0$
is unramified over p, and that
![]() $v_0$
either splits in F or is inert in F. Suppose, moreover, that the hermitian space
$v_0$
either splits in F or is inert in F. Suppose, moreover, that the hermitian space
![]() $W_{v_0}$
is split. If there exists a prime v of
$W_{v_0}$
is split. If there exists a prime v of
![]() $F_0$
above p that is non-split in F, we assume additionally that
$F_0$
above p that is non-split in F, we assume additionally that
![]() $p\neq 2$
. We choose a vertex lattice
$p\neq 2$
. We choose a vertex lattice
![]() $\Lambda _v$
in the
$\Lambda _v$
in the
![]() $F_v/F_{0,v}$
-hermitian space
$F_v/F_{0,v}$
-hermitian space
![]() $W_v$
. For now, we assume that
$W_v$
. For now, we assume that
![]() $\Lambda _{v_0}$
is self-dual. We recall that an
$\Lambda _{v_0}$
is self-dual. We recall that an
![]() $\mathcal {O}_{F,v}$
-lattice
$\mathcal {O}_{F,v}$
-lattice
![]() $\Lambda $
in an
$\Lambda $
in an
![]() $F_v/F_{0,v}$
-hermitian space is called a vertex lattice of type r if
$F_v/F_{0,v}$
-hermitian space is called a vertex lattice of type r if
![]() $\Lambda \subset ^r\Lambda ^{*}\subset \pi _v^{-1}\Lambda $
.Footnote
6
An
$\Lambda \subset ^r\Lambda ^{*}\subset \pi _v^{-1}\Lambda $
.Footnote
6
An
![]() $\mathcal {O}_{F,v}$
-lattice
$\mathcal {O}_{F,v}$
-lattice
![]() $\Lambda $
in an
$\Lambda $
in an
![]() $F_v/F_{0,v}$
-hermitian space is called a vertex lattice if it is a vertex lattice of type r for some r. Here,
$F_v/F_{0,v}$
-hermitian space is called a vertex lattice if it is a vertex lattice of type r for some r. Here,
![]() $\pi _v$
is a uniformizer in
$\pi _v$
is a uniformizer in
![]() $F_v:=F\otimes _FF_{0,v}$
, where
$F_v:=F\otimes _FF_{0,v}$
, where
![]() $F_{0,v}$
is the v-adic completion of
$F_{0,v}$
is the v-adic completion of
![]() $F_0$
for a place v of
$F_0$
for a place v of
![]() $F_0$
. In particular, a self-dual lattice is simply a vertex lattice of type
$F_0$
. In particular, a self-dual lattice is simply a vertex lattice of type
![]() $0$
. Assume that
$0$
. Assume that
![]() $K_{G,v}=\mathrm {Stab}(\Lambda _v)\subset G(F_{0,v})$
.
$K_{G,v}=\mathrm {Stab}(\Lambda _v)\subset G(F_{0,v})$
.
B.1.27
Let
![]() $\mathcal {M}_{K_{\widetilde {G}}}(\widetilde {G})$
be the moduli functor which associates to each locally Noetherian
$\mathcal {M}_{K_{\widetilde {G}}}(\widetilde {G})$
be the moduli functor which associates to each locally Noetherian
![]() $\mathcal {O}_{E,(\nu )}$
-scheme S the groupoid of triples
$\mathcal {O}_{E,(\nu )}$
-scheme S the groupoid of triples
![]() $\mathcal {M}_{K_{\widetilde {G}}}(\widetilde {G})(S):=(A_0,\iota _0,\lambda _0, A,\iota ,\lambda ,\overline {\eta }^p)$
, where
$\mathcal {M}_{K_{\widetilde {G}}}(\widetilde {G})(S):=(A_0,\iota _0,\lambda _0, A,\iota ,\lambda ,\overline {\eta }^p)$
, where
-
•
 $(A_0,\iota _0,\lambda _0)\in \mathcal {M}_0^{\xi }(S)$
as is defined in B.1.25;
$(A_0,\iota _0,\lambda _0)\in \mathcal {M}_0^{\xi }(S)$
as is defined in B.1.25; -
•
 $(A,\iota )$
is an abelian scheme over S, equipped with an
$(A,\iota )$
is an abelian scheme over S, equipped with an
 $\mathcal {O}_F\otimes \mathbb {Z}_{(p)}$
-endomorphism structure
$\mathcal {O}_F\otimes \mathbb {Z}_{(p)}$
-endomorphism structure
 $\iota $
satisfying the Kottwitz condition of signature
$\iota $
satisfying the Kottwitz condition of signature
 $((1,n-1)_{\varphi _0},(0,n)_{\varphi \in \Phi \setminus \{\varphi _0\}})$
; that is,
$((1,n-1)_{\varphi _0},(0,n)_{\varphi \in \Phi \setminus \{\varphi _0\}})$
; that is,  $$\begin{align*}{\mathrm{Char}}(\iota(a)|{\mathrm{Lie}} A)=(T-\varphi_0(a))(T-\varphi_0(\overline{a}))^{n-1}\prod\limits_{\varphi\in\Phi\setminus\{\varphi_0\}}(T-\varphi(\overline{a}))^n\quad\text{ for all }a\in F;\end{align*}$$
$$\begin{align*}{\mathrm{Char}}(\iota(a)|{\mathrm{Lie}} A)=(T-\varphi_0(a))(T-\varphi_0(\overline{a}))^{n-1}\prod\limits_{\varphi\in\Phi\setminus\{\varphi_0\}}(T-\varphi(\overline{a}))^n\quad\text{ for all }a\in F;\end{align*}$$
-
•
 $\lambda $
is a polarization of A such that the associated Rosati involution induces the nontrivial Galois automorphism of
$\lambda $
is a polarization of A such that the associated Rosati involution induces the nontrivial Galois automorphism of
 $F/F_0$
on
$F/F_0$
on
 $\mathcal {O}_F\otimes \mathbb {Z}_{(p)}$
via
$\mathcal {O}_F\otimes \mathbb {Z}_{(p)}$
via
 $\iota $
, and such that the following additional assumption in [Reference Rapoport, Smithling and ZhangRSZ20, (4.2)] is also satisfied: the action of
$\iota $
, and such that the following additional assumption in [Reference Rapoport, Smithling and ZhangRSZ20, (4.2)] is also satisfied: the action of
 $\mathcal {O}_{F_0}\otimes \mathbb {Z}_p{\ \simeq \ }\prod \limits _{v|p}\mathcal {O}_{F_0,v}$
on the p-divisible group
$\mathcal {O}_{F_0}\otimes \mathbb {Z}_p{\ \simeq \ }\prod \limits _{v|p}\mathcal {O}_{F_0,v}$
on the p-divisible group
 $A[p^{\infty }]$
induces a decomposition
$A[p^{\infty }]$
induces a decomposition
 $ A[p^{\infty }]=\prod \limits _{v|p}A[v^{\infty }],$
where v ranges over the places of
$ A[p^{\infty }]=\prod \limits _{v|p}A[v^{\infty }],$
where v ranges over the places of
 $F_0$
above p; the polarization
$F_0$
above p; the polarization
 $\lambda $
then induces a polarization (B.1.28)for each v; we require
$\lambda $
then induces a polarization (B.1.28)for each v; we require $$ \begin{align} \lambda_v: A[v^{\infty}]\to A^{\vee}[v^{\infty}]{\ \simeq \ } A[v^{\vee}]^{\vee} \end{align} $$
$$ \begin{align} \lambda_v: A[v^{\infty}]\to A^{\vee}[v^{\infty}]{\ \simeq \ } A[v^{\vee}]^{\vee} \end{align} $$
 $\ker \lambda _v$
to be contained in
$\ker \lambda _v$
to be contained in
 $A[\iota (\pi _v)]$
of rank
$A[\iota (\pi _v)]$
of rank
 $\#(\Lambda _v^{*}/\Lambda _v)$
for each place v of
$\#(\Lambda _v^{*}/\Lambda _v)$
for each place v of
 $F_0$
above p;
$F_0$
above p;
-
•
 $\overline {\eta }^p$
is a
$\overline {\eta }^p$
is a
 $K_G^p$
-orbit of the
$K_G^p$
-orbit of the
 $\mathbb {A}^p_{F,f}$
-linear isometry (B.1.29)where the hermitian form on the left-hand side is
$\mathbb {A}^p_{F,f}$
-linear isometry (B.1.29)where the hermitian form on the left-hand side is $$ \begin{align} {\mathrm{Hom}}_F(\widehat{V}^p(A_0),\widehat{V}^p(A))\ \simeq \ -W\otimes_F \mathbb{A}^p_{F,f}, \end{align} $$
$$ \begin{align} {\mathrm{Hom}}_F(\widehat{V}^p(A_0),\widehat{V}^p(A))\ \simeq \ -W\otimes_F \mathbb{A}^p_{F,f}, \end{align} $$
 $(x,y)\mapsto \lambda _0^{-1}\circ y^{\vee }\circ \lambda \circ x.$
$(x,y)\mapsto \lambda _0^{-1}\circ y^{\vee }\circ \lambda \circ x.$
-
• For each
 $v\neq v_0$
over p, we impose the sign condition and Eisenstein condition at v [Reference Rapoport, Smithling and ZhangRSZ20, (4.4), (4.10)].
$v\neq v_0$
over p, we impose the sign condition and Eisenstein condition at v [Reference Rapoport, Smithling and ZhangRSZ20, (4.4), (4.10)].
By [Reference Rapoport, Smithling and ZhangRSZ20, Theorem 4.1], the forgetful map
![]() $(A_0,\iota _0,\lambda _0,A,\iota ,\lambda ,\overline {\eta }^p)\mapsto (A_0,\iota _0,\lambda _0)$
is representable and induces a morphism of
$(A_0,\iota _0,\lambda _0,A,\iota ,\lambda ,\overline {\eta }^p)\mapsto (A_0,\iota _0,\lambda _0)$
is representable and induces a morphism of
![]() $\mathcal {O}_{E,(\nu )}$
-schemes
$\mathcal {O}_{E,(\nu )}$
-schemes
On the level of generic fibres, (B.1.30) recovers the map (B.1.21).
B.2 Comparison of integral models
B.2.1
Let
![]() $\mathscr {S}_{K_{\widetilde {G}}}(\widetilde {G},\{h_{\widetilde {G}}\})$
be the integral model defined over
$\mathscr {S}_{K_{\widetilde {G}}}(\widetilde {G},\{h_{\widetilde {G}}\})$
be the integral model defined over
![]() $\mathcal {O}_{E,(\nu )}$
for
$\mathcal {O}_{E,(\nu )}$
for
![]() ${\mathrm {Sh}}_{K_{\widetilde {G}}}(\widetilde {G},\{h_{\widetilde {G}}\})$
as constructed in [Reference Kisin and PappasKP18,
${\mathrm {Sh}}_{K_{\widetilde {G}}}(\widetilde {G},\{h_{\widetilde {G}}\})$
as constructed in [Reference Kisin and PappasKP18,
![]() $\S$
4.6]. Recall that the abelian type integral model
$\S$
4.6]. Recall that the abelian type integral model
![]() $\mathscr {S}_{K_{\widetilde {G}}}(\widetilde {G},\{h_{\widetilde {G}}\})$
is built out of the integral model
$\mathscr {S}_{K_{\widetilde {G}}}(\widetilde {G},\{h_{\widetilde {G}}\})$
is built out of the integral model
![]() $\mathscr {S}(G^{\mathbb {Q}},\{h_{G^{\mathbb {Q}}}\})$
for a corresponding Hodge type Shimura variety associated to the abelian type
$\mathscr {S}(G^{\mathbb {Q}},\{h_{G^{\mathbb {Q}}}\})$
for a corresponding Hodge type Shimura variety associated to the abelian type
![]() ${\mathrm {Sh}}_{K_{\widetilde {G}}}(\widetilde {G},\{h_{\widetilde {G}}\})$
, which, as in [Reference Kisin and PappasKP18, 4.6.21] (see also [Reference KisinKis10, 3.4.13] and [Reference DeligneDel79] for more details), is
${\mathrm {Sh}}_{K_{\widetilde {G}}}(\widetilde {G},\{h_{\widetilde {G}}\})$
, which, as in [Reference Kisin and PappasKP18, 4.6.21] (see also [Reference KisinKis10, 3.4.13] and [Reference DeligneDel79] for more details), is
![]() ${\mathrm {Sh}}_{K_{G^{\mathbb {Q}}}}(G^{\mathbb {Q}},\{h_{G^{\mathbb {Q}}}\})$
. Recall that
${\mathrm {Sh}}_{K_{G^{\mathbb {Q}}}}(G^{\mathbb {Q}},\{h_{G^{\mathbb {Q}}}\})$
. Recall that
![]() $\mathscr {S}(G^{\mathbb {Q}},\{h_{G^{\mathbb {Q}}}\})$
is the
$\mathscr {S}(G^{\mathbb {Q}},\{h_{G^{\mathbb {Q}}}\})$
is the
![]() $\mathcal {O}_{F,(\nu )}$
-scheme constructed by taking the flat closure
$\mathcal {O}_{F,(\nu )}$
-scheme constructed by taking the flat closure
![]() $\mathscr {S}^-_{}(G^{\mathbb {Q}},\{h_{G^{\mathbb {Q}}}\})$
of the generic fibre
$\mathscr {S}^-_{}(G^{\mathbb {Q}},\{h_{G^{\mathbb {Q}}}\})$
of the generic fibre
![]() ${\mathrm {Sh}}_{}(G^{\mathbb {Q}},\{h_{G^{\mathbb {Q}}}\})$
inside some suitable Siegel integral model
${\mathrm {Sh}}_{}(G^{\mathbb {Q}},\{h_{G^{\mathbb {Q}}}\})$
inside some suitable Siegel integral model
![]() $\mathscr {S}_{K'}({\mathrm {GSp}},S^{\pm })_{\mathcal {O}_{F,(\nu )}}$
for some prime
$\mathscr {S}_{K'}({\mathrm {GSp}},S^{\pm })_{\mathcal {O}_{F,(\nu )}}$
for some prime
![]() $\nu $
of F above a fixed prime p. For convenience of expositions, we shall fix a symplectic embedding
$\nu $
of F above a fixed prime p. For convenience of expositions, we shall fix a symplectic embedding
![]() $i:(G^{\mathbb {Q}},\{h_{G^{\mathbb {Q}}}\})\hookrightarrow ({\mathrm {GSp}}(V,\psi ),S^{\pm })$
.Footnote
7
By [Reference XuXu21, Reference XuXu25],Footnote
8
this flat closure
$i:(G^{\mathbb {Q}},\{h_{G^{\mathbb {Q}}}\})\hookrightarrow ({\mathrm {GSp}}(V,\psi ),S^{\pm })$
.Footnote
7
By [Reference XuXu21, Reference XuXu25],Footnote
8
this flat closure
![]() $\mathscr {S}^-_{}(G^{\mathbb {Q}},\{h_{G^{\mathbb {Q}}}\}){\ \simeq \ } \mathscr {S}_{}(G^{\mathbb {Q}},\{h_{G^{\mathbb {Q}}}\})$
is the desired integral model.Footnote
9
We shall use the model for
$\mathscr {S}^-_{}(G^{\mathbb {Q}},\{h_{G^{\mathbb {Q}}}\}){\ \simeq \ } \mathscr {S}_{}(G^{\mathbb {Q}},\{h_{G^{\mathbb {Q}}}\})$
is the desired integral model.Footnote
9
We shall use the model for
![]() ${\mathrm {Sh}}(G^{\mathbb {Q}},\{h_{G^{\mathbb {Q}}}\})$
as building blocks for integral models for
${\mathrm {Sh}}(G^{\mathbb {Q}},\{h_{G^{\mathbb {Q}}}\})$
as building blocks for integral models for
![]() ${\mathrm {Sh}}_{K_{\widetilde {G}}}(\widetilde {G},\{h_{\widetilde {G}}\})$
and
${\mathrm {Sh}}_{K_{\widetilde {G}}}(\widetilde {G},\{h_{\widetilde {G}}\})$
and
![]() ${\mathrm {Sh}}_{K_G}(G,\{h_G\})$
.
${\mathrm {Sh}}_{K_G}(G,\{h_G\})$
.
Fix a connected component
![]() $\{h_{G^{\mathbb {Q}}}\}^+\subset \{h_{G^{\mathbb {Q}}}\}$
, and let
$\{h_{G^{\mathbb {Q}}}\}^+\subset \{h_{G^{\mathbb {Q}}}\}$
, and let
![]() ${\mathrm {Sh}}(G^{\mathbb {Q}},\{h_{G^{\mathbb {Q}}}\})^+\subset {\mathrm {Sh}}(G^{\mathbb {Q}},\{h_{G^{\mathbb {Q}}}\})$
be the geometrically connected component which is the image of
${\mathrm {Sh}}(G^{\mathbb {Q}},\{h_{G^{\mathbb {Q}}}\})^+\subset {\mathrm {Sh}}(G^{\mathbb {Q}},\{h_{G^{\mathbb {Q}}}\})$
be the geometrically connected component which is the image of
![]() $\{h_{G^{\mathbb {Q}}}\}^+\times 1$
. Let
$\{h_{G^{\mathbb {Q}}}\}^+\times 1$
. Let
![]() $F^p\subset \overline {F}$
be the maximal extension of F that is unramified at primes dividing p. By [Reference DeligneDel79, Theorem 2.6.3], the action of
$F^p\subset \overline {F}$
be the maximal extension of F that is unramified at primes dividing p. By [Reference DeligneDel79, Theorem 2.6.3], the action of
![]() ${\mathrm {Gal}}(\overline {F}/F)$
on
${\mathrm {Gal}}(\overline {F}/F)$
on
![]() ${\mathrm {Sh}}_{K_{G^{\mathbb {Q}},p}}(G^{\mathbb {Q}},\{h_{G^{\mathbb {Q}}}\})^+$
factors through
${\mathrm {Sh}}_{K_{G^{\mathbb {Q}},p}}(G^{\mathbb {Q}},\{h_{G^{\mathbb {Q}}}\})^+$
factors through
![]() ${\mathrm {Gal}}(\overline {F}^p/F)$
. We abuse the notation and still denote
${\mathrm {Gal}}(\overline {F}^p/F)$
. We abuse the notation and still denote
![]() ${\mathrm {Sh}}_{K_{G^{\mathbb {Q}},p}}(G^{\mathbb {Q}},\{h_{G^{\mathbb {Q}}}\})^+$
as the
${\mathrm {Sh}}_{K_{G^{\mathbb {Q}},p}}(G^{\mathbb {Q}},\{h_{G^{\mathbb {Q}}}\})^+$
as the
![]() $F^p$
-scheme obtained via descent. Let
$F^p$
-scheme obtained via descent. Let
![]() $\mathscr {S}_{K_{G^{\mathbb {Q}},p}}(G^{\mathbb {Q}})^+$
be the closure of
$\mathscr {S}_{K_{G^{\mathbb {Q}},p}}(G^{\mathbb {Q}})^+$
be the closure of
![]() ${\mathrm {Sh}}_{K_{G^{\mathbb {Q}},p}}(G^{\mathbb {Q}},\{h_{G^{\mathbb {Q}}}\})^+$
in
${\mathrm {Sh}}_{K_{G^{\mathbb {Q}},p}}(G^{\mathbb {Q}},\{h_{G^{\mathbb {Q}}}\})^+$
in
![]() $\mathscr {S}_{K_{G^{\mathbb {Q}},p}}^-(G^{\mathbb {Q}},\{h_{G^{\mathbb {Q}}}\})\otimes _{\mathcal {O}_{F,(\nu )}}\mathcal {O}_{F^p,(\nu )}$
. Here, the notation
$\mathscr {S}_{K_{G^{\mathbb {Q}},p}}^-(G^{\mathbb {Q}},\{h_{G^{\mathbb {Q}}}\})\otimes _{\mathcal {O}_{F,(\nu )}}\mathcal {O}_{F^p,(\nu )}$
. Here, the notation
![]() $\mathcal {O}_{F^p,(\nu )}$
denotes the ring of integers of
$\mathcal {O}_{F^p,(\nu )}$
denotes the ring of integers of
![]() $F^p$
localized at
$F^p$
localized at
![]() $(p)$
.Footnote
10
$(p)$
.Footnote
10
Let
![]() $\mathscr {A}(\widetilde {G}_{\mathbb {Z}_{(p)}})$
(resp.
$\mathscr {A}(\widetilde {G}_{\mathbb {Z}_{(p)}})$
(resp.
![]() $\mathscr {A}(G^{\mathbb {Q}}_{\mathbb {Z}_{(p)}})^{\circ }$
) be the group defined in [Reference Kisin and PappasKP18, 4.6.8] for
$\mathscr {A}(G^{\mathbb {Q}}_{\mathbb {Z}_{(p)}})^{\circ }$
) be the group defined in [Reference Kisin and PappasKP18, 4.6.8] for
![]() $\widetilde {G}$
(resp.
$\widetilde {G}$
(resp.
![]() $G^{\mathbb {Q}}$
), which was originally defined in [Reference DeligneDel79]. We recall that
$G^{\mathbb {Q}}$
), which was originally defined in [Reference DeligneDel79]. We recall that
and
![]() $\mathscr {A}(G^{\mathbb {Q}}_{\mathbb {Z}_{(p)}})^{\circ }:=(G^{\mathbb {Q}})^{\circ }(\mathbb {Z}_{(p)})_+^-/Z(\mathbb {Z}_{(p)})^-*_{(G^{\mathbb {Q}})^{\circ }(\mathbb {Z}_{(p)})_+/Z(\mathbb {Z}_{(p)})}(G^{\mathbb {Q}})^{{\mathrm {ad}}\circ }(\mathbb {Z}_{(p)})^+$
, where
$\mathscr {A}(G^{\mathbb {Q}}_{\mathbb {Z}_{(p)}})^{\circ }:=(G^{\mathbb {Q}})^{\circ }(\mathbb {Z}_{(p)})_+^-/Z(\mathbb {Z}_{(p)})^-*_{(G^{\mathbb {Q}})^{\circ }(\mathbb {Z}_{(p)})_+/Z(\mathbb {Z}_{(p)})}(G^{\mathbb {Q}})^{{\mathrm {ad}}\circ }(\mathbb {Z}_{(p)})^+$
, where
![]() $(G^{\mathbb {Q}})^{\circ }(\mathbb {Z}_{(p)})_+^-$
is the closure of
$(G^{\mathbb {Q}})^{\circ }(\mathbb {Z}_{(p)})_+^-$
is the closure of
![]() $(G^{\mathbb {Q}})^{\circ }(\mathbb {Z}_{(p)})_+$
in
$(G^{\mathbb {Q}})^{\circ }(\mathbb {Z}_{(p)})_+$
in
![]() $(G^{\mathbb {Q}})(\mathbb {A}_f^p)$
. By [Reference Kisin and PappasKP18, Lemma 4.6.10], we have an inclusion
$(G^{\mathbb {Q}})(\mathbb {A}_f^p)$
. By [Reference Kisin and PappasKP18, Lemma 4.6.10], we have an inclusion
Here,
![]() $\mathscr {A}(\widetilde {G}):=\widetilde {G}(\mathbb {A}_f)/\widetilde {Z}(\mathbb {Q})^-*_{\widetilde {G}(\mathbb {Q})_+/\widetilde {Z}(\mathbb {Q})}\widetilde {G}^{{\mathrm {ad}}}(\mathbb {Q})^+$
, where
$\mathscr {A}(\widetilde {G}):=\widetilde {G}(\mathbb {A}_f)/\widetilde {Z}(\mathbb {Q})^-*_{\widetilde {G}(\mathbb {Q})_+/\widetilde {Z}(\mathbb {Q})}\widetilde {G}^{{\mathrm {ad}}}(\mathbb {Q})^+$
, where
![]() $\widetilde {Z}(\mathbb {Q})^-$
denotes the closure of
$\widetilde {Z}(\mathbb {Q})^-$
denotes the closure of
![]() $Z_{\widetilde {G}}(\mathbb {Q})$
in
$Z_{\widetilde {G}}(\mathbb {Q})$
in
![]() $\widetilde {G}(\mathbb {A}_f)$
, and
$\widetilde {G}(\mathbb {A}_f)$
, and
where
![]() $G^{\mathbb {Q}}(\mathbb {Q})_+^-$
denotes the closure of
$G^{\mathbb {Q}}(\mathbb {Q})_+^-$
denotes the closure of
![]() $G^{\mathbb {Q}}(\mathbb {Q})_+$
in
$G^{\mathbb {Q}}(\mathbb {Q})_+$
in
![]() $G^{\mathbb {Q}}(\mathbb {A}_f)$
. Let
$G^{\mathbb {Q}}(\mathbb {A}_f)$
. Let
![]() $\widetilde {J}\subset \widetilde {G}(\mathbb {Q}_p)$
denote a set which maps bijectively to a set of coset representatives for the image of
$\widetilde {J}\subset \widetilde {G}(\mathbb {Q}_p)$
denote a set which maps bijectively to a set of coset representatives for the image of
![]() $\mathscr {A}(\widetilde {G}_{\mathbb {Z}_{(p)}})$
in
$\mathscr {A}(\widetilde {G}_{\mathbb {Z}_{(p)}})$
in
![]() $\mathscr {A}(G^{\mathbb {Q}})^{\circ }\backslash \mathscr {A}(\widetilde {G})/K_{\widetilde {G},p}$
under (B.2.3). Recall from [Reference Kisin and PappasKP18, 4.6.15], we have
$\mathscr {A}(G^{\mathbb {Q}})^{\circ }\backslash \mathscr {A}(\widetilde {G})/K_{\widetilde {G},p}$
under (B.2.3). Recall from [Reference Kisin and PappasKP18, 4.6.15], we have
Note that by analogous arguments as loc.cit., the right-hand side of (B.2.4) has a natural structure of a
![]() $\mathcal {O}_{E,(\nu )}:=\mathcal {O}_E\otimes _{\mathcal {O}_F}\mathcal {O}_{F,(\nu )}$
-scheme with
$\mathcal {O}_{E,(\nu )}:=\mathcal {O}_E\otimes _{\mathcal {O}_F}\mathcal {O}_{F,(\nu )}$
-scheme with
![]() $\widetilde {G}(\mathbb {A}_f^p)$
-action and is a model for
$\widetilde {G}(\mathbb {A}_f^p)$
-action and is a model for
![]() ${\mathrm {Sh}}_{K_{\widetilde {G},p}}(\widetilde {G},\{h_{\widetilde {G}}\})$
. Moreover, for sufficiently small
${\mathrm {Sh}}_{K_{\widetilde {G},p}}(\widetilde {G},\{h_{\widetilde {G}}\})$
. Moreover, for sufficiently small
![]() $K_{\widetilde {G}}^p$
, the quotient
$K_{\widetilde {G}}^p$
, the quotient
![]() $\mathscr {S}_{K_{\widetilde {G},p}}(\widetilde {G},\{h_{\widetilde {G}}\})/K_{\widetilde {G}}^p:=\mathscr {S}_{K_{\widetilde {G}}}(\widetilde {G},\{h_{\widetilde {G}}\})$
is a finite type
$\mathscr {S}_{K_{\widetilde {G},p}}(\widetilde {G},\{h_{\widetilde {G}}\})/K_{\widetilde {G}}^p:=\mathscr {S}_{K_{\widetilde {G}}}(\widetilde {G},\{h_{\widetilde {G}}\})$
is a finite type
![]() $\mathcal {O}_{E,(\nu )}$
-scheme extending
$\mathcal {O}_{E,(\nu )}$
-scheme extending
![]() ${\mathrm {Sh}}_{K_{\widetilde {G}}}(\widetilde {G},\{h_{\widetilde {G}}\})$
.
${\mathrm {Sh}}_{K_{\widetilde {G}}}(\widetilde {G},\{h_{\widetilde {G}}\})$
.
Lemma B.2.5.
![]() $\mathcal {M}_{K_{\widetilde {G}}}(\widetilde {G},\{h_{\widetilde {G}}\}){\ \simeq \ }\mathscr {S}_{K_{\widetilde {G}}}(\widetilde {G},\{h_{\widetilde {G}}\})$
as
$\mathcal {M}_{K_{\widetilde {G}}}(\widetilde {G},\{h_{\widetilde {G}}\}){\ \simeq \ }\mathscr {S}_{K_{\widetilde {G}}}(\widetilde {G},\{h_{\widetilde {G}}\})$
as
![]() $\operatorname {\mathrm {Spec}}\mathcal {O}_{E,(\nu )}$
-schemes.
$\operatorname {\mathrm {Spec}}\mathcal {O}_{E,(\nu )}$
-schemes.
Proof. The moduli description for
![]() $\mathcal {M}_{K_{\widetilde {G}}}(\widetilde {G},\{h_{\widetilde {G}}\})$
in B.1.26 induces a natural map
$\mathcal {M}_{K_{\widetilde {G}}}(\widetilde {G},\{h_{\widetilde {G}}\})$
in B.1.26 induces a natural map
by simply forgetting the component
![]() $(A_0,\iota _0,\lambda _0,\overline {\eta }^p)$
in the tuple. Note that the map (B.2.6) is proper, and in particular closed. We fix an arbitrary
$(A_0,\iota _0,\lambda _0,\overline {\eta }^p)$
in the tuple. Note that the map (B.2.6) is proper, and in particular closed. We fix an arbitrary
![]() $(A^{\star },\iota ^{\star },\lambda ^{\star })\in \mathscr {S}_{K_{G^{\mathbb {Q}},p}}(G^{\mathbb {Q}})^+$
, and suppose
$(A^{\star },\iota ^{\star },\lambda ^{\star })\in \mathscr {S}_{K_{G^{\mathbb {Q}},p}}(G^{\mathbb {Q}})^+$
, and suppose
under the map (B.2.6). Take any
![]() $(h,\gamma ^{-1})\in \mathscr {A}(\widetilde {G}_{\mathbb {Z}_{(p)}})$
. As in [Reference Kisin and PappasKP18, 4.5.3], let
$(h,\gamma ^{-1})\in \mathscr {A}(\widetilde {G}_{\mathbb {Z}_{(p)}})$
. As in [Reference Kisin and PappasKP18, 4.5.3], let
![]() $\widetilde {\mathcal {P}}_{\gamma }\subset \widetilde {G}$
be the torsor given by the fibre over
$\widetilde {\mathcal {P}}_{\gamma }\subset \widetilde {G}$
be the torsor given by the fibre over
![]() $\gamma \in \widetilde {G}^{{\mathrm {ad}}}(\mathbb {Z}_{(p)})$
. First we check that
$\gamma \in \widetilde {G}^{{\mathrm {ad}}}(\mathbb {Z}_{(p)})$
. First we check that
gives another point in the fibre over
![]() $(A^{\star },\iota ^{\star },\lambda ^{\star })$
under the map (B.2.6). This is clear as we only need to check that
$(A^{\star },\iota ^{\star },\lambda ^{\star })$
under the map (B.2.6). This is clear as we only need to check that
![]() $(\eta ^{\star })^{\widetilde {\mathcal {P}}_{\gamma }}$
are
$(\eta ^{\star })^{\widetilde {\mathcal {P}}_{\gamma }}$
are
![]() $\mathbb {A}_{F,f}$
-linear isometries
$\mathbb {A}_{F,f}$
-linear isometries
but this is simply given by the composite
![]() $\widetilde {\gamma }^{-1}\circ \eta ^{\star }\circ \iota _{\widetilde {\gamma }}^{-1}$
, where
$\widetilde {\gamma }^{-1}\circ \eta ^{\star }\circ \iota _{\widetilde {\gamma }}^{-1}$
, where
![]() $\iota _{\widetilde {\gamma }}$
is as defined in [Reference Kisin and PappasKP18, 4.5.3].
$\iota _{\widetilde {\gamma }}$
is as defined in [Reference Kisin and PappasKP18, 4.5.3].
It then remains to check that
![]() $\ker (\mathscr {A}(G^{\mathbb {Q}}_{\mathbb {Z}_{(p)}})^{\circ }\to \mathscr {A}(\widetilde {G}_{\mathbb {Z}_{(p)}}))$
acts freely on
$\ker (\mathscr {A}(G^{\mathbb {Q}}_{\mathbb {Z}_{(p)}})^{\circ }\to \mathscr {A}(\widetilde {G}_{\mathbb {Z}_{(p)}}))$
acts freely on
![]() $\mathscr {S}_{K_{G^{\mathbb {Q}},p}}(G^{\mathbb {Q}})^+$
, and this follows from [Reference Kisin and PappasKP18, 4.6.17] and the fact that
$\mathscr {S}_{K_{G^{\mathbb {Q}},p}}(G^{\mathbb {Q}})^+$
, and this follows from [Reference Kisin and PappasKP18, 4.6.17] and the fact that
![]() $\ker (\mathscr {A}(G^{\mathbb {Q}}_{\mathbb {Z}_{(p)}})^{\circ }\to \mathscr {A}(\widetilde {G}_{\mathbb {Z}_{(p)}}))$
is a subgroup of
$\ker (\mathscr {A}(G^{\mathbb {Q}}_{\mathbb {Z}_{(p)}})^{\circ }\to \mathscr {A}(\widetilde {G}_{\mathbb {Z}_{(p)}}))$
is a subgroup of
![]() $\Delta (G^{\mathbb {Q}},(G^{\mathbb {Q}})^{{\mathrm {ad}}}):=\ker (\mathscr {A}(G^{\mathbb {Q}}_{\mathbb {Z}_{(p)}})\to \mathscr {A}(G^{\mathbb {Q}{\mathrm {ad}}}_{\mathbb {Z}_{(p)}}))$
. Thus,
$\Delta (G^{\mathbb {Q}},(G^{\mathbb {Q}})^{{\mathrm {ad}}}):=\ker (\mathscr {A}(G^{\mathbb {Q}}_{\mathbb {Z}_{(p)}})\to \mathscr {A}(G^{\mathbb {Q}{\mathrm {ad}}}_{\mathbb {Z}_{(p)}}))$
. Thus,
In particular,
![]() $\mathcal {M}_{K_{\widetilde {G}}}(\widetilde {G},\{h_{\widetilde {G}}\}){\ \simeq \ }\mathscr {S}_{K_{\widetilde {G}}}(\widetilde {G},\{h_{\widetilde {G}}\})$
.
$\mathcal {M}_{K_{\widetilde {G}}}(\widetilde {G},\{h_{\widetilde {G}}\}){\ \simeq \ }\mathscr {S}_{K_{\widetilde {G}}}(\widetilde {G},\{h_{\widetilde {G}}\})$
.
B.2.10
For an arbitrary extension
![]() $L/E$
, taking the fibre in (B.1.30) over a fixed
$L/E$
, taking the fibre in (B.1.30) over a fixed
![]() $\mathcal {O}_{L,(\nu )}$
-point
$\mathcal {O}_{L,(\nu )}$
-point
![]() $(A_0^{\star },\iota _0^{\star },\lambda _0^{\star })$
of
$(A_0^{\star },\iota _0^{\star },\lambda _0^{\star })$
of
![]() $\mathcal {M}_0^{\mathcal {O}_F,\xi }$
gives a flat integral model
$\mathcal {M}_0^{\mathcal {O}_F,\xi }$
gives a flat integral model
![]() $\mathcal {M}^{\star }_{K_G}(G,\{h_G\})$
over
$\mathcal {M}^{\star }_{K_G}(G,\{h_G\})$
over
![]() $\mathcal {O}_L$
. Here, we use the upper script
$\mathcal {O}_L$
. Here, we use the upper script
![]() $\star $
to emphasize that the model
$\star $
to emphasize that the model
![]() $\mathcal {M}^{\star }_{K_G}(G,\{h_G\})$
thus obtained a priori depends on the choice of a base point
$\mathcal {M}^{\star }_{K_G}(G,\{h_G\})$
thus obtained a priori depends on the choice of a base point
![]() $(A_0^{\star },\iota _0^{\star },\lambda _0^{\star })$
. However, recall from B.1.17 that the reflex field for
$(A_0^{\star },\iota _0^{\star },\lambda _0^{\star })$
. However, recall from B.1.17 that the reflex field for
![]() $(G,\{h_G\})$
is F, by [Reference Kisin and PappasKP18] we also have a normal integral model
$(G,\{h_G\})$
is F, by [Reference Kisin and PappasKP18] we also have a normal integral model
![]() $\mathscr {S}_{K_G}(G,\{h_G\})$
over
$\mathscr {S}_{K_G}(G,\{h_G\})$
over
![]() $\operatorname {\mathrm {Spec}} \mathcal {O}_{F,(v)}$
, which is given by
$\operatorname {\mathrm {Spec}} \mathcal {O}_{F,(v)}$
, which is given by
Here,
![]() $\mathscr {A}(G_{\mathbb {Z}_{(p)}})$
is the analogous group for G as defined in (B.2.2), and
$\mathscr {A}(G_{\mathbb {Z}_{(p)}})$
is the analogous group for G as defined in (B.2.2), and
![]() $J\subset G(\mathbb {Q}_p)$
denotes the set analogous to
$J\subset G(\mathbb {Q}_p)$
denotes the set analogous to
![]() $\widetilde {J}$
defined above (B.2.4), using the analogous map for G as in (B.2.3).
$\widetilde {J}$
defined above (B.2.4), using the analogous map for G as in (B.2.3).
Lemma B.2.12.
![]() $\mathcal {M}_{K_G}(G,\{h_G\}){\ \simeq \ }\mathscr {S}_{K_G}(G,\{h_G\})_{\mathcal {O}_{L,(\nu )}}$
as
$\mathcal {M}_{K_G}(G,\{h_G\}){\ \simeq \ }\mathscr {S}_{K_G}(G,\{h_G\})_{\mathcal {O}_{L,(\nu )}}$
as
![]() $\operatorname {\mathrm {Spec}}\mathcal {O}_{L,(\nu )}$
-schemes.
$\operatorname {\mathrm {Spec}}\mathcal {O}_{L,(\nu )}$
-schemes.
Proof. Consider the map
given by forgetting the component
![]() $(A_0^{\star },\iota _0^{\star },\lambda _0^{\star })$
in the tuple. Let
$(A_0^{\star },\iota _0^{\star },\lambda _0^{\star })$
in the tuple. Let
![]() $\mathscr {S}_{K_{G^{\mathbb {Q}},p}}^{\star }(G^{\mathbb {Q}}) _{\mathcal {O}_{L,(\nu )}}$
denote the image of the map (B.2.13). We take an arbitrary
$\mathscr {S}_{K_{G^{\mathbb {Q}},p}}^{\star }(G^{\mathbb {Q}}) _{\mathcal {O}_{L,(\nu )}}$
denote the image of the map (B.2.13). We take an arbitrary
![]() $(A,\iota ,\lambda )\in \mathscr {S}_{K_{G^{\mathbb {Q}},p}}^{\star }(G^{\mathbb {Q}})^+_{\mathcal {O}_{L,(\nu )}}$
, and thus by construction of
$(A,\iota ,\lambda )\in \mathscr {S}_{K_{G^{\mathbb {Q}},p}}^{\star }(G^{\mathbb {Q}})^+_{\mathcal {O}_{L,(\nu )}}$
, and thus by construction of
![]() $\mathcal {M}^{\star }_{K_{G}}(G,\{h_{G}\})$
, we clearly have
$\mathcal {M}^{\star }_{K_{G}}(G,\{h_{G}\})$
, we clearly have
Take any
![]() $(h,\gamma ^{-1})\in \mathscr {A}(G_{\mathbb {Z}_{(p)}})$
. In particular,
$(h,\gamma ^{-1})\in \mathscr {A}(G_{\mathbb {Z}_{(p)}})$
. In particular,
![]() $\gamma \in G^{{\mathrm {ad}}}{\ \simeq \ } (G^{\mathbb {Q}})^{{\mathrm {ad}}}$
. Again as in [Reference Kisin and PappasKP18, 4.5.3], let
$\gamma \in G^{{\mathrm {ad}}}{\ \simeq \ } (G^{\mathbb {Q}})^{{\mathrm {ad}}}$
. Again as in [Reference Kisin and PappasKP18, 4.5.3], let
![]() $\mathcal {P}_{\gamma }\subset G^{\mathbb {Q}}$
be the torsor given by the fibre over
$\mathcal {P}_{\gamma }\subset G^{\mathbb {Q}}$
be the torsor given by the fibre over
![]() $\gamma \in (G^{\mathbb {Q}})^{{\mathrm {ad}}}(\mathbb {Z}_{(p)})$
. By the same reasoning as in the proof of Lemma B.2.5, we also have
$\gamma \in (G^{\mathbb {Q}})^{{\mathrm {ad}}}(\mathbb {Z}_{(p)})$
. By the same reasoning as in the proof of Lemma B.2.5, we also have
gives another point in the fibre over
![]() $(A_0^{\star },\iota _0^{\star },\lambda _0^{\star })$
under the map (B.1.30). The rest of the argument proceeds similarly as in the proof of Lemma B.2.5 – that is, the kernel
$(A_0^{\star },\iota _0^{\star },\lambda _0^{\star })$
under the map (B.1.30). The rest of the argument proceeds similarly as in the proof of Lemma B.2.5 – that is, the kernel
![]() $\ker (\mathscr {A}(G^{\mathbb {Q}}_{\mathbb {Z}_{(p)}})^{\circ }\to \mathscr {A}(G_{\mathbb {Z}_{(p)}}))$
acts freely on
$\ker (\mathscr {A}(G^{\mathbb {Q}}_{\mathbb {Z}_{(p)}})^{\circ }\to \mathscr {A}(G_{\mathbb {Z}_{(p)}}))$
acts freely on
![]() $\mathscr {S}_{K_{G^{\mathbb {Q}},p}}(G^{\mathbb {Q}})^+$
. In particular, we have
$\mathscr {S}_{K_{G^{\mathbb {Q}},p}}(G^{\mathbb {Q}})^+$
. In particular, we have
and thus,
![]() $\mathcal {M}^{\star }_{K_G}(G){\ \simeq \ }\mathscr {S}_{K_G}(G)_{\mathcal {O}_{L,(\nu )}}$
. (Since the choice of base point
$\mathcal {M}^{\star }_{K_G}(G){\ \simeq \ }\mathscr {S}_{K_G}(G)_{\mathcal {O}_{L,(\nu )}}$
. (Since the choice of base point
![]() $\star $
does not affect the proof, we may drop the upper script
$\star $
does not affect the proof, we may drop the upper script
![]() $\star $
from our notations.)
$\star $
from our notations.)
B.2.17
We consider the Drinfeld level structure integral models analogous to those in [Reference Rapoport, Smithling and ZhangRSZ20,
![]() $\S$
4.3]. Consider the embedding
$\S$
4.3]. Consider the embedding
![]() $\widetilde {\nu }: \overline {\mathbb {Q}}\hookrightarrow \overline {\mathbb {Q}}_p$
, which identifies
$\widetilde {\nu }: \overline {\mathbb {Q}}\hookrightarrow \overline {\mathbb {Q}}_p$
, which identifies
The above identification (B.2.18) then gives an identification
where
![]() $w_{\varphi }$
denotes the p-adic place in F induced by
$w_{\varphi }$
denotes the p-adic place in F induced by
![]() $\widetilde {\nu }\circ \varphi $
.
$\widetilde {\nu }\circ \varphi $
.
We fix a place
![]() $v_0$
of F over p that is split in F (and possibly ramified over p) into
$v_0$
of F over p that is split in F (and possibly ramified over p) into
![]() $w_0$
and another place
$w_0$
and another place
![]() $\overline {w}_0$
in F. We require, moreover, that the CM type
$\overline {w}_0$
in F. We require, moreover, that the CM type
![]() $\Phi $
considered in (B.1.2) and the chosen place
$\Phi $
considered in (B.1.2) and the chosen place
![]() $\nu $
of E above p satisfy the following matching condition:
$\nu $
of E above p satisfy the following matching condition:
This condition (B.2.20) only depends on the place
![]() $\nu $
of E induced by
$\nu $
of E induced by
![]() $\widetilde {\nu }$
.
$\widetilde {\nu }$
.
Now we introduce a Drinfeld level structure at
![]() $v_0$
. Recall the level structure subgroup
$v_0$
. Recall the level structure subgroup
![]() $K_G$
from (B.1.20). We define a variant compact open subgroup
$K_G$
from (B.1.20). We define a variant compact open subgroup
![]() $K_G^m\subset G(\mathbb {A}_{F_0,f})$
in exactly the same way as
$K_G^m\subset G(\mathbb {A}_{F_0,f})$
in exactly the same way as
![]() $K_G$
, except that, in the
$K_G$
, except that, in the
![]() $v_0$
-factor, we require
$v_0$
-factor, we require
![]() $K_{G,v_0}^m\subset G(F_{0,v_0})$
to be the principal congruence subgroup modulo
$K_{G,v_0}^m\subset G(F_{0,v_0})$
to be the principal congruence subgroup modulo
![]() $\mathfrak {p}_{v_0}^m$
inside
$\mathfrak {p}_{v_0}^m$
inside
![]() $K_{G,v_0}$
. Clearly,
$K_{G,v_0}$
. Clearly,
![]() $K_G=K_G^{m=0}$
. As in (B.1.20), we define
$K_G=K_G^{m=0}$
. As in (B.1.20), we define
![]() $K_{\widetilde {G}}^m=K_{Z^{\mathbb {Q}}}\times K_G^m$
.
$K_{\widetilde {G}}^m=K_{Z^{\mathbb {Q}}}\times K_G^m$
.
Let
![]() $\Lambda _{v_0}=\Lambda _{w_0}\oplus \Lambda _{\overline {w}_0}$
denote the natural decomposition of the lattice
$\Lambda _{v_0}=\Lambda _{w_0}\oplus \Lambda _{\overline {w}_0}$
denote the natural decomposition of the lattice
![]() $\Lambda _{v_0}$
attached to the split place
$\Lambda _{v_0}$
attached to the split place
![]() $v_0$
. For a point
$v_0$
. For a point
![]() $(A_0,\iota _0,\lambda _0,A,\iota ,\lambda ,\overline {\eta }^p)\in \mathcal {M}_{K_{\widetilde {G}}}(\widetilde {G})(S)$
, we have a decomposition of p-divisible groups
$(A_0,\iota _0,\lambda _0,A,\iota ,\lambda ,\overline {\eta }^p)\in \mathcal {M}_{K_{\widetilde {G}}}(\widetilde {G})(S)$
, we have a decomposition of p-divisible groups
where w ranges over the places of F lying over p. Moreover, we further decompose the
![]() $v_0$
-term in (B.2.21) and consider
$v_0$
-term in (B.2.21) and consider
where, when p is locally nilpotent on S, the p-divisible group
![]() $A[w_0^{\infty }]$
satisfies the Kottwitz condition of type
$A[w_0^{\infty }]$
satisfies the Kottwitz condition of type
![]() $r|_{w_0}$
for the action of
$r|_{w_0}$
for the action of
![]() $\mathcal {O}_{F,w_0}$
on its Lie algebra, in the sense of [Reference Rapoport and ZinkRZ17,
$\mathcal {O}_{F,w_0}$
on its Lie algebra, in the sense of [Reference Rapoport and ZinkRZ17,
![]() $\S$
8]. Here,
$\S$
8]. Here,
![]() $r|_{w_0}$
denotes the restriction of the function r on
$r|_{w_0}$
denotes the restriction of the function r on
![]() ${\mathrm {Hom}}_{\mathbb {Q}}(F,\overline {\mathbb {Q}})$
to
${\mathrm {Hom}}_{\mathbb {Q}}(F,\overline {\mathbb {Q}})$
to
![]() ${\mathrm {Hom}}_{\mathbb {Q}_p}(F_{w_0},\overline {\mathbb {Q}}_p)$
under (B.2.19).
${\mathrm {Hom}}_{\mathbb {Q}_p}(F_{w_0},\overline {\mathbb {Q}}_p)$
under (B.2.19).
Likewise, we have the same decomposition as (B.2.22) for
![]() $A_0$
; that is, we have
$A_0$
; that is, we have
Let
![]() $\pi _{w_0}$
be a uniformizer of
$\pi _{w_0}$
be a uniformizer of
![]() $F_{0,w_0}$
. In addition to the moduli functor
$F_{0,w_0}$
. In addition to the moduli functor
![]() $\mathcal {M}_{K_{\widetilde {G}}}(\widetilde {G})$
which classifies tuples
$\mathcal {M}_{K_{\widetilde {G}}}(\widetilde {G})$
which classifies tuples
![]() $(A_0,\iota _0,\lambda _0,A,\iota ,\lambda ,\overline {\eta }^p)$
, we impose the following additional Drinfeld level structure as in [Reference Harris and TaylorHT01,
$(A_0,\iota _0,\lambda _0,A,\iota ,\lambda ,\overline {\eta }^p)$
, we impose the following additional Drinfeld level structure as in [Reference Harris and TaylorHT01,
![]() $\S$
II.2]; that is,
$\S$
II.2]; that is,
-
• an
 $\mathcal {O}_{F,w_0}$
-linear homomorphism of finite flat group schemes (B.2.24)
$\mathcal {O}_{F,w_0}$
-linear homomorphism of finite flat group schemes (B.2.24) $$ \begin{align} \eta:\pi_{w_0}^{-m}\Lambda_{w_0}/\Lambda_{w_0}\to \underline{{\mathrm{Hom}}}_{\mathcal{O}_{F,w_0}}(A_0[w_0^m],A[w_0^m]). \end{align} $$
$$ \begin{align} \eta:\pi_{w_0}^{-m}\Lambda_{w_0}/\Lambda_{w_0}\to \underline{{\mathrm{Hom}}}_{\mathcal{O}_{F,w_0}}(A_0[w_0^m],A[w_0^m]). \end{align} $$
We denote the resulting moduli problem by
![]() $\mathcal {M}_{K_{\widetilde {G}}^m}(\widetilde {G})$
, which is relatively representable by a finite flat morphism to
$\mathcal {M}_{K_{\widetilde {G}}^m}(\widetilde {G})$
, which is relatively representable by a finite flat morphism to
![]() $\mathcal {M}_{K_{\widetilde {G}}}(\widetilde {G})$
. In fact,
$\mathcal {M}_{K_{\widetilde {G}}}(\widetilde {G})$
. In fact,
![]() $\mathcal {M}_{K_{\widetilde {G}}^m}(\widetilde {G})$
is regular and flat over
$\mathcal {M}_{K_{\widetilde {G}}^m}(\widetilde {G})$
is regular and flat over
![]() $\operatorname {\mathrm {Spec}}\mathcal {O}_{E,(\nu )}$
by [Reference Harris and TaylorHT01, Lemma III.4.1].
$\operatorname {\mathrm {Spec}}\mathcal {O}_{E,(\nu )}$
by [Reference Harris and TaylorHT01, Lemma III.4.1].
B.2.25
Recall the integral model
![]() $\mathscr {S}_{K_{\widetilde {G}}}(\widetilde {G},\{h_{\widetilde {G}}\})$
(resp.
$\mathscr {S}_{K_{\widetilde {G}}}(\widetilde {G},\{h_{\widetilde {G}}\})$
(resp.
![]() $\mathscr {S}_{K_G}(G,\{h_G\})$
) defined in (B.2.4) (resp. (B.2.11)). We define
$\mathscr {S}_{K_G}(G,\{h_G\})$
) defined in (B.2.4) (resp. (B.2.11)). We define
![]() $\mathscr {S}_{K_{\widetilde {G}}^m}(\widetilde {G},\{h_{\widetilde {G}}\})$
(resp.
$\mathscr {S}_{K_{\widetilde {G}}^m}(\widetilde {G},\{h_{\widetilde {G}}\})$
(resp.
![]() $\mathscr {S}_{K_G^m}(G,\{h_G\})_{\mathcal {O}_{L,(\nu )}}$
) as the normalization of
$\mathscr {S}_{K_G^m}(G,\{h_G\})_{\mathcal {O}_{L,(\nu )}}$
) as the normalization of
![]() $\mathscr {S}_{K_{\widetilde {G}}}(\widetilde {G},\{h_{\widetilde {G}}\})$
(resp.
$\mathscr {S}_{K_{\widetilde {G}}}(\widetilde {G},\{h_{\widetilde {G}}\})$
(resp.
![]() $\mathscr {S}_{K_G}(G,\{h_G\})_{\mathcal {O}_{L, (\nu )}}$
) inside
$\mathscr {S}_{K_G}(G,\{h_G\})_{\mathcal {O}_{L, (\nu )}}$
) inside
![]() ${\mathrm {Sh}}_{K_{\widetilde {G}}^m}(\widetilde {G},\{h_{\widetilde {G}}\}){\ \simeq \ } M_{K_{\widetilde {G}}^m}(\widetilde {G})$
(resp.
${\mathrm {Sh}}_{K_{\widetilde {G}}^m}(\widetilde {G},\{h_{\widetilde {G}}\}){\ \simeq \ } M_{K_{\widetilde {G}}^m}(\widetilde {G})$
(resp.
![]() ${\mathrm {Sh}}_{{K_G^m}}(G,\{h_G\})_L{\ \simeq \ } M_{{K_G^m}}(G)_L$
).
${\mathrm {Sh}}_{{K_G^m}}(G,\{h_G\})_L{\ \simeq \ } M_{{K_G^m}}(G)_L$
).
Corollary B.2.26.
![]() $\mathscr {S}_{K_{\widetilde {G}}^m}(\widetilde {G},\{h_{\widetilde {G}}\}){\ \simeq \ } \mathcal {M}_{K_{\widetilde {G}}^m}(\widetilde {G})$
as
$\mathscr {S}_{K_{\widetilde {G}}^m}(\widetilde {G},\{h_{\widetilde {G}}\}){\ \simeq \ } \mathcal {M}_{K_{\widetilde {G}}^m}(\widetilde {G})$
as
![]() $\operatorname {\mathrm {Spec}}\mathcal {O}_{E,(\nu )}$
-schemes, and
$\operatorname {\mathrm {Spec}}\mathcal {O}_{E,(\nu )}$
-schemes, and
as
![]() $\operatorname {\mathrm {Spec}}\mathcal {O}_{L,(\nu )}$
-schemes.
$\operatorname {\mathrm {Spec}}\mathcal {O}_{L,(\nu )}$
-schemes.
Proof. By Lemma B.2.5 (resp. B.2.12),
![]() $\mathscr {S}_{K_{\widetilde {G}}^m}(\widetilde {G},\{h_{\widetilde {G}}\})$
(resp.
$\mathscr {S}_{K_{\widetilde {G}}^m}(\widetilde {G},\{h_{\widetilde {G}}\})$
(resp.
![]() $\mathscr {S}_{K_G^m}(G,\{h_G\})_{\mathcal {O}_L}$
) is the normalization of
$\mathscr {S}_{K_G^m}(G,\{h_G\})_{\mathcal {O}_L}$
) is the normalization of
![]() $\mathscr {S}_{K_{\widetilde {G}}}(\widetilde {G},\{h_{\widetilde {G}}\}){\ \simeq \ } \mathcal {M}_{K_{\widetilde {G}}}(\widetilde {G},\{h_{\widetilde {G}}\})$
(resp.
$\mathscr {S}_{K_{\widetilde {G}}}(\widetilde {G},\{h_{\widetilde {G}}\}){\ \simeq \ } \mathcal {M}_{K_{\widetilde {G}}}(\widetilde {G},\{h_{\widetilde {G}}\})$
(resp.
![]() $\mathscr {S}_{K_G}(G,\{h_G\})_{\mathcal {O}_L}{\ \simeq \ } \mathcal {M}_{K_G}(G,\{h_G\})$
) inside
$\mathscr {S}_{K_G}(G,\{h_G\})_{\mathcal {O}_L}{\ \simeq \ } \mathcal {M}_{K_G}(G,\{h_G\})$
) inside
![]() ${\mathrm {Sh}}_{K_{\widetilde {G}}^m}(\widetilde {G},\{h_{\widetilde {G}}\}){\ \simeq \ } M_{K_{\widetilde {G}}^m}(\widetilde {G})$
(resp.
${\mathrm {Sh}}_{K_{\widetilde {G}}^m}(\widetilde {G},\{h_{\widetilde {G}}\}){\ \simeq \ } M_{K_{\widetilde {G}}^m}(\widetilde {G})$
(resp.
![]() ${\mathrm {Sh}}_{{K_G^m}}(G)_L{\ \simeq \ } M_{{K_G^m}}(G)_L$
). Since
${\mathrm {Sh}}_{{K_G^m}}(G)_L{\ \simeq \ } M_{{K_G^m}}(G)_L$
). Since
![]() $\mathcal {M}_{K_{\widetilde {G}}^m}(\widetilde {G})$
is regular and flat, in particular it is normal. Thus, by [Reference GrothendieckGro67, IV-2, 6.14.1],
$\mathcal {M}_{K_{\widetilde {G}}^m}(\widetilde {G})$
is regular and flat, in particular it is normal. Thus, by [Reference GrothendieckGro67, IV-2, 6.14.1],
![]() $\mathcal {M}_{K_G^m}(G)$
is normal (even though it may not necessarily be regular). By [Reference ProjectSta18, 035I] applied to the scheme
$\mathcal {M}_{K_G^m}(G)$
is normal (even though it may not necessarily be regular). By [Reference ProjectSta18, 035I] applied to the scheme
![]() $\mathcal {M}_{K_{\widetilde {G}}^m}(\widetilde {G})$
(resp.
$\mathcal {M}_{K_{\widetilde {G}}^m}(\widetilde {G})$
(resp.
![]() $\mathcal {M}_{K_G^m}(G)$
), there exists a unique morphism
$\mathcal {M}_{K_G^m}(G)$
), there exists a unique morphism
![]() $\mathscr {S}_{K_{\widetilde {G}}^m}(\widetilde {G},\{h_{\widetilde {G}}\})\to \mathcal {M}_{K_{\widetilde {G}}^m}(\widetilde {G})$
(resp.
$\mathscr {S}_{K_{\widetilde {G}}^m}(\widetilde {G},\{h_{\widetilde {G}}\})\to \mathcal {M}_{K_{\widetilde {G}}^m}(\widetilde {G})$
(resp.
![]() $\mathscr {S}_{K_{G}^m}(G,\{h_{G}\})\to \mathcal {M}_{K_{G}^m}(G)$
), which is the normalization of
$\mathscr {S}_{K_{G}^m}(G,\{h_{G}\})\to \mathcal {M}_{K_{G}^m}(G)$
), which is the normalization of
![]() $\mathcal {M}_{K_{\widetilde {G}}^m}(\widetilde {G})$
(resp.
$\mathcal {M}_{K_{\widetilde {G}}^m}(\widetilde {G})$
(resp.
![]() $\mathcal {M}_{K_G^m}(G)$
) in
$\mathcal {M}_{K_G^m}(G)$
) in
![]() ${\mathrm {Sh}}_{K_{\widetilde {G}}^m}(\widetilde {G},\{h_{\widetilde {G}}\})$
(resp.
${\mathrm {Sh}}_{K_{\widetilde {G}}^m}(\widetilde {G},\{h_{\widetilde {G}}\})$
(resp.
![]() ${\mathrm {Sh}}_{K_G^m}(G,\{h_G\})$
). Since
${\mathrm {Sh}}_{K_G^m}(G,\{h_G\})$
). Since
![]() $\mathcal {M}_{K_{\widetilde {G}}^m}(\widetilde {G})$
(resp.
$\mathcal {M}_{K_{\widetilde {G}}^m}(\widetilde {G})$
(resp.
![]() $\mathcal {M}_{K_G^m}(G)$
) is already normal, we have an isomorphism
$\mathcal {M}_{K_G^m}(G)$
) is already normal, we have an isomorphism
![]() $\mathscr {S}_{K_{\widetilde {G}}^m}(\widetilde {G},\{h_{\widetilde {G}}\}){\ \simeq \ } \mathcal {M}_{K_{\widetilde {G}}^m}(\widetilde {G})$
(resp.
$\mathscr {S}_{K_{\widetilde {G}}^m}(\widetilde {G},\{h_{\widetilde {G}}\}){\ \simeq \ } \mathcal {M}_{K_{\widetilde {G}}^m}(\widetilde {G})$
(resp.
![]() $\mathcal {M}_{K_G^m}(G,\{h_G\}){\ \simeq \ }\mathscr {S}_{K_G^m}(G,\{h_G\})_{\mathcal {O}_{L,(\nu )}}$
).
$\mathcal {M}_{K_G^m}(G,\{h_G\}){\ \simeq \ }\mathscr {S}_{K_G^m}(G,\{h_G\})_{\mathcal {O}_{L,(\nu )}}$
).
B.2.28
In this last section, we recall the construction of semi-global integral models with AT parahoric level as in [Reference Rapoport, Smithling and ZhangRSZ20,
![]() $\S$
4.4]. Recall the notion of vertex lattice from §B.1.26. We say that a vertex lattice
$\S$
4.4]. Recall the notion of vertex lattice from §B.1.26. We say that a vertex lattice
![]() $\Lambda $
is almost self-dual if it is a vertex lattice of type
$\Lambda $
is almost self-dual if it is a vertex lattice of type
![]() $1$
. We say that a vertex lattice
$1$
. We say that a vertex lattice
![]() $\Lambda $
is
$\Lambda $
is
![]() $\pi _v$
-modular (resp. almost
$\pi _v$
-modular (resp. almost
![]() $\pi _v$
-modular) if
$\pi _v$
-modular) if
![]() $\Lambda ^{*}=\pi _v^{-1}\Lambda $
(resp.
$\Lambda ^{*}=\pi _v^{-1}\Lambda $
(resp.
![]() $\Lambda \subset \Lambda ^{*}\subset ^1 \pi _v^{-1}\Lambda $
).
$\Lambda \subset \Lambda ^{*}\subset ^1 \pi _v^{-1}\Lambda $
).
Suppose
![]() $p\neq 2$
and
$p\neq 2$
and
![]() $v_0$
is unramified over p. As in §B.1.26, we take a vertex lattice
$v_0$
is unramified over p. As in §B.1.26, we take a vertex lattice
![]() $\Lambda _v\subset W_v$
for each prime v of
$\Lambda _v\subset W_v$
for each prime v of
![]() $F_0$
above p. Unlike in §B.1.26, let
$F_0$
above p. Unlike in §B.1.26, let
![]() $(v_0,\Lambda _{v_0})$
be of one of the following types:
$(v_0,\Lambda _{v_0})$
be of one of the following types:
-
1.
 $v_0$
is inert in F and
$v_0$
is inert in F and
 $\Lambda _{v_0}$
is almost self-dual as an
$\Lambda _{v_0}$
is almost self-dual as an
 $\mathcal {O}_{F,v_0}$
-lattice;
$\mathcal {O}_{F,v_0}$
-lattice; -
2. n is even,
 $v_0$
ramifies in F and
$v_0$
ramifies in F and
 $\Lambda _{v_0}$
is
$\Lambda _{v_0}$
is
 $\pi _{v_0}$
-modular;
$\pi _{v_0}$
-modular; -
3. n is odd,
 $v_0$
ramifies in F and
$v_0$
ramifies in F and
 $\Lambda _{v_0}$
is almost
$\Lambda _{v_0}$
is almost
 $\pi _{v_0}$
-modular;
$\pi _{v_0}$
-modular; -
4.
 $n=2$
,
$n=2$
,
 $v_0$
ramifies in F and
$v_0$
ramifies in F and
 $\Lambda _{v_0}$
is self-dual.
$\Lambda _{v_0}$
is self-dual.
To the moduli functor
![]() $\mathcal {M}_{K_{\widetilde {G}}}(\widetilde {G})$
which classifies tuples
$\mathcal {M}_{K_{\widetilde {G}}}(\widetilde {G})$
which classifies tuples
![]() $(A_0,\iota _0,\lambda _0,A,\iota ,\lambda ,\overline {\eta }^p)$
as in §B.1.26 (except that the condition on
$(A_0,\iota _0,\lambda _0,A,\iota ,\lambda ,\overline {\eta }^p)$
as in §B.1.26 (except that the condition on
![]() $(v_0,\Lambda _{v_0})$
is different), we impose the following additional condition:
$(v_0,\Lambda _{v_0})$
is different), we impose the following additional condition:
-
• When the pair
 $(v_0,\Lambda _{v_0})$
is of AT type (2), (3) or (4), we impose the Eisenstein condition on the summand
$(v_0,\Lambda _{v_0})$
is of AT type (2), (3) or (4), we impose the Eisenstein condition on the summand
 ${\mathrm {Lie}}_{\psi }A[v_0^{\infty }]$
[Reference Rapoport, Smithling and ZhangRSZ20, 4.10];
${\mathrm {Lie}}_{\psi }A[v_0^{\infty }]$
[Reference Rapoport, Smithling and ZhangRSZ20, 4.10]; -
• When the pair
 $(v_0,\Lambda _{v_0})$
is of AT type (2), we impose additionally the wedge condition [Reference Rapoport, Smithling and ZhangRSZ20, 4.27] and the spin condition [Reference Rapoport, Smithling and ZhangRSZ20, 4.28]
$(v_0,\Lambda _{v_0})$
is of AT type (2), we impose additionally the wedge condition [Reference Rapoport, Smithling and ZhangRSZ20, 4.27] and the spin condition [Reference Rapoport, Smithling and ZhangRSZ20, 4.28] -
• When the pair
 $(v_0,\Lambda _{v_0})$
is of AT type (3), we impose additionally the refined spin condition [Reference Rapoport, Smithling and ZhangRSZ18, (7.9)] on
$(v_0,\Lambda _{v_0})$
is of AT type (3), we impose additionally the refined spin condition [Reference Rapoport, Smithling and ZhangRSZ18, (7.9)] on
 ${\mathrm {Lie}}_{\psi _0}A[v_0^{\infty }]$
.
${\mathrm {Lie}}_{\psi _0}A[v_0^{\infty }]$
.
By [Reference Rapoport, Smithling and ZhangRSZ20, Theorem 4.7], the moduli functor above is representable by a Deligne-Mumford stack flat over
![]() $\operatorname {\mathrm {Spec}}\mathcal {O}_{E,(\nu )}$
and relatively representable over
$\operatorname {\mathrm {Spec}}\mathcal {O}_{E,(\nu )}$
and relatively representable over
![]() $\mathcal {M}_0^{\mathcal {O}_F,\xi }$
, i.e. (B.1.30) still holds in this case. To see that
$\mathcal {M}_0^{\mathcal {O}_F,\xi }$
, i.e. (B.1.30) still holds in this case. To see that
![]() $\mathcal {M}_{K_{\widetilde {G}}}(\widetilde {G},\{h_{\widetilde {G}}\}){\ \simeq \ }\mathscr {S}_{K_{\widetilde {G}}}(\widetilde {G},\{h_{\widetilde {G}}\})$
as
$\mathcal {M}_{K_{\widetilde {G}}}(\widetilde {G},\{h_{\widetilde {G}}\}){\ \simeq \ }\mathscr {S}_{K_{\widetilde {G}}}(\widetilde {G},\{h_{\widetilde {G}}\})$
as
![]() $\operatorname {\mathrm {Spec}}\mathcal {O}_{E,(\nu )}$
-schemes, one simply proceeds as in Lemma B.2.5.
$\operatorname {\mathrm {Spec}}\mathcal {O}_{E,(\nu )}$
-schemes, one simply proceeds as in Lemma B.2.5.
Acknowledgements
The author thanks Yifeng Liu for his many useful comments and suggestions. He also thanks Xinyi Yuan for sharing his manuscript and answering the author’s questions. He is grateful to Shouwu Zhang for proposing the arithmetic mixed Siegel-Weil formula and for his help on the revision of the paper. He thanks Jan Hendrik Bruinier, Stephan Ehlen, Ziqi Guo, Chao Li, and Siddarth Sankaran, Wei Zhang, Yihang Zhu and Jialiang Zou for their help. He also thanks Yujie Xu for providing Appendix B. He also thanks the anonymous referees for their advice to improve the presentation of this paper. The research is partially supported by the NSF grant DMS-2000533.
Competing interest
The authors have no competing interests to declare.






