Hostname: page-component-7dd5485656-zlgnt Total loading time: 0 Render date: 2025-10-30T21:24:23.180Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE IRREGULAR HODGE FILTRATION OF EXPONENTIALLY TWISTED MIXED HODGE MODULES

Part of: Singularities (Co)homology theory

Published online by Cambridge University Press:  25 May 2015

CLAUDE SABBAH  and
JENG-DAW YU
CLAUDE SABBAH
Affiliation:
UMR 7640 du CNRS, Centre de Mathématiques Laurent Schwartz, École polytechnique, F-91128 Palaiseau cedex, France; Claude.Sabbah@polytechnique.edu
JENG-DAW YU
Affiliation:
Department of Mathematics, National Taiwan University, Taipei 10617, Taiwan; jdyu@ntu.edu.tw

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Given a mixed Hodge module 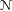$\mathcal{N}$ and a meromorphic function 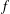$f$ on a complex manifold, we associate to these data a filtration (the irregular Hodge filtration) on the exponentially twisted holonomic module 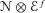$\mathcal{N}\otimes \mathcal{E}^{f}$, which extends the construction of Esnault et al. (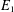$E_{1}$-degeneration of the irregular Hodge filtration (with an appendix by Saito), J. reine angew. Math. (2015),doi:10.1515/crelle-2014-0118). We show the strictness of the push-forward filtered 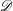${\mathcal{D}}$-module through any projective morphism 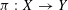${\it\pi}:X\rightarrow Y$, by using the theory of mixed twistor 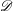${\mathcal{D}}$-modules of Mochizuki. We consider the example of the rescaling of a regular function 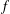$f$, which leads to an expression of the irregular Hodge filtration of the Laplace transform of the Gauss–Manin systems of 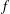$f$ in terms of the Harder–Narasimhan filtration of the Kontsevich bundles associated with 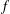$f$.

MSC classification

Primary: 14F40: de Rham cohomology 32S35: Mixed Hodge theory of singular varieties 32S40: Monodromy; relations with differential equations and $D$-modules

Information

Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 3 , 2015 , e9
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/3.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2015

References

Beilinson, A. A, Bernstein, J. N and Deligne, P., ‘Faisceaux pervers’, inAnalyse et topologie sur les espaces singuliers, Astérisque, 100 (Société Mathématique de France, Paris, 1982), 7–171.Google Scholar
Borisov, L. A, Chen, L. and Smith, G. G, ‘The orbifold Chow ring of toric Deligne-Mumford stacks’, J. Amer. Math. Soc. 18(1) (2005), 193–215.CrossRefGoogle Scholar
Brieskorn, E., ‘Die Monodromie der isolierten Singularitäten von Hyperflächen’, Manuscripta Math. 2 (1970), 103–161.Google Scholar
Deligne, P., Équations différentielles à points singuliers réguliers, Lecture Notes in Mathematics, 163 (Springer, Berlin, Heidelberg, New York, 1970).Google Scholar
Deligne, P., ‘Théorie de Hodge II’, Publ. Math. Inst. Hautes Études Sci. 40 (1971), 5–57.Google Scholar
Deligne, P., ‘Un théorème de finitude pour la monodromie’, inDiscrete Groups in Geometry and Analysis, New Haven, CT, 1984, Progress in Mathematics, 67 (Birkhäuser, Boston, MA, 1987), 1–19.Google Scholar
Deligne, P., ‘Théorie de Hodge irrégulière (mars 1984 & août 2006)’, inSingularités irrégulières, Correspondance et documents, Documents mathématiques, 5 (Société Mathématique de France, Paris, 2007), 109–114, 115–128.Google Scholar
Douai, A. and Sabbah, C., ‘Gauss–Manin systems, Brieskorn lattices and Frobenius structures (I)’, Ann. Inst. Fourier (Grenoble) 53(4) (2003), 1055–1116.CrossRefGoogle Scholar
Esnault, H., Sabbah, C. and Yu, J.-D., ‘E 1 -degeneration of the irregular Hodge filtration (with an appendix by M. Saito)’, J. reine angew. Math. (2015), doi:10.1515/crelle-2014-0118, online arXiv:1302.4537.Google Scholar
Fulton, W., Introduction to Toric Varieties, Annals of Mathematics Studies, 131 (Princeton University Press, Princeton, NJ, 1993).CrossRefGoogle Scholar
Hotta, R., Takeuchi, K. and Tanisaki, T., D-Modules, Perverse Sheaves, and Representation Theory, Progress in Mathematics, 236 (Birkhäuser, Boston, Basel, Berlin, 2008), in Japanese: 1995.Google Scholar
Kashiwara, M., ‘B-functions and holonomic systems’, Invent. Math. 38 (1976), 33–53.Google Scholar
Katz, N., Exponential Sums and Differential Equations, Annals of Mathematics Studies, 124 (Princeton University Press, Princeton, NJ, 1990).CrossRefGoogle Scholar
Kontsevich, M., ‘Holonomic D-modules and positive characteristic’, Japan. J. Math. 4 (2009), 1–25. doi:10.1007/s11537-009-0852-x.Google Scholar
Kouchnirenko, A. G, ‘Polyèdres de Newton et nombres de Milnor’, Invent. Math. 32 (1976), 1–31.Google Scholar
Mebkhout, Z., ‘Le théorème de positivité, le théorème de comparaison et le théorème d’existence de Riemann’, inÉléments de la théorie des systèmes différentiels géométriques, Séminaires & Congrès, 8 (Société Mathématique de France, Paris, 2004), 165–310.Google Scholar
Mochizuki, T., Asymptotic Behaviour of Tame Harmonic Bundles and an Application to Pure Twistor D-Modules, vol. 185, Memoirs of the American Mathematical Society, 869–870 (American Mathematical Society, Providence, RI, 2007), arXiv:math.DG/0312230,arXiv:math.DG/0402122.Google Scholar
Mochizuki, T., Wild Harmonic Bundles and Wild pure Twistor D-Modules, Astérisque, 340 (Société Mathématique de France, Paris, 2011).Google Scholar
Mochizuki, T., ‘Mixed twistor D-Modules’, Preprint (2011), arXiv:1104.3366.Google Scholar
Mochizuki, T., ‘A twistor approach to the Kontsevich complexes’, Preprint (2015),arXiv:1501.04145.Google Scholar
Roucairol, C., ‘Formal structure of direct image of holonomic D-modules of exponential type’, Manuscripta Math. 124(3) (2007), 299–318.Google Scholar
Sabbah, C., ‘Monodromy at infinity and Fourier transform’, Publ. RIMS Kyoto Univ. 33(4) (1997), 643–685.Google Scholar
Sabbah, C., ‘On a twisted de Rham complex’, Tôhoku Math. J. 51 (1999), 125–140.Google Scholar
Sabbah, C., ‘Fourier–Laplace transform of irreducible regular differential systems on the Riemann sphere’, Russian Math. Surveys 59(6) (2004), 1165–1180; II, Moscow Math. J. 9(4) (2009), 885–898.Google Scholar
Sabbah, C., Polarizable twistor D-modules, Astérisque, 300 (Société Mathématique de France, Paris, 2005).Google Scholar
Sabbah, C., ‘Hypergeometric periods for a tame polynomial’, Portugal. Math. 63(2) (2006), 173–226. arXiv:math.AG/9805077.Google Scholar
Sabbah, C., ‘Monodromy at infinity and Fourier transform II’, Publ. RIMS Kyoto Univ. 42 (2006), 803–835.Google Scholar
Sabbah, C., ‘Fourier–Laplace transform of a variation of polarized complex Hodge structure’, J. reine angew. Math. 621 (2008), 123–158. arXiv:math.AG/0508551.Google Scholar
Sabbah, C., ‘Wild twistor D-modules’, inAlgebraic Analysis and Around, Advanced Studies in Pure Mathematics, 54 (Mathematical Society of Japan, Tokyo, 2009), 293–353. arXiv:0803.0287.Google Scholar
Sabbah, C., ‘Fourier–Laplace transform of a variation of polarized complex Hodge structure, II’, inNew developments in Algebraic Geometry, Integrable Systems and Mirror symmetry, Kyoto, January 2008, Advanced Studies in Pure Mathematics, 59 (Mathematical Society of Japan, Tokyo, 2010), 289–347. arXiv:0804.4328.Google Scholar
Sabbah, C., Introduction to Stokes Structures, Lecture Notes in Mathematics, 2060 (Springer, Heidelberg, New York, Dordrecht, London, 2013), doi:10.1007/978-3-642-31695-1,arXiv:0912.2762.Google Scholar
Saito, M., ‘Modules de Hodge polarisables’, Publ. RIMS Kyoto Univ. 24 (1988), 849–995.Google Scholar
Saito, M., ‘Mixed Hodge Modules’, Publ. RIMS, Kyoto Univ. 26 (1990), 221–333.Google Scholar
Saito, M., ‘On Kollár’s conjecture’, inSeveral Complex Variables and Complex Geometry, Part 2, Santa Cruz, CA, 1989, Proceedings of the Symposium on Pure Mathematics, 52 (American Mathematical Society, Providence, RI, 1991), 509–517.Google Scholar
Yu, J.-D., ‘Irregular Hodge filtration on twisted de Rham cohomology’, Manuscripta Math. 144(1–2) (2014), 99–133. arXiv:1203.2338.Google Scholar