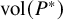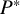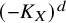1 Introduction
1.1 Background and results
Let
![]() $N\cong \mathbb {Z}^d$
be a lattice of rank d. A convex polytope
$N\cong \mathbb {Z}^d$
be a lattice of rank d. A convex polytope
![]() $P\subset N_{\mathbb {R}}$
, where
$P\subset N_{\mathbb {R}}$
, where
![]() , is called a lattice polytope if the vertices
, is called a lattice polytope if the vertices
![]() $\operatorname {vert}(P)$
of P are contained in N. Two lattice polytopes
$\operatorname {vert}(P)$
of P are contained in N. Two lattice polytopes
![]() $P,Q\subset N_{\mathbb {R}}$
are said to be unimodular equivalent if there exists an affine lattice automorphism
$P,Q\subset N_{\mathbb {R}}$
are said to be unimodular equivalent if there exists an affine lattice automorphism
![]() $\varphi \in \operatorname {GL}_d(\mathbb {Z})\ltimes \mathbb {Z}^d$
of N such that
$\varphi \in \operatorname {GL}_d(\mathbb {Z})\ltimes \mathbb {Z}^d$
of N such that
![]() $\varphi _{\mathbb {R}}(P)=Q$
. Unless stated otherwise, we regard lattice polytopes as being defined only up to unimodular equivalence.
$\varphi _{\mathbb {R}}(P)=Q$
. Unless stated otherwise, we regard lattice polytopes as being defined only up to unimodular equivalence.
Let
![]() $P\subset N_{\mathbb {R}}$
be a lattice polytope of dimension d (that is, P is of maximum dimension in
$P\subset N_{\mathbb {R}}$
be a lattice polytope of dimension d (that is, P is of maximum dimension in
![]() $N_{\mathbb {R}}$
) containing exactly one lattice point in its (strict) interior: that is,
$N_{\mathbb {R}}$
) containing exactly one lattice point in its (strict) interior: that is,
![]() $\left |{\operatorname {int}(P)\cap N}\right |=1$
. We can assume that this interior point is the origin
$\left |{\operatorname {int}(P)\cap N}\right |=1$
. We can assume that this interior point is the origin
![]() $\boldsymbol {0}\in N$
. For reasons explained in Section 1.2 below, we call P a canonical Fano polytope. As a consequence of results by Hensley [Reference Hensley9, Theorem 3.6] and Lagarias–Ziegler [Reference Lagarias and Ziegler15, Theorem 2], there are finitely many canonical Fano polytopes (up to unimodular equivalence) in each dimension d.
$\boldsymbol {0}\in N$
. For reasons explained in Section 1.2 below, we call P a canonical Fano polytope. As a consequence of results by Hensley [Reference Hensley9, Theorem 3.6] and Lagarias–Ziegler [Reference Lagarias and Ziegler15, Theorem 2], there are finitely many canonical Fano polytopes (up to unimodular equivalence) in each dimension d.
Canonical Fano polytopes in dimensions
![]() $d\leq 3$
have been classified [Reference Kasprzyk10], and we find that
$d\leq 3$
have been classified [Reference Kasprzyk10], and we find that
![]() ${\operatorname {vol}(P)\leq 12}$
. For
${\operatorname {vol}(P)\leq 12}$
. For
![]() $d\geq 4$
, it is conjectured that the volume of a d-dimensional canonical Fano polytope is bounded by
$d\geq 4$
, it is conjectured that the volume of a d-dimensional canonical Fano polytope is bounded by
where
![]() $s_i$
denotes the ith term of the Sylvester sequence:
$s_i$
denotes the ith term of the Sylvester sequence:
Moreover, the case of equality in equation (1.1) is expected to be attained only by the canonical Fano simplex

Here
![]() $\{e_1,\ldots ,e_d\}$
is a basis of N. This conjecture is hinted at in [Reference Lagarias and Ziegler15, Reference Reid19, Reference Zaks, Perles and Wills21], explicitly stated in [Reference Nill16, Conjecture 1.7] and proved by Averkov–Krümpelmann–Nill [Reference Averkov, Krümpelmann and Nill3] for the case when P is a canonical Fano simplex. The conjecture remains open for a general canonical Fano polytope. The current best upper bound on the volume of a canonical Fano polytope that is not a simplex is established in [Reference Averkov, Krümpelmann and Nill3, Theorem 2.7] (improving upon a result by Pikhurko [Reference Pikhurko17]); however, this is presumed to be far from sharp:
$\{e_1,\ldots ,e_d\}$
is a basis of N. This conjecture is hinted at in [Reference Lagarias and Ziegler15, Reference Reid19, Reference Zaks, Perles and Wills21], explicitly stated in [Reference Nill16, Conjecture 1.7] and proved by Averkov–Krümpelmann–Nill [Reference Averkov, Krümpelmann and Nill3] for the case when P is a canonical Fano simplex. The conjecture remains open for a general canonical Fano polytope. The current best upper bound on the volume of a canonical Fano polytope that is not a simplex is established in [Reference Averkov, Krümpelmann and Nill3, Theorem 2.7] (improving upon a result by Pikhurko [Reference Pikhurko17]); however, this is presumed to be far from sharp:
Instead of bounding
![]() $\operatorname {vol}(P)$
, it is also natural to consider the volume of the dual polytope
$\operatorname {vol}(P)$
, it is also natural to consider the volume of the dual polytope
![]() $P^*$
(see Section 1.4 for the definition of the dual polytope). The main result of this paper is:
$P^*$
(see Section 1.4 for the definition of the dual polytope). The main result of this paper is:
Theorem 1.1. Let
![]() $P\subset N_{\mathbb {R}}$
be a d-dimensional canonical Fano polytope, where
$P\subset N_{\mathbb {R}}$
be a d-dimensional canonical Fano polytope, where
![]() $d\geq 4$
. Then
$d\geq 4$
. Then
with equality if and only if
![]() $P=R_{(d)}^*$
.
$P=R_{(d)}^*$
.
In three dimensions, the expected bound
![]() $\operatorname {vol}(P^*)\leq 12$
is proved in [Reference Kasprzyk10, Theorem 4.6]. In this case, however, equality is obtained by the duals of two distinct simplices:
$\operatorname {vol}(P^*)\leq 12$
is proved in [Reference Kasprzyk10, Theorem 4.6]. In this case, however, equality is obtained by the duals of two distinct simplices:
The analogue of Theorem 1.1 is proved in [Reference Averkov, Krümpelmann and Nill3, Theorem 2.5(b)] for d-dimensional canonical Fano simplices.
Probably one of the most studied classes of canonical Fano polytopes is the reflexive polytopes, consisting of those
![]() $P\subset N_{\mathbb {R}}$
such that the dual
$P\subset N_{\mathbb {R}}$
such that the dual
![]() $P^*$
is also a canonical Fano polytope (for a brief survey, see [Reference Kasprzyk and Nill12]). Note that
$P^*$
is also a canonical Fano polytope (for a brief survey, see [Reference Kasprzyk and Nill12]). Note that
![]() $R_{(d)}$
is a reflexive simplex [Reference Nill16]. An immediate consequence of Theorem 1.1 is a proof of the conjectured inequality in equation (1.1) in the case of reflexive polytopes:
$R_{(d)}$
is a reflexive simplex [Reference Nill16]. An immediate consequence of Theorem 1.1 is a proof of the conjectured inequality in equation (1.1) in the case of reflexive polytopes:
Corollary 1.2. Let
![]() $P\subset N_{\mathbb {R}}$
be a d-dimensional reflexive polytope, where
$P\subset N_{\mathbb {R}}$
be a d-dimensional reflexive polytope, where
![]() $d\geq 4$
. Then
$d\geq 4$
. Then
with equality if and only if
![]() $P=R_{(d)}$
.
$P=R_{(d)}$
.
The analogue of Corollary 1.2 in the case of reflexive simplices is proved in [Reference Nill16, Theorem A].
1.2 Toric geometry and Fano varieties
Canonical Fano polytopes arise naturally in algebraic geometry. To each d-dimensional canonical Fano polytope
![]() $P\subset N_{\mathbb {R}}$
, we can associate a d-dimensional projective toric variety
$P\subset N_{\mathbb {R}}$
, we can associate a d-dimensional projective toric variety
![]() $X_P$
whose fan is given by the cones in
$X_P$
whose fan is given by the cones in
![]() $N_{\mathbb {R}}$
spanning the faces of P (here we require that the unique interior point of P is taken to be the origin
$N_{\mathbb {R}}$
spanning the faces of P (here we require that the unique interior point of P is taken to be the origin
![]() $\boldsymbol {0}$
of N). This variety is Fano – recall that a variety X is Fano if its anti-canonical divisor
$\boldsymbol {0}$
of N). This variety is Fano – recall that a variety X is Fano if its anti-canonical divisor
![]() $-K_X$
is ample – and has at worst canonical singularities. In fact, this construction is reversible, and there exists a one-to-one correspondence between (unimodular equivalence classes of) canonical Fano polytopes and (isomorphism classes of) Fano toric varieties with at worst canonical singularities. For details on canonical singularities and their importance in algebraic geometry, see [Reference Reid20]; for details on toric geometry, see [Reference Danilov8]; and for additional background material, see the survey [Reference Kasprzyk and Nill12].
$-K_X$
is ample – and has at worst canonical singularities. In fact, this construction is reversible, and there exists a one-to-one correspondence between (unimodular equivalence classes of) canonical Fano polytopes and (isomorphism classes of) Fano toric varieties with at worst canonical singularities. For details on canonical singularities and their importance in algebraic geometry, see [Reference Reid20]; for details on toric geometry, see [Reference Danilov8]; and for additional background material, see the survey [Reference Kasprzyk and Nill12].
The classification of Fano varieties is a long-standing open problem. An important advance would be to bound the degree
![]() $(-K_X)^d$
. In the case when X is nonsingular, the bound
$(-K_X)^d$
. In the case when X is nonsingular, the bound
was established by Kollár–Miyaoka–Mori [Reference Kollár, Miyaoka and Mori13], although this is almost certainly not sharp. Very little is known when X has canonical singularities; however, Prokhorov [Reference Prokhorov18] proved that if X is a three-dimensional Fano with Gorenstein canonical singularities, then the degree is bounded by
![]() $(-K_X)^3\leq 72$
. In this case, the maximum degree is obtained by the two weighted projective spaces
$(-K_X)^3\leq 72$
. In this case, the maximum degree is obtained by the two weighted projective spaces
![]() $\mathbb {P}(1,1,1,3)$
and
$\mathbb {P}(1,1,1,3)$
and
![]() $\mathbb {P}(1,1,4,6)$
, and these two toric varieties correspond to the two canonical Fano simplices in equation (1.2). It is tempting to conjecture that in higher dimensions, the maximum degree is obtained by a Fano toric variety. Recalling that
$\mathbb {P}(1,1,4,6)$
, and these two toric varieties correspond to the two canonical Fano simplices in equation (1.2). It is tempting to conjecture that in higher dimensions, the maximum degree is obtained by a Fano toric variety. Recalling that
![]() $(-K_{X_P})^d=d!\operatorname {vol}(P^*)$
, Theorem 1.1 provides a sharp bound on the degree when X is toric:
$(-K_{X_P})^d=d!\operatorname {vol}(P^*)$
, Theorem 1.1 provides a sharp bound on the degree when X is toric:
Corollary 1.3. Let X be a d-dimensional Fano toric variety with at worst canonical singularities, where
![]() $d\ge 4$
. Then
$d\ge 4$
. Then
with equality if and only if X is isomorphic to the weighted projective space
This extends [Reference Nill16, Theorem A] and [Reference Averkov, Krümpelmann and Nill3, Theorem 2.11], where analogous results are stated when X is a Gorenstein fake weighted projective space and when X is a fake weighted projective space with at worst canonical singularities, respectively. Corollary 1.3 also generalises the three-dimensional bound of [Reference Kasprzyk10, Theorem 4.6].
Finally, Corollary 1.3 also has implications for current attempts to classify nonsingular Fano varieties via mirror symmetry [Reference Coates, Corti, Galkin and Kasprzyk7]. Here the hope is that a nonsingular Fano variety X with
![]() $-K_X$
very ample has a
$-K_X$
very ample has a
![]() $\mathbb {Q}$
-Gorenstein deformation to a Gorenstein canonical Fano toric variety
$\mathbb {Q}$
-Gorenstein deformation to a Gorenstein canonical Fano toric variety
![]() $X_P$
. Since this deformation would leave the degree unchanged, the bound of Corollary 1.3 would apply to X. It is interesting to note that in this case, the bound in equation (1.4) is significantly smaller than the bound in equation (1.3) of Kollár–Miyaoka–Mori.
$X_P$
. Since this deformation would leave the degree unchanged, the bound of Corollary 1.3 would apply to X. It is interesting to note that in this case, the bound in equation (1.4) is significantly smaller than the bound in equation (1.3) of Kollár–Miyaoka–Mori.
1.3 Overview of the proof
Our strategy to prove Theorem 1.1 is as follows. In Section 2, we reduce the problem to canonical Fano polytopes satisfying some minimality condition. We observe that such polytopes admit a decomposition into canonical Fano simplices (following [Reference Kasprzyk10] and compare with the decomposition used in [Reference Kreuzer and Skarke14]), for which the statement is already known [Reference Averkov, Krümpelmann and Nill3]. In Section 3, we use this decomposition, together with the monotonicity of the normalised volume, to prove Theorem 1.1 in the majority of cases (Corollary 3.1). Finally, the remaining cases are proved in Section 6 using a mixture of integration techniques (developed in Sections 4–5) and explicit classifications.
1.4 Notation and terminology
Let
![]() $P\subset N_{\mathbb {R}}$
be a lattice polytope of maximum dimension in a rank d lattice
$P\subset N_{\mathbb {R}}$
be a lattice polytope of maximum dimension in a rank d lattice
![]() $N\cong \mathbb {Z}^d$
, and let
$N\cong \mathbb {Z}^d$
, and let
be the lattice dual to N. The dual (or polar) polyhedron of P is
If
![]() $\boldsymbol {0}\in P$
, then
$\boldsymbol {0}\in P$
, then
![]() $P^*$
is a convex polytope, although typically
$P^*$
is a convex polytope, although typically
![]() $P^*$
has rational vertices and so is not a lattice polytope.
$P^*$
has rational vertices and so is not a lattice polytope.
Let P and Q be two maximum-dimensional polytopes in
![]() $(N_P)_{\mathbb {R}}\cong \mathbb {R}^p$
and
$(N_P)_{\mathbb {R}}\cong \mathbb {R}^p$
and
![]() $(N_Q)_{\mathbb {R}}\cong \mathbb {R}^q$
, respectively. Suppose that P and Q contain the origin
$(N_Q)_{\mathbb {R}}\cong \mathbb {R}^q$
, respectively. Suppose that P and Q contain the origin
![]() $\boldsymbol {0}_{P}\in N_P$
and
$\boldsymbol {0}_{P}\in N_P$
and
![]() $\boldsymbol {0}_{Q}\in N_Q$
of their respective ambient spaces. The free sum (or direct sum) is the maximum-dimensional polytope
$\boldsymbol {0}_{Q}\in N_Q$
of their respective ambient spaces. The free sum (or direct sum) is the maximum-dimensional polytope
The product is the polytope
Free sums and products of polytopes are related via duality by
On the affine hull
![]() $\operatorname {aff}(P)$
, there exists a volume form called the relative lattice volume that is normalised by setting the volume of a fundamental parallelepiped of
$\operatorname {aff}(P)$
, there exists a volume form called the relative lattice volume that is normalised by setting the volume of a fundamental parallelepiped of
![]() $\operatorname {aff}_{\mathbb {Z}}(P)$
equal to
$\operatorname {aff}_{\mathbb {Z}}(P)$
equal to
![]() $1$
. We denote the relative lattice volume of P by
$1$
. We denote the relative lattice volume of P by
![]() $\operatorname {vol}_N(P)$
. The volume
$\operatorname {vol}_N(P)$
. The volume
![]() is often called the normalised lattice volume of P. If
is often called the normalised lattice volume of P. If
![]() $N'\subseteq N$
is a sublattice of N, then for
$N'\subseteq N$
is a sublattice of N, then for
![]() $S\subseteq \operatorname {lin}(N')$
, we have
$S\subseteq \operatorname {lin}(N')$
, we have
![]() $\operatorname {vol}_{N'}(S)\leq \operatorname {vol}_N(S)$
. If in addition we have that
$\operatorname {vol}_{N'}(S)\leq \operatorname {vol}_N(S)$
. If in addition we have that
![]() $N'\to N$
splits over
$N'\to N$
splits over
![]() $\mathbb {Z}$
, then
$\mathbb {Z}$
, then
![]() $\operatorname {vol}_{N'}(S)=\operatorname {vol}_N(S)$
.
$\operatorname {vol}_{N'}(S)=\operatorname {vol}_N(S)$
.
2 Decomposition of minimal polytopes
The case of canonical Fano simplices is already considered in [Reference Averkov, Krümpelmann and Nill3]. Our focus is on the case when P is not a simplex. Notice that if
![]() $P\subsetneq Q$
, then
$P\subsetneq Q$
, then
![]() $Q^*\subsetneq P^*$
, and hence
$Q^*\subsetneq P^*$
, and hence
![]() $\operatorname {vol}(Q^*)<\operatorname {vol}(P^*)$
. It is therefore sufficient to prove Theorem 1.1 for ‘small’ polytopes P: that is, for the minimal canonical Fano polytopes:
$\operatorname {vol}(Q^*)<\operatorname {vol}(P^*)$
. It is therefore sufficient to prove Theorem 1.1 for ‘small’ polytopes P: that is, for the minimal canonical Fano polytopes:
Definition 2.1 [Reference Kasprzyk10, Definition 2.2]
A d-dimensional canonical Fano polytope
![]() $P\subset N_{\mathbb {R}}$
is minimal if for each vertex of P, the polytope obtained by removing this vertex is not a d-dimensional canonical Fano polytope: that is, if
$P\subset N_{\mathbb {R}}$
is minimal if for each vertex of P, the polytope obtained by removing this vertex is not a d-dimensional canonical Fano polytope: that is, if
![]() $\operatorname {conv}(P\cap N\setminus \{v\})$
is not a d-dimensional canonical Fano polytope for each
$\operatorname {conv}(P\cap N\setminus \{v\})$
is not a d-dimensional canonical Fano polytope for each
![]() $v\in \operatorname {vert}(P)$
.
$v\in \operatorname {vert}(P)$
.
Each canonical Fano polytope Q can be reduced to a minimal polytope
![]() $P\subset Q$
via successive removal of vertices. Of course, P need not be uniquely determined. Minimal canonical Fano polytopes admit a decomposition in terms of lower-dimensional minimal canonical Fano simplices:
$P\subset Q$
via successive removal of vertices. Of course, P need not be uniquely determined. Minimal canonical Fano polytopes admit a decomposition in terms of lower-dimensional minimal canonical Fano simplices:
Proposition 2.2 [Reference Kasprzyk10, Proposition 3.2]
Let P be a minimal canonical Fano d-polytope that is not a simplex. Then there exists a minimal canonical Fano k-simplex S contained in P with
![]() $\operatorname {vert}(S)\subset \operatorname {vert}(P)$
for some
$\operatorname {vert}(S)\subset \operatorname {vert}(P)$
for some
![]() $1\le k<d$
. For any such S, there exists a minimal canonical Fano
$1\le k<d$
. For any such S, there exists a minimal canonical Fano
![]() $(d-k+s)$
-polytope
$(d-k+s)$
-polytope
![]() $P'$
with
$P'$
with
![]() $\operatorname {vert}(P')\subset \operatorname {vert}(P)$
such that
$\operatorname {vert}(P')\subset \operatorname {vert}(P)$
such that
![]() $P=\operatorname {conv}(S\cup P')$
,
$P=\operatorname {conv}(S\cup P')$
,
![]() $s=\left |{\operatorname {vert}(S)\cap \operatorname {vert}(P')}\right |$
and
$s=\left |{\operatorname {vert}(S)\cap \operatorname {vert}(P')}\right |$
and
![]() $0\leq s < k$
.
$0\leq s < k$
.
For brevity, we write ‘d-polytope’ rather than ‘polytope of dimension d’ and ‘k-simplex’ rather than ‘simplex of dimension k’.
Corollary 2.3. Let P be a minimal canonical Fano d-polytope that is not a simplex. Then for some
![]() $2\le t\le d$
, there exist minimal canonical Fano simplices
$2\le t\le d$
, there exist minimal canonical Fano simplices
![]() $S_1,\ldots ,S_t$
such that
$S_1,\ldots ,S_t$
such that
![]() $P=\operatorname {conv}(S_1\cup \cdots \cup S_t)$
, where
$P=\operatorname {conv}(S_1\cup \cdots \cup S_t)$
, where
![]() $\dim (S_i)=d_i\geq 1$
and
$\dim (S_i)=d_i\geq 1$
and
![]() $\operatorname {vert}(S_i)\subset \operatorname {vert}(P)$
, for each
$\operatorname {vert}(S_i)\subset \operatorname {vert}(P)$
, for each
![]() $1\leq i\leq t$
. Set
$1\leq i\leq t$
. Set
![]() , and for each
, and for each
![]() $2\leq i\leq t$
, set
$2\leq i\leq t$
, set
![]() , where
, where
![]() . Then
. Then
An example of this decomposition is illustrated in Figure 1.

Figure 1 An example of a three-dimensional minimal canonical Fano polytope P, which decomposes into two canonical Fano simplices
![]() $S_1$
and
$S_1$
and
![]() $S_2$
sharing a common vertex v. In the notation of Corollary 2.3,
$S_2$
sharing a common vertex v. In the notation of Corollary 2.3,
![]() $d=3$
,
$d=3$
,
![]() $t=2$
,
$t=2$
,
![]() $d_1=d_2=2$
and
$d_1=d_2=2$
and
![]() $r_2=1$
.
$r_2=1$
.
Proof. We apply Proposition 2.2 iteratively, at each step choosing S to be of smallest possible dimension. Thus P can be written as
![]() $P=\operatorname {conv}(S_1\cup \cdots \cup S_t)$
for some
$P=\operatorname {conv}(S_1\cup \cdots \cup S_t)$
for some
![]() $t\geq 1$
, where the
$t\geq 1$
, where the
![]() $S_i$
are minimal canonical Fano simplices of dimension
$S_i$
are minimal canonical Fano simplices of dimension
![]() $d_i\ge 1$
with
$d_i\ge 1$
with
![]() $\operatorname {vert}(S_i)\subseteq \operatorname {vert}(P)$
having
$\operatorname {vert}(S_i)\subseteq \operatorname {vert}(P)$
having
![]() $r_i$
common vertices with
$r_i$
common vertices with
![]() $P^{(i-1)}$
, such that
$P^{(i-1)}$
, such that
![]() $d_t\le d_{t-1}\le \cdots \le d_1$
. The case
$d_t\le d_{t-1}\le \cdots \le d_1$
. The case
![]() $P^{(0)}$
is taken to be the empty set, giving
$P^{(0)}$
is taken to be the empty set, giving
![]() $r_1=0$
. At each step, the dimension of
$r_1=0$
. At each step, the dimension of
![]() $P^{(i)}$
can be obtained from Proposition 2.2:
$P^{(i)}$
can be obtained from Proposition 2.2:
![]() $\dim (P^{(i)})=\dim (P^{(i-1)})+\dim (S_i)-r_i$
. Hence
$\dim (P^{(i)})=\dim (P^{(i-1)})+\dim (S_i)-r_i$
. Hence
![]() $d=\sum _{i=1}^t(d_i-r_i)$
, so equation (2.1) holds. Once again using Proposition 2.2, since
$d=\sum _{i=1}^t(d_i-r_i)$
, so equation (2.1) holds. Once again using Proposition 2.2, since
![]() $\dim (S_i)>r_i$
,
$\dim (S_i)>r_i$
,
![]() $\dim (P^{(i)})\geq \dim (P^{(i-1)})+1$
. It follows that
$\dim (P^{(i)})\geq \dim (P^{(i-1)})+1$
. It follows that
![]() $t\leq d$
, so
$t\leq d$
, so
![]() $d_1\leq d-t+1$
. Hence our choice of simplices implies equation (2.2). Finally, the number of vertices of
$d_1\leq d-t+1$
. Hence our choice of simplices implies equation (2.2). Finally, the number of vertices of
![]() $P^{(i)}$
is
$P^{(i)}$
is
![]() $\left |{\operatorname {vert}(P^{(i-1)})}\right |+\left |{\operatorname {vert}(S_i)}\right |-r_i$
. This implies that
$\left |{\operatorname {vert}(P^{(i-1)})}\right |+\left |{\operatorname {vert}(S_i)}\right |-r_i$
. This implies that
![]() $\left |{\operatorname {vert}(P)}\right |=\sum _{i=1}^t(d_i+1)-r$
, and from equation (2.1), we deduce that equation (2.3) holds.
$\left |{\operatorname {vert}(P)}\right |=\sum _{i=1}^t(d_i+1)-r$
, and from equation (2.1), we deduce that equation (2.3) holds.
Notice that equality (2.3), combined with the bound
![]() $t\leq d$
, implies that a minimal canonical Fano polytope P satisfies
$t\leq d$
, implies that a minimal canonical Fano polytope P satisfies
![]() $\left |{\operatorname {vert}(P)}\right |\leq 2 d$
(this is known as Steinitz’s inequality).
$\left |{\operatorname {vert}(P)}\right |\leq 2 d$
(this is known as Steinitz’s inequality).
3 Bounding the volume of
 $P^*$
via monotonicity of the normalised volume
$P^*$
via monotonicity of the normalised volume
As noted above, it is sufficient to prove Theorem 1.1 for minimal canonical Fano polytopes that are not simplices. Let
![]() $P\subset N_{\mathbb {R}}$
be such a polytope of dimension
$P\subset N_{\mathbb {R}}$
be such a polytope of dimension
![]() $d\geq 4$
. Fix a decomposition of P, and use the notation
$d\geq 4$
. Fix a decomposition of P, and use the notation
![]() $t,S_i,d_i,r_i,r$
as defined in Corollary 2.3. In this section, we prove Theorem 1.1 for the majority of decompositions. The decompositions not addressed in this section and whose proof is the focus of Sections 4–5 below are listed in Corollary 3.1.
$t,S_i,d_i,r_i,r$
as defined in Corollary 2.3. In this section, we prove Theorem 1.1 for the majority of decompositions. The decompositions not addressed in this section and whose proof is the focus of Sections 4–5 below are listed in Corollary 3.1.
Corollary 3.1. To prove Theorem 1.1, it is enough to verify that the inequality
holds for all minimal canonical Fano polytopes
![]() $P\subset N_{\mathbb {R}}$
of dimension
$P\subset N_{\mathbb {R}}$
of dimension
![]() $d\ge 4$
whose decomposition into minimal canonical Fano simplices falls into one of the following five cases:
$d\ge 4$
whose decomposition into minimal canonical Fano simplices falls into one of the following five cases:
-
1.
 $t=2$
and
$t=2$
and
 $d_1=d_2=d-1$
; or
$d_1=d_2=d-1$
; or -
2.
 $t=2$
,
$t=2$
,
 $d=4$
,
$d=4$
,
 $d_1=3$
and
$d_1=3$
and
 $d_2=2$
; or
$d_2=2$
; or -
3.
 $t=2$
,
$t=2$
,
 $d=5$
,
$d=5$
,
 $d_1=4$
and
$d_1=4$
and
 $d_2=3$
; or
$d_2=3$
; or -
4.
 $t=3$
,
$t=3$
,
 $d=4$
and
$d=4$
and
 $d_1=d_2=d_3=2$
; or
$d_1=d_2=d_3=2$
; or -
5.
 $t=3$
,
$t=3$
,
 $d=5$
and
$d=5$
and
 $d_1=d_2=d_3=3$
.
$d_1=d_2=d_3=3$
.
To prove Corollary 3.1, we use the monotonicity of the normalised volume. Let
be the sublattice of lattice points in the linear hull of
![]() $S_i$
(recall that
$S_i$
(recall that
![]() $\boldsymbol {0}\in \operatorname {int}(S_i)$
, so this really is a sublattice) for each
$\boldsymbol {0}\in \operatorname {int}(S_i)$
, so this really is a sublattice) for each
![]() $1\leq i\le t$
. Define the map
$1\leq i\le t$
. Define the map
 $$\begin{align*}\varphi\colon N_1\oplus\cdots\oplus N_t\to N,\qquad(x_1,\ldots,x_t)\mapsto\sum_{i=1}^{t} x_i. \end{align*}$$
$$\begin{align*}\varphi\colon N_1\oplus\cdots\oplus N_t\to N,\qquad(x_1,\ldots,x_t)\mapsto\sum_{i=1}^{t} x_i. \end{align*}$$
Notice that
![]() $\varphi $
may not be surjective; however, since its image has the same rank as N, the extension
$\varphi $
may not be surjective; however, since its image has the same rank as N, the extension
![]() $\varphi _{\mathbb {R}}$
of
$\varphi _{\mathbb {R}}$
of
![]() $\varphi $
to a map of vector spaces is surjective. Moreover,
$\varphi $
to a map of vector spaces is surjective. Moreover,
![]() $\varphi _{\mathbb {R}}$
gives the following representation of P:
$\varphi _{\mathbb {R}}$
gives the following representation of P:
Let
![]() $M,M_1,\ldots ,M_t$
denote the lattices dual to
$M,M_1,\ldots ,M_t$
denote the lattices dual to
![]() $N,N_1,\ldots ,N_t$
, respectively. The map
$N,N_1,\ldots ,N_t$
, respectively. The map
![]() $\varphi _{\mathbb {R}}^*$
dual to
$\varphi _{\mathbb {R}}^*$
dual to
![]() $\varphi _{\mathbb {R}}$
is an injection, and in particular
$\varphi _{\mathbb {R}}$
is an injection, and in particular
where M is naturally embedded via
![]() $\varphi ^*$
into
$\varphi ^*$
into
![]() $M_1\oplus \cdots \oplus M_t$
. This situation will be studied in more detail in Section 4. Using the monotonicity of the normalised volume, finding an upper bound for the normalised volume of
$M_1\oplus \cdots \oplus M_t$
. This situation will be studied in more detail in Section 4. Using the monotonicity of the normalised volume, finding an upper bound for the normalised volume of
![]() $S_1^*\times \cdots \times S_t^*$
yields an upper bound for the normalised volume of
$S_1^*\times \cdots \times S_t^*$
yields an upper bound for the normalised volume of
![]() $P^*$
. Specifically, we know that
$P^*$
. Specifically, we know that
 $$ \begin{align} \begin{aligned} \operatorname{Vol}_M(P^*)&\leq\operatorname{Vol}_{M_1\oplus\cdots\oplus M_t}(S_1^*\times\cdots\times S_t^*)\\ &=(d_1+\cdots+d_t)!\operatorname{vol}_{M_1\oplus\cdots\oplus M_t}(S_1^*\times\cdots\times S_t^*)\\ &=(d_1+\cdots+d_t)!\prod_{i=1}^t\operatorname{vol}_{M_i}(S_i^*)\\ &=\frac{(d_1+\cdots+d_t)!}{d_1!\cdots d_t!}\prod_{i=1}^t\operatorname{Vol}_{M_i}(S_i^*). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \operatorname{Vol}_M(P^*)&\leq\operatorname{Vol}_{M_1\oplus\cdots\oplus M_t}(S_1^*\times\cdots\times S_t^*)\\ &=(d_1+\cdots+d_t)!\operatorname{vol}_{M_1\oplus\cdots\oplus M_t}(S_1^*\times\cdots\times S_t^*)\\ &=(d_1+\cdots+d_t)!\prod_{i=1}^t\operatorname{vol}_{M_i}(S_i^*)\\ &=\frac{(d_1+\cdots+d_t)!}{d_1!\cdots d_t!}\prod_{i=1}^t\operatorname{Vol}_{M_i}(S_i^*). \end{aligned} \end{align} $$
The normalised volume of
![]() $S_i^*$
is bounded from above (see [Reference Kasprzyk10] and [Reference Averkov, Krümpelmann and Nill3, Theorem 2.5(b)]):
$S_i^*$
is bounded from above (see [Reference Kasprzyk10] and [Reference Averkov, Krümpelmann and Nill3, Theorem 2.5(b)]):

Hence the inequality in equation (3.1) becomes
 $$\begin{align*}\operatorname{Vol}_M(P^*)\leq\frac{(d_1+\cdots+d_t)!}{d_1!\cdots d_t!}\,\prod_{i=1}^t B_{d_i}. \end{align*}$$
$$\begin{align*}\operatorname{Vol}_M(P^*)\leq\frac{(d_1+\cdots+d_t)!}{d_1!\cdots d_t!}\,\prod_{i=1}^t B_{d_i}. \end{align*}$$
At this point, Theorem 1.1 would follow from
 $$ \begin{align} \frac{(d_1+\cdots+d_t)!}{d_1!\cdots d_t!}\,\prod_{i=1}^t B_{d_i}< B_d. \end{align} $$
$$ \begin{align} \frac{(d_1+\cdots+d_t)!}{d_1!\cdots d_t!}\,\prod_{i=1}^t B_{d_i}< B_d. \end{align} $$
Unfortunately,the inequality in equation (3.2) does not always hold: for example, it fails when
![]() $t=2$
and
$t=2$
and
![]() $d_1=d_2=d-1$
, for any
$d_1=d_2=d-1$
, for any
![]() $d\geq 3$
. Nevertheless, this technique is sufficient to prove Theorem 1.1 for a large number of cases:
$d\geq 3$
. Nevertheless, this technique is sufficient to prove Theorem 1.1 for a large number of cases:
Lemma 3.2. The inequality in equation (3.2) – and therefore Theorem 1.1 – holds whenever:
-
1.
 $t\geq 3$
, with the exception of the following six cases:
$t\geq 3$
, with the exception of the following six cases:-
(a)
 $t=3$
,
$t=3$
,
 $d=4$
and
$d=4$
and
 $d_1=d_2=d_3=2$
; or
$d_1=d_2=d_3=2$
; or -
(b)
 $t=3$
,
$t=3$
,
 $d=5$
and
$d=5$
and
 $d_1=d_2=d_3=3$
; or
$d_1=d_2=d_3=3$
; or -
(c)
 $t=3$
,
$t=3$
,
 $d=4$
,
$d=4$
,
 $d_1=d_2=2$
and
$d_1=d_2=2$
and
 $d_3=1$
; or
$d_3=1$
; or -
(d)
 $t=3$
,
$t=3$
,
 $d=5$
,
$d=5$
,
 $d_1=d_2=3$
and
$d_1=d_2=3$
and
 $d_3=2$
; or
$d_3=2$
; or -
(e)
 $t=3$
,
$t=3$
,
 $d=6$
and
$d=6$
and
 $d_1=d_2=d_3=4$
; or
$d_1=d_2=d_3=4$
; or -
(f)
 $t=4$
,
$t=4$
,
 $d=5$
and
$d=5$
and
 $d_1=d_2=d_3=d_4=2$
;
$d_1=d_2=d_3=d_4=2$
;
-
-
2.
 $t=2$
, with the exceptions of the following three cases:
$t=2$
, with the exceptions of the following three cases:-
(a)
 $d_1=d_2=d-1$
; or
$d_1=d_2=d-1$
; or -
(b)
 $d=4$
,
$d=4$
,
 $d_1=3$
and
$d_1=3$
and
 $d_2=2$
; or
$d_2=2$
; or -
(c)
 $d=5$
,
$d=5$
,
 $d_1=4$
and
$d_1=4$
and
 $d_2=3$
.
$d_2=3$
.
-
Proof. We prove equation (1) and equation (2) separately but by the same general technique: first we show that the statement is true for large values of d; then we check the finite number of remaining values.
-
(1) Since the quantity
increases as the $$\begin{align*}\frac{(d_1 +\cdots + d_t)!}{d_1!\cdots d_t!}\,\prod_{i=1}^t B_{d_i} \end{align*}$$
$$\begin{align*}\frac{(d_1 +\cdots + d_t)!}{d_1!\cdots d_t!}\,\prod_{i=1}^t B_{d_i} \end{align*}$$
 $d_i$
increase, by equation (2.2), it is enough to prove the inequality in equation (3.2) when
$d_i$
increase, by equation (2.2), it is enough to prove the inequality in equation (3.2) when
 $d_i=d-t+1$
for all i. That is, it is sufficient to show that (3.3)From
$d_i=d-t+1$
for all i. That is, it is sufficient to show that (3.3)From $$ \begin{align} \frac{(t(d-t+1))!}{(d-t+1)!^t}\, (B_{d-t+1})^{t} < B_d. \end{align} $$
$$ \begin{align} \frac{(t(d-t+1))!}{(d-t+1)!^t}\, (B_{d-t+1})^{t} < B_d. \end{align} $$
 $n!\leq 2\cdot 2^2\cdots 2^{n-1} = 2^{n(n-1)/2}$
(which is strict when
$n!\leq 2\cdot 2^2\cdots 2^{n-1} = 2^{n(n-1)/2}$
(which is strict when
 $n\ge 3$
), we obtain
$n\ge 3$
), we obtain  $$\begin{align*}\frac{(t(d-t+1))!}{(d-t+1)!^t}\le (t(d-t+1))! < 2^{\frac{1}{2}t(d-t+1)(t(d-t+1)-1)}. \end{align*}$$
$$\begin{align*}\frac{(t(d-t+1))!}{(d-t+1)!^t}\le (t(d-t+1))! < 2^{\frac{1}{2}t(d-t+1)(t(d-t+1)-1)}. \end{align*}$$
Therefore, if the inequality
(3.4)holds, so too does the inequality in equation (3.3). $$ \begin{align} 2^{\frac{1}{2}t(d-t+1)(t(d-t+1)-1)}2^t(B_{d-t+1})^{t}\leq B_d \end{align} $$
$$ \begin{align} 2^{\frac{1}{2}t(d-t+1)(t(d-t+1)-1)}2^t(B_{d-t+1})^{t}\leq B_d \end{align} $$
To prove equation (3.4), we make use of the well-known description due to Aho–Sloane [Reference Aho and Sloane1, Example 2.5] of the Sylvester sequence in terms of the constant
 $c\approx 1.2640847353\dots $
: Notice that
$c\approx 1.2640847353\dots $
: Notice that $$\begin{align*}s_n=\left\lfloor c^{2^n}+\frac{1}{2}\right\rfloor. \end{align*}$$
$$\begin{align*}s_n=\left\lfloor c^{2^n}+\frac{1}{2}\right\rfloor. \end{align*}$$
 $B_d=2(s_d-1)^2>(s_d + 1)^2$
whenever
$B_d=2(s_d-1)^2>(s_d + 1)^2$
whenever
 $d\geq 3$
. Since
$d\geq 3$
. Since
 $s_d+1>c^{2^d}$
, the right-hand side of equation (3.4) is bounded from below: Moreover,
$s_d+1>c^{2^d}$
, the right-hand side of equation (3.4) is bounded from below: Moreover, $$\begin{align*}B_d=2(s_d-1)^2> (s_d + 1)^2 > c^{2^{d+1}}. \end{align*}$$
$$\begin{align*}B_d=2(s_d-1)^2> (s_d + 1)^2 > c^{2^{d+1}}. \end{align*}$$
 $B_{d-t+1}/2 < c^{2^{d-t+2}}$
. Since
$B_{d-t+1}/2 < c^{2^{d-t+2}}$
. Since
 $c^3> 2$
, the left-hand side of equation (3.4) is bounded from above: We shall show that
$c^3> 2$
, the left-hand side of equation (3.4) is bounded from above: We shall show that $$\begin{align*}2^{\frac{1}{2}t(d-t+1)(t(d-t+1)-1)} 2^t\left(\frac{B_{d-t+1}}{2}\right)^{t} <c^{\frac{3}{2}t(d-t+1)(t(d-t+1)-1)} c^{3t} c^{2^{d-t+2}t}. \end{align*}$$
$$\begin{align*}2^{\frac{1}{2}t(d-t+1)(t(d-t+1)-1)} 2^t\left(\frac{B_{d-t+1}}{2}\right)^{t} <c^{\frac{3}{2}t(d-t+1)(t(d-t+1)-1)} c^{3t} c^{2^{d-t+2}t}. \end{align*}$$
 $c^{\frac {3}{2}t(d-t+1)(t(d-t+1)-1)} c^{3t} c^{2^{d-t+2}t}\leq c^{2^{d+1}}$
, from which we conclude that the inequality in equation (3.4) holds. Taking
$c^{\frac {3}{2}t(d-t+1)(t(d-t+1)-1)} c^{3t} c^{2^{d-t+2}t}\leq c^{2^{d+1}}$
, from which we conclude that the inequality in equation (3.4) holds. Taking
 $\log _c$
, we have to verify that the inequality is satisfied. Rewrite this inequality as
$\log _c$
, we have to verify that the inequality is satisfied. Rewrite this inequality as $$ \begin{align*} \frac{3}{2}t(d-t+1)(t(d-t+1)-1) + 3t + 2^{d-t+2} t\leq 2^{d+1} \end{align*} $$
Since
$$ \begin{align*} \frac{3}{2}t(d-t+1)(t(d-t+1)-1) + 3t + 2^{d-t+2} t\leq 2^{d+1} \end{align*} $$
Since $$\begin{align*}3t(d-t+1)(t(d-t+1)-1) + 6t\leq 2^{d+2}\left(1-\frac{t}{2^{t-1}}\right). \end{align*}$$
$$\begin{align*}3t(d-t+1)(t(d-t+1)-1) + 6t\leq 2^{d+2}\left(1-\frac{t}{2^{t-1}}\right). \end{align*}$$
 $t\ge 3$
, by setting
$t\ge 3$
, by setting
 $t=3$
in the right-most factor, it is enough to prove that Since
$t=3$
in the right-most factor, it is enough to prove that Since $$ \begin{align*} 3t(d-t+1)(t(d-t+1)-1) + 6t\leq 2^{d}. \end{align*} $$
$$ \begin{align*} 3t(d-t+1)(t(d-t+1)-1) + 6t\leq 2^{d}. \end{align*} $$
 $t(d-t+1)$
is maximised when
$t(d-t+1)$
is maximised when
 $t=(d+1)/2$
, and since
$t=(d+1)/2$
, and since
 $6t\leq 6d$
, the above inequality is valid when This holds when
$6t\leq 6d$
, the above inequality is valid when This holds when $$\begin{align*}\frac{3(d+1)}{2}\left(d-\frac{d+1}{2}+1\right)\left(\frac{d+1}{2}\left(d-\frac{d+1}{2}+1\right)-1\right) + 6d\leq 2^{d}. \end{align*}$$
$$\begin{align*}\frac{3(d+1)}{2}\left(d-\frac{d+1}{2}+1\right)\left(\frac{d+1}{2}\left(d-\frac{d+1}{2}+1\right)-1\right) + 6d\leq 2^{d}. \end{align*}$$
 $d\geq 13$
. Recalling that d bounds the quantities
$d\geq 13$
. Recalling that d bounds the quantities
 $t,d_1,\ldots ,d_t$
, we are left with finitely many cases to verify. The inequality in equation (3.2) holds in all but six cases, as listed in the statement.
$t,d_1,\ldots ,d_t$
, we are left with finitely many cases to verify. The inequality in equation (3.2) holds in all but six cases, as listed in the statement.
-
(2) By the same monotonicity argument used at the beginning of the previous case, we choose
 $d_1$
and
$d_1$
and
 $d_2$
as large as possible: that is, we fix
$d_2$
as large as possible: that is, we fix
 $d_1=d-1$
and
$d_1=d-1$
and
 $d_2=d-2$
(we noted above that the inequality in equation (3.2) is not satisfied when
$d_2=d-2$
(we noted above that the inequality in equation (3.2) is not satisfied when
 $d_1=d_2=d-1$
). The inequality in equation (3.2) becomes Proceeding as above, we reduce the problem to proving the inequality
$d_1=d_2=d-1$
). The inequality in equation (3.2) becomes Proceeding as above, we reduce the problem to proving the inequality $$\begin{align*}\frac{(2d-3)!}{(d-2)! (d-1)!}\, B_{d-2} B_{d-1} < B_d. \end{align*}$$
This holds when
$$\begin{align*}\frac{(2d-3)!}{(d-2)! (d-1)!}\, B_{d-2} B_{d-1} < B_d. \end{align*}$$
This holds when $$\begin{align*}3(2d^2-7d+8)+2^{d-1}+2^d\le 2^{d+1}. \end{align*}$$
$$\begin{align*}3(2d^2-7d+8)+2^{d-1}+2^d\le 2^{d+1}. \end{align*}$$
 $d\geq 10$
. Removing the assumptions
$d\geq 10$
. Removing the assumptions
 $d_1=d-1$
and
$d_1=d-1$
and
 $d_2=d-2$
on
$d_2=d-2$
on
 $d_1$
and
$d_1$
and
 $d_2$
, the finitely many cases for
$d_2$
, the finitely many cases for
 $4\leq d\leq 9$
can be directly verified against the inequality in equation (3.2). We find the exceptional cases listed in the statement of the lemma.
$4\leq d\leq 9$
can be directly verified against the inequality in equation (3.2). We find the exceptional cases listed in the statement of the lemma.
Proof of Corollary 3.1
By Lemma 3.2, we need to show that proving Theorem 1.1 for all decompositions listed in the statement of Corollary 3.1 also proves it in these four cases:
-
1.
 $t=3$
,
$t=3$
,
 $d=4$
,
$d=4$
,
 $d_1=d_2=2$
and
$d_1=d_2=2$
and
 $d_3=1$
; or
$d_3=1$
; or -
2.
 $t=3$
,
$t=3$
,
 $d=5$
,
$d=5$
,
 $d_1=d_2=3$
and
$d_1=d_2=3$
and
 $d_3=2$
; or
$d_3=2$
; or -
3.
 $t=3$
,
$t=3$
,
 $d=6$
and
$d=6$
and
 $d_1=d_2=d_3=4$
; or
$d_1=d_2=d_3=4$
; or -
4.
 $t=4$
,
$t=4$
,
 $d=5$
and
$d=5$
and
 $d_1=d_2=d_3=d_4=2$
.
$d_1=d_2=d_3=d_4=2$
.
In each case, we have that either
![]() $t=3$
or
$t=3$
or
![]() $t=4$
. By Corollary 2.3, we can express P as
$t=4$
. By Corollary 2.3, we can express P as
![]() $P = P'\cup S_t$
, where
$P = P'\cup S_t$
, where
![]() $P' = S_1\cup \cdots \cup S_{t-1}$
is a minimal polytope of dimension
$P' = S_1\cup \cdots \cup S_{t-1}$
is a minimal polytope of dimension
![]() $d'$
decomposed into
$d'$
decomposed into
![]() $t'=t-1$
minimal simplices. Note that in all four cases,
$t'=t-1$
minimal simplices. Note that in all four cases,
![]() $d'=d-1$
. We now proceed exactly as in the first part of this section. Let
$d'=d-1$
. We now proceed exactly as in the first part of this section. Let
![]() be the sublattice of N of lattice points in the linear hull of
be the sublattice of N of lattice points in the linear hull of
![]() $P'$
. We define the map
$P'$
. We define the map
![]() $\varphi '\colon N'\oplus N_{t}\to N$
by
$\varphi '\colon N'\oplus N_{t}\to N$
by
![]() $(x_1,x_2)\mapsto x_1 + x_2$
, whose extension
$(x_1,x_2)\mapsto x_1 + x_2$
, whose extension
![]() $\varphi _{\mathbb {R}}$
to a map of vector spaces is surjective and gives the following representation of P:
$\varphi _{\mathbb {R}}$
to a map of vector spaces is surjective and gives the following representation of P:
Let
![]() $M'$
denote the lattice dual to
$M'$
denote the lattice dual to
![]() $N'$
. The map
$N'$
. The map
![]() $(\varphi ')_{\mathbb {R}}^*$
dual to
$(\varphi ')_{\mathbb {R}}^*$
dual to
![]() $(\varphi ')_{\mathbb {R}}$
is an injection, and in particular
$(\varphi ')_{\mathbb {R}}$
is an injection, and in particular
As in equation (3.1), by the monotonicity of the normalised volume,
By our assumption and Lemma 3.2, Theorem 1.1 holds for
![]() $t'=2$
and for
$t'=2$
and for
![]() $t'=3$
,
$t'=3$
,
![]() $d'=4$
,
$d'=4$
,
![]() $d_1=d_2=d_3=2$
. Hence, in all four cases, Theorem 1.1 holds for
$d_1=d_2=d_3=2$
. Hence, in all four cases, Theorem 1.1 holds for
![]() $P'$
: that is,
$P'$
: that is,
![]() $\operatorname {Vol}_{M'}((P')^*) < B_{d-1}$
. Since
$\operatorname {Vol}_{M'}((P')^*) < B_{d-1}$
. Since
![]() $\operatorname {Vol}_{M_{t}}(S_{t}^*)\leq B_{d_{t}}$
and
$\operatorname {Vol}_{M_{t}}(S_{t}^*)\leq B_{d_{t}}$
and
![]() $d'=d-1$
,
$d'=d-1$
,
Hence it is enough to prove that
This inequality can be directly checked in all four cases.
4 Slicing minimal polytopes
We now develop the foundations for a finer technique that we use in Section 6 to help prove the remaining cases of Theorem 1.1. In particular, we shall explain how minimal polytopes can be described as a particular union of slices that are products of slices of simplices (see Figure 2). Using this construction, in Section 5, we give a better estimate of the dual volume via integration.

Figure 2 The dual
![]() $P^*$
of the polytope P from Figure 1, together with the dual triangles
$P^*$
of the polytope P from Figure 1, together with the dual triangles
![]() $(S^{\prime }_1)^*\subset (M^{\prime }_1)_{\mathbb {R}}$
and
$(S^{\prime }_1)^*\subset (M^{\prime }_1)_{\mathbb {R}}$
and
![]() $(S^{\prime }_2)^*\subset (M^{\prime }_2)_{\mathbb {R}}$
. In the left-most picture, the grey slice is
$(S^{\prime }_2)^*\subset (M^{\prime }_2)_{\mathbb {R}}$
. In the left-most picture, the grey slice is
![]() $H_{1,\boldsymbol {0}}\times H_{2,\boldsymbol {0}}$
. We refer to Section 4.2 for the precise definitions.
$H_{1,\boldsymbol {0}}\times H_{2,\boldsymbol {0}}$
. We refer to Section 4.2 for the precise definitions.
4.1 Embedding the dual polytope
As above, we are in the setup of Corollary 2.3:
![]() $P\subset N_{\mathbb {R}}$
is a d-dimensional minimal canonical Fano polytope decomposed into minimal canonical Fano simplices
$P\subset N_{\mathbb {R}}$
is a d-dimensional minimal canonical Fano polytope decomposed into minimal canonical Fano simplices
![]() $S_1,\ldots ,S_t$
for some
$S_1,\ldots ,S_t$
for some
![]() $t\geq 2$
. We define
$t\geq 2$
. We define
to be the set of those vertices of P that occur multiple times amongst the vertices of the
![]() $S_i$
, and we define
$S_i$
, and we define
. For example, in Figure 1, we have
![]() $\mathcal {V}=\mathcal {V}_1=\mathcal {V}_2=\{v\}$
.
$\mathcal {V}=\mathcal {V}_1=\mathcal {V}_2=\{v\}$
.
It will be convenient to coarsen the lattice N. We note that coarsening the ambient lattice N to a lattice
![]() $N'$
is an assumption we can make. Indeed, if
$N'$
is an assumption we can make. Indeed, if
![]() $P_M^*$
and
$P_M^*$
and
![]() $P_{M'}^*$
denote the duals of P with respect to the lattices
$P_{M'}^*$
denote the duals of P with respect to the lattices
![]() $M=N^*$
and
$M=N^*$
and
![]() $M'=(N')^*$
, respectively, then the volume of
$M'=(N')^*$
, respectively, then the volume of
![]() $P_{M'}^*$
is equal to the volume of
$P_{M'}^*$
is equal to the volume of
![]() $P_M^*$
multiplied by the index of
$P_M^*$
multiplied by the index of
![]() $M'$
as a subgroup of M (which is a positive integer).
$M'$
as a subgroup of M (which is a positive integer).
Let
![]() $N^{\prime }_i$
denote some sublattice of
$N^{\prime }_i$
denote some sublattice of
![]() $N_i=\operatorname {lin}_{\mathbb {R}}(S_i)\cap N$
of rank
$N_i=\operatorname {lin}_{\mathbb {R}}(S_i)\cap N$
of rank
![]() $d_i$
with
$d_i$
with
![]() $\mathcal {V}_i\subset N^{\prime }_i$
(a specific choice of
$\mathcal {V}_i\subset N^{\prime }_i$
(a specific choice of
![]() $N^{\prime }_i$
will be given in Section 4.2). Notice that
$N^{\prime }_i$
will be given in Section 4.2). Notice that
![]() $S_i$
may no longer be a lattice simplex with respect to
$S_i$
may no longer be a lattice simplex with respect to
![]() $N^{\prime }_i$
. Therefore, to avoid any confusion, we denote by
$N^{\prime }_i$
. Therefore, to avoid any confusion, we denote by
![]() $S^{\prime }_i\subseteq (N^{\prime }_i)_{\mathbb {R}}=(N_i)_{\mathbb {R}}$
the rational simplex with vertices
$S^{\prime }_i\subseteq (N^{\prime }_i)_{\mathbb {R}}=(N_i)_{\mathbb {R}}$
the rational simplex with vertices
![]() $\operatorname {vert}(S_i)$
with respect to the lattice
$\operatorname {vert}(S_i)$
with respect to the lattice
![]() $N^{\prime }_i$
. Now, by possibly coarsening the lattice N, we may suppose that N is the image of the lattice
$N^{\prime }_i$
. Now, by possibly coarsening the lattice N, we may suppose that N is the image of the lattice
![]() $N^{\prime }_1\oplus \cdots \oplus N^{\prime }_t$
via the map
$N^{\prime }_1\oplus \cdots \oplus N^{\prime }_t$
via the map
 $$ \begin{align} \begin{array}{r@{\ }c@{\ }l} \varphi\colon N^{\prime}_1\oplus\cdots\oplus N^{\prime}_t &\to&N\\ (x_1,\ldots,x_t) &\mapsto&{\displaystyle\sum_{i=1}^{t}x_i}. \end{array} \end{align} $$
$$ \begin{align} \begin{array}{r@{\ }c@{\ }l} \varphi\colon N^{\prime}_1\oplus\cdots\oplus N^{\prime}_t &\to&N\\ (x_1,\ldots,x_t) &\mapsto&{\displaystyle\sum_{i=1}^{t}x_i}. \end{array} \end{align} $$
Hence we can assume that this map is surjective. Notice that the polytope P may no longer be a lattice polytope with respect to this ambient lattice. We extend the map
![]() $\varphi $
to the map of real vector spaces
$\varphi $
to the map of real vector spaces
![]() $\varphi _{\mathbb {R}}\colon (N^{\prime }_1)_{\mathbb {R}}\oplus \cdots \oplus (N^{\prime }_t)_{\mathbb {R}}\to N_{\mathbb {R}}$
. As in the previous section, we can describe P as
$\varphi _{\mathbb {R}}\colon (N^{\prime }_1)_{\mathbb {R}}\oplus \cdots \oplus (N^{\prime }_t)_{\mathbb {R}}\to N_{\mathbb {R}}$
. As in the previous section, we can describe P as
By definition,
![]() $\varphi $
is a surjective map, so we have the exact sequence
$\varphi $
is a surjective map, so we have the exact sequence
which splits over
![]() $\mathbb {Z}$
. From equation (2.1), we have that
$\mathbb {Z}$
. From equation (2.1), we have that
![]() $N^{\prime }_1\oplus \cdots \oplus N^{\prime }_t$
splits into parts of rank d and r. As a consequence, the dual sequence
$N^{\prime }_1\oplus \cdots \oplus N^{\prime }_t$
splits into parts of rank d and r. As a consequence, the dual sequence
is exact and splits too. Here we used the notation
![]() $M^{\prime }_1,\ldots ,M^{\prime }_t$
for the dual lattices of
$M^{\prime }_1,\ldots ,M^{\prime }_t$
for the dual lattices of
![]() $N^{\prime }_1,\ldots ,N^{\prime }_t$
, respectively. Let
$N^{\prime }_1,\ldots ,N^{\prime }_t$
, respectively. Let
![]() $(\ker \varphi )^{\perp }$
denote the elements of
$(\ker \varphi )^{\perp }$
denote the elements of
![]() $M^{\prime }_1\oplus \cdots \oplus M^{\prime }_t$
vanishing on
$M^{\prime }_1\oplus \cdots \oplus M^{\prime }_t$
vanishing on
![]() $\ker \varphi $
. By the exactness of the dual sequence,
$\ker \varphi $
. By the exactness of the dual sequence,
![]() $\varphi ^*(M)=(\ker \varphi )^{\perp }$
: that is, the lattices M and
$\varphi ^*(M)=(\ker \varphi )^{\perp }$
: that is, the lattices M and
![]() $(\ker \varphi )^{\perp }$
are isomorphic via
$(\ker \varphi )^{\perp }$
are isomorphic via
![]() $\varphi ^*$
. In particular,
$\varphi ^*$
. In particular,
![]() $(\ker \varphi )^{\perp } = (M^{\prime }_1\oplus \cdots \oplus M^{\prime }_t)\cap (\ker \varphi )^{\perp }_{\mathbb {R}}$
is a direct summand of
$(\ker \varphi )^{\perp } = (M^{\prime }_1\oplus \cdots \oplus M^{\prime }_t)\cap (\ker \varphi )^{\perp }_{\mathbb {R}}$
is a direct summand of
![]() $M^{\prime }_1\oplus \cdots \oplus M^{\prime }_t$
of rank d.
$M^{\prime }_1\oplus \cdots \oplus M^{\prime }_t$
of rank d.
By tensoring by
![]() $\mathbb {R}$
to extend the maps to the ambient real vector spaces, it follows that the following polytopes are isomorphic as rational polytopes with respect to their respective lattices:
$\mathbb {R}$
to extend the maps to the ambient real vector spaces, it follows that the following polytopes are isomorphic as rational polytopes with respect to their respective lattices:
 $$ \begin{align} \begin{aligned} P^* &\cong\varphi_{\mathbb{R}} ^* (P^*)\\ &=(S^{\prime}_1\oplus\cdots\oplus S^{\prime}_t)^*\cap (\ker\varphi)_{\mathbb{R}}^{\perp}\\ &=((S^{\prime}_1)^*\times\cdots\times (S^{\prime}_t)^*)\cap (\ker\varphi)_{\mathbb{R}}^{\perp}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} P^* &\cong\varphi_{\mathbb{R}} ^* (P^*)\\ &=(S^{\prime}_1\oplus\cdots\oplus S^{\prime}_t)^*\cap (\ker\varphi)_{\mathbb{R}}^{\perp}\\ &=((S^{\prime}_1)^*\times\cdots\times (S^{\prime}_t)^*)\cap (\ker\varphi)_{\mathbb{R}}^{\perp}. \end{aligned} \end{align} $$
We now describe a set of generators of
![]() $(\ker \varphi )_{\mathbb {R}}$
. For this, let us identify
$(\ker \varphi )_{\mathbb {R}}$
. For this, let us identify
![]() $N^{\prime }_i$
with the corresponding direct summand in
$N^{\prime }_i$
with the corresponding direct summand in
![]() $N^{\prime }_1\oplus \cdots \oplus N^{\prime }_t$
. In this way, we can identify
$N^{\prime }_1\oplus \cdots \oplus N^{\prime }_t$
. In this way, we can identify
![]() $v\in \operatorname {vert}(S^{\prime }_i)$
with
$v\in \operatorname {vert}(S^{\prime }_i)$
with
![]() $e_{i,v}\in N^{\prime }_1\oplus \cdots \oplus N^{\prime }_t$
: that is,
$e_{i,v}\in N^{\prime }_1\oplus \cdots \oplus N^{\prime }_t$
: that is,
![]() $(e_{i,v})_i = v\in N^{\prime }_i$
and
$(e_{i,v})_i = v\in N^{\prime }_i$
and
![]() $(e_{i,v})_j =\boldsymbol {0}_{N^{\prime }_j}$
for
$(e_{i,v})_j =\boldsymbol {0}_{N^{\prime }_j}$
for
![]() $j\not =i$
. Recall that
$j\not =i$
. Recall that
![]() $\dim _{\mathbb {R}} (\ker \varphi )_{\mathbb {R}} = r$
. Let
$\dim _{\mathbb {R}} (\ker \varphi )_{\mathbb {R}} = r$
. Let
![]() $1\leq i_1 < i_2\leq t$
and
$1\leq i_1 < i_2\leq t$
and
![]() $v\in \mathcal {V}_{i_1}\cap \mathcal {V}_{i_2}$
. We denote by
$v\in \mathcal {V}_{i_1}\cap \mathcal {V}_{i_2}$
. We denote by
![]() $w_{v,i_1,i_2}$
the element
$w_{v,i_1,i_2}$
the element
![]() $e_{i_2,v}-e_{i_1,v}\in N^{\prime }_1\oplus \cdots \oplus N^{\prime }_t$
.
$e_{i_2,v}-e_{i_1,v}\in N^{\prime }_1\oplus \cdots \oplus N^{\prime }_t$
.
Lemma 4.1. With notation as above,
![]() $\ker \varphi _{\mathbb {R}}$
is generated by the set
$\ker \varphi _{\mathbb {R}}$
is generated by the set
Proof. We prove that the subset
of
![]() $\Omega $
is a basis of
$\Omega $
is a basis of
![]() $\ker \varphi _{\mathbb {R}}$
. Since for
$\ker \varphi _{\mathbb {R}}$
. Since for
![]() $2\le i\leq t$
, we have
$2\le i\leq t$
, we have
![]() $\left |{\{w_{v,i_1,i}\in \Omega '\,\colon i_2=i\}}\right |=r_i$
, this implies that
$\left |{\{w_{v,i_1,i}\in \Omega '\,\colon i_2=i\}}\right |=r_i$
, this implies that
![]() $\left |{\Omega '}\right |=\sum _{i=2}^t r_i = r$
. Hence it is enough to prove that the elements of
$\left |{\Omega '}\right |=\sum _{i=2}^t r_i = r$
. Hence it is enough to prove that the elements of
![]() $\Omega '$
are linearly independent.
$\Omega '$
are linearly independent.
Denote the elements of
![]() $\Omega '$
by
$\Omega '$
by
![]() $\boldsymbol {x}_1,\ldots ,\boldsymbol {x}_r$
, where
$\boldsymbol {x}_1,\ldots ,\boldsymbol {x}_r$
, where
![]() $\boldsymbol {x}_j=((\boldsymbol {x}_j)_1,\ldots ,(\boldsymbol {x}_j)_t)\in N^{\prime }_1\oplus \cdots \oplus N^{\prime }_t$
. Assume there exists a nontrivial relation
$\boldsymbol {x}_j=((\boldsymbol {x}_j)_1,\ldots ,(\boldsymbol {x}_j)_t)\in N^{\prime }_1\oplus \cdots \oplus N^{\prime }_t$
. Assume there exists a nontrivial relation
![]() $\mu _1\boldsymbol {x}_1 +\ldots +\mu _r\boldsymbol {x}_r =\boldsymbol {0}$
with
$\mu _1\boldsymbol {x}_1 +\ldots +\mu _r\boldsymbol {x}_r =\boldsymbol {0}$
with
. Let us define
Let
![]() $i\in \{1,\ldots , t\}$
be the largest integer such that there exists an integer
$i\in \{1,\ldots , t\}$
be the largest integer such that there exists an integer
![]() $j\in \operatorname {supp}(\boldsymbol {\mu })$
, an index
$j\in \operatorname {supp}(\boldsymbol {\mu })$
, an index
![]() $1\le i_1 < i$
and a vertex
$1\le i_1 < i$
and a vertex
![]() $v\in \mathcal {V}_{i_1}\cap \mathcal {V}_i$
, with
$v\in \mathcal {V}_{i_1}\cap \mathcal {V}_i$
, with
![]() $w_{v,i_1,i}=\boldsymbol {x}_j$
. By definition of i and
$w_{v,i_1,i}=\boldsymbol {x}_j$
. By definition of i and
![]() $\Omega '$
, all elements in
$\Omega '$
, all elements in
![]() $\{(\boldsymbol {x}_j)_i\,\colon j\in \operatorname {supp}(\boldsymbol {\mu }), (\boldsymbol {x}_j)_i\not =\boldsymbol {0}_{N^{\prime }_i}\}\neq \varnothing $
are pairwise distinct vertices in
$\{(\boldsymbol {x}_j)_i\,\colon j\in \operatorname {supp}(\boldsymbol {\mu }), (\boldsymbol {x}_j)_i\not =\boldsymbol {0}_{N^{\prime }_i}\}\neq \varnothing $
are pairwise distinct vertices in
![]() $\mathcal {V}_i\cap \operatorname {vert}(P^{(i-1)})$
. Hence
$\mathcal {V}_i\cap \operatorname {vert}(P^{(i-1)})$
. Hence
 $$\begin{align*}\sum_{j\in\operatorname{supp}(\boldsymbol{\mu})}\mu_j\, (\boldsymbol{x}_j)_i =\boldsymbol{0}_{N^{\prime}_i} \end{align*}$$
$$\begin{align*}\sum_{j\in\operatorname{supp}(\boldsymbol{\mu})}\mu_j\, (\boldsymbol{x}_j)_i =\boldsymbol{0}_{N^{\prime}_i} \end{align*}$$
implies a nontrivial relation of a non-empty subset of the vertices in
![]() $\mathcal {V}_i\cap \operatorname {vert}(P^{(i-1)})$
. However, as
$\mathcal {V}_i\cap \operatorname {vert}(P^{(i-1)})$
. However, as
![]() $S_i$
contains the origin in its interior, any proper subset of the set of vertices of
$S_i$
contains the origin in its interior, any proper subset of the set of vertices of
![]() $S_i$
is linearly independent, so
$S_i$
is linearly independent, so
![]() $\mathcal {V}_i\cap \operatorname {vert}(P^{(i-1)}) =\operatorname {vert}(S_i)$
. Hence
$\mathcal {V}_i\cap \operatorname {vert}(P^{(i-1)}) =\operatorname {vert}(S_i)$
. Hence
![]() $r_i=d_i+1$
, a contradiction to equation (2.2).
$r_i=d_i+1$
, a contradiction to equation (2.2).
We now apply Lemma 4.1 to equation (4.2):
 $$ \begin{align} \begin{aligned} P^*&\cong\varphi^*_{\mathbb{R}} (P^*)\\ &=((S^{\prime}_1)^*\times\cdots\times (S^{\prime}_t)^*)\cap (\ker\varphi)_{\mathbb{R}}^{\perp}\\ &=\{(y_1,\ldots , y_t)\in (S^{\prime}_1)^*\times\cdots\times (S^{\prime}_t)^*\,\colon\langle (y_1,\ldots,y_t) ,\omega\rangle = 0\text{ for each }\omega\in (\ker\varphi)_{\mathbb{R}}\}\\ &=\{(y_1,\ldots , y_t)\in (S^{\prime}_1)^*\times\cdots\times (S^{\prime}_t)^*\,\colon\langle y_{i_1} , e_{i_1,v}\rangle =\langle y_{i_2} , e_{i_2,v}\rangle\text{ for each } w_{v,i_1,i_2}\in\Omega\}\\ &=\{(y_1,\ldots , y_t)\in (S^{\prime}_1)^*\times\cdots\times (S^{\prime}_t)^*\,\colon\langle y_{i_1} , e_{i_1,v}\rangle =\langle y_{i_2} , e_{i_2,v}\rangle\text{ for each } v\in\mathcal{V}_{i_1}\cap\mathcal{V}_{i_2}\}.\\ \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} P^*&\cong\varphi^*_{\mathbb{R}} (P^*)\\ &=((S^{\prime}_1)^*\times\cdots\times (S^{\prime}_t)^*)\cap (\ker\varphi)_{\mathbb{R}}^{\perp}\\ &=\{(y_1,\ldots , y_t)\in (S^{\prime}_1)^*\times\cdots\times (S^{\prime}_t)^*\,\colon\langle (y_1,\ldots,y_t) ,\omega\rangle = 0\text{ for each }\omega\in (\ker\varphi)_{\mathbb{R}}\}\\ &=\{(y_1,\ldots , y_t)\in (S^{\prime}_1)^*\times\cdots\times (S^{\prime}_t)^*\,\colon\langle y_{i_1} , e_{i_1,v}\rangle =\langle y_{i_2} , e_{i_2,v}\rangle\text{ for each } w_{v,i_1,i_2}\in\Omega\}\\ &=\{(y_1,\ldots , y_t)\in (S^{\prime}_1)^*\times\cdots\times (S^{\prime}_t)^*\,\colon\langle y_{i_1} , e_{i_1,v}\rangle =\langle y_{i_2} , e_{i_2,v}\rangle\text{ for each } v\in\mathcal{V}_{i_1}\cap\mathcal{V}_{i_2}\}.\\ \end{aligned} \end{align} $$
4.2 The integration map
From here onward, we will assume that the decomposition of P into the simplices
![]() $S_i$
is irredundant: that is,
$S_i$
is irredundant: that is,
![]() $\mathcal {V}_i\subsetneq \operatorname {vert}(S_i)$
for
$\mathcal {V}_i\subsetneq \operatorname {vert}(S_i)$
for
![]() $i=1,\ldots , t$
. Under this assumption, we describe a specific choice for
$i=1,\ldots , t$
. Under this assumption, we describe a specific choice for
![]() $N^{\prime }_i$
. For this, we choose a vertex
$N^{\prime }_i$
. For this, we choose a vertex
![]() $v_i\in \operatorname {vert}(S_i)\setminus \mathcal {V}_i$
and set
$v_i\in \operatorname {vert}(S_i)\setminus \mathcal {V}_i$
and set
We have
![]() $\mathcal {V}_i\subset \widehat {\mathcal {V}}_i$
. We define
$\mathcal {V}_i\subset \widehat {\mathcal {V}}_i$
. We define
![]() $N^{\prime }_i$
to be the lattice spanned by
$N^{\prime }_i$
to be the lattice spanned by
![]() $\widehat {\mathcal {V}}_i$
: that is,
$\widehat {\mathcal {V}}_i$
: that is,
By construction, the
![]() $d_i$
vertices in
$d_i$
vertices in
![]() $\widehat {\mathcal {V}}_i$
form a lattice basis
$\widehat {\mathcal {V}}_i$
form a lattice basis
of
![]() $N^{\prime }_i$
(as a sublattice of
$N^{\prime }_i$
(as a sublattice of
![]() $N^{\prime }_1\oplus \cdots \oplus N^{\prime }_t$
). Note that the vertex
$N^{\prime }_1\oplus \cdots \oplus N^{\prime }_t$
). Note that the vertex
![]() $v_i$
need not be a lattice point in
$v_i$
need not be a lattice point in
![]() $N^{\prime }_i$
. We again assume that N is given as the image of
$N^{\prime }_i$
. We again assume that N is given as the image of
![]() $\varphi $
– see equation (4.1) – and we will refer to
$\varphi $
– see equation (4.1) – and we will refer to
![]() $S_i$
as
$S_i$
as
![]() $S^{\prime }_i$
when referring to it with respect to the lattice
$S^{\prime }_i$
when referring to it with respect to the lattice
![]() $N^{\prime }_i$
. This choice of lattice will allow us to prove Lemma 4.2, which simplifies the considerations in Section 5. In particular, it will yield a convenient explicit description of
$N^{\prime }_i$
. This choice of lattice will allow us to prove Lemma 4.2, which simplifies the considerations in Section 5. In particular, it will yield a convenient explicit description of
![]() $(S^{\prime }_i)^*$
(see Lemma 5.1).
$(S^{\prime }_i)^*$
(see Lemma 5.1).
Set
![]() and
and
![]() for
for
![]() $i=1,\ldots , t$
. We define
$i=1,\ldots , t$
. We define
![]() $\Psi $
to be the map
$\Psi $
to be the map
 $$ \begin{align*} \Psi: (\ker\varphi)^{\perp} &\to\bigoplus_{v\in\mathcal{V}}\mathbb{Z}\cong\mathbb{Z}^q\\ (y_1,\ldots,y_t) &\mapsto (\langle y_{i_v} , e_{i_v,v}\rangle)_{v\in\mathcal{V}}, \end{align*} $$
$$ \begin{align*} \Psi: (\ker\varphi)^{\perp} &\to\bigoplus_{v\in\mathcal{V}}\mathbb{Z}\cong\mathbb{Z}^q\\ (y_1,\ldots,y_t) &\mapsto (\langle y_{i_v} , e_{i_v,v}\rangle)_{v\in\mathcal{V}}, \end{align*} $$
where for each v,
![]() $i_v$
is any index such that
$i_v$
is any index such that
![]() $v\in \mathcal {V}_{i_v}$
. Since
$v\in \mathcal {V}_{i_v}$
. Since
![]() $\langle y_{i_1} , e_{i_1,v}\rangle =\langle y_{i_2} , e_{i_2,v}\rangle $
whenever
$\langle y_{i_1} , e_{i_1,v}\rangle =\langle y_{i_2} , e_{i_2,v}\rangle $
whenever
![]() $v\in \mathcal {V}_{i_1}\cap \mathcal {V}_{i_2}$
,
$v\in \mathcal {V}_{i_1}\cap \mathcal {V}_{i_2}$
,
![]() $\Psi $
is a well-defined map. In an analogous fashion to the definition of
$\Psi $
is a well-defined map. In an analogous fashion to the definition of
![]() $\Psi $
, for each
$\Psi $
, for each
![]() $i\in \{1,\ldots ,t\}$
, we define the map
$i\in \{1,\ldots ,t\}$
, we define the map
 $$ \begin{align*} \Psi_i: M^{\prime}_i &\to\bigoplus_{v\in\mathcal{V}_i}\mathbb{Z}\cong\mathbb{Z}^{q_i}\\ y &\mapsto (\langle y , e_{i,v}\rangle)_{v\in\mathcal{V}_i}. \end{align*} $$
$$ \begin{align*} \Psi_i: M^{\prime}_i &\to\bigoplus_{v\in\mathcal{V}_i}\mathbb{Z}\cong\mathbb{Z}^{q_i}\\ y &\mapsto (\langle y , e_{i,v}\rangle)_{v\in\mathcal{V}_i}. \end{align*} $$
Lemma 4.2. The maps
![]() $\Psi ,\Psi _1,\ldots ,\Psi _t$
are surjective.
$\Psi ,\Psi _1,\ldots ,\Psi _t$
are surjective.
Proof. Let
![]() $\{\epsilon _{i,v}\}_{v\in \mathcal {V}_i}$
be the standard basis of
$\{\epsilon _{i,v}\}_{v\in \mathcal {V}_i}$
be the standard basis of
![]() $\bigoplus _{v\in \mathcal {V}_i}\mathbb {Z}$
and
$\bigoplus _{v\in \mathcal {V}_i}\mathbb {Z}$
and
![]() $\{e_{i,v}^*\}_{v\in \widehat {\mathcal {V}}_i}$
the lattice basis of
$\{e_{i,v}^*\}_{v\in \widehat {\mathcal {V}}_i}$
the lattice basis of
![]() $M^{\prime }_i$
dual to the lattice basis
$M^{\prime }_i$
dual to the lattice basis
![]() $\{e_{i,v}\}_{v\in \widehat {\mathcal {V}}_i}$
of
$\{e_{i,v}\}_{v\in \widehat {\mathcal {V}}_i}$
of
![]() $N^{\prime }_i$
. The maps
$N^{\prime }_i$
. The maps
![]() $\Psi _i$
are surjective, since each element
$\Psi _i$
are surjective, since each element
![]() $e_{i,v}^*$
is mapped into
$e_{i,v}^*$
is mapped into
![]() $\epsilon _{i,v}$
, for
$\epsilon _{i,v}$
, for
![]() $v\in \mathcal {V}_i$
.
$v\in \mathcal {V}_i$
.
We now prove that
![]() $\Psi $
is surjective. Since the codomains of the maps
$\Psi $
is surjective. Since the codomains of the maps
![]() $\Psi _i$
span the codomain of
$\Psi _i$
span the codomain of
![]() $\Psi $
, it is enough to check that for each
$\Psi $
, it is enough to check that for each
![]() $i\in \{1,\ldots ,t\}$
and for each
$i\in \{1,\ldots ,t\}$
and for each
![]() $v\in \mathcal {V}_i$
, there exists an element
$v\in \mathcal {V}_i$
, there exists an element
![]() $(y_1,\ldots ,y_t)\in (\ker \varphi )^{\perp }\subset M^{\prime }_1\oplus \cdots \oplus M^{\prime }_t$
such that
$(y_1,\ldots ,y_t)\in (\ker \varphi )^{\perp }\subset M^{\prime }_1\oplus \cdots \oplus M^{\prime }_t$
such that
![]() $y_i=e_{i,v}^*$
. This is true since it suffices to choose
$y_i=e_{i,v}^*$
. This is true since it suffices to choose
![]() $(y_1,\ldots ,y_t)$
as
$(y_1,\ldots ,y_t)$
as
As a consequence of Lemma 4.2, the extensions of
![]() $\Psi ,\Psi _1,\ldots ,\Psi _t$
to the real vector space maps
$\Psi ,\Psi _1,\ldots ,\Psi _t$
to the real vector space maps
are linear surjective maps. We define natural projections
as the identity over
![]() $\bigoplus _{v\in \mathcal {V}_i}\mathbb {R}$
and the zero map over
$\bigoplus _{v\in \mathcal {V}_i}\mathbb {R}$
and the zero map over
![]() $\bigoplus _{v\in \mathcal {V}\setminus \mathcal {V}_i}\mathbb {R}$
.
$\bigoplus _{v\in \mathcal {V}\setminus \mathcal {V}_i}\mathbb {R}$
.
Let
![]() $\mathcal {D}$
be the set of parameters
$\mathcal {D}$
be the set of parameters
Given a point
![]() $\boldsymbol {\lambda }=(\lambda _v)_{v\in \mathcal {V}}\in \mathcal {D}$
, define the fibre
$\boldsymbol {\lambda }=(\lambda _v)_{v\in \mathcal {V}}\in \mathcal {D}$
, define the fibre
Denote by
![]() $F^*_i$
the
$F^*_i$
the
![]() $(d_i-q_i)$
-dimensional face of
$(d_i-q_i)$
-dimensional face of
![]() $(S^{\prime }_i)^*$
given by
$(S^{\prime }_i)^*$
given by
From equation (4.3), we obtain the desired decomposition of
![]() $P^*$
:
$P^*$
:
 $$ \begin{align} \begin{aligned} P^* &\cong\bigsqcup_{(\lambda_v)_{v\in\mathcal{V}}\in\mathcal{D}}\{(y_1,\ldots , y_t)\in (S^{\prime}_1)^*\times\cdots\times (S^{\prime}_t)^*\,\colon\langle y_i , e_{i,v}\rangle =\lambda_v\text{ for all } v\in\mathcal{V}_i,\, i = 1,\ldots, t\}\\ &=\bigsqcup_{\boldsymbol{\lambda}\in\mathcal{D}} H_{1,\boldsymbol{\lambda}}\times\cdots\times H_{t,\boldsymbol{\lambda}}.\\ \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} P^* &\cong\bigsqcup_{(\lambda_v)_{v\in\mathcal{V}}\in\mathcal{D}}\{(y_1,\ldots , y_t)\in (S^{\prime}_1)^*\times\cdots\times (S^{\prime}_t)^*\,\colon\langle y_i , e_{i,v}\rangle =\lambda_v\text{ for all } v\in\mathcal{V}_i,\, i = 1,\ldots, t\}\\ &=\bigsqcup_{\boldsymbol{\lambda}\in\mathcal{D}} H_{1,\boldsymbol{\lambda}}\times\cdots\times H_{t,\boldsymbol{\lambda}}.\\ \end{aligned} \end{align} $$
In other words,
![]() $P^*$
is sliced into a disjoint union of sections (see Figure 2).
$P^*$
is sliced into a disjoint union of sections (see Figure 2).
5 Bounding the volume of
 $P^*$
via integration
$P^*$
via integration
In this section, we apply equation (4.5) to obtain a finer bound on the volume of
![]() $P^*$
in the case when P decomposes into just two simplices. From here onward, we assume we are in the setup of Corollary 2.3 with
$P^*$
in the case when P decomposes into just two simplices. From here onward, we assume we are in the setup of Corollary 2.3 with
![]() $t=2$
: that is, P decomposes in two minimal canonical simplices
$t=2$
: that is, P decomposes in two minimal canonical simplices
![]() $S_1$
and
$S_1$
and
![]() $S_2$
of dimensions
$S_2$
of dimensions
![]() $d_1$
and
$d_1$
and
![]() $d_2$
, respectively. As P is not a simplex, clearly this decomposition is irredundant, so the results of Section 4.2 apply. We will continue to use the notation introduced in Section 4, in particular the choice of
$d_2$
, respectively. As P is not a simplex, clearly this decomposition is irredundant, so the results of Section 4.2 apply. We will continue to use the notation introduced in Section 4, in particular the choice of
![]() $N^{\prime }_i,N,S^{\prime }_i$
in Section 4.2. Note that
$N^{\prime }_i,N,S^{\prime }_i$
in Section 4.2. Note that
![]() $q=r_2=r = |\mathcal {V}| = |\mathcal {V}_1| = |\mathcal {V}_2|$
is the number of common vertices of
$q=r_2=r = |\mathcal {V}| = |\mathcal {V}_1| = |\mathcal {V}_2|$
is the number of common vertices of
![]() $S_1$
and
$S_1$
and
![]() $S_2$
.
$S_2$
.
The equality in equation (4.5) and Lemma 4.2 allow us to calculate the volume
![]() $\operatorname {vol}_M(P^*)$
by integrating the sections over the possible values of
$\operatorname {vol}_M(P^*)$
by integrating the sections over the possible values of
![]() $\boldsymbol {\lambda }$
. In particular,
$\boldsymbol {\lambda }$
. In particular,
Before attempting to bound such a value, we present an alternative description of
![]() $\mathcal {D}$
. For
$\mathcal {D}$
. For
![]() $i=1,2$
, we define
$i=1,2$
, we define
![]() $\mathcal {D}_i$
as
$\mathcal {D}_i$
as
and we note that (since the maps
![]() $p_i$
defined in the previous section correspond to the identity maps here)
$p_i$
defined in the previous section correspond to the identity maps here)
Recall that a lattice basis
![]() $\{e_{i,v}\}$
for
$\{e_{i,v}\}$
for
![]() $N^{\prime }_i$
is given by the elements of
$N^{\prime }_i$
is given by the elements of
![]() $\widehat {\mathcal {V}}_i=\operatorname {vert}(S_i)\setminus \{v_i\}$
. Denote by
$\widehat {\mathcal {V}}_i=\operatorname {vert}(S_i)\setminus \{v_i\}$
. Denote by
![]() $(\beta _{i,v})_{v\in \operatorname {vert}(S_i)}$
the barycentric coordinates of the origin in the simplex
$(\beta _{i,v})_{v\in \operatorname {vert}(S_i)}$
the barycentric coordinates of the origin in the simplex
![]() $S_i$
: that is,
$S_i$
: that is,
![]() $\sum _{v\in \operatorname {vert}(S_i)}\beta _{i,v} v =\boldsymbol {0}$
, where
$\sum _{v\in \operatorname {vert}(S_i)}\beta _{i,v} v =\boldsymbol {0}$
, where
![]() $\sum _{v\in \operatorname {vert}(S_i)}\beta _{i,v} = 1$
. Note that
$\sum _{v\in \operatorname {vert}(S_i)}\beta _{i,v} = 1$
. Note that
![]() $\beta _{i,v}> 0$
for any
$\beta _{i,v}> 0$
for any
![]() $v\in \operatorname {vert}(S_i)$
. Hence we can express
$v\in \operatorname {vert}(S_i)$
. Hence we can express
![]() $v_i$
as
$v_i$
as
 $$\begin{align*}v_i= -\sum_{v\in\widehat{\mathcal{V}}_i}\frac{\beta_{i,v}}{\beta_{i,v_i}}e_{i,v}.\end{align*}$$
$$\begin{align*}v_i= -\sum_{v\in\widehat{\mathcal{V}}_i}\frac{\beta_{i,v}}{\beta_{i,v_i}}e_{i,v}.\end{align*}$$
Let us denote by
![]() $\{\epsilon _{i,v}\}_{v\in \mathcal {V}_i}$
the standard basis of
$\{\epsilon _{i,v}\}_{v\in \mathcal {V}_i}$
the standard basis of
![]() $\bigoplus _{v\in \mathcal {V}_i}\mathbb {Z}$
. Lemma 5.1 below gives an explicit description for
$\bigoplus _{v\in \mathcal {V}_i}\mathbb {Z}$
. Lemma 5.1 below gives an explicit description for
![]() $(S^{\prime }_i)^*$
and
$(S^{\prime }_i)^*$
and
![]() $\mathcal {D}_i$
in terms of our chosen lattice bases. We omit the straightforward proof.
$\mathcal {D}_i$
in terms of our chosen lattice bases. We omit the straightforward proof.
Lemma 5.1. With notation as above, for
![]() $i=1,2$
,
$i=1,2$
,
 $$\begin{align*}(S^{\prime}_i)^* =\operatorname{conv}\left(\left\{-\sum_{v\in\mathcal{V}} e^*_{i,v}\right\}\cup\left\{\left(\frac{1}{\beta_{i,w}}-1\right)e^*_{i,w}-\sum_{v\in\mathcal{V}\setminus\{w\}} e^*_{i,v}\right\}_{w\in\widehat{\mathcal{V}}_i}\right), \end{align*}$$
$$\begin{align*}(S^{\prime}_i)^* =\operatorname{conv}\left(\left\{-\sum_{v\in\mathcal{V}} e^*_{i,v}\right\}\cup\left\{\left(\frac{1}{\beta_{i,w}}-1\right)e^*_{i,w}-\sum_{v\in\mathcal{V}\setminus\{w\}} e^*_{i,v}\right\}_{w\in\widehat{\mathcal{V}}_i}\right), \end{align*}$$
 $$\begin{align*}\quad\!\!\!\mathcal{D}_i =\operatorname{conv}\left(\left\{-\sum_{v\in\mathcal{V}}\epsilon^*_{i,v}\right\}\cup\left\{\left(\frac{1}{\beta_{i,w}}-1\right)\epsilon^*_{i,w}-\sum_{v\in\mathcal{V}\setminus\{w\}}\epsilon^*_{i,v}\right\}_{w\in\mathcal{V}}\right). \end{align*}$$
$$\begin{align*}\quad\!\!\!\mathcal{D}_i =\operatorname{conv}\left(\left\{-\sum_{v\in\mathcal{V}}\epsilon^*_{i,v}\right\}\cup\left\{\left(\frac{1}{\beta_{i,w}}-1\right)\epsilon^*_{i,w}-\sum_{v\in\mathcal{V}\setminus\{w\}}\epsilon^*_{i,v}\right\}_{w\in\mathcal{V}}\right). \end{align*}$$
By using the inequality
![]() $f_1 f_2\leq \frac {f_1^2+f_2^2}{2}$
, we can bound equation (5.1) via
$f_1 f_2\leq \frac {f_1^2+f_2^2}{2}$
, we can bound equation (5.1) via
 $$ \begin{align} \begin{aligned} \operatorname{vol}_{M}(P^*) &\leq\int_{\boldsymbol{\lambda}\in\mathcal{D}}\frac{\operatorname{vol}_{M^{\prime}_1}(H_{1,\boldsymbol{\lambda}})^2 +\operatorname{vol}_{M^{\prime}_2}(H_{2,\boldsymbol{\lambda}})^2}{2}\,d\boldsymbol{\lambda}\\ &=\frac{1}{2}\int_{\boldsymbol{\lambda}\in\mathcal{D}}\operatorname{vol}_{M^{\prime}_1}(H_{1,\boldsymbol{\lambda}})^2\,d\boldsymbol{\lambda} +\frac{1}{2}\int_{\boldsymbol{\lambda}\in\mathcal{D}}\operatorname{vol}_{M^{\prime}_2}(H_{2,\boldsymbol{\lambda}})^2\,d\boldsymbol{\lambda}\\ &\leq\frac{1}{2}\int_{\boldsymbol{\lambda}\in\mathcal{D}_1}\operatorname{vol}_{M^{\prime}_1}(H_{1,\boldsymbol{\lambda}})^2\,d\boldsymbol{\lambda} +\frac{1}{2}\int_{\boldsymbol{\lambda}\in\mathcal{D}_2}\operatorname{vol}_{M^{\prime}_2}(H_{2,\boldsymbol{\lambda}})^2\,d\boldsymbol{\lambda},\\ \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \operatorname{vol}_{M}(P^*) &\leq\int_{\boldsymbol{\lambda}\in\mathcal{D}}\frac{\operatorname{vol}_{M^{\prime}_1}(H_{1,\boldsymbol{\lambda}})^2 +\operatorname{vol}_{M^{\prime}_2}(H_{2,\boldsymbol{\lambda}})^2}{2}\,d\boldsymbol{\lambda}\\ &=\frac{1}{2}\int_{\boldsymbol{\lambda}\in\mathcal{D}}\operatorname{vol}_{M^{\prime}_1}(H_{1,\boldsymbol{\lambda}})^2\,d\boldsymbol{\lambda} +\frac{1}{2}\int_{\boldsymbol{\lambda}\in\mathcal{D}}\operatorname{vol}_{M^{\prime}_2}(H_{2,\boldsymbol{\lambda}})^2\,d\boldsymbol{\lambda}\\ &\leq\frac{1}{2}\int_{\boldsymbol{\lambda}\in\mathcal{D}_1}\operatorname{vol}_{M^{\prime}_1}(H_{1,\boldsymbol{\lambda}})^2\,d\boldsymbol{\lambda} +\frac{1}{2}\int_{\boldsymbol{\lambda}\in\mathcal{D}_2}\operatorname{vol}_{M^{\prime}_2}(H_{2,\boldsymbol{\lambda}})^2\,d\boldsymbol{\lambda},\\ \end{aligned} \end{align} $$
where the final inequality follows from equation (5.2). It is convenient to perform a change of variables for
![]() $i=1,2$
via the maps
$i=1,2$
via the maps
By Lemma 5.1, the integration domain
![]() $\mathcal {D}_i$
becomes the unimodular q-dimensional simplex
$\mathcal {D}_i$
becomes the unimodular q-dimensional simplex
![]() $\Delta _{(q)}$
: that is, the convex hull of the origin and the standard basis of
$\Delta _{(q)}$
: that is, the convex hull of the origin and the standard basis of
![]() $\mathbb {Z}^q$
. Hence equation (5.3) can be rewritten as
$\mathbb {Z}^q$
. Hence equation (5.3) can be rewritten as
 $$ \begin{align} \operatorname{vol}_{M}(P^*)\leq\frac{1}{2}\prod_{v\in\mathcal{V}}\frac{1}{\beta_{1,v}}\int_{\boldsymbol{\alpha}\in\Delta_{(q)}}\!\!\operatorname{vol}_{M^{\prime}_1}(H_{1,f_1(\boldsymbol{\alpha})})^2\,d\boldsymbol{\alpha} +\frac{1}{2}\prod_{v\in\mathcal{V}}\frac{1}{\beta_{2,v}}\int_{\boldsymbol{\alpha}\in\Delta_{(q)}}\!\!\operatorname{vol}_{M^{\prime}_2}(H_{2,f_2(\boldsymbol{\alpha})})^2\,d\boldsymbol{\alpha}. \end{align} $$
$$ \begin{align} \operatorname{vol}_{M}(P^*)\leq\frac{1}{2}\prod_{v\in\mathcal{V}}\frac{1}{\beta_{1,v}}\int_{\boldsymbol{\alpha}\in\Delta_{(q)}}\!\!\operatorname{vol}_{M^{\prime}_1}(H_{1,f_1(\boldsymbol{\alpha})})^2\,d\boldsymbol{\alpha} +\frac{1}{2}\prod_{v\in\mathcal{V}}\frac{1}{\beta_{2,v}}\int_{\boldsymbol{\alpha}\in\Delta_{(q)}}\!\!\operatorname{vol}_{M^{\prime}_2}(H_{2,f_2(\boldsymbol{\alpha})})^2\,d\boldsymbol{\alpha}. \end{align} $$
Lemma 5.2 [Reference Averkov2, Lemma 3.5 III]
With notation as above, for
![]() $i=1,2$
,
$i=1,2$
,
 $$\begin{align*}\operatorname{vol}_{M^{\prime}_i}(H_{i,f_i(\boldsymbol{\alpha})})=\operatorname{vol}_{M^{\prime}_i}(F^*_i)\left( 1 -\sum_{v\in\mathcal{V}_i}\alpha_v\right) ^{d_i-q}, \end{align*}$$
$$\begin{align*}\operatorname{vol}_{M^{\prime}_i}(H_{i,f_i(\boldsymbol{\alpha})})=\operatorname{vol}_{M^{\prime}_i}(F^*_i)\left( 1 -\sum_{v\in\mathcal{V}_i}\alpha_v\right) ^{d_i-q}, \end{align*}$$
where
![]() $F_i$
is the
$F_i$
is the
![]() $(d_i-q)$
-dimensional face of
$(d_i-q)$
-dimensional face of
![]() $(S^{\prime }_i)^*$
defined in equation (4.4).
$(S^{\prime }_i)^*$
defined in equation (4.4).
The inequality in equation (5.4) can now be rewritten as
 $$ \begin{align} \begin{aligned} \operatorname{vol}_{M}(P^*) &\leq \frac{1}{2}\prod_{v\in\mathcal{V}}\frac{1}{\beta_{1,v}}\operatorname{vol}_{M^{\prime}_1}(F^*_1)^t\int_{\boldsymbol{\alpha}\in\Delta_{(q)}}\left( 1 -\sum_{v\in\mathcal{V}}\alpha_v\right) ^{2(d_1-q)}\,d\boldsymbol{\alpha}\\& \quad + \frac{1}{2}\prod_{v\in\mathcal{V}}\frac{1}{\beta_{2,v}}\operatorname{vol}_{M^{\prime}_2}(F^*_2)^t\int_{\boldsymbol{\alpha}\in\Delta_{(q)}}\left( 1 -\sum_{v\in\mathcal{V}}\alpha_v\right) ^{2(d_2-q)}\,d\boldsymbol{\alpha}.\\ \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \operatorname{vol}_{M}(P^*) &\leq \frac{1}{2}\prod_{v\in\mathcal{V}}\frac{1}{\beta_{1,v}}\operatorname{vol}_{M^{\prime}_1}(F^*_1)^t\int_{\boldsymbol{\alpha}\in\Delta_{(q)}}\left( 1 -\sum_{v\in\mathcal{V}}\alpha_v\right) ^{2(d_1-q)}\,d\boldsymbol{\alpha}\\& \quad + \frac{1}{2}\prod_{v\in\mathcal{V}}\frac{1}{\beta_{2,v}}\operatorname{vol}_{M^{\prime}_2}(F^*_2)^t\int_{\boldsymbol{\alpha}\in\Delta_{(q)}}\left( 1 -\sum_{v\in\mathcal{V}}\alpha_v\right) ^{2(d_2-q)}\,d\boldsymbol{\alpha}.\\ \end{aligned} \end{align} $$
The following lemma derives from a special case of a well-known representation of the beta function (see, for example, [Reference Carlson6, Representation 4.3-2]).
Lemma 5.3.
 $$\begin{align*}\int_{\boldsymbol{\alpha}\in\Delta_{(a)}}( 1 -\alpha_1 -\ldots -\alpha_a )^b\,d\boldsymbol{\alpha} =\frac{b!}{(a+b)!}. \end{align*}$$
$$\begin{align*}\int_{\boldsymbol{\alpha}\in\Delta_{(a)}}( 1 -\alpha_1 -\ldots -\alpha_a )^b\,d\boldsymbol{\alpha} =\frac{b!}{(a+b)!}. \end{align*}$$
Applying Lemma 5.3 to equation (5.5) yields
 $$ \begin{align} \operatorname{vol}_{M}(P^*)\leq\frac{1}{2}\prod_{v\in\mathcal{V}}\frac{1}{\beta_{1,v}}\operatorname{vol}_{M^{\prime}_1}(F^*_1)^2\frac{(2(d_1-q))!}{(q+2(d_1-q))!} +\frac{1}{2}\prod_{v\in\mathcal{V}}\frac{1}{\beta_{2,v}}\operatorname{vol}_{M^{\prime}_2}(F^*_2)^2\frac{(2(d_2-q))!}{(q+(2(d_2-q))!}. \end{align} $$
$$ \begin{align} \operatorname{vol}_{M}(P^*)\leq\frac{1}{2}\prod_{v\in\mathcal{V}}\frac{1}{\beta_{1,v}}\operatorname{vol}_{M^{\prime}_1}(F^*_1)^2\frac{(2(d_1-q))!}{(q+2(d_1-q))!} +\frac{1}{2}\prod_{v\in\mathcal{V}}\frac{1}{\beta_{2,v}}\operatorname{vol}_{M^{\prime}_2}(F^*_2)^2\frac{(2(d_2-q))!}{(q+(2(d_2-q))!}. \end{align} $$
The volume of
![]() $F^*_i$
is computed in Lemma 5.4 below. Its proof is omitted since it is a straightforward consequence of the description of
$F^*_i$
is computed in Lemma 5.4 below. Its proof is omitted since it is a straightforward consequence of the description of
![]() $(S^{\prime }_i)^*$
given in Lemma 5.1.
$(S^{\prime }_i)^*$
given in Lemma 5.1.
Lemma 5.4. With notation as above, for
![]() $i=1,2$
,
$i=1,2$
,
 $$\begin{align*}\operatorname{vol}_{M^{\prime}_i}(F_i^*)=\frac{1}{(d_i-q)!}\prod_{v\in\widehat{\mathcal{V}}_i\setminus\mathcal{V}}\frac{1}{\beta_{i,v}}. \end{align*}$$
$$\begin{align*}\operatorname{vol}_{M^{\prime}_i}(F_i^*)=\frac{1}{(d_i-q)!}\prod_{v\in\widehat{\mathcal{V}}_i\setminus\mathcal{V}}\frac{1}{\beta_{i,v}}. \end{align*}$$
Finally, applying Lemma 5.4 to equation (5.6) gives the following bound for
![]() $\operatorname {vol}_{M}(P^*)$
:
$\operatorname {vol}_{M}(P^*)$
:
 $$ \begin{align} \begin{aligned} \operatorname{vol}_{M}(P^*)\leq\frac{1}{2}&\frac{(2(d_1-q))!}{(q+2(d_1-q))!((d_1-q)!)^2}\prod_{v\in\mathcal{V}}\frac{1}{\beta_{1,v}}\prod_{v\in\widehat{\mathcal{V}}_1\setminus\mathcal{V} }\frac{1}{\beta_{1,v}^2}\\ &+\frac{1}{2}\frac{(2(d_2-q))!}{(q+2(d_2-q))!((d_2-q)!)^2}\prod_{v\in\mathcal{V}}\frac{1}{\beta_{2,v}}\prod_{v\in\widehat{\mathcal{V}}_2\setminus\mathcal{V} }\frac{1}{\beta_{2,v}^2}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \operatorname{vol}_{M}(P^*)\leq\frac{1}{2}&\frac{(2(d_1-q))!}{(q+2(d_1-q))!((d_1-q)!)^2}\prod_{v\in\mathcal{V}}\frac{1}{\beta_{1,v}}\prod_{v\in\widehat{\mathcal{V}}_1\setminus\mathcal{V} }\frac{1}{\beta_{1,v}^2}\\ &+\frac{1}{2}\frac{(2(d_2-q))!}{(q+2(d_2-q))!((d_2-q)!)^2}\prod_{v\in\mathcal{V}}\frac{1}{\beta_{2,v}}\prod_{v\in\widehat{\mathcal{V}}_2\setminus\mathcal{V} }\frac{1}{\beta_{2,v}^2}. \end{aligned} \end{align} $$
6 Final cases
In this final section, we address the remaining cases of Corollary 3.1. That is, we prove that the decompositions
-
1.
 $t=2$
,
$t=2$
,
 $d_1=d_2=d-1$
, for
$d_1=d_2=d-1$
, for
 $d\geq 4$
$d\geq 4$
-
2.
 $t=2$
,
$t=2$
,
 $d_1=d-1$
,
$d_1=d-1$
,
 $d_2=d-2$
,
$d_2=d-2$
,
 $d\in \{4,5\}$
$d\in \{4,5\}$
-
3.
 $t=3$
,
$t=3$
,
 $d_1=d_2=d_3=d-2$
,
$d_1=d_2=d_3=d-2$
,
 $d\in \{4,5\}$
$d\in \{4,5\}$
satisfy Theorem 1.1.
6.1 The case
 $t=2$
,
$t=2$
,
 $d_1=d_2=d-1$
$d_1=d_2=d-1$
By equation (2.1), we have
![]() $q=d-2$
. Hence the inequality in equation (5.7) can be rewritten as
$q=d-2$
. Hence the inequality in equation (5.7) can be rewritten as
 $$ \begin{align} \operatorname{vol}_{M}(P^*)\leq\frac{1}{d!}\left(\prod_{v\in\mathcal{V}}\frac{1}{\beta_{1,v}}\prod_{v\in\widehat{\mathcal{V}}_1\setminus\mathcal{V} }\frac{1}{\beta_{1,v}^2} +\prod_{v\in\mathcal{V}}\frac{1}{\beta_{2,v}}\prod_{v\in\widehat{\mathcal{V}}_2\setminus\mathcal{V} }\frac{1}{\beta_{2,v}^2}\right). \end{align} $$
$$ \begin{align} \operatorname{vol}_{M}(P^*)\leq\frac{1}{d!}\left(\prod_{v\in\mathcal{V}}\frac{1}{\beta_{1,v}}\prod_{v\in\widehat{\mathcal{V}}_1\setminus\mathcal{V} }\frac{1}{\beta_{1,v}^2} +\prod_{v\in\mathcal{V}}\frac{1}{\beta_{2,v}}\prod_{v\in\widehat{\mathcal{V}}_2\setminus\mathcal{V} }\frac{1}{\beta_{2,v}^2}\right). \end{align} $$
We focus on the product
 $$\begin{align*}\prod_{v\in\mathcal{V}}\frac{1}{\beta_{i,v}}\prod_{v\in\widehat{\mathcal{V}}_i\setminus\mathcal{V} }\frac{1}{\beta_{i,v}^2} \end{align*}$$
$$\begin{align*}\prod_{v\in\mathcal{V}}\frac{1}{\beta_{i,v}}\prod_{v\in\widehat{\mathcal{V}}_i\setminus\mathcal{V} }\frac{1}{\beta_{i,v}^2} \end{align*}$$
for each
![]() $i=1,2$
. Note that in Section 4.2, we chose to exclude one of the vertices (called
$i=1,2$
. Note that in Section 4.2, we chose to exclude one of the vertices (called
![]() $v_i$
) of
$v_i$
) of
![]() $\operatorname {vert}(S_i)\setminus \mathcal {V}$
from appearing in
$\operatorname {vert}(S_i)\setminus \mathcal {V}$
from appearing in
![]() $\widehat {\mathcal {V}}_i$
. As there are two such vertices (say,
$\widehat {\mathcal {V}}_i$
. As there are two such vertices (say,
![]() $\operatorname {vert}(S_i)\setminus \mathcal {V}=\{v_i, u_i\}$
), we can exclude the one whose corresponding barycentric coordinate is smaller: that is,
$\operatorname {vert}(S_i)\setminus \mathcal {V}=\{v_i, u_i\}$
), we can exclude the one whose corresponding barycentric coordinate is smaller: that is,
![]() $\beta _{i,{v_i}}\le \beta _{i,{u_i}}$
. This yields
$\beta _{i,{v_i}}\le \beta _{i,{u_i}}$
. This yields
 $$ \begin{align} \prod_{v\in\mathcal{V}}\frac{1}{\beta_{i,v}}\prod_{v\in\widehat{\mathcal{V}}_i\setminus\mathcal{V} }\frac{1}{\beta_{i,v}^2} =\left(\prod_{v\in\mathcal{V}}\frac{1}{\beta_{i,v}}\right)\frac{1}{\beta_{i,{u_i}}^2}\le\left(\prod_{v\in\mathcal{V}}\frac{1}{\beta_{i,v}}\right)\frac{1}{\beta_{i,{u_i}}}\frac{1}{\beta_{i,{v_i}}} =\frac{1}{\beta_{i,0}\cdots\beta_{i,d-1}}, \end{align} $$
$$ \begin{align} \prod_{v\in\mathcal{V}}\frac{1}{\beta_{i,v}}\prod_{v\in\widehat{\mathcal{V}}_i\setminus\mathcal{V} }\frac{1}{\beta_{i,v}^2} =\left(\prod_{v\in\mathcal{V}}\frac{1}{\beta_{i,v}}\right)\frac{1}{\beta_{i,{u_i}}^2}\le\left(\prod_{v\in\mathcal{V}}\frac{1}{\beta_{i,v}}\right)\frac{1}{\beta_{i,{u_i}}}\frac{1}{\beta_{i,{v_i}}} =\frac{1}{\beta_{i,0}\cdots\beta_{i,d-1}}, \end{align} $$
where
![]() $\{\beta _{i,v}\,\colon v\in \operatorname {vert}(S_i)\} =\{\beta _{i,j}\,\colon j=0,\ldots , d-1\}$
. Notice that the equality in equation (6.2) is attained if and only if
$\{\beta _{i,v}\,\colon v\in \operatorname {vert}(S_i)\} =\{\beta _{i,j}\,\colon j=0,\ldots , d-1\}$
. Notice that the equality in equation (6.2) is attained if and only if
![]() $\beta _{i,u_i} =\beta _{i,v_i}$
.
$\beta _{i,u_i} =\beta _{i,v_i}$
.
For each
![]() $i=1,2$
, let us order the barycentric coordinates such that
$i=1,2$
, let us order the barycentric coordinates such that
![]() $\beta _{i,0}\ge \beta _{i,1}\ge \cdots \ge \beta _{i,d-1}$
.
$\beta _{i,0}\ge \beta _{i,1}\ge \cdots \ge \beta _{i,d-1}$
.
Lemma 6.1 [Reference Averkov, Krümpelmann and Nill3, Lemma 4.2(d)]
With notation as above,
with equality if and only if
 $$ \begin{align} \left(\beta_{i,0},\ldots,\beta_{i,d-1}\right) =\left(\frac{1}{s_1},\ldots,\frac{1}{s_{d-1}},\frac{1}{s_d-1}\right). \end{align} $$
$$ \begin{align} \left(\beta_{i,0},\ldots,\beta_{i,d-1}\right) =\left(\frac{1}{s_1},\ldots,\frac{1}{s_{d-1}},\frac{1}{s_d-1}\right). \end{align} $$
Applying Lemma 6.1 and equations (6.2)–(6.1), we obtain
This inequality is strict, since the condition that
![]() $\beta _{i,u_i} =\beta _{i,v_i}$
from equation (6.2) and the condition in equation (6.3) from Lemma 6.1 cannot hold simultaneously.
$\beta _{i,u_i} =\beta _{i,v_i}$
from equation (6.2) and the condition in equation (6.3) from Lemma 6.1 cannot hold simultaneously.
6.2 The cases
 $t=2$
,
$t=2$
,
 $d_1=d-1$
,
$d_1=d-1$
,
 $d_2=d-2$
,
$d_2=d-2$
,
 $d\in \{4,5\}$
$d\in \{4,5\}$
The barycentric coordinates of the canonical Fano simplices up to and including dimension four are classified in [Reference Kasprzyk11]. Hence we can verify that in this situation, the right-hand side of equation (5.7) is always strictly less than
![]() $2(s_d-1)^2/d!$
.
$2(s_d-1)^2/d!$
.
6.3 The cases
 $t=3$
,
$t=3$
,
 $d_1=d_2=d_3=d-2$
,
$d_1=d_2=d_3=d-2$
,
 $d\in \{4,5\}$
$d\in \{4,5\}$
Corollary 2.3 implies that
![]() $r_2=r_3=d-3$
. To prove the inequality in these final cases, we explicitly construct every minimal polytope P of dimension four or five that admits a decomposition into three minimal simplices of dimensions two or three, respectively, such that the vertices of P generate the ambient lattice N. Under this setting, we note that P is uniquely determined by
$r_2=r_3=d-3$
. To prove the inequality in these final cases, we explicitly construct every minimal polytope P of dimension four or five that admits a decomposition into three minimal simplices of dimensions two or three, respectively, such that the vertices of P generate the ambient lattice N. Under this setting, we note that P is uniquely determined by
-
1. the barycentric coordinates of the simplices
 $S_1,S_2,S_3$
in the decomposition; and
$S_1,S_2,S_3$
in the decomposition; and -
2. the choice of
 $d-3$
vertices in common with
$d-3$
vertices in common with
 $S_2$
and
$S_2$
and
 $S_1$
, together with the choice of
$S_1$
, together with the choice of
 $d-3$
vertices in common with
$d-3$
vertices in common with
 $S_3$
and
$S_3$
and
 $S_1\cup S_2$
.
$S_1\cup S_2$
.
This follows from the following general construction. The (reduced) weights of a canonical Fano simplex S of dimension n are the positive integers
![]() $(k\beta _0,\ldots , k\beta _n)$
given by the barycentric coordinates
$(k\beta _0,\ldots , k\beta _n)$
given by the barycentric coordinates
![]() $(\beta _0,\ldots ,\beta _n)$
of the origin (with respect to the vertices of S), where k is the smallest positive integer such that the
$(\beta _0,\ldots ,\beta _n)$
of the origin (with respect to the vertices of S), where k is the smallest positive integer such that the
![]() $k\beta _i$
are all integral. In particular, the weights of a canonical Fano simplex are coprime. Moreover, since the vertices of a canonical Fano simplex are primitive lattice points, the weights are well-formed: that is, any n of them are coprime. Let us use the fact that any minimal polytope P has a decomposition into t minimal simplices. We proceed invariantly since we do not know the embedding of these simplices into the lattice N. Let
$k\beta _i$
are all integral. In particular, the weights of a canonical Fano simplex are coprime. Moreover, since the vertices of a canonical Fano simplex are primitive lattice points, the weights are well-formed: that is, any n of them are coprime. Let us use the fact that any minimal polytope P has a decomposition into t minimal simplices. We proceed invariantly since we do not know the embedding of these simplices into the lattice N. Let
![]() $\underline {\lambda }^{(n)}=(\lambda _0,\ldots ,\lambda _n)$
denote the (reduced, well-formed) weights of a minimal canonical Fano simplex of dimension n. Fix weights
$\underline {\lambda }^{(n)}=(\lambda _0,\ldots ,\lambda _n)$
denote the (reduced, well-formed) weights of a minimal canonical Fano simplex of dimension n. Fix weights
![]() $\underline {\lambda }^{(d_1)},\ldots ,\underline {\lambda }^{(d_t)}$
. For each pair
$\underline {\lambda }^{(d_1)},\ldots ,\underline {\lambda }^{(d_t)}$
. For each pair
![]() $(i,j)$
with
$(i,j)$
with
![]() $1\leq i < j\leq t$
, we pick a (possibly empty) subset
$1\leq i < j\leq t$
, we pick a (possibly empty) subset
![]() $V_{ij}\subset \{0,\ldots ,d_i\}\times \{0,\ldots ,d_j\}$
such that
$V_{ij}\subset \{0,\ldots ,d_i\}\times \{0,\ldots ,d_j\}$
such that
![]() $V_{ij}:\pi _1(V_{ij})\to \pi _2(V_{ij})$
is a bijection (here
$V_{ij}:\pi _1(V_{ij})\to \pi _2(V_{ij})$
is a bijection (here
![]() $\pi _k$
denotes the projection on the kth factor). Let
$\pi _k$
denotes the projection on the kth factor). Let
![]() $\iota _j:\mathbb {Z}^{d_j+1}\to \bigoplus _{i=1}^t\mathbb {Z}^{d_i+1}$
,
$\iota _j:\mathbb {Z}^{d_j+1}\to \bigoplus _{i=1}^t\mathbb {Z}^{d_i+1}$
,
![]() $1\leq j\leq t$
, be the natural inclusion on the jth factor. Define
$1\leq j\leq t$
, be the natural inclusion on the jth factor. Define

Applying
![]() $-\otimes \mathbb {R}$
ensures torsion-freeness of the quotient
$-\otimes \mathbb {R}$
ensures torsion-freeness of the quotient
![]() $\left (\bigoplus _{i=1}^t\mathbb {Z}^{d_i+1}\right )/(W + V)$
, and therefore we get the exact sequence
$\left (\bigoplus _{i=1}^t\mathbb {Z}^{d_i+1}\right )/(W + V)$
, and therefore we get the exact sequence
 $$\begin{align*}0\to (W + V)\otimes\mathbb{R}\to\left(\bigoplus_{i=1}^t\mathbb{Z}^{d_i+1}\right)\otimes\mathbb{R}\xrightarrow{\varphi_{\mathbb{R}}} N\otimes\mathbb{R}\to 0, \end{align*}$$
$$\begin{align*}0\to (W + V)\otimes\mathbb{R}\to\left(\bigoplus_{i=1}^t\mathbb{Z}^{d_i+1}\right)\otimes\mathbb{R}\xrightarrow{\varphi_{\mathbb{R}}} N\otimes\mathbb{R}\to 0, \end{align*}$$
where N is the lattice obtained as the quotient
![]() $\left (\bigoplus _{i=1}^t\mathbb {Z}^{d_i+1}\right )/K$
, where K is the direct summand defined by
$\left (\bigoplus _{i=1}^t\mathbb {Z}^{d_i+1}\right )/K$
, where K is the direct summand defined by
![]() $\left (\bigoplus _{i=1}^t\mathbb {Z}^{d_i+1}\right )\cap \left ((W + V)\otimes \mathbb {R}\right )$
. We now define
$\left (\bigoplus _{i=1}^t\mathbb {Z}^{d_i+1}\right )\cap \left ((W + V)\otimes \mathbb {R}\right )$
. We now define

which by construction is a polytope whose vertices generate its ambient lattice N. In general, Q may not be a minimal polytope; however, if P is a minimal lattice polytope of dimension d whose vertices generate its ambient lattice, then there exists a choice of integers
![]() $t,d_1,\ldots ,d_t$
, weights
$t,d_1,\ldots ,d_t$
, weights
![]() $\underline {\lambda }^{(d_1)},\ldots ,\underline {\lambda }^{(d_t)}$
of minimal Fano simplices
$\underline {\lambda }^{(d_1)},\ldots ,\underline {\lambda }^{(d_t)}$
of minimal Fano simplices
![]() $S_1,\ldots ,S_t$
of dimensions
$S_1,\ldots ,S_t$
of dimensions
![]() $d_1,\ldots ,d_t$
and subsets
$d_1,\ldots ,d_t$
and subsets
![]() $V_{ij}$
(for
$V_{ij}$
(for
![]() $1\leq i < j\leq t$
) such that the polytope Q constructed above is equal to P. The fact that we can recover P from the construction of Q is a consequence of Lemma 4.1, while the existence of the parameters
$1\leq i < j\leq t$
) such that the polytope Q constructed above is equal to P. The fact that we can recover P from the construction of Q is a consequence of Lemma 4.1, while the existence of the parameters
![]() $t,d_1,\ldots ,d_t$
and the weights follows from Corollary 2.3.
$t,d_1,\ldots ,d_t$
and the weights follows from Corollary 2.3.
We now specialise this construction to the case
![]() $t=3$
,
$t=3$
,
![]() $d_1=d_2=d_3=d-2$
for
$d_1=d_2=d_3=d-2$
for
![]() $d\in \{4,5\}$
. The weights of the minimal canonical Fano simplices of dimensions two and three have been classified [Reference Kasprzyk10, Figure 1 and Proposition 4.3]. There are two possible weights in dimension two:
$d\in \{4,5\}$
. The weights of the minimal canonical Fano simplices of dimensions two and three have been classified [Reference Kasprzyk10, Figure 1 and Proposition 4.3]. There are two possible weights in dimension two:
![]() $(1,1,1)$
and
$(1,1,1)$
and
![]() $(1,1,2)$
. In dimension three, there are
$(1,1,2)$
. In dimension three, there are
![]() $13$
possible weights,Footnote 1 recorded in Table 1. Since the choices for the common vertices (encoded in the sets
$13$
possible weights,Footnote 1 recorded in Table 1. Since the choices for the common vertices (encoded in the sets
![]() $V_{ij}$
,
$V_{ij}$
,
![]() $1\leq i < j\leq 3$
) are finite, all the minimal canonical Fano polytopes P admitting such a decomposition and whose vertices generate the ambient lattice N can be classified.
$1\leq i < j\leq 3$
) are finite, all the minimal canonical Fano polytopes P admitting such a decomposition and whose vertices generate the ambient lattice N can be classified.
Table 1 The weights of the minimal canonical Fano simplices in dimension three.

We use the computer algebra system Magma [Reference Bosma, Cannon and Playoust5] to derive the classification. Source code and output can be downloaded from Zenodo [Reference Balletti, Kasprzyk and Nill4]. In the first case (
![]() $d_1=d_2=d_3=2$
), there are exactly four such four-dimensional polytopes, and in each case, the inequality of Theorem 1.1 holds. To solve the second case (
$d_1=d_2=d_3=2$
), there are exactly four such four-dimensional polytopes, and in each case, the inequality of Theorem 1.1 holds. To solve the second case (
![]() $d_1=d_2=d_3=3$
), we first build all possible four-dimensional minimal polytopes
$d_1=d_2=d_3=3$
), we first build all possible four-dimensional minimal polytopes
![]() $P'$
whose vertices generate the ambient lattice and admit a decomposition into two three-dimensional minimal canonical Fano simplices
$P'$
whose vertices generate the ambient lattice and admit a decomposition into two three-dimensional minimal canonical Fano simplices
![]() $S_1$
and
$S_1$
and
![]() $S_2$
. We then verify that any five-dimensional polytope P decomposing as
$S_2$
. We then verify that any five-dimensional polytope P decomposing as
![]() $S_1$
,
$S_1$
,
![]() $S_2$
and
$S_2$
and
![]() $S_3$
satisfies the inequality in equation (3.5) for each choice of three-dimensional minimal canonical Fano simplex
$S_3$
satisfies the inequality in equation (3.5) for each choice of three-dimensional minimal canonical Fano simplex
![]() $S_3$
; that is, we verify that
$S_3$
; that is, we verify that
holds in each case. There are
![]() $147$
minimal four-dimensional polytopes with a decomposition into two three-dimensional minimal canonical Fano simplices and whose vertices generate the lattice N, and in each case, the inequality holds. This completes the proof of Theorem 1.1.
$147$
minimal four-dimensional polytopes with a decomposition into two three-dimensional minimal canonical Fano simplices and whose vertices generate the lattice N, and in each case, the inequality holds. This completes the proof of Theorem 1.1.
6.4 Bounding the volume of P
Unfortunately, the methods used here to prove a sharp upper bound on the volume of
![]() $P^*$
do not immediately help provide an upper bound on the volume of P. Since there is no known decomposition result for maximal canonical Fano polytopes, we would again have to pass to the dual side and consider minimal ‘canonical’ subpolytopes of
$P^*$
do not immediately help provide an upper bound on the volume of P. Since there is no known decomposition result for maximal canonical Fano polytopes, we would again have to pass to the dual side and consider minimal ‘canonical’ subpolytopes of
![]() $P^*$
. One could still decompose these into ‘canonical’ simplices. However, they would no longer be lattice simplices, and there are no known applicable bounds on the corresponding barycentric coordinates of the origin in the rational case.
$P^*$
. One could still decompose these into ‘canonical’ simplices. However, they would no longer be lattice simplices, and there are no known applicable bounds on the corresponding barycentric coordinates of the origin in the rational case.
Conflict of Interest
The authors have no conflict of interest to declare.
Financial support
GB was supported by the Stiftelsen GS Magnusons Fund and by a Jubileumsfond grant from the Knut and Alice Wallenbergs Foundation. BN would like to thank the Fields Institute for financial support to participate in the thematic program ‘Combinatorial Algebraic Geometry’ and Stockholm University for his time spent as an affiliated researcher. In addition, GB and BN were supported by Vetenskapsrådet grant NT:2014-3991. AK was supported by EPSRC Fellowship EP/N022513/1.