1 Introduction
In diverse areas of mathematics, posets and simplicial complexes arising from algebraic, combinatorial or geometric objects are widely studied. Usually, one tries to answer questions or determine intrinsic properties of a mathematical object by looking into the combinatorics and topology of associated combinatorial structures. One of the most classical examples is the poset of subspaces of a finite-dimensional vector space, which has been extensively studied in connection with the combinatorics, representation theory and cohomology of linear groups. Sometimes one even endeavors to associate several posets or simplicial complexes with a given object, establish relations among them, and then achieve stronger results. In this direction, many works provide resembling constructions and morphisms between the various combinatorial structures, analyzed often via ‘Quillen’s fiber theorem’ type tools. In some cases, these yield wedge/join decompositions, allowing us to translate or interchange combinatorial and homotopy properties from one structure to another.
This paper aims to present a general framework in which many of these constructions are particular cases. We discuss fundamental combinatorial properties that are intrinsic to our approach and show how they can be used to establish comparison results between the different posets and simplicial complexes arising from the same mathematical object. These results provide a toolset for verifying homotopical properties such as high connectivity, sphericity or even Cohen-Macaulayness, and also for computing Euler characteristics (or, more generally, the module afforded in the homology). These are goals prevalent in the literature.
The starting point of our constructions is the subobject poset of a given object X in some category
![]() ${\mathcal C}$
. However, from a combinatorial point of view, this poset is often not suitable since it may contain infinite chains, as is, for example, the case of the subgroup poset of a free group, or even the subgroup poset of a free Abelian group. Infinite chains obstruct the construction of ‘natural’ posets of decompositions and frame complexes associated with X. For that reason, we will keep only the subobjects that are complemented with respect to a suitable product. Thus, we shift gears and work instead with an initial category
${\mathcal C}$
. However, from a combinatorial point of view, this poset is often not suitable since it may contain infinite chains, as is, for example, the case of the subgroup poset of a free group, or even the subgroup poset of a free Abelian group. Infinite chains obstruct the construction of ‘natural’ posets of decompositions and frame complexes associated with X. For that reason, we will keep only the subobjects that are complemented with respect to a suitable product. Thus, we shift gears and work instead with an initial category
![]() ${\mathcal C}$
equipped with a symmetric monoidal product
${\mathcal C}$
equipped with a symmetric monoidal product
![]() $\sqcup $
, which will often be the coproduct of
$\sqcup $
, which will often be the coproduct of
![]() ${\mathcal C}$
. With this additional structure at hand, we can extract more ‘interesting’ subobject posets and decompositions that encode different ways of resembling the original object from sets or tuples of subobjects whose
${\mathcal C}$
. With this additional structure at hand, we can extract more ‘interesting’ subobject posets and decompositions that encode different ways of resembling the original object from sets or tuples of subobjects whose
![]() $\sqcup $
-product is isomorphic to X.
$\sqcup $
-product is isomorphic to X.
To be more precise, the constructions in this article are built up from a so-called poset of complemented subobjects
![]() ${\mathcal {S}}(X,\sqcup )$
of a fixed object X in our initial category
${\mathcal {S}}(X,\sqcup )$
of a fixed object X in our initial category
![]() ${\mathcal C}$
with symmetric monoidal product
${\mathcal C}$
with symmetric monoidal product
![]() $\sqcup $
. A prominent example to keep in mind is the above-mentioned poset of subspaces
$\sqcup $
. A prominent example to keep in mind is the above-mentioned poset of subspaces
![]() ${{\mathcal S}}(V)$
of a vector space V of dimension n over a field
${{\mathcal S}}(V)$
of a vector space V of dimension n over a field
![]() ${\mathbb {K}}$
. In this case, we consider the category of vector spaces over
${\mathbb {K}}$
. In this case, we consider the category of vector spaces over
![]() ${\mathbb {K}}$
with
${\mathbb {K}}$
with
![]() $\sqcup $
being just the usual coproduct. The order complex of
$\sqcup $
being just the usual coproduct. The order complex of
![]() ${{\mathcal S}}(V)$
is the Tits building of
${{\mathcal S}}(V)$
is the Tits building of
![]() $\operatorname {\mathrm {SL}}_n({\mathbb {K}})$
, and it has been widely studied in many areas of mathematics. Then we define the posets of
$\operatorname {\mathrm {SL}}_n({\mathbb {K}})$
, and it has been widely studied in many areas of mathematics. Then we define the posets of
![]() $\sqcup $
-decompositions and partial
$\sqcup $
-decompositions and partial
![]() $\sqcup $
-decompositions (see Definition 2.15). In our example case, the former corresponds to the poset
$\sqcup $
-decompositions (see Definition 2.15). In our example case, the former corresponds to the poset
![]() ${\mathcal D}(V)$
of collections of nonzero subspaces
${\mathcal D}(V)$
of collections of nonzero subspaces
![]() $\{S_1,\ldots , S_r\}$
which are in internal direct sum and span the whole space V; that is,
$\{S_1,\ldots , S_r\}$
which are in internal direct sum and span the whole space V; that is,
![]() $S_1\oplus \cdots \oplus S_r \cong \left \langle S_1,\ldots ,S_r\right \rangle = V$
. The latter, denoted by
$S_1\oplus \cdots \oplus S_r \cong \left \langle S_1,\ldots ,S_r\right \rangle = V$
. The latter, denoted by
![]() ${\mathcal {PD}}(V)$
, consists of collections of nonzero subspaces in direct sum, the span being just a subspace. Both posets are ordered by refinement. Direct sum decompositions of vector spaces over finite fields were shown to be homotopically Cohen-Macaulay in [Reference WelkerWel]. Indeed, the same result for arbitrary fields is already implicit in [Reference CharneyC], as we explain later in the article (see Proposition 4.15 and Subsection 6.2). For partial direct sum decompositions of vector spaces over finite fields, Cohen-Macaulayness was established in the unpublished work [Reference Hanlon, Hersh and ShareshianHHS]. For infinite fields, the proper part of
${\mathcal {PD}}(V)$
, consists of collections of nonzero subspaces in direct sum, the span being just a subspace. Both posets are ordered by refinement. Direct sum decompositions of vector spaces over finite fields were shown to be homotopically Cohen-Macaulay in [Reference WelkerWel]. Indeed, the same result for arbitrary fields is already implicit in [Reference CharneyC], as we explain later in the article (see Proposition 4.15 and Subsection 6.2). For partial direct sum decompositions of vector spaces over finite fields, Cohen-Macaulayness was established in the unpublished work [Reference Hanlon, Hersh and ShareshianHHS]. For infinite fields, the proper part of
![]() ${\mathcal {PD}}(V)$
is spherical by results of [Reference Brück, Piterman and WelkerBPW, Reference Miller, Patzt and WilsonMPW], as we explain in Subsection 6.2. However, Cohen-Macaulayness has not been established yet in the case of infinite fields. Then we define a simplicial complex of frames. In the vector space case, a frame is a partial decomposition into
${\mathcal {PD}}(V)$
is spherical by results of [Reference Brück, Piterman and WelkerBPW, Reference Miller, Patzt and WilsonMPW], as we explain in Subsection 6.2. However, Cohen-Macaulayness has not been established yet in the case of infinite fields. Then we define a simplicial complex of frames. In the vector space case, a frame is a partial decomposition into
![]() $1$
-dimensional subspaces. A further construction is obtained as the inflation of the frame complex. That is, we replace vertices of the frame complex with sets (interpreted as sets of generators or bases). This yields the complex of partial bases. From subobject posets and frame complexes, one can also build the augmented Bergman complex – which in the matroid case recently gained a lot of attention through [Reference Braden, Huh, Matherne, Proudfoot and WangBHMPW].
$1$
-dimensional subspaces. A further construction is obtained as the inflation of the frame complex. That is, we replace vertices of the frame complex with sets (interpreted as sets of generators or bases). This yields the complex of partial bases. From subobject posets and frame complexes, one can also build the augmented Bergman complex – which in the matroid case recently gained a lot of attention through [Reference Braden, Huh, Matherne, Proudfoot and WangBHMPW].
For (partial) decompositions, frames and partial bases, there also exist ordered versions. These are posets whose elements are all linear orders on sets and simplices in the unordered poset or simplicial complex (see Definition 4.5). Our key result regarding the ordered versions is that they exhibit a nice wedge decomposition in terms of their unordered counterparts. Therefore, properties such as sphericity or Cohen-Macaulayness can be transferred back and forth. In our vector space example, the ordered partial decompositions are linearly ordered sets of subspaces that form internal direct sums, and ordered decompositions are in close relationship to a complex studied in [Reference CharneyC], which in our setting we call the Charney complex. The ordered versions of the frame complex and the partial basis complex essentially correspond to the associated complex of injective words (see [Reference Jonsson and WelkerJW, Reference Reiner and WebbReW]).
Our results about properties and connections among these different posets and complexes allow us to specialize them to important cases. We summarize the main examples to which we apply our theory in Table 1. In the row of this table corresponding to vector spaces with forms, we take the category of vector spaces with suitable forms, and morphisms are isometries. Even though this category misses most of the coproducts, the natural candidate for it is the orthogonal sum, and that is the monoidal product we consider. Also observe that in the matroid case, there is no categorical approach developed so far that suits our purposes. The problem relies on the fact that the main poset we want to study is the lattice of flats, but the matroid obtained from the join of two flats depends specifically on the matroid we are working with. Hence, in that case, we regard the lattice of flats as a poset-category, and the monoidal product is just the join.
Table 1 Main examples of the paper.

Finally, we would like to emphasize that our results are based on combinatorial and topological methods that apply mainly to finite-dimensional complexes and posets.
A related categorical approach is developed in [Reference Galatius, Kupers and Randal-WilliamsGKRW, Reference Randal-WilliamsRW, Reference Randal-Williams and WahlRWW], where certain complexes are constructed from complemented subobjects. While our focus is the analysis of the combinatorics and the homotopy types of our constructions, these works address homological stability problems for quite general families of groups by starting out with high connectivity assumptions. Thus, in a certain sense, our work complements [Reference Galatius, Kupers and Randal-WilliamsGKRW, Reference Randal-WilliamsRW, Reference Randal-Williams and WahlRWW] by establishing a set of posets and simplicial complexes together with properties and relations among them that can be used to prove Cohen-Macaulayness or high connectivity. We expect that our results will yield new classes of complexes, which then can be fed into the sophisticated machinery devised in these works.
A different but related problem where our results may provide new input data is the search for dualizing modules (see, for example, [Reference Church and PutmanCP, Reference Church, Farb and PutmanCFP]). If V is an n-dimensional vector space over
![]() ${\mathbb {K}}$
, the order complex of the proper part of the poset of subspaces of V is the Tits building of
${\mathbb {K}}$
, the order complex of the proper part of the poset of subspaces of V is the Tits building of
![]() $\operatorname {\mathrm {SL}}_n({\mathbb {K}})$
. The top-dimensional homology group of this complex is the well-known Steinberg module of
$\operatorname {\mathrm {SL}}_n({\mathbb {K}})$
. The top-dimensional homology group of this complex is the well-known Steinberg module of
![]() $\operatorname {\mathrm {SL}}_n({\mathbb {K}})$
, and by Borel-Serre [Reference Borel and SerreBS73], it is a rational dualizing module for
$\operatorname {\mathrm {SL}}_n({\mathbb {K}})$
, and by Borel-Serre [Reference Borel and SerreBS73], it is a rational dualizing module for
![]() $\operatorname {\mathrm {SL}}_n({{\mathcal O}})$
, when
$\operatorname {\mathrm {SL}}_n({{\mathcal O}})$
, when
![]() ${\mathbb {K}}$
is a number field and
${\mathbb {K}}$
is a number field and
![]() ${{\mathcal O}}$
is its ring of integers. The explicit determination of a dualizing module may be a difficult and often unsolved problem. For example, a question raised by Hatcher and Vogtmann [Reference Hatcher and VogtmannHV98a] asked whether the top dimensional cohomology group of the free factor complex
${{\mathcal O}}$
is its ring of integers. The explicit determination of a dualizing module may be a difficult and often unsolved problem. For example, a question raised by Hatcher and Vogtmann [Reference Hatcher and VogtmannHV98a] asked whether the top dimensional cohomology group of the free factor complex
![]() $\operatorname {\mathrm {FC}}(F_n)$
of the free group
$\operatorname {\mathrm {FC}}(F_n)$
of the free group
![]() $F_n$
of rank n yields a dualizing module for
$F_n$
of rank n yields a dualizing module for
![]() $\operatorname {\mathrm {Aut}}(F_n)$
. However, a negative answer to this question was recently given in the case
$\operatorname {\mathrm {Aut}}(F_n)$
. However, a negative answer to this question was recently given in the case
![]() $n = 5$
in [Reference Himes, Miller, Nariman and PutmanHMNP]. In general, the homology (or even the ‘Lefschetz module’) of
$n = 5$
in [Reference Himes, Miller, Nariman and PutmanHMNP]. In general, the homology (or even the ‘Lefschetz module’) of
![]() ${\mathcal {S}}(X,\sqcup )$
can be regarded as a Steinberg module for a suitable group of automorphisms of this poset, prompting consideration for a similar interpretation in other contexts.
${\mathcal {S}}(X,\sqcup )$
can be regarded as a Steinberg module for a suitable group of automorphisms of this poset, prompting consideration for a similar interpretation in other contexts.
From the combinatorial perspective, this paper explores a unified approach to many well-studied poset constructions (see, for example, [Reference StanleySt78, Reference StanleySt12, Reference WachsWac]). It comprises important complexes and posets associated with matroids including the lattice of flats, the independence complex and the recently studied augmented Bergman complex (see, for example, [Reference BjörnerBj92, Reference Braden, Huh, Matherne, Proudfoot and WangBHMPW]). In both cases, new constructions and results are added. These yield results on homotopy types about ‘natural’ combinatorially defined posets and complexes. When looking at the reduced Euler characteristic or equivalently the Möbius number, new enumerative identities follow, which will be addressed in an upcoming work [Reference Piterman, Shareshian and WelkerPSW].
The paper is organized as follows. In Section 2, we give precise definitions of the framework we want to work with and provide definitions of complemented elements and decompositions arising from subobjects in a certain monoidal category. In Section 3, we establish basic properties of the posets of decompositions and partial decompositions, and in Section 4, we define other posets that can also be constructed from decompositions. In particular, we include here the definition of the frame complex, the partial basis complex, their ordered versions, the augmented Bergman complex and the Charney complex. In Section 5, we prove results on the homotopy types of posets and simplicial complexes defined in Section 2 and Section 4. Typical results from this paragraph express the homotopy type of one class of posets in terms of another class. Through these formulas for the homotopy types, we can define conditions under which properties, such as sphericity or Cohen-Macaulayness are transferred. In general, results from this section provide innovative tools to investigate the topology of combinatorially defined simplicial complexes.
Finally, in Section 6, we prove a variety of new results on the homotopy types and Euler characteristic of posets and simplicial complexes built in the preceding sections for a wide range of combinatorial, algebraic and geometric objects (e.g., subspaces of vector spaces, nondegenerate subspaces, matroids, set-partitions, etc.). The proofs use a combination of methods developed in Section 4 & Section 5 and additional enumerative results. Throughout that section, we pose some questions and present open problems.
2 Poset of decompositions into subobjects
We start our poset constructions with a purely combinatorial approach. We will see that this approach, even though vital for subsequent developments, fails to cover important classes of posets that otherwise perfectly fit our setting. For that reason, we will use category theory language later in this section.
First, we recall some basic notations and definitions. A poset
![]() ${{\mathcal S}}$
is a (not necessarily finite) set with a partial order
${{\mathcal S}}$
is a (not necessarily finite) set with a partial order
![]() $\leq $
. We call
$\leq $
. We call
![]() ${{\mathcal S}}$
bounded if it has a unique minimal element
${{\mathcal S}}$
bounded if it has a unique minimal element
![]() $0_{{{\mathcal S}}}$
and a unique maximal element
$0_{{{\mathcal S}}}$
and a unique maximal element
![]() $1_{{{\mathcal S}}}$
. When the reference poset
$1_{{{\mathcal S}}}$
. When the reference poset
![]() ${{\mathcal S}}$
is clear from the context, we just write
${{\mathcal S}}$
is clear from the context, we just write
![]() $0$
and
$0$
and
![]() $1$
for the minimum and maximum of
$1$
for the minimum and maximum of
![]() ${{\mathcal S}}$
. For a bounded poset
${{\mathcal S}}$
. For a bounded poset
![]() ${{\mathcal S}}$
, we denote by
${{\mathcal S}}$
, we denote by
![]() ${{\mathcal S}}^{*} = {{\mathcal S}}\setminus \{0_{{{\mathcal S}}},1_{{{\mathcal S}}}\}$
its proper part. Also if
${{\mathcal S}}^{*} = {{\mathcal S}}\setminus \{0_{{{\mathcal S}}},1_{{{\mathcal S}}}\}$
its proper part. Also if
![]() ${{\mathcal S}}$
has just a unique maximum element
${{\mathcal S}}$
has just a unique maximum element
![]() $1_{{{\mathcal S}}}$
, we set
$1_{{{\mathcal S}}}$
, we set
![]() ${{\mathcal S}}^{\circ } = {{\mathcal S}}\setminus \{1_{{{\mathcal S}}}\}$
. For
${{\mathcal S}}^{\circ } = {{\mathcal S}}\setminus \{1_{{{\mathcal S}}}\}$
. For
![]() $x \in {{\mathcal S}}$
, we write
$x \in {{\mathcal S}}$
, we write
![]() ${{\mathcal S}}_{\leq x}$
for the subposet
${{\mathcal S}}_{\leq x}$
for the subposet
![]() $\{ \,y \in {{\mathcal S}}~|~y \leq x\}$
. Analogously defined are
$\{ \,y \in {{\mathcal S}}~|~y \leq x\}$
. Analogously defined are
![]() ${{\mathcal S}}_{< x}$
,
${{\mathcal S}}_{< x}$
,
![]() ${{\mathcal S}}_{\geq x}$
and
${{\mathcal S}}_{\geq x}$
and
![]() ${{\mathcal S}}_{> x}$
.
${{\mathcal S}}_{> x}$
.
The order complex of a poset
![]() ${{\mathcal S}}$
is the simplicial complex
${{\mathcal S}}$
is the simplicial complex
![]() $\Delta ({{\mathcal S}})$
whose i-simplices are the finite chains
$\Delta ({{\mathcal S}})$
whose i-simplices are the finite chains
![]() $x_0 < \cdots < x_i$
of
$x_0 < \cdots < x_i$
of
![]() $i+1$
distinct elements from
$i+1$
distinct elements from
![]() ${{\mathcal S}}$
. When we speak of topological properties of a poset, we mean the corresponding property of the geometric realization of its order complex. For an element x of
${{\mathcal S}}$
. When we speak of topological properties of a poset, we mean the corresponding property of the geometric realization of its order complex. For an element x of
![]() ${{\mathcal S}}$
, we let
${{\mathcal S}}$
, we let
![]() $h(x)$
be the dimension of the order complex of
$h(x)$
be the dimension of the order complex of
![]() ${{\mathcal S}}_{\leq x}$
and call
${{\mathcal S}}_{\leq x}$
and call
![]() $h(x)$
the height of x in
$h(x)$
the height of x in
![]() ${{\mathcal S}}$
. The height of
${{\mathcal S}}$
. The height of
![]() ${{\mathcal S}}$
is the supremum of the heights of its elements or, equivalently, the dimension of its order complex. All poset constructions we want to unify in this paper yield posets of finite height. Nevertheless, during the construction process, we will sometimes have to go through infinite-height posets.
${{\mathcal S}}$
is the supremum of the heights of its elements or, equivalently, the dimension of its order complex. All poset constructions we want to unify in this paper yield posets of finite height. Nevertheless, during the construction process, we will sometimes have to go through infinite-height posets.
In a poset
![]() ${{\mathcal S}}$
, we say for a subset
${{\mathcal S}}$
, we say for a subset
![]() $\sigma $
that the join of
$\sigma $
that the join of
![]() $\sigma $
exists in
$\sigma $
exists in
![]() ${{\mathcal S}}$
if
${{\mathcal S}}$
if
![]() $\{ y \in {{\mathcal S}}~|~y \geq x $
for all
$\{ y \in {{\mathcal S}}~|~y \geq x $
for all
![]() $x \in \sigma \}$
has a unique minimal element. In this case, we write
$x \in \sigma \}$
has a unique minimal element. In this case, we write
![]() $\bigvee _{x \in \sigma } x$
for the join of
$\bigvee _{x \in \sigma } x$
for the join of
![]() $\sigma $
. Analogously, we say that the meet of
$\sigma $
. Analogously, we say that the meet of
![]() $\sigma $
exists in
$\sigma $
exists in
![]() ${{\mathcal S}}$
if
${{\mathcal S}}$
if
![]() $\{ y \in {{\mathcal S}}~|~y \leq x $
for all
$\{ y \in {{\mathcal S}}~|~y \leq x $
for all
![]() $x \in \sigma \}$
has a unique maximal element, and write
$x \in \sigma \}$
has a unique maximal element, and write
![]() $\bigwedge _{x \in \sigma } x$
for the meet of
$\bigwedge _{x \in \sigma } x$
for the meet of
![]() $\sigma $
. Here, we adopt the usual convention that in a bounded poset, the join over the empty set is
$\sigma $
. Here, we adopt the usual convention that in a bounded poset, the join over the empty set is
![]() $0_{{{\mathcal S}}}$
and the meet over the empty set is
$0_{{{\mathcal S}}}$
and the meet over the empty set is
![]() $1_{{{\mathcal S}}}$
.
$1_{{{\mathcal S}}}$
.
We denote by
![]() $|\sigma |$
the size of a set
$|\sigma |$
the size of a set
![]() $\sigma $
.
$\sigma $
.
Definition 2.1. Let
![]() ${{\mathcal S}}$
be a bounded poset. We say that a nonempty subset
${{\mathcal S}}$
be a bounded poset. We say that a nonempty subset
![]() $\sigma \subseteq {{\mathcal S}} $
is a (full) decomposition of
$\sigma \subseteq {{\mathcal S}} $
is a (full) decomposition of
![]() ${{\mathcal S}}$
if
${{\mathcal S}}$
if
-
(1) for all
 $\tau \subseteq \sigma $
, the join
$\tau \subseteq \sigma $
, the join
 $\bigvee _{x \in \tau } x$
exists in
$\bigvee _{x \in \tau } x$
exists in
 ${{\mathcal S}}$
and
${{\mathcal S}}$
and  $$\begin{align*}h\big(\bigvee_{x\in \tau} x\big) = \sum_{x\in \tau} h(x),\end{align*}$$
$$\begin{align*}h\big(\bigvee_{x\in \tau} x\big) = \sum_{x\in \tau} h(x),\end{align*}$$
-
(2)
 $\big \{\,\bigvee _{x \in \tau } x \,\big |\, \tau \subseteq \sigma \,\big \} \subseteq {{\mathcal S}}$
with suprema and infima taken in
$\big \{\,\bigvee _{x \in \tau } x \,\big |\, \tau \subseteq \sigma \,\big \} \subseteq {{\mathcal S}}$
with suprema and infima taken in
 ${{\mathcal S}}$
is a Boolean lattice on
${{\mathcal S}}$
is a Boolean lattice on
 $|\sigma |$
elements with maximal element
$|\sigma |$
elements with maximal element
 $1_{{\mathcal S}}$
.
$1_{{\mathcal S}}$
.
We say
![]() $\tau \subseteq {{\mathcal S}}$
is a partial decomposition if it is a subset of a decomposition. We denote by
$\tau \subseteq {{\mathcal S}}$
is a partial decomposition if it is a subset of a decomposition. We denote by
![]() ${\mathcal {PD}}({{\mathcal S}})$
the set of all partial decompositions and by
${\mathcal {PD}}({{\mathcal S}})$
the set of all partial decompositions and by
![]() ${\mathcal D}({{\mathcal S}})$
the set of decompositions of
${\mathcal D}({{\mathcal S}})$
the set of decompositions of
![]() ${{\mathcal S}}$
. We order
${{\mathcal S}}$
. We order
![]() ${\mathcal {PD}}({{\mathcal S}})$
and
${\mathcal {PD}}({{\mathcal S}})$
and
![]() ${\mathcal D}({{\mathcal S}})$
by refinement. That is,
${\mathcal D}({{\mathcal S}})$
by refinement. That is,
![]() $\tau \leq \sigma $
if and only if for all
$\tau \leq \sigma $
if and only if for all
![]() $x\in \tau $
, there exists
$x\in \tau $
, there exists
![]() $y\in \sigma $
such that
$y\in \sigma $
such that
![]() $x\leq y$
.
$x\leq y$
.
Note that
![]() $0_{{{\mathcal S}}}$
cannot be part of a decomposition. It also follows from the definition that
$0_{{{\mathcal S}}}$
cannot be part of a decomposition. It also follows from the definition that
![]() ${\mathcal {PD}}({{\mathcal S}})$
is a bounded poset where the empty set
${\mathcal {PD}}({{\mathcal S}})$
is a bounded poset where the empty set
![]() $\emptyset $
is the unique minimal element, and
$\emptyset $
is the unique minimal element, and
![]() $\{1_{{{\mathcal S}}}\}$
is the unique maximal element. The subposet
$\{1_{{{\mathcal S}}}\}$
is the unique maximal element. The subposet
![]() ${\mathcal D}({{\mathcal S}})$
is an upper-order ideal of
${\mathcal D}({{\mathcal S}})$
is an upper-order ideal of
![]() ${\mathcal {PD}}({{\mathcal S}})$
which may not have a unique minimal element. We study the case where
${\mathcal {PD}}({{\mathcal S}})$
which may not have a unique minimal element. We study the case where
![]() ${\mathcal D}({{\mathcal S}})$
has a unique minimal element in Corollary 5.19.
${\mathcal D}({{\mathcal S}})$
has a unique minimal element in Corollary 5.19.
The following simple properties of full and partial decompositions are immediate consequences of the definition.
Lemma 2.2. Let
![]() ${{\mathcal S}}$
be a bounded poset and
${{\mathcal S}}$
be a bounded poset and
![]() $\sigma ,\tau \in {\mathcal D}({{\mathcal S}})$
.
$\sigma ,\tau \in {\mathcal D}({{\mathcal S}})$
.
-
(1) if
 $\tau \subseteq \sigma $
, then
$\tau \subseteq \sigma $
, then
 $\tau = \sigma $
.
$\tau = \sigma $
. -
(2) if
 $\tau \leq \sigma $
and
$\tau \leq \sigma $
and
 $|\tau |=|\sigma |$
, then
$|\tau |=|\sigma |$
, then
 $\tau = \sigma $
.
$\tau = \sigma $
.
Remark 2.3. There are several natural orders on
![]() ${\mathcal {PD}}({{\mathcal S}})$
:
${\mathcal {PD}}({{\mathcal S}})$
:
-
• the order
 $\leq $
we have defined (i.e., order by refinement);
$\leq $
we have defined (i.e., order by refinement); -
• the order
 $\leq '$
where
$\leq '$
where
 $\tau \leq '\sigma $
if
$\tau \leq '\sigma $
if
 $\tau \leq \sigma $
and also there exist decompositions
$\tau \leq \sigma $
and also there exist decompositions
 $\hat {\tau }\leq \hat {\sigma }$
with
$\hat {\tau }\leq \hat {\sigma }$
with
 $\tau \subseteq \hat {\tau }$
and
$\tau \subseteq \hat {\tau }$
and
 $\sigma \subseteq \hat {\sigma }$
;
$\sigma \subseteq \hat {\sigma }$
; -
• the order
 $\subseteq $
induced by set-inclusion.
$\subseteq $
induced by set-inclusion.
The ordering
![]() $\leq '$
coincides with
$\leq '$
coincides with
![]() $\leq $
if
$\leq $
if
![]() $\tau ,\sigma \in {\mathcal D}({{\mathcal S}})$
. Although in general
$\tau ,\sigma \in {\mathcal D}({{\mathcal S}})$
. Although in general
![]() $\leq '$
is more restrictive than
$\leq '$
is more restrictive than
![]() $\leq $
, they will coincide in many important examples discussed later. See Section 6.
$\leq $
, they will coincide in many important examples discussed later. See Section 6.
However, we will not address the poset structure obtained from the ordering
![]() $\subseteq $
. See Remark 6.25 for an example comparing the inclusion and the refinement orderings.
$\subseteq $
. See Remark 6.25 for an example comparing the inclusion and the refinement orderings.
Example 2.4. If
![]() ${{\mathcal S}}$
is the Boolean lattice of all subsets of a set
${{\mathcal S}}$
is the Boolean lattice of all subsets of a set
![]() $\tau $
ordered by refinement, then
$\tau $
ordered by refinement, then
![]() ${\mathcal D}({{\mathcal S}})$
is the partition lattice
${\mathcal D}({{\mathcal S}})$
is the partition lattice
![]() $\Pi (\tau )$
. It is easily checked that for a decomposition
$\Pi (\tau )$
. It is easily checked that for a decomposition
![]() $\sigma \in {\mathcal D}({{\mathcal S}})$
, the upper interval
$\sigma \in {\mathcal D}({{\mathcal S}})$
, the upper interval
![]() ${\mathcal D}({{\mathcal S}})_{\geq \sigma }$
is isomorphic to
${\mathcal D}({{\mathcal S}})_{\geq \sigma }$
is isomorphic to
![]() $\Pi (\sigma )$
. Recall that the Möbius number of
$\Pi (\sigma )$
. Recall that the Möbius number of
![]() $\Pi (\tau )$
is
$\Pi (\tau )$
is
![]() $(-1)^{|\tau |-1}(|\tau |-1)!$
if
$(-1)^{|\tau |-1}(|\tau |-1)!$
if
![]() $|\tau |\geq 2$
.
$|\tau |\geq 2$
.
For instance, let us consider the case
![]() $\tau = \{1,2,3\}$
. The Hasse diagram of the poset of full decompositions (partitions in blue) and partial decompositions (partial partitions in blue or black) of the Boolean lattice on three elements is depicted in Figure 1. Here, we use the usual notation for set partition instead of the formal definition of (partial) decompositions – for example,
$\tau = \{1,2,3\}$
. The Hasse diagram of the poset of full decompositions (partitions in blue) and partial decompositions (partial partitions in blue or black) of the Boolean lattice on three elements is depicted in Figure 1. Here, we use the usual notation for set partition instead of the formal definition of (partial) decompositions – for example,
![]() $1|23$
instead of
$1|23$
instead of
![]() $\{\{1\},\{2,3\}\}$
.
$\{\{1\},\{2,3\}\}$
.
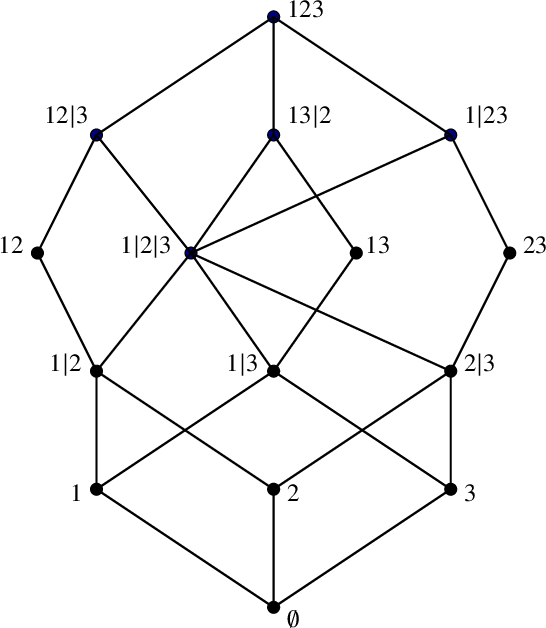
Figure 1 Full and partial set-partitions of
![]() $\{1,2,3\}$
.
$\{1,2,3\}$
.
Indeed, one reason for including the height condition in the definition of a decomposition is that we want to control upper intervals in
![]() ${\mathcal D}({{\mathcal S}})$
in the same way we do it in the partition lattice.
${\mathcal D}({{\mathcal S}})$
in the same way we do it in the partition lattice.
Lemma 2.5. For a bounded poset
![]() ${{\mathcal S}}$
and
${{\mathcal S}}$
and
![]() $\tau \in {\mathcal D}({{\mathcal S}})$
, we have
$\tau \in {\mathcal D}({{\mathcal S}})$
, we have
![]() ${\mathcal D}({{\mathcal S}})_{\geq \tau } \cong \Pi (\tau )$
.
${\mathcal D}({{\mathcal S}})_{\geq \tau } \cong \Pi (\tau )$
.
Proof. By definition, it is clear that for every partition
![]() $\pi $
of
$\pi $
of
![]() $\tau $
, the set
$\tau $
, the set
![]() $\{ \bigvee _{y\in p} y \mathrel {{\: : \: }} p\in \pi \}$
is a decomposition. Now suppose that
$\{ \bigvee _{y\in p} y \mathrel {{\: : \: }} p\in \pi \}$
is a decomposition. Now suppose that
![]() $\tau \leq \sigma $
. For
$\tau \leq \sigma $
. For
![]() $x\in \sigma $
, let
$x\in \sigma $
, let
![]() $x' = \bigvee _{y\in \tau \mathrel {{\: : \: }} y\leq x} y$
. Then
$x' = \bigvee _{y\in \tau \mathrel {{\: : \: }} y\leq x} y$
. Then
![]() $\sigma ' = \{x' \mathrel {{\: : \: }} x\in \sigma \}$
is a decomposition since it is obtained from a suitable partition of
$\sigma ' = \{x' \mathrel {{\: : \: }} x\in \sigma \}$
is a decomposition since it is obtained from a suitable partition of
![]() $\tau $
, with
$\tau $
, with
![]() $|\sigma '| = |\sigma |$
and
$|\sigma '| = |\sigma |$
and
![]() $\sigma '\leq \sigma $
. By Lemma 2.2,
$\sigma '\leq \sigma $
. By Lemma 2.2,
![]() $\sigma ' = \sigma $
. This means that elements of
$\sigma ' = \sigma $
. This means that elements of
![]() $\sigma $
are obtained by joining elements of
$\sigma $
are obtained by joining elements of
![]() $\tau $
. Thus
$\tau $
. Thus
![]() ${\mathcal D}({{\mathcal S}})_{\geq \tau } \cong \Pi (\tau )$
.
${\mathcal D}({{\mathcal S}})_{\geq \tau } \cong \Pi (\tau )$
.
The lower intervals in
![]() ${\mathcal D}({{\mathcal S}})$
and
${\mathcal D}({{\mathcal S}})$
and
![]() ${\mathcal {PD}}({{\mathcal S}})$
are not necessarily direct products of decomposition or partial decomposition posets if we do not require additional ‘relative-extension” properties. We have the following characterization.
${\mathcal {PD}}({{\mathcal S}})$
are not necessarily direct products of decomposition or partial decomposition posets if we do not require additional ‘relative-extension” properties. We have the following characterization.
Lemma 2.6. Let
![]() ${{\mathcal S}}$
be a bounded poset such that for every
${{\mathcal S}}$
be a bounded poset such that for every
![]() $\sigma \in {\mathcal {PD}}({{\mathcal S}})$
, it holds:
$\sigma \in {\mathcal {PD}}({{\mathcal S}})$
, it holds:
-
(E1)
 ${\mathcal {PD}}({{\mathcal S}}_{\leq x}) = {\mathcal {PD}}({{\mathcal S}})_{\leq \{x\}}$
for all
${\mathcal {PD}}({{\mathcal S}}_{\leq x}) = {\mathcal {PD}}({{\mathcal S}})_{\leq \{x\}}$
for all
 $x\in \sigma $
, and
$x\in \sigma $
, and -
(E2) if
 $\tau _x\in {\mathcal {PD}}({{\mathcal S}}_{\leq x})$
for
$\tau _x\in {\mathcal {PD}}({{\mathcal S}}_{\leq x})$
for
 $x\in \sigma $
, then
$x\in \sigma $
, then
 $\cup _{x\in \sigma } \tau _x\in {\mathcal {PD}}({{\mathcal S}})_{\leq \sigma }$
.
$\cup _{x\in \sigma } \tau _x\in {\mathcal {PD}}({{\mathcal S}})_{\leq \sigma }$
.
Then for every
![]() $\sigma \in {\mathcal {PD}}({{\mathcal S}})$
, we have
$\sigma \in {\mathcal {PD}}({{\mathcal S}})$
, we have
![]() ${\mathcal {PD}}({{\mathcal S}})_{\leq \sigma } = \prod _{x\in \sigma } {\mathcal {PD}}({{\mathcal S}}_{\leq x})$
. If
${\mathcal {PD}}({{\mathcal S}})_{\leq \sigma } = \prod _{x\in \sigma } {\mathcal {PD}}({{\mathcal S}}_{\leq x})$
. If
![]() $\sigma \in {\mathcal D}({{\mathcal S}})$
, then also
$\sigma \in {\mathcal D}({{\mathcal S}})$
, then also
![]() ${\mathcal D}({{\mathcal S}})_{\leq \sigma } = \prod _{x\in \sigma } {\mathcal D}({{\mathcal S}}_{\leq x})$
.
${\mathcal D}({{\mathcal S}})_{\leq \sigma } = \prod _{x\in \sigma } {\mathcal D}({{\mathcal S}}_{\leq x})$
.
Conversely, if we naturally have
![]() ${\mathcal {PD}}({{\mathcal S}})_{\leq \sigma } = \prod _{x\in \sigma } {\mathcal {PD}}({{\mathcal S}}_{\leq x})$
, then (E1) and (E2) hold.
${\mathcal {PD}}({{\mathcal S}})_{\leq \sigma } = \prod _{x\in \sigma } {\mathcal {PD}}({{\mathcal S}}_{\leq x})$
, then (E1) and (E2) hold.
Proof. Let
![]() $\tau \leq \sigma $
and define
$\tau \leq \sigma $
and define
![]() $\tau _x = \sigma \cap {{\mathcal S}}_{\leq x}$
. Then by (E1),
$\tau _x = \sigma \cap {{\mathcal S}}_{\leq x}$
. Then by (E1),
![]() $\tau _x\in {\mathcal {PD}}({{\mathcal S}}_{\leq x})$
. Therefore, we have a well-defined order-preserving map
$\tau _x\in {\mathcal {PD}}({{\mathcal S}}_{\leq x})$
. Therefore, we have a well-defined order-preserving map
![]() ${\mathcal {PD}}({{\mathcal S}})_{\leq \sigma }\to \prod _{x\in \sigma } {\mathcal {PD}}({{\mathcal S}}_{\leq x})$
given by
${\mathcal {PD}}({{\mathcal S}})_{\leq \sigma }\to \prod _{x\in \sigma } {\mathcal {PD}}({{\mathcal S}}_{\leq x})$
given by
![]() $\tau \mapsto (\tau _x)_{x\in \sigma }$
. This map is clearly an embedding by definition of the ordering. Property (E2) also implies that this is surjective: indeed, if
$\tau \mapsto (\tau _x)_{x\in \sigma }$
. This map is clearly an embedding by definition of the ordering. Property (E2) also implies that this is surjective: indeed, if
![]() $\tau _x\in {\mathcal {PD}}({{\mathcal S}}_{\leq x})$
, then
$\tau _x\in {\mathcal {PD}}({{\mathcal S}}_{\leq x})$
, then
![]() $\tau = \cup _{x\in \sigma }\tau _x \in {\mathcal {PD}}({{\mathcal S}})_{\leq \sigma }$
by (E2), and
$\tau = \cup _{x\in \sigma }\tau _x \in {\mathcal {PD}}({{\mathcal S}})_{\leq \sigma }$
by (E2), and
![]() $\tau \cap {{\mathcal S}}_{\leq x} = \tau _x$
.
$\tau \cap {{\mathcal S}}_{\leq x} = \tau _x$
.
The structure of the lower interval in the decomposition poset follows immediately from the result in the partial decompositions. We leave the proof of the reverse implication for the reader.
If we drop the requirement on the heights in Definition 2.1, we may encounter situations where we have two distinct comparable decompositions of the same size. In particular, the conclusions of Lemma 2.5 may fail. This leads us to the definition of weak decompositions.
Definition 2.7. Let
![]() ${{\mathcal S}}$
be a bounded poset (not necessarily of finite height), and let
${{\mathcal S}}$
be a bounded poset (not necessarily of finite height), and let
![]() $\sigma \subseteq {{\mathcal S}}$
. We say that
$\sigma \subseteq {{\mathcal S}}$
. We say that
![]() $\sigma $
is a weak decomposition if for all
$\sigma $
is a weak decomposition if for all
![]() $\tau \subseteq \sigma $
,
$\tau \subseteq \sigma $
,
![]() $\bigvee _{x\in \tau } x$
exists and the subposet
$\bigvee _{x\in \tau } x$
exists and the subposet
![]() $\{ \bigvee _{x\in \tau } x \mathrel {{\: : \: }} \tau \subseteq \sigma \}$
, with suprema and infima taken in
$\{ \bigvee _{x\in \tau } x \mathrel {{\: : \: }} \tau \subseteq \sigma \}$
, with suprema and infima taken in
![]() ${{\mathcal S}}$
, is a Boolean lattice on
${{\mathcal S}}$
, is a Boolean lattice on
![]() $|\sigma |$
elements with maximal element
$|\sigma |$
elements with maximal element
![]() $1_{{\mathcal S}}$
. We analogously define the posets of weak decompositions
$1_{{\mathcal S}}$
. We analogously define the posets of weak decompositions
![]() ${\mathcal D}_w({{\mathcal S}})$
and weak partial decompositions
${\mathcal D}_w({{\mathcal S}})$
and weak partial decompositions
![]() ${\mathcal {PD}}_w({{\mathcal S}})$
, both ordered by refinement.
${\mathcal {PD}}_w({{\mathcal S}})$
, both ordered by refinement.
Clearly, decompositions are weak decompositions, so
![]() ${\mathcal D}({{\mathcal S}})\subseteq {\mathcal D}_w({{\mathcal S}})$
and
${\mathcal D}({{\mathcal S}})\subseteq {\mathcal D}_w({{\mathcal S}})$
and
![]() ${\mathcal {PD}}({{\mathcal S}})\subseteq {\mathcal {PD}}_w({{\mathcal S}})$
are subposets.
${\mathcal {PD}}({{\mathcal S}})\subseteq {\mathcal {PD}}_w({{\mathcal S}})$
are subposets.
Note that in Example 2.4, weak decompositions are decompositions. So in that case,
![]() ${\mathcal {PD}}({\mathcal {S}}) = {\mathcal {PD}}_w({\mathcal {S}})$
. However, the following example shows that weak decompositions are not always decompositions and that upper-intervals in
${\mathcal {PD}}({\mathcal {S}}) = {\mathcal {PD}}_w({\mathcal {S}})$
. However, the following example shows that weak decompositions are not always decompositions and that upper-intervals in
![]() ${\mathcal D}_w({{\mathcal S}})$
may not be partition lattices.
${\mathcal D}_w({{\mathcal S}})$
may not be partition lattices.
Example 2.8. Let
![]() ${{\mathcal S}}$
be a bounded poset. Then
${{\mathcal S}}$
be a bounded poset. Then
![]() $d\in {\mathcal D}_w({{\mathcal S}})$
if and only if
$d\in {\mathcal D}_w({{\mathcal S}})$
if and only if
-
• either
 $d = \{x,y\}$
, with x and y belonging to different connected components of
$d = \{x,y\}$
, with x and y belonging to different connected components of
 ${{\mathcal S}}^{*}$
, or
${{\mathcal S}}^{*}$
, or -
• else
 $d\in {\mathcal D}_w(C \cup \{0_{{{\mathcal S}}},1_{{{\mathcal S}}}\})$
, where C is a connected component of
$d\in {\mathcal D}_w(C \cup \{0_{{{\mathcal S}}},1_{{{\mathcal S}}}\})$
, where C is a connected component of
 ${{\mathcal S}}^{*}$
.
${{\mathcal S}}^{*}$
.
Indeed, if
![]() $d\in {\mathcal D}_w({{\mathcal S}})$
contains elements
$d\in {\mathcal D}_w({{\mathcal S}})$
contains elements
![]() $x,y$
in different connected components, then
$x,y$
in different connected components, then
![]() $x\vee y = 1$
. Thus, for
$x\vee y = 1$
. Thus, for
![]() $z\in d$
, we have
$z\in d$
, we have
![]() $z \wedge (x\vee y) = z$
, which implies that
$z \wedge (x\vee y) = z$
, which implies that
![]() $z = x$
or y. Note also that if
$z = x$
or y. Note also that if
![]() $C_1,C_2$
are two different connected components of
$C_1,C_2$
are two different connected components of
![]() ${{\mathcal S}}^{*}$
and
${{\mathcal S}}^{*}$
and
![]() $x,y,z\in {{\mathcal S}}^{*}$
are elements such that
$x,y,z\in {{\mathcal S}}^{*}$
are elements such that
![]() $x \leq y \in C_1$
and
$x \leq y \in C_1$
and
![]() $z\in C_2$
, then
$z\in C_2$
, then
![]() $\{x,z\}\leq \{y,z\}$
and both are weak decompositions of
$\{x,z\}\leq \{y,z\}$
and both are weak decompositions of
![]() ${{\mathcal S}}$
. In particular,
${{\mathcal S}}$
. In particular,
![]() ${\mathcal D}_w({{\mathcal S}})_{\geq \{x,z\}} = {{\mathcal S}}_{\geq x} \times {{\mathcal S}}_{\geq z}$
, so the upper interval is not necessarily a partition lattice.
${\mathcal D}_w({{\mathcal S}})_{\geq \{x,z\}} = {{\mathcal S}}_{\geq x} \times {{\mathcal S}}_{\geq z}$
, so the upper interval is not necessarily a partition lattice.
Indeed, suppose that
![]() ${{\mathcal S}} = \{0,a,b,c,d,1\}$
with minimum
${{\mathcal S}} = \{0,a,b,c,d,1\}$
with minimum
![]() $0$
, maximum
$0$
, maximum
![]() $1$
,
$1$
,
![]() $a<c$
and
$a<c$
and
![]() $b<d$
. We have
$b<d$
. We have
![]() ${\mathcal D}_w({{\mathcal S}}) = \{ \{a,b\}, \{b,c\}, \{a,d\}, \{c,d\}, \{1\} \}$
, and the upper-interval
${\mathcal D}_w({{\mathcal S}}) = \{ \{a,b\}, \{b,c\}, \{a,d\}, \{c,d\}, \{1\} \}$
, and the upper-interval
![]() ${\mathcal D}_w({{\mathcal S}})_{\geq \{a,b\}}$
is not a partition lattice. See Figure 2 for the Hasse diagrams of
${\mathcal D}_w({{\mathcal S}})_{\geq \{a,b\}}$
is not a partition lattice. See Figure 2 for the Hasse diagrams of
![]() ${{\mathcal S}}$
,
${{\mathcal S}}$
,
![]() ${\mathcal {PD}}_w({{\mathcal S}})$
and
${\mathcal {PD}}_w({{\mathcal S}})$
and
![]() ${\mathcal {PD}}(S)$
, and the corresponding decomposition posets which are depicted in blue. Note that
${\mathcal {PD}}(S)$
, and the corresponding decomposition posets which are depicted in blue. Note that
![]() ${{\mathcal S}}$
is a lattice but
${{\mathcal S}}$
is a lattice but
![]() ${\mathcal {PD}}({{\mathcal S}})$
is not.
${\mathcal {PD}}({{\mathcal S}})$
is not.
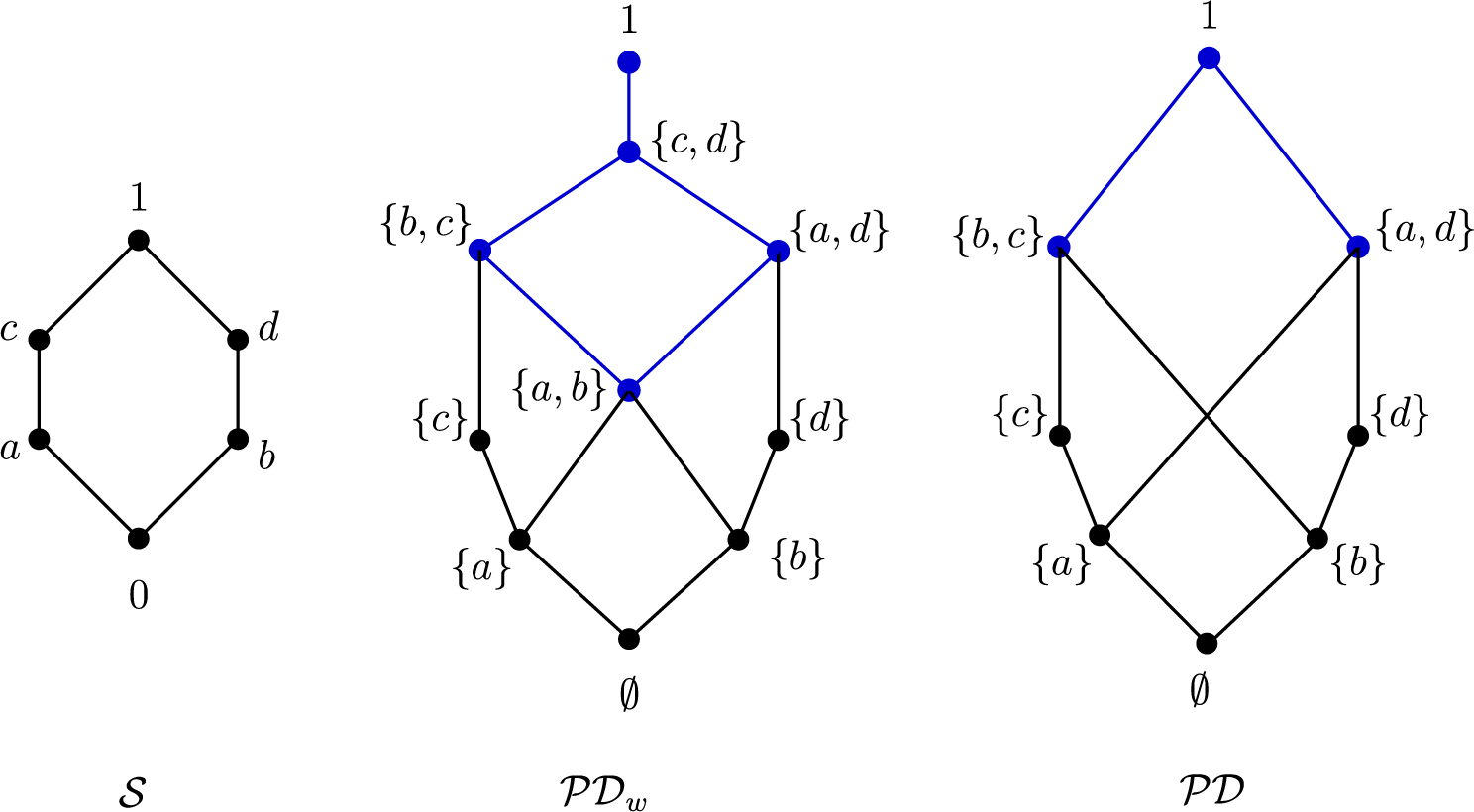
Figure 2 From left to right, Hasse diagrams of posets
![]() ${{\mathcal S}}$
,
${{\mathcal S}}$
,
![]() ${\mathcal {PD}}_w({{\mathcal S}})$
and
${\mathcal {PD}}_w({{\mathcal S}})$
and
![]() ${\mathcal {PD}}({{\mathcal S}})$
, respectively. The corresponding decomposition posets are displayed in blue.
${\mathcal {PD}}({{\mathcal S}})$
, respectively. The corresponding decomposition posets are displayed in blue.
This example also shows that
![]() $({\mathcal {PD}}({{\mathcal S}}),\leq )\neq ({\mathcal {PD}}({{\mathcal S}}),\leq ')$
, where
$({\mathcal {PD}}({{\mathcal S}}),\leq )\neq ({\mathcal {PD}}({{\mathcal S}}),\leq ')$
, where
![]() $\leq '$
is the ordering defined in Remark 2.3. The latter poset is displayed in Figure 3.
$\leq '$
is the ordering defined in Remark 2.3. The latter poset is displayed in Figure 3.
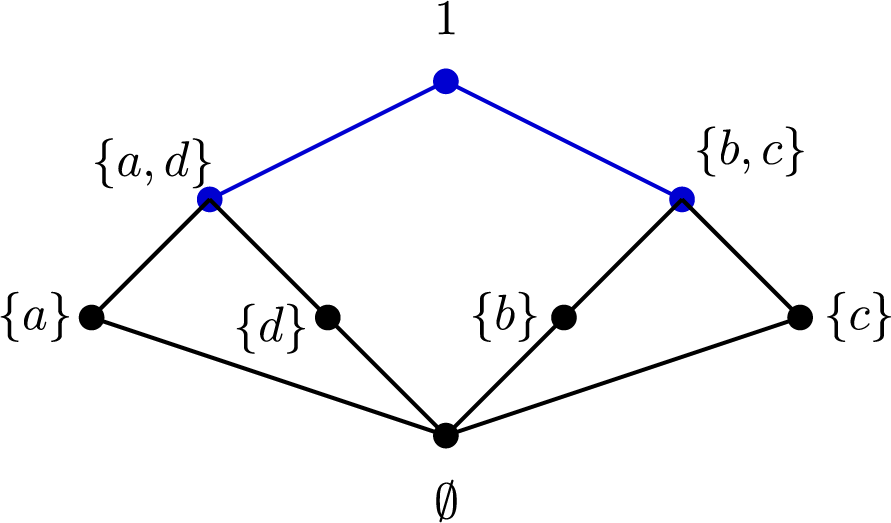
Figure 3 Poset
![]() $({\mathcal {PD}}({{\mathcal S}}),\leq ')$
.
$({\mathcal {PD}}({{\mathcal S}}),\leq ')$
.
Let us analyze now some examples in subgroup posets.
Example 2.9. Let
![]() $G = S_3$
be the symmetric group on
$G = S_3$
be the symmetric group on
![]() $3$
letters. Then the poset of subgroups of G, denoted by
$3$
letters. Then the poset of subgroups of G, denoted by
![]() ${{\mathcal S}}(G)$
, consists of a unique minimal element (the trivial subgroup, denoted by
${{\mathcal S}}(G)$
, consists of a unique minimal element (the trivial subgroup, denoted by
![]() $1$
in this example), a unique maximal element (the whole group G), a subgroup of order
$1$
in this example), a unique maximal element (the whole group G), a subgroup of order
![]() $3$
generated by a
$3$
generated by a
![]() $3$
-cycle, and three subgroups of order
$3$
-cycle, and three subgroups of order
![]() $2$
(one for each transposition). Then
$2$
(one for each transposition). Then
![]() ${{\mathcal S}}(G)^{*}$
is a discrete poset with
${{\mathcal S}}(G)^{*}$
is a discrete poset with
![]() $4$
points. Hence, a decomposition of
$4$
points. Hence, a decomposition of
![]() ${{\mathcal S}}(G)$
different from
${{\mathcal S}}(G)$
different from
![]() $\{G\}$
is a set of two nontrivial proper subgroups of G.
$\{G\}$
is a set of two nontrivial proper subgroups of G.
Example 2.10. Let G be a cyclic group of order m. If
![]() $m = p^n$
is a prime power, then
$m = p^n$
is a prime power, then
![]() ${{\mathcal S}}(G)$
, the lattice of subgroups of G, has height n, and
${{\mathcal S}}(G)$
, the lattice of subgroups of G, has height n, and
![]() ${\mathcal {PD}}({{\mathcal S}}(G)) = {\mathcal D}({{\mathcal S}}(G)) = \{ \{G\} \}$
.
${\mathcal {PD}}({{\mathcal S}}(G)) = {\mathcal D}({{\mathcal S}}(G)) = \{ \{G\} \}$
.
Suppose
![]() $G = C_{p_1^{n_1}}\times \cdots \times C_{p_r^{n_r}}$
for different primes
$G = C_{p_1^{n_1}}\times \cdots \times C_{p_r^{n_r}}$
for different primes
![]() $p_j$
. Let
$p_j$
. Let
![]() $G_j = C_{p_j^{n_j}}$
. Then the height of a subgroup of G equals the number of primes (counted with multiplicity) of its order. In particular,
$G_j = C_{p_j^{n_j}}$
. Then the height of a subgroup of G equals the number of primes (counted with multiplicity) of its order. In particular,
![]() $h({{\mathcal S}}(G)) = \sum _j n_j$
. Therefore, the only possible decompositions of G are those obtained by coarsening the decomposition
$h({{\mathcal S}}(G)) = \sum _j n_j$
. Therefore, the only possible decompositions of G are those obtained by coarsening the decomposition
![]() $\{G_1,\ldots ,G_r\}$
. Hence,
$\{G_1,\ldots ,G_r\}$
. Hence,
![]() ${\mathcal D}({{\mathcal S}}(G))$
is the partition lattice on the set
${\mathcal D}({{\mathcal S}}(G))$
is the partition lattice on the set
![]() $\{G_1,\ldots ,G_r\}$
.
$\{G_1,\ldots ,G_r\}$
.
2.1 Monoidal categories and restricted decompositions
The constructions above will not cover all the structures we would like to study. For example, consider the case of a nontrivial finitely generated free Abelian group A. Its poset of subgroups is a lattice of infinite height. Therefore, we cannot talk about decompositions given the finite-dimensional requirement in Definition 2.1. Nevertheless, it is implicit here that decompositions should be sets of subgroups
![]() $A_1,\ldots , A_r$
which span a Boolean lattice inside the poset of subgroups with join
$A_1,\ldots , A_r$
which span a Boolean lattice inside the poset of subgroups with join
![]() $A_1\oplus \cdots \oplus A_r = \left \langle A_1,\ldots ,A_r\right \rangle = A$
. Thus, if we instead consider the subposet of complemented subgroups of A (or summands), this is a bounded poset of finite height. However, there is still a problem in this subposet: even if
$A_1\oplus \cdots \oplus A_r = \left \langle A_1,\ldots ,A_r\right \rangle = A$
. Thus, if we instead consider the subposet of complemented subgroups of A (or summands), this is a bounded poset of finite height. However, there is still a problem in this subposet: even if
![]() $\{A_1,A_2\}$
is a (weak) decomposition in the poset sense, it is not clear that
$\{A_1,A_2\}$
is a (weak) decomposition in the poset sense, it is not clear that
![]() $A_1\vee A_2$
coincides with the direct sum
$A_1\vee A_2$
coincides with the direct sum
![]() $A_1\oplus A_2$
. For example, if
$A_1\oplus A_2$
. For example, if
![]() $A = {\mathbb {Z}}^2$
, then
$A = {\mathbb {Z}}^2$
, then
![]() $A_1=\left \langle (1,2)\right \rangle $
and
$A_1=\left \langle (1,2)\right \rangle $
and
![]() $A_2=\left \langle (1,0)\right \rangle $
are summands of A such that
$A_2=\left \langle (1,0)\right \rangle $
are summands of A such that
![]() $A_1\wedge A_2 = 0$
and
$A_1\wedge A_2 = 0$
and
![]() $A_1\vee A_2 = A$
in the poset of summands of A, but
$A_1\vee A_2 = A$
in the poset of summands of A, but
![]() $A_1+A_2 = A_1\oplus A_2 < A$
.
$A_1+A_2 = A_1\oplus A_2 < A$
.
A similar situation arises if we consider instead a free group of rank
![]() $\geq 2$
. By a decomposition here, we want not only the Boolean lattice condition but also ‘free’ spans. That is, if F is a free group of rank
$\geq 2$
. By a decomposition here, we want not only the Boolean lattice condition but also ‘free’ spans. That is, if F is a free group of rank
![]() $\geq 2$
and
$\geq 2$
and
![]() $H,K$
are two subgroups, then
$H,K$
are two subgroups, then
![]() $H,K$
is a weak decomposition if
$H,K$
is a weak decomposition if
![]() $H\cap K = 1$
and
$H\cap K = 1$
and
![]() $H\vee K = \left \langle H,K\right \rangle =F$
. But the span
$H\vee K = \left \langle H,K\right \rangle =F$
. But the span
![]() $\left \langle H,K\right \rangle $
forgets the relation between the elements of H and K, and we may actually want
$\left \langle H,K\right \rangle $
forgets the relation between the elements of H and K, and we may actually want
![]() $\left \langle H,K\right \rangle $
to be equal to the free product of H and K. An adaptation of the Abelian-case example with
$\left \langle H,K\right \rangle $
to be equal to the free product of H and K. An adaptation of the Abelian-case example with
![]() ${\mathbb {Z}}^2$
shows that there are free factors
${\mathbb {Z}}^2$
shows that there are free factors
![]() $H,K$
of the free group
$H,K$
of the free group
![]() $F_2$
of rank
$F_2$
of rank
![]() $2$
such that
$2$
such that
![]() $H\cap K = 1$
but
$H\cap K = 1$
but
![]() $H\vee K = \left \langle H,K\right \rangle = F$
is not the free product of H and K.
$H\vee K = \left \langle H,K\right \rangle = F$
is not the free product of H and K.
To cover these and other cases, we extend our purely combinatorial setting by using concepts from category theory. We start with some notation.
For a category
![]() ${\mathcal C}$
and an object
${\mathcal C}$
and an object
![]() $X\in {\mathcal C}$
, write
$X\in {\mathcal C}$
, write
![]() $\operatorname {\mathrm {Hom}}_{\mathcal C}(Y,X)$
for the homomorphisms from an object Y to X, and
$\operatorname {\mathrm {Hom}}_{\mathcal C}(Y,X)$
for the homomorphisms from an object Y to X, and
![]() $\operatorname {\mathrm {Aut}}_{\mathcal C}(X)$
for the isomorphisms of X. Let
$\operatorname {\mathrm {Aut}}_{\mathcal C}(X)$
for the isomorphisms of X. Let
![]() ${\mathcal C} \downarrow X$
be the comma category with objects
${\mathcal C} \downarrow X$
be the comma category with objects
![]() $(Y,f)$
, where
$(Y,f)$
, where
![]() $Y \in {\mathcal C}$
and
$Y \in {\mathcal C}$
and
![]() $f \in \operatorname {\mathrm {Hom}}_{{\mathcal C}}(Y,X)$
, and morphisms between
$f \in \operatorname {\mathrm {Hom}}_{{\mathcal C}}(Y,X)$
, and morphisms between
![]() $(Y,f)$
and
$(Y,f)$
and
![]() $(Z,g)$
being
$(Z,g)$
being
![]() $h \in \operatorname {\mathrm {Hom}}_{{\mathcal C}}(Y,Z)$
with
$h \in \operatorname {\mathrm {Hom}}_{{\mathcal C}}(Y,Z)$
with
![]() $f = gh$
. We consider the subcategory
$f = gh$
. We consider the subcategory ![]() with objects
with objects
![]() $(Y,i)$
such that i is a monomorphism, and morphisms inherited from
$(Y,i)$
such that i is a monomorphism, and morphisms inherited from
![]() ${\mathcal C} \downarrow X$
. Note that a morphism
${\mathcal C} \downarrow X$
. Note that a morphism
![]() $h : (Y,i) \rightarrow (Z,j)$
in
$h : (Y,i) \rightarrow (Z,j)$
in ![]() comes indeed from a monomorphism
comes indeed from a monomorphism
![]() $h:Y\to Z$
.
$h:Y\to Z$
.
A subobject of X is an isomorphism class of objects in ![]() , where
, where
![]() $(Y,i)$
and
$(Y,i)$
and
![]() $(Z,j)$
are isomorphic if and only if there exists an isomorphism
$(Z,j)$
are isomorphic if and only if there exists an isomorphism
![]() $\phi :Y\to Z$
such that
$\phi :Y\to Z$
such that
![]() $i = j\phi $
. We write
$i = j\phi $
. We write
![]() $[(Y,i)]$
for the subobject represented by
$[(Y,i)]$
for the subobject represented by
![]() $(Y,i)$
. Let
$(Y,i)$
. Let
![]() ${\mathcal {S}}(X)$
denote the collection of subobjects of X, which is a poset-category (that is, there is at most one arrow between any two objects, and this defines an anti-symmetric relation). We gather some properties in the following lemma.
${\mathcal {S}}(X)$
denote the collection of subobjects of X, which is a poset-category (that is, there is at most one arrow between any two objects, and this defines an anti-symmetric relation). We gather some properties in the following lemma.
Lemma 2.11. Let X be an object of a category
![]() ${\mathcal C}$
. The following hold:
${\mathcal C}$
. The following hold:
-
(1)
 is a pre-order with
is a pre-order with
 $x\lesssim y$
if there is an arrow from x to y. Namely, there is at most one arrow between any two objects.
$x\lesssim y$
if there is an arrow from x to y. Namely, there is at most one arrow between any two objects. -
(2)
 ${\mathcal {S}}(X)$
is a skeleton of the category
${\mathcal {S}}(X)$
is a skeleton of the category  .
. -
(3) If
 ${\mathcal C}$
has an initial object
${\mathcal C}$
has an initial object
 $0$
, then
$0$
, then
 $0\in {\mathcal {S}}(X)$
is the unique minimum of this poset.
$0\in {\mathcal {S}}(X)$
is the unique minimum of this poset. -
(4) The poset
 ${\mathcal {S}}(X)$
has a unique maximum given by the class of
${\mathcal {S}}(X)$
has a unique maximum given by the class of
 $(X,i)$
, where i is any isomorphism of X. We denote this class just by X.
$(X,i)$
, where i is any isomorphism of X. We denote this class just by X. -
(5) If
 $z\in {\mathcal {S}}(X)$
, then there is a poset isomorphism
$z\in {\mathcal {S}}(X)$
, then there is a poset isomorphism
 ${\mathcal {S}}(X)_{\leq z} \cong {\mathcal {S}}(Z)$
for any representative
${\mathcal {S}}(X)_{\leq z} \cong {\mathcal {S}}(Z)$
for any representative
 $(Z,i)\in z$
.
$(Z,i)\in z$
.
Proof. These are straightforward facts from the definitions.
Note that item 5 also implies that if
![]() $i,i':Z\to X$
are two monomorphisms and
$i,i':Z\to X$
are two monomorphisms and
![]() $z:=[(Z,i)]$
,
$z:=[(Z,i)]$
,
![]() $z':=[(Z,i')]$
, then
$z':=[(Z,i')]$
, then
![]() ${\mathcal {S}}(X)_{\leq z}\cong {\mathcal {S}}(Z) \cong {\mathcal {S}}(X)_{\leq z'}$
. In particular, if
${\mathcal {S}}(X)_{\leq z}\cong {\mathcal {S}}(Z) \cong {\mathcal {S}}(X)_{\leq z'}$
. In particular, if
![]() $i:X\to X$
is a monomorphism, then
$i:X\to X$
is a monomorphism, then
![]() ${\mathcal {S}}(X)_{\leq [(X,i)]} \cong {\mathcal {S}}(X)$
.
${\mathcal {S}}(X)_{\leq [(X,i)]} \cong {\mathcal {S}}(X)$
.
Warning.
![]() ${\mathcal {S}}(X)$
is always a bounded poset but, in general, of infinite height.
${\mathcal {S}}(X)$
is always a bounded poset but, in general, of infinite height.
We want to restrict the collection of decompositions to those that have a particular shape. To specify the ‘shape’ of the decompositions, we define beforehand a ‘product of objects’, and then we select the decompositions whose join equals the product. This naturally leads us to the definition of a monoidal product in our category. However, we will require this product to have some particular properties closer to a coproduct.
Definition 2.12. An initial symmetric monoidal category, or ISM-category for short, is an initial monoidal category
![]() $({\mathcal C},\sqcup )$
, where
$({\mathcal C},\sqcup )$
, where
![]() $\sqcup $
is a naturally associative and commutative product, and the initial object of the category is also a neutral element for
$\sqcup $
is a naturally associative and commutative product, and the initial object of the category is also a neutral element for
![]() $\sqcup $
.
$\sqcup $
.
The notation ‘
![]() $\sqcup $
’ suggests a similarity with the coproduct. Indeed, sometimes
$\sqcup $
’ suggests a similarity with the coproduct. Indeed, sometimes
![]() $\sqcup $
will be the coproduct of the category. However, in many cases, the category
$\sqcup $
will be the coproduct of the category. However, in many cases, the category
![]() ${\mathcal C}$
may not have all coproducts, and so
${\mathcal C}$
may not have all coproducts, and so
![]() $\sqcup $
will serve as a remedy.
$\sqcup $
will serve as a remedy.
Remark 2.13. Note that, for any two objects X, Y, we have a canonical map
![]() $\iota _X:X\to X\sqcup Y$
arising from
$\iota _X:X\to X\sqcup Y$
arising from
where
![]() $i_0:0\to Y$
.
$i_0:0\to Y$
.
To define decompositions in
![]() ${\mathcal {S}}(X)$
, we need finite height, and
${\mathcal {S}}(X)$
, we need finite height, and
![]() ${\mathcal {S}}(X)$
may have infinite dimension in general (for example, when X is a nontrivial free group in the category of groups, see Example 2.18). For that reason, we will work with the subposet
${\mathcal {S}}(X)$
may have infinite dimension in general (for example, when X is a nontrivial free group in the category of groups, see Example 2.18). For that reason, we will work with the subposet
![]() ${\mathcal {S}}(X,\sqcup )$
of
${\mathcal {S}}(X,\sqcup )$
of
![]() $\sqcup $
-complemented subobjects defined below, which we expect to have finite height and whose elements are eligible to be part of decompositions. To that end, we introduce first the notion of
$\sqcup $
-complemented subobjects defined below, which we expect to have finite height and whose elements are eligible to be part of decompositions. To that end, we introduce first the notion of
![]() $\sqcup $
-compatible joins of elements.
$\sqcup $
-compatible joins of elements.
Definition 2.14. Let
![]() $({\mathcal C},\sqcup )$
be an ISM-category,
$({\mathcal C},\sqcup )$
be an ISM-category,
![]() $X\in {\mathcal C}$
and
$X\in {\mathcal C}$
and
![]() $\sigma = \{x_1,\ldots , x_r\}\subseteq {\mathcal T}\subseteq {\mathcal {S}}(X)$
. We say that
$\sigma = \{x_1,\ldots , x_r\}\subseteq {\mathcal T}\subseteq {\mathcal {S}}(X)$
. We say that
![]() $\sigma $
is
$\sigma $
is
![]() $\sqcup $
-compatible in
$\sqcup $
-compatible in
![]() ${\mathcal T}$
if there are suitable representatives
${\mathcal T}$
if there are suitable representatives
![]() $x_i = [(X_i, j_i)]$
such that the following conditions hold:
$x_i = [(X_i, j_i)]$
such that the following conditions hold:
-
(1) For all
 $\emptyset \neq I \subseteq I' \subseteq [r]$
, we have natural monomorphismsFootnote 1
$\emptyset \neq I \subseteq I' \subseteq [r]$
, we have natural monomorphismsFootnote 1  $$ \begin{align*}j_{I,I'} : \bigsqcup_{i\in I} X_i \rightarrow \bigsqcup_{i\in I'} X_i \qquad \text{ and } \qquad j_{I}:\bigsqcup_{i\in I} X_i \rightarrow X;\end{align*} $$
$$ \begin{align*}j_{I,I'} : \bigsqcup_{i\in I} X_i \rightarrow \bigsqcup_{i\in I'} X_i \qquad \text{ and } \qquad j_{I}:\bigsqcup_{i\in I} X_i \rightarrow X;\end{align*} $$
-
(2) for any
 $\emptyset \neq I\subseteq [r]$
, there exists the join
$\emptyset \neq I\subseteq [r]$
, there exists the join
 $\bigvee _{i\in I} x_i$
in
$\bigvee _{i\in I} x_i$
in
 ${\mathcal T}$
and
${\mathcal T}$
and  $$ \begin{align*}\Big[\,\big(\, \bigsqcup_{i \in I} X_i,j_I\,\big)\, \Big] = \bigvee_{i\in I} x_i;\end{align*} $$
$$ \begin{align*}\Big[\,\big(\, \bigsqcup_{i \in I} X_i,j_I\,\big)\, \Big] = \bigvee_{i\in I} x_i;\end{align*} $$
-
(3) the following diagram commutes for all
 $\emptyset \neq I \subseteq I' \subseteq [r]$
and
$\emptyset \neq I \subseteq I' \subseteq [r]$
and
 $k\in I$
:
$k\in I$
: 
We now define posets of subobjects compatible with the monoidal product
![]() $\sqcup $
:
$\sqcup $
:
Definition 2.15. Let
![]() $({\mathcal C},\sqcup )$
be an ISM-category and let
$({\mathcal C},\sqcup )$
be an ISM-category and let
![]() $X\in {\mathcal C}$
be an object.
$X\in {\mathcal C}$
be an object.
-
(1) An element
 $x\in {\mathcal {S}}(X)$
is
$x\in {\mathcal {S}}(X)$
is
 $\sqcup $
-complemented if there exists a poset-complement
$\sqcup $
-complemented if there exists a poset-complement
 $y\in {\mathcal {S}}(X)$
of x (that is,
$y\in {\mathcal {S}}(X)$
of x (that is,
 $x\wedge y = 0$
and
$x\wedge y = 0$
and
 $x\vee y = 1$
) such that the set
$x\vee y = 1$
) such that the set
 $\{x,y\}\subseteq {\mathcal {S}}(X)$
is
$\{x,y\}\subseteq {\mathcal {S}}(X)$
is
 $\sqcup $
-compatible in
$\sqcup $
-compatible in
 ${\mathcal {S}}(X)$
.
${\mathcal {S}}(X)$
. -
(2) We define
 ${\mathcal {S}}(X,\sqcup )$
to be the subposet of
${\mathcal {S}}(X,\sqcup )$
to be the subposet of
 $\sqcup $
-complemented elements of
$\sqcup $
-complemented elements of
 ${\mathcal {S}}(X)$
.
${\mathcal {S}}(X)$
. -
(3) If
 ${\mathcal {S}}(X,\sqcup )$
has finite height, a
${\mathcal {S}}(X,\sqcup )$
has finite height, a
 $\sqcup $
-decomposition of X is a decomposition
$\sqcup $
-decomposition of X is a decomposition
 $\sigma \in {\mathcal D}({\mathcal {S}}(X,\sqcup ))$
which is
$\sigma \in {\mathcal D}({\mathcal {S}}(X,\sqcup ))$
which is
 $\sqcup $
-compatible in
$\sqcup $
-compatible in
 ${\mathcal {S}}(X,\sqcup )$
.
${\mathcal {S}}(X,\sqcup )$
. -
(4) Denote by
 ${\mathcal D}(X,\sqcup )$
the subposet of
${\mathcal D}(X,\sqcup )$
the subposet of
 ${\mathcal D}({\mathcal {S}}(X,\sqcup ))$
consisting of
${\mathcal D}({\mathcal {S}}(X,\sqcup ))$
consisting of
 $\sqcup $
-decompositions, and by
$\sqcup $
-decompositions, and by
 ${\mathcal {PD}}(X,\sqcup )$
the subposet of
${\mathcal {PD}}(X,\sqcup )$
the subposet of
 ${\mathcal {PD}}({\mathcal {S}}(X,\sqcup ))$
consisting of the subsets of
${\mathcal {PD}}({\mathcal {S}}(X,\sqcup ))$
consisting of the subsets of
 $\sqcup $
-decompositions.
$\sqcup $
-decompositions.
Similarly, we define
![]() $\sqcup $
-weak (partial) decompositions but without the need to require finite height for
$\sqcup $
-weak (partial) decompositions but without the need to require finite height for
![]() ${\mathcal {S}}(X,\sqcup )$
.
${\mathcal {S}}(X,\sqcup )$
.
Note that by definition,
![]() ${\mathcal {S}}(X,\sqcup )$
is bounded with maximum X and minimum
${\mathcal {S}}(X,\sqcup )$
is bounded with maximum X and minimum
![]() $0$
(the initial object), and all its elements are
$0$
(the initial object), and all its elements are
![]() $\sqcup $
-complemented, and in particular complemented. Also,
$\sqcup $
-complemented, and in particular complemented. Also,
![]() ${\mathcal {PD}}(X,\sqcup )$
is bounded with maximum
${\mathcal {PD}}(X,\sqcup )$
is bounded with maximum
![]() $\{X\}$
and minimum
$\{X\}$
and minimum
![]() $\emptyset $
. Moreover,
$\emptyset $
. Moreover,
![]() ${\mathcal D}(X,\sqcup )$
is a nonempty order ideal of
${\mathcal D}(X,\sqcup )$
is a nonempty order ideal of
![]() ${\mathcal {PD}}(X,\sqcup )$
and, in particular,
${\mathcal {PD}}(X,\sqcup )$
and, in particular,
![]() $\{X\}$
is the unique maximal element of
$\{X\}$
is the unique maximal element of
![]() ${\mathcal D}(X,\sqcup )$
.
${\mathcal D}(X,\sqcup )$
.
Example 2.16. Let
![]() ${\mathcal C}$
be the category of groups, so
${\mathcal C}$
be the category of groups, so
![]() ${\mathcal {S}}(X)$
is the subgroup lattice for a group X. We choose ‘
${\mathcal {S}}(X)$
is the subgroup lattice for a group X. We choose ‘
![]() $\sqcup $
’ to be the direct product of groups. In order to get a finite-dimensional poset
$\sqcup $
’ to be the direct product of groups. In order to get a finite-dimensional poset
![]() ${\mathcal {S}}(X,\sqcup )$
, we work with a finite group X. Hence,
${\mathcal {S}}(X,\sqcup )$
, we work with a finite group X. Hence,
![]() ${\mathcal {S}}(X,\sqcup )$
is the subposet of subgroups of X which are direct-product factors of X. That is,
${\mathcal {S}}(X,\sqcup )$
is the subposet of subgroups of X which are direct-product factors of X. That is,
![]() $H\leq X$
is
$H\leq X$
is
![]() $\sqcup $
-complemented if and only if there exists a subgroup
$\sqcup $
-complemented if and only if there exists a subgroup
![]() $K\leq X$
such that
$K\leq X$
such that
![]() $H\cap K=1$
,
$H\cap K=1$
,
![]() $[H,K]=1$
and
$[H,K]=1$
and
![]() $H\times K \cong HK = X$
. Recall that, by the Krull-Schmidt theorem for finite groups, there exists a unique direct product decomposition of a finite group into indecomposable factors, up to permutation and isomorphism of the factors. In particular, the minimal elements of
$H\times K \cong HK = X$
. Recall that, by the Krull-Schmidt theorem for finite groups, there exists a unique direct product decomposition of a finite group into indecomposable factors, up to permutation and isomorphism of the factors. In particular, the minimal elements of
![]() ${\mathcal {S}}(X,\sqcup )$
are the indecomposable factors of X and the height of an element
${\mathcal {S}}(X,\sqcup )$
are the indecomposable factors of X and the height of an element
![]() $H\in {\mathcal {S}}(X,\sqcup )$
is the number of (nontrivial) indecomposable direct product factors. Therefore,
$H\in {\mathcal {S}}(X,\sqcup )$
is the number of (nontrivial) indecomposable direct product factors. Therefore,
![]() ${\mathcal D}_w(X,\sqcup )$
is the poset of all (internal) direct-product decompositions of X ordered by refinement, and
${\mathcal D}_w(X,\sqcup )$
is the poset of all (internal) direct-product decompositions of X ordered by refinement, and
![]() ${\mathcal D}(X,\sqcup )$
equals
${\mathcal D}(X,\sqcup )$
equals
![]() ${\mathcal D}_w(X,\sqcup )$
.
${\mathcal D}_w(X,\sqcup )$
.
In view of the previous example and Example 2.10, we propose the following question:
Question 2.17. If G is the direct product of groups
![]() $G_1,\ldots ,G_r$
of relatively prime orders, do we have
$G_1,\ldots ,G_r$
of relatively prime orders, do we have
![]() ${\mathcal D}({{\mathcal S}}(G),\times ) = \Pi (r)\times {\mathcal D}(G_1,\times )\times \cdots \times {\mathcal D}(G_r,\times )$
?
${\mathcal D}({{\mathcal S}}(G),\times ) = \Pi (r)\times {\mathcal D}(G_1,\times )\times \cdots \times {\mathcal D}(G_r,\times )$
?
Example 2.18. Recall that the coproduct in the category of groups is the free product. So we choose ‘
![]() $\sqcup $
’ to be the free product of groups and X a free group of finite rank. Then
$\sqcup $
’ to be the free product of groups and X a free group of finite rank. Then
![]() ${\mathcal {S}}(X)$
is a lattice with infinite height, and we cannot apply our definition of decompositions. However,
${\mathcal {S}}(X)$
is a lattice with infinite height, and we cannot apply our definition of decompositions. However,
![]() ${\mathcal {S}}(X,\sqcup )$
does have finite height. Indeed, we claim that
${\mathcal {S}}(X,\sqcup )$
does have finite height. Indeed, we claim that
![]() ${\mathcal {S}}(X,\sqcup )$
is the poset
${\mathcal {S}}(X,\sqcup )$
is the poset
![]() $\operatorname {\mathrm {FC}}(X)$
of free factors of X. To see this, let
$\operatorname {\mathrm {FC}}(X)$
of free factors of X. To see this, let
![]() $H\in {\mathcal {S}}(X,\sqcup )$
and let
$H\in {\mathcal {S}}(X,\sqcup )$
and let
![]() $K\in {\mathcal {S}}(X)$
be a
$K\in {\mathcal {S}}(X)$
be a
![]() $\sqcup $
-complement for H. This means that
$\sqcup $
-complement for H. This means that
![]() $H\cap K = 1$
and
$H\cap K = 1$
and
![]() $H*K$
is naturally isomorphic to
$H*K$
is naturally isomorphic to
![]() $\left \langle H,K\right \rangle = X$
. That is,
$\left \langle H,K\right \rangle = X$
. That is,
![]() $X = H*K$
, so
$X = H*K$
, so
![]() $H,K$
are free factors of X. Since a free factor of X belongs to
$H,K$
are free factors of X. Since a free factor of X belongs to
![]() ${\mathcal {S}}(X,\sqcup )$
, we conclude that
${\mathcal {S}}(X,\sqcup )$
, we conclude that
![]() ${\mathcal {S}}(X, \sqcup ) = \operatorname {\mathrm {FC}}(X)$
. In particular,
${\mathcal {S}}(X, \sqcup ) = \operatorname {\mathrm {FC}}(X)$
. In particular,
![]() $\operatorname {\mathrm {FC}}(X)$
is a graded poset, and if
$\operatorname {\mathrm {FC}}(X)$
is a graded poset, and if
![]() $H\in \operatorname {\mathrm {FC}}(X)$
, then its height equals
$H\in \operatorname {\mathrm {FC}}(X)$
, then its height equals
![]() $\operatorname {\mathrm {rk}}(H)$
, the rank of H as a (free) group. Moreover, since
$\operatorname {\mathrm {rk}}(H)$
, the rank of H as a (free) group. Moreover, since
![]() $\operatorname {\mathrm {rk}}(H*K) = \operatorname {\mathrm {rk}}(H)+\operatorname {\mathrm {rk}}(K)$
, we conclude that
$\operatorname {\mathrm {rk}}(H*K) = \operatorname {\mathrm {rk}}(H)+\operatorname {\mathrm {rk}}(K)$
, we conclude that
![]() $\sqcup $
-weak decompositions are
$\sqcup $
-weak decompositions are
![]() $\sqcup $
-decompositions. Therefore,
$\sqcup $
-decompositions. Therefore,
![]() ${\mathcal D}_w(X,\sqcup ) = {\mathcal D}(X,\sqcup )$
is the poset of decompositions
${\mathcal D}_w(X,\sqcup ) = {\mathcal D}(X,\sqcup )$
is the poset of decompositions
![]() $\{H_1,\ldots , H_k\}$
of X into free factors
$\{H_1,\ldots , H_k\}$
of X into free factors
![]() $X = H_1 * \cdots * H_k$
.
$X = H_1 * \cdots * H_k$
.
Example 2.19. Let
![]() ${{\mathcal S}}$
be a lattice. Then we have the induced poset-category
${{\mathcal S}}$
be a lattice. Then we have the induced poset-category
![]() ${\mathcal C}$
whose objects are the elements of
${\mathcal C}$
whose objects are the elements of
![]() ${{\mathcal S}}$
with arrows
${{\mathcal S}}$
with arrows
![]() $x\to y$
if and only if
$x\to y$
if and only if
![]() $x\leq y$
. Then
$x\leq y$
. Then
![]() ${\mathcal {S}}(1_{{{\mathcal S}}}) = {{\mathcal S}}$
. Moreover,
${\mathcal {S}}(1_{{{\mathcal S}}}) = {{\mathcal S}}$
. Moreover,
![]() ${\mathcal C}$
is an ISM-category with
${\mathcal C}$
is an ISM-category with
![]() $\sqcup $
given by the join of elements in
$\sqcup $
given by the join of elements in
![]() ${{\mathcal S}}$
(i.e.,
${{\mathcal S}}$
(i.e.,
![]() $x\sqcup y = x\vee y$
). It is straightforward to verify then that
$x\sqcup y = x\vee y$
). It is straightforward to verify then that
![]() ${\mathcal {S}}(1_{{{\mathcal S}}},\sqcup )$
is the subposet of complemented elements of
${\mathcal {S}}(1_{{{\mathcal S}}},\sqcup )$
is the subposet of complemented elements of
![]() ${{\mathcal S}}$
. In particular, if every element of
${{\mathcal S}}$
. In particular, if every element of
![]() ${{\mathcal S}}$
is complemented, then
${{\mathcal S}}$
is complemented, then
![]() ${{\mathcal S}} = {\mathcal {S}}(1_{{{\mathcal S}}},\sqcup )$
,
${{\mathcal S}} = {\mathcal {S}}(1_{{{\mathcal S}}},\sqcup )$
,
![]() ${\mathcal D}({{\mathcal S}}) = {\mathcal D}({{\mathcal S}},\sqcup )$
and
${\mathcal D}({{\mathcal S}}) = {\mathcal D}({{\mathcal S}},\sqcup )$
and
![]() ${\mathcal {PD}}({{\mathcal S}}) = {\mathcal {PD}}(1_{{{\mathcal S}}},\sqcup )$
.
${\mathcal {PD}}({{\mathcal S}}) = {\mathcal {PD}}(1_{{{\mathcal S}}},\sqcup )$
.
3 Properties of decomposition posets
From now on, we assume that X is an object of an ISM-category
![]() $({\mathcal C},\sqcup )$
such that
$({\mathcal C},\sqcup )$
such that
![]() ${\mathcal {S}}(X,\sqcup )$
has finite height. Recall by Example 2.19 that we can regard a complemented lattice
${\mathcal {S}}(X,\sqcup )$
has finite height. Recall by Example 2.19 that we can regard a complemented lattice
![]() ${{\mathcal S}}$
as some poset
${{\mathcal S}}$
as some poset
![]() ${{\mathcal S}}(X,\sqcup )$
where also
${{\mathcal S}}(X,\sqcup )$
where also
![]() ${\mathcal D}({{\mathcal S}}) = {\mathcal D}(X,\sqcup )$
and
${\mathcal D}({{\mathcal S}}) = {\mathcal D}(X,\sqcup )$
and
![]() ${\mathcal {PD}}({{\mathcal S}}) = {\mathcal {PD}}(X,\sqcup )$
. Therefore, the results of this section are also valid for complemented lattices of finite height.
${\mathcal {PD}}({{\mathcal S}}) = {\mathcal {PD}}(X,\sqcup )$
. Therefore, the results of this section are also valid for complemented lattices of finite height.
The following proposition recovers the structure of upper intervals of decompositions, and it is an immediate consequence of the definitions.
Proposition 3.1. For
![]() $\sigma \in {\mathcal D}(X,\sqcup )$
we have
$\sigma \in {\mathcal D}(X,\sqcup )$
we have
![]() ${\mathcal D}(X,\sqcup )_{\geq \sigma } \cong \Pi (\sigma )$
.
${\mathcal D}(X,\sqcup )_{\geq \sigma } \cong \Pi (\sigma )$
.
Proof. This follows from Lemma 2.5 and the fact that
![]() ${\mathcal D}(X,\sqcup )$
is an upper order ideal in
${\mathcal D}(X,\sqcup )$
is an upper order ideal in
![]() ${\mathcal D}({\mathcal {S}}(X,\sqcup ))$
.
${\mathcal D}({\mathcal {S}}(X,\sqcup ))$
.
In some important cases, we also have control over the lower intervals, and the following property holds:
Definition 3.2. We say that X satisfies property (LI) if the following condition holds:
-
(LI) For all
 $\sigma \in {\mathcal {PD}}(X,\sqcup )$
we have
$\sigma \in {\mathcal {PD}}(X,\sqcup )$
we have
 ${\mathcal {PD}}(X,\sqcup )_{\leq \sigma } = \prod _{y\in \sigma } {\mathcal {PD}}(Y,\sqcup )$
, for suitable representatives
${\mathcal {PD}}(X,\sqcup )_{\leq \sigma } = \prod _{y\in \sigma } {\mathcal {PD}}(Y,\sqcup )$
, for suitable representatives
 $(Y,i_y)\in y$
.
$(Y,i_y)\in y$
.
Here, (LI) stands for Lower Interval.
In particular, property (LI) implies that the lower interval
![]() ${\mathcal D}(X,\sqcup )_{\leq \sigma }$
is also a product
${\mathcal D}(X,\sqcup )_{\leq \sigma }$
is also a product
![]() $\prod _{y\in \sigma } {\mathcal D}(Y,\sqcup )$
. Conditions analogous to those from Lemma 2.6 imply property (LI).
$\prod _{y\in \sigma } {\mathcal D}(Y,\sqcup )$
. Conditions analogous to those from Lemma 2.6 imply property (LI).
The following proposition provides some information on the heights of the posets of decompositions and partial decompositions.
Proposition 3.3. Let
![]() ${\mathcal {S}}(X,\sqcup )$
be of height n. Then every decomposition in
${\mathcal {S}}(X,\sqcup )$
be of height n. Then every decomposition in
![]() ${\mathcal D}(X,\sqcup )$
has size at most n. In particular,
${\mathcal D}(X,\sqcup )$
has size at most n. In particular,
![]() $h({\mathcal {PD}}(X,\sqcup )) \leq 2n-1$
and
$h({\mathcal {PD}}(X,\sqcup )) \leq 2n-1$
and
![]() $h({\mathcal D}(X,\sqcup ))\leq n-1$
. Moreover, the following are equivalent:
$h({\mathcal D}(X,\sqcup ))\leq n-1$
. Moreover, the following are equivalent:
-
(1) there exists a decomposition of size n.
-
(2)
 $h({\mathcal {PD}}(X,\sqcup )) = 2n-1$
.
$h({\mathcal {PD}}(X,\sqcup )) = 2n-1$
. -
(3)
 $h({\mathcal D}(X,\sqcup )) = n-1$
.
$h({\mathcal D}(X,\sqcup )) = n-1$
.
If one of the preceding conditions holds, then the following are equivalent:
-
1’. for every decomposition
 $\sigma $
, there exists a decomposition
$\sigma $
, there exists a decomposition
 $\tau $
of size n with
$\tau $
of size n with
 $\tau \leq \sigma $
.
$\tau \leq \sigma $
. -
3’.
 ${\mathcal D}(X,\sqcup )$
is graded.
${\mathcal D}(X,\sqcup )$
is graded.
Proof. The bound on the size of elements of
![]() ${\mathcal D}(X,\sqcup )$
is an immediate consequence of the definitions. The bound on the height of
${\mathcal D}(X,\sqcup )$
is an immediate consequence of the definitions. The bound on the height of
![]() ${\mathcal D}(X,\sqcup )$
then follows from Proposition 3.1. For
${\mathcal D}(X,\sqcup )$
then follows from Proposition 3.1. For
![]() ${\mathcal {PD}}(X,\sqcup )$
, we argue as follows. Suppose that
${\mathcal {PD}}(X,\sqcup )$
, we argue as follows. Suppose that
![]() $\sigma \in {\mathcal {PD}}(X,\sqcup )$
,
$\sigma \in {\mathcal {PD}}(X,\sqcup )$
,
![]() $\sigma \neq \emptyset $
, and consider a saturated chain
$\sigma \neq \emptyset $
, and consider a saturated chain
![]() $\gamma $
in
$\gamma $
in
![]() ${\mathcal {PD}}(X,\sqcup )$
with maximal element
${\mathcal {PD}}(X,\sqcup )$
with maximal element
![]() $\sigma $
. In particular,
$\sigma $
. In particular,
![]() $\gamma $
contains the empty partial decomposition. Then, a covering relation
$\gamma $
contains the empty partial decomposition. Then, a covering relation
![]() $\tau \prec \tau '$
in
$\tau \prec \tau '$
in
![]() $\gamma $
means that either we ‘split’ some elements of
$\gamma $
means that either we ‘split’ some elements of
![]() $\tau '$
(meaning that for some
$\tau '$
(meaning that for some
![]() $x\in \tau '$
, there are
$x\in \tau '$
, there are
![]() $y,z \in \tau $
with
$y,z \in \tau $
with
![]() $x \geq y \vee z$
and
$x \geq y \vee z$
and
![]() $x \not \in \tau $
) or we eliminated an ‘unsplittable’ element (i.e., there is
$x \not \in \tau $
) or we eliminated an ‘unsplittable’ element (i.e., there is
![]() $x\in \tau '$
which cannot be split and
$x\in \tau '$
which cannot be split and
![]() $\tau = \tau '\setminus \{x\}$
). Therefore, for
$\tau = \tau '\setminus \{x\}$
). Therefore, for
![]() $x \in \tau $
, we can perform at most
$x \in \tau $
, we can perform at most
![]() $h(x)-1$
splittings and eliminate at most
$h(x)-1$
splittings and eliminate at most
![]() $h(x)$
elements. Thus, the maximal chain
$h(x)$
elements. Thus, the maximal chain
![]() $\gamma $
has size at most
$\gamma $
has size at most
This implies that
![]() $h({\mathcal {PD}}(X,\sqcup ))\leq 2n-1$
.
$h({\mathcal {PD}}(X,\sqcup ))\leq 2n-1$
.
The equivalence of items 1 and 3 immediately follows from Proposition 3.1. The equivalence of items 1 and 2 is a consequence of the proof of the bound
![]() $h({\mathcal {PD}}(X,\sqcup )) \leq 2n-1$
.
$h({\mathcal {PD}}(X,\sqcup )) \leq 2n-1$
.
Given the equivalent conditions of items 1, 2 and 3, again Proposition 3.1 implies the equivalence of 1’ and 3’.
In general,
![]() ${\mathcal D}(X,\sqcup )$
has a unique maximal but not necessarily a unique minimal element. As defined at the beginning of Section 2, for a poset
${\mathcal D}(X,\sqcup )$
has a unique maximal but not necessarily a unique minimal element. As defined at the beginning of Section 2, for a poset
![]() ${{\mathcal S}}$
with a unique maximal element, we write
${{\mathcal S}}$
with a unique maximal element, we write
![]() ${{\mathcal S}}^{\circ }$
for the subposet obtained by removing the unique maximal element, and in case
${{\mathcal S}}^{\circ }$
for the subposet obtained by removing the unique maximal element, and in case
![]() ${{\mathcal S}}$
has also a unique minimal element, we denote by
${{\mathcal S}}$
has also a unique minimal element, we denote by
![]() ${{\mathcal S}}^{*}$
the subposet obtained by removing both the unique minimal and the unique maximal element. When
${{\mathcal S}}^{*}$
the subposet obtained by removing both the unique minimal and the unique maximal element. When
![]() ${\mathcal {S}}(X,\sqcup )$
is the Boolean lattice with
${\mathcal {S}}(X,\sqcup )$
is the Boolean lattice with
![]() $\sqcup $
the disjoint union,
$\sqcup $
the disjoint union,
![]() ${\mathcal D}(X,\sqcup )$
is the partition lattice which has a unique minimal element and in the literature
${\mathcal D}(X,\sqcup )$
is the partition lattice which has a unique minimal element and in the literature
![]() ${\mathcal D}(X,\sqcup )^{*}$
is studied extensively. However, given that
${\mathcal D}(X,\sqcup )^{*}$
is studied extensively. However, given that
![]() ${\mathcal D}(X,\sqcup )$
usually has more than one minimal element, in our approach, it is more natural to consider the topology of the partition lattice after removing the maximal element only. As a consequence, we will usually study
${\mathcal D}(X,\sqcup )$
usually has more than one minimal element, in our approach, it is more natural to consider the topology of the partition lattice after removing the maximal element only. As a consequence, we will usually study
![]() ${\mathcal D}(X,\sqcup )^{\circ }$
.
${\mathcal D}(X,\sqcup )^{\circ }$
.
In the following proposition, we see that
![]() ${\mathcal D}(X,\sqcup )$
is a lattice if we add an extra minimum.
${\mathcal D}(X,\sqcup )$
is a lattice if we add an extra minimum.
Proposition 3.4. The poset
![]() ${\mathcal D}(X,\sqcup )$
is a lattice after adding an extra minimum element.
${\mathcal D}(X,\sqcup )$
is a lattice after adding an extra minimum element.
Proof. We show that two
![]() $\sqcup $
-decompositions
$\sqcup $
-decompositions
![]() $\sigma _1,\sigma _2$
, bounded below by some element
$\sigma _1,\sigma _2$
, bounded below by some element
![]() $\tau \in {\mathcal D}(X,\sqcup )$
, have a meet in
$\tau \in {\mathcal D}(X,\sqcup )$
, have a meet in
![]() ${\mathcal D}(X,\sqcup )$
. Indeed, since
${\mathcal D}(X,\sqcup )$
. Indeed, since
![]() $\sigma _1,\sigma _2\in {\mathcal D}(X,\sqcup )_{\geq \tau } \cong \Pi (\tau )$
is a partition lattice, they have a meet in this poset, which we denote by
$\sigma _1,\sigma _2\in {\mathcal D}(X,\sqcup )_{\geq \tau } \cong \Pi (\tau )$
is a partition lattice, they have a meet in this poset, which we denote by
![]() $\sigma $
. Let
$\sigma $
. Let
![]() $e:2^{\tau } \to {{\mathcal S}}(X,\sqcup )$
be the lattice embedding of the Boolean lattice on
$e:2^{\tau } \to {{\mathcal S}}(X,\sqcup )$
be the lattice embedding of the Boolean lattice on
![]() $\tau $
. If
$\tau $
. If
![]() $x\in \sigma _1$
and
$x\in \sigma _1$
and
![]() $y\in \sigma _2$
, then there exist unique sets
$y\in \sigma _2$
, then there exist unique sets
![]() $\tau _x,\tau _y\subseteq \tau $
such that
$\tau _x,\tau _y\subseteq \tau $
such that
![]() $x = \bigvee _{a\in \tau _x} a$
and
$x = \bigvee _{a\in \tau _x} a$
and
![]() $y = \bigvee _{b\in \tau _y} b$
, where the join is taken in the poset
$y = \bigvee _{b\in \tau _y} b$
, where the join is taken in the poset
![]() ${\mathcal {S}}(X,\sqcup )$
. Hence,
${\mathcal {S}}(X,\sqcup )$
. Hence,
![]() $e(\tau _x) = x$
,
$e(\tau _x) = x$
,
![]() $e(\tau _y) = y$
and
$e(\tau _y) = y$
and
![]() $e(\tau _x\cap \tau _y) = x\wedge y$
. The decomposition
$e(\tau _x\cap \tau _y) = x\wedge y$
. The decomposition
![]() $\sigma $
can be described as follows:
$\sigma $
can be described as follows:
But then, by definition of e,
where the meet is taken in
![]() ${\mathcal {S}}(X,\sqcup )$
. This description of
${\mathcal {S}}(X,\sqcup )$
. This description of
![]() $\sigma $
does not depend on
$\sigma $
does not depend on
![]() $\tau $
, and clearly
$\tau $
, and clearly
![]() $\sigma \geq \tau $
. Therefore,
$\sigma \geq \tau $
. Therefore,
![]() $\sigma _1\wedge \sigma _2$
exists in
$\sigma _1\wedge \sigma _2$
exists in
![]() ${\mathcal D}(X,\sqcup )$
, and it is equal to the element
${\mathcal D}(X,\sqcup )$
, and it is equal to the element
![]() $\sigma $
described above.
$\sigma $
described above.
The poset
![]() ${\mathcal {PD}}(X,\sqcup )$
is not a lattice in general, as it is seen in the poset of Figure 2 in Example 2.8. The next example also shows that weak decomposition and weak partial decomposition posets might not be lattices. Here, we invoke Example 2.19.
${\mathcal {PD}}(X,\sqcup )$
is not a lattice in general, as it is seen in the poset of Figure 2 in Example 2.8. The next example also shows that weak decomposition and weak partial decomposition posets might not be lattices. Here, we invoke Example 2.19.
Example 3.5. Let
![]() $G = S_4$
be the symmetric group on
$G = S_4$
be the symmetric group on
![]() $4$
letters. Then for
$4$
letters. Then for
![]() ${{\mathcal S}}(G)$
, the lattice of subgroups of G, we have that
${{\mathcal S}}(G)$
, the lattice of subgroups of G, we have that
![]() ${\mathcal D}_w({{\mathcal S}}(G))$
is not a lattice after adding a minimal element, and hence nor is
${\mathcal D}_w({{\mathcal S}}(G))$
is not a lattice after adding a minimal element, and hence nor is
![]() ${\mathcal {PD}}_w({{\mathcal S}}(G))$
. This was shown by using GAP. To be more concrete, we have weak decompositions
${\mathcal {PD}}_w({{\mathcal S}}(G))$
. This was shown by using GAP. To be more concrete, we have weak decompositions
for which their join in
![]() ${\mathcal D}_w({{\mathcal S}}(G))$
does not exist since the elements above both of them in
${\mathcal D}_w({{\mathcal S}}(G))$
does not exist since the elements above both of them in
![]() ${\mathcal D}_w({{\mathcal S}}(G))$
are
${\mathcal D}_w({{\mathcal S}}(G))$
are
Moreover,
![]() ${\mathcal {PD}}({{\mathcal S}}(G))$
is not a lattice either since the join fails for the partial decompositions
${\mathcal {PD}}({{\mathcal S}}(G))$
is not a lattice either since the join fails for the partial decompositions
In view of our definition of decompositions in terms of heights, it will be useful to work with complements of elements which also have the correct height.
Definition 3.6. Let
![]() ${{\mathcal S}}$
be a poset.
${{\mathcal S}}$
be a poset.
-
• Let
 $y\in {{\mathcal S}}$
and suppose that
$y\in {{\mathcal S}}$
and suppose that
 ${{\mathcal S}}_{\leq y}$
is bounded of finite height. We say that
${{\mathcal S}}_{\leq y}$
is bounded of finite height. We say that
 $x\in {{\mathcal S}}_{\leq y}$
is h-complemented in y if there exists
$x\in {{\mathcal S}}_{\leq y}$
is h-complemented in y if there exists
 $x'\leq y$
such that
$x'\leq y$
such that
 $x'\wedge x = 0$
and
$x'\wedge x = 0$
and
 $x\vee x' = y$
(meet and join taken in
$x\vee x' = y$
(meet and join taken in
 ${{\mathcal S}}$
) and
${{\mathcal S}}$
) and
 $h(x) + h(x') = h(y)$
.
$h(x) + h(x') = h(y)$
.
Suppose now that
![]() ${{\mathcal S}}$
is bounded of finite height.
${{\mathcal S}}$
is bounded of finite height.
-
• An element
 $x\in {{\mathcal S}}$
is called h-complemented if x is h-complemented in
$x\in {{\mathcal S}}$
is called h-complemented if x is h-complemented in
 $1_{{{\mathcal S}}}$
. We denote by
$1_{{{\mathcal S}}}$
. We denote by
 ${{\mathcal S}}_h$
the subposet of h-complemented elements.
${{\mathcal S}}_h$
the subposet of h-complemented elements. -
• We say that
 ${{\mathcal S}}$
is h-complemented if
${{\mathcal S}}$
is h-complemented if
 ${{\mathcal S}} = {{\mathcal S}}_h$
.
${{\mathcal S}} = {{\mathcal S}}_h$
. -
• If for every
 $x\leq y$
in
$x\leq y$
in
 ${{\mathcal S}}$
there exists a (unique) h-complement of x in y, then we say that
${{\mathcal S}}$
there exists a (unique) h-complement of x in y, then we say that
 ${{\mathcal S}}$
is (uniquely) downward h-complemented.
${{\mathcal S}}$
is (uniquely) downward h-complemented.
Next, we define the analogous concepts in posets
![]() ${\mathcal {S}}(X,\sqcup )$
by taking into account the monoidal product
${\mathcal {S}}(X,\sqcup )$
by taking into account the monoidal product
![]() $\sqcup $
. These concepts will play an important role later in Section 5. For instance, the unique downward
$\sqcup $
. These concepts will play an important role later in Section 5. For instance, the unique downward
![]() $(\sqcup ,h)$
-complementation property, as defined below, will arise in examples like posets of nondegenerate subspaces with the orthogonal complementation, or the Boolean lattice with the usual set complementation. Recall that we are assuming that
$(\sqcup ,h)$
-complementation property, as defined below, will arise in examples like posets of nondegenerate subspaces with the orthogonal complementation, or the Boolean lattice with the usual set complementation. Recall that we are assuming that
![]() ${\mathcal {S}}(X,\sqcup )$
has finite height.
${\mathcal {S}}(X,\sqcup )$
has finite height.
Definition 3.7. Let X and
![]() $\sqcup $
be as above.
$\sqcup $
be as above.
-
• If
 $z\leq y\in {\mathcal {S}}(X,\sqcup )$
, a
$z\leq y\in {\mathcal {S}}(X,\sqcup )$
, a
 $(\sqcup ,h)$
-complement of z in y is an h-complement w of z in y such that
$(\sqcup ,h)$
-complement of z in y is an h-complement w of z in y such that
 $\{z,w\}$
is
$\{z,w\}$
is
 $\sqcup $
-compatible in
$\sqcup $
-compatible in
 ${\mathcal {S}}(X,\sqcup )$
. We denote by
${\mathcal {S}}(X,\sqcup )$
. We denote by
 ${\mathcal {S}}_h(X,\sqcup )$
the subposet of
${\mathcal {S}}_h(X,\sqcup )$
the subposet of
 ${\mathcal {S}}(X,\sqcup )$
whose elements have a
${\mathcal {S}}(X,\sqcup )$
whose elements have a
 $(\sqcup ,h)$
-complement in
$(\sqcup ,h)$
-complement in
 ${\mathcal {S}}(X,\sqcup )$
.
${\mathcal {S}}(X,\sqcup )$
. -
• We say that
 ${\mathcal {S}}(X,\sqcup )$
is
${\mathcal {S}}(X,\sqcup )$
is
 $(\sqcup ,h)$
-complemented if
$(\sqcup ,h)$
-complemented if
 ${\mathcal {S}}_h(X,\sqcup ) = {\mathcal {S}}(X, \sqcup )$
.
${\mathcal {S}}_h(X,\sqcup ) = {\mathcal {S}}(X, \sqcup )$
. -
• We say that
 ${\mathcal {S}}(X,\sqcup )$
is (uniquely) downward
${\mathcal {S}}(X,\sqcup )$
is (uniquely) downward
 $(\sqcup ,h)$
-complemented if for all
$(\sqcup ,h)$
-complemented if for all
 $z\leq y \in {\mathcal {S}}(X,\sqcup )$
, there exists a (unique)
$z\leq y \in {\mathcal {S}}(X,\sqcup )$
, there exists a (unique)
 $(\sqcup ,h)$
-complement of z in y. In the case of uniqueness, we denote by
$(\sqcup ,h)$
-complement of z in y. In the case of uniqueness, we denote by
 $z^{\perp _y}$
the unique
$z^{\perp _y}$
the unique
 $(\sqcup ,h)$
-complement of z in y, and by
$(\sqcup ,h)$
-complement of z in y, and by
 $z^\perp $
the unique
$z^\perp $
the unique
 $(\sqcup ,h)$
-complement of z in
$(\sqcup ,h)$
-complement of z in
 ${\mathcal {S}}(X,\sqcup )$
.
${\mathcal {S}}(X,\sqcup )$
.
Note that
![]() ${{\mathcal S}}_h$
(resp.
${{\mathcal S}}_h$
(resp.
![]() ${\mathcal {S}}_h(X,\sqcup )$
) contains the unique minimum element and those elements which belong to some
${\mathcal {S}}_h(X,\sqcup )$
) contains the unique minimum element and those elements which belong to some
![]() $\sigma \in {\mathcal D}({{\mathcal S}})$
(reps.
$\sigma \in {\mathcal D}({{\mathcal S}})$
(reps.
![]() $\sigma \in {\mathcal D}(X,\sqcup )$
).
$\sigma \in {\mathcal D}(X,\sqcup )$
).
Even if
![]() ${\mathcal {S}}(X,\sqcup )$
is uniquely
${\mathcal {S}}(X,\sqcup )$
is uniquely
![]() $(\sqcup ,h)$
-complemented, the complements in the purely poset-theoretic sense need not be unique. For example, for the poset of nondegenerate subspaces of a finite-dimensional vector space equipped with a nondegenerate sesquilinear form and
$(\sqcup ,h)$
-complemented, the complements in the purely poset-theoretic sense need not be unique. For example, for the poset of nondegenerate subspaces of a finite-dimensional vector space equipped with a nondegenerate sesquilinear form and
![]() $\sqcup $
the orthogonal sum, complements and even h-complements of nondegenerate subspaces are not unique. However, the poset is uniquely downward
$\sqcup $
the orthogonal sum, complements and even h-complements of nondegenerate subspaces are not unique. However, the poset is uniquely downward
![]() $(\sqcup ,h)$
-complemented (i.e.,
$(\sqcup ,h)$
-complemented (i.e.,
![]() $(\sqcup ,h)$
-complements are unique). See Subsection 6.3 for more details.
$(\sqcup ,h)$
-complements are unique). See Subsection 6.3 for more details.
The following lemma is an immediate consequence of the definitions.
Lemma 3.8. The map
![]() $\Phi : {\mathcal {PD}}(X,\sqcup ) \to {\mathcal {S}}(X,\sqcup )$
sending
$\Phi : {\mathcal {PD}}(X,\sqcup ) \to {\mathcal {S}}(X,\sqcup )$
sending
![]() $\sigma $
to
$\sigma $
to
![]() $\Phi (\sigma ) = \bigvee _{x\in \sigma }x$
is an order-preserving map with
$\Phi (\sigma ) = \bigvee _{x\in \sigma }x$
is an order-preserving map with
![]() $\Phi ^{-1}(0) = \{ \emptyset \}$
and
$\Phi ^{-1}(0) = \{ \emptyset \}$
and
![]() $\Phi ^{-1}(1) = {\mathcal D}(X,\sqcup )$
. Its image is the poset
$\Phi ^{-1}(1) = {\mathcal D}(X,\sqcup )$
. Its image is the poset
![]() ${\mathcal {S}}_h(X,\sqcup )$
. Thus,
${\mathcal {S}}_h(X,\sqcup )$
. Thus,
![]() $\Phi $
is surjective if and only if
$\Phi $
is surjective if and only if
![]() ${\mathcal {S}}(X,\sqcup )$
is
${\mathcal {S}}(X,\sqcup )$
is
![]() $(\sqcup ,h)$
-complemented.
$(\sqcup ,h)$
-complemented.
Similarly, for a bounded poset
![]() ${{\mathcal S}}$
of finite height and
${{\mathcal S}}$
of finite height and
![]() $x\in {{\mathcal S}}$
, we have that
$x\in {{\mathcal S}}$
, we have that
![]() $\{x\}$
is a partial decomposition of
$\{x\}$
is a partial decomposition of
![]() ${{\mathcal S}}$
if and only if
${{\mathcal S}}$
if and only if
![]() $x\neq 0$
and it is h-complemented in
$x\neq 0$
and it is h-complemented in
![]() ${{\mathcal S}}$
.
${{\mathcal S}}$
.
We have the following necessary condition for the lattice property on
![]() ${\mathcal {PD}}(X,\sqcup )$
.
${\mathcal {PD}}(X,\sqcup )$
.
Lemma 3.9. If
![]() ${\mathcal {PD}}(X,\sqcup )$
is a lattice, then
${\mathcal {PD}}(X,\sqcup )$
is a lattice, then
![]() ${\mathcal {S}}_h(X,\sqcup )$
is also a lattice.
${\mathcal {S}}_h(X,\sqcup )$
is also a lattice.
Proof. Suppose that
![]() $x,y\in {\mathcal {S}}_h(X,\sqcup )$
have a lower bound
$x,y\in {\mathcal {S}}_h(X,\sqcup )$
have a lower bound
![]() $0\neq z\in {\mathcal {S}}_h(X,\sqcup )$
. Then
$0\neq z\in {\mathcal {S}}_h(X,\sqcup )$
. Then
![]() $\{z\}\leq \{x\},\{y\}$
in
$\{z\}\leq \{x\},\{y\}$
in
![]() ${\mathcal {PD}}(X,\sqcup )$
. Since
${\mathcal {PD}}(X,\sqcup )$
. Since
![]() ${\mathcal {PD}}(X,\sqcup )$
is a lattice, there exists
${\mathcal {PD}}(X,\sqcup )$
is a lattice, there exists
![]() $\sigma \in {\mathcal {PD}}(X,\sqcup )$
such that
$\sigma \in {\mathcal {PD}}(X,\sqcup )$
such that
![]() $\sigma = \{x\} \wedge \{y\}$
, and therefore,
$\sigma = \{x\} \wedge \{y\}$
, and therefore,
![]() $\{z\}\leq \sigma $
. But this implies that
$\{z\}\leq \sigma $
. But this implies that
![]() $\Phi (\sigma )\leq x,y$
, so we must have
$\Phi (\sigma )\leq x,y$
, so we must have
![]() $\sigma = \{ \Phi (\sigma )\}$
. Hence,
$\sigma = \{ \Phi (\sigma )\}$
. Hence,
![]() $z \leq \Phi (\sigma )\in {\mathcal {S}}_h(X,\sqcup )$
and
$z \leq \Phi (\sigma )\in {\mathcal {S}}_h(X,\sqcup )$
and
![]() $x\wedge y = \Phi (\sigma )$
.
$x\wedge y = \Phi (\sigma )$
.
The converse of this lemma does not hold, as the lattice of Example 3.5 shows.
We will work with the following properties. These are motivated by the question of whether a decomposition of a subobject of X can be extended to a decomposition of X. Essentially, they will give us natural ways of constructing new partial decompositions and will help us to establish stronger relations among the different posets and complexes, in particular when combined with downward
![]() $(\sqcup ,h)$
-complementation. In well-known scenarios (cf. Section 6), these properties are usually easy to verify, or else they are consequences of known theorems.
$(\sqcup ,h)$
-complementation. In well-known scenarios (cf. Section 6), these properties are usually easy to verify, or else they are consequences of known theorems.
Definition 3.10. Let X and
![]() $\sqcup $
be as above. We define the following properties:
$\sqcup $
be as above. We define the following properties:
-
(EX) If
 $y \in \sigma \in {\mathcal {PD}}(X,\sqcup )$
and
$y \in \sigma \in {\mathcal {PD}}(X,\sqcup )$
and
 $\tau \in {\mathcal D}( {\mathcal {S}}(X,\sqcup )_{\leq y})$
is
$\tau \in {\mathcal D}( {\mathcal {S}}(X,\sqcup )_{\leq y})$
is
 $\sqcup $
-compatible in
$\sqcup $
-compatible in
 ${\mathcal {S}}(X,\sqcup )$
, then
${\mathcal {S}}(X,\sqcup )$
, then
 $\left ( \sigma \setminus \{y\} \right )\cup \tau \in {\mathcal {PD}}(X,\sqcup )$
.
$\left ( \sigma \setminus \{y\} \right )\cup \tau \in {\mathcal {PD}}(X,\sqcup )$
. -
(CM) If
 $\{x,y\}, \{x',y'\}\in {\mathcal D}(X,\sqcup )$
are such that
$\{x,y\}, \{x',y'\}\in {\mathcal D}(X,\sqcup )$
are such that
 $x\leq x'$
and
$x\leq x'$
and
 $y'\leq y$
, then
$y'\leq y$
, then
 $x'\wedge y$
exists and
$x'\wedge y$
exists and
 $\{x'\wedge y,x,y'\}\setminus \{0\}\in {\mathcal D}(X,\sqcup )$
.
$\{x'\wedge y,x,y'\}\setminus \{0\}\in {\mathcal D}(X,\sqcup )$
.
Here, (EX) stands for the Extension property, and (CM) for the Complementation property. For instance, we will see later in Subsection 6.2 that in the case of vector spaces with the direct sum, properties (EX) and (CM) hold.
Remark 3.11. Note that in the definition of property (EX), if
![]() $\sigma \in {\mathcal D}(X,\sqcup )$
is a decomposition, then
$\sigma \in {\mathcal D}(X,\sqcup )$
is a decomposition, then
![]() $\left ( \sigma \setminus \{y\} \right )\cup \tau \in {\mathcal D}(X,\sqcup )$
by height. Basically, property (EX) means that any time we take a partial decomposition, we can replace any of its subobjects with a full decomposition of this subobject. In the vector space example, where partial decompositions of a given vector space V are sets of subspaces in internal direct sum, this means that we can replace any subspace S by an internal direct sum of S and still obtain a partial decomposition of V.
$\left ( \sigma \setminus \{y\} \right )\cup \tau \in {\mathcal D}(X,\sqcup )$
by height. Basically, property (EX) means that any time we take a partial decomposition, we can replace any of its subobjects with a full decomposition of this subobject. In the vector space example, where partial decompositions of a given vector space V are sets of subspaces in internal direct sum, this means that we can replace any subspace S by an internal direct sum of S and still obtain a partial decomposition of V.
However, in property (CM),
![]() $\{x'\wedge y, y'\}\in {\mathcal D}( {\mathcal {S}}(X,\sqcup )_{\leq y})$
since
$\{x'\wedge y, y'\}\in {\mathcal D}( {\mathcal {S}}(X,\sqcup )_{\leq y})$
since
![]() $(x'\wedge y) \vee y'$
exists, it is below y, and the height condition
$(x'\wedge y) \vee y'$
exists, it is below y, and the height condition
![]() $h(x'\wedge y) + h(y') = h(1) - h(x) = h(y)$
guarantees
$h(x'\wedge y) + h(y') = h(1) - h(x) = h(y)$
guarantees
![]() $(x'\wedge y) \vee y' = y$
. Roughly, property (CM) says that given two decompositions of size two as above, we can easily construct their meet in the decomposition poset by just taking the meet (in the original poset) of the ‘largest’ elements. For instance, this property clearly holds in the vector space example by the dimension theorem. See Subsection 6.2 for more details.
$(x'\wedge y) \vee y' = y$
. Roughly, property (CM) says that given two decompositions of size two as above, we can easily construct their meet in the decomposition poset by just taking the meet (in the original poset) of the ‘largest’ elements. For instance, this property clearly holds in the vector space example by the dimension theorem. See Subsection 6.2 for more details.
In general, property (EX) might not hold (not even for lattices).
Example 3.12. The poset
![]() ${{\mathcal S}}$
with Hasse diagram as in Figure 4 is easily seen to be a lattice. Let
${{\mathcal S}}$
with Hasse diagram as in Figure 4 is easily seen to be a lattice. Let
![]() $X = {{\mathcal S}}$
and
$X = {{\mathcal S}}$
and
![]() $\sqcup = \vee $
be the join operation. Then
$\sqcup = \vee $
be the join operation. Then
![]() $y = e \in \sigma = \{a,e\} \in {\mathcal D}(X,\sqcup ) \subseteq {\mathcal {PD}}(X,\sqcup )$
. We also have that
$y = e \in \sigma = \{a,e\} \in {\mathcal D}(X,\sqcup ) \subseteq {\mathcal {PD}}(X,\sqcup )$
. We also have that
![]() $\tau = \{b,c\} \in {\mathcal D}(X,\sqcup )_{\leq e})$
, but
$\tau = \{b,c\} \in {\mathcal D}(X,\sqcup )_{\leq e})$
, but
![]() $(\sigma \setminus \{y\}) \cup \tau = \{a,b,c\} \not \in {\mathcal {PD}}(X,\sqcup )$
. Thus,
$(\sigma \setminus \{y\}) \cup \tau = \{a,b,c\} \not \in {\mathcal {PD}}(X,\sqcup )$
. Thus,
![]() $(X,\sqcup )$
does not satisfy (EX).
$(X,\sqcup )$
does not satisfy (EX).

Figure 4 Lattice failing properties (EX) and (CM).
The property (CM) fails in this example, too. We have
![]() $\{x=a,y=e\},\{x'=d,y'=c\}\in {\mathcal D}(X,\sqcup )$
with
$\{x=a,y=e\},\{x'=d,y'=c\}\in {\mathcal D}(X,\sqcup )$
with
![]() $x=a\leq d=x'$
and
$x=a\leq d=x'$
and
![]() $y'=c\leq e=y$
, but
$y'=c\leq e=y$
, but
![]() $\{x'\wedge y,x,y'\} = \{d\wedge e, a, c\} = \{ b,a,c\}\notin {\mathcal D}(X,\sqcup )$
.
$\{x'\wedge y,x,y'\} = \{d\wedge e, a, c\} = \{ b,a,c\}\notin {\mathcal D}(X,\sqcup )$
.
We will see later that property (CM) fails in the case when X is a finitely generated free group in the category of groups with
![]() $\sqcup $
being the free product. See Example 6.1.
$\sqcup $
being the free product. See Example 6.1.
Corollary 3.13. If
![]() ${\mathcal {S}}(X,\sqcup )$
is uniquely downward
${\mathcal {S}}(X,\sqcup )$
is uniquely downward
![]() $(\sqcup ,h)$
-complemented and property (EX) holds, then the following hold:
$(\sqcup ,h)$
-complemented and property (EX) holds, then the following hold:
-
(1) the map
 $x\mapsto x^\perp $
is an anti-isomorphism of
$x\mapsto x^\perp $
is an anti-isomorphism of
 ${\mathcal {S}}(X,\sqcup )$
;
${\mathcal {S}}(X,\sqcup )$
; -
(2) if
 $x\leq y\leq z$
, then
$x\leq y\leq z$
, then
 $\{x,x^{\perp _y},y^{\perp _z},z^\perp \}\setminus \{0\} \in {\mathcal D}(X,\sqcup )$
and
$\{x,x^{\perp _y},y^{\perp _z},z^\perp \}\setminus \{0\} \in {\mathcal D}(X,\sqcup )$
and
 $x^{\perp _y}\vee y^{\perp _z} = x^{\perp _z}$
;
$x^{\perp _y}\vee y^{\perp _z} = x^{\perp _z}$
; -
(3) property (CM) is satisfied.
Proof. We first prove item 2. The assertion is trivial for
![]() $z = 0$
, so we assume that
$z = 0$
, so we assume that
![]() $z\neq 0$
and let
$z\neq 0$
and let
![]() $x\leq y\leq z$
and
$x\leq y\leq z$
and
![]() $\sigma = \{z,z^\perp \}\setminus \{0\} $
. Clearly,
$\sigma = \{z,z^\perp \}\setminus \{0\} $
. Clearly,
![]() $\sigma \in {\mathcal D}(X,\sqcup )$
and
$\sigma \in {\mathcal D}(X,\sqcup )$
and
![]() $\{y,y^{\perp _z}\}\setminus \{0\} \in {\mathcal D}({\mathcal {S}}(X,\sqcup )_{\leq z})$
is
$\{y,y^{\perp _z}\}\setminus \{0\} \in {\mathcal D}({\mathcal {S}}(X,\sqcup )_{\leq z})$
is
![]() $\sqcup $
-compatible in
$\sqcup $
-compatible in
![]() ${\mathcal {S}}(X,\sqcup )$
by definition. Hence, by property (EX),
${\mathcal {S}}(X,\sqcup )$
by definition. Hence, by property (EX),
![]() $\{z^\perp ,y,y^{\perp _z}\}\setminus \{0\} \in {\mathcal D}(X,\sqcup )$
. Similarly,
$\{z^\perp ,y,y^{\perp _z}\}\setminus \{0\} \in {\mathcal D}(X,\sqcup )$
. Similarly,
![]() $\{x, x^{\perp _y}\}\setminus \{0\} \in {\mathcal D}({\mathcal {S}}(X,\sqcup )_{\leq y})$
, and it is
$\{x, x^{\perp _y}\}\setminus \{0\} \in {\mathcal D}({\mathcal {S}}(X,\sqcup )_{\leq y})$
, and it is
![]() $\sqcup $
-compatible in
$\sqcup $
-compatible in
![]() ${\mathcal {S}}(X,\sqcup )$
, so
${\mathcal {S}}(X,\sqcup )$
, so
![]() $\{z^\perp ,x, x^{\perp _y},y^{\perp _z}\}\setminus \{0\} \in {\mathcal D}(X,\sqcup )$
. Then
$\{z^\perp ,x, x^{\perp _y},y^{\perp _z}\}\setminus \{0\} \in {\mathcal D}(X,\sqcup )$
. Then
![]() $z = x\vee x^{\perp _y} \vee y^{\perp _z}$
, and by uniqueness, we conclude that
$z = x\vee x^{\perp _y} \vee y^{\perp _z}$
, and by uniqueness, we conclude that
![]() $x^{\perp _z} = x^{\perp _y}\vee y^{\perp _z}$
. This establishes item 2. Moreover, by putting
$x^{\perp _z} = x^{\perp _y}\vee y^{\perp _z}$
. This establishes item 2. Moreover, by putting
![]() $z=1$
the maximal element, we see that
$z=1$
the maximal element, we see that
![]() $x^\perp = x^{\perp _y}\vee y^\perp $
, i.e.,
$x^\perp = x^{\perp _y}\vee y^\perp $
, i.e.,
![]() $x^\perp \geq y^\perp $
. Thus, the map
$x^\perp \geq y^\perp $
. Thus, the map
![]() $x\mapsto x^\perp $
is an anti-isomorphism, which proves item 1.
$x\mapsto x^\perp $
is an anti-isomorphism, which proves item 1.
For item 3, we can take decompositions
![]() $\{x,x^\perp \}$
and
$\{x,x^\perp \}$
and
![]() $\{x',x^{\prime \perp }\}$
where
$\{x',x^{\prime \perp }\}$
where
![]() $x\leq x'$
(by uniqueness and item 1). We show that
$x\leq x'$
(by uniqueness and item 1). We show that
![]() $x'\wedge x^\perp = x^{\perp _{x'}}$
. Let
$x'\wedge x^\perp = x^{\perp _{x'}}$
. Let
![]() $z\leq x^\perp ,x'$
. By item 1,
$z\leq x^\perp ,x'$
. By item 1,
![]() $z^\perp \geq x,x^{\prime \perp }$
. Since
$z^\perp \geq x,x^{\prime \perp }$
. Since
![]() $\{x,x^{\perp _{x'}},x^{\prime \perp }\}\setminus \{0\}\in {\mathcal D}(X,\sqcup )$
by item 2,
$\{x,x^{\perp _{x'}},x^{\prime \perp }\}\setminus \{0\}\in {\mathcal D}(X,\sqcup )$
by item 2,
![]() $x\vee x^{\prime \perp }$
exists and so
$x\vee x^{\prime \perp }$
exists and so
![]() $z^\perp \geq x\vee x^{\prime \perp }$
. Taking complements again by item 1, we see that
$z^\perp \geq x\vee x^{\prime \perp }$
. Taking complements again by item 1, we see that
![]() $z\leq (x\vee x^{\prime \perp })^\perp $
, and the latter is equal to
$z\leq (x\vee x^{\prime \perp })^\perp $
, and the latter is equal to
![]() $x^{\perp _{x'}}$
by uniqueness – that is,
$x^{\perp _{x'}}$
by uniqueness – that is,
![]() $z\leq x^{\perp _{x'}}$
. Therefore,
$z\leq x^{\perp _{x'}}$
. Therefore,
![]() $x^\perp \wedge x'$
exists, and it is
$x^\perp \wedge x'$
exists, and it is
![]() $x^{\perp _{x'}}$
. Thus, property (CM) holds.
$x^{\perp _{x'}}$
. Thus, property (CM) holds.
4 Simplicial complexes and posets derived from decompositions
In this section, we define additional posets and complexes related to decompositions, most of them inspired by analogous constructions in specific cases. We continue with our usual assumptions, so X is an object of an ISM-category
![]() ${\mathcal C}$
with product
${\mathcal C}$
with product
![]() $\sqcup $
and such that
$\sqcup $
and such that
![]() ${\mathcal {S}}(X,\sqcup )$
has finite height. At the end of this section, the reader can find a table with the names of the combinatorial structures defined here, except for the ordered versions. See Table 2.
${\mathcal {S}}(X,\sqcup )$
has finite height. At the end of this section, the reader can find a table with the names of the combinatorial structures defined here, except for the ordered versions. See Table 2.
Table 2 Structures associated to an object X of an ISM-category
![]() $({\mathcal C},\sqcup )$
for which
$({\mathcal C},\sqcup )$
for which
![]() ${\mathcal {S}}(X,\sqcup )$
has finite height.
${\mathcal {S}}(X,\sqcup )$
has finite height.

4.1 Frames and partial bases
Definition 4.1 (Frame)
A partial frame of X is a
![]() $\sqcup $
-partial decomposition
$\sqcup $
-partial decomposition
![]() $\sigma \in {\mathcal {PD}}(X,\sqcup )$
where all elements of
$\sigma \in {\mathcal {PD}}(X,\sqcup )$
where all elements of
![]() $\sigma $
are atoms of
$\sigma $
are atoms of
![]() ${\mathcal {S}}(X,\sqcup )$
. We write
${\mathcal {S}}(X,\sqcup )$
. We write
![]() ${\mathcal {PF}}(X,\sqcup )$
for the subposet of
${\mathcal {PF}}(X,\sqcup )$
for the subposet of
![]() ${\mathcal {PD}}(X,\sqcup )$
consisting of all partial frames of X.
${\mathcal {PD}}(X,\sqcup )$
consisting of all partial frames of X.
A partial frame
![]() $\sigma $
is called a full frame of X if
$\sigma $
is called a full frame of X if
![]() $\sigma \in {\mathcal D}(X,\sqcup )$
. We write
$\sigma \in {\mathcal D}(X,\sqcup )$
. We write
![]() ${\mathcal F}(X,\sqcup )$
for the subposet of
${\mathcal F}(X,\sqcup )$
for the subposet of
![]() ${\mathcal {PF}}(X,\sqcup )$
consisting of partial frames contained in full frames.
${\mathcal {PF}}(X,\sqcup )$
consisting of partial frames contained in full frames.
The following property follows immediately from the definition.
Lemma 4.2. The posets
![]() ${\mathcal F}(X,\sqcup )\subseteq {\mathcal {PF}}(X,\sqcup )$
are lower intervals of
${\mathcal F}(X,\sqcup )\subseteq {\mathcal {PF}}(X,\sqcup )$
are lower intervals of
![]() ${\mathcal {PD}}(X,\sqcup )$
. Moreover, the refinement ordering
${\mathcal {PD}}(X,\sqcup )$
. Moreover, the refinement ordering
![]() $\leq $
in
$\leq $
in
![]() ${\mathcal F}(X,\sqcup )$
and
${\mathcal F}(X,\sqcup )$
and
![]() ${\mathcal {PF}}(X,\sqcup )$
coincides with the inclusion ordering
${\mathcal {PF}}(X,\sqcup )$
coincides with the inclusion ordering
![]() $\subseteq $
, and hence, these posets are simplicial complexes.
$\subseteq $
, and hence, these posets are simplicial complexes.
Now we use frames to recover the idea of bases. We propose the following definition for the partial basis complexes, based on inflation complexes.
Definition 4.3. Let K be a simplicial complex with vertex set
![]() $\mathcal {A}$
. For every vertex x of K, take a nonempty set
$\mathcal {A}$
. For every vertex x of K, take a nonempty set
![]() $P_x$
, and set
$P_x$
, and set
![]() $P = (P_x)_{x\in \mathcal {A}}$
. The inflation complex
$P = (P_x)_{x\in \mathcal {A}}$
. The inflation complex
![]() $(K,P)$
is the simplicial complex whose vertices are the pairs
$(K,P)$
is the simplicial complex whose vertices are the pairs
![]() $(x,a)$
, with
$(x,a)$
, with
![]() $a\in P_x$
, and simplices are sets of vertices
$a\in P_x$
, and simplices are sets of vertices
![]() $\{ (x_1,a_1), \ldots , (x_r,a_r)\}$
such that
$\{ (x_1,a_1), \ldots , (x_r,a_r)\}$
such that
![]() $x_i\neq x_j$
if
$x_i\neq x_j$
if
![]() $i\neq j$
and
$i\neq j$
and
![]() $\{x_1,\ldots , x_r\}$
is a simplex of K.
$\{x_1,\ldots , x_r\}$
is a simplex of K.
Write
![]() $p_{(K,P)}$
(or simply p) for the simplicial map
$p_{(K,P)}$
(or simply p) for the simplicial map
![]() $(K,P)\to K$
obtained by projecting the vertices of
$(K,P)\to K$
obtained by projecting the vertices of
![]() $(K,P)$
onto their first variable (the deflation map).
$(K,P)$
onto their first variable (the deflation map).
If each
![]() $P_{x}$
is finite, then
$P_{x}$
is finite, then
![]() $(K,P)$
is an inflation of K in the sense of [Reference Björner, Wachs and WelkerBWW, Section 6]. We will see that results analogous to those from [Reference Björner, Wachs and WelkerBWW] hold in the general situation, where the sets
$(K,P)$
is an inflation of K in the sense of [Reference Björner, Wachs and WelkerBWW, Section 6]. We will see that results analogous to those from [Reference Björner, Wachs and WelkerBWW] hold in the general situation, where the sets
![]() $P_x$
are not necessarily finite or have the same size.
$P_x$
are not necessarily finite or have the same size.
Definition 4.4 (Partial bases)
Let
![]() $\mathcal {A}$
be the set of vertices of
$\mathcal {A}$
be the set of vertices of
![]() ${\mathcal {PF}}(X,\sqcup )$
and
${\mathcal {PF}}(X,\sqcup )$
and
![]() $(P_x)_{x \in \mathcal {A}}$
be a collection of nonempty sets. A simplex B in the inflation complex
$(P_x)_{x \in \mathcal {A}}$
be a collection of nonempty sets. A simplex B in the inflation complex
![]() $({\mathcal {PF}}(X,\sqcup ), P)$
is termed a partial basis of X. We say that B extends to a full basis if
$({\mathcal {PF}}(X,\sqcup ), P)$
is termed a partial basis of X. We say that B extends to a full basis if
![]() $p(B)\in {\mathcal F}(X,\sqcup )$
. Denote by
$p(B)\in {\mathcal F}(X,\sqcup )$
. Denote by
![]() $\mathcal {PB}(X,\sqcup ,P) = ({\mathcal {PF}}(X,\sqcup ), P)$
the complex of partial bases with respect to the collection P, and by
$\mathcal {PB}(X,\sqcup ,P) = ({\mathcal {PF}}(X,\sqcup ), P)$
the complex of partial bases with respect to the collection P, and by
![]() $\mathcal {B}(X,\sqcup ,P)$
the complex of partial bases that extend to a full basis.
$\mathcal {B}(X,\sqcup ,P)$
the complex of partial bases that extend to a full basis.
Intuitively, we think of
![]() $P_x$
as a set of suitable bases of the atom x. For example, if x represents a
$P_x$
as a set of suitable bases of the atom x. For example, if x represents a
![]() $1$
-dimensional vector space in the subspace poset, then
$1$
-dimensional vector space in the subspace poset, then
![]() $P_x$
can represent the set of nonzero vectors in x. If x represents a
$P_x$
can represent the set of nonzero vectors in x. If x represents a
![]() $1$
-dimensional nondegenerate subspace in the nondegenerate subspace poset of a unitary space, we can take
$1$
-dimensional nondegenerate subspace in the nondegenerate subspace poset of a unitary space, we can take
![]() $P_x$
to be the set of normal vectors
$P_x$
to be the set of normal vectors
![]() $v\in x$
.
$v\in x$
.
To simplify the notation, we will usually drop the P from the notation and leave the collection implicit. When the stated results strongly depend on the collection P, we will use the notation again.
4.2 Ordered versions
We define the ordered versions of the posets attached to
![]() ${\mathcal {S}}(X,\sqcup )$
.
${\mathcal {S}}(X,\sqcup )$
.
Definition 4.5. Let
![]() ${\mathcal T}$
be one of the symbols
${\mathcal T}$
be one of the symbols
![]() ${\mathcal D}, {\mathcal {PD}}, {\mathcal F}, {\mathcal {PF}}, \mathcal {B},\mathcal {PB}$
. The ordered poset
${\mathcal D}, {\mathcal {PD}}, {\mathcal F}, {\mathcal {PF}}, \mathcal {B},\mathcal {PB}$
. The ordered poset
![]() $\mathcal {O}{\mathcal T}(X,\sqcup )$
consists of distinct-element tuples
$\mathcal {O}{\mathcal T}(X,\sqcup )$
consists of distinct-element tuples
![]() $(x_1,\ldots ,x_r)$
,
$(x_1,\ldots ,x_r)$
,
![]() $r\geq 0$
, such that
$r\geq 0$
, such that
![]() $\{x_1,\ldots ,x_r\}\in {\mathcal T}(X,\sqcup )$
. The order in
$\{x_1,\ldots ,x_r\}\in {\mathcal T}(X,\sqcup )$
. The order in
![]() $\mathcal {O}{\mathcal T}(X,\sqcup )$
is given by order-preserving refinement; that is,
$\mathcal {O}{\mathcal T}(X,\sqcup )$
is given by order-preserving refinement; that is,
We denote by
![]() $F_{\mathcal T}:\mathcal {O}{\mathcal T}(X,\sqcup )\to {\mathcal T}(X,\sqcup )$
the forgetful poset map.
$F_{\mathcal T}:\mathcal {O}{\mathcal T}(X,\sqcup )\to {\mathcal T}(X,\sqcup )$
the forgetful poset map.
Remark 4.6. For a simplicial complex K, let
![]() $\mathcal {O} K$
be the complex of injective words on K. That is,
$\mathcal {O} K$
be the complex of injective words on K. That is,
![]() $\mathcal {O} K$
is a set whose elements are tuples
$\mathcal {O} K$
is a set whose elements are tuples
![]() $z = (v_1,\ldots ,v_r)$
consisting of distinct vertices of K and such that
$z = (v_1,\ldots ,v_r)$
consisting of distinct vertices of K and such that
![]() $F_K(z) = \{v_1,\ldots ,v_r\}$
is a simplex of K. Similar to the previous definition,
$F_K(z) = \{v_1,\ldots ,v_r\}$
is a simplex of K. Similar to the previous definition,
![]() $\mathcal {O} K$
is a poset ordered by order-preserving inclusion, and we have a forgetful poset map
$\mathcal {O} K$
is a poset ordered by order-preserving inclusion, and we have a forgetful poset map
![]() $F_K:\mathcal {O} K\to K$
. However,
$F_K:\mathcal {O} K\to K$
. However,
![]() $\mathcal {O} K$
is not a simplicial complex in general.
$\mathcal {O} K$
is not a simplicial complex in general.
We see then that the poset
![]() $\mathcal {O} {\mathcal T}(X,\sqcup )$
, for
$\mathcal {O} {\mathcal T}(X,\sqcup )$
, for
![]() ${\mathcal T}\in \{{\mathcal F},{\mathcal {PF}}, \mathcal {B},\mathcal {PB}\}$
, is exactly the complex of injective words over
${\mathcal T}\in \{{\mathcal F},{\mathcal {PF}}, \mathcal {B},\mathcal {PB}\}$
, is exactly the complex of injective words over
![]() ${\mathcal T}(X,\sqcup )$
. As a consequence, we will be able to invoke results from [Reference Jonsson and WelkerJW].
${\mathcal T}(X,\sqcup )$
. As a consequence, we will be able to invoke results from [Reference Jonsson and WelkerJW].
The following example gives us some idea of the structure of the ordered versions:
Example 4.7. Let
![]() $X = \mathbb {F}_{2}^2$
be the
$X = \mathbb {F}_{2}^2$
be the
![]() $2$
-dimensional vector space over the field with two elements. For the monoidal product, we take
$2$
-dimensional vector space over the field with two elements. For the monoidal product, we take
![]() $\sqcup =\oplus $
, the direct sum in the category of vector spaces over
$\sqcup =\oplus $
, the direct sum in the category of vector spaces over
![]() $\mathbb {F}_{2}$
. There are exactly three nontrivial proper subspaces, which we may denote by
$\mathbb {F}_{2}$
. There are exactly three nontrivial proper subspaces, which we may denote by
![]() $U_1, U_2, U_{3}$
. Then
$U_1, U_2, U_{3}$
. Then
![]() ${\mathcal {S}}(X,\sqcup )={\mathcal {S}}(V)$
, the poset of subspaces of V, has the following structure:
${\mathcal {S}}(X,\sqcup )={\mathcal {S}}(V)$
, the poset of subspaces of V, has the following structure:
From the Hasse diagram of
![]() ${\mathcal {S}}(V)$
, we see that there are three full decompositions
${\mathcal {S}}(V)$
, we see that there are three full decompositions
From this, one easily determines the partial decomposition poset
![]() ${\mathcal {PD}}(X,\sqcup )={\mathcal {PD}}(V)$
and its ordered version. See Figure 5.
${\mathcal {PD}}(X,\sqcup )={\mathcal {PD}}(V)$
and its ordered version. See Figure 5.
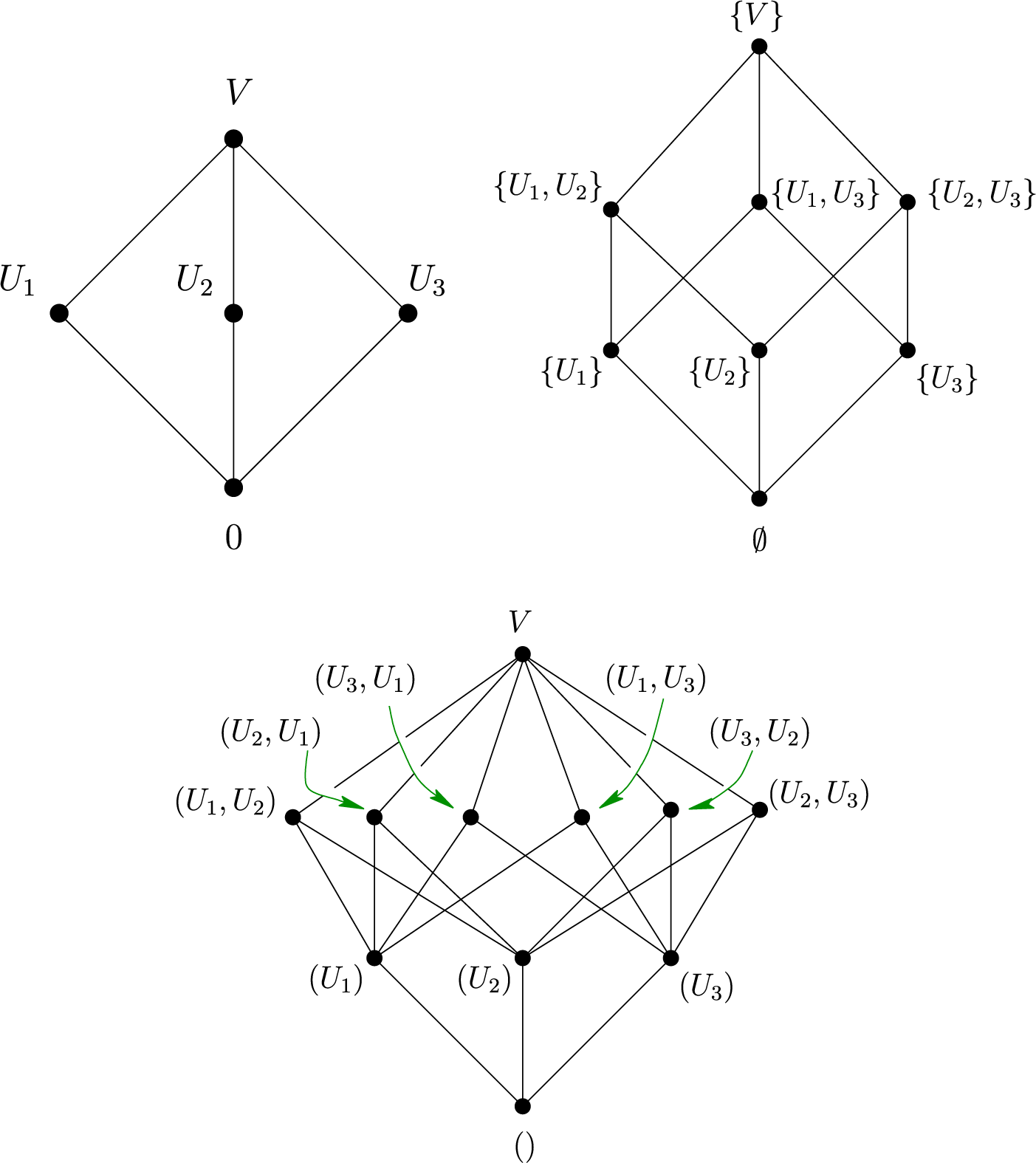
Figure 5 Poset of subspaces of
![]() $V = \mathbb {F}_{2}^2$
(top left), poset of partial decompositions of V (top right) and poset of ordered partial decompositions of V (bottom). Here,
$V = \mathbb {F}_{2}^2$
(top left), poset of partial decompositions of V (top right) and poset of ordered partial decompositions of V (bottom). Here,
![]() $U_1 = \left \langle (1,0)\right \rangle $
,
$U_1 = \left \langle (1,0)\right \rangle $
,
![]() $U_2 = \left \langle (1,1)\right \rangle $
, and
$U_2 = \left \langle (1,1)\right \rangle $
, and
![]() $U_3 = \left \langle (0,1)\right \rangle $
.
$U_3 = \left \langle (0,1)\right \rangle $
.
Example 4.8. Let
![]() $X = \{1,\ldots , n\}$
be in the category of sets with
$X = \{1,\ldots , n\}$
be in the category of sets with
![]() $\sqcup = \coprod $
the disjoint union. Then
$\sqcup = \coprod $
the disjoint union. Then
![]() ${\mathcal {S}}(X,\sqcup )$
is the Boolean lattice,
${\mathcal {S}}(X,\sqcup )$
is the Boolean lattice,
![]() ${\mathcal D}(X,\sqcup ) = \Pi (n)$
is the partition lattice, and
${\mathcal D}(X,\sqcup ) = \Pi (n)$
is the partition lattice, and
![]() ${\mathcal {PD}}(X,\sqcup )$
is the partial partition lattice. The ordered partial partition poset
${\mathcal {PD}}(X,\sqcup )$
is the partial partition lattice. The ordered partial partition poset
![]() ${{\mathcal O}}{\mathcal {PD}}(X,\sqcup )$
for the case
${{\mathcal O}}{\mathcal {PD}}(X,\sqcup )$
for the case
![]() $n=3$
is given in Figure 6. The blue subposet shows the ordered partition poset
$n=3$
is given in Figure 6. The blue subposet shows the ordered partition poset
![]() ${{\mathcal O}}{\mathcal D}(X,\sqcup )$
.
${{\mathcal O}}{\mathcal D}(X,\sqcup )$
.
Figure 6 Ordered partial and full partition poset.
Proposition 1.4 of [Reference Billera and SarangarajanBS96] states that the ordered partition lattice is the face lattice of the permutohedron
![]() $P_n$
of order n.
$P_n$
of order n.
Since we aim to relate later the homotopy type of
![]() $\mathcal {O} {\mathcal T}(X,\sqcup )$
with that of
$\mathcal {O} {\mathcal T}(X,\sqcup )$
with that of
![]() ${\mathcal T}(X,\sqcup )$
, in the following lemmas, we take a closer look at the fibers by the canonical forgetful maps and the intervals in the ordered versions.
${\mathcal T}(X,\sqcup )$
, in the following lemmas, we take a closer look at the fibers by the canonical forgetful maps and the intervals in the ordered versions.
Lemma 4.9. The following hold:
-
(1)
 $F_{\mathcal D}^{-1}( {\mathcal D}(X,\sqcup )_{\geq \sigma } )$
is the ordered partition lattice on the set
$F_{\mathcal D}^{-1}( {\mathcal D}(X,\sqcup )_{\geq \sigma } )$
is the ordered partition lattice on the set
 $\sigma $
, which is the face poset of a permutohedron of order
$\sigma $
, which is the face poset of a permutohedron of order
 $|\sigma |$
. Thus,
$|\sigma |$
. Thus,
 $F_{\mathcal D}^{-1}( {\mathcal D}(X,\sqcup )^{\circ }_{\geq \sigma } )$
is a sphere of dimension
$F_{\mathcal D}^{-1}( {\mathcal D}(X,\sqcup )^{\circ }_{\geq \sigma } )$
is a sphere of dimension
 $|\sigma |-2$
(and also Cohen-Macaulay).
$|\sigma |-2$
(and also Cohen-Macaulay). -
(2) If
 $\sigma \in {\mathcal {PD}}(X,\sqcup )^{*}\setminus {\mathcal D}(X,\sqcup )^{\circ }$
, then
$\sigma \in {\mathcal {PD}}(X,\sqcup )^{*}\setminus {\mathcal D}(X,\sqcup )^{\circ }$
, then
 $F_{{\mathcal {PD}}}^{-1}\big ( \ ({\mathcal {PD}}(X,\sqcup )^{*})_{\geq \sigma } \ \big )$
is contractible.
$F_{{\mathcal {PD}}}^{-1}\big ( \ ({\mathcal {PD}}(X,\sqcup )^{*})_{\geq \sigma } \ \big )$
is contractible. -
(3) For a simplicial complex K and
 $\sigma \in K$
,
$\sigma \in K$
,
 $F_{K}^{-1}( K_{\leq \sigma } )$
is the ordered version of the Boolean lattice – namely, the poset of injective words. In particular,
$F_{K}^{-1}( K_{\leq \sigma } )$
is the ordered version of the Boolean lattice – namely, the poset of injective words. In particular,
 $F_{K}^{-1}( K_{\leq \sigma } )$
is shellable of dimension
$F_{K}^{-1}( K_{\leq \sigma } )$
is shellable of dimension
 $|\sigma |-1$
, and the number of spheres is the number of derangements on
$|\sigma |-1$
, and the number of spheres is the number of derangements on
 $|\sigma |$
points:
$|\sigma |$
points:  $$\begin{align*}\sum_{i=0}^{|\sigma|} (-1)^{i} \frac{|\sigma|!}{i!}.\end{align*}$$
$$\begin{align*}\sum_{i=0}^{|\sigma|} (-1)^{i} \frac{|\sigma|!}{i!}.\end{align*}$$
Proof. Since
![]() ${\mathcal D}(X,\sqcup )_{\geq \sigma }$
is the partition lattice on the set
${\mathcal D}(X,\sqcup )_{\geq \sigma }$
is the partition lattice on the set
![]() $\sigma $
by Lemma 2.5, it is clear that
$\sigma $
by Lemma 2.5, it is clear that
![]() $F_{\mathcal D}^{-1}( {\mathcal D}(X,\sqcup )_{\geq \sigma } )$
is the ordered partition lattice on the set
$F_{\mathcal D}^{-1}( {\mathcal D}(X,\sqcup )_{\geq \sigma } )$
is the ordered partition lattice on the set
![]() $\sigma $
. Now, by Proposition 1.4 of [Reference Billera and SarangarajanBS96], this is the face lattice of the permutahedron of order
$\sigma $
. Now, by Proposition 1.4 of [Reference Billera and SarangarajanBS96], this is the face lattice of the permutahedron of order
![]() $|\sigma |$
. The second part of item 1 now follows since the order complex of the face lattice of a polytope is a sphere.
$|\sigma |$
. The second part of item 1 now follows since the order complex of the face lattice of a polytope is a sphere.
Item 3 follows similarly, and the shellability is implied by Theorem 6.1 of [Reference Björner and WachsBW].
For item 2, we construct a homotopy between the identity and a constant map. Since
![]() $\sigma $
is a nonempty
$\sigma $
is a nonempty
![]() $\sqcup $
-partial decomposition (not full), there exists
$\sqcup $
-partial decomposition (not full), there exists
![]() $x = \bigvee _{y\in \sigma } y$
, and this is different from
$x = \bigvee _{y\in \sigma } y$
, and this is different from
![]() $1$
and
$1$
and
![]() $0$
. Let
$0$
. Let
![]() $\tau \in F^{-1}_{{\mathcal {PD}}}( ({\mathcal {PD}}(X,\sqcup )^{*})_{\geq \sigma })$
, and write
$\tau \in F^{-1}_{{\mathcal {PD}}}( ({\mathcal {PD}}(X,\sqcup )^{*})_{\geq \sigma })$
, and write
![]() $\tau = (z_1,\ldots ,z_s)$
. Define
$\tau = (z_1,\ldots ,z_s)$
. Define
and let
![]() $r(\tau )$
be the tuple
$r(\tau )$
be the tuple
![]() $(z_1',\ldots ,z_s')$
after removing the
$(z_1',\ldots ,z_s')$
after removing the
![]() $0$
elements. We see that
$0$
elements. We see that
![]() $F_{{\mathcal {PD}}}(r(\tau ))$
is a
$F_{{\mathcal {PD}}}(r(\tau ))$
is a
![]() $\sqcup $
-partial decomposition obtained by joining elements of
$\sqcup $
-partial decomposition obtained by joining elements of
![]() $\sigma $
, so
$\sigma $
, so
![]() $F_{{\mathcal {PD}}}(r(\tau ))\geq \sigma $
. Thus, we have well-defined order-preserving maps
$F_{{\mathcal {PD}}}(r(\tau ))\geq \sigma $
. Thus, we have well-defined order-preserving maps
This implies that
![]() $F^{-1}_{{\mathcal {PD}}}( ({\mathcal {PD}}(X,\sqcup )^{*})_{\geq \sigma })$
is contractible.
$F^{-1}_{{\mathcal {PD}}}( ({\mathcal {PD}}(X,\sqcup )^{*})_{\geq \sigma })$
is contractible.
We describe now some intervals in the ordered versions. Recall property (LI) from Definition 3.2. Here,
![]() $|z|$
denotes the size of an ordered tuple z – that is, the number of (distinct) elements of the tuple.
$|z|$
denotes the size of an ordered tuple z – that is, the number of (distinct) elements of the tuple.
Lemma 4.10. The following hold:
-
(1) For
 $z\in \mathcal {O}{\mathcal D}(X,\sqcup )$
,
$z\in \mathcal {O}{\mathcal D}(X,\sqcup )$
,
 $\mathcal {O}{\mathcal D}(X,\sqcup )_{\geq z}$
is the Boolean lattice on a set of size
$\mathcal {O}{\mathcal D}(X,\sqcup )_{\geq z}$
is the Boolean lattice on a set of size
 $|z|-1$
. In particular, if
$|z|-1$
. In particular, if
 ${\mathcal D}(X,\sqcup )$
is finite, then
${\mathcal D}(X,\sqcup )$
is finite, then  $$\begin{align*}\tilde{\chi}\left(\mathcal{O}{\mathcal D}(X,\sqcup)^{\circ}\right) = \sum_{k\geq 1} (-1)^{k} \cdot k! \cdot \# \{\sigma\in {\mathcal D}(X,\sqcup) \mathrel{{\: : \: }} |\sigma| = k\}.\end{align*}$$
$$\begin{align*}\tilde{\chi}\left(\mathcal{O}{\mathcal D}(X,\sqcup)^{\circ}\right) = \sum_{k\geq 1} (-1)^{k} \cdot k! \cdot \# \{\sigma\in {\mathcal D}(X,\sqcup) \mathrel{{\: : \: }} |\sigma| = k\}.\end{align*}$$
-
(2) Suppose that property (LI) holds. Then for
 $z\in \mathcal {O}{\mathcal {PD}}(X,\sqcup )$
, we have and if
$z\in \mathcal {O}{\mathcal {PD}}(X,\sqcup )$
, we have and if $$\begin{align*}\mathcal{O}{\mathcal{PD}}(X,\sqcup)_{\leq z} \cong \prod_{y\in z} \mathcal{O} {\mathcal{PD}}(Y,\sqcup), \end{align*}$$
$$\begin{align*}\mathcal{O}{\mathcal{PD}}(X,\sqcup)_{\leq z} \cong \prod_{y\in z} \mathcal{O} {\mathcal{PD}}(Y,\sqcup), \end{align*}$$
 $z\in \mathcal {O}{\mathcal D}(X,\sqcup )$
, then also
$z\in \mathcal {O}{\mathcal D}(X,\sqcup )$
, then also  $$\begin{align*}\mathcal{O}{\mathcal D}(X,\sqcup)_{\leq z} \cong \prod_{y\in z} \mathcal{O} {\mathcal D}(Y,\sqcup). \end{align*}$$
$$\begin{align*}\mathcal{O}{\mathcal D}(X,\sqcup)_{\leq z} \cong \prod_{y\in z} \mathcal{O} {\mathcal D}(Y,\sqcup). \end{align*}$$
Here,
 $(Y,i_y)\in y$
denote suitable representatives for
$(Y,i_y)\in y$
denote suitable representatives for
 $y\in z$
.
$y\in z$
. -
(3) Let K be a simplicial complex and
 $z\in \mathcal {O} K$
. Then
$z\in \mathcal {O} K$
. Then
 $\mathcal {O} K_{>z} \cong \mathcal {O}\operatorname {\mathrm {Lk}}_{K}(z)$
and
$\mathcal {O} K_{>z} \cong \mathcal {O}\operatorname {\mathrm {Lk}}_{K}(z)$
and
 $\mathcal {O} K_{\leq z}$
is the Boolean lattice on
$\mathcal {O} K_{\leq z}$
is the Boolean lattice on
 $F_{K}(z)$
.
$F_{K}(z)$
.
Proof. These are straightforward.
Finally, we establish a connection between the ordered version of the poset of decompositions and the subposet of
![]() $(\sqcup ,h)$
-complemented subobjects.
$(\sqcup ,h)$
-complemented subobjects.
Definition 4.11. Let
![]() $G:\mathcal {O}{\mathcal {PD}}(X,\sqcup )^{*} \to {(\Delta {\mathcal {S}}_h(X,\sqcup )^{*})}^{\mathrm {op}} \cup \{\emptyset \}$
be the function
$G:\mathcal {O}{\mathcal {PD}}(X,\sqcup )^{*} \to {(\Delta {\mathcal {S}}_h(X,\sqcup )^{*})}^{\mathrm {op}} \cup \{\emptyset \}$
be the function
It is clear that if
![]() $\{x_1,\ldots ,x_r\}$
is a
$\{x_1,\ldots ,x_r\}$
is a
![]() $\sqcup $
-partial decomposition, then any join of its elements is
$\sqcup $
-partial decomposition, then any join of its elements is
![]() $(\sqcup ,h)$
-complemented, and hence belongs to
$(\sqcup ,h)$
-complemented, and hence belongs to
![]() ${\mathcal {S}}_h(X,\sqcup )$
. Thus, G is a well-defined function. However, G is not order-preserving for partial decompositions: for example, if
${\mathcal {S}}_h(X,\sqcup )$
. Thus, G is a well-defined function. However, G is not order-preserving for partial decompositions: for example, if
![]() $x\leq y$
and
$x\leq y$
and
![]() $\{x,z\}, \{y,z\}$
are
$\{x,z\}, \{y,z\}$
are
![]() $\sqcup $
-partial decompositions, then
$\sqcup $
-partial decompositions, then
![]() $(x,z)\leq (y,z)$
but
$(x,z)\leq (y,z)$
but
![]() $G(x,z) = \{x\}\not \subseteq \{y\} = G(y,z) $
. Nevertheless, this is a poset map when restricted to decompositions:
$G(x,z) = \{x\}\not \subseteq \{y\} = G(y,z) $
. Nevertheless, this is a poset map when restricted to decompositions:
Lemma 4.12. The restriction
![]() $G: \mathcal {O}{\mathcal D}(X,\sqcup )^{\circ }\to {\left (\Delta \big ( {\mathcal {S}}_h(X,\sqcup )^{*}\big ) \right )}^{\mathrm {op}}$
is an order-preserving map.
$G: \mathcal {O}{\mathcal D}(X,\sqcup )^{\circ }\to {\left (\Delta \big ( {\mathcal {S}}_h(X,\sqcup )^{*}\big ) \right )}^{\mathrm {op}}$
is an order-preserving map.
Proof. This follows since elements of
![]() $\mathcal {O}{\mathcal D}(X,\sqcup )_{>\tau }$
are obtained by joining adjacent blocks of an ordered decomposition
$\mathcal {O}{\mathcal D}(X,\sqcup )_{>\tau }$
are obtained by joining adjacent blocks of an ordered decomposition
![]() $\tau $
. That is, if
$\tau $
. That is, if
![]() $\sigma>\tau $
and
$\sigma>\tau $
and
![]() $\tau = (x_1,\ldots ,x_r)$
, we can write
$\tau = (x_1,\ldots ,x_r)$
, we can write
 $$\begin{align*}\sigma = \bigg( {\bigvee_{i=1}^{t_1}}x_i, \bigvee_{i=t_1+1}^{t_2} x_i,\ldots, \bigvee_{i=t_{s-1}+1}^{r}x_i\bigg)\end{align*}$$
$$\begin{align*}\sigma = \bigg( {\bigvee_{i=1}^{t_1}}x_i, \bigvee_{i=t_1+1}^{t_2} x_i,\ldots, \bigvee_{i=t_{s-1}+1}^{r}x_i\bigg)\end{align*}$$
for suitable
![]() $1 \leq t_1 < t_2 < \cdots < t_s = r$
. Thus,
$1 \leq t_1 < t_2 < \cdots < t_s = r$
. Thus,
![]() $G(\tau )$
contains
$G(\tau )$
contains
![]() $G(\sigma )$
.
$G(\sigma )$
.
We will see later that this map turns out to be an isomorphism under unique complementation and suitable extension properties. See Lemma 5.17 and Lemma 5.18.
4.3 The augmented Bergman complex
We introduce now a (simplified) version of the augmented Bergman complex in our context. This complex was first defined for matroids, and it gained substantial attention due to the work [Reference Braden, Huh, Matherne, Proudfoot and WangBHMPW] where its Stanley-Reisner ring is a key object in the proofs of the Top-Heavy conjecture (raised by Dowling and Wilson), and the non-negativity of the coefficients of Kazhdan-Lusztig polynomials for all matroids. Its topology in the matroid case was carefully analyzed in [Reference Bullock, Kelley, Reiner, Ren, Shemy, Shen, Sun and ZhangBKR].
Definition 4.13 (Bergman)
Take disjoint copies of the vertices of
![]() ${\mathcal F}(X,\sqcup )$
and the atoms of
${\mathcal F}(X,\sqcup )$
and the atoms of
![]() ${\mathcal {S}}(X,\sqcup )$
.
${\mathcal {S}}(X,\sqcup )$
.
In
![]() $\Delta (X,\sqcup )$
, we collect all sets
$\Delta (X,\sqcup )$
, we collect all sets
![]() $\sigma \cup \{ x_1 \lneq x_2 \lneq \cdots \lneq x_r\}$
where
$\sigma \cup \{ x_1 \lneq x_2 \lneq \cdots \lneq x_r\}$
where
![]() $\sigma \in {\mathcal F}(X,\sqcup )$
and
$\sigma \in {\mathcal F}(X,\sqcup )$
and
![]() $\Phi (\sigma ) \leq x_1,\ldots , x_r \in {\mathcal {S}}(X,\sqcup )^{\circ }$
. We call
$\Phi (\sigma ) \leq x_1,\ldots , x_r \in {\mathcal {S}}(X,\sqcup )^{\circ }$
. We call
![]() $\Delta (X,\sqcup )$
the augmented Bergman complex of X.
$\Delta (X,\sqcup )$
the augmented Bergman complex of X.
It is a direct consequence of the definition that the augmented Bergman complex
![]() $\Delta (X,\sqcup )$
is indeed a simplicial complex. Note that if
$\Delta (X,\sqcup )$
is indeed a simplicial complex. Note that if
![]() $\sigma \in {\mathcal F}(X,\sqcup )$
is a full frame, then
$\sigma \in {\mathcal F}(X,\sqcup )$
is a full frame, then
![]() $\sigma \in \Delta (X,\sqcup )$
is a maximal simplex. Also note that
$\sigma \in \Delta (X,\sqcup )$
is a maximal simplex. Also note that
![]() $0 \in {\mathcal {S}}(X,\sqcup )$
is a vertex of
$0 \in {\mathcal {S}}(X,\sqcup )$
is a vertex of
![]() $\Delta (X,\sqcup )$
, and a simplex containing
$\Delta (X,\sqcup )$
, and a simplex containing
![]() $0$
must be a flag of
$0$
must be a flag of
![]() ${\mathcal {S}}(X,\sqcup )^{\circ }$
.
${\mathcal {S}}(X,\sqcup )^{\circ }$
.
4.4 The Charney poset
A different version of the ordered decompositions was introduced by R. Charney in [Reference CharneyC]. There she works with the poset of summands of a finitely generated free module over a Dedekind domain, and defines a poset whose elements are ordered direct sum decompositions of size two with a zigzag ordering. Another version of Charney’s poset appears in the context of split buildings for spaces with a certain form, and we interpret decompositions of size two there as direct sum decomposition pairs
![]() $(V_1,V_2)$
such that
$(V_1,V_2)$
such that
![]() $V_1$
and the orthogonal complement of
$V_1$
and the orthogonal complement of
![]() $V_2$
are totally isotropic subspaces (see [Reference Lehrer and RylandsLR]).
$V_2$
are totally isotropic subspaces (see [Reference Lehrer and RylandsLR]).
We adapt the definition of this poset to our context.
Definition 4.14. The Charney poset associated with X is the poset
![]() $\mathcal {G}(X,\sqcup )$
whose underlying set consists of ordered decompositions of size two:
$\mathcal {G}(X,\sqcup )$
whose underlying set consists of ordered decompositions of size two:
and the ordering is given by
The following proposition relates the ordered decompositions to the Charney complex.
Proposition 4.15. Let
![]() $\beta $
be the function
$\beta $
be the function
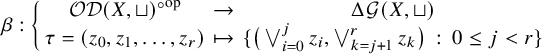 $$\begin{align*}\beta :\left\{ \begin{array}{ccc} {{\mathcal{OD}}(X,\sqcup)^{\circ}}^{\mathrm{op}} & \to & \Delta \mathcal{G}(X,\sqcup)\\ \tau=(z_0,z_1,\ldots,z_r) & \mapsto & \{ \big(\bigvee_{i=0}^j z_i, \bigvee_{k=j+1}^r z_k\big) \mathrel{{\: : \: }} 0\leq j <r \} \end{array} \right.\end{align*}$$
$$\begin{align*}\beta :\left\{ \begin{array}{ccc} {{\mathcal{OD}}(X,\sqcup)^{\circ}}^{\mathrm{op}} & \to & \Delta \mathcal{G}(X,\sqcup)\\ \tau=(z_0,z_1,\ldots,z_r) & \mapsto & \{ \big(\bigvee_{i=0}^j z_i, \bigvee_{k=j+1}^r z_k\big) \mathrel{{\: : \: }} 0\leq j <r \} \end{array} \right.\end{align*}$$
Then
![]() $\beta $
is a rank-preserving poset embedding whose image is downward closed.
$\beta $
is a rank-preserving poset embedding whose image is downward closed.
Moreover, if properties (EX) and (CM) from Definition 3.10 hold, then
![]() $\beta $
is surjective and therefore an isomorphism.
$\beta $
is surjective and therefore an isomorphism.
Proof. It is clear that
![]() $\beta $
is a well-defined, order-preserving and rank-preserving map, and also injective: if
$\beta $
is a well-defined, order-preserving and rank-preserving map, and also injective: if
![]() $\beta (z_0,\ldots ,z_r) = \{ (x_0,y_0) < \cdots < (x_{r-1}, y_{r-1}) \}$
, then
$\beta (z_0,\ldots ,z_r) = \{ (x_0,y_0) < \cdots < (x_{r-1}, y_{r-1}) \}$
, then
 $$ \begin{align} z_j = (\bigvee_{i=0}^j z_i\big) \wedge \big( \bigvee_{k=j}^r z_k\big) = x_j \wedge y_{j-1}. \end{align} $$
$$ \begin{align} z_j = (\bigvee_{i=0}^j z_i\big) \wedge \big( \bigvee_{k=j}^r z_k\big) = x_j \wedge y_{j-1}. \end{align} $$
Note that this meet always exists by definition of a decomposition. By convention, we set
![]() $x_{-1}=0, y_{-1}=1$
and
$x_{-1}=0, y_{-1}=1$
and
![]() $x_r=1,y_r=0$
.
$x_r=1,y_r=0$
.
We show now that
![]() $\beta $
is an embedding. Suppose that
$\beta $
is an embedding. Suppose that
![]() $\beta (\tau )\supseteq \beta (\sigma )$
with
$\beta (\tau )\supseteq \beta (\sigma )$
with
For
![]() $0\leq i\leq s-1$
, we take the unique index
$0\leq i\leq s-1$
, we take the unique index
![]() $0\leq j_i\leq r-1$
such that
$0\leq j_i\leq r-1$
such that
![]() $(u_i,v_i) = (x_{j_i},y_{j_i})$
. Since
$(u_i,v_i) = (x_{j_i},y_{j_i})$
. Since
![]() $(u_{-1},v_{-1}) = (x_{-1},y_{-1})$
and
$(u_{-1},v_{-1}) = (x_{-1},y_{-1})$
and
![]() $(u_s,v_s) = (x_r,y_r)$
, we set
$(u_s,v_s) = (x_r,y_r)$
, we set
![]() $j_{-1} = -1$
and
$j_{-1} = -1$
and
![]() $j_s = r$
. It is clear that
$j_s = r$
. It is clear that
![]() $(j_i)_{i=-1}^{s}$
is a strictly monotone increasing sequence. Then, for all
$(j_i)_{i=-1}^{s}$
is a strictly monotone increasing sequence. Then, for all
![]() $0\leq i\leq s$
, we have
$0\leq i\leq s$
, we have
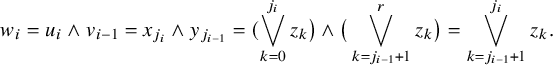 $$\begin{align*}w_i = u_i\wedge v_{i-1} = x_{j_i}\wedge y_{j_{i-1}} = (\bigvee_{k=0}^{j_i} z_k\big) \wedge \big( \bigvee_{k=j_{i-1}+1}^r z_k\big) = \bigvee_{k=j_{i-1}+1}^{j_i}z_k.\end{align*}$$
$$\begin{align*}w_i = u_i\wedge v_{i-1} = x_{j_i}\wedge y_{j_{i-1}} = (\bigvee_{k=0}^{j_i} z_k\big) \wedge \big( \bigvee_{k=j_{i-1}+1}^r z_k\big) = \bigvee_{k=j_{i-1}+1}^{j_i}z_k.\end{align*}$$
This implies that
![]() $\tau \leq \sigma $
, so
$\tau \leq \sigma $
, so
![]() $\beta $
is a poset embedding. It is also clear that if
$\beta $
is a poset embedding. It is also clear that if
![]() $\omega \subseteq \beta (z)$
, then
$\omega \subseteq \beta (z)$
, then
![]() $\omega \in \mathrm {Im}(\beta )$
.
$\omega \in \mathrm {Im}(\beta )$
.
Finally, we show that
![]() $\beta $
is surjective under properties (EX) and (CM). We argue by induction on the size r of a chain
$\beta $
is surjective under properties (EX) and (CM). We argue by induction on the size r of a chain
![]() $s \in \Delta \mathcal {G}(X,\sqcup )$
and in view of (1), we show that if
$s \in \Delta \mathcal {G}(X,\sqcup )$
and in view of (1), we show that if
then
![]() $y_{i-1}\wedge x_i$
exists for all
$y_{i-1}\wedge x_i$
exists for all
![]() $1\leq i\leq r$
and, if we set
$1\leq i\leq r$
and, if we set
![]() $y_{-1} = 1$
and
$y_{-1} = 1$
and
![]() $x_{r+1} = 1$
, then
$x_{r+1} = 1$
, then
![]() $\{x_i \wedge y_{i-1} \mathrel {{\: : \: }} 0\leq i\leq r+1\}\in {\mathcal D}(X,\sqcup )$
.
$\{x_i \wedge y_{i-1} \mathrel {{\: : \: }} 0\leq i\leq r+1\}\in {\mathcal D}(X,\sqcup )$
.
The case
![]() $r = 0$
is trivial. Suppose then that
$r = 0$
is trivial. Suppose then that
![]() $r> 0$
and that
$r> 0$
and that
![]() $s = \{ (x_0,y_0) < \cdots < (x_r,y_r)\}$
. By induction, we have a
$s = \{ (x_0,y_0) < \cdots < (x_r,y_r)\}$
. By induction, we have a
![]() $\sqcup $
-decomposition
$\sqcup $
-decomposition
By property (CM) applied to
![]() $(x_{r-1},y_{r-1}) < (x_r,y_r)$
, we have
$(x_{r-1},y_{r-1}) < (x_r,y_r)$
, we have
![]() $\tau := \{x_r\wedge y_{r-1}, x_{r-1}, y_{r}\}\in {\mathcal D}(X,\sqcup )$
. Hence,
$\tau := \{x_r\wedge y_{r-1}, x_{r-1}, y_{r}\}\in {\mathcal D}(X,\sqcup )$
. Hence,
![]() $\{x_r\wedge y_{r-1},y_r\}\in {\mathcal D}( {\mathcal {S}}(X,\sqcup )_{\leq y_{r-1}})$
by Remark 3.11 and it is
$\{x_r\wedge y_{r-1},y_r\}\in {\mathcal D}( {\mathcal {S}}(X,\sqcup )_{\leq y_{r-1}})$
by Remark 3.11 and it is
![]() $\sqcup $
-compatible in
$\sqcup $
-compatible in
![]() ${\mathcal {S}}(X,\sqcup )$
, so by property (EX), we have
${\mathcal {S}}(X,\sqcup )$
, so by property (EX), we have
But note that
This concludes the induction, and thus,
![]() $\beta $
is surjective since
$\beta $
is surjective since
We summarize the non-ordered constructions in Table 2.
Remark 4.16. Most of the structures we defined for an object of an ISM-category, along with their corresponding properties, can be translated to the context of posets according to Definition 2.1. In the case of lattices, they coincide with the definitions in the categorical context as discussed in Example 2.19. However, we will not present those analogous results here; the interested reader can verify the validity of the results presented in this article within the context of posets.
5 Homotopy equivalences and isomorphisms
5.1 General homotopy formulas
In this section, we first recall some known facts about homotopy types of posets and then apply them to the posets we defined in the previous sections. When writing down explicit formulas for the homotopy type, we identify the poset with its order complex. For example,
![]() ${\mathcal T} \simeq {{\mathcal S}} \vee {{\mathcal S}}$
means that the geometric realization of the order complex of
${\mathcal T} \simeq {{\mathcal S}} \vee {{\mathcal S}}$
means that the geometric realization of the order complex of
![]() ${\mathcal T}$
is homotopy equivalent to a wedge sum of two copies of the geometric realization of the order complex of
${\mathcal T}$
is homotopy equivalent to a wedge sum of two copies of the geometric realization of the order complex of
![]() ${{\mathcal S}}$
. If we need to emphasize the topological spaces behind our results and constructions, we write
${{\mathcal S}}$
. If we need to emphasize the topological spaces behind our results and constructions, we write
![]() $|{{\mathcal S}}|$
for the geometric realization of the order complex of a poset
$|{{\mathcal S}}|$
for the geometric realization of the order complex of a poset
![]() ${{\mathcal S}}$
.
${{\mathcal S}}$
.
Assume that
![]() ${{\mathcal S}}$
is a poset of finite height n. We say that
${{\mathcal S}}$
is a poset of finite height n. We say that
![]() ${{\mathcal S}}$
is spherical if it is
${{\mathcal S}}$
is spherical if it is
![]() $(n-1)$
-connected or, equivalently, homotopy equivalent to a wedge of n-spheres. The poset
$(n-1)$
-connected or, equivalently, homotopy equivalent to a wedge of n-spheres. The poset
![]() ${{\mathcal S}}$
is Cohen-Macaulay if
${{\mathcal S}}$
is Cohen-Macaulay if
![]() ${{\mathcal S}}$
is spherical and for all
${{\mathcal S}}$
is spherical and for all
![]() $x,y\in {{\mathcal S}}$
, the intervals
$x,y\in {{\mathcal S}}$
, the intervals
![]() ${{\mathcal S}}_{>x}$
,
${{\mathcal S}}_{>x}$
,
![]() ${{\mathcal S}}_{<y}$
and
${{\mathcal S}}_{<y}$
and
![]() ${{\mathcal S}}_{> x} \cap {{\mathcal S}}_{< y}$
(if
${{\mathcal S}}_{> x} \cap {{\mathcal S}}_{< y}$
(if
![]() $x<y$
) are spherical of height
$x<y$
) are spherical of height
![]() $n-h(x)-1$
,
$n-h(x)-1$
,
![]() $h(y)-1$
and
$h(y)-1$
and
![]() $h(y)-h(x)-2$
, respectively. This is the classical notion of homotopically Cohen-Macaulayness of a poset or simplicial complex. This implies Cohen-Macaulayness over any field, which is defined by the corresponding high homological connectedness.
$h(y)-h(x)-2$
, respectively. This is the classical notion of homotopically Cohen-Macaulayness of a poset or simplicial complex. This implies Cohen-Macaulayness over any field, which is defined by the corresponding high homological connectedness.
Recall that if
![]() $f,g:{\mathcal T}\to {{\mathcal S}}$
are order-preserving maps such that
$f,g:{\mathcal T}\to {{\mathcal S}}$
are order-preserving maps such that
![]() $f(x)\leq g(x)$
for all
$f(x)\leq g(x)$
for all
![]() $x\in {\mathcal T}$
, then f and g are homotopy equivalent. We will repeatedly use this fact throughout this paper to obtain homotopy equivalences and establish the contractibility of some posets.
$x\in {\mathcal T}$
, then f and g are homotopy equivalent. We will repeatedly use this fact throughout this paper to obtain homotopy equivalences and establish the contractibility of some posets.
The first tool we will need is a consequence of Propositions 3.1, 3.5 and 3.7 from [Reference Welker, Ziegler and ŽivaljevićWZZ]. Note that in [Reference Welker, Ziegler and ŽivaljevićWZZ], Proposition 3.1 was formulated only for diagrams over finite posets, but the proof only relies on paracompactness of the spaces involved (see, for example, [Reference SegalSe]). As a consequence, the results from [Reference Welker, Ziegler and ŽivaljevićWZZ] can be applied to finite height posets.
Proposition 5.1. Let
![]() ${{\mathcal S}},{\mathcal T}$
be posets of finite height and
${{\mathcal S}},{\mathcal T}$
be posets of finite height and
![]() $f:{\mathcal T}\to {{\mathcal S}}$
a poset map such that for all
$f:{\mathcal T}\to {{\mathcal S}}$
a poset map such that for all
![]() $x\in {{\mathcal S}}$
, the inclusion
$x\in {{\mathcal S}}$
, the inclusion
![]() $f^{-1}\big (\,{{\mathcal S}}_{<x}\,\big ) \hookrightarrow f^{-1}\big (\,{{\mathcal S}}_{\leq x}\,\big )$
is homotopy equivalent to the constant map with image
$f^{-1}\big (\,{{\mathcal S}}_{<x}\,\big ) \hookrightarrow f^{-1}\big (\,{{\mathcal S}}_{\leq x}\,\big )$
is homotopy equivalent to the constant map with image
![]() $c_x\in f^{-1}({{\mathcal S}}_{\leq x})$
. Then there is a homotopy equivalence
$c_x\in f^{-1}({{\mathcal S}}_{\leq x})$
. Then there is a homotopy equivalence
where the wedge identifies
![]() $x\in {{\mathcal S}}$
with
$x\in {{\mathcal S}}$
with
![]() $c_x\in f^{-1}({{\mathcal S}}_{\leq x})$
.
$c_x\in f^{-1}({{\mathcal S}}_{\leq x})$
.
The following well-known fact will be useful for verifying the requirements of Proposition 5.1.
Lemma 5.2. Let
![]() ${\mathcal Q}\subseteq {{\mathcal S}}$
be posets such that
${\mathcal Q}\subseteq {{\mathcal S}}$
be posets such that
![]() ${{\mathcal S}}$
is k-connected and
${{\mathcal S}}$
is k-connected and
![]() ${\mathcal Q}$
has dimension at most k. Then the inclusion
${\mathcal Q}$
has dimension at most k. Then the inclusion
![]() ${\mathcal Q}\hookrightarrow {{\mathcal S}}$
is null-homotopic.
${\mathcal Q}\hookrightarrow {{\mathcal S}}$
is null-homotopic.
Then from Proposition 5.1 and Lemma 5.2, we can derive the following version of Quillen’s fiber theorem, which we will use repeatedly.
Theorem 5.3 (Quillen’s fiber theorem)
Let
![]() $f:{\mathcal T}\to {{\mathcal S}}$
be a map between posets of finite height. Let
$f:{\mathcal T}\to {{\mathcal S}}$
be a map between posets of finite height. Let
![]() $m\geq -1$
, and suppose that for all
$m\geq -1$
, and suppose that for all
![]() $x\in {{\mathcal S}}$
,
$x\in {{\mathcal S}}$
,
![]() $f^{-1}({{\mathcal S}}_{\leq x}) * {{\mathcal S}}_{>x}$
is m-connected. Then f is an
$f^{-1}({{\mathcal S}}_{\leq x}) * {{\mathcal S}}_{>x}$
is m-connected. Then f is an
![]() $(m+1)$
-equivalence.
$(m+1)$
-equivalence.
We will also use the non-Hausdorff mapping cylinder (see [Reference Barmak and MinianBM]) of a map
![]() $f:{\mathcal T}\to {{\mathcal S}}$
between posets. This is the poset
$f:{\mathcal T}\to {{\mathcal S}}$
between posets. This is the poset
![]() $M_f = {\mathcal T}\coprod {{\mathcal S}}$
such that its ordering
$M_f = {\mathcal T}\coprod {{\mathcal S}}$
such that its ordering
![]() $\leq $
restricts to the given ordering in
$\leq $
restricts to the given ordering in
![]() ${\mathcal T}$
and
${\mathcal T}$
and
![]() ${{\mathcal S}}$
, and for
${{\mathcal S}}$
, and for
![]() $x\in {\mathcal T}$
and
$x\in {\mathcal T}$
and
![]() $y\in {{\mathcal S}}$
, we have
$y\in {{\mathcal S}}$
, we have
![]() $x < y$
if
$x < y$
if
![]() $f(x)\leq y$
. Note that if
$f(x)\leq y$
. Note that if
![]() ${{\mathcal S}}$
has a unique maximal element
${{\mathcal S}}$
has a unique maximal element
![]() $1_{{{\mathcal S}}}$
, then this is also the unique maximal element of
$1_{{{\mathcal S}}}$
, then this is also the unique maximal element of
![]() $M_f$
, and we can write
$M_f$
, and we can write
![]() $M_f^{\circ } = M_f \setminus \{1_{{{\mathcal S}}}\}$
.
$M_f^{\circ } = M_f \setminus \{1_{{{\mathcal S}}}\}$
.
Example 5.4. Let
![]() ${\mathcal T}$
be the poset with points
${\mathcal T}$
be the poset with points
![]() $(0,0),(0,1),(1,0),(1,1)$
, with
$(0,0),(0,1),(1,0),(1,1)$
, with
![]() $(a,b)\leq (c,d)$
if and only if
$(a,b)\leq (c,d)$
if and only if
![]() $a\leq c$
. Let
$a\leq c$
. Let
![]() ${{\mathcal S}}$
be the poset
${{\mathcal S}}$
be the poset
![]() $\{0 < 1\}$
, and consider the projection
$\{0 < 1\}$
, and consider the projection
![]() $f:{\mathcal T}\to {{\mathcal S}}$
defined by
$f:{\mathcal T}\to {{\mathcal S}}$
defined by
![]() $f(a,b)=a$
. Then the non-Hausdorff mapping cylinder of f is the poset displayed in Figure 7.
$f(a,b)=a$
. Then the non-Hausdorff mapping cylinder of f is the poset displayed in Figure 7.
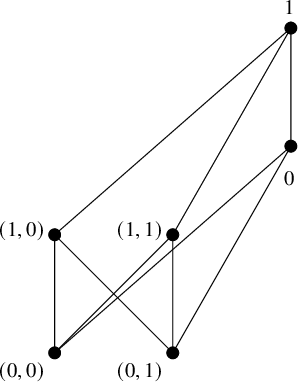
Figure 7 Hasse diagram of the non-Hausdorff mapping cylinder of the poset map
![]() $f:{\mathcal T}\to {{\mathcal S}}$
.
$f:{\mathcal T}\to {{\mathcal S}}$
.
The adjective non-Hausdorff is motivated by the non-Hausdorffness of the construction when considering finite posets as finite topological spaces. We refer the reader to [Reference Barmak and MinianBM] for a more detailed discussion.
Lemma 5.5. Let
![]() $f:{\mathcal T}\to {{\mathcal S}}$
be a map of posets of finite height, where
$f:{\mathcal T}\to {{\mathcal S}}$
be a map of posets of finite height, where
![]() ${{\mathcal S}}$
is bounded. If
${{\mathcal S}}$
is bounded. If
![]() $M := \{ x \in {\mathcal T}~|~f(x) = 1_{{{\mathcal S}}}\}$
is an antichain, then
$M := \{ x \in {\mathcal T}~|~f(x) = 1_{{{\mathcal S}}}\}$
is an antichain, then
![]() $M_f^{\circ } = M_f \setminus \{1_{{{\mathcal S}}}\}$
is homotopy equivalent to
$M_f^{\circ } = M_f \setminus \{1_{{{\mathcal S}}}\}$
is homotopy equivalent to
Proof. Note that
![]() $M_f^{\circ }\setminus M$
is contractible since
$M_f^{\circ }\setminus M$
is contractible since
![]() ${{\mathcal S}}^{\circ }$
is contractible and the map
${{\mathcal S}}^{\circ }$
is contractible and the map
![]() $r:M_f^{\circ }\setminus M \to {{\mathcal S}}^{\circ }$
, defined by
$r:M_f^{\circ }\setminus M \to {{\mathcal S}}^{\circ }$
, defined by
![]() $r(x) = f(x)$
if
$r(x) = f(x)$
if
![]() $x\in {\mathcal T}$
or
$x\in {\mathcal T}$
or
![]() $r(x)=x$
if
$r(x)=x$
if
![]() $x\in {{\mathcal S}}$
, is a homotopy equivalence with inverse given by the natural inclusion of
$x\in {{\mathcal S}}$
, is a homotopy equivalence with inverse given by the natural inclusion of
![]() ${{\mathcal S}}^{\circ }$
in
${{\mathcal S}}^{\circ }$
in
![]() $M_f^{\circ }$
. Therefore,
$M_f^{\circ }$
. Therefore,
![]() $|M_f^{\circ }| \simeq |M_f^{\circ }|/|M_f^{\circ }\setminus M|$
, and since M is an antichain, we conclude that
$|M_f^{\circ }| \simeq |M_f^{\circ }|/|M_f^{\circ }\setminus M|$
, and since M is an antichain, we conclude that
![]() $|M_f^{\circ }|/|M_f^{\circ }\setminus M|$
is homotopy equivalent to the wedge of the suspension of the links in
$|M_f^{\circ }|/|M_f^{\circ }\setminus M|$
is homotopy equivalent to the wedge of the suspension of the links in
![]() $|M_f^{\circ }|$
of
$|M_f^{\circ }|$
of
![]() $x\in M$
. The fact that
$x\in M$
. The fact that
![]() $\operatorname {\mathrm {Lk}}_{|M_f^{\circ }|}(x) = |{\mathcal T}_{<x}|$
then concludes the proof.
$\operatorname {\mathrm {Lk}}_{|M_f^{\circ }|}(x) = |{\mathcal T}_{<x}|$
then concludes the proof.
Let us apply Lemma 5.5 to the map f from Example 5.4.
Example 5.6. Let
![]() ${\mathcal T}$
,
${\mathcal T}$
,
![]() ${{\mathcal S}}$
and f be as in Example 5.4. Note that
${{\mathcal S}}$
and f be as in Example 5.4. Note that
![]() ${{\mathcal S}}$
is bounded. Following the notation of Lemma 5.5, we have that
${{\mathcal S}}$
is bounded. Following the notation of Lemma 5.5, we have that
![]() $M = \{ (1,0), (1,1)\}$
is an antichain. Thus,
$M = \{ (1,0), (1,1)\}$
is an antichain. Thus,
![]() $M_f^{\circ }$
is the poset obtained from
$M_f^{\circ }$
is the poset obtained from
![]() ${\mathcal T}$
after adding an extra element
${\mathcal T}$
after adding an extra element
![]() $0$
above
$0$
above
![]() $(0,0)$
and
$(0,0)$
and
![]() $(0,1)$
. The order complex of this poset is depicted in Figure 8, which clearly has the homotopy type of
$(0,1)$
. The order complex of this poset is depicted in Figure 8, which clearly has the homotopy type of
![]() $S^1\vee S^1$
. This coincides with the description given in Lemma 5.5.
$S^1\vee S^1$
. This coincides with the description given in Lemma 5.5.
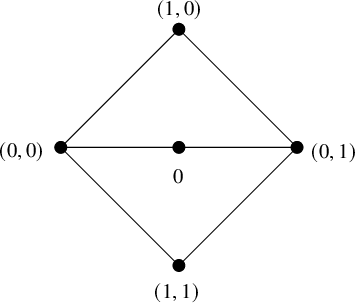
Figure 8 Geometric realization of the poset
![]() $M_f^{\circ }$
from Example 5.4.
$M_f^{\circ }$
from Example 5.4.
In general, we also have the following formula relating the Euler characteristic of posets related by an order-preserving map (see, for example, Corollary 3.2 of [Reference WalkerWal81]).
Lemma 5.7. Let
![]() $f:{\mathcal T}\to {{\mathcal S}}$
be a map of finite posets. Then
$f:{\mathcal T}\to {{\mathcal S}}$
be a map of finite posets. Then
5.2 Homotopy formulas and results for posets from Section 2 - Section 4
Our first homotopy equivalence relates the strictly partial decomposition with the subposet of
![]() $(\sqcup ,h)$
-complemented subobjects. We refer the reader to Definition 3.7 for the different notions of complementation employed here, as well as for the definition of the subposet
$(\sqcup ,h)$
-complemented subobjects. We refer the reader to Definition 3.7 for the different notions of complementation employed here, as well as for the definition of the subposet
![]() ${\mathcal {S}}_h(X,\sqcup )$
. Recall that
${\mathcal {S}}_h(X,\sqcup )$
. Recall that
![]() $\Phi (\sigma ) = \bigvee _{x\in \sigma } x$
for a partial decomposition
$\Phi (\sigma ) = \bigvee _{x\in \sigma } x$
for a partial decomposition
![]() $\sigma \in {\mathcal {PD}}(X,\sqcup )$
.
$\sigma \in {\mathcal {PD}}(X,\sqcup )$
.
The main applications of the results in this subsection can be found in Section 6. Here, we will give just some small examples.
Proposition 5.8. The map
![]() $\Phi :{\mathcal {PD}}(X,\sqcup )^{*} \setminus {\mathcal D}(X,\sqcup )\to {\mathcal {S}}_h(X,\sqcup )^{*}$
is a homotopy equivalence with inverse
$\Phi :{\mathcal {PD}}(X,\sqcup )^{*} \setminus {\mathcal D}(X,\sqcup )\to {\mathcal {S}}_h(X,\sqcup )^{*}$
is a homotopy equivalence with inverse
![]() $i:{\mathcal {S}}_h(X,\sqcup )^{*}\to {\mathcal {PD}}(X,\sqcup )^{*} \setminus {\mathcal D}(X,\sqcup )$
given by
$i:{\mathcal {S}}_h(X,\sqcup )^{*}\to {\mathcal {PD}}(X,\sqcup )^{*} \setminus {\mathcal D}(X,\sqcup )$
given by
![]() $i(x) = \{x\}$
. In particular,
$i(x) = \{x\}$
. In particular,
![]() ${\mathcal {S}}_h(X,\sqcup )^{*}$
is a deformation retract of
${\mathcal {S}}_h(X,\sqcup )^{*}$
is a deformation retract of
![]() ${\mathcal {PD}}(X,\sqcup )^{*} \setminus {\mathcal D}(X,\sqcup )$
.
${\mathcal {PD}}(X,\sqcup )^{*} \setminus {\mathcal D}(X,\sqcup )$
.
Moreover,
![]() $\mathcal {O}{\mathcal {PD}}(X,\sqcup )^{*}\setminus \mathcal {O}{\mathcal D}(X,\sqcup )$
is also homotopy equivalent to
$\mathcal {O}{\mathcal {PD}}(X,\sqcup )^{*}\setminus \mathcal {O}{\mathcal D}(X,\sqcup )$
is also homotopy equivalent to
![]() ${\mathcal {S}}_h(X,\sqcup )^{*}$
.
${\mathcal {S}}_h(X,\sqcup )^{*}$
.
Proof. This follows from Lemma 3.8, the definition of
![]() ${\mathcal {S}}_h(X,\sqcup )$
and the relations
${\mathcal {S}}_h(X,\sqcup )$
and the relations
![]() $\Phi (i(x)) = x$
and
$\Phi (i(x)) = x$
and
![]() $i(\Phi (\sigma )) \geq \sigma $
.
$i(\Phi (\sigma )) \geq \sigma $
.
Now we apply the wedge-decomposition result to relate the ordered and unordered versions of the posets
![]() ${\mathcal D},{\mathcal {PD}},{\mathcal F},{\mathcal {PF}}, \mathcal {B}, \mathcal {PB}$
. Recall the definition of
${\mathcal D},{\mathcal {PD}},{\mathcal F},{\mathcal {PF}}, \mathcal {B}, \mathcal {PB}$
. Recall the definition of
![]() $\mathcal {O} K$
for a simplicial complex K from Remark 4.6. We will sometimes write CM for Cohen-Macaulay (do not confuse with property (CM) from Definition 3.10).
$\mathcal {O} K$
for a simplicial complex K from Remark 4.6. We will sometimes write CM for Cohen-Macaulay (do not confuse with property (CM) from Definition 3.10).
Theorem 5.9. If
![]() ${\mathcal {S}}(X,\sqcup )$
has finite height, the following hold:
${\mathcal {S}}(X,\sqcup )$
has finite height, the following hold:
-
(1)
 $$ \begin{align*}\mathcal{O}{\mathcal D}(X,\sqcup)^{\circ} \simeq {\mathcal D}(X,\sqcup)^{\circ} \vee \bigvee_{\sigma \in {\mathcal D}(X,\sqcup)^{\circ}} S^{|\sigma|-2} * {\mathcal D}(X,\sqcup)^{\circ}_{< \sigma}.\end{align*} $$
$$ \begin{align*}\mathcal{O}{\mathcal D}(X,\sqcup)^{\circ} \simeq {\mathcal D}(X,\sqcup)^{\circ} \vee \bigvee_{\sigma \in {\mathcal D}(X,\sqcup)^{\circ}} S^{|\sigma|-2} * {\mathcal D}(X,\sqcup)^{\circ}_{< \sigma}.\end{align*} $$
Hence,
 $\mathcal {O}{\mathcal D}(X,\sqcup )$
is Cohen-Macaulay if
$\mathcal {O}{\mathcal D}(X,\sqcup )$
is Cohen-Macaulay if
 ${\mathcal D}(X,\sqcup )$
is.
${\mathcal D}(X,\sqcup )$
is. -
(2)
 $$ \begin{align*}\mathcal{O}{\mathcal{PD}}(X,\sqcup)^{*} \simeq {\mathcal{PD}}(X,\sqcup)^{*} \vee \bigvee_{\sigma \in {\mathcal D}(X,\sqcup)^{\circ}} S^{|\sigma|-2} * ({\mathcal{PD}}(X,\sqcup)^{*})_{< \sigma}.\end{align*} $$
$$ \begin{align*}\mathcal{O}{\mathcal{PD}}(X,\sqcup)^{*} \simeq {\mathcal{PD}}(X,\sqcup)^{*} \vee \bigvee_{\sigma \in {\mathcal D}(X,\sqcup)^{\circ}} S^{|\sigma|-2} * ({\mathcal{PD}}(X,\sqcup)^{*})_{< \sigma}.\end{align*} $$
Hence,
 $\mathcal {O}{\mathcal {PD}}(X,\sqcup )$
is Cohen-Macaulay if
$\mathcal {O}{\mathcal {PD}}(X,\sqcup )$
is Cohen-Macaulay if
 ${\mathcal {PD}}(X,\sqcup )$
is.
${\mathcal {PD}}(X,\sqcup )$
is. -
(3) If K is a finite-dimensional simplicial complex, then
 $$ \begin{align*}\mathcal{O} K \simeq K \vee \bigvee_{\sigma \in K} \bigg( \bigvee_{D(|\sigma|)} S^{|\sigma|-1} \bigg) * \operatorname{\mathrm{Lk}}_{K}(\sigma),\end{align*} $$
$$ \begin{align*}\mathcal{O} K \simeq K \vee \bigvee_{\sigma \in K} \bigg( \bigvee_{D(|\sigma|)} S^{|\sigma|-1} \bigg) * \operatorname{\mathrm{Lk}}_{K}(\sigma),\end{align*} $$
where
 $D(n) = \sum _{i=0}^n(-1)^i \frac {n!}{i!}$
. Moreover, K is homotopically CM (resp. CM over a ring R) if and only if
$D(n) = \sum _{i=0}^n(-1)^i \frac {n!}{i!}$
. Moreover, K is homotopically CM (resp. CM over a ring R) if and only if
 $\mathcal {O} K$
is homotopically CM (resp. CM over R). In particular, this applies to the complexes
$\mathcal {O} K$
is homotopically CM (resp. CM over R). In particular, this applies to the complexes
 ${\mathcal F}, {\mathcal {PF}}, \mathcal {B}$
or
${\mathcal F}, {\mathcal {PF}}, \mathcal {B}$
or
 $\mathcal {PB}$
.
$\mathcal {PB}$
.
Proof. These conclusions follow from the description of the fibers in Lemma 4.9 in conjunction with Lemma 5.2 and Proposition 5.1. Note that when K is a simplicial complex regarded as a poset, then
![]() $K_{>\sigma }$
is isomorphic to
$K_{>\sigma }$
is isomorphic to
![]() $\operatorname {\mathrm {Lk}}_K(\sigma )$
for any simplex
$\operatorname {\mathrm {Lk}}_K(\sigma )$
for any simplex
![]() $\sigma \in K$
. The Cohen-Macaulay implication in items 1 and 2 follows from Lemma 4.9 items 1 and 2, respectively, jointly with Corollary 9.7 of [Reference QuillenQ].
$\sigma \in K$
. The Cohen-Macaulay implication in items 1 and 2 follows from Lemma 4.9 items 1 and 2, respectively, jointly with Corollary 9.7 of [Reference QuillenQ].
The ‘only if’ implication of the Cohen-Macaulay part of item 3 follows by an application of Theorem 5.1 of [Reference Björner, Wachs and WelkerBWW] by noting that if
![]() $\sigma \in K$
, then
$\sigma \in K$
, then
![]() $F_{K}^{-1}(K_{\leq \sigma })$
is Cohen-Macaulay. That is,
$F_{K}^{-1}(K_{\leq \sigma })$
is Cohen-Macaulay. That is,
![]() $F_K^{-1}(K_{\leq \sigma })$
is the poset of injective words on the alphabet
$F_K^{-1}(K_{\leq \sigma })$
is the poset of injective words on the alphabet
![]() $\sigma $
, and this was proved to be shellable (and hence Cohen-Macaulay) by [Reference Björner and WachsBW].
$\sigma $
, and this was proved to be shellable (and hence Cohen-Macaulay) by [Reference Björner and WachsBW].
For the ‘if’ implication, it remains to prove that if
![]() $\mathcal {O} K$
is Cohen-Macaulay, then the links
$\mathcal {O} K$
is Cohen-Macaulay, then the links
![]() $\operatorname {\mathrm {Lk}}_K(\sigma )$
are spherical. It is not hard to show that they have the correct dimension. Now fix
$\operatorname {\mathrm {Lk}}_K(\sigma )$
are spherical. It is not hard to show that they have the correct dimension. Now fix
![]() $\sigma \in K$
, and let
$\sigma \in K$
, and let
![]() $z\in F_{K}^{-1}(\sigma )$
. Let
$z\in F_{K}^{-1}(\sigma )$
. Let
![]() $(v_i)_{i\in I}$
be a total ordering of the vertices of
$(v_i)_{i\in I}$
be a total ordering of the vertices of
![]() $\operatorname {\mathrm {Lk}}_K(\sigma )$
. Consider the map
$\operatorname {\mathrm {Lk}}_K(\sigma )$
. Consider the map
![]() $H:\operatorname {\mathrm {Lk}}_K(\sigma )\to \mathcal {O} K_{>z}$
given by
$H:\operatorname {\mathrm {Lk}}_K(\sigma )\to \mathcal {O} K_{>z}$
given by
![]() $H(\tau ) = (z,v_{i_1},\ldots ,v_{i_k})$
if
$H(\tau ) = (z,v_{i_1},\ldots ,v_{i_k})$
if
![]() $\tau = \{v_{i_1}<\cdots <v_{i_k}\}$
. Clearly, H is a well-defined order-preserving poset map. Let
$\tau = \{v_{i_1}<\cdots <v_{i_k}\}$
. Clearly, H is a well-defined order-preserving poset map. Let
![]() $F':\mathcal {O} K_{>z}\to \operatorname {\mathrm {Lk}}_K(\sigma )$
be the map that forgets the ordering and deletes the vertices in
$F':\mathcal {O} K_{>z}\to \operatorname {\mathrm {Lk}}_K(\sigma )$
be the map that forgets the ordering and deletes the vertices in
![]() $\sigma $
; that is,
$\sigma $
; that is,
![]() $F'(w) = F_{K}(w) \setminus \sigma $
. Thus,
$F'(w) = F_{K}(w) \setminus \sigma $
. Thus,
![]() $F'H(\tau ) = \tau $
is the identity map, so
$F'H(\tau ) = \tau $
is the identity map, so
![]() $F'$
induces a surjective map on the homotopy (and homology) groups. Since
$F'$
induces a surjective map on the homotopy (and homology) groups. Since
![]() $\mathcal {O} K_{>z}$
is spherical of the same dimension than
$\mathcal {O} K_{>z}$
is spherical of the same dimension than
![]() $\operatorname {\mathrm {Lk}}_K(\sigma )$
, we conclude that
$\operatorname {\mathrm {Lk}}_K(\sigma )$
, we conclude that
![]() $\operatorname {\mathrm {Lk}}_K(\sigma )$
is spherical. This concludes the proof.
$\operatorname {\mathrm {Lk}}_K(\sigma )$
is spherical. This concludes the proof.
We study now natural maps between our posets that might be useful to compute the homotopy type relations between them. We begin with the relation between the complex of partial bases
![]() $\mathcal {B}(X,\sqcup ,P)$
and the frame complex. Since these are inflation complexes in the sense of [Reference Björner, Wachs and WelkerBWW] (see Definition 4.3), by their Theorem 6.2 adapted to the infinite situation, we can prove:
$\mathcal {B}(X,\sqcup ,P)$
and the frame complex. Since these are inflation complexes in the sense of [Reference Björner, Wachs and WelkerBWW] (see Definition 4.3), by their Theorem 6.2 adapted to the infinite situation, we can prove:
Proposition 5.10. Let K be a finite-dimensional simplicial complex and
![]() $P = (P_x)_{x\in \mathcal {A}}$
a collection of nonempty sets
$P = (P_x)_{x\in \mathcal {A}}$
a collection of nonempty sets
![]() $P_x$
indexed by the set of vertices
$P_x$
indexed by the set of vertices
![]() $\mathcal {A}$
of K. Let
$\mathcal {A}$
of K. Let
![]() $p:(K,P)\to K$
be the deflation map. Then we have the following homotopy equivalence:
$p:(K,P)\to K$
be the deflation map. Then we have the following homotopy equivalence:
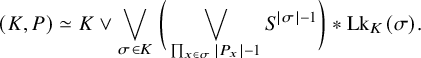 $$\begin{align*}(K,P) \simeq K \vee \bigvee_{\sigma\in K} \bigg( \bigvee_{\prod_{x\in \sigma} |P_x|-1} S^{|\sigma|-1} \bigg) * \operatorname{\mathrm{Lk}}_K(\sigma).\end{align*}$$
$$\begin{align*}(K,P) \simeq K \vee \bigvee_{\sigma\in K} \bigg( \bigvee_{\prod_{x\in \sigma} |P_x|-1} S^{|\sigma|-1} \bigg) * \operatorname{\mathrm{Lk}}_K(\sigma).\end{align*}$$
Furthermore,
![]() $p^{-1}(K_{\leq \sigma }) = P_{x_1} * \cdots * P_{x_r}$
for
$p^{-1}(K_{\leq \sigma }) = P_{x_1} * \cdots * P_{x_r}$
for
![]() $\sigma = \{x_1,\ldots , x_r\}\in K$
(where the
$\sigma = \{x_1,\ldots , x_r\}\in K$
(where the
![]() $P_x$
are regarded as discrete complexes), and K is homotopically CM if and only if
$P_x$
are regarded as discrete complexes), and K is homotopically CM if and only if
![]() $(K,P)$
is homotopically CM. The same conclusions hold for Cohen-Macaulayness over a ring.
$(K,P)$
is homotopically CM. The same conclusions hold for Cohen-Macaulayness over a ring.
In particular, this applies to
![]() $K = {\mathcal {PF}}(X,\sqcup )$
or
$K = {\mathcal {PF}}(X,\sqcup )$
or
![]() ${\mathcal F}(X,\sqcup )$
with
${\mathcal F}(X,\sqcup )$
with
![]() $(K,P) = \mathcal {PB}(X,\sqcup ,P)$
or
$(K,P) = \mathcal {PB}(X,\sqcup ,P)$
or
![]() $\mathcal {B}(X,\sqcup ,P)$
, respectively.
$\mathcal {B}(X,\sqcup ,P)$
, respectively.
Proof. The homotopy equivalence is a consequence of [Reference Björner, Wachs and WelkerBWW, Theorem 6.2] adapted to the infinite case, regarding a simplicial complex as a poset via its face poset. Alternatively, this follows from Proposition 5.1 since
![]() $p^{-1}(K_{\leq \sigma }) = P_{x_1} * \cdots * P_{x_r}$
for
$p^{-1}(K_{\leq \sigma }) = P_{x_1} * \cdots * P_{x_r}$
for
![]() $\sigma = \{x_1,\ldots ,x_r\} \in K$
. Also recall that
$\sigma = \{x_1,\ldots ,x_r\} \in K$
. Also recall that
![]() $K_{>\sigma } \cong \operatorname {\mathrm {Lk}}_K(\sigma )$
.
$K_{>\sigma } \cong \operatorname {\mathrm {Lk}}_K(\sigma )$
.
Then by [Reference QuillenQ, Corollary 9.7], since the lower fibers
![]() $p^{-1}(K_{\leq \sigma })$
are homotopically CM of the correct dimension, if K is homotopically CM, then
$p^{-1}(K_{\leq \sigma })$
are homotopically CM of the correct dimension, if K is homotopically CM, then
![]() $(K,P)$
is homotopically CM as well.
$(K,P)$
is homotopically CM as well.
Conversely, suppose that
![]() $(K,P)$
is homotopically CM. By the wedge decomposition, K is spherical. It remains to prove that the links of its simplices are spherical of the correct dimension. Let
$(K,P)$
is homotopically CM. By the wedge decomposition, K is spherical. It remains to prove that the links of its simplices are spherical of the correct dimension. Let
![]() $\sigma \in K$
and consider a simplex
$\sigma \in K$
and consider a simplex
![]() $B\in (K,P)$
with
$B\in (K,P)$
with
![]() $p(B) = \sigma $
. Then
$p(B) = \sigma $
. Then
![]() $\operatorname {\mathrm {Lk}}_{(K,P)}(B)$
is isomorphic to the inflation complex
$\operatorname {\mathrm {Lk}}_{(K,P)}(B)$
is isomorphic to the inflation complex
![]() $(\operatorname {\mathrm {Lk}}_{K}(\sigma ), P^B)$
, where
$(\operatorname {\mathrm {Lk}}_{K}(\sigma ), P^B)$
, where
![]() $P^B:=(P_x)_{x \in \mathcal {A}_{\sigma }}$
and
$P^B:=(P_x)_{x \in \mathcal {A}_{\sigma }}$
and
![]() $\mathcal {A}_{\sigma }$
is the set of vertices of
$\mathcal {A}_{\sigma }$
is the set of vertices of
![]() $\operatorname {\mathrm {Lk}}_{K}(\sigma )$
. Since
$\operatorname {\mathrm {Lk}}_{K}(\sigma )$
. Since
![]() $\operatorname {\mathrm {Lk}}_{(K,P)}(B)$
is spherical by Cohen-Macaulayness, by the wedge decomposition, again we conclude that
$\operatorname {\mathrm {Lk}}_{(K,P)}(B)$
is spherical by Cohen-Macaulayness, by the wedge decomposition, again we conclude that
![]() $\operatorname {\mathrm {Lk}}_{K}(\sigma )$
is spherical.
$\operatorname {\mathrm {Lk}}_{K}(\sigma )$
is spherical.
The homological version of CM over a given ring is obtained by a similar argument.
We refer to Section 6 for concrete applications of these results. For instance, in the case of (finite) matroids (see Subsection 6.4), it is well-known that the independence complex is shellable and hence homotopically Cohen-Macaulay. In our language, this is the partial basis complex associated with the lattice of flats. Therefore, as a consequence of the previous result, the corresponding frame complex is homotopically Cohen-Macaulay.
We derive some results on the augmented Bergman complex using the non-Hausdorff mapping cylinder.
Lemma 5.11.
![]() $\Delta (X,\sqcup )$
is homotopy equivalent to
$\Delta (X,\sqcup )$
is homotopy equivalent to
![]() $M_\Phi ^{\circ }$
, where
$M_\Phi ^{\circ }$
, where
![]() $M_{\Phi }$
is the non-Hausdorff mapping cylinder of the map
$M_{\Phi }$
is the non-Hausdorff mapping cylinder of the map
![]() $\Phi :{\mathcal F}(X,\sqcup )\to {\mathcal {S}}(X,\sqcup )$
.
$\Phi :{\mathcal F}(X,\sqcup )\to {\mathcal {S}}(X,\sqcup )$
.
Proof. Consider the map
![]() $\varphi : \Delta (X,\sqcup ) \to M_\Phi ^{\circ }$
given by
$\varphi : \Delta (X,\sqcup ) \to M_\Phi ^{\circ }$
given by
 $$\begin{align*}\varphi(\sigma \cup \{x_1,\ldots,x_r\}) = \begin{cases} \sigma & r = 0,\\ x_r & r> 0. \end{cases}\end{align*}$$
$$\begin{align*}\varphi(\sigma \cup \{x_1,\ldots,x_r\}) = \begin{cases} \sigma & r = 0,\\ x_r & r> 0. \end{cases}\end{align*}$$
Clearly,
![]() $\varphi $
is a well-defined order-preserving map. To prove it is a homotopy equivalence, we show that the lower homotopy fibers are contractible. Indeed, for
$\varphi $
is a well-defined order-preserving map. To prove it is a homotopy equivalence, we show that the lower homotopy fibers are contractible. Indeed, for
![]() $\sigma \in {\mathcal F}(X,\sqcup )$
, we have
$\sigma \in {\mathcal F}(X,\sqcup )$
, we have
On the other hand, for
![]() $x\in {\mathcal {S}}(X,\sqcup )^{\circ }$
, we get
$x\in {\mathcal {S}}(X,\sqcup )^{\circ }$
, we get
When
![]() $r>0$
, the condition
$r>0$
, the condition
![]() $\Phi (\sigma )\leq x$
follows immediately from
$\Phi (\sigma )\leq x$
follows immediately from
![]() $x_r\leq x$
. In this way, we can construct a contraction homotopy inside this fiber:
$x_r\leq x$
. In this way, we can construct a contraction homotopy inside this fiber:
Note that all these terms lie in
![]() $\varphi ^{-1} \big ( {M_\Phi ^{\circ }}_{\leq \sigma } \big )$
.
$\varphi ^{-1} \big ( {M_\Phi ^{\circ }}_{\leq \sigma } \big )$
.
Since the lower homotopy fibers are contractible, by Quillen’s fiber theorem (see Theorem 5.3), we conclude that
![]() $\varphi $
is a homotopy equivalence.
$\varphi $
is a homotopy equivalence.
Since the elements of the poset
![]() ${\mathcal F}(X,\sqcup )$
whose join is the unique maximal element of
${\mathcal F}(X,\sqcup )$
whose join is the unique maximal element of
![]() ${\mathcal {S}}(X,\sqcup )$
consist of exactly the set of full frames, they form an antichain. In conjunction with Lemma 5.5, this immediately implies the following result, which is well-known in the matroid case (see [Reference Bullock, Kelley, Reiner, Ren, Shemy, Shen, Sun and ZhangBKR]).
${\mathcal {S}}(X,\sqcup )$
consist of exactly the set of full frames, they form an antichain. In conjunction with Lemma 5.5, this immediately implies the following result, which is well-known in the matroid case (see [Reference Bullock, Kelley, Reiner, Ren, Shemy, Shen, Sun and ZhangBKR]).
Proposition 5.12. Let M be the set of full frames of
![]() ${\mathcal {S}}(X,\sqcup )$
. Then
${\mathcal {S}}(X,\sqcup )$
. Then
![]() $\Delta (X,\sqcup )$
is homotopy equivalent to
$\Delta (X,\sqcup )$
is homotopy equivalent to
In particular,
![]() $\Delta (X,\sqcup )$
is spherical, and if M is empty (i.e., there are no full frames), then
$\Delta (X,\sqcup )$
is spherical, and if M is empty (i.e., there are no full frames), then
![]() $\Delta (X,\sqcup )$
is contractible.
$\Delta (X,\sqcup )$
is contractible.
We have the following partial result on the connectivity of
![]() ${\mathcal {PD}}(X,\sqcup )^{*}$
if we have information on the lower intervals of both
${\mathcal {PD}}(X,\sqcup )^{*}$
if we have information on the lower intervals of both
![]() ${\mathcal {S}}_h(X,\sqcup )$
and the partial decompositions. We will use property (LI) from Definition 3.2 to prove the following theorem.
${\mathcal {S}}_h(X,\sqcup )$
and the partial decompositions. We will use property (LI) from Definition 3.2 to prove the following theorem.
Theorem 5.13. Let n denote the height of
![]() ${\mathcal {S}}(X,\sqcup )$
. Assume that property (LI) holds and that for all
${\mathcal {S}}(X,\sqcup )$
. Assume that property (LI) holds and that for all
![]() $y\in {\mathcal {S}}_h(X,\sqcup )$
, the poset
$y\in {\mathcal {S}}_h(X,\sqcup )$
, the poset
![]() ${\mathcal {S}}_h(Y,\sqcup )^{*}$
is spherical of dimension
${\mathcal {S}}_h(Y,\sqcup )^{*}$
is spherical of dimension
![]() $h(y)-2$
. Then
$h(y)-2$
. Then
![]() ${\mathcal {PD}}(X,\sqcup )^{*}$
is
${\mathcal {PD}}(X,\sqcup )^{*}$
is
![]() $(n-3)$
-connected. Moreover, the inclusion
$(n-3)$
-connected. Moreover, the inclusion
![]() ${\mathcal {S}}_h(X,\sqcup )^{*}\hookrightarrow {\mathcal {PD}}(X,\sqcup )^{*}$
is an
${\mathcal {S}}_h(X,\sqcup )^{*}\hookrightarrow {\mathcal {PD}}(X,\sqcup )^{*}$
is an
![]() $(n-2)$
-equivalence.
$(n-2)$
-equivalence.
Proof. Note that
![]() ${\mathcal {S}}_h(X,\sqcup )^{*}$
is spherical of dimension
${\mathcal {S}}_h(X,\sqcup )^{*}$
is spherical of dimension
![]() $n-2$
by hypothesis, and that the inclusion
$n-2$
by hypothesis, and that the inclusion
![]() ${\mathcal {S}}_h(X,\sqcup )^{*}\hookrightarrow {\mathcal {PD}}(X,\sqcup )^{*}\setminus {\mathcal D}(X,\sqcup )$
is a homotopy equivalence by Proposition 5.8. Therefore, it is enough to show that the inclusion
${\mathcal {S}}_h(X,\sqcup )^{*}\hookrightarrow {\mathcal {PD}}(X,\sqcup )^{*}\setminus {\mathcal D}(X,\sqcup )$
is a homotopy equivalence by Proposition 5.8. Therefore, it is enough to show that the inclusion
![]() $i:{\mathcal {PD}}(X,\sqcup )^{*}\setminus {\mathcal D}(X,\sqcup ) \hookrightarrow {\mathcal {PD}}(X,\sqcup )^{*}$
is an
$i:{\mathcal {PD}}(X,\sqcup )^{*}\setminus {\mathcal D}(X,\sqcup ) \hookrightarrow {\mathcal {PD}}(X,\sqcup )^{*}$
is an
![]() $(n-2)$
-equivalence.
$(n-2)$
-equivalence.
We analyze the lower fibers of full decompositions for the map i and apply Quillen’s fiber theorem later. Let
![]() $\sigma _0\in {\mathcal D}(X,\sqcup )^{\circ }$
. By property (LI), the lower fiber
$\sigma _0\in {\mathcal D}(X,\sqcup )^{\circ }$
. By property (LI), the lower fiber
![]() $i^{-1}({\mathcal D}(X,\sqcup )^{\circ })$
can be identified with the poset
$i^{-1}({\mathcal D}(X,\sqcup )^{\circ })$
can be identified with the poset
Write
![]() $\sigma _0 = \{y_1,\ldots ,y_r\}$
, and
$\sigma _0 = \{y_1,\ldots ,y_r\}$
, and
![]() ${\mathcal {PD}}(y_i) := {\mathcal {PD}}(Y_i,\sqcup )$
,
${\mathcal {PD}}(y_i) := {\mathcal {PD}}(Y_i,\sqcup )$
,
![]() ${\mathcal D}(y_i) := {\mathcal D}(Y_i,\sqcup )$
and
${\mathcal D}(y_i) := {\mathcal D}(Y_i,\sqcup )$
and
![]() ${\mathcal {S}}_h(y_i) := {\mathcal {S}}_h(Y_i,\sqcup )$
. We claim that
${\mathcal {S}}_h(y_i) := {\mathcal {S}}_h(Y_i,\sqcup )$
. We claim that
![]() $F_{\sigma _0}$
is homotopy equivalent to
$F_{\sigma _0}$
is homotopy equivalent to
![]() ${\mathcal T} := \big ( \prod _{i=1}^r {\mathcal {S}}_h(y_i) \big )^{*}$
.
${\mathcal T} := \big ( \prod _{i=1}^r {\mathcal {S}}_h(y_i) \big )^{*}$
.
Let
![]() $\Psi :F_{\sigma _0}\to {\mathcal T}$
be the map such that
$\Psi :F_{\sigma _0}\to {\mathcal T}$
be the map such that
Clearly,
![]() $\Psi $
is well-defined and order-preserving.
$\Psi $
is well-defined and order-preserving.
On the other hand, we have a map
![]() $\Gamma : {\mathcal T} \to F_{\sigma _0}$
which is just the canonical inclusion
$\Gamma : {\mathcal T} \to F_{\sigma _0}$
which is just the canonical inclusion
![]() $\Gamma (x_1,\ldots ,x_r) = ( \{x_1\} \setminus \{0\}, \ldots , \{x_r\}\setminus \{0\})$
. Then
$\Gamma (x_1,\ldots ,x_r) = ( \{x_1\} \setminus \{0\}, \ldots , \{x_r\}\setminus \{0\})$
. Then
![]() $\Psi \circ \Gamma $
is the identity map on
$\Psi \circ \Gamma $
is the identity map on
![]() ${\mathcal T}$
, and
${\mathcal T}$
, and
Now,
![]() ${\mathcal T}$
is the proper part of the direct product of bounded posets, and hence, it is a standard fact that the geometric realization of
${\mathcal T}$
is the proper part of the direct product of bounded posets, and hence, it is a standard fact that the geometric realization of
![]() ${\mathcal T}$
is isomorphic to an iterated suspension of a join of the spaces
${\mathcal T}$
is isomorphic to an iterated suspension of a join of the spaces
![]() $|{\mathcal {S}}_h(y_i)^{*}|$
:
$|{\mathcal {S}}_h(y_i)^{*}|$
:
See [Reference WalkerWal88]. Since
![]() ${\mathcal {S}}_h(y_i)^{*}$
is
${\mathcal {S}}_h(y_i)^{*}$
is
![]() $(h(y_i)-3)$
-connected by hypothesis, we conclude that
$(h(y_i)-3)$
-connected by hypothesis, we conclude that
![]() ${\mathcal T}$
is
${\mathcal T}$
is
connected. However, we know that
![]() ${\mathcal D}(X,\sqcup )^{\circ }_{>\sigma _0}$
is the proper part of the partition lattice on
${\mathcal D}(X,\sqcup )^{\circ }_{>\sigma _0}$
is the proper part of the partition lattice on
![]() $\sigma _0$
, so it is spherical of dimension
$\sigma _0$
, so it is spherical of dimension
![]() $r-3$
, and hence
$r-3$
, and hence
![]() $(r-4)$
-connected (the empty space is
$(r-4)$
-connected (the empty space is
![]() $(-2)$
-connected by convention). Thus,
$(-2)$
-connected by convention). Thus,
![]() $F_{\sigma _0} * {\mathcal D}(X,\sqcup )^{\circ }_{>\sigma _0}$
is
$F_{\sigma _0} * {\mathcal D}(X,\sqcup )^{\circ }_{>\sigma _0}$
is
connected. In particular, since
![]() $r\geq 2$
, these are
$r\geq 2$
, these are
![]() $(n-3)$
-connected. By Theorem 5.3, we conclude that i is an
$(n-3)$
-connected. By Theorem 5.3, we conclude that i is an
![]() $(n-2)$
-equivalence, and therefore,
$(n-2)$
-equivalence, and therefore,
![]() ${\mathcal {PD}}(X,\sqcup )^{*}$
is
${\mathcal {PD}}(X,\sqcup )^{*}$
is
![]() $(n-3)$
-connected.
$(n-3)$
-connected.
Example 5.14. Let L be the lattice of subsets of
![]() $\{1,2,3,4\}$
of size different from three. In Subsection 6.4, we will see that this is the lattice of flats of the uniform matroid
$\{1,2,3,4\}$
of size different from three. In Subsection 6.4, we will see that this is the lattice of flats of the uniform matroid
![]() $U_{4,3}$
. Then, by Example 2.19,
$U_{4,3}$
. Then, by Example 2.19,
![]() $L = {\mathcal {S}}(X,\sqcup )$
if L is regarded as a category with monoidal product
$L = {\mathcal {S}}(X,\sqcup )$
if L is regarded as a category with monoidal product
![]() $\sqcup =\vee $
, and
$\sqcup =\vee $
, and
![]() $X=\{1,2,3,4\}$
the maximal element. Note L has height three, and
$X=\{1,2,3,4\}$
the maximal element. Note L has height three, and
![]() ${\mathcal {PD}}(L) = {\mathcal {PD}}(X,\sqcup )$
. Also,
${\mathcal {PD}}(L) = {\mathcal {PD}}(X,\sqcup )$
. Also,
![]() $L = {\mathcal {S}}_h(X,\sqcup )$
, and by the previous theorem, we conclude that the inclusion
$L = {\mathcal {S}}_h(X,\sqcup )$
, and by the previous theorem, we conclude that the inclusion
![]() $i:L^{*} \hookrightarrow {\mathcal {PD}}(L)^{*}$
is a
$i:L^{*} \hookrightarrow {\mathcal {PD}}(L)^{*}$
is a
![]() $1$
-equivalence. Since
$1$
-equivalence. Since
![]() $L^{*}$
is connected, we see that
$L^{*}$
is connected, we see that
![]() ${\mathcal {PD}}(L)^{*}$
is connected. Now we show that
${\mathcal {PD}}(L)^{*}$
is connected. Now we show that
![]() ${\mathcal {PD}}(L)^{*}$
is simply connected, so the inclusion i induces the trivial map in the fundamental groups.
${\mathcal {PD}}(L)^{*}$
is simply connected, so the inclusion i induces the trivial map in the fundamental groups.
If we regard
![]() $L^{*}$
as a
$L^{*}$
as a
![]() $1$
-dimensional simplicial complex, it is not hard to see that
$1$
-dimensional simplicial complex, it is not hard to see that
![]() $L^{*}$
becomes simply connected after attaching
$L^{*}$
becomes simply connected after attaching
![]() $2$
-cells to the cycles of the form
$2$
-cells to the cycles of the form
Thus,
![]() ${\mathcal {PD}}(L)^{*}$
is simply connected if each such cycle is null-homotopic when included in
${\mathcal {PD}}(L)^{*}$
is simply connected if each such cycle is null-homotopic when included in
![]() ${\mathcal {PD}}(L)^{*}$
. Let C denote the cycle from (2), seen as a subposet of
${\mathcal {PD}}(L)^{*}$
. Let C denote the cycle from (2), seen as a subposet of
![]() $L^{*}$
. Then
$L^{*}$
. Then
![]() $i:C\to {\mathcal {PD}}(L)^{*}$
is null-homotopic via the following equivalences of maps:
$i:C\to {\mathcal {PD}}(L)^{*}$
is null-homotopic via the following equivalences of maps:
From this, we can conclude that
![]() ${\mathcal {PD}}(L)^{*}$
is at least
${\mathcal {PD}}(L)^{*}$
is at least
![]() $1$
-connected. Moreover, it is not hard to show that
$1$
-connected. Moreover, it is not hard to show that
![]() ${\mathcal {PD}}(L)^{*}$
collapses to the subposet whose elements are the nonempty subsets of size at most three of
${\mathcal {PD}}(L)^{*}$
collapses to the subposet whose elements are the nonempty subsets of size at most three of
![]() $\{1,2,3,4\}$
(which is the proper part of the Boolean lattice of rank four). Since this poset has dimension two and it is
$\{1,2,3,4\}$
(which is the proper part of the Boolean lattice of rank four). Since this poset has dimension two and it is
![]() $1$
-connected, we conclude that
$1$
-connected, we conclude that
![]() ${\mathcal {PD}}(L)^{*}$
has the homotopy type of a wedge of
${\mathcal {PD}}(L)^{*}$
has the homotopy type of a wedge of
![]() $2$
-spheres.
$2$
-spheres.
In the following two results, we will see that the situation in the previous example actually generalizes to a more general setting.
Proposition 5.15. Let n be the height of
![]() ${\mathcal {S}}(X,\sqcup )$
and suppose
${\mathcal {S}}(X,\sqcup )$
and suppose
![]() $\sigma \in {\mathcal F}(X,\sqcup )$
is a full frame (i.e., a decomposition of size n). Then the Coxeter complex
$\sigma \in {\mathcal F}(X,\sqcup )$
is a full frame (i.e., a decomposition of size n). Then the Coxeter complex
![]() $S_{\sigma }$
associated with
$S_{\sigma }$
associated with
![]() $\sigma $
gives a nonzero class
$\sigma $
gives a nonzero class
![]() $[S_\sigma ]\in \widetilde {H}_{n-2}( {\mathcal {S}}_h(X,\sqcup )^{*},{\mathbb {Z}}) \subseteq \widetilde {H}_{n-2}( {\mathcal {S}}(X,\sqcup )^{*},{\mathbb {Z}})$
.
$[S_\sigma ]\in \widetilde {H}_{n-2}( {\mathcal {S}}_h(X,\sqcup )^{*},{\mathbb {Z}}) \subseteq \widetilde {H}_{n-2}( {\mathcal {S}}(X,\sqcup )^{*},{\mathbb {Z}})$
.
Moreover,
![]() $S_{\sigma }$
is null-homotopic when embedded in
$S_{\sigma }$
is null-homotopic when embedded in
![]() ${\mathcal {PD}}(X,\sqcup )^{*}$
via the canonical inclusion
${\mathcal {PD}}(X,\sqcup )^{*}$
via the canonical inclusion
![]() ${\mathcal {S}}_h(X,\sqcup )^{*}\hookrightarrow {\mathcal {PD}}(X,\sqcup )^{*}$
.
${\mathcal {S}}_h(X,\sqcup )^{*}\hookrightarrow {\mathcal {PD}}(X,\sqcup )^{*}$
.
Proof. There is an
![]() $(n-2)$
-dimensional sphere embedded in the order complex of
$(n-2)$
-dimensional sphere embedded in the order complex of
![]() ${\mathcal {S}}_h(X,\sqcup )$
which is obtained by taking the usual apartment of a basis, here regarded as a frame. Concretely, this sphere is a Coxeter complex obtained as the order complex of the subposet
${\mathcal {S}}_h(X,\sqcup )$
which is obtained by taking the usual apartment of a basis, here regarded as a frame. Concretely, this sphere is a Coxeter complex obtained as the order complex of the subposet
Since
![]() $S_{\sigma }$
is an
$S_{\sigma }$
is an
![]() $(n-2)$
-dimensional sphere, its class gives a nonzero cycle for the
$(n-2)$
-dimensional sphere, its class gives a nonzero cycle for the
![]() $(n-2)$
-homology group of
$(n-2)$
-homology group of
![]() ${\mathcal {S}}_h(X,\sqcup )^{*}$
, which is naturally included in
${\mathcal {S}}_h(X,\sqcup )^{*}$
, which is naturally included in
![]() $\widetilde {H}_{n-2}( {\mathcal {S}}(X,\sqcup )^{*},{\mathbb {Z}})$
.
$\widetilde {H}_{n-2}( {\mathcal {S}}(X,\sqcup )^{*},{\mathbb {Z}})$
.
On the other hand, note that the image of
![]() $S_{\sigma }$
under the canonical map
$S_{\sigma }$
under the canonical map
![]() ${\mathcal {S}}_h(X,\sqcup )^{*}\to {\mathcal {PD}}(X,\sqcup )^{*}$
is contained in the subposet
${\mathcal {S}}_h(X,\sqcup )^{*}\to {\mathcal {PD}}(X,\sqcup )^{*}$
is contained in the subposet
Then
![]() $T_{\sigma }$
is the proper part of the partial decomposition poset of the Boolean lattice on
$T_{\sigma }$
is the proper part of the partial decomposition poset of the Boolean lattice on
![]() $\sigma $
. In particular, by Corollary 5.19, the poset
$\sigma $
. In particular, by Corollary 5.19, the poset
![]() $T_{\sigma }$
is contractible. Hence, the inclusion of the sphere
$T_{\sigma }$
is contractible. Hence, the inclusion of the sphere
![]() $S_{\sigma } \hookrightarrow {\mathcal {PD}}(X,\sqcup )^{*}$
is null-homotopic (and thus trivial in homology).
$S_{\sigma } \hookrightarrow {\mathcal {PD}}(X,\sqcup )^{*}$
is null-homotopic (and thus trivial in homology).
Corollary 5.16. Let n be the height of
![]() ${\mathcal {S}}(X,\sqcup )$
, and assume the following conditions hold:
${\mathcal {S}}(X,\sqcup )$
, and assume the following conditions hold:
-
• property (LI);
-
• for all
 $y\in {\mathcal {S}}_h(X,\sqcup )$
, the poset
$y\in {\mathcal {S}}_h(X,\sqcup )$
, the poset
 ${\mathcal {S}}_h(Y,\sqcup )^{*}$
is spherical of dimension
${\mathcal {S}}_h(Y,\sqcup )^{*}$
is spherical of dimension
 $h(y)-2$
;
$h(y)-2$
; -
• the spheres
 $S_{\sigma }$
, for
$S_{\sigma }$
, for
 $\sigma $
a full frame, generate the
$\sigma $
a full frame, generate the
 $(n-2)$
th homotopy group of
$(n-2)$
th homotopy group of
 ${\mathcal {S}}_h(X,\sqcup )^{*}$
.
${\mathcal {S}}_h(X,\sqcup )^{*}$
.
Then
![]() ${\mathcal {S}}_h(X,\sqcup )^{*}\hookrightarrow {\mathcal {PD}}(X,\sqcup )^{*}$
is null-homotopic. In particular,
${\mathcal {S}}_h(X,\sqcup )^{*}\hookrightarrow {\mathcal {PD}}(X,\sqcup )^{*}$
is null-homotopic. In particular,
![]() ${\mathcal {PD}}(X,\sqcup )^{*}$
is
${\mathcal {PD}}(X,\sqcup )^{*}$
is
![]() $(n-2)$
-connected.
$(n-2)$
-connected.
Proof. By Theorem 5.13, it is enough to show that
![]() ${\mathcal {S}}_h(X,\sqcup )^{*}\hookrightarrow {\mathcal {PD}}(X,\sqcup )^{*}$
maps a set of generators of the
${\mathcal {S}}_h(X,\sqcup )^{*}\hookrightarrow {\mathcal {PD}}(X,\sqcup )^{*}$
maps a set of generators of the
![]() $(n-2)$
th homotopy group to the trivial subgroup. By hypothesis, we can take as a generating set the classes of the spheres obtained as the order complexes of
$(n-2)$
th homotopy group to the trivial subgroup. By hypothesis, we can take as a generating set the classes of the spheres obtained as the order complexes of
![]() $S_{\sigma }$
for the full frames
$S_{\sigma }$
for the full frames
![]() $\sigma $
. By Proposition 5.15, these spheres are null-homotopic in
$\sigma $
. By Proposition 5.15, these spheres are null-homotopic in
![]() ${\mathcal {PD}}(X,\sqcup )^{*}$
. The result follows.
${\mathcal {PD}}(X,\sqcup )^{*}$
. The result follows.
5.3 Unique complementation
Now we explore some consequences of the relations between the different posets we defined when we additionally have unique downward
![]() $(\sqcup ,h)$
-complementation and property (EX) holds. Recall that property (EX) states that if we have a partial decomposition
$(\sqcup ,h)$
-complementation and property (EX) holds. Recall that property (EX) states that if we have a partial decomposition
![]() $\sigma $
of
$\sigma $
of
![]() ${\mathcal {S}}(X,\sqcup )$
and we pick a full decomposition
${\mathcal {S}}(X,\sqcup )$
and we pick a full decomposition
![]() $\tau \in {\mathcal D}({\mathcal {S}}(X,\sqcup )_{\leq y})$
of the lower interval of one of its elements
$\tau \in {\mathcal D}({\mathcal {S}}(X,\sqcup )_{\leq y})$
of the lower interval of one of its elements
![]() $y\in \sigma $
which is
$y\in \sigma $
which is
![]() $\sqcup $
-compatible in
$\sqcup $
-compatible in
![]() ${\mathcal {S}}(X,\sqcup )$
, then
${\mathcal {S}}(X,\sqcup )$
, then
![]() $( \sigma \setminus \{y\})\cup \tau $
is a partial decomposition of X. See Definition 3.10.
$( \sigma \setminus \{y\})\cup \tau $
is a partial decomposition of X. See Definition 3.10.
Lemma 5.17. If
![]() ${\mathcal {S}}(X,\sqcup )$
is uniquely downward
${\mathcal {S}}(X,\sqcup )$
is uniquely downward
![]() $(\sqcup ,h)$
-complemented and the map G defined in Lemma 4.12 is surjective, then G is an isomorphism between
$(\sqcup ,h)$
-complemented and the map G defined in Lemma 4.12 is surjective, then G is an isomorphism between
![]() $\mathcal {O}{\mathcal D}(X,\sqcup )^{\circ }$
and the opposite poset of
$\mathcal {O}{\mathcal D}(X,\sqcup )^{\circ }$
and the opposite poset of
![]() $\Delta {\mathcal {S}}(X,\sqcup )^{*}$
.
$\Delta {\mathcal {S}}(X,\sqcup )^{*}$
.
Proof. Since G is a surjective poset map by hypothesis, it is enough to prove that
![]() $G(\tau ) \supseteq G(\sigma )$
implies that
$G(\tau ) \supseteq G(\sigma )$
implies that
![]() $\tau \leq \sigma $
.
$\tau \leq \sigma $
.
Assume then that
![]() $G(\tau )\supseteq G(\sigma )$
. Write
$G(\tau )\supseteq G(\sigma )$
. Write
![]() $\tau =(z_1,\ldots ,z_r)$
and
$\tau =(z_1,\ldots ,z_r)$
and
![]() $\sigma =(w_1,\ldots ,w_s)$
. For
$\sigma =(w_1,\ldots ,w_s)$
. For
![]() $1\leq j\leq s-1$
, let
$1\leq j\leq s-1$
, let
![]() $1\leq \beta (j) \leq r$
be such that
$1\leq \beta (j) \leq r$
be such that
We claim that
Indeed,
![]() $w_{j+1}$
is the unique
$w_{j+1}$
is the unique
![]() $(\sqcup ,h)$
-complement of
$(\sqcup ,h)$
-complement of
in
But also
![]() $z_{\beta (j)+1} \vee \cdots \vee z_{\beta (j)}$
is the unique
$z_{\beta (j)+1} \vee \cdots \vee z_{\beta (j)}$
is the unique
![]() $(\sqcup ,h)$
-complement of
$(\sqcup ,h)$
-complement of
![]() $y_j$
in
$y_j$
in
![]() $y_j \vee w_{j+1}$
. Thus, they must coincide. This shows that
$y_j \vee w_{j+1}$
. Thus, they must coincide. This shows that
![]() $\tau \leq \sigma $
.
$\tau \leq \sigma $
.
Lemma 5.18. If
![]() ${\mathcal {S}}(X,\sqcup )$
is uniquely downward
${\mathcal {S}}(X,\sqcup )$
is uniquely downward
![]() $(\sqcup ,h)$
-complemented and satisfies property (EX), then the map G is surjective. In particular,
$(\sqcup ,h)$
-complemented and satisfies property (EX), then the map G is surjective. In particular,
![]() $\mathcal {O}{\mathcal D}(X,\sqcup )^{\circ }$
is isomorphic to
$\mathcal {O}{\mathcal D}(X,\sqcup )^{\circ }$
is isomorphic to
![]() $(\Delta {\mathcal {S}}(X,\sqcup )^{*})^{\mathrm {op}}$
.
$(\Delta {\mathcal {S}}(X,\sqcup )^{*})^{\mathrm {op}}$
.
Proof. We prove this by induction on the size of a chain. Let
![]() $c = \{ z_0 < z_1 \cdots < z_r \} \in \Delta {\mathcal {S}}(X,\sqcup )^{*}$
be a chain. If
$c = \{ z_0 < z_1 \cdots < z_r \} \in \Delta {\mathcal {S}}(X,\sqcup )^{*}$
be a chain. If
![]() $r = 0$
, let
$r = 0$
, let
![]() $w_0$
be the unique
$w_0$
be the unique
![]() $(\sqcup ,h)$
-complement of
$(\sqcup ,h)$
-complement of
![]() $z_0$
. Thus,
$z_0$
. Thus,
![]() $\{z_0,w_0\}$
is a
$\{z_0,w_0\}$
is a
![]() $\sqcup $
-decomposition and
$\sqcup $
-decomposition and
![]() $G(z_0,w_0) = (z_0)$
. Assume then that
$G(z_0,w_0) = (z_0)$
. Assume then that
![]() $r> 0$
, and let
$r> 0$
, and let
![]() $c' = c\setminus \{z_r\}$
. Hence, there exists an ordered
$c' = c\setminus \{z_r\}$
. Hence, there exists an ordered
![]() $\sqcup $
-decomposition
$\sqcup $
-decomposition
![]() $(x_0,\ldots ,x_r)$
with
$(x_0,\ldots ,x_r)$
with
![]() $z_i = x_0 \vee \cdots \vee x_i$
, for
$z_i = x_0 \vee \cdots \vee x_i$
, for
![]() $0\leq i \leq r-1$
. By uniqueness, we have
$0\leq i \leq r-1$
. By uniqueness, we have
![]() $x_r = z_{r-1}^\perp> z_r^{\perp }$
. Let u be the unique
$x_r = z_{r-1}^\perp> z_r^{\perp }$
. Let u be the unique
![]() $(\sqcup ,h)$
-complement of
$(\sqcup ,h)$
-complement of
![]() $z_r^\perp $
in
$z_r^\perp $
in
![]() $x_r$
. Then
$x_r$
. Then
![]() $\{u,z_r^{\perp }\}\in {\mathcal D}( {\mathcal {S}}(X,\sqcup )_{\leq x_r})$
and it is
$\{u,z_r^{\perp }\}\in {\mathcal D}( {\mathcal {S}}(X,\sqcup )_{\leq x_r})$
and it is
![]() $\sqcup $
-compatible in
$\sqcup $
-compatible in
![]() ${\mathcal {S}}(X,\sqcup )$
. By property (EX), we see that
${\mathcal {S}}(X,\sqcup )$
. By property (EX), we see that
![]() $\{x_0,\ldots ,x_{r-1},u,z_r^{\perp }\}\in {\mathcal D}(X,\sqcup )$
and also
$\{x_0,\ldots ,x_{r-1},u,z_r^{\perp }\}\in {\mathcal D}(X,\sqcup )$
and also
![]() $z_r = z_{r-1}\vee u$
. Hence,
$z_r = z_{r-1}\vee u$
. Hence,
![]() $G(x_0,\ldots ,x_{r-1},u,z_r^{\perp }) = (z_0,\ldots ,z_{r-1},z_r)$
.
$G(x_0,\ldots ,x_{r-1},u,z_r^{\perp }) = (z_0,\ldots ,z_{r-1},z_r)$
.
Corollary 5.19. Suppose that
![]() ${\mathcal D}(X,\sqcup )$
has a unique minimum element
${\mathcal D}(X,\sqcup )$
has a unique minimum element
![]() $\sigma _0$
. Then
$\sigma _0$
. Then
![]() ${\mathcal D}(X,\sqcup )$
is the partition lattice on
${\mathcal D}(X,\sqcup )$
is the partition lattice on
![]() $\sigma _0$
,
$\sigma _0$
,
![]() ${\mathcal {S}}_h(X,\sqcup )$
is a Boolean lattice on the set
${\mathcal {S}}_h(X,\sqcup )$
is a Boolean lattice on the set
![]() $\sigma _0$
and
$\sigma _0$
and
![]() ${\mathcal {PD}}(X,\sqcup )^{*}$
is contractible. Moreover,
${\mathcal {PD}}(X,\sqcup )^{*}$
is contractible. Moreover,
![]() ${\mathcal {S}}_h(X,\sqcup )$
,
${\mathcal {S}}_h(X,\sqcup )$
,
![]() ${\mathcal D}(X,\sqcup )$
,
${\mathcal D}(X,\sqcup )$
,
![]() ${\mathcal {PD}}(X,\sqcup )$
are Cohen-Macaulay.
${\mathcal {PD}}(X,\sqcup )$
are Cohen-Macaulay.
Proof. By Proposition 3.1,
![]() ${\mathcal D}(X,\sqcup )$
is the partition lattice on
${\mathcal D}(X,\sqcup )$
is the partition lattice on
![]() $\sigma _0$
. Since, any element of
$\sigma _0$
. Since, any element of
![]() $x\in {\mathcal {S}}_h(X,\sqcup )$
is part of a
$x\in {\mathcal {S}}_h(X,\sqcup )$
is part of a
![]() $\sqcup $
-decomposition, there exists a unique set
$\sqcup $
-decomposition, there exists a unique set
![]() $\tau \subseteq \sigma _0$
such that x is the join of the elements of
$\tau \subseteq \sigma _0$
such that x is the join of the elements of
![]() $\tau $
. Therefore,
$\tau $
. Therefore,
![]() ${\mathcal {S}}_h(X,\sqcup )$
is the Boolean lattice on the set
${\mathcal {S}}_h(X,\sqcup )$
is the Boolean lattice on the set
![]() $\sigma _0$
. In particular,
$\sigma _0$
. In particular,
![]() ${\mathcal {S}}_h(X,\sqcup )$
and
${\mathcal {S}}_h(X,\sqcup )$
and
![]() ${\mathcal D}(X,\sqcup )$
are Cohen-Macaulay.
${\mathcal D}(X,\sqcup )$
are Cohen-Macaulay.
Now we prove that
![]() ${\mathcal {PD}}(X,\sqcup )^{*}$
is contractible. In fact, we show that if
${\mathcal {PD}}(X,\sqcup )^{*}$
is contractible. In fact, we show that if
![]() $\sigma \in {\mathcal {PD}}(X,\sqcup )\setminus {\mathcal D}(X,\sqcup )$
, then
$\sigma \in {\mathcal {PD}}(X,\sqcup )\setminus {\mathcal D}(X,\sqcup )$
, then
![]() ${\mathcal {PD}}(X,\sqcup )_{>\sigma } \setminus \{ \{1\}\}$
is contractible (so
${\mathcal {PD}}(X,\sqcup )_{>\sigma } \setminus \{ \{1\}\}$
is contractible (so
![]() ${\mathcal {PD}}(X,\sqcup )^{*}$
is contractible by taking
${\mathcal {PD}}(X,\sqcup )^{*}$
is contractible by taking
![]() $\sigma = \{\}$
).
$\sigma = \{\}$
).
Let
![]() $\sigma \in {\mathcal {PD}}(X,\sqcup )\setminus {\mathcal D}(X,\sqcup )$
. Then
$\sigma \in {\mathcal {PD}}(X,\sqcup )\setminus {\mathcal D}(X,\sqcup )$
. Then
![]() $\sigma $
is contained in some
$\sigma $
is contained in some
![]() $\sqcup $
-decomposition (i.e., partition)
$\sqcup $
-decomposition (i.e., partition)
![]() $\tau $
and every element
$\tau $
and every element
![]() $y\in \sigma $
can be obtained by joining elements of
$y\in \sigma $
can be obtained by joining elements of
![]() $\sigma _0$
. Thus, the set
$\sigma _0$
. Thus, the set
is a partition of
![]() $\sigma _0$
. Now we fix
$\sigma _0$
. Now we fix
![]() $\sigma $
, and let
$\sigma $
, and let
![]() $\sigma '>\sigma $
. Then
$\sigma '>\sigma $
. Then
![]() $f(\sigma ') \geq \sigma '> \sigma $
. Since
$f(\sigma ') \geq \sigma '> \sigma $
. Since
![]() $\sigma \notin {\mathcal D}(X,\sqcup )$
and
$\sigma \notin {\mathcal D}(X,\sqcup )$
and
![]() $f(\sigma )\in {\mathcal D}(X,\sqcup )$
, we see that
$f(\sigma )\in {\mathcal D}(X,\sqcup )$
, we see that
![]() $f(\sigma )>\sigma $
. Thus, we have the following inequalities in
$f(\sigma )>\sigma $
. Thus, we have the following inequalities in
![]() ${\mathcal {PD}}(X,\sqcup )_{>\sigma }\setminus \{ \{1\} \}$
:
${\mathcal {PD}}(X,\sqcup )_{>\sigma }\setminus \{ \{1\} \}$
:
This proves that
![]() ${\mathcal {PD}}(X,\sqcup )_{>\sigma }\setminus \{ \{1\} \}$
is contractible. It is also not hard to show that this interval has the correct dimension.
${\mathcal {PD}}(X,\sqcup )_{>\sigma }\setminus \{ \{1\} \}$
is contractible. It is also not hard to show that this interval has the correct dimension.
Since
![]() $f(\emptyset ) = \sigma _0$
, the homotopy above is
$f(\emptyset ) = \sigma _0$
, the homotopy above is
Hence,
![]() ${\mathcal {PD}}(X,\sqcup )^{*}$
is contractible.
${\mathcal {PD}}(X,\sqcup )^{*}$
is contractible.
On the other hand, if
![]() $\sigma \in {\mathcal D}(X,\sqcup )$
, then
$\sigma \in {\mathcal D}(X,\sqcup )$
, then
which is a Cohen-Macaulay poset. Therefore, upper intervals in the poset
![]() ${\mathcal {PD}}(X,\sqcup )^{*}$
are spherical of the correct dimension.
${\mathcal {PD}}(X,\sqcup )^{*}$
are spherical of the correct dimension.
Finally, since lower intervals in
![]() ${\mathcal {PD}}(X,\sqcup )$
are products of partial decomposition posets, which are partial decompositions of Boolean lattices, we conclude that
${\mathcal {PD}}(X,\sqcup )$
are products of partial decomposition posets, which are partial decompositions of Boolean lattices, we conclude that
![]() ${\mathcal {PD}}(X,\sqcup )$
is a Cohen-Macaulay poset.
${\mathcal {PD}}(X,\sqcup )$
is a Cohen-Macaulay poset.
Proposition 5.20. If
![]() ${\mathcal {S}}(X,\sqcup )$
is uniquely downward
${\mathcal {S}}(X,\sqcup )$
is uniquely downward
![]() $(\sqcup ,h)$
-complemented and satisfies property (EX), then there is a deformation retract of
$(\sqcup ,h)$
-complemented and satisfies property (EX), then there is a deformation retract of
![]() ${\mathcal {PD}}(X,\sqcup )^{*}$
onto
${\mathcal {PD}}(X,\sqcup )^{*}$
onto
![]() ${\mathcal D}(X,\sqcup )^{\circ }$
.
${\mathcal D}(X,\sqcup )^{\circ }$
.
Proof. We prove that for any
![]() $\tau \in {\mathcal {PD}}(X,\sqcup )^{*} \setminus {\mathcal D}(X,\sqcup )$
, the interval
$\tau \in {\mathcal {PD}}(X,\sqcup )^{*} \setminus {\mathcal D}(X,\sqcup )$
, the interval
![]() ${\mathcal D}_{\tau }:={\mathcal D}(X,\sqcup )^{\circ }_{\geq \tau }$
is contractible. Let
${\mathcal D}_{\tau }:={\mathcal D}(X,\sqcup )^{\circ }_{\geq \tau }$
is contractible. Let
![]() $\sigma \in {\mathcal D}_{\tau }$
. For
$\sigma \in {\mathcal D}_{\tau }$
. For
![]() $y\in \sigma $
, let
$y\in \sigma $
, let
![]() $\tau _y := \{x\in \tau \mathrel {{\: : \: }} x\leq y\}$
and
$\tau _y := \{x\in \tau \mathrel {{\: : \: }} x\leq y\}$
and
![]() $\alpha (y) := \bigvee _{x\in \tau _y}x$
. Then
$\alpha (y) := \bigvee _{x\in \tau _y}x$
. Then
![]() $\alpha (y)\leq y$
. Let
$\alpha (y)\leq y$
. Let
![]() $\beta (y)\leq y$
be the unique
$\beta (y)\leq y$
be the unique
![]() $(\sqcup ,h)$
-complement for
$(\sqcup ,h)$
-complement for
![]() $\alpha (y)$
in y. Hence, we get a decomposition
$\alpha (y)$
in y. Hence, we get a decomposition
![]() $\{\alpha (y),\beta (y)\}\setminus \{0\} \in {\mathcal D}({\mathcal {S}}(X,\sqcup )_{\leq y})$
which is
$\{\alpha (y),\beta (y)\}\setminus \{0\} \in {\mathcal D}({\mathcal {S}}(X,\sqcup )_{\leq y})$
which is
![]() $\sqcup $
-compatible in
$\sqcup $
-compatible in
![]() ${\mathcal {S}}(X,\sqcup )$
. By property (EX),
${\mathcal {S}}(X,\sqcup )$
. By property (EX),
is a
![]() $\sqcup $
-decomposition of
$\sqcup $
-decomposition of
![]() ${\mathcal {S}}(X,\sqcup )$
. We can continue in this way until producing a
${\mathcal {S}}(X,\sqcup )$
. We can continue in this way until producing a
![]() $\sqcup $
-decomposition
$\sqcup $
-decomposition
Note that
![]() $\Lambda (\sigma )\leq \sigma $
and
$\Lambda (\sigma )\leq \sigma $
and
![]() $\tau \leq \Lambda (\sigma )$
. Now, let x be the join of the elements of
$\tau \leq \Lambda (\sigma )$
. Now, let x be the join of the elements of
![]() $\tau $
and
$\tau $
and
![]() $x'$
be the
$x'$
be the
![]() $(\sqcup ,h)$
-complement of x in
$(\sqcup ,h)$
-complement of x in
![]() ${\mathcal {S}}(X,\sqcup )$
. We claim that
${\mathcal {S}}(X,\sqcup )$
. We claim that
![]() $\beta (y)\leq x'$
. Since
$\beta (y)\leq x'$
. Since
![]() $x = \bigvee _{y \in \sigma } \alpha (y)$
, if
$x = \bigvee _{y \in \sigma } \alpha (y)$
, if
![]() $x" = \bigvee _{y\in \sigma } \beta (y)$
, then
$x" = \bigvee _{y\in \sigma } \beta (y)$
, then
![]() $\{x,x"\}\in {\mathcal D}(X,\sqcup )$
, so
$\{x,x"\}\in {\mathcal D}(X,\sqcup )$
, so
![]() $x,x"$
are
$x,x"$
are
![]() $(\sqcup ,h)$
-complements of each other since
$(\sqcup ,h)$
-complements of each other since
![]() $\Lambda (\sigma )$
is a
$\Lambda (\sigma )$
is a
![]() $\sqcup $
-decomposition. By uniqueness,
$\sqcup $
-decomposition. By uniqueness,
![]() $x" = x'$
, and this implies that
$x" = x'$
, and this implies that
![]() $\beta (y)\leq x'$
. Hence, we have the following zigzag whose elements lie in
$\beta (y)\leq x'$
. Hence, we have the following zigzag whose elements lie in
![]() ${\mathcal D}_{\tau }$
:
${\mathcal D}_{\tau }$
:
It remains to prove that the map
![]() $\sigma \mapsto \Lambda (\sigma )$
is order-preserving. For simplicity, we prove it for covering relations, so assume that
$\sigma \mapsto \Lambda (\sigma )$
is order-preserving. For simplicity, we prove it for covering relations, so assume that
![]() $\sigma \leq \rho $
, where
$\sigma \leq \rho $
, where
![]() $\rho $
is obtained by joining two elements
$\rho $
is obtained by joining two elements
![]() $y_1,y_2$
of
$y_1,y_2$
of
![]() $\sigma $
. Then we have the
$\sigma $
. Then we have the
![]() $\sqcup $
-decompositions by
$\sqcup $
-decompositions by
![]() $(\sqcup ,h)$
-complements
$(\sqcup ,h)$
-complements
![]() $y_1 = \alpha (y_1) \vee \beta (y_1)$
and
$y_1 = \alpha (y_1) \vee \beta (y_1)$
and
![]() $y_2 = \alpha (y_2)\vee \beta (y_2)$
. Clearly,
$y_2 = \alpha (y_2)\vee \beta (y_2)$
. Clearly,
![]() $\alpha (y_1\vee y_2) = \alpha (y_1)\vee \alpha (y_2)$
. Let
$\alpha (y_1\vee y_2) = \alpha (y_1)\vee \alpha (y_2)$
. Let
![]() $z = \beta (y_1)\vee \beta (y_2)$
, which exists since
$z = \beta (y_1)\vee \beta (y_2)$
, which exists since
![]() $\Lambda (\sigma )$
is a
$\Lambda (\sigma )$
is a
![]() $\sqcup $
-decomposition. This also implies that
$\sqcup $
-decomposition. This also implies that
![]() $h(z) = h(\beta (y_1)) + h(\beta (y_2))$
, and that
$h(z) = h(\beta (y_1)) + h(\beta (y_2))$
, and that
![]() $z \wedge (\alpha (y_1)\vee \alpha (y_2)) = 0$
. We also have that
$z \wedge (\alpha (y_1)\vee \alpha (y_2)) = 0$
. We also have that
![]() $z\vee \alpha (y_1)\vee \alpha (y_2) = y_1\vee y_2$
. Therefore, z is an
$z\vee \alpha (y_1)\vee \alpha (y_2) = y_1\vee y_2$
. Therefore, z is an
![]() $(\sqcup ,h)$
-complement for
$(\sqcup ,h)$
-complement for
![]() $\alpha (y_1)\vee \alpha (y_2)$
in
$\alpha (y_1)\vee \alpha (y_2)$
in
![]() $y_1\vee y_2$
. By uniqueness,
$y_1\vee y_2$
. By uniqueness,
![]() $z = \beta (y_1\vee y_2)$
. Hence,
$z = \beta (y_1\vee y_2)$
. Hence,
![]() $\Lambda (\rho )$
is obtained from
$\Lambda (\rho )$
is obtained from
![]() $\Lambda (\sigma )$
after taking the joins
$\Lambda (\sigma )$
after taking the joins
![]() $\alpha (y_1)\vee \alpha (y_2)$
and
$\alpha (y_1)\vee \alpha (y_2)$
and
![]() $\beta (y_1)\vee \beta (y_2)$
. Thus,
$\beta (y_1)\vee \beta (y_2)$
. Thus,
![]() $\Lambda (\sigma )\leq \Lambda (\rho )$
.
$\Lambda (\sigma )\leq \Lambda (\rho )$
.
Corollary 5.21. Suppose that
![]() ${\mathcal {S}}(X,\sqcup )$
is uniquely downward
${\mathcal {S}}(X,\sqcup )$
is uniquely downward
![]() $(\sqcup ,h)$
-complemented, and let
$(\sqcup ,h)$
-complemented, and let
![]() ${\sigma \in {\mathcal {PF}}(X,\sqcup )}$
be a simplex of size
${\sigma \in {\mathcal {PF}}(X,\sqcup )}$
be a simplex of size
![]() $n-1$
. Then the following hold:
$n-1$
. Then the following hold:
-
(1)
 $\sigma $
is contained in a unique maximal simplex.
$\sigma $
is contained in a unique maximal simplex. -
(2) There is a deformation retract of
 ${\mathcal F}(X,\sqcup )$
, viewed as a poset, onto the subposet
${\mathcal F}(X,\sqcup )$
, viewed as a poset, onto the subposet
 $\widehat {{\mathcal F}}(X,\sqcup )$
of frames of size
$\widehat {{\mathcal F}}(X,\sqcup )$
of frames of size
 $\neq n-1$
.
$\neq n-1$
. -
(3) If property (EX) holds, then we have a poset inclusion
 $\widehat {{\mathcal F}}(X,\sqcup )^{\mathrm {op}} \hookrightarrow {\mathcal D}(X,\sqcup )^{\circ }$
given by
$\widehat {{\mathcal F}}(X,\sqcup )^{\mathrm {op}} \hookrightarrow {\mathcal D}(X,\sqcup )^{\circ }$
given by
 ${\tau \mapsto \tau \cup \{ \big (\bigvee _{x\in \tau }x \big )^\perp \}}$
.
${\tau \mapsto \tau \cup \{ \big (\bigvee _{x\in \tau }x \big )^\perp \}}$
.
Proof. Let
![]() $\sigma \in {\mathcal {PF}}(X,\sqcup )$
be a frame of size
$\sigma \in {\mathcal {PF}}(X,\sqcup )$
be a frame of size
![]() $n-1$
, and recall that
$n-1$
, and recall that
![]() $\Phi (\sigma )$
is the join of the elements of
$\Phi (\sigma )$
is the join of the elements of
![]() $\sigma $
. Since
$\sigma $
. Since
![]() $\sigma $
is a partial decomposition,
$\sigma $
is a partial decomposition,
![]() $\sigma \cup \{\Phi (\sigma )^\perp \}\in {\mathcal D}(X,\sqcup )$
. Now,
$\sigma \cup \{\Phi (\sigma )^\perp \}\in {\mathcal D}(X,\sqcup )$
. Now,
![]() $|\sigma |=n-1$
implies that
$|\sigma |=n-1$
implies that
![]() $h(\Phi (\sigma )) = n-1$
and
$h(\Phi (\sigma )) = n-1$
and
![]() $h(\Phi (\sigma )^\perp ) = 1$
. Therefore,
$h(\Phi (\sigma )^\perp ) = 1$
. Therefore,
![]() $\sigma \cup \{\Phi (\sigma )^\perp \}$
is a frame of size n, and clearly,
$\sigma \cup \{\Phi (\sigma )^\perp \}$
is a frame of size n, and clearly,
![]() ${\mathcal {PF}}(X,\sqcup )_{>\sigma } = \{ \sigma \cup \{\Phi (\sigma )^\perp \}\} $
by uniqueness of the complement. This proves item 1.
${\mathcal {PF}}(X,\sqcup )_{>\sigma } = \{ \sigma \cup \{\Phi (\sigma )^\perp \}\} $
by uniqueness of the complement. This proves item 1.
Item 2 is an easy consequence of item 1. We write down the deformation retract. Let
![]() $\widehat {{\mathcal F}}(X,\sqcup )$
be the subposet of
$\widehat {{\mathcal F}}(X,\sqcup )$
be the subposet of
![]() ${\mathcal F}(X,\sqcup )$
consisting of frames of size
${\mathcal F}(X,\sqcup )$
consisting of frames of size
![]() $\neq n-1$
. By the previous paragraph,
$\neq n-1$
. By the previous paragraph,
![]() ${\mathcal F}(X,\sqcup )_{>\sigma } = \{ \sigma \cup \{\Phi (\sigma )^\perp \}\}$
for any frame
${\mathcal F}(X,\sqcup )_{>\sigma } = \{ \sigma \cup \{\Phi (\sigma )^\perp \}\}$
for any frame
![]() $\sigma $
of size
$\sigma $
of size
![]() $n-1$
. Therefore, the retraction
$n-1$
. Therefore, the retraction
![]() $r:{\mathcal F}(X,\sqcup )\to \widehat {{\mathcal F}}(X,\sqcup )$
that takes a frame of size
$r:{\mathcal F}(X,\sqcup )\to \widehat {{\mathcal F}}(X,\sqcup )$
that takes a frame of size
![]() $n-1$
to the unique maximal frame of size n containing it is an order-preserving map such that
$n-1$
to the unique maximal frame of size n containing it is an order-preserving map such that
![]() $r(\sigma )\geq \sigma $
for all
$r(\sigma )\geq \sigma $
for all
![]() $\sigma \in {\mathcal F}(X,\sqcup )$
, and it is the identity on
$\sigma \in {\mathcal F}(X,\sqcup )$
, and it is the identity on
![]() $\widehat {{\mathcal F}}(X,\sqcup )$
. Hence,
$\widehat {{\mathcal F}}(X,\sqcup )$
. Hence,
![]() ${\mathcal F}(X,\sqcup ) \simeq \widehat {{\mathcal F}}(X,\sqcup )$
.
${\mathcal F}(X,\sqcup ) \simeq \widehat {{\mathcal F}}(X,\sqcup )$
.
The function
![]() $\widehat {{\mathcal F}}(X,\sqcup )^{\mathrm {op}} \hookrightarrow {\mathcal D}(X,\sqcup )^{\circ }$
defined in item 3 is an inclusion of posets by Corollary 3.13.
$\widehat {{\mathcal F}}(X,\sqcup )^{\mathrm {op}} \hookrightarrow {\mathcal D}(X,\sqcup )^{\circ }$
defined in item 3 is an inclusion of posets by Corollary 3.13.
Corollary 5.22. Assume the following hold for
![]() ${\mathcal {S}}(X,\sqcup )$
:
${\mathcal {S}}(X,\sqcup )$
:
-
(1)
 ${\mathcal {S}}(X,\sqcup )$
is finite and uniquely downward
${\mathcal {S}}(X,\sqcup )$
is finite and uniquely downward
 $(\sqcup ,h)$
-complemented.
$(\sqcup ,h)$
-complemented. -
(2) For
 $y\in {\mathcal {S}}(X,\sqcup )$
,
$y\in {\mathcal {S}}(X,\sqcup )$
,
 ${\mathcal {S}}(X,\sqcup )_{\leq y} = {\mathcal {S}}(Y,\sqcup )$
for a representative
${\mathcal {S}}(X,\sqcup )_{\leq y} = {\mathcal {S}}(Y,\sqcup )$
for a representative
 $y = [(Y,i)]$
.
$y = [(Y,i)]$
. -
(3) Property (EX) holds.
-
(4) The lower intervals in
 ${\mathcal D}(X,\sqcup )$
and
${\mathcal D}(X,\sqcup )$
and
 ${\mathcal {PD}}(X,\sqcup )$
decompose as in Lemma 4.10(2).
${\mathcal {PD}}(X,\sqcup )$
decompose as in Lemma 4.10(2).
Then
![]() $\tilde {\chi }(\mathcal {O}{\mathcal {PD}}(X,\sqcup )^{*}) = -1$
.
$\tilde {\chi }(\mathcal {O}{\mathcal {PD}}(X,\sqcup )^{*}) = -1$
.
Proof. We compute
![]() $\tilde {\chi }(\mathcal {O}{\mathcal {PD}}(X,\sqcup )^{*})$
by using the wedge decomposition given in Theorem 5.9(2) and the following formula for the Euler characteristic of a finite poset:
$\tilde {\chi }(\mathcal {O}{\mathcal {PD}}(X,\sqcup )^{*})$
by using the wedge decomposition given in Theorem 5.9(2) and the following formula for the Euler characteristic of a finite poset:
First, note that
![]() ${\mathcal {S}}(Y,\sqcup )$
is also uniquely downward
${\mathcal {S}}(Y,\sqcup )$
is also uniquely downward
![]() $(\sqcup ,h)$
-complemented since it coincides with
$(\sqcup ,h)$
-complemented since it coincides with
![]() ${\mathcal {S}}(X,\sqcup )_{\leq y}$
for
${\mathcal {S}}(X,\sqcup )_{\leq y}$
for
![]() $y = [(Y,i)]$
. From this, it is also not hard to see that property (EX) holds for
$y = [(Y,i)]$
. From this, it is also not hard to see that property (EX) holds for
![]() ${\mathcal {S}}(Y,\sqcup )$
. Thus, by Proposition 5.20,
${\mathcal {S}}(Y,\sqcup )$
. Thus, by Proposition 5.20,
![]() ${\mathcal {PD}}(Y,\sqcup )^{*} \simeq {\mathcal D}(Y,\sqcup )^{\circ }$
for any
${\mathcal {PD}}(Y,\sqcup )^{*} \simeq {\mathcal D}(Y,\sqcup )^{\circ }$
for any
![]() $y = [(Y,i)]\in {\mathcal {S}}(X,\sqcup )$
.
$y = [(Y,i)]\in {\mathcal {S}}(X,\sqcup )$
.
Now let
![]() $\sigma = \{y_1,\ldots ,y_r\}\in {\mathcal D}(X,\sqcup )^{\circ }$
, with representatives
$\sigma = \{y_1,\ldots ,y_r\}\in {\mathcal D}(X,\sqcup )^{\circ }$
, with representatives
![]() $y_i = [(Y_i,j_i)]$
. We have
$y_i = [(Y_i,j_i)]$
. We have
 $$ \begin{align*} \tilde{\chi}( ({\mathcal{PD}}(X,\sqcup)^{*})_{<\sigma} ) & = \tilde{\chi}\bigg( \big(\prod_i {\mathcal{PD}}(Y_i,\sqcup) \big) ^{*} \bigg) = \prod_i \tilde{\chi}\big( {\mathcal{PD}}(Y_i,\sqcup)^{*} \big) = \prod_i \tilde{\chi}\big( {\mathcal D}(Y_i,\sqcup)^{\circ} \big), \end{align*} $$
$$ \begin{align*} \tilde{\chi}( ({\mathcal{PD}}(X,\sqcup)^{*})_{<\sigma} ) & = \tilde{\chi}\bigg( \big(\prod_i {\mathcal{PD}}(Y_i,\sqcup) \big) ^{*} \bigg) = \prod_i \tilde{\chi}\big( {\mathcal{PD}}(Y_i,\sqcup)^{*} \big) = \prod_i \tilde{\chi}\big( {\mathcal D}(Y_i,\sqcup)^{\circ} \big), \end{align*} $$
and
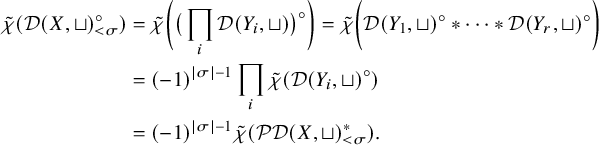 $$ \begin{align*} \tilde{\chi}( {\mathcal D}(X,\sqcup)^{\circ}_{<\sigma} ) & = \tilde{\chi}\bigg( \big(\prod_i {\mathcal D}(Y_i,\sqcup) \big) ^{\circ} \bigg) = \tilde{\chi}\bigg( {\mathcal D}(Y_1,\sqcup)^{\circ} * \cdots * {\mathcal D}(Y_r,\sqcup)^{\circ} \bigg)\\ & = (-1)^{|\sigma|-1} \prod_i \tilde{\chi}( {\mathcal D}(Y_i,\sqcup)^{\circ} ) \\ & = (-1)^{|\sigma|-1} \tilde{\chi}( {\mathcal{PD}}(X,\sqcup)^{*}_{<\sigma} ). \end{align*} $$
$$ \begin{align*} \tilde{\chi}( {\mathcal D}(X,\sqcup)^{\circ}_{<\sigma} ) & = \tilde{\chi}\bigg( \big(\prod_i {\mathcal D}(Y_i,\sqcup) \big) ^{\circ} \bigg) = \tilde{\chi}\bigg( {\mathcal D}(Y_1,\sqcup)^{\circ} * \cdots * {\mathcal D}(Y_r,\sqcup)^{\circ} \bigg)\\ & = (-1)^{|\sigma|-1} \prod_i \tilde{\chi}( {\mathcal D}(Y_i,\sqcup)^{\circ} ) \\ & = (-1)^{|\sigma|-1} \tilde{\chi}( {\mathcal{PD}}(X,\sqcup)^{*}_{<\sigma} ). \end{align*} $$
By item 2 of Theorem 5.9 and the above equalities, we get
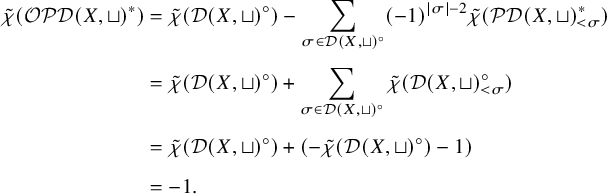 $$ \begin{align*} \tilde{\chi}(\mathcal{O}{\mathcal{PD}}(X,\sqcup)^{*}) & = \tilde{\chi}({\mathcal D}(X,\sqcup)^{\circ}) - \sum_{\sigma\in {\mathcal D}(X,\sqcup)^{\circ}} (-1)^{|\sigma|-2} \tilde{\chi}( {\mathcal{PD}}(X,\sqcup)^{*}_{<\sigma} )\\[4pt] & = \tilde{\chi}({\mathcal D}(X,\sqcup)^{\circ}) + \sum_{\sigma\in {\mathcal D}(X,\sqcup)^{\circ}} \tilde{\chi}( {\mathcal D}(X,\sqcup)^{\circ}_{<\sigma} )\\[4pt] & = \tilde{\chi}({\mathcal D}(X,\sqcup)^{\circ}) + (-\tilde{\chi}({\mathcal D}(X,\sqcup)^{\circ}) - 1)\\[4pt] & = -1.\\[-38pt] \end{align*} $$
$$ \begin{align*} \tilde{\chi}(\mathcal{O}{\mathcal{PD}}(X,\sqcup)^{*}) & = \tilde{\chi}({\mathcal D}(X,\sqcup)^{\circ}) - \sum_{\sigma\in {\mathcal D}(X,\sqcup)^{\circ}} (-1)^{|\sigma|-2} \tilde{\chi}( {\mathcal{PD}}(X,\sqcup)^{*}_{<\sigma} )\\[4pt] & = \tilde{\chi}({\mathcal D}(X,\sqcup)^{\circ}) + \sum_{\sigma\in {\mathcal D}(X,\sqcup)^{\circ}} \tilde{\chi}( {\mathcal D}(X,\sqcup)^{\circ}_{<\sigma} )\\[4pt] & = \tilde{\chi}({\mathcal D}(X,\sqcup)^{\circ}) + (-\tilde{\chi}({\mathcal D}(X,\sqcup)^{\circ}) - 1)\\[4pt] & = -1.\\[-38pt] \end{align*} $$
The next example shows that
![]() $\mathcal {O}{\mathcal {PD}}(X,\sqcup )^{*}$
has the homotopy type of a sphere of the maximal possible dimension.
$\mathcal {O}{\mathcal {PD}}(X,\sqcup )^{*}$
has the homotopy type of a sphere of the maximal possible dimension.
Example 5.23. Let
![]() $L = {\mathcal {S}}(X,\sqcup )$
be the Boolean lattice on n elements, and hence of height n. Since this is a uniquely downward
$L = {\mathcal {S}}(X,\sqcup )$
be the Boolean lattice on n elements, and hence of height n. Since this is a uniquely downward
![]() $(\sqcup ,h)$
-complemented geometric lattice (see Subsection 6.4), it satisfies hypotheses of Corollary 5.22. Moreover,
$(\sqcup ,h)$
-complemented geometric lattice (see Subsection 6.4), it satisfies hypotheses of Corollary 5.22. Moreover,
![]() ${\mathcal {PD}}(L)$
is the partial partition lattice, and its proper part retracts onto
${\mathcal {PD}}(L)$
is the partial partition lattice, and its proper part retracts onto
![]() ${\mathcal D}(L)^{\circ }$
by Proposition 5.20, which is contractible (recall it has a unique minimal element
${\mathcal D}(L)^{\circ }$
by Proposition 5.20, which is contractible (recall it has a unique minimal element
![]() $\sigma _0$
given by the partition into one-blocks).
$\sigma _0$
given by the partition into one-blocks).
By Theorem 5.9, we see that
Now, by property (LI), for
![]() $\sigma \in {\mathcal D}(K)^{\circ }$
, it is not hard to see that
$\sigma \in {\mathcal D}(K)^{\circ }$
, it is not hard to see that
![]() ${\mathcal {PD}}(L)_{\leq \sigma }$
is the product of the partial partition lattices on the subsets of
${\mathcal {PD}}(L)_{\leq \sigma }$
is the product of the partial partition lattices on the subsets of
![]() $\sigma $
. Hence, after removing the top and minimal element of this product, we see that this is contractible if
$\sigma $
. Hence, after removing the top and minimal element of this product, we see that this is contractible if
![]() $\sigma $
contains a block of size at least two. Hence,
$\sigma $
contains a block of size at least two. Hence,
Now,
![]() $({\mathcal {PD}}(L)^{*})_{<\sigma _0}$
is the poset of proper faces of the simplex of size
$({\mathcal {PD}}(L)^{*})_{<\sigma _0}$
is the poset of proper faces of the simplex of size
![]() $|\sigma _0|$
. Therefore,
$|\sigma _0|$
. Therefore,
![]() $({\mathcal {PD}}(L)^{*})_{<\sigma _0}$
is a sphere of dimension
$({\mathcal {PD}}(L)^{*})_{<\sigma _0}$
is a sphere of dimension
![]() $|\sigma _0|-2=n-2$
. From the join decomposition, we see that
$|\sigma _0|-2=n-2$
. From the join decomposition, we see that
![]() $\mathcal {O}{\mathcal {PD}}(L)^{*}$
has the homotopy type of a sphere of dimension
$\mathcal {O}{\mathcal {PD}}(L)^{*}$
has the homotopy type of a sphere of dimension
![]() $2n-3$
.
$2n-3$
.
For instance, for
![]() $n = 2$
,
$n = 2$
,
![]() $|\mathcal {O}{\mathcal {PD}}(L)^{*}|$
is the triangulation of the
$|\mathcal {O}{\mathcal {PD}}(L)^{*}|$
is the triangulation of the
![]() $1$
-dimensional sphere with exactly four vertices and four edges, as depicted in Figure 9.
$1$
-dimensional sphere with exactly four vertices and four edges, as depicted in Figure 9.
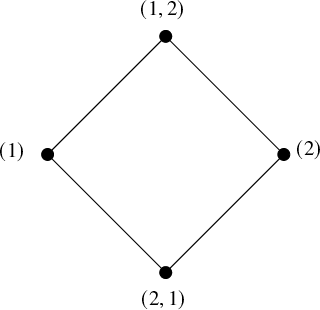
Figure 9 Geometric realization of
![]() $\mathcal {O}{\mathcal {PD}}^{*}$
for the Boolean lattice on
$\mathcal {O}{\mathcal {PD}}^{*}$
for the Boolean lattice on
![]() $\{1,2\}$
.
$\{1,2\}$
.
The following example shows that, in the conditions of Corollary 5.22,
![]() $\mathcal {O}{\mathcal {PD}}(X,\sqcup )^{*}$
might be a wedge of several spheres of different dimensions. See Subsection 6.3 for more details.
$\mathcal {O}{\mathcal {PD}}(X,\sqcup )^{*}$
might be a wedge of several spheres of different dimensions. See Subsection 6.3 for more details.
Example 5.24. Let
![]() $n=2$
and take a field
$n=2$
and take a field
![]() ${\mathbb {K}}$
of characteristic
${\mathbb {K}}$
of characteristic
![]() $\neq 2$
. Consider
$\neq 2$
. Consider
![]() $V= {\mathbb {K}}^2$
with bilinear form given by the identity matrix on the canonical basis. Here, we consider the category of finite-dimensional
$V= {\mathbb {K}}^2$
with bilinear form given by the identity matrix on the canonical basis. Here, we consider the category of finite-dimensional
![]() ${\mathbb {K}}$
-vector spaces with a nondegenerate bilinear form, with monoidal product
${\mathbb {K}}$
-vector spaces with a nondegenerate bilinear form, with monoidal product
![]() $\sqcup $
given by the orthogonal product
$\sqcup $
given by the orthogonal product ![]() . Taking as our object
. Taking as our object
![]() $X=V$
, we see that
$X=V$
, we see that
![]() ${\mathcal {S}}(X,\sqcup )$
is the poset of nondegenerate subspaces of V. Thus,
${\mathcal {S}}(X,\sqcup )$
is the poset of nondegenerate subspaces of V. Thus,
![]() ${\mathcal {S}}(X,\sqcup )$
is uniquely downward
${\mathcal {S}}(X,\sqcup )$
is uniquely downward
![]() $(\sqcup ,h)$
-complemented, where the complement is given by the orthogonal complement. Indeed, it fulfills the hypotheses of Corollary 5.22 except maybe for the finiteness condition in item 1 (which is equivalent to the finiteness of
$(\sqcup ,h)$
-complemented, where the complement is given by the orthogonal complement. Indeed, it fulfills the hypotheses of Corollary 5.22 except maybe for the finiteness condition in item 1 (which is equivalent to the finiteness of
![]() ${\mathbb {K}}$
).
${\mathbb {K}}$
).
Then,
![]() $\mathcal {O}{\mathcal {PD}}(X,\sqcup )^{*}$
is the disjoint union of
$\mathcal {O}{\mathcal {PD}}(X,\sqcup )^{*}$
is the disjoint union of
![]() $1$
-spheres indexed by the full frames of V. That is, the disjoint union of the posets given in Figure 10, one for each set
$1$
-spheres indexed by the full frames of V. That is, the disjoint union of the posets given in Figure 10, one for each set
![]() $\{S,S^\perp \}$
, where S is a nondegenerate
$\{S,S^\perp \}$
, where S is a nondegenerate
![]() $1$
-dimensional subspace of V. In particular, if
$1$
-dimensional subspace of V. In particular, if
![]() ${\mathbb {K}}$
is finite, the reduced Euler characteristic of the space is
${\mathbb {K}}$
is finite, the reduced Euler characteristic of the space is
![]() $-1$
, but spheres of different dimensions arise. If
$-1$
, but spheres of different dimensions arise. If
![]() ${\mathbb {K}}$
is infinite, then an infinite number of
${\mathbb {K}}$
is infinite, then an infinite number of
![]() $1$
-spheres and
$1$
-spheres and
![]() $0$
-spheres appear.
$0$
-spheres appear.
Figure 10 Connected components of the poset
![]() $\mathcal {O}{\mathcal {PD}}^{*}$
of a vector space of dimension two equipped with a nondegenerate bilinear form.
$\mathcal {O}{\mathcal {PD}}^{*}$
of a vector space of dimension two equipped with a nondegenerate bilinear form.
6 Application to classical examples
This section shows how our constructions give rise to well-studied objects. In particular, for each particular case, we will check properties (LI), (EX) and (CM). We will see that usually (LI) and (EX) hold, but (CM) might fail.
6.1 Finitely generated free groups
Let
![]() ${\mathcal C}$
be the category of groups. We take
${\mathcal C}$
be the category of groups. We take
![]() $\sqcup $
to be the coproduct of this category, which is the free product of groups, denoted by
$\sqcup $
to be the coproduct of this category, which is the free product of groups, denoted by
![]() $*$
. Then, for a group X, we have that
$*$
. Then, for a group X, we have that
![]() ${\mathcal {S}}(X)$
is the lattice of subgroups. If X is a free group of finite rank n,
${\mathcal {S}}(X)$
is the lattice of subgroups. If X is a free group of finite rank n,
![]() ${\mathcal {S}}(X,*) = \operatorname {\mathrm {FC}}(X) = \operatorname {\mathrm {FC}}_n$
is the poset of free factors of X. Hatcher and Vogtmann studied this poset in several articles (see, for example, [Reference Hatcher and VogtmannHV98a, Reference Hatcher and VogtmannHV98b, Reference Hatcher and VogtmannHV22]), and they proved it is Cohen-Macaulay of dimension n. Note that this poset is ranked, and the poset-rank of an element is exactly its rank as a free group. Moreover,
${\mathcal {S}}(X,*) = \operatorname {\mathrm {FC}}(X) = \operatorname {\mathrm {FC}}_n$
is the poset of free factors of X. Hatcher and Vogtmann studied this poset in several articles (see, for example, [Reference Hatcher and VogtmannHV98a, Reference Hatcher and VogtmannHV98b, Reference Hatcher and VogtmannHV22]), and they proved it is Cohen-Macaulay of dimension n. Note that this poset is ranked, and the poset-rank of an element is exactly its rank as a free group. Moreover,
![]() $\operatorname {\mathrm {FC}}(X)$
is indeed a lattice by the Kurosh subgroup theorem, and for
$\operatorname {\mathrm {FC}}(X)$
is indeed a lattice by the Kurosh subgroup theorem, and for
![]() $H\in \operatorname {\mathrm {FC}}(X)$
, we have
$H\in \operatorname {\mathrm {FC}}(X)$
, we have
![]() $\operatorname {\mathrm {FC}}(X)_{\leq H} = \operatorname {\mathrm {FC}}(H)$
.
$\operatorname {\mathrm {FC}}(X)_{\leq H} = \operatorname {\mathrm {FC}}(H)$
.
On the other hand, if
![]() $H_1 * H_2 * \cdots * H_r\in \operatorname {\mathrm {FC}}(X)$
, then
$H_1 * H_2 * \cdots * H_r\in \operatorname {\mathrm {FC}}(X)$
, then
![]() $\{H_1,\ldots ,H_r\}$
spans a Boolean lattice such that the map
$\{H_1,\ldots ,H_r\}$
spans a Boolean lattice such that the map
![]() $I\subseteq \{1,\ldots ,r\} \mapsto \langle H_i \mathrel {{\: : \: }} i\in I\rangle \in \operatorname {\mathrm {FC}}(X)$
is a lattice embedding. Therefore,
$I\subseteq \{1,\ldots ,r\} \mapsto \langle H_i \mathrel {{\: : \: }} i\in I\rangle \in \operatorname {\mathrm {FC}}(X)$
is a lattice embedding. Therefore,
![]() ${\mathcal D}(X,*)$
is the poset of decompositions into free factors, and we may just denote it by
${\mathcal D}(X,*)$
is the poset of decompositions into free factors, and we may just denote it by
![]() ${\mathcal D}(X)$
. That is, its elements are sets of nontrivial free factors
${\mathcal D}(X)$
. That is, its elements are sets of nontrivial free factors
![]() $\{H_1,\ldots ,H_r\}$
such that
$\{H_1,\ldots ,H_r\}$
such that
![]() $H_1 * \cdots * H_r = X$
. This coincides with the poset defined by Hatcher and Vogtmann in [Reference Hatcher and VogtmannHV22]. It is proved in [Reference Hatcher and VogtmannHV22] that
$H_1 * \cdots * H_r = X$
. This coincides with the poset defined by Hatcher and Vogtmann in [Reference Hatcher and VogtmannHV22]. It is proved in [Reference Hatcher and VogtmannHV22] that
![]() ${\mathcal D}(X)^{\circ }$
is spherical of dimension
${\mathcal D}(X)^{\circ }$
is spherical of dimension
![]() $n-2$
.
$n-2$
.
The poset
![]() $\operatorname {\mathrm {FC}}(X)$
is (non-uniquely) downward
$\operatorname {\mathrm {FC}}(X)$
is (non-uniquely) downward
![]() $(\sqcup ,h)$
-complemented, and it satisfies property (EX). However, property (CM) fails in this case, as the following example shows.
$(\sqcup ,h)$
-complemented, and it satisfies property (EX). However, property (CM) fails in this case, as the following example shows.
Example 6.1. Let X be the free group of rank
![]() $3$
with basis
$3$
with basis
![]() $\{ a,b,c \}$
. Consider the free decompositions
$\{ a,b,c \}$
. Consider the free decompositions
![]() $X = \left \langle a\right \rangle * \left \langle ca,cb\right \rangle = \left \langle a,b\right \rangle * \left \langle ca\right \rangle $
. Then we have
$X = \left \langle a\right \rangle * \left \langle ca,cb\right \rangle = \left \langle a,b\right \rangle * \left \langle ca\right \rangle $
. Then we have
![]() $\left \langle a\right \rangle \leq \left \langle a,b\right \rangle $
and
$\left \langle a\right \rangle \leq \left \langle a,b\right \rangle $
and
![]() $\left \langle ca,cb\right \rangle \geq \left \langle ca\right \rangle $
. However,
$\left \langle ca,cb\right \rangle \geq \left \langle ca\right \rangle $
. However,
Thus, X fails property (CM).
The same example can be generalized to show that property (CM) fails on any free group of finite rank
![]() $\geq 3$
.
$\geq 3$
.
We naturally have
![]() ${\mathcal {PD}}(X)_{\leq \sigma } = \prod _{H\in \sigma } {\mathcal {PD}}(H)$
for any
${\mathcal {PD}}(X)_{\leq \sigma } = \prod _{H\in \sigma } {\mathcal {PD}}(H)$
for any
![]() $\sigma \in {\mathcal {PD}}(X)$
, so property (LI) also holds. Moreover, upper intervals in
$\sigma \in {\mathcal {PD}}(X)$
, so property (LI) also holds. Moreover, upper intervals in
![]() ${\mathcal D}(X)$
are partition lattices by Lemma 2.5, and lower intervals are products of smaller decomposition posets. Thus, we conclude that
${\mathcal D}(X)$
are partition lattices by Lemma 2.5, and lower intervals are products of smaller decomposition posets. Thus, we conclude that
![]() ${\mathcal D}(X)$
is Cohen-Macaulay.
${\mathcal D}(X)$
is Cohen-Macaulay.
Theorem 6.2 (Hatcher-Vogtmann)
Let X be a free group of finite rank n. Then the posets
![]() $\operatorname {\mathrm {FC}}(X)$
and
$\operatorname {\mathrm {FC}}(X)$
and
![]() ${\mathcal D}(X)$
are Cohen-Macaulay of dimension n and
${\mathcal D}(X)$
are Cohen-Macaulay of dimension n and
![]() $n-1$
, respectively.
$n-1$
, respectively.
By Theorem 5.9, we obtain the following corollary.
Corollary 6.3. Let X be a free group of finite rank n. Then the poset
![]() $\mathcal {O}{\mathcal D}(X)$
is Cohen-Macaulay of dimension
$\mathcal {O}{\mathcal D}(X)$
is Cohen-Macaulay of dimension
![]() $n-1$
.
$n-1$
.
Next, note that every partial frame
![]() $\{H_1,\ldots ,H_r\}$
of X extends to a full frame. Hence,
$\{H_1,\ldots ,H_r\}$
of X extends to a full frame. Hence,
![]() ${\mathcal {PF}}(X,*) = {\mathcal F}(X,*)$
, and the set
${\mathcal {PF}}(X,*) = {\mathcal F}(X,*)$
, and the set
![]() $\mathcal {A}$
of vertices of
$\mathcal {A}$
of vertices of
![]() ${\mathcal F}(X,*)$
is exactly the set of free factors of X of rank
${\mathcal F}(X,*)$
is exactly the set of free factors of X of rank
![]() $1$
. We denote this complex simply by
$1$
. We denote this complex simply by
![]() ${\mathcal F}(X)$
.
${\mathcal F}(X)$
.
For the partial basis complex, we choose the family
![]() $P = (P_H)_{H\in \mathcal {A}}$
, where
$P = (P_H)_{H\in \mathcal {A}}$
, where
![]() $P_H = \{ x\in H \mathrel {{\: : \: }} \left \langle x\right \rangle = H\} \cong \{ \pm 1\}$
. Then
$P_H = \{ x\in H \mathrel {{\: : \: }} \left \langle x\right \rangle = H\} \cong \{ \pm 1\}$
. Then
![]() $\mathcal {B}(X,*)$
is exactly the complex of partial bases of a free group; that is, the maximal simplices are bases of X. This complex is also denoted by
$\mathcal {B}(X,*)$
is exactly the complex of partial bases of a free group; that is, the maximal simplices are bases of X. This complex is also denoted by
![]() $\operatorname {\mathrm {PB}}(X) = \operatorname {\mathrm {PB}}_n$
, and it was shown to be Cohen-Macaulay of dimension
$\operatorname {\mathrm {PB}}(X) = \operatorname {\mathrm {PB}}_n$
, and it was shown to be Cohen-Macaulay of dimension
![]() $n-1$
by Sadofschi Costa [Reference Sadofschi CostaSC]. In particular, by Proposition 5.10, we conclude that
$n-1$
by Sadofschi Costa [Reference Sadofschi CostaSC]. In particular, by Proposition 5.10, we conclude that
![]() ${\mathcal F}(X)$
is Cohen-Macaulay.
${\mathcal F}(X)$
is Cohen-Macaulay.
Theorem 6.4 (Sadofschi Costa)
Let X be a free group of finite rank n. Then the posets
![]() ${\mathcal F}(X)$
and
${\mathcal F}(X)$
and
![]() $\operatorname {\mathrm {PB}}(X)$
are Cohen-Macaulay of dimension
$\operatorname {\mathrm {PB}}(X)$
are Cohen-Macaulay of dimension
![]() $n-1$
.
$n-1$
.
Again, Theorem 5.9 yields the following corollary.
Corollary 6.5. Let X be a free group of finite rank n. Then the posets
![]() $\mathcal {O}{\mathcal F}(X)$
and
$\mathcal {O}{\mathcal F}(X)$
and
![]() $\mathcal {O}\operatorname {\mathrm {PB}}(X)$
are Cohen-Macaulay of dimension
$\mathcal {O}\operatorname {\mathrm {PB}}(X)$
are Cohen-Macaulay of dimension
![]() $n-1$
.
$n-1$
.
However, little is known about the homotopy type of the poset of partial decompositions
![]() ${\mathcal {PD}}(X) := {\mathcal {PD}}(X,*)$
. Thus, we propose the following question.
${\mathcal {PD}}(X) := {\mathcal {PD}}(X,*)$
. Thus, we propose the following question.
Question 6.6. Let X be a free group of rank n. Are the proper parts of
![]() ${\mathcal {PD}}(X)$
and
${\mathcal {PD}}(X)$
and
![]() $\mathcal {O}{\mathcal {PD}}(X)$
spherical (of dimension
$\mathcal {O}{\mathcal {PD}}(X)$
spherical (of dimension
![]() $2n-3$
)? If so, are they Cohen-Macaulay?
$2n-3$
)? If so, are they Cohen-Macaulay?
By Theorem 5.13, Theorem 6.2 and property (LI), we see that
![]() ${\mathcal {PD}}(X)^{*}$
is at least
${\mathcal {PD}}(X)^{*}$
is at least
![]() $(n-3)$
-connected.
$(n-3)$
-connected.
If
![]() $n = 2$
, then
$n = 2$
, then
![]() ${\mathcal {PD}}(X)^{*} = {\mathcal F}(X)$
, which is connected by Theorem 6.4. Thus,
${\mathcal {PD}}(X)^{*} = {\mathcal F}(X)$
, which is connected by Theorem 6.4. Thus,
![]() ${\mathcal {PD}}(X)^{*}$
is connected for all
${\mathcal {PD}}(X)^{*}$
is connected for all
![]() $n\geq 2$
. Moreover,
$n\geq 2$
. Moreover,
![]() ${\mathcal {PD}}(X)^{*}$
is simply connected for
${\mathcal {PD}}(X)^{*}$
is simply connected for
![]() $n\geq 3$
:
$n\geq 3$
:
Proposition 6.7. If
![]() $n\geq 3$
, then
$n\geq 3$
, then
![]() ${\mathcal {PD}}(X)^{*}$
is simply connected.
${\mathcal {PD}}(X)^{*}$
is simply connected.
Proof. We only need to analyze the case
![]() $n = 3$
. By Corollary 5.16, it is enough to show that homotopy classes of the standard apartments generate the fundamental group of
$n = 3$
. By Corollary 5.16, it is enough to show that homotopy classes of the standard apartments generate the fundamental group of
![]() $\operatorname {\mathrm {FC}}(X)^{*}$
. But this follows from Proposition 5.8 of [Reference Sadofschi CostaSC] applied to the empty partial basis there.
$\operatorname {\mathrm {FC}}(X)^{*}$
. But this follows from Proposition 5.8 of [Reference Sadofschi CostaSC] applied to the empty partial basis there.
6.2 Vector spaces
Let
![]() ${\mathcal C}$
be the category of vector spaces over a field
${\mathcal C}$
be the category of vector spaces over a field
![]() ${\mathbb {K}}$
, and let X be a
${\mathbb {K}}$
, and let X be a
![]() ${\mathbb {K}}$
-vector space of finite dimension n. Here, we take
${\mathbb {K}}$
-vector space of finite dimension n. Here, we take
![]() $\sqcup $
to be the coproduct of the category – that is, the direct sum
$\sqcup $
to be the coproduct of the category – that is, the direct sum
![]() $\oplus $
of vector spaces. Then
$\oplus $
of vector spaces. Then
![]() ${\mathcal {S}}(X) = {\mathcal {S}}(X,\oplus )$
is the poset of subspaces of X since every subspace has a direct sum complement. The order complex of
${\mathcal {S}}(X) = {\mathcal {S}}(X,\oplus )$
is the poset of subspaces of X since every subspace has a direct sum complement. The order complex of
![]() ${\mathcal {S}}(X)^{*}$
is the Tits building of
${\mathcal {S}}(X)^{*}$
is the Tits building of
![]() $\operatorname {\mathrm {SL}}(X)$
, which is spherical by the famous Solomon-Tits theorem [Reference Solomon, Brauer and SahSo69]. Intervals in
$\operatorname {\mathrm {SL}}(X)$
, which is spherical by the famous Solomon-Tits theorem [Reference Solomon, Brauer and SahSo69]. Intervals in
![]() ${\mathcal {S}}(X)$
are subspace posets again, so
${\mathcal {S}}(X)$
are subspace posets again, so
![]() ${\mathcal {S}}(X)$
is indeed Cohen-Macaulay of dimension n. This poset is also ranked, and the rank of an element coincides with its dimension as a
${\mathcal {S}}(X)$
is indeed Cohen-Macaulay of dimension n. This poset is also ranked, and the rank of an element coincides with its dimension as a
![]() ${\mathbb {K}}$
-vector space. Note that
${\mathbb {K}}$
-vector space. Note that
![]() $\{V_1,\ldots ,V_r\}\subseteq {\mathcal {S}}(X)$
are subspaces in internal direct sum if and only if
$\{V_1,\ldots ,V_r\}\subseteq {\mathcal {S}}(X)$
are subspaces in internal direct sum if and only if
![]() $\sum _i \dim (V_i) = \dim (V_1+\cdots +V_r)$
. Hence,
$\sum _i \dim (V_i) = \dim (V_1+\cdots +V_r)$
. Hence,
![]() ${\mathcal D}(X,\oplus )$
is the poset of sets of nonzero subspaces which are in internal direct sum and span X. We denote it simply by
${\mathcal D}(X,\oplus )$
is the poset of sets of nonzero subspaces which are in internal direct sum and span X. We denote it simply by
![]() ${\mathcal D}(X)$
. This poset was shown to be shellable for finite fields in [Reference WelkerWel], and in particular Cohen-Macaulay. In the case
${\mathcal D}(X)$
. This poset was shown to be shellable for finite fields in [Reference WelkerWel], and in particular Cohen-Macaulay. In the case
![]() $X = \mathbb {F}_{q}^n$
, the reduced Euler characteristic of
$X = \mathbb {F}_{q}^n$
, the reduced Euler characteristic of
![]() ${\mathcal D}(X)$
is
${\mathcal D}(X)$
is
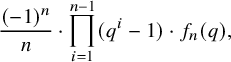 $$ \begin{align} \frac{(-1)^n}{n} \cdot \prod_{i=1}^{n-1} (q^i-1) \cdot f_n(q), \end{align} $$
$$ \begin{align} \frac{(-1)^n}{n} \cdot \prod_{i=1}^{n-1} (q^i-1) \cdot f_n(q), \end{align} $$
where
![]() $f_n(q)$
is a monic polynomial of degree
$f_n(q)$
is a monic polynomial of degree
![]() $\binom {n}{2}$
and positive integer coefficients related to a q-analog of Catalan numbers. The coefficient sequences of these polynomials seem to be always unimodal (see [Reference WelkerWel, pp.241-242]).
$\binom {n}{2}$
and positive integer coefficients related to a q-analog of Catalan numbers. The coefficient sequences of these polynomials seem to be always unimodal (see [Reference WelkerWel, pp.241-242]).
On the other hand, for arbitrary fields, we show later that
![]() ${\mathcal D}(X)^{*}$
is spherical by invoking the results from [Reference CharneyC] on the Charney poset
${\mathcal D}(X)^{*}$
is spherical by invoking the results from [Reference CharneyC] on the Charney poset
![]() $\mathcal {G}(X,\oplus )$
(see Definition 4.14).
$\mathcal {G}(X,\oplus )$
(see Definition 4.14).
Similar to the case of the free factor poset,
![]() ${\mathcal F}(X) := {\mathcal F}(X,\oplus ) = {\mathcal {PF}}(X,\oplus )$
, and we take
${\mathcal F}(X) := {\mathcal F}(X,\oplus ) = {\mathcal {PF}}(X,\oplus )$
, and we take
![]() $\operatorname {\mathrm {PB}}(X) := \mathcal {B}(X,\oplus )$
to be the complex of partial bases of X (i.e., linearly independent sets of vectors). For finite vector spaces X, the complexes
$\operatorname {\mathrm {PB}}(X) := \mathcal {B}(X,\oplus )$
to be the complex of partial bases of X (i.e., linearly independent sets of vectors). For finite vector spaces X, the complexes
![]() ${\mathcal F}(X)$
and
${\mathcal F}(X)$
and
![]() $\operatorname {\mathrm {PB}}(X)$
are matroid complexes, which are shellable and in particular Cohen-Macaulay of dimension
$\operatorname {\mathrm {PB}}(X)$
are matroid complexes, which are shellable and in particular Cohen-Macaulay of dimension
![]() $n-1$
(see [Reference BjörnerBj92] and Proposition 5.10). For infinite fields, this follows from Theorem 2.6 of [Reference van der KallenvdK] since fields satisfy the Bass’ stable range condition
$n-1$
(see [Reference BjörnerBj92] and Proposition 5.10). For infinite fields, this follows from Theorem 2.6 of [Reference van der KallenvdK] since fields satisfy the Bass’ stable range condition
![]() $\mathrm {SR}_2$
. By item (i) of this theorem, we see that
$\mathrm {SR}_2$
. By item (i) of this theorem, we see that
![]() $\mathcal {O} \operatorname {\mathrm {PB}}(X)$
is spherical of dimension
$\mathcal {O} \operatorname {\mathrm {PB}}(X)$
is spherical of dimension
![]() $n-1$
, and by (ii), there also the intervals
$n-1$
, and by (ii), there also the intervals
![]() $\mathcal {O} \operatorname {\mathrm {PB}}(X)_{>z}$
, for
$\mathcal {O} \operatorname {\mathrm {PB}}(X)_{>z}$
, for
![]() $z\in \mathcal {O} \operatorname {\mathrm {PB}}(X)$
, are spherical. This implies that
$z\in \mathcal {O} \operatorname {\mathrm {PB}}(X)$
, are spherical. This implies that
![]() $\mathcal {O} \operatorname {\mathrm {PB}}(X)$
is Cohen-Macaulay of dimension
$\mathcal {O} \operatorname {\mathrm {PB}}(X)$
is Cohen-Macaulay of dimension
![]() $n-1$
. Then by Theorem 5.9,
$n-1$
. Then by Theorem 5.9,
![]() $\operatorname {\mathrm {PB}}(X)$
is Cohen-Macaulay of dimension
$\operatorname {\mathrm {PB}}(X)$
is Cohen-Macaulay of dimension
![]() $n-1$
. By Proposition 5.10,
$n-1$
. By Proposition 5.10,
![]() ${\mathcal F}(X)$
is Cohen-Macaulay of dimension
${\mathcal F}(X)$
is Cohen-Macaulay of dimension
![]() $n-1$
. Again, by Theorem 5.9, we see that
$n-1$
. Again, by Theorem 5.9, we see that
![]() $\mathcal {O} {\mathcal F}(X)$
is Cohen-Macaulay of dimension
$\mathcal {O} {\mathcal F}(X)$
is Cohen-Macaulay of dimension
![]() $n-1$
.
$n-1$
.
Finally,
![]() ${\mathcal {PD}}(X) := {\mathcal {PD}}(X,\oplus )$
is the poset of partial direct sum decompositions of X; that is, its elements are sets of nonzero subspaces of X which are in internal direct sum. An unpublished work by Hanlon, Hersh and Shareshian [Reference Hanlon, Hersh and ShareshianHHS] proves that
${\mathcal {PD}}(X) := {\mathcal {PD}}(X,\oplus )$
is the poset of partial direct sum decompositions of X; that is, its elements are sets of nonzero subspaces of X which are in internal direct sum. An unpublished work by Hanlon, Hersh and Shareshian [Reference Hanlon, Hersh and ShareshianHHS] proves that
![]() ${\mathcal {PD}}(X)^{*}$
is Cohen-Macaulay of dimension
${\mathcal {PD}}(X)^{*}$
is Cohen-Macaulay of dimension
![]() $2n-3$
, and in particular spherical, if
$2n-3$
, and in particular spherical, if
![]() $X = \mathbb {F}_{q}^ n$
. Moreover, they show that the reduced Euler characteristic of this poset is
$X = \mathbb {F}_{q}^ n$
. Moreover, they show that the reduced Euler characteristic of this poset is
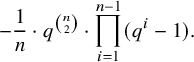 $$ \begin{align} - \frac{1}{n} \cdot q^{ \binom{n}{2} } \cdot \prod_{i=1}^{n-1} (q^i-1). \end{align} $$
$$ \begin{align} - \frac{1}{n} \cdot q^{ \binom{n}{2} } \cdot \prod_{i=1}^{n-1} (q^i-1). \end{align} $$
Note that this formula is closely related to the Euler characteristic of the join of the poset of proper nonzero subspaces and
![]() ${\mathcal D}(X)$
. The former has Euler characteristic
${\mathcal D}(X)$
. The former has Euler characteristic
![]() $(-1)^n q^ {\binom {n}{2}}$
, and the Euler characteristic of the latter is given in (4). The join of two posets has as its Euler characteristic the negative of the product of the two Euler characteristics, so in (5) the polynomial
$(-1)^n q^ {\binom {n}{2}}$
, and the Euler characteristic of the latter is given in (4). The join of two posets has as its Euler characteristic the negative of the product of the two Euler characteristics, so in (5) the polynomial
![]() $f_n(q)$
is missing.
$f_n(q)$
is missing.
For finite-dimensional vector spaces X over arbitrary fields, the poset
![]() ${\mathcal {PD}}(X)$
is homotopy equivalent to
${\mathcal {PD}}(X)$
is homotopy equivalent to
![]() $\operatorname {\mathrm {CB}}(X)$
(see [Reference Brück, Piterman and WelkerBPW]), which was proved to be
$\operatorname {\mathrm {CB}}(X)$
(see [Reference Brück, Piterman and WelkerBPW]), which was proved to be
![]() $(2n-4)$
-connected in [Reference Miller, Patzt and WilsonMPW]. Hence,
$(2n-4)$
-connected in [Reference Miller, Patzt and WilsonMPW]. Hence,
![]() ${\mathcal {PD}}(X)$
is spherical of dimension
${\mathcal {PD}}(X)$
is spherical of dimension
![]() $2n-3$
. By Theorem 6.8 and Theorem 5.9, we can also conclude that
$2n-3$
. By Theorem 6.8 and Theorem 5.9, we can also conclude that
![]() $\mathcal {O}{\mathcal {PD}}(X)^{*}$
is spherical.
$\mathcal {O}{\mathcal {PD}}(X)^{*}$
is spherical.
To conclude Cohen-Macaulayness for
![]() ${\mathcal {PD}}(X)$
, we must show that intervals are spherical. Note that property (LI) holds, so if
${\mathcal {PD}}(X)$
, we must show that intervals are spherical. Note that property (LI) holds, so if
![]() $\sigma \in {\mathcal {PD}}(X)$
, then
$\sigma \in {\mathcal {PD}}(X)$
, then
![]() ${\mathcal {PD}}(X)_{\leq \sigma } \cong \prod _{S\in \sigma } {\mathcal {PD}}(S)$
is spherical by induction. However, upper intervals do not have a clear description, unless we have full decomposition. That is, if
${\mathcal {PD}}(X)_{\leq \sigma } \cong \prod _{S\in \sigma } {\mathcal {PD}}(S)$
is spherical by induction. However, upper intervals do not have a clear description, unless we have full decomposition. That is, if
![]() $\sigma \in {\mathcal D}(X)$
, then
$\sigma \in {\mathcal D}(X)$
, then
![]() ${\mathcal {PD}}(X)_{\geq \sigma } = {\mathcal D}(X)_{\geq \sigma }$
is the partition lattice on
${\mathcal {PD}}(X)_{\geq \sigma } = {\mathcal D}(X)_{\geq \sigma }$
is the partition lattice on
![]() $\sigma $
, whose proper part is spherical.
$\sigma $
, whose proper part is spherical.
Finally, note
![]() ${\mathcal {S}}(X)$
is downward
${\mathcal {S}}(X)$
is downward
![]() $(\sqcup ,h)$
-complemented for
$(\sqcup ,h)$
-complemented for
![]() $\sqcup = \oplus $
, and it satisfies properties (EX) and (CM). Hence, by Proposition 4.15, the Charney complex
$\sqcup = \oplus $
, and it satisfies properties (EX) and (CM). Hence, by Proposition 4.15, the Charney complex
![]() $\Delta \mathcal {G}(X,\oplus )$
is isomorphic to the poset
$\Delta \mathcal {G}(X,\oplus )$
is isomorphic to the poset
![]() $( \mathcal {O} {\mathcal D}(X,\oplus )^{\circ } )^{\mathrm {op}}$
. Since the
$( \mathcal {O} {\mathcal D}(X,\oplus )^{\circ } )^{\mathrm {op}}$
. Since the
![]() $\mathcal {G}(X,\oplus )$
is spherical by [Reference CharneyC], we conclude that
$\mathcal {G}(X,\oplus )$
is spherical by [Reference CharneyC], we conclude that
![]() $\mathcal {O} {\mathcal D}(X)^{\circ }=\mathcal {O} {\mathcal D}(X,\oplus )^{\circ }$
is spherical of dimension
$\mathcal {O} {\mathcal D}(X)^{\circ }=\mathcal {O} {\mathcal D}(X,\oplus )^{\circ }$
is spherical of dimension
![]() $n-2$
. Thus,
$n-2$
. Thus,
![]() ${\mathcal D}(X)^{\circ }$
is spherical of dimension
${\mathcal D}(X)^{\circ }$
is spherical of dimension
![]() $n-2$
by Theorem 5.9.
$n-2$
by Theorem 5.9.
We conclude the following theorem, whose pieces follow from the references and arguments in the preceding paragraphs.
Theorem 6.8. Let X be a vector space of finite dimension n over a field
![]() ${\mathbb {K}}$
. Then the posets
${\mathbb {K}}$
. Then the posets
![]() $\operatorname {\mathrm {PB}}(X)$
,
$\operatorname {\mathrm {PB}}(X)$
,
![]() $\mathcal {O}\operatorname {\mathrm {PB}}(X)$
,
$\mathcal {O}\operatorname {\mathrm {PB}}(X)$
,
![]() ${\mathcal F}(X)$
,
${\mathcal F}(X)$
,
![]() $\mathcal {O}{\mathcal F}(X)$
,
$\mathcal {O}{\mathcal F}(X)$
,
![]() ${\mathcal {S}}(X)$
,
${\mathcal {S}}(X)$
,
![]() ${\mathcal D}(X)$
and
${\mathcal D}(X)$
and
![]() $\mathcal {O}{\mathcal D}(X)$
are Cohen-Macaulay.
$\mathcal {O}{\mathcal D}(X)$
are Cohen-Macaulay.
The posets
![]() ${\mathcal {PD}}(X)^{*}$
and
${\mathcal {PD}}(X)^{*}$
and
![]() $\mathcal {O}{\mathcal {PD}}(X)^{*}$
are spherical of dimension
$\mathcal {O}{\mathcal {PD}}(X)^{*}$
are spherical of dimension
![]() $2n-3$
. If
$2n-3$
. If
![]() ${\mathbb {K}}$
is a finite field, then
${\mathbb {K}}$
is a finite field, then
![]() ${\mathcal {PD}}(X)$
and
${\mathcal {PD}}(X)$
and
![]() $\mathcal {O}{\mathcal {PD}}(X)$
are Cohen-Macaulay.
$\mathcal {O}{\mathcal {PD}}(X)$
are Cohen-Macaulay.
As we mentioned above, the upper intervals in the partial decomposition posets are harder to compute. We leave open then the following question.
Question 6.9. Are the posets
![]() ${\mathcal {PD}}(X)$
and
${\mathcal {PD}}(X)$
and
![]() $\mathcal {O}{\mathcal {PD}}(X)$
Cohen-Macaulay, for any finite-dimensional vector space X?
$\mathcal {O}{\mathcal {PD}}(X)$
Cohen-Macaulay, for any finite-dimensional vector space X?
We close this section with a brief discussion on the Euler characteristic of frames, partial decompositions and some of the ordered versions.
For
![]() $X=\mathbb {F}_{q}^n$
, it is easily checked that the Euler characteristic of
$X=\mathbb {F}_{q}^n$
, it is easily checked that the Euler characteristic of
![]() $\mathcal {O}{\mathcal F}(X)$
is a q-analog of the derangement numbers. Figure 11 provides a list for small n, and Figure 12 contains the values for the unordered version. These polynomials do not seem to be well-behaved, and we do not know of any other proposed q-analog of derangement numbers coinciding with them. Similarly, the reduced Euler characteristic of
$\mathcal {O}{\mathcal F}(X)$
is a q-analog of the derangement numbers. Figure 11 provides a list for small n, and Figure 12 contains the values for the unordered version. These polynomials do not seem to be well-behaved, and we do not know of any other proposed q-analog of derangement numbers coinciding with them. Similarly, the reduced Euler characteristic of
![]() $\mathcal {O}{\mathcal D}(X)$
does not suggest any nice pattern.
$\mathcal {O}{\mathcal D}(X)$
does not suggest any nice pattern.
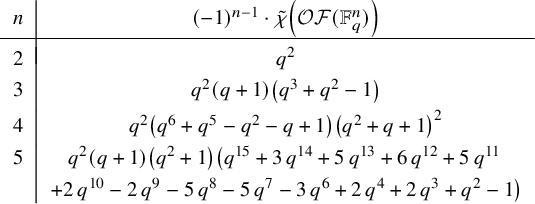
Figure 11 Euler characteristic of
![]() $\mathcal {O}{\mathcal F}(\mathbb {F}_{q}^n)$
.
$\mathcal {O}{\mathcal F}(\mathbb {F}_{q}^n)$
.
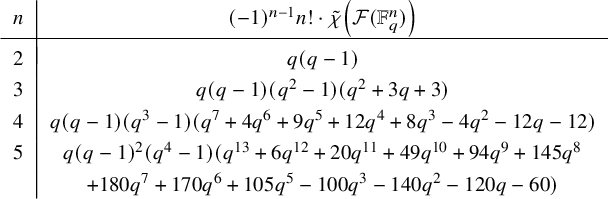
Figure 12 Euler characteristic of
![]() ${\mathcal F}(\mathbb {F}_{q}^n)$
.
${\mathcal F}(\mathbb {F}_{q}^n)$
.
In the following theorem, we compute the reduced Euler characteristic of
![]() $\mathcal {O}{\mathcal {PD}}(X)$
for an n-dimensional vector space X over the finite field
$\mathcal {O}{\mathcal {PD}}(X)$
for an n-dimensional vector space X over the finite field
![]() $\mathbb {F}_{q}$
.
$\mathbb {F}_{q}$
.
Theorem 6.10. For
![]() $n\geq 1$
and q a prime power, if
$n\geq 1$
and q a prime power, if
![]() $X = \mathbb {F}_{q}^n$
, then
$X = \mathbb {F}_{q}^n$
, then
![]() $\tilde {\chi }(\mathcal {O}{\mathcal {PD}}(X)^{*}) = -q^{n(n-1)}$
.
$\tilde {\chi }(\mathcal {O}{\mathcal {PD}}(X)^{*}) = -q^{n(n-1)}$
.
Proof. We argue by induction on n. The cases
![]() $n = 1$
and
$n = 1$
and
![]() $n = 2$
are straightforward to verify. Hence, we assume
$n = 2$
are straightforward to verify. Hence, we assume
![]() $n\geq 3$
. Let
$n\geq 3$
. Let
![]() ${\mathcal U} = \mathcal {O}{\mathcal {PD}}(X)^{*}\setminus \mathcal {O}{\mathcal D}(X)$
. Then, by item 2 of Theorem 5.9, we have
${\mathcal U} = \mathcal {O}{\mathcal {PD}}(X)^{*}\setminus \mathcal {O}{\mathcal D}(X)$
. Then, by item 2 of Theorem 5.9, we have
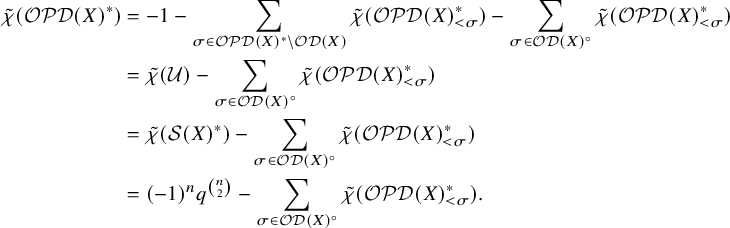 $$ \begin{align*} \tilde{\chi}(\mathcal{O}{\mathcal{PD}}(X)^{*}) & = -1 - \sum_{\sigma\in \mathcal{O}{\mathcal{PD}}(X)^{*}\setminus \mathcal{O}{\mathcal D}(X)} \tilde{\chi}(\mathcal{O}{\mathcal{PD}}(X)^{*}_{<\sigma}) - \sum_{\sigma\in \mathcal{O}{\mathcal D}(X)^{\circ}} \tilde{\chi}(\mathcal{O}{\mathcal{PD}}(X)^{*}_{<\sigma})\\ & = \tilde{\chi}({\mathcal U}) - \sum_{\sigma\in \mathcal{O}{\mathcal D}(X)^{\circ}} \tilde{\chi}(\mathcal{O}{\mathcal{PD}}(X)^{*}_{<\sigma})\\ & = \tilde{\chi}({{\mathcal S}}(X)^{*}) - \sum_{\sigma\in \mathcal{O}{\mathcal D}(X)^{\circ}} \tilde{\chi}(\mathcal{O}{\mathcal{PD}}(X)^{*}_{<\sigma})\\ & = (-1)^nq^{\binom{n}{2}} - \sum_{\sigma\in \mathcal{O}{\mathcal D}(X)^{\circ}} \tilde{\chi}(\mathcal{O}{\mathcal{PD}}(X)^{*}_{<\sigma}). \end{align*} $$
$$ \begin{align*} \tilde{\chi}(\mathcal{O}{\mathcal{PD}}(X)^{*}) & = -1 - \sum_{\sigma\in \mathcal{O}{\mathcal{PD}}(X)^{*}\setminus \mathcal{O}{\mathcal D}(X)} \tilde{\chi}(\mathcal{O}{\mathcal{PD}}(X)^{*}_{<\sigma}) - \sum_{\sigma\in \mathcal{O}{\mathcal D}(X)^{\circ}} \tilde{\chi}(\mathcal{O}{\mathcal{PD}}(X)^{*}_{<\sigma})\\ & = \tilde{\chi}({\mathcal U}) - \sum_{\sigma\in \mathcal{O}{\mathcal D}(X)^{\circ}} \tilde{\chi}(\mathcal{O}{\mathcal{PD}}(X)^{*}_{<\sigma})\\ & = \tilde{\chi}({{\mathcal S}}(X)^{*}) - \sum_{\sigma\in \mathcal{O}{\mathcal D}(X)^{\circ}} \tilde{\chi}(\mathcal{O}{\mathcal{PD}}(X)^{*}_{<\sigma})\\ & = (-1)^nq^{\binom{n}{2}} - \sum_{\sigma\in \mathcal{O}{\mathcal D}(X)^{\circ}} \tilde{\chi}(\mathcal{O}{\mathcal{PD}}(X)^{*}_{<\sigma}). \end{align*} $$
Let
Thus,
![]() $\tilde {\chi }(\mathcal {O}{\mathcal {PD}}(X)^{*}) = -q^{n(n-1)}$
if and only if
$\tilde {\chi }(\mathcal {O}{\mathcal {PD}}(X)^{*}) = -q^{n(n-1)}$
if and only if
We write
![]() $S\in \sigma $
if S lies in the underlying set of
$S\in \sigma $
if S lies in the underlying set of
![]() $\sigma \in \mathcal {O}{\mathcal D}(X)$
. Now we expand
$\sigma \in \mathcal {O}{\mathcal D}(X)$
. Now we expand
![]() $\alpha $
by taking into account the inductive hypothesis:
$\alpha $
by taking into account the inductive hypothesis:
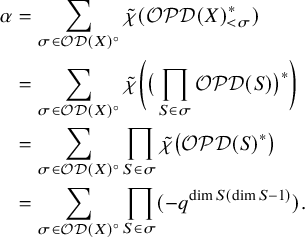 $$ \begin{align*} \alpha & = \sum_{\sigma\in \mathcal{O}{\mathcal D}(X)^{\circ}} \tilde{\chi}(\mathcal{O}{\mathcal{PD}}(X)^{*}_{<\sigma})\\ & = \sum_{\sigma\in \mathcal{O}{\mathcal D}(X)^{\circ}} \tilde{\chi}\bigg( \big( \prod_{S\in \sigma} \mathcal{O}{\mathcal{PD}}(S) \big)^{*} \bigg)\\ & = \sum_{\sigma\in \mathcal{O}{\mathcal D}(X)^{\circ}} \prod_{S\in \sigma}\tilde{\chi}\big( \mathcal{O}{\mathcal{PD}}(S)^{*} \big)\\ & = \sum_{\sigma\in \mathcal{O}{\mathcal D}(X)^{\circ}} \prod_{S\in \sigma}(-q^{\dim S(\dim S -1)}). \end{align*} $$
$$ \begin{align*} \alpha & = \sum_{\sigma\in \mathcal{O}{\mathcal D}(X)^{\circ}} \tilde{\chi}(\mathcal{O}{\mathcal{PD}}(X)^{*}_{<\sigma})\\ & = \sum_{\sigma\in \mathcal{O}{\mathcal D}(X)^{\circ}} \tilde{\chi}\bigg( \big( \prod_{S\in \sigma} \mathcal{O}{\mathcal{PD}}(S) \big)^{*} \bigg)\\ & = \sum_{\sigma\in \mathcal{O}{\mathcal D}(X)^{\circ}} \prod_{S\in \sigma}\tilde{\chi}\big( \mathcal{O}{\mathcal{PD}}(S)^{*} \big)\\ & = \sum_{\sigma\in \mathcal{O}{\mathcal D}(X)^{\circ}} \prod_{S\in \sigma}(-q^{\dim S(\dim S -1)}). \end{align*} $$
Fixing
![]() $2\leq m\leq n$
and positive integers
$2\leq m\leq n$
and positive integers
![]() $k_1,\ldots ,k_m$
such that
$k_1,\ldots ,k_m$
such that
![]() $k_1+\cdots +k_m=n$
, the number of ordered decompositions
$k_1+\cdots +k_m=n$
, the number of ordered decompositions
![]() $\sigma =(S_1,\ldots ,S_m)\in \mathcal {O}{\mathcal D}(X)^{\circ }$
such that
$\sigma =(S_1,\ldots ,S_m)\in \mathcal {O}{\mathcal D}(X)^{\circ }$
such that
![]() $\dim S_i = k_i$
equals
$\dim S_i = k_i$
equals
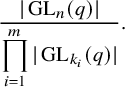 $$\begin{align*}\frac{|\operatorname{\mathrm{GL}}_n(q)|}{\displaystyle{\prod_{i=1}^m |\operatorname{\mathrm{GL}}_{k_i}(q)|}}.\end{align*}$$
$$\begin{align*}\frac{|\operatorname{\mathrm{GL}}_n(q)|}{\displaystyle{\prod_{i=1}^m |\operatorname{\mathrm{GL}}_{k_i}(q)|}}.\end{align*}$$
Denote by
![]() $\mathcal {O}_{n,m}$
the set of sequences
$\mathcal {O}_{n,m}$
the set of sequences
![]() $\mathbf {k} = (k_1,\ldots ,k_m)$
of positive integers with
$\mathbf {k} = (k_1,\ldots ,k_m)$
of positive integers with
 $\displaystyle {\sum _{i=1}^ m} k_i = n$
. Then
$\displaystyle {\sum _{i=1}^ m} k_i = n$
. Then
 $$ \begin{align} \begin{aligned} \alpha - q^{n(n-1)} & = \sum_{m=1}^n \,\sum_{\mathbf{k} \in \mathcal{O}_{n,m}} \frac{|\operatorname{\mathrm{GL}}_n(q)|}{\displaystyle{\prod_{i=1}^ m |\operatorname{\mathrm{GL}}_{k_i}(q)|}} \,\prod_{i=1}^m(-q^{k_i(k_i-1)})\\ & = \sum_{m=1}^n (-1)^m \sum_{\mathbf{k} \in \mathcal{O}_{n,m}} \frac{|\operatorname{\mathrm{GL}}_n(q)|}{\displaystyle{\prod_{i=1}^ m |\operatorname{\mathrm{GL}}_{k_i}(q)|}} \,\,q^{-n + {\sum_{i=1}^ m} k_i^2}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \alpha - q^{n(n-1)} & = \sum_{m=1}^n \,\sum_{\mathbf{k} \in \mathcal{O}_{n,m}} \frac{|\operatorname{\mathrm{GL}}_n(q)|}{\displaystyle{\prod_{i=1}^ m |\operatorname{\mathrm{GL}}_{k_i}(q)|}} \,\prod_{i=1}^m(-q^{k_i(k_i-1)})\\ & = \sum_{m=1}^n (-1)^m \sum_{\mathbf{k} \in \mathcal{O}_{n,m}} \frac{|\operatorname{\mathrm{GL}}_n(q)|}{\displaystyle{\prod_{i=1}^ m |\operatorname{\mathrm{GL}}_{k_i}(q)|}} \,\,q^{-n + {\sum_{i=1}^ m} k_i^2}. \end{aligned} \end{align} $$
On the other hand, the Euler characteristic of the poset of subspaces is given by the following formula:
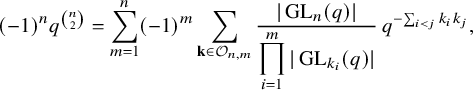 $$ \begin{align} (-1)^n q^{\binom{n}{2}} = \sum_{m=1}^n (-1)^m \sum_{\mathbf{k}\in \mathcal{O}_{n,m}} \frac{|\operatorname{\mathrm{GL}}_n(q)|}{\displaystyle{\prod_{i=1}^ m |\operatorname{\mathrm{GL}}_{k_i}(q)|}} \, q^{ -{\sum_{i<j}k_ik_j}}, \end{align} $$
$$ \begin{align} (-1)^n q^{\binom{n}{2}} = \sum_{m=1}^n (-1)^m \sum_{\mathbf{k}\in \mathcal{O}_{n,m}} \frac{|\operatorname{\mathrm{GL}}_n(q)|}{\displaystyle{\prod_{i=1}^ m |\operatorname{\mathrm{GL}}_{k_i}(q)|}} \, q^{ -{\sum_{i<j}k_ik_j}}, \end{align} $$
which arises by counting flags of subspaces
![]() $0<V_1<\cdots <V_{m-1}<X$
. This is also known as the Solomon identity [Reference SolomonSo66, Corollary 1.1]. Hence, we must show that (6) and (7) coincide.
$0<V_1<\cdots <V_{m-1}<X$
. This is also known as the Solomon identity [Reference SolomonSo66, Corollary 1.1]. Hence, we must show that (6) and (7) coincide.
Note that
 $-n+\displaystyle {\sum _{i=1}^m k_i^2} = n^2-n - 2 \displaystyle {\sum _{1 \leq i<j \leq m}} k_ik_j$
. Thus, in (6), we get
$-n+\displaystyle {\sum _{i=1}^m k_i^2} = n^2-n - 2 \displaystyle {\sum _{1 \leq i<j \leq m}} k_ik_j$
. Thus, in (6), we get
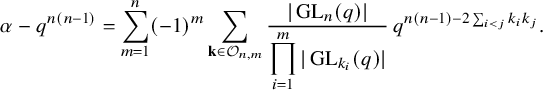 $$ \begin{align} \alpha-q^{n(n-1)} = \sum_{m=1}^n (-1)^m \sum_{\mathbf{k} \in \mathcal{O}_{n,m}} \frac{|\operatorname{\mathrm{GL}}_n(q)|}{\displaystyle{\prod_{i=1}^m |\operatorname{\mathrm{GL}}_{k_i}(q)|}} \,q^{n(n-1) - 2 \sum_{i<j} k_ik_j}. \end{align} $$
$$ \begin{align} \alpha-q^{n(n-1)} = \sum_{m=1}^n (-1)^m \sum_{\mathbf{k} \in \mathcal{O}_{n,m}} \frac{|\operatorname{\mathrm{GL}}_n(q)|}{\displaystyle{\prod_{i=1}^m |\operatorname{\mathrm{GL}}_{k_i}(q)|}} \,q^{n(n-1) - 2 \sum_{i<j} k_ik_j}. \end{align} $$
If we let
![]() $\beta := q^{-n(n-1)}(\alpha -q^{n(n-1)})$
, we must show that
$\beta := q^{-n(n-1)}(\alpha -q^{n(n-1)})$
, we must show that
![]() $\beta = (-1)^n q^{-\binom {n}{2}}$
. This identity now follows by replacing q by
$\beta = (-1)^n q^{-\binom {n}{2}}$
. This identity now follows by replacing q by
![]() $q^{-1}$
in (7) and observing that
$q^{-1}$
in (7) and observing that
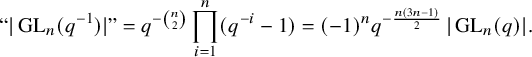 $$\begin{align*}\text{"}|\operatorname{\mathrm{GL}}_n(q^{-1})|\text{"} = q^{-\binom{n}{2}} \prod_{i=1}^n (q^{-i}-1) = (-1)^n q^{-\frac{n(3n-1)}{2}}\, |\operatorname{\mathrm{GL}}_n(q)|.\\[-48pt]\end{align*}$$
$$\begin{align*}\text{"}|\operatorname{\mathrm{GL}}_n(q^{-1})|\text{"} = q^{-\binom{n}{2}} \prod_{i=1}^n (q^{-i}-1) = (-1)^n q^{-\frac{n(3n-1)}{2}}\, |\operatorname{\mathrm{GL}}_n(q)|.\\[-48pt]\end{align*}$$
6.3 Vector spaces with forms
In this section, we consider vector spaces equipped with forms. This case will require some preparation before we can turn our attention to the concrete posets and complexes.
Recall that for a vector space V over a field
![]() ${\mathbb {K}}$
, a form is just a map
${\mathbb {K}}$
, a form is just a map
![]() $\Psi :V\times V\to {\mathbb {K}}$
. In our setting, we require
$\Psi :V\times V\to {\mathbb {K}}$
. In our setting, we require
![]() $\Psi $
to be bi-additive and such that
$\Psi $
to be bi-additive and such that
![]() $\Psi (-,v)$
is
$\Psi (-,v)$
is
![]() ${\mathbb {K}}$
-linear for all
${\mathbb {K}}$
-linear for all
![]() $v\in V$
. We call this property almost
$v\in V$
. We call this property almost
![]() ${\mathbb {K}}$
-bilinear. The form
${\mathbb {K}}$
-bilinear. The form
![]() $\Psi $
is reflexive if for all
$\Psi $
is reflexive if for all
![]() $v,w\in V$
, we have that
$v,w\in V$
, we have that
![]() $\Psi (v,w) = 0$
if and only if
$\Psi (v,w) = 0$
if and only if
![]() $\Psi (w,v) = 0$
. The radical
$\Psi (w,v) = 0$
. The radical
![]() $\operatorname {\mathrm {Rad}}(V) = \{v\in V\mathrel {{\: : \: }} v\perp w $
for all
$\operatorname {\mathrm {Rad}}(V) = \{v\in V\mathrel {{\: : \: }} v\perp w $
for all
![]() $ w\in V\}$
and the orthogonal complement
$ w\in V\}$
and the orthogonal complement
![]() $S^\perp = \big \{\,v\in V\mathrel {{\: : \: }} v\perp w $
for all
$S^\perp = \big \{\,v\in V\mathrel {{\: : \: }} v\perp w $
for all
![]() $ w\in S\,\big \}$
of a subset
$ w\in S\,\big \}$
of a subset
![]() $S\subseteq V$
are subspaces of V by
$S\subseteq V$
are subspaces of V by
![]() ${\mathbb {K}}$
-linearity in the first variable. Here,
${\mathbb {K}}$
-linearity in the first variable. Here,
![]() $v\perp w$
if
$v\perp w$
if
![]() $\Psi (v,w) = 0$
. A subspace
$\Psi (v,w) = 0$
. A subspace
![]() $S\leq V$
is nondegenerate if its radical
$S\leq V$
is nondegenerate if its radical
![]() $\operatorname {\mathrm {Rad}}(S) = S\cap S^\perp $
is zero. In particular, V is nondegenerate if
$\operatorname {\mathrm {Rad}}(S) = S\cap S^\perp $
is zero. In particular, V is nondegenerate if
![]() $\operatorname {\mathrm {Rad}}(V) = 0$
. In this case, we also say
$\operatorname {\mathrm {Rad}}(V) = 0$
. In this case, we also say
![]() $\Psi $
is nondegenerate. If
$\Psi $
is nondegenerate. If
![]() $S\leq V$
, we regard S as a vector space with a form by restricting
$S\leq V$
, we regard S as a vector space with a form by restricting
![]() $\Psi $
to
$\Psi $
to
![]() $S\times S$
. We usually denote this restriction by
$S\times S$
. We usually denote this restriction by
![]() $\Psi _S$
, or simply
$\Psi _S$
, or simply
![]() $\Psi $
when it is clear from the context. Note that if
$\Psi $
when it is clear from the context. Note that if
![]() $\Psi $
is reflexive, then so is
$\Psi $
is reflexive, then so is
![]() $\Psi _S$
for any
$\Psi _S$
for any
![]() $S\leq V$
.
$S\leq V$
.
Consider the category
![]() $\operatorname {\mathrm {IVec}}_{\mathbb {K}}$
whose objects are pairs
$\operatorname {\mathrm {IVec}}_{\mathbb {K}}$
whose objects are pairs
![]() $(V,\Psi _V)$
, where V is a vector space over
$(V,\Psi _V)$
, where V is a vector space over
![]() ${\mathbb {K}}$
and
${\mathbb {K}}$
and
![]() $\Psi _V:V\times V\to {\mathbb {K}}$
is an almost
$\Psi _V:V\times V\to {\mathbb {K}}$
is an almost
![]() ${\mathbb {K}}$
-bilinear form, and maps are isometries. That is, a map
${\mathbb {K}}$
-bilinear form, and maps are isometries. That is, a map
![]() $f:(V,\Psi _V)\to (W,\Psi _W)$
is a linear map
$f:(V,\Psi _V)\to (W,\Psi _W)$
is a linear map
![]() $f:V\to W$
such that
$f:V\to W$
such that
![]() $\Psi _W(f(v),f(w)) = \Psi _V(v,w)$
for all
$\Psi _W(f(v),f(w)) = \Psi _V(v,w)$
for all
![]() $v,w\in V$
. We also consider the full subcategory
$v,w\in V$
. We also consider the full subcategory
![]() $\operatorname {\mathrm {RIVec}}_{\mathbb {K}}$
of reflexive forms.
$\operatorname {\mathrm {RIVec}}_{\mathbb {K}}$
of reflexive forms.
Since we want to work with posets of subobjects, we characterize in the following proposition the monomorphisms of these categories.
Lemma 6.11. In the categories
![]() $\operatorname {\mathrm {IVec}}_{\mathbb {K}}$
and
$\operatorname {\mathrm {IVec}}_{\mathbb {K}}$
and
![]() $\operatorname {\mathrm {RIVec}}_{\mathbb {K}}$
, monomorphisms are exactly the injective isometries (that is, monomorphisms when regarded as linear maps).
$\operatorname {\mathrm {RIVec}}_{\mathbb {K}}$
, monomorphisms are exactly the injective isometries (that is, monomorphisms when regarded as linear maps).
In particular, if
![]() ${\mathcal C} = \operatorname {\mathrm {IVec}}_{{\mathbb {K}}}$
or
${\mathcal C} = \operatorname {\mathrm {IVec}}_{{\mathbb {K}}}$
or
![]() ${\mathcal C} = \operatorname {\mathrm {RIVec}}_{{\mathbb {K}}}$
and
${\mathcal C} = \operatorname {\mathrm {RIVec}}_{{\mathbb {K}}}$
and
![]() $(V,\Psi )\in {\mathcal C}$
, then
$(V,\Psi )\in {\mathcal C}$
, then
![]() ${\mathcal {S}}_{{\mathcal C}}(V,\Psi )$
is the poset of subspaces of V.
${\mathcal {S}}_{{\mathcal C}}(V,\Psi )$
is the poset of subspaces of V.
Proof. The proof is the same for both categories. It is clear that if
![]() $f:(V,\Psi _V)\to (W,\Psi _W)$
is an injective isometry, then f is a monomorphism of the category. Conversely, assume that f is a monomorphism in the category, and suppose that
$f:(V,\Psi _V)\to (W,\Psi _W)$
is an injective isometry, then f is a monomorphism of the category. Conversely, assume that f is a monomorphism in the category, and suppose that
![]() $f(v) = 0$
. We prove that
$f(v) = 0$
. We prove that
![]() $v=0$
. Since f is an isometry,
$v=0$
. Since f is an isometry,
![]() $\Psi _V(\lambda v, \lambda ' v) = 0$
for all
$\Psi _V(\lambda v, \lambda ' v) = 0$
for all
![]() $\lambda ,\lambda '\in {\mathbb {K}}$
. Let
$\lambda ,\lambda '\in {\mathbb {K}}$
. Let
![]() $S = \left \langle v\right \rangle $
with
$S = \left \langle v\right \rangle $
with
![]() $\Psi _S = \Psi _V|_S$
, which is the null form (and in particular, it is reflexive). Consider the maps
$\Psi _S = \Psi _V|_S$
, which is the null form (and in particular, it is reflexive). Consider the maps
![]() $g_1,g_2:S\to V$
given by
$g_1,g_2:S\to V$
given by
![]() $g_1(v) = v$
and
$g_1(v) = v$
and
![]() $g_2(v) = 0$
. Then
$g_2(v) = 0$
. Then
![]() $g_1$
and
$g_1$
and
![]() $g_2$
are isometries and
$g_2$
are isometries and
![]() $fg_1 = 0 = fg_2$
. Thus,
$fg_1 = 0 = fg_2$
. Thus,
![]() $g_1,g_2:(S,\Psi _S)\to (V,\Psi _V)$
are maps in
$g_1,g_2:(S,\Psi _S)\to (V,\Psi _V)$
are maps in
![]() $\operatorname {\mathrm {IVec}}_{\mathbb {K}}$
(and also in
$\operatorname {\mathrm {IVec}}_{\mathbb {K}}$
(and also in
![]() $\operatorname {\mathrm {RIVec}}_{{\mathbb {K}}}$
if
$\operatorname {\mathrm {RIVec}}_{{\mathbb {K}}}$
if
![]() $\Psi _V$
is reflexive). Since
$\Psi _V$
is reflexive). Since
![]() $fg_1=fg_2$
, we conclude that
$fg_1=fg_2$
, we conclude that
![]() $g_1=g_2$
; that is,
$g_1=g_2$
; that is,
![]() $v=0$
.
$v=0$
.
We will also need the following dimension formula for orthogonal complements of subspaces in a vector space with a reflexive almost
![]() ${\mathbb {K}}$
-bilinear form. The proof follows the same ideas as the original proof for
${\mathbb {K}}$
-bilinear form. The proof follows the same ideas as the original proof for
![]() $\sigma $
-sesquilinear forms, and we leave the details to the reader.
$\sigma $
-sesquilinear forms, and we leave the details to the reader.
Proposition 6.12 (Dimension-formula)
Let V be a finite-dimensional vector space and let
![]() $\Psi $
be a reflexive almost
$\Psi $
be a reflexive almost
![]() ${\mathbb {K}}$
-bilinear form on V. Then, for all
${\mathbb {K}}$
-bilinear form on V. Then, for all
![]() $S\leq V$
, we have
$S\leq V$
, we have
In particular,
![]() $(S^\perp )^\perp = S + \operatorname {\mathrm {Rad}}(V)$
and
$(S^\perp )^\perp = S + \operatorname {\mathrm {Rad}}(V)$
and
![]() $\operatorname {\mathrm {Rad}}(S^\perp ) = \operatorname {\mathrm {Rad}}(S) + \operatorname {\mathrm {Rad}}(V)$
.
$\operatorname {\mathrm {Rad}}(S^\perp ) = \operatorname {\mathrm {Rad}}(S) + \operatorname {\mathrm {Rad}}(V)$
.
Having reviewed basic properties of the relevant categories, we now define a suitable monoidal product. For any two objects
![]() $(V,\Psi _V),(W,\Psi _W)$
of
$(V,\Psi _V),(W,\Psi _W)$
of
![]() $\operatorname {\mathrm {IVec}}_{{\mathbb {K}}}$
, there is a natural orthogonal sum
$\operatorname {\mathrm {IVec}}_{{\mathbb {K}}}$
, there is a natural orthogonal sum ![]() where
where
We denote this construction by ![]() . The following lemma is a simple consequence of the definitions.
. The following lemma is a simple consequence of the definitions.
Lemma 6.13. For any two objects
![]() $(V,\Psi _V),(W,\Psi _W)$
of
$(V,\Psi _V),(W,\Psi _W)$
of
![]() $\operatorname {\mathrm {IVec}}_{{\mathbb {K}}}$
,
$\operatorname {\mathrm {IVec}}_{{\mathbb {K}}}$
, ![]() is almost
is almost
![]() ${\mathbb {K}}$
-bilinear. Moreover, if
${\mathbb {K}}$
-bilinear. Moreover, if
![]() $i_V: V\to V\oplus W$
,
$i_V: V\to V\oplus W$
,
![]() $v\mapsto v\oplus 0$
and
$v\mapsto v\oplus 0$
and
![]() $i_W: W\to V\oplus W$
,
$i_W: W\to V\oplus W$
,
![]() $w\mapsto 0\oplus w$
are the canonical embeddings, then
$w\mapsto 0\oplus w$
are the canonical embeddings, then
![]() $i_V, i_W$
are injective isometries and
$i_V, i_W$
are injective isometries and
![]() $V\leq W^\perp $
and
$V\leq W^\perp $
and
![]() $W\leq V^\perp $
in
$W\leq V^\perp $
in ![]() .
.
Note that ![]() might not be reflexive even if
might not be reflexive even if
![]() $\Psi _V$
and
$\Psi _V$
and
![]() $\Psi _W$
are. Nevertheless, this is the case for many important examples such as
$\Psi _W$
are. Nevertheless, this is the case for many important examples such as
![]() $\sigma $
-sesquilinear forms.
$\sigma $
-sesquilinear forms.
Example 6.14. Let
![]() ${\mathbb {K}}$
be a field of characteristic different from
${\mathbb {K}}$
be a field of characteristic different from
![]() $2$
. Let
$2$
. Let
![]() $({\mathbb {K}},\Psi _1)$
be the
$({\mathbb {K}},\Psi _1)$
be the
![]() $1$
-dimensional vector space with
$1$
-dimensional vector space with
![]() $\Psi _1$
the product of
$\Psi _1$
the product of
![]() ${\mathbb {K}}$
, that is,
${\mathbb {K}}$
, that is,
![]() $\Psi _1(x,y) = xy$
. Consider also
$\Psi _1(x,y) = xy$
. Consider also
![]() $({\mathbb {K}}^2,\Psi _2)$
, the symplectic space of dimension
$({\mathbb {K}}^2,\Psi _2)$
, the symplectic space of dimension
![]() $2$
. Here,
$2$
. Here,
![]() $\Psi _2( (x_1,x_2), (y_1,y_2)) = x_1y_2-x_2y_1$
. Then
$\Psi _2( (x_1,x_2), (y_1,y_2)) = x_1y_2-x_2y_1$
. Then ![]() where
where
Therefore, both
![]() $\Psi _1,\Psi _2$
are
$\Psi _1,\Psi _2$
are
![]() ${\mathbb {K}}$
-bilinear and reflexive, and
${\mathbb {K}}$
-bilinear and reflexive, and
![]() $\Psi _3$
is
$\Psi _3$
is
![]() ${\mathbb {K}}$
-bilinear but not reflexive. For instance, take
${\mathbb {K}}$
-bilinear but not reflexive. For instance, take
![]() $x,y\in {\mathbb {K}}^3$
with
$x,y\in {\mathbb {K}}^3$
with
![]() $x_1=y_1=1$
,
$x_1=y_1=1$
,
![]() $x_3=y_2=1$
and
$x_3=y_2=1$
and
![]() $x_2=y_3=0$
. Then
$x_2=y_3=0$
. Then
It is also important to observe that ![]() is not a coproduct in the category
is not a coproduct in the category
![]() $\operatorname {\mathrm {IVec}}_{\mathbb {K}}$
. For example, it fails the universal property for the orthogonal sum of two non-orthogonal lines embedded in the real plane. In fact, the coproduct of ‘most’ pairs of objects of this category does not exist. Nevertheless, it is easily seen that the operation
$\operatorname {\mathrm {IVec}}_{\mathbb {K}}$
. For example, it fails the universal property for the orthogonal sum of two non-orthogonal lines embedded in the real plane. In fact, the coproduct of ‘most’ pairs of objects of this category does not exist. Nevertheless, it is easily seen that the operation ![]() turns
turns
![]() $\operatorname {\mathrm {IVec}}_{\mathbb {K}}$
into an ISM-category. However, by Example 6.14, the product
$\operatorname {\mathrm {IVec}}_{\mathbb {K}}$
into an ISM-category. However, by Example 6.14, the product ![]() does not restrict to a monoidal product in
does not restrict to a monoidal product in
![]() $\operatorname {\mathrm {RIVec}}_{\mathbb {K}}$
.
$\operatorname {\mathrm {RIVec}}_{\mathbb {K}}$
.
The following proposition describes the ![]() -complemented subspaces of V, where
-complemented subspaces of V, where
![]() $(V,\Psi )\in \operatorname {\mathrm {IVec}}_{{\mathbb {K}}}$
. We identify subobjects with subspaces by restricting the form
$(V,\Psi )\in \operatorname {\mathrm {IVec}}_{{\mathbb {K}}}$
. We identify subobjects with subspaces by restricting the form
![]() $\Psi $
.
$\Psi $
.
Proposition 6.15. Let
![]() $(V,\Psi )\in \operatorname {\mathrm {IVec}}_{{\mathbb {K}}}$
and
$(V,\Psi )\in \operatorname {\mathrm {IVec}}_{{\mathbb {K}}}$
and
![]() $S,W\leq V$
such that
$S,W\leq V$
such that
![]() $S\cap W = 0$
. The following are equivalent:
$S\cap W = 0$
. The following are equivalent:
-
(1)
 $S,W\in {\mathcal {S}}(V,\Psi )$
are
$S,W\in {\mathcal {S}}(V,\Psi )$
are  -complements of each other in
-complements of each other in
 ${\mathcal {S}}(S\oplus W,\Psi )$
,
${\mathcal {S}}(S\oplus W,\Psi )$
, -
(2)
 $W\leq S^\perp $
,
$W\leq S^\perp $
,
 $S\leq W^\perp $
.
$S\leq W^\perp $
.
Moreover, if
![]() $\Psi $
is reflexive, then
$\Psi $
is reflexive, then
![]() $S\leq V$
is
$S\leq V$
is ![]() -complemented if and only if
-complemented if and only if
![]() $\operatorname {\mathrm {Rad}}(S)\leq \operatorname {\mathrm {Rad}}(V)$
. In particular, nondegenerate subspaces are
$\operatorname {\mathrm {Rad}}(S)\leq \operatorname {\mathrm {Rad}}(V)$
. In particular, nondegenerate subspaces are ![]() -complemented, and if
-complemented, and if
![]() $\Psi $
is also nondegenerate, then
$\Psi $
is also nondegenerate, then ![]() is the poset of nondegenerate subspaces.
is the poset of nondegenerate subspaces.
Proof. The equivalences in the first part follow easily from the definitions.
Suppose that
![]() $\Psi $
is reflexive and let
$\Psi $
is reflexive and let
![]() $S \leq V$
. First we assume that
$S \leq V$
. First we assume that
![]() $\operatorname {\mathrm {Rad}}(S) \leq \operatorname {\mathrm {Rad}}(V)$
and show that S is
$\operatorname {\mathrm {Rad}}(S) \leq \operatorname {\mathrm {Rad}}(V)$
and show that S is ![]() -complemented. Let
-complemented. Let
![]() $W\leq S$
be a subspace complement for the radical; that is,
$W\leq S$
be a subspace complement for the radical; that is,
![]() $S = \operatorname {\mathrm {Rad}}(S) \oplus W$
. We claim that
$S = \operatorname {\mathrm {Rad}}(S) \oplus W$
. We claim that
![]() $\operatorname {\mathrm {Rad}}(W) = 0$
. By construction, for a given
$\operatorname {\mathrm {Rad}}(W) = 0$
. By construction, for a given
![]() $s\in S$
, there are
$s\in S$
, there are
![]() $r \in \operatorname {\mathrm {Rad}}(S)$
and
$r \in \operatorname {\mathrm {Rad}}(S)$
and
![]() $w \in W$
such that
$w \in W$
such that
![]() $s = r+w$
. Also for any
$s = r+w$
. Also for any
![]() $v \in \operatorname {\mathrm {Rad}}(W)$
, we have
$v \in \operatorname {\mathrm {Rad}}(W)$
, we have
![]() $\Psi (v,w) = 0$
and by reflexivity
$\Psi (v,w) = 0$
and by reflexivity
![]() $\Psi (w,v) = 0$
. It follows that
$\Psi (w,v) = 0$
. It follows that
This shows that
![]() $\operatorname {\mathrm {Rad}}(W)\leq \operatorname {\mathrm {Rad}}(S)\cap W = 0$
, and hence,
$\operatorname {\mathrm {Rad}}(W)\leq \operatorname {\mathrm {Rad}}(S)\cap W = 0$
, and hence,
![]() $W\cap W^\perp = \operatorname {\mathrm {Rad}}(W) = 0$
.
$W\cap W^\perp = \operatorname {\mathrm {Rad}}(W) = 0$
.
Decompose
![]() $W^ \perp = \operatorname {\mathrm {Rad}}(V) \oplus W'$
and
$W^ \perp = \operatorname {\mathrm {Rad}}(V) \oplus W'$
and
![]() $\operatorname {\mathrm {Rad}}(V) = \operatorname {\mathrm {Rad}}(S) \oplus R$
. We claim that
$\operatorname {\mathrm {Rad}}(V) = \operatorname {\mathrm {Rad}}(S) \oplus R$
. We claim that
![]() $V = S\oplus (R\oplus W')$
. By Proposition 6.12,
$V = S\oplus (R\oplus W')$
. By Proposition 6.12,
Since
![]() $W\cap \operatorname {\mathrm {Rad}}(V) \leq \operatorname {\mathrm {Rad}}(W) = 0$
, we see that
$W\cap \operatorname {\mathrm {Rad}}(V) \leq \operatorname {\mathrm {Rad}}(W) = 0$
, we see that
Hence, we obtain
This shows that
![]() $R\oplus W'$
is a complement for S. Finally, note that
$R\oplus W'$
is a complement for S. Finally, note that
![]() $R\oplus W'\perp S$
and
$R\oplus W'\perp S$
and
![]() $(R\oplus W')\cap S = 0$
, and by the first part of the proposition, we conclude that
$(R\oplus W')\cap S = 0$
, and by the first part of the proposition, we conclude that
![]() $R\oplus W'$
is a
$R\oplus W'$
is a ![]() -complement for S.
-complement for S.
Now we show that if S is ![]() -complemented, then
-complemented, then
![]() $\operatorname {\mathrm {Rad}}(S) \leq \operatorname {\mathrm {Rad}}(V)$
. Let W be a
$\operatorname {\mathrm {Rad}}(S) \leq \operatorname {\mathrm {Rad}}(V)$
. Let W be a ![]() -complement of S in
-complement of S in
![]() ${\mathcal {S}}(V,\Psi )$
. By definition, we have
${\mathcal {S}}(V,\Psi )$
. By definition, we have
![]() $S\oplus W = V$
, and the first part of the proposition implies that
$S\oplus W = V$
, and the first part of the proposition implies that
![]() $S\leq W^\perp $
and
$S\leq W^\perp $
and
![]() $W\leq S^\perp $
. Since
$W\leq S^\perp $
. Since
![]() $S\leq \operatorname {\mathrm {Rad}}(S)^\perp $
and
$S\leq \operatorname {\mathrm {Rad}}(S)^\perp $
and
![]() $W\leq \operatorname {\mathrm {Rad}}(S)^\perp $
, we conclude by reflexivity that
$W\leq \operatorname {\mathrm {Rad}}(S)^\perp $
, we conclude by reflexivity that
![]() $V = S\oplus W \leq \operatorname {\mathrm {Rad}}(S)^\perp $
, and hence,
$V = S\oplus W \leq \operatorname {\mathrm {Rad}}(S)^\perp $
, and hence,
![]() $\operatorname {\mathrm {Rad}}(S) \leq \operatorname {\mathrm {Rad}}(V)$
.
$\operatorname {\mathrm {Rad}}(S) \leq \operatorname {\mathrm {Rad}}(V)$
.
Remark 6.16. Note that if
![]() $(V,\Psi )$
is reflexive,
$(V,\Psi )$
is reflexive, ![]() and
and ![]() , then
, then
![]() $\operatorname {\mathrm {Rad}}(T)\leq \operatorname {\mathrm {Rad}}(S)\leq \operatorname {\mathrm {Rad}}(V)$
and so
$\operatorname {\mathrm {Rad}}(T)\leq \operatorname {\mathrm {Rad}}(S)\leq \operatorname {\mathrm {Rad}}(V)$
and so ![]() . This means that
. This means that ![]() .
.
Next, we identify the elements of ![]() under a suitable hypothesis. For that, we call a collection
under a suitable hypothesis. For that, we call a collection
![]() $\sigma = \{V_1,\ldots ,V_r\}$
of subspaces of V an orthogonal decomposition of V if V is the (internal) direct sum of the
$\sigma = \{V_1,\ldots ,V_r\}$
of subspaces of V an orthogonal decomposition of V if V is the (internal) direct sum of the
![]() $V_1,\ldots , V_r$
and
$V_1,\ldots , V_r$
and
![]() $V_i \perp V_j$
for all
$V_i \perp V_j$
for all
![]() $i\neq j$
. Any subset of an orthogonal decomposition is called a partial orthogonal decomposition. In
$i\neq j$
. Any subset of an orthogonal decomposition is called a partial orthogonal decomposition. In
![]() ${\mathcal D}(V,\Psi )$
, we collect all orthogonal decompositions of V and in
${\mathcal D}(V,\Psi )$
, we collect all orthogonal decompositions of V and in
![]() ${\mathcal {PD}}(V,\Psi )$
all partial orthogonal decompositions of V. Both posets are ordered by refinement and hence are subposets of
${\mathcal {PD}}(V,\Psi )$
all partial orthogonal decompositions of V. Both posets are ordered by refinement and hence are subposets of
![]() ${\mathcal {PD}}(V)$
and
${\mathcal {PD}}(V)$
and
![]() ${\mathcal D}(V)$
. The following is now an immediate consequence of Proposition 6.15.
${\mathcal D}(V)$
. The following is now an immediate consequence of Proposition 6.15.
Corollary 6.17. Let
![]() $(V,\Psi ) \in \operatorname {\mathrm {IVec}}_{\mathbb {K}}$
with V finite-dimensional and
$(V,\Psi ) \in \operatorname {\mathrm {IVec}}_{\mathbb {K}}$
with V finite-dimensional and
![]() $\Psi $
reflexive and nondegenerate. Then we have the following:
$\Psi $
reflexive and nondegenerate. Then we have the following:
-
(1) The poset
 satisfies properties (EX) and (CM), and it is uniquely downward
satisfies properties (EX) and (CM), and it is uniquely downward
 $(\sqcup ,h)$
-complemented for
$(\sqcup ,h)$
-complemented for  .
. -
(2)
 and
and  .
. -
(3) Property (LI) holds; that is,
 .
. -
(4) For
 , we have
, we have  .
.
Using Proposition 6.15 and Proposition 5.20, as well as by Lemma 4.12, Lemma 5.17 and Lemma 5.18, we conclude the following:
Corollary 6.18. Let
![]() $(V,\Psi ) \in \operatorname {\mathrm {IVec}}_{\mathbb {K}}$
with V finite-dimensional and
$(V,\Psi ) \in \operatorname {\mathrm {IVec}}_{\mathbb {K}}$
with V finite-dimensional and
![]() $\Psi $
reflexive and nondegenerate. Then we have
$\Psi $
reflexive and nondegenerate. Then we have
-
(1)
 ${\mathcal {PD}}(V,\Psi )^{*} \simeq {\mathcal D}(V,\Psi )^{\circ }$
.
${\mathcal {PD}}(V,\Psi )^{*} \simeq {\mathcal D}(V,\Psi )^{\circ }$
. -
(2)
 .
. -
(3)
 $\tilde {\chi }( \mathcal {O}{\mathcal {PD}}(V,\Psi )^{*} ) = -1$
.
$\tilde {\chi }( \mathcal {O}{\mathcal {PD}}(V,\Psi )^{*} ) = -1$
.
Proof. Item 1 follows by Proposition 5.20, item 2 by Lemma 4.12, Lemma 5.17 and Lemma 5.18, and item 3 by Corollary 5.22. In all cases, we invoke the properties described in Corollary 6.17.
Remark 6.19. By Corollary 6.18, the posets
![]() $\mathcal {O}{\mathcal {PD}}(V,\Psi )^{*}$
and
$\mathcal {O}{\mathcal {PD}}(V,\Psi )^{*}$
and
![]() ${\mathcal {PD}}(V,\Psi )^{*}$
cannot be spherical since the latter is homotopy equivalent to
${\mathcal {PD}}(V,\Psi )^{*}$
cannot be spherical since the latter is homotopy equivalent to
![]() ${\mathcal D}(V,\Psi )^{\circ }$
which has dimension
${\mathcal D}(V,\Psi )^{\circ }$
which has dimension
![]() $n-2$
and is not contractible in general, and
$n-2$
and is not contractible in general, and
![]() $\mathcal {O}{\mathcal {PD}}(V,\Psi )^{*}$
is a wedge of
$\mathcal {O}{\mathcal {PD}}(V,\Psi )^{*}$
is a wedge of
![]() ${\mathcal {PD}}(V,\Psi )^{*}$
and suspension of intervals. In particular,
${\mathcal {PD}}(V,\Psi )^{*}$
and suspension of intervals. In particular,
![]() $\mathcal {O}{\mathcal {PD}}(V,\Psi )$
and
$\mathcal {O}{\mathcal {PD}}(V,\Psi )$
and
![]() ${\mathcal {PD}}(V,\Psi )$
are not Cohen-Macaulay.
${\mathcal {PD}}(V,\Psi )$
are not Cohen-Macaulay.
For general
![]() $\Psi $
, we do not know of results about the homotopy type or Cohen-Macaulayness of the posets discussed in this paper. In the following theorem, we collect a few known results for
$\Psi $
, we do not know of results about the homotopy type or Cohen-Macaulayness of the posets discussed in this paper. In the following theorem, we collect a few known results for
![]() $\sigma $
-Hermitian and symplectic forms. Recall that for a field involution
$\sigma $
-Hermitian and symplectic forms. Recall that for a field involution
![]() $\sigma $
of
$\sigma $
of
![]() ${\mathbb {K}}$
and
${\mathbb {K}}$
and
![]() $\epsilon \in \{1,-1\}$
, an almost
$\epsilon \in \{1,-1\}$
, an almost
![]() ${\mathbb {K}}$
-bilinear form
${\mathbb {K}}$
-bilinear form
![]() $\Psi $
is
$\Psi $
is
![]() $(\sigma ,\epsilon )$
-Hermitian if
$(\sigma ,\epsilon )$
-Hermitian if
![]() $\Psi (v,w) = \epsilon \sigma ( \,\Psi (w,v)\,)$
. Note that
$\Psi (v,w) = \epsilon \sigma ( \,\Psi (w,v)\,)$
. Note that
![]() $(\sigma ,\epsilon )$
-Hermitian forms are always reflexive. If
$(\sigma ,\epsilon )$
-Hermitian forms are always reflexive. If
![]() $\epsilon = 1$
, we just say that
$\epsilon = 1$
, we just say that
![]() $\Psi $
is
$\Psi $
is
![]() $\sigma $
-Hermitian. When
$\sigma $
-Hermitian. When
![]() $\epsilon = 1$
and
$\epsilon = 1$
and
![]() $\sigma $
has order
$\sigma $
has order
![]() $2$
, we get a Hermitian form, and if in addition
$2$
, we get a Hermitian form, and if in addition
![]() $\Psi $
is nondegenerate, we say that
$\Psi $
is nondegenerate, we say that
![]() $\Psi $
is a unitary form and V a unitary space. If
$\Psi $
is a unitary form and V a unitary space. If
![]() $\epsilon =-1$
,
$\epsilon =-1$
,
![]() $\sigma $
is the identity and
$\sigma $
is the identity and
![]() $\Psi (v,v) = 0$
for all
$\Psi (v,v) = 0$
for all
![]() $v\in V$
, we get a symplectic form. For
$v\in V$
, we get a symplectic form. For
![]() $\epsilon = 1$
and
$\epsilon = 1$
and
![]() $\sigma $
the identity map, we get an orthogonal form.
$\sigma $
the identity map, we get an orthogonal form.
Theorem 6.20.
-
(1) Let
 ${\mathbb {K}}$
be a field and
${\mathbb {K}}$
be a field and
 $\sigma $
an automorphism of
$\sigma $
an automorphism of
 ${\mathbb {K}}$
of order one or two. If
${\mathbb {K}}$
of order one or two. If
 $\sigma $
is the identity, then we assume that
$\sigma $
is the identity, then we assume that
 ${\mathbb {K}}$
has odd characteristic. Let V be an
${\mathbb {K}}$
has odd characteristic. Let V be an
 $(n+1)$
-dimensional
$(n+1)$
-dimensional
 ${\mathbb {K}}$
-vector space and
${\mathbb {K}}$
-vector space and
 $\Psi $
a nondegenerate
$\Psi $
a nondegenerate
 $\sigma $
-Hermitian form. If
$\sigma $
-Hermitian form. If
 ${\mathbb {K}}$
is a finite field
${\mathbb {K}}$
is a finite field
 $\mathbb {F}_{q}$
, then assume
$\mathbb {F}_{q}$
, then assume
 $2^{n}<q$
in the case
$2^{n}<q$
in the case
 $\sigma $
is the identity and
$\sigma $
is the identity and
 $2^{n-1}\,(\sqrt {q}+1)<q$
in case
$2^{n-1}\,(\sqrt {q}+1)<q$
in case
 $\sigma $
has order
$\sigma $
has order
 $2$
. Then the following posets are Cohen-Macaulay:
$2$
. Then the following posets are Cohen-Macaulay:-
(b)
 $\mathcal {O}{\mathcal D}(V,\Psi )$
.
$\mathcal {O}{\mathcal D}(V,\Psi )$
. -
(c)
 ${\mathcal D}(V,\Psi )$
.
${\mathcal D}(V,\Psi )$
.
-
(2) Let
 ${\mathbb {K}}$
be a finite field of size
${\mathbb {K}}$
be a finite field of size
 $>2$
and V a
$>2$
and V a
 ${\mathbb {K}}$
-vector space of dimension
${\mathbb {K}}$
-vector space of dimension
 $2n$
equipped with a nondegenerate symplectic form
$2n$
equipped with a nondegenerate symplectic form
 $\Psi $
. Then the following posets are Cohen-Macaulay:
$\Psi $
. Then the following posets are Cohen-Macaulay:-
(a) [Reference DasD]
 .
. -
(b)
 $\mathcal {O}{\mathcal D}(V,\Psi )$
.
$\mathcal {O}{\mathcal D}(V,\Psi )$
. -
(c)
 ${\mathcal D}(V,\Psi )$
.
${\mathcal D}(V,\Psi )$
.
-
In both cases,
![]() $\mathcal {O}{\mathcal {PD}}(V,\Psi )^{*}$
is homotopy equivalent to a wedge of spheres.
$\mathcal {O}{\mathcal {PD}}(V,\Psi )^{*}$
is homotopy equivalent to a wedge of spheres.
Proof. The conclusions on ![]() are the main results of [Reference Devillers, Gramlich and MühlherrDGM] and [Reference DasD]. By item 2 of Corollary 6.18 and Lemma 4.10, we have that (a) implies (b) both in items 1 and 2. By induction on the dimensions of V, Theorem 5.9 implies that
are the main results of [Reference Devillers, Gramlich and MühlherrDGM] and [Reference DasD]. By item 2 of Corollary 6.18 and Lemma 4.10, we have that (a) implies (b) both in items 1 and 2. By induction on the dimensions of V, Theorem 5.9 implies that
![]() ${\mathcal D}(V,\Psi )^{\circ }$
is spherical. By Corollary 6.17 and Lemma 2.5, all proper intervals are spherical. Thus
${\mathcal D}(V,\Psi )^{\circ }$
is spherical. By Corollary 6.17 and Lemma 2.5, all proper intervals are spherical. Thus
![]() ${\mathcal D}(V,\Psi )$
is Cohen-Macaulay in both cases. Again, Theorem 5.9 shows that
${\mathcal D}(V,\Psi )$
is Cohen-Macaulay in both cases. Again, Theorem 5.9 shows that
![]() $\mathcal {O}{\mathcal {PD}}(V,\Psi )^{*}$
is homotopy equivalent to a wedge of spheres.
$\mathcal {O}{\mathcal {PD}}(V,\Psi )^{*}$
is homotopy equivalent to a wedge of spheres.
The restriction to characteristic
![]() $\neq 2$
in item 1 of Theorem 6.20 is not present in [Reference Devillers, Gramlich and MühlherrDGM, Main Theorem]. Nevertheless, in [Reference Devillers, Gramlich and MühlherrDGM], the Main Theorem is derived from Theorem 4.4 there, which applies to Phan geometries, and it requires the existence of non-isotropic vectors (see [Reference Devillers, Gramlich and MühlherrDGM, Definition 3.2]). The latter is not guaranteed in characteristic
$\neq 2$
in item 1 of Theorem 6.20 is not present in [Reference Devillers, Gramlich and MühlherrDGM, Main Theorem]. Nevertheless, in [Reference Devillers, Gramlich and MühlherrDGM], the Main Theorem is derived from Theorem 4.4 there, which applies to Phan geometries, and it requires the existence of non-isotropic vectors (see [Reference Devillers, Gramlich and MühlherrDGM, Definition 3.2]). The latter is not guaranteed in characteristic
![]() $2$
and for
$2$
and for
![]() $\sigma $
the identity. We consider the validity of item 1 of Theorem 6.20 for characteristic
$\sigma $
the identity. We consider the validity of item 1 of Theorem 6.20 for characteristic
![]() $2$
and
$2$
and
![]() $\sigma $
the identity open. Even if the answer is affirmative, the dimension of the spheres provided in [Reference Devillers, Gramlich and MühlherrDGM, Main Theorem] needs some clarification in that case. Note that if
$\sigma $
the identity open. Even if the answer is affirmative, the dimension of the spheres provided in [Reference Devillers, Gramlich and MühlherrDGM, Main Theorem] needs some clarification in that case. Note that if
![]() ${\mathbb {K}}$
is a field of characteristic
${\mathbb {K}}$
is a field of characteristic
![]() $2$
and
$2$
and
![]() $\sigma $
the identity, then
$\sigma $
the identity, then
![]() $\Psi (v,w) = \sum _{i=1}^n v_iw_{n-i+1}$
gives a nondegenerate
$\Psi (v,w) = \sum _{i=1}^n v_iw_{n-i+1}$
gives a nondegenerate
![]() $\sigma $
-Hermitian form (in the sense of [Reference Devillers, Gramlich and MühlherrDGM]) over a vector space of even dimension n. However,
$\sigma $
-Hermitian form (in the sense of [Reference Devillers, Gramlich and MühlherrDGM]) over a vector space of even dimension n. However,
![]() $(V,\Psi )$
is also a symplectic space, so the dimension of the order complex of
$(V,\Psi )$
is also a symplectic space, so the dimension of the order complex of
![]() ${{\mathcal S}}(V,\Psi )$
is not
${{\mathcal S}}(V,\Psi )$
is not
![]() $n-2$
, but
$n-2$
, but
![]() $\frac {n}{2}-2$
.
$\frac {n}{2}-2$
.
On the other hand, Das [Reference DasD] works with nondegenerate symplectic forms over finite fields of size
![]() $> 2$
, so this is where our restriction on the size of the field comes from. Indeed, we expect these results to be true also for infinite fields. Furthermore, by the proof of item 2 of Theorem 6.20, Cohen-Macaulayness will follow for the decomposition posets once the following conjecture is resolved.
$> 2$
, so this is where our restriction on the size of the field comes from. Indeed, we expect these results to be true also for infinite fields. Furthermore, by the proof of item 2 of Theorem 6.20, Cohen-Macaulayness will follow for the decomposition posets once the following conjecture is resolved.
Conjecture 6.21. Let
![]() ${\mathbb {K}}$
be any field and V a finite-dimensional
${\mathbb {K}}$
be any field and V a finite-dimensional
![]() ${\mathbb {K}}$
-vector space with a nondegenerate symplectic form
${\mathbb {K}}$
-vector space with a nondegenerate symplectic form
![]() $\Psi $
. Then
$\Psi $
. Then ![]() is Cohen-Macaulay.
is Cohen-Macaulay.
We also mention that some vanishing results for the rational homology of the frame complex of unitary and symplectic spaces were obtained in [Reference PitermanP, Reference Piterman and WelkerPW24], by using Garland’s method. Note that, by Corollary 6.17 and Corollary 5.21, ![]() is homotopy equivalent to the poset
is homotopy equivalent to the poset
![]() $\hat {{\mathcal F}}(V,\Psi )$
of nonempty frames of size
$\hat {{\mathcal F}}(V,\Psi )$
of nonempty frames of size
![]() $\neq n-1$
.
$\neq n-1$
.
Theorem 6.22. Let V be a finite-dimensional vector space over
![]() ${\mathbb {K}}$
.
${\mathbb {K}}$
.
-
(1) If
 $(V,\Psi )$
is a unitary space of dimension n and
$(V,\Psi )$
is a unitary space of dimension n and
 ${\mathbb {K}} = \mathbb {F}_{q^2}$
, then the following hold:
${\mathbb {K}} = \mathbb {F}_{q^2}$
, then the following hold:-
(a) If
 $n < q+1$
, then
$n < q+1$
, then
 $\hat {{\mathcal F}}(V,\Psi )$
,
$\hat {{\mathcal F}}(V,\Psi )$
,  and
and
 ${\mathcal D}(V,\Psi )^{\circ }$
are Cohen-Macaulay of dimension
${\mathcal D}(V,\Psi )^{\circ }$
are Cohen-Macaulay of dimension
 $n-2$
over
$n-2$
over
 $\mathbb {Q}$
.
$\mathbb {Q}$
. -
(b) For
 $n \geq 11$
, the posets
$n \geq 11$
, the posets
 $\hat {{\mathcal F}}(V,\Psi )$
,
$\hat {{\mathcal F}}(V,\Psi )$
,
 ${\mathcal {S}}(V,\Psi )^{*}$
and
${\mathcal {S}}(V,\Psi )^{*}$
and
 ${\mathcal D}(V,\Psi )^{\circ }$
are
${\mathcal D}(V,\Psi )^{\circ }$
are
 $([2n/3]-1)$
-connected over
$([2n/3]-1)$
-connected over
 $\mathbb {Q}$
.
$\mathbb {Q}$
. -
(c) If
 $n \geq q(q-1)+1$
, then
$n \geq q(q-1)+1$
, then
 $\hat {{\mathcal F}}(V,\Psi )$
is not Cohen-Macaulay over
$\hat {{\mathcal F}}(V,\Psi )$
is not Cohen-Macaulay over
 $\mathbb {Q}$
.
$\mathbb {Q}$
.
-
-
(2) If
 $(V,\Psi )$
is a nondegenerate symplectic space of dimension
$(V,\Psi )$
is a nondegenerate symplectic space of dimension
 $2n$
and
$2n$
and
 ${\mathbb {K}} = \mathbb {F}_{q}$
, then the following hold:
${\mathbb {K}} = \mathbb {F}_{q}$
, then the following hold:-
(a) If
 $n<q+3$
, then
$n<q+3$
, then
 $\hat {{\mathcal F}}(V,\Psi )$
is Cohen-Macaulay of dimension
$\hat {{\mathcal F}}(V,\Psi )$
is Cohen-Macaulay of dimension
 $n-2$
over
$n-2$
over
 $\mathbb {Q}$
.
$\mathbb {Q}$
. -
(b) If
 $n\geq 7$
, then
$n\geq 7$
, then
 $\hat {{\mathcal F}}(V,\Psi )$
is
$\hat {{\mathcal F}}(V,\Psi )$
is
 $[n/2]$
-connected over
$[n/2]$
-connected over
 $\mathbb {Q}$
.
$\mathbb {Q}$
. -
(c) If
 $n>q^2(q^2+1) + n(n-2)q^{-4}(q^4+q^2+1)^{-1}$
, then
$n>q^2(q^2+1) + n(n-2)q^{-4}(q^4+q^2+1)^{-1}$
, then
 $\hat {{\mathcal F}}(V,\Psi )$
is not Cohen-Macaulay over
$\hat {{\mathcal F}}(V,\Psi )$
is not Cohen-Macaulay over
 $\mathbb {Q}$
.
$\mathbb {Q}$
.
-
The reader can verify that these results on Cohen-Macaulayness over
![]() $\mathbb {Q}$
also hold for the corresponding ordered versions (under the given relations between the dimension and the size of the field).
$\mathbb {Q}$
also hold for the corresponding ordered versions (under the given relations between the dimension and the size of the field).
On the other hand, results by Vogtmann [Reference VogtmannV] show that the complex of orthonormal bases of an orthogonal space (under suitable conditions on the ground field) is at least ‘
![]() $n/3$
’-connected. In fact, Vogtmann’s proof can be extended to our context by using our definition of the partial basis complex. Here, for an atom S of
$n/3$
’-connected. In fact, Vogtmann’s proof can be extended to our context by using our definition of the partial basis complex. Here, for an atom S of
![]() ${\mathcal {S}}(V,\Psi )$
, we take as
${\mathcal {S}}(V,\Psi )$
, we take as
![]() $P_S$
in the definition of
$P_S$
in the definition of ![]() a suitable set of bases of S. For example, if
a suitable set of bases of S. For example, if
![]() $\Psi $
is unitary, then S has dimension
$\Psi $
is unitary, then S has dimension
![]() $1$
, and we can take the set of those vectors
$1$
, and we can take the set of those vectors
![]() $v\in S$
such that
$v\in S$
such that
![]() $\Psi (v,v) = 1$
. Similar considerations can be made for the orthogonal case, but note that there may not exist vectors of norm
$\Psi (v,v) = 1$
. Similar considerations can be made for the orthogonal case, but note that there may not exist vectors of norm
![]() $1$
. In such cases, we can fix a non-square scalar d of the ground field and take those vectors
$1$
. In such cases, we can fix a non-square scalar d of the ground field and take those vectors
![]() $v\in S$
with
$v\in S$
with
![]() $\Psi (v,v) = d$
. In the symplectic case, we can consider for example symplectic bases – that is, pairs
$\Psi (v,v) = d$
. In the symplectic case, we can consider for example symplectic bases – that is, pairs
![]() $(v,w)$
such that
$(v,w)$
such that
![]() $\Psi (v,w) = 1$
.
$\Psi (v,w) = 1$
.
We close this subsection with some comments on the Euler characteristics of the different decomposition posets for unitary and symplectic spaces over finite fields.
If
![]() $\Psi $
is unitary or symplectic, then
$\Psi $
is unitary or symplectic, then
![]() ${\mathcal D}(V,\Psi )$
is an exponential structure in the sense of Stanley [Reference StanleySt78]. Hence, generating function techniques, analogous to those applied in [Reference WelkerWel] which yield (4), can also be used to study the reduced Euler characteristic of
${\mathcal D}(V,\Psi )$
is an exponential structure in the sense of Stanley [Reference StanleySt78]. Hence, generating function techniques, analogous to those applied in [Reference WelkerWel] which yield (4), can also be used to study the reduced Euler characteristic of
![]() ${\mathcal D}(V,\Psi )^{\circ }$
. Therefore, one can derive the following results. For
${\mathcal D}(V,\Psi )^{\circ }$
. Therefore, one can derive the following results. For
![]() ${\mathbb {K}} = {\mathbb {F}}_{q^2}$
and
${\mathbb {K}} = {\mathbb {F}}_{q^2}$
and
![]() $\Psi $
unitary on
$\Psi $
unitary on
![]() $V = {\mathbb {F}}_{q^ 2}^ n$
, the reduced Euler characteristic of
$V = {\mathbb {F}}_{q^ 2}^ n$
, the reduced Euler characteristic of
![]() ${\mathcal D}(V,\Psi )^{\circ }$
is
${\mathcal D}(V,\Psi )^{\circ }$
is
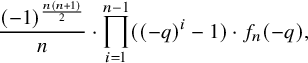 $$ \begin{align} \frac{(-1)^{\frac{n(n+1)}{2}}}{n} \cdot \prod_{i=1}^{n-1} ((-q)^i-1) \cdot f_n(-q), \end{align} $$
$$ \begin{align} \frac{(-1)^{\frac{n(n+1)}{2}}}{n} \cdot \prod_{i=1}^{n-1} ((-q)^i-1) \cdot f_n(-q), \end{align} $$
where
![]() $f_n(q)$
is the same polynomial as in (4). Indeed, (10) is the evaluation of (4) in
$f_n(q)$
is the same polynomial as in (4). Indeed, (10) is the evaluation of (4) in
![]() $-q$
, which makes it another manifestation of Ennola duality.
$-q$
, which makes it another manifestation of Ennola duality.
For
![]() ${\mathbb {K}} = {\mathbb {F}}_{q}$
and
${\mathbb {K}} = {\mathbb {F}}_{q}$
and
![]() $\Psi $
symplectic on
$\Psi $
symplectic on
![]() $V = {\mathbb {F}}_{q}^{2n}$
, the reduced Euler characteristic of
$V = {\mathbb {F}}_{q}^{2n}$
, the reduced Euler characteristic of
![]() ${\mathcal D}(V,\Psi )^{\circ }$
is
${\mathcal D}(V,\Psi )^{\circ }$
is
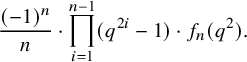 $$ \begin{align} \frac{(-1)^n}{n} \cdot \prod_{i=1}^{n-1} (q^{2i}-1) \cdot f_n(q^2). \end{align} $$
$$ \begin{align} \frac{(-1)^n}{n} \cdot \prod_{i=1}^{n-1} (q^{2i}-1) \cdot f_n(q^2). \end{align} $$
Again,
![]() $f_n(q)$
is the polynomial from (4).
$f_n(q)$
is the polynomial from (4).
We expect similar behavior in case
![]() $\Psi $
is a nondegenerate bilinear form, or even a quadratic form. Since in this case there is no unique form up to isometry,
$\Psi $
is a nondegenerate bilinear form, or even a quadratic form. Since in this case there is no unique form up to isometry,
![]() ${\mathcal D}(V,\Psi )^{\circ }$
does not have to be an exponential structure and the calculations above need to be amended.
${\mathcal D}(V,\Psi )^{\circ }$
does not have to be an exponential structure and the calculations above need to be amended.
Question 6.23. Let V be a finite-dimensional vector space over a finite field and
![]() $\Psi $
a nondegenerate quadratic form on V. What is the reduced Euler characteristic of
$\Psi $
a nondegenerate quadratic form on V. What is the reduced Euler characteristic of
![]() ${\mathcal D}(V,\Psi )^{\circ }$
?
${\mathcal D}(V,\Psi )^{\circ }$
?
6.4 Matroids
Matroids are a natural generalization of vector spaces. Nevertheless, as we will see, due to a lack of a categorical setting suiting our approach, we have to proceed differently.
Recall (see, for example, [Reference BjörnerBj92]), that a matroid is a pair
![]() $(M,I(M))$
, where
$(M,I(M))$
, where
![]() $I(M)$
is a pure finite-dimensional simplicial complex on the set M such that if
$I(M)$
is a pure finite-dimensional simplicial complex on the set M such that if
![]() $\sigma ,\tau \in I(M)$
and
$\sigma ,\tau \in I(M)$
and
![]() $|\tau |<|\sigma |$
, then there exists
$|\tau |<|\sigma |$
, then there exists
![]() $y\in \sigma $
such that
$y\in \sigma $
such that
![]() $\tau \cup \{y\}\in I(M)$
(this is usually referred as the exchange property). The simplices of
$\tau \cup \{y\}\in I(M)$
(this is usually referred as the exchange property). The simplices of
![]() $I(M)$
are called independent sets, and the rank of M is the size dimension of
$I(M)$
are called independent sets, and the rank of M is the size dimension of
![]() $I(M)$
– that is, the size of a maximal independent set. We will later recognize
$I(M)$
– that is, the size of a maximal independent set. We will later recognize
![]() $I(M)$
as the complex of partial bases of the matroid. Note that in our definition of a matroid, we allow infinite sets M. Even though this definition for infinite M may not be a satisfactory concept from the point of view of matroid theory, it still allows the construction of interesting posets, and many of our results hold in this generality.
$I(M)$
as the complex of partial bases of the matroid. Note that in our definition of a matroid, we allow infinite sets M. Even though this definition for infinite M may not be a satisfactory concept from the point of view of matroid theory, it still allows the construction of interesting posets, and many of our results hold in this generality.
A subset
![]() $\sigma \subseteq M$
is called dependent if
$\sigma \subseteq M$
is called dependent if
![]() $\sigma \notin I(M)$
. Two elements
$\sigma \notin I(M)$
. Two elements
![]() $x,y\in M$
are parallel if
$x,y\in M$
are parallel if
![]() $\{x,y\}$
is a dependent set. A loop is an element
$\{x,y\}$
is a dependent set. A loop is an element
![]() $x\in M$
such that
$x\in M$
such that
![]() $\{x\}$
is not an independent set.
$\{x\}$
is not an independent set.
The rank
![]() $\operatorname {\mathrm {rk}}(F)$
of a subset
$\operatorname {\mathrm {rk}}(F)$
of a subset
![]() $F \subseteq M$
is the maximum size of an independent set contained in F. A flat of M is a subset
$F \subseteq M$
is the maximum size of an independent set contained in F. A flat of M is a subset
![]() $F\subseteq M$
such that for all
$F\subseteq M$
such that for all
![]() $x\in M\setminus F$
, we have
$x\in M\setminus F$
, we have
![]() $\operatorname {\mathrm {rk}}(F \cup \{x\})> \operatorname {\mathrm {rk}}(F)$
. In particular, the set of loops, which we denote by
$\operatorname {\mathrm {rk}}(F \cup \{x\})> \operatorname {\mathrm {rk}}(F)$
. In particular, the set of loops, which we denote by
![]() $0$
, is a flat, and also M is a flat. The poset of flats, denoted by
$0$
, is a flat, and also M is a flat. The poset of flats, denoted by
![]() ${{\mathcal L}}(M)$
, is the set of all flats of M ordered by inclusion. This is a geometric and hence graded lattice with minimal element
${{\mathcal L}}(M)$
, is the set of all flats of M ordered by inclusion. This is a geometric and hence graded lattice with minimal element
![]() $0$
, maximal element M and rank function
$0$
, maximal element M and rank function
![]() $\operatorname {\mathrm {rk}}$
. Moreover, for flats F and G, the rank function satisfies
$\operatorname {\mathrm {rk}}$
. Moreover, for flats F and G, the rank function satisfies
This rank inequality is known as the upper semimodular condition (see [Reference StanleySt12]). Note that the rank of M coincides with the value
![]() $\operatorname {\mathrm {rk}}(M)$
of the rank function, which is the height of
$\operatorname {\mathrm {rk}}(M)$
of the rank function, which is the height of
![]() ${{\mathcal L}}(M)$
.
${{\mathcal L}}(M)$
.
We are interested in analyzing the posets and simplicial complexes arising from
![]() ${{\mathcal L}}(M)$
and its decomposition poset
${{\mathcal L}}(M)$
and its decomposition poset
![]() ${\mathcal D}({{\mathcal L}}(M))$
. For the sake of brevity, we will write
${\mathcal D}({{\mathcal L}}(M))$
. For the sake of brevity, we will write
![]() ${\mathcal D}(M)$
for
${\mathcal D}(M)$
for
![]() ${\mathcal D}({{\mathcal L}}(M))$
and
${\mathcal D}({{\mathcal L}}(M))$
and
![]() ${\mathcal {PD}}(M)$
for
${\mathcal {PD}}(M)$
for
![]() ${\mathcal {PD}}({{\mathcal L}}(M))$
. If M is a finite matroid, then
${\mathcal {PD}}({{\mathcal L}}(M))$
. If M is a finite matroid, then
![]() ${{\mathcal L}}(M)$
is well-known to be shellable and hence Cohen-Macaulay (see [Reference BjörnerBj92]). We are not aware of a proof of a similar result in the case M is an infinite matroid of finite rank. The proof for infinite matroids will be provided in an upcoming work [Reference Piterman and WelkerPW25].
${{\mathcal L}}(M)$
is well-known to be shellable and hence Cohen-Macaulay (see [Reference BjörnerBj92]). We are not aware of a proof of a similar result in the case M is an infinite matroid of finite rank. The proof for infinite matroids will be provided in an upcoming work [Reference Piterman and WelkerPW25].
There is some literature on the category of matroids (see, for example, [Reference Heunen and PattaHP]). Unfortunately, these results do not allow us to consider matroids as an ISM-category. Indeed, there is no natural monoidal product of matroids which, when restricted to disjoint flats of a fixed matroid, yields the matroid of the flat which is the join. For example, rank one flats from different projective planes are indistinguishable, but the join of two flats of rank one already distinguishes the planes. Consequently, for matroids, we have to resort to the combinatorial construction of
![]() ${\mathcal D}(M)$
. Nevertheless, since
${\mathcal D}(M)$
. Nevertheless, since
![]() ${{\mathcal L}}(M)$
is a complemented lattice of finite height, by Example 2.19, if we regard
${{\mathcal L}}(M)$
is a complemented lattice of finite height, by Example 2.19, if we regard
![]() ${{\mathcal L}}(M)$
as a poset category with
${{\mathcal L}}(M)$
as a poset category with
![]() $\sqcup = \vee $
, then
$\sqcup = \vee $
, then
![]() ${{\mathcal L}}(M) = {\mathcal {S}}(M,\vee )$
. In particular, we can apply all our results.
${{\mathcal L}}(M) = {\mathcal {S}}(M,\vee )$
. In particular, we can apply all our results.
In [Reference WelkerWel], the lattice
![]() ${\mathcal D}(M)$
and related structures associated to rank selections of
${\mathcal D}(M)$
and related structures associated to rank selections of
![]() ${{\mathcal L}}(M)$
are studied. Recall first that if M is a matroid of rank n with rank function
${{\mathcal L}}(M)$
are studied. Recall first that if M is a matroid of rank n with rank function
![]() $\operatorname {\mathrm {rk}}$
, then a collection of flats
$\operatorname {\mathrm {rk}}$
, then a collection of flats
![]() $F_1,\ldots , F_k$
is a partial direct sum decomposition if and only if the sum of their ranks equals the rank of their join
$F_1,\ldots , F_k$
is a partial direct sum decomposition if and only if the sum of their ranks equals the rank of their join
![]() $F_1\vee \cdots \vee F_j$
. It is not hard to see that partial direct sum decompositions in matroids always extend to direct sum decompositions, and the latter are exactly the decomposition as in Definition 2.1. Thus, the poset of (partial) direct sum decompositions of a matroid, ordered by refinement, is exactly the poset of (partial) decompositions of the lattice of flats. Therefore,
$F_1\vee \cdots \vee F_j$
. It is not hard to see that partial direct sum decompositions in matroids always extend to direct sum decompositions, and the latter are exactly the decomposition as in Definition 2.1. Thus, the poset of (partial) direct sum decompositions of a matroid, ordered by refinement, is exactly the poset of (partial) decompositions of the lattice of flats. Therefore,
![]() ${\mathcal D}(M) = {\mathcal D}(M,\vee )$
and
${\mathcal D}(M) = {\mathcal D}(M,\vee )$
and
![]() ${\mathcal {PD}}(M) = {\mathcal {PD}}(M,\vee )$
. Moreover, if M has rank n, by Proposition 3.3, we see that
${\mathcal {PD}}(M) = {\mathcal {PD}}(M,\vee )$
. Moreover, if M has rank n, by Proposition 3.3, we see that
![]() ${\mathcal D}(M)$
and
${\mathcal D}(M)$
and
![]() ${\mathcal {PD}}(M)$
have height
${\mathcal {PD}}(M)$
have height
![]() $n-1$
and
$n-1$
and
![]() $2n-1$
, respectively. It is shown in [Reference WelkerWel] that, for modularly complemented (finite) matroids,
$2n-1$
, respectively. It is shown in [Reference WelkerWel] that, for modularly complemented (finite) matroids,
![]() ${\mathcal D}(M)$
is shellable and hence homotopically Cohen-Macaulay.
${\mathcal D}(M)$
is shellable and hence homotopically Cohen-Macaulay.
For matroids in which all flats of the same rank define isomorphic matroids,
![]() ${\mathcal D}(M)$
is an exponential structure in the sense of Stanley [Reference StanleySt78]. This occurs, for example, when M is the matroid defined by the projective geometry derived from a finite vector space of dimension n over a field with q elements. Note that M is also modularly complemented, so
${\mathcal D}(M)$
is an exponential structure in the sense of Stanley [Reference StanleySt78]. This occurs, for example, when M is the matroid defined by the projective geometry derived from a finite vector space of dimension n over a field with q elements. Note that M is also modularly complemented, so
![]() ${\mathcal D}(M)$
is shellable. In fact, the Euler characteristic of
${\mathcal D}(M)$
is shellable. In fact, the Euler characteristic of
![]() ${\mathcal D}(M)$
is computed in [Reference WelkerWel] by using the exponential structure machinery from [Reference StanleySt78] (see Eq. (4)). Although this case was already treated from a different perspective in Subsection 6.2, we see that the shellability of
${\mathcal D}(M)$
is computed in [Reference WelkerWel] by using the exponential structure machinery from [Reference StanleySt78] (see Eq. (4)). Although this case was already treated from a different perspective in Subsection 6.2, we see that the shellability of
![]() ${\mathcal D}(M)$
is obtained from purely theoretical matroid properties.
${\mathcal D}(M)$
is obtained from purely theoretical matroid properties.
Another case for which
![]() ${\mathcal D}(M)$
is an exponential structure and M is modularly complemented is when
${\mathcal D}(M)$
is an exponential structure and M is modularly complemented is when
![]() ${{\mathcal L}}(M)$
is the Boolean lattice of subsets of an n-element set. Here,
${{\mathcal L}}(M)$
is the Boolean lattice of subsets of an n-element set. Here,
![]() ${\mathcal D}(M)$
is the partition lattice
${\mathcal D}(M)$
is the partition lattice
![]() $\Pi _n$
, and in particular, it has a unique minimal element. As a consequence of Corollary 5.19, we then get the following well-known fact.
$\Pi _n$
, and in particular, it has a unique minimal element. As a consequence of Corollary 5.19, we then get the following well-known fact.
Corollary 6.24. The proper part of the poset of partial partitions of
![]() $[n]$
is contractible and Cohen-Macaulay.
$[n]$
is contractible and Cohen-Macaulay.
Remark 6.25. As mentioned in Remark 2.3, there is an alternative ordering in
![]() ${\mathcal {PD}}(M)$
, namely, the contention ordering, which makes
${\mathcal {PD}}(M)$
, namely, the contention ordering, which makes
![]() ${\mathcal {PD}}(M)$
a simplicial complex. A recent work [Reference GottsteinG] shows that the simplicial complex of partial partitions of
${\mathcal {PD}}(M)$
a simplicial complex. A recent work [Reference GottsteinG] shows that the simplicial complex of partial partitions of
![]() $[n]$
, denoted by
$[n]$
, denoted by
![]() $D_n$
, is non-pure shellable. Indeed,
$D_n$
, is non-pure shellable. Indeed,
![]() $D_n$
has nonzero homology in different degrees. See Theorem 4.4 of [Reference GottsteinG].
$D_n$
has nonzero homology in different degrees. See Theorem 4.4 of [Reference GottsteinG].
Recall that if there are no parallel elements in the matroid M, then
![]() ${{\mathcal L}}(M)$
is the Boolean lattice on n elements if and only if M is the uniform matroid
${{\mathcal L}}(M)$
is the Boolean lattice on n elements if and only if M is the uniform matroid
![]() $U_{n,n}$
. In general, for
$U_{n,n}$
. In general, for
![]() $1 \leq k \leq n$
, the uniform matroid
$1 \leq k \leq n$
, the uniform matroid
![]() $U_{n,k}$
is the matroid on the set
$U_{n,k}$
is the matroid on the set
![]() $[n]$
whose independent sets are the subsets of size
$[n]$
whose independent sets are the subsets of size
![]() $\leq k$
. Then
$\leq k$
. Then
![]() $U_{n,k}$
has rank k, and
$U_{n,k}$
has rank k, and
![]() ${{\mathcal L}}(U_{n,k})$
is the lattice of all subsets of
${{\mathcal L}}(U_{n,k})$
is the lattice of all subsets of
![]() $[n]$
of size n or
$[n]$
of size n or
![]() $< k$
, from which it follows that
$< k$
, from which it follows that
![]() ${\mathcal D}(U_{n,k})$
is an exponential structure. Assume
${\mathcal D}(U_{n,k})$
is an exponential structure. Assume
![]() $k \leq n-1$
. In general,
$k \leq n-1$
. In general,
![]() ${\mathcal {PD}}(U_{n,k})$
consists of the trivial partition
${\mathcal {PD}}(U_{n,k})$
consists of the trivial partition
![]() $[n]$
and partial partitions of
$[n]$
and partial partitions of
![]() $[n]$
with block sizes
$[n]$
with block sizes
![]() $< k$
and sum of block sizes
$< k$
and sum of block sizes
![]() $\leq k$
. We can map such a partial partition to the partition with only singleton blocks and one singleton block for each element appearing in the partition. This map is a downward closure operator on
$\leq k$
. We can map such a partial partition to the partition with only singleton blocks and one singleton block for each element appearing in the partition. This map is a downward closure operator on
![]() ${\mathcal {PD}}(U_{n,k})^{*}$
whose image is isomorphic to the poset of nonempty subsets of
${\mathcal {PD}}(U_{n,k})^{*}$
whose image is isomorphic to the poset of nonempty subsets of
![]() $[n]$
of size
$[n]$
of size
![]() $\leq k$
. This is exactly the proper part of the lattice of flats of
$\leq k$
. This is exactly the proper part of the lattice of flats of
![]() $U_{n,k+1}$
, which is indeed the
$U_{n,k+1}$
, which is indeed the
![]() $(k-1)$
-skeleton of the n-simplex. Thus,
$(k-1)$
-skeleton of the n-simplex. Thus,
![]() ${\mathcal {PD}}(U_{n,k})^{*}$
has homology concentrated in dimension
${\mathcal {PD}}(U_{n,k})^{*}$
has homology concentrated in dimension
![]() $k-1$
, and its
$k-1$
, and its
![]() $(k-1)$
th homology group is free of rank
$(k-1)$
th homology group is free of rank
![]() $\binom {n-1}{k}$
. This already shows that for
$\binom {n-1}{k}$
. This already shows that for
![]() $2 < k \leq n-1$
the poset
$2 < k \leq n-1$
the poset
![]() ${\mathcal {PD}}(U_{n,k})^{*}$
is not spherical. Similarly, the downward closure operator restricts to
${\mathcal {PD}}(U_{n,k})^{*}$
is not spherical. Similarly, the downward closure operator restricts to
![]() ${\mathcal D}(U_{n,k})^{\circ }$
with image an antichain of
${\mathcal D}(U_{n,k})^{\circ }$
with image an antichain of
![]() $\binom {n}{k}$
elements. This shows that again for
$\binom {n}{k}$
elements. This shows that again for
![]() $2 < k \leq n-1$
, the poset
$2 < k \leq n-1$
, the poset
![]() ${\mathcal D}(U_{n,k})$
is not Cohen-Macaulay and
${\mathcal D}(U_{n,k})$
is not Cohen-Macaulay and
![]() ${\mathcal D}(U_{n,k})^{\circ }$
is not spherical.
${\mathcal D}(U_{n,k})^{\circ }$
is not spherical.
If
![]() ${\mathcal D}(M)$
is not an exponential structure, the computation of the Euler characteristic becomes even more challenging. This is the case for the partition lattice. Since the lattice of partitions
${\mathcal D}(M)$
is not an exponential structure, the computation of the Euler characteristic becomes even more challenging. This is the case for the partition lattice. Since the lattice of partitions
![]() $\Pi _n$
is itself a geometric lattice, there is a matroid M with
$\Pi _n$
is itself a geometric lattice, there is a matroid M with
![]() ${{\mathcal L}}(M) = \Pi _n$
. Note that this matroid has rank
${{\mathcal L}}(M) = \Pi _n$
. Note that this matroid has rank
![]() $n-1$
and the rank of a flat (=partition)
$n-1$
and the rank of a flat (=partition)
![]() $\pi $
is
$\pi $
is
![]() $n - |\pi |$
. A decomposition of this matroid is, therefore, a set
$n - |\pi |$
. A decomposition of this matroid is, therefore, a set
![]() $\{ \pi _1,\ldots ,\pi _k\}$
of partitions
$\{ \pi _1,\ldots ,\pi _k\}$
of partitions
![]() $\pi _j$
such that
$\pi _j$
such that
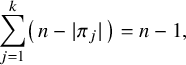 $$ \begin{align*}\displaystyle{\sum_{j=1}^k} \big(\,n - |\pi_j|\,\big) = n-1,\end{align*} $$
$$ \begin{align*}\displaystyle{\sum_{j=1}^k} \big(\,n - |\pi_j|\,\big) = n-1,\end{align*} $$
and
![]() $\pi _1\vee \cdots \vee \pi _k$
is the coarsest partition. Since
$\pi _1\vee \cdots \vee \pi _k$
is the coarsest partition. Since
![]() $\Pi _n$
is modularly complemented, by [Reference WelkerWel], we see that
$\Pi _n$
is modularly complemented, by [Reference WelkerWel], we see that
![]() ${\mathcal D}(\Pi _n)$
is Cohen-Macaulay and hence
${\mathcal D}(\Pi _n)$
is Cohen-Macaulay and hence
![]() ${\mathcal D}(\Pi _n)^{\circ }$
spherical of dimension
${\mathcal D}(\Pi _n)^{\circ }$
spherical of dimension
![]() $n-3$
.
$n-3$
.
In the following result, we relate partial decompositions of
![]() $\Pi _n$
to hyperforests and compute the Euler characteristic of
$\Pi _n$
to hyperforests and compute the Euler characteristic of
![]() ${\mathcal D}(\Pi _n)^{\circ }$
and
${\mathcal D}(\Pi _n)^{\circ }$
and
![]() ${\mathcal {PD}}(\Pi _n)^{*}$
. Denote by
${\mathcal {PD}}(\Pi _n)^{*}$
. Denote by
![]() $\operatorname {\mathrm {HF}}_n$
the poset of hyperforests on an n-element set ordered by refinement (see [Reference BacherBa]), and by
$\operatorname {\mathrm {HF}}_n$
the poset of hyperforests on an n-element set ordered by refinement (see [Reference BacherBa]), and by
![]() $\operatorname {\mathrm {HT}}_n$
the subposet of
$\operatorname {\mathrm {HT}}_n$
the subposet of
![]() $\operatorname {\mathrm {HF}}_n$
consisting of hypertrees (see [Reference McCammond and MeierMcCM]).
$\operatorname {\mathrm {HF}}_n$
consisting of hypertrees (see [Reference McCammond and MeierMcCM]).
Proposition 6.26. Let M be a matroid such that
![]() ${{\mathcal L}}(M) = \Pi _n$
. Then the following holds:
${{\mathcal L}}(M) = \Pi _n$
. Then the following holds:
-
(1)
 ${\mathcal D}(M)^{\circ }$
is homotopy equivalent to the proper part of
${\mathcal D}(M)^{\circ }$
is homotopy equivalent to the proper part of
 $\operatorname {\mathrm {HT}}_n$
. It follows that
$\operatorname {\mathrm {HT}}_n$
. It follows that
 ${\mathcal D}(M)$
is Cohen-Macaulay and its Möbius number is
${\mathcal D}(M)$
is Cohen-Macaulay and its Möbius number is
 ${\mathcal D}(M)^{\circ }$
is
${\mathcal D}(M)^{\circ }$
is
 $(-1)^{n-1} (n-1)^{n-2}$
.
$(-1)^{n-1} (n-1)^{n-2}$
. -
(2)
 ${\mathcal {PD}}(M)^{*}$
is homotopy equivalent to the proper part of
${\mathcal {PD}}(M)^{*}$
is homotopy equivalent to the proper part of
 $\operatorname {\mathrm {HF}}_n$
. In particular, the reduced Euler characteristic of
$\operatorname {\mathrm {HF}}_n$
. In particular, the reduced Euler characteristic of
 ${\mathcal {PD}}^{*}_n$
is
${\mathcal {PD}}^{*}_n$
is
 $-(n-2)!$
.
$-(n-2)!$
.
Proof. We prove first the homotopy equivalence in each case. We show that if a partial decomposition
![]() $\sigma $
contains a partition with at least two blocks of size bigger than one, then
$\sigma $
contains a partition with at least two blocks of size bigger than one, then
![]() ${\mathcal {PD}}(M)^{*}_{< \sigma }$
and
${\mathcal {PD}}(M)^{*}_{< \sigma }$
and
![]() ${\mathcal D}(M)^{\circ }_{< \sigma }$
(if
${\mathcal D}(M)^{\circ }_{< \sigma }$
(if
![]() $\sigma $
is also a full decomposition) are contractible. This will yield a homotopy equivalence between
$\sigma $
is also a full decomposition) are contractible. This will yield a homotopy equivalence between
![]() ${\mathcal D}(M)^{\circ }$
(resp.
${\mathcal D}(M)^{\circ }$
(resp.
![]() ${\mathcal {PD}}(M)^{*}$
) and the subposet
${\mathcal {PD}}(M)^{*}$
) and the subposet
![]() $X_n$
(resp.
$X_n$
(resp.
![]() $Y_n$
) of (resp. partial) direct sum decompositions whose partitions have precisely one block of size bigger than one. But these posets
$Y_n$
) of (resp. partial) direct sum decompositions whose partitions have precisely one block of size bigger than one. But these posets
![]() $X_n$
and
$X_n$
and
![]() $Y_n$
are exactly the proper parts of
$Y_n$
are exactly the proper parts of
![]() $\operatorname {\mathrm {HT}}_n$
and
$\operatorname {\mathrm {HT}}_n$
and
![]() $\operatorname {\mathrm {HF}}_n$
, respectively.
$\operatorname {\mathrm {HF}}_n$
, respectively.
Let
![]() $\pi $
be a partition of
$\pi $
be a partition of
![]() $[n]$
. Consider the following partial decomposition:
$[n]$
. Consider the following partial decomposition:
If
![]() $\pi $
contains just one block of size
$\pi $
contains just one block of size
![]() $\geq 2$
, then
$\geq 2$
, then
![]() $\sigma _\pi = \{\,\pi \,\}$
. It is also not difficult to see that the sum of the ranks of the partitions belonging to
$\sigma _\pi = \{\,\pi \,\}$
. It is also not difficult to see that the sum of the ranks of the partitions belonging to
![]() $\sigma _\pi $
equals the rank of
$\sigma _\pi $
equals the rank of
![]() $\pi $
. Also, we have
$\pi $
. Also, we have
![]() $\pi = \bigvee _{\rho \in \sigma _\pi } \rho $
, since the latter is the smallest partition that contains all the blocks
$\pi = \bigvee _{\rho \in \sigma _\pi } \rho $
, since the latter is the smallest partition that contains all the blocks
![]() $B\in \pi $
of size
$B\in \pi $
of size
![]() $\geq 2$
. Therefore,
$\geq 2$
. Therefore,
![]() $\sigma _\pi $
is a direct sum decomposition of
$\sigma _\pi $
is a direct sum decomposition of
![]() $\pi $
.
$\pi $
.
Now, let
![]() $\tau = \{\pi _1,\ldots ,\pi _r\} \in {\mathcal {PD}}(M)^{*}$
be a partial direct sum decomposition. Define the map
$\tau = \{\pi _1,\ldots ,\pi _r\} \in {\mathcal {PD}}(M)^{*}$
be a partial direct sum decomposition. Define the map
![]() $f(\tau ) = \bigcup _{i=1}^r \sigma _{\pi _i}$
. We claim that
$f(\tau ) = \bigcup _{i=1}^r \sigma _{\pi _i}$
. We claim that
![]() $f(\tau )$
is also a partial direct sum decomposition:
$f(\tau )$
is also a partial direct sum decomposition:
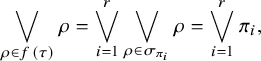 $$\begin{align*}\bigvee_{\rho\in f(\tau)} \rho = \bigvee_{i=1}^r \bigvee_{\rho\in \sigma_{\pi_i}}\rho = \bigvee_{i=1}^r \pi_i,\end{align*}$$
$$\begin{align*}\bigvee_{\rho\in f(\tau)} \rho = \bigvee_{i=1}^r \bigvee_{\rho\in \sigma_{\pi_i}}\rho = \bigvee_{i=1}^r \pi_i,\end{align*}$$
and this implies that the sum of the ranks must be correct:
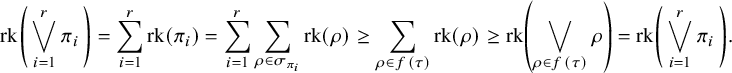 $$\begin{align*}\operatorname{\mathrm{rk}}\left( \,\bigvee_{i=1}^r \pi_i\, \right) = \sum_{i=1}^r \operatorname{\mathrm{rk}}(\pi_i) = \sum_{i=1}^r \sum_{\rho\in \sigma_{\pi_i}} \operatorname{\mathrm{rk}}(\rho) \geq \sum_{\rho\in f(\tau)} \operatorname{\mathrm{rk}}(\rho) \geq \operatorname{\mathrm{rk}}\left(\bigvee_{\rho\in f(\tau)} \rho\right) = \operatorname{\mathrm{rk}}\left(\,\bigvee_{i=1}^r \pi_i\,\right).\end{align*}$$
$$\begin{align*}\operatorname{\mathrm{rk}}\left( \,\bigvee_{i=1}^r \pi_i\, \right) = \sum_{i=1}^r \operatorname{\mathrm{rk}}(\pi_i) = \sum_{i=1}^r \sum_{\rho\in \sigma_{\pi_i}} \operatorname{\mathrm{rk}}(\rho) \geq \sum_{\rho\in f(\tau)} \operatorname{\mathrm{rk}}(\rho) \geq \operatorname{\mathrm{rk}}\left(\bigvee_{\rho\in f(\tau)} \rho\right) = \operatorname{\mathrm{rk}}\left(\,\bigvee_{i=1}^r \pi_i\,\right).\end{align*}$$
Thus,
![]() $f:{\mathcal {PD}}(M)^{*} \to Y_n$
is a well-defined and surjective function that restricts to a surjective map
$f:{\mathcal {PD}}(M)^{*} \to Y_n$
is a well-defined and surjective function that restricts to a surjective map
![]() ${\mathcal D}(M)^{\circ } \to X_n$
. Finally, it is straightforward to verify that if
${\mathcal D}(M)^{\circ } \to X_n$
. Finally, it is straightforward to verify that if
![]() $\rho $
is finer than
$\rho $
is finer than
![]() $\pi $
, then
$\pi $
, then
![]() $\sigma _\rho \leq \sigma _\pi $
, and so f is an order-preserving map. Since we have
$\sigma _\rho \leq \sigma _\pi $
, and so f is an order-preserving map. Since we have
![]() $f(\tau ) \leq \tau $
and f is the identity on
$f(\tau ) \leq \tau $
and f is the identity on
![]() $Y_n$
, we conclude that f is a homotopy equivalence. Moreover, this also shows that the lower intervals
$Y_n$
, we conclude that f is a homotopy equivalence. Moreover, this also shows that the lower intervals
![]() ${{\mathcal {PD}}(M)^{*}}_{< \tau }$
and
${{\mathcal {PD}}(M)^{*}}_{< \tau }$
and
![]() ${{\mathcal D}(M)^{\circ }}_{< \tau }$
(if
${{\mathcal D}(M)^{\circ }}_{< \tau }$
(if
![]() $\tau $
is a decomposition) are contractible for
$\tau $
is a decomposition) are contractible for
![]() $\tau \in {\mathcal {PD}}(M)^{*} \setminus Y_n$
since for
$\tau \in {\mathcal {PD}}(M)^{*} \setminus Y_n$
since for
![]() $\tau ' < \tau $
, we have
$\tau ' < \tau $
, we have
![]() $\tau ' \geq f(\tau ') \leq f(\tau ) < \tau $
.
$\tau ' \geq f(\tau ') \leq f(\tau ) < \tau $
.
We have already seen that
![]() ${\mathcal D}(M)$
is Cohen-Macaulay by [Reference WelkerWel]. The value of the Euler characteristic of
${\mathcal D}(M)$
is Cohen-Macaulay by [Reference WelkerWel]. The value of the Euler characteristic of
![]() ${\mathcal D}(M)^{\circ }$
follows from the homotopy equivalence with the proper part of the hypertree lattice
${\mathcal D}(M)^{\circ }$
follows from the homotopy equivalence with the proper part of the hypertree lattice
![]() $\operatorname {\mathrm {HT}}_n$
and Theorem 1.1 of [Reference McCammond and MeierMcCM]. For hyperforests, this follows from Proposition 19 of [Reference BacherBa].
$\operatorname {\mathrm {HT}}_n$
and Theorem 1.1 of [Reference McCammond and MeierMcCM]. For hyperforests, this follows from Proposition 19 of [Reference BacherBa].
Concerning the ordered versions, we conclude from item 1 in Theorem 5.9 that
![]() $\mathcal {O}{\mathcal D}(M)^{\circ }$
is Cohen-Macaulay of dimension
$\mathcal {O}{\mathcal D}(M)^{\circ }$
is Cohen-Macaulay of dimension
![]() $n-3$
if
$n-3$
if
![]() ${{\mathcal L}}(M) = \Pi _n$
. In [Reference Piterman, Shareshian and WelkerPSW], we show that the Möbius number in this case is
${{\mathcal L}}(M) = \Pi _n$
. In [Reference Piterman, Shareshian and WelkerPSW], we show that the Möbius number in this case is
![]() $(-1)^{n-1} \, (2n-1)^{n-2}$
. In the same work, we also show that the Möbius number of
$(-1)^{n-1} \, (2n-1)^{n-2}$
. In the same work, we also show that the Möbius number of
![]() $\mathcal {O}{\mathcal {PD}}(M)^{*}$
is
$\mathcal {O}{\mathcal {PD}}(M)^{*}$
is
![]() $-(n-1)! \cdot C_{n-1}$
, where
$-(n-1)! \cdot C_{n-1}$
, where
![]() $C_{n-1}$
is the
$C_{n-1}$
is the
![]() $(n-1)$
st Catalan number.
$(n-1)$
st Catalan number.
However, we do not have information on the sphericity of
![]() ${\mathcal {PD}}(M)^{*}$
and
${\mathcal {PD}}(M)^{*}$
and
![]() $\mathcal {O}{\mathcal {PD}}(M)^{*}$
. Preliminary computations show that these posets should be Cohen-Macaulay (and even shellable). So we propose the following question:
$\mathcal {O}{\mathcal {PD}}(M)^{*}$
. Preliminary computations show that these posets should be Cohen-Macaulay (and even shellable). So we propose the following question:
Question 6.27. Let M be a matroid such that
![]() ${{\mathcal L}}(M)$
is isomorphic to
${{\mathcal L}}(M)$
is isomorphic to
![]() $\Pi _n$
,
$\Pi _n$
,
![]() $n \geq 2$
. Are
$n \geq 2$
. Are
![]() ${\mathcal {PD}}(M)$
and
${\mathcal {PD}}(M)$
and
![]() $\mathcal {O}{\mathcal {PD}}(M)$
Cohen-Macaulay?
$\mathcal {O}{\mathcal {PD}}(M)$
Cohen-Macaulay?
When M is the matroid such that
![]() ${{\mathcal L}}(M)$
is the Boolean lattice, then we have already used the well-known fact that
${{\mathcal L}}(M)$
is the Boolean lattice, then we have already used the well-known fact that
![]() $\mathcal {O}{\mathcal D}(M)^{\circ }$
is the face poset of the permutohedron and hence its order complex is homeomorphic to a sphere. The latter is also a consequence of Lemma 5.17. More interesting is
$\mathcal {O}{\mathcal D}(M)^{\circ }$
is the face poset of the permutohedron and hence its order complex is homeomorphic to a sphere. The latter is also a consequence of Lemma 5.17. More interesting is
![]() $\mathcal {O}{\mathcal {PD}}(M)^{*}$
. By Corollary 5.22, its Euler characteristic is
$\mathcal {O}{\mathcal {PD}}(M)^{*}$
. By Corollary 5.22, its Euler characteristic is
![]() $-1$
. Using item 2 of Theorem 5.9 and the fact that the interval
$-1$
. Using item 2 of Theorem 5.9 and the fact that the interval
![]() ${\mathcal {PD}}(M)^{*}_{< \sigma }$
below a full decomposition
${\mathcal {PD}}(M)^{*}_{< \sigma }$
below a full decomposition
![]() $\sigma \in {\mathcal D}(M)^{*}$
is contractible, it even follows that
$\sigma \in {\mathcal D}(M)^{*}$
is contractible, it even follows that
![]() $\mathcal {O}{\mathcal {PD}}(M)^{*}$
is homotopy equivalent to a sphere arising from the wedge-term in item 2 of Theorem 5.9 corresponding to the unique minimal element of
$\mathcal {O}{\mathcal {PD}}(M)^{*}$
is homotopy equivalent to a sphere arising from the wedge-term in item 2 of Theorem 5.9 corresponding to the unique minimal element of
![]() ${\mathcal D}(M)$
. Summarizing these results, we obtain the following:
${\mathcal D}(M)$
. Summarizing these results, we obtain the following:
Proposition 6.28. Let M be a matroid such that
![]() ${{\mathcal L}}(M)$
is a Boolean lattice on n elements. Then:
${{\mathcal L}}(M)$
is a Boolean lattice on n elements. Then:
-
(1)
 $\mathcal {O}{\mathcal D}(M)^{\circ }$
is homeomorphic to a polytopal sphere of dimension
$\mathcal {O}{\mathcal D}(M)^{\circ }$
is homeomorphic to a polytopal sphere of dimension
 $n-2$
.
$n-2$
. -
(2)
 $\mathcal {O}{\mathcal {PD}}(M)^{*}$
is homotopy equivalent to a sphere of dimension
$\mathcal {O}{\mathcal {PD}}(M)^{*}$
is homotopy equivalent to a sphere of dimension
 $2n-3$
.
$2n-3$
.
It remains open if, in this case,
![]() $\mathcal {O}{\mathcal {PD}}(M)^{*}$
is actually homeomorphic to a sphere. Note that there is a construction of a polytopal sphere based on ordered partial partitions – the elements of
$\mathcal {O}{\mathcal {PD}}(M)^{*}$
is actually homeomorphic to a sphere. Note that there is a construction of a polytopal sphere based on ordered partial partitions – the elements of
![]() $\mathcal {O}{\mathcal {PD}}(M)$
– in [Reference Houston, Goucher and JohnstonHGJ]. This construction seems to be unrelated to
$\mathcal {O}{\mathcal {PD}}(M)$
– in [Reference Houston, Goucher and JohnstonHGJ]. This construction seems to be unrelated to
![]() $\mathcal {O}{\mathcal {PD}}(M)$
and its order complex, though. It is easily seen that, in general, the poset
$\mathcal {O}{\mathcal {PD}}(M)$
and its order complex, though. It is easily seen that, in general, the poset
![]() $\mathcal {O}{\mathcal {PD}}(M)$
is not a lattice and hence not a face lattice of a polytope. Nevertheless,
$\mathcal {O}{\mathcal {PD}}(M)$
is not a lattice and hence not a face lattice of a polytope. Nevertheless,
![]() $\mathcal {O}{\mathcal {PD}}(M)^{*}$
is the face poset of a regular CW-complex (see, for instance, Proposition 3.1 in [Reference BjörnerBj84]).
$\mathcal {O}{\mathcal {PD}}(M)^{*}$
is the face poset of a regular CW-complex (see, for instance, Proposition 3.1 in [Reference BjörnerBj84]).
Question 6.29. Let M be a matroid such that
![]() ${{\mathcal L}}(M)$
is the Boolean lattice on n elements. Is the geometric realization of
${{\mathcal L}}(M)$
is the Boolean lattice on n elements. Is the geometric realization of
![]() $\mathcal {O}{\mathcal {PD}}(M)^{*}$
homeomorphic to the sphere of dimension
$\mathcal {O}{\mathcal {PD}}(M)^{*}$
homeomorphic to the sphere of dimension
![]() $2n-3$
?
$2n-3$
?
Finally, we discuss the frame complex and the complex of partial bases of a matroid M. Indeed, in our definition, we can regard
![]() $\mathcal {B}(M,\vee ,P)$
as the initial independence complex of M by letting
$\mathcal {B}(M,\vee ,P)$
as the initial independence complex of M by letting
![]() $P_F$
be the set of parallel elements in a flat
$P_F$
be the set of parallel elements in a flat
![]() $F\in {{\mathcal L}}(M)$
of rank one. Hence,
$F\in {{\mathcal L}}(M)$
of rank one. Hence,
![]() $\mathcal {B}(M,\vee ,P) = I(M)$
. For a finite matroid, this is a well-studied and important object, which, as we mentioned at the beginning of this section, is well-known to be Cohen-Macaulay. We deduce then that, for a finite matroid M, the frame complex
$\mathcal {B}(M,\vee ,P) = I(M)$
. For a finite matroid, this is a well-studied and important object, which, as we mentioned at the beginning of this section, is well-known to be Cohen-Macaulay. We deduce then that, for a finite matroid M, the frame complex
![]() ${\mathcal F}(M)$
is also Cohen-Macaulay. In fact,
${\mathcal F}(M)$
is also Cohen-Macaulay. In fact,
![]() ${\mathcal F}(M)$
is also the independence complex of the matroid
${\mathcal F}(M)$
is also the independence complex of the matroid
![]() $M'$
whose ground set is the vertex set of
$M'$
whose ground set is the vertex set of
![]() ${\mathcal F}(M)$
(and so
${\mathcal F}(M)$
(and so
![]() ${{\mathcal L}}(M)$
is isomorphic to
${{\mathcal L}}(M)$
is isomorphic to
![]() ${{\mathcal L}}(M')$
). Thus, in both cases, the ordered versions are Cohen-Macaulay by Theorem 5.9.
${{\mathcal L}}(M')$
). Thus, in both cases, the ordered versions are Cohen-Macaulay by Theorem 5.9.
As for
![]() ${{\mathcal L}}(M)$
in the situation when the matroid is infinite, we do not know of a suitable reference proving Cohen-Macaulayness. In [Reference Piterman and WelkerPW25], we also show that
${{\mathcal L}}(M)$
in the situation when the matroid is infinite, we do not know of a suitable reference proving Cohen-Macaulayness. In [Reference Piterman and WelkerPW25], we also show that
![]() $I(M)$
is Cohen-Macaulay of dimension
$I(M)$
is Cohen-Macaulay of dimension
![]() $n-1$
if M is an infinite matroid of finite rank n. In particular, we see that the frame complex
$n-1$
if M is an infinite matroid of finite rank n. In particular, we see that the frame complex
![]() ${\mathcal F}(M)$
is Cohen-Macaulay of dimension
${\mathcal F}(M)$
is Cohen-Macaulay of dimension
![]() $n-1$
by Proposition 5.10.
$n-1$
by Proposition 5.10.
As mentioned above, the results from Proposition 5.12 on the topology of the augmented Bergman complex in the (finite) matroid case are well-known (see [Reference Bullock, Kelley, Reiner, Ren, Shemy, Shen, Sun and ZhangBKR]).
6.5 Modules over Dedekind domains
Let M be a left module over a ring R. In the category of (left) R-modules with monoidal product equal to the coproduct (i.e., the direct sum),
![]() ${\mathcal {S}}(M)$
is the poset of submodules and
${\mathcal {S}}(M)$
is the poset of submodules and
![]() ${\mathcal {S}}(M,\oplus )$
is the subposet of direct summands of M. Without further requirements,
${\mathcal {S}}(M,\oplus )$
is the subposet of direct summands of M. Without further requirements,
![]() ${\mathcal {S}}(M,\oplus )$
may have infinite height. Hence, we assume that M is a finitely generated module over a Dedekind domain R. Then we have a structure theorem: M decomposes as the direct sum
${\mathcal {S}}(M,\oplus )$
may have infinite height. Hence, we assume that M is a finitely generated module over a Dedekind domain R. Then we have a structure theorem: M decomposes as the direct sum
![]() $T_M\oplus P_M$
, where
$T_M\oplus P_M$
, where
![]() $T_M$
is the torsion submodule and
$T_M$
is the torsion submodule and
![]() $P_M$
is a projective module. Moreover,
$P_M$
is a projective module. Moreover,
![]() $T_M$
decomposes as a finite direct sum of cyclic torsion modules. However,
$T_M$
decomposes as a finite direct sum of cyclic torsion modules. However,
![]() $P_M$
may not be a free module, but it decomposes as the direct sum of a free module
$P_M$
may not be a free module, but it decomposes as the direct sum of a free module
![]() $R^{n-1}$
and a rank-
$R^{n-1}$
and a rank-
![]() $1$
projective module I. Thus, M is a Noetherian module, and it is projective if and only if it is torsion-free.
$1$
projective module I. Thus, M is a Noetherian module, and it is projective if and only if it is torsion-free.
The following lemma describes the poset
![]() ${\mathcal {S}}(M,\oplus )$
in terms of the torsion submodule and the projective part.
${\mathcal {S}}(M,\oplus )$
in terms of the torsion submodule and the projective part.
Lemma 6.30. Let R be a Dedekind domain and M a finitely generated R-module. Denote by
![]() $T_M$
the torsion submodule of M and
$T_M$
the torsion submodule of M and
![]() $P = M/T_M$
. If
$P = M/T_M$
. If
![]() $q:M\to M/T_M$
is the quotient map, then
$q:M\to M/T_M$
is the quotient map, then
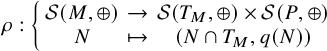 $$\begin{align*}\rho :\left\{ \begin{array}{ccc} {\mathcal{S}}(M,\oplus) & \to & {\mathcal{S}}(T_M,\oplus) \times {\mathcal{S}}(P,\oplus)\\ N & \mapsto & (N\cap T_M, q(N)) \end{array} \right.\end{align*}$$
$$\begin{align*}\rho :\left\{ \begin{array}{ccc} {\mathcal{S}}(M,\oplus) & \to & {\mathcal{S}}(T_M,\oplus) \times {\mathcal{S}}(P,\oplus)\\ N & \mapsto & (N\cap T_M, q(N)) \end{array} \right.\end{align*}$$
is an isomorphism with inverse
![]() $(T,R)\mapsto i(T)+s(R)$
, where
$(T,R)\mapsto i(T)+s(R)$
, where
![]() $s:P\to M$
is a section of q and
$s:P\to M$
is a section of q and
![]() $i:T_M\to M$
is the inclusion map.
$i:T_M\to M$
is the inclusion map.
Proof. Let
![]() $N\in {\mathcal {S}}(M,\oplus )$
. Then N is also finitely generated and the torsion submodule of N is
$N\in {\mathcal {S}}(M,\oplus )$
. Then N is also finitely generated and the torsion submodule of N is
![]() $T_N = N\cap T_M$
. Indeed, we also have
$T_N = N\cap T_M$
. Indeed, we also have
![]() $N = T_N\oplus s(q(N))$
since the sequence
$N = T_N\oplus s(q(N))$
since the sequence
![]() $0\to T_N\to N \to q(N) \to 0$
splits with section
$0\to T_N\to N \to q(N) \to 0$
splits with section
![]() $s|_{q(N)}$
. It is not hard to show that if
$s|_{q(N)}$
. It is not hard to show that if
![]() $N'$
is a complement of N in M, then
$N'$
is a complement of N in M, then
![]() $N'\cap T_M$
is a complement of
$N'\cap T_M$
is a complement of
![]() $N\cap T_M$
in
$N\cap T_M$
in
![]() $T_M$
and
$T_M$
and
![]() $q(N')$
is a complement of
$q(N')$
is a complement of
![]() $q(N)$
in P. Hence,
$q(N)$
in P. Hence,
![]() $\rho $
is a well-defined order-preserving map, and it is an isomorphism with inverse given by
$\rho $
is a well-defined order-preserving map, and it is an isomorphism with inverse given by
![]() $(T,R)\mapsto i(T) + s(R)$
.
$(T,R)\mapsto i(T) + s(R)$
.
The structure of the poset of direct summands
![]() ${\mathcal {S}}(T,\oplus )$
of a torsion module T over a Dedekind domain is closely related to the poset of direct summands in an Abelian group. In this article, we will not study the torsion part and thus only focus on the poset of direct summands of a projective module of finite rank.
${\mathcal {S}}(T,\oplus )$
of a torsion module T over a Dedekind domain is closely related to the poset of direct summands in an Abelian group. In this article, we will not study the torsion part and thus only focus on the poset of direct summands of a projective module of finite rank.
Lemma 6.31. Let M be a finitely generated projective module of rank n over a Dedekind domain R with field of fractions
![]() ${\mathbb {K}}$
. The following hold:
${\mathbb {K}}$
. The following hold:
-
(1) Let
 $V = M\otimes _R {\mathbb {K}} \cong {\mathbb {K}}^n$
. Then the map
$V = M\otimes _R {\mathbb {K}} \cong {\mathbb {K}}^n$
. Then the map
 $N\mapsto N\otimes _R {\mathbb {K}}$
gives an isomorphism
$N\mapsto N\otimes _R {\mathbb {K}}$
gives an isomorphism
 ${\mathcal {S}}(M,\oplus ) \to {\mathcal {S}}(V)$
, where the latter is the poset of subspaces of V.
${\mathcal {S}}(M,\oplus ) \to {\mathcal {S}}(V)$
, where the latter is the poset of subspaces of V. -
(2) If
 $N,N'\in {\mathcal {S}}(M,\oplus )$
, then
$N,N'\in {\mathcal {S}}(M,\oplus )$
, then
 $N\cap N'\in {\mathcal {S}}(M,\oplus )$
. Thus,
$N\cap N'\in {\mathcal {S}}(M,\oplus )$
. Thus,
 $N\wedge N' = N\cap N'$
.
$N\wedge N' = N\cap N'$
. -
(3) For
 $P\in M$
, it holds
$P\in M$
, it holds
 ${\mathcal {S}}(M,\oplus )_{\leq P} = {\mathcal {S}}(P,\oplus )$
. In particular,
${\mathcal {S}}(M,\oplus )_{\leq P} = {\mathcal {S}}(P,\oplus )$
. In particular,
 ${\mathcal {S}}(M,\oplus )$
is downward
${\mathcal {S}}(M,\oplus )$
is downward
 $(\sqcup ,h)$
-complemented, with
$(\sqcup ,h)$
-complemented, with
 $\sqcup = \oplus $
.
$\sqcup = \oplus $
. -
(4) Property (LI).
-
(5) Property (EX).
-
(6) Property (CM).
Proof. Item 1 is discussed in [Reference CharneyC, p. 3] and item 2 in [Reference CharneyC, Lemma 1.2]. Item 3 is a consequence of the modular law.
Next, suppose that
![]() $\sigma \in {\mathcal {PD}}(M,\oplus )$
and let
$\sigma \in {\mathcal {PD}}(M,\oplus )$
and let
![]() $\tau _P\in {\mathcal D}(P,\oplus )$
. Fix
$\tau _P\in {\mathcal D}(P,\oplus )$
. Fix
![]() $P'\in {\mathcal {S}}(M,\oplus )$
such that
$P'\in {\mathcal {S}}(M,\oplus )$
such that
![]() $\sigma \cup \{P'\}\in {\mathcal D}(M,\oplus )$
. Then
$\sigma \cup \{P'\}\in {\mathcal D}(M,\oplus )$
. Then
![]() $\bigcup _{P\in \sigma } \tau _P \cup \{P'\}\in {\mathcal D}(M,\oplus )$
. Reciprocally, by item 3, if
$\bigcup _{P\in \sigma } \tau _P \cup \{P'\}\in {\mathcal D}(M,\oplus )$
. Reciprocally, by item 3, if
![]() $\sigma \in {\mathcal {PD}}(M,\oplus )$
and
$\sigma \in {\mathcal {PD}}(M,\oplus )$
and
![]() $\Phi (\sigma )\leq P$
, then
$\Phi (\sigma )\leq P$
, then
![]() $\Phi (\sigma )\in {\mathcal {S}}(P,\oplus )$
, and if
$\Phi (\sigma )\in {\mathcal {S}}(P,\oplus )$
, and if
![]() $\{ \Phi (\sigma ), U \}\in {\mathcal D}(P,\oplus )$
and
$\{ \Phi (\sigma ), U \}\in {\mathcal D}(P,\oplus )$
and
![]() $\{P,P'\}\in {\mathcal D}(M,\oplus )$
, then
$\{P,P'\}\in {\mathcal D}(M,\oplus )$
, then
![]() $\sigma \cup \{U,P'\}\in {\mathcal D}(M,\oplus )$
. From this, it is not hard to conclude that item 4 holds.
$\sigma \cup \{U,P'\}\in {\mathcal D}(M,\oplus )$
. From this, it is not hard to conclude that item 4 holds.
Property (EX) also holds by similar arguments involving the use of modular law.
Finally, we show that property (CM) holds. Let
![]() $(P,P'), (N,N')$
two direct sum decompositions of M such that
$(P,P'), (N,N')$
two direct sum decompositions of M such that
![]() $P\leq P'$
and
$P\leq P'$
and
![]() $N\geq N'$
. Then, by item 2,
$N\geq N'$
. Then, by item 2,
![]() $P'\cap N = P'\wedge N \in {\mathcal {S}}(M,\oplus )$
. Also, the submodules
$P'\cap N = P'\wedge N \in {\mathcal {S}}(M,\oplus )$
. Also, the submodules
![]() $\{P, P'\cap N, N'\}$
are clearly in direct sum, and their span is M. Thus,
$\{P, P'\cap N, N'\}$
are clearly in direct sum, and their span is M. Thus,
![]() $\{P,P'\cap N, N'\}\setminus \{0\}\in {\mathcal D}(M,\oplus )$
.
$\{P,P'\cap N, N'\}\setminus \{0\}\in {\mathcal D}(M,\oplus )$
.
In [Reference CharneyC], Charney proved that if R is a Dedekind domain and M is a projective module of rank n, then
![]() $\mathcal {G}(M,\oplus )$
is spherical of dimension
$\mathcal {G}(M,\oplus )$
is spherical of dimension
![]() $n-2$
. By Proposition 4.15 and Lemma 6.31, we see that
$n-2$
. By Proposition 4.15 and Lemma 6.31, we see that
![]() $\Delta \mathcal {G}(M,\oplus ) \cong {\mathcal {O}{\mathcal D}(M,\oplus )^{\circ }}^{\mathrm {op}}$
. Now, by Lemma 4.10 and Lemma 6.31, the intervals
$\Delta \mathcal {G}(M,\oplus ) \cong {\mathcal {O}{\mathcal D}(M,\oplus )^{\circ }}^{\mathrm {op}}$
. Now, by Lemma 4.10 and Lemma 6.31, the intervals
![]() $\mathcal {O}{\mathcal D}(M,\oplus )^{\circ }_{< z}$
and
$\mathcal {O}{\mathcal D}(M,\oplus )^{\circ }_{< z}$
and
![]() $\mathcal {O}{\mathcal D}(M,\oplus )^{\circ }_{> z}$
are spherical of the correct dimension for
$\mathcal {O}{\mathcal D}(M,\oplus )^{\circ }_{> z}$
are spherical of the correct dimension for
![]() $z\in \mathcal {O}{\mathcal D}(M,\oplus )$
. Thus,
$z\in \mathcal {O}{\mathcal D}(M,\oplus )$
. Thus,
![]() $\mathcal {O}{\mathcal D}(M,\oplus )$
is Cohen-Macaulay (so
$\mathcal {O}{\mathcal D}(M,\oplus )$
is Cohen-Macaulay (so
![]() $\mathcal {G}(M,\oplus )$
is Cohen-Macaulay as well). By Theorem 5.9,
$\mathcal {G}(M,\oplus )$
is Cohen-Macaulay as well). By Theorem 5.9,
![]() ${\mathcal D}(M,\oplus )^{\circ }$
is spherical. Since its intervals are intervals in partition lattices or products of smaller decomposition posets, we also conclude that
${\mathcal D}(M,\oplus )^{\circ }$
is spherical. Since its intervals are intervals in partition lattices or products of smaller decomposition posets, we also conclude that
![]() ${\mathcal D}(M,\oplus )$
is Cohen-Macaulay.
${\mathcal D}(M,\oplus )$
is Cohen-Macaulay.
Hence, by Charney’s result we get the following:
Theorem 6.32 (Charney)
Let M be a finitely generated projective module of rank n over a Dedekind domain R. Then
![]() ${\mathcal {S}}(M,\oplus )$
,
${\mathcal {S}}(M,\oplus )$
,
![]() ${\mathcal D}(M,\oplus )$
,
${\mathcal D}(M,\oplus )$
,
![]() $\mathcal {O}{\mathcal D}(M,\oplus )$
and
$\mathcal {O}{\mathcal D}(M,\oplus )$
and
![]() $\mathcal {G}(M,\oplus )$
are Cohen-Macaulay posets of dimension n,
$\mathcal {G}(M,\oplus )$
are Cohen-Macaulay posets of dimension n,
![]() $n-1$
,
$n-1$
,
![]() $n-1$
and
$n-1$
and
![]() $n-2$
, respectively. In particular, this holds when R is a PID.
$n-2$
, respectively. In particular, this holds when R is a PID.
On the other hand, the complex of partial bases of a projective module of finite rank over a Dedekind domain is widely studied. But first, we need to make a few remarks on its definition. According to the work by Van der Kallen [Reference van der KallenvdK], the poset
![]() ${\mathcal U}(M)$
of unimodular sequences of an R-module M is the set of ordered sequences of distinct elements of M which form a basis of a free summand of M, ordered in the usual way. That is, if
${\mathcal U}(M)$
of unimodular sequences of an R-module M is the set of ordered sequences of distinct elements of M which form a basis of a free summand of M, ordered in the usual way. That is, if
![]() $z,w\in {\mathcal U}(M)$
, then
$z,w\in {\mathcal U}(M)$
, then
![]() $z\leq w$
if and only if z is obtained by deleting elements of the tuple w.
$z\leq w$
if and only if z is obtained by deleting elements of the tuple w.
However, the definition of
![]() ${\mathcal U}(M)$
does not always coincide with our definition of (ordered) frames and partial bases for M. To be more precise, let
${\mathcal U}(M)$
does not always coincide with our definition of (ordered) frames and partial bases for M. To be more precise, let
![]() ${\mathcal C}$
be the category of R-modules, where R is a Dedekind domain,
${\mathcal C}$
be the category of R-modules, where R is a Dedekind domain,
![]() $\sqcup = \oplus $
, and let
$\sqcup = \oplus $
, and let
![]() $M=R^n$
be the free R-module of rank
$M=R^n$
be the free R-module of rank
![]() $n\geq 2$
. Then there are frames
$n\geq 2$
. Then there are frames
![]() $\{N_1,\ldots ,N_n\}$
of M such that not all the
$\{N_1,\ldots ,N_n\}$
of M such that not all the
![]() $N_i$
are free, but just projective of rank one. Indeed, this is the case if R is not a PID. This leads to the question of which definition we should also employ for the complex of partial bases. For example, a natural choice for the partial basis complex is to take, for each rank-
$N_i$
are free, but just projective of rank one. Indeed, this is the case if R is not a PID. This leads to the question of which definition we should also employ for the complex of partial bases. For example, a natural choice for the partial basis complex is to take, for each rank-
![]() $1$
summand N of M, the set of generating sets of N of minimal possible size. In the case N is free, this is exactly the set of bases of N. But if N is non-free, these generating sets have size
$1$
summand N of M, the set of generating sets of N of minimal possible size. In the case N is free, this is exactly the set of bases of N. But if N is non-free, these generating sets have size
![]() $2$
. We denote our ‘natural’ choice for the partial basis complex by
$2$
. We denote our ‘natural’ choice for the partial basis complex by
![]() $\mathcal {B}(M,\oplus )$
(note that
$\mathcal {B}(M,\oplus )$
(note that
![]() ${\mathcal {PF}}(M,\oplus ) = {\mathcal F}(M,\oplus )$
). When R is a PID,
${\mathcal {PF}}(M,\oplus ) = {\mathcal F}(M,\oplus )$
). When R is a PID,
![]() $\mathcal {O}\mathcal {B}(M,\oplus ) = {\mathcal U}(M)$
.
$\mathcal {O}\mathcal {B}(M,\oplus ) = {\mathcal U}(M)$
.
If we work instead in the category of free R-modules with
![]() $\sqcup = \oplus $
, then a rank-
$\sqcup = \oplus $
, then a rank-
![]() $1$
summand of
$1$
summand of
![]() $M = R^n$
is always free, and therefore,
$M = R^n$
is always free, and therefore,
![]() ${\mathcal U}(M)$
coincides with the ordered version of the complex of partial bases as we defined. To avoid confusion on these different approaches and definitions, we write
${\mathcal U}(M)$
coincides with the ordered version of the complex of partial bases as we defined. To avoid confusion on these different approaches and definitions, we write
![]() $\mathcal {B}(M)$
,
$\mathcal {B}(M)$
,
![]() ${\mathcal F}(M)$
, etc., for the versions of these posets and complexes that only involve decompositions into free summands (so working in the category of free R-modules). We reserve notation with
${\mathcal F}(M)$
, etc., for the versions of these posets and complexes that only involve decompositions into free summands (so working in the category of free R-modules). We reserve notation with
![]() $\oplus $
– namely,
$\oplus $
– namely,
![]() $\mathcal {B}(M,\oplus )$
,
$\mathcal {B}(M,\oplus )$
,
![]() ${\mathcal F}(M,\oplus )$
, etc. – for the corresponding versions in the category of R-modules (so decompositions might involve non-free projective summands). With this notation,
${\mathcal F}(M,\oplus )$
, etc. – for the corresponding versions in the category of R-modules (so decompositions might involve non-free projective summands). With this notation,
We recall now some results on these posets and complexes. By Theorem 2.6 of [Reference van der KallenvdK],
![]() ${\mathcal U}(R^n)$
has dimension
${\mathcal U}(R^n)$
has dimension
![]() $n-1$
and it is
$n-1$
and it is
![]() $(n-3)$
-connected. This result settled a conjecture raised by Quillen on higher connectivity of the posets of unimodular sequences on finite-dimensional Noetherian rings. Moreover, by Theorem 5.9, the unordered version of this poset (i.e., the complex
$(n-3)$
-connected. This result settled a conjecture raised by Quillen on higher connectivity of the posets of unimodular sequences on finite-dimensional Noetherian rings. Moreover, by Theorem 5.9, the unordered version of this poset (i.e., the complex
![]() ${\mathcal B}(R^n)$
) is
${\mathcal B}(R^n)$
) is
![]() $(n-3)$
-connected. In particular,
$(n-3)$
-connected. In particular,
![]() ${\mathcal F}(R^n)$
is
${\mathcal F}(R^n)$
is
![]() $(n-3)$
-connected by Proposition 5.10.
$(n-3)$
-connected by Proposition 5.10.
However, it was more recently shown [Reference Church, Farb and PutmanCFP, Theorem 2.1] that
![]() ${\mathcal U}(R^n)$
might not be spherical, and hence, the family of complexes
${\mathcal U}(R^n)$
might not be spherical, and hence, the family of complexes
![]() ${\mathcal U}(R^n)$
is not Cohen-Macaulay in general (and thus neither is
${\mathcal U}(R^n)$
is not Cohen-Macaulay in general (and thus neither is
![]() ${\mathcal F}(R^n)$
by Proposition 5.10). For example, for
${\mathcal F}(R^n)$
by Proposition 5.10). For example, for
![]() $R = {\mathbb {Z}}[\sqrt {-5}]$
and
$R = {\mathbb {Z}}[\sqrt {-5}]$
and
![]() $n=2$
, the complex
$n=2$
, the complex
![]() ${\mathcal U}(R^2)$
is disconnected. Nevertheless, Theorem E of [Reference Church, Farb and PutmanCFP] establishes the Cohen-Macaulay property for the complex
${\mathcal U}(R^2)$
is disconnected. Nevertheless, Theorem E of [Reference Church, Farb and PutmanCFP] establishes the Cohen-Macaulay property for the complex
![]() ${\mathcal U}(R_S^n)$
if
${\mathcal U}(R_S^n)$
if
![]() $R_S$
is a Dedekind domain of arithmetic type constructed from a global field or number field K, and S is a set of places of K of size at least two (and infinite if K is a number field), which also contains a non-complex place. In particular, its unordered version is Cohen-Macaulay by Theorem 5.9. Also by Proposition 5.10,
$R_S$
is a Dedekind domain of arithmetic type constructed from a global field or number field K, and S is a set of places of K of size at least two (and infinite if K is a number field), which also contains a non-complex place. In particular, its unordered version is Cohen-Macaulay by Theorem 5.9. Also by Proposition 5.10,
![]() ${\mathcal F}(R_S^n)$
is Cohen-Macaulay.
${\mathcal F}(R_S^n)$
is Cohen-Macaulay.
We propose the study of the partial decompositions in this context:
Question 6.33. For which Dedekind domains R are
![]() ${\mathcal {PD}}(R^n)^{*}$
and
${\mathcal {PD}}(R^n)^{*}$
and
![]() ${\mathcal {PD}}(R^n,\oplus )^{*}$
spherical?
${\mathcal {PD}}(R^n,\oplus )^{*}$
spherical?
Note that in the example above for
![]() $R = {\mathbb {Z}}[\sqrt {-5}]$
,
$R = {\mathbb {Z}}[\sqrt {-5}]$
,
![]() ${\mathcal {PD}}(R^2)^{*} = {\mathcal F}(R^2)$
is disconnected since
${\mathcal {PD}}(R^2)^{*} = {\mathcal F}(R^2)$
is disconnected since
![]() $\mathcal {B}(R^2) = {\mathcal U}(R^2)$
is. But also
$\mathcal {B}(R^2) = {\mathcal U}(R^2)$
is. But also
![]() ${\mathcal {PD}}(R^2,\oplus )^{*} = {\mathcal F}(R^2,\oplus )$
is disconnected, as we show below.
${\mathcal {PD}}(R^2,\oplus )^{*} = {\mathcal F}(R^2,\oplus )$
is disconnected, as we show below.
Lemma 6.34. Let R be a Dedekind domain. If
![]() ${\mathcal F}(R^2)$
is disconnected, then so is
${\mathcal F}(R^2)$
is disconnected, then so is
![]() ${\mathcal F}(R^2,\oplus )$
.
${\mathcal F}(R^2,\oplus )$
.
Proof. We prove first that for a frame
![]() $\{N_1,N_2\}\in {\mathcal F}(R^2,\oplus )$
,
$\{N_1,N_2\}\in {\mathcal F}(R^2,\oplus )$
,
![]() $N_1$
is free if and only if
$N_1$
is free if and only if
![]() $N_2$
is. Indeed, the
$N_2$
is. Indeed, the
![]() $N_i$
are rank-
$N_i$
are rank-
![]() $1$
projective R-modules, and hence can be regarded as ideals of R. To be more precise, if
$1$
projective R-modules, and hence can be regarded as ideals of R. To be more precise, if
![]() $R^2 = N_1\oplus N_2$
then, regarding
$R^2 = N_1\oplus N_2$
then, regarding
![]() $N_1,N_2$
as ideals, in the class group, we have that
$N_1,N_2$
as ideals, in the class group, we have that
![]() $1 = [R]^2 = [R^2] = [N_1][N_2]$
, which means that
$1 = [R]^2 = [R^2] = [N_1][N_2]$
, which means that
![]() $N_1$
is the inverse of
$N_1$
is the inverse of
![]() $N_2$
. Now note that
$N_2$
. Now note that
![]() $N_1$
is free if and only if it is a principal ideal; that is,
$N_1$
is free if and only if it is a principal ideal; that is,
![]() $[N_1] =1$
. Thus,
$[N_1] =1$
. Thus,
![]() $N_1$
is free if and only if
$N_1$
is free if and only if
![]() $N_2$
is.
$N_2$
is.
On the other hand, a frame
![]() $\{N_1,N_2\}\in {\mathcal F}(R^2,\oplus )$
contains either two rank-
$\{N_1,N_2\}\in {\mathcal F}(R^2,\oplus )$
contains either two rank-
![]() $1$
free modules or two non-free rank-
$1$
free modules or two non-free rank-
![]() $1$
projective modules. Thus, two frames of free rank-
$1$
projective modules. Thus, two frames of free rank-
![]() $1$
submodules that are in different connected components in
$1$
submodules that are in different connected components in
![]() ${\mathcal F}(R^2)$
cannot be connected by using non-free rank-
${\mathcal F}(R^2)$
cannot be connected by using non-free rank-
![]() $1$
projective summands in
$1$
projective summands in
![]() ${\mathcal F}(R^2,\oplus )$
. This shows that
${\mathcal F}(R^2,\oplus )$
. This shows that
![]() ${\mathcal F}(R^2,\oplus )$
is disconnected if
${\mathcal F}(R^2,\oplus )$
is disconnected if
![]() ${\mathcal F}(R^2)$
is.
${\mathcal F}(R^2)$
is.
On the other hand, by Charney’s results and Theorem 5.13, we can conclude that
![]() ${\mathcal {PD}}(M,\oplus )^{*}$
is at least
${\mathcal {PD}}(M,\oplus )^{*}$
is at least
![]() $(n-3)$
-connected for a rank-n projective module M.
$(n-3)$
-connected for a rank-n projective module M.
Acknowledgements
We are very grateful to Benjamin Brück for the many discussions during his research visit to Marburg and for providing us with several motivational examples and references. We thank Jesper Møller for pointing out to us that the Solomon identity can be used to simplify the proof of Theorem 6.10 from an earlier version of this paper. We also thank the anonymous referee for valuable suggestions, which greatly improved the presentation of this article.
The first author is supported by a Postdoctoral fellowship granted by the Alexander von Humboldt Stiftung and the FWO grant 12K1223N.
Competing interest
The authors have no competing interests to declare.