Hostname: page-component-8448b6f56d-mp689 Total loading time: 0 Render date: 2024-04-25T06:24:14.685Z Has data issue: false hasContentIssue false
  • English
  • Français

ROUQUIER’S CONJECTURE AND DIAGRAMMATIC ALGEBRA

Part of: Categories with structure Rings and algebras arising under various constructions Representation theory of rings and algebras Lie algebras and Lie superalgebras

Published online by Cambridge University Press:  16 November 2017

BEN WEBSTER
BEN WEBSTER*
Affiliation:
Department of Mathematics, University of Virginia, Charlottesville, VA, USA
*
†Current address: Department of Pure Mathematics, University of Waterloo & Perimeter Institute for Mathematical Physics, Waterloo, ON, Canada; email: ben.webster@uwaterloo.ca, bwebster@perimeterinstitute.ca

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove a conjecture of Rouquier relating the decomposition numbers in category 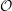${\mathcal{O}}$ for a cyclotomic rational Cherednik algebra to Uglov’s canonical basis of a higher level Fock space. Independent proofs of this conjecture have also recently been given by Rouquier, Shan, Varagnolo and Vasserot and by Losev, using different methods. Our approach is to develop two diagrammatic models for this category 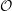${\mathcal{O}}$; while inspired by geometry, these are purely diagrammatic algebras, which we believe are of some intrinsic interest. In particular, we can quite explicitly describe the representations of the Hecke algebra that are hit by projectives under the 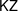$\mathsf{KZ}$-functor from the Cherednik category 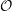${\mathcal{O}}$ in this case, with an explicit basis. This algebra has a number of beautiful structures including categorifications of many aspects of Fock space. It can be understood quite explicitly using a homogeneous cellular basis which generalizes such a basis given by Hu and Mathas for cyclotomic KLR algebras. Thus, we can transfer results proven in this diagrammatic formalism to category 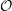${\mathcal{O}}$ for a cyclotomic rational Cherednik algebra, including the connection of decomposition numbers to canonical bases mentioned above, and an action of the affine braid group by derived equivalences between different blocks.

MSC classification

Primary: 16G99: None of the above, but in this section 18D99: None of the above, but in this section 16S37: Quadratic and Koszul algebras 17B10: Representations, algebraic theory (weights) 17B67: Kac-Moody (super)algebras; extended affine Lie algebras; toroidal Lie algebras
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 5 , 2017 , e27
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author 2017

References

Ariki, S., Representations of Quantum Algebras and Combinatorics of Young Tableaux, University Lecture Series, 26 (American Mathematical Society, Providence, RI, 2002), Translated from the 2000 Japanese edition and revised by the author.Google Scholar
Beilinson, A., Ginzburg, V. and Soergel, W., ‘Koszul duality patterns in representation theory’, J. Amer. Math. Soc. 9(2) (1996), 473–527.Google Scholar
Bezrukavnikov, R., ‘Quasi-exceptional sets and equivariant coherent sheaves on the nilpotent cone’, Represent. Theory 7 (2003), 1–18, (electronic).CrossRefGoogle Scholar
Bezrukavnikov, R. and Etingof, P., ‘Parabolic induction and restriction functors for rational Cherednik algebras’, Selecta Math. (N.S.) 14(3–4) (2009), 397–425.CrossRefGoogle Scholar
Braden, T., Licata, A., Proudfoot, N. and Webster, B., ‘Quantizations of conical symplectic resolutions II: category 𝓞 and symplectic duality’, Astérisque 2016(384) (2016), 75–179. with an appendix by I. Losev. MR 3594665.Google Scholar
Brundan, J. and Kleshchev, A., ‘Blocks of cyclotomic Hecke algebras and Khovanov–Lauda algebras’, Invent. Math. 178 (2009), 451–484.Google Scholar
Brundan, J., Losev, I. and Webster, B., ‘Tensor Product Categorifications and the Super Kazhdan–Lusztig Conjecture’, Int. Math. Res. Not. IMRN 2017(20) (2017), 6329–6410. MR 3712200.Google Scholar
Cautis, S. and Licata, A., ‘Heisenberg categorification and Hilbert schemes’, Duke Math. J. 161(13) (2012), 2469–2547.Google Scholar
Chuang, J. and Miyachi, H., Hidden Hecke algebras and Koszul duality, Preprint.Google Scholar
Chuang, J. and Rouquier, R., ‘Derived equivalences for symmetric groups and sl2 -categorification’, Ann. of Math. (2) 167(1) (2008), 245–298.Google Scholar
Dipper, R., James, G. and Mathas, A., ‘Cyclotomic q-Schur algebras’, Math. Z. 229(3) (1998), 385–416.Google Scholar
Dipper, R. and Mathas, A., ‘Morita equivalences of Ariki–Koike algebras’, Math. Z. 240(3) (2002), 579–610.Google Scholar
Frenkel, I. B. and Savage, A., ‘Bases of representations of type A affine Lie algebras via quiver varieties and statistical mechanics’, Int. Math. Res. Not. IMRN (28) (2003), 1521–1547.Google Scholar
Ginzburg, V., Guay, N., Opdam, E. and Rouquier, R., ‘On the category 𝓞 for rational Cherednik algebras’, Invent. Math. 154(3) (2003), 617–651.Google Scholar
Gordon, I. G. and Losev, I., ‘On category 𝓞 for cyclotomic rational Cherednik algebras’, J. Eur. Math. Soc. (JEMS) 16(5) (2014), 1017–1079.Google Scholar
Hu, J. and Mathas, A., ‘Graded cellular bases for the cyclotomic Khovanov–Lauda–Rouquier algebras of type A ’, Adv. Math. 225(2) (2010), 598–642.Google Scholar
Khovanov, M. and Lauda, A. D., ‘A diagrammatic approach to categorification of quantum groups. I’, Represent. Theory 13 (2009), 309–347.Google Scholar
König, S. and Xi, C., ‘When is a cellular algebra quasi-hereditary?’, Math. Ann. 315(2) (1999), 281–293.Google Scholar
Losev, I., ‘Towards multiplicities for cyclotomic rational Cherednik algebras’, Preprint, 2012, arXiv:1207.1299.Google Scholar
Losev, I., ‘Highest weight sl2 -categorifications I: crystals’, Math. Z. 274(3–4) (2013), 1231–1247.Google Scholar
Losev, I., ‘Proof of Varagnolo–Vasserot conjecture on cyclotomic categories 𝓞’, Selecta Math. (N.S.) 22(2) (2016), 631–668.Google Scholar
Losev, I. and Webster, B., ‘On uniqueness of tensor products of irreducible categorifications’, Selecta Math. (N.S.) 21(2) (2015), 345–377.Google Scholar
Maksimau, R., ‘Quiver Schur algebras and Koszul duality’, J. Algebra 406 (2014), 91–133.Google Scholar
Rouquier, R., ‘2-Kac–Moody algebras’, Preprint, 2008, arXiv:0812.5023.Google Scholar
Rouquier, R., ‘ q-Schur algebras and complex reflection groups’, Mosc. Math. J. 8(1) (2008), 119–158, 184.Google Scholar
Rouquier, R., Shan, P., Varagnolo, M. and Vasserot, E., ‘Categorifications and cyclotomic rational double affine Hecke algebras’, Invent. Math. 204(3) (2016), 671–786.Google Scholar
Ram, A. and Tingley, P., ‘Universal Verma modules and the Misra–Miwa Fock space’, Int. J. Math. Math. Sci. (2010), Art. ID 326247, 19.CrossRefGoogle Scholar
Shan, P., ‘Crystals of Fock spaces and cyclotomic rational double affine Hecke algebras’, Ann. Sci. Éc. Norm. Supér. (4) 44(1) (2011), 147–182.Google Scholar
Shan, P., ‘Graded decomposition matrices of v-Schur algebras via Jantzen filtration’, Represent. Theory 16 (2012), 212–269.Google Scholar
Shan, P., Varagnolo, M. and Vasserot, E., ‘Koszul duality of affine Kac–Moody algebras and cyclotomic rational double affine Hecke algebras’, Adv. Math. 262 (2014), 370–435.Google Scholar
Soergel, W., ‘Kategorie 𝓞, perverse Garben und Moduln über den Koinvarianten zur Weylgruppe’, J. Amer. Math. Soc. 3(2) (1990), 421–445.Google Scholar
Soergel, W., ‘The combinatorics of Harish–Chandra bimodules’, J. Reine Angew. Math. 429 (1992), 49–74.Google Scholar
Stroppel, C. and Webster, B., ‘Quiver Schur algebras and $q$ -Fock space’, Preprint, 2011, arXiv:1110.1115.Google Scholar
Tingley, P., ‘Three combinatorial models for sl̂ n crystals, with applications to cylindric plane partitions’, Int. Math. Res. Not. IMRN (2) (2008), Art. ID rnm143, 40.Google Scholar
Uglov, D., ‘Canonical bases of higher-level q-deformed Fock spaces and Kazhdan–Lusztig polynomials’, inPhysical Combinatorics (Kyoto, 1999), Progress in Mathematics, 191 (Birkhäuser, Boston, 2000), 249–299.Google Scholar
Varagnolo, M. and Vasserot, E., ‘Cyclotomic double affine Hecke algebras and affine parabolic category O’, Adv. Math. 225(3) (2010), 1523–1588.Google Scholar
Webster, B., ‘Weighted Khovanov–Lauda–Rouquier algebras’, Preprint, 2012, arXiv:1209.2463.Google Scholar
Webster, B., ‘Knot invariants and higher representation theory’, Mem. Amer. Math. Soc. 250(1191) (2017), 141.Google Scholar
Webster, B., ‘On graded presentations of Hecke algebras and their generalizations’, Preprint, 2013, arXiv:1305.0599.Google Scholar
Webster, B., ‘On generalized category 𝓞 for a quiver variety’, Math. Ann. 368(1) (2017), 483–536.Google Scholar