1 Introduction and statements of results
Let
![]() $\Phi $
be a crystallographic root system in an r-dimensional Euclidean space V, and
$\Phi $
be a crystallographic root system in an r-dimensional Euclidean space V, and
![]() $W\subseteq \operatorname {\mathrm {GL}}(V)$
be its corresponding Weyl group. Coxeter–Catalan combinatorics is the study of the W-Catalan number
$W\subseteq \operatorname {\mathrm {GL}}(V)$
be its corresponding Weyl group. Coxeter–Catalan combinatorics is the study of the W-Catalan number
 $$ \begin{align} \operatorname{\mathrm{Cat}}(W) := \prod_{i=1}^{r} \frac{d_i+h}{d_i}, \end{align} $$
$$ \begin{align} \operatorname{\mathrm{Cat}}(W) := \prod_{i=1}^{r} \frac{d_i+h}{d_i}, \end{align} $$
where
![]() $d_1\leq \cdots \leq d_r$
are the degrees of W and
$d_1\leq \cdots \leq d_r$
are the degrees of W and
![]() $h=d_r$
is its Coxeter number. Although not obvious, it is true that
$h=d_r$
is its Coxeter number. Although not obvious, it is true that
![]() $\operatorname {\mathrm {Cat}}(W)$
is an integer. It counts several collections of objects associated to
$\operatorname {\mathrm {Cat}}(W)$
is an integer. It counts several collections of objects associated to
![]() $\Phi $
, including the following:
$\Phi $
, including the following:
-
• W-nonnesting partitions (i.e., antichains of the poset
 $\Phi ^+$
of positive roots)
$\Phi ^+$
of positive roots) -
• W-noncrossing partitions (i.e., elements of W between the identity e and a fixed Coxeter element c in absolute order)
We let
![]() $\operatorname {\mathrm {NN}}(W)$
and
$\operatorname {\mathrm {NN}}(W)$
and
![]() $\operatorname {\mathrm {NC}}(W)$
denote the sets of W-nonnesting and W-noncrossing partitions, respectively (see, e.g., [Reference Armstrong1, Chapter 1] for a general introduction to Coxeter–Catalan combinatorics).
$\operatorname {\mathrm {NC}}(W)$
denote the sets of W-nonnesting and W-noncrossing partitions, respectively (see, e.g., [Reference Armstrong1, Chapter 1] for a general introduction to Coxeter–Catalan combinatorics).
Although there has been a tremendous amount of work done in Coxeter–Catalan combinatorics in the past 20-plus years, the connection between the nonnesting and noncrossing worlds remains deeply mysterious. As an example of the divide between nonnesting and noncrossing, we note that there is a uniform proof of the product formula (1.1) for nonnesting objects [Reference Cellini and Papi12, Reference Haiman15], but the only known proof of this formula for noncrossing objects is case by case [Reference Bessis4]. On the other hand, the noncrossing definition of the W-Catalan number extends directly to all finite Coxeter groups, whereas the naive generalisation of the nonnesting definition fails to work properly in noncrystallographic types.
The present work focuses on another difference between the nonnesting and noncrossing worlds, this one concerning a refinement of the W-Catalan number. Namely, for
![]() $0\leq k \leq r$
, the kth W-Narayana number
$0\leq k \leq r$
, the kth W-Narayana number
![]() $\operatorname {\mathrm {Nar}}(W,k)$
can be defined as either:
$\operatorname {\mathrm {Nar}}(W,k)$
can be defined as either:
-
• the number of nonnesting partitions in
 $\operatorname {\mathrm {NN}}(W)$
of cardinality k or
$\operatorname {\mathrm {NN}}(W)$
of cardinality k or -
• the number of noncrossing partitions in
 $\operatorname {\mathrm {NC}}(W)$
of rank k.
$\operatorname {\mathrm {NC}}(W)$
of rank k.
Evidently, the Narayana numbers refine the Catalan numbers in the sense that
![]() $\operatorname {\mathrm {Cat}}(W)=\sum _{k=0}^{r}\operatorname {\mathrm {Nar}}(W,k)$
.
$\operatorname {\mathrm {Cat}}(W)=\sum _{k=0}^{r}\operatorname {\mathrm {Nar}}(W,k)$
.
The property of the Narayana numbers that will most concern us here is their symmetry:
for all
![]() $0\leq k \leq r$
. This symmetry is easily seen using the noncrossing definition of the Narayana numbers: it follows from the fact that the lattice of noncrossing partitions is self-dual. (A particular duality of
$0\leq k \leq r$
. This symmetry is easily seen using the noncrossing definition of the Narayana numbers: it follows from the fact that the lattice of noncrossing partitions is self-dual. (A particular duality of
![]() $\operatorname {\mathrm {NC}}(W)$
, the Kreweras complement, will feature prominently in what follows.) However, this symmetry is far from obvious using the nonnesting definition of the Narayana numbers.
$\operatorname {\mathrm {NC}}(W)$
, the Kreweras complement, will feature prominently in what follows.) However, this symmetry is far from obvious using the nonnesting definition of the Narayana numbers.
In this paper, we take up the following problem:
Problem 1.1. Explain the symmetry (1.2) of the nonnesting W-Narayana numbers.
This problem was mentioned, for instance, in [Reference Fomin and Reading14, Remark 5.10]. Our approach to it will build upon a program of Panyushev [Reference Panyushev21, Reference Panyushev22]. In particular, we will study the following conjecture of Panyushev:
Conjecture 1.2 Panyushev [Reference Panyushev21, Conjecture 6.1]
There is a ‘natural’ involution
![]() $\mathfrak {P}\colon \operatorname {\mathrm {NN}}(W)\to \operatorname {\mathrm {NN}}(W)$
for which
$\mathfrak {P}\colon \operatorname {\mathrm {NN}}(W)\to \operatorname {\mathrm {NN}}(W)$
for which
![]() $\#A + \#\mathfrak {P}(A)=r$
for all
$\#A + \#\mathfrak {P}(A)=r$
for all
![]() $A \in \operatorname {\mathrm {NN}}(W)$
.
$A \in \operatorname {\mathrm {NN}}(W)$
.
Remark 1.3. Let
![]() $\mathfrak {g}$
be the complex semisimple Lie algebra corresponding to the root system
$\mathfrak {g}$
be the complex semisimple Lie algebra corresponding to the root system
![]() $\Phi $
, and let
$\Phi $
, and let
![]() $\mathfrak {b}$
be the Borel subalgebra of
$\mathfrak {b}$
be the Borel subalgebra of
![]() $\mathfrak {g}$
corresponding to the choice of positive roots
$\mathfrak {g}$
corresponding to the choice of positive roots
![]() $\Phi ^+$
. The nonnesting partitions
$\Phi ^+$
. The nonnesting partitions
![]() $\operatorname {\mathrm {NN}}(W)$
are in bijection with the ad-nilpotent ideals in
$\operatorname {\mathrm {NN}}(W)$
are in bijection with the ad-nilpotent ideals in
![]() $\mathfrak {b}$
; under this bijection, the cardinality of the antichain becomes the minimal number of generators of the ideal. Hence, Panyushev described his conjectural
$\mathfrak {b}$
; under this bijection, the cardinality of the antichain becomes the minimal number of generators of the ideal. Hence, Panyushev described his conjectural
![]() $\mathfrak {P}$
as a duality for ad-nilpotent ideals of
$\mathfrak {P}$
as a duality for ad-nilpotent ideals of
![]() $\mathfrak {b}$
, which sends an ideal with k generators to one with
$\mathfrak {b}$
, which sends an ideal with k generators to one with
![]() $r-k$
generators.
$r-k$
generators.
It is immediate from equation (1.2) that there is some involution satisfying the condition in Conjecture 1.2, so the word ‘natural’ is doing all the work in this conjecture. Actually, Panyushev listed some specific desiderata for
![]() $\mathfrak {P}$
that we will review later (see Conjecture 2.11). But, for instance, one thing we could want is that
$\mathfrak {P}$
that we will review later (see Conjecture 2.11). But, for instance, one thing we could want is that
![]() $\mathfrak {P}(A)$
be easily computable from A. Another thing we could want is that the definition of
$\mathfrak {P}(A)$
be easily computable from A. Another thing we could want is that the definition of
![]() $\mathfrak {P}$
be purely ‘poset-theoretic’ (using only the poset structure of
$\mathfrak {P}$
be purely ‘poset-theoretic’ (using only the poset structure of
![]() $\Phi ^+$
), since the definition of the Narayana numbers in terms of
$\Phi ^+$
), since the definition of the Narayana numbers in terms of
![]() $\operatorname {\mathrm {NN}}(W)$
is poset-theoretic in this sense.
$\operatorname {\mathrm {NN}}(W)$
is poset-theoretic in this sense.
Panyushev was unable to define
![]() $\mathfrak {P}$
in general, but in [Reference Panyushev21] he was able to come up with a definition in type A. In fact, Panyushev’s involution
$\mathfrak {P}$
in general, but in [Reference Panyushev21] he was able to come up with a definition in type A. In fact, Panyushev’s involution
![]() $\mathfrak {P}$
in type A is equivalent to the Lalanne–Kreweras involution on Dyck paths [Reference Hopkins and Joseph18]. A simple ‘folding’ argument allows one to obtain the appropriate involution
$\mathfrak {P}$
in type A is equivalent to the Lalanne–Kreweras involution on Dyck paths [Reference Hopkins and Joseph18]. A simple ‘folding’ argument allows one to obtain the appropriate involution
![]() $\mathfrak {P}$
in types B/C from the one in type A, so Panyushev was also able to treat types B/C.
$\mathfrak {P}$
in types B/C from the one in type A, so Panyushev was also able to treat types B/C.
What’s more, in a follow-up paper Panyushev [Reference Panyushev22] conjectured a way to do something ‘close’ to defining
![]() $\mathfrak {P}$
for all root systems. He considered the rowmotion operator
$\mathfrak {P}$
for all root systems. He considered the rowmotion operator
![]() $\operatorname {\mathrm {Row}} \colon \operatorname {\mathrm {NN}}(W)\to \operatorname {\mathrm {NN}}(W)$
acting on nonnesting partitions, and conjectured that it has very good behavior. Specifically, he conjectured that:
$\operatorname {\mathrm {Row}} \colon \operatorname {\mathrm {NN}}(W)\to \operatorname {\mathrm {NN}}(W)$
acting on nonnesting partitions, and conjectured that it has very good behavior. Specifically, he conjectured that:
-
•
 $\operatorname {\mathrm {Row}} ^{h}$
is the involutive poset automorphism
$\operatorname {\mathrm {Row}} ^{h}$
is the involutive poset automorphism
 $-w_0\colon \Phi ^+\to \Phi ^+$
, where
$-w_0\colon \Phi ^+\to \Phi ^+$
, where
 $w_0\in W$
is the longest element (hence,
$w_0\in W$
is the longest element (hence,
 $\operatorname {\mathrm {Row}} ^{2h}$
is the identity), and
$\operatorname {\mathrm {Row}} ^{2h}$
is the identity), and -
• the average cardinality of the antichains in any
 $\operatorname {\mathrm {Row}} $
-orbit is
$\operatorname {\mathrm {Row}} $
-orbit is
 $\frac {r}{2}$
.
$\frac {r}{2}$
.
This rowmotion conjecture is ‘close’ to Conjecture 1.2 because it says that
![]() $\operatorname {\mathrm {NN}}(W)$
can be partitioned into blocks of sizes dividing
$\operatorname {\mathrm {NN}}(W)$
can be partitioned into blocks of sizes dividing
![]() $2h$
such that the average cardinality in each block is
$2h$
such that the average cardinality in each block is
![]() $\frac {r}{2}$
, whereas Conjecture 1.2 says that
$\frac {r}{2}$
, whereas Conjecture 1.2 says that
![]() $\operatorname {\mathrm {NN}}(W)$
can be partitioned into blocks of sizes dividing
$\operatorname {\mathrm {NN}}(W)$
can be partitioned into blocks of sizes dividing
![]() $2$
such that the average cardinality in each block is
$2$
such that the average cardinality in each block is
![]() $\frac {r}{2}$
. Panyushev’s rowmotion conjecture was proved by Armstrong, Stump and Thomas [Reference Armstrong, Stump and Thomas2].
$\frac {r}{2}$
. Panyushev’s rowmotion conjecture was proved by Armstrong, Stump and Thomas [Reference Armstrong, Stump and Thomas2].
Although Panyushev was not the first to consider rowmotion (which is defined more generally as acting on the antichains of any poset), his investigation of rowmotion on root posets rekindled interest in this operator. Indeed, the past 10 or so years have seen the emergence of the subfield of dynamical algebraic combinatorics [Reference Roby27, Reference Striker31], in which rowmotion features prominently. Furthermore, Panyushev’s observation of ‘constant average cardinality along orbits’ was one of the first instances of homomesy [Reference Propp and Roby23], a phenomenon that again is at the heart of dynamical algebraic combinatorics.
In the present paper, we demonstrate how ideas from dynamical algebraic combinatorics can be used to address (more of) Conjecture 1.2.
As shown by Cameron and Fon-der-Flaass [Reference Cameron and Fon-Der-Flaass10] (see also [Reference Joseph19]), rowmotion acting on the antichains of any poset can be written as a composition of toggles, which are certain simple involutions that add elements to or remove elements from subsets. For any ranked poset, there is another canonical composition of toggles that gives a related involutive operator called rowvacuation. The names ‘rowmotion’ and ‘rowvacuation’ come from Schützenberger’s promotion and evacuation operators on linear extensions. Rowmotion and rowvacuation share many properties with promotion and evacuation: for instance, they generate a dihedral group action.
Rowvacuation is easy to compute (because it is a composition of toggles), and its definition is inherently poset-theoretic. Our main result is the following:
Theorem 1.4. If
![]() $\Phi $
is one of the classical types A, B, C or D, then the rowvacuation operator
$\Phi $
is one of the classical types A, B, C or D, then the rowvacuation operator
![]() $\operatorname {\mathrm {Rvac}}\colon \operatorname {\mathrm {NN}}(W)\to \operatorname {\mathrm {NN}}(W)$
is Panyushev’s conjectured involution
$\operatorname {\mathrm {Rvac}}\colon \operatorname {\mathrm {NN}}(W)\to \operatorname {\mathrm {NN}}(W)$
is Panyushev’s conjectured involution
![]() $\mathfrak {P}$
from Conjecture 1.2.
$\mathfrak {P}$
from Conjecture 1.2.
For
![]() $\Phi =G_2$
, it is easy to see there is a unique choice of
$\Phi =G_2$
, it is easy to see there is a unique choice of
![]() $\mathfrak {P}$
which in fact agrees with rowvacuation. Unfortunately, for the other exceptional types
$\mathfrak {P}$
which in fact agrees with rowvacuation. Unfortunately, for the other exceptional types
![]() $E_6$
,
$E_6$
,
![]() $E_7$
,
$E_7$
,
![]() $E_8$
and
$E_8$
and
![]() $F_4$
, there exist
$F_4$
, there exist
![]() $A \in \operatorname {\mathrm {NN}}(W)$
with
$A \in \operatorname {\mathrm {NN}}(W)$
with
![]() $\#A+\#\operatorname {\mathrm {Rvac}}(A)\neq r$
(see Remark 2.12), so we are unable to resolve Conjecture 1.2 in these exceptional types.
$\#A+\#\operatorname {\mathrm {Rvac}}(A)\neq r$
(see Remark 2.12), so we are unable to resolve Conjecture 1.2 in these exceptional types.
It was recently shown by the second author and Joseph [Reference Hopkins and Joseph18] that the Lalanne–Kreweras involution is rowvacuation for the root posets of type A. Together with Panyushev’s prior work from [Reference Panyushev21], this proves Theorem 1.4 for types A, B and C. So the only case we have to address here is type D.Footnote
1
However, along the way we prove results concerning rowvacuation of
![]() $\operatorname {\mathrm {NN}}(W)$
for arbitrary
$\operatorname {\mathrm {NN}}(W)$
for arbitrary
![]() $\Phi $
.
$\Phi $
.
More precisely, we extend some results of Armstrong, Stump and Thomas [Reference Armstrong, Stump and Thomas2]. In order to resolve Panyushev’s rowmotion conjecture, as well as a related conjecture of Bessis and Reiner [Reference Bessis and Reiner5], they constructed a bijection
![]() $\Theta _W\colon \operatorname {\mathrm {NN}}(W)\to \operatorname {\mathrm {NC}}(W)$
between the nonnesting and noncrossing partitions that is uniquely specified by a handful of properties (see Theorem 3.1). The most important of these properties is that
$\Theta _W\colon \operatorname {\mathrm {NN}}(W)\to \operatorname {\mathrm {NC}}(W)$
between the nonnesting and noncrossing partitions that is uniquely specified by a handful of properties (see Theorem 3.1). The most important of these properties is that
where
![]() $\operatorname {\mathrm {Krew}}\colon \operatorname {\mathrm {NC}}(W)\to \operatorname {\mathrm {NC}}(W)$
denotes the Kreweras complement defined by
$\operatorname {\mathrm {Krew}}\colon \operatorname {\mathrm {NC}}(W)\to \operatorname {\mathrm {NC}}(W)$
denotes the Kreweras complement defined by
![]() $\operatorname {\mathrm {Krew}}(w) := cw^{-1}$
. We show the following:
$\operatorname {\mathrm {Krew}}(w) := cw^{-1}$
. We show the following:
Theorem 1.5. For the bijection
![]() $\Theta _W\colon \operatorname {\mathrm {NN}}(W)\to \operatorname {\mathrm {NC}}(W)$
from [Reference Armstrong, Stump and Thomas2], we have
$\Theta _W\colon \operatorname {\mathrm {NN}}(W)\to \operatorname {\mathrm {NC}}(W)$
from [Reference Armstrong, Stump and Thomas2], we have
 $$ \begin{align*} \Theta_W \cdot \left(\operatorname{\mathrm{Row}}^{-1} \cdot \operatorname{\mathrm{Rvac}}\right) = \operatorname{\mathrm{Flip}}\cdot \Theta_W, \end{align*} $$
$$ \begin{align*} \Theta_W \cdot \left(\operatorname{\mathrm{Row}}^{-1} \cdot \operatorname{\mathrm{Rvac}}\right) = \operatorname{\mathrm{Flip}}\cdot \Theta_W, \end{align*} $$
where
![]() $\operatorname {\mathrm {Flip}}\colon \operatorname {\mathrm {NC}}(W)\to \operatorname {\mathrm {NC}}(W)$
is the involutive poset automorphism defined by
$\operatorname {\mathrm {Flip}}\colon \operatorname {\mathrm {NC}}(W)\to \operatorname {\mathrm {NC}}(W)$
is the involutive poset automorphism defined by
![]() $\operatorname {\mathrm {Flip}}(w) := gw^{-1}g^{-1}$
(for the appropriate involution
$\operatorname {\mathrm {Flip}}(w) := gw^{-1}g^{-1}$
(for the appropriate involution
![]() $g\in W$
depending on c).
$g\in W$
depending on c).
Note that we prove Theorem 1.5 just by appealing to the general properties satisfied by
![]() $\Theta _W$
, not via any case-by-case reasoning. Nevertheless, a lot of intricate combinatorial reasoning particular to the classical types does go into our proof of Theorem 1.4. For example, in these classical types, there are models of noncrossing partitions where
$\Theta _W$
, not via any case-by-case reasoning. Nevertheless, a lot of intricate combinatorial reasoning particular to the classical types does go into our proof of Theorem 1.4. For example, in these classical types, there are models of noncrossing partitions where
![]() $\operatorname {\mathrm {Krew}}$
corresponds to rotation; we show that
$\operatorname {\mathrm {Krew}}$
corresponds to rotation; we show that
![]() $\operatorname {\mathrm {Flip}}$
corresponds to reflection across a diameter in these models (hence the name).
$\operatorname {\mathrm {Flip}}$
corresponds to reflection across a diameter in these models (hence the name).
Remark 1.6. Before we end this introduction, let us briefly discuss an alternate approach to Problem 1.1 that we will not pursue. This alternate approach concerns an even further refinement of the Catalan numbers. Let
![]() $\Pi (\Phi )$
denote the lattice of flats of the Coxeter arrangement of
$\Pi (\Phi )$
denote the lattice of flats of the Coxeter arrangement of
![]() $\Phi $
. There are natural embeddings
$\Phi $
. There are natural embeddings
 $$ \begin{align*} \iota_{\operatorname{\mathrm{NN}}}\colon \operatorname{\mathrm{NN}}(W) &\hookrightarrow \Pi(\Phi)\\ \iota_{\operatorname{\mathrm{NC}}}\colon \operatorname{\mathrm{NC}}(W) &\hookrightarrow \Pi(\Phi). \end{align*} $$
$$ \begin{align*} \iota_{\operatorname{\mathrm{NN}}}\colon \operatorname{\mathrm{NN}}(W) &\hookrightarrow \Pi(\Phi)\\ \iota_{\operatorname{\mathrm{NC}}}\colon \operatorname{\mathrm{NC}}(W) &\hookrightarrow \Pi(\Phi). \end{align*} $$
Define the type
Footnote
2
of
![]() $A\in \operatorname {\mathrm {NN}}(W)$
to be the W-orbit of
$A\in \operatorname {\mathrm {NN}}(W)$
to be the W-orbit of
![]() $\iota _{\operatorname {\mathrm {NN}}}(A)$
, and define the type of
$\iota _{\operatorname {\mathrm {NN}}}(A)$
, and define the type of
![]() $w \in \operatorname {\mathrm {NC}}(W)$
similarly. It is known [Reference Athanasiadis and Reiner3, Theorem 6.3] that for any
$w \in \operatorname {\mathrm {NC}}(W)$
similarly. It is known [Reference Athanasiadis and Reiner3, Theorem 6.3] that for any
![]() $X \in \Pi (\Phi )/W$
, the number of nonnesting partitions of type X is the same as the number of noncrossing partitions of type X. These numbers are called the W-Kreweras numbers.Footnote
3
Moreover, the codimension of
$X \in \Pi (\Phi )/W$
, the number of nonnesting partitions of type X is the same as the number of noncrossing partitions of type X. These numbers are called the W-Kreweras numbers.Footnote
3
Moreover, the codimension of
![]() $\iota _{\operatorname {\mathrm {NN}}}(A)$
is the same as the cardinality of
$\iota _{\operatorname {\mathrm {NN}}}(A)$
is the same as the cardinality of
![]() $A \in \operatorname {\mathrm {NN}}(W)$
, and the codimension of
$A \in \operatorname {\mathrm {NN}}(W)$
, and the codimension of
![]() $\iota _{\operatorname {\mathrm {NC}}}(w)$
is the same as the rank of
$\iota _{\operatorname {\mathrm {NC}}}(w)$
is the same as the rank of
![]() $w \in \operatorname {\mathrm {NC}}(W)$
. Since, as already mentioned, the symmetry of the Narayana numbers is easy to see in the noncrossing world, a type-preserving bijection between nonnesting and noncrossing partitions would therefore constitute a solution to Problem 1.1. There are a handful of type-preserving bijections between the nonnesting and noncrossing partitions in the literature [Reference Fink and Iriarte Giraldo13, Reference Kim20]; but these constructions are all ad hoc and thus unsatisfactory in some sense. No uniform type-preserving bijection is known.
$w \in \operatorname {\mathrm {NC}}(W)$
. Since, as already mentioned, the symmetry of the Narayana numbers is easy to see in the noncrossing world, a type-preserving bijection between nonnesting and noncrossing partitions would therefore constitute a solution to Problem 1.1. There are a handful of type-preserving bijections between the nonnesting and noncrossing partitions in the literature [Reference Fink and Iriarte Giraldo13, Reference Kim20]; but these constructions are all ad hoc and thus unsatisfactory in some sense. No uniform type-preserving bijection is known.
The rest of the paper is structured as follows. In Section 2, we review necessary background concerning root posets, rowmotion and rowvacuation, and Panyushev’s Conjecture 1.2. In Section 3, we review noncrossing partitions, the Kreweras complement and the Armstrong–Stump–Thomas bijection. We also introduce the
![]() $\operatorname {\mathrm {Flip}}$
operator and prove Theorem 1.5 there. Armstrong, Stump and Thomas gave explicit combinatorial descriptions of their bijections in classical types. We review their description in type A in Section 4 and parts of their description in type D in Section 5. These sections also establish some lemmas, concerning how rowvacuation interacts with these combinatorial constructions, that will be needed in the proof of Theorem 1.4. In Section 6, we tie up the remaining loose ends and prove that rowvacuation serves as Panyushev’s
$\operatorname {\mathrm {Flip}}$
operator and prove Theorem 1.5 there. Armstrong, Stump and Thomas gave explicit combinatorial descriptions of their bijections in classical types. We review their description in type A in Section 4 and parts of their description in type D in Section 5. These sections also establish some lemmas, concerning how rowvacuation interacts with these combinatorial constructions, that will be needed in the proof of Theorem 1.4. In Section 6, we tie up the remaining loose ends and prove that rowvacuation serves as Panyushev’s
![]() $\mathfrak {P}$
in type D, thus completing the proof of Theorem 1.4.
$\mathfrak {P}$
in type D, thus completing the proof of Theorem 1.4.
2 Posets
2.1 Root posets
We assume the reader is familiar with the basics concerning posets as laid out, for instance, in [Reference Stanley28, Chapter 3]. All posets we consider in this paper are finite, and we drop this adjective from now on. We say a poset P is ranked if there exists a rank function
![]() $\operatorname {\mathrm {rk}}\colon P \to \mathbb {N}$
for which
$\operatorname {\mathrm {rk}}\colon P \to \mathbb {N}$
for which
-
•
 $\operatorname {\mathrm {rk}}(p)=0$
for all minimal elements of P and
$\operatorname {\mathrm {rk}}(p)=0$
for all minimal elements of P and -
•
 $\operatorname {\mathrm {rk}}(y)=\operatorname {\mathrm {rk}}(x)+1$
if
$\operatorname {\mathrm {rk}}(y)=\operatorname {\mathrm {rk}}(x)+1$
if
 $x,y\in P$
are such that
$x,y\in P$
are such that
 $x \lessdot y$
.
$x \lessdot y$
.
A rank function is unique if it exists. The rank
![]() $\operatorname {\mathrm {rk}}(P)$
of a ranked poset P is the maximum value of its rank function. From now on, all posets we consider will be ranked. For
$\operatorname {\mathrm {rk}}(P)$
of a ranked poset P is the maximum value of its rank function. From now on, all posets we consider will be ranked. For
![]() $i\in \mathbb {N}$
, we use the notation
$i\in \mathbb {N}$
, we use the notation
Note that
![]() $P_i$
is empty unless
$P_i$
is empty unless
![]() $0\leq i \leq \operatorname {\mathrm {rk}}(P)$
. The nonempty
$0\leq i \leq \operatorname {\mathrm {rk}}(P)$
. The nonempty
![]() $P_i$
are called the ranks of P. We use
$P_i$
are called the ranks of P. We use
![]() $\mathcal {A}(P)$
to denote the set of antichains of P. Evidently,
$\mathcal {A}(P)$
to denote the set of antichains of P. Evidently,
![]() $P_i\in \mathcal {A}(P)$
for all
$P_i\in \mathcal {A}(P)$
for all
![]() $i \in \mathbb {N}$
.
$i \in \mathbb {N}$
.
As in Section 1, let
![]() $\Phi $
be a crystallographic root system in an r-dimensional vector space V with Weyl group
$\Phi $
be a crystallographic root system in an r-dimensional vector space V with Weyl group
![]() $W\subseteq \operatorname {\mathrm {GL}}(V)$
. For basic background on root systems, see, for example, [Reference Bourbaki6]. We assume we have chosen a system of simple roots
$W\subseteq \operatorname {\mathrm {GL}}(V)$
. For basic background on root systems, see, for example, [Reference Bourbaki6]. We assume we have chosen a system of simple roots
![]() $\{\alpha _1,\ldots ,\alpha _r\}$
and hence a corresponding set
$\{\alpha _1,\ldots ,\alpha _r\}$
and hence a corresponding set
![]() $\Phi ^+$
of positive roots (those that are nonnegative linear combinations of the simple roots). The root poset of
$\Phi ^+$
of positive roots (those that are nonnegative linear combinations of the simple roots). The root poset of
![]() $\Phi $
is the partial order on
$\Phi $
is the partial order on
![]() $\Phi ^+$
whereby
$\Phi ^+$
whereby
![]() $\alpha \leq \beta $
if
$\alpha \leq \beta $
if
![]() $\beta -\alpha $
is a nonnegative sum of simple roots. By abuse of notation, we use
$\beta -\alpha $
is a nonnegative sum of simple roots. By abuse of notation, we use
![]() $\Phi ^+$
to denote the root poset; if
$\Phi ^+$
to denote the root poset; if
![]() $\Phi $
has type X, we also use
$\Phi $
has type X, we also use
![]() $\Phi ^+(X)$
to denote this poset. The root poset is ranked, with the rank function being
$\Phi ^+(X)$
to denote this poset. The root poset is ranked, with the rank function being
![]() $\operatorname {\mathrm {rk}}(\alpha )=\operatorname {\mathrm {ht}}(\alpha )-1$
, where the height of a positive root
$\operatorname {\mathrm {rk}}(\alpha )=\operatorname {\mathrm {ht}}(\alpha )-1$
, where the height of a positive root
![]() $\alpha = \sum _{i}a_i\alpha _i \in \Phi ^+$
is
$\alpha = \sum _{i}a_i\alpha _i \in \Phi ^+$
is
![]() $\operatorname {\mathrm {ht}}(\alpha ):= \sum _{i}a_i$
. The minimal elements of
$\operatorname {\mathrm {ht}}(\alpha ):= \sum _{i}a_i$
. The minimal elements of
![]() $\Phi ^+$
are the simple roots. If
$\Phi ^+$
are the simple roots. If
![]() $\Phi $
is irreducible, then it has a unique maximal element called the highest root. Again, if
$\Phi $
is irreducible, then it has a unique maximal element called the highest root. Again, if
![]() $\Phi $
is irreducible, then the rank of
$\Phi $
is irreducible, then the rank of
![]() $\Phi ^+$
is
$\Phi ^+$
is
![]() $\operatorname {\mathrm {rk}}(\Phi ^+)=h-2$
, where we recall that h denotes the Coxeter number of W. (In fact, all the degrees of W can similarly be read off from the sizes of ranks of
$\operatorname {\mathrm {rk}}(\Phi ^+)=h-2$
, where we recall that h denotes the Coxeter number of W. (In fact, all the degrees of W can similarly be read off from the sizes of ranks of
![]() $\Phi ^+$
.) The poset
$\Phi ^+$
.) The poset
![]() $\Phi ^+$
has a canonical involutive automorphism
$\Phi ^+$
has a canonical involutive automorphism
![]() $\alpha \mapsto -w_0(\alpha )$
, where
$\alpha \mapsto -w_0(\alpha )$
, where
![]() $w_0\in W$
is the longest element.
$w_0\in W$
is the longest element.
As discussed in Section 1, we call the antichains of
![]() $\Phi ^+$
the W-nonnesting partitions. This name is due to Postnikov, who first suggested studying them as Catalan objects (see [Reference Reiner25, Remark 2]). In Section 1 we denoted this set of antichains by
$\Phi ^+$
the W-nonnesting partitions. This name is due to Postnikov, who first suggested studying them as Catalan objects (see [Reference Reiner25, Remark 2]). In Section 1 we denoted this set of antichains by
![]() $\operatorname {\mathrm {NN}}(W)$
, but from now on we will use the notation
$\operatorname {\mathrm {NN}}(W)$
, but from now on we will use the notation
![]() $\mathcal {A}(\Phi ^+)$
.
$\mathcal {A}(\Phi ^+)$
.
We now describe specific realisations of the root posets of classical-type root systems. In anticipation of our detailed analysis of these posets, we will also highlight connections between them and define some subsets
![]() $\mathcal {L},\mathcal {S} \subseteq \Phi ^+$
of particular interest. We use the standard notation
$\mathcal {L},\mathcal {S} \subseteq \Phi ^+$
of particular interest. We use the standard notation
![]() $[i,j] := \{i,i+1,\ldots ,j\}$
for intervals, and we also use
$[i,j] := \{i,i+1,\ldots ,j\}$
for intervals, and we also use
![]() $[n]:= [1,n]$
and
$[n]:= [1,n]$
and
![]() $-[n]:= [-n,-1]$
. For
$-[n]:= [-n,-1]$
. For
![]() $1\leq i \leq n$
, let
$1\leq i \leq n$
, let
![]() $e_i$
denote the ith standard basis vector in
$e_i$
denote the ith standard basis vector in
![]() $\mathbb R^n$
.
$\mathbb R^n$
.
The elements of the root poset
![]() $\Phi ^+(A_{n-1})$
are
$\Phi ^+(A_{n-1})$
are
![]() $e_i-e_j$
for
$e_i-e_j$
for
![]() $1\leq i < j \leq n$
. The simple roots
$1\leq i < j \leq n$
. The simple roots
![]() $\alpha _1,\ldots ,\alpha _{n-1}$
are
$\alpha _1,\ldots ,\alpha _{n-1}$
are
![]() $\alpha _i=e_i-e_{i+1}$
. We identify
$\alpha _i=e_i-e_{i+1}$
. We identify
![]() $\Phi ^+(A_{n-1})$
with the set of intervals
$\Phi ^+(A_{n-1})$
with the set of intervals
![]() $\{[i,j]\subseteq [n]\colon 1 \leq i < j \leq n\}$
ordered by containment, where the root
$\{[i,j]\subseteq [n]\colon 1 \leq i < j \leq n\}$
ordered by containment, where the root
![]() $e_i-e_j$
corresponds to the interval
$e_i-e_j$
corresponds to the interval
![]() $[i,j]$
. Figure 1 presents the Hasse diagram of
$[i,j]$
. Figure 1 presents the Hasse diagram of
![]() $\Phi ^+(A_9)$
. The poset
$\Phi ^+(A_9)$
. The poset
![]() $\Phi ^+(A_{n-1})$
has an involutive automorphism
$\Phi ^+(A_{n-1})$
has an involutive automorphism
![]() $\eta :\Phi ^+(A_{n-1})\to \Phi ^+(A_{n-1})$
given by
$\eta :\Phi ^+(A_{n-1})\to \Phi ^+(A_{n-1})$
given by
![]() $\eta ([i,j])=[n+1-j,n+1-i]$
, which, simply put, is reflection of the Hasse diagram across the central vertical axis. In fact,
$\eta ([i,j])=[n+1-j,n+1-i]$
, which, simply put, is reflection of the Hasse diagram across the central vertical axis. In fact,
![]() $\eta =-w_0$
. We denote the set of elements of
$\eta =-w_0$
. We denote the set of elements of
![]() $\Phi ^+(A_{n-1})$
that are fixed by
$\Phi ^+(A_{n-1})$
that are fixed by
![]() $\eta $
by
$\eta $
by
![]() $\mathcal L_{A_{n-1}}:= \{[i,n+1-i]\colon 1\leq i\leq \left \lfloor n/2\right \rfloor \}$
.
$\mathcal L_{A_{n-1}}:= \{[i,n+1-i]\colon 1\leq i\leq \left \lfloor n/2\right \rfloor \}$
.

Figure 1 The root poset
![]() $\Phi ^+(A_9)$
. The minimal elements are the simple roots, which can be identified with the intervals
$\Phi ^+(A_9)$
. The minimal elements are the simple roots, which can be identified with the intervals
![]() $[1,2],[2,3],\ldots ,[9,10]$
(ordered as they appear from left to right in the Hasse diagram). The set
$[1,2],[2,3],\ldots ,[9,10]$
(ordered as they appear from left to right in the Hasse diagram). The set
![]() $\mathcal L_{A_{9}}$
consists of the five elements circled in blue. The set
$\mathcal L_{A_{9}}$
consists of the five elements circled in blue. The set
![]() $\mathcal {S}_{A_{9}}$
consists of the nine elements circled in red.
$\mathcal {S}_{A_{9}}$
consists of the nine elements circled in red.
The root posets of types B and C are isomorphic, so we will focus our attention on type C. The elements of
![]() $\Phi ^+(C_n)$
are
$\Phi ^+(C_n)$
are
![]() $e_i\pm e_j$
for
$e_i\pm e_j$
for
![]() $1\leq i<j\leq n$
, together with
$1\leq i<j\leq n$
, together with
![]() $2e_i$
for
$2e_i$
for
![]() $1\leq i \leq n$
. The simple roots
$1\leq i \leq n$
. The simple roots
![]() $\alpha _1,\ldots ,\alpha _n$
are
$\alpha _1,\ldots ,\alpha _n$
are
 $$ \begin{align*} \alpha_i = \begin{cases} e_i - e_{i+1} &\text{if } 1\leq i \leq n-1, \\ 2e_n &\text{if } i=n.\end{cases} \end{align*} $$
$$ \begin{align*} \alpha_i = \begin{cases} e_i - e_{i+1} &\text{if } 1\leq i \leq n-1, \\ 2e_n &\text{if } i=n.\end{cases} \end{align*} $$
The poset
![]() $\Phi ^+(C_n)$
can be realised as the quotient of
$\Phi ^+(C_n)$
can be realised as the quotient of
![]() $\Phi ^+(A_{2n-1})$
by the action of
$\Phi ^+(A_{2n-1})$
by the action of
![]() $\eta $
. In other words, the Hasse diagram of
$\eta $
. In other words, the Hasse diagram of
![]() $\Phi ^+(C_n)$
is obtained by ‘folding’
$\Phi ^+(C_n)$
is obtained by ‘folding’
![]() $\Phi ^+(A_{2n-1})$
along its central vertical axis. Figure 2 presents the Hasse diagram of
$\Phi ^+(A_{2n-1})$
along its central vertical axis. Figure 2 presents the Hasse diagram of
![]() $\Phi ^+(C_5)$
. There is a natural injection
$\Phi ^+(C_5)$
. There is a natural injection
![]() $\iota \colon \mathcal P(\Phi ^+(C_n))\to \mathcal P(\Phi ^+(A_{2n-1}))$
obtained by ‘unfolding,’ where
$\iota \colon \mathcal P(\Phi ^+(C_n))\to \mathcal P(\Phi ^+(A_{2n-1}))$
obtained by ‘unfolding,’ where
![]() $\mathcal {P}(X)$
denotes the power set of X. Thus, the image of
$\mathcal {P}(X)$
denotes the power set of X. Thus, the image of
![]() $\iota $
is the collection of subsets of
$\iota $
is the collection of subsets of
![]() $\Phi ^+(A_{2n-1})$
that are symmetric about the central vertical axis. We denote by
$\Phi ^+(A_{2n-1})$
that are symmetric about the central vertical axis. We denote by
![]() $\mathcal L_{C_n}$
the set of long roots in
$\mathcal L_{C_n}$
the set of long roots in
![]() $\Phi ^+(C_n)$
, which correspond to the singleton
$\Phi ^+(C_n)$
, which correspond to the singleton
![]() $\eta $
-orbits in
$\eta $
-orbits in
![]() $\Phi ^+(A_{2n-1})$
(i.e., the elements lying on the ‘crease of the fold’). Equivalently, we have
$\Phi ^+(A_{2n-1})$
(i.e., the elements lying on the ‘crease of the fold’). Equivalently, we have
![]() $\mathcal L_{C_n}=\iota ^{-1}\left (\mathcal L_{A_{2n-1}}\right )$
.
$\mathcal L_{C_n}=\iota ^{-1}\left (\mathcal L_{A_{2n-1}}\right )$
.

Figure 2 The root poset
![]() $\Phi ^+(C_5)$
. The set
$\Phi ^+(C_5)$
. The set
![]() $\mathcal L_{C_5}$
consists of the five elements circled in blue. The set
$\mathcal L_{C_5}$
consists of the five elements circled in blue. The set
![]() $\mathcal {S}_{C_5}$
consists of the five elements circled in red.
$\mathcal {S}_{C_5}$
consists of the five elements circled in red.
The elements of the root poset
![]() $\Phi ^+(D_n)$
are
$\Phi ^+(D_n)$
are
![]() $e_i\pm e_j$
for
$e_i\pm e_j$
for
![]() $1\leq i<j\leq n$
. The simple roots
$1\leq i<j\leq n$
. The simple roots
![]() $\alpha _1,\ldots ,\alpha _n$
are
$\alpha _1,\ldots ,\alpha _n$
are
 $$ \begin{align*} \alpha_i = \begin{cases} e_i - e_{i+1} &\text{if } 1\leq i \leq n-1, \\ e_{n-1}+e_n &\text{if } i=n.\end{cases} \end{align*} $$
$$ \begin{align*} \alpha_i = \begin{cases} e_i - e_{i+1} &\text{if } 1\leq i \leq n-1, \\ e_{n-1}+e_n &\text{if } i=n.\end{cases} \end{align*} $$
See Figure 3 for a depiction of
![]() $\Phi ^+(D_6)$
. There is an involutive automorphism
$\Phi ^+(D_6)$
. There is an involutive automorphism
![]() $\delta $
of the Dynkin diagram of
$\delta $
of the Dynkin diagram of
![]() $\Phi (D_n)$
that swaps the nodes
$\Phi (D_n)$
that swaps the nodes
![]() $n-1$
and n. This induces an automorphism of the poset
$n-1$
and n. This induces an automorphism of the poset
![]() $\Phi ^+(D_n)$
that swaps every occurrence of
$\Phi ^+(D_n)$
that swaps every occurrence of
![]() $\alpha _{n-1}$
appearing in an expansion of a root with
$\alpha _{n-1}$
appearing in an expansion of a root with
![]() $\alpha _n$
and vice versa; we also denote this automorphism by
$\alpha _n$
and vice versa; we also denote this automorphism by
![]() $\delta \colon \Phi ^+(D_n) \to \Phi ^+(D_n)$
. We have
$\delta \colon \Phi ^+(D_n) \to \Phi ^+(D_n)$
. We have
![]() $\delta (e_i-e_n)=e_i+e_n$
and
$\delta (e_i-e_n)=e_i+e_n$
and
![]() $\delta (e_i+e_n)=e_i-e_n$
for each
$\delta (e_i+e_n)=e_i-e_n$
for each
![]() $1\leq i\leq n-1$
; all of the other positive roots are fixed by
$1\leq i\leq n-1$
; all of the other positive roots are fixed by
![]() $\delta $
. (Note that
$\delta $
. (Note that
![]() $\delta =-w_0$
when n is odd; but
$\delta =-w_0$
when n is odd; but
![]() $-w_0$
, unlike
$-w_0$
, unlike
![]() $\delta $
, is trivial when n is even.) In Figure 3, the roots of the form
$\delta $
, is trivial when n is even.) In Figure 3, the roots of the form
![]() $e_i+e_6$
are coloured white. Furthermore, for each
$e_i+e_6$
are coloured white. Furthermore, for each
![]() $1\leq i\leq 5$
, we draw the root
$1\leq i\leq 5$
, we draw the root
![]() $e_i-e_6$
immediately to the right of
$e_i-e_6$
immediately to the right of
![]() $e_i+e_6$
in the figure. There is a natural bijection between the
$e_i+e_6$
in the figure. There is a natural bijection between the
![]() $\delta $
-orbits in
$\delta $
-orbits in
![]() $\Phi ^+(D_n)$
and the elements of
$\Phi ^+(D_n)$
and the elements of
![]() $\Phi ^+(C_{n-1})$
, yielding the quotient map
$\Phi ^+(C_{n-1})$
, yielding the quotient map
![]() $\gamma :\Phi ^+(D_n)\to \Phi ^+(C_{n-1})$
. Referring to Figure 3 again, we see that
$\gamma :\Phi ^+(D_n)\to \Phi ^+(C_{n-1})$
. Referring to Figure 3 again, we see that
![]() $\gamma $
essentially ‘glues’ each white element to the black element drawn immediately to the right of it. Let us define
$\gamma $
essentially ‘glues’ each white element to the black element drawn immediately to the right of it. Let us define
![]() $\mathcal L_{D_n}:=\gamma ^{-1}\left (\mathcal L_{C_{n-1}}\right )$
.
$\mathcal L_{D_n}:=\gamma ^{-1}\left (\mathcal L_{C_{n-1}}\right )$
.

Figure 3 The root poset
![]() $\Phi ^+(D_6)$
. The set
$\Phi ^+(D_6)$
. The set
![]() $\mathcal L_{D_6}$
consists of the six elements circled in blue. The set
$\mathcal L_{D_6}$
consists of the six elements circled in blue. The set
![]() $\mathcal {S}_{D_6}$
consists of the
$\mathcal {S}_{D_6}$
consists of the
![]() $10$
elements circled in red.
$10$
elements circled in red.
We define
![]() $\mathcal {S}_{C_n}\subseteq \Phi ^+(C_n)$
to be the set of elements
$\mathcal {S}_{C_n}\subseteq \Phi ^+(C_n)$
to be the set of elements
![]() $\alpha \in \Phi ^+(C_n)$
for which
$\alpha \in \Phi ^+(C_n)$
for which
![]() $\gamma ^{-1}(\alpha )$
consists of two elements; all other
$\gamma ^{-1}(\alpha )$
consists of two elements; all other
![]() $\alpha \in \Phi ^+(C_n)$
have
$\alpha \in \Phi ^+(C_n)$
have
![]() $\#\gamma ^{-1}(\alpha )=1$
. (Under the isomorphism
$\#\gamma ^{-1}(\alpha )=1$
. (Under the isomorphism
![]() $\Phi ^+(C_n)\simeq \Phi ^+(B_n)$
,
$\Phi ^+(C_n)\simeq \Phi ^+(B_n)$
,
![]() $\mathcal {S}_{C_n}$
consists of the short roots in
$\mathcal {S}_{C_n}$
consists of the short roots in
![]() $\Phi ^+(B_n)$
.) We also define
$\Phi ^+(B_n)$
.) We also define
![]() $\mathcal {S}_{A_{2n-1}}\subseteq \Phi ^+(A_{2n-1})$
to be
$\mathcal {S}_{A_{2n-1}}\subseteq \Phi ^+(A_{2n-1})$
to be
![]() $\iota \left (\mathcal {S}_{C_n}\right )$
, and
$\iota \left (\mathcal {S}_{C_n}\right )$
, and
![]() $\mathcal {S}_{D_n}\subseteq \Phi ^+(D_n)$
to be
$\mathcal {S}_{D_n}\subseteq \Phi ^+(D_n)$
to be
![]() $\gamma ^{-1}\left (\mathcal {S}_{C_{n-1}}\right )$
. Equivalently,
$\gamma ^{-1}\left (\mathcal {S}_{C_{n-1}}\right )$
. Equivalently,
![]() $\mathcal {S}_{A_{2n-1}}$
consists of those
$\mathcal {S}_{A_{2n-1}}$
consists of those
![]() $[i,j] \in \Phi ^+(A_{2n-1})$
for which either
$[i,j] \in \Phi ^+(A_{2n-1})$
for which either
![]() $i=n$
or
$i=n$
or
![]() $j=n+1$
. These subsets
$j=n+1$
. These subsets
![]() $\mathcal {S}$
are also depicted in Figures 1 to 3.
$\mathcal {S}$
are also depicted in Figures 1 to 3.
Remark 2.1. The processes of obtaining
![]() $\Phi ^+(B_n)$
(
$\Phi ^+(B_n)$
(
![]() $\simeq \Phi ^+(C_n)$
) as a quotient of
$\simeq \Phi ^+(C_n)$
) as a quotient of
![]() $\Phi ^+(A_n)$
and of obtaining
$\Phi ^+(A_n)$
and of obtaining
![]() $\Phi ^+(C_n)$
as a quotient of
$\Phi ^+(C_n)$
as a quotient of
![]() $\Phi ^+(D_n)$
are special cases of a more general procedure from the theory of root systems referred to as folding. Given a simply laced root system
$\Phi ^+(D_n)$
are special cases of a more general procedure from the theory of root systems referred to as folding. Given a simply laced root system
![]() $\Phi $
and an automorphism
$\Phi $
and an automorphism
![]() $\sigma $
of the Dynkin diagram of
$\sigma $
of the Dynkin diagram of
![]() $\Phi $
(subject to a certain technical condition), folding produces a new root system
$\Phi $
(subject to a certain technical condition), folding produces a new root system
![]() $\Phi ^{\sigma }$
whose roots correspond to
$\Phi ^{\sigma }$
whose roots correspond to
![]() $\sigma $
-orbits. Since we only need the cases of folding we have already described explicitly, we will not give a precise account of folding here; see [Reference Stembridge29] for such an account. We also warn that while the symbols
$\sigma $
-orbits. Since we only need the cases of folding we have already described explicitly, we will not give a precise account of folding here; see [Reference Stembridge29] for such an account. We also warn that while the symbols
![]() $\mathcal {L}$
and
$\mathcal {L}$
and
![]() $\mathcal {S}$
were chosen to evoke the words ‘long’ and ‘short,’ the simply laced types A and D of course do not have roots of different lengths, so this notation is just meant to be suggestive.
$\mathcal {S}$
were chosen to evoke the words ‘long’ and ‘short,’ the simply laced types A and D of course do not have roots of different lengths, so this notation is just meant to be suggestive.
2.2 Rowmotion and rowvacuation
Now we review the rowmotion and rowvacuation operators acting on the antichains of a ranked poset P.Footnote 4
Rowmotion,
![]() $\operatorname {\mathrm {Row}} \colon \mathcal {A}(P)\to \mathcal {A}(P)$
, is given by
$\operatorname {\mathrm {Row}} \colon \mathcal {A}(P)\to \mathcal {A}(P)$
, is given by
for all
![]() $A\in \mathcal {A}(P)$
, where
$A\in \mathcal {A}(P)$
, where
![]() $\min (X)$
means the set of minimal elements of a subset
$\min (X)$
means the set of minimal elements of a subset
![]() $X\subseteq P$
. Rowmotion is a bijection. Before Panyushev [Reference Panyushev21], rowmotion was studied by Brouwer and Schrijver [Reference Brouwer and Schrijver9] and Cameron and Fon-der-Flaass [Reference Cameron and Fon-Der-Flaass10], among others.
$X\subseteq P$
. Rowmotion is a bijection. Before Panyushev [Reference Panyushev21], rowmotion was studied by Brouwer and Schrijver [Reference Brouwer and Schrijver9] and Cameron and Fon-der-Flaass [Reference Cameron and Fon-Der-Flaass10], among others.
Example 2.2. The two orbits of rowmotion on
![]() $\mathcal {A}(\Phi ^+(A_2))$
are as follows:
$\mathcal {A}(\Phi ^+(A_2))$
are as follows:

The elements of each antichain are depicted with red squares. Observe that
![]() $\operatorname {\mathrm {Row}} ^3=\eta $
, and the average of
$\operatorname {\mathrm {Row}} ^3=\eta $
, and the average of
![]() $\#A$
along any
$\#A$
along any
![]() $\operatorname {\mathrm {Row}} $
-orbit is
$\operatorname {\mathrm {Row}} $
-orbit is
![]() $1$
.
$1$
.
As discussed in Section 1, Armstrong, Stump and Thomas [Reference Armstrong, Stump and Thomas2] proved the following conjecture of Panyushev concerning rowmotion of nonnesting partitions:
Theorem 2.3 Armstrong–Stump–Thomas [Reference Armstrong, Stump and Thomas2, Theorem 1.2]
For rowmotion of nonnesting partitions
![]() $\operatorname {\mathrm {Row}} \colon \mathcal {A}(\Phi ^+)\to \mathcal {A}(\Phi ^+)$
, we have the following:
$\operatorname {\mathrm {Row}} \colon \mathcal {A}(\Phi ^+)\to \mathcal {A}(\Phi ^+)$
, we have the following:
-
•
 $\operatorname {\mathrm {Row}} ^{2h}$
is the identity (and
$\operatorname {\mathrm {Row}} ^{2h}$
is the identity (and
 $\operatorname {\mathrm {Row}} ^h=-w_0$
if
$\operatorname {\mathrm {Row}} ^h=-w_0$
if
 $\Phi $
is irreducible) and
$\Phi $
is irreducible) and -
•
 $\frac {1}{\#O} \sum _{A \in O} \#A = \frac {r}{2}$
for any
$\frac {1}{\#O} \sum _{A \in O} \#A = \frac {r}{2}$
for any
 $\operatorname {\mathrm {Row}} $
-orbit
$\operatorname {\mathrm {Row}} $
-orbit
 $O\subseteq \mathcal {A}(\Phi ^+)$
.
$O\subseteq \mathcal {A}(\Phi ^+)$
.
As shown by Cameron and Fon-der-Flaass [Reference Cameron and Fon-Der-Flaass10], and further emphasised by Striker and Williams [Reference Striker and Williams32], there is an alternate way to describe rowmotion as a composition of certain local involutions called toggles. However, in [Reference Cameron and Fon-Der-Flaass10, Reference Striker and Williams32], the order ideal variant of rowmotion and toggles are considered. We prefer to stick to antichains, and hence will focus on a description due to Joseph [Reference Joseph19] of rowmotion as a composition of antichain toggles. For
![]() $p\in P$
, define the toggle at p,
$p\in P$
, define the toggle at p,
![]() $\tau _p\colon \mathcal {A}(P)\to \mathcal {A}(P)$
, to be the involution
$\tau _p\colon \mathcal {A}(P)\to \mathcal {A}(P)$
, to be the involution
 $$ \begin{align*} \tau_p(A):= \begin{cases} A\setminus \{p\} &\text{if } p\in A, \\ A\cup \{p\} &\text{if } p \notin A \text{ and } A\cup \{p\} \in \mathcal{A}(P),\\ A &\text{otherwise}.\end{cases} \end{align*} $$
$$ \begin{align*} \tau_p(A):= \begin{cases} A\setminus \{p\} &\text{if } p\in A, \\ A\cup \{p\} &\text{if } p \notin A \text{ and } A\cup \{p\} \in \mathcal{A}(P),\\ A &\text{otherwise}.\end{cases} \end{align*} $$
Let us emphasise that these antichain toggles are not the same as order ideal toggles. Also, if
![]() $p,p'\in P$
are incomparable, then the toggles
$p,p'\in P$
are incomparable, then the toggles
![]() $\tau _p$
and
$\tau _p$
and
![]() $\tau _{p'}$
commute.
$\tau _{p'}$
commute.
Proposition 2.4. Joseph [Reference Joseph19, Proposition 2.24]
![]() $\operatorname {\mathrm {Row}} =\tau _{p_n} \tau _{p_{n-1}}\cdots \tau _{p_1}$
for any linear extension
$\operatorname {\mathrm {Row}} =\tau _{p_n} \tau _{p_{n-1}}\cdots \tau _{p_1}$
for any linear extension
![]() $p_1,p_2,\ldots ,p_n$
of P.
$p_1,p_2,\ldots ,p_n$
of P.
Next we define rowvacuation, which, unlike rowmotion, requires our poset to be ranked. For
![]() $i=0,1,\ldots ,\operatorname {\mathrm {rk}}(P)$
, we define the rank toggle
$i=0,1,\ldots ,\operatorname {\mathrm {rk}}(P)$
, we define the rank toggle
![]() $\boldsymbol {\tau }_i\colon \mathcal {A}(P)\to \mathcal {A}(P)$
to be
$\boldsymbol {\tau }_i\colon \mathcal {A}(P)\to \mathcal {A}(P)$
to be
![]() $\boldsymbol {\tau }_i := \prod _{p \in P_i} \tau _p$
. All the toggles
$\boldsymbol {\tau }_i := \prod _{p \in P_i} \tau _p$
. All the toggles
![]() $\tau _p$
for
$\tau _p$
for
![]() $p\in P_i$
commute, so this product makes sense. Evidently,
$p\in P_i$
commute, so this product makes sense. Evidently,
Rowvacuation,
![]() $\operatorname {\mathrm {Rvac}}\colon \mathcal {A}(P) \to \mathcal {A}(P)$
, is a different product of these rank toggles:
$\operatorname {\mathrm {Rvac}}\colon \mathcal {A}(P) \to \mathcal {A}(P)$
, is a different product of these rank toggles:
We write
![]() $\operatorname {\mathrm {Row}}_P$
and
$\operatorname {\mathrm {Row}}_P$
and
![]() $\operatorname {\mathrm {Rvac}}_P$
when we wish to emphasise the underlying poset P; this will be useful when we consider multiple posets at once.
$\operatorname {\mathrm {Rvac}}_P$
when we wish to emphasise the underlying poset P; this will be useful when we consider multiple posets at once.
Example 2.5. We show how to compute
![]() $\operatorname {\mathrm {Rvac}}(A)$
for one particular antichain
$\operatorname {\mathrm {Rvac}}(A)$
for one particular antichain
![]() $A\in \mathcal {A}(\Phi ^+(D_4))$
:
$A\in \mathcal {A}(\Phi ^+(D_4))$
:

Observe that
![]() $\#A+\#\operatorname {\mathrm {Rvac}}(A)=2+2=4$
.
$\#A+\#\operatorname {\mathrm {Rvac}}(A)=2+2=4$
.
Rowvacuation was first formally defined, briefly, in [Reference Hopkins17, §5.1] and was further studied in [Reference Hopkins and Joseph18]. As mentioned in Section 1, rowmotion and rowvacuation are ‘partner’ operators in exactly the same way that Schützenberger’s promotion and evacuation operators are. For instance, together they always generate a dihedral group action:
Proposition 2.6 [Reference Hopkins17, Proposition 5.1], [Reference Hopkins and Joseph18, Proposition 2.18]
For any P:
-
•
 $\operatorname {\mathrm {Rvac}}$
is an involution and
$\operatorname {\mathrm {Rvac}}$
is an involution and -
•
 $\operatorname {\mathrm {Rvac}}\cdot \operatorname {\mathrm {Row}}= \operatorname {\mathrm {Row}}^{-1} \cdot \operatorname {\mathrm {Rvac}}$
.
$\operatorname {\mathrm {Rvac}}\cdot \operatorname {\mathrm {Row}}= \operatorname {\mathrm {Row}}^{-1} \cdot \operatorname {\mathrm {Rvac}}$
.
In general, it seems hard to ‘describe’ the rowvacuation of an antichain. But in [Reference Hopkins and Joseph18], the second author and Joseph showed that rowvacuation acting on a root poset of type A can be computed as follows:
Theorem 2.7 Hopkins–Joseph [Reference Hopkins and Joseph18, Theorem 3.5]
Set
![]() $A\in \mathcal {A}(\Phi ^+(A_{n-1}))$
. Note that A is of the form
$A\in \mathcal {A}(\Phi ^+(A_{n-1}))$
. Note that A is of the form
![]() $A=\{[i_1,j_1],\ldots ,[i_k,j_k]\}$
with
$A=\{[i_1,j_1],\ldots ,[i_k,j_k]\}$
with
![]() $i_1 < i_2 < \cdots < i_k$
and
$i_1 < i_2 < \cdots < i_k$
and
![]() $j_1 < j_2 < \cdots < j_k$
. Then
$j_1 < j_2 < \cdots < j_k$
. Then
 $$ \begin{align*} \operatorname{\mathrm{Rvac}}(A) = \left\{ \left[i'_1,j'_1\right],\ldots, \left[i'_{n-1-k},j'_{n-1-k}\right]\right\}, \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Rvac}}(A) = \left\{ \left[i'_1,j'_1\right],\ldots, \left[i'_{n-1-k},j'_{n-1-k}\right]\right\}, \end{align*} $$
where
 $$\begin{align*} \phantom{the eq}\left\{i'_1 < i'_2 < \cdots < i'_{n-1-k}\right\} &:= \{1,2,\ldots,n-1\}\setminus \{j_1-1,j_2-1,\ldots,j_k-1\}, \end{align*}$$
$$\begin{align*} \phantom{the eq}\left\{i'_1 < i'_2 < \cdots < i'_{n-1-k}\right\} &:= \{1,2,\ldots,n-1\}\setminus \{j_1-1,j_2-1,\ldots,j_k-1\}, \end{align*}$$
 $$\begin{align*} \left\{j'_1 < j'_2 < \cdots < j'_{n-1-k}\right\} &:= \{2,3,\ldots,n\}\setminus \{i_1+1,i_2+1,\ldots,i_k+1\}. \end{align*}$$
$$\begin{align*} \left\{j'_1 < j'_2 < \cdots < j'_{n-1-k}\right\} &:= \{2,3,\ldots,n\}\setminus \{i_1+1,i_2+1,\ldots,i_k+1\}. \end{align*}$$
The formula in Theorem 2.7 immediately gives
![]() $\#A+\#\operatorname {\mathrm {Rvac}}(A)=n-1$
. As explained in [Reference Hopkins and Joseph18, §1], this formula is equivalent to the Lalanne–Kreweras involution on Dyck paths via a simple bijection between the antichains in
$\#A+\#\operatorname {\mathrm {Rvac}}(A)=n-1$
. As explained in [Reference Hopkins and Joseph18, §1], this formula is equivalent to the Lalanne–Kreweras involution on Dyck paths via a simple bijection between the antichains in
![]() $\mathcal {A}(\Phi ^+(A_{n-1}))$
and the Dyck paths of length
$\mathcal {A}(\Phi ^+(A_{n-1}))$
and the Dyck paths of length
![]() $2n$
. Rowvacuation clearly commutes with any poset automorphism. Therefore, by embedding
$2n$
. Rowvacuation clearly commutes with any poset automorphism. Therefore, by embedding
![]() $\mathcal {A}(\Phi ^+(C_n))$
into
$\mathcal {A}(\Phi ^+(C_n))$
into
![]() $\mathcal {A}(\Phi ^+(A_{2n-1}))$
via
$\mathcal {A}(\Phi ^+(A_{2n-1}))$
via
![]() $\iota $
, Theorem 2.7 also yields a simple description of rowvacuation acting on
$\iota $
, Theorem 2.7 also yields a simple description of rowvacuation acting on
![]() $\mathcal {A}(\Phi ^+(C_n))$
.
$\mathcal {A}(\Phi ^+(C_n))$
.
Example 2.8. If
![]() $A=\{[1,3]\}\in \mathcal {A}(\Phi ^+(A_3))$
, then
$A=\{[1,3]\}\in \mathcal {A}(\Phi ^+(A_3))$
, then
![]() $\operatorname {\mathrm {Rvac}}(A)=\{[1,3],[3,4]\}$
:
$\operatorname {\mathrm {Rvac}}(A)=\{[1,3],[3,4]\}$
:

The reader may check that this agrees with Theorem 2.7.
Before we move on to discuss Panyushev’s conjectured duality for root poset antichains, let us prove a few more general properties of rowvacuation that will show that it is a good candidate for this duality.
Proposition 2.9. We have
![]() $\operatorname {\mathrm {Rvac}}(P_i)=P_{\operatorname {\mathrm {rk}}(P)+1-i}$
for any
$\operatorname {\mathrm {Rvac}}(P_i)=P_{\operatorname {\mathrm {rk}}(P)+1-i}$
for any
![]() $i=0,1,\ldots ,\operatorname {\mathrm {rk}}(P)+1$
.
$i=0,1,\ldots ,\operatorname {\mathrm {rk}}(P)+1$
.
Proof. Define
![]() $d_k := \left (\boldsymbol {\tau }_{\operatorname {\mathrm {rk}}(P)} \boldsymbol {\tau }_{\operatorname {\mathrm {rk}}(P)-1} \cdots \boldsymbol {\tau }_k\right )$
for
$d_k := \left (\boldsymbol {\tau }_{\operatorname {\mathrm {rk}}(P)} \boldsymbol {\tau }_{\operatorname {\mathrm {rk}}(P)-1} \cdots \boldsymbol {\tau }_k\right )$
for
![]() $k=0,\ldots ,\operatorname {\mathrm {rk}}(P)$
, so that
$k=0,\ldots ,\operatorname {\mathrm {rk}}(P)$
, so that
It is easy to see that for
![]() $i=0,\ldots ,\operatorname {\mathrm {rk}}(P)+1$
,
$i=0,\ldots ,\operatorname {\mathrm {rk}}(P)+1$
,
 $$ \begin{align*} d_k (P_i) = \begin{cases} P_{k} &\text{if } i=\operatorname{\mathrm{rk}}(P)+1, \\ P_{i+1} &\text{if } k\leq i\leq \operatorname{\mathrm{rk}}(P), \\ P_i &\text{otherwise}. \end{cases} \end{align*} $$
$$ \begin{align*} d_k (P_i) = \begin{cases} P_{k} &\text{if } i=\operatorname{\mathrm{rk}}(P)+1, \\ P_{i+1} &\text{if } k\leq i\leq \operatorname{\mathrm{rk}}(P), \\ P_i &\text{otherwise}. \end{cases} \end{align*} $$
Therefore,
 $$ \begin{align*} \operatorname{\mathrm{Rvac}}(P_i) &= d_{\operatorname{\mathrm{rk}}(P)} d_{\operatorname{\mathrm{rk}}(P)-1} \cdots d_1 d_0(P_i) \\ &= d_{\operatorname{\mathrm{rk}}(P)} d_{\operatorname{\mathrm{rk}}(P)-1} \cdots d_{\operatorname{\mathrm{rk}}(P)+1-i} \left(P_{\operatorname{\mathrm{rk}}(P)+1}\right) \\ &= d_{\operatorname{\mathrm{rk}}(P)} d_{\operatorname{\mathrm{rk}}(P)-1} \cdots d_{\operatorname{\mathrm{rk}}(P)+2-i} \left(P_{\operatorname{\mathrm{rk}}(P)+1-i}\right) \\ &= P_{\operatorname{\mathrm{rk}}(P)+1-i}, \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Rvac}}(P_i) &= d_{\operatorname{\mathrm{rk}}(P)} d_{\operatorname{\mathrm{rk}}(P)-1} \cdots d_1 d_0(P_i) \\ &= d_{\operatorname{\mathrm{rk}}(P)} d_{\operatorname{\mathrm{rk}}(P)-1} \cdots d_{\operatorname{\mathrm{rk}}(P)+1-i} \left(P_{\operatorname{\mathrm{rk}}(P)+1}\right) \\ &= d_{\operatorname{\mathrm{rk}}(P)} d_{\operatorname{\mathrm{rk}}(P)-1} \cdots d_{\operatorname{\mathrm{rk}}(P)+2-i} \left(P_{\operatorname{\mathrm{rk}}(P)+1-i}\right) \\ &= P_{\operatorname{\mathrm{rk}}(P)+1-i}, \end{align*} $$
as claimed.
Proposition 2.10. Let
![]() $p \in P_0$
be a minimal element. Set
$p \in P_0$
be a minimal element. Set
![]() $P' := \left \{q\in P\colon q \not \geq p\right \}$
. Then for any
$P' := \left \{q\in P\colon q \not \geq p\right \}$
. Then for any
![]() $A \in \mathcal {A}(P)$
, we have the following:
$A \in \mathcal {A}(P)$
, we have the following:
-
• if
 $A\subseteq P'$
, then
$A\subseteq P'$
, then
 $\operatorname {\mathrm {Rvac}}(A) = \{p\} \cup \operatorname {\mathrm {Rvac}}_{P'}(A)$
;
$\operatorname {\mathrm {Rvac}}(A) = \{p\} \cup \operatorname {\mathrm {Rvac}}_{P'}(A)$
; -
• if
 $p \in A$
, then
$p \in A$
, then
 $\operatorname {\mathrm {Rvac}}(A) = \operatorname {\mathrm {Rvac}}_{P'}(A\setminus \{p\})$
.
$\operatorname {\mathrm {Rvac}}(A) = \operatorname {\mathrm {Rvac}}_{P'}(A\setminus \{p\})$
.
Proof. Let us prove the first bulleted item. If
![]() $A\subseteq P'$
, then
$A\subseteq P'$
, then
![]() $p \not \in A$
. Hence, when we carry out the rank toggles
$p \not \in A$
. Hence, when we carry out the rank toggles
the application of
![]() $\boldsymbol {\tau }_0$
will add p to A. From then on, no
$\boldsymbol {\tau }_0$
will add p to A. From then on, no
![]() $q \geq p$
can be added to A. Therefore, the effect of carrying out this sequence of rank toggles will be the same as if we carried them out just on
$q \geq p$
can be added to A. Therefore, the effect of carrying out this sequence of rank toggles will be the same as if we carried them out just on
![]() $P'$
, except that we also have to add p. This is exactly what the equality
$P'$
, except that we also have to add p. This is exactly what the equality
![]() $\operatorname {\mathrm {Rvac}}(A) = \{p\} \cup \operatorname {\mathrm {Rvac}}_{P'}(A)$
asserts.
$\operatorname {\mathrm {Rvac}}(A) = \{p\} \cup \operatorname {\mathrm {Rvac}}_{P'}(A)$
asserts.
For the second item: if
![]() $p\in A$
, then A is of the form
$p\in A$
, then A is of the form
![]() $A=\{p\}\cup A'$
for some antichain
$A=\{p\}\cup A'$
for some antichain
![]() $A' \subseteq P'$
. So this item actually follows from the first item and the fact that
$A' \subseteq P'$
. So this item actually follows from the first item and the fact that
![]() $\operatorname {\mathrm {Rvac}}$
is an involution (see Proposition 2.6).
$\operatorname {\mathrm {Rvac}}$
is an involution (see Proposition 2.6).
2.3 Panyushev’s nonnesting-partition duality conjecture
We now give a more precise version of Conjecture 1.2:
Conjecture 2.11 Panyushev [Reference Panyushev21, Conjecture 6.1]
There is an involution on the set of nonnesting partitions
![]() $\mathfrak {P}\colon \mathcal {A}(\Phi ^+)\to \mathcal {A}(\Phi ^+)$
which satisfies the following properties. First of all, if
$\mathfrak {P}\colon \mathcal {A}(\Phi ^+)\to \mathcal {A}(\Phi ^+)$
which satisfies the following properties. First of all, if
![]() $\Phi =\Phi '\sqcup \Phi ''$
is reducible, then
$\Phi =\Phi '\sqcup \Phi ''$
is reducible, then
for all
![]() $A \in \mathcal {A}(\Phi ^+)$
. And if
$A \in \mathcal {A}(\Phi ^+)$
. And if
![]() $\Phi $
is irreducible, then for all
$\Phi $
is irreducible, then for all
![]() $A\in \mathcal {A}(\Phi ^+)$
we have the following:
$A\in \mathcal {A}(\Phi ^+)$
we have the following:
-
(i)
 $\#A+\#\mathfrak {P}(A)=r$
.
$\#A+\#\mathfrak {P}(A)=r$
. -
(ii) The distribution of long and short roots in the multiset union
 $A\cup \mathfrak {P}(A)$
is the same as in the set of simple roots
$A\cup \mathfrak {P}(A)$
is the same as in the set of simple roots
 $\{\alpha _1,\ldots ,\alpha _r\}$
.
$\{\alpha _1,\ldots ,\alpha _r\}$
. -
(iii) If
 $A = \Phi ^+_i$
, then
$A = \Phi ^+_i$
, then
 $\mathfrak {P}(A)=\Phi ^+_{h-1-i}$
for all
$\mathfrak {P}(A)=\Phi ^+_{h-1-i}$
for all
 $i=0,\ldots ,h-1$
.
$i=0,\ldots ,h-1$
. -
(iv) If
 $\alpha \in A$
for a simple root
$\alpha \in A$
for a simple root
 $\alpha $
, then
$\alpha $
, then
 $\mathfrak {P}(A)=\mathfrak {P}_{\Phi '}(A\setminus \{\alpha \})$
, where
$\mathfrak {P}(A)=\mathfrak {P}_{\Phi '}(A\setminus \{\alpha \})$
, where
 $\Phi '\subseteq \Phi $
is the maximal parabolic subroot system of
$\Phi '\subseteq \Phi $
is the maximal parabolic subroot system of
 $\Phi $
obtained by removing
$\Phi $
obtained by removing
 $\alpha $
from the system of simple roots.
$\alpha $
from the system of simple roots. -
(v) If
 $A \subseteq (\Phi ')^+$
, where
$A \subseteq (\Phi ')^+$
, where
 $\Phi '\subseteq \Phi $
is the maximal parabolic subroot system of
$\Phi '\subseteq \Phi $
is the maximal parabolic subroot system of
 $\Phi $
obtained by removing some simple root
$\Phi $
obtained by removing some simple root
 $\alpha $
, then
$\alpha $
, then
 $\mathfrak {P}(A)=\{\alpha \}\cup \mathfrak {P}_{\Phi '}(A)$
.
$\mathfrak {P}(A)=\{\alpha \}\cup \mathfrak {P}_{\Phi '}(A)$
.
Remember that we are trying to show that rowvacuation is Panyushev’s
![]() $\mathfrak {P}$
: Theorem 1.4 asserts that
$\mathfrak {P}$
: Theorem 1.4 asserts that
![]() $\mathfrak {P}=\operatorname {\mathrm {Rvac}}$
for the classical types. So let us check which of the properties in Conjecture 2.11 rowvacuation satisfies.
$\mathfrak {P}=\operatorname {\mathrm {Rvac}}$
for the classical types. So let us check which of the properties in Conjecture 2.11 rowvacuation satisfies.
![]() $\operatorname {\mathrm {Rvac}}$
evidently respects the decomposition of a root system into its irreducible components, which at the level of root posets corresponds to the decomposition into connected posets. Furthermore, property (iii) for
$\operatorname {\mathrm {Rvac}}$
evidently respects the decomposition of a root system into its irreducible components, which at the level of root posets corresponds to the decomposition into connected posets. Furthermore, property (iii) for
![]() $\operatorname {\mathrm {Rvac}}$
is Proposition 2.9, and properties (iv) and (v) are Proposition 2.10. So the only properties that we do not yet know
$\operatorname {\mathrm {Rvac}}$
is Proposition 2.9, and properties (iv) and (v) are Proposition 2.10. So the only properties that we do not yet know
![]() $\operatorname {\mathrm {Rvac}}$
satisfies are (i) and (ii). Of course, (i) is the property we really care about: it says that
$\operatorname {\mathrm {Rvac}}$
satisfies are (i) and (ii). Of course, (i) is the property we really care about: it says that
![]() $\mathfrak {P}$
combinatorially exhibits the symmetry of the W-Narayana numbers.
$\mathfrak {P}$
combinatorially exhibits the symmetry of the W-Narayana numbers.
In [Reference Panyushev21, §4], Panyushev showed that defining
![]() $\mathfrak {P}$
in type
$\mathfrak {P}$
in type
![]() $A_{n-1}$
using the formula in Theorem 2.7 gives an involution satisfying the conditions of Conjecture 2.11. Hence,
$A_{n-1}$
using the formula in Theorem 2.7 gives an involution satisfying the conditions of Conjecture 2.11. Hence,
![]() $\mathfrak {P}=\operatorname {\mathrm {Rvac}}$
for type A. He also showed [Reference Panyushev21, §5.1] that defining
$\mathfrak {P}=\operatorname {\mathrm {Rvac}}$
for type A. He also showed [Reference Panyushev21, §5.1] that defining
![]() $\mathfrak {P}$
for type C by embedding it into the type A root poset via
$\mathfrak {P}$
for type C by embedding it into the type A root poset via
![]() $\iota $
and using the type A definition of
$\iota $
and using the type A definition of
![]() $\mathfrak {P}$
also gives an involution satisfying Conjecture 2.11; so
$\mathfrak {P}$
also gives an involution satisfying Conjecture 2.11; so
![]() $\mathfrak {P}=\operatorname {\mathrm {Rvac}}$
for type C as well. And he showed the same for type B [Reference Panyushev21, §5.2]; thus
$\mathfrak {P}=\operatorname {\mathrm {Rvac}}$
for type C as well. And he showed the same for type B [Reference Panyushev21, §5.2]; thus
![]() $\mathfrak {P}=\operatorname {\mathrm {Rvac}}$
again for type B. Hence, the only remaining case of Theorem 1.4 is type D. As mentioned, only properties (i) and (ii) of Conjecture 2.11 for
$\mathfrak {P}=\operatorname {\mathrm {Rvac}}$
again for type B. Hence, the only remaining case of Theorem 1.4 is type D. As mentioned, only properties (i) and (ii) of Conjecture 2.11 for
![]() $\operatorname {\mathrm {Rvac}}$
are in doubt. In fact, since type D is simply laced, (ii) is vacuous because all roots in the root system have the same length. Consequently, all we have left to show is that
$\operatorname {\mathrm {Rvac}}$
are in doubt. In fact, since type D is simply laced, (ii) is vacuous because all roots in the root system have the same length. Consequently, all we have left to show is that
![]() $\#A+\#\operatorname {\mathrm {Rvac}}(A)=n$
for all
$\#A+\#\operatorname {\mathrm {Rvac}}(A)=n$
for all
![]() $A\in \mathcal {A}(\Phi ^+(D_n))$
.
$A\in \mathcal {A}(\Phi ^+(D_n))$
.
Showing that
![]() $\#A+\#\operatorname {\mathrm {Rvac}}(A)=n$
for all
$\#A+\#\operatorname {\mathrm {Rvac}}(A)=n$
for all
![]() $A\in \mathcal {A}(\Phi ^+(D_n))$
will take up the remainder of the paper and require quite a lot of work. In particular, we will have to use the bijection of Armstrong, Stump and Thomas [Reference Armstrong, Stump and Thomas2] between nonnesting and noncrossing partitions, which we discuss in the next section.
$A\in \mathcal {A}(\Phi ^+(D_n))$
will take up the remainder of the paper and require quite a lot of work. In particular, we will have to use the bijection of Armstrong, Stump and Thomas [Reference Armstrong, Stump and Thomas2] between nonnesting and noncrossing partitions, which we discuss in the next section.
Remark 2.12. As mentioned in Section 1, the identity
![]() $\#A +\#\operatorname {\mathrm {Rvac}}(A)=r$
fails to hold when
$\#A +\#\operatorname {\mathrm {Rvac}}(A)=r$
fails to hold when
![]() $\Phi $
is one of the exceptional types other than
$\Phi $
is one of the exceptional types other than
![]() $G_2$
. Figure 4 gives an example of such a failure for
$G_2$
. Figure 4 gives an example of such a failure for
![]() $F_4$
; there are similar examples for
$F_4$
; there are similar examples for
![]() $E_6$
,
$E_6$
,
![]() $E_7$
and
$E_7$
and
![]() $E_8$
. It would be interesting to try to modify rowvacuation somehow to obtain Panyushev’s desired involution
$E_8$
. It would be interesting to try to modify rowvacuation somehow to obtain Panyushev’s desired involution
![]() $\mathfrak {P}$
in the exceptional types.
$\mathfrak {P}$
in the exceptional types.

Figure 4 An antichain
![]() $A\in \mathcal {A}(\Phi ^+(F_4))$
(left) and its rowvacuation (right). In this example,
$A\in \mathcal {A}(\Phi ^+(F_4))$
(left) and its rowvacuation (right). In this example,
![]() $\#A +\#\operatorname {\mathrm {Rvac}}(A)\neq 4$
.
$\#A +\#\operatorname {\mathrm {Rvac}}(A)\neq 4$
.
Remark 2.13. In [Reference Hopkins and Joseph18, §2.8] it is explained that if there is a constant
![]() $c\in \mathbb {N}$
for which
$c\in \mathbb {N}$
for which
![]() $\#A+\#\operatorname {\mathrm {Rvac}}(A)=c$
for every antichain
$\#A+\#\operatorname {\mathrm {Rvac}}(A)=c$
for every antichain
![]() $A\in \mathcal {A}(P)$
of a ranked poset P, then necessarily
$A\in \mathcal {A}(P)$
of a ranked poset P, then necessarily
 $\frac {1}{\#O}\sum _{A \in O} \#A=\frac {c}{2}$
for every
$\frac {1}{\#O}\sum _{A \in O} \#A=\frac {c}{2}$
for every
![]() $\operatorname {\mathrm {Row}} $
-orbit
$\operatorname {\mathrm {Row}} $
-orbit
![]() $O\subseteq \mathcal {A}(P)$
as well. Hence, Theorem 1.4 implies the second item in Theorem 2.3 for the classical types. However, since we use a lot of the machinery of [Reference Armstrong, Stump and Thomas2] to prove Theorem 1.4, this does not really qualify as a new proof of this homomesy result.
$O\subseteq \mathcal {A}(P)$
as well. Hence, Theorem 1.4 implies the second item in Theorem 2.3 for the classical types. However, since we use a lot of the machinery of [Reference Armstrong, Stump and Thomas2] to prove Theorem 1.4, this does not really qualify as a new proof of this homomesy result.
3 Noncrossing partitions and the AST bijection
In this section, we review the W-noncrossing partitions and then describe the Armstrong–Stump–Thomas (AST) [Reference Armstrong, Stump and Thomas2] bijection between nonnesting and noncrossing partitions, which interacts very nicely with both rowmotion and rowvacuation.
3.1 Noncrossing partitions
We continue to fix a root system
![]() $\Phi $
in V with Weyl group
$\Phi $
in V with Weyl group
![]() $W\subseteq \operatorname {\mathrm {GL}}(V)$
. We use
$W\subseteq \operatorname {\mathrm {GL}}(V)$
. We use
![]() $s_i \in \operatorname {\mathrm {GL}}(V)$
to denote the simple reflection corresponding to a simple root
$s_i \in \operatorname {\mathrm {GL}}(V)$
to denote the simple reflection corresponding to a simple root
![]() $\alpha _i$
. Recall that W is generated by
$\alpha _i$
. Recall that W is generated by
![]() $\{s_1,\ldots ,s_r\}$
. A Coxeter element
$\{s_1,\ldots ,s_r\}$
. A Coxeter element
![]() $c\in W$
is a product of all the simple reflections
$c\in W$
is a product of all the simple reflections
![]() $s_1,\ldots ,s_r$
in some order. From now on, fix a choice of a Coxeter element c. The order of c is, by definition, the Coxeter number h.
$s_1,\ldots ,s_r$
in some order. From now on, fix a choice of a Coxeter element c. The order of c is, by definition, the Coxeter number h.
We use
![]() $T\subseteq W$
to denote the set of reflections – that is, all W-conjugates of
$T\subseteq W$
to denote the set of reflections – that is, all W-conjugates of
![]() $s_1,\ldots ,s_r$
. The absolute length of an element
$s_1,\ldots ,s_r$
. The absolute length of an element
![]() $w\in W$
, denoted
$w\in W$
, denoted
![]() $\ell _T(w)$
, is the minimum length of an expression for w as a product of elements of T. The absolute order on W is the partial order where
$\ell _T(w)$
, is the minimum length of an expression for w as a product of elements of T. The absolute order on W is the partial order where
![]() $u \leq w$
if and only if
$u \leq w$
if and only if
![]() $\ell _T(w) = \ell _T(u) + \ell _T\left (u^{-1}w\right )$
. The identity element e is the minimal element of absolute order; the Coxeter elements form a subset of the maximal elements. The poset of W-noncrossing partitions
$\ell _T(w) = \ell _T(u) + \ell _T\left (u^{-1}w\right )$
. The identity element e is the minimal element of absolute order; the Coxeter elements form a subset of the maximal elements. The poset of W-noncrossing partitions
![]() $\operatorname {\mathrm {NC}}(W,c)$
is defined to be the interval
$\operatorname {\mathrm {NC}}(W,c)$
is defined to be the interval
![]() $[e,w] \subseteq W$
in absolute order between the identity element e and the Coxeter element c. For fixed W and varying c, the posets
$[e,w] \subseteq W$
in absolute order between the identity element e and the Coxeter element c. For fixed W and varying c, the posets
![]() $\operatorname {\mathrm {NC}}(W,c)$
are isomorphic, since all Coxeter elements are conjugate; this is why we just used the notation
$\operatorname {\mathrm {NC}}(W,c)$
are isomorphic, since all Coxeter elements are conjugate; this is why we just used the notation
![]() $\operatorname {\mathrm {NC}}(W)$
for this poset in Section 1. But from now on, we use the notation
$\operatorname {\mathrm {NC}}(W)$
for this poset in Section 1. But from now on, we use the notation
![]() $\operatorname {\mathrm {NC}}(W,c)$
to emphasise the choice of c.
$\operatorname {\mathrm {NC}}(W,c)$
to emphasise the choice of c.
The W-noncrossing partitions were first introduced by Brady and Watt [Reference Brady and Watt7] and independently by Bessis [Reference Bessis4], following work of Reiner [Reference Reiner25] in the classical types (see also [Reference Athanasiadis and Reiner3]). The poset
![]() $\operatorname {\mathrm {NC}}(W,c)$
is ranked with rank function
$\operatorname {\mathrm {NC}}(W,c)$
is ranked with rank function
![]() $\ell _T$
, and its rank is
$\ell _T$
, and its rank is
![]() $\operatorname {\mathrm {rk}}(\operatorname {\mathrm {NC}}(W,c))=\ell _T(c)=r$
. It is known [Reference Brady and Watt8] that
$\operatorname {\mathrm {rk}}(\operatorname {\mathrm {NC}}(W,c))=\ell _T(c)=r$
. It is known [Reference Brady and Watt8] that
![]() $\operatorname {\mathrm {NC}}(W,c)$
is always a lattice. Furthermore,
$\operatorname {\mathrm {NC}}(W,c)$
is always a lattice. Furthermore,
![]() $\operatorname {\mathrm {NC}}(W,c)$
is self-dual. In fact, the Kreweras complement
$\operatorname {\mathrm {NC}}(W,c)$
is self-dual. In fact, the Kreweras complement
![]() $\operatorname {\mathrm {Krew}}\colon \operatorname {\mathrm {NC}}(W,c)\to \operatorname {\mathrm {NC}}(W,c)$
defined by
$\operatorname {\mathrm {Krew}}\colon \operatorname {\mathrm {NC}}(W,c)\to \operatorname {\mathrm {NC}}(W,c)$
defined by
![]() $\operatorname {\mathrm {Krew}}(w):= cw^{-1}$
is an antiautomorphism of
$\operatorname {\mathrm {Krew}}(w):= cw^{-1}$
is an antiautomorphism of
![]() $\operatorname {\mathrm {NC}}(W,c)$
.
$\operatorname {\mathrm {NC}}(W,c)$
.
Since we will work mostly with the classical types, let us review (some of) their Weyl groups and noncrossing partitions. The Weyl group
![]() $W(A_{n-1})$
of type
$W(A_{n-1})$
of type
![]() $A_{n-1}$
is isomorphic to the symmetric group
$A_{n-1}$
is isomorphic to the symmetric group
![]() $\mathfrak S_n$
. When we view
$\mathfrak S_n$
. When we view
![]() $W(A_{n-1})$
as
$W(A_{n-1})$
as
![]() $\mathfrak S_n$
, the simple reflection
$\mathfrak S_n$
, the simple reflection
![]() $s_i$
is the simple transposition
$s_i$
is the simple transposition
![]() $(i,i+1)$
. A standard choice of Coxeter element is
$(i,i+1)$
. A standard choice of Coxeter element is
![]() $c=s_1s_2\cdots s_{n-1} = (1,2,3,\ldots ,n)$
(in cycle notation). Figure 5 depicts the lattice of noncrossing partitions in
$c=s_1s_2\cdots s_{n-1} = (1,2,3,\ldots ,n)$
(in cycle notation). Figure 5 depicts the lattice of noncrossing partitions in
![]() $\mathfrak S_3$
for the standard choice of Coxeter element. Note that
$\mathfrak S_3$
for the standard choice of Coxeter element. Note that
![]() $\operatorname {\mathrm {NC}}(\mathfrak {S}_n)$
is isomorphic to the classical lattice of noncrossing set partitions of
$\operatorname {\mathrm {NC}}(\mathfrak {S}_n)$
is isomorphic to the classical lattice of noncrossing set partitions of
![]() $[n]$
, with the Kreweras complement being the classical Kreweras complement of noncrossing set partitions. Meanwhile, the Weyl group
$[n]$
, with the Kreweras complement being the classical Kreweras complement of noncrossing set partitions. Meanwhile, the Weyl group
![]() $W(D_n)$
of type
$W(D_n)$
of type
![]() $D_n$
can be viewed as the group of permutations w of the set
$D_n$
can be viewed as the group of permutations w of the set
![]() $(-[n])\cup [n]$
such that
$(-[n])\cup [n]$
such that
![]() $w(-i)=-w(i)$
for all
$w(-i)=-w(i)$
for all
![]() $i\in [n]$
and for which the quantity
$i\in [n]$
and for which the quantity
![]() $\#\{i\in [n]\colon w(i)<0\}$
is even. Viewing
$\#\{i\in [n]\colon w(i)<0\}$
is even. Viewing
![]() $W(D_n)$
as a group of permutations of
$W(D_n)$
as a group of permutations of
![]() $(-[n])\cup [n]$
, we have
$(-[n])\cup [n]$
, we have
 $$ \begin{align*} s_i = \begin{cases} (i,i+1)(-i,-i-1) &\text{if } 1\leq i \leq n-1, \\ (n,-n+1)(n-1,-n) &\text{if } i=n.\end{cases} \end{align*} $$
$$ \begin{align*} s_i = \begin{cases} (i,i+1)(-i,-i-1) &\text{if } 1\leq i \leq n-1, \\ (n,-n+1)(n-1,-n) &\text{if } i=n.\end{cases} \end{align*} $$

Figure 5 The lattice of noncrossing partitions
![]() $\operatorname {\mathrm {NC}}(\mathfrak {S}_3)$
.
$\operatorname {\mathrm {NC}}(\mathfrak {S}_3)$
.
3.2 The AST bijection
The Kreweras complement is usually not an involution: it has order h or
![]() $2h$
. For instance, in type A,
$2h$
. For instance, in type A,
![]() $\operatorname {\mathrm {Krew}}^{2}$
corresponds to rotation of noncrossing set partitions. Hence, one might wonder about the orbit structure of
$\operatorname {\mathrm {Krew}}^{2}$
corresponds to rotation of noncrossing set partitions. Hence, one might wonder about the orbit structure of
![]() $\operatorname {\mathrm {Krew}}$
. This is where the connection to Panyushev’s work arises. After Panyushev had experimentally exhibited the remarkable properties of rowmotion acting on the root poset in [Reference Panyushev22], Bessis and Reiner [Reference Bessis and Reiner5] conjectured that the orbit structure of
$\operatorname {\mathrm {Krew}}$
. This is where the connection to Panyushev’s work arises. After Panyushev had experimentally exhibited the remarkable properties of rowmotion acting on the root poset in [Reference Panyushev22], Bessis and Reiner [Reference Bessis and Reiner5] conjectured that the orbit structure of
![]() $\operatorname {\mathrm {Row}}$
acting on
$\operatorname {\mathrm {Row}}$
acting on
![]() $\mathcal {A}(\Phi ^+)$
is the same as the orbit structure of
$\mathcal {A}(\Phi ^+)$
is the same as the orbit structure of
![]() $\operatorname {\mathrm {Krew}}$
acting on
$\operatorname {\mathrm {Krew}}$
acting on
![]() $\operatorname {\mathrm {NC}}(W,c)$
. Armstrong, Stump and Thomas [Reference Armstrong, Stump and Thomas2] proved this conjecture of Bessis and Reiner by defining an explicit bijection between
$\operatorname {\mathrm {NC}}(W,c)$
. Armstrong, Stump and Thomas [Reference Armstrong, Stump and Thomas2] proved this conjecture of Bessis and Reiner by defining an explicit bijection between
![]() $\mathcal {A}(\Phi ^+)$
and
$\mathcal {A}(\Phi ^+)$
and
![]() $\operatorname {\mathrm {NC}}(W,c)$
that equivariantly maps rowmotion to Kreweras complement.
$\operatorname {\mathrm {NC}}(W,c)$
that equivariantly maps rowmotion to Kreweras complement.
In order to describe their bijection, we need to assume that our Coxeter element is bipartite – that is, that
![]() $c = c_L c_R$
, where
$c = c_L c_R$
, where
![]() $L\sqcup R = [r]$
is a bipartition of the nodes of the Dynkin diagram of
$L\sqcup R = [r]$
is a bipartition of the nodes of the Dynkin diagram of
![]() $\Phi $
and
$\Phi $
and
![]() $c_X := \prod _{i\in X} s_i$
(the products
$c_X := \prod _{i\in X} s_i$
(the products
![]() $c_L$
and
$c_L$
and
![]() $c_R$
are well defined, since the bipartite assumption guarantees that these simple reflections commute). Since the Dynkin diagram of
$c_R$
are well defined, since the bipartite assumption guarantees that these simple reflections commute). Since the Dynkin diagram of
![]() $\Phi $
is always a tree, a bipartite Coxeter element exists. Because all Coxeter elements are conjugate, there is no loss of generality in assuming bipartiteness.
$\Phi $
is always a tree, a bipartite Coxeter element exists. Because all Coxeter elements are conjugate, there is no loss of generality in assuming bipartiteness.
For
![]() $J\subseteq [r]$
, the parabolic subgroup
$J\subseteq [r]$
, the parabolic subgroup
![]() $W_J$
is the subgroup of W generated by the simple reflections
$W_J$
is the subgroup of W generated by the simple reflections
![]() $s_i$
for
$s_i$
for
![]() $i \in J$
. If
$i \in J$
. If
![]() $c_Lc_R$
is a bipartite Coxeter element of W, then
$c_Lc_R$
is a bipartite Coxeter element of W, then
![]() $c_{L'}c_{R'}$
is a bipartite Coxeter element of
$c_{L'}c_{R'}$
is a bipartite Coxeter element of
![]() $W_J$
, where
$W_J$
, where
![]() $L' := L\cap J$
and
$L' := L\cap J$
and
![]() $R' := R\cap J$
; we have a natural inclusion
$R' := R\cap J$
; we have a natural inclusion
![]() $\operatorname {\mathrm {NC}}\left (W_J,c_{L'}c_{R'}\right )\subseteq \operatorname {\mathrm {NC}}(W,c_Lc_R)$
. Meanwhile, we use
$\operatorname {\mathrm {NC}}\left (W_J,c_{L'}c_{R'}\right )\subseteq \operatorname {\mathrm {NC}}(W,c_Lc_R)$
. Meanwhile, we use
![]() $\Phi ^+_J$
to denote the corresponding parabolic root poset, which is
$\Phi ^+_J$
to denote the corresponding parabolic root poset, which is
![]() $\Phi ^+_J := \left \{\alpha \in \Phi ^+\colon \alpha \not \geq \alpha _i \text { for all } i\in [r]\setminus J\right \}$
.Footnote
5
For an antichain
$\Phi ^+_J := \left \{\alpha \in \Phi ^+\colon \alpha \not \geq \alpha _i \text { for all } i\in [r]\setminus J\right \}$
.Footnote
5
For an antichain
![]() $A \in \mathcal {A}(\Phi ^+)$
, we define its support to be
$A \in \mathcal {A}(\Phi ^+)$
, we define its support to be
We can view any antichain
![]() $A \in \mathcal {A}(\Phi ^+)$
as also an antichain in
$A \in \mathcal {A}(\Phi ^+)$
as also an antichain in
 $\mathcal {A}\left (\Phi _{\operatorname {\mathrm {supp}}(A)}^+\right )$
.
$\mathcal {A}\left (\Phi _{\operatorname {\mathrm {supp}}(A)}^+\right )$
.
With all this notation in hand, we can now describe the Armstrong–Stump–Thomas nonnesting-to-noncrossing bijection that sends rowmotion to Kreweras complement. As we will see, it is defined inductively, so it is important that we allow the possibility that
![]() $\Phi ^+$
is reducible, as we have been doing throughout.
$\Phi ^+$
is reducible, as we have been doing throughout.
Theorem 3.1 Armstrong–Stump–Thomas [Reference Armstrong, Stump and Thomas2]
Fix a bipartition
![]() $L\sqcup R = [r]$
of the Dynkin diagram of
$L\sqcup R = [r]$
of the Dynkin diagram of
![]() $\Phi $
. Then there is a unique bijection
$\Phi $
. Then there is a unique bijection
![]() $\Theta _{W}\colon \mathcal {A}(\Phi ^+)\xrightarrow {\sim } \operatorname {\mathrm {NC}}(W,c_Lc_R)$
for which:
$\Theta _{W}\colon \mathcal {A}(\Phi ^+)\xrightarrow {\sim } \operatorname {\mathrm {NC}}(W,c_Lc_R)$
for which:
-
• (base case)
 $\Theta _W(\{\alpha _i\colon i \in L\})=e$
;
$\Theta _W(\{\alpha _i\colon i \in L\})=e$
; -
• (equivariance)
 $\Theta _W \cdot \operatorname {\mathrm {Row}}= \operatorname {\mathrm {Krew}}\cdot \Theta _W$
;
$\Theta _W \cdot \operatorname {\mathrm {Row}}= \operatorname {\mathrm {Krew}}\cdot \Theta _W$
; -
• (parabolic induction)
 $\Theta _W(A) = \prod _{i \in L\setminus \operatorname {\mathrm {supp}}(A)} s_i \cdot \Theta _{W_{\operatorname {\mathrm {supp}}(A)}}(A)$
for
$\Theta _W(A) = \prod _{i \in L\setminus \operatorname {\mathrm {supp}}(A)} s_i \cdot \Theta _{W_{\operatorname {\mathrm {supp}}(A)}}(A)$
for
 $A \in \mathcal {A}(\Phi ^+)$
, where
$A \in \mathcal {A}(\Phi ^+)$
, where
 $ \Theta _{W_{\operatorname {\mathrm {supp}}(A)}}(A) \in \operatorname {\mathrm {NC}}\left (W_{\operatorname {\mathrm {supp}}(A)},c_{L\cap \operatorname {\mathrm {supp}}(A)}c_{R\cap \operatorname {\mathrm {supp}}(A)}\right )\subseteq \operatorname {\mathrm {NC}}(W,c_Lc_R)$
.
$ \Theta _{W_{\operatorname {\mathrm {supp}}(A)}}(A) \in \operatorname {\mathrm {NC}}\left (W_{\operatorname {\mathrm {supp}}(A)},c_{L\cap \operatorname {\mathrm {supp}}(A)}c_{R\cap \operatorname {\mathrm {supp}}(A)}\right )\subseteq \operatorname {\mathrm {NC}}(W,c_Lc_R)$
.
Remark 3.2. Armstrong, Stump and Thomas [Reference Armstrong, Stump and Thomas2] used Theorem 3.1 to prove Theorem 2.3. But also, affirming a conjecture of Bessis and Reiner [Reference Bessis and Reiner5], they used Theorem 3.1 to show that
![]() $\operatorname {\mathrm {Row}}$
acting on
$\operatorname {\mathrm {Row}}$
acting on
![]() $\mathcal {A}(\Phi ^+)$
satisfies a cyclic sieving phenomenon [Reference Reiner, Stanton and White26], where the sieving polynomial is a natural q-analogue of
$\mathcal {A}(\Phi ^+)$
satisfies a cyclic sieving phenomenon [Reference Reiner, Stanton and White26], where the sieving polynomial is a natural q-analogue of
![]() $\operatorname {\mathrm {Cat}}(W)$
. Recently there has been interest in extending sieving phenomena to dihedral group actions as well [Reference Hopkins16, Reference Rao and Suk24, Reference Stier, Wellman and Xu30]. Hence, it might be interesting to explore sieving phenomenona for
$\operatorname {\mathrm {Cat}}(W)$
. Recently there has been interest in extending sieving phenomena to dihedral group actions as well [Reference Hopkins16, Reference Rao and Suk24, Reference Stier, Wellman and Xu30]. Hence, it might be interesting to explore sieving phenomenona for
![]() $\langle \operatorname {\mathrm {Row}}, \operatorname {\mathrm {Rvac}} \rangle $
acting on
$\langle \operatorname {\mathrm {Row}}, \operatorname {\mathrm {Rvac}} \rangle $
acting on
![]() $\mathcal {A}(\Phi ^+)$
.
$\mathcal {A}(\Phi ^+)$
.
3.3 Flip
Now that we have stated the Armstrong–Stump–Thomas bijection, we want to bring rowvacuation into the story. In other words, we need an involution on the set of noncrossing partitions of
![]() $\Phi $
that plays the role that rowvacuation plays for the nonnesting partitions. Since the Kreweras complement is a kind of ‘rotation’, and this hypothetical involution on noncrossing partitions ought to generate a dihedral action with the Kreweras complement, we will refer to it as flip. As before, we use the bipartite Coxeter element
$\Phi $
that plays the role that rowvacuation plays for the nonnesting partitions. Since the Kreweras complement is a kind of ‘rotation’, and this hypothetical involution on noncrossing partitions ought to generate a dihedral action with the Kreweras complement, we will refer to it as flip. As before, we use the bipartite Coxeter element
![]() $c=c_Lc_R$
. We define
$c=c_Lc_R$
. We define
![]() $\operatorname {\mathrm {Flip}}\colon \operatorname {\mathrm {NC}}(W,c_Lc_R)\to \operatorname {\mathrm {NC}}(W,c_Lc_R)$
by
$\operatorname {\mathrm {Flip}}\colon \operatorname {\mathrm {NC}}(W,c_Lc_R)\to \operatorname {\mathrm {NC}}(W,c_Lc_R)$
by
 $\operatorname {\mathrm {Flip}}(w) := c_L w^{-1} c_L^{-1}$
. Note that since
$\operatorname {\mathrm {Flip}}(w) := c_L w^{-1} c_L^{-1}$
. Note that since
![]() $c_L$
is an involution,
$c_L$
is an involution,
![]() $\operatorname {\mathrm {Flip}}$
is also an involution. It fixes c and permutes the set of reflections, so it is an automorphism of
$\operatorname {\mathrm {Flip}}$
is also an involution. It fixes c and permutes the set of reflections, so it is an automorphism of
![]() $\operatorname {\mathrm {NC}}(W,c_Lc_R)$
. It is also easily seen that
$\operatorname {\mathrm {NC}}(W,c_Lc_R)$
. It is also easily seen that
Remark 3.3. For nonbipartite c, we can define
![]() $\operatorname {\mathrm {Flip}}\colon \operatorname {\mathrm {NC}}(W,c)\to \operatorname {\mathrm {NC}}(W,c)$
by conjugating to a bipartite c. In fact, it is not hard to show that the
$\operatorname {\mathrm {Flip}}\colon \operatorname {\mathrm {NC}}(W,c)\to \operatorname {\mathrm {NC}}(W,c)$
by conjugating to a bipartite c. In fact, it is not hard to show that the
![]() $g\in W$
that conjugate c to
$g\in W$
that conjugate c to
![]() $c^{-1}$
form a (left and right)
$c^{-1}$
form a (left and right)
![]() $\langle c \rangle $
-coset and that they are all necessarily involutions. (The one thing needed to prove this is the well-known fact that the centraliser of c in W is
$\langle c \rangle $
-coset and that they are all necessarily involutions. (The one thing needed to prove this is the well-known fact that the centraliser of c in W is
![]() $\langle c \rangle $
.) When h is odd, this
$\langle c \rangle $
.) When h is odd, this
![]() $\langle c \rangle $
-coset is a single
$\langle c \rangle $
-coset is a single
![]() $\langle c \rangle $
-conjugacy class; when h is even, it consists of two
$\langle c \rangle $
-conjugacy class; when h is even, it consists of two
![]() $\langle c \rangle $
-conjugacy classes.
$\langle c \rangle $
-conjugacy classes.
Remark 3.4. Extending the previous remark, we note there are other involutive automorphisms of
![]() $\operatorname {\mathrm {NC}}(W,c_Lc_R)$
such as the map
$\operatorname {\mathrm {NC}}(W,c_Lc_R)$
such as the map
![]() $\operatorname {\mathrm {Flip}}'\colon \operatorname {\mathrm {NC}}(W,c_Lc_R)\to \operatorname {\mathrm {NC}}(W,c_Lc_R)$
defined by
$\operatorname {\mathrm {Flip}}'\colon \operatorname {\mathrm {NC}}(W,c_Lc_R)\to \operatorname {\mathrm {NC}}(W,c_Lc_R)$
defined by
 $\operatorname {\mathrm {Flip}}'(w) := c_R w^{-1} c_R^{-1}$
, and others obtained by conjugating
$\operatorname {\mathrm {Flip}}'(w) := c_R w^{-1} c_R^{-1}$
, and others obtained by conjugating
![]() $\operatorname {\mathrm {Flip}}$
or
$\operatorname {\mathrm {Flip}}$
or
![]() $\operatorname {\mathrm {Flip}}'$
by powers of c. These various involutive automorphisms of
$\operatorname {\mathrm {Flip}}'$
by powers of c. These various involutive automorphisms of
![]() $\operatorname {\mathrm {NC}}(W,c_Lc_R)$
were previously considered, for instance, by Armstrong in [Reference Armstrong1, §4.3.4]. Our focus on
$\operatorname {\mathrm {NC}}(W,c_Lc_R)$
were previously considered, for instance, by Armstrong in [Reference Armstrong1, §4.3.4]. Our focus on
![]() $\operatorname {\mathrm {Flip}}$
is ultimately a matter of convention.
$\operatorname {\mathrm {Flip}}$
is ultimately a matter of convention.
Remark 3.5. That c is conjugate by an involution to its inverse is not a special property of Coxeter elements; Carter [Reference Carter11, Theorem C(iii)] proved that every element of a Weyl group is conjugate by an involution to its inverse.
With this definition of
![]() $\operatorname {\mathrm {Flip}}$
, we can upgrade the equivalence of cyclic actions in Theorem 3.1 to an equivalence of dihedral actions essentially ‘for free’, using just the general properties of the bijection listed in that theorem. This is what we asserted in Theorem 1.5:
$\operatorname {\mathrm {Flip}}$
, we can upgrade the equivalence of cyclic actions in Theorem 3.1 to an equivalence of dihedral actions essentially ‘for free’, using just the general properties of the bijection listed in that theorem. This is what we asserted in Theorem 1.5:
 $$ \begin{align*} \Theta_W \cdot \left(\operatorname{\mathrm{Row}}^{-1}\cdot \operatorname{\mathrm{Rvac}}\right) = \operatorname{\mathrm{Flip}}\cdot \Theta_W. \end{align*} $$
$$ \begin{align*} \Theta_W \cdot \left(\operatorname{\mathrm{Row}}^{-1}\cdot \operatorname{\mathrm{Rvac}}\right) = \operatorname{\mathrm{Flip}}\cdot \Theta_W. \end{align*} $$
The reason that we need to use
![]() $\operatorname {\mathrm {Row}}^{-1}\cdot \operatorname {\mathrm {Rvac}}$
instead of just
$\operatorname {\mathrm {Row}}^{-1}\cdot \operatorname {\mathrm {Rvac}}$
instead of just
![]() $\operatorname {\mathrm {Rvac}}$
in Theorem 1.5 is that sometimes there are no
$\operatorname {\mathrm {Rvac}}$
in Theorem 1.5 is that sometimes there are no
![]() $A \in \mathcal {A}(\Phi ^+)$
fixed by
$A \in \mathcal {A}(\Phi ^+)$
fixed by
![]() $\operatorname {\mathrm {Rvac}}$
, whereas there will always be some fixed points of
$\operatorname {\mathrm {Rvac}}$
, whereas there will always be some fixed points of
![]() $\operatorname {\mathrm {Flip}}$
(e.g., e and c).
$\operatorname {\mathrm {Flip}}$
(e.g., e and c).
In order to prove Theorem 1.5, we need to show that
![]() $\operatorname {\mathrm {Row}}^{-1}\cdot \operatorname {\mathrm {Rvac}}$
behaves well with respect to parabolic induction. In fact, this is true for any poset P. Namely, for an antichain
$\operatorname {\mathrm {Row}}^{-1}\cdot \operatorname {\mathrm {Rvac}}$
behaves well with respect to parabolic induction. In fact, this is true for any poset P. Namely, for an antichain
![]() $A \in \mathcal {A}(P)$
, slightly abusing notation, let us define its support to be
$A \in \mathcal {A}(P)$
, slightly abusing notation, let us define its support to be
![]() $\operatorname {\mathrm {supp}}(A):= \{p \in P_0\colon p\leq q \text { for some } q\in A\}$
. For a subset
$\operatorname {\mathrm {supp}}(A):= \{p \in P_0\colon p\leq q \text { for some } q\in A\}$
. For a subset
![]() $X\subseteq P_0$
, define
$X\subseteq P_0$
, define
![]() $P_{X} := \left \{q \in P\colon q \not \geq p \text { for all } p \in P_0\setminus X\right \}$
. We can view any antichain
$P_{X} := \left \{q \in P\colon q \not \geq p \text { for all } p \in P_0\setminus X\right \}$
. We can view any antichain
![]() $A \in \mathcal {A}(P)$
as an antichain in
$A \in \mathcal {A}(P)$
as an antichain in
![]() $\mathcal {A}\left (P_{\operatorname {\mathrm {supp}}(A)}\right )$
. We let
$\mathcal {A}\left (P_{\operatorname {\mathrm {supp}}(A)}\right )$
. We let
 $\left (\operatorname {\mathrm {Row}}^{-1}\cdot \operatorname {\mathrm {Rvac}}\right )_{\operatorname {\mathrm {supp}}(A)}(A)$
denote the image of A under
$\left (\operatorname {\mathrm {Row}}^{-1}\cdot \operatorname {\mathrm {Rvac}}\right )_{\operatorname {\mathrm {supp}}(A)}(A)$
denote the image of A under
 $\operatorname {\mathrm {Row}}^{-1}\cdot \operatorname {\mathrm {Rvac}}\colon \mathcal {A}\left (P_{\operatorname {\mathrm {supp}}(A)}\right )\to \mathcal {A}\left (P_{\operatorname {\mathrm {supp}}(A)}\right )$
.
$\operatorname {\mathrm {Row}}^{-1}\cdot \operatorname {\mathrm {Rvac}}\colon \mathcal {A}\left (P_{\operatorname {\mathrm {supp}}(A)}\right )\to \mathcal {A}\left (P_{\operatorname {\mathrm {supp}}(A)}\right )$
.
Lemma 3.6. For any P and
![]() $A \in \mathcal {A}(P)$
, we have the following:
$A \in \mathcal {A}(P)$
, we have the following:
-
•
 $\operatorname {\mathrm {supp}}\left (\left (\operatorname {\mathrm {Row}}^{-1}\cdot \operatorname {\mathrm {Rvac}}\right )(A)\right ) = \operatorname {\mathrm {supp}}(A)$
and
$\operatorname {\mathrm {supp}}\left (\left (\operatorname {\mathrm {Row}}^{-1}\cdot \operatorname {\mathrm {Rvac}}\right )(A)\right ) = \operatorname {\mathrm {supp}}(A)$
and -
•
 $\operatorname {\mathrm {Row}}^{-1}\cdot \operatorname {\mathrm {Rvac}}(A) = \left (\operatorname {\mathrm {Row}}^{-1}\cdot \operatorname {\mathrm {Rvac}}\right )_{\operatorname {\mathrm {supp}}(A)}(A)$
.
$\operatorname {\mathrm {Row}}^{-1}\cdot \operatorname {\mathrm {Rvac}}(A) = \left (\operatorname {\mathrm {Row}}^{-1}\cdot \operatorname {\mathrm {Rvac}}\right )_{\operatorname {\mathrm {supp}}(A)}(A)$
.
Proof. The argument is very similar to the proof of Proposition 2.10. Let us prove the second bulleted item first. We write
![]() $\operatorname {\mathrm {Row}}^{-1}\cdot \operatorname {\mathrm {Rvac}}$
as
$\operatorname {\mathrm {Row}}^{-1}\cdot \operatorname {\mathrm {Rvac}}$
as
When we apply the first
![]() $\boldsymbol {\tau }_0$
to A, it will add to our antichain all of
$\boldsymbol {\tau }_0$
to A, it will add to our antichain all of
![]() $P_0\setminus \operatorname {\mathrm {supp}}(A)$
, and until those elements are removed by the
$P_0\setminus \operatorname {\mathrm {supp}}(A)$
, and until those elements are removed by the
![]() $\boldsymbol {\tau }_0$
at the end of this sequence of toggles (which they will be), no element of
$\boldsymbol {\tau }_0$
at the end of this sequence of toggles (which they will be), no element of
![]() $P\setminus P_{\operatorname {\mathrm {supp}}(A)}$
can be toggled into our antichain. Meanwhile, the status of elements of
$P\setminus P_{\operatorname {\mathrm {supp}}(A)}$
can be toggled into our antichain. Meanwhile, the status of elements of
![]() $P_0\setminus \operatorname {\mathrm {supp}}(A)$
has no effect on the toggles
$P_0\setminus \operatorname {\mathrm {supp}}(A)$
has no effect on the toggles
![]() $\tau _p$
for
$\tau _p$
for
![]() $p\in P_{\operatorname {\mathrm {supp}}(A)}$
. So indeed, applying this sequence of toggles to A will have the same effect as if we applied only the toggles
$p\in P_{\operatorname {\mathrm {supp}}(A)}$
. So indeed, applying this sequence of toggles to A will have the same effect as if we applied only the toggles
![]() $\tau _p$
for
$\tau _p$
for
![]() $p \in P_{\operatorname {\mathrm {supp}}(A)}$
. This proves the second bulleted item.
$p \in P_{\operatorname {\mathrm {supp}}(A)}$
. This proves the second bulleted item.
From the previous paragraph we have
 $\operatorname {\mathrm {supp}}\left (\left (\operatorname {\mathrm {Row}}^{-1}\cdot \operatorname {\mathrm {Rvac}}\right )(A)\right ) \subseteq \operatorname {\mathrm {supp}}(A)$
. But since
$\operatorname {\mathrm {supp}}\left (\left (\operatorname {\mathrm {Row}}^{-1}\cdot \operatorname {\mathrm {Rvac}}\right )(A)\right ) \subseteq \operatorname {\mathrm {supp}}(A)$
. But since
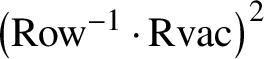 $\left (\operatorname {\mathrm {Row}}^{-1}\cdot \operatorname {\mathrm {Rvac}}\right )^2$
is the identity, this also implies that we have the reverse containment
$\left (\operatorname {\mathrm {Row}}^{-1}\cdot \operatorname {\mathrm {Rvac}}\right )^2$
is the identity, this also implies that we have the reverse containment
 $\operatorname {\mathrm {supp}}(A)\subseteq \operatorname {\mathrm {supp}}\left (\left (\operatorname {\mathrm {Row}}^{-1}\cdot \operatorname {\mathrm {Rvac}}\right )(A)\right )$
, thus proving the first bulleted item as well.
$\operatorname {\mathrm {supp}}(A)\subseteq \operatorname {\mathrm {supp}}\left (\left (\operatorname {\mathrm {Row}}^{-1}\cdot \operatorname {\mathrm {Rvac}}\right )(A)\right )$
, thus proving the first bulleted item as well.
Proof of Theorem 1.5. In showing that the bijection
![]() $\Theta _{W}\colon \mathcal {A}(\Phi ^+)\xrightarrow {\sim } \operatorname {\mathrm {NC}}(W,c_Lc_R)$
is uniquely defined by the listed properties, Armstrong, Stump and Thomas [Reference Armstrong, Stump and Thomas2] explained that for every
$\Theta _{W}\colon \mathcal {A}(\Phi ^+)\xrightarrow {\sim } \operatorname {\mathrm {NC}}(W,c_Lc_R)$
is uniquely defined by the listed properties, Armstrong, Stump and Thomas [Reference Armstrong, Stump and Thomas2] explained that for every
![]() $A \in \mathcal {A}(\Phi ^+)$
, there is a
$A \in \mathcal {A}(\Phi ^+)$
, there is a
![]() $k \geq 0$
such that
$k \geq 0$
such that
 $\operatorname {\mathrm {supp}}\left (\operatorname {\mathrm {Row}} ^{k}(A)\right ) \neq [r]$
. Hence, the bijection can be computed inductively as follows: we let
$\operatorname {\mathrm {supp}}\left (\operatorname {\mathrm {Row}} ^{k}(A)\right ) \neq [r]$
. Hence, the bijection can be computed inductively as follows: we let
![]() $A' := \operatorname {\mathrm {Row}} ^{k}(A)$
, where
$A' := \operatorname {\mathrm {Row}} ^{k}(A)$
, where
![]() $k\geq 0$
is minimal so that
$k\geq 0$
is minimal so that
![]() $\operatorname {\mathrm {supp}}(A') \neq [r]$
; we then compute
$\operatorname {\mathrm {supp}}(A') \neq [r]$
; we then compute
![]() $w' := \Theta _{W_{\operatorname {\mathrm {supp}}\left (A'\right )}}(A')$
on the smaller Weyl group
$w' := \Theta _{W_{\operatorname {\mathrm {supp}}\left (A'\right )}}(A')$
on the smaller Weyl group
![]() $W_{\operatorname {\mathrm {supp}}\left (A'\right )}$
; finally, we set
$W_{\operatorname {\mathrm {supp}}\left (A'\right )}$
; finally, we set
 $\Theta _{W}(A) := \operatorname {\mathrm {Krew}}^{-k}\left (\prod _{i \in L\setminus \operatorname {\mathrm {supp}}\left (A'\right ) }s_i \cdot w'\right )$
. The base case of this induction is where we use the condition
$\Theta _{W}(A) := \operatorname {\mathrm {Krew}}^{-k}\left (\prod _{i \in L\setminus \operatorname {\mathrm {supp}}\left (A'\right ) }s_i \cdot w'\right )$
. The base case of this induction is where we use the condition
![]() $\Theta _W(\{\alpha _i\colon i \in L\})=e$
.Footnote
6
$\Theta _W(\{\alpha _i\colon i \in L\})=e$
.Footnote
6
Thus, to prove this theorem, it suffices to show the following:
-
• As a base case,
 $\Theta _W \left ( \left (\operatorname {\mathrm {Row}}^{-1}\cdot \operatorname {\mathrm {Rvac}}\right )(\{\alpha _i\colon i \in L\})\right ) = \operatorname {\mathrm {Flip}}(e)$
.
$\Theta _W \left ( \left (\operatorname {\mathrm {Row}}^{-1}\cdot \operatorname {\mathrm {Rvac}}\right )(\{\alpha _i\colon i \in L\})\right ) = \operatorname {\mathrm {Flip}}(e)$
. -
• If
 $\Theta _W\left ( \left (\operatorname {\mathrm {Row}}^{-1}\cdot \operatorname {\mathrm {Rvac}}\right )(A)\right ) = \operatorname {\mathrm {Flip}}(\Theta _W(A))$
, then
$\Theta _W\left ( \left (\operatorname {\mathrm {Row}}^{-1}\cdot \operatorname {\mathrm {Rvac}}\right )(A)\right ) = \operatorname {\mathrm {Flip}}(\Theta _W(A))$
, then  $$ \begin{align*} \Theta_W\left(\left(\operatorname{\mathrm{Row}}^{-1}\cdot \operatorname{\mathrm{Rvac}}\right)\left(\operatorname{\mathrm{Row}}^{-1}(A)\right)\right) = \operatorname{\mathrm{Flip}}\left(\operatorname{\mathrm{Krew}}^{-1} (\Theta_W(A))\right). \end{align*} $$
$$ \begin{align*} \Theta_W\left(\left(\operatorname{\mathrm{Row}}^{-1}\cdot \operatorname{\mathrm{Rvac}}\right)\left(\operatorname{\mathrm{Row}}^{-1}(A)\right)\right) = \operatorname{\mathrm{Flip}}\left(\operatorname{\mathrm{Krew}}^{-1} (\Theta_W(A))\right). \end{align*} $$
-
• If
 $\Theta _{W_{\operatorname {\mathrm {supp}}(A)}}\left ( \left (\operatorname {\mathrm {Row}}^{-1}\cdot \operatorname {\mathrm {Rvac}}\right )_{\operatorname {\mathrm {supp}}(A)} (A)\right ) = \operatorname {\mathrm {Flip}}_{W_{\operatorname {\mathrm {supp}}(A)}}\left (\Theta _{W_{\operatorname {\mathrm {supp}}(A)}}(A) \right )$
, then
$\Theta _{W_{\operatorname {\mathrm {supp}}(A)}}\left ( \left (\operatorname {\mathrm {Row}}^{-1}\cdot \operatorname {\mathrm {Rvac}}\right )_{\operatorname {\mathrm {supp}}(A)} (A)\right ) = \operatorname {\mathrm {Flip}}_{W_{\operatorname {\mathrm {supp}}(A)}}\left (\Theta _{W_{\operatorname {\mathrm {supp}}(A)}}(A) \right )$
, then  $$ \begin{align*} \Theta_W\left(\left(\operatorname{\mathrm{Row}}^{-1}\cdot \operatorname{\mathrm{Rvac}}\right)(A)\right) = \operatorname{\mathrm{Flip}}\left({\textstyle\prod_{i \in L\setminus \operatorname{\mathrm{supp}} (A)}} s_i \cdot \Theta_{W_{\operatorname{\mathrm{supp}}(A)}}(A)\right)=\operatorname{\mathrm{Flip}}(\Theta_W(A)).\end{align*} $$
$$ \begin{align*} \Theta_W\left(\left(\operatorname{\mathrm{Row}}^{-1}\cdot \operatorname{\mathrm{Rvac}}\right)(A)\right) = \operatorname{\mathrm{Flip}}\left({\textstyle\prod_{i \in L\setminus \operatorname{\mathrm{supp}} (A)}} s_i \cdot \Theta_{W_{\operatorname{\mathrm{supp}}(A)}}(A)\right)=\operatorname{\mathrm{Flip}}(\Theta_W(A)).\end{align*} $$
The first bulleted item is clear, since
 $$ \begin{align*} \left(\operatorname{\mathrm{Row}}^{-1}\cdot \operatorname{\mathrm{Rvac}}\right)(\{\alpha_i\colon i \in L\})=\operatorname{\mathrm{Row}}^{-1}(\{\alpha_i\colon i \in R\}) =\{\alpha_i\colon i \in L\} \end{align*} $$
$$ \begin{align*} \left(\operatorname{\mathrm{Row}}^{-1}\cdot \operatorname{\mathrm{Rvac}}\right)(\{\alpha_i\colon i \in L\})=\operatorname{\mathrm{Row}}^{-1}(\{\alpha_i\colon i \in R\}) =\{\alpha_i\colon i \in L\} \end{align*} $$
and
![]() $\operatorname {\mathrm {Flip}}(e)=e$
.
$\operatorname {\mathrm {Flip}}(e)=e$
.
For the second bulleted item, we use Proposition 2.6 and equation (3.1) to see that
 $$ \begin{align*} \Theta_W\left(\left(\operatorname{\mathrm{Row}}^{-1}\cdot \operatorname{\mathrm{Rvac}}\right) \left(\operatorname{\mathrm{Row}}^{-1}(A)\right)\right) &= \Theta_W\left(\left(\operatorname{\mathrm{Row}}\cdot \operatorname{\mathrm{Row}}^{-1} \operatorname{\mathrm{Rvac}}\right)(A)\right) \\ &= \operatorname{\mathrm{Krew}} \left(\Theta_W\left(\left(\operatorname{\mathrm{Row}}^{-1}\cdot \operatorname{\mathrm{Rvac}}\right)(A)\right)\right) \\ &= \operatorname{\mathrm{Krew}} (\operatorname{\mathrm{Flip}}(\Theta_W(A))) = \operatorname{\mathrm{Flip}}\left( \operatorname{\mathrm{Krew}}^{-1}(\Theta_W(A))\right). \end{align*} $$
$$ \begin{align*} \Theta_W\left(\left(\operatorname{\mathrm{Row}}^{-1}\cdot \operatorname{\mathrm{Rvac}}\right) \left(\operatorname{\mathrm{Row}}^{-1}(A)\right)\right) &= \Theta_W\left(\left(\operatorname{\mathrm{Row}}\cdot \operatorname{\mathrm{Row}}^{-1} \operatorname{\mathrm{Rvac}}\right)(A)\right) \\ &= \operatorname{\mathrm{Krew}} \left(\Theta_W\left(\left(\operatorname{\mathrm{Row}}^{-1}\cdot \operatorname{\mathrm{Rvac}}\right)(A)\right)\right) \\ &= \operatorname{\mathrm{Krew}} (\operatorname{\mathrm{Flip}}(\Theta_W(A))) = \operatorname{\mathrm{Flip}}\left( \operatorname{\mathrm{Krew}}^{-1}(\Theta_W(A))\right). \end{align*} $$
For the third bulleted item, we use Lemma 3.6 and the fact that, by definition,
![]() $\Theta _{W_{\operatorname {\mathrm {supp}}(A)}}(A) = \prod _{i \in L\setminus \operatorname {\mathrm {supp}}(A)} s_i \cdot \Theta _W (A)$
to see that
$\Theta _{W_{\operatorname {\mathrm {supp}}(A)}}(A) = \prod _{i \in L\setminus \operatorname {\mathrm {supp}}(A)} s_i \cdot \Theta _W (A)$
to see that
 $$ \begin{align*} \Theta_W\left(\left(\operatorname{\mathrm{Row}}^{-1}\cdot \operatorname{\mathrm{Rvac}}\right)(A)\right) &= \Theta_W\left(\left(\operatorname{\mathrm{Row}}^{-1}\cdot \operatorname{\mathrm{Rvac}}\right)_{\operatorname{\mathrm{supp}}(A)}(A)\right) \\ &= \prod_{i \in L\setminus \operatorname{\mathrm{supp}}(A)} s_i \cdot \Theta_{W_{\operatorname{\mathrm{supp}}(A)}}\left( \left(\operatorname{\mathrm{Row}}^{-1}\cdot \operatorname{\mathrm{Rvac}}\right)_{\operatorname{\mathrm{supp}}(A)} (A)\right) \\ &= \prod_{i \in L\setminus \operatorname{\mathrm{supp}}(A)} s_i \cdot \operatorname{\mathrm{Flip}}_{W_{\operatorname{\mathrm{supp}}(A)}}\left(\Theta_{W_{\operatorname{\mathrm{supp}}(A)}}(A) \right) \\ &= \prod_{i \in L\setminus \operatorname{\mathrm{supp}}(A)} s_i \cdot \operatorname{\mathrm{Flip}}_{W_{\operatorname{\mathrm{supp}}(A)}} \left(\prod_{i \in L\setminus \operatorname{\mathrm{supp}}(A)} s_i \cdot \Theta_W (A) \right)\\ &=\prod_{i \in L\setminus \operatorname{\mathrm{supp}}(A)} s_i \cdot c_{L \cap \operatorname{\mathrm{supp}}(A)} \cdot \Theta_W (A)^{-1} \cdot \prod_{i \in L\setminus \operatorname{\mathrm{supp}}(A)} s_i \cdot c_{L \cap \operatorname{\mathrm{supp}}(A)} \\ &= c_L \left(\Theta_W (A)^{-1}\right) c_L \\ &= \operatorname{\mathrm{Flip}}(\Theta_W (A)). \end{align*} $$
$$ \begin{align*} \Theta_W\left(\left(\operatorname{\mathrm{Row}}^{-1}\cdot \operatorname{\mathrm{Rvac}}\right)(A)\right) &= \Theta_W\left(\left(\operatorname{\mathrm{Row}}^{-1}\cdot \operatorname{\mathrm{Rvac}}\right)_{\operatorname{\mathrm{supp}}(A)}(A)\right) \\ &= \prod_{i \in L\setminus \operatorname{\mathrm{supp}}(A)} s_i \cdot \Theta_{W_{\operatorname{\mathrm{supp}}(A)}}\left( \left(\operatorname{\mathrm{Row}}^{-1}\cdot \operatorname{\mathrm{Rvac}}\right)_{\operatorname{\mathrm{supp}}(A)} (A)\right) \\ &= \prod_{i \in L\setminus \operatorname{\mathrm{supp}}(A)} s_i \cdot \operatorname{\mathrm{Flip}}_{W_{\operatorname{\mathrm{supp}}(A)}}\left(\Theta_{W_{\operatorname{\mathrm{supp}}(A)}}(A) \right) \\ &= \prod_{i \in L\setminus \operatorname{\mathrm{supp}}(A)} s_i \cdot \operatorname{\mathrm{Flip}}_{W_{\operatorname{\mathrm{supp}}(A)}} \left(\prod_{i \in L\setminus \operatorname{\mathrm{supp}}(A)} s_i \cdot \Theta_W (A) \right)\\ &=\prod_{i \in L\setminus \operatorname{\mathrm{supp}}(A)} s_i \cdot c_{L \cap \operatorname{\mathrm{supp}}(A)} \cdot \Theta_W (A)^{-1} \cdot \prod_{i \in L\setminus \operatorname{\mathrm{supp}}(A)} s_i \cdot c_{L \cap \operatorname{\mathrm{supp}}(A)} \\ &= c_L \left(\Theta_W (A)^{-1}\right) c_L \\ &= \operatorname{\mathrm{Flip}}(\Theta_W (A)). \end{align*} $$
Armstrong, Stump and Thomas proved Theorem 3.1 by explicitly constructing the map
![]() $\Theta _W$
in each of the classical types. In the next two sections, we review their constructions in types A and D. Thanks to Theorem 1.5, these explicit constructions will help us understand the effect that
$\Theta _W$
in each of the classical types. In the next two sections, we review their constructions in types A and D. Thanks to Theorem 1.5, these explicit constructions will help us understand the effect that
![]() $\operatorname {\mathrm {Rvac}}$
has on an antichain
$\operatorname {\mathrm {Rvac}}$
has on an antichain
![]() $A\in \mathcal {A}(\Phi ^+(D_n))$
.
$A\in \mathcal {A}(\Phi ^+(D_n))$
.
4 The AST bijection in type A
In this section, we review the construction of the Armstong–Stump–Thomas bijection in type A. It uses noncrossing matchings.
Let
![]() $A=\{[i_1,j_1],\ldots ,[i_m,j_m]\} \in \mathcal {A}(\Phi ^+(A_{n-1}))$
, with
$A=\{[i_1,j_1],\ldots ,[i_m,j_m]\} \in \mathcal {A}(\Phi ^+(A_{n-1}))$
, with
![]() $i_1< \cdots < i_m$
. Place
$i_1< \cdots < i_m$
. Place
![]() $2n$
vertices labelled
$2n$
vertices labelled
![]() $1^{(0)},2^{(0)},\ldots ,n^{(0)},n^{(1)},\ldots ,2^{(1)},1^{(1)}$
in clockwise order at evenly-spaced positions around a circle. For
$1^{(0)},2^{(0)},\ldots ,n^{(0)},n^{(1)},\ldots ,2^{(1)},1^{(1)}$
in clockwise order at evenly-spaced positions around a circle. For
![]() $1\leq \ell \leq m$
, add a marker on the vertex
$1\leq \ell \leq m$
, add a marker on the vertex
 $j_\ell ^{(0)}$
with marking
$j_\ell ^{(0)}$
with marking
![]() $i_\ell $
. Then for each
$i_\ell $
. Then for each
![]() $i\in [n]\setminus \{i_1,\ldots ,i_m\}$
, add a marker on
$i\in [n]\setminus \{i_1,\ldots ,i_m\}$
, add a marker on
![]() $i^{(1)}$
with marking i. We now add n (straight) edges to the configuration, one at a time. The ith edge that we add connects the vertex with marking i to the closest unmarked vertex that is not already connected to an edge. Here, ‘closest’ is determined by moving counterclockwise from the vertex with marking i if that vertex has a
$i^{(1)}$
with marking i. We now add n (straight) edges to the configuration, one at a time. The ith edge that we add connects the vertex with marking i to the closest unmarked vertex that is not already connected to an edge. Here, ‘closest’ is determined by moving counterclockwise from the vertex with marking i if that vertex has a
![]() $(0)$
superscript and clockwise from that vertex if it has a
$(0)$
superscript and clockwise from that vertex if it has a
![]() $(1)$
superscript. The resulting diagram is denoted by
$(1)$
superscript. The resulting diagram is denoted by
![]() $\psi _{A_{n-1}}(A)$
. The markings are only used to help with the construction of
$\psi _{A_{n-1}}(A)$
. The markings are only used to help with the construction of
![]() $\psi _{A_{n-1}}(A)$
; we do not consider them to be part of the diagram.
$\psi _{A_{n-1}}(A)$
; we do not consider them to be part of the diagram.
Example 4.1. If A is the antichain
![]() $\{[1,3],[2,6],[3,7],[4,8],[5,9],[8,10]\}$
in
$\{[1,3],[2,6],[3,7],[4,8],[5,9],[8,10]\}$
in
![]() $\Phi ^+(A_9)$
shown on the top of Figure 6, then
$\Phi ^+(A_9)$
shown on the top of Figure 6, then
![]() $\psi _{A_9}(A)$
is the diagram shown on the bottom. The markings (which are not considered to be part of the diagram
$\psi _{A_9}(A)$
is the diagram shown on the bottom. The markings (which are not considered to be part of the diagram
![]() $\psi _{A_9}(A)$
) are represented by purple numbers. For example, the fact that
$\psi _{A_9}(A)$
) are represented by purple numbers. For example, the fact that
![]() $[1,3]\in A$
tells us that the vertex
$[1,3]\in A$
tells us that the vertex
![]() $3^{(0)}$
should be given the marking
$3^{(0)}$
should be given the marking
![]() ${\color {purple}1}$
. Once the markings are placed, the edges are drawn as prescribed.
${\color {purple}1}$
. Once the markings are placed, the edges are drawn as prescribed.

Figure 6 An antichain
![]() $A\in \mathcal A(\Phi ^+(A_9))$
(top) and the corresponding diagram
$A\in \mathcal A(\Phi ^+(A_9))$
(top) and the corresponding diagram
![]() $\psi _{A_9}(A)$
(bottom).
$\psi _{A_9}(A)$
(bottom).
The next step is to relabel the vertices in
![]() $\psi _{A_{n-1}}(A)$
according to a bipartite Coxeter element
$\psi _{A_{n-1}}(A)$
according to a bipartite Coxeter element
![]() $c=c_Lc_R\in W(A_{n-1})$
. We choose
$c=c_Lc_R\in W(A_{n-1})$
. We choose
![]() $L\sqcup R$
to be the unique bipartition of the Dynkin diagram of
$L\sqcup R$
to be the unique bipartition of the Dynkin diagram of
![]() $\Phi (A_{n-1})$
such that
$\Phi (A_{n-1})$
such that
![]() $1\in L$
. This means that
$1\in L$
. This means that
![]() $c_L=s_1s_3\cdots s_{n-2}$
if n is odd and
$c_L=s_1s_3\cdots s_{n-2}$
if n is odd and
![]() $c_L=s_1s_3\cdots s_{n-1}$
if n is even. Let
$c_L=s_1s_3\cdots s_{n-1}$
if n is even. Let
![]() $p_1,\ldots ,p_n$
be the sequence obtained by listing the even elements of
$p_1,\ldots ,p_n$
be the sequence obtained by listing the even elements of
![]() $[n]$
in increasing order and then listing the odd elements of
$[n]$
in increasing order and then listing the odd elements of
![]() $[n]$
in decreasing order. The cycle decomposition of c (viewed as a permutation in
$[n]$
in decreasing order. The cycle decomposition of c (viewed as a permutation in
![]() $\mathfrak S_n$
) is
$\mathfrak S_n$
) is
![]() $(p_1,\ldots ,p_n)$
. In the diagram
$(p_1,\ldots ,p_n)$
. In the diagram
![]() $\psi _{A_{n-1}}(A)$
, relabel the vertices
$\psi _{A_{n-1}}(A)$
, relabel the vertices
![]() $1^{(0)},2^{(0)},\ldots ,n^{(0)},n^{(1)},\ldots ,2^{(1)},1^{(1)}$
as
$1^{(0)},2^{(0)},\ldots ,n^{(0)},n^{(1)},\ldots ,2^{(1)},1^{(1)}$
as
 $p_1^{(0)},p_1^{(1)},p_2^{(0)},p_2^{(1)},\ldots ,p_n^{(0)},p_n^{(1)}$
, respectively. Let us call the relabelled diagram
$p_1^{(0)},p_1^{(1)},p_2^{(0)},p_2^{(1)},\ldots ,p_n^{(0)},p_n^{(1)}$
, respectively. Let us call the relabelled diagram
![]() $\varphi _{A_{n-1}}(A)$
.
$\varphi _{A_{n-1}}(A)$
.
In [Reference Armstrong, Stump and Thomas2], it is shown that
![]() $\varphi _{A_{n-1}}(A)$
is a noncrossing matching, meaning that each vertex is incident to exactly one edge and that no two edges cross each other. Furthermore, each edge has one endpoint with a
$\varphi _{A_{n-1}}(A)$
is a noncrossing matching, meaning that each vertex is incident to exactly one edge and that no two edges cross each other. Furthermore, each edge has one endpoint with a
![]() $(0)$
superscript and one endpoint with a
$(0)$
superscript and one endpoint with a
![]() $(1)$
superscript. This allows us to define a permutation
$(1)$
superscript. This allows us to define a permutation
![]() $w\in \mathfrak S_n$
by declaring
$w\in \mathfrak S_n$
by declaring
![]() $w(i)=j$
whenever
$w(i)=j$
whenever
![]() $i^{(1)}$
is connected to
$i^{(1)}$
is connected to
![]() $j^{(0)}$
via an edge in
$j^{(0)}$
via an edge in
![]() $\varphi _{A_{n-1}}(A)$
. Armstrong, Stump and Thomas proved that this definition yields the bijection
$\varphi _{A_{n-1}}(A)$
. Armstrong, Stump and Thomas proved that this definition yields the bijection
![]() $\Theta _{W\left (A_{n-1}\right )}$
from Theorem 3.1.
$\Theta _{W\left (A_{n-1}\right )}$
from Theorem 3.1.
Theorem 4.2 [Reference Armstrong, Stump and Thomas2, §3.1]
Let
![]() $\Theta _{W\left (A_{n-1}\right )}\colon \mathcal A(\Phi ^+(A_{n-1}))\to \operatorname {\mathrm {NC}}(W(A_{n-1}),c)$
be the bijection from Theorem 3.1, where
$\Theta _{W\left (A_{n-1}\right )}\colon \mathcal A(\Phi ^+(A_{n-1}))\to \operatorname {\mathrm {NC}}(W(A_{n-1}),c)$
be the bijection from Theorem 3.1, where
![]() $c=c_Lc_R=(p_1,\ldots ,p_n)$
is the bipartite Coxeter element already defined. Then we have
$c=c_Lc_R=(p_1,\ldots ,p_n)$
is the bipartite Coxeter element already defined. Then we have
![]() $\Theta _{W\left (A_{n-1}\right )}(A)(i)=j$
if and only if
$\Theta _{W\left (A_{n-1}\right )}(A)(i)=j$
if and only if
![]() $i^{(1)}$
is connected to
$i^{(1)}$
is connected to
![]() $j^{(0)}$
via an edge in
$j^{(0)}$
via an edge in
![]() $\varphi _{A_{n-1}}(A)$
, for every
$\varphi _{A_{n-1}}(A)$
, for every
![]() $A\in \mathcal A(\Phi ^+(A_{n-1}))$
.
$A\in \mathcal A(\Phi ^+(A_{n-1}))$
.
Example 4.3. Let A be as in Example 4.1. By relabelling the vertices of
![]() $\psi _{A_{9}}(A)$
in the manner described, we obtain the diagram
$\psi _{A_{9}}(A)$
in the manner described, we obtain the diagram
![]() $\varphi _{A_{9}}(A)$
shown on the left in Figure 7. Theorem 4.2 tells us that
$\varphi _{A_{9}}(A)$
shown on the left in Figure 7. Theorem 4.2 tells us that
![]() $\Theta _{W\left (A_9\right )}(A)\in \operatorname {\mathrm {NC}}(W(A_9),c)$
is the permutation in
$\Theta _{W\left (A_9\right )}(A)\in \operatorname {\mathrm {NC}}(W(A_9),c)$
is the permutation in
![]() $\mathfrak S_{10}$
with cycle decomposition
$\mathfrak S_{10}$
with cycle decomposition
![]() $(1,10)(2,4,8)(3,9,7)(5)(6)$
.
$(1,10)(2,4,8)(3,9,7)(5)(6)$
.

Figure 7 The diagrams
![]() $\varphi _{A_{9}}(A)$
(left) and
$\varphi _{A_{9}}(A)$
(left) and
![]() $\varphi _{A_9}(\operatorname {\mathrm {Row}}\cdot \operatorname {\mathrm {Rvac}}(A))$
(right), where A is the antichain from Example 4.1. We have also drawn the line M in each diagram. Note that
$\varphi _{A_9}(\operatorname {\mathrm {Row}}\cdot \operatorname {\mathrm {Rvac}}(A))$
(right), where A is the antichain from Example 4.1. We have also drawn the line M in each diagram. Note that
![]() $\varphi _{A_9}(\operatorname {\mathrm {Row}}\cdot \operatorname {\mathrm {Rvac}}(A))$
is obtained from
$\varphi _{A_9}(\operatorname {\mathrm {Row}}\cdot \operatorname {\mathrm {Rvac}}(A))$
is obtained from
![]() $\varphi _{A_9}(A)$
by reflecting the edges through M.
$\varphi _{A_9}(A)$
by reflecting the edges through M.
To end this section, we find a simple relationship between the diagrams
![]() $\varphi _{A_{n-1}}(A)$
and
$\varphi _{A_{n-1}}(A)$
and
![]() $\varphi _{A_{n-1}}(\operatorname {\mathrm {Row}}\cdot \operatorname {\mathrm {Rvac}}(A))$
that we will need later. By combining Proposition 2.6 with Theorem 1.5 and 3.1, we find that
$\varphi _{A_{n-1}}(\operatorname {\mathrm {Row}}\cdot \operatorname {\mathrm {Rvac}}(A))$
that we will need later. By combining Proposition 2.6 with Theorem 1.5 and 3.1, we find that
 $$ \begin{align*} \Theta_{W\left(A_{n-1}\right)}\cdot\operatorname{\mathrm{Row}}\cdot\operatorname{\mathrm{Rvac}}=\Theta_{W\left(A_{n-1}\right)}\cdot\operatorname{\mathrm{Row}}^2\cdot\operatorname{\mathrm{Row}}^{-1}\cdot\operatorname{\mathrm{Rvac}}=\operatorname{\mathrm{Krew}}^2\cdot\operatorname{\mathrm{Flip}} \cdot\Theta_{W\left(A_{n-1}\right)}, \end{align*} $$
$$ \begin{align*} \Theta_{W\left(A_{n-1}\right)}\cdot\operatorname{\mathrm{Row}}\cdot\operatorname{\mathrm{Rvac}}=\Theta_{W\left(A_{n-1}\right)}\cdot\operatorname{\mathrm{Row}}^2\cdot\operatorname{\mathrm{Row}}^{-1}\cdot\operatorname{\mathrm{Rvac}}=\operatorname{\mathrm{Krew}}^2\cdot\operatorname{\mathrm{Flip}} \cdot\Theta_{W\left(A_{n-1}\right)}, \end{align*} $$
so
 $$ \begin{align*} \Theta_{W\left(A_{n-1}\right)}(\operatorname{\mathrm{Row}}\cdot \operatorname{\mathrm{Rvac}}(A))&=\operatorname{\mathrm{Krew}}^2\cdot \operatorname{\mathrm{Flip}}\left(\Theta_{W\left(A_{n-1}\right)}(A)\right)=c\operatorname{\mathrm{Flip}}\left(\Theta_{W\left(A_{n-1}\right)}(A)\right)c^{-1}\\ &=c_Lc_Rc_L\Theta_{W\left(A_{n-1}\right)}(A)^{-1}c_Lc_Rc_L. \end{align*} $$
$$ \begin{align*} \Theta_{W\left(A_{n-1}\right)}(\operatorname{\mathrm{Row}}\cdot \operatorname{\mathrm{Rvac}}(A))&=\operatorname{\mathrm{Krew}}^2\cdot \operatorname{\mathrm{Flip}}\left(\Theta_{W\left(A_{n-1}\right)}(A)\right)=c\operatorname{\mathrm{Flip}}\left(\Theta_{W\left(A_{n-1}\right)}(A)\right)c^{-1}\\ &=c_Lc_Rc_L\Theta_{W\left(A_{n-1}\right)}(A)^{-1}c_Lc_Rc_L. \end{align*} $$
In each of the diagrams
![]() $\varphi _{A_{n-1}}(A)$
and
$\varphi _{A_{n-1}}(A)$
and
![]() $\varphi _{A_{n-1}}(\operatorname {\mathrm {Row}} \cdot \operatorname {\mathrm {Rvac}}(A))$
, let M be the line through the centre of the circle that is equidistant from
$\varphi _{A_{n-1}}(\operatorname {\mathrm {Row}} \cdot \operatorname {\mathrm {Rvac}}(A))$
, let M be the line through the centre of the circle that is equidistant from
![]() $2^{(0)}$
and
$2^{(0)}$
and
![]() $2^{(1)}$
, as shown in Figure 7. Let
$2^{(1)}$
, as shown in Figure 7. Let
![]() $\Omega $
be the reflection of the plane through the line M. We think of
$\Omega $
be the reflection of the plane through the line M. We think of
![]() $\Omega $
as acting on the diagrams
$\Omega $
as acting on the diagrams
![]() $\varphi _{A_{n-1}}(A)$
and
$\varphi _{A_{n-1}}(A)$
and
![]() $\varphi _{A_{n-1}}(\operatorname {\mathrm {Row}}\cdot \operatorname {\mathrm {Rvac}}(A))$
. For each
$\varphi _{A_{n-1}}(\operatorname {\mathrm {Row}}\cdot \operatorname {\mathrm {Rvac}}(A))$
. For each
![]() $i\in [n]$
, we readily compute that
$i\in [n]$
, we readily compute that
 $\Omega \left (i^{(0)}\right )=(c_Lc_Rc_L(i))^{(1)}$
and
$\Omega \left (i^{(0)}\right )=(c_Lc_Rc_L(i))^{(1)}$
and
 $\Omega \left (i^{(1)}\right )=(c_Lc_Rc_L(i))^{(0)}$
. With these observations in hand, the next lemma follows immediately from Theorem 4.2. Figure 7 illustrates this lemma.
$\Omega \left (i^{(1)}\right )=(c_Lc_Rc_L(i))^{(0)}$
. With these observations in hand, the next lemma follows immediately from Theorem 4.2. Figure 7 illustrates this lemma.
Lemma 4.4. Let
![]() $A\in \mathcal A(\Phi ^+(A))$
, and preserve the notation from before. The diagram
$A\in \mathcal A(\Phi ^+(A))$
, and preserve the notation from before. The diagram
![]() $\varphi _{A_{n-1}}(\operatorname {\mathrm {Row}}\cdot \operatorname {\mathrm {Rvac}}(A))$
is obtained from
$\varphi _{A_{n-1}}(\operatorname {\mathrm {Row}}\cdot \operatorname {\mathrm {Rvac}}(A))$
is obtained from
![]() $\varphi _{A_{n-1}}(A)$
by reflecting all of the edges through the line M (and leaving the vertices unchanged).
$\varphi _{A_{n-1}}(A)$
by reflecting all of the edges through the line M (and leaving the vertices unchanged).
5 The AST bijection in type D
In this section, we review the pieces of the Armstrong–Stump–Thomas bijection in type D that we will need later. We then use those pieces to prove a lemma that will be crucial in the next section.
Recall from Section 2.1 the automorphism
![]() $\delta \colon \Phi ^+(D_n)\to \Phi ^+(D_n)$
, the natural quotient map
$\delta \colon \Phi ^+(D_n)\to \Phi ^+(D_n)$
, the natural quotient map
![]() $\gamma \colon \Phi ^+(D_n)\to \Phi ^+(C_{n-1})$
induced by
$\gamma \colon \Phi ^+(D_n)\to \Phi ^+(C_{n-1})$
induced by
![]() $\delta $
, and the natural inclusion
$\delta $
, and the natural inclusion
![]() $\iota \colon \mathcal P(\Phi ^+(C_{n-1}))\to \mathcal P(\Phi ^+(A_{2n-3}))$
obtained by ‘unfolding’.
$\iota \colon \mathcal P(\Phi ^+(C_{n-1}))\to \mathcal P(\Phi ^+(A_{2n-3}))$
obtained by ‘unfolding’.
The antichains A of
![]() $\Phi ^+(D_n)$
with
$\Phi ^+(D_n)$
with
![]() $\delta (A)=A$
descend to antichains of
$\delta (A)=A$
descend to antichains of
![]() $\Phi ^+(C_{n-1})$
and so are easily dealt with. Thus, in this section, we fix an
$\Phi ^+(C_{n-1})$
and so are easily dealt with. Thus, in this section, we fix an
![]() $A \in \mathcal {A}(\Phi ^+(D_n))$
for which
$A \in \mathcal {A}(\Phi ^+(D_n))$
for which
![]() $\delta (A)\neq A$
. Then
$\delta (A)\neq A$
. Then
![]() $\iota (\gamma (A))$
is a subset of
$\iota (\gamma (A))$
is a subset of
![]() $\Phi ^+(A_{2n-3})$
that is symmetric about the central vertical axis. Note that
$\Phi ^+(A_{2n-3})$
that is symmetric about the central vertical axis. Note that
![]() $\iota (\gamma (A))$
is not necessarily an antichain. As before, we identify the elements of
$\iota (\gamma (A))$
is not necessarily an antichain. As before, we identify the elements of
![]() $\Phi ^+(A_{2n-3})$
with the intervals
$\Phi ^+(A_{2n-3})$
with the intervals
![]() $[i,j]\subseteq [2n-2]$
, with
$[i,j]\subseteq [2n-2]$
, with
![]() $1\leq i<j\leq 2n-2$
. Let
$1\leq i<j\leq 2n-2$
. Let
![]() $\mathcal {Q}$
be the set of elements
$\mathcal {Q}$
be the set of elements
![]() $[i,j]\in \Phi ^+(A_{2n-3})$
such that
$[i,j]\in \Phi ^+(A_{2n-3})$
such that
![]() $i\leq n-1$
and
$i\leq n-1$
and
![]() $j\geq n$
. Equivalently,
$j\geq n$
. Equivalently,
![]() $\mathcal Q$
consists of the elements greater than or equal to the minimal element
$\mathcal Q$
consists of the elements greater than or equal to the minimal element
![]() $[n-1,n]$
. Let
$[n-1,n]$
. Let
![]() $[i_1,j_1],\ldots ,[i_k,j_k]$
be the elements of
$[i_1,j_1],\ldots ,[i_k,j_k]$
be the elements of
![]() $\iota (\gamma (A))\cap \mathcal {Q}$
written in lexicographic order. (Note that
$\iota (\gamma (A))\cap \mathcal {Q}$
written in lexicographic order. (Note that
![]() $\delta (A)\neq A$
implies
$\delta (A)\neq A$
implies
![]() $k\geq 1$
.) Let
$k\geq 1$
.) Let
![]() $\widehat A$
be the set of elements of
$\widehat A$
be the set of elements of
![]() $\Phi ^+(A_{2n-3})$
obtained from
$\Phi ^+(A_{2n-3})$
obtained from
![]() $\iota (\gamma (A))$
by removing the elements of
$\iota (\gamma (A))$
by removing the elements of
![]() $\iota (\gamma (A))\cap \mathcal {Q}$
and replacing them with
$\iota (\gamma (A))\cap \mathcal {Q}$
and replacing them with
![]() $[i_1,j_2],[i_2,j_3],\ldots ,[i_{k-1},j_k]$
. From [Reference Armstrong, Stump and Thomas2],
$[i_1,j_2],[i_2,j_3],\ldots ,[i_{k-1},j_k]$
. From [Reference Armstrong, Stump and Thomas2],
![]() $\widehat A$
is an antichain of
$\widehat A$
is an antichain of
![]() $\Phi ^+(A_{2n-3})$
that is symmetric about the central vertical axis – that is, with
$\Phi ^+(A_{2n-3})$
that is symmetric about the central vertical axis – that is, with
 $\eta \left (\widehat {A}\right )=\widehat {A}$
.
$\eta \left (\widehat {A}\right )=\widehat {A}$
.
Example 5.1. If A is the antichain of
![]() $\Phi ^+(D_6)$
shown in red in the top left of Figure 8, then
$\Phi ^+(D_6)$
shown in red in the top left of Figure 8, then
![]() $\iota (\gamma (A))$
is the subset of
$\iota (\gamma (A))$
is the subset of
![]() $\Phi ^+(A_9)$
shown in red in the top right. The set
$\Phi ^+(A_9)$
shown in red in the top right. The set
![]() $\mathcal {Q}$
consists of the elements of
$\mathcal {Q}$
consists of the elements of
![]() $\Phi ^+(A_9)$
lying inside the green square in the figure. The elements of
$\Phi ^+(A_9)$
lying inside the green square in the figure. The elements of
![]() $\iota (\gamma (A))\cap \mathcal {Q}$
are
$\iota (\gamma (A))\cap \mathcal {Q}$
are
![]() $[2,6]$
,
$[2,6]$
,
![]() $[3,6]$
,
$[3,6]$
,
![]() $[4,7]$
,
$[4,7]$
,
![]() $[5,8]$
and
$[5,8]$
and
![]() $[5,9]$
;
$[5,9]$
;
![]() $\widehat A\in \mathcal A(\Phi ^+(A_9))$
is obtained from
$\widehat A\in \mathcal A(\Phi ^+(A_9))$
is obtained from
![]() $\iota (\gamma (A))$
by replacing these five elements with
$\iota (\gamma (A))$
by replacing these five elements with
![]() $[2,6]$
,
$[2,6]$
,
![]() $[3,7]$
,
$[3,7]$
,
![]() $[4,8]$
and
$[4,8]$
and
![]() $[5,9]$
. Notice that
$[5,9]$
. Notice that
![]() $\widehat A$
, which is depicted in red in the bottom of Figure 8, is indeed an antichain of
$\widehat A$
, which is depicted in red in the bottom of Figure 8, is indeed an antichain of
![]() $\Phi ^+(A_9)$
. In fact,
$\Phi ^+(A_9)$
. In fact,
![]() $\widehat A$
is the same as the antichain from Figure 6.
$\widehat A$
is the same as the antichain from Figure 6.

Figure 8 From the antichain
![]() $A\in \mathcal A(\Phi ^+(D_6))$
(top left), we obtain the set
$A\in \mathcal A(\Phi ^+(D_6))$
(top left), we obtain the set
![]() $\iota (\gamma (A))\subseteq \Phi ^+(A_9)$
(top right) and the antichain
$\iota (\gamma (A))\subseteq \Phi ^+(A_9)$
(top right) and the antichain
![]() $\widehat A\in \mathcal A(\Phi ^+(A_9))$
(bottom). Note that
$\widehat A\in \mathcal A(\Phi ^+(A_9))$
(bottom). Note that
![]() $\iota (\gamma (A))$
is not an antichain.
$\iota (\gamma (A))$
is not an antichain.
Since
![]() $\widehat A$
is an antichain of
$\widehat A$
is an antichain of
![]() $\Phi ^+(A_{2n-3})$
, we can consider the diagram
$\Phi ^+(A_{2n-3})$
, we can consider the diagram
 $\varphi _{A_{2n-3}}\left (\widehat A\right )$
defined in Section 4. Recall that M is the line through the centre of the circle that is equidistant from
$\varphi _{A_{2n-3}}\left (\widehat A\right )$
defined in Section 4. Recall that M is the line through the centre of the circle that is equidistant from
![]() $2^{(0)}$
and
$2^{(0)}$
and
![]() $2^{(1)}$
. Let
$2^{(1)}$
. Let
![]() $M^\perp $
denote the line through the centre of the circle that is perpendicular to M. Let H be the set of vertices in the diagram that are on the same side of
$M^\perp $
denote the line through the centre of the circle that is perpendicular to M. Let H be the set of vertices in the diagram that are on the same side of
![]() $M^\perp $
as
$M^\perp $
as
![]() $2^{(0)}$
, and let
$2^{(0)}$
, and let
![]() $\overline H$
be the set of vertices in the diagram that are on the opposite side of
$\overline H$
be the set of vertices in the diagram that are on the opposite side of
![]() $M^\perp $
. We say an edge in the diagram is transverse if it has one endpoint in H and one endpoint in
$M^\perp $
. We say an edge in the diagram is transverse if it has one endpoint in H and one endpoint in
![]() $\overline H$
. From [Reference Armstrong, Stump and Thomas2] we have the implication that there are at least two transverse edges in
$\overline H$
. From [Reference Armstrong, Stump and Thomas2] we have the implication that there are at least two transverse edges in
 $\varphi _{A_{2n-3}}\left (\widehat A\right )$
; by removing the two transverse edges that are closest to the centre of the circle, we obtain a new diagram that we denote by
$\varphi _{A_{2n-3}}\left (\widehat A\right )$
; by removing the two transverse edges that are closest to the centre of the circle, we obtain a new diagram that we denote by
 $\xi _{A_{2n-3}}\left (\widehat A\right )$
.
$\xi _{A_{2n-3}}\left (\widehat A\right )$
.
We now relabel the vertices in
 $\xi _{A_{2n-3}}\left (\widehat A\right )$
according to a bipartite Coxeter element
$\xi _{A_{2n-3}}\left (\widehat A\right )$
according to a bipartite Coxeter element
![]() $c=c_Lc_R\in W(D_n)$
. We choose
$c=c_Lc_R\in W(D_n)$
. We choose
![]() $L\sqcup R$
to be the unique bipartition of the Dynkin diagram of
$L\sqcup R$
to be the unique bipartition of the Dynkin diagram of
![]() $\Phi (D_n)$
such that
$\Phi (D_n)$
such that
![]() $1\in L$
. This means that
$1\in L$
. This means that
![]() $c_L=s_1s_3\cdots s_{n-4}s_{n-2}$
if n is odd and
$c_L=s_1s_3\cdots s_{n-4}s_{n-2}$
if n is odd and
![]() $c_L=s_1s_3\cdots s_{n-3}s_{n-1}s_n$
if n is even. Let
$c_L=s_1s_3\cdots s_{n-3}s_{n-1}s_n$
if n is even. Let
![]() $q_1,\ldots ,q_{2n-2}$
be the sequence of numbers obtained by listing the even elements of
$q_1,\ldots ,q_{2n-2}$
be the sequence of numbers obtained by listing the even elements of
![]() $[n-1]$
in increasing order, then listing the odd elements of
$[n-1]$
in increasing order, then listing the odd elements of
![]() $-[n-1]$
in increasing order, then listing the even elements of
$-[n-1]$
in increasing order, then listing the even elements of
![]() $-[n-1]$
in decreasing order and finally listing the odd elements of
$-[n-1]$
in decreasing order and finally listing the odd elements of
![]() $[n-1]$
in decreasing order. The cycle decomposition of c is
$[n-1]$
in decreasing order. The cycle decomposition of c is
![]() $(q_1,\ldots ,q_{2n-2})(n,-n)$
. Relabel the vertices in the diagram
$(q_1,\ldots ,q_{2n-2})(n,-n)$
. Relabel the vertices in the diagram
 $\xi _{A_{2n-3}}\left (\widehat A\right )$
, starting at
$\xi _{A_{2n-3}}\left (\widehat A\right )$
, starting at
![]() $2^{(0)}$
and moving clockwise, as
$2^{(0)}$
and moving clockwise, as
 $$ \begin{align*} q_1^{(0)},q_1^{(1)},q_2^{(0)},q_2^{(1)},\ldots,q_{2n-2}^{(0)},q_{2n-2}^{(1)}. \end{align*} $$
$$ \begin{align*} q_1^{(0)},q_1^{(1)},q_2^{(0)},q_2^{(1)},\ldots,q_{2n-2}^{(0)},q_{2n-2}^{(1)}. \end{align*} $$
Let us call the relabelled diagram
![]() $\varphi _{D_n}(A)$
.
$\varphi _{D_n}(A)$
.
Example 5.2. Let A and
![]() $\widehat A$
be as in Example 5.1. The diagram
$\widehat A$
be as in Example 5.1. The diagram
 $\varphi _{A_9}\left (\widehat A\right )$
, which we computed in Example 4.3, is drawn again on the left in Figure 9. We have now included the line
$\varphi _{A_9}\left (\widehat A\right )$
, which we computed in Example 4.3, is drawn again on the left in Figure 9. We have now included the line
![]() $M^\perp $
in the figure. Furthermore, we have coloured the vertices in H red and the vertices in
$M^\perp $
in the figure. Furthermore, we have coloured the vertices in H red and the vertices in
![]() $\overline H$
blue. The two transverse edges that are closest to the centre of the circle are the one connecting
$\overline H$
blue. The two transverse edges that are closest to the centre of the circle are the one connecting
![]() $1^{(1)}$
to
$1^{(1)}$
to
![]() $10^{(0)}$
and the one connecting
$10^{(0)}$
and the one connecting
![]() $10^{(1)}$
to
$10^{(1)}$
to
![]() $1^{(0)}$
; these two edges are removed to produce
$1^{(0)}$
; these two edges are removed to produce
 $\xi _{A_9}\left (\widehat A\right )$
. After relabelling the vertices of
$\xi _{A_9}\left (\widehat A\right )$
. After relabelling the vertices of
 $\xi _{A_9}\left (\widehat A\right )$
in the manner already described, we obtain the diagram
$\xi _{A_9}\left (\widehat A\right )$
in the manner already described, we obtain the diagram
![]() $\varphi _{D_6}(A)$
shown on the right in Figure 9.
$\varphi _{D_6}(A)$
shown on the right in Figure 9.

Figure 9 The diagrams
 $\varphi _{A_9}(\widehat A)$
(left) and
$\varphi _{A_9}(\widehat A)$
(left) and
![]() $\varphi _{D_6}(A)$
(right) from Example 5.2.
$\varphi _{D_6}(A)$
(right) from Example 5.2.
Armstrong, Stump and Thomas used the diagrams we have constructed in this section to give an explicit description of the map
![]() $\Theta _{W\left (D_n\right )}$
. We will need only part of their description, which we state in the following theorem. Recall that we view
$\Theta _{W\left (D_n\right )}$
. We will need only part of their description, which we state in the following theorem. Recall that we view
![]() $W(D_n)$
as the group of permutations w of
$W(D_n)$
as the group of permutations w of
![]() $(-[n])\cup [n]$
such that
$(-[n])\cup [n]$
such that
![]() $w(-i)=-w(i)$
for all
$w(-i)=-w(i)$
for all
![]() $i\in [n]$
and such that
$i\in [n]$
and such that
![]() $\#\{i\in [n]:w(i)<0\}$
is even.
$\#\{i\in [n]:w(i)<0\}$
is even.
Theorem 5.3 [Reference Armstrong, Stump and Thomas2, §3.3]
Let
![]() $\Theta _{W\left (D_n\right )}\colon \mathcal A(\Phi ^+(D_n))\to \operatorname {\mathrm {NC}}(W(D_n),c)$
be the bijection from Theorem 3.1, where
$\Theta _{W\left (D_n\right )}\colon \mathcal A(\Phi ^+(D_n))\to \operatorname {\mathrm {NC}}(W(D_n),c)$
be the bijection from Theorem 3.1, where
![]() $c=c_Lc_R=(q_1,\ldots ,q_{2n-2})(n,-n)$
is the bipartite Coxeter element previously defined. Let
$c=c_Lc_R=(q_1,\ldots ,q_{2n-2})(n,-n)$
is the bipartite Coxeter element previously defined. Let
![]() $A\in \mathcal A(\Phi ^+(D_n))$
be such that
$A\in \mathcal A(\Phi ^+(D_n))$
be such that
![]() $\delta (A)\neq A$
. The diagram
$\delta (A)\neq A$
. The diagram
![]() $\varphi _{D_n}(A)$
defined previously is left unchanged if we rotate each of the edges by
$\varphi _{D_n}(A)$
defined previously is left unchanged if we rotate each of the edges by
![]() $180^\circ $
about the centre of the circle. If there is an edge in
$180^\circ $
about the centre of the circle. If there is an edge in
![]() $\varphi _{D_n}(A)$
with endpoints
$\varphi _{D_n}(A)$
with endpoints
![]() $i^{(1)}$
and
$i^{(1)}$
and
![]() $j^{(0)}$
, then
$j^{(0)}$
, then
![]() $\Theta _{W\left (D_n\right )}(A)(i)=j$
. There exist
$\Theta _{W\left (D_n\right )}(A)(i)=j$
. There exist
![]() $x_A,y_A\in [n-1]$
such that the four vertices of
$x_A,y_A\in [n-1]$
such that the four vertices of
![]() $\varphi _{D_n}(A)$
not incident to any edges are
$\varphi _{D_n}(A)$
not incident to any edges are
 $x_A^{(0)},-x_A^{(0)},y_A^{(1)},-y_A^{(1)}$
and such that
$x_A^{(0)},-x_A^{(0)},y_A^{(1)},-y_A^{(1)}$
and such that
![]() $\Theta _{W\left (D_n\right )}(A)(\{n,-n\})=\{x_A,-x_A\}$
and
$\Theta _{W\left (D_n\right )}(A)(\{n,-n\})=\{x_A,-x_A\}$
and
![]() $\Theta _{W\left (D_n\right )}(A)(\{y_A,-y_A\})=\{n,-n\}$
.
$\Theta _{W\left (D_n\right )}(A)(\{y_A,-y_A\})=\{n,-n\}$
.
Example 5.4. Let A be as in Examples 5.1
and 5.2. The diagram
![]() $\varphi _{D_6}(A)$
(shown on the right in Figure 9) is clearly left unchanged when its edges are rotated by
$\varphi _{D_6}(A)$
(shown on the right in Figure 9) is clearly left unchanged when its edges are rotated by
![]() $180^\circ $
about the centre of the circle. Theorem 5.3 tells us that most of the values of
$180^\circ $
about the centre of the circle. Theorem 5.3 tells us that most of the values of
![]() $\Theta _{W\left (D_6\right )}(A)$
are determined by
$\Theta _{W\left (D_6\right )}(A)$
are determined by
![]() $\varphi _{D_6}(A)$
. For example, the edge between
$\varphi _{D_6}(A)$
. For example, the edge between
![]() $-3^{(1)}$
and
$-3^{(1)}$
and
![]() $2^{(0)}$
tells us that
$2^{(0)}$
tells us that
![]() $\Theta _{W\left (D_6\right )}(A)(-3)=2$
. In this example,
$\Theta _{W\left (D_6\right )}(A)(-3)=2$
. In this example,
![]() $x_A=y_A=1$
, so Theorem 5.3 tells us that
$x_A=y_A=1$
, so Theorem 5.3 tells us that
![]() $\Theta _{W\left (D_6\right )}(A)(\{1,-1\})=\{6,-6\}$
and
$\Theta _{W\left (D_6\right )}(A)(\{1,-1\})=\{6,-6\}$
and
![]() $\Theta _{W\left (D_6\right )}(A)(\{6,-6\})=\{1,-1\}$
.
$\Theta _{W\left (D_6\right )}(A)(\{6,-6\})=\{1,-1\}$
.
We are now in a position to prove the main lemma of this section, which states that
 $\operatorname {\mathrm {Row}} \cdot \operatorname {\mathrm {Rvac}}\left (\widehat A\right )=\widehat {\operatorname {\mathrm {Row}}\cdot \operatorname {\mathrm {Rvac}}(A)}$
. When we compute
$\operatorname {\mathrm {Row}} \cdot \operatorname {\mathrm {Rvac}}\left (\widehat A\right )=\widehat {\operatorname {\mathrm {Row}}\cdot \operatorname {\mathrm {Rvac}}(A)}$
. When we compute
 $\operatorname {\mathrm {Row}}\cdot \operatorname {\mathrm {Rvac}}\left (\widehat A\right )$
, we are viewing
$\operatorname {\mathrm {Row}}\cdot \operatorname {\mathrm {Rvac}}\left (\widehat A\right )$
, we are viewing
![]() $\operatorname {\mathrm {Row}}$
and
$\operatorname {\mathrm {Row}}$
and
![]() $\operatorname {\mathrm {Rvac}}$
as operators on
$\operatorname {\mathrm {Rvac}}$
as operators on
![]() $\mathcal A(\Phi ^+(A_{2n-3}))$
; when we compute
$\mathcal A(\Phi ^+(A_{2n-3}))$
; when we compute
 $\widehat {\operatorname {\mathrm {Row}}\cdot \operatorname {\mathrm {Rvac}}(A)}$
, we are viewing them as operators on
$\widehat {\operatorname {\mathrm {Row}}\cdot \operatorname {\mathrm {Rvac}}(A)}$
, we are viewing them as operators on
![]() $\mathcal A(\Phi ^+(D_n))$
. Note that for any antichain
$\mathcal A(\Phi ^+(D_n))$
. Note that for any antichain
![]() $B \in \Phi ^+(D_n)$
obtained from A via a series of rowmotions and rowvacuations, we still have
$B \in \Phi ^+(D_n)$
obtained from A via a series of rowmotions and rowvacuations, we still have
![]() $\delta (B)\neq B$
, because rowvacuation and rowmotion commute with poset automorphisms like
$\delta (B)\neq B$
, because rowvacuation and rowmotion commute with poset automorphisms like
![]() $\delta $
. Hence, it makes sense to speak of
$\delta $
. Hence, it makes sense to speak of
![]() $\widehat {B}$
.
$\widehat {B}$
.
Lemma 5.5. If
![]() $A\in \mathcal A(\Phi ^+(D_n))$
is such that
$A\in \mathcal A(\Phi ^+(D_n))$
is such that
![]() $\delta (A)\neq A$
, then
$\delta (A)\neq A$
, then
 $$ \begin{align*} \operatorname{\mathrm{Row}}\cdot \operatorname{\mathrm{Rvac}}\left(\widehat A\right)=\widehat{\operatorname{\mathrm{Row}}\cdot \operatorname{\mathrm{Rvac}}(A)}. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Row}}\cdot \operatorname{\mathrm{Rvac}}\left(\widehat A\right)=\widehat{\operatorname{\mathrm{Row}}\cdot \operatorname{\mathrm{Rvac}}(A)}. \end{align*} $$
Proof. To ease notation, let
![]() $B=\operatorname {\mathrm {Row}}\cdot \operatorname {\mathrm {Rvac}}(A)$
. By combining Proposition 2.6 with Theorem 1.5 and 3.1, we find that
$B=\operatorname {\mathrm {Row}}\cdot \operatorname {\mathrm {Rvac}}(A)$
. By combining Proposition 2.6 with Theorem 1.5 and 3.1, we find that
 $$ \begin{align*} \Theta_{W\left(D_n\right)}\cdot\operatorname{\mathrm{Row}}\cdot\operatorname{\mathrm{Rvac}}=\Theta_{W\left(D_n\right)} \cdot\operatorname{\mathrm{Row}}^2\cdot\operatorname{\mathrm{Row}}^{-1}\cdot\operatorname{\mathrm{Rvac}}=\operatorname{\mathrm{Krew}}^2\cdot\operatorname{\mathrm{Flip}}\cdot\Theta_{W\left(D_n\right)}, \end{align*} $$
$$ \begin{align*} \Theta_{W\left(D_n\right)}\cdot\operatorname{\mathrm{Row}}\cdot\operatorname{\mathrm{Rvac}}=\Theta_{W\left(D_n\right)} \cdot\operatorname{\mathrm{Row}}^2\cdot\operatorname{\mathrm{Row}}^{-1}\cdot\operatorname{\mathrm{Rvac}}=\operatorname{\mathrm{Krew}}^2\cdot\operatorname{\mathrm{Flip}}\cdot\Theta_{W\left(D_n\right)}, \end{align*} $$
so
 $$ \begin{align*} \Theta_{W\left(D_n\right)}(B)&=\operatorname{\mathrm{Krew}}^2\cdot \operatorname{\mathrm{Flip}}\left(\Theta_{W\left(D_n\right)}(A)\right)=c\operatorname{\mathrm{Flip}}\left(\Theta_{W\left(D_n\right)}(A)\right)c^{-1}\\ &=c_Lc_Rc_L\Theta_{W\left(D_n\right)}(A)^{-1}c_Lc_Rc_L, \end{align*} $$
$$ \begin{align*} \Theta_{W\left(D_n\right)}(B)&=\operatorname{\mathrm{Krew}}^2\cdot \operatorname{\mathrm{Flip}}\left(\Theta_{W\left(D_n\right)}(A)\right)=c\operatorname{\mathrm{Flip}}\left(\Theta_{W\left(D_n\right)}(A)\right)c^{-1}\\ &=c_Lc_Rc_L\Theta_{W\left(D_n\right)}(A)^{-1}c_Lc_Rc_L, \end{align*} $$
where
![]() $c=c_Lc_R\in W(D_n)$
is the bipartite Coxeter element previously defined. In each of the diagrams
$c=c_Lc_R\in W(D_n)$
is the bipartite Coxeter element previously defined. In each of the diagrams
![]() $\varphi _{D_n}(A)$
and
$\varphi _{D_n}(A)$
and
![]() $\varphi _{D_n}(B)$
, let M be the line through the centre of the circle that is equidistant from
$\varphi _{D_n}(B)$
, let M be the line through the centre of the circle that is equidistant from
![]() $2^{(0)}$
and
$2^{(0)}$
and
![]() $2^{(1)}$
(this is the same as the line M shown on the left in Figure 9). Let
$2^{(1)}$
(this is the same as the line M shown on the left in Figure 9). Let
![]() $\Omega $
be the reflection of the plane through the line M. Notice that
$\Omega $
be the reflection of the plane through the line M. Notice that
![]() $\Omega (H)=H$
and
$\Omega (H)=H$
and
 $\Omega \left (\overline H\right )=\overline H$
. We think of
$\Omega \left (\overline H\right )=\overline H$
. We think of
![]() $\Omega $
as acting on
$\Omega $
as acting on
![]() $\varphi _{D_n}(A)$
and
$\varphi _{D_n}(A)$
and
![]() $\varphi _{D_n}(B)$
. For each
$\varphi _{D_n}(B)$
. For each
![]() $i\in (-[n-1])\cup [n-1]$
, we readily compute that
$i\in (-[n-1])\cup [n-1]$
, we readily compute that
 $\Omega \left (i^{(0)}\right )=(c_Lc_Rc_L(i))^{(1)}$
and
$\Omega \left (i^{(0)}\right )=(c_Lc_Rc_L(i))^{(1)}$
and
 $\Omega \left (i^{(1)}\right )=(c_Lc_Rc_L(i))^{(0)}$
. Combining these observations with Theorem 5.3, we find that
$\Omega \left (i^{(1)}\right )=(c_Lc_Rc_L(i))^{(0)}$
. Combining these observations with Theorem 5.3, we find that
![]() $\varphi _{D_n}(B)$
is obtained from
$\varphi _{D_n}(B)$
is obtained from
![]() $\varphi _{D_n}(A)$
by reflecting all of the edges through M (and leaving the vertices unchanged). Note that we are heavily using the fact that
$\varphi _{D_n}(A)$
by reflecting all of the edges through M (and leaving the vertices unchanged). Note that we are heavily using the fact that
![]() $\Omega $
preserves H and
$\Omega $
preserves H and
![]() $\overline H$
; indeed, this guarantees that if E and
$\overline H$
; indeed, this guarantees that if E and
![]() $E'$
are the transverse edges that are removed from
$E'$
are the transverse edges that are removed from
 $\varphi _{A_{2n-3}}\left (\widehat A\right )$
in the construction of
$\varphi _{A_{2n-3}}\left (\widehat A\right )$
in the construction of
![]() $\varphi _{D_n}(A)$
, then
$\varphi _{D_n}(A)$
, then
![]() $\Omega (E)$
and
$\Omega (E)$
and
![]() $\Omega (E')$
are still transverse. These are precisely the edges that are removed from
$\Omega (E')$
are still transverse. These are precisely the edges that are removed from
 $\varphi _{A_{2n-3}}\left (\widehat B\right )$
in the construction of
$\varphi _{A_{2n-3}}\left (\widehat B\right )$
in the construction of
![]() $\varphi _{D_n}(B)$
.
$\varphi _{D_n}(B)$
.
We now know that
![]() $\varphi _{D_n}(B)$
is obtained from
$\varphi _{D_n}(B)$
is obtained from
![]() $\varphi _{D_n}(A)$
by reflecting all of the edges through M. It follows that
$\varphi _{D_n}(A)$
by reflecting all of the edges through M. It follows that
 $\varphi _{A_{2n-3}}\left (\widehat B\right )$
is obtained from
$\varphi _{A_{2n-3}}\left (\widehat B\right )$
is obtained from
 $\varphi _{A_{2n-3}}\left (\widehat A\right )$
by reflecting all of the edges through
$\varphi _{A_{2n-3}}\left (\widehat A\right )$
by reflecting all of the edges through
 $M \ \Big ($
we are using the fact that
$M \ \Big ($
we are using the fact that
 $\varphi _{A_{2n-3}}\left (\widehat A\right )$
and
$\varphi _{A_{2n-3}}\left (\widehat A\right )$
and
 $\varphi _{A_{2n-3}}\left (\widehat B\right )$
are noncrossing to see that they can be reconstructed uniquely from
$\varphi _{A_{2n-3}}\left (\widehat B\right )$
are noncrossing to see that they can be reconstructed uniquely from
 $\xi _{A_{2n-3}}\left (\widehat A\right )$
and
$\xi _{A_{2n-3}}\left (\widehat A\right )$
and
 $\xi _{A_{2n-3}}\left (\widehat B\right )\Big )$
. We also know by Lemma 4.4 that
$\xi _{A_{2n-3}}\left (\widehat B\right )\Big )$
. We also know by Lemma 4.4 that
 $\varphi _{A_{2n-3}}\left (\operatorname {\mathrm {Row}}\cdot \operatorname {\mathrm {Rvac}}\left (\widehat A\right )\right )$
is obtained from
$\varphi _{A_{2n-3}}\left (\operatorname {\mathrm {Row}}\cdot \operatorname {\mathrm {Rvac}}\left (\widehat A\right )\right )$
is obtained from
 $\varphi _{A_{2n-3}}\left (\widehat A\right )$
by reflecting all of the edges through M. This means that
$\varphi _{A_{2n-3}}\left (\widehat A\right )$
by reflecting all of the edges through M. This means that
 $\varphi _{A_{2n-3}}\left (\widehat B\right )=\varphi _{A_{2n-3}}\left (\operatorname {\mathrm {Row}}\cdot \operatorname {\mathrm {Rvac}}\left (\widehat A\right )\right )$
, so it follows from Theorem 4.2 that
$\varphi _{A_{2n-3}}\left (\widehat B\right )=\varphi _{A_{2n-3}}\left (\operatorname {\mathrm {Row}}\cdot \operatorname {\mathrm {Rvac}}\left (\widehat A\right )\right )$
, so it follows from Theorem 4.2 that
 $\Theta _{W\left (A_{2n-3}\right )}\left (\widehat B\right )=\Theta _{W\left (A_{2n-3}\right )}\left (\operatorname {\mathrm {Row}}\cdot \operatorname {\mathrm {Rvac}}\left (\widehat A\right )\right )$
. Because
$\Theta _{W\left (A_{2n-3}\right )}\left (\widehat B\right )=\Theta _{W\left (A_{2n-3}\right )}\left (\operatorname {\mathrm {Row}}\cdot \operatorname {\mathrm {Rvac}}\left (\widehat A\right )\right )$
. Because
![]() $\Theta _{W\left (A_{2n-3}\right )}$
is a bijection, we must have
$\Theta _{W\left (A_{2n-3}\right )}$
is a bijection, we must have
 $\widehat B=\operatorname {\mathrm {Row}}\cdot \operatorname {\mathrm {Rvac}}\left (\widehat A\right )$
, as desired.
$\widehat B=\operatorname {\mathrm {Row}}\cdot \operatorname {\mathrm {Rvac}}\left (\widehat A\right )$
, as desired.
Example 5.6. Let
![]() $A\in \mathcal A(\Phi ^+(D_6))$
and
$A\in \mathcal A(\Phi ^+(D_6))$
and
![]() $\widehat A\in \mathcal A(\Phi ^+(A_9))$
be the antichains from Example 5.1, as depicted in Figure 8. Then
$\widehat A\in \mathcal A(\Phi ^+(A_9))$
be the antichains from Example 5.1, as depicted in Figure 8. Then
![]() $\operatorname {\mathrm {Row}}\cdot \operatorname {\mathrm {Rvac}}(A)$
and
$\operatorname {\mathrm {Row}}\cdot \operatorname {\mathrm {Rvac}}(A)$
and
 $\operatorname {\mathrm {Row}}\cdot \operatorname {\mathrm {Rvac}}\left (\widehat A\right )$
are the antichains shown in blue in Figure 10. It is straightforward to check that
$\operatorname {\mathrm {Row}}\cdot \operatorname {\mathrm {Rvac}}\left (\widehat A\right )$
are the antichains shown in blue in Figure 10. It is straightforward to check that
 $\operatorname {\mathrm {Row}}\cdot \operatorname {\mathrm {Rvac}}\left (\widehat A\right )$
is the same as
$\operatorname {\mathrm {Row}}\cdot \operatorname {\mathrm {Rvac}}\left (\widehat A\right )$
is the same as
 $\widehat {\operatorname {\mathrm {Row}}\cdot \operatorname {\mathrm {Rvac}}(A)}$
in this case, as predicted by Lemma 5.5. Let
$\widehat {\operatorname {\mathrm {Row}}\cdot \operatorname {\mathrm {Rvac}}(A)}$
in this case, as predicted by Lemma 5.5. Let
![]() $B=\operatorname {\mathrm {Row}}\cdot \operatorname {\mathrm {Rvac}}(A)$
. To help illustrate part of the proof of Lemma 5.5, we have drawn the diagrams
$B=\operatorname {\mathrm {Row}}\cdot \operatorname {\mathrm {Rvac}}(A)$
. To help illustrate part of the proof of Lemma 5.5, we have drawn the diagrams
 $\varphi _{A_9}\left (\widehat B\right )$
and
$\varphi _{A_9}\left (\widehat B\right )$
and
![]() $\varphi _{D_6}(B)$
in Figure 11. The diagrams
$\varphi _{D_6}(B)$
in Figure 11. The diagrams
 $\varphi _{A_9}\left (\widehat A\right )$
and
$\varphi _{A_9}\left (\widehat A\right )$
and
![]() $\varphi _{D_6}(A)$
are shown in Figure 9. Notice that
$\varphi _{D_6}(A)$
are shown in Figure 9. Notice that
 $\varphi _{A_9}\left (\widehat B\right )$
and
$\varphi _{A_9}\left (\widehat B\right )$
and
![]() $\varphi _{D_6}(B)$
are obtained by reflecting the edges in
$\varphi _{D_6}(B)$
are obtained by reflecting the edges in
 $\varphi _{A_9}\left (\widehat A\right )$
and
$\varphi _{A_9}\left (\widehat A\right )$
and
![]() $\varphi _{D_6}(A)$
, respectively, through the line M.
$\varphi _{D_6}(A)$
, respectively, through the line M.

Figure 10 The antichains
![]() $\operatorname {\mathrm {Row}}\cdot \operatorname {\mathrm {Rvac}}(A)$
(left) and
$\operatorname {\mathrm {Row}}\cdot \operatorname {\mathrm {Rvac}}(A)$
(left) and
 $\operatorname {\mathrm {Row}}\cdot \operatorname {\mathrm {Rvac}}\left (\widehat A\right )$
(right), where A and
$\operatorname {\mathrm {Row}}\cdot \operatorname {\mathrm {Rvac}}\left (\widehat A\right )$
(right), where A and
![]() $\widehat A$
are the antichains from Example 5.1.
$\widehat A$
are the antichains from Example 5.1.

Figure 11 The diagrams
 $\varphi _{A_9}\left (\widehat B\right )$
(left) and
$\varphi _{A_9}\left (\widehat B\right )$
(left) and
![]() $\varphi _{D_6}(B)$
(right) from Example 5.6.
$\varphi _{D_6}(B)$
(right) from Example 5.6.
Recall our notation
![]() $\alpha _1,\ldots ,\alpha _n$
for the simple roots of
$\alpha _1,\ldots ,\alpha _n$
for the simple roots of
![]() $\Phi ^+(D_n)$
. We will now combine Lemma 5.5 with the following result of [Reference Armstrong, Stump and Thomas2] to say that, for most A with
$\Phi ^+(D_n)$
. We will now combine Lemma 5.5 with the following result of [Reference Armstrong, Stump and Thomas2] to say that, for most A with
![]() $\delta (A)\neq A$
, we have
$\delta (A)\neq A$
, we have
 $\widehat {\operatorname {\mathrm {Rvac}}(A)} = \operatorname {\mathrm {Rvac}}\left (\widehat {A}\right )$
:
$\widehat {\operatorname {\mathrm {Rvac}}(A)} = \operatorname {\mathrm {Rvac}}\left (\widehat {A}\right )$
:
Lemma 5.7. Let
![]() $A\in \mathcal A(\Phi ^+(D_n))$
be such that
$A\in \mathcal A(\Phi ^+(D_n))$
be such that
![]() $\delta (A)\neq A$
and
$\delta (A)\neq A$
and
![]() $\{\alpha _{n-1},\alpha _n\}\cap A = \varnothing $
. Then
$\{\alpha _{n-1},\alpha _n\}\cap A = \varnothing $
. Then
 $$ \begin{align*} \operatorname{\mathrm{Row}}\left(\widehat A\right)=\widehat{\operatorname{\mathrm{Row}}(A)}. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Row}}\left(\widehat A\right)=\widehat{\operatorname{\mathrm{Row}}(A)}. \end{align*} $$
Proof. This is basically [Reference Armstrong, Stump and Thomas2]. Specifically, that lemma says that if
![]() $A\in \mathcal A(\Phi ^+(D_n))$
is such that
$A\in \mathcal A(\Phi ^+(D_n))$
is such that
![]() $\delta (A)\neq A$
and
$\delta (A)\neq A$
and
![]() $\widehat {A}\cap \mathcal {Q} \neq \varnothing $
, then
$\widehat {A}\cap \mathcal {Q} \neq \varnothing $
, then
 $\operatorname {\mathrm {Row}}\left (\widehat A\right )=\widehat {\operatorname {\mathrm {Row}}(A)}$
. Hence, we must show that
$\operatorname {\mathrm {Row}}\left (\widehat A\right )=\widehat {\operatorname {\mathrm {Row}}(A)}$
. Hence, we must show that
![]() $\widehat {A}\cap \mathcal {Q} \neq \varnothing $
. Recall the definition of
$\widehat {A}\cap \mathcal {Q} \neq \varnothing $
. Recall the definition of
![]() $\mathcal {S}_{D_n}$
from Section 2.1. Because
$\mathcal {S}_{D_n}$
from Section 2.1. Because
![]() $\delta (A)\neq A$
and
$\delta (A)\neq A$
and
![]() $\{\alpha _{n-1},\alpha _n\}\cap A=\varnothing $
, there must be some
$\{\alpha _{n-1},\alpha _n\}\cap A=\varnothing $
, there must be some
![]() $\alpha \in A\cap \mathcal {S}_{D_n}$
that is not in
$\alpha \in A\cap \mathcal {S}_{D_n}$
that is not in
![]() $\{\alpha _{n-1},\alpha _n\}$
. Then
$\{\alpha _{n-1},\alpha _n\}$
. Then
![]() $\iota (\gamma (\alpha ))$
consists of two elements belonging to
$\iota (\gamma (\alpha ))$
consists of two elements belonging to
![]() $\mathcal {Q}$
, so
$\mathcal {Q}$
, so
![]() $\#(\iota (\gamma (A))\cap \mathcal Q)\geq 2$
. It is then immediate from the definition of
$\#(\iota (\gamma (A))\cap \mathcal Q)\geq 2$
. It is then immediate from the definition of
![]() $\widehat {A}$
that
$\widehat {A}$
that
 $\#\left (\widehat {A}\cap \mathcal {Q}\right ) = \#(\iota (\gamma (A))\cap \mathcal {Q})-1\geq 1$
.
$\#\left (\widehat {A}\cap \mathcal {Q}\right ) = \#(\iota (\gamma (A))\cap \mathcal {Q})-1\geq 1$
.
Corollary 5.8. If
![]() $A\in \mathcal A(\Phi ^+(D_n))$
is such that
$A\in \mathcal A(\Phi ^+(D_n))$
is such that
![]() $\delta (A)\neq A$
and
$\delta (A)\neq A$
and
![]() $\{\alpha _{n-1},\alpha _n\}\cap A = \varnothing $
, then
$\{\alpha _{n-1},\alpha _n\}\cap A = \varnothing $
, then
 $$ \begin{align*} \operatorname{\mathrm{Rvac}}\left(\widehat A\right)=\widehat{\operatorname{\mathrm{Rvac}}(A)}. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Rvac}}\left(\widehat A\right)=\widehat{\operatorname{\mathrm{Rvac}}(A)}. \end{align*} $$
Proof. From Lemma 5.7 we have
 $$ \begin{align*} \operatorname{\mathrm{Row}}\left(\widehat{A}\right) = \widehat{\operatorname{\mathrm{Row}}(A)}. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Row}}\left(\widehat{A}\right) = \widehat{\operatorname{\mathrm{Row}}(A)}. \end{align*} $$
As already mentioned, rowmotion commutes with poset automorphisms, so it is still the case that
![]() $\delta (\operatorname {\mathrm {Row}}(A)) \neq \operatorname {\mathrm {Row}}(A)$
. Then we can apply Lemma 5.5 to say that
$\delta (\operatorname {\mathrm {Row}}(A)) \neq \operatorname {\mathrm {Row}}(A)$
. Then we can apply Lemma 5.5 to say that
 $$ \begin{align*} \operatorname{\mathrm{Row}}\cdot \operatorname{\mathrm{Rvac}}\cdot \operatorname{\mathrm{Row}}\left(\widehat A\right)= \operatorname{\mathrm{Row}}\cdot \operatorname{\mathrm{Rvac}} \left(\widehat{\operatorname{\mathrm{Row}}(A)}\right) =\widehat{\operatorname{\mathrm{Row}}\cdot \operatorname{\mathrm{Rvac}}\cdot \operatorname{\mathrm{Row}}(A)}.\end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Row}}\cdot \operatorname{\mathrm{Rvac}}\cdot \operatorname{\mathrm{Row}}\left(\widehat A\right)= \operatorname{\mathrm{Row}}\cdot \operatorname{\mathrm{Rvac}} \left(\widehat{\operatorname{\mathrm{Row}}(A)}\right) =\widehat{\operatorname{\mathrm{Row}}\cdot \operatorname{\mathrm{Rvac}}\cdot \operatorname{\mathrm{Row}}(A)}.\end{align*} $$
The result follows from Proposition 2.6, which says that
![]() $\operatorname {\mathrm {Row}}\cdot \operatorname {\mathrm {Rvac}}\cdot \operatorname {\mathrm {Row}}=\operatorname {\mathrm {Rvac}}$
.
$\operatorname {\mathrm {Row}}\cdot \operatorname {\mathrm {Rvac}}\cdot \operatorname {\mathrm {Row}}=\operatorname {\mathrm {Rvac}}$
.
Example 5.9. Let
![]() $A\in \mathcal A(\Phi ^+(D_6))$
and
$A\in \mathcal A(\Phi ^+(D_6))$
and
![]() $\widehat A\in \mathcal A(\Phi ^+(A_9))$
be the antichains from Example 5.1, as depicted in Figure 8. Then
$\widehat A\in \mathcal A(\Phi ^+(A_9))$
be the antichains from Example 5.1, as depicted in Figure 8. Then
![]() $\operatorname {\mathrm {Rvac}}(A)$
and
$\operatorname {\mathrm {Rvac}}(A)$
and
 $\operatorname {\mathrm {Rvac}}\left (\widehat A\right )$
are the antichains shown in red in Figure 12. It is straightforward to check that
$\operatorname {\mathrm {Rvac}}\left (\widehat A\right )$
are the antichains shown in red in Figure 12. It is straightforward to check that
 $\operatorname {\mathrm {Rvac}}\left (\widehat A\right )$
is the same as
$\operatorname {\mathrm {Rvac}}\left (\widehat A\right )$
is the same as
 $\widehat {\operatorname {\mathrm {Rvac}}(A)}$
in this case, as predicted by Corollary 5.8.
$\widehat {\operatorname {\mathrm {Rvac}}(A)}$
in this case, as predicted by Corollary 5.8.

Figure 12 The antichains
![]() $\operatorname {\mathrm {Rvac}}(A)$
(left) and
$\operatorname {\mathrm {Rvac}}(A)$
(left) and
 $\operatorname {\mathrm {Rvac}}\left (\widehat A\right )$
(right), where A and
$\operatorname {\mathrm {Rvac}}\left (\widehat A\right )$
(right), where A and
![]() $\widehat A$
are the antichains from Example 5.1.
$\widehat A$
are the antichains from Example 5.1.
Remark 5.10. The assumption
![]() $\{\alpha _{n-1},\alpha _n\}\cap A = \varnothing $
in Corollary 5.8 is required. For example, if
$\{\alpha _{n-1},\alpha _n\}\cap A = \varnothing $
in Corollary 5.8 is required. For example, if
![]() $A=\{\alpha _n\}$
, then
$A=\{\alpha _n\}$
, then
![]() $\widehat {A}=\varnothing $
, so
$\widehat {A}=\varnothing $
, so
 $\operatorname {\mathrm {Rvac}}\left (\widehat {A}\right )$
consists of all minimal elements of
$\operatorname {\mathrm {Rvac}}\left (\widehat {A}\right )$
consists of all minimal elements of
![]() $\Phi ^+({A_{2n-3}})$
; but
$\Phi ^+({A_{2n-3}})$
; but
 $\widehat {\operatorname {\mathrm {Rvac}}(A)} = \widehat {\{\alpha _1,\ldots ,\alpha _{n-1}\}}$
consists of all but one of the minimal elements of
$\widehat {\operatorname {\mathrm {Rvac}}(A)} = \widehat {\{\alpha _1,\ldots ,\alpha _{n-1}\}}$
consists of all but one of the minimal elements of
![]() $\Phi ^+({A_{2n-3}})$
(it is missing the ‘middle’ simple root
$\Phi ^+({A_{2n-3}})$
(it is missing the ‘middle’ simple root
![]() $[n-1,n]$
).
$[n-1,n]$
).
6 Proof of Panyushev’s conjecture in type D
Recall from Section 2.3 that our goal is to prove the following theorem:
Theorem 6.1. For every
![]() $A\in \mathcal A(\Phi ^+(D_n))$
, we have
$A\in \mathcal A(\Phi ^+(D_n))$
, we have
![]() $\#A+\#\operatorname {\mathrm {Rvac}}(A)=n$
.
$\#A+\#\operatorname {\mathrm {Rvac}}(A)=n$
.
In proving Theorem 6.1, we will make heavy use of Theorem 1.4 for types A and C. As a consequence, we will need to consider the action of rowvacuation on different posets. As before, we will use subscripts as in the notation
![]() $\operatorname {\mathrm {Rvac}}_P$
when referring to an operator on
$\operatorname {\mathrm {Rvac}}_P$
when referring to an operator on
![]() $\mathcal A(P)$
. We will primarily be concerned with the poset
$\mathcal A(P)$
. We will primarily be concerned with the poset
![]() $\Phi ^+(D_n)$
, so operators without subscripts will be assumed to act on
$\Phi ^+(D_n)$
, so operators without subscripts will be assumed to act on
![]() $\mathcal {A}(\Phi ^+(D_n))$
.
$\mathcal {A}(\Phi ^+(D_n))$
.
Before we start with the proof of Theorem 6.1, we need two simple propositions about rowvacuation of
![]() $\eta $
-symmetric antichains in type A. Recall the definitions of the special subsets
$\eta $
-symmetric antichains in type A. Recall the definitions of the special subsets
![]() $\mathcal {L}$
,
$\mathcal {L}$
,
![]() $\mathcal {S}$
of the root posets of classical types from Section 2.1.
$\mathcal {S}$
of the root posets of classical types from Section 2.1.
Proposition 6.2. Let
![]() $B\in \mathcal {A}(\Phi ^+(A_{2n-1}))$
be such that
$B\in \mathcal {A}(\Phi ^+(A_{2n-1}))$
be such that
![]() $\eta (B)=B$
. Then exactly one of B or
$\eta (B)=B$
. Then exactly one of B or
![]() $\operatorname {\mathrm {Rvac}}_{\Phi ^+\left (A_{2n-1}\right )}(B)$
contains an element of
$\operatorname {\mathrm {Rvac}}_{\Phi ^+\left (A_{2n-1}\right )}(B)$
contains an element of
![]() $\mathcal {L}_{A_{2n-1}}$
.
$\mathcal {L}_{A_{2n-1}}$
.
Proposition 6.3. Let
![]() $B\in \mathcal {A}(\Phi ^+(A_{2n-1}))$
be such that
$B\in \mathcal {A}(\Phi ^+(A_{2n-1}))$
be such that
![]() $\eta (B)=B$
. Then exactly one of B or
$\eta (B)=B$
. Then exactly one of B or
![]() $\operatorname {\mathrm {Rvac}}_{\Phi ^+\left (A_{2n-1}\right )}(B)$
contains an element of
$\operatorname {\mathrm {Rvac}}_{\Phi ^+\left (A_{2n-1}\right )}(B)$
contains an element of
![]() $\mathcal {S}_{A_{2n-1}}$
.
$\mathcal {S}_{A_{2n-1}}$
.
Proof.
Proposition 6.2 can be seen as the type C case of Conjecture 2.11(ii) – that is, the fact that
 $\iota ^{-1}(B)\cup \operatorname {\mathrm {Rvac}}_{\Phi ^+\left (C_n\right )}\left (\iota ^{-1}(B)\right )$
has the right distribution of long and short roots. Similarly, Proposition 6.3 can be seen as the type B case of Conjecture 2.11(ii) – that is, the fact that
$\iota ^{-1}(B)\cup \operatorname {\mathrm {Rvac}}_{\Phi ^+\left (C_n\right )}\left (\iota ^{-1}(B)\right )$
has the right distribution of long and short roots. Similarly, Proposition 6.3 can be seen as the type B case of Conjecture 2.11(ii) – that is, the fact that
![]() $\operatorname {\mathrm {Rvac}}$
on the type B root poset has the right distribution of long and short roots. So they can be thought of as consequences of Panyushev’s work in [Reference Panyushev21, §5]. However, they are also both immediate from the formula for type A rowvacuation in Theorem 2.7.
$\operatorname {\mathrm {Rvac}}$
on the type B root poset has the right distribution of long and short roots. So they can be thought of as consequences of Panyushev’s work in [Reference Panyushev21, §5]. However, they are also both immediate from the formula for type A rowvacuation in Theorem 2.7.
Our proof of Theorem 6.1 will consist of several cases. We first dispense with the case of Theorem 6.1 in which
![]() $\delta (A)=A$
:
$\delta (A)=A$
:
Lemma 6.4. If
![]() $A\in \mathcal A(\Phi ^+(D_n))$
is such that
$A\in \mathcal A(\Phi ^+(D_n))$
is such that
![]() $\delta (A)=A$
, then
$\delta (A)=A$
, then
![]() $\#A+\#\operatorname {\mathrm {Rvac}}(A)=n$
.
$\#A+\#\operatorname {\mathrm {Rvac}}(A)=n$
.
Proof. Because
![]() $\mathcal {S}_{C_{n-1}}$
is a chain, each antichain of
$\mathcal {S}_{C_{n-1}}$
is a chain, each antichain of
![]() $\Phi ^+(C_{n-1})$
contains at most one element of
$\Phi ^+(C_{n-1})$
contains at most one element of
![]() $\mathcal {S}_{C_{n-1}}$
. Given an antichain B of
$\mathcal {S}_{C_{n-1}}$
. Given an antichain B of
![]() $\Phi ^+(C_{n-1})$
, let
$\Phi ^+(C_{n-1})$
, let
![]() $\varepsilon (B)$
be
$\varepsilon (B)$
be
![]() $1$
if B contains an element of
$1$
if B contains an element of
![]() $\mathcal {S}_{C_{n-1}}$
and
$\mathcal {S}_{C_{n-1}}$
and
![]() $0$
otherwise. We have
$0$
otherwise. We have
![]() $\#\gamma ^{-1}(B)=\#B+\varepsilon (B)$
.
$\#\gamma ^{-1}(B)=\#B+\varepsilon (B)$
.
Because rowvacuation commutes with the poset automorphism
![]() $\delta $
, we have
$\delta $
, we have
![]() $\delta (\operatorname {\mathrm {Rvac}}(A))=\operatorname {\mathrm {Rvac}}(A)$
. One can easily check that
$\delta (\operatorname {\mathrm {Rvac}}(A))=\operatorname {\mathrm {Rvac}}(A)$
. One can easily check that
![]() $\gamma (A)$
is an antichain of
$\gamma (A)$
is an antichain of
![]() $\Phi ^+(C_{n-1})$
for which
$\Phi ^+(C_{n-1})$
for which
![]() $\operatorname {\mathrm {Rvac}}_{\Phi ^+\left (C_{n-1}\right )}(\gamma (A))=\gamma (\operatorname {\mathrm {Rvac}}(A))$
. So, using
$\operatorname {\mathrm {Rvac}}_{\Phi ^+\left (C_{n-1}\right )}(\gamma (A))=\gamma (\operatorname {\mathrm {Rvac}}(A))$
. So, using
![]() $\ast $
to denote the quantity
$\ast $
to denote the quantity
![]() $\#A+ \#\operatorname {\mathrm {Rvac}}(A)$
, we have
$\#A+ \#\operatorname {\mathrm {Rvac}}(A)$
, we have
 $$ \begin{align*} \ast &=\#\gamma^{-1}(\gamma(A))+\#\gamma^{-1}(\gamma(\operatorname{\mathrm{Rvac}}(A)))\\ &=\#\gamma^{-1}(\gamma(A))+\#\gamma^{-1}\left(\operatorname{\mathrm{Rvac}}_{\Phi^+\left(C_{n-1}\right)}(\gamma(A))\right)\\ &=\#\gamma(A)+\varepsilon(\gamma(A))+\#\operatorname{\mathrm{Rvac}}_{\Phi^+\left(C_{n-1}\right)}(\gamma(A))+\varepsilon\left(\operatorname{\mathrm{Rvac}}_{\Phi^+\left(C_{n-1}\right)}(\gamma(A))\right). \end{align*} $$
$$ \begin{align*} \ast &=\#\gamma^{-1}(\gamma(A))+\#\gamma^{-1}(\gamma(\operatorname{\mathrm{Rvac}}(A)))\\ &=\#\gamma^{-1}(\gamma(A))+\#\gamma^{-1}\left(\operatorname{\mathrm{Rvac}}_{\Phi^+\left(C_{n-1}\right)}(\gamma(A))\right)\\ &=\#\gamma(A)+\varepsilon(\gamma(A))+\#\operatorname{\mathrm{Rvac}}_{\Phi^+\left(C_{n-1}\right)}(\gamma(A))+\varepsilon\left(\operatorname{\mathrm{Rvac}}_{\Phi^+\left(C_{n-1}\right)}(\gamma(A))\right). \end{align*} $$
We saw in Section 2.3 that rowvacuation serves as Panyushev’s
![]() $\mathfrak {P}$
in type C, which means that
$\mathfrak {P}$
in type C, which means that
![]() $\#\gamma (A)+\#\operatorname {\mathrm {Rvac}}_{\Phi ^+\left (C_{n-1}\right )}(\gamma (A))=n-1$
. Hence, in order to prove
$\#\gamma (A)+\#\operatorname {\mathrm {Rvac}}_{\Phi ^+\left (C_{n-1}\right )}(\gamma (A))=n-1$
. Hence, in order to prove
![]() $\#A+\#\operatorname {\mathrm {Rvac}}(A)=n$
, we need to show that
$\#A+\#\operatorname {\mathrm {Rvac}}(A)=n$
, we need to show that
In other words, we need to show that
![]() $\gamma (A)$
contains an element of
$\gamma (A)$
contains an element of
![]() $\mathcal {S}_{C_{n-1}}$
if and only if
$\mathcal {S}_{C_{n-1}}$
if and only if
![]() $\operatorname {\mathrm {Rvac}}_{\Phi ^+\left (C_{n-1}\right )}(\gamma (A))$
does not contain an element of
$\operatorname {\mathrm {Rvac}}_{\Phi ^+\left (C_{n-1}\right )}(\gamma (A))$
does not contain an element of
![]() $\mathcal {S}_{C_{n-1}}$
. It suffices to show that
$\mathcal {S}_{C_{n-1}}$
. It suffices to show that
![]() $\iota (\gamma (A))$
contains an element of
$\iota (\gamma (A))$
contains an element of
![]() $\mathcal {S}_{A_{2n-3}}$
if and only if
$\mathcal {S}_{A_{2n-3}}$
if and only if
![]() $\iota \left (\operatorname {\mathrm {Rvac}}_{\Phi ^+\left (C_{n-1}\right )}(\gamma (A))\right )$
does not contain an element of
$\iota \left (\operatorname {\mathrm {Rvac}}_{\Phi ^+\left (C_{n-1}\right )}(\gamma (A))\right )$
does not contain an element of
![]() $\mathcal {S}_{A_{2n-3}}$
. Since
$\mathcal {S}_{A_{2n-3}}$
. Since
this follows from Proposition 6.3.
Now we consider the case where
![]() $\delta (A)\neq A$
. Actually, we have two cases here, depending on whether A contains an element of
$\delta (A)\neq A$
. Actually, we have two cases here, depending on whether A contains an element of
![]() $\{\alpha _{n-1},\alpha _n\}$
or not.
$\{\alpha _{n-1},\alpha _n\}$
or not.
Lemma 6.5. If
![]() $A\in \mathcal A(\Phi ^+(D_n))$
is such that
$A\in \mathcal A(\Phi ^+(D_n))$
is such that
![]() $\delta (A)\neq A$
and
$\delta (A)\neq A$
and
![]() $\{\alpha _{n-1},\alpha _n\}\cap A =\varnothing $
, then
$\{\alpha _{n-1},\alpha _n\}\cap A =\varnothing $
, then
![]() $\#A+\#\operatorname {\mathrm {Rvac}}(A)=n$
.
$\#A+\#\operatorname {\mathrm {Rvac}}(A)=n$
.
Proof. Recall the antichain
![]() $\widehat {A}\in \mathcal {A}(\Phi ^+(A_{2n-3}))$
defined in terms of A in Section 5. From the definition of
$\widehat {A}\in \mathcal {A}(\Phi ^+(A_{2n-3}))$
defined in terms of A in Section 5. From the definition of
![]() $\widehat {A}$
, it is immediate that
$\widehat {A}$
, it is immediate that
 $$ \begin{align*} \#\widehat{A} = \begin{cases} 2\cdot\#A - 1& \text{if } A\cap \mathcal{L}_{D_n}=\varnothing, \\ 2\cdot\#A - 2 &\text{if } A\cap \mathcal{L}_{D_n}\neq \varnothing.\end{cases} \end{align*} $$
$$ \begin{align*} \#\widehat{A} = \begin{cases} 2\cdot\#A - 1& \text{if } A\cap \mathcal{L}_{D_n}=\varnothing, \\ 2\cdot\#A - 2 &\text{if } A\cap \mathcal{L}_{D_n}\neq \varnothing.\end{cases} \end{align*} $$
Given an antichain B of
![]() $\Phi ^+(A_{2n-3})$
, let
$\Phi ^+(A_{2n-3})$
, let
![]() $\varepsilon (B)$
be
$\varepsilon (B)$
be
![]() $1$
if B contains an element of
$1$
if B contains an element of
![]() $\mathcal {L}_{A_{2n-3}}$
and
$\mathcal {L}_{A_{2n-3}}$
and
![]() $0$
otherwise. It is straightforward to check from the definition of
$0$
otherwise. It is straightforward to check from the definition of
![]() $\widehat {A}$
that
$\widehat {A}$
that
![]() $A\cap \mathcal {L}_{D_n}=\varnothing $
if and only if
$A\cap \mathcal {L}_{D_n}=\varnothing $
if and only if
 $\widehat {A}\cap \mathcal {L}_{A_{2n-3}}\neq \varnothing $
. Hence,
$\widehat {A}\cap \mathcal {L}_{A_{2n-3}}\neq \varnothing $
. Hence,
 $\#\widehat {A} = 2\cdot \#A - 2 +\varepsilon \left (\widehat {A}\right )$
. Similarly, we have
$\#\widehat {A} = 2\cdot \#A - 2 +\varepsilon \left (\widehat {A}\right )$
. Similarly, we have
 $\#\widehat {\operatorname {\mathrm {Rvac}}(A)} = 2\cdot \#\operatorname {\mathrm {Rvac}}(A) - 2 +\varepsilon \left (\widehat {\operatorname {\mathrm {Rvac}}(A)}\right )$
.
$\#\widehat {\operatorname {\mathrm {Rvac}}(A)} = 2\cdot \#\operatorname {\mathrm {Rvac}}(A) - 2 +\varepsilon \left (\widehat {\operatorname {\mathrm {Rvac}}(A)}\right )$
.
From Corollary 5.8, we get
 $$ \begin{align*} \#\widehat{A}+\#\operatorname{\mathrm{Rvac}}_{\Phi^+\left({A_{2n-3}}\right)}\left(\widehat{A}\right) &= \#\widehat{A}+\#\widehat{\operatorname{\mathrm{Rvac}}(A)} \\ &= 2(\#A+\#\operatorname{\mathrm{Rvac}}(A)) - 4 +\varepsilon\left(\widehat{A}\right)+\varepsilon\left(\widehat{\operatorname{\mathrm{Rvac}}(A)}\right)\\ &= 2(\#A+\#\operatorname{\mathrm{Rvac}}(A)) - 4 +\varepsilon\left(\widehat{A}\right)+\varepsilon\left(\operatorname{\mathrm{Rvac}}_{\Phi^+\left({A_{2n-3}}\right)}\left(\widehat{A}\right)\right). \end{align*} $$
$$ \begin{align*} \#\widehat{A}+\#\operatorname{\mathrm{Rvac}}_{\Phi^+\left({A_{2n-3}}\right)}\left(\widehat{A}\right) &= \#\widehat{A}+\#\widehat{\operatorname{\mathrm{Rvac}}(A)} \\ &= 2(\#A+\#\operatorname{\mathrm{Rvac}}(A)) - 4 +\varepsilon\left(\widehat{A}\right)+\varepsilon\left(\widehat{\operatorname{\mathrm{Rvac}}(A)}\right)\\ &= 2(\#A+\#\operatorname{\mathrm{Rvac}}(A)) - 4 +\varepsilon\left(\widehat{A}\right)+\varepsilon\left(\operatorname{\mathrm{Rvac}}_{\Phi^+\left({A_{2n-3}}\right)}\left(\widehat{A}\right)\right). \end{align*} $$
But Proposition 6.2 tells us that
 $\varepsilon \left (\widehat {A}\right )+\varepsilon \left (\operatorname {\mathrm {Rvac}}_{\Phi ^+\left ({A_{2n-3}}\right )}\left (\widehat {A}\right )\right )=1$
, so
$\varepsilon \left (\widehat {A}\right )+\varepsilon \left (\operatorname {\mathrm {Rvac}}_{\Phi ^+\left ({A_{2n-3}}\right )}\left (\widehat {A}\right )\right )=1$
, so
 $$ \begin{align*} \#\widehat{A}+\#\operatorname{\mathrm{Rvac}}_{\Phi^+\left({A_{2n-3}}\right)}\left(\widehat{A}\right)=2(\#A+\#\operatorname{\mathrm{Rvac}}(A)) - 3. \end{align*} $$
$$ \begin{align*} \#\widehat{A}+\#\operatorname{\mathrm{Rvac}}_{\Phi^+\left({A_{2n-3}}\right)}\left(\widehat{A}\right)=2(\#A+\#\operatorname{\mathrm{Rvac}}(A)) - 3. \end{align*} $$
As we saw in Section 2.3, rowvacuation serves as Panyushev’s
![]() $\mathfrak {P}$
in type A, so
$\mathfrak {P}$
in type A, so
 $\#\widehat {A}+\#\operatorname {\mathrm {Rvac}}_{\Phi ^+\left ({A_{2n-3}}\right )}\left (\widehat {A}\right )=2n-3$
. Hence,
$\#\widehat {A}+\#\operatorname {\mathrm {Rvac}}_{\Phi ^+\left ({A_{2n-3}}\right )}\left (\widehat {A}\right )=2n-3$
. Hence,
![]() $\#A+\#\operatorname {\mathrm {Rvac}}(A)=n$
.
$\#A+\#\operatorname {\mathrm {Rvac}}(A)=n$
.
Lemma 6.6. If
![]() $A\in \mathcal A(\Phi ^+(D_n))$
is such that
$A\in \mathcal A(\Phi ^+(D_n))$
is such that
![]() $\delta (A)\neq A$
and
$\delta (A)\neq A$
and
![]() $\{\alpha _{n-1},\alpha _n\}\cap A \neq \varnothing $
, then
$\{\alpha _{n-1},\alpha _n\}\cap A \neq \varnothing $
, then
![]() $\#A+\#\operatorname {\mathrm {Rvac}}(A)=n$
.
$\#A+\#\operatorname {\mathrm {Rvac}}(A)=n$
.
Proof. Assume without loss of generality that
![]() $\alpha _n\in A$
. Let
$\alpha _n\in A$
. Let
![]() $\Phi '$
be the maximal parabolic subroot system of
$\Phi '$
be the maximal parabolic subroot system of
![]() $\Phi ^+(D_n)$
obtained by removing
$\Phi ^+(D_n)$
obtained by removing
![]() $\alpha _n$
from the system of simple roots. Clearly,
$\alpha _n$
from the system of simple roots. Clearly,
![]() $\Phi '\simeq A_{n-1}$
. From the fact that rowvacuation respects parabolic induction – that is, from Conjecture 2.11(iv) or, more precisely, Proposition 2.10 – we know that
$\Phi '\simeq A_{n-1}$
. From the fact that rowvacuation respects parabolic induction – that is, from Conjecture 2.11(iv) or, more precisely, Proposition 2.10 – we know that
![]() $\operatorname {\mathrm {Rvac}}(A)=\operatorname {\mathrm {Rvac}}_{\left (\Phi '\right )^+}(A\setminus \{\alpha _n\})$
. But since we know that rowvacuation is
$\operatorname {\mathrm {Rvac}}(A)=\operatorname {\mathrm {Rvac}}_{\left (\Phi '\right )^+}(A\setminus \{\alpha _n\})$
. But since we know that rowvacuation is
![]() $\mathfrak {P}$
in type A, we know that
$\mathfrak {P}$
in type A, we know that
![]() $\#\operatorname {\mathrm {Rvac}}_{\left (\Phi '\right )^+}(A\setminus \{\alpha _n\})=(n-1)-(\#A-1)=n-\#A$
. Hence,
$\#\operatorname {\mathrm {Rvac}}_{\left (\Phi '\right )^+}(A\setminus \{\alpha _n\})=(n-1)-(\#A-1)=n-\#A$
. Hence,
![]() $\#A+\#\operatorname {\mathrm {Rvac}}(A)=n$
. (Note that we did not need the hypothesis
$\#A+\#\operatorname {\mathrm {Rvac}}(A)=n$
. (Note that we did not need the hypothesis
![]() $\delta (A)\neq A$
.)
$\delta (A)\neq A$
.)
All together, Lemmas 6.4 to 6.6 imply Theorem 6.1. Hence, we have completed the proof of Theorem 1.4.
Acknowledgements
We thank the organisers of the 2020 BIRS Online Workshop on dynamical algebraic combinatorics for giving us the opportunity to collaborate on this project. We thank Theo Douvropoulos, Michael Joseph, Hugh Thomas and Nathan Williams for useful discussion during that workshop. The second author gives a special thanks to Nathan Williams for suggesting the correct involution g to use in the definition of
![]() $\operatorname {\mathrm {Flip}}$
for root systems of arbitrary type.
$\operatorname {\mathrm {Flip}}$
for root systems of arbitrary type.
The first author was supported by a Fannie and John Hertz Foundation Fellowship and an NSF Graduate Research Fellowship (grant DGE-1656466). The second author was supported by an NSF Mathematical Sciences Postdoctoral Research Fellowship.
Conflict of Interest
None.