1 Introduction
In 1965, Richard Thompson defined the three groups
$ F < T < V $
that are now known as Thompson’s groups. They have been studied extensively in the last fifty years, as they arise naturally in many different areas of mathematics (geometric group theory and homotopy theory, to name a few). For a historical overview on Thompson’s groups, we refer to the excellent survey by Cannon, Floyd and Parry [Reference Cannon, Floyd and Parry8].
Different points of view mean that Thompson’s groups can be defined in many different ways. For example, one can define them combinatorially, as groups of certain partial automorphisms of a binary tree, or dynamically, as subgroups of homeomorphisms (with possibly some discontinuities, in the case of V) from the circle to itself.
Despite receiving a lot of attention, many questions about these groups are still open, the most famous arguably being whether F is amenable.
Being finitely presented groups, an interesting problem is computing their Dehn functions. Indeed, the Dehn function is a natural quasi-isometric invariant associated to finitely presented groups; geometrically, it can be seen as the isoperimetric function associated to the presentation complex of the group.
Equivalently, one can also interpret the Dehn function combinatorially as the number of relations from the presentation that one needs to apply to reduce a word of length n representing the identity to the empty word. In this sense, it is also related to the complexity of the word problem; for example, the latter is decidable if and only if the Dehn function is computable.
Note that the Dehn function of a finitely presented group is always either linear, in which case the group is hyperbolic [Reference Gromov12], or it is at least quadratic [Reference Yu18].
The Dehn function of Thompson’s group F was proven by Guba [Reference Guba16] to be quadratic. While the lower bound follows easily from the fact that F contains
$ {\mathbb {Z}}^2 $
as a subgroup and is therefore not hyperbolic, the upper bound required a lot of work. Gersten first managed to prove an exponential upper bound [Reference Gersten10] that was brought down to sub-exponential [Reference Guba and Sapir15], then to
$n^5$
[Reference Guba13], and finally to quadratic [Reference Guba16].
Thompson’s groups T and V are also not hyperbolic, so their Dehn functions are at least quadratic. In fact, both are conjectured to have quadratic Dehn functions (see, for example, [Reference Zaremsky21]). It was proven by Guba [Reference Guba14] that the Dehn functions of T and V have polynomial upper bounds of
$ n^7 $
and
$ n^{11} $
, respectively. The upper bound for T was later improved to
$n^5$
[Reference Wang, Zheng and Zhang20].
In this paper, we prove the conjecture for Thompson’s group T.
Theorem A. The Dehn function of Thompson’s group T is quadratic.
The proof relies on the fact that F has quadratic Dehn function.
If in the combinatorial definition of Thompson’s groups one replaces the binary tree with an n-ary tree, one gets three families of groups
$ F_n, T_n, V_n $
. The family
$V_n$
was introduced by Higman [Reference Higman17], while later, Brown [Reference Brown3] naturally extended the definition to
$F_n$
and
$T_n$
; these groups are sometimes referred to as Higman–Thompson groups.
The same techniques used for proving Theorem A apply also for the family
$ T_n $
.
Theorem B. The Dehn function of the Higman–Thompson group
$T_n$
is quadratic.
Here, we exploit the fact that by a result of Zhang [Reference Zhang22], the groups
$F_n$
have quadratic Dehn functions.
1.1 Strategy of the proof
Thompson’s groups F and T both have a finite and an infinite generating set that are well established in the literature; the advantage of the infinite one is that it admits a more symmetric (infinite) presentation.
Both groups admit normal forms, sometimes called
$ pq $
and
$ pcq $
factorization (see [Reference Cannon, Floyd and Parry8, Corollary 2.7, Theorem 5.7]), both of which use the infinite presentation; Guba used this normal form to prove that F has quadratic Dehn function. For T, the situation is slightly more complicated: if we rewrite the normal form of an element of T in terms of a finite generating set, the resulting word may be much longer than the actual norm of the element with respect to the word metric. Therefore, we introduce two different normal forms for F and T that use finite generating sets.
We look at Thompson’s groups from the dynamical point of view, so T is viewed as a certain subgroup of orientation-preserving self-homeomorphisms of the circle. If we parametrize the circle as the interval
$[0,1]$
with the endpoints identified, then F can be described as the subgroup of elements of T that fix the point
$0 \equiv 1$
. By considering the subgroup of elements that fix both
$0$
and
$\frac 12$
, we get a subgroup
$H < F$
that is naturally isomorphic to
$ F \times F $
.
We choose a finite generating set for H. From this, we construct a finite generating set for F by adding an element
$X_0 \in F$
that does not fix
$ \frac 12 $
. Similarly, from the generating set for F, we construct a generating set for T by adding the rotation of the circle
$C_0 \in T$
of order two. By studying the dynamics of these groups
$ H < F < T $
on the circle, we can prove that every element of F is represented by a word with at most one instance of
$X_0$
, and every element of T is represented by a word with at most one instance of
$C_0$
. Such words are our chosen normal forms for F and T; these are not unique, but this is not an issue for our purposes.
By a standard argument, it suffices to show that all triangular loops in the Cayley graph where the edges are normal forms have quadratic area. To perform this computation, we exploit the fact that in a triangular loop, almost all the letters are generators of H. Since
$C_0$
stabilizes
$ \{{0, \frac 12} \}$
, it normalizes
$ H $
; in fact, the generating set chosen for H is invariant under conjugation by
$C_0$
. So we can commute the letter
$C_0$
with every generator of H, by replacing the latter with its conjugate. This allows us to eliminate all instances of
$C_0$
in the word, and then we conclude using that the Dehn function of F is quadratic.
For Theorem B the strategy is similar, except now we consider the subgroup of
$F_n$
that fixes all the points
$ \frac 1n, \dots , \frac {n-1}n $
, and we work with the rotation of order n.
Note that one can prove Theorem B directly without proving the particular case for Thompson’s group
$ T = T_2 $
. However, we choose to first give the proof for Theorem A, as the reader might be more familiar with Thompson’s groups F and T than their generalizations, and the former have more established conventions for their generating sets. This makes the proof of Theorem A more explicit and hopefully easier to read, and in turn it helps to understand the proof of Theorem B.
1.2 Structure of the paper
We start in Section 2 by recalling the definition of Dehn function, and we introduce Thompson’s group F and T, together with their generating sets, presentation, and some useful properties. In Section 3, we show that F admits a normal form with at most one instance of the generator
$X_0$
, and in Section 4, we introduce the normal form for T that we use to prove Theorem A. In Section 5, we generalize all the arguments in the previous sections to prove Theorem B. We conclude with some remarks in Section 6.
2 Preliminaries
We start by fixing some notation. Let G be a finitely generated group, and
$S=\{{s_1, \dots , s_k}\}$
be a finite subset of G. If w is a word in the alphabet
$S \cup S^{-1}$
, then we write
$ w(S) $
or
$ w(s_1, \dots , s_k) $
to make the alphabet explicit. We denote the length of w by
$ \lvert w\rvert $
. If
$g \in G$
, and S is a generating set, we denote by
$ \lVert {g}\rVert _S $
the minimal length of a word representing g (that is, the distance of g from the identity with respect to the word metric). If the generating set is clear, we also write
$ \lVert {g}\rVert _G $
.
We say that a word
$w(S)$
is null-homotopic if it represents the trivial element of G. If G has a finite presentation
$ \langle S|{\mathcal R} \rangle $
, and w is a null-homotopic word, then w can be written as a product of conjugates of k relations, for some
$ k \in \mathbb {N} $
; we call the minimum such k the area of w, and denote it by
$ \operatorname {\mathrm {Area}}(w) $
.
The Dehn function of G encodes the growth of the area in terms of the length of the word. More precisely, it is a function
$ \delta _{G} \colon \mathbb {N} \to \mathbb {N} $
defined by
$$\begin{align*}\delta_{G} (N) = \max \{ {\operatorname{\mathrm{Area}}(w) : w \text{ null-homotopic},\,\lvert {w}\rvert \leq N}\}. \end{align*}$$
The Dehn function as defined above depends on the chosen presentation for G; to solve this problem, one introduces the following equivalence relation.
If
$ f,g \colon \mathbb {N} \to \mathbb {N} $
, we say that
$ f \preccurlyeq g $
if there exists
$ C>0 $
such that for all
$ N \in \mathbb {N} $
, we have
$ f(N) \leq C g(CN+C) + CN + C $
. If
$ f \preccurlyeq g \preccurlyeq f $
, we write
$ f \asymp g $
; different presentations of the same group (and more generally of quasi-isometric groups) have equivalent Dehn functions. A group G has quadratic Dehn function if
$ \delta _{G} \asymp (N \mapsto N^2) $
.
Throughout the paper, we identify the circle with the interval
$[0,1]$
with the endpoints glued together. Thompson’s group T is the group of self-homeomorphisms of the circle that send dyadic rationals to dyadic rationals, are linear except on finitely many dyadic rationals, and the derivative is a power of
$2$
(with integer exponent) wherever it is defined. The subgroup of T consisting of the homeomorphisms that fix the point
$0$
is Thompson’s group F. We refer to [Reference Cannon, Floyd and Parry8] for an introduction on these groups.
Let
$ X_0, X_1, \dots $
denote the standard generators of Thompson’s group F. They are defined as follows:
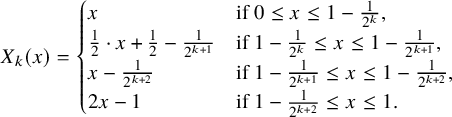$$\begin{align*}X_k(x) = \begin{cases} x & \text{if } 0 \leq x \leq 1-\frac1{2^k}, \\ \frac12 \cdot x + \frac12 - \frac1{2^{k+1}} & \text{if } 1-\frac1{2^k}\leq x \leq 1-\frac{1}{2^{k+1}}, \\ x-\frac1{2^{k+2}} & \text{if } 1-\frac1{2^{k+1}} \leq x \leq 1-\frac1{2^{k+2}}, \\ 2x-1 & \text{if } 1-\frac1{2^{k+2}} \leq x \leq 1. \end{cases} \end{align*}$$
Thompson’s group F admits both an infinite presentation
$$\begin{align*}\langle {X_0, X_1, \dots }| { X_j X_i = X_i X_{j+1} \text{ for all } i < j}\rangle, \end{align*}$$
involving all the
$X_i$
, with
$i \in \mathbb {N}$
, and a finite one with two generators
$ X_0, X_1 $
, given by
$$\begin{align*}\langle {X_0,X_1}| { [X_0X_1^{-1}, X_0^{-1}X_1X_0], [X_0X_1^{-1}, X_0^{-2}X_1X_0^2]}\rangle. \end{align*}$$
In particular, all the other generators can be expressed in terms of the
$X_i$
by the formula
$ X_{i+1} = X_0^{-i} X_1 X_0^i $
.
To obtain a generating set for T, we need to add another homeomorphism that does not fix
$0$
. To this end, let
$C_0$
be the homeomorphism defined by
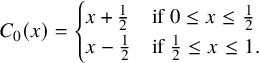$$\begin{align*}C_0(x) = \begin{cases} x+\frac12 & \text{if } 0 \leq x \leq \frac12 \\ x-\frac12 & \text{if } \frac12 \leq x \leq 1. \\ \end{cases} \end{align*}$$
In other words,
$C_0$
is the rotation of the circle of order two.
Remark 2.1. One can also define elements
$C_i$
of order
$ i+2 $
for all
$ i \geq 0 $
, as done in [Reference Cannon, Floyd and Parry8], and get an infinite presentation. To obtain a finite generating set, it suffices to add only one of the
$C_i$
to the generators of F, and the usual choice is to use
$C_1$
instead of
$C_0$
. To translate between the presentations found in the literature and the one we use here, it is helpful to keep in mind that
$ C_1 = X_0^{-1} C_0 $
.
We also define
$ Y_i := C_0 X_i C_0 $
for
$ i\geq 1 $
. Since
$X_i$
has
$ \frac 12 $
as a fixed point for
$ i \geq 1 $
, it follows that
$ Y_i \in F $
. In this paper, we choose
$ S_F := \{ {X_0^{\pm 1}, X_1^{\pm 1}, X_2^{\pm 1}, Y_1^{\pm 1}, Y_2^{\pm 1}}\}$
as a generating set for F, and
$S_T:= S_F \cup \{ {C_0}\}$
as a generating set for T. In Figure 1, we have drawn the rectangular diagrams for the generators: the top border represents the domain, while the bottom border represents the codomain (see [Reference Cannon, Floyd and Parry8] for more details).
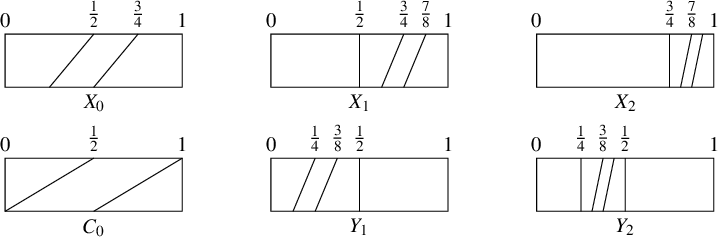
Figure 1 Rectangular diagrams for the generators
$ S_T $
.
Lemma 2.2. Thompson’s group F admits the following presentation:
$$\begin{align*}\langle {S_F}| { [Y_1, X_1], [Y_1, X_2], X_0 X_2=X_1 X_0, Y_1 = X_0^2 X_1^{-1} X_0^{-1}, Y_{2} = X_0 X_1^2 X_2^{-1} X_1^{-1} X_0^{-1}}\rangle. \end{align*}$$
Proof. By using the rectangular diagrams, one can check that the relations hold in F. Moreover, one can use the last three relations to express
$ X_2, Y_1, Y_2 $
in terms of
$X_0, X_1$
; after doing this, it turns out that the remaining two relations are conjugate to
$ [X_0X_1^{-1}, X_0^{-1}X_1X_0], [X_0X_1^{-1}, X_0^{-2}X_1X_0^2]$
, so the above presentation is equivalent to the standard presentation for F.
The reason why we introduced these additional generators is that
$\{ {X_1,X_2}\} $
and
$ \{{Y_1,Y_2} \} $
generate two subgroups of F that are both isomorphic to F itself. More generally, given two dyadic numbers
$ 0 \leq a < b \leq 1 $
with
$ b-a=2^{-k} $
for some integer
$ k $
, we may consider the subgroup of F consisting of homeomorphisms that are the identity outside
$ (a,b) $
; denote this group by
$ F[a,b] $
.
Theorem 2.3 [Reference Burillo4, Theorem 3.1.3, 5.1.1].
For all dyadic numbers
$ 0 \leq a < b \leq 1 $
, the subgroup
$ F[a,b] $
is isomorphic to F and undistorted.
In particular,
$ X_1, X_2 $
generate
$ F[\frac 12, 1] $
, while
$Y_1,Y_2$
generate
$ F[0, \frac 12] $
; the element
$C_0 \in T$
conjugates
$ F[0, \frac 12] $
to
$ F[\frac 12, 1] $
and vice versa, as we can see from the following.
Lemma 2.4. Thompson’s group T is generated by the elements
$ S_T $
and satisfies the following relations:
-
1.
$[Y_1, X_1]$
, -
2.
$[Y_1, X_2]$
, -
3.
$X_0 X_2=X_1 X_0$
, -
4.
$Y_1 = X_0^2 X_1^{-1} X_0^{-1}$
, -
5.
$ X_0^{-1} Y_2 X_0 = X_1^2 X_2^{-1} X_1^{-1} $
, -
6.
$ C_0^2 = 1 $
, -
7.
$ (C_0 X_0)^3 = 1 $
, -
8.
$ C_0 X_2 = Y_2 C_0 $
, -
9.
$ C_0 X_1 = Y_1 C_0 $
.
Proof. The first five relations are the relations from F, while the last four can be checked directly by composing the homeomorphisms.
Remark 2.5. It is possible to show that the above relations yield a presentation for T, as they can be obtained by manipulating the finite presentations for T found in the literature [Reference Cannon, Floyd and Parry8, Reference Burillo, Cleary, Stein and Taback7], but showing this equivalence by hand is a bit tedious. Luckily, we can avoid doing this computation: while proving that the Dehn function of T is quadratic, we actually show that for some constant
$C>0$
, any null-homotopic word of length n in the generating set
$S_T$
can be reduced to the trivial word by applying at most
$ C \cdot n^2 $
relations (1)-(9), which implies that the above is a presentation for T.
3 A normal form for F
Except for
$X_0$
, the generators for F interact quite nicely with
$C_0$
, as
$ C_0 X_i = Y_i C_0 $
for
$ i \geq 1 $
. The aim of this section is to show that every element of F can be expressed as a word in the generators
$S_F$
with at most one instance of
$X_0$
(or its inverse). This defines a normal form for F, which will be very useful when computing the Dehn function of T.
Before doing so, we need some estimates on the word metric of F. An efficient way to estimate the word length is obtained by looking at the so-called reduced tree diagrams for elements in F [Reference Burillo5]. We translate this notion in terms of self-homeomorphisms of the interval.
Given
$f \in F$
, there exist subdivisions
$ 0=x_0 < \dots < x_k=1 $
and
$ 0 = y_0 < \dots < y_k = 1 $
, with every interval
$ [x_i, x_{i+1}] $
and
$ [y_i, y_{i+1}] $
of the form
$ [\frac {a}{2^{\ell }}, \frac {a+1}{2^\ell }] $
, such that f sends
$ x_i $
to
$ y_i $
and is affine on every
$ [x_i, x_{i+1}] $
. If the subdivision is minimal, then the number of intervals k is quasi-equivalent to the norm
$ \lVert {f}\rVert _{F} $
; that is,
$ \frac 1Ck - C \leq \lVert {f}\rVert _{F} \leq Ck + C $
for some constant
$C> 0$
independent of f.
From this, we get the following lemmas.
Lemma 3.1. There exists a constant
$C>0$
such that the following holds. Let
$ 0<a=\frac {d}{2^k}<1 $
be a dyadic number, with d odd. There exists an element
$ f\in F $
such that
$ f(a) = \frac 12 $
and
$ \lVert {f}\rVert _{F} \leq C \cdot k + C$
. Moreover, all
$ f \in F $
with
$ f(a) = \frac 12 $
satisfy
$ \lVert {f}\rVert _{F} \geq \frac 1C k-C $
.
Proof. There is a subdivision
$ x_0 < \dots < x_{k+1} $
where
$ x_j = a $
for some j; this can be constructed by iteratively bisecting the interval containing a. Then choose a subdivision
$ y_0 < \dots < y_{k+1} $
such that
$y_j = \frac 12$
; the map associated to these subdivisions satisfies the requirements.
For the second statement, let
$ f \in F $
be any map with
$ f(a)=\frac 12 $
, and choose subdivisions associated to f. Since
$ \frac 12 $
is a point of the second subdivision (unless f is the identity), then
$ a $
must be a point of the first subdivision, and so the two subdivisions must have at least
$k+1$
intervals; from this, we conclude.
Lemma 3.2. There exists
$C>0$
such that the following holds. Let
$ 0<a=\frac {d}{2^k} <1 $
be a dyadic number, with
$ a \neq \frac 12 $
and d odd. There exists an element
$ f\in F $
with
$ f(a) = \frac 12 $
that can be represented as a word of length at most
$ C \cdot k $
of the form
$$ \begin{align*} X_0 & \cdot w(X_1,X_2) & & \text{if } a>\tfrac12 \\ X_0^{-1} & \cdot w(Y_1, Y_2) & & \text{if } a < \tfrac12. \end{align*} $$
Proof. If
$ a> \frac 12 $
, by Lemma 3.1, we can obtain an element of F that sends
$2a-1$
to
$ \frac 12 $
: by rescaling with
$ x \mapsto \frac 12(x+1) $
, we get
$ g \in F[\frac 12, 1] $
with
$ \lVert {g}\rVert _{F[\frac 12, 1]} \leq C(k-1) $
and
$ g(a) = \frac 34 $
. If
$w(X_1,X_2)$
is a shortest representative for g, then
$ X_0 w(X_1,X_2) $
satisfies the hypotheses.
If
$ a<\frac 12 $
, the construction is analogous by choosing
$ g \in F[0, \frac 12] $
with
$g(a)=\frac 14$
, and using
$ X_0^{-1} w(Y_1,Y_2) $
.
We are now able to show that elements of F can be represented by words that have at most one instance of the letter
$ X_0 $
.
Proposition 3.3. Let
$ f \in F $
. Then f is represented by a word
$w(S)$
of the form
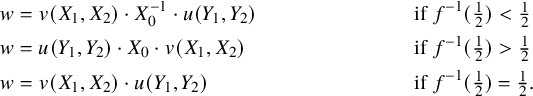$$ \begin{align*} w & = v(X_1,X_2) \cdot X_0^{-1} \cdot u(Y_1,Y_2) & & \text{if } f^{-1}(\tfrac12) < \tfrac12 \\ w & = u(Y_1, Y_2) \cdot X_0 \cdot v(X_1,X_2) & & \text{if } f^{-1}(\tfrac12)> \tfrac12 \\ w & = v(X_1,X_2) \cdot u(Y_1, Y_2) & & \text{if } f^{-1}(\tfrac12) = \tfrac12. \end{align*} $$
Moreover, the word w can be chosen of length bounded above by
$ C \cdot \lVert {f}\rVert _F $
, for some constant C independent of f.
Proof. Let 
; assume that
$ a> \frac 12 $
. Let
$f_1$
be the function with
$f_1(a) = \frac 12$
given by Lemma 3.2, represented by the word
$ X_0 w_1(X_1,X_2) $
of length at most
$ C \cdot k$
. By Lemma 3.1, this means that the length of
$w_1$
is bounded linearly in terms of
$ \lVert {f}\rVert _{F} $
.
Since
$ f_1 \circ f^{-1} $
fixes
$ \frac 12 $
, then it belongs to the subgroup
$ F[0,\frac 12] \times F[\frac 12, 1] $
, which is undistorted by Theorem 2.3. There exists
$ f_2 \in F[0,\frac 12] $
,
$ f_3 \in F[\frac 12, 1] $
, such that
$ f_1 \circ f^{-1} = f_3 \circ f_2 $
; let
$ w_2(Y_1,Y_2) $
and
$w_3(X_1,X_2)$
be words representing
$ f_2 $
and
$f_3 $
, with
$$\begin{align*}\lvert {w_2}\rvert + \lvert {w_3}\rvert \leq C' \cdot \lVert {f_1 \circ f^{-1}}\rVert_F \leq C' \cdot (\lVert {f}\rVert_F + \lVert{f_1} \rVert_F), \end{align*}$$
so the length of both
$ w_2 $
and
$ w_3 $
is bounded by a linear function of
$ \lVert {f}\rVert _{F} $
.
So
$ f = f_2^{-1} \circ f_3^{-1} \circ f_1$
is represented by
$$\begin{align*}w_2^{-1} (Y_1,Y_2) \cdot w_3^{-1} (X_1, X_2) \cdot X_0 \cdot w_1(X_1,X_2). \end{align*}$$
Finally, since for
$ \varepsilon \in \{ {\pm 1}\} $
we have
$$\begin{align*}X_1^{\varepsilon} X_0 = X_0 X_2^{\varepsilon}, \qquad X_2^{\varepsilon} X_0 = X_0 X_3^{\varepsilon} = X_0 X_1^{-1} X_2^{\varepsilon} X_1, \end{align*}$$
we obtain that
$ w_3^{-1}(X_1,X_2) X_0 = X_0 w_4(X_1,X_2) $
for some word
$w_4$
. Therefore, f is represented by
$$\begin{align*}w_2^{-1}(Y_1,Y_2) \cdot X_0 \cdot w_4(X_1,X_2), \end{align*}$$
with
$w_4$
bounded by a linear function of
$\lVert {f}\rVert _F$
.
If
$f^{-1}(\frac 12) < \frac 12$
, then
$ f(\frac 12)> \frac 12 $
, so the result follows by applying the above on
$ f^{-1} $
, and then taking the inverse at the end.
If
$f(\frac 12)=\frac 12$
, then we conclude by noting that
$f \in F[0,\frac 12] \times F[\frac 12,1]$
and by using that the latter is an undistorted subgroup of F by Theorem 2.3.
4 The Dehn function of T
The estimates for the word length based on tree diagrams hold for Thompson’s group T as well (see [Reference Burillo, Cleary, Stein and Taback7]). In particular, by the same arguments, we get the following.
Lemma 4.1. There exists
$ C>0 $
such that for every
$ f \in T $
, if
$ f(0) = \frac {d}{2^k} $
with d odd, then
$ \lVert {f}\rVert _{T} \geq \frac 1C k - C $
.
Proposition 4.2. There exists
$ C>0 $
such that every
$ f \in T \setminus F $
is represented by a word
$$\begin{align*}w = u(S_F) \cdot C_0 \cdot v(S_F), \end{align*}$$
such that
$\lvert w \rvert \leq C \cdot \lVert {f}\rVert _T $
.
Proof. Let
$ a= \frac {d}{2^k} := f^{-1}(0) $
. Let
$ f_1 \in F $
be the element that sends
$ a $
to
$ \frac 12 $
given by Lemma 3.1. By Lemma 4.1, and since F is undistorted in T [Reference Burillo, Cleary, Stein and Taback7, Corollary 5.2], we have
$\lVert {f_1}\rVert _F \leq C' \lVert {f}\rVert _{T} + C'$
for some constant
$C'$
.
Now
$ f_2 := f \circ f_1^{-1} \circ C_0 $
fixes the point
$0$
, so it belongs to F; moreover,
$$\begin{align*}\lVert {f_2}\rVert_F \leq C" \lVert {f_2}\rVert_T \leq C" (\lVert {f}\rVert_T + \lVert{f_1} \rVert_T + 1). \end{align*}$$
Since
$ f = f_2 \circ C_0 \circ f_1 $
, we may conclude by choosing short representatives
$ w_1(S_F), w_2(S_F) $
for
$ f_1, f_2 $
.
We have shown that each element of T is represented by a word containing at most one letter
$C_0$
, and whose length is bounded by a linear function of the norm of the element; we can employ these nice representatives to compute the Dehn function of T.
A standard argument, employed for example in [Reference Gersten and Short11, Reference Carter and Forester9, Reference Ascari, Bertolotti, Italiano, Isenrich and Migliorini1], shows that it suffices to bound the area of triangular loops. This fact can be stated generally as follows:
Proposition 4.3. Let
$G = \langle S|{\mathcal R} \rangle $
be a finitely presented group, and for each
$g \in G$
, choose a subset
$W_g$
of words in S that represent the element g. Suppose that there exists
$C>0$
such the following hold:
-
• for every
$g \in G$
, there is
$ w \in W_g $
with
$ \lvert {w}\rvert \leq C \cdot \lVert {g}\rVert _G $
; -
• for every null-homotopic word
$ w = w_1 w_2 w_3 $
, with
$w_i \in W_{g_i}$
for some elements
$ g_1, g_2, g_3 $
, we have that
$ \operatorname {\mathrm {Area}}(w) \leq C \lvert {w}\rvert ^2 $
.
Then the Dehn function of G is quadratic.
The set
$ W_g $
should be thought as some preferred word representatives for g. In our setting, the set
$ W_g $
consists of the word representatives for
$g \in T$
that have at most one
$C_0$
; they exist by Proposition 4.2.
The proposition can be proven by subdividing a Van Kampen diagram for a generic loop into triangular cells, as explained in [Reference Carter and Forester9], or even directly by induction [Reference Ascari, Bertolotti, Italiano, Isenrich and Migliorini1, Theorem 5.9]. Note that it is non-restrictive to prove the proposition for the case
$ \lvert {W_g} \rvert = 1 $
(that is, when using a unique normal form) as restricting every
$W_g$
to a singleton can only weaken the hypotheses.
This simplifies our work considerably, as it suffices to compute the area of null-homotopic words containing up to three instances of
$C_0$
. Note that a word containing exactly one instance of
$C_0$
cannot be null-homotopic, as it cannot send the point
$0$
to itself. So there are just two cases to check.
Proposition 4.4. There exists
$ C>0 $
such that every null-homotopic word of the form
$$\begin{align*}w=C_0 \cdot w_1(S_F) \cdot C_0 \cdot w_2(S_F) \end{align*}$$
has area at most
$ C \cdot \lvert {w} \rvert ^2 $
.
Proof. Let
$ f_2 \in F $
be the element represented by
$ w_2 $
and
$ C_0 w_1^{-1} C_0 $
. Since
$ C_0 w_1 C_0 $
fixes the point
$ \frac 12 $
, then
$ f_2 $
can be represented by a word
$ u(X_1,X_2,Y_1,Y_2)$
of length bounded by
$ C \lvert {w_2}\rvert $
, for some
$ C>0 $
. Therefore, using
$ \delta _{F}((C+1) \cdot \lvert {w_2} \rvert )$
many instances of relations (1)–(5), we can replace
$w_2$
by u, obtaining the word
$$\begin{align*}C_0 \cdot w_1(S_F) \cdot C_0 \cdot u(X_1,X_2,Y_1,Y_2). \end{align*}$$
Now using relations (8), (9), we can shift all letters in u to the left of
$C_0$
, obtaining
$$\begin{align*}C_0 \cdot w_1(S_F) \cdot u(Y_1,Y_2,X_1,X_2) \cdot C_0, \end{align*}$$
where with
$u(Y_1,Y_2,X_1,X_2)$
, we denote the word obtained by
$ u(X_1,X_2,Y_1,Y_2) $
replacing
$ X_1 \rightsquigarrow Y_1 $
,
$ X_2 \rightsquigarrow Y_2 $
,
$Y_1 \rightsquigarrow X_1$
and
$ Y_2 \rightsquigarrow X_2$
(note that
$ C_0 X_1 = Y_1 C_0 $
is conjugate to
$ C_0 Y_1 = X_1 C_0 $
, since
$C_0$
is an involution). After conjugating by
$C_0$
, we get a word in
$S_F$
. The result follows from the fact that F has quadratic Dehn function [Reference Guba16].
Proposition 4.5. There exists
$ C>0 $
such that every null-homotopic word of the form
$$\begin{align*}w=C_0 \cdot w_1(S_F) \cdot C_0 \cdot w_2(S_F) \cdot C_0 \cdot w_3(S_F) \end{align*}$$
has area at most
$ C \cdot \lvert {w} \rvert ^2 $
.
Proof. Let
$f_2 \in F$
be the element represented by
$ w_2 $
. If
$f_2(\frac 12)=\frac 12$
, then it would follow that
$ w(0) = \frac 12 $
, so w did not represent the identity of T. Therefore, assume that
$f_2^{-1}(\frac 12)> \frac 12$
(the other case is equivalent by taking the inverse of w), and let
$u(Y_1,Y_2) \cdot X_0 \cdot v(X_1,X_2) $
be the representative for
$f_2$
given by Proposition 3.3.
We can replace
$w_2$
by
$u \cdot X_0 \cdot v$
using a number of relations that is at most quadratic in
$\lvert {w_2}\rvert $
, since the Dehn function of F is quadratic. We obtain
$$\begin{align*}C_0 \cdot w_1(S_F) \cdot C_0 \cdot u(Y_1,Y_2) \cdot X_0 \cdot v(X_1,X_2) \cdot C_0 \cdot w_3(S_F). \end{align*}$$
Now use relations (8), (9) to shift u to the left of
$C_0$
, and v to the right of the other
$C_0$
. We get
$$\begin{align*}C_0 \cdot w_1(S_F) \cdot u(X_1, X_2) \cdot C_0 \cdot X_0 \cdot C_0 \cdot v(Y_1,Y_2) \cdot w_3(S_F). \end{align*}$$
Using
$ (C_0X_0)^3 = 1 $
, we have that
$ C_0X_0C_0 = X_0^{-1} C_0 X_0^{-1} $
. After this substitution, the word contains only two
$C_0$
letters, so we conclude by the previous lemma.
The proof of Theorem A is now complete.
5 Higman-Thompson groups
We now generalize the result to the Higman-Thompson groups
$ T_n $
. They are defined for
$ n\geq 2 $
as the groups of piecewise-linear homeomorphisms of the circle
$ [0,1]/\sim $
, whose singularities are n-adic numbers (that is, of the form
$ \frac {a}{n^b} $
for some
$ a,b \in \mathbb {N} $
) and with derivative at every other point of the form
$ n^k $
for some
$ k \in {\mathbb {Z}} $
[Reference Brown3, Section 4B]. The subgroup of
$ T_{n} $
of homeomorphisms that fix
$0$
is denoted by
$ F_{n} $
. These are generalizations of
$ T $
and F, since
$ T=T_{2} $
and
$ F=F_{2} $
.
It is convenient to keep in mind the description of elements of
$F_n$
as tree diagrams [Reference Burillo, Cleary and Stein6]. Every finite rooted n-ary tree is in natural correspondence to a subdivision of
$ [0,1] $
in intervals of the form
$ [\frac a{n^k}, \frac {a+1}{n^k}] $
. Given two finite rooted n-ary trees with the same number of leaves, we may construct a unique map
$f \in F_n$
that sends the i-th interval of the first subdivision to the i-th interval of the second subdivision via an affine function. This pair of trees is usually referred to as a tree diagram for f.
Given a tree diagram, one may choose an integer i and append an n-caret (i.e., an n-ary tree with only the root and n leaves) to the i-th leaf on both trees; doing so does not change the associated map. A tree diagram is called reduced if it is not obtained from another tree diagram by applying the previous operation.
The word length of an element
$ f \in F_{n} $
can be estimated by using the number of carets
$ N(f) $
appearing in either tree of the reduced diagram.
Theorem 5.1 [Reference Burillo, Cleary and Stein6, Theorem 5].
There is a constant
$C>0$
such that for all
$ f \in F_{n} $
, then
$$\begin{align*}\frac1C N(f) \leq \lVert {f}\rVert_{F_{n}} \leq CN(f). \end{align*}$$
For n-adic rationals
$ 0 \leq a < b \leq 1 $
, denote by
$ F_{n}[a,b] $
the subgroup of
$ F_{n} $
that contains all homeomorphisms that are the identity outside
$ (a,b) $
. To ease notation, for
$ i \in \{1, \dots , n\} $
, we also denote with
$ F_n^{(i)} $
the subgroup
$ F_n[\frac {i-1}{n}, \frac in] $
.
Lemma 5.2. For every
$ i \in \{1, \dots , n\} $
, the subgroup
$ F_n^{(i)}$
is isomorphic to
$F_n$
and undistorted inside
$ F_{n} $
.
Proof. The isomorphism is induced by linearly rescaling
$ [0,1] $
to
$ [\frac {i-1}n, \frac {i}n] $
. This sends the map
$ f \in F_n $
with associated tree diagram
$({\mathcal {T}}_1,{\mathcal {T}}_2)$
to the map
$ f' \in F_n^{(i)} $
with tree diagram
$ ({\mathcal {T}}_1^{\prime },{\mathcal {T}}_2^{\prime }) $
, where for
$ j \in \{1, 2\} $
, the tree
${\mathcal {T}}_j^{\prime }$
is obtained by attaching the root of
${\mathcal {T}}_j$
to the i-th leaf of an n-caret.
In particular,
$ N(f')=N(f) + 1 $
, so by Theorem 5.1, we get that the map above is a quasi-isometric embedding (i.e., the subgroup is undistorted).
Denote by
$ {\mathcal {T}}[i] $
the tree obtained by attaching an n-caret to the i-th leaf of another n-caret. Following [Reference Brown3, Section 4.11], define for
$ i,j \in \{1, \dots , n\} $
the glide
$ \gamma _{i,j} \in F_n $
as the element with associated tree diagram
$ ({\mathcal {T}}[i], {\mathcal {T}}[j]) $
, and let
$ \gamma _i := \gamma _{i,i+1} $
for
$ i \in \{1, \dots , n-1 \} $
. Let
$ \rho \in T_{n} $
be the rotation of order n defined by
$ x \mapsto x+\frac 1n\ \pmod {\mathbb {Z}} $
.
Figure 2 The tree diagram for the glide
$ \gamma _{i,j} $
.
Remark 5.3. When comparing with [Reference Brown3], be careful that we are using the convention that maps are applied from right to left, while in [Reference Brown3], they are applied from left to right.
Moreover, Brown considers a more general class of groups
$ T_{n,r} $
, that one may interpret as self-homeomorphisms of the circle described as the interval
$ [0,r] / \sim $
. Here, we are looking in the special case
$ n=r $
: it is easy to see that
$ T_n = T_{n,1} \cong T_{n,n} $
by rescaling.
Remark 5.4. In the case
$ n=2 $
, then
$ \gamma _1 = X_0^{-1}$
with respect to the notation in the previous section.
Both
$F_n$
and
$T_n$
are finitely presented. We will not need the explicit presentation to compute the Dehn function; below, we recall some useful properties.
Lemma 5.5. The following hold.
-
1.
$ \gamma _{j,k}\gamma _{i,j}$
=
$ \gamma _{i,k} $
; -
2.
$ \rho \gamma _i \rho ^{-1} = \gamma _{i+1} $
for
$ i \in \{1, \dots , {n-2}\} $
; -
3.
$ \rho ^{-k} \gamma _{k}^{-1} \rho ^{k} = \gamma _{1,n-1} \rho ^{-1} \gamma _{1,n-1}$
for
$ k \in \{1, \dots , {n-1}\} $
; -
4.
$ \rho F_n^{(i)} \rho ^{-1} = F_n^{(i+1)} $
for
$ i \in \{1, \dots , {n-1}\} $
; -
5.
$ \rho F_n^{(n)} \rho ^{-1} = F_n^{(i)} $
; -
6.
$ \gamma _i^{-1} F_n^{(i)} \gamma _i \subset F_n^{(i)}$
; -
7.
$ \gamma _i F_n^{(i+1)}\gamma _i^{-1} \subset F_n^{(i+1)}$
.
Proof. Most of the computations are straightforward. For (3), one may either check the equality directly using tree diagrams or obtain it from expression (iv) in [Reference Brown3, Section 4.11], where in our case,
$ r=n $
.
For (6) and (7), we use that
$ \gamma _i^{-1}([\frac {i-1}n, \frac {i}n]) = [\frac {i-1}n, \frac {i-1}n + \frac 1{n^2}] $
and
$ \gamma _i([\frac {i}n, \frac {i+1}n]) = [\frac {i+1}n - \frac {1}{n^2}, \frac {i+1}n] $
.
We now generalize the arguments in Section 3 to the case
$ n>2 $
. The only substantial difference is that we need to be careful, as the action of
$ F_n $
is not transitive on the
$ n $
-adic numbers. The following lemma is well known to experts, but we provide a proof for the convenience of the reader.
Lemma 5.6. Let
$ x=\frac {a}{n^k}, y=\frac {b}{n^\ell } $
be two n-adic numbers in
$ (0,1) $
. There exists
$ f \in F_n $
with
$ f(x)=y $
if and only if
$ a \equiv b\ \pmod {n-1}$
.
Moreover, if such an f exists, it can be chosen such that
$ \lVert {f}\rVert _{F_n} \leq C(k+\ell ) $
, for some constant
$C>0$
independent of x and y.
Proof. We may assume that a and b are not multiples of n, as dividing by n does not change the residual class modulo
$n-1$
.
Say that an n-ary tree contains an n-adic rational q if q is an endpoint of the corresponding subdivision. For such a tree, the leaves left (right) of q are the leaves corresponding to intervals that are to the left (right) of q.
We show that if a tree contains x, the residual class modulo
$n-1$
of the number of leaves left of x is the same as a. To this end, consider the minimal n-ary tree
$ {\mathcal {T}}_x $
that contains x. It is immediate to note that the number of leaves to the left of x is the sum of the digits of x written in base n; this has the same residual class modulo
$n-1$
as a. Every other tree that contains x is obtained by attaching carets to
${\mathcal {T}}_x$
; since attaching a caret increases the number of leaves by
$n-1$
, the residual class modulo
$n-1$
of the number of leaves left of x is the same as a for every tree containing x. Similarly, the number of leaves left to y in a tree containing y is congruent to
$ b $
modulo
$n-1$
.
If
$f \in F$
sends x to y, we can find a tree diagram
$({\mathcal {T}},{\mathcal {T}}')$
for
$ f $
. By possibly attaching carets, we may assume that
$ {\mathcal {T}} $
contains x and
$ {\mathcal {T}}' $
contains y. Since x is sent to y, the number of leaves of
${\mathcal {T}}$
left of x coincides with the number of leaves of
${\mathcal {T}}'$
left of y, and so
$ a \equiv b\ \pmod {n-1} $
.
Vice versa, assume
$ a \equiv b\ \pmod {n-1} $
and consider the minimal trees
$ {\mathcal {T}}_x $
and
$ {\mathcal {T}}_y $
: they have, respectively,
$ k $
and
$ \ell $
carets. Let
$L_x$
and
$R_x$
be the number of leaves, respectively, left and right of x in
${\mathcal {T}}_x$
, and
$ L_y $
,
$ R_y $
be the number of leaves left and right of y in
${\mathcal {T}}_y$
.
If
$ n-1 $
divides
$ a-b $
, then it also divides
$ L_x-L_y $
by the arguments above. Since
$ L_x+R_x \equiv L_y+R_y \equiv 1\ \pmod {n-1} $
, then
$n-1$
also divides
$ R_x-R_y $
.
If
$ L_x \leq L_y $
, we attach
$ \frac {L_y-L_x}{n-1} $
carets to the left of x in
$T_x$
; otherwise, we attach
$ \frac {L_x-L_y}{n-1} $
to the left of y in
$T_y$
. After that, the numbers of leaves to the left of x in
$T_x$
and to the left of y in
$ {\mathcal {T}}_y $
coincide and are equal to
$$\begin{align*}\max\{{L_x, L_y} \} \leq L_x + L_y - 1. \end{align*}$$
We perform the same procedure on the right. In the end, we obtain two trees forming a tree diagram
$ ({\mathcal {T}}_x^{\prime }, {\mathcal {T}}_y^{\prime }) $
. The map associated to it sends x to y by construction; the tree diagram has at most
$ L_x + R_x - 1 + L_y + R_y -1$
leaves and therefore at most
$ k + \ell $
carets, so the estimate follows.
Let
$S_1 = \{ {s_{1,1}, \dots s_{1,\ell }} \}$
be a finite set of generators for the subgroup
$F_n^{(1)}$
, and for
$ k \in \{1, \dots , n \} $
, let
$ S_k = \{ {s_{k,1}, \dots , s_{k, \ell }}\}$
be a generating set for
$ F_n^{(k)} $
defined by
$ s_{k,i} = \rho ^{k-1} s_{1,i} \rho ^{-(k-1)} $
. Let
$S_{F_n}$
be
$ S_1 \cup \dots \cup S_{n} \cup \{ {\gamma _1^{\pm 1}, \dots , \gamma _{n-1}^{\pm 1}}\}$
, and
$ S_{T_n} = S_{F_n} \cup \{{\rho ^{\pm 1}} \}$
.
Proposition 5.7. The set
$ S_{F_n} $
generates
$ F_n $
. Moreover, there exists a constant
$ C> 0 $
such that every element
$f \in F_n$
is represented by a word
$w(S_{F_n})$
of length at most
$ C \cdot \lVert {f}\rVert _{F_n} $
with the following property: for every
$ k \in \{1, \dots , {n-1} \} $
, there is at most one instance of
$ \gamma _k^{\pm 1} $
, and
$ \gamma _k^{\pm 1} $
appears in w if and only if
$ f(\frac kn) \neq \frac kn $
.
Proof. Note that if
$ f $
fixes all the points of the form
$ \frac kn $
, then the result follows from the fact that
$ F_n^{(1)} \times \dots \times F_n^{(n)} $
is undistorted inside
$ F_n $
by Lemma 5.2.
Otherwise, let
$ k \in \{1, \dots , {n-1}\}$
be the least such that
$ f(\frac kn) \neq \frac kn $
. It suffices to prove the following claim.
Claim. We can decompose f as either
$ f' \circ \gamma _k \circ f_k $
or
$ f_k \circ \gamma _k^{-1} \circ f' $
, where
$ f' $
fixes
$ \frac in $
for
$ i \in \{1, \dots , k\}$
and
$ f_k \in F_n^{(k)} $
with
$ \lVert {f_k}\rVert \leq C \lVert {f}\rVert $
.
Indeed, if we assume the claim, we may apply it first on f, then on
$f'$
, and so on, until we obtain a decomposition of f into a product of some
$ f_k \in F_n^{(k)} $
and some
$ \gamma _k^{\pm 1} $
(in some order), with each
$ \gamma _k^{\pm 1} $
appearing at most once. The last part of the statement of the proposition follows from the fact that
$ \gamma _k $
is the only generator that does not fix
$ \frac kn $
.
Let us prove the claim. By possibly replacing f with its inverse, we may assume that
$ f^{-1}(\frac kn) < \frac kn $
. Since
$ f $
fixes
$ \frac {k-1}n $
, then it also means that
$ f^{-1}(\frac kn)> \frac {k-1}{n} $
. We can write
$ f^{-1}(\frac kn) $
as
$ \frac {k-1}n + \frac d{n^\ell } $
.
By Lemma 5.6, we get that
$ d \equiv 1\ \pmod {n-1} $
. Using the same lemma, we may construct
$ f_k \in F_n^{(k)} $
that sends
$ f^{-1}(\frac kn) $
to
$\frac {k-1}{n} + \frac 1 {n^2}$
, and this can be chosen with norm bounded linearly in terms of
$\ell $
, and therefore in terms of
$ \lVert {f}\rVert _{F_n} $
by Theorem 5.1 and Lemma 5.2.
So
$f' := f \circ f_k^{-1} \circ \gamma _k^{-1} $
fixes the point
$ \frac kn $
, and clearly also fixes
$ \frac in $
for
$i<k$
. Therefore, we get
$$\begin{align*}f = f' \circ \gamma_k \circ f_k, \end{align*}$$
as required.
Proposition 5.8. Every
$ f \in T_n $
is represented by a word of the form
$$\begin{align*}w(S_{F_n}) \cdot \rho^{-k} \cdot \gamma \cdot v(S_{m}), \end{align*}$$
for some
$ k \in \{0, \dots , {n-1}\}$
, some
$ m \in \{1, \dots , {n}\} $
, and some glide
$ \gamma \in F_n $
(possibly the trivial one). Moreover, w and v can be chosen of length at most
$ C \cdot \lVert {f}\rVert _{T_n} $
, for some constant
$C>0$
independent of f.
Proof. If
$ f \in F_n $
, then the result follows from the fact that
$ F_n $
is undistorted in
$ T_n $
[Reference Sheng19].
Otherwise, let
$ f^{-1}(0) =: \frac {a}n + \frac b{n^\ell } \neq 0 $
, with
$ \frac b{n^\ell } < \frac 1n $
, and let k be the unique integer in
$ \{1, \dots , {n-1} \}$
so that
$ k \equiv a + b\ \pmod {n-1} $
. If
$b=0$
, we are done as
$ f= f' \circ \rho ^{-a} $
for some
$ f' \in F_n $
, so assume
$ b \neq 0 $
.
Let
$f_{a+1} \in F_n^{(a+1)} $
be a function sending
$\frac {a}n + \frac b{n^\ell }$
to
$ \frac an + \frac {c}{n^2} $
, where
$ c \in \{1, \dots , {n-1}\} $
with
$ b \equiv c\ \pmod {n-1} $
. We now choose a glide
$\gamma $
that sends
$ \frac an + \frac {c}{n^2} $
to
$ \frac kn $
; one possible choice is
-
• either
$ \gamma _{a+1,n} $
, if
$ a+c = k $
, -
• or
$ \gamma _{a+1,1} $
if
$ a+c=k+n-1 $
.
This can be checked by looking at tree diagrams for
$ \gamma _{k,1} $
and
$ \gamma _{k,n} $
.
In conclusion, the map
$ f \circ f_{a+1}^{-1} \circ \gamma ^{-1} \circ \rho ^{k} $
stabilizes the point
$0$
, so it is equal to some
$ f' \in F_n $
.
So we have obtained
$$\begin{align*}f = f' \circ \rho^{-k} \circ \gamma \circ f_{a+1}, \end{align*}$$
and we conclude by choosing representatives for the elements
$ f_{a+1} \in F_n^{(a+1)}, f' \in F_n $
.
The estimate follows from the fact that we can choose
$f_{a+1}$
with small norm thanks to Lemma 5.6, and from the fact that
$ F_n $
is undistorted inside
$T_n$
[Reference Sheng19, Theorem 3.7].
As done for T, since every
$ f \in {T_n} $
is represented by a word of linear length in
$ \lVert {f}\rVert _{T_n} $
containing at most one power of
$ \rho $
, by applying Proposition 4.3 we only need to check that the words containing at most three powers of
$ \rho $
have quadratic area.
Proposition 5.9. Let
$$\begin{align*}w=\rho^{-k_1} \cdot w_1(S_{F_n}) \cdot \rho^{k_2} \cdot w_2(S_{F_n}) \end{align*}$$
be a null-homotopic word, where
$ k_1,k_2 \in \{0, \dots , {n-1}\}$
. Then
$ k_1=k_2 $
and
$ \operatorname {\mathrm {Area}}(w) $
is quadratic.
Proof. If
$ k_1=k_2=0 $
, the result follows from the fact that
$ F_n $
[Reference Zhang22] has quadratic Dehn function. Otherwise, both
$k_1$
and
$k_2 $
must be nonzero, or the resulting word could not have
$0$
as a fixed point (and would not be null-homotopic).
Let
$f_1$
be the element of
$F_{n}$
represented by
$w_1$
. Since w is null-homotopic, the map
$ \rho ^{-k_1} f_1 \rho ^{k_2} $
belongs to
$ F_n $
, so in particular,
$ f_1(\frac {k_2}n) = \frac {k_1}n $
, from which we get by Lemma 5.6 that 
.
By [Reference Zhang22], we can replace
$w_1$
with a word
$w_3$
of the form given by Proposition 5.7 using a quadratic amount of relations. Since
$ f_1 $
fixes
$ \frac kn $
, the word
$w_3$
does not contain the generator
$ \gamma _k^{\pm 1} $
(i.e., every letter of
$w_3$
fixes the point
$ \frac kn $
).
So for every letter s of
$w_3$
, the conjugate
$ \rho ^{-k} \cdot s \cdot \rho ^k $
is still an element of
$F_n$
. So we can shift the
$ \rho ^k $
to the left, using that for every letter s in
$w_3$
, then
$ s \rho ^k = \rho ^k s' $
for some
$ s' \in F_n $
.
After using a number of relations that is linear in
$\lvert w_3\rvert$
, the powers of
$ \rho $
cancel, and we are left with a word in
$S_{F_n}$
that has quadratic area by [Reference Zhang22].
Proposition 5.10. Let
$$\begin{align*}w=\rho^{k_1} \cdot w_1(S_F) \cdot \rho^{k_2} \cdot w_2(S_F) \cdot \rho^{k_3} \cdot w_3 (S_F) \end{align*}$$
be a null-homotopic word, where
$ k_1,k_2,k_3 \in \{1, \dots , {n-1}\} $
. Then
$ \operatorname {\mathrm {Area}}(w) $
is quadratic.
Proof. By Proposition 5.8, we can rewrite
$ \rho ^{k_1} \cdot w_1(S_{F_n}) $
as
$ w_4(S_{F_n}) \cdot \rho ^{k_1} \cdot \gamma \cdot w_5(S_{m}) $
. This can be done with a quadratic amount of relations by Proposition 5.9.
Now we shift
$w_5$
to the right of
$ \rho ^{k_2} $
, obtaining
$$\begin{align*}w_4(S_{F_n}) \cdot \rho^{k_1} \cdot \gamma \cdot \rho^{k_2} \cdot w_5(S_{m-k}) \cdot w_2(S_F) \cdot \rho^{k_3} \cdot w_3(S_F), \end{align*}$$
where the index
$ m-k $
is to be intended mod
$ n $
.
Now by Proposition 5.8, we can replace
$ \rho ^{k_1} \gamma \rho ^{k_2} $
, that has length at most
$3n$
(a constant), by some word
$ w_6(S_{F_n}) \rho ^h w_7(S_{F_n}) $
; the number of relations we need is bounded above by a constant that does not depend on w. After doing this, we conclude by the previous lemma.
We now apply Proposition 4.3, where
$W_g$
is defined as the words representing
$ g \in T_n $
of the form given by Proposition 5.8; the area of all triangular diagrams is quadratic by Propositions 5.9 and 5.10. The proof of Theorem B is complete.
6 Final remarks
Higman and Brown defined more generally groups
$ F_{n,r}, T_{n,r} $
[Reference Brown3] and
$ V_{n,r} $
[Reference Higman17] for
$ n \geq 2 $
and
$ r \geq 1 $
. Brown shows that
$ F_{n,r} \cong F_n $
for all
$ r \geq 1 $
, but the same cannot hold for
$ T_{n,r} $
, for example, because the order of torsion elements in
$T_n$
satisfies some restrictions [Reference Sheng19] while in
$T_{n,r}$
, there is always a torsion element of order r.
It is very likely that the same techniques can be used to prove that the Dehn function of
$ T_{n,r} $
is quadratic; however, one should make sure that all the technical lemmas involving distortion still hold in the more general case. In particular, we could not find a reference in the literature proving that
$ F_{n,r} $
is undistorted in
$ T_{n,r} $
.
However, the situation seems intrinsically more difficult when trying to prove that the Dehn function of V is quadratic. First, unlike what happens for F and T, the word metric cannot be estimated as nicely in terms of the reduced tree diagram: the best result one can get [Reference Birget2] is that
$$\begin{align*}\frac 1C N(f) \leq \lVert {f}\rVert_V \leq C N(f) \log N(f), \end{align*}$$
where
$N(f)$
denotes the number of carets for a reduced tree diagram for f. The second obstacle is that, while elements of T can be expressed by a word containing at most one instance of
$C_0$
, a similar result cannot hold for V, as the number of discontinuities for a function
$f \in V$
gives a lower bound for the number of generators not belonging to T in a representative of f.
Acknowledgements
We would like to thank Claudio Llosa Isenrich for pointing us to this question, and for useful discussions. We would also like to thank the anonymous referee for their careful review.
Competing interest
The author has no competing interests to declare.
Funding statement
The author gratefully acknowledges funding by the DFG 281869850 (RTG 2229) and would like to thank INdAM as a member of GNSAGA.
Ethical standards
The research meets all ethical guidelines, including adherence to the legal requirements of the study country.
Open access
