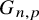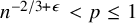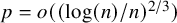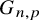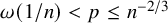1. Introduction
An independent set in a graph
![]() $ G = (V,E)$
is a set of vertices that contains no edge of the graph. The independence number of G, denoted
$ G = (V,E)$
is a set of vertices that contains no edge of the graph. The independence number of G, denoted
![]() $\alpha (G)$
, is the maximum number of vertices in an independent set in G. The binomial random graph
$\alpha (G)$
, is the maximum number of vertices in an independent set in G. The binomial random graph
![]() $ G_{n,p}$
has a vertex set of cardinality n, and each potential edge appears independently with probability p, where
$ G_{n,p}$
has a vertex set of cardinality n, and each potential edge appears independently with probability p, where
![]() $p=p(n)$
can vary with n. We say that an integer-valued random variable X defined on
$p=p(n)$
can vary with n. We say that an integer-valued random variable X defined on
![]() $G_{n,p}$
is concentrated on
$G_{n,p}$
is concentrated on
![]() $k = k(n)$
values if there is a function
$k = k(n)$
values if there is a function
![]() $f(n)$
such that
$f(n)$
such that
In this work, we address the following question: For which probabilities
![]() $p =p(n)$
is
$p =p(n)$
is
![]() $ \alpha ( G_{n,p})$
concentrated on two values?
$ \alpha ( G_{n,p})$
concentrated on two values?
The independence number of
![]() $ G_{n,p}$
has been a central issue in the study of the random graph since the beginning. In the 1970s, Bollobás and Erdős [Reference Bollobás and Erdős5] and Matula [Reference Matula17] independently showed that
$ G_{n,p}$
has been a central issue in the study of the random graph since the beginning. In the 1970s, Bollobás and Erdős [Reference Bollobás and Erdős5] and Matula [Reference Matula17] independently showed that
![]() $ \alpha ( G_{n,p})$
is concentrated on two values when p is a constant. In the late 1980s, Frieze [Reference Frieze9] showed that if
$ \alpha ( G_{n,p})$
is concentrated on two values when p is a constant. In the late 1980s, Frieze [Reference Frieze9] showed that if
![]() $ \omega (1/n) < p < o(1)$
, then
$ \omega (1/n) < p < o(1)$
, then
with high probability. This celebrated result combines the second moment method with a large deviation inequality in a surprising way. Dani and Moore [Reference Dani and Moore8] give the best-known lower bound on the independence number of
![]() $ G_{n,p}$
when p is a constant over n. For further discussion of
$ G_{n,p}$
when p is a constant over n. For further discussion of
![]() $ \alpha (G_{n,p})$
, see the canonical random graphs texts [Reference Bollobás4] [Reference Frieze and Karońksi10] [Reference Janson, Łuczak and Ruciński14].
$ \alpha (G_{n,p})$
, see the canonical random graphs texts [Reference Bollobás4] [Reference Frieze and Karońksi10] [Reference Janson, Łuczak and Ruciński14].
The algorithmic question of finding a large independent set in a random graph is also a central issue. An influential work of Karp and Sipser [Reference Karp and Sipser15] introduced a simple randomized algorithm that determines the independence number of
![]() $ G_{n,p}$
for
$ G_{n,p}$
for
![]() $ p = c/n$
such that
$ p = c/n$
such that
![]() $c < e$
. However, the computational problem of finding a maximum independent set in
$c < e$
. However, the computational problem of finding a maximum independent set in
![]() $ G_{n,p}$
for larger p appears to be a very difficult problem; for example, Coja-Oghlan and Efthymiou [Reference Coja-Oghlan and Efthymious6] showed that the space of independent sets in
$ G_{n,p}$
for larger p appears to be a very difficult problem; for example, Coja-Oghlan and Efthymiou [Reference Coja-Oghlan and Efthymious6] showed that the space of independent sets in
![]() $ G_{n,p}$
that are larger than roughly half the independence number form an ‘intricately ragged landscape’ that foils local search algorithms.
$ G_{n,p}$
that are larger than roughly half the independence number form an ‘intricately ragged landscape’ that foils local search algorithms.
Interest in the concentration of the independence number of
![]() $ G_{n,p}$
is also motivated by the study of the chromatic number of
$ G_{n,p}$
is also motivated by the study of the chromatic number of
![]() $ G_{n,p}$
. An influential series of works starting with Shamir and Spencer [Reference Shamir and Spencer19] and culminating in the result of Alon and Krivelevich [Reference Alon and Krivelevich2] establish two point concentration of the chromatic number of
$ G_{n,p}$
. An influential series of works starting with Shamir and Spencer [Reference Shamir and Spencer19] and culminating in the result of Alon and Krivelevich [Reference Alon and Krivelevich2] establish two point concentration of the chromatic number of
![]() $ G_{n,p}$
for
$ G_{n,p}$
for
![]() $ p < n^{-1/2 - \epsilon }$
(also see [Reference Łuczak16], [Reference Achlioptas and Naor1], [Reference Coja-Oghlan, Panagiotou and Steger7], [Reference Surya and Warnke20]). More recently, Heckel [Reference Heckel12] showed that the chromatic number of
$ p < n^{-1/2 - \epsilon }$
(also see [Reference Łuczak16], [Reference Achlioptas and Naor1], [Reference Coja-Oghlan, Panagiotou and Steger7], [Reference Surya and Warnke20]). More recently, Heckel [Reference Heckel12] showed that the chromatic number of
![]() $ G_{n,1/2}$
is not concentrated on any interval of length smaller then
$ G_{n,1/2}$
is not concentrated on any interval of length smaller then
![]() $ n^{1/4- \epsilon }$
. Heckel and Riordan [Reference Heckel and Riordan13] then improved this lower bound on the length of the interval on which the chromatic number is concentrated to
$ n^{1/4- \epsilon }$
. Heckel and Riordan [Reference Heckel and Riordan13] then improved this lower bound on the length of the interval on which the chromatic number is concentrated to
![]() $ n^{1/2 - \epsilon }$
. They also state a fascinating conjecture regarding fine detail of the concentration of the chromatic number of
$ n^{1/2 - \epsilon }$
. They also state a fascinating conjecture regarding fine detail of the concentration of the chromatic number of
![]() $ G_{n,1/2}$
. Determining the extent of concentration of the chromatic number of
$ G_{n,1/2}$
. Determining the extent of concentration of the chromatic number of
![]() $ G_{n,p}$
for
$ G_{n,p}$
for
![]() $ n^{-1/2} \le p < o(1)$
is another central and interesting question. Two point concentration of the domination number of
$ n^{-1/2} \le p < o(1)$
is another central and interesting question. Two point concentration of the domination number of
![]() $ G_{n,p}$
has also been established for a wide range of values of p [Reference Glebov, Liebenau and Szabó11].
$ G_{n,p}$
has also been established for a wide range of values of p [Reference Glebov, Liebenau and Szabó11].
Despite this extensive interest in two point concentration of closely related parameters, two point concentration of
![]() $ \alpha (G_{n,p})$
itself has not been addressed since the early pioneering results of Bollobás and Erdős and Matula. Our main result is as follows.
$ \alpha (G_{n,p})$
itself has not been addressed since the early pioneering results of Bollobás and Erdős and Matula. Our main result is as follows.
Theorem 1. Let
![]() $ \epsilon>0$
. If
$ \epsilon>0$
. If
![]() $ n^{-2/3+\epsilon } < p \le 1$
, then
$ n^{-2/3+\epsilon } < p \le 1$
, then
![]() $ \alpha ( G_{n,p})$
is concentrated on two values.
$ \alpha ( G_{n,p})$
is concentrated on two values.
Soon after the original version of this manuscript was posted to the ArXiv, Sah and Sawhney observed that Theorem 1 is roughly best possible.
Theorem 2 (Sah and Sawhney [Reference Sah and Sawhney18]).
Suppose
![]() $ p = p(n)$
satisfies
$ p = p(n)$
satisfies
![]() $ p = \omega (1/n)$
and
$ p = \omega (1/n)$
and
![]() $ {p < (\log (n)/(12n))^{2/3}}$
. Then there exists
$ {p < (\log (n)/(12n))^{2/3}}$
. Then there exists
![]() $ q = q(n)$
such that
$ q = q(n)$
such that
![]() $ p \le q \le 2p$
and
$ p \le q \le 2p$
and
![]() $ \alpha ( G_{n,q})$
is not concentrated on fewer than
$ \alpha ( G_{n,q})$
is not concentrated on fewer than
![]() $ n^{-1}p^{-3/2} \log (np) / 2$
values.
$ n^{-1}p^{-3/2} \log (np) / 2$
values.
Note that this anti-concentration statement is somewhat weak as it is compatible with two point concentration for some functions
![]() $ p < n^{-2/3}$
. On the other hand, it is natural to suspect that the extent of concentration of the independence number is monotone in the regime. See the Conclusion for further discussion.
$ p < n^{-2/3}$
. On the other hand, it is natural to suspect that the extent of concentration of the independence number is monotone in the regime. See the Conclusion for further discussion.
Now, the second moment method is the main tool in the proof of Theorem 1. Let
![]() $X_k$
be the number of independent sets of size k in
$X_k$
be the number of independent sets of size k in
![]() $G_{n,p}$
. We have
$G_{n,p}$
. We have
 $$\begin{align*}\mathbb{E}[ X_k ] = \binom{n}{k} (1-p)^{\binom{k}{2}}, \end{align*}$$
$$\begin{align*}\mathbb{E}[ X_k ] = \binom{n}{k} (1-p)^{\binom{k}{2}}, \end{align*}$$
and if k is large enough for this expectation to vanish, then there are no independent sets of size k with high probability. This simple observation provides a general upper bound on
![]() $ \alpha ( G_{n,p})$
. As far as we are aware, this is the only upper bound on
$ \alpha ( G_{n,p})$
. As far as we are aware, this is the only upper bound on
![]() $ \alpha ( G_{n,p})$
that appears in the literature. It turns out this upper bound is sufficient to establish two point concentration when
$ \alpha ( G_{n,p})$
that appears in the literature. It turns out this upper bound is sufficient to establish two point concentration when
![]() $ n^{-1/2 + \epsilon } < p \le 1$
. (This was recently observed by the authors [Reference Bohman and Hofstad3] for
$ n^{-1/2 + \epsilon } < p \le 1$
. (This was recently observed by the authors [Reference Bohman and Hofstad3] for
![]() $n^{-1/3+ \epsilon } < p < o(1)$
.) However, for smaller values of p this upper bound turns out not to be sufficient for two point concentration as the independence number is actually somewhat smaller than the largest value of k for which
$n^{-1/3+ \epsilon } < p < o(1)$
.) However, for smaller values of p this upper bound turns out not to be sufficient for two point concentration as the independence number is actually somewhat smaller than the largest value of k for which
![]() $\mathbb {E}[X_k]= \omega (1)$
with high probability.
$\mathbb {E}[X_k]= \omega (1)$
with high probability.
In the regime
![]() $ n^{-2/3+ \epsilon } < p < n^{-1/2 + \epsilon }$
, we need to consider a more general object. We define an augmented independent set of order k to be a set S of
$ n^{-2/3+ \epsilon } < p < n^{-1/2 + \epsilon }$
, we need to consider a more general object. We define an augmented independent set of order k to be a set S of
![]() $k+r$
vertices such that the graph induced on S is a matching with r edges and every vertex
$k+r$
vertices such that the graph induced on S is a matching with r edges and every vertex
![]() $v \notin S$
has at least two neighbors in S. Clearly, such an augmented independent set contains
$v \notin S$
has at least two neighbors in S. Clearly, such an augmented independent set contains
![]() $2^r$
independent sets of size k, and so
$2^r$
independent sets of size k, and so
![]() $\mathbb {E}[X_k]$
can be quite large even when the expected number of augmented independent sets of order k vanishes. As the appearance of a single independent set of size k implies the appearance of an augmented independent set of order at least k, it follows from this observation that the appearance of augmented independent sets containing large induced matchings can create a situation in which
$\mathbb {E}[X_k]$
can be quite large even when the expected number of augmented independent sets of order k vanishes. As the appearance of a single independent set of size k implies the appearance of an augmented independent set of order at least k, it follows from this observation that the appearance of augmented independent sets containing large induced matchings can create a situation in which
![]() $ \alpha ( G_{n,p}) $
is less then k with high probability (whp) even though
$ \alpha ( G_{n,p}) $
is less then k with high probability (whp) even though
![]() $ \mathbb {E}[X_k]$
tends to infinity. Furthermore, it turns out the variance in the number of augmented independent sets of order k is small enough to allow us to establish two point concentration using the second moment method in the regime in question.
$ \mathbb {E}[X_k]$
tends to infinity. Furthermore, it turns out the variance in the number of augmented independent sets of order k is small enough to allow us to establish two point concentration using the second moment method in the regime in question.
The remainder of this paper is organized as follows. In the following section, we make some preliminary calculations. We then prove our main result, Theorem 1, in Section 3. Theorem 2 is proved in Section 4. In Section 5, we observe that if
![]() $ p = c/n$
for some constant c, then there is a constant K such that
$ p = c/n$
for some constant c, then there is a constant K such that
![]() $ \alpha ( G_{n,p})$
is not concentrated on any interval of length
$ \alpha ( G_{n,p})$
is not concentrated on any interval of length
![]() $ K\sqrt {n}$
. We conclude by making some remarks regarding the concentration
$ K\sqrt {n}$
. We conclude by making some remarks regarding the concentration
![]() $ \alpha ( G_{n,p})$
for
$ \alpha ( G_{n,p})$
for
![]() $ \omega (1/n) < p \le n^{-2/3}$
in Section 6.
$ \omega (1/n) < p \le n^{-2/3}$
in Section 6.
We mentioned above that the second moment method applied to
![]() $X_k$
is sufficient to establish two point concentration down to
$X_k$
is sufficient to establish two point concentration down to
![]() $ p = n^{-1/3+ \epsilon }$
(see [Reference Bohman and Hofstad3] for this proof). It turns out that the second moment method applied to the number of maximal independent sets of size k suffices to establish two point concentration down to
$ p = n^{-1/3+ \epsilon }$
(see [Reference Bohman and Hofstad3] for this proof). It turns out that the second moment method applied to the number of maximal independent sets of size k suffices to establish two point concentration down to
![]() $ p = n^{-1/2 + \epsilon }$
. We include this proof in an appendix.
$ p = n^{-1/2 + \epsilon }$
. We include this proof in an appendix.
2. Preliminary calculations
Throughout Sections 2 and 3, we restrict our attention to
![]() $p = p(n)$
, where
$p = p(n)$
, where
![]() $p =n^{-2/3 + \epsilon } < p < 1/ \log (n)^2$
for some
$p =n^{-2/3 + \epsilon } < p < 1/ \log (n)^2$
for some
![]() $\epsilon>0$
. This is valid as the classical results of Bollobás and Erdős and Matula treat the case
$\epsilon>0$
. This is valid as the classical results of Bollobás and Erdős and Matula treat the case
![]() $ p> 1/ \log (n)^2$
. It is a classical result of Frieze that for all such p we have
$ p> 1/ \log (n)^2$
. It is a classical result of Frieze that for all such p we have
with high probability. As we are interested in refinements of this result, we will need some estimates regarding numbers in this range.
Recall that
![]() $ X_k$
is the number of independent sets of size k in
$ X_k$
is the number of independent sets of size k in
![]() $ G_{n,p}$
. The upper bound in Frieze’s result is achieved by simply identifying a value of k such that
$ G_{n,p}$
. The upper bound in Frieze’s result is achieved by simply identifying a value of k such that
![]() $\mathbb {E} [X_k] = o(1)$
. In order to make comparisons with this bound, we define
$\mathbb {E} [X_k] = o(1)$
. In order to make comparisons with this bound, we define
![]() $ k_x$
to be the largest value of k for which
$ k_x$
to be the largest value of k for which
 $$\begin{align*}\mathbb{E}[X_k] = \binom{n}{k} (1-p)^{\binom{k}{2}}> n^{2\epsilon}. \end{align*}$$
$$\begin{align*}\mathbb{E}[X_k] = \binom{n}{k} (1-p)^{\binom{k}{2}}> n^{2\epsilon}. \end{align*}$$
We note in passing that the exact value in the exponent of this cut-off function is not crucial; we simply need it to be small (in particular, we need
![]() $ \mathbb {E}[ X_{k_x+2}] = o(1)$
) and greater than the exponent in the polynomial function bound that we use to define the variable
$ \mathbb {E}[ X_{k_x+2}] = o(1)$
) and greater than the exponent in the polynomial function bound that we use to define the variable
![]() $k_z$
below.
$k_z$
below.
Now, suppose
![]() $ k = k_x \pm o(1/p)$
. In other words, consider
$ k = k_x \pm o(1/p)$
. In other words, consider
(Note that impact of the
![]() $ 2 \epsilon $
in the definition of
$ 2 \epsilon $
in the definition of
![]() $ k_x$
is absorbed in the
$ k_x$
is absorbed in the
![]() $ o(1)$
term.) Our first observation is that, for such a k, we have
$ o(1)$
term.) Our first observation is that, for such a k, we have
 $$ \begin{align*} \frac{ne}k (1-p)^{k/2} = (1+o(1)) \frac{ne}k \exp\{ - \log(np) + \log( \log(np)) - \log( e/2) + o(1)\} \\ = ( 1 +o(1)) \frac{ \log(np) }{ \log(np) - \log\log(np) + \log(e/2) - o(1)} = 1+o(1). \end{align*} $$
$$ \begin{align*} \frac{ne}k (1-p)^{k/2} = (1+o(1)) \frac{ne}k \exp\{ - \log(np) + \log( \log(np)) - \log( e/2) + o(1)\} \\ = ( 1 +o(1)) \frac{ \log(np) }{ \log(np) - \log\log(np) + \log(e/2) - o(1)} = 1+o(1). \end{align*} $$
So, we have
It follows that we have
 $$ \begin{align} \left( 1 - ( 1 -p)^k\right)^{n-k} = \left( 1 - (1+o(1)) \left( \frac{k}{en}\right)^2 \right)^{n-k} = e^{ - (1 +o(1)) \frac{k^2}{ e^2 n}}. \end{align} $$
$$ \begin{align} \left( 1 - ( 1 -p)^k\right)^{n-k} = \left( 1 - (1+o(1)) \left( \frac{k}{en}\right)^2 \right)^{n-k} = e^{ - (1 +o(1)) \frac{k^2}{ e^2 n}}. \end{align} $$
Similarly,
3. Two-point concentration
In this section, we show that two point concentration of
![]() $\alpha (G_{n,p})$
persists for p as low as
$\alpha (G_{n,p})$
persists for p as low as
![]() $n^{-2/3+\epsilon }$
but at a value that does not equal
$n^{-2/3+\epsilon }$
but at a value that does not equal
![]() $k_x$
for small p. Our main technical result is as follows. We write
$k_x$
for small p. Our main technical result is as follows. We write
![]() $ f(n) \sim g(n)$
if
$ f(n) \sim g(n)$
if
![]() $ \lim _{n \to \infty } f/g =1 $
.
$ \lim _{n \to \infty } f/g =1 $
.
Theorem 3. If
![]() $ n^{-2/3+\epsilon } < p < 1 / \log (n)^2 $
for some
$ n^{-2/3+\epsilon } < p < 1 / \log (n)^2 $
for some
![]() $\epsilon>0$
, then there exists an integer
$\epsilon>0$
, then there exists an integer
![]() $k_{z} = k_{z}(n)$
such that
$k_{z} = k_{z}(n)$
such that
![]() $\alpha (G_{n,p}) \in \{k_{z},k_{z}+1\}$
whp. Furthermore, we have
$\alpha (G_{n,p}) \in \{k_{z},k_{z}+1\}$
whp. Furthermore, we have
 $$\begin{align*}k_x - k_{z} \begin{cases} = 0 & \text{ if } p = \omega\left( \log(n) n^{-1/2} \right)\\ = \xi_n & \text{ if } p = C \log(n) n^{-1/2} \\ \sim \frac{k_x^2}{e^2 n} \sim \frac{ 4 \log(np)^2}{ e^2 p^2 n} & \text{ if } p = o\left( \log(n) n^{-1/2} \right), \end{cases} \end{align*}$$
$$\begin{align*}k_x - k_{z} \begin{cases} = 0 & \text{ if } p = \omega\left( \log(n) n^{-1/2} \right)\\ = \xi_n & \text{ if } p = C \log(n) n^{-1/2} \\ \sim \frac{k_x^2}{e^2 n} \sim \frac{ 4 \log(np)^2}{ e^2 p^2 n} & \text{ if } p = o\left( \log(n) n^{-1/2} \right), \end{cases} \end{align*}$$
where
![]() $ \xi _n \in \left ( \frac {1}{ e^2C^2} -\frac {5}{2}, \frac {1}{ e^2C^2} +\frac {3}{2} \right ) $
.
$ \xi _n \in \left ( \frac {1}{ e^2C^2} -\frac {5}{2}, \frac {1}{ e^2C^2} +\frac {3}{2} \right ) $
.
We emphasize that the sequence
![]() $ \xi _n$
for the case
$ \xi _n$
for the case
![]() $ p = C \log (n) n^{-1/2}$
does not converge to a particular value; rather, it ranges over the specified interval. Indeed,
$ p = C \log (n) n^{-1/2}$
does not converge to a particular value; rather, it ranges over the specified interval. Indeed,
![]() $ \xi _n$
is more precisely given by the following expression
$ \xi _n$
is more precisely given by the following expression
 $$\begin{align*}\xi_n = \left\lceil \frac{1}{e^2C^2} - \frac{2\log(\mathbb{E}[X_{k_x}])}{\log(n)} + 2\epsilon \pm o(1) \right\rceil. \end{align*}$$
$$\begin{align*}\xi_n = \left\lceil \frac{1}{e^2C^2} - \frac{2\log(\mathbb{E}[X_{k_x}])}{\log(n)} + 2\epsilon \pm o(1) \right\rceil. \end{align*}$$
As
![]() $ \mathbb {E}[ X_{k_x}]$
can take a wide range of values as n varies, we have persistent variation of
$ \mathbb {E}[ X_{k_x}]$
can take a wide range of values as n varies, we have persistent variation of
![]() $ \xi _n$
over a small list of values. The remainder of this section is a proof of Theorem 3.
$ \xi _n$
over a small list of values. The remainder of this section is a proof of Theorem 3.
Recall that an augmented independent set of order k in a graph G is defined to be a set of vertices S for which there exists some
![]() $r \geq 0$
such that
$r \geq 0$
such that
![]() $|S| = k+r$
and S contains exactly r edges that form a matching (i.e., these edges are pairwise disjoint) and all vertices outside of S have at least two neighbors in S. To motivate this definition, first note that such a set S contains
$|S| = k+r$
and S contains exactly r edges that form a matching (i.e., these edges are pairwise disjoint) and all vertices outside of S have at least two neighbors in S. To motivate this definition, first note that such a set S contains
![]() $2^r$
independent sets of size k, so this structure is well suited for isolating large variations in the number of independent sets of size k. The fact that we are interested in studying the number of independent sets of size k where k is close to the independence number of G motivates the condition regarding vertices outside of S. Indeed, suppose S is a set such that the induced graph on S is a (not necessarily perfect) matching and v is a vertex outside of S that has one neighbor in S. If v is adjacent to a vertex u that is not in the matching then adding v to S creates an augmented independent set of order k with an additional edge in its matching. So in this situation we would want to include v in S in order to isolate as much variation in the number of independent sets of k as possible. On the other hand, if v is adjacent to a vertex u that is part of the matching, then
$2^r$
independent sets of size k, so this structure is well suited for isolating large variations in the number of independent sets of size k. The fact that we are interested in studying the number of independent sets of size k where k is close to the independence number of G motivates the condition regarding vertices outside of S. Indeed, suppose S is a set such that the induced graph on S is a (not necessarily perfect) matching and v is a vertex outside of S that has one neighbor in S. If v is adjacent to a vertex u that is not in the matching then adding v to S creates an augmented independent set of order k with an additional edge in its matching. So in this situation we would want to include v in S in order to isolate as much variation in the number of independent sets of k as possible. On the other hand, if v is adjacent to a vertex u that is part of the matching, then
![]() $ S \setminus \{u\} \cup \{v\}$
contains an independent set of size
$ S \setminus \{u\} \cup \{v\}$
contains an independent set of size
![]() $k+1$
.
$k+1$
.
Lemma 4. For any graph G,
![]() $\alpha (G) = k$
if and only if G has an augmented independent set of order k but no augmented independent set of any larger order.
$\alpha (G) = k$
if and only if G has an augmented independent set of order k but no augmented independent set of any larger order.
Proof. Let
![]() $ \hat {\alpha }(G)$
be the largest k for which there is an augmented independent set of order k. As an augmented independent set of order k contains an independent set on k vertices, we have
$ \hat {\alpha }(G)$
be the largest k for which there is an augmented independent set of order k. As an augmented independent set of order k contains an independent set on k vertices, we have
Now, suppose that G has a maximum independent set S of size k. Let T be a maximum set of vertices that contains S and has the additional property that the graph induced on T is a matching. We claim that T is an augmented independent set; that is, every vertex outside of T has two neighbors in T. Clearly, every vertex outside T has a neighbor in T (since S is a maximum independent set). If v is a vertex outside of T with only one neighbor in T, then this neighbor u is in one of the matching edges (since T is chosen to be a maximum set with the given property), but in this situation the set
![]() $ (T \setminus \{u\}) \cup \{v\}$
contains an independent set that is larger than S, which is a contradiction. So, T is an augmented independent set of order at least k. Therefore,
$ (T \setminus \{u\}) \cup \{v\}$
contains an independent set that is larger than S, which is a contradiction. So, T is an augmented independent set of order at least k. Therefore,
We prove Theorem 3 by applying the second moment method to the random variable Z, which counts the number of augmented independent sets of order
![]() $k_z$
with a prescribed number of edges
$k_z$
with a prescribed number of edges
![]() $r_z$
. This requires some relatively delicate estimates to determine the optimal values of the parameters
$r_z$
. This requires some relatively delicate estimates to determine the optimal values of the parameters
![]() $k_z$
and
$k_z$
and
![]() $r_z$
. We begin with those calculations. We then move on to the first moment and second moment calculations for Z that suffice to prove Theorem 3.
$r_z$
. We begin with those calculations. We then move on to the first moment and second moment calculations for Z that suffice to prove Theorem 3.
3.1. Defining and estimating
 $k_z$
and
$k_z$
and
 $r_z$
$r_z$
In this section, we define
![]() $ k_z$
and
$ k_z$
and
![]() $r_z$
, and establish a number of estimates of these quantities.
$r_z$
, and establish a number of estimates of these quantities.
To start, let
![]() $E(n,k,r)$
denote the expected number of augmented independent sets of order k with exactly r edges in
$E(n,k,r)$
denote the expected number of augmented independent sets of order k with exactly r edges in
![]() $G_{n,p}$
. There are
$G_{n,p}$
. There are
![]() $\binom {n}{k+r}$
ways to choose the location of our set, and given this set there are
$\binom {n}{k+r}$
ways to choose the location of our set, and given this set there are
![]() $\frac {(k+r)!}{(k-r)! 2^r r!}$
ways to choose the locations of the r disjoint edges. The probability of choosing internal edges accordingly is
$\frac {(k+r)!}{(k-r)! 2^r r!}$
ways to choose the locations of the r disjoint edges. The probability of choosing internal edges accordingly is
and finally, the probability that every vertex outside our set has at least two neighbors within the set is
![]() $ F(n,k,r)^{n-k-r}$
where we set
$ F(n,k,r)^{n-k-r}$
where we set
Thus, we have
 $$ \begin{align} E(n,k,r) =\binom{n}{k+r}\frac{(k+r)!}{(k-r)! 2^r r!}p^r(1-p)^{\binom{k+r}{2}-r} F(n,k,r)^{n-k-r}. \end{align} $$
$$ \begin{align} E(n,k,r) =\binom{n}{k+r}\frac{(k+r)!}{(k-r)! 2^r r!}p^r(1-p)^{\binom{k+r}{2}-r} F(n,k,r)^{n-k-r}. \end{align} $$
Now, we define
![]() $k_z = k_z(n)$
to be the largest
$k_z = k_z(n)$
to be the largest
![]() $k \le k_x$
for which there exists an r such that
$k \le k_x$
for which there exists an r such that
![]() $ E(n,k,r)> n^{\epsilon }$
.Footnote 1
$ E(n,k,r)> n^{\epsilon }$
.Footnote 1
Our first observation is that, while
![]() $k_z$
is not equal to
$k_z$
is not equal to
![]() $k_x$
when p is sufficiently small, the difference between the two numbers is relatively small.
$k_x$
when p is sufficiently small, the difference between the two numbers is relatively small.
Lemma 5. If
![]() $ p = \omega ( \log (n)/ \sqrt {n} )$
, then
$ p = \omega ( \log (n)/ \sqrt {n} )$
, then
![]() $ k_z = k_x$
. Otherwise, we have
$ k_z = k_x$
. Otherwise, we have
 $$ \begin{align*} k_z \ge k_x - O \left( \frac{ k_x^2}{n} \right) \ge k_x - o( k_x^{1/2}). \end{align*} $$
$$ \begin{align*} k_z \ge k_x - O \left( \frac{ k_x^2}{n} \right) \ge k_x - o( k_x^{1/2}). \end{align*} $$
Proof. This observation follows from considering
![]() $r=0$
and
$r=0$
and
![]() $ k = k_x - \frac { C k_x^2}{n}$
, where C is a sufficiently large constant and applying Equations (4) and (6). We first note that if
$ k = k_x - \frac { C k_x^2}{n}$
, where C is a sufficiently large constant and applying Equations (4) and (6). We first note that if
![]() $ p = \omega ( \log (n)/ \sqrt {n})$
, then the expression in Equation (6) is subpolynomial. In this case, we have
$ p = \omega ( \log (n)/ \sqrt {n})$
, then the expression in Equation (6) is subpolynomial. In this case, we have
![]() $ E(n,k_x,0)> n^{\epsilon }$
and
$ E(n,k_x,0)> n^{\epsilon }$
and
![]() $ k_z = k_x$
.
$ k_z = k_x$
.
Restricting our attention to
![]() $ p = O ( \log (n)/ \sqrt {n})$
, note that for
$ p = O ( \log (n)/ \sqrt {n})$
, note that for
![]() $ k = k_x - O( k_x^2/n)$
we have
$ k = k_x - O( k_x^2/n)$
we have
 $$ \begin{align} \frac{ \binom{n}{k} (1-p)^{\binom{k}{2}} }{ \binom{n}{k+1} (1-p)^{\binom{k+1}{2}} } = \frac{ k+1}{n-k} (1-p)^{-k} = (1+o(1)) \frac{ ne^2}{k}, \end{align} $$
$$ \begin{align} \frac{ \binom{n}{k} (1-p)^{\binom{k}{2}} }{ \binom{n}{k+1} (1-p)^{\binom{k+1}{2}} } = \frac{ k+1}{n-k} (1-p)^{-k} = (1+o(1)) \frac{ ne^2}{k}, \end{align} $$
and thus
 $$ \begin{align*} \begin{split} E(n,k,0) &=\binom{n}{k} (1-p)^{ \binom{k}{2} } \exp \left\{- (1+o(1)) \frac{p k^3}{ e^2 n} \right\} \nonumber \\& \ge \left( \frac{ ne^2}{ 2k} \right)^{ \frac{ C k^2}{n}} \exp \left\{- (1+o(1)) \frac{p k^3}{ e^2 n} \right\}. \end{split} \end{align*} $$
$$ \begin{align*} \begin{split} E(n,k,0) &=\binom{n}{k} (1-p)^{ \binom{k}{2} } \exp \left\{- (1+o(1)) \frac{p k^3}{ e^2 n} \right\} \nonumber \\& \ge \left( \frac{ ne^2}{ 2k} \right)^{ \frac{ C k^2}{n}} \exp \left\{- (1+o(1)) \frac{p k^3}{ e^2 n} \right\}. \end{split} \end{align*} $$
Therefore,
![]() $E(n,k,0)> n^{\epsilon }$
if C is a sufficiently large constant.
$E(n,k,0)> n^{\epsilon }$
if C is a sufficiently large constant.
Note that we may henceforth assume that the estimates given in Equations 3–6 hold for
![]() $k_z \le k \le k_x$
.
$k_z \le k \le k_x$
.
Next, for
![]() $ k_z \le k \le k_x$
define
$ k_z \le k \le k_x$
define
We are now ready to define the random variable Z. Set
![]() $ r_z = r_M(k_z)$
, and let the variable Z count the number of augmented independent sets of order
$ r_z = r_M(k_z)$
, and let the variable Z count the number of augmented independent sets of order
![]() $k_z$
with exactly
$k_z$
with exactly
![]() $r_z$
internal edges. Note that such sets have
$r_z$
internal edges. Note that such sets have
![]() $k_{z}+r_z$
vertices and
$k_{z}+r_z$
vertices and
![]() $\mathbb {E}(Z) = E(n,k_z,r_z)> n^\epsilon $
.
$\mathbb {E}(Z) = E(n,k_z,r_z)> n^\epsilon $
.
We now move on to more accurate estimates for
![]() $k_z$
and
$k_z$
and
![]() $r_z$
, starting with an estimate for
$r_z$
, starting with an estimate for
![]() $r_z$
that we obtain by estimating the ratio of consecutive terms of Equation (8). Note that we always have
$r_z$
that we obtain by estimating the ratio of consecutive terms of Equation (8). Note that we always have
![]() $r \leq k$
, which we will use a couple of times below. First, we show that
$r \leq k$
, which we will use a couple of times below. First, we show that
![]() $F(n,k,r)^{n-k-r}$
will have an insignificant effect on the ratio. One can easily verify, using Equation (4), that
$F(n,k,r)^{n-k-r}$
will have an insignificant effect on the ratio. One can easily verify, using Equation (4), that
![]() $F(n,k,r) = 1-o(1)$
. Furthermore,
$F(n,k,r) = 1-o(1)$
. Furthermore,
exactly. Therefore, we have
 $$ \begin{align*} \frac{F(n,k,r+1)^{n-k-r-1}}{F(n,k,r)^{n-k-r}} & = \left(\frac{F(n,k,r+1)}{F(n,k,r)}\right)^{n-k-r} F(n,k,r+1)^{-1} \\ & = (1 +o(1)) \left( 1 + \frac{ (k+r)p^2(1 -p)^{k+r-1}}{ F(n,k,r)} \right)^{n-k-r} \\ & = (1 +o(1)) \left( 1 + (1+o(1)) (k+r)p^2(1 -p)^{k+r-1} \right)^{n-k-r}. \end{align*} $$
$$ \begin{align*} \frac{F(n,k,r+1)^{n-k-r-1}}{F(n,k,r)^{n-k-r}} & = \left(\frac{F(n,k,r+1)}{F(n,k,r)}\right)^{n-k-r} F(n,k,r+1)^{-1} \\ & = (1 +o(1)) \left( 1 + \frac{ (k+r)p^2(1 -p)^{k+r-1}}{ F(n,k,r)} \right)^{n-k-r} \\ & = (1 +o(1)) \left( 1 + (1+o(1)) (k+r)p^2(1 -p)^{k+r-1} \right)^{n-k-r}. \end{align*} $$
Since
it follows that
 $$ \begin{align} \frac{F(n,k,r+1)^{n-k-r-1}}{F(n,k,r)^{n-k-r}} = 1+o(1), \end{align} $$
$$ \begin{align} \frac{F(n,k,r+1)^{n-k-r-1}}{F(n,k,r)^{n-k-r}} = 1+o(1), \end{align} $$
as desired.
With this bound on the ratio
![]() $ F(n,k,r+1)^{n-k-r-1}/ F(n,k,r)^{n-k-r}$
in hand and applying Equation (4) as in Equation (9), we conclude that if
$ F(n,k,r+1)^{n-k-r-1}/ F(n,k,r)^{n-k-r}$
in hand and applying Equation (4) as in Equation (9), we conclude that if
![]() $r = o(1/p)$
, then we have
$r = o(1/p)$
, then we have
 $$ \begin{align}\nonumber \frac{E(n,k,r+1)}{E(n,k,r)} &=(1+o(1)) \frac{ \binom{n}{k+r+1} (1-p)^{\binom{k+r+1}{2}} }{ \binom{n}{k+r} (1-p)^{\binom{k+r}{2}} } \left(\frac{(k+r+1)(k-r)p}{2(r+1)}\right)\\& = (1+o(1)) \left(\frac{k}{e^2 n}\right) \left(\frac{(k+r+1)(k-r)p}{2(r+1)}\right) \end{align} $$
$$ \begin{align}\nonumber \frac{E(n,k,r+1)}{E(n,k,r)} &=(1+o(1)) \frac{ \binom{n}{k+r+1} (1-p)^{\binom{k+r+1}{2}} }{ \binom{n}{k+r} (1-p)^{\binom{k+r}{2}} } \left(\frac{(k+r+1)(k-r)p}{2(r+1)}\right)\\& = (1+o(1)) \left(\frac{k}{e^2 n}\right) \left(\frac{(k+r+1)(k-r)p}{2(r+1)}\right) \end{align} $$
 $$ \begin{align} &= (1+o(1))\frac{k^3p}{2e^2n(r+1)}(1-r^2/k^2).\qquad \end{align} $$
$$ \begin{align} &= (1+o(1))\frac{k^3p}{2e^2n(r+1)}(1-r^2/k^2).\qquad \end{align} $$
This calculation provides the desired estimate for
![]() $r_z$
.
$r_z$
.
Lemma 6.
 $$\begin{align*}r_z = \left\lceil (1+o(1)) \frac{4 \log(np)^3 }{ e^2 n p^2} -1 \right\rceil. \end{align*}$$
$$\begin{align*}r_z = \left\lceil (1+o(1)) \frac{4 \log(np)^3 }{ e^2 n p^2} -1 \right\rceil. \end{align*}$$
Proof. First, note that the form of Equation (12) suggests that
![]() $ r_M(k)$
should be roughly
$ r_M(k)$
should be roughly
![]() $ k^3p/n$
as this is the regime in which the ratio is roughly one. Since
$ k^3p/n$
as this is the regime in which the ratio is roughly one. Since
![]() $k^3p/n = o(1/p)$
, the estimate given by Equation (12) holds in the vicinity of
$k^3p/n = o(1/p)$
, the estimate given by Equation (12) holds in the vicinity of
![]() $ r = k^3p/n$
. Furthermore, for
$ r = k^3p/n$
. Furthermore, for
![]() $ r= \Omega (1/p)$
the arguments above can be easily adapted to show that
$ r= \Omega (1/p)$
the arguments above can be easily adapted to show that
![]() $ E(n,k,r+1)/E(n,k,r)$
is bounded above by the expression in Equation (12). It follows that we have
$ E(n,k,r+1)/E(n,k,r)$
is bounded above by the expression in Equation (12). It follows that we have
Hence, we can conclude that
 $$ \begin{align} r_M(k) \le \frac{k^3p}{e^2n} = O\left( \frac{\log(np) k^2}{n} \right). \end{align} $$
$$ \begin{align} r_M(k) \le \frac{k^3p}{e^2n} = O\left( \frac{\log(np) k^2}{n} \right). \end{align} $$
Note that if
![]() $r = O( k^3p/n )$
then the
$r = O( k^3p/n )$
then the
![]() $(1-r^2/k^2) $
term in Equation (12) is equal to
$(1-r^2/k^2) $
term in Equation (12) is equal to
![]() $ 1+o(1)$
. We conclude that we have
$ 1+o(1)$
. We conclude that we have
 $$ \begin{align} r_M(k) = \left\lceil \frac{k^3p}{ 2 e^2n} (1+o(1)) -1 \right\rceil. \end{align} $$
$$ \begin{align} r_M(k) = \left\lceil \frac{k^3p}{ 2 e^2n} (1+o(1)) -1 \right\rceil. \end{align} $$
In light of Lemma 5, the proof is complete.
We note in passing that Lemma 6 implies that
![]() $ r_z $
becomes relevant at
$ r_z $
becomes relevant at
![]() $ p = \Theta ( \log (n)^{3/2}/ n^{1/2}) $
, as
$ p = \Theta ( \log (n)^{3/2}/ n^{1/2}) $
, as
![]() $ r_z=0$
for p larger than this regime. Furthermore, for all p that we contemplate in this section (i.e., for
$ r_z=0$
for p larger than this regime. Furthermore, for all p that we contemplate in this section (i.e., for
![]() $p> n^{-2/3 + \epsilon }$
) we have
$p> n^{-2/3 + \epsilon }$
) we have
Finally, we turn to estimating
![]() $ k_z $
. Note that we may assume
$ k_z $
. Note that we may assume
![]() $ p = O( \log (n) n^{-1/2})$
as we have
$ p = O( \log (n) n^{-1/2})$
as we have
![]() $ k_z= k_x $
for larger p by Lemma 5. Note further that Equation (15) implies that
$ k_z= k_x $
for larger p by Lemma 5. Note further that Equation (15) implies that
![]() $ r_M(k) = \Omega ( \log (n))$
for
$ r_M(k) = \Omega ( \log (n))$
for
![]() $ k_z \le k \le k_x$
for p in this regime. Recall that, appealing to Equation (6), we have
$ k_z \le k \le k_x$
for p in this regime. Recall that, appealing to Equation (6), we have
Next, observe that, since
![]() $F(n,k+1,r) = F(n,k,r+1)$
, we can easily adapt the argument that proves Equation (10) to establish
$F(n,k+1,r) = F(n,k,r+1)$
, we can easily adapt the argument that proves Equation (10) to establish
 $$\begin{align*}\frac{F(n,k+1,r)^{n-k-r-1}}{F(n,k,r)^{n-k-r}} = 1+o(1) \end{align*}$$
$$\begin{align*}\frac{F(n,k+1,r)^{n-k-r-1}}{F(n,k,r)^{n-k-r}} = 1+o(1) \end{align*}$$
for
![]() $ k_z \le k \le k_x$
and
$ k_z \le k \le k_x$
and
![]() $r = o(1/p)$
. So we can calculate the ratio over a change in k in the same way that we established Equation (12). Thus, for
$r = o(1/p)$
. So we can calculate the ratio over a change in k in the same way that we established Equation (12). Thus, for
![]() $ k_z \le k \le k_x$
and
$ k_z \le k \le k_x$
and
![]() $r = o(1/p)$
we have
$r = o(1/p)$
we have
Using Equations (6), (17), (12) and (15), we write
 $$ \begin{align*} \begin{split} E(n,k,r_M(k)) & = E(n,k_x,0) \prod_{\ell=k}^{k_x-1} \frac{E (n,\ell,0)}{ E(n, \ell+1,0) } \prod_{r=0}^{r_M(k)-1} \frac{E(n,k,r+1)}{ E(n,k,r)} \\ & = \mathbb{E}[ X_{k_x}] e^{- (1+o(1)) \frac{p k_x^3}{ e^2 n} } \left( \frac{e^2n}{k} (1+o(1)) \right)^{k_x-k} \left((1+o(1))\frac{k^3p}{2e^2n} \right)^{r_M(k)} \frac{1}{ r_M(k)!} \\ & = \mathbb{E}[ X_{k_x}] e^{- (1+o(1)) \frac{p k_x^3}{ 2 e^2 n} } \left( \frac{e^2n}{k} (1+o(1)) \right)^{k_x-k}. \end{split} \end{align*} $$
$$ \begin{align*} \begin{split} E(n,k,r_M(k)) & = E(n,k_x,0) \prod_{\ell=k}^{k_x-1} \frac{E (n,\ell,0)}{ E(n, \ell+1,0) } \prod_{r=0}^{r_M(k)-1} \frac{E(n,k,r+1)}{ E(n,k,r)} \\ & = \mathbb{E}[ X_{k_x}] e^{- (1+o(1)) \frac{p k_x^3}{ e^2 n} } \left( \frac{e^2n}{k} (1+o(1)) \right)^{k_x-k} \left((1+o(1))\frac{k^3p}{2e^2n} \right)^{r_M(k)} \frac{1}{ r_M(k)!} \\ & = \mathbb{E}[ X_{k_x}] e^{- (1+o(1)) \frac{p k_x^3}{ 2 e^2 n} } \left( \frac{e^2n}{k} (1+o(1)) \right)^{k_x-k}. \end{split} \end{align*} $$
This estimate suffices to establish the following.
Lemma 7.
 $$ \begin{align*} n^{-2/3 + \epsilon} < p \ll \log(n) n^{-1/2} & \hskip5mm \Rightarrow & k_x - k_z = (1+o(1)) \frac{ k_x^2 }{ e^2 n } = (1+o(1)) \frac{ 4 \log(np)^2 }{ e^2p^2n} \\ p = C \log(n) n^{-1/2} & \hskip5mm \Rightarrow & k_x - k_z = \left\lceil \frac{1}{e^2C^2} - \frac{2\log(\mathbb{E}[X_{k_x}])}{\log(n)} + 2 \epsilon \pm o(1) \right\rceil. \end{align*} $$
$$ \begin{align*} n^{-2/3 + \epsilon} < p \ll \log(n) n^{-1/2} & \hskip5mm \Rightarrow & k_x - k_z = (1+o(1)) \frac{ k_x^2 }{ e^2 n } = (1+o(1)) \frac{ 4 \log(np)^2 }{ e^2p^2n} \\ p = C \log(n) n^{-1/2} & \hskip5mm \Rightarrow & k_x - k_z = \left\lceil \frac{1}{e^2C^2} - \frac{2\log(\mathbb{E}[X_{k_x}])}{\log(n)} + 2 \epsilon \pm o(1) \right\rceil. \end{align*} $$
Proof. First, note that for p in these ranges we have
It follows that
![]() $ k_x - k_z$
is the smallest integer
$ k_x - k_z$
is the smallest integer
![]() $ \kappa $
such that
$ \kappa $
such that
If
![]() $ p \ll \log (n) n^{-1/2}$
, then
$ p \ll \log (n) n^{-1/2}$
, then
![]() $ \log \mathbb {E}[X_k] = O( \log (n)) = o( k_x^3p/n)$
and the first part of the Lemma follows. On the other hand, if
$ \log \mathbb {E}[X_k] = O( \log (n)) = o( k_x^3p/n)$
and the first part of the Lemma follows. On the other hand, if
![]() $ p = C \log (n) n^{-1/2}$
, then
$ p = C \log (n) n^{-1/2}$
, then
![]() $ k_x^3 p /n = (1+o(1))\log (n)/C^2$
and
$ k_x^3 p /n = (1+o(1))\log (n)/C^2$
and
![]() $ p k_x = \log (n) (1+o(1))$
and we recover the second part of the lemma.
$ p k_x = \log (n) (1+o(1))$
and we recover the second part of the lemma.
3.2. First moment
Here, we show that, with high probability, no augmented independent set of order k appears for any
![]() $ k_{z}+2 \le k \le k_x+1$
. This is sufficient because we can simply consider the expected number of independent sets of size
$ k_{z}+2 \le k \le k_x+1$
. This is sufficient because we can simply consider the expected number of independent sets of size
![]() $k_x + 2$
to rule out the appearance of any larger independent set. We emphasize that we are restricting our attention to k that satisfy Equation (3). We begin with a simple observation.
$k_x + 2$
to rule out the appearance of any larger independent set. We emphasize that we are restricting our attention to k that satisfy Equation (3). We begin with a simple observation.
Lemma 8. For all k that satisfy Equation (3), we have
 $$ \begin{align*}\displaystyle\sum_{r=0}^{k} E(n,k,r) \leq 4 \sum_{r=0}^{2r_M(k)} E(n,k,r).\end{align*} $$
$$ \begin{align*}\displaystyle\sum_{r=0}^{k} E(n,k,r) \leq 4 \sum_{r=0}^{2r_M(k)} E(n,k,r).\end{align*} $$
Proof. We begin by noting that Equation (12) can be adapted to show
 $$\begin{align*}\frac{ E(n,k,r+1) }{ E(n,k,r)} \le (1+o(1))\frac{k^3p}{2e^2n(r+1)}. \end{align*}$$
$$\begin{align*}\frac{ E(n,k,r+1) }{ E(n,k,r)} \le (1+o(1))\frac{k^3p}{2e^2n(r+1)}. \end{align*}$$
Now, we consider cases depending on the value of
![]() $ r_M = r_M(k)$
. First, note that if
$ r_M = r_M(k)$
. First, note that if
![]() $ r_M = 0$
then we have
$ r_M = 0$
then we have
![]() $ k^3p/ (2e^2n) < 1 +o(1) $
and
$ k^3p/ (2e^2n) < 1 +o(1) $
and
 $$\begin{align*}\sum_{r=0}^k E(n,k,r) \le (1+o(1)) E(n,k,0) \sum_{r=0}^\infty \frac{1}{r!} \le 4 E(n,k,0). \end{align*}$$
$$\begin{align*}\sum_{r=0}^k E(n,k,r) \le (1+o(1)) E(n,k,0) \sum_{r=0}^\infty \frac{1}{r!} \le 4 E(n,k,0). \end{align*}$$
Now, suppose
![]() $ r_M \ge 1$
. Recalling Equation (15), note that if
$ r_M \ge 1$
. Recalling Equation (15), note that if
![]() $r> 2r_M$
, then we have
$r> 2r_M$
, then we have
So we have
 $$ \begin{align*} \displaystyle\sum_{r=0}^{k} E(n,k,r) &= \sum_{r=0}^{2r_M} E(n,k,r) + \sum_{r =2r_M+1}^k E(n,k,r) \\ &\le \left(\sum_{r=0}^{2r_M} E(n,k,r)\right) + 3 E(n,k,2r_M+1) \le \left(\sum_{r=0}^{2r_M} E(n,k,r)\right) + 3 E(n,k,2r_M).\quad\qquad\\[-52pt] \end{align*} $$
$$ \begin{align*} \displaystyle\sum_{r=0}^{k} E(n,k,r) &= \sum_{r=0}^{2r_M} E(n,k,r) + \sum_{r =2r_M+1}^k E(n,k,r) \\ &\le \left(\sum_{r=0}^{2r_M} E(n,k,r)\right) + 3 E(n,k,2r_M+1) \le \left(\sum_{r=0}^{2r_M} E(n,k,r)\right) + 3 E(n,k,2r_M).\quad\qquad\\[-52pt] \end{align*} $$
Note that it follows from the proof of Lemma 8 that we have
Applying this observation together with Lemma 8 and Equation (17), we have
 $$ \begin{align*} \sum_{r=0}^{k+1}E(n,k+1,r) &< \frac{5}{3} \sum_{r=0}^k E(n,k+1,r) \\&< \frac{20}{3} \sum_{r=0}^{2 r_M(k+1)} E(n,k+1,r)\\&< \frac{k}{n} \sum_{r=0}^{2 r_M(k+1)} E(n,k,r)\\&< \frac{k}{n} \sum_{r=0}^{k}E(n,k,r). \end{align*} $$
$$ \begin{align*} \sum_{r=0}^{k+1}E(n,k+1,r) &< \frac{5}{3} \sum_{r=0}^k E(n,k+1,r) \\&< \frac{20}{3} \sum_{r=0}^{2 r_M(k+1)} E(n,k+1,r)\\&< \frac{k}{n} \sum_{r=0}^{2 r_M(k+1)} E(n,k,r)\\&< \frac{k}{n} \sum_{r=0}^{k}E(n,k,r). \end{align*} $$
Therefore, by Lemma 8 and Equation (14), we have
 $$ \begin{align*} \displaystyle\sum_{k=k_z+2}^{k_x+1} \left(\sum_{r=0}^{k}E(n,k,r)\right) &< \frac{2k_z}{n} \sum_{r=0}^{k_z+1} E(n,k_z+1,r) \\[4pt]&\leq \frac{8k_z}{n} \sum_{r=0}^{2r_M(k_z+1)} E(n,k_z+1,r) \\[4pt]&\leq \left(\frac{8k_z}{n}\right)\left(\frac{3k_z^3 p}{e^2 n}\right) E(n,k_z+1,r_M( k_z+1)) \\[4pt]&\leq \left(\frac{8k_z}{n}\right)\left(\frac{3k_z^3 p}{e^2 n}\right) n^\epsilon \\[4pt]&= O(\log(n)^4n^{-2\epsilon}). \end{align*} $$
$$ \begin{align*} \displaystyle\sum_{k=k_z+2}^{k_x+1} \left(\sum_{r=0}^{k}E(n,k,r)\right) &< \frac{2k_z}{n} \sum_{r=0}^{k_z+1} E(n,k_z+1,r) \\[4pt]&\leq \frac{8k_z}{n} \sum_{r=0}^{2r_M(k_z+1)} E(n,k_z+1,r) \\[4pt]&\leq \left(\frac{8k_z}{n}\right)\left(\frac{3k_z^3 p}{e^2 n}\right) E(n,k_z+1,r_M( k_z+1)) \\[4pt]&\leq \left(\frac{8k_z}{n}\right)\left(\frac{3k_z^3 p}{e^2 n}\right) n^\epsilon \\[4pt]&= O(\log(n)^4n^{-2\epsilon}). \end{align*} $$
Hence, whp no augmented independent set of order k for any
![]() $k \geq k_z+2$
appears and by Lemma 4, we have
$k \geq k_z+2$
appears and by Lemma 4, we have
![]() $\alpha (G) \leq k_z+1$
whp.
$\alpha (G) \leq k_z+1$
whp.
3.3. Second moment method applied to Z
Here, we prove by the second moment method that an augmented independent set of order
![]() $k_z$
appears with high probability; more specifically, we prove that such a set with
$k_z$
appears with high probability; more specifically, we prove that such a set with
![]() $k_z+r_z$
vertices and
$k_z+r_z$
vertices and
![]() $r_z = r_M( k_z)$
internal edges appears whp. For convenience we let
$r_z = r_M( k_z)$
internal edges appears whp. For convenience we let
throughout the rest of this subsection. Recall that the random variable Z counts the number of augmented independent sets of order k with r edges, and by the definition of
![]() $r_M$
and Z we have
$r_M$
and Z we have
and our goal is to show that
![]() $ Z>0$
whp.
$ Z>0$
whp.
We now break up Z into a sum of indicator random variables. Let
![]() $ \mathbb {S}$
be the collection of all pairs
$ \mathbb {S}$
be the collection of all pairs
![]() $ (S, m_S)$
, where S is a set of
$ (S, m_S)$
, where S is a set of ![]() vertices and
vertices and
![]() $ m_S$
is a matching consisting of r edges all of which are contained in S. Note that
$ m_S$
is a matching consisting of r edges all of which are contained in S. Note that

For each pair
![]() $ (S, m_S) \in \mathbb {S}$
, let
$ (S, m_S) \in \mathbb {S}$
, let
![]() $ Z_{S,m_S}$
be the indicator random variable for the event that S is an augmented independent set with matching
$ Z_{S,m_S}$
be the indicator random variable for the event that S is an augmented independent set with matching
![]() $m_S$
. We have
$m_S$
. We have
 $$ \begin{align*} &\text{Var}(Z) \leq \sum_{(S,m_S) \in \mathbb{S}} \text{Var}(Z_{S,m_S})+ \sum_{S \neq T} \text{Cov}(Z_{S,m_S},Z_{T,m_T})\qquad\qquad\qquad\qquad\qquad\qquad \\[4pt] &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\leq \mathbb{E}(Z) + \sum_{S \neq T} \mathbb{E}(Z_{S,m_S} Z_{T,m_T}) - \mathbb{E}(Z_{S,m_S})\mathbb{E}(Z_{T,m_T}), \end{align*} $$
$$ \begin{align*} &\text{Var}(Z) \leq \sum_{(S,m_S) \in \mathbb{S}} \text{Var}(Z_{S,m_S})+ \sum_{S \neq T} \text{Cov}(Z_{S,m_S},Z_{T,m_T})\qquad\qquad\qquad\qquad\qquad\qquad \\[4pt] &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\leq \mathbb{E}(Z) + \sum_{S \neq T} \mathbb{E}(Z_{S,m_S} Z_{T,m_T}) - \mathbb{E}(Z_{S,m_S})\mathbb{E}(Z_{T,m_T}), \end{align*} $$
where here and throughout this section such summations are over all
![]() $ (S,m_S), (T,m_T) \in \mathbb {S}$
that have the specified S and/or T. Note that we are making use of the full covariance; we will see below that this is necessary to handle sets
$ (S,m_S), (T,m_T) \in \mathbb {S}$
that have the specified S and/or T. Note that we are making use of the full covariance; we will see below that this is necessary to handle sets
![]() $S,T$
such that
$S,T$
such that
![]() $ |S\cap T|$
is roughly
$ |S\cap T|$
is roughly
![]() $ k^2/n$
. Next, let
$ k^2/n$
. Next, let
 $$ \begin{align} h_i &:= \frac{1}{\mathbb{E}(Z)^2}\sum_{|S \cap T| = i} \mathbb{E}(Z_{S,m_S} Z_{T,m_T}) - \mathbb{E}(Z_{S,m_S}) \mathbb{E}(Z_{T,m_T}) \end{align} $$
$$ \begin{align} h_i &:= \frac{1}{\mathbb{E}(Z)^2}\sum_{|S \cap T| = i} \mathbb{E}(Z_{S,m_S} Z_{T,m_T}) - \mathbb{E}(Z_{S,m_S}) \mathbb{E}(Z_{T,m_T}) \end{align} $$
 $$ \begin{align}&= \left(\frac{1 }{ |\mathbb{S}| }\right)^2\sum_{|S \cap T| = i} \left(\frac{\mathbb{E}(Z_{T,m_T} | Z_{S, m_S} = 1)}{\mathbb{E}(Z_{S,m_S})} - 1\right).\qquad\quad\ \end{align} $$
$$ \begin{align}&= \left(\frac{1 }{ |\mathbb{S}| }\right)^2\sum_{|S \cap T| = i} \left(\frac{\mathbb{E}(Z_{T,m_T} | Z_{S, m_S} = 1)}{\mathbb{E}(Z_{S,m_S})} - 1\right).\qquad\quad\ \end{align} $$
Applying the second moment method, we have
![]() $ \mathbb {P}( Z = 0) \le \text {Var}[Z]/ \mathbb {E}[Z]^2 $
. Thus, our goal is to show
$ \mathbb {P}( Z = 0) \le \text {Var}[Z]/ \mathbb {E}[Z]^2 $
. Thus, our goal is to show

We emphasize that
![]() $ \mathbb {E}(Z)$
can be significantly different from
$ \mathbb {E}(Z)$
can be significantly different from
![]() $ \mathbb {E}(X)$
here. We consider three ranges of i to establish the desired bounds on
$ \mathbb {E}(X)$
here. We consider three ranges of i to establish the desired bounds on
![]() $ \sum h_i$
.
$ \sum h_i$
.
3.3.1. Case 1:
 $i < \frac {1}{ \log (n) p}$
.
$i < \frac {1}{ \log (n) p}$
.
Fix a pair
![]() $(S, m_S) \in \mathbb {S}$
, and define
$(S, m_S) \in \mathbb {S}$
, and define
![]() $ \mathcal {E} $
to be the event that
$ \mathcal {E} $
to be the event that
![]() $ Z_{S,m_S} =1 $
. In other words,
$ Z_{S,m_S} =1 $
. In other words,
![]() $ \mathcal {E} $
is the event that S gives an augmented independent set with the prescribed matching
$ \mathcal {E} $
is the event that S gives an augmented independent set with the prescribed matching
![]() $m_S$
. Let
$m_S$
. Let
![]() $ \mathcal {E}_T$
be the event
$ \mathcal {E}_T$
be the event
![]() $ Z_{T,m_T} =1 $
. Recalling Equation (20), we seek to bound
$ Z_{T,m_T} =1 $
. Recalling Equation (20), we seek to bound
 $$ \begin{align} h_i = \frac{1}{|\mathbb{S}|} \sum_{T: |S \cap T|=i } \left( \frac{ \mathbb{P}( {\mathcal{E}}_T \mid \mathcal{E})}{ \mathbb{P} ( \mathcal{E}) } - 1 \right). \end{align} $$
$$ \begin{align} h_i = \frac{1}{|\mathbb{S}|} \sum_{T: |S \cap T|=i } \left( \frac{ \mathbb{P}( {\mathcal{E}}_T \mid \mathcal{E})}{ \mathbb{P} ( \mathcal{E}) } - 1 \right). \end{align} $$
Now, for
![]() $ \ell = 0, \dots , r $
let
$ \ell = 0, \dots , r $
let
![]() $ \mathbb {S}_\ell $
be the collection of pairs
$ \mathbb {S}_\ell $
be the collection of pairs
![]() $(T, m_T) \in \mathbb {S}$
with the property that
$(T, m_T) \in \mathbb {S}$
with the property that
![]() $ m_S$
and
$ m_S$
and
![]() $m_T$
have exactly
$m_T$
have exactly
![]() $\ell $
edges in common. Define
$\ell $
edges in common. Define
 $$\begin{align*}B = \left\lceil \frac{1}{\sqrt{p\ln(n)}}\right\rceil,\end{align*}$$
$$\begin{align*}B = \left\lceil \frac{1}{\sqrt{p\ln(n)}}\right\rceil,\end{align*}$$
and, for
![]() $ B < i < B^2$
, let
$ B < i < B^2$
, let
![]() $\mathbb {S}_{i,\ell }$
be the collection of pairs
$\mathbb {S}_{i,\ell }$
be the collection of pairs
![]() $(T, m_T) \in \mathbb {S}_\ell $
such that
$(T, m_T) \in \mathbb {S}_\ell $
such that
![]() $|T \cap S| = i$
. Finally, let
$|T \cap S| = i$
. Finally, let
![]() $\mathbb {S}^{\prime }_\ell $
be the collection of pairs
$\mathbb {S}^{\prime }_\ell $
be the collection of pairs
![]() $(T, m_T) \in \mathbb {S}_\ell $
with the additional property that
$(T, m_T) \in \mathbb {S}_\ell $
with the additional property that
![]() $ |T \cap S| \le B$
. We make two claims.
$ |T \cap S| \le B$
. We make two claims.
Lemma 9. If
![]() $(T, m_T) \in \mathbb {S}_{i,\ell }$
and
$(T, m_T) \in \mathbb {S}_{i,\ell }$
and
![]() $ i < \frac {1}{\log (n)p }$
then
$ i < \frac {1}{\log (n)p }$
then
 $$\begin{align*}\mathbb{P}( \mathcal{E}_T \mid \mathcal{E} ) \le e^{O(k^3p^2i/n) +o(1)} \frac{ \mathbb{P}( \mathcal{E}) }{ p^\ell (1-p)^{\binom{i}{2}}}. \end{align*}$$
$$\begin{align*}\mathbb{P}( \mathcal{E}_T \mid \mathcal{E} ) \le e^{O(k^3p^2i/n) +o(1)} \frac{ \mathbb{P}( \mathcal{E}) }{ p^\ell (1-p)^{\binom{i}{2}}}. \end{align*}$$
Proof. In order to discuss the conditioning on the event
![]() $ \mathcal {E}$
, we need to define an additional parameter. Let w be the number of edges in
$ \mathcal {E}$
, we need to define an additional parameter. Let w be the number of edges in
![]() $m_T$
that have exactly one vertex in
$m_T$
that have exactly one vertex in
![]() $ S\cap T$
and let W be the vertices in
$ S\cap T$
and let W be the vertices in
![]() $T \setminus S$
that are included in such edges. To be precise, we define
$T \setminus S$
that are included in such edges. To be precise, we define
For each vertex
![]() $ v \in W$
, let
$ v \in W$
, let
![]() $ vv'$
be the edge of
$ vv'$
be the edge of
![]() $m_T$
that contains v.
$m_T$
that contains v.
We condition as follows. First, we simply condition on all pairs within S appearing as edges and nonedges as required for the event
![]() $ \mathcal {E}$
. But we proceed more carefully for vertices v that are not in S. For such vertices, we must reveal information about the neighbors of v in S. We do this by observing whether or not the potential edges of the form
$ \mathcal {E}$
. But we proceed more carefully for vertices v that are not in S. For such vertices, we must reveal information about the neighbors of v in S. We do this by observing whether or not the potential edges of the form
![]() $vu$
, where
$vu$
, where
![]() $u \in S$
actually are edges one at a time, starting with potential neighbors
$u \in S$
actually are edges one at a time, starting with potential neighbors
![]() $ u \in S \setminus T$
, and stopping as soon as we observe at least two such neighbors. For vertices
$ u \in S \setminus T$
, and stopping as soon as we observe at least two such neighbors. For vertices
![]() $v\in W$
, we add the restriction that the edge
$v\in W$
, we add the restriction that the edge
![]() $ vv' \in m_T $
is the last edge observed in this process. So, for a vertex
$ vv' \in m_T $
is the last edge observed in this process. So, for a vertex
![]() $v \in T \setminus S$
, this process either observes two edges between v and
$v \in T \setminus S$
, this process either observes two edges between v and
![]() $ S \setminus T$
– and therefore observes no potential edges between v and
$ S \setminus T$
– and therefore observes no potential edges between v and
![]() $S \cap T$
– or the process observes at most one edge between v and
$S \cap T$
– or the process observes at most one edge between v and
![]() $ S \setminus T$
and therefore observes edges between v and
$ S \setminus T$
and therefore observes edges between v and
![]() $S \cap T$
and reveals that at least one such edge appears. In this latter case, the conditional probability of
$S \cap T$
and reveals that at least one such edge appears. In this latter case, the conditional probability of
![]() $ \mathcal {E}_T$
is zero unless this vertex v is in W and the observed edge is
$ \mathcal {E}_T$
is zero unless this vertex v is in W and the observed edge is
![]() $vv'$
.
$vv'$
.
For each set
![]() $ U \subset T \setminus S$
, we define
$ U \subset T \setminus S$
, we define
![]() $ \mathcal {F}_{U}$
to be the event that
$ \mathcal {F}_{U}$
to be the event that
![]() $\mathcal {E}$
holds and U is the set of vertices
$\mathcal {E}$
holds and U is the set of vertices
![]() $ v \in T \setminus S$
with the property that our process reveals edges between
$ v \in T \setminus S$
with the property that our process reveals edges between
![]() $ v$
and
$ v$
and
![]() $ S \cap T$
. Note that we have
$ S \cap T$
. Note that we have
and
Next, let
![]() $I = S \cap T$
, and define
$I = S \cap T$
, and define
![]() $ \mathcal {I}$
to be the event that the process detailed above resorts to revealing potential edges between v and I for more than
$ \mathcal {I}$
to be the event that the process detailed above resorts to revealing potential edges between v and I for more than
![]() $ \log ^2(n) k $
vertices
$ \log ^2(n) k $
vertices
![]() $ v \not \in S$
. Note that the probability that a particular vertex
$ v \not \in S$
. Note that the probability that a particular vertex
![]() $ v \not \in S $
resorts to observing potential edges to I is
$ v \not \in S $
resorts to observing potential edges to I is

Thus, the expected number of vertices that observe edges to
![]() $ I$
is
$ I$
is
![]() $ O(\log (n)^2 k^2/n) = o(k)$
. As these events are independent, the Chernoff bound (see Corollary 21.9 in [Reference Frieze and Karońksi10]) then implies
$ O(\log (n)^2 k^2/n) = o(k)$
. As these events are independent, the Chernoff bound (see Corollary 21.9 in [Reference Frieze and Karońksi10]) then implies
Now, we are ready to put everything together. Applying the law of total probability, we have
 $$ \begin{align*} \begin{split} \mathbb{P}( \mathcal{E}_T \mid \mathcal{E} ) & = \sum_{ U \subseteq T \setminus S} \left(\mathbb{P}( \mathcal{E}_T \mid \mathcal{F}_{U} \wedge \mathcal{I}) \cdot \frac{ \mathbb{P}( \mathcal{F}_{U} \wedge \mathcal{I})}{ \mathbb{P}( \mathcal{E})} + \mathbb{P}( \mathcal{E}_T \mid \mathcal{F}_{U} \wedge \overline{\mathcal{I}}) \cdot \frac{ \mathbb{P}( \mathcal{F}_{U} \wedge \overline{ \mathcal{I}})}{ \mathbb{P}( \mathcal{E})} \right) \\ & \le \frac{ \mathbb{P}( \mathcal{I})}{ \mathbb{P}( \mathcal{E} ) } + \sum_{ U \subseteq T \setminus S } \mathbb{P}( \mathcal{E}_T \mid \mathcal{F}_{U} \wedge \overline{\mathcal{I}}) \cdot \frac{ \mathbb{P}( \mathcal{F}_{U} )}{ \mathbb{P}( \mathcal{E})} \\ & = \frac{ \mathbb{P}( \mathcal{I})}{ \mathbb{P}( \mathcal{E} ) } + \sum_{ U \subseteq W } \mathbb{P}( \mathcal{E}_T \mid \mathcal{F}_{U} \wedge \overline{\mathcal{I}}) \cdot \frac{ \mathbb{P}( \mathcal{F}_{U} )}{ \mathbb{P}( \mathcal{E})}. \end{split} \end{align*} $$
$$ \begin{align*} \begin{split} \mathbb{P}( \mathcal{E}_T \mid \mathcal{E} ) & = \sum_{ U \subseteq T \setminus S} \left(\mathbb{P}( \mathcal{E}_T \mid \mathcal{F}_{U} \wedge \mathcal{I}) \cdot \frac{ \mathbb{P}( \mathcal{F}_{U} \wedge \mathcal{I})}{ \mathbb{P}( \mathcal{E})} + \mathbb{P}( \mathcal{E}_T \mid \mathcal{F}_{U} \wedge \overline{\mathcal{I}}) \cdot \frac{ \mathbb{P}( \mathcal{F}_{U} \wedge \overline{ \mathcal{I}})}{ \mathbb{P}( \mathcal{E})} \right) \\ & \le \frac{ \mathbb{P}( \mathcal{I})}{ \mathbb{P}( \mathcal{E} ) } + \sum_{ U \subseteq T \setminus S } \mathbb{P}( \mathcal{E}_T \mid \mathcal{F}_{U} \wedge \overline{\mathcal{I}}) \cdot \frac{ \mathbb{P}( \mathcal{F}_{U} )}{ \mathbb{P}( \mathcal{E})} \\ & = \frac{ \mathbb{P}( \mathcal{I})}{ \mathbb{P}( \mathcal{E} ) } + \sum_{ U \subseteq W } \mathbb{P}( \mathcal{E}_T \mid \mathcal{F}_{U} \wedge \overline{\mathcal{I}}) \cdot \frac{ \mathbb{P}( \mathcal{F}_{U} )}{ \mathbb{P}( \mathcal{E})}. \end{split} \end{align*} $$
Now, observe that we have

and if
![]() $ U \subseteq W $
, then we have
$ U \subseteq W $
, then we have

where we use
![]() $ |U| \le \min \{i,r\} $
and
$ |U| \le \min \{i,r\} $
and
![]() $ k^4 p < n^{2 - 2\epsilon } $
. Thus,
$ k^4 p < n^{2 - 2\epsilon } $
. Thus,
 $$ \begin{align*} &\sum_{ U \subseteq W } \mathbb{P}( \mathcal{E}_T \mid \mathcal{F}_{U} \wedge \overline{\mathcal{I}}) \cdot \frac{ \mathbb{P}( \mathcal{F}_{U} )}{ \mathbb{P}( \mathcal{E})} \\ &\quad\le \frac{ (1+o(1)) e^{O(k^3p^2i/n)} \mathbb{P}( \mathcal{E} )}{ p^\ell (1-p)^{i^2/2}} \sum_{u=0}^{w} \binom{w}{u} \left[ (1+o(1))\frac{ k^3}{ e^2 i n^2} \right] ^{u} = \frac{ (1+o(1)) e^{O(k^3p^2i/n)} \mathbb{P}( \mathcal{E} )}{ p^\ell (1-p)^{i^2/2}}, \end{align*} $$
$$ \begin{align*} &\sum_{ U \subseteq W } \mathbb{P}( \mathcal{E}_T \mid \mathcal{F}_{U} \wedge \overline{\mathcal{I}}) \cdot \frac{ \mathbb{P}( \mathcal{F}_{U} )}{ \mathbb{P}( \mathcal{E})} \\ &\quad\le \frac{ (1+o(1)) e^{O(k^3p^2i/n)} \mathbb{P}( \mathcal{E} )}{ p^\ell (1-p)^{i^2/2}} \sum_{u=0}^{w} \binom{w}{u} \left[ (1+o(1))\frac{ k^3}{ e^2 i n^2} \right] ^{u} = \frac{ (1+o(1)) e^{O(k^3p^2i/n)} \mathbb{P}( \mathcal{E} )}{ p^\ell (1-p)^{i^2/2}}, \end{align*} $$
where we use
![]() $ w \le i$
to bound the sum. We finally note that we have
$ w \le i$
to bound the sum. We finally note that we have
And the proof of the lemma is complete.
Lemma 10. For
![]() $\ell =1, \dots , r$
, we have
$\ell =1, \dots , r$
, we have
 $$\begin{align*}| \mathbb{S}_\ell| \le | \mathbb{S}| \left( \frac{ 3 r^2}{ n^2} \right)^\ell. \end{align*}$$
$$\begin{align*}| \mathbb{S}_\ell| \le | \mathbb{S}| \left( \frac{ 3 r^2}{ n^2} \right)^\ell. \end{align*}$$
Furthermore, we have

Proof. We have

Thus,

The calculation for the second part of the lemma is similar.

Thus,

We are now ready to show that
![]() $\sum _{i=0}^{1/(p \log (n))} h_i = o(1)$
using Lemmas 9 and 10. We will split this into two subranges.
$\sum _{i=0}^{1/(p \log (n))} h_i = o(1)$
using Lemmas 9 and 10. We will split this into two subranges.
Subcase 1.1:
![]() $i \leq B$
.
$i \leq B$
.
In this case, by Lemma 9 we have
![]() $\mathbb {P}(\mathcal {E}_T \mid \mathcal {E}) \leq (1+o(1))\frac {\mathbb {P}(\mathcal {E})}{p^{\ell }}$
, hence
$\mathbb {P}(\mathcal {E}_T \mid \mathcal {E}) \leq (1+o(1))\frac {\mathbb {P}(\mathcal {E})}{p^{\ell }}$
, hence
 $$ \begin{align*} \begin{split} \sum_{i=0}^{B}h_i & = \frac{1}{|\mathbb{S}|} \sum_{\ell = 0}^r \sum_{ (T, m_T) \in \mathbb{S}_\ell' } \left( \frac{ \mathbb{P}( \mathcal{E}_T \mid \mathcal{E})}{ \mathbb{P} ( \mathcal{E}) } - 1 \right) \\ & = \frac{ o( | \mathbb{S}_0'| )}{ |\mathbb{S}|} + \sum_{\ell=1}^r \left( \frac{ 4 r^2}{ p n^2} \right)^\ell \\ & \le o(1) + \sum_{\ell=1}^r \left( \frac{1}{ n^{2/3}} \right)^\ell \\ & = o(1). \end{split} \end{align*} $$
$$ \begin{align*} \begin{split} \sum_{i=0}^{B}h_i & = \frac{1}{|\mathbb{S}|} \sum_{\ell = 0}^r \sum_{ (T, m_T) \in \mathbb{S}_\ell' } \left( \frac{ \mathbb{P}( \mathcal{E}_T \mid \mathcal{E})}{ \mathbb{P} ( \mathcal{E}) } - 1 \right) \\ & = \frac{ o( | \mathbb{S}_0'| )}{ |\mathbb{S}|} + \sum_{\ell=1}^r \left( \frac{ 4 r^2}{ p n^2} \right)^\ell \\ & \le o(1) + \sum_{\ell=1}^r \left( \frac{1}{ n^{2/3}} \right)^\ell \\ & = o(1). \end{split} \end{align*} $$
Subcase 1.2:
![]() $B < i < B^2$
.
$B < i < B^2$
.
Here, we have

Since ![]() and
and ![]() , we have
, we have
 $$ \begin{align*} \sum_{i=B}^{B^2} h_i = o(1). \end{align*} $$
$$ \begin{align*} \sum_{i=B}^{B^2} h_i = o(1). \end{align*} $$
3.3.2. Case 2:  .
.
In this case, we can afford to be lenient with our bounds; in particular, we do not need to make use of the condition that vertices outside S have at least two neighbors in S. We begin by bounding
![]() $ \frac {1}{ \mathbb {E}( Z_{S,m_S})} \sum _{m_S, m_T} \mathbb {E}( Z_{S, m_S} Z_{T, m_T}) $
for a fixed pair of sets
$ \frac {1}{ \mathbb {E}( Z_{S,m_S})} \sum _{m_S, m_T} \mathbb {E}( Z_{S, m_S} Z_{T, m_T}) $
for a fixed pair of sets
![]() $S,T$
such that
$S,T$
such that
![]() $ |S \cap T| =i$
. If there are
$ |S \cap T| =i$
. If there are
![]() $\ell $
edges in the intersection, a bound for the number of ways to choose
$\ell $
edges in the intersection, a bound for the number of ways to choose
![]() $m_S$
and
$m_S$
and
![]() $m_T$
is
$m_T$
is ![]() (we have
(we have
![]() $2r-\ell $
edges total; each has less than
$2r-\ell $
edges total; each has less than ![]() choices.) Thus, we have
choices.) Thus, we have

Recalling Equation (6), we have

It follows that

As
![]() $ r =o(k^{1/2}) = o(i) $
, we have
$ r =o(k^{1/2}) = o(i) $
, we have

3.3.3. Case 3: 
We calculate
![]() $h_i$
as defined in Equation (19). For simplicity, let
$h_i$
as defined in Equation (19). For simplicity, let ![]() . For some fixed i (hence j), there are
. For some fixed i (hence j), there are ![]() ways to choose S and T. Now, fix sets S and T.
ways to choose S and T. Now, fix sets S and T.
We now consider the number of ways to choose the matchings
![]() $m_S$
and
$m_S$
and
![]() $m_T$
that are compatible with the event
$m_T$
that are compatible with the event
![]() $ \{ Z_{S,m_S} Z_{T, m_T} =1 \}$
. Let
$ \{ Z_{S,m_S} Z_{T, m_T} =1 \}$
. Let
![]() $R_I$
be the set of matching edges contained in
$R_I$
be the set of matching edges contained in
![]() $S \cap T$
, and let
$S \cap T$
, and let
![]() $r_I:=|R_I|$
(so
$r_I:=|R_I|$
(so
![]() $r_I$
is the same as
$r_I$
is the same as
![]() $\ell $
from Cases 1 and 2). Secondly, let
$\ell $
from Cases 1 and 2). Secondly, let
![]() $R_O$
be the set of edges in
$R_O$
be the set of edges in
![]() $m_S$
that are not in
$m_S$
that are not in
![]() $R_I$
, and let
$R_I$
, and let
![]() $R^{\prime }_O$
be the set of edges of
$R^{\prime }_O$
be the set of edges of
![]() $m_T$
that are not in
$m_T$
that are not in
![]() $R_I$
, and define
$R_I$
, and define
![]() $r_O := |R_O| = |R^{\prime }_O|$
(‘I’ stands for ‘inner’, and ‘O’ stands for ‘outer’). Hence,
$r_O := |R_O| = |R^{\prime }_O|$
(‘I’ stands for ‘inner’, and ‘O’ stands for ‘outer’). Hence,
![]() $r = r_O + r_I$
. Finally, let
$r = r_O + r_I$
. Finally, let
![]() $R_S$
be the matching edges in
$R_S$
be the matching edges in
![]() $R_O$
which are contained completely in
$R_O$
which are contained completely in
![]() $S \setminus T$
, and let
$S \setminus T$
, and let
![]() $r_S = |R_S|$
. See Figure 1.
$r_S = |R_S|$
. See Figure 1.

Figure 1 A depiction of the edges appearing in intersecting augmented independent sets.
We now count the number of ways to choose edges in
![]() $R_O$
if
$R_O$
if
![]() $r_O$
is fixed. To do this, we first note that if
$r_O$
is fixed. To do this, we first note that if
![]() $r_S$
is also fixed, then the number of ways to choose the edges that comprise
$r_S$
is also fixed, then the number of ways to choose the edges that comprise
![]() $R_S$
is
$R_S$
is
Then the number of ways to choose the rest of the rest of the edges in
![]() $R_O$
is
$R_O$
is

therefore, the total number of ways to choose
![]() $R_O$
is
$R_O$
is

By a symmetric argument, Equation (23) is an upper bound for the number of ways to choose the edges in
![]() $R^{\prime }_O$
as well.
$R^{\prime }_O$
as well.
Next, note that the number of ways to choose edges in
![]() $R_I$
is bounded by
$R_I$
is bounded by ![]() . Putting these together, the number of ways to choose
. Putting these together, the number of ways to choose
![]() $m_S$
and
$m_S$
and
![]() $m_T$
is at most
$m_T$
is at most

(assuming that
![]() $r^{r_O} = 1$
if
$r^{r_O} = 1$
if
![]() $r = r_O = 0$
).
$r = r_O = 0$
).
Now, we estimate the probability of the event
![]() $ \{ Z_{S,{m_S}} Z_{T,m_T} = 1 \}$
. The probability the edges within S and within T are chosen accordingly is
$ \{ Z_{S,{m_S}} Z_{T,m_T} = 1 \}$
. The probability the edges within S and within T are chosen accordingly is
Now, consider pairs of vertices from
![]() $S \backslash T$
to
$S \backslash T$
to
![]() $T \backslash S$
. Recall that a vertex
$T \backslash S$
. Recall that a vertex
![]() $ v \in S \setminus T$
has at least two neighbors in T. So, if
$ v \in S \setminus T$
has at least two neighbors in T. So, if
![]() $ v $
is already incident with an edge that goes into T among the edges already specified, then there is at least one edge from v to
$ v $
is already incident with an edge that goes into T among the edges already specified, then there is at least one edge from v to
![]() $T \backslash S$
(since each from
$T \backslash S$
(since each from
![]() $S \backslash T$
can send at most one edge to
$S \backslash T$
can send at most one edge to
![]() $S \cap T$
). Such an edge appears with probability
$S \cap T$
). Such an edge appears with probability
![]() $1 - (1-p)^{j} \le jp$
. If a vertex
$1 - (1-p)^{j} \le jp$
. If a vertex
![]() $ v \in S \backslash T$
is not in an edge of
$ v \in S \backslash T$
is not in an edge of
![]() $m_S$
that intersects
$m_S$
that intersects
![]() $ S \cap T$
, then v is incident with at least two edges going to
$ S \cap T$
, then v is incident with at least two edges going to
![]() $T \backslash S$
. The probability of these two edges appearing is at most
$T \backslash S$
. The probability of these two edges appearing is at most
![]() $j^2 p^2$
by the union bound. Since the number of vertices in the first category is at most
$j^2 p^2$
by the union bound. Since the number of vertices in the first category is at most
![]() $r_O$
, the total probability of all edges between
$r_O$
, the total probability of all edges between
![]() $S \backslash T$
and
$S \backslash T$
and
![]() $T \backslash S$
being chosen accordingly is at most
$T \backslash S$
being chosen accordingly is at most
![]() $(jp)^{2j-r_O}$
. Hence, the probability that the edges within
$(jp)^{2j-r_O}$
. Hence, the probability that the edges within
![]() $ S \cup T$
appear in accordance with the event
$ S \cup T$
appear in accordance with the event
![]() $ \{ Z_{S,{m_S}} Z_{T,m_T} = 1 \}$
is at most
$ \{ Z_{S,{m_S}} Z_{T,m_T} = 1 \}$
is at most
Finally, the probability that all vertices outside
![]() $S \cup T$
have at least two neighbors in S is at most
$S \cup T$
have at least two neighbors in S is at most ![]() . Note that, since
. Note that, since

we have
Multiplying this probability estimate by the estimate for the number of choices for
![]() $ m_S$
and
$ m_S$
and
![]() $m_T$
given by Equation (24) and summing over
$m_T$
given by Equation (24) and summing over
![]() $r_O$
, we see that for a fixed S and T we have
$r_O$
, we see that for a fixed S and T we have
 $$\begin{align*}\frac{ 1 }{\mathbb{P}( Z_{S, m_S} =1 ) } \sum_{ m_S, m_T} \mathbb{P}\left( Z_{S,m_S} Z_{T,m_T} = 1 \right) \end{align*}$$
$$\begin{align*}\frac{ 1 }{\mathbb{P}( Z_{S, m_S} =1 ) } \sum_{ m_S, m_T} \mathbb{P}\left( Z_{S,m_S} Z_{T,m_T} = 1 \right) \end{align*}$$
is at most

where we use
![]() $ r = o( k^{1/2}) $
in the last step (and assume
$ r = o( k^{1/2}) $
in the last step (and assume
![]() $r^{r_O} = 1$
if
$r^{r_O} = 1$
if
![]() $r = r_O = 0$
). Recalling that
$r = r_O = 0$
). Recalling that ![]() and that the number of choices for the pair of sets
and that the number of choices for the pair of sets
![]() $S,T$
is
$S,T$
is ![]() , we have
, we have

As
![]() $ r = o( k^{1/2})$
and
$ r = o( k^{1/2})$
and
![]() $ k = O ( \log (n) n^{2/3 - \epsilon })$
, we have
$ k = O ( \log (n) n^{2/3 - \epsilon })$
, we have ![]() , as desired.
, as desired.
4. Weak anti-concentration of
 $\alpha (G_{n,p})$
for
$\alpha (G_{n,p})$
for
 $ n^{-1} < p < n^{-2/3}$
$ n^{-1} < p < n^{-2/3}$
In this section, we present the argument of Sah and Sawhney that shows that two-point concentration of the independence number does not extend to
![]() $p = n^{\gamma }$
if
$p = n^{\gamma }$
if
![]() $\gamma \leq -2/3$
; that is, we prove Theorem 2. We note in passing that this proof is similar to an argument that appears in [Reference Alon and Krivelevich2] (see the last item in the ‘concluding remarks and open problems’ section of [Reference Alon and Krivelevich2]). Throughout this section, we assume
$\gamma \leq -2/3$
; that is, we prove Theorem 2. We note in passing that this proof is similar to an argument that appears in [Reference Alon and Krivelevich2] (see the last item in the ‘concluding remarks and open problems’ section of [Reference Alon and Krivelevich2]). Throughout this section, we assume
![]() $ \omega ( 1/n ) < p< ( \log (n)/n)^{2/3} $
. Recall Theorem 2:
$ \omega ( 1/n ) < p< ( \log (n)/n)^{2/3} $
. Recall Theorem 2:
Theorem 2 (Sah and Sawhney [Reference Sah and Sawhney18]).
Let
![]() $p = p(n)$
satisfy
$p = p(n)$
satisfy
![]() $ \omega ( 1/n ) < p< ( \log (n)/(12n))^{2/3} $
, and set
$ \omega ( 1/n ) < p< ( \log (n)/(12n))^{2/3} $
, and set
Then there exists
![]() $ q = q(n)$
such that
$ q = q(n)$
such that
![]() $p \leq q \leq 2p$
such that
$p \leq q \leq 2p$
such that
![]() $ \alpha ( G_{n,q})$
is not concentrated on
$ \alpha ( G_{n,q})$
is not concentrated on
![]() $ \ell $
values.
$ \ell $
values.
For p in the specified range, we define
We first observe that this choice of
![]() $p'$
is close enough to p to ensure that there is no ‘separation’ of the intervals over which
$p'$
is close enough to p to ensure that there is no ‘separation’ of the intervals over which
![]() $ G_{n,p}$
and
$ G_{n,p}$
and
![]() $ G_{n,p'}$
are respectively concentrated. To be precise, we establish the following:
$ G_{n,p'}$
are respectively concentrated. To be precise, we establish the following:
Lemma 11. If
![]() $ \omega (n^{-1}) < p < o(1)$
, then there is a sequence
$ \omega (n^{-1}) < p < o(1)$
, then there is a sequence
![]() $ k = k(n)$
such that
$ k = k(n)$
such that
for n sufficiently large.
Proof. First, observe that, since the distributions of
![]() $e(G_{n,p})$
and
$e(G_{n,p})$
and
![]() $e\left (G_{n,p'}\right )$
are approximately Gaussian with equal variances and with means that are
$e\left (G_{n,p'}\right )$
are approximately Gaussian with equal variances and with means that are
![]() $1/\sqrt {2}$
standard deviations apart, there is some value
$1/\sqrt {2}$
standard deviations apart, there is some value
![]() $ m$
such that
$ m$
such that
Now let k be the median value of
![]() $ \alpha ( G_{n,m} )$
. As the addition of edges does not increase the independence number, the lemma follows.
$ \alpha ( G_{n,m} )$
. As the addition of edges does not increase the independence number, the lemma follows.
Now, we prove Theorem 2. Assume for the sake of contradiction that if n is sufficiently large and
![]() $ p \le q \le 2p$
, then there is an interval I such that
$ p \le q \le 2p$
, then there is an interval I such that
![]() $ |I| \le \ell $
and
$ |I| \le \ell $
and
Consider the sequence
![]() $p_0, p_1, p_2, \dots $
, where
$p_0, p_1, p_2, \dots $
, where
![]() $p_0 = p$
and
$p_0 = p$
and
![]() $p_{i+1} = p_i'$
for
$p_{i+1} = p_i'$
for
![]() $i \geq 0$
, and let z be the lowest integer such that
$i \geq 0$
, and let z be the lowest integer such that
![]() $p_z \geq 2p$
; it is easy to see that
$p_z \geq 2p$
; it is easy to see that
![]() $z \leq n\sqrt {p}$
. Let
$z \leq n\sqrt {p}$
. Let
![]() $ I_0 = [a_0,b_0], I_1 = [a_1, b_1], \dots , I_{z-1} = [a_{z-1},b_{z-1}]$
be intervals of
$ I_0 = [a_0,b_0], I_1 = [a_1, b_1], \dots , I_{z-1} = [a_{z-1},b_{z-1}]$
be intervals of
![]() $\ell $
values such that
$\ell $
values such that
![]() $ \alpha ( G_{n,p_i} )$
lies in
$ \alpha ( G_{n,p_i} )$
lies in
![]() $ I_i$
with probability at least
$ I_i$
with probability at least
![]() $ 49/50$
for each i. By Lemma 11, we have
$ 49/50$
for each i. By Lemma 11, we have
![]() $a_{i} \leq b_{i+1}$
for all
$a_{i} \leq b_{i+1}$
for all
![]() $i < z$
. This implies
$i < z$
. This implies
![]() $ b_{i+1} \ge b_i - \ell $
. Iterating this observation gives
$ b_{i+1} \ge b_i - \ell $
. Iterating this observation gives
On the other hand, by Equation (1), we have
This is a contradiction.
5. Anti-concentration of
 $\alpha (G_{n,p})$
for
$\alpha (G_{n,p})$
for
 $p = c/n$
$p = c/n$
In this section, we establish anti-concentration of the independence number of
![]() $ G_{n,p}$
for
$ G_{n,p}$
for
![]() $ p = c/n$
, where c is a constant. We note in passing that for very small
$ p = c/n$
, where c is a constant. We note in passing that for very small
![]() $p(n)$
it is easy to show that
$p(n)$
it is easy to show that
![]() $\alpha (G)$
is not narrowly concentrated. Indeed, if
$\alpha (G)$
is not narrowly concentrated. Indeed, if
![]() $p = n^{\gamma }$
for some
$p = n^{\gamma }$
for some
![]() $\gamma \in (-2,-3/2)$
, then whp no two edges intersect, and hence the independence number is determined by the number of edges that appear. Since the distribution of the number of edges is roughly Poisson with mean
$\gamma \in (-2,-3/2)$
, then whp no two edges intersect, and hence the independence number is determined by the number of edges that appear. Since the distribution of the number of edges is roughly Poisson with mean
![]() $\mu \approx n^{2+\gamma }/2$
, then we will not have concentration of
$\mu \approx n^{2+\gamma }/2$
, then we will not have concentration of
![]() $\alpha (G)$
on fewer than
$\alpha (G)$
on fewer than
![]() $\Theta (n^{1+\gamma /2})$
values.
$\Theta (n^{1+\gamma /2})$
values.
We now state our anti-concentration result.
Theorem 12. Let
![]() $p = c/n$
, where
$p = c/n$
, where
![]() $ c>0$
is a constant, and let
$ c>0$
is a constant, and let
![]() $ k = k(n)$
be an arbitrary sequence of integers. There exists a constant
$ k = k(n)$
be an arbitrary sequence of integers. There exists a constant
![]() $L>0$
such that
$L>0$
such that
![]() $ \mathbb {P}( \alpha (G_{n,p}) = k) \le Ln^{-1/2}$
for n sufficiently large.
$ \mathbb {P}( \alpha (G_{n,p}) = k) \le Ln^{-1/2}$
for n sufficiently large.
Theorem 12 implies that
![]() $ \alpha ( G_{n, c/n})$
is not concentrated on fewer than
$ \alpha ( G_{n, c/n})$
is not concentrated on fewer than
![]() $ \sqrt {n}/(2L)$
values. Note that this is the best possible anti-concentration result in this regime (up to the constant) as standard martingale methods (such as Hoeffding–Azuma or Talagrand’s inequality) show that, for any function
$ \sqrt {n}/(2L)$
values. Note that this is the best possible anti-concentration result in this regime (up to the constant) as standard martingale methods (such as Hoeffding–Azuma or Talagrand’s inequality) show that, for any function
![]() ${k(n) = \omega (\sqrt {n})}$
, the independence number is concentrated on some interval of length
${k(n) = \omega (\sqrt {n})}$
, the independence number is concentrated on some interval of length
![]() $k(n)$
(this assertion holds for any value of p).
$k(n)$
(this assertion holds for any value of p).
For a fixed graph G, let
![]() $T (G)$
be the subgraph of G given by all connected components that are trees on
$T (G)$
be the subgraph of G given by all connected components that are trees on
![]() $4$
vertices. Let
$4$
vertices. Let
![]() $t(G)$
be the number of components in
$t(G)$
be the number of components in
![]() $T(G)$
. Finally, let
$T(G)$
. Finally, let
![]() $\bar {T}(G)$
be the remainder of the graph G (so
$\bar {T}(G)$
be the remainder of the graph G (so
![]() $ G = T(G) + \overline {T}(G)$
). Let
$ G = T(G) + \overline {T}(G)$
). Let
![]() $p =c/n$
and let
$p =c/n$
and let
![]() $ G = G_{n,p}$
. We set
$ G = G_{n,p}$
. We set
![]() $ \mu = \mu (c)=\frac {2 c^3 e^{-4c}}{ 3}$
. Note that we have
$ \mu = \mu (c)=\frac {2 c^3 e^{-4c}}{ 3}$
. Note that we have
 $$\begin{align*}E[t(G)] = \binom{n}{4} \cdot 16 \cdot p^3 (1-p)^{3+4(n-4)} =(1+o(1)) \frac{16 c^3 e^{-4c}n}{ 24} = (1+o(1)) \mu n. \end{align*}$$
$$\begin{align*}E[t(G)] = \binom{n}{4} \cdot 16 \cdot p^3 (1-p)^{3+4(n-4)} =(1+o(1)) \frac{16 c^3 e^{-4c}n}{ 24} = (1+o(1)) \mu n. \end{align*}$$
We note that
![]() $t(G)$
is a well concentrated random variable.
$t(G)$
is a well concentrated random variable.
Lemma 13.
 $$\begin{align*}\mathbb{P}( t(G) < \mu n/2) = O \left( \frac{1}{n} \right). \end{align*}$$
$$\begin{align*}\mathbb{P}( t(G) < \mu n/2) = O \left( \frac{1}{n} \right). \end{align*}$$
Proof. Here, we use standard second moment method once again. For vertex set S with
![]() $|S| = 4$
, let
$|S| = 4$
, let
![]() $W_S$
be the random variable that indicates if the graph induced on S is an isolated tree. Set
$W_S$
be the random variable that indicates if the graph induced on S is an isolated tree. Set
![]() $ W =t(G)$
, and note that
$ W =t(G)$
, and note that
![]() $ t(G)$
is the sum of all
$ t(G)$
is the sum of all
![]() $\binom {n}{4}$
indicators. By Chebychev, we have
$\binom {n}{4}$
indicators. By Chebychev, we have
 $$ \begin{align*} \mathbb{P}\left(W < \frac{\mu n}{2}\right) \leq \mathbb{P}\left(|W - \mathbb{E}(W)| \geq \frac{\mathbb{E}(W)}{3}\right) \leq \frac{9\text{Var}(W)}{\mathbb{E}(W)^2}. \end{align*} $$
$$ \begin{align*} \mathbb{P}\left(W < \frac{\mu n}{2}\right) \leq \mathbb{P}\left(|W - \mathbb{E}(W)| \geq \frac{\mathbb{E}(W)}{3}\right) \leq \frac{9\text{Var}(W)}{\mathbb{E}(W)^2}. \end{align*} $$
Hence
 $$ \begin{align*} \mathbb{P}\left(W < \frac{ \mu n}{2}\right) \leq \frac{9\text{Var}(W)}{\mathbb{E}(W)^2} < 9\left(\frac{1}{\mathbb{E}(W)} + \max_{S,T}\left\{\frac{\mathbb{E}(W_S W_{T}) - \mathbb{E}(W_S)\mathbb{E}(W_{T})}{\mathbb{E}(W_S)^2}\right\}\right). \end{align*} $$
$$ \begin{align*} \mathbb{P}\left(W < \frac{ \mu n}{2}\right) \leq \frac{9\text{Var}(W)}{\mathbb{E}(W)^2} < 9\left(\frac{1}{\mathbb{E}(W)} + \max_{S,T}\left\{\frac{\mathbb{E}(W_S W_{T}) - \mathbb{E}(W_S)\mathbb{E}(W_{T})}{\mathbb{E}(W_S)^2}\right\}\right). \end{align*} $$
Note that the only case where we get a positive covariance is where
![]() $S \cap T = \emptyset $
, and in this case, we have
$S \cap T = \emptyset $
, and in this case, we have
Therefore,
 $$ \begin{align*} \mathbb{P}\left( t(G) < \frac{ \mu n}{2}\right) < \frac{9 +o(1)}{ \mu n} + \frac{144 c+o(1)}{n} =O\left(\frac{1}{n} \right).\\[-46pt] \end{align*} $$
$$ \begin{align*} \mathbb{P}\left( t(G) < \frac{ \mu n}{2}\right) < \frac{9 +o(1)}{ \mu n} + \frac{144 c+o(1)}{n} =O\left(\frac{1}{n} \right).\\[-46pt] \end{align*} $$
With this observation in hand, we are ready to proceed to the proof of Theorem 12. Let k be a fixed integer. Let
![]() $ \mathcal {T}$
be the collection of all graphs H on
$ \mathcal {T}$
be the collection of all graphs H on
![]() $v_H \le n$
vertices such that
$v_H \le n$
vertices such that
![]() $ 4 \mid n - v_H$
and H has no connected component that is a tree on four vertices. Let
$ 4 \mid n - v_H$
and H has no connected component that is a tree on four vertices. Let
![]() $ \mathcal {T}'$
be the collection of graphs in
$ \mathcal {T}'$
be the collection of graphs in
![]() $H \in \mathcal {T}$
such that
$H \in \mathcal {T}$
such that
![]() $ v_H \le n - 2 \mu n$
vertices. Applying the law of total probability, we have
$ v_H \le n - 2 \mu n$
vertices. Applying the law of total probability, we have
 $$ \begin{align*} \mathbb{P}( \alpha( G) = k) &= \sum_{H \in \mathcal{T}} \mathbb{P}( \alpha( G) = k \mid \overline{T}( G) = H) \mathbb{P}( \overline{T}(G) = H) \\ &\le \mathbb{P} (t(G) \le \mu n/2) + \sum_{H \in \mathcal{T}'} \mathbb{P}( \alpha( G) = k \mid \overline{T}( G) = H) \mathbb{P}( \overline{T}(G) = H). \end{align*} $$
$$ \begin{align*} \mathbb{P}( \alpha( G) = k) &= \sum_{H \in \mathcal{T}} \mathbb{P}( \alpha( G) = k \mid \overline{T}( G) = H) \mathbb{P}( \overline{T}(G) = H) \\ &\le \mathbb{P} (t(G) \le \mu n/2) + \sum_{H \in \mathcal{T}'} \mathbb{P}( \alpha( G) = k \mid \overline{T}( G) = H) \mathbb{P}( \overline{T}(G) = H). \end{align*} $$
So, it suffices to bound the conditional probability
where H is a graph in
![]() $ \mathcal {T}'$
. Under this conditioning, the graph G is H together with a forest of
$ \mathcal {T}'$
. Under this conditioning, the graph G is H together with a forest of
![]() $ (n - v_H)/4$
trees on four vertices. Furthermore, the number of trees in this forest which are stars on four vertices is a binomial random variable with
$ (n - v_H)/4$
trees on four vertices. Furthermore, the number of trees in this forest which are stars on four vertices is a binomial random variable with
![]() $ (n - v_H)/4$
trials with probability of success
$ (n - v_H)/4$
trials with probability of success
![]() $ 1/4$
on each trial. Let B be this random variable, and note that if G is drawn from the conditional probability space on the collection of graphs with
$ 1/4$
on each trial. Let B be this random variable, and note that if G is drawn from the conditional probability space on the collection of graphs with
![]() $\overline {T}( G) = H $
, then we have
$\overline {T}( G) = H $
, then we have
Therefore, we have
But B is a binomial random variable with a linear number of trials, and therefore the probability that B is any particular value is at most
![]() $ L/\sqrt {n}$
for some constant L.
$ L/\sqrt {n}$
for some constant L.
6. Conclusion
In this section, we present some remarks and open questions related to the extent of concentration of
![]() $ \alpha ( G_{n,p})$
for
$ \alpha ( G_{n,p})$
for
![]() $ p < n^{-2/3}$
. We write
$ p < n^{-2/3}$
. We write ![]() if
if
![]() $ f/g$
is bounded above by a polylogarithmic function and
$ f/g$
is bounded above by a polylogarithmic function and ![]() if
if
![]() $ f/g$
is bounded below by a polylogarithmic function.
$ f/g$
is bounded below by a polylogarithmic function.
-
○ The precise extent of concentration of
 $ \alpha ( G_{n,p})$
for
$ \alpha ( G_{n,p})$
for
 $ p = n^{\gamma }$
with
$ p = n^{\gamma }$
with
 $ -1 < \gamma < -2/3$
remains an interesting open question. Note that Theorem 2 gives a lower bound of
$ -1 < \gamma < -2/3$
remains an interesting open question. Note that Theorem 2 gives a lower bound of  on the extent of concentration in this range. Furthermore, Theorems 1 and 12 show that this lower bound is of the correct order at either end of the interval. So it is natural to ask if this lower bound is actually tight throughout this range.
on the extent of concentration in this range. Furthermore, Theorems 1 and 12 show that this lower bound is of the correct order at either end of the interval. So it is natural to ask if this lower bound is actually tight throughout this range.Question 14. Suppose
 $ p = n^{\gamma }$
where
$ p = n^{\gamma }$
where
 $\gamma $
is a constant such that
$\gamma $
is a constant such that
 $ -1 < \gamma < -2/3$
. Is
$ -1 < \gamma < -2/3$
. Is
 $ \alpha ( G_{n,p} )$
concentrated on
$ \alpha ( G_{n,p} )$
concentrated on  values?
values? -
○ We do not see a way to adapt the argument given in Section 4 to prove anti-concentration of
 $ \alpha (G_{n,m})$
for
$ \alpha (G_{n,m})$
for
 $m \le n^{4/3}$
. We conjecture that we have such anti-concentration.At the moment, we have no lower bound on the extent of concentration
$m \le n^{4/3}$
. We conjecture that we have such anti-concentration.At the moment, we have no lower bound on the extent of concentrationConjecture 15. Suppose
 $ m = n^{ \eta }$
, where
$ m = n^{ \eta }$
, where
 $\eta $
is a constant such that
$\eta $
is a constant such that
 $ 1 < \eta < 4/3$
. Then
$ 1 < \eta < 4/3$
. Then
 $ \alpha (G_{n,m})$
is not concentrated on
$ \alpha (G_{n,m})$
is not concentrated on
 $ n^{ 2 - 3\eta /2 - \epsilon } $
values.
$ n^{ 2 - 3\eta /2 - \epsilon } $
values. $ \alpha ( G_{n,m})$
in this regime. It seems natural to suspect that Conjecture 15 is closely related to the questions of proving a stronger, uniform form of anti-concentration of
$ \alpha ( G_{n,m})$
in this regime. It seems natural to suspect that Conjecture 15 is closely related to the questions of proving a stronger, uniform form of anti-concentration of
 $ \alpha ( G_{n,p})$
for
$ \alpha ( G_{n,p})$
for
 $ p = n^{\gamma }$
with
$ p = n^{\gamma }$
with
 $ -1 < \gamma < -2/3$
. We believe that the following strengthening of Theorem 2 holds.Note that we proved Conjecture 16 for
$ -1 < \gamma < -2/3$
. We believe that the following strengthening of Theorem 2 holds.Note that we proved Conjecture 16 forConjecture 16. If
 $ p = n^{\gamma }$
where
$ p = n^{\gamma }$
where
 $ \gamma $
is a constant such that
$ \gamma $
is a constant such that
 $-1 < \gamma < -2/3$
, then we have
$-1 < \gamma < -2/3$
, then we have 
for any sequence
 $k = k(n)$
.
$k = k(n)$
. $ \gamma =-1$
(i.e.,
$ \gamma =-1$
(i.e.,
 $ p = 1/n$
) in Section 5.
$ p = 1/n$
) in Section 5.
-
○ We conclude by noting that the first moment argument using augmented independent sets given in Section 3.2 can be adapted in straightforward way to give the following upper bound on the independence number of
 $ G_{n,p}$
for
$ G_{n,p}$
for
 $ p \le n^{-2/3}$
.This improvement can be extended to give a small linear improvement on the best known upper bound on
$ p \le n^{-2/3}$
.This improvement can be extended to give a small linear improvement on the best known upper bound onTheorem 17. If
 $ \omega ( 1/n) < p \le n^{-2/3}$
, then we have
$ \omega ( 1/n) < p \le n^{-2/3}$
, then we have  $$\begin{align*}\alpha (G_{n,p}) \le k_x - \Omega\left( \frac{ \log(np)^2 }{ p^2n} \right) \end{align*}$$
$$\begin{align*}\alpha (G_{n,p}) \le k_x - \Omega\left( \frac{ \log(np)^2 }{ p^2n} \right) \end{align*}$$
with high probability, where
 $k_x$
is the largest integer such that
$k_x$
is the largest integer such that
 $ \binom {n}{k_x}(1-p)^{\binom {k_x}{2}}> 1$
.
$ \binom {n}{k_x}(1-p)^{\binom {k_x}{2}}> 1$
. $ \alpha ( G_{n,p} )$
, where
$ \alpha ( G_{n,p} )$
, where
 $ p = c/n$
and c is a constant. In fact, a first moment argument using maximal independent sets is sufficient to give a linear improvement on the upper bound in this context. As the precise magnitude of the optimal improvement requires a lengthy calculation, we exclude this in the interest of brevity.
$ p = c/n$
and c is a constant. In fact, a first moment argument using maximal independent sets is sufficient to give a linear improvement on the upper bound in this context. As the precise magnitude of the optimal improvement requires a lengthy calculation, we exclude this in the interest of brevity.
7. Appendix: two-point concentration of
 $ \alpha (G_{n,p})$
for
$ \alpha (G_{n,p})$
for
 $n^{-1/2+ \epsilon } < p< 1/ \log (n)^2$
$n^{-1/2+ \epsilon } < p< 1/ \log (n)^2$
Here, we show that the second moment method applied to the random variable
![]() $Y_k$
, which is the number of maximal independent sets of size k, suffices to establish two point concentration of
$Y_k$
, which is the number of maximal independent sets of size k, suffices to establish two point concentration of
![]() $ \alpha (G_{n,p}) $
for
$ \alpha (G_{n,p}) $
for
![]() $n^{-1/2+ \epsilon } < p< 1/ \log (n)^2$
.
$n^{-1/2+ \epsilon } < p< 1/ \log (n)^2$
.
Recall that
![]() $X_k$
is the random variable which counts the number of independent sets of size k in
$X_k$
is the random variable which counts the number of independent sets of size k in
![]() $ G_{n,p}$
, and we defined
$ G_{n,p}$
, and we defined
![]() $k_x$
to be the largest integer such that
$k_x$
to be the largest integer such that
Set
![]() $ X = X_{k_x}$
and
$ X = X_{k_x}$
and
![]() $ Y = Y_{x_k}$
.
$ Y = Y_{x_k}$
.
Theorem 18. Consider
![]() $p = p(n)$
such that
$p = p(n)$
such that
![]() $ n^{-1/2 + \epsilon } < p< 1/ \log (n)^2$
. Then
$ n^{-1/2 + \epsilon } < p< 1/ \log (n)^2$
. Then
![]() $\alpha (G_{n,p}) \in \{k_x,k_x+1\}$
whp.
$\alpha (G_{n,p}) \in \{k_x,k_x+1\}$
whp.
Proof. Set
![]() $k = k_x$
. First, we show by the standard first moment method that no independent set of size
$k = k_x$
. First, we show by the standard first moment method that no independent set of size
![]() $k+2$
appear whp:
$k+2$
appear whp:
 $$ \begin{align*} \mathbb{P}( \alpha( G_{n,p}) \ge k +2) &\leq \binom{n}{k +2}(1-p)^{\binom{k+2}{2}} \\&= \binom{n}{k+1}(1-p)^{\binom{k+1}{2}}\Bigg(\frac{n-k-1}{k+2}(1-p)^{k+1} \Bigg) \\&= (1+o(1))\binom{n}{k+1}(1-p)^{\binom{k+1}{2}} \frac{n}{k} \left( \frac{k}{ne} \right)^2 \\& = o \left( \frac{k}{n^{1/2}} \right) \\&= o(1), \end{align*} $$
$$ \begin{align*} \mathbb{P}( \alpha( G_{n,p}) \ge k +2) &\leq \binom{n}{k +2}(1-p)^{\binom{k+2}{2}} \\&= \binom{n}{k+1}(1-p)^{\binom{k+1}{2}}\Bigg(\frac{n-k-1}{k+2}(1-p)^{k+1} \Bigg) \\&= (1+o(1))\binom{n}{k+1}(1-p)^{\binom{k+1}{2}} \frac{n}{k} \left( \frac{k}{ne} \right)^2 \\& = o \left( \frac{k}{n^{1/2}} \right) \\&= o(1), \end{align*} $$
where we use the fact that
![]() $ k = o(n^{1/2}) $
when
$ k = o(n^{1/2}) $
when
![]() $p> n^{-1/2+\epsilon }$
in the last line.
$p> n^{-1/2+\epsilon }$
in the last line.
Next, we show that an independent set of size k exists whp. Here, we use the second moment method, but the variance of X itself is too large. So we work with the random variable Y which counts the number of maximal independent sets of size k. The first moment calculation is straightforward, using Equation (5):
 $$ \begin{align} \mathbb{E}(Y) &= \binom{n}{k}(1-p)^{\binom{k}{2}} (1-(1-p)^{k})^{n-k} \nonumber \\&= \binom{n}{k}(1-p)^{\binom{k}{2}}e^{- O( k^2/n)} \end{align} $$
$$ \begin{align} \mathbb{E}(Y) &= \binom{n}{k}(1-p)^{\binom{k}{2}} (1-(1-p)^{k})^{n-k} \nonumber \\&= \binom{n}{k}(1-p)^{\binom{k}{2}}e^{- O( k^2/n)} \end{align} $$
 $$ \begin{align}&= \mathbb{E}(X)(1-o(1))\qquad\qquad\ \ \,\\&= \omega(1).\qquad\qquad\ \ \, \nonumber \end{align} $$
$$ \begin{align}&= \mathbb{E}(X)(1-o(1))\qquad\qquad\ \ \,\\&= \omega(1).\qquad\qquad\ \ \, \nonumber \end{align} $$
By Chebyshev’s inequality, all that is left to show is that
![]() $\frac {Var(Y)}{\mathbb {E}(Y)^2} = o(1)$
. We write Y as the sum of indicator variables
$\frac {Var(Y)}{\mathbb {E}(Y)^2} = o(1)$
. We write Y as the sum of indicator variables
![]() $Y_S$
, over all sets S such that
$Y_S$
, over all sets S such that
![]() $|K| = k$
, of the random variable
$|K| = k$
, of the random variable
![]() $Y_S$
which is the indicator for the event that S is a maximal independent vertex set. We define indicator variables
$Y_S$
which is the indicator for the event that S is a maximal independent vertex set. We define indicator variables
![]() $X_S$
for not necessarily maximal independent sets analogously. Then we have
$X_S$
for not necessarily maximal independent sets analogously. Then we have
Next, define, for all relevant i:
 $$ \begin{align*} &f_i = \frac{1}{\mathbb{E}(X)^2}\sum_{|S \cap T| = i} \mathbb{E}(X_S X_{T}) = \frac{\binom{k}{i}\binom{n-k}{k-i}}{\binom{n}{k}} (1-p)^{-\binom{i}{2}}, \\& g_i = \frac{1}{\mathbb{E}(Y)^2}\sum_{|S \cap T| = i} \mathbb{E}(Y_S Y_{T}), \text{ and} \\& \kappa_i = \frac{f_{i+1}}{f_i}. \end{align*} $$
$$ \begin{align*} &f_i = \frac{1}{\mathbb{E}(X)^2}\sum_{|S \cap T| = i} \mathbb{E}(X_S X_{T}) = \frac{\binom{k}{i}\binom{n-k}{k-i}}{\binom{n}{k}} (1-p)^{-\binom{i}{2}}, \\& g_i = \frac{1}{\mathbb{E}(Y)^2}\sum_{|S \cap T| = i} \mathbb{E}(Y_S Y_{T}), \text{ and} \\& \kappa_i = \frac{f_{i+1}}{f_i}. \end{align*} $$
Since
![]() $\mathbb {E}(Y) = \omega (1)$
, our goal is to show that
$\mathbb {E}(Y) = \omega (1)$
, our goal is to show that
 $$ \begin{align*} \sum_{i=0}^{k-1} g_i = o(1). \end{align*} $$
$$ \begin{align*} \sum_{i=0}^{k-1} g_i = o(1). \end{align*} $$
We consider three ranges of i:
![]() $i < \frac {\epsilon }{2} k_x$
,
$i < \frac {\epsilon }{2} k_x$
,
![]() $\frac {\epsilon }{2} k_x \leq i \leq (1-\epsilon )k_x$
, and
$\frac {\epsilon }{2} k_x \leq i \leq (1-\epsilon )k_x$
, and
![]() $i> (1-\epsilon ) k_x$
(where
$i> (1-\epsilon ) k_x$
(where
![]() $\epsilon $
is the constant in the statement of the Theorem). For each range, we show that the sum of variables
$\epsilon $
is the constant in the statement of the Theorem). For each range, we show that the sum of variables
![]() $g_i$
within that range is
$g_i$
within that range is
![]() $o(1)$
. For the first two ranges, we will actually work with variables
$o(1)$
. For the first two ranges, we will actually work with variables
![]() $f_i$
instead, noting that, since
$f_i$
instead, noting that, since
![]() $Y_S \leq X_S$
and by similar reasoning to Equation (27),
$Y_S \leq X_S$
and by similar reasoning to Equation (27),
![]() $g_i \leq f_i(1+o(1))$
.
$g_i \leq f_i(1+o(1))$
.
First, consider
![]() $i < \frac {\epsilon }{2} k$
. Using the explicit formula for
$i < \frac {\epsilon }{2} k$
. Using the explicit formula for
![]() $f_i$
we have
$f_i$
we have
 $$ \begin{align*} \kappa_i = \frac{(k-i)^2(1-p)^{-i}}{(i+1)(n-2k+i+1)} < \frac{ k^2 (1-p)^{-\epsilon k/2}}{n} = (1+o(1)) \frac{ k^2}{n} \left( \frac{ ne}{k} \right)^{\epsilon} = O \left( \frac{ \log(n)^2}{ n^{\epsilon}} \right) = o(1). \end{align*} $$
$$ \begin{align*} \kappa_i = \frac{(k-i)^2(1-p)^{-i}}{(i+1)(n-2k+i+1)} < \frac{ k^2 (1-p)^{-\epsilon k/2}}{n} = (1+o(1)) \frac{ k^2}{n} \left( \frac{ ne}{k} \right)^{\epsilon} = O \left( \frac{ \log(n)^2}{ n^{\epsilon}} \right) = o(1). \end{align*} $$
As
![]() $ f_2 = O( k^4/n^2) = o(1)$
then
$ f_2 = O( k^4/n^2) = o(1)$
then
![]() $\sum _{i=2}^{\epsilon k/2} f_i$
is a geometric sum with leading term and ratio in
$\sum _{i=2}^{\epsilon k/2} f_i$
is a geometric sum with leading term and ratio in
![]() $o(1)$
.
$o(1)$
.
Next, consider the range
![]() $\frac {\epsilon }{2} k \leq i \leq (1-\epsilon ) k$
. We have
$\frac {\epsilon }{2} k \leq i \leq (1-\epsilon ) k$
. We have
 $$ \begin{align} f_i & \le 2^{k} \left( \frac{k}{n} \right)^i (1-p)^{-\binom{i}{2}} \nonumber\\ & \le \left[ 2^{k/i} \frac{k}{n} \left( (1-p)^{-k/2} \right)^{i/k} \right]^i \nonumber\\ & \le \left[ (1+o(1)) 2^{ 2/ \epsilon } \frac{k}{n} \left( \frac{ne}{k} \right)^{1-\epsilon} \right]^i \\ & \le \left[ (1+o(1)) 2^{ 2/ \epsilon } e^{1-\epsilon} \left( \frac{k}{n} \right)^\epsilon \right]^i. \nonumber \end{align} $$
$$ \begin{align} f_i & \le 2^{k} \left( \frac{k}{n} \right)^i (1-p)^{-\binom{i}{2}} \nonumber\\ & \le \left[ 2^{k/i} \frac{k}{n} \left( (1-p)^{-k/2} \right)^{i/k} \right]^i \nonumber\\ & \le \left[ (1+o(1)) 2^{ 2/ \epsilon } \frac{k}{n} \left( \frac{ne}{k} \right)^{1-\epsilon} \right]^i \\ & \le \left[ (1+o(1)) 2^{ 2/ \epsilon } e^{1-\epsilon} \left( \frac{k}{n} \right)^\epsilon \right]^i. \nonumber \end{align} $$
Hence, the sum of variables
![]() $f_i$
over
$f_i$
over
![]() $\frac {\epsilon }{2} k_x \leq i \leq (1-\epsilon )k_x$
is
$\frac {\epsilon }{2} k_x \leq i \leq (1-\epsilon )k_x$
is
![]() $o(1)$
.
$o(1)$
.
The range where
![]() $i> (1-\epsilon ) k$
is where we use the variables
$i> (1-\epsilon ) k$
is where we use the variables
![]() $g_i$
instead of
$g_i$
instead of
![]() $f_i$
. Given two vertex sets S and T with intersection size i, and given that they are both independent, consider the probability that both are maximal independent sets. This probability is bounded above by the probability that each vertex in
$f_i$
. Given two vertex sets S and T with intersection size i, and given that they are both independent, consider the probability that both are maximal independent sets. This probability is bounded above by the probability that each vertex in
![]() $S \backslash T$
is adjacent to at least one vertex in
$S \backslash T$
is adjacent to at least one vertex in
![]() $T \backslash S$
, which is equal to
$T \backslash S$
, which is equal to
![]() $(1-(1-p)^{k-i})^{k-i} \leq ((k-i)p)^{k-i}$
. Therefore, we have
$(1-(1-p)^{k-i})^{k-i} \leq ((k-i)p)^{k-i}$
. Therefore, we have
 $$ \begin{align*} g_i &\leq (1+o(1)) \frac{\binom{k}{i}\binom{n-k}{k-i}}{\binom{n}{k}} (1-p)^{-\binom{i}{2}} ((k-i)p)^{k-i} \\&= \frac{1+o(1)}{\mathbb{E}[X]} \Bigg(\binom{k}{k-i} (k-i)^{k-i}\Bigg) \Bigg(\binom{n-k}{k-i}(1-p)^{\binom{k}{2}-\binom{i}{2}}p^{k-i} \Bigg) \\&< \frac{1+o(1)}{\mathbb{E}[X]} (ke)^{k-i} n^{k-i} (1-p)^{(1-\epsilon)k(k-i)}p^{k-i} \\&< \frac{1}{\mathbb{E}[X]} \Bigg((1+o(1)) e k n p \left( \frac{ k}{ ne} \right)^{2(1 -\epsilon)} \Bigg)^{k-i} \\&< \frac{1}{\mathbb{E}[X]} \Bigg( 22 \log(n)^3 n^{-\epsilon + 2\epsilon^2} \Bigg)^{k-i}, \end{align*} $$
$$ \begin{align*} g_i &\leq (1+o(1)) \frac{\binom{k}{i}\binom{n-k}{k-i}}{\binom{n}{k}} (1-p)^{-\binom{i}{2}} ((k-i)p)^{k-i} \\&= \frac{1+o(1)}{\mathbb{E}[X]} \Bigg(\binom{k}{k-i} (k-i)^{k-i}\Bigg) \Bigg(\binom{n-k}{k-i}(1-p)^{\binom{k}{2}-\binom{i}{2}}p^{k-i} \Bigg) \\&< \frac{1+o(1)}{\mathbb{E}[X]} (ke)^{k-i} n^{k-i} (1-p)^{(1-\epsilon)k(k-i)}p^{k-i} \\&< \frac{1}{\mathbb{E}[X]} \Bigg((1+o(1)) e k n p \left( \frac{ k}{ ne} \right)^{2(1 -\epsilon)} \Bigg)^{k-i} \\&< \frac{1}{\mathbb{E}[X]} \Bigg( 22 \log(n)^3 n^{-\epsilon + 2\epsilon^2} \Bigg)^{k-i}, \end{align*} $$
so
![]() $\sum _{i>(1-\epsilon ) k} g_i = o(1)$
, as desired.
$\sum _{i>(1-\epsilon ) k} g_i = o(1)$
, as desired.
Acknowledgments
We thank the anonymous referee for useful comments and suggestions.
Competing interest
The authors have no competing interest to declare.
Funding statement
This work was supported in part by a grant from the Simons Foundation (587088, TB).