Article contents
UPPER BOUNDS FOR SUNFLOWER-FREE SETS
Published online by Cambridge University Press: 27 June 2017
Abstract
A collection of 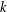 $k$ sets is said to form a
$k$ sets is said to form a 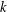 $k$ -sunflower, or
$k$ -sunflower, or 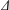 $\unicode[STIX]{x1D6E5}$ -system, if the intersection of any two sets from the collection is the same, and we call a family of sets
$\unicode[STIX]{x1D6E5}$ -system, if the intersection of any two sets from the collection is the same, and we call a family of sets 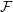 ${\mathcal{F}}$ sunflower-free if it contains no
${\mathcal{F}}$ sunflower-free if it contains no 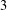 $3$ -sunflowers. Following the recent breakthrough of Ellenberg and Gijswijt (‘On large subsets of
$3$ -sunflowers. Following the recent breakthrough of Ellenberg and Gijswijt (‘On large subsets of  $\mathbb{F}_{q}^{n}$ with no three-term arithmetic progression’, Ann. of Math. (2) 185 (2017), 339–343); (‘Progression-free sets in
$\mathbb{F}_{q}^{n}$ with no three-term arithmetic progression’, Ann. of Math. (2) 185 (2017), 339–343); (‘Progression-free sets in 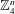 $\mathbb{Z}_{4}^{n}$ are exponentially small’, Ann. of Math. (2) 185 (2017), 331–337) we apply the polynomial method directly to Erdős–Szemerédi sunflower problem (Erdős and Szemerédi, ‘Combinatorial properties of systems of sets’, J. Combin. Theory Ser. A 24 (1978), 308–313) and prove that any sunflower-free family
$\mathbb{Z}_{4}^{n}$ are exponentially small’, Ann. of Math. (2) 185 (2017), 331–337) we apply the polynomial method directly to Erdős–Szemerédi sunflower problem (Erdős and Szemerédi, ‘Combinatorial properties of systems of sets’, J. Combin. Theory Ser. A 24 (1978), 308–313) and prove that any sunflower-free family 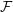 ${\mathcal{F}}$ of subsets of
${\mathcal{F}}$ of subsets of  $\{1,2,\ldots ,n\}$ has size at most
$\{1,2,\ldots ,n\}$ has size at most 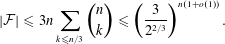 $$\begin{eqnarray}|{\mathcal{F}}|\leqslant 3n\mathop{\sum }_{k\leqslant n/3}\binom{n}{k}\leqslant \left(\frac{3}{2^{2/3}}\right)^{n(1+o(1))}.\end{eqnarray}$$
$$\begin{eqnarray}|{\mathcal{F}}|\leqslant 3n\mathop{\sum }_{k\leqslant n/3}\binom{n}{k}\leqslant \left(\frac{3}{2^{2/3}}\right)^{n(1+o(1))}.\end{eqnarray}$$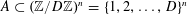 $A\subset (\mathbb{Z}/D\mathbb{Z})^{n}=\{1,2,\ldots ,D\}^{n}$ for
$A\subset (\mathbb{Z}/D\mathbb{Z})^{n}=\{1,2,\ldots ,D\}^{n}$ for 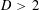 $D>2$ is sunflower-free if for every distinct triple
$D>2$ is sunflower-free if for every distinct triple 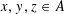 $x,y,z\in A$ there exists a coordinate
$x,y,z\in A$ there exists a coordinate 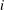 $i$ where exactly two of
$i$ where exactly two of 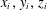 $x_{i},y_{i},z_{i}$ are equal. Using a version of the polynomial method with characters
$x_{i},y_{i},z_{i}$ are equal. Using a version of the polynomial method with characters 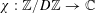 $\unicode[STIX]{x1D712}:\mathbb{Z}/D\mathbb{Z}\rightarrow \mathbb{C}$ instead of polynomials, we show that any sunflower-free set
$\unicode[STIX]{x1D712}:\mathbb{Z}/D\mathbb{Z}\rightarrow \mathbb{C}$ instead of polynomials, we show that any sunflower-free set 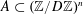 $A\subset (\mathbb{Z}/D\mathbb{Z})^{n}$ has size
$A\subset (\mathbb{Z}/D\mathbb{Z})^{n}$ has size 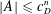 $$\begin{eqnarray}|A|\leqslant c_{D}^{n}\end{eqnarray}$$
$$\begin{eqnarray}|A|\leqslant c_{D}^{n}\end{eqnarray}$$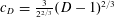 $c_{D}=\frac{3}{2^{2/3}}(D-1)^{2/3}$ . This can be seen as making further progress on a possible approach to proving the Erdős and Rado sunflower conjecture (‘Intersection theorems for systems of sets’,J. Lond. Math. Soc. (2) 35 (1960), 85–90), which by the work of Alon et al. (‘On sunflowers and matrix multiplication’, Comput. Complexity22 (2013), 219–243; Theorem 2.6) is equivalent to proving that
$c_{D}=\frac{3}{2^{2/3}}(D-1)^{2/3}$ . This can be seen as making further progress on a possible approach to proving the Erdős and Rado sunflower conjecture (‘Intersection theorems for systems of sets’,J. Lond. Math. Soc. (2) 35 (1960), 85–90), which by the work of Alon et al. (‘On sunflowers and matrix multiplication’, Comput. Complexity22 (2013), 219–243; Theorem 2.6) is equivalent to proving that 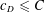 $c_{D}\leqslant C$ for some constant
$c_{D}\leqslant C$ for some constant 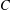 $C$ independent of
$C$ independent of 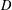 $D$ .
$D$ .
Information
- Type
- Research Article
- Information
- Creative Commons
- This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
- Copyright
- © The Author(s) 2017
References
- 28
- Cited by


