[Agg17]
Aggarwal, A., ‘Dynamical stochastic higher spin vertex models’, Selecta Math.
24(3) (2018), 2659–2735.
[ABB18]
Aggarwal, A., Borodin, A. and Bufetov, A., ‘Stochasticization of solutions to the Yang-Baxter equation’, Ann. Henri Poincaré
20(8) (2019), 2495–2554.
[BDJ99]
Baik, J., Deift, P. and Johansson, K., ‘On the distribution of the length of the longest increasing subsequence of random permutations’, J. Amer. Math. Soc.
12(4) (1999), 1119–1178.
[Bar01]
Baryshnikov, Y., ‘GUEs and queues’, Probab. Theory Related Fields
119 (2001), 256–274.
[Bax07]
Baxter, R., Exactly Solved Models in Statistical Mechanics (Courier Dover Publications, Mineola, NY, 2007).
[BBB+14]
Betea, D., Boutillier, C., Bouttier, J., Chapuy, G., Corteel, S. and Vuletić, M., ‘Perfect sampling algorithm for Schur processes’, Markov Process. Related Fields
24(3) (2017), 381–418.
[BW16]
Betea, D. and Wheeler, M., ‘Refined Cauchy and Littlewood identities, plane partitions and symmetry classes of alternating sign matrices’, J. Combin. Theory Ser A
137 (2016), 126–165.
[BWZJ15]
Betea, D., Wheeler, M. and Zinn-Justin, P., ‘Refined Cauchy/Littlewood identities and six-vertex model partition functions: II. Proofs and new conjectures’, J. Algebraic Combin.
42(2) (2015), 555–603.
[Bor11]
Borodin, A., ‘Schur dynamics of the Schur processes’, Adv. Math.
228(4) (2011), 2268–2291.
[Bor16]
Borodin, A., ‘Stochastic higher spin six vertex model and Macdonald measures’, J. Math. Phys.
59(2) (2018), 023301.
[Bor17a]
Borodin, A., ‘On a family of symmetric rational functions’, Adv. Math.
306 (2017), 973–1018.
[Bor17b]
Borodin, A., ‘Symmetric elliptic functions, IRF models, and dynamic exclusion processes’, Preprint, 2017, arXiv:1701.05239 [math-ph]. [BBW18]
Borodin, A., Bufetov, A. and Wheeler, M., ‘Between the stochastic six vertex model and Hall–Littlewood processes’, Duke Math. J.
167(13) (2018), 2457–2529.
[BC14]
Borodin, A. and Corwin, I., ‘Macdonald processes’, Probab. Theory Related Fields
158 (2014), 225–400.
[BC15]
Borodin, A. and Corwin, I., ‘Discrete time q-TASEPs’, Int. Math. Res. Not. IMRN
2015(2) (2015), 499–537.
[BC17]
Borodin, A. and Corwin, I., ‘Dynamic ASEP, duality and continuous
$q^{-1}$
-Hermite polynomials’, Preprint, 2017, arXiv:1705.01980 [math.PR]. [BCFV15]
Borodin, A., Corwin, I., Ferrari, P. and Veto, B., ‘Height fluctuations for the stationary KPZ equation’, Math. Phys. Anal. Geom.
18(1) (2015), 1–95.
[BCG16]
Borodin, A., Corwin, I. and Gorin, V., ‘Stochastic six-vertex model’, Duke J. Math.
165(3) (2016), 563–624.
[BCGS16]
Borodin, A., Corwin, I., Gorin, V. and Shakirov, S., ‘Observables of Macdonald processes’, Trans. Amer. Math. Soc.
368(3) (2016), 1517–1558.
[BCPS15a]
Borodin, A., Corwin, I., Petrov, L. and Sasamoto, T., ‘Spectral theory for interacting particle systems solvable by coordinate Bethe ansatz’, Commun. Math. Phys.
339(3) (2015), 1167–1245.
[BCPS15b]
Borodin, A., Corwin, I., Petrov, L. and Sasamoto, T., ‘Spectral theory for the q-Boson particle system’, Compos. Math.
151(1) (2015), 1–67.
[BF08]
Borodin, A. and Ferrari, P., ‘Large time asymptotics of growth models on space-like paths I: PushASEP’, Electron. J. Probab.
13 (2008), 1380–1418.
[BF14]
Borodin, A. and Ferrari, P., ‘Anisotropic growth of random surfaces in 2 + 1 dimensions’, Commun. Math. Phys.
325 (2014), 603–684.
[BG15]
Borodin, A. and Gorin, V., ‘General 𝛽-Jacobi corners process and the Gaussian free field’, Comm. Pure Appl. Math.
68(10) (2015), 1774–1844.
[BP14]
Borodin, A. and Petrov, L., ‘Integrable probability: From representation theory to Macdonald processes’, Probab. Surv.
11 (2014), 1–58.
[BP16]
Borodin, A. and Petrov, L., ‘Nearest neighbor Markov dynamics on Macdonald processes’, Adv. Math.
300 (2016), 71–155.
[BP18a]
Borodin, A. and Petrov, L., ‘Higher spin six vertex model and symmetric rational functions’, Selecta Math.
24(2) (2018), 751–874.
[BP18b]
Borodin, A. and Petrov, L., ‘Inhomogeneous exponential jump model’, Probab. Theory Related Fields
172 (2018), 323–385.
[BM18]
Bufetov, A. and Matveev, K., ‘Hall–Littlewood RSK field’, Selecta Math.
24(5) (2018), 4839–4884.
[BP15]
Bufetov, A. and Petrov, L., ‘Law of large numbers for infinite random matrices over a finite field’, Selecta Math.
21(4) (2015), 1271–1338.
[Cor12]
Corwin, I., ‘The Kardar–Parisi–Zhang equation and universality class’, Random Matrices Theory Appl.
1(1) (2012), 1130001.
[Cor16]
Corwin, I., ‘Kardar–Parisi–Zhang universality’, Notices Amer. Math. Soc.
63(3) (2016), 230–239.
[COSZ14]
Corwin, I., O’Connell, N., Seppäläinen, T. and Zygouras, N., ‘Tropical combinatorics and Whittaker functions’, Duke J. Math.
163(3) (2014), 513–563.
[CP15]
Corwin, I. and Petrov, L., ‘The q-PushASEP: a new integrable model for traffic in 1 + 1 dimension’, J. Stat. Phys.
160(4) (2015), 1005–1026.
[CP16]
Corwin, I. and Petrov, L., ‘Stochastic higher spin vertex models on the line’, Comm. Math. Phys.
343(2) (2016), 651–700.
[DF90]
Diaconis, P. and Fill, J. A., ‘Strong stationary times via a new form of duality’, Ann. Probab.
18 (1990), 1483–1522.
[Dim16]
Dimitrov, E., ‘KPZ and Airy limits of Hall–Littlewood random plane partitions’, Ann. Inst. Henri Poincaré Probab. Stat.
54(2) (2018), 640–693.
[DLSS91]
Derrida, B., Lebowitz, J., Speer, E. and Spohn, H., ‘Dynamics of an anchored Toom interface’, J. Phys. A
24(20) (1991), 4805–4834.
[Fer08]
Ferrari, P., ‘The universal Airy1 and Airy2 processes in the totally asymmetric simple exclusion process’, inIntegrable Systems and Random Matrices: In Honor of Percy Deift, (eds. Baik, J., Kriecherbauer, T., Li, L.-C., McLaughlin, K. T.-R. and Tomei, C.) Contemporary Mathematics (American Mathematical Society, Providence, RI, 2008), 321–332.
[Fom86]
Fomin, S., ‘Generalized Robinson-Schnested-Knuth correspondence’, Zap. Nauchn. Sem. (LOMI)
155 (1986), 156–175 (in Russian).
[Fom95]
Fomin, S., ‘Schensted algorithms for dual graded graphs’, J. Algebraic Combin.
4(1) (1995), 5–45.
[GM14]
Gimmett, G. and Manolescu, I., ‘Bond percolation on isoradial graphs: criticality and universality’, Probab. Theory Related Fields
159(1–2) (2014), 273–327.
[GS92]
Gwa, L.-H. and Spohn, H., ‘Six-vertex model, roughened surfaces, and an asymmetric spin Hamiltonian’, Phys. Rev. Lett.
68(6) (1992), 725–728.
[HHT15]
Halpin-Healy, T. and Takeuchi, K., ‘A KPZ cocktail-shaken, not stirred …’, J. Stat. Phys.
160(4) (2015), 794–814.
[Joh00]
Johansson, K., ‘Shape fluctuations and random matrices’, Comm. Math. Phys.
209(2) (2000), 437–476.
[Kir01]
Kirillov, A. N., ‘Introduction to tropical combinatorics’, inPhysics and Combinatorics, Proceedings of the Nagoya 2000 International Workshop (Singapore) (eds. Kirillov, A. N. and Liskova, N.) (World Scientific, Singapore, 2001), 82–150.
[KR87]
Kirillov, A. N. and Reshetikhin, N., ‘Exact solution of the integrable XXZ Heisenberg model with arbitrary spin. I. The ground state and the excitation spectrum’, J. Phys. A
20(6) (1987), 1565–1585.
[KBI93]
Korepin, V., Bogoliubov, N. and Izergin, A., Quantum Inverse Scattering Method and Correlation Functions, (Cambridge University Press, Cambridge, 1993).
[KR83]
Kulish, P. and Reshetikhin, N., ‘Quantum linear problem for the Sine–Gordon equation and higher representations’, New York J. Math. Sci.
23 (1983), 2435–2441.
[KRS81]
Kulish, P., Reshetikhin, N. and Sklyanin, E., ‘Yang–Baxter equation and representation theory: I’, Lett. Math. Phys.
5 (1981), 393–403.
[Lie67]
Lieb, E. H., ‘Residual entropy of square ice’, Phys. Rev.
162(1) (1967), 162–172.
[MGP68]
MacDonald, C., Gibbs, J. and Pipkin, A., ‘Kinetics of biopolymerization on nucleic acid templates’, Biopolymers
6(1) (1968), 1–25.
[Mac95]
Macdonald, I. G., Symmetric Functions and Hall Polynomials, 2nd edn, (Oxford University Press, Oxford, UK, 1995).
[Man14]
Mangazeev, V., ‘On the Yang–Baxter equation for the six-vertex model’, Nuclear Phys. B
882 (2014), 70–96.
[MP17]
Matveev, K. and Petrov, L., ‘
q-randomized Robinson–Schensted–Knuth correspondences and random polymers’, Ann. Inst. Henri Poincare D
4(1) (2017), 1–123.
[NY04]
Noumi, M. and Yamada, Y., ‘Tropical Robinson–Schensted–Knuth correspondence and birational Weyl group actions’, inRepresentation Theory of Algebraic Groups and Quantum Groups, Adv. Stud. Pure Math., 40 (Math. Soc. Japan, Tokyo, 2004), 371–442.
[O’C03a]
O’Connell, N., ‘A path-transformation for random walks and the Robinson–Schensted correspondence’, Trans. Amer. Math. Soc.
355(9) (2003), 3669–3697.
[O’C03b]
O’Connell, N., ‘Conditioned random walks and the RSK correspondence’, J. Phys. A
36(12) (2003), 3049–3066.
[O’C12]
O’Connell, N., ‘Directed polymers and the quantum Toda lattice’, Ann. Probab.
40(2) (2012), 437–458.
[OP13]
O’Connell, N. and Pei, Y., ‘A q-weighted version of the Robinson–Schensted algorithm’, Electron. J. Probab.
18(95) (2013), 1–25.
[OSZ14]
O’Connell, N., Seppäläinen, T. and Zygouras, N., ‘Geometric RSK correspondence, Whittaker functions and symmetrized random polymers’, Invent. Math.
197 (2014), 361–416.
[OY02]
O’Connell, N. and Yor, M., ‘A representation for non-colliding random walks’, Electron. Commun. Probab.
7 (2002), 1–12.
[Oko01]
Okounkov, A., ‘Infinite wedge and random partitions’, Selecta Math.
7(1) (2001), 57–81.
[OR03]
Okounkov, A. and Reshetikhin, N., ‘Correlation function of Schur process with application to local geometry of a random 3-dimensional Young diagram’, J. Amer. Math. Soc.
16(3) (2003), 581–603.
[Pau35]
Pauling, L., ‘The structure and entropy of ice and of other crystals with some randomness of atomic arrangement’, J. Amer. Chem. Soc.
57(12) (1935), 2680–2684.
[Pei13]
Pei, Y., ‘A symmetry property for q-weighted Robinson–Schensted algorithms and other branching insertion algorithms’, J. Algebraic Combin.
40 (2013), 743–770.
[Pei16]
Pei, Y., ‘A
$q$
-Robinson–Schensted–Knuth Algorithm and a
$q$
-polymer’, Preprint, 2016, arXiv:1610.03692 [math.CO]. [Pet20]
Petrov, L., ‘PushTASEP in inhomogeneous space’, In preparation, 2020.
[Pov13]
Povolotsky, A., ‘On integrability of zero-range chipping models with factorized steady state’, J. Phys. A
46
465205 (2013).
[PS02]
Prähofer, M. and Spohn, H., ‘Scale invariance of the PNG droplet and the Airy process’, J. Stat. Phys.
108 (2002), 1071–1106.
[Sep12]
Seppäläinen, T., ‘Scaling for a one-dimensional directed polymer with boundary conditions’, Ann. Probab.
40(1) (2012), 19–73.
[Spi70]
Spitzer, F., ‘Interaction of Markov processes’, Adv. Math.
5(2) (1970), 246–290.
[Spo15]
Sportiello, A., Personal communication, 2015.
[Tsi06]
Tsilevich, N., ‘Quantum inverse scattering method for the q-boson model and symmetric functions’, Funct. Anal. Appl.
40(3) (2006), 207–217.
[VK86]
Vershik, A. and Kerov, S., ‘The characters of the infinite symmetric group and probability properties of the Robinson–Shensted–Knuth algorithm’, SIAM J. Algebra Discrete Math.
7(1) (1986), 116–124.
[WW09]
Warren, J. and Windridge, P., ‘Some examples of dynamics for Gelfand–Tsetlin patterns’, Electron. J. Probab.
14 (2009), 1745–1769.
[Wey97]
Weyl, H., The Classical Groups. Their Invariants and Representations, (Princeton University Press, Princeton, NJ, 1997).
[WZJ16]
Wheeler, M. and Zinn-Justin, P., ‘Refined Cauchy/Littlewood identities and six-vertex model partition functions: III. Deformed bosons’, Adv. Math.
299 (2016), 543–600.
[Yan67]
Yang, C. N., ‘Some exact results for the many-body problem in one dimension with repulsive delta-function interaction’, Phys. Rev. Lett.
19(23) (1967), 1312.
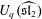$U_{q}(\widehat{\mathfrak{sl}_{2}})$
. Combining these moves leads to a new object which we call the spin Hall–Littlewood Yang–Baxter field—a probability distribution on two-dimensional arrays of particle configurations on the discrete line. We identify joint distributions along down-right paths in the Yang–Baxter field with spin Hall–Littlewood processes, a generalization of Schur processes. We consider various degenerations of the Yang–Baxter field leading to new dynamic versions of the stochastic six-vertex model and of the Asymmetric Simple Exclusion Process.
$q^{-1}$
-Hermite polynomials’, Preprint, 2017, arXiv:1705.01980 [math.PR].
$q$
-Robinson–Schensted–Knuth Algorithm and a
$q$
-polymer’, Preprint, 2016, arXiv:1610.03692 [math.CO].
