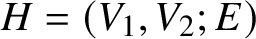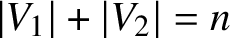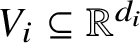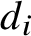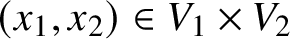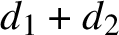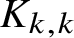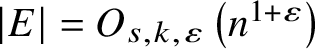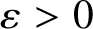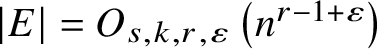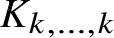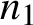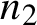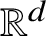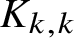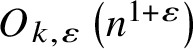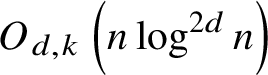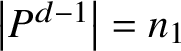1. Introduction
We fix
![]() $r \in \mathbb {N}_{\geq 2}$
and let
$r \in \mathbb {N}_{\geq 2}$
and let
![]() $H = \left (V_1, \dotsc , V_r; E \right )$
be an r-partite and r-uniform hypergraph (or just an r-hypergraph for brevity) with vertex sets
$H = \left (V_1, \dotsc , V_r; E \right )$
be an r-partite and r-uniform hypergraph (or just an r-hypergraph for brevity) with vertex sets
![]() $V_1, \dotsc , V_r$
having
$V_1, \dotsc , V_r$
having
![]() $\lvert V_i\rvert = n_i$
, (hyper-) edge set E and a total number
$\lvert V_i\rvert = n_i$
, (hyper-) edge set E and a total number
![]() $n = \sum _{i=1}^r n_i$
of vertices.
$n = \sum _{i=1}^r n_i$
of vertices.
Zarankiewicz’s problem asks for the maximum number of edges in such a hypergraph H (as a function of
![]() $n_1, \dotsc , n_r$
) assuming that it does not contain the complete r-hypergraph
$n_1, \dotsc , n_r$
) assuming that it does not contain the complete r-hypergraph
![]() $K_{k, \dotsc , k}$
with
$K_{k, \dotsc , k}$
with
![]() $k> 0$
a fixed number of vertices in each part. The following classical upper bound is due to Kővári, Sós and Turán [Reference Kővári, Sós and Turán14] for
$k> 0$
a fixed number of vertices in each part. The following classical upper bound is due to Kővári, Sós and Turán [Reference Kővári, Sós and Turán14] for
![]() $r=2$
and Erdős [Reference Erdős9] for a general r: if H is
$r=2$
and Erdős [Reference Erdős9] for a general r: if H is
![]() $K_{k, \dotsc , k}$
-free, then
$K_{k, \dotsc , k}$
-free, then
 $\lvert E\rvert = O_{r,k} \left (n^{r - \frac {1}{k^{r-1}}} \right )$
. A probabilistic construction in [Reference Erdős9] also shows that the exponent cannot be substantially improved.
$\lvert E\rvert = O_{r,k} \left (n^{r - \frac {1}{k^{r-1}}} \right )$
. A probabilistic construction in [Reference Erdős9] also shows that the exponent cannot be substantially improved.
However, stronger bounds are known for restricted families of hypergraphs arising in geometric settings. For example, if H is the incidence graph of a set of
![]() $n_1$
points and
$n_1$
points and
![]() $n_2$
lines in
$n_2$
lines in
![]() $\mathbb {R}^2$
, then H is
$\mathbb {R}^2$
, then H is
![]() $K_{2,2}$
-free, and the Kővári–Sós–Turán Theorem implies
$K_{2,2}$
-free, and the Kővári–Sós–Turán Theorem implies
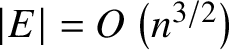 $\lvert E\rvert = O\left ( n^{3/2}\right )$
. The Szemerédi–Trotter Theorem [Reference Szemerédi and Trotter20] improves this and gives the optimal bound
$\lvert E\rvert = O\left ( n^{3/2}\right )$
. The Szemerédi–Trotter Theorem [Reference Szemerédi and Trotter20] improves this and gives the optimal bound
 $\lvert E\rvert = O\left (n^{4/3}\right )$
. More generally, [Reference Fox, Pach, Sheffer, Suk and Zahl12] gives improved bounds for semialgebraic graphs of bounded description complexity. This is generalised to semialgebraic hypergraphs in [Reference Do8]. In a different direction, the results in [Reference Fox, Pach, Sheffer, Suk and Zahl12] are generalised to graphs definable in o-minimal structures in [Reference Basu and Raz2] and, more generally, in distal structures in [Reference Chernikov, Galvin and Starchenko4].
$\lvert E\rvert = O\left (n^{4/3}\right )$
. More generally, [Reference Fox, Pach, Sheffer, Suk and Zahl12] gives improved bounds for semialgebraic graphs of bounded description complexity. This is generalised to semialgebraic hypergraphs in [Reference Do8]. In a different direction, the results in [Reference Fox, Pach, Sheffer, Suk and Zahl12] are generalised to graphs definable in o-minimal structures in [Reference Basu and Raz2] and, more generally, in distal structures in [Reference Chernikov, Galvin and Starchenko4].
A related highly nontrivial problem is to understand when the bounds offered by the results in the preceding paragraph are sharp. When H is the incidence graph of
![]() $n_1$
points and
$n_1$
points and
![]() $n_2$
circles of unit radius in
$n_2$
circles of unit radius in
![]() $\mathbb {R}^2$
, the best known upper bound is
$\mathbb {R}^2$
, the best known upper bound is
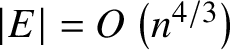 $\lvert E\rvert =O\left (n^{4/3}\right )$
, proven in [Reference Spencer, Szemerédi and Trotter19] and also implied by the general bound for semialgebraic graphs. Any improvement to this bound will be a step toward resolving the long-standing unit-distance conjecture of Erdős (an almost-linear bound of the form
$\lvert E\rvert =O\left (n^{4/3}\right )$
, proven in [Reference Spencer, Szemerédi and Trotter19] and also implied by the general bound for semialgebraic graphs. Any improvement to this bound will be a step toward resolving the long-standing unit-distance conjecture of Erdős (an almost-linear bound of the form
 $\lvert E\rvert =O\left (n^{1+c/\log \log n}\right )$
will positively resolve it).
$\lvert E\rvert =O\left (n^{1+c/\log \log n}\right )$
will positively resolve it).
This paper was originally motivated by the following incidence problem: Let H be the incidence graph of a set of
![]() $n_1$
points and a set of
$n_1$
points and a set of
![]() $n_2$
solid rectangles with axis-parallel sides (which we refer to as boxes) in
$n_2$
solid rectangles with axis-parallel sides (which we refer to as boxes) in
![]() $\mathbb {R}^2$
. Assuming that H is
$\mathbb {R}^2$
. Assuming that H is
![]() $K_{2,2}$
-free – that is, no two points belong to two rectangles simultaneously – what is the maximum number of incidences
$K_{2,2}$
-free – that is, no two points belong to two rectangles simultaneously – what is the maximum number of incidences
![]() $\lvert E\rvert $
? In the following theorem, we obtain an almost-linear bound (which is much stronger than the bound implied by the aforementioned general result for semialgebraic graphs) and demonstrate that it is close to optimal:
$\lvert E\rvert $
? In the following theorem, we obtain an almost-linear bound (which is much stronger than the bound implied by the aforementioned general result for semialgebraic graphs) and demonstrate that it is close to optimal:
Theorem (A).
-
1. For any set P of
 $n_1$
points in
$n_1$
points in
 $\mathbb {R}^2$
and any set R of
$\mathbb {R}^2$
and any set R of
 $n_2$
boxes in
$n_2$
boxes in
 $\mathbb {R}^2$
, if the incidence graph on
$\mathbb {R}^2$
, if the incidence graph on
 $P \times R$
is
$P \times R$
is
 $K_{k,k}$
-free, then it contains at most
$K_{k,k}$
-free, then it contains at most
 $O_k \left (n \log ^{4}(n) \right )$
incidences (Corollary 2.38 with
$O_k \left (n \log ^{4}(n) \right )$
incidences (Corollary 2.38 with
 $d=2$
).
$d=2$
). -
2. If all boxes in R are dyadic (i.e., direct products of intervals of the form
 $\left [s2^t, (s+1)2^t\right )$
for some integers
$\left [s2^t, (s+1)2^t\right )$
for some integers
 $s,t$
), then the number of incidences is at most
$s,t$
), then the number of incidences is at most
 $O_k \left ( n \frac {\log \left (100+n_1\right )}{\log \log \left (100+n_1\right )} \right )$
(Theorem 4.7).
$O_k \left ( n \frac {\log \left (100+n_1\right )}{\log \log \left (100+n_1\right )} \right )$
(Theorem 4.7). -
3. For an arbitrarily large n, there exists a set of n points and n dyadic boxes in
 $\mathbb {R}^2$
so that the incidence graph is
$\mathbb {R}^2$
so that the incidence graph is
 $K_{2,2}$
-free and the number of incidences is
$K_{2,2}$
-free and the number of incidences is
 $\Omega \left (n \frac {\log (n)}{\log \log (n)} \right )$
(Proposition 3.5).
$\Omega \left (n \frac {\log (n)}{\log \log (n)} \right )$
(Proposition 3.5).
Problem 1.1. While the bound for dyadic boxes is tight, we leave it as an open problem to close the gap between the upper and lower bounds for arbitrary boxes.
Remark 1.2. A related result in [Reference Fox and Pach11] demonstrates that every
![]() $K_{k,k}$
-free intersection graph of n convex sets on the plane satisfies
$K_{k,k}$
-free intersection graph of n convex sets on the plane satisfies
![]() $\lvert E\rvert = O_{k}(n)$
. Note that in Theorem (B) we consider a
$\lvert E\rvert = O_{k}(n)$
. Note that in Theorem (B) we consider a
![]() $K_{k,k}$
-free bipartite graph, so in particular there is no restriction on the intersection graph of the boxes in R.
$K_{k,k}$
-free bipartite graph, so in particular there is no restriction on the intersection graph of the boxes in R.
Theorem (A.1) admits the following generalisation to higher dimensions and more general polytopes:
Theorem (B).
-
1. For any set P of
 $n_1$
points and any set B of
$n_1$
points and any set B of
 $n_2$
boxes in
$n_2$
boxes in
 $\mathbb {R}^d$
, if the incidence graph on
$\mathbb {R}^d$
, if the incidence graph on
 $P \times B$
is
$P \times B$
is
 $K_{k,k}$
-free, then it contains at most
$K_{k,k}$
-free, then it contains at most
 $O_{d,k} \left ( n \log ^{2 d} n \right )$
incidences (Corollary 2.38).
$O_{d,k} \left ( n \log ^{2 d} n \right )$
incidences (Corollary 2.38). -
2. More generally, given finitely many half-spaces
 $H_1, \dotsc , H_s$
in
$H_1, \dotsc , H_s$
in
 $\mathbb {R}^d$
, let
$\mathbb {R}^d$
, let
 $\mathcal {F}$
be the family of all possible polytopes in
$\mathcal {F}$
be the family of all possible polytopes in
 $\mathbb {R}^d$
cut out by arbitrary translates of
$\mathbb {R}^d$
cut out by arbitrary translates of
 $H_1, \dotsc , H_s$
. Then for any set P of
$H_1, \dotsc , H_s$
. Then for any set P of
 $n_1$
points in
$n_1$
points in
 $\mathbb {R}^d$
and any set F of
$\mathbb {R}^d$
and any set F of
 $n_2$
polytopes in
$n_2$
polytopes in
 $\mathcal {F}$
, if the incidence graph on
$\mathcal {F}$
, if the incidence graph on
 $P \times F$
is
$P \times F$
is
 $K_{k,k}$
-free, then it contains at most
$K_{k,k}$
-free, then it contains at most
 $O_{k,s}\left ( n \log ^{s} n \right )$
incidences (Corollary 2.37).
$O_{k,s}\left ( n \log ^{s} n \right )$
incidences (Corollary 2.37).
Problem 1.3. What is the optimal bound on the power of
![]() $\log n$
in Theorem (B)? In particular, does it actually have to grow with the dimension d?
$\log n$
in Theorem (B)? In particular, does it actually have to grow with the dimension d?
Remark 1.4. A bound similar to Theorem (B.1) and an improved bound for Theorem (A.1) in the
![]() $K_{2,2}$
-free case are established independently by Tomon and Zakharov in [Reference Tomon and Zakharov22], in which they also use our Theorem (A.3) to provide a counterexample to a conjecture of Alon et al. [Reference Alon, Basavaraju, Chandran, Mathew and Rajendraprasad1] about the number of edges in a graph of bounded separation dimension, as well as to a conjecture of Kostochka from [Reference Kostochka13]. Some further Ramsey properties of semilinear graphs are demonstrated by Tomon in [Reference Tomon21].
$K_{2,2}$
-free case are established independently by Tomon and Zakharov in [Reference Tomon and Zakharov22], in which they also use our Theorem (A.3) to provide a counterexample to a conjecture of Alon et al. [Reference Alon, Basavaraju, Chandran, Mathew and Rajendraprasad1] about the number of edges in a graph of bounded separation dimension, as well as to a conjecture of Kostochka from [Reference Kostochka13]. Some further Ramsey properties of semilinear graphs are demonstrated by Tomon in [Reference Tomon21].
The upper bounds in Theorems (A.1) and (B) are obtained as immediate applications of a general upper bound for Zarankiewicz’s problem for semilinear hypergraphs of bounded description complexity.
Definition 1.5. Let V be an ordered vector space over an ordered division ring R (e.g.,
![]() $\mathbb {R}$
viewed as a vector space over itself). A set
$\mathbb {R}$
viewed as a vector space over itself). A set
![]() $X \subseteq V^d$
is semilinear, of description complexity
$X \subseteq V^d$
is semilinear, of description complexity
![]() $(s,t)$
, if X is a union of at most t sets of the form
$(s,t)$
, if X is a union of at most t sets of the form
 $$ \begin{align*} \left\{ \bar{x}\in V^{d}:f_{1}\left(\bar{x}\right) \leq 0, \dotsc, f_{p} \left(\bar{x}\right) \leq 0,f_{p+1}\left(\bar{x}\right)<0,\dotsc,f_{s}\left(\bar{x}\right)<0\right\}, \end{align*} $$
$$ \begin{align*} \left\{ \bar{x}\in V^{d}:f_{1}\left(\bar{x}\right) \leq 0, \dotsc, f_{p} \left(\bar{x}\right) \leq 0,f_{p+1}\left(\bar{x}\right)<0,\dotsc,f_{s}\left(\bar{x}\right)<0\right\}, \end{align*} $$
where
![]() $p \leq s \in \mathbb {N}$
and each
$p \leq s \in \mathbb {N}$
and each
![]() $f_i: V^d \to V$
is a linear function – that is, of the form
$f_i: V^d \to V$
is a linear function – that is, of the form
for some
![]() $\lambda _{i}\in R$
and
$\lambda _{i}\in R$
and
![]() $a\in V$
.
$a\in V$
.
We focus on the case
![]() $V=R = \mathbb {R}$
in the introduction, when these are precisely the semialgebraic sets that can be defined using only linear polynomials.
$V=R = \mathbb {R}$
in the introduction, when these are precisely the semialgebraic sets that can be defined using only linear polynomials.
Remark 1.6. By a standard quantifier elimination result [Reference Van den Dries23, §7], every set definable in an ordered vector space over an ordered division ring, in the sense of model theory, is semilinear (equivalently, a projection of a semilinear set is a finite union of semilinear sets).
Definition 1.7. We say that an r-hypergraph H is semilinear, of description complexity
![]() $(s,t)$
, if there exist some
$(s,t)$
, if there exist some
![]() $d_i \in \mathbb {N}, V_i \subseteq \mathbb {R}^{d_i}$
and a semilinear set
$d_i \in \mathbb {N}, V_i \subseteq \mathbb {R}^{d_i}$
and a semilinear set
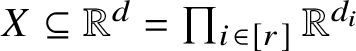 $X \subseteq \mathbb {R}^d = \prod _{i \in [r]} \mathbb {R}^{d_i}$
of description complexity
$X \subseteq \mathbb {R}^d = \prod _{i \in [r]} \mathbb {R}^{d_i}$
of description complexity
![]() $(s,t)$
so that H is isomorphic to the r-hypergraph
$(s,t)$
so that H is isomorphic to the r-hypergraph
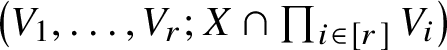 $\left (V_1, \dotsc , V_r; X \cap \prod _{i \in [r]} V_i \right )$
.
$\left (V_1, \dotsc , V_r; X \cap \prod _{i \in [r]} V_i \right )$
.
We stress that there is no restriction on the dimensions
![]() $d_i$
in this definition. We obtain the following general upper bound:
$d_i$
in this definition. We obtain the following general upper bound:
Theorem (C). If H is a semilinear r-hypergraph of description complexity
![]() $(s,t)$
and H is
$(s,t)$
and H is
![]() $K_{k, \dotsc , k}$
-free, then
$K_{k, \dotsc , k}$
-free, then
 $$ \begin{align*}\lvert E\rvert = O_{r,s,t,k} \left( n^{r-1} \log^{s\left(2^{r-1}-1\right)}(n) \right).\end{align*} $$
$$ \begin{align*}\lvert E\rvert = O_{r,s,t,k} \left( n^{r-1} \log^{s\left(2^{r-1}-1\right)}(n) \right).\end{align*} $$
In particular,
![]() $\lvert E\rvert = O_{r,s,t,k,\varepsilon } \left ( n^{r-1 + \varepsilon } \right )$
for any
$\lvert E\rvert = O_{r,s,t,k,\varepsilon } \left ( n^{r-1 + \varepsilon } \right )$
for any
![]() $\varepsilon>0$
in this case. For a more precise statement, see Corollary 2.36 (in particular, the dependence of the constant in
$\varepsilon>0$
in this case. For a more precise statement, see Corollary 2.36 (in particular, the dependence of the constant in
![]() $O_{r,s,t,k}$
on k is at most linear).
$O_{r,s,t,k}$
on k is at most linear).
Remark 1.8. It is demonstrated in [Reference Mustafa and Pach17] that a similar bound holds in the situation when H is the intersection hypergraph of
![]() $(d-1)$
-dimensional simplices in
$(d-1)$
-dimensional simplices in
![]() $\mathbb {R}^d$
.
$\mathbb {R}^d$
.
One can get rid of the logarithmic factor entirely by restricting to the family of all finite r-hypergraphs induced by a given
![]() $K_{k, \dotsc , k}$
-free semilinear relation (as opposed to all
$K_{k, \dotsc , k}$
-free semilinear relation (as opposed to all
![]() $K_{k, \dotsc , k}$
-free r-hypergraphs induced by a given arbitrary semilinear relation, as in Theorem (C)).
$K_{k, \dotsc , k}$
-free r-hypergraphs induced by a given arbitrary semilinear relation, as in Theorem (C)).
Theorem (D). Assume that
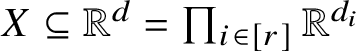 $X \subseteq \mathbb {R}^d = \prod _{i \in [r]} \mathbb {R}^{d_i}$
is semilinear and X does not contain the direct product of r infinite sets (e.g., if X is
$X \subseteq \mathbb {R}^d = \prod _{i \in [r]} \mathbb {R}^{d_i}$
is semilinear and X does not contain the direct product of r infinite sets (e.g., if X is
![]() $K_{k, \dotsc , k}$
-free for some k). Then for any r-hypergraph H of the form
$K_{k, \dotsc , k}$
-free for some k). Then for any r-hypergraph H of the form
 $\left (V_1, \dotsc , V_r; X \cap \prod _{i \in [r]} V_i \right )$
for some finite
$\left (V_1, \dotsc , V_r; X \cap \prod _{i \in [r]} V_i \right )$
for some finite
![]() $V_i \subseteq \mathbb {R}^{d_i}$
, we have
$V_i \subseteq \mathbb {R}^{d_i}$
, we have
![]() $\lvert E\rvert = O_X\left (n^{r-1}\right )$
.
$\lvert E\rvert = O_X\left (n^{r-1}\right )$
.
This is Corollary 5.12 and follows from a more general Theorem 5.6 connecting linear Zarankiewicz bounds to a model-theoretic notion of linearity of a first-order structure (in the sense that the matroid given by the algebraic closure operator behaves like the linear span in a vector space, as opposed to the algebraic closure in an algebraically closed field – see Definition 5.3).
In particular, for every
![]() $K_{k,k}$
-free semilinear relation
$K_{k,k}$
-free semilinear relation
![]() $X \subseteq \mathbb {R}^{d_1} \times \mathbb {R}^{d_2}$
(equivalently, X definable with parameters in the first-order structure
$X \subseteq \mathbb {R}^{d_1} \times \mathbb {R}^{d_2}$
(equivalently, X definable with parameters in the first-order structure
![]() $(\mathbb {R}, <, +)$
by Remark 1.6) we have
$(\mathbb {R}, <, +)$
by Remark 1.6) we have
![]() $\lvert X \cap (V_1 \times V_2)\rvert = O(n)$
for all
$\lvert X \cap (V_1 \times V_2)\rvert = O(n)$
for all
 $V_i \subseteq \mathbb {R}^{d_i}_i$
,
$V_i \subseteq \mathbb {R}^{d_i}_i$
,
![]() $\lvert V_i\rvert = n_i$
,
$\lvert V_i\rvert = n_i$
,
![]() $n = n_1 + n_2$
. One the other hand, by optimality of the Szemerédi–Trotter bound, for the semialgebraic
$n = n_1 + n_2$
. One the other hand, by optimality of the Szemerédi–Trotter bound, for the semialgebraic
![]() $K_{2,2}$
-free point-line incidence graph
$K_{2,2}$
-free point-line incidence graph
 $X = \left \{(x_1,x_2; y_1, y_2) \in \mathbb {R}^4 : x_2 = y_1 x_1 + y_2 \right \}\subseteq \mathbb {R}^2 \times \mathbb {R}^2$
we have
$X = \left \{(x_1,x_2; y_1, y_2) \in \mathbb {R}^4 : x_2 = y_1 x_1 + y_2 \right \}\subseteq \mathbb {R}^2 \times \mathbb {R}^2$
we have
 $\lvert X \cap (V_1 \times V_2)\rvert = \Omega \left (n^{\frac {4}{3}}\right )$
. Note that in order to define it we use both addition and multiplication – that is, the field structure. This is not coincidental; as a consequence of the trichotomy theorem in o-minimal structures [Reference Peterzil and Starchenko18], we observe that the failure of a linear Zarankiewicz bound always allows us to recover the field in a definable way (Corollary 5.11). In the semialgebraic case, we have the following corollary that is easy to state (Corollary 5.14):
$\lvert X \cap (V_1 \times V_2)\rvert = \Omega \left (n^{\frac {4}{3}}\right )$
. Note that in order to define it we use both addition and multiplication – that is, the field structure. This is not coincidental; as a consequence of the trichotomy theorem in o-minimal structures [Reference Peterzil and Starchenko18], we observe that the failure of a linear Zarankiewicz bound always allows us to recover the field in a definable way (Corollary 5.11). In the semialgebraic case, we have the following corollary that is easy to state (Corollary 5.14):
Theorem (E). Assume that
 $X \subseteq \mathbb {R}^d = \prod _{i \in [r]} \mathbb {R}^{d_i}$
for some
$X \subseteq \mathbb {R}^d = \prod _{i \in [r]} \mathbb {R}^{d_i}$
for some
![]() $r,d_i \in \mathbb {N}$
is semialgebraic and
$r,d_i \in \mathbb {N}$
is semialgebraic and
![]() $K_{k, \dotsc , k}$
-free, but
$K_{k, \dotsc , k}$
-free, but
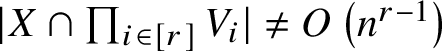 $\lvert X \cap \prod _{i \in [r]} V_i\rvert \neq O\left (n^{r-1}\right )$
. Then the graph of multiplication
$\lvert X \cap \prod _{i \in [r]} V_i\rvert \neq O\left (n^{r-1}\right )$
. Then the graph of multiplication
![]() $\times \restriction _{[0,1]}$
restricted to the unit box is definable in
$\times \restriction _{[0,1]}$
restricted to the unit box is definable in
![]() $(\mathbb {R}, <, +, X)$
.
$(\mathbb {R}, <, +, X)$
.
We conclude with a brief overview of the paper.
In Section 2 we introduce a more general class of hypergraphs definable in terms of coordinate-wise monotone functions (Definition 2.1) and prove an upper Zarankiewicz bound for it (Theorem 2.17). Theorems (A.1), (B) and (C) are then deduced from it in Section 2.5.
In Section 3 we prove Theorem (A.3) by establishing a lower bound on the number of incidences between points and dyadic boxes on the plane, demonstrating that the logarithmic factor is unavoidable (Proposition 3.5).
In Section 4, we establish Theorem (A.2) by obtaining a stronger bound on the number of incidences with dyadic boxes on the plane (Theorem 4.7). We use a different argument, relying on a certain partial order specific to the dyadic case, to reduce from
![]() $\log ^4(n)$
given by the general theorem to
$\log ^4(n)$
given by the general theorem to
![]() $\log (n)$
. Up to a constant factor, this implies the same bound for incidences with general boxes when one counts only incidences that are bounded away from the border (Remark 4.8).
$\log (n)$
. Up to a constant factor, this implies the same bound for incidences with general boxes when one counts only incidences that are bounded away from the border (Remark 4.8).
Finally, in Section 5 we prove a general Zarankiewicz bound for definable relations in weakly locally modular geometric first-order structures (Theorem 5.6), deduce Theorem (D) from it (Corollary 5.12) and observe how to recover a real closed field from the failure of Theorem (D) in the o-minimal case (Corollary 5.11).
2. Upper bounds
2.1. Coordinate-wise monotone functions and basic sets
For an integer
![]() $r\in \mathbb N_{>0}$
, by an r-grid (or a grid, if r is clear from the context) we mean a cartesian product
$r\in \mathbb N_{>0}$
, by an r-grid (or a grid, if r is clear from the context) we mean a cartesian product
![]() $B=B_1{{\times }\dotsb {\times }} B_r$
of some sets
$B=B_1{{\times }\dotsb {\times }} B_r$
of some sets
![]() $B_1, \dotsc , B_r$
. As usual,
$B_1, \dotsc , B_r$
. As usual,
![]() $[r]$
denotes the set
$[r]$
denotes the set
![]() $\left \{1, 2, \dotsc , r \right \}$
.
$\left \{1, 2, \dotsc , r \right \}$
.
If
![]() $B=B_1{{\times }\dotsb {\times }} B_r$
is a grid, then by a subgrid we mean a subset
$B=B_1{{\times }\dotsb {\times }} B_r$
is a grid, then by a subgrid we mean a subset
![]() $C \subseteq B$
of the form
$C \subseteq B$
of the form
![]() $C=C_1{{\times }\dotsb {\times }} C_r$
for some
$C=C_1{{\times }\dotsb {\times }} C_r$
for some
![]() $C_i \subseteq B_i$
.
$C_i \subseteq B_i$
.
Let B be an r-grid, S an arbitrary set and
![]() $f: B \to S$
a function. For
$f: B \to S$
a function. For
![]() $i \in [r]$
, set
$i \in [r]$
, set
and let
![]() $\pi _i: B \to B_i$
and
$\pi _i: B \to B_i$
and
![]() $\pi ^i: B \to B^i$
be the projection maps.
$\pi ^i: B \to B^i$
be the projection maps.
For
![]() $a \in B^i $
and
$a \in B^i $
and
![]() $b \in B_i$
, we write
$b \in B_i$
, we write
![]() $a \oplus _i b$
for the element
$a \oplus _i b$
for the element
![]() $c \in B$
with
$c \in B$
with
![]() $\pi ^i(c) = a$
and
$\pi ^i(c) = a$
and
![]() $\pi _i(c) = b$
. In particular, when
$\pi _i(c) = b$
. In particular, when
![]() $i = r$
,
$i = r$
,
![]() $a \oplus _r b = (a, b)$
.
$a \oplus _r b = (a, b)$
.
Definition 2.1. Let B be an r-grid and
![]() $(S,<)$
a linearly ordered set. A function
$(S,<)$
a linearly ordered set. A function
![]() $f\colon B\to S$
is coordinate-wise monotone if for any
$f\colon B\to S$
is coordinate-wise monotone if for any
![]() $i\in [r]$
,
$i\in [r]$
,
![]() $a,a'\in B^i$
and
$a,a'\in B^i$
and
![]() $b,b'\in B_i$
, we have
$b,b'\in B_i$
, we have
Remark 2.2. Let
![]() $B =B_1{{\times }\dotsb {\times }} B_r$
be an r-grid and
$B =B_1{{\times }\dotsb {\times }} B_r$
be an r-grid and
![]() $\Gamma $
an ordered abelian group. We say that a function
$\Gamma $
an ordered abelian group. We say that a function
![]() $f\colon B\to \Gamma $
is quasi-linear if there exist some functions
$f\colon B\to \Gamma $
is quasi-linear if there exist some functions
![]() $f_i\colon B_i\to \Gamma $
,
$f_i\colon B_i\to \Gamma $
,
![]() $i\in [r]$
, such that
$i\in [r]$
, such that
Then every quasi-linear function is coordinate-wise monotone (as
![]() $ f(a\oplus _i b) \leq f({a} \oplus _i b') \Leftrightarrow f_i(b) \leq f_i(b')$
for any
$ f(a\oplus _i b) \leq f({a} \oplus _i b') \Leftrightarrow f_i(b) \leq f_i(b')$
for any
![]() $a \in B^i$
).
$a \in B^i$
).
Example 2.3. Suppose that V is an ordered vector space over an ordered division ring R,
![]() $d_i \in \mathbb {N}$
for
$d_i \in \mathbb {N}$
for
![]() $i \in [r]$
, and
$i \in [r]$
, and
![]() $f: V^{d_1} {{\times }\dotsb {\times }} V^{d_r} \to V $
is a linear function. Then f is obviously quasi-linear, and hence coordinate-wise monotone.
$f: V^{d_1} {{\times }\dotsb {\times }} V^{d_r} \to V $
is a linear function. Then f is obviously quasi-linear, and hence coordinate-wise monotone.
Remark 2.4. Let B be a grid and
![]() $C \subseteq B$
a subgrid. If
$C \subseteq B$
a subgrid. If
![]() $f\colon B\to S$
is a coordinate-wise monotone function, then the restriction
$f\colon B\to S$
is a coordinate-wise monotone function, then the restriction
![]() $f{\restriction C}$
is a coordinate-wise monotone function on C.
$f{\restriction C}$
is a coordinate-wise monotone function on C.
Definition 2.5. Let B be an r-grid. A subset
![]() $X\subseteq B$
is a basic set if there exists a linearly ordered set
$X\subseteq B$
is a basic set if there exists a linearly ordered set
![]() $(S,<)$
, a coordinate-wise monotone function
$(S,<)$
, a coordinate-wise monotone function
![]() $f\colon B\to S$
and
$f\colon B\to S$
and
![]() $l\in S$
such that
$l\in S$
such that
![]() $X= \left \{ b\in B \colon f(b) < l\right \}$
.
$X= \left \{ b\in B \colon f(b) < l\right \}$
.
Remark 2.6. If
![]() $r=1$
, then every subset of
$r=1$
, then every subset of
![]() $B=B_1$
is basic.
$B=B_1$
is basic.
Remark 2.7. If
![]() $X\subseteq B$
is given by
$X\subseteq B$
is given by
![]() $X= \left \{ b\in B \colon f(b) \leq l\right \}$
for some coordinate-wise monotone function
$X= \left \{ b\in B \colon f(b) \leq l\right \}$
for some coordinate-wise monotone function
![]() $f\colon B\to S$
, then X is a basic set as well. Indeed, we can just add a new element
$f\colon B\to S$
, then X is a basic set as well. Indeed, we can just add a new element
![]() $l'$
to S so that it is a successor of l, and then
$l'$
to S so that it is a successor of l, and then
![]() $X=\left \{b \in B: f(b)< l'\right \}$
.
$X=\left \{b \in B: f(b)< l'\right \}$
.
Similarly, the sets
![]() $\left \{ b\in B \colon f(b)> l\right \}, \left \{ b\in B \colon f(b) \geq l\right \}$
are basic, by inverting the order on S.
$\left \{ b\in B \colon f(b)> l\right \}, \left \{ b\in B \colon f(b) \geq l\right \}$
are basic, by inverting the order on S.
We have the following ‘coordinate-splitting’ presentation for basic sets:
Proposition 2.8. Let
![]() $B=B_1{{\times }\dotsb {\times }} B_r$
be an r-grid and
$B=B_1{{\times }\dotsb {\times }} B_r$
be an r-grid and
![]() $X\subseteq B$
a basic set. Then there is a linearly ordered set
$X\subseteq B$
a basic set. Then there is a linearly ordered set
![]() $(S,<)$
, a coordinate-wise monotone function
$(S,<)$
, a coordinate-wise monotone function
![]() $f^r\colon B^r \to S$
and a function
$f^r\colon B^r \to S$
and a function
![]() $f_r\colon B_r\to S$
such that
$f_r\colon B_r\to S$
such that
![]() $X=\left \{ b^r \oplus _{r} b_r \colon f^r(b^r) < f_r(b_r) \right \}$
.
$X=\left \{ b^r \oplus _{r} b_r \colon f^r(b^r) < f_r(b_r) \right \}$
.
Remark 2.9. The converse of this proposition is also true: an arbitrary linear order
![]() $(S,<)$
can be realised as a subset of some ordered abelian group
$(S,<)$
can be realised as a subset of some ordered abelian group
![]() $(G, +, <)$
with the induced ordering (we can take
$(G, +, <)$
with the induced ordering (we can take
![]() $G := \mathbb {Q}$
when S is at most countable); then define
$G := \mathbb {Q}$
when S is at most countable); then define
![]() $f: B \to S$
by setting
$f: B \to S$
by setting
Proof of Proposition 2.8. Assume that we are given a coordinate-wise monotone function
![]() $f\colon B\to S$
and
$f\colon B\to S$
and
![]() $l\in S$
with
$l\in S$
with
![]() $X= \left \{ b\in B \colon f(b) < l\right \}$
.
$X= \left \{ b\in B \colon f(b) < l\right \}$
.
For
![]() $i\in [r]$
, let
$i\in [r]$
, let
![]() $\leq _i$
be the preorder on
$\leq _i$
be the preorder on
![]() $B_i$
induced by f – namely, for
$B_i$
induced by f – namely, for
![]() $b,b'\in B_i$
we set
$b,b'\in B_i$
we set
![]() $b\leq _i b'$
if and only if for some (equivalently, any)
$b\leq _i b'$
if and only if for some (equivalently, any)
![]() $a\in B^i$
we have
$a\in B^i$
we have
![]() $f(a \oplus _i b)\leq f(a \oplus _i b')$
.
$f(a \oplus _i b)\leq f(a \oplus _i b')$
.
Quotienting
![]() $B_i$
by the equivalence relation corresponding to the preorder
$B_i$
by the equivalence relation corresponding to the preorder
![]() $\leq _i$
if needed, we may assume that each
$\leq _i$
if needed, we may assume that each
![]() $\leq _i$
is actually a linear order.
$\leq _i$
is actually a linear order.
Let
![]() $<^r$
be the partial order on
$<^r$
be the partial order on
![]() $B^r$
with
$B^r$
with
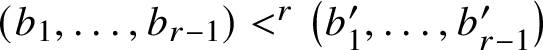 $(b_1,\dotsc ,b_{r-1}) <^r \left (b^{\prime }_1,\dotsc ,b^{\prime }_{r-1}\right )$
if and only if
$(b_1,\dotsc ,b_{r-1}) <^r \left (b^{\prime }_1,\dotsc ,b^{\prime }_{r-1}\right )$
if and only if
 $$ \begin{align*} (b_1,\dotsc,b_{r-1}) \neq \left(b^{\prime}_1,\dotsc,b^{\prime}_{r-1}\right) \text{ and } b_j\leq_j b^{\prime}_j \text{ for all } j\in[r-1]. \end{align*} $$
$$ \begin{align*} (b_1,\dotsc,b_{r-1}) \neq \left(b^{\prime}_1,\dotsc,b^{\prime}_{r-1}\right) \text{ and } b_j\leq_j b^{\prime}_j \text{ for all } j\in[r-1]. \end{align*} $$
Define
![]() $T := B^r \dot \cup B_r$
, where
$T := B^r \dot \cup B_r$
, where
![]() $\dot \cup $
denotes the disjoint union. Clearly
$\dot \cup $
denotes the disjoint union. Clearly
![]() $<^r$
is a strict partial order on T – that is, a transitive and antisymmetric (hence irreflexive) relation.
$<^r$
is a strict partial order on T – that is, a transitive and antisymmetric (hence irreflexive) relation.
For any
![]() $b^r\in B^r$
and
$b^r\in B^r$
and
![]() $b_r\in B_r$
, we define
$b_r\in B_r$
, we define
Claim 2.10. Set
![]() $a_1,a_2\in B^r$
and
$a_1,a_2\in B^r$
and
![]() $b_1,b_2\in B_r$
.
$b_1,b_2\in B_r$
.
-
1. If
 $a_1\triangleleft b_1 \triangleleft a_2 \triangleleft b_2$
, then
$a_1\triangleleft b_1 \triangleleft a_2 \triangleleft b_2$
, then
 $b_2 <_r b_1$
and
$b_2 <_r b_1$
and
 $a_1\triangleleft b_2$
.
$a_1\triangleleft b_2$
. -
2. If
 $b_1\triangleleft a_1 \triangleleft b_2 \triangleleft a_2$
, then
$b_1\triangleleft a_1 \triangleleft b_2 \triangleleft a_2$
, then
 $b_2 <_r b_1$
and
$b_2 <_r b_1$
and
 $b_1\triangleleft a_2$
.
$b_1\triangleleft a_2$
.
Proof. (1). We have
![]() $f(a_2 \oplus _r b_1) \geq l$
and
$f(a_2 \oplus _r b_1) \geq l$
and
![]() $f(a_2 \oplus _{r} b_2) < l$
, hence
$f(a_2 \oplus _{r} b_2) < l$
, hence
![]() $b_2 <_r b_1$
. Since
$b_2 <_r b_1$
. Since
![]() $f(a_1 \oplus _r b_1)<l$
and
$f(a_1 \oplus _r b_1)<l$
and
![]() $b_2 <_r b_1$
we also have
$b_2 <_r b_1$
we also have
![]() $f(a_1 \oplus _r b_2)<l$
.
$f(a_1 \oplus _r b_2)<l$
.
(2) is similar.
Let
![]() $\triangleleft ^t$
be the transitive closure of
$\triangleleft ^t$
be the transitive closure of
![]() $\triangleleft $
. It follows from the preceding claim that
$\triangleleft $
. It follows from the preceding claim that
![]() $\triangleleft ^t=\triangleleft \cup \triangleleft {\circ }\triangleleft $
. More explicitly, for
$\triangleleft ^t=\triangleleft \cup \triangleleft {\circ }\triangleleft $
. More explicitly, for
![]() $b_1,b_2 \in B_r$
, we have
$b_1,b_2 \in B_r$
, we have
![]() $b_1 \triangleleft ^t b_2$
if
$b_1 \triangleleft ^t b_2$
if
![]() $b_2 <_r b_1$
, and for
$b_2 <_r b_1$
, and for
![]() $a_1,a_2 \in B^r$
, we have
$a_1,a_2 \in B^r$
, we have
![]() $a_1 \triangleleft ^t a_2$
if
$a_1 \triangleleft ^t a_2$
if
![]() $f(a_1 \oplus b) < l < f(a_2 \oplus b)$
for some
$f(a_1 \oplus b) < l < f(a_2 \oplus b)$
for some
![]() $b \in B_r$
. It is not hard to see then that
$b \in B_r$
. It is not hard to see then that
![]() $\triangleleft ^t$
is antisymmetric, and hence it is a strict partial order on T.
$\triangleleft ^t$
is antisymmetric, and hence it is a strict partial order on T.
Claim 2.11. The union
![]() $<^r \cup \triangleleft ^t$
is a strict partial order on T.
$<^r \cup \triangleleft ^t$
is a strict partial order on T.
Proof. We first show transitivity. Note that
![]() $<^r$
and
$<^r$
and
![]() $\triangleleft ^t$
are both transitive, so it suffices to show for
$\triangleleft ^t$
are both transitive, so it suffices to show for
![]() $x, y, z \in T$
that if either
$x, y, z \in T$
that if either
![]() $x <^r y \triangleleft ^t z$
or
$x <^r y \triangleleft ^t z$
or
![]() $x \triangleleft ^t y <^r z$
, then
$x \triangleleft ^t y <^r z$
, then
![]() $x \triangleleft ^t z$
. Furthermore, since
$x \triangleleft ^t z$
. Furthermore, since
![]() $\triangleleft ^t=\triangleleft \cup \triangleleft {\circ }\triangleleft $
, we may restrict our attention to the following cases: If
$\triangleleft ^t=\triangleleft \cup \triangleleft {\circ }\triangleleft $
, we may restrict our attention to the following cases: If
![]() $a_1 <^r a_2\triangleleft b$
with
$a_1 <^r a_2\triangleleft b$
with
![]() $a_1,a_2\in B^r$
and
$a_1,a_2\in B^r$
and
![]() $b\in B_r$
, then
$b\in B_r$
, then
![]() $f(a_1 \oplus _r b)<f(a_2 \oplus _r b)<l$
, and so
$f(a_1 \oplus _r b)<f(a_2 \oplus _r b)<l$
, and so
![]() $a_1\triangleleft b$
. If
$a_1\triangleleft b$
. If
![]() $b\triangleleft a_1 <^r a_2$
with
$b\triangleleft a_1 <^r a_2$
with
![]() $a_1,a_2\in B^r$
and
$a_1,a_2\in B^r$
and
![]() $b\in B_r$
, then
$b\in B_r$
, then
![]() $f(a_2 \oplus _r b)>f(a_1 \oplus _r b)\geq l$
, and so
$f(a_2 \oplus _r b)>f(a_1 \oplus _r b)\geq l$
, and so
![]() $b\triangleleft a_2$
.
$b\triangleleft a_2$
.
To check antisymmetry, assume
![]() $a_1 <^r a_2$
and
$a_1 <^r a_2$
and
![]() $a_2 \triangleleft ^t a_1$
. Since
$a_2 \triangleleft ^t a_1$
. Since
![]() $a_1,a_2\in B^r$
, we have
$a_1,a_2\in B^r$
, we have
![]() $a_2\triangleleft b \triangleleft a_1$
for some
$a_2\triangleleft b \triangleleft a_1$
for some
![]() $b\in B_r$
. We have
$b\in B_r$
. We have
![]() $f(a_1 \oplus _r b)\geq l> f(a_2 \oplus _r b)$
, contradicting
$f(a_1 \oplus _r b)\geq l> f(a_2 \oplus _r b)$
, contradicting
![]() $a_1<^r a_2$
.
$a_1<^r a_2$
.
Finally, let
![]() $\prec $
be an arbitrary linear order on
$\prec $
be an arbitrary linear order on
![]() $T=B^r\dot \cup B_r$
extending
$T=B^r\dot \cup B_r$
extending
![]() $<^r \cup \triangleleft ^t$
. Since
$<^r \cup \triangleleft ^t$
. Since
![]() $\prec $
extends
$\prec $
extends
![]() $\triangleleft $
, for
$\triangleleft $
, for
![]() $a\in B^r$
and
$a\in B^r$
and
![]() $b\in B_r$
we have
$b\in B_r$
we have
![]() $(a,b)\in X$
if and only if
$(a,b)\in X$
if and only if
![]() $a\prec b$
.
$a\prec b$
.
We take
![]() $f^r\colon B^r\to T$
and
$f^r\colon B^r\to T$
and
![]() $f_r\colon B_r\to T$
to be the identity maps. Since
$f_r\colon B_r\to T$
to be the identity maps. Since
![]() $\prec $
extends
$\prec $
extends
![]() $<^r$
, the map
$<^r$
, the map
![]() $f^r$
is coordinate-wise monotone.
$f^r$
is coordinate-wise monotone.
2.2. Main theorem
Definition 2.12. Let
![]() $B=B_1{{\times }\dotsb {\times }} B_r$
be an r-grid.
$B=B_1{{\times }\dotsb {\times }} B_r$
be an r-grid.
-
1. Given
 $s \in \mathbb {N}$
, we say that a set
$s \in \mathbb {N}$
, we say that a set
 $X\subseteq B$
has grid-complexity s (in B) if X is the intersection of B with at most s basic subsets of B.
$X\subseteq B$
has grid-complexity s (in B) if X is the intersection of B with at most s basic subsets of B.We say that X has finite grid-complexity if it has grid-complexity s for some
 $s \in \mathbb {N}$
.
$s \in \mathbb {N}$
. -
2. For integers
 $k_1,\dotsc , k_r$
we say that
$k_1,\dotsc , k_r$
we say that
 $X\subseteq B$
is
$X\subseteq B$
is
 $K_{k_1,\dotsc ,k_r}$
-free if X does not contain a subgrid
$K_{k_1,\dotsc ,k_r}$
-free if X does not contain a subgrid
 $C_1{{\times }\dotsb {\times }} C_r\subseteq S$
with
$C_1{{\times }\dotsb {\times }} C_r\subseteq S$
with
 $\lvert C_i\rvert =k_i$
.
$\lvert C_i\rvert =k_i$
.
In particular, B itself is the only subset of B of grid-complexity
![]() $0$
.
$0$
.
Example 2.13. Suppose that V is an ordered vector space over an ordered division ring,
![]() $d = d_1 + \dotsb + d_r \in \mathbb {N}$
and
$d = d_1 + \dotsb + d_r \in \mathbb {N}$
and
 $$ \begin{align*} X = \left\{ \bar{x} \in V^{d}:f_{1}\left(\bar{x}\right) \leq 0, \dotsc, f_{p}\left(\bar{x}\right) \leq 0,f_{p+1}\left(\bar{x}\right)<0,\dotsc,f_{s}\left(\bar{x}\right)<0\right\}, \end{align*} $$
$$ \begin{align*} X = \left\{ \bar{x} \in V^{d}:f_{1}\left(\bar{x}\right) \leq 0, \dotsc, f_{p}\left(\bar{x}\right) \leq 0,f_{p+1}\left(\bar{x}\right)<0,\dotsc,f_{s}\left(\bar{x}\right)<0\right\}, \end{align*} $$
for some linear functions
![]() $f_i: V^d \to V, i \in [s]$
. Then each
$f_i: V^d \to V, i \in [s]$
. Then each
![]() $f_i$
is coordinate-wise monotone (Example 2.3), and hence each of the sets
$f_i$
is coordinate-wise monotone (Example 2.3), and hence each of the sets
 $$ \begin{align*}\left\{\bar{x} \in V^d : f_i(\bar{x}) <0 \right\}, \left\{\bar{x} \in V^d : f_i(\bar{x}) \leq 0 \right\}\end{align*} $$
$$ \begin{align*}\left\{\bar{x} \in V^d : f_i(\bar{x}) <0 \right\}, \left\{\bar{x} \in V^d : f_i(\bar{x}) \leq 0 \right\}\end{align*} $$
is a basic subset of the grid
![]() $V^{d_1} {{\times }\dotsb {\times }} V^{d_r}$
(the latter by Remark 2.7), and
$V^{d_1} {{\times }\dotsb {\times }} V^{d_r}$
(the latter by Remark 2.7), and
![]() $X \subseteq V^{d_1} {{\times }\dotsb {\times }} V^{d_r}$
as an intersection of these s basic sets has grid-complexity s.
$X \subseteq V^{d_1} {{\times }\dotsb {\times }} V^{d_r}$
as an intersection of these s basic sets has grid-complexity s.
Remark 2.14.
-
1. Let B be an r-grid and
 $A\subseteq B$
a subset of B of grid-complexity s. If
$A\subseteq B$
a subset of B of grid-complexity s. If
 $C \subseteq B$
is a subgrid containing A, then A is also a subset of C of grid-complexity s.
$C \subseteq B$
is a subgrid containing A, then A is also a subset of C of grid-complexity s. -
2. In particular, if
 $A\subseteq B$
is a subset of grid-complexity s, then A is a subset of grid-complexity
$A\subseteq B$
is a subset of grid-complexity s, then A is a subset of grid-complexity
 $ s$
of the grid
$ s$
of the grid
 $A_1{{\times }\dotsb {\times }} A_r$
, where
$A_1{{\times }\dotsb {\times }} A_r$
, where
 $A_i :=\pi _i(A)$
is the projection of A on
$A_i :=\pi _i(A)$
is the projection of A on
 $B_i$
(it is the smallest subgrid of B containing A).
$B_i$
(it is the smallest subgrid of B containing A).
Definition 2.15. Let
![]() $B=B_1{{\times }\dotsb {\times }} B_r$
be a finite r-grid and set
$B=B_1{{\times }\dotsb {\times }} B_r$
be a finite r-grid and set
![]() $n_i :=\lvert B_i\rvert $
. For
$n_i :=\lvert B_i\rvert $
. For
![]() $j\in \{0,\dotsc , r\}$
, we will denote by
$j\in \{0,\dotsc , r\}$
, we will denote by
 $\delta _j^r(B)$
the integer
$\delta _j^r(B)$
the integer
 $$ \begin{align*} \delta_j^r(B) := \sum_{ i_1<i_2<\dotsb< i_j \in [r]} n_{i_1} \cdot n_{i_2} \cdot \dotsb \cdot n_{i_j}.\end{align*} $$
$$ \begin{align*} \delta_j^r(B) := \sum_{ i_1<i_2<\dotsb< i_j \in [r]} n_{i_1} \cdot n_{i_2} \cdot \dotsb \cdot n_{i_j}.\end{align*} $$
Example 2.16. We have
![]() $\delta ^r_0(B)=1$
,
$\delta ^r_0(B)=1$
,
![]() $\delta ^r_1(B)=n_1+\dotsb +n_r$
,
$\delta ^r_1(B)=n_1+\dotsb +n_r$
,
![]() $\delta _r^r(B)=n_1n_2\dotsb n_r$
.
$\delta _r^r(B)=n_1n_2\dotsb n_r$
.
We can now state the main theorem:
Theorem 2.17. For all integers
![]() $r\geq 2, s\geq 0, k\geq 2$
, there are
$r\geq 2, s\geq 0, k\geq 2$
, there are
![]() $\alpha =\alpha (r,s,k)\in \mathbb {R}$
and
$\alpha =\alpha (r,s,k)\in \mathbb {R}$
and
![]() $\beta =\beta (r,s)\in \mathbb N$
such that for any finite r-grid B and
$\beta =\beta (r,s)\in \mathbb N$
such that for any finite r-grid B and
![]() $K_{k,\dotsc ,k}$
-free subset
$K_{k,\dotsc ,k}$
-free subset
![]() $A \subseteq B$
of grid-complexity s, we have
$A \subseteq B$
of grid-complexity s, we have
 $$ \begin{align*} |A| \leq \alpha \delta^r_{r-1}(B) \log^\beta \left( \delta^r_{r-1}(B)+1 \right). \end{align*} $$
$$ \begin{align*} |A| \leq \alpha \delta^r_{r-1}(B) \log^\beta \left( \delta^r_{r-1}(B)+1 \right). \end{align*} $$
Moreover, we can take
![]() $\beta (r,s) := s\left (2^{r-1}-1\right )$
.
$\beta (r,s) := s\left (2^{r-1}-1\right )$
.
Remark 2.18. Inspecting the proof in Sections 2.3 and 2.4, it can be verified that the dependence of
![]() $\alpha $
on k in Theorem 2.17 s at most linear.
$\alpha $
on k in Theorem 2.17 s at most linear.
Remark 2.19. We use
 $\log ^\beta \left ( \delta ^r_{r-1}(B)+1 \right )$
instead of
$\log ^\beta \left ( \delta ^r_{r-1}(B)+1 \right )$
instead of
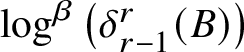 $\log ^\beta \left ( \delta ^r_{r-1}(B) \right )$
to include the case
$\log ^\beta \left ( \delta ^r_{r-1}(B) \right )$
to include the case
![]() $\delta ^r_{r-1}(B)\leq 1$
.
$\delta ^r_{r-1}(B)\leq 1$
.
Remark 2.20. If, in Theorem 2.17, A is only assumed to be a union of at most t sets of grid-complexity s, then the same bound holds with
![]() $\alpha ' := t \cdot \alpha $
(if
$\alpha ' := t \cdot \alpha $
(if
![]() $A = \bigcup _{i \in [t]} A_i$
is
$A = \bigcup _{i \in [t]} A_i$
is
![]() $K_{k,\dotsc ,k}$
-free, then each
$K_{k,\dotsc ,k}$
-free, then each
![]() $A_i$
is also
$A_i$
is also
![]() $K_{k,\dotsc ,k}$
-free, so we can apply Theorem 2.17 to each
$K_{k,\dotsc ,k}$
-free, so we can apply Theorem 2.17 to each
![]() $A_i$
and bound
$A_i$
and bound
![]() $\lvert A\rvert $
by the sum of their bounds).
$\lvert A\rvert $
by the sum of their bounds).
Definition 2.21. Let
![]() $B=B_1{{\times }\dotsb {\times }} B_r$
be a grid. We extend the definition of
$B=B_1{{\times }\dotsb {\times }} B_r$
be a grid. We extend the definition of
![]() $\delta ^r_j$
to arbitrary finite subsets of B as follows: let
$\delta ^r_j$
to arbitrary finite subsets of B as follows: let
![]() $A\subseteq B$
be a finite subset, and let
$A\subseteq B$
be a finite subset, and let
![]() $A_i :=\pi _i(A)$
,
$A_i :=\pi _i(A)$
,
![]() $i\in [r]$
, be the projections of A. We define
$i\in [r]$
, be the projections of A. We define
 $\delta ^r_j(A) :=\delta ^r_j(A_1{{\times }\dotsb {\times }} A_r)$
.
$\delta ^r_j(A) :=\delta ^r_j(A_1{{\times }\dotsb {\times }} A_r)$
.
If B is a finite r-grid and
![]() $A\subseteq B$
, then obviously
$A\subseteq B$
, then obviously
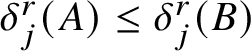 $\delta ^r_j(A)\leq \delta ^r_j(B)$
. Thus Theorem 2.17 is equivalent to the following:
$\delta ^r_j(A)\leq \delta ^r_j(B)$
. Thus Theorem 2.17 is equivalent to the following:
Proposition 2.22. For all integers
![]() $r\geq 2, s\geq 0, k\geq 2$
, there are
$r\geq 2, s\geq 0, k\geq 2$
, there are
![]() $\alpha =\alpha (r,s,k)\in \mathbb {R}$
and
$\alpha =\alpha (r,s,k)\in \mathbb {R}$
and
![]() $\beta =s\left (2^{r-1}-1\right ) \in \mathbb N$
such that for any r-grid B and
$\beta =s\left (2^{r-1}-1\right ) \in \mathbb N$
such that for any r-grid B and
![]() $K_{k,\dotsc ,k}$
-free finite subset
$K_{k,\dotsc ,k}$
-free finite subset
![]() $A \subseteq B$
of grid-complexity
$A \subseteq B$
of grid-complexity
![]() $\leq s$
, we have
$\leq s$
, we have
 $$ \begin{align*} \lvert A\rvert \leq \alpha \delta^r_{r-1}(A) \log^\beta\left(\delta^r_{r-1}(A)+1\right). \end{align*} $$
$$ \begin{align*} \lvert A\rvert \leq \alpha \delta^r_{r-1}(A) \log^\beta\left(\delta^r_{r-1}(A)+1\right). \end{align*} $$
Definition 2.23. For
![]() $r\geq 1, s\geq 0, k\geq 2$
and
$r\geq 1, s\geq 0, k\geq 2$
and
![]() $n\in \mathbb N$
, let
$n\in \mathbb N$
, let
![]() $F_{r,k}(s,n)$
be the maximal size of a
$F_{r,k}(s,n)$
be the maximal size of a
![]() $K_{k,\dotsc ,k}$
-free subset A of grid-complexity s of some r-grid B with
$K_{k,\dotsc ,k}$
-free subset A of grid-complexity s of some r-grid B with
![]() $\delta _{r-1}^r(B)\leq n$
.
$\delta _{r-1}^r(B)\leq n$
.
Then Proposition 2.22 can be restated as follows:
Proposition 2.24. For all integers
![]() $r\geq 2, s\geq 0, k\geq 2$
, there are
$r\geq 2, s\geq 0, k\geq 2$
, there are
![]() $\alpha =\alpha (r,s,k)\in \mathbb {R}$
and
$\alpha =\alpha (r,s,k)\in \mathbb {R}$
and
![]() $\beta =\beta (r,s)\in \mathbb N$
such that
$\beta =\beta (r,s)\in \mathbb N$
such that
Remark 2.25. Notice that
![]() $F_{r,k}(s,0)=0$
.
$F_{r,k}(s,0)=0$
.
In the rest of the section we prove Proposition 2.24 by induction on r, where for each r it is proved by induction on s. We will use the following simple recurrence bound:
Fact 2.26. Let
![]() $\mu \colon \mathbb N \to \mathbb N$
be a function satisfying
$\mu \colon \mathbb N \to \mathbb N$
be a function satisfying
![]() $\mu (0)=0$
and
$\mu (0)=0$
and
![]() $\mu (n)\leq 2\mu (\lfloor n/2\rfloor ) + \alpha n \log ^\beta (n+1)$
for some
$\mu (n)\leq 2\mu (\lfloor n/2\rfloor ) + \alpha n \log ^\beta (n+1)$
for some
![]() $\alpha \in \mathbb {R}$
and
$\alpha \in \mathbb {R}$
and
![]() $\beta \in \mathbb N$
. Then
$\beta \in \mathbb N$
. Then
![]() $\mu (n)\leq \alpha ' n \log ^{\beta +1} (n+1)$
for some
$\mu (n)\leq \alpha ' n \log ^{\beta +1} (n+1)$
for some
![]() $\alpha '=\alpha '(\alpha ,\beta )\in \mathbb {R}$
.
$\alpha '=\alpha '(\alpha ,\beta )\in \mathbb {R}$
.
2.3. The base case
 $r=2$
$r=2$
Let
![]() $B=B_1{\times } B_2$
be a finite grid and
$B=B_1{\times } B_2$
be a finite grid and
![]() $A\subseteq B$
a subset of grid-complexity s. We will proceed by induction on s.
$A\subseteq B$
a subset of grid-complexity s. We will proceed by induction on s.
If
![]() $s=0$
, then
$s=0$
, then
![]() $A=B_1\times B_2$
. If A is
$A=B_1\times B_2$
. If A is
![]() $K_{k,k}$
-free, then one of the sets
$K_{k,k}$
-free, then one of the sets
![]() $B_1, B_2$
must have size at most k. Hence
$B_1, B_2$
must have size at most k. Hence
 $\lvert A\rvert \leq k(\lvert B_1\rvert +\lvert B_2\rvert )=k\delta ^2_1(B)$
.
$\lvert A\rvert \leq k(\lvert B_1\rvert +\lvert B_2\rvert )=k\delta ^2_1(B)$
.
Thus
Remark 2.27. The same argument shows that
![]() $F_{r,k}(0,n) \leq k n$
for all
$F_{r,k}(0,n) \leq k n$
for all
![]() $r \geq 2$
.
$r \geq 2$
.
Assume now that the theorem is proved for
![]() $r=2$
and all
$r=2$
and all
![]() $s'<s$
. Define
$s'<s$
. Define
![]() $n_1 :=\lvert B_1\rvert $
,
$n_1 :=\lvert B_1\rvert $
,
![]() $n_2 :=\lvert B_2\rvert $
and
$n_2 :=\lvert B_2\rvert $
and
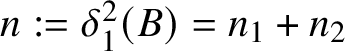 $n :=\delta ^2_1(B)=n_1+n_2$
.
$n :=\delta ^2_1(B)=n_1+n_2$
.
We choose basic sets
![]() $X_1,\dotsc , X_s \subseteq B$
such that
$X_1,\dotsc , X_s \subseteq B$
such that
![]() $A=B \cap \bigcap _{j \in [s]} X_j$
.
$A=B \cap \bigcap _{j \in [s]} X_j$
.
By Proposition 2.8, we can choose a finite linear order
![]() $(S,<)$
and functions
$(S,<)$
and functions
![]() $f_1\colon B_1\to S$
and
$f_1\colon B_1\to S$
and
![]() $f_2\colon B_2\to S$
so that
$f_2\colon B_2\to S$
so that
For
![]() $l\in S$
,
$l\in S$
,
![]() $i\in \{1,2\}$
and
$i\in \{1,2\}$
and
![]() $\square \in \{ <,=,>, \leq , \geq \}$
, let
$\square \in \{ <,=,>, \leq , \geq \}$
, let
 $$ \begin{align*} B_i^{\square l} = \left\{ b\in B_i \colon f_i(b) \square l \right\}. \end{align*} $$
$$ \begin{align*} B_i^{\square l} = \left\{ b\in B_i \colon f_i(b) \square l \right\}. \end{align*} $$
We choose
![]() $h\in S$
such that
$h\in S$
such that
 $$ \begin{align*} \left\lvert B_1^{<h}\right\rvert+\left\lvert B_2^{<h}\right\rvert \leq n/2 \text{ and } \left\lvert B_1^{>h}\right\rvert+\left\lvert B_2^{>h}\right\rvert \leq n/2. \end{align*} $$
$$ \begin{align*} \left\lvert B_1^{<h}\right\rvert+\left\lvert B_2^{<h}\right\rvert \leq n/2 \text{ and } \left\lvert B_1^{>h}\right\rvert+\left\lvert B_2^{>h}\right\rvert \leq n/2. \end{align*} $$
For example, we can take h to be the minimal element in
![]() $f_1(B_1)\cup f_2(B_2)$
with
$f_1(B_1)\cup f_2(B_2)$
with
 $ \left \lvert B_1^{\leq h}\right \rvert +\left \lvert B_2^{ \leq h}\right \rvert \geq n/2$
. Then
$ \left \lvert B_1^{\leq h}\right \rvert +\left \lvert B_2^{ \leq h}\right \rvert \geq n/2$
. Then
 $$ \begin{align*} X_s = \left[\left(B_1^{<h}\times B_2^{<h}\right) \cap X_s \right] \cup \left[ \left(B_1^{>h}\times B_2^{>h} \right) \cap X_s \right] \cup \left(B_1^{<h}\times B_2^{\geq h} \right) \cup \left(B_1^{=h}\times B_2^{>h}\right). \end{align*} $$
$$ \begin{align*} X_s = \left[\left(B_1^{<h}\times B_2^{<h}\right) \cap X_s \right] \cup \left[ \left(B_1^{>h}\times B_2^{>h} \right) \cap X_s \right] \cup \left(B_1^{<h}\times B_2^{\geq h} \right) \cup \left(B_1^{=h}\times B_2^{>h}\right). \end{align*} $$
Hence we conclude
Applying the induction hypothesis on s and using Fact 2.26 and Remark 2.25, we obtain
![]() $F_{2,k}(s,n)\leq \alpha n (\log n)^\beta $
for some
$F_{2,k}(s,n)\leq \alpha n (\log n)^\beta $
for some
![]() $\alpha =\alpha (s,k)\in \mathbb {R}$
and
$\alpha =\alpha (s,k)\in \mathbb {R}$
and
![]() $\beta =\beta (s)\in \mathbb N$
.
$\beta =\beta (s)\in \mathbb N$
.
This finishes the base case
![]() $r=2$
.
$r=2$
.
2.4. Induction step
We fix
![]() $r \in \mathbb {N}_{\geq 3}$
and assume that Proposition 2.24 holds for all pairs
$r \in \mathbb {N}_{\geq 3}$
and assume that Proposition 2.24 holds for all pairs
![]() $(r',s)$
with
$(r',s)$
with
![]() $r'<r$
and
$r'<r$
and
![]() $s \in \mathbb {N}$
.
$s \in \mathbb {N}$
.
Definition 2.28. Let
![]() $B=B_1{{\times }\dotsb {\times }} B_r$
be a finite r-grid.
$B=B_1{{\times }\dotsb {\times }} B_r$
be a finite r-grid.
-
1. For integers
 $t, u\in \mathbb N$
, we say that a subset
$t, u\in \mathbb N$
, we say that a subset
 $A\subseteq B$
is of split grid-complexity
$A\subseteq B$
is of split grid-complexity
 $(t, u)$
if there are basic sets
$(t, u)$
if there are basic sets
 $X_1,\dotsc , X_{u} \subseteq B$
, a subset
$X_1,\dotsc , X_{u} \subseteq B$
, a subset
 $A^r\subseteq B_1{{\times }\dotsb {\times }} B_{r-1}$
of grid-complexity t and a subset
$A^r\subseteq B_1{{\times }\dotsb {\times }} B_{r-1}$
of grid-complexity t and a subset
 $A_r\subseteq B_{r}$
such that
$A_r\subseteq B_{r}$
such that
 $A=(A^r\times A_r)\cap \bigcap _{i \in [u]} X_i$
.
$A=(A^r\times A_r)\cap \bigcap _{i \in [u]} X_i$
. -
2. For
 $t, u \geq 0, k\geq 2$
and
$t, u \geq 0, k\geq 2$
and
 $n\in \mathbb N$
, let
$n\in \mathbb N$
, let
 $G_{k}(t,u,n)$
be the maximal size of a
$G_{k}(t,u,n)$
be the maximal size of a
 $K_{k,\dotsc ,k}$
-free subset A of an r-grid B of split grid-complexity
$K_{k,\dotsc ,k}$
-free subset A of an r-grid B of split grid-complexity
 $(t,u)$
with
$(t,u)$
with
 $\delta _{r-1}^r(B)\leq n$
.
$\delta _{r-1}^r(B)\leq n$
.
Remark 2.29.
-
1. Note that
 $A_r$
has grid-complexity at most
$A_r$
has grid-complexity at most
 $1$
, which is the reason we do not include a parameter for the grid-complexity of
$1$
, which is the reason we do not include a parameter for the grid-complexity of
 $A_r$
in the split grid-complexity of A.
$A_r$
in the split grid-complexity of A. -
2. If
 $A\subseteq B$
is of grid-complexity s, then it is of split grid-complexity
$A\subseteq B$
is of grid-complexity s, then it is of split grid-complexity
 $(0,s)$
.
$(0,s)$
. -
3. If
 $A\subseteq B$
is of split grid-complexity
$A\subseteq B$
is of split grid-complexity
 $(t, u)$
, then it is of grid-complexity
$(t, u)$
, then it is of grid-complexity
 $t + u$
.
$t + u$
.
For the rest of the proof, we abuse notation slightly and refer to the split grid-complexity of a set as simply the grid-complexity. To complete the induction step we will prove the following proposition:
Proposition 2.30. For any integers
![]() $t,u\geq 0, k\geq 2, r \geq 3$
, there are
$t,u\geq 0, k\geq 2, r \geq 3$
, there are
![]() $\alpha ' = \alpha '(r,k,t,u)\in \mathbb {R}$
and
$\alpha ' = \alpha '(r,k,t,u)\in \mathbb {R}$
and
![]() $\beta ' = \beta '(r,k,t,u)\in \mathbb N$
such that
$\beta ' = \beta '(r,k,t,u)\in \mathbb N$
such that
We will use the following notations throughout the section:
-
•
 $B=B_1{{\times }\dotsb {\times }} B_r$
is a finite grid with
$B=B_1{{\times }\dotsb {\times }} B_r$
is a finite grid with
 $n=\delta ^r_{r-1}(B)$
;
$n=\delta ^r_{r-1}(B)$
; -
•
 $A\subseteq B$
is a subset of grid-complexity
$A\subseteq B$
is a subset of grid-complexity
 $(t,u)$
;
$(t,u)$
; -
•
 $B^r$
is the
$B^r$
is the
 $(r-1)$
-grid
$(r-1)$
-grid
 $B^r :=B_1{{\times }\dotsb {\times }} B_{r-1}$
;
$B^r :=B_1{{\times }\dotsb {\times }} B_{r-1}$
; -
•
 $A^r \subseteq B^r$
is a subset of grid-complexity t,
$A^r \subseteq B^r$
is a subset of grid-complexity t,
 $A_r \subseteq B_r$
, and
$A_r \subseteq B_r$
, and
 $X_1,\dotsc X_{u} \subseteq B$
are basic subsets such that
$X_1,\dotsc X_{u} \subseteq B$
are basic subsets such that
 $A= (A^r{\times } A_r)\cap \bigcap _{i \in [u]} X_i$
.
$A= (A^r{\times } A_r)\cap \bigcap _{i \in [u]} X_i$
.
We proceed by induction on u.
The base case
![]() $u=0$
of Proposition 2.30.
$u=0$
of Proposition 2.30.
In this case,
![]() $A=A^r\times A_r$
. If A is
$A=A^r\times A_r$
. If A is
![]() $K_{k,\dotsc ,k}$
-free, then either
$K_{k,\dotsc ,k}$
-free, then either
![]() $A^r$
is
$A^r$
is
![]() $K_{k,\dotsc ,k}$
-free or
$K_{k,\dotsc ,k}$
-free or
![]() $\lvert A_r\rvert <k$
.
$\lvert A_r\rvert <k$
.
In the first case, by the induction hypothesis on r, there are
![]() $\alpha =\alpha (r-1, t,k)$
and
$\alpha =\alpha (r-1, t,k)$
and
![]() $\beta =\beta (r-1, t)$
such that
$\beta =\beta (r-1, t)$
such that
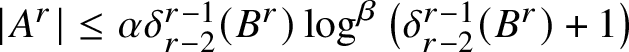 $\lvert A^r\rvert \leq \alpha \delta ^{r-1}_{r-2}(B^r)\log ^\beta \left ( \delta ^{r-1}_{r-2}(B^r)+1\right )$
. In the second case, we have
$\lvert A^r\rvert \leq \alpha \delta ^{r-1}_{r-2}(B^r)\log ^\beta \left ( \delta ^{r-1}_{r-2}(B^r)+1\right )$
. In the second case, we have
 $\lvert A\rvert \leq \lvert B^r\rvert k=\delta ^{r-1}_{r-1}(B^r)k$
.
$\lvert A\rvert \leq \lvert B^r\rvert k=\delta ^{r-1}_{r-1}(B^r)k$
.
Since
 $n=\delta ^r_{r-1}(B)=\delta ^{r-1}_{r-1}(B^r)+\delta ^{r-1}_{r-2}(B^r) \lvert B_r\rvert $
, the conclusion of the proposition follows with
$n=\delta ^r_{r-1}(B)=\delta ^{r-1}_{r-1}(B^r)+\delta ^{r-1}_{r-2}(B^r) \lvert B_r\rvert $
, the conclusion of the proposition follows with
![]() $\alpha ' := \alpha , \beta ' := \beta $
.
$\alpha ' := \alpha , \beta ' := \beta $
.
Induction step of Proposition 2.30.
We assume now that the proposition holds for all pairs
![]() $(t,u')$
with
$(t,u')$
with
![]() $u'<u$
and
$u'<u$
and
![]() $t \in \mathbb {N}$
.
$t \in \mathbb {N}$
.
Given a tuple
![]() $x = (x_1, \dotsc , x_r) \in B$
, we set
$x = (x_1, \dotsc , x_r) \in B$
, we set
![]() $x^r := (x_1, \dotsc , x_{r-1})$
. By Proposition 2.8, we can choose a finite linear order
$x^r := (x_1, \dotsc , x_{r-1})$
. By Proposition 2.8, we can choose a finite linear order
![]() $(S,<)$
, a coordinate-wise monotone function
$(S,<)$
, a coordinate-wise monotone function
![]() $f^r\colon B^r\to S$
and a function
$f^r\colon B^r\to S$
and a function
![]() $f_r\colon B_r\to S$
so that
$f_r\colon B_r\to S$
so that
Moreover, by Remark 2.9 we may assume without loss of generality that the coordinate-wise monotone function defining
![]() $X_u$
is given by
$X_u$
is given by
Definition 2.31. Given an arbitrary set
![]() $C^r \subseteq B^r$
, we say that a set
$C^r \subseteq B^r$
, we say that a set
![]() $H^r \subseteq C^r$
is an
$H^r \subseteq C^r$
is an
![]() $f^r$
-strip in
$f^r$
-strip in
![]() $C^r$
if
$C^r$
if
for some
![]() $l_1,l_2\in S$
,
$l_1,l_2\in S$
,
![]() $\triangleleft _1, \triangleleft _2\in \{ <,\leq \}$
. Likewise, given an arbitrary set
$\triangleleft _1, \triangleleft _2\in \{ <,\leq \}$
. Likewise, given an arbitrary set
![]() $C_r \subseteq B_r$
, we say that
$C_r \subseteq B_r$
, we say that
![]() $H_r \subseteq C_r$
is an
$H_r \subseteq C_r$
is an
![]() $f_r$
-strip in
$f_r$
-strip in
![]() $C_r$
if
$C_r$
if
for some
![]() $l_1,l_2\in S$
,
$l_1,l_2\in S$
,
![]() $\triangleleft _1, \triangleleft _2\in \{ <,\leq \}$
. If
$\triangleleft _1, \triangleleft _2\in \{ <,\leq \}$
. If
![]() $C^r = A^r$
or
$C^r = A^r$
or
![]() $C_r = A_r$
, we simply say an
$C_r = A_r$
, we simply say an
![]() $f^r$
-strip or
$f^r$
-strip or
![]() $f_r$
-strip, respectively.
$f_r$
-strip, respectively.
Remark 2.32. Note the following:
-
1.
 $A^r$
is an
$A^r$
is an
 $f^r$
-strip, and
$f^r$
-strip, and
 $A_r$
is an
$A_r$
is an
 $f_r$
-strip.
$f_r$
-strip. -
2. Every
 $f^r$
-strip is a subset of the
$f^r$
-strip is a subset of the
 $(r-1)$
-grid
$(r-1)$
-grid
 $B^r$
of grid-complexity
$B^r$
of grid-complexity
 $t+2$
(using Remark 2.7).
$t+2$
(using Remark 2.7). -
3. The intersection of any two
 $f^r$
-strips is an
$f^r$
-strips is an
 $f^r$
-strip; the same conclusion holds for
$f^r$
-strip; the same conclusion holds for
 $f_r$
-strips.
$f_r$
-strips.
Definition 2.33.
-
1. We say that a subset
 $H\subseteq B$
is an f-grid if
$H\subseteq B$
is an f-grid if
 $H=H^r\times H_r$
, where
$H=H^r\times H_r$
, where
 $H^r\subseteq B^r$
is an
$H^r\subseteq B^r$
is an
 $f^r$
-strip in
$f^r$
-strip in
 $B^r$
and
$B^r$
and
 $H_r \subseteq B_r$
is an
$H_r \subseteq B_r$
is an
 $f_r$
-strip in
$f_r$
-strip in
 $B_r$
.
$B_r$
. -
2. If
 $H=H^r\times H_r$
is an f-grid, we set Note that if H is a sub-grid of B, then
$H=H^r\times H_r$
is an f-grid, we set Note that if H is a sub-grid of B, then $$ \begin{align*} \Delta(H) :=\lvert H^r\rvert + \delta^{r-1}_{r-2}(H^r)\lvert H_r\rvert \text{ (see Definition~2.21 for } \delta^{r-1}_{r-2}). \end{align*} $$
$$ \begin{align*} \Delta(H) :=\lvert H^r\rvert + \delta^{r-1}_{r-2}(H^r)\lvert H_r\rvert \text{ (see Definition~2.21 for } \delta^{r-1}_{r-2}). \end{align*} $$
 $\Delta (H)=\delta ^r_{r-1}(H)$
.
$\Delta (H)=\delta ^r_{r-1}(H)$
.
-
3. For an f-grid H, we will denote by
 $A_H$
the set
$A_H$
the set
 $A\cap H$
.
$A\cap H$
.
The induction step for Proposition 2.30 will follow from the following proposition:
Proposition 2.34. For all integers
![]() $k\geq 2, r \geq 3$
, there are
$k\geq 2, r \geq 3$
, there are
![]() $\alpha ' = \alpha '(r,k,t,u)\in \mathbb {R}$
and
$\alpha ' = \alpha '(r,k,t,u)\in \mathbb {R}$
and
![]() $\beta '=\beta '(r,t,u) \in \mathbb N$
such that, for any f-grid H, if the set
$\beta '=\beta '(r,t,u) \in \mathbb N$
such that, for any f-grid H, if the set
![]() $A_H$
is
$A_H$
is
![]() $K_{k,\dotsc ,k}$
-free then
$K_{k,\dotsc ,k}$
-free then
We should stress that in this proposition,
![]() $\alpha '$
and
$\alpha '$
and
![]() $\beta '$
do not depend on
$\beta '$
do not depend on
![]() $f^r, f_r$
, B,
$f^r, f_r$
, B,
![]() $A^r$
, and
$A^r$
, and
![]() $A_r$
, but they may depend on our fixed t and u.
$A_r$
, but they may depend on our fixed t and u.
Given Proposition 2.34, we can apply it to the f-grid
![]() $H := A^r\times A_r$
(so
$H := A^r\times A_r$
(so
![]() $A_H = A$
) and get
$A_H = A$
) and get
It is easy to see that
![]() $\Delta (A^r\times A_r)\leq \delta ^r_{r-1}(B)$
, and hence Proposition 2.30 follows with the same
$\Delta (A^r\times A_r)\leq \delta ^r_{r-1}(B)$
, and hence Proposition 2.30 follows with the same
![]() $\alpha '$
and
$\alpha '$
and
![]() $\beta '$
.
$\beta '$
.
We proceed with the proof of Proposition 2.34:
Proof of Proposition 2.34. Fix
![]() $m\in \mathbb N$
, and let
$m\in \mathbb N$
, and let
![]() $L(m)$
be the maximal size of a
$L(m)$
be the maximal size of a
![]() $K_{k,\dotsc ,k}$
-free set
$K_{k,\dotsc ,k}$
-free set
![]() $A_H$
among all f-grids
$A_H$
among all f-grids
![]() $H \subseteq B$
with
$H \subseteq B$
with
![]() $\Delta (H)\leq m$
. We need to show that for some
$\Delta (H)\leq m$
. We need to show that for some
![]() $\alpha '=\alpha '(k)\in \mathbb {R}$
and
$\alpha '=\alpha '(k)\in \mathbb {R}$
and
![]() $\beta ' \in \mathbb N$
we have
$\beta ' \in \mathbb N$
we have
Let
![]() $H=H^r\times H_r$
be an f-grid with
$H=H^r\times H_r$
be an f-grid with
![]() $\Delta (H)\leq m$
.
$\Delta (H)\leq m$
.
For
![]() $l\in S$
and
$l\in S$
and
![]() $\square \in \{ <,=,>, \leq , \geq \}$
, define
$\square \in \{ <,=,>, \leq , \geq \}$
, define
and
Note that for every
![]() $l \in S$
,
$l \in S$
,
![]() $H^{r,\square l}$
is an
$H^{r,\square l}$
is an
![]() $f^r$
-strip in
$f^r$
-strip in
![]() $H^r$
,
$H^r$
,
![]() $H_r^{\square l}$
is an
$H_r^{\square l}$
is an
![]() $f_r$
-strip in
$f_r$
-strip in
![]() $H_r$
and their product is an f-grid.
$H_r$
and their product is an f-grid.
Claim 2.35. There is
![]() $h\in S$
such that
$h\in S$
such that
 $$ \begin{align*} \Delta\left(H^{r,<h}\times H_r^{<h}\right) \leq m/2 \text{ and } \Delta\left(H^{r,>h}\times H_r^{>h}\right) \leq m/2.\end{align*} $$
$$ \begin{align*} \Delta\left(H^{r,<h}\times H_r^{<h}\right) \leq m/2 \text{ and } \Delta\left(H^{r,>h}\times H_r^{>h}\right) \leq m/2.\end{align*} $$
Proof. Set
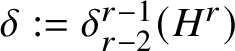 $\delta :=\delta ^{r-1}_{r-2}(H^r)$
.
$\delta :=\delta ^{r-1}_{r-2}(H^r)$
.
Let h be the minimal element in
![]() $f^r(H^r)\cup f_r(H_r)$
with
$f^r(H^r)\cup f_r(H_r)$
with
 $$ \begin{align*} \left\lvert H^{r,\leq h }\right\rvert+\delta \left\lvert H_r^{\leq h}\right\rvert \geq m/2.\end{align*} $$
$$ \begin{align*} \left\lvert H^{r,\leq h }\right\rvert+\delta \left\lvert H_r^{\leq h}\right\rvert \geq m/2.\end{align*} $$
Then
 $ \left \lvert H^{r,< h }\right \rvert +\delta \left \lvert H_r^{< h}\right \rvert \leq m/2$
and
$ \left \lvert H^{r,< h }\right \rvert +\delta \left \lvert H_r^{< h}\right \rvert \leq m/2$
and
 $ \left \lvert H^{r,> h }\right \rvert +\delta \left \lvert H_r^{> h}\right \rvert \leq m/2$
. Since
$ \left \lvert H^{r,> h }\right \rvert +\delta \left \lvert H_r^{> h}\right \rvert \leq m/2$
. Since
![]() $H^{r,< h}, H^{r,> h} \subseteq H^r$
, we have
$H^{r,< h}, H^{r,> h} \subseteq H^r$
, we have
 $\delta ^{r-1}_{r-2}\left (H^{r,< h}\right ), \delta ^{r-1}_{r-2}\left (H^{r,> h}\right ) \leq \delta $
. The claim follows.
$\delta ^{r-1}_{r-2}\left (H^{r,< h}\right ), \delta ^{r-1}_{r-2}\left (H^{r,> h}\right ) \leq \delta $
. The claim follows.
Let h be as in the claim. It is not hard to see that the following hold:
 $$ \begin{gather*} \left( H^{r, \leq h} \times H_r^{\geq h} \right) \cap X_u = \left( H^{r, < h} \times H_{r}^{\geq h} \right) \cup \left( H^{r, =h} \times H_r^{>h} \right),\\ \left( H^{r, \geq h} \times H_r^{\leq h} \right) \cap X_u = \emptyset. \end{gather*} $$
$$ \begin{gather*} \left( H^{r, \leq h} \times H_r^{\geq h} \right) \cap X_u = \left( H^{r, < h} \times H_{r}^{\geq h} \right) \cup \left( H^{r, =h} \times H_r^{>h} \right),\\ \left( H^{r, \geq h} \times H_r^{\leq h} \right) \cap X_u = \emptyset. \end{gather*} $$
It follows that
 $$ \begin{align*} A_H \cap X_u = \left[\left(H^{r,<h}\times H_r^{<h}\right) \cap X_u \right] \cup \left[\left(H^{r,>h}\times H_r^{>h}\right) \cap X_u \right] \cup \left(H^{r,<h}\times H_r^{\geq h}\right) \cup \left(H^{r,=h}\times H_r^{>h}\right). \end{align*} $$
$$ \begin{align*} A_H \cap X_u = \left[\left(H^{r,<h}\times H_r^{<h}\right) \cap X_u \right] \cup \left[\left(H^{r,>h}\times H_r^{>h}\right) \cap X_u \right] \cup \left(H^{r,<h}\times H_r^{\geq h}\right) \cup \left(H^{r,=h}\times H_r^{>h}\right). \end{align*} $$
Hence, by the choice of h and using Remark 2.32(2),
Applying the induction hypothesis on u and using Fact 2.26, we obtain
![]() $L(m)\leq \alpha ' m \log ^{\beta '}(m+1)$
for some
$L(m)\leq \alpha ' m \log ^{\beta '}(m+1)$
for some
![]() $\alpha '=\alpha '(k)\in \mathbb {R}$
and
$\alpha '=\alpha '(k)\in \mathbb {R}$
and
![]() $\beta '\in \mathbb N$
.
$\beta '\in \mathbb N$
.
This finishes the proof of Proposition 2.34, and hence of the induction step of Proposition 2.24.
Finally, inspecting the proof, we have shown the following:
-
1.
 $\beta (2,s) \leq s$
for all
$\beta (2,s) \leq s$
for all
 $s \in \mathbb {N}$
.
$s \in \mathbb {N}$
. -
2.
 $\beta '(r,t, 0) \leq \beta (r-1,t)$
for all
$\beta '(r,t, 0) \leq \beta (r-1,t)$
for all
 $r \geq 3$
and
$r \geq 3$
and
 $t \in \mathbb {N}$
.
$t \in \mathbb {N}$
. -
3.
 $\beta '(r,t,u) \leq \beta '(r, t+2, u-1) + 1$
for all
$\beta '(r,t,u) \leq \beta '(r, t+2, u-1) + 1$
for all
 $r \geq 3, t \geq 0, u \geq 1$
.
$r \geq 3, t \geq 0, u \geq 1$
.
Iterating (3), for every
![]() $r \geq 3, s \geq 1$
we have
$r \geq 3, s \geq 1$
we have
![]() $\beta (r,s) \leq \beta '(r,0,s) \leq \beta '(r, 2s, 0) + s$
. Hence, by (2),
$\beta (r,s) \leq \beta '(r,0,s) \leq \beta '(r, 2s, 0) + s$
. Hence, by (2),
![]() $\beta (r,s) \leq \beta (r-1, 2s) + s$
for every
$\beta (r,s) \leq \beta (r-1, 2s) + s$
for every
![]() $r \geq 3$
and
$r \geq 3$
and
![]() $s \geq 1$
. Iterating this, we get
$s \geq 1$
. Iterating this, we get
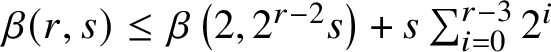 $\beta (r,s) \leq \beta \left (2, 2^{r-2}s\right ) + s \sum _{i=0}^{r-3}2^i$
. Using (1), this implies
$\beta (r,s) \leq \beta \left (2, 2^{r-2}s\right ) + s \sum _{i=0}^{r-3}2^i$
. Using (1), this implies
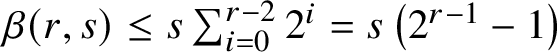 $\beta (r,s) \leq s \sum _{i=0}^{r-2}2^i = s\left (2^{r-1}-1\right )$
for all
$\beta (r,s) \leq s \sum _{i=0}^{r-2}2^i = s\left (2^{r-1}-1\right )$
for all
![]() $r \geq 3, s \geq 1$
. Hence, by Remark 2.27 and (1) again,
$r \geq 3, s \geq 1$
. Hence, by Remark 2.27 and (1) again,
![]() $\beta (r,s) \leq s\left (2^{r-1}-1\right )$
for all
$\beta (r,s) \leq s\left (2^{r-1}-1\right )$
for all
![]() $r \geq 2, s \geq 0$
.
$r \geq 2, s \geq 0$
.
2.5. Some applications
We observe several immediate applications of Theorem 2.17, starting with the following bound for semilinear hypergraphs:
Corollary 2.36. For every
![]() $r,s,t,k \in \mathbb {N}, r \geq 2$
, there exist some
$r,s,t,k \in \mathbb {N}, r \geq 2$
, there exist some
![]() $\alpha =\alpha (r,s,t,k)\in \mathbb {R}$
and
$\alpha =\alpha (r,s,t,k)\in \mathbb {R}$
and
![]() $\beta (r,s) := s\left (2^{r-1}-1\right )$
satisfying the following: for any semilinear
$\beta (r,s) := s\left (2^{r-1}-1\right )$
satisfying the following: for any semilinear
![]() $K_{k, \dotsc , k}$
-free r-hypergraph
$K_{k, \dotsc , k}$
-free r-hypergraph
![]() $H = (V_1, \dotsc , V_r;E)$
of description complexity
$H = (V_1, \dotsc , V_r;E)$
of description complexity
![]() $(s,t)$
(see Definition 1.7), taking
$(s,t)$
(see Definition 1.7), taking
![]() $V:= \prod _{i \in [r]}V_i$
we have
$V:= \prod _{i \in [r]}V_i$
we have
 $$ \begin{align*} \lvert E\rvert \leq \alpha \delta^r_{r-1}(V) \log^\beta \left( \delta^r_{r-1}(V)+1 \right). \end{align*} $$
$$ \begin{align*} \lvert E\rvert \leq \alpha \delta^r_{r-1}(V) \log^\beta \left( \delta^r_{r-1}(V)+1 \right). \end{align*} $$
Proof. By assumption, the edge relation E can be defined by a union of t sets, each of which is defined by s linear equalities and inequalities, hence of grid-complexity
![]() $\leq s$
(see Example 2.13). The conclusion follows by Theorem 2.17 and Remark 2.20.
$\leq s$
(see Example 2.13). The conclusion follows by Theorem 2.17 and Remark 2.20.
As a special case with
![]() $r=2$
, this implies a bound for the following incidence problem:
$r=2$
, this implies a bound for the following incidence problem:
Corollary 2.37. For every
![]() $s,k \in \mathbb {N}$
there exists some
$s,k \in \mathbb {N}$
there exists some
![]() $\alpha =\alpha (s,k)\in \mathbb {R}$
satisfying the following:
$\alpha =\alpha (s,k)\in \mathbb {R}$
satisfying the following:
Let
![]() $d \in \mathbb {N}$
and
$d \in \mathbb {N}$
and
![]() $H_1, \dotsc , H_s \subseteq \mathbb {R}^d$
be finitely many (closed or open) half-spaces in
$H_1, \dotsc , H_s \subseteq \mathbb {R}^d$
be finitely many (closed or open) half-spaces in
![]() $\mathbb {R}^d$
. Let
$\mathbb {R}^d$
. Let
![]() $\mathcal {F}$
be the (infinite) family of all possible polytopes in
$\mathcal {F}$
be the (infinite) family of all possible polytopes in
![]() $\mathbb {R}^d$
cut out by arbitrary translates of
$\mathbb {R}^d$
cut out by arbitrary translates of
![]() $H_1, \dotsc , H_s$
.
$H_1, \dotsc , H_s$
.
For any set P of
![]() $n_1$
points in
$n_1$
points in
![]() $\mathbb {R}^d$
and any set F of
$\mathbb {R}^d$
and any set F of
![]() $n_2$
polytopes in
$n_2$
polytopes in
![]() $\mathcal {F}$
, if the incidence graph on
$\mathcal {F}$
, if the incidence graph on
![]() $P \times F$
is
$P \times F$
is
![]() $K_{k,k}$
-free, then it contains at most
$K_{k,k}$
-free, then it contains at most
![]() $\alpha n \log ^{s} n$
incidences.
$\alpha n \log ^{s} n$
incidences.
Proof. We can write
 $$ \begin{align*}H_i = \left\{\bar{x} = (x_1, \dotsc, x_d) \in \mathbb{R}^d : \sum_{j \in [d]} a_{i,j} x_j \square_i b_i \right\},\end{align*} $$
$$ \begin{align*}H_i = \left\{\bar{x} = (x_1, \dotsc, x_d) \in \mathbb{R}^d : \sum_{j \in [d]} a_{i,j} x_j \square_i b_i \right\},\end{align*} $$
where
![]() $a_{i,j},b_i \in \mathbb {R}$
and
$a_{i,j},b_i \in \mathbb {R}$
and
![]() $\square _i \in \{>, \geq \}$
for
$\square _i \in \{>, \geq \}$
for
![]() $i \in [s], j \in [d]$
depending on whether
$i \in [s], j \in [d]$
depending on whether
![]() $H_i$
is an open or a closed half-space.
$H_i$
is an open or a closed half-space.
Every polytope
![]() $F \in \mathcal {F}$
is of the form
$F \in \mathcal {F}$
is of the form
![]() $\bigcap _{i \in [s]} (\bar {y}_i + H_i)$
for some
$\bigcap _{i \in [s]} (\bar {y}_i + H_i)$
for some
![]() $(\bar {y}_1, \dotsc , \bar {y}_s) \in \mathbb {R}^{sd}$
, where
$(\bar {y}_1, \dotsc , \bar {y}_s) \in \mathbb {R}^{sd}$
, where
![]() $\bar {y}_i + H_i$
is the translate of
$\bar {y}_i + H_i$
is the translate of
![]() $H_i$
by the vector
$H_i$
by the vector
![]() $\bar {y}_i = \left (y_{i,1}, \dotsc , y_{i,d}\right ) \in \mathbb {R}^d$
– that is,
$\bar {y}_i = \left (y_{i,1}, \dotsc , y_{i,d}\right ) \in \mathbb {R}^d$
– that is,
 $$ \begin{align*}\bar{y}_i + H_i = \left\{ \bar{x} \in \mathbb{R}^d : \sum_{j \in [d]} a_{i,j} x_j + \sum_{j \in [d]}\left(-a_{i,j}\right)y_j \square_i b_i \right\}.\end{align*} $$
$$ \begin{align*}\bar{y}_i + H_i = \left\{ \bar{x} \in \mathbb{R}^d : \sum_{j \in [d]} a_{i,j} x_j + \sum_{j \in [d]}\left(-a_{i,j}\right)y_j \square_i b_i \right\}.\end{align*} $$
Then the incidence relation between points in
![]() $\mathbb {R}^d$
and polytopes in
$\mathbb {R}^d$
and polytopes in
![]() $\mathcal {F}$
can be identified with the semilinear set
$\mathcal {F}$
can be identified with the semilinear set
 $$ \begin{align*}\left\{ \left(\bar{x}; \left(y_{i,j}\right)_{i \in [s], j \in [d]} \right) \in \mathbb{R}^d \times \mathbb{R}^{sd} : \bigwedge_{i \in [s]} \sum_{j \in [d]} a_{i,j} x_j + \sum_{j \in [d]}\left(-a_{i,j}\right)y_{i,j} \square_i b_i \right\}\end{align*} $$
$$ \begin{align*}\left\{ \left(\bar{x}; \left(y_{i,j}\right)_{i \in [s], j \in [d]} \right) \in \mathbb{R}^d \times \mathbb{R}^{sd} : \bigwedge_{i \in [s]} \sum_{j \in [d]} a_{i,j} x_j + \sum_{j \in [d]}\left(-a_{i,j}\right)y_{i,j} \square_i b_i \right\}\end{align*} $$
defined by s linear inequalities. The conclusion now follows by Corollary 2.36 with
![]() $r=2$
.
$r=2$
.
In particular, we get a bound for the original question that motivated this paper.
Corollary 2.38. Let
![]() $\mathcal {F}_d$
be the family of all (closed or open) boxes in
$\mathcal {F}_d$
be the family of all (closed or open) boxes in
![]() $\mathbb {R}^d$
. Then for every k there exists some
$\mathbb {R}^d$
. Then for every k there exists some
![]() $\alpha = \alpha (d,k)$
satisfying the following: for any set P of
$\alpha = \alpha (d,k)$
satisfying the following: for any set P of
![]() $n_1$
points in
$n_1$
points in
![]() $\mathbb {R}^d$
and any set F of
$\mathbb {R}^d$
and any set F of
![]() $n_2$
boxes in
$n_2$
boxes in
![]() $\mathcal {F}_d$
, if the incidence graph on
$\mathcal {F}_d$
, if the incidence graph on
![]() $P \times F$
is
$P \times F$
is
![]() $K_{k,k}$
-free, then it contains at most
$K_{k,k}$
-free, then it contains at most
![]() $\alpha n \log ^{2 d} n $
incidences.
$\alpha n \log ^{2 d} n $
incidences.
Proof. This is immediate from Corollary 2.37, since we have
![]() $2d$
half-spaces in
$2d$
half-spaces in
![]() $\mathbb {R}^d$
such that every box in
$\mathbb {R}^d$
such that every box in
![]() $\mathbb {R}^d$
is cut out by the intersection of their translates.
$\mathbb {R}^d$
is cut out by the intersection of their translates.
3. Lower bounds
While we do not know if the bound
![]() $\beta (2,s) \leq s$
in Theorem 2.17 is optimal, in this section we show that at least the logarithmic factor is unavoidable already for the incidence relation between points and dyadic boxes in
$\beta (2,s) \leq s$
in Theorem 2.17 is optimal, in this section we show that at least the logarithmic factor is unavoidable already for the incidence relation between points and dyadic boxes in
![]() $\mathbb {R}^2$
.
$\mathbb {R}^2$
.
We describe a slightly more general construction first. Fix
![]() $d \in \mathbb {N}_{>0}$
.
$d \in \mathbb {N}_{>0}$
.
Definition 3.1. Given finite tuples
![]() $\bar {p}=(p_1, \dotsc , p_{n}), \bar {q}=(q_1, \dotsc ,q_n)$
and
$\bar {p}=(p_1, \dotsc , p_{n}), \bar {q}=(q_1, \dotsc ,q_n)$
and
![]() $\bar {r}=(r_1, \dotsc , r_m)$
with
$\bar {r}=(r_1, \dotsc , r_m)$
with
![]() $p_i,q_i,r_i \in \mathbb {R}^d$
– say
$p_i,q_i,r_i \in \mathbb {R}^d$
– say
![]() $p_i = \left (p_{i,1}, \dotsc , p_{i,d}\right ), q_i = \left (q_{i,1}, \dotsc , q_{i,d}\right ), r_i = \left (r_{i,1}, \dotsc , r_{i,d}\right )$
– we say that
$p_i = \left (p_{i,1}, \dotsc , p_{i,d}\right ), q_i = \left (q_{i,1}, \dotsc , q_{i,d}\right ), r_i = \left (r_{i,1}, \dotsc , r_{i,d}\right )$
– we say that
![]() $\bar {p}$
and
$\bar {p}$
and
![]() $\bar {q}$
have the same order-type over
$\bar {q}$
have the same order-type over
![]() $\bar {r}$
if
$\bar {r}$
if
 $$ \begin{gather*} p_{i,j} \square p_{i',j'} \iff q_{i,j} \square q_{i',j'} \text{ and} \\ p_{i,j} \square r_{k,j'} \iff q_{i,j} \square r_{k,j'} \end{gather*} $$
$$ \begin{gather*} p_{i,j} \square p_{i',j'} \iff q_{i,j} \square q_{i',j'} \text{ and} \\ p_{i,j} \square r_{k,j'} \iff q_{i,j} \square r_{k,j'} \end{gather*} $$
for all
![]() $\square \in \{<,>,= \}$
,
$\square \in \{<,>,= \}$
,
![]() $1 \leq i,i' \leq n, 1 \leq j,j' \leq d$
and
$1 \leq i,i' \leq n, 1 \leq j,j' \leq d$
and
![]() $1 \leq k \leq m$
.
$1 \leq k \leq m$
.
In other words, the tuples
![]() $\left (p_{i,j} : 1 \leq i \leq n, 1\leq j \leq d\right )$
and
$\left (p_{i,j} : 1 \leq i \leq n, 1\leq j \leq d\right )$
and
![]() $\left (q_{i,j} : 1 \leq i \leq n, 1\leq j \leq d\right )$
have the same quantifier-free type over the set
$\left (q_{i,j} : 1 \leq i \leq n, 1\leq j \leq d\right )$
have the same quantifier-free type over the set
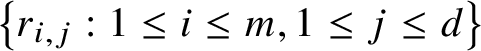 $\left \{r_{i,j} : 1 \leq i \leq m, 1 \leq j \leq d \right \}$
in the structure
$\left \{r_{i,j} : 1 \leq i \leq m, 1 \leq j \leq d \right \}$
in the structure
![]() $(\mathbb {R}, <)$
.
$(\mathbb {R}, <)$
.
Remark 3.2. Assume that
![]() $P =\{ p_1, \dotsc , p_{n} \} \subseteq \mathbb {R}^d$
is a finite set of points and B is a finite set of d-dimensional open boxes with axis-parallel sides, with I incidences between P and B.
$P =\{ p_1, \dotsc , p_{n} \} \subseteq \mathbb {R}^d$
is a finite set of points and B is a finite set of d-dimensional open boxes with axis-parallel sides, with I incidences between P and B.
-
1. By perturbing P and B slightly, we may assume that for every
 $1 \leq j \leq d$
, all points in P have pairwise distinct jth coordinates
$1 \leq j \leq d$
, all points in P have pairwise distinct jth coordinates
 $p_{1,j}, \dotsc , p_{n,j}$
, and none of the points in P belongs to the border of any of the boxes in B, while the incidence graph between P and B remains unchanged.
$p_{1,j}, \dotsc , p_{n,j}$
, and none of the points in P belongs to the border of any of the boxes in B, while the incidence graph between P and B remains unchanged. -
2. Let
 $\bar {r}$
be the tuple listing all corners of all boxes in B. If
$\bar {r}$
be the tuple listing all corners of all boxes in B. If
 $P' = \left \{p^{\prime }_1, \dotsc , p^{\prime }_n\right \} \subseteq \mathbb {R}^d$
is an arbitrary set of points with the same order-type as P over
$P' = \left \{p^{\prime }_1, \dotsc , p^{\prime }_n\right \} \subseteq \mathbb {R}^d$
is an arbitrary set of points with the same order-type as P over
 $\bar {r}$
, then the incidence graph on
$\bar {r}$
, then the incidence graph on
 $P \times B$
is isomorphic to the incidence graph on
$P \times B$
is isomorphic to the incidence graph on
 $P' \times B$
.
$P' \times B$
.
We have the following lemma for combining point-box incidence configurations in a higher-dimensional space:
Lemma 3.3. Given any
![]() $d,n_1,n_2,n^{\prime }_1, n^{\prime }_2, m,m' \in \mathbb {N}_{>0}$
, assume that:
$d,n_1,n_2,n^{\prime }_1, n^{\prime }_2, m,m' \in \mathbb {N}_{>0}$
, assume that:
-
1. there exists a set of points
 $P^{d-1} \subseteq \mathbb {R}^{d-1}$
with
$P^{d-1} \subseteq \mathbb {R}^{d-1}$
with
 $\left \lvert P^{d-1}\right \rvert = n_1$
and a set of
$\left \lvert P^{d-1}\right \rvert = n_1$
and a set of
 $(d-1)$
-dimensional boxes
$(d-1)$
-dimensional boxes
 $B^{d-1}$
with
$B^{d-1}$
with
 $\left \lvert B^{d-1}\right \rvert = n_2$
, with m incidences between them and the incidence graph
$\left \lvert B^{d-1}\right \rvert = n_2$
, with m incidences between them and the incidence graph
 $K_{2,2}$
-free; and
$K_{2,2}$
-free; and -
2. there exists a set of points
 $P^d \subseteq \mathbb {R}^d$
with
$P^d \subseteq \mathbb {R}^d$
with
 $\left \lvert P^d\right \rvert = n^{\prime }_1$
and a set of d-dimensional boxes
$\left \lvert P^d\right \rvert = n^{\prime }_1$
and a set of d-dimensional boxes
 $B^d$
with
$B^d$
with
 $\left \lvert B^d\right \rvert =n^{\prime }_2$
, with
$\left \lvert B^d\right \rvert =n^{\prime }_2$
, with
 $m'$
incidences between them and the incidence graph
$m'$
incidences between them and the incidence graph
 $K_{2,2}$
-free.
$K_{2,2}$
-free.
Then there exists a set of points
![]() $P \subseteq \mathbb {R}^d$
with
$P \subseteq \mathbb {R}^d$
with
![]() $\lvert P\rvert = n_1 n^{\prime }_1$
and a set of d-dimensional boxes B with
$\lvert P\rvert = n_1 n^{\prime }_1$
and a set of d-dimensional boxes B with
![]() $\lvert B\rvert = n_1n^{\prime }_2+n^{\prime }_1n_2$
, so that there are
$\lvert B\rvert = n_1n^{\prime }_2+n^{\prime }_1n_2$
, so that there are
![]() $n_1m' + m n^{\prime }_1$
incidences between P and B and their incidence graph is still
$n_1m' + m n^{\prime }_1$
incidences between P and B and their incidence graph is still
![]() $K_{2,2}$
-free.
$K_{2,2}$
-free.
Proof. By Remark 3.2(1) we may assume that for every
![]() $1 \leq j \leq d$
, all points in
$1 \leq j \leq d$
, all points in
![]() $P^d$
have pairwise distinct jth coordinates; for every
$P^d$
have pairwise distinct jth coordinates; for every
![]() $1 \leq j \leq d-1$
, all points in
$1 \leq j \leq d-1$
, all points in
![]() $P^{d-1}$
have pairwise distinct jth coordinates; and none of the points is on the border of any of the boxes. Write
$P^{d-1}$
have pairwise distinct jth coordinates; and none of the points is on the border of any of the boxes. Write
![]() $P^{d-1}$
as
$P^{d-1}$
as
![]() $p_1, \dotsc , p_{n_1}$
. Let
$p_1, \dotsc , p_{n_1}$
. Let
![]() $\bar {r}$
be the tuple listing all corners of all boxes in
$\bar {r}$
be the tuple listing all corners of all boxes in
![]() $B^{d-1}$
.
$B^{d-1}$
.
Using this, for each
![]() $p_i$
we can choose a very small
$p_i$
we can choose a very small
![]() $(d-1)$
-dimensional box
$(d-1)$
-dimensional box
![]() $\beta _i$
with
$\beta _i$
with
![]() $p_i \in \beta _{i}$
and such that for any choice of points
$p_i \in \beta _{i}$
and such that for any choice of points
![]() $p^{\prime }_i \in \beta _i, 1 \leq i \leq n_1$
, we have that
$p^{\prime }_i \in \beta _i, 1 \leq i \leq n_1$
, we have that
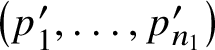 $\left (p^{\prime }_1, \dotsc , p^{\prime }_{n_1}\right )$
has the same order-type as
$\left (p^{\prime }_1, \dotsc , p^{\prime }_{n_1}\right )$
has the same order-type as
![]() $(p_1, \dotsc , p_{n_1})$
over
$(p_1, \dotsc , p_{n_1})$
over
![]() $\bar {r}$
. In particular, every
$\bar {r}$
. In particular, every
![]() $\beta _i$
is pairwise disjoint, and the incidence graph between
$\beta _i$
is pairwise disjoint, and the incidence graph between
![]() $P^{d-1}$
and
$P^{d-1}$
and
![]() $B^{d-1}$
is isomorphic to the incidence graph between
$B^{d-1}$
is isomorphic to the incidence graph between
 $\left (p^{\prime }_i, \dotsc , p^{\prime }_{n_1}\right )$
and
$\left (p^{\prime }_i, \dotsc , p^{\prime }_{n_1}\right )$
and
![]() $B^{d-1}$
by Remark 3.2(2).
$B^{d-1}$
by Remark 3.2(2).
Contracting and translating while keeping the dth coordinate unchanged, for each
![]() $1 \leq i \leq n_1$
we can find a copy
$1 \leq i \leq n_1$
we can find a copy
 $\left (P^{d}_i, B^d_i\right )$
of the configuration
$\left (P^{d}_i, B^d_i\right )$
of the configuration
![]() $\left (P^d, B^d\right )$
entirely contained in the box
$\left (P^d, B^d\right )$
entirely contained in the box
![]() $\beta _i \times \mathbb {R}$
– that is,
$\beta _i \times \mathbb {R}$
– that is,
-
• all points in
 $P^{d}_i$
and boxes in
$P^{d}_i$
and boxes in
 $ B^d_i$
are contained in
$ B^d_i$
are contained in
 $\beta _i \times \mathbb {R}$
;
$\beta _i \times \mathbb {R}$
; -
• the incidence graph on
 $\left (P^{d}_i, B^d_i\right )$
is isomorphic to the incidence graph on
$\left (P^{d}_i, B^d_i\right )$
is isomorphic to the incidence graph on
 $\left (P^{d}, B^d\right )$
; and
$\left (P^{d}, B^d\right )$
; and -
• for all i, the dth coordinate of every point in
 $P_i^d$
is the same as the dth coordinate of the corresponding point in
$P_i^d$
is the same as the dth coordinate of the corresponding point in
 $P^d$
.
$P^d$
.
Set
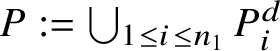 $P := \bigcup _{1 \leq i \leq n_1} P^d_i$
and
$P := \bigcup _{1 \leq i \leq n_1} P^d_i$
and
 $B' := \bigcup _{1 \leq i \leq n_1} B^d_i$
; then
$B' := \bigcup _{1 \leq i \leq n_1} B^d_i$
; then
![]() $\lvert P\rvert = n_1n^{\prime }_1, \lvert B'\rvert = n_1n^{\prime }_2$
and there are
$\lvert P\rvert = n_1n^{\prime }_1, \lvert B'\rvert = n_1n^{\prime }_2$
and there are
![]() $n_1m'$
incidences between P and
$n_1m'$
incidences between P and
![]() $B'$
.
$B'$
.
Write
![]() $P^d$
as
$P^d$
as
![]() $q_1, \dotsc , q_{n^{\prime }_1}$
and
$q_1, \dotsc , q_{n^{\prime }_1}$
and
![]() $B^{d-1}$
as
$B^{d-1}$
as
![]() $c_1, \dotsc , c_{n_2}$
. As all of the dth coordinates of the points in
$c_1, \dotsc , c_{n_2}$
. As all of the dth coordinates of the points in
![]() $P^d$
are pairwise disjoint, for each
$P^d$
are pairwise disjoint, for each
![]() $1 \leq j \leq n^{\prime }_1$
we can choose a small interval
$1 \leq j \leq n^{\prime }_1$
we can choose a small interval
![]() $I_j \subseteq \mathbb {R}$
with
$I_j \subseteq \mathbb {R}$
with
![]() $q_{j,d} \in I_j$
and such that all of the intervals
$q_{j,d} \in I_j$
and such that all of the intervals
![]() $I_j, 1 \leq j \leq n^{\prime }_1$
, are pairwise disjoint. For each
$I_j, 1 \leq j \leq n^{\prime }_1$
, are pairwise disjoint. For each
![]() $1 \leq j \leq n^{\prime }_1$
and
$1 \leq j \leq n^{\prime }_1$
and
![]() $c_l \in B^{d-1}$
, we consider the d-dimensional box
$c_l \in B^{d-1}$
, we consider the d-dimensional box
![]() $c_{j,l} :=c_l \times I_j$
. Define
$c_{j,l} :=c_l \times I_j$
. Define
 $B_j := \left \{c_{j,l} : 1 \leq l \leq n_2 \right \}$
. For each
$B_j := \left \{c_{j,l} : 1 \leq l \leq n_2 \right \}$
. For each
![]() $1 \leq i \leq n_1$
and
$1 \leq i \leq n_1$
and
![]() $1 \leq j \leq n^{\prime }_1$
,
$1 \leq j \leq n^{\prime }_1$
,
![]() $(\beta _i \times \mathbb {R}) \cap \left (\mathbb {R}^{d-1} \times I_j\right )$
contains exactly one point
$(\beta _i \times \mathbb {R}) \cap \left (\mathbb {R}^{d-1} \times I_j\right )$
contains exactly one point
![]() $q_{i,j}$
(given by the copy of
$q_{i,j}$
(given by the copy of
![]() $q_{j}$
in
$q_{j}$
in
![]() $P_i^d$
), and the projection
$P_i^d$
), and the projection
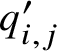 $q^{\prime }_{i,j}$
of
$q^{\prime }_{i,j}$
of
![]() $q_{i,j}$
onto the first
$q_{i,j}$
onto the first
![]() $d-1$
coordinates is in
$d-1$
coordinates is in
![]() $\beta _i$
. Hence the incidence graph between P and
$\beta _i$
. Hence the incidence graph between P and
![]() $B_j$
is isomorphic to the incidence graph between
$B_j$
is isomorphic to the incidence graph between
![]() $P^{d-1}$
and
$P^{d-1}$
and
![]() $B^{d-1}$
by the choice of the
$B^{d-1}$
by the choice of the
![]() $\beta _i$
s, and in particular the number of incidences is m.
$\beta _i$
s, and in particular the number of incidences is m.
Finally, define
 $B := B' \cup \bigcup _{1 \leq j \leq n^{\prime }_1} B_j$
; then
$B := B' \cup \bigcup _{1 \leq j \leq n^{\prime }_1} B_j$
; then
![]() $\lvert B\rvert = n_1n^{\prime }_2 + n^{\prime }_1n_2$
. Note that
$\lvert B\rvert = n_1n^{\prime }_2 + n^{\prime }_1n_2$
. Note that
![]() $c_{j,l} \cap c_{j',l'} = \emptyset $
for
$c_{j,l} \cap c_{j',l'} = \emptyset $
for
![]() $j \neq j'$
and any
$j \neq j'$
and any
![]() $l,l'$
– that is, no box in
$l,l'$
– that is, no box in
![]() $B_j$
intersects any of the boxes in
$B_j$
intersects any of the boxes in
![]() $B_{j'}$
for
$B_{j'}$
for
![]() $j\neq j'$
. It is now not hard to check that the incidence graph between P and B is
$j\neq j'$
. It is now not hard to check that the incidence graph between P and B is
![]() $K_{2,2}$
-free, by construction and the assumptions of
$K_{2,2}$
-free, by construction and the assumptions of
![]() $K_{2,2}$
-freeness of
$K_{2,2}$
-freeness of
![]() $\left (P^d,B^d\right )$
and
$\left (P^d,B^d\right )$
and
![]() $\left (P^{d-1}, B^{d-1}\right )$
, and that there are
$\left (P^{d-1}, B^{d-1}\right )$
, and that there are
![]() $n_1m'+mn^{\prime }_1$
incidences between P and B.
$n_1m'+mn^{\prime }_1$
incidences between P and B.
Remark 3.4. It follows from the proof that if all the boxes in
![]() $B^{d-1}$
and
$B^{d-1}$
and
![]() $B^d$
are dyadic (see Definition 4.6), then we can choose the boxes in B to be dyadic as well.
$B^d$
are dyadic (see Definition 4.6), then we can choose the boxes in B to be dyadic as well.
Proposition 3.5. For any
![]() $\ell \in \mathbb {N}$
, there exist a set P of
$\ell \in \mathbb {N}$
, there exist a set P of
![]() $ \ell ^{\ell }$
points and a set B of
$ \ell ^{\ell }$
points and a set B of
![]() $\ell ^{\ell }$
dyadic boxes in
$\ell ^{\ell }$
dyadic boxes in
![]() $\mathbb {R}^2$
such that their incidence graph is
$\mathbb {R}^2$
such that their incidence graph is
![]() $K_{2,2}$
-free and the number of incidences is
$K_{2,2}$
-free and the number of incidences is
![]() $\ell \ell ^{\ell }$
.
$\ell \ell ^{\ell }$
.
In particular, substituting
![]() $n := \ell ^{\ell }$
, this shows that the number of incidences grows as
$n := \ell ^{\ell }$
, this shows that the number of incidences grows as
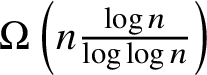 $\Omega \left (n \frac {\log n}{\log \log n} \right )$
.
$\Omega \left (n \frac {\log n}{\log \log n} \right )$
.
Proof. Given d, assume that there exist
![]() $K_{2,2}$
-free ‘point–dyadic box’ configurations satisfying Lemma 3.3(1) and (2) for some parameters
$K_{2,2}$
-free ‘point–dyadic box’ configurations satisfying Lemma 3.3(1) and (2) for some parameters
![]() $d, n_1, n_2, n^{\prime }_1, n^{\prime }_2, m, m'$
. Then for any
$d, n_1, n_2, n^{\prime }_1, n^{\prime }_2, m, m'$
. Then for any
![]() $j \in \mathbb {N}$
, we can iterate the lemma j times and find a
$j \in \mathbb {N}$
, we can iterate the lemma j times and find a
![]() $K_{2,2}$
-free ‘point–dyadic box’ configuration in
$K_{2,2}$
-free ‘point–dyadic box’ configuration in
![]() $\mathbb {R}^d$
with
$\mathbb {R}^d$
with
 $n_1^j n^{\prime }_1$
points,
$n_1^j n^{\prime }_1$
points,
 $n_1^j n^{\prime }_2 + j n_1^{j-1} n^{\prime }_1 n_2$
dyadic boxes (Remark 3.4) and
$n_1^j n^{\prime }_2 + j n_1^{j-1} n^{\prime }_1 n_2$
dyadic boxes (Remark 3.4) and
 $n_1^j m' + j n_1^{j-1} n^{\prime }_1 m$
incidences.
$n_1^j m' + j n_1^{j-1} n^{\prime }_1 m$
incidences.
In particular, let
![]() $d = 2$
and let
$d = 2$
and let
![]() $\ell $
be arbitrary. We can start with
$\ell $
be arbitrary. We can start with
![]() $n_1 = \ell , n_2 = 1, m=\ell $
(one dyadic interval containing
$n_1 = \ell , n_2 = 1, m=\ell $
(one dyadic interval containing
![]() $n_1$
points in
$n_1$
points in
![]() $\mathbb {R}$
) and
$\mathbb {R}$
) and
![]() $n^{\prime }_1=1, n^{\prime }_2=0, m' = 0$
(one point and zero dyadic boxes in
$n^{\prime }_1=1, n^{\prime }_2=0, m' = 0$
(one point and zero dyadic boxes in
![]() $\mathbb {R}^2$
). Taking
$\mathbb {R}^2$
). Taking
![]() $j := \ell $
, we then find a
$j := \ell $
, we then find a
![]() $K_{2,2}$
-free configuration with
$K_{2,2}$
-free configuration with
![]() $\ell ^{\ell }$
points,
$\ell ^{\ell }$
points,
![]() $\ell ^\ell $
dyadic boxes and
$\ell ^\ell $
dyadic boxes and
![]() $\ell \ell ^{\ell }$
incidences. Hence for
$\ell \ell ^{\ell }$
incidences. Hence for
![]() $n := k^k$
, we have n points, n boxes and
$n := k^k$
, we have n points, n boxes and
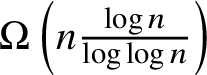 $\Omega \left (n \frac {\log n}{\log \log n} \right )$
incidences.
$\Omega \left (n \frac {\log n}{\log \log n} \right )$
incidences.
Remark 3.6. We remark that the construction in Lemma 3.3 cannot produce a
![]() $K_{2,2}$
-free configuration with more than
$K_{2,2}$
-free configuration with more than
 $O \left ( n \frac {\log n}{\log \log n} \right )$
incidences in
$O \left ( n \frac {\log n}{\log \log n} \right )$
incidences in
![]() $\mathbb {R}^d$
for any d.
$\mathbb {R}^d$
for any d.
Indeed, using the ‘coordinates’
 $\left ( \log n^{\prime }_1, \frac {n^{\prime }_2}{n^{\prime }_1}, \frac {m'}{n^{\prime }_1} \right )$
instead of
$\left ( \log n^{\prime }_1, \frac {n^{\prime }_2}{n^{\prime }_1}, \frac {m'}{n^{\prime }_1} \right )$
instead of
 $\left (n^{\prime }_1,n^{\prime }_2,m'\right )$
, where the coordinates correspond to the number of points, boxes and incidences, respectively, the lemma says that if
$\left (n^{\prime }_1,n^{\prime }_2,m'\right )$
, where the coordinates correspond to the number of points, boxes and incidences, respectively, the lemma says that if
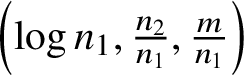 $\left ( \log n_1, \frac {n_2}{n_1}, \frac {m}{n_1} \right )$
is attainable in
$\left ( \log n_1, \frac {n_2}{n_1}, \frac {m}{n_1} \right )$
is attainable in
![]() $d-1$
dimensions and
$d-1$
dimensions and
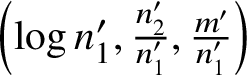 $\left ( \log n^{\prime }_1, \frac {n^{\prime }_2}{n^{\prime }_1}, \frac {m'}{n^{\prime }_1} \right )$
is attainable in d dimensions, then
$\left ( \log n^{\prime }_1, \frac {n^{\prime }_2}{n^{\prime }_1}, \frac {m'}{n^{\prime }_1} \right )$
is attainable in d dimensions, then
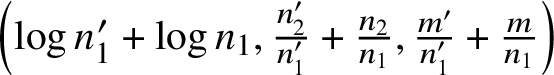 $\left ( \log n^{\prime }_1 + \log n_1, \frac {n^{\prime }_2}{n^{\prime }_1} + \frac {n_2}{n_1}, \frac {m'}{n^{\prime }_1} + \frac {m}{n_1} \right )$
is attainable in d dimensions. Thus, one adds the vector
$\left ( \log n^{\prime }_1 + \log n_1, \frac {n^{\prime }_2}{n^{\prime }_1} + \frac {n_2}{n_1}, \frac {m'}{n^{\prime }_1} + \frac {m}{n_1} \right )$
is attainable in d dimensions. Thus, one adds the vector
 $\left (\frac {n_2}{n_1}, \frac {m}{n_1} \right )$
to
$\left (\frac {n_2}{n_1}, \frac {m}{n_1} \right )$
to
 $\left ( \frac {n^{\prime }_2}{n^{\prime }_1},\frac {m'}{n^{\prime }_1} \right )$
. We want to maximise the second coordinate of this vector while keeping the first coordinate below
$\left ( \frac {n^{\prime }_2}{n^{\prime }_1},\frac {m'}{n^{\prime }_1} \right )$
. We want to maximise the second coordinate of this vector while keeping the first coordinate below
![]() $1$
, and the optimal way to do this essentially is to add
$1$
, and the optimal way to do this essentially is to add
![]() $n_1$
times the vector
$n_1$
times the vector
 $\left (\frac {1}{n_1},1 \right )$
, which increases
$\left (\frac {1}{n_1},1 \right )$
, which increases
![]() $\log n^{\prime }_1$
by
$\log n^{\prime }_1$
by
![]() $n_1 \log n_1$
and gives the
$n_1 \log n_1$
and gives the
 $\frac {\log n}{\log \log n}$
lower bound.
$\frac {\log n}{\log \log n}$
lower bound.
We thus ask whether in the ‘point-box’ incidence bound in
![]() $\mathbb {R}^d$
the power of
$\mathbb {R}^d$
the power of
![]() $\log n$
has to grow with the dimension d (see Problem 1.3).
$\log n$
has to grow with the dimension d (see Problem 1.3).
4. Dyadic rectangles
In this section we strengthen the bound on the number of incidences with rectangles on the plane with axis-parallel sides given by Corollary 2.38 – that is,
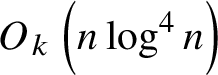 $O_{k} \left ( n \log ^{4} n \right )$
– in the special case of dyadic rectangles, using a different argument (which relies on a certain partial order specific to the dyadic case).
$O_{k} \left ( n \log ^{4} n \right )$
– in the special case of dyadic rectangles, using a different argument (which relies on a certain partial order specific to the dyadic case).
4.1. Locally d-linear orders
Throughout this section, let
![]() $(P, \leq )$
be a partially ordered set of size at most
$(P, \leq )$
be a partially ordered set of size at most
![]() $n_1$
, and let L be a collection of subsets of P (possibly with repetitions) of size at most
$n_1$
, and let L be a collection of subsets of P (possibly with repetitions) of size at most
![]() $n_2$
. As before, we let
$n_2$
. As before, we let
![]() $n = n_1 + n_2$
.
$n = n_1 + n_2$
.
Definition 4.1. We say that a set
![]() $S \subseteq P$
is d-linear if it contains no antichains of size greater than d, and
$S \subseteq P$
is d-linear if it contains no antichains of size greater than d, and
![]() $(P, \leq )$
is locally d-linear if any interval
$(P, \leq )$
is locally d-linear if any interval
![]() $[a,b] = \{ x \in P : a \leq x \leq b \}$
is d-linear.
$[a,b] = \{ x \in P : a \leq x \leq b \}$
is d-linear.
Note that d-linearity is preserved under removing points from P.
Definition 4.2. The collection L is said to be a
![]() $K_{k,k}$
-free arrangement if for any
$K_{k,k}$
-free arrangement if for any
![]() $a_1 \neq \dotsb \neq a_k \in P$
, there are at most
$a_1 \neq \dotsb \neq a_k \in P$
, there are at most
![]() $k-1$
sets from L containing all of them simultaneously.
$k-1$
sets from L containing all of them simultaneously.
Observe that if one removes any number of points from P or removes any number of sets from L, one still obtains a
![]() $K_{k,k}$
-free arrangement. We now state the main theorem of this section:
$K_{k,k}$
-free arrangement. We now state the main theorem of this section:
Theorem 4.3. Suppose
![]() $(P,<)$
is locally d-linear and L is a
$(P,<)$
is locally d-linear and L is a
![]() $K_{k,k}$
-free arrangement of d-linear subsets of P. Then
$K_{k,k}$
-free arrangement of d-linear subsets of P. Then
 $$ \begin{align*}\sum_{\ell \in L} \lvert\ell\rvert = O_{d,k}\left( n \frac{\log(100+n_1)}{\log \log(100+n_1)} \right).\end{align*} $$
$$ \begin{align*}\sum_{\ell \in L} \lvert\ell\rvert = O_{d,k}\left( n \frac{\log(100+n_1)}{\log \log(100+n_1)} \right).\end{align*} $$
To prove this theorem, we first need some definitions and a lemma. If
![]() $x \in P$
, define a parent of x to be an element
$x \in P$
, define a parent of x to be an element
![]() $y \in P$
with
$y \in P$
with
![]() $y>x$
and no element between x and y, and similarly define a child of x to be an element
$y>x$
and no element between x and y, and similarly define a child of x to be an element
![]() $z \in P$
with
$z \in P$
with
![]() $z<x$
and no element between z and x. We say that z is a strict t-descendant of x if there are some elements
$z<x$
and no element between z and x. We say that z is a strict t-descendant of x if there are some elements
![]() $z_0 = x> z_1 > \dotsb > z_{t} = z$
such that
$z_0 = x> z_1 > \dotsb > z_{t} = z$
such that
![]() $z_{i+1}$
is a child of
$z_{i+1}$
is a child of
![]() $z_i$
, and that z is a t-descendant of x if it is a strict s-descendant for some
$z_i$
, and that z is a t-descendant of x if it is a strict s-descendant for some
![]() $0 \leq s \leq t$
.
$0 \leq s \leq t$
.
Lemma 4.4. Fix
![]() $d,k \in \mathbb {N}$
. Let L be a
$d,k \in \mathbb {N}$
. Let L be a
![]() $K_{k,k}$
-free arrangement of d-linear subsets of P and let
$K_{k,k}$
-free arrangement of d-linear subsets of P and let
![]() $m> 0$
. Let
$m> 0$
. Let
![]() $P'$
denote the set of all elements in P which have a
$P'$
denote the set of all elements in P which have a
![]() $(k-1)$
-descendant with more than m children. Then
$(k-1)$
-descendant with more than m children. Then
 $$ \begin{align*}\sum_{\ell \in L} \lvert\ell\rvert \leq \sum_{\ell \in L} \lvert\ell \cap P'\rvert + d(k-1)\lvert L\rvert + (k-1) m^{k-1} (\lvert P\rvert - \lvert P'\rvert ).\end{align*} $$
$$ \begin{align*}\sum_{\ell \in L} \lvert\ell\rvert \leq \sum_{\ell \in L} \lvert\ell \cap P'\rvert + d(k-1)\lvert L\rvert + (k-1) m^{k-1} (\lvert P\rvert - \lvert P'\rvert ).\end{align*} $$
Proof. Let
![]() $P'' := P \backslash P'$
denote the set of elements
$P'' := P \backslash P'$
denote the set of elements
![]() $x \in P$
such that every
$x \in P$
such that every
![]() $(k-1)$
-descendant of x has at most m children. Then we can rearrange the desired inequality as
$(k-1)$
-descendant of x has at most m children. Then we can rearrange the desired inequality as
 $$ \begin{align*}\sum_{\ell \in L} \lvert \ell \cap P''\rvert \leq d(k-1)\lvert L\rvert + (k-1)m^{k-1} \lvert P''\rvert.\end{align*} $$
$$ \begin{align*}\sum_{\ell \in L} \lvert \ell \cap P''\rvert \leq d(k-1)\lvert L\rvert + (k-1)m^{k-1} \lvert P''\rvert.\end{align*} $$
The quantity
![]() $\sum _{\ell \in L} \lvert \ell \cap P''\rvert $
is counting incidences
$\sum _{\ell \in L} \lvert \ell \cap P''\rvert $
is counting incidences
![]() $(x,\ell )$
where
$(x,\ell )$
where
![]() $\ell \in L$
and
$\ell \in L$
and
![]() $x \in P'' \cap \ell $
.
$x \in P'' \cap \ell $
.
Given
![]() $\ell \in L$
, call a point
$\ell \in L$
, call a point
![]() $x \in \ell $
low if it has no descending chain of length
$x \in \ell $
low if it has no descending chain of length
![]() $k-1$
under it in
$k-1$
under it in
![]() $\ell $
. Every
$\ell $
. Every
![]() $\ell $
can contain at most
$\ell $
can contain at most
![]() $d(k-1)$
low points. Indeed, as
$d(k-1)$
low points. Indeed, as
![]() $\ell $
is d-linear, it has at most d minimal elements. Removing them, we obtain a d-linear set
$\ell $
is d-linear, it has at most d minimal elements. Removing them, we obtain a d-linear set
![]() $\ell _1 \subseteq \ell $
such that every point in it contains an element under it in
$\ell _1 \subseteq \ell $
such that every point in it contains an element under it in
![]() $\ell $
, and
$\ell $
, and
![]() $\ell _1$
itself has at most d minimal elements. Remove them to obtain a d-linear set
$\ell _1$
itself has at most d minimal elements. Remove them to obtain a d-linear set
![]() $\ell _2 \subseteq \ell _1$
such that each point in it contains a descending chain of length
$\ell _2 \subseteq \ell _1$
such that each point in it contains a descending chain of length
![]() $2$
under it in
$2$
under it in
![]() $\ell $
, and so on.
$\ell $
, and so on.
Hence each
![]() $\ell \in L$
contributes at most
$\ell \in L$
contributes at most
![]() $d(k-1)$
incidences with its low points, giving a total contribution of at most
$d(k-1)$
incidences with its low points, giving a total contribution of at most
![]() $d(k-1)\lvert L\rvert $
to the sum. If x is not a low point on
$d(k-1)\lvert L\rvert $
to the sum. If x is not a low point on
![]() $\ell $
, then there are some
$\ell $
, then there are some
![]() $z_1 < \dotsb < z_{k-1} < x$
in
$z_1 < \dotsb < z_{k-1} < x$
in
![]() $\ell $
, with each one a child of the next one. As L is a
$\ell $
, with each one a child of the next one. As L is a
![]() $K_{k,k}$
-free arrangement, among the sets
$K_{k,k}$
-free arrangement, among the sets
![]() $\ell \in L$
there are at most
$\ell \in L$
there are at most
![]() $k-1$
containing all these points. By the definition of
$k-1$
containing all these points. By the definition of
![]() $P''$
, for each
$P''$
, for each
![]() $x \in P''$
there are at most
$x \in P''$
there are at most
![]() $m^{k-1}$
choices for such tuples
$m^{k-1}$
choices for such tuples
![]() $(z_1, \dotsc , z_{k-1})$
. Hence x is incident to at most
$(z_1, \dotsc , z_{k-1})$
. Hence x is incident to at most
![]() $(k-1)m^{k-1}$
sets
$(k-1)m^{k-1}$
sets
![]() $\ell \in L$
for which it is not low, and the total number of contributions of incidences in this case is at most
$\ell \in L$
for which it is not low, and the total number of contributions of incidences in this case is at most
![]() $(k-1) m^{k-1} \lvert P''\rvert $
, so the claim follows.
$(k-1) m^{k-1} \lvert P''\rvert $
, so the claim follows.
Now we prove Theorem 4.3. Let t be a natural number to be chosen later and
![]() $m>0$
be another parameter to be chosen later. Define the subsets
$m>0$
be another parameter to be chosen later. Define the subsets
of P by defining
![]() $P_0 := P$
, and for each
$P_0 := P$
, and for each
![]() $i=0,\dots ,t-1$
, defining
$i=0,\dots ,t-1$
, defining
![]() $P_{i+1}$
to be the set of points in
$P_{i+1}$
to be the set of points in
![]() $P_i$
that have a
$P_i$
that have a
![]() $(k-1)$
-descendant with more than m children in
$(k-1)$
-descendant with more than m children in
![]() $(P_i, <)$
. By Lemma 4.4, we have
$(P_i, <)$
. By Lemma 4.4, we have
 $$ \begin{align*}\sum_{\ell \in L} \lvert\ell \cap P_i\rvert \leq \sum_{\ell \in L} \lvert\ell \cap P_{i+1}\rvert + d(k-1)\lvert L\rvert + (k-1)m^{k-1} (\lvert P_i\rvert - \lvert P_{i+1}\rvert )\end{align*} $$
$$ \begin{align*}\sum_{\ell \in L} \lvert\ell \cap P_i\rvert \leq \sum_{\ell \in L} \lvert\ell \cap P_{i+1}\rvert + d(k-1)\lvert L\rvert + (k-1)m^{k-1} (\lvert P_i\rvert - \lvert P_{i+1}\rvert )\end{align*} $$
for all
![]() $i=0,\dots ,t-1$
, and hence on telescoping,
$i=0,\dots ,t-1$
, and hence on telescoping,
 $$ \begin{align*}\sum_{\ell \in L} \lvert\ell\rvert \leq \sum_{\ell \in L} \lvert\ell \cap P_t\rvert + d(k-1) t \lvert L\rvert + (k-1) m^{k-1} n_1.\end{align*} $$
$$ \begin{align*}\sum_{\ell \in L} \lvert\ell\rvert \leq \sum_{\ell \in L} \lvert\ell \cap P_t\rvert + d(k-1) t \lvert L\rvert + (k-1) m^{k-1} n_1.\end{align*} $$
Claim 4.5. Let x be a point in
![]() $P_t$
. Then it has at least
$P_t$
. Then it has at least
 $ \frac {m^t}{\left (k d^k\right )^{t-1}}$
distinct descendants in P.
$ \frac {m^t}{\left (k d^k\right )^{t-1}}$
distinct descendants in P.
Proof. By definition of
![]() $P_t$
there is some
$P_t$
there is some
![]() $(k-1)$
-descendant
$(k-1)$
-descendant
![]() $x' \in P_{t-1}$
of x which has at least
$x' \in P_{t-1}$
of x which has at least
![]() $ m$
children in
$ m$
children in
![]() $P_{t-1}$
. Let
$P_{t-1}$
. Let
![]() $S_{t-1} \subseteq P_{t-1}$
denote the set of children of
$S_{t-1} \subseteq P_{t-1}$
denote the set of children of
![]() $x'$
, so
$x'$
, so
![]() $\lvert S_{t-1}\rvert \geq m$
. By reverse induction for
$\lvert S_{t-1}\rvert \geq m$
. By reverse induction for
![]() $i= t-1, t-2, \dotsc , 0$
, we choose sets
$i= t-1, t-2, \dotsc , 0$
, we choose sets
![]() $S_{i} \subseteq P_i$
of descendants of x so that
$S_{i} \subseteq P_i$
of descendants of x so that
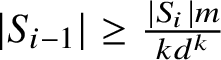 $\lvert S_{i-1}\rvert \geq \frac {\lvert S_i\rvert m }{k d^k}$
. Then
$\lvert S_{i-1}\rvert \geq \frac {\lvert S_i\rvert m }{k d^k}$
. Then
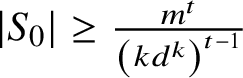 $\lvert S_0\rvert \geq \frac { m^t}{\left (k d^k\right )^{t-1}} $
, as wanted.
$\lvert S_0\rvert \geq \frac { m^t}{\left (k d^k\right )^{t-1}} $
, as wanted.
Let
![]() $S_i$
be given. By the definition of
$S_i$
be given. By the definition of
![]() $P_{i}$
and the pigeonhole principle, there is some
$P_{i}$
and the pigeonhole principle, there is some
![]() $0 \leq s \leq k-1$
and
$0 \leq s \leq k-1$
and
![]() $S^{\prime }_i \subseteq S_i$
such that
$S^{\prime }_i \subseteq S_i$
such that
 $\left \lvert S^{\prime }_i\right \rvert \geq \frac {\lvert S_i\rvert }{k}$
and every
$\left \lvert S^{\prime }_i\right \rvert \geq \frac {\lvert S_i\rvert }{k}$
and every
![]() $y \in S^{\prime }_i$
has a strict s-descendant
$y \in S^{\prime }_i$
has a strict s-descendant
![]() $z_y \in P_{i-1}$
with at least m children in
$z_y \in P_{i-1}$
with at least m children in
![]() $P_{i-1}$
. Fix a path
$P_{i-1}$
. Fix a path
![]() $I_y$
of length s connecting y to
$I_y$
of length s connecting y to
![]() $z_y$
, and for
$z_y$
, and for
![]() $0 \leq r \leq s$
let
$0 \leq r \leq s$
let
![]() $z^r_y$
denote the rth element on the path
$z^r_y$
denote the rth element on the path
![]() $I_y$
(so
$I_y$
(so
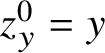 $z_y^0 = y $
,
$z_y^0 = y $
,
![]() $z_y^s = z_y$
and
$z_y^s = z_y$
and
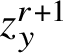 $z_y^{r+1}$
is a child of
$z_y^{r+1}$
is a child of
![]() $z_y^r$
). Define
$z_y^r$
). Define
 $I^r := \left \{ z^r_y : y \in S^{\prime }_i\right \}$
, so
$I^r := \left \{ z^r_y : y \in S^{\prime }_i\right \}$
, so
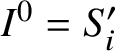 $I^0 = S^{\prime }_i$
. Then
$I^0 = S^{\prime }_i$
. Then
 $\left \lvert I^{r+1}\right \rvert \geq \frac {\lvert I^r\rvert }{d}$
(otherwise there is some element
$\left \lvert I^{r+1}\right \rvert \geq \frac {\lvert I^r\rvert }{d}$
(otherwise there is some element
![]() $z \in I^{r+1}$
which has at least
$z \in I^{r+1}$
which has at least
![]() $d+1$
different parents in
$d+1$
different parents in
![]() $I^r$
, which would then form an antichain of size
$I^r$
, which would then form an antichain of size
![]() $d+1$
, contradicting the local d-linearity of P). Hence
$d+1$
, contradicting the local d-linearity of P). Hence
 $$ \begin{align*}\lvert I^s\rvert \geq \frac{\left\lvert I^0\right\rvert}{d^{s}} \geq \frac{\left\lvert S^{\prime}_i\right\rvert}{d^{k-1}} \geq \frac{\lvert S_i\rvert}{k d^{k-1}}.\end{align*} $$
$$ \begin{align*}\lvert I^s\rvert \geq \frac{\left\lvert I^0\right\rvert}{d^{s}} \geq \frac{\left\lvert S^{\prime}_i\right\rvert}{d^{k-1}} \geq \frac{\lvert S_i\rvert}{k d^{k-1}}.\end{align*} $$
Now by hypothesis every element in
![]() $I^s$
has at least m children in
$I^s$
has at least m children in
![]() $P_{i-1}$
; denote the set of all the children of the elements in
$P_{i-1}$
; denote the set of all the children of the elements in
![]() $I^s$
by
$I^s$
by
![]() $S_{i-1} \subseteq P_{i-1}$
. Then, again by d-linearity,
$S_{i-1} \subseteq P_{i-1}$
. Then, again by d-linearity,
 $\lvert S_{i-1}\rvert \geq \frac {\lvert I^s\rvert m}{d} \geq \frac {\lvert S_i\rvert m }{k d^k}$
.
$\lvert S_{i-1}\rvert \geq \frac {\lvert I^s\rvert m}{d} \geq \frac {\lvert S_i\rvert m }{k d^k}$
.
Thus if we choose
![]() $m, t$
such that
$m, t$
such that
 $$ \begin{align*}\left( \frac{m}{kd^k} \right)^t> n_1,\end{align*} $$
$$ \begin{align*}\left( \frac{m}{kd^k} \right)^t> n_1,\end{align*} $$
then we will get a contradiction, unless
![]() $P_t$
is empty. We conclude, for such m and t, that
$P_t$
is empty. We conclude, for such m and t, that
 $$ \begin{align*}\sum_{\ell \in L} \lvert\ell\rvert \leq d(k-1) t \lvert L\rvert + (k-1) m^{k-1} n_1.\end{align*} $$
$$ \begin{align*}\sum_{\ell \in L} \lvert\ell\rvert \leq d(k-1) t \lvert L\rvert + (k-1) m^{k-1} n_1.\end{align*} $$
If we take
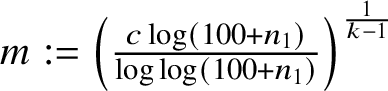 $m := \left ( \frac {c \log \left (100+n_1\right )}{\log \log \left (100+n_1\right )} \right )^{\frac {1}{k-1}}$
and t to be the integer part of
$m := \left ( \frac {c \log \left (100+n_1\right )}{\log \log \left (100+n_1\right )} \right )^{\frac {1}{k-1}}$
and t to be the integer part of
 $\frac {c \log \left (100+n_1\right )}{\log \log \left (100+n_1\right )}$
, and assume that c is sufficiently large relative to k and d, then the claim follows.
$\frac {c \log \left (100+n_1\right )}{\log \log \left (100+n_1\right )}$
, and assume that c is sufficiently large relative to k and d, then the claim follows.
4.2. Reduction for dyadic rectangles
Definition 4.6.
-
1. Define a dyadic interval to be a half-open interval I of the form
 $I = \left [s2^t, (s+1)2^t\right )$
for integers
$I = \left [s2^t, (s+1)2^t\right )$
for integers
 $s,t$
; we use
$s,t$
; we use
 $\lvert I\rvert = 2^t$
to denote the length of such an interval.
$\lvert I\rvert = 2^t$
to denote the length of such an interval. -
2. Define a dyadic box in
 $\mathbb {R}^d$
(a dyadic rectangle when
$\mathbb {R}^d$
(a dyadic rectangle when
 $d=2$
) to be a product
$d=2$
) to be a product
 $I_1 {{\times }\dotsb {\times }} I_d$
of dyadic intervals.
$I_1 {{\times }\dotsb {\times }} I_d$
of dyadic intervals.
Note that if two dyadic intervals intersect, then one must be contained in the other.
Theorem 4.7. Fix
![]() $k \in \mathbb {N}$
. Assume we have a collection P of
$k \in \mathbb {N}$
. Assume we have a collection P of
![]() $n_1$
points in
$n_1$
points in
![]() $\mathbb {R}^2$
and a collection R of
$\mathbb {R}^2$
and a collection R of
![]() $n_2$
dyadic rectangles in
$n_2$
dyadic rectangles in
![]() $\mathbb {R}^2$
, with the property that the incidence graph contains no
$\mathbb {R}^2$
, with the property that the incidence graph contains no
![]() $K_{k,k}$
, and
$K_{k,k}$
, and
![]() $n = n_1 + n_2$
. Then the number of incidences
$n = n_1 + n_2$
. Then the number of incidences
![]() $(p,I \times J)$
with
$(p,I \times J)$
with
![]() $p \in P$
and
$p \in P$
and
![]() $p \in I \times J \in R$
is at most
$p \in I \times J \in R$
is at most
 $$ \begin{align*} O_k \left( n \frac{\log(100+n_1)}{\log\log(100+n_1)} \right). \end{align*} $$
$$ \begin{align*} O_k \left( n \frac{\log(100+n_1)}{\log\log(100+n_1)} \right). \end{align*} $$
Proof. Suppose that we have some nested dyadic rectangles
![]() $D_1 \supseteq D_2 \supseteq \dotsb \supseteq D_k$
in R. As the incidence graph is
$D_1 \supseteq D_2 \supseteq \dotsb \supseteq D_k$
in R. As the incidence graph is
![]() $K_{k,k}$
-free by hypothesis,
$K_{k,k}$
-free by hypothesis,
![]() $D_k$
may contain at most
$D_k$
may contain at most
![]() $(k-1)$
points from P. Removing all such rectangles repeatedly, we lose only
$(k-1)$
points from P. Removing all such rectangles repeatedly, we lose only
![]() $(k-1) n_2$
incidences, and thus may assume that any nested sequence in R is of length at most
$(k-1) n_2$
incidences, and thus may assume that any nested sequence in R is of length at most
![]() $k-1$
. In particular, any rectangle can be repeated at most
$k-1$
. In particular, any rectangle can be repeated at most
![]() $k-1$
times in R. Then, possibly increasing the number of incidences by a multiple of
$k-1$
times in R. Then, possibly increasing the number of incidences by a multiple of
![]() $(k-1)$
, we may assume that there are no repetitions in R.
$(k-1)$
, we may assume that there are no repetitions in R.
We now define a relation
![]() $\leq $
on R by declaring
$\leq $
on R by declaring
![]() $I \times J \leq I' \times J'$
if
$I \times J \leq I' \times J'$
if
![]() $I \subseteq I'$
and
$I \subseteq I'$
and
![]() $J \supseteq J'$
. This is a locally
$J \supseteq J'$
. This is a locally
![]() $(k-1)$
-linear partial order (by the previous paragraph: antisymmetry holds, as there are no repetitions in R, and using the fact that all rectangles are dyadic, any antichain of size k inside an interval would give a nested sequence of rectangles of length k).
$(k-1)$
-linear partial order (by the previous paragraph: antisymmetry holds, as there are no repetitions in R, and using the fact that all rectangles are dyadic, any antichain of size k inside an interval would give a nested sequence of rectangles of length k).
For each point p in P, let
![]() $\ell _p$
be a subset of R consisting of all those rectangles in R that contain p; then
$\ell _p$
be a subset of R consisting of all those rectangles in R that contain p; then
![]() $\ell _p$
is a
$\ell _p$
is a
![]() $(k-1)$
-linear set (again, any antichain gives a nested sequence of rectangles of the same length). Finally,
$(k-1)$
-linear set (again, any antichain gives a nested sequence of rectangles of the same length). Finally,
![]() $p \in R \iff R \in \ell _p$
, hence the collection
$p \in R \iff R \in \ell _p$
, hence the collection
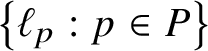 $\left \{ \ell _p : p \in P \right \}$
is a
$\left \{ \ell _p : p \in P \right \}$
is a
![]() $K_{k,k}$
-free arrangement and the claim now follows from Theorem 4.3 with
$K_{k,k}$
-free arrangement and the claim now follows from Theorem 4.3 with
![]() $d := k-1$
.
$d := k-1$
.
Remark 4.8. For a nondyadic rectangle R, let
![]() $0.99 R$
denote the rectangle with the same centre as R but whose lengths and heights have been shrunk by a factor of
$0.99 R$
denote the rectangle with the same centre as R but whose lengths and heights have been shrunk by a factor of
![]() $0.99$
. Define a good incidence to be a pair
$0.99$
. Define a good incidence to be a pair
![]() $(p,R)$
where p is a point lying in
$(p,R)$
where p is a point lying in
![]() $0.99 R$
, not just in R. Then the dyadic bound in Theorem 4.7 implies that for a family of arbitrary (not necessarily dyadic) rectangles with no
$0.99 R$
, not just in R. Then the dyadic bound in Theorem 4.7 implies that for a family of arbitrary (not necessarily dyadic) rectangles with no
![]() $K_{k,k}$
s, one still gets the
$K_{k,k}$
s, one still gets the
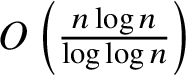 $O \left (\frac {n \log n}{ \log \log n} \right )$
-type bound for the number of good incidences.
$O \left (\frac {n \log n}{ \log \log n} \right )$
-type bound for the number of good incidences.
The reason is as follows. First, we can randomly translate and dilate (nonisotropically, with the horizontal and vertical coordinates dilated separately) the configuration of points and rectangles by some translation parameter and a pair of dilation parameters
![]() $(s,t)$
for each of the coordinates. While there is no invariant probability measure on the space of dilations, one can, for instance, pick a large number N (much larger than the number of points and rectangles, etc.) and dilate horizontally by a random dilation between
$(s,t)$
for each of the coordinates. While there is no invariant probability measure on the space of dilations, one can, for instance, pick a large number N (much larger than the number of points and rectangles, etc.) and dilate horizontally by a random dilation between
![]() $1/N$
and N (using, say, the
$1/N$
and N (using, say, the
![]() $dt/t$
Haar measure), making (with positive probability) the horizontal side length close to a power of
$dt/t$
Haar measure), making (with positive probability) the horizontal side length close to a power of
![]() $2$
; then a vertical dilation will achieve a similar effect for the vertical side length; and then one can translate by a random amount in
$2$
; then a vertical dilation will achieve a similar effect for the vertical side length; and then one can translate by a random amount in
![]() $[-N,N]^2$
(chosen uniformly at random), placing the rectangle very close to a dyadic one with positive probability. If R is a rectangle that is randomly dilated and translated in this way, then with probability
$[-N,N]^2$
(chosen uniformly at random), placing the rectangle very close to a dyadic one with positive probability. If R is a rectangle that is randomly dilated and translated in this way, then with probability
![]() $>10^{-10}$
, there will be a dyadic rectangle
$>10^{-10}$
, there will be a dyadic rectangle
![]() $R'$
stuck between R and
$R'$
stuck between R and
![]() $0.99 R$
. If the original rectangles have no
$0.99 R$
. If the original rectangles have no
![]() $K_{k,k}$
, then neither will these new dyadic rectangles. The expected number of incidences amongst the dyadic rectangles is at least
$K_{k,k}$
, then neither will these new dyadic rectangles. The expected number of incidences amongst the dyadic rectangles is at least
![]() $10^{-10}$
times the number of good incidences amongst the original rectangles. Hence any incidence bound we get on dyadic rectangles implies the corresponding bound for good incidences for nondyadic rectangles (losing a factor of
$10^{-10}$
times the number of good incidences amongst the original rectangles. Hence any incidence bound we get on dyadic rectangles implies the corresponding bound for good incidences for nondyadic rectangles (losing a factor of
![]() $10^{10}$
).
$10^{10}$
).
5. A connection to model-theoretic linearity
In this section we obtain a stronger bound in Theorem 2.17 (without the logarithmic factor) under a stronger assumption that the whole semilinear relation X is
![]() $K_{k, \dotsc ,k}$
-free (Corollary 5.12). And we show that if this stronger bound does not hold for a given semialgebraic relation, then the field operations can be recovered from this relation (see Corollary 5.14 for the precise statement). These results are deduced in Section 5.2 from a more general model-theoretic theorem proved in Section 5.1.
$K_{k, \dotsc ,k}$
-free (Corollary 5.12). And we show that if this stronger bound does not hold for a given semialgebraic relation, then the field operations can be recovered from this relation (see Corollary 5.14 for the precise statement). These results are deduced in Section 5.2 from a more general model-theoretic theorem proved in Section 5.1.
5.1. Main theorem
We recall some standard model-theoretic notation and definitions, and refer to [Reference Marker15] for a general introduction to model theory and [Reference Berenstein and Vassiliev3] for further details on geometric structures.
Recall that
![]() $\operatorname {acl}$
denotes the algebraic closure operator – that is, if
$\operatorname {acl}$
denotes the algebraic closure operator – that is, if
![]() $\mathcal {M} = (M, \dotsc )$
is a first-order structure,
$\mathcal {M} = (M, \dotsc )$
is a first-order structure,
![]() $A \subseteq M$
and a is a finite tuple in M, then
$A \subseteq M$
and a is a finite tuple in M, then
![]() $a \in \operatorname {acl}(A)$
if it belongs to some finite A-definable subset of
$a \in \operatorname {acl}(A)$
if it belongs to some finite A-definable subset of
![]() $M^{\lvert a\rvert }$
(this generalises the linear span in vector spaces and algebraic closure in fields). Throughout this section, we follow the standard model-theoretic notation: depending on the context, writing
$M^{\lvert a\rvert }$
(this generalises the linear span in vector spaces and algebraic closure in fields). Throughout this section, we follow the standard model-theoretic notation: depending on the context, writing
![]() $BC$
denotes either the union of two subsets
$BC$
denotes either the union of two subsets
![]() $B,C$
of M or the tuple obtained by concatenating the (possibly infinite) tuples
$B,C$
of M or the tuple obtained by concatenating the (possibly infinite) tuples
![]() $B,C$
of elements of M.
$B,C$
of elements of M.
Definition 5.1. A complete first-order theory T in a language
![]() $\mathcal {L}$
is geometric if for any model
$\mathcal {L}$
is geometric if for any model
![]() $\mathcal {M} = (M, \dotsc ) \models T$
we have the following:
$\mathcal {M} = (M, \dotsc ) \models T$
we have the following:
-
1. The algebraic closure in
 $\mathcal {M}$
satisfies the exchange principle:
$\mathcal {M}$
satisfies the exchange principle:if
 $a,b$
are singletons in
$a,b$
are singletons in
 $\mathcal {M}$
,
$\mathcal {M}$
,
 $A \subseteq M$
and
$A \subseteq M$
and
 $b \in \operatorname {acl}(A,a) \setminus \operatorname {acl}(A)$
, then
$b \in \operatorname {acl}(A,a) \setminus \operatorname {acl}(A)$
, then
 $a \in \operatorname {acl} (A,b)$
.
$a \in \operatorname {acl} (A,b)$
. -
2. T eliminates the
 $\exists ^{\infty }$
quantifier:
$\exists ^{\infty }$
quantifier:for every
 $\mathcal {L}$
-formula
$\mathcal {L}$
-formula
 $\varphi (x,y)$
with x a single variable and y a tuple of variables, there exists some
$\varphi (x,y)$
with x a single variable and y a tuple of variables, there exists some
 $k \in \mathbb {N}$
such that for every
$k \in \mathbb {N}$
such that for every
 $b \in M^{\lvert y\rvert }$
, if
$b \in M^{\lvert y\rvert }$
, if
 $\varphi (x,b)$
has more than k solutions in M, then it has infinitely many solutions in M.
$\varphi (x,b)$
has more than k solutions in M, then it has infinitely many solutions in M.
In models of a geometric theory, the algebraic closure operator
![]() $\operatorname {acl}$
gives rise to a matroid, and given a a finite tuple in M and
$\operatorname {acl}$
gives rise to a matroid, and given a a finite tuple in M and
![]() $A \subseteq M$
,
$A \subseteq M$
,
![]() $\dim (a/A)$
is the minimal cardinality of a subtuple
$\dim (a/A)$
is the minimal cardinality of a subtuple
![]() $a'$
of a such that
$a'$
of a such that
![]() $\operatorname {acl}(a \cup A) = \operatorname {acl}(a' \cup A)$
(in an algebraically closed field, this is just the transcendence degree of a over the field generated by A). Finally, given a finite tuple a and sets
$\operatorname {acl}(a \cup A) = \operatorname {acl}(a' \cup A)$
(in an algebraically closed field, this is just the transcendence degree of a over the field generated by A). Finally, given a finite tuple a and sets
![]() $C,B \subseteq M$
, we write
$C,B \subseteq M$
, we write
![]() to denote that
to denote that
![]() $\dim \left (a/BC \right ) = \dim \left (a / C \right )$
.
$\dim \left (a/BC \right ) = \dim \left (a / C \right )$
.
Remark 5.2. If T is geometric, then it is easy to check that
![]() is an independence relation – that is, it satisfies the following properties for all tuples
is an independence relation – that is, it satisfies the following properties for all tuples
![]() $a,a', b,b',d$
and
$a,a', b,b',d$
and
![]() $C,D \subseteq M$
:
$C,D \subseteq M$
:
-
•
 .
. -
• (Extension) If
 and d is arbitrary, then there exists some
and d is arbitrary, then there exists some
 $a'$
such that
$a'$
such that
 and
and
 $a' \equiv _{Cb} a$
(which means that
$a' \equiv _{Cb} a$
(which means that
 $a'$
belongs to exactly the same
$a'$
belongs to exactly the same
 $Cb$
-definable subsets of
$Cb$
-definable subsets of
 $M^{\lvert a\rvert }$
as a).
$M^{\lvert a\rvert }$
as a). -
• (Monotonicity)
 .
. -
• (Symmetry)
 .
. -
• (Transitivity)
 and
and
 .
. -
• (Nondegeneracy) If
 and
and
 $d \in \operatorname {acl}(a,C) \cap \operatorname {acl}(b,C)$
, then
$d \in \operatorname {acl}(a,C) \cap \operatorname {acl}(b,C)$
, then
 $d \in \operatorname {acl}(C)$
.
$d \in \operatorname {acl}(C)$
.
The following property expresses that the matroid defined by the algebraic closure is linear, in the sense that the closure operator behaves more like the span in vector spaces, as opposed to algebraic closure in fields:
Definition 5.3 [Reference Berenstein and Vassiliev3, Definition 2.1]
A geometric theory T is weakly locally modular if for any saturated
![]() $\mathcal {M} \models T$
and
$\mathcal {M} \models T$
and
![]() $A,B$
small subsets of
$A,B$
small subsets of
![]() $\mathcal {M}$
there exists some small set
$\mathcal {M}$
there exists some small set
![]() such that
such that
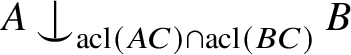 .
.
Recall that a linearly ordered structure
![]() $\mathcal {M}=(M,<, \dotsc )$
is o-minimal if every definable subset of M is a finite union of intervals (see, e.g., [Reference Van den Dries23]).
$\mathcal {M}=(M,<, \dotsc )$
is o-minimal if every definable subset of M is a finite union of intervals (see, e.g., [Reference Van den Dries23]).
Example 5.4 [Reference Berenstein and Vassiliev3, Section 3.2]
An o-minimal structure is linear (i.e., any normal interpretable family of plane curves in T has dimension
![]() $\leq 1$
) if and only if it is weakly locally modular.
$\leq 1$
) if and only if it is weakly locally modular.
In particular, every theory of an ordered vector space over an ordered division ring is weakly locally modular (so Theorem 5.6 applies to semilinear relations).
The following is a key model-theoretic lemma:
Lemma 5.5. Assume that T is geometric and weakly locally modular, and
![]() $\mathcal {M} = (M, \dotsc ) \models T $
is
$\mathcal {M} = (M, \dotsc ) \models T $
is
![]() $\aleph _1$
-saturated. Assume that
$\aleph _1$
-saturated. Assume that
![]() $E \subseteq M^{d_1} {{\times }\dotsb {\times }} M^{d_r}$
is an r-ary relation defined by a formula with parameters in a finite tuple b, and E contains no r-grid
$E \subseteq M^{d_1} {{\times }\dotsb {\times }} M^{d_r}$
is an r-ary relation defined by a formula with parameters in a finite tuple b, and E contains no r-grid
![]() $A=\prod _{i \in [r]}A_i$
with each
$A=\prod _{i \in [r]}A_i$
with each
![]() $A_i \subseteq M^{d_i}$
infinite. Then for any
$A_i \subseteq M^{d_i}$
infinite. Then for any
![]() $(a_1, \dotsc , a_r) \in E$
there exists some
$(a_1, \dotsc , a_r) \in E$
there exists some
![]() $i \in [r]$
such that
$i \in [r]$
such that
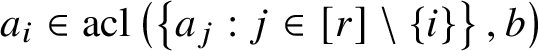 $a_i \in \operatorname {acl} \left ( \left \{a_j : j \in [r] \setminus \{i\} \right \}, b\right )$
.
$a_i \in \operatorname {acl} \left ( \left \{a_j : j \in [r] \setminus \{i\} \right \}, b\right )$
.
Proof. Assume the lemma is untrue; then there exist some
![]() $(a_1, \dotsc , a_r)$
in
$(a_1, \dotsc , a_r)$
in
![]() $\mathcal {M}$
such that
$\mathcal {M}$
such that
![]() $(a_1,\dotsc , a_r) \in E$
, but
$(a_1,\dotsc , a_r) \in E$
, but
![]() $a_i \notin \operatorname {acl} \left ( a_{\neq i}, b \right )$
for every
$a_i \notin \operatorname {acl} \left ( a_{\neq i}, b \right )$
for every
![]() $i \in [r]$
, where
$i \in [r]$
, where
 $a_{\neq i} := \left \{a_j : j \in [r] \setminus \{i\} \right \}$
.
$a_{\neq i} := \left \{a_j : j \in [r] \setminus \{i\} \right \}$
.
By weak local modularity, for each
![]() $i \in [r]$
there exists some small set
$i \in [r]$
there exists some small set
![]() $C_i \subseteq \mathcal {M}$
such that
$C_i \subseteq \mathcal {M}$
such that

By extension of
![]() , we may assume that
, we may assume that
![]() for all
for all
![]() $i \in [r]$
. Hence by transitivity,
$i \in [r]$
. Hence by transitivity,
![]() , where
, where
![]() $C := \bigcup _{i \in [r]} C_i$
.
$C := \bigcup _{i \in [r]} C_i$
.
Set
![]() $D := \bigcap _{i \in [r]} \operatorname {acl} \left ( a_{\neq i}, b, C\right )$
.
$D := \bigcap _{i \in [r]} \operatorname {acl} \left ( a_{\neq i}, b, C\right )$
.
Claim A. For every
![]() $i \in [r]$
,
$i \in [r]$
,
![]() .
.
Proof. Fix
![]() $i \in [r]$
. As
$i \in [r]$
. As
and
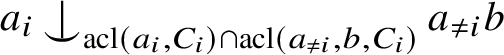
, by symmetry and transitivity we have

Note that
![]() $\operatorname {acl}(a_i,C_i) \subseteq \operatorname {acl}\left (a_{\neq j},C\right )$
for every
$\operatorname {acl}(a_i,C_i) \subseteq \operatorname {acl}\left (a_{\neq j},C\right )$
for every
![]() $i \neq j \in [r]$
, and hence
$i \neq j \in [r]$
, and hence
![]() $\operatorname {acl}(a_i,C_i) \cap \operatorname {acl}(a_{\neq i},b,C_i) \subseteq D$
, and clearly
$\operatorname {acl}(a_i,C_i) \cap \operatorname {acl}(a_{\neq i},b,C_i) \subseteq D$
, and clearly
![]() $D \subseteq \operatorname {acl}(a_{\neq i},b,C)$
. Hence
$D \subseteq \operatorname {acl}(a_{\neq i},b,C)$
. Hence
![]() , and in particular
, and in particular
![]() .
.
Claim B. For every
![]() $i \in [r]$
,
$i \in [r]$
,
![]() $a_i \notin \operatorname {acl}(D)$
.
$a_i \notin \operatorname {acl}(D)$
.
Proof. Fix
![]() $i \in [r]$
. Then
$i \in [r]$
. Then
![]() $\operatorname {acl}(D) \subseteq \operatorname {acl}(a_{\neq i}, b, C)$
by definition. But as
$\operatorname {acl}(D) \subseteq \operatorname {acl}(a_{\neq i}, b, C)$
by definition. But as
 by transitivity, if
by transitivity, if
![]() $a_i \in \operatorname {acl}(a_{\neq i}, b, C)$
then we would get
$a_i \in \operatorname {acl}(a_{\neq i}, b, C)$
then we would get
![]() $a_i \in \operatorname {acl}(a_{\neq i},b)$
, contradicting the assumption.
$a_i \in \operatorname {acl}(a_{\neq i},b)$
, contradicting the assumption.
By induction we will choose sequences of tuples
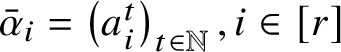 $\bar {\alpha }_i = \left (a_i^{t}\right )_{t \in \mathbb {N}}, i \in [r]$
, in
$\bar {\alpha }_i = \left (a_i^{t}\right )_{t \in \mathbb {N}}, i \in [r]$
, in
![]() $\mathcal {M}$
such that for every
$\mathcal {M}$
such that for every
![]() $i \in [r]$
we have:
$i \in [r]$
we have:
-
1.
 $a^t_i \equiv _{D \bar {\alpha }_{<i} a_{>i}} a_i$
for all
$a^t_i \equiv _{D \bar {\alpha }_{<i} a_{>i}} a_i$
for all
 $t \in \mathbb {N}$
;
$t \in \mathbb {N}$
; -
2.
 $a^t_i \neq a_i^{s}$
(as tuples) for all
$a^t_i \neq a_i^{s}$
(as tuples) for all
 $s \neq t \in \mathbb {N}$
;
$s \neq t \in \mathbb {N}$
; -
3.
 .
.
Fix
![]() $i \in [r]$
and assume that we already chose some sequences
$i \in [r]$
and assume that we already chose some sequences
![]() $\bar {a}_j$
for
$\bar {a}_j$
for
![]() $1 \leq j < i$
satisfying (1)–(3).
$1 \leq j < i$
satisfying (1)–(3).
Claim C. We have
![]() .
.
Proof. If
![]() $i=1$
, this claim becomes
$i=1$
, this claim becomes
, hence holds by Claim (A). So assume
![]() $i \geq 2$
. We will show by induction that for each
$i \geq 2$
. We will show by induction that for each
![]() $l = 1, \dotsc , i-1$
we have
$l = 1, \dotsc , i-1$
we have

For
![]() $l =1$
this is equivalent to
$l =1$
this is equivalent to
, which holds by (3) for
![]() $i-1$
. So we assume this holds for
$i-1$
. So we assume this holds for
![]() $l < i-1$
– that is, we have
$l < i-1$
– that is, we have
– and show it for
![]() $l+1$
. By assumption and transitivity, we have
$l+1$
. By assumption and transitivity, we have

Also,
by (3) for
![]() $i-(l+1) < i$
. Then by transitivity again,
$i-(l+1) < i$
. Then by transitivity again,
, which concludes the inductive step.
In particular, for
![]() $l = i-1$
we get
$l = i-1$
we get
![]() – that is,
– that is,
![]() . By transitivity and Claim (A), this implies
. By transitivity and Claim (A), this implies
![]() , and we conclude by symmetry.
, and we conclude by symmetry.
Using Claim (C) and extension of
![]() , we can choose a sequence
, we can choose a sequence
 $\bar {\alpha }_i = \left (a^t_i\right )_{t \in \mathbb {N}}$
so that
$\bar {\alpha }_i = \left (a^t_i\right )_{t \in \mathbb {N}}$
so that
![]() $a^t_i \equiv _{D \bar {\alpha }_{<i} a_{>i}} a_i$
and
$a^t_i \equiv _{D \bar {\alpha }_{<i} a_{>i}} a_i$
and
 for every
for every
![]() $t \in \mathbb {N}$
. By Claim (B) we have
$t \in \mathbb {N}$
. By Claim (B) we have
![]() $a_i \notin \operatorname {acl}(D)$
, hence
$a_i \notin \operatorname {acl}(D)$
, hence
![]() $a_i^t \notin \operatorname {acl}(D)$
, hence
$a_i^t \notin \operatorname {acl}(D)$
, hence
 $a^t_i \notin \operatorname {acl}\left (\bar {\alpha }_{<i}, a_{>i}, a_i^{<t} \right )$
, so in particular all the tuples
$a^t_i \notin \operatorname {acl}\left (\bar {\alpha }_{<i}, a_{>i}, a_i^{<t} \right )$
, so in particular all the tuples
 $\left (a^t_i\right )_{t \in \mathbb {N}}$
are pairwise-distinct and
$\left (a^t_i\right )_{t \in \mathbb {N}}$
are pairwise-distinct and
![]() $\bar {\alpha }_i$
satisfies (1) and (2). By symmetry and transitivity of
$\bar {\alpha }_i$
satisfies (1) and (2). By symmetry and transitivity of
![]() , we get
, we get
![]() . This concludes the inductive step in the construction of the sequences.
. This concludes the inductive step in the construction of the sequences.
Finally, as (1) holds for all
![]() $i \in [r]$
and b is contained in D, it follows that
$i \in [r]$
and b is contained in D, it follows that
 $\left (a^{t_1}_{1}, \dotsc , a^{t_r}_r\right ) \equiv _{b} (a_1, \dotsc , a_r)$
, and hence
$\left (a^{t_1}_{1}, \dotsc , a^{t_r}_r\right ) \equiv _{b} (a_1, \dotsc , a_r)$
, and hence
 $\left (a^{t_1}_{1}, \dotsc , a^{t_r}_r\right ) \in E$
for every
$\left (a^{t_1}_{1}, \dotsc , a^{t_r}_r\right ) \in E$
for every
![]() $(t_1, \dotsc , t_r) \in \mathbb {N}^r$
. By (1), each of the sets
$(t_1, \dotsc , t_r) \in \mathbb {N}^r$
. By (1), each of the sets
 $\left \{a^{t}_i : t \in \mathbb {N} \right \}, i \in [r]$
, is infinite – contradicting the assumption on E. This concludes the proof of the lemma.
$\left \{a^{t}_i : t \in \mathbb {N} \right \}, i \in [r]$
, is infinite – contradicting the assumption on E. This concludes the proof of the lemma.
Theorem 5.6. Assume that T is a geometric, weakly locally modular theory, and
![]() $\mathcal {M} \models T$
. Assume that
$\mathcal {M} \models T$
. Assume that
![]() $r \in \mathbb {N}_{\geq 2}$
and
$r \in \mathbb {N}_{\geq 2}$
and
![]() $\varphi (\bar {x}_1, \dotsc , \bar {x}_r,\bar {y})$
is an
$\varphi (\bar {x}_1, \dotsc , \bar {x}_r,\bar {y})$
is an
![]() $\mathcal {L}$
-formula without parameters, with
$\mathcal {L}$
-formula without parameters, with
![]() $\lvert \bar {x}_i\rvert = d_i, \lvert \bar {y}\rvert = e$
. Then there exists some
$\lvert \bar {x}_i\rvert = d_i, \lvert \bar {y}\rvert = e$
. Then there exists some
![]() $\alpha = \alpha (\varphi ) \in \mathbb {R}_{>0}$
satisfying the following:
$\alpha = \alpha (\varphi ) \in \mathbb {R}_{>0}$
satisfying the following:
Given
![]() $b \in M^{e}$
, consider the r-ary relation
$b \in M^{e}$
, consider the r-ary relation
 $$ \begin{align*}E_b := \left\{(a_1, \dotsc, a_r) \in M^{d_1} {{\times}\dotsb{\times}} M^{d_r} : \mathcal{M} \models \varphi(a_1, \dotsc, a_r, b) \right\}.\end{align*} $$
$$ \begin{align*}E_b := \left\{(a_1, \dotsc, a_r) \in M^{d_1} {{\times}\dotsb{\times}} M^{d_r} : \mathcal{M} \models \varphi(a_1, \dotsc, a_r, b) \right\}.\end{align*} $$
Then for every
![]() $b \in M^e$
, exactly one of the following two cases must occur:
$b \in M^e$
, exactly one of the following two cases must occur:
-
1.
 $E_b$
is not
$E_b$
is not
 $K_{k, \dotsc , k}$
-free for any
$K_{k, \dotsc , k}$
-free for any
 $k \in \mathbb {N}$
, or
$k \in \mathbb {N}$
, or -
2. for any finite r-grid
 $B \subseteq \prod _{i \in [r]} M^{d_i}$
, we have
$B \subseteq \prod _{i \in [r]} M^{d_i}$
, we have  $$ \begin{align*} \lvert E_b \cap B\rvert \leq \alpha \delta^r_{r-1}(B). \end{align*} $$
$$ \begin{align*} \lvert E_b \cap B\rvert \leq \alpha \delta^r_{r-1}(B). \end{align*} $$
Proof. Assume that
![]() $\mathcal {N} = (N, \dotsc )$
is an elementary extension of
$\mathcal {N} = (N, \dotsc )$
is an elementary extension of
![]() $\mathcal {M}$
and
$\mathcal {M}$
and
![]() $b \in M^{e}$
. Then for a fixed
$b \in M^{e}$
. Then for a fixed
![]() $k \in \mathbb {N}$
,
$k \in \mathbb {N}$
,
 $$ \begin{align*}E_b = \left\{(a_1, \dotsc, a_r) \in M^{d_1} {{\times}\dotsb{\times}} M^{d_r} : \mathcal{M} \models \varphi(a_1, \dotsc, a_r, b) \right\}\end{align*} $$
$$ \begin{align*}E_b = \left\{(a_1, \dotsc, a_r) \in M^{d_1} {{\times}\dotsb{\times}} M^{d_r} : \mathcal{M} \models \varphi(a_1, \dotsc, a_r, b) \right\}\end{align*} $$
is
![]() $K_{k, \dotsc , k}$
-free if and only if
$K_{k, \dotsc , k}$
-free if and only if
 $$ \begin{align*}E^{\prime}_b = \left\{(a_1, \dotsc, a_r) \in N^{d_1} {{\times}\dotsb{\times}} N^{d_r} : \mathcal{N} \models \varphi(a_1, \dotsc, a_r, b) \right\}\end{align*} $$
$$ \begin{align*}E^{\prime}_b = \left\{(a_1, \dotsc, a_r) \in N^{d_1} {{\times}\dotsb{\times}} N^{d_r} : \mathcal{N} \models \varphi(a_1, \dotsc, a_r, b) \right\}\end{align*} $$
is
![]() $K_{k, \dotsc , k}$
-free, as this can be expressed by a first-order formula
$K_{k, \dotsc , k}$
-free, as this can be expressed by a first-order formula
![]() $\psi (y)$
and
$\psi (y)$
and
![]() $\mathcal {M} \models \psi (b) \iff \mathcal {N} \models \psi (b)$
. Similarly, for a fixed
$\mathcal {M} \models \psi (b) \iff \mathcal {N} \models \psi (b)$
. Similarly, for a fixed
![]() $\alpha \in \mathbb {R}$
,
$\alpha \in \mathbb {R}$
,
![]() $\lvert E_b \cap B\rvert \leq \alpha \delta ^r_{r-1}(B)$
for every finite r-grid
$\lvert E_b \cap B\rvert \leq \alpha \delta ^r_{r-1}(B)$
for every finite r-grid
 $B \subseteq \prod _{i \in [r]} M^{d_i}$
if and only if
$B \subseteq \prod _{i \in [r]} M^{d_i}$
if and only if
 $\left \lvert E^{\prime }_b \cap B\right \rvert \leq \alpha \delta ^r_{r-1}(B)$
for every finite r-grid
$\left \lvert E^{\prime }_b \cap B\right \rvert \leq \alpha \delta ^r_{r-1}(B)$
for every finite r-grid
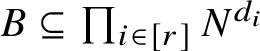 $B \subseteq \prod _{i \in [r]} N^{d_i}$
(as for all fixed sizes of
$B \subseteq \prod _{i \in [r]} N^{d_i}$
(as for all fixed sizes of
![]() $B_1, \dotsc , B_r$
, this condition can be expressed by a first-order formula). Hence, passing to an elementary extension, we may assume that
$B_1, \dotsc , B_r$
, this condition can be expressed by a first-order formula). Hence, passing to an elementary extension, we may assume that
![]() $\mathcal {M}$
is
$\mathcal {M}$
is
![]() $\aleph _1$
-saturated.
$\aleph _1$
-saturated.
As T eliminates
![]() $\exists ^{\infty }$
, there exists some
$\exists ^{\infty }$
, there exists some
![]() $m = m(\varphi ) \in \mathbb {N}$
such that for any
$m = m(\varphi ) \in \mathbb {N}$
such that for any
![]() $i \in [r]$
,
$i \in [r]$
,
![]() $b \in M^e$
and tuple
$b \in M^e$
and tuple
![]() $\bar {a} := \left ( a_j \in M^{d_j} : j \in [r] \setminus \{i\} \right )$
, the fibre
$\bar {a} := \left ( a_j \in M^{d_j} : j \in [r] \setminus \{i\} \right )$
, the fibre
 $$ \begin{align*}E^i_{\bar{a}; b} := \left\{ a^* \in M^{d_i} : \mathcal{M} \models \varphi\left(a_1, \dotsc, a_{i-1}, a^*, a_{i+1}, \dotsc, a_{r}; b\right)\right\}\end{align*} $$
$$ \begin{align*}E^i_{\bar{a}; b} := \left\{ a^* \in M^{d_i} : \mathcal{M} \models \varphi\left(a_1, \dotsc, a_{i-1}, a^*, a_{i+1}, \dotsc, a_{r}; b\right)\right\}\end{align*} $$
is finite if and only if it has size
![]() $\leq m$
.
$\leq m$
.
Given an arbitrary
![]() $b \in M^{e}$
such that
$b \in M^{e}$
such that
![]() $E_b$
is
$E_b$
is
![]() $K_{k, \dotsc , k}$
-free, Lemma 5.5 and compactness imply that for every tuple
$K_{k, \dotsc , k}$
-free, Lemma 5.5 and compactness imply that for every tuple
![]() $(a_1, \dotsc , a_r) \in E_b$
, there exists some
$(a_1, \dotsc , a_r) \in E_b$
, there exists some
![]() $i \in [r]$
such that the fibre
$i \in [r]$
such that the fibre
 $E^i_{\bar {a}; b}$
is finite, hence
$E^i_{\bar {a}; b}$
is finite, hence
 $\left \lvert E^i_{\bar {a}; b}\right \rvert \leq m$
. This easily implies that for any finite r-grid
$\left \lvert E^i_{\bar {a}; b}\right \rvert \leq m$
. This easily implies that for any finite r-grid
 $B \subseteq \prod _{i \in [r]} M^{d_i}$
, we have
$B \subseteq \prod _{i \in [r]} M^{d_i}$
, we have
![]() $\lvert E_b\cap B\rvert \leq m \delta ^r_{r-1}(B)$
.
$\lvert E_b\cap B\rvert \leq m \delta ^r_{r-1}(B)$
.
Remark 5.7. In the binary case, a similar observation was made by Evans in the context of certain stable theories [Reference Evans10, Proposition 3.1].
Restricting to distal structures, we can relax the assumption ‘
![]() $E_b$
is
$E_b$
is
![]() $K_{k, \dotsc , k}$
-free for some k’ to ‘
$K_{k, \dotsc , k}$
-free for some k’ to ‘
![]() $E_b$
does not contain a direct product of infinite sets’ in Theorem 5.6 (we refer to, e.g., the introduction in [Reference Chernikov and Starchenko6] or [Reference Chernikov, Galvin and Starchenko4] for a general discussion of model-theoretic distality and its connections to combinatorics).
$E_b$
does not contain a direct product of infinite sets’ in Theorem 5.6 (we refer to, e.g., the introduction in [Reference Chernikov and Starchenko6] or [Reference Chernikov, Galvin and Starchenko4] for a general discussion of model-theoretic distality and its connections to combinatorics).
Corollary 5.8. Assume that T is a distal, geometric, weakly locally modular theory,
![]() $\mathcal {M} \models T$
,
$\mathcal {M} \models T$
,
![]() $r \in \mathbb {N}_{\geq 2}$
and
$r \in \mathbb {N}_{\geq 2}$
and
![]() $\varphi (\bar {x}_1, \dotsc , \bar {x}_r,\bar {y})$
is an
$\varphi (\bar {x}_1, \dotsc , \bar {x}_r,\bar {y})$
is an
![]() $\mathcal {L}$
-formula without parameters, with
$\mathcal {L}$
-formula without parameters, with
![]() $\lvert \bar {x}_i\rvert = d_i, \lvert \bar {y}\rvert = e$
. Then there exists some
$\lvert \bar {x}_i\rvert = d_i, \lvert \bar {y}\rvert = e$
. Then there exists some
![]() $\alpha = \alpha (\varphi ) \in \mathbb {R}_{>0}$
satisfying the following:
$\alpha = \alpha (\varphi ) \in \mathbb {R}_{>0}$
satisfying the following:
Assume that
![]() $b \in M^{e}$
and the r-ary relation
$b \in M^{e}$
and the r-ary relation
![]() $E_b$
does not contain an r-grid
$E_b$
does not contain an r-grid
![]() $A = \prod _{i \in [r]}A_i$
with each
$A = \prod _{i \in [r]}A_i$
with each
![]() $A_i \subseteq M^{d_i}$
infinite. Then
$A_i \subseteq M^{d_i}$
infinite. Then
![]() $\lvert E_b \cap B\rvert \leq \alpha \delta ^r_{r-1}(B)$
for any finite r-grid B.
$\lvert E_b \cap B\rvert \leq \alpha \delta ^r_{r-1}(B)$
for any finite r-grid B.
Proof. By [Reference Chernikov, Galvin and Starchenko4, Theorem 5.12], if
![]() $\mathcal {M}$
is a distal structure with elimination of
$\mathcal {M}$
is a distal structure with elimination of
![]() $\exists ^{\infty }$
, then there exists some
$\exists ^{\infty }$
, then there exists some
![]() $k = k(\varphi ) \in \mathbb {N}$
such that for every
$k = k(\varphi ) \in \mathbb {N}$
such that for every
![]() $b \in M^{e}$
,
$b \in M^{e}$
,
![]() $E_b$
is not
$E_b$
is not
![]() $K_{k, \dotsc , k}$
-free if and only if
$K_{k, \dotsc , k}$
-free if and only if
![]() $\prod _{i \in [r]} A_i \subseteq E_b$
for some infinite
$\prod _{i \in [r]} A_i \subseteq E_b$
for some infinite
![]() $A_i \subseteq M^{d_i}$
. The conclusion now follows by Theorem 5.6.
$A_i \subseteq M^{d_i}$
. The conclusion now follows by Theorem 5.6.
Remark 5.9. Weaker bounds for noncartesian relations definable in arbitrary distal theories are established in [Reference Chernikov and Starchenko7, Reference Chernikov, Peterzil and Starchenko5].
Now we show that in the o-minimal case, this result actually characterises weak local modularity. By the trichotomy theorem in o-minimal structures [Reference Peterzil and Starchenko18], we have the following equivalence:
Fact 5.10. Let
![]() $\mathcal {M}$
be an o-minimal (
$\mathcal {M}$
be an o-minimal (
![]() $\aleph _1$
-)saturated structure. The following are equivalent:
$\aleph _1$
-)saturated structure. The following are equivalent:
-
•
 $\mathcal {M}$
is not linear (see Example 5.4).
$\mathcal {M}$
is not linear (see Example 5.4). -
•
 $\mathcal {M}$
is not weakly locally modular.
$\mathcal {M}$
is not weakly locally modular. -
• There exists a real closed field definable in
 $\mathcal {M}$
.
$\mathcal {M}$
.
Corollary 5.11. Let
![]() $\mathcal {M}$
be an o-minimal structure. The following are equivalent:
$\mathcal {M}$
be an o-minimal structure. The following are equivalent:
-
1.
 $\mathcal {M}$
is weakly locally modular.
$\mathcal {M}$
is weakly locally modular. -
2. Corollary 5.8 holds in
 $\mathcal {M}$
.
$\mathcal {M}$
. -
3. For every
 $d_1,d_2 \in \mathbb {N}$
and every definable (with parameters)
$d_1,d_2 \in \mathbb {N}$
and every definable (with parameters)
 $X \subseteq M^{d_1} \times M^{d_2}$
, if X is
$X \subseteq M^{d_1} \times M^{d_2}$
, if X is
 $K_{k,k}$
-free for some
$K_{k,k}$
-free for some
 $k \in \mathbb {N}$
, then there exist some
$k \in \mathbb {N}$
, then there exist some
 $\beta < \frac {4}{3}$
and
$\beta < \frac {4}{3}$
and
 $\alpha $
such that for any n and
$\alpha $
such that for any n and
 $B_i \subseteq M^{d_i}$
with
$B_i \subseteq M^{d_i}$
with
 $\lvert B_i\rvert = n$
, we have
$\lvert B_i\rvert = n$
, we have  $$ \begin{align*} \lvert X \cap B_1 \times B_2\rvert \leq \alpha n^{\beta}. \end{align*} $$
$$ \begin{align*} \lvert X \cap B_1 \times B_2\rvert \leq \alpha n^{\beta}. \end{align*} $$
-
4. There is no infinite field definable in
 $\mathcal {M}$
.
$\mathcal {M}$
.
Proof. (1)
![]() $\Rightarrow $
(2) by Corollary 5.8, and (2)
$\Rightarrow $
(2) by Corollary 5.8, and (2)
![]() $\Rightarrow $
(3) is obvious.
$\Rightarrow $
(3) is obvious.
For (3)
![]() $\Rightarrow $
(4), assume that
$\Rightarrow $
(4), assume that
![]() $\mathcal {R}$
is an infinite field definable in
$\mathcal {R}$
is an infinite field definable in
![]() $\mathcal {M}$
,
$\mathcal {M}$
,
![]() $\textrm {char}(\mathcal {R}) = 0$
by o-minimality. Then the point-line incidence relation on
$\textrm {char}(\mathcal {R}) = 0$
by o-minimality. Then the point-line incidence relation on
![]() $\mathcal {R}^2$
corresponds to a
$\mathcal {R}^2$
corresponds to a
![]() $K_{2,2}$
-free definable relation
$K_{2,2}$
-free definable relation
![]() $E \subseteq \mathcal {M}^{d} \times \mathcal {M}^d$
for some d. By the standard lower bound for Szemerédi–Trotter, the number of incidences satisfies
$E \subseteq \mathcal {M}^{d} \times \mathcal {M}^d$
for some d. By the standard lower bound for Szemerédi–Trotter, the number of incidences satisfies
 $\Omega \left (n^{4/3}\right )$
, hence E cannot satisfy (3).
$\Omega \left (n^{4/3}\right )$
, hence E cannot satisfy (3).
For (4)
![]() $\Rightarrow $
(1), if
$\Rightarrow $
(1), if
![]() $\mathcal {M}$
is not weakly locally modular, then by Fact 5.10 a real closed field
$\mathcal {M}$
is not weakly locally modular, then by Fact 5.10 a real closed field
![]() $\mathcal {R}$
is definable in
$\mathcal {R}$
is definable in
![]() $\mathcal {M}$
.
$\mathcal {M}$
.
5.2. Applications to semialgebraic relations
Corollary 5.12. Assume that
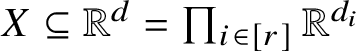 $X \subseteq \mathbb {R}^d = \prod _{i \in [r]} \mathbb {R}^{d_i}$
is semilinear and X does not contain a direct product of r infinite sets (e.g., if X is
$X \subseteq \mathbb {R}^d = \prod _{i \in [r]} \mathbb {R}^{d_i}$
is semilinear and X does not contain a direct product of r infinite sets (e.g., if X is
![]() $K_{k, \dotsc , k}$
-free for some k). Then there exists some
$K_{k, \dotsc , k}$
-free for some k). Then there exists some
![]() $\alpha = \alpha (X)$
such that for any r-hypergraph H of the form
$\alpha = \alpha (X)$
such that for any r-hypergraph H of the form
 $\left (V_1, \dotsc , V_r; X \cap \prod _{i \in [r]} V_i \right )$
for some finite
$\left (V_1, \dotsc , V_r; X \cap \prod _{i \in [r]} V_i \right )$
for some finite
![]() $V_i \subseteq \mathbb {R}^{d_i}$
, with
$V_i \subseteq \mathbb {R}^{d_i}$
, with
![]() $\sum _{i =1}^r \lvert V_i\rvert =n$
, we have
$\sum _{i =1}^r \lvert V_i\rvert =n$
, we have
![]() $\lvert E\rvert \leq \alpha n^{r-1}$
.
$\lvert E\rvert \leq \alpha n^{r-1}$
.
Proof. As every o-minimal structure is distal and every semilinear relation is definable in an ordered vector space over
![]() $\mathbb {R}$
which is o-minimal and locally modular (Example 5.4), the result follows by Corollary 5.8.
$\mathbb {R}$
which is o-minimal and locally modular (Example 5.4), the result follows by Corollary 5.8.
We recall the following special case of the trichotomy theorem in o-minimal structures restricted to semialgebraic relations:
Fact 5.13
([Reference Marker, Peterzil and Pillay16, Theorem 1.3]). Let
![]() $X \subseteq \mathbb {R}^n$
be a semialgebraic but not semilinear set. Then
$X \subseteq \mathbb {R}^n$
be a semialgebraic but not semilinear set. Then
![]() $\times \restriction _{[0,1]^2}$
(i.e., the graph of multiplication restricted to the unit box) is definable in the first-order structure
$\times \restriction _{[0,1]^2}$
(i.e., the graph of multiplication restricted to the unit box) is definable in the first-order structure
![]() $(\mathbb {R},<,+,X)$
.
$(\mathbb {R},<,+,X)$
.
Using this fact, we have the following more explicit variant of Corollary 5.11 in the semialgebraic case:
Corollary 5.14. Let
![]() $X \subseteq \mathbb {R}^d$
be a semialgebraic set, and consider the first-order structure
$X \subseteq \mathbb {R}^d$
be a semialgebraic set, and consider the first-order structure
![]() $\mathcal {M} = (\mathbb {R}, <,+,X)$
. Then the following are equivalent:
$\mathcal {M} = (\mathbb {R}, <,+,X)$
. Then the following are equivalent:
-
1. For any
 $r \in \mathbb {N}$
and any r-ary relation
$r \in \mathbb {N}$
and any r-ary relation
 $Y \subseteq \prod _{i \in [r]}\mathbb {R}^{d_i}$
not containing an r-grid
$Y \subseteq \prod _{i \in [r]}\mathbb {R}^{d_i}$
not containing an r-grid
 $A = \prod _{i \in [r]}A_i$
with each
$A = \prod _{i \in [r]}A_i$
with each
 $A_i \subseteq \mathbb {R}^{d_i}$
infinite, there exists some
$A_i \subseteq \mathbb {R}^{d_i}$
infinite, there exists some
 $\alpha \in \mathbb {R}$
such that
$\alpha \in \mathbb {R}$
such that
 $\lvert Y \cap B\rvert \leq \alpha \delta ^r_{r-1}(B)$
for every finite r-grid B.
$\lvert Y \cap B\rvert \leq \alpha \delta ^r_{r-1}(B)$
for every finite r-grid B. -
2. For every
 $d_1,d_2 \in \mathbb {N}$
and
$d_1,d_2 \in \mathbb {N}$
and
 $Y \subseteq \mathbb {R}^{d_1} \times \mathbb {R}^{d_2}$
definable (with parameters) in
$Y \subseteq \mathbb {R}^{d_1} \times \mathbb {R}^{d_2}$
definable (with parameters) in
 $\mathcal {M}$
, if Y is
$\mathcal {M}$
, if Y is
 $K_{k,k}$
-free for some
$K_{k,k}$
-free for some
 $k \in \mathbb {N}$
, then there exist some
$k \in \mathbb {N}$
, then there exist some
 $\beta < \frac {4}{3}$
and
$\beta < \frac {4}{3}$
and
 $\alpha $
such that for any n and
$\alpha $
such that for any n and
 $B_i \subseteq \mathbb {R}^{d_i}$
with
$B_i \subseteq \mathbb {R}^{d_i}$
with
 $\lvert B_i\rvert = n$
, we have
$\lvert B_i\rvert = n$
, we have  $$ \begin{align*} \lvert X \cap B_1 \times B_2\rvert \leq \alpha n^{\beta}. \end{align*} $$
$$ \begin{align*} \lvert X \cap B_1 \times B_2\rvert \leq \alpha n^{\beta}. \end{align*} $$
-
3.
 $\times \restriction _{[0,1]^2}$
is not definable in
$\times \restriction _{[0,1]^2}$
is not definable in
 $\mathcal {M}$
.
$\mathcal {M}$
.
Proof. (1)
![]() $\Rightarrow $
(2) is obvious.
$\Rightarrow $
(2) is obvious.
For (2)
![]() $\Rightarrow $
(3), using
$\Rightarrow $
(3), using
![]() $\times \restriction _{[0,1]^2}$
the
$\times \restriction _{[0,1]^2}$
the
![]() $K_{2,2}$
-free point-line incidence relation in
$K_{2,2}$
-free point-line incidence relation in
![]() $\mathbb {R}^2$
is definable restricted to
$\mathbb {R}^2$
is definable restricted to
![]() $[0,1]^2$
, and the standard configurations witnessing the lower bound in Szemerédi–Trotter can be scaled down to the unit box.
$[0,1]^2$
, and the standard configurations witnessing the lower bound in Szemerédi–Trotter can be scaled down to the unit box.
For (3)
![]() $\Rightarrow $
(1), assume that (1) does not hold in
$\Rightarrow $
(1), assume that (1) does not hold in
![]() $(\mathbb {R},<,+,X)$
. Then necessarily some Y definable in
$(\mathbb {R},<,+,X)$
. Then necessarily some Y definable in
![]() $(\mathbb {R},<,+,X)$
is not semilinear, by Corollary 5.12. By Fact 5.13, if Y is not semilinear, then
$(\mathbb {R},<,+,X)$
is not semilinear, by Corollary 5.12. By Fact 5.13, if Y is not semilinear, then
![]() $\times \restriction _{[0,1]^2}$
is definable in the structure
$\times \restriction _{[0,1]^2}$
is definable in the structure
![]() $(\mathbb {R},<,+,Y)$
, hence in
$(\mathbb {R},<,+,Y)$
, hence in
![]() $(\mathbb {R},<,+,X)$
.
$(\mathbb {R},<,+,X)$
.
Acknowledgments
We thank the referees for their very helpful suggestions on improving the paper. The second author is grateful to Adam Sheffer for some very helpful conversations.
The second author was partially supported by NSF CAREER grant DMS-1651321 and by a Simons Fellowship. He is grateful to the American Insitute of Mathematics for additional support. The third author was supported by NSF Research Grant DMS-1800806. The fourth author was partially supported by NSF grant DMS-1764034 and by a Simons Investigator Award.
Conflict of Interest
None.